Probing the electronic relaxation pathways and photostability of the synthetic nucleobase Z via laser interfaced mass spectrometry

Abstract

The photostability of synthetic (unnatural) nucleobases is important in establishing the integrity of new genetic alphabets, and critical for developing healthy semisynthetic organisms. Here, we report the first study to explore the photostability and electronic decay pathways of the synthetic nucleobase, Z (6-amino-5-nitro-2(1H)-pyridone), combining UV laser photodissociation and collisional dissociation measurements to characterise the decay pathways across the region from 3.1–4.9 eV. Photoexcitation across this region produced the m/z 138 ion as the dominant photofragment, mirroring the dominant fragment produced upon higher-energy collisional excitation. Analysis of the ion-yield production curve profile for the m/z 138 ion indicates that it is produced following ultrafast excited state decay with boil off of the OH functional group of Z from the hot electronic ground state. Electronic structure calculations provide physical insight into why this is the dominant fragmentation pathway, since a node in the electron density along the C–OH bond is found for all tautomers of Z. While the dominant decay pathway for Z is consistent with ultrafast excited state decay, we also identify several minor dissociative photochemistry decay pathways, associated with intrinsic photoinstability. The results presented here can be used to guide the development of more photostable synthetic nucleobases.

---

1. Introduction

The expansion of the genetic alphabet has been a key long-term scientific objective, to enhance storage and retrieval of genetic information.^1,2 Interest in this field has increased due to potential biotechnology applications, including the production of novel amino acids, and site-specific tagging of oligonucleotides.^3,4 However, recent work developing non-natural nucleobases and semisynthetic organisms has largely overlooked the photostability of the new nucleobase moieties. This is surprising given the wide-scale acceptance that the natural DNA nucleobases were selected not just due to their ability to encode genetic information, but also due to their photostability in the presence of UV light.^5,6 Crespo-Hernandez and co-workers have studied the photostability of the synthetic nucleobase dTPT3 ((2-deoxy-β-D-erythro-pentofuranosyl)-thieno[3,4]pyridine-2-thione), finding that it is a photosensitizer upon the absorption of UVA to near-visible radiation, thus possessing the potential to oxidatively damage DNA and other biomolecules in vivo.⁷ Their results have been supported by subsequent theoretical work from Cui and co-workers,⁸ and further recent experimental work by Li and co-workers.⁹ These studies on dTPT3 show the importance of characterising the photostability of new synthetic nucleobases as part of broader efforts to assess their suitability for biochemical deployment.

Gas-phase laser spectroscopy has provided detailed information on the intrinsic photostability of a wide range of biological molecules over the last two decades. These studies seek to contribute to a broader understanding of photostability either in bulk solutions or in biological media. This insight can be gained through comparison of the gas-phase data for the isolated biological molecule, with the related computational chemistry results that can then be extended to include the effect of solvent. However, recent results from our group on biological molecules (e.g. riboflavin),¹⁰ as well as sunscreen molecules,¹¹ have shown that such gas-phase measurements can be directly linked to solution-phase photostability. In the current work, we use these gas-phase laser photodissociation techniques to probe the intrinsic photostability of a synthetic nucleobase as an isolated molecule for the first time.

The development of synthetic nucleobases is challenging for a variety of reasons, aside from photochemical considerations. The case of the unnatural base pair (UBP) dNaM-dTPT3 provides an illustrative example. In 2017, the Romesberg group reported that the UBP dNaM-dTPT3 had been successfully incorporated into the E. coli genome.^12,13 Importantly, this synthetic UBP was shown to retain its genetic information indefinitely, and displayed excellent replication and retention properties.^14,15 Despite the positive qualities displayed by dNaM-dTPT3, it was notable that this UBP did not exhibit the H-bonding interaction of a natural nucleobase pair, with base-pair complementarity instead being achieved via intermolecular hydrophobic interactions resulting in nucleobase stacking.¹⁶ This led to the development of further UBPs where, as in DNA, recognition occurs from H-bonding interactions.¹⁷

The Z:P (2-aminoimidazo[1,2-a]-1,3,5-triazin4(8H)-one) combination is one such UBP where the nucleobases bind through three hydrogen bonds. Fig. 1 illustrates the structures of the Z and P nucleobases, along with their base-paired geometry. Hydrogen-bonded UBPs are thought to offer advantages over non-hydrogen bonding base-pairs due to better structural compatibility within a DNA duplex.^18,19 Indeed, studies of Z:P have shown that this UBP closely mimics G:C in terms of geometry and stability,^20,21 as well as displaying excellent replication by cellular components.^22,23 All of these features indicate that the Z:P pair has excellent potential for future biotechnology applications. Furthermore, the presence of the unique NO₂ group functionality of Z may offer selective recognition by proteins, hence facilitating novel clinical applications.^20,24

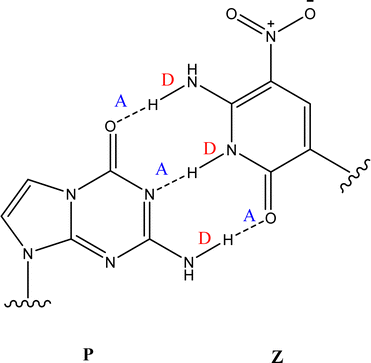Fig. 1 The geometric structure of the Z:P UBP, showing that Z displays a donor, donor, acceptor (D, D, A) arrangement of hydrogen bonds that is complemented by P (A, A, D).

In this work, we perform the first photochemical characterisation of the Z nucleobase (6-amino-5-nitro-2(1H)-pyridone). Our measurements have been performed on the protonated form of Z, i.e. Z·H⁺, to allow the system to be studied in the gas-phase using laser interfaced mass spectrometry (LIMS). The LIMS approach is an efficient method for characterising the intrinsic photochemical properties of molecules and ensembles away from the complications of the condensed-phase medium. Previous gas-phase studies of the photodynamics of protonated uracil have shown that this form displays the same photostability as the unprotonated form. Similarly, the protonated form of the non-natural nucleobase, 2-thiouracil, is photounstable, like the photounstable non-protonated form.²⁵ These results indicate that the protonated forms, which can be readily produced via electrospray ionization (ESI) and mass-selected, are excellent proxies for the non-protonated forms which would be more challenging to produce in the gas-phase.²⁶

Both natural and non-natural nucleobases are known to exhibit a variety of relatively low-energy tautomeric forms.²⁶ LIMS is able to distinguish such isomers,^27,28 which are often differentially produced when electrospraying from protic and non-protic solvents. To help establish whether tautomeric forms of Z·H⁺ are present in our experiments, the experiments presented here have been performed on ions that have been electrosprayed from both water and acetonitrile solutions.

To gain further insight into the photofragmentation pathways, it is advantageous to perform complementary higher-energy collisional dissociation (HCD) experiments.²⁹ This technique allows characterization of the ground-state fragmentation pathways, as a function of increasing internal energy and therefore provides information on thermal dissociation of the electronic ground state of a system. For molecular systems where the produced photofragments correlate with the thermal ground-state dissociation fragments, the photodecay of the excited state is described as a “statistical decay” process.²⁵ In contrast, if dissociation occurs directly from the excited state without the involvement of a conical intersection to return the system to a near-starting point geometry, a “non-statistical” decay process is occurring.³⁰ In non-statistical decay, the photofragments obtained will be significantly different in terms of their identities and relative intensities from the ground electronic-state thermal fragments. Previous high-level computational calculations of the excited state potential energy surfaces have underlined the strength of combining insight from the two complementary experimental methods.^31,32 Here, we use this approach to gain fundamental insight into the ultrafast vs. non-ultrafast regimes^33,34 of the Z nucleobase.

2. Experimental and computational procedures

Gas-phase UV photodissociation spectra were recorded in vacuo via laser-interfaced mass spectrometry using a Bruker Amazon quadrupole ion-trap (QIT) mass spectrometer that has been modified for conducting laser experiments as described in detail elsewhere.³⁵ Spectra were recorded via an action spectroscopy approach. UV photons were produced using a Nd:YAG (10 Hz, Surelite) pumped OPO (Horizon) laser scanning over the range 230–400 nm (3.10–5.39 eV) using a step size of 2 nm and laser power of 0.20 ± 0.03 mJ.

Solutions of Z (5 × 10⁻⁴ mol dm⁻³) in deionised water or acetonitrile were introduced into the mass spectrometer via ESI using a nebulising gas pressure of 10.0 psi, an injection rate of 330 μL h⁻¹ a drying gas flow rate of 8 dm³ min⁻¹ and a capillary temperature of 240 °C. 6-Amino-5-nitro-2(1H)-pyridone (Z) was purchased as a powder (≥95% purity) from MedChemExpress and used without further purification.

For photofragmentation experiments, the ion accumulation time was 100 ms and the fragmentation time 100 ms, such that each mass-selected ion packet interacted with one laser pulse, thus decreasing the probability of multi-photon absorption events. This was verified by conducting laser-power experiments at the approximate gas-phase absorption maximum (320 nm) to demonstrate the linear relationship between photodepletion intensity and photon energy over the working UV range, as consistent with single-photon absorption conditions (see S1 of ESI†). Photodepletion action spectra and photofragmentation production spectra were acquired simultaneously where photodepletion intensity (PD) and photofragmentation production (PF) are calculated using eqn (1) and (2):^{11,29,36–38}

where I_OFF and I_ON are the peak intensities with the laser off and on respectively, I_FRAG is the photofragment intensity due to laser irradiation, λ is the excitation wavelength (nm) and P is the laser pulse energy (mJ). All PD and PF intensities reported are an average of three repeats for water and two repeats for acetonitrile.

Collision-induced dissociation (CID) experiments were conducted using a higher-energy C-trap dissociation (HCD) Bruker Esquire ESI mass spectrometer.³⁹ Solutions of Z (5 × 10⁻⁴ mol dm⁻³) in deionised water were introduced into the mass spectrometer via ESI with the following parameters: capillary voltage, −3800 V; drying-gas flow rate, 8 dm³ min⁻¹; nebulising-gas pressure, 10.0 psi; injection rate, 300 μL h⁻¹; capillary temperature 275 °C. The % HCD energy was increased stepwise from 0% to 60% in intervals of 2%, with 30 s of data acquisition at each interval.

Preliminary calculations were performed to determine the relative energies of different protomers of Z·H⁺, at the MP2/cc-pVTZ level of theory in Gaussian 16.⁴⁰ Frequency calculations were performed to confirm that all optimised structures correspond to true minima. Excited state calculations were performed using time-dependent density functional theory (TDDFT) calculations using the Tamm-Dancoff approximation⁴¹ (50 states, triplets and singlets). These excited-state calculations were used to identify gaseous absorption spectra and vertical excitation energies for the most experimentally relevant protomers of Z·H⁺.

3. Results and discussion

3.1. Quantum chemical calculations of protomeric forms of Z·H⁺

The Z nucleobase can exist as either an enol or keto tautomer, in which the keto tautomer exhibits the complementary H-bonding motif for selective recognition of the P nucleobase in the Z:P UBP, shown in Fig. 1.^22,23 In order to gain insight into the physical properties of the protonated Z nucleobase, we have investigated the relative energetics of the different protomeric forms of Z·H⁺ using electronic structure methods. The three lowest-energy Z·H⁺ protomers, optimised at the MP2/cc-pVTZ level of theory, are shown in Fig. 2. These structures were selected for optimization based on previous studies of protonated uracil and protonated thiouracil.²⁵

Fig. 2 Geometric structures of the lowest-energy isomers of Z·H⁺ optimised at the MP2/cc-pVTZ level of theory. Enol-type structures can exist as rotamers, due to hindered rotation about the C–OH bond of the –OH substituent. Where relevant, the orientation of the dihedral angle NCOH > corresponds to the lowest energy rotamer. The numbering scheme used for all isomers is shown on enol-N4.

Relative energies of the isolated protomers in the gas phase are shown in Table 1, alongside calculated Boltzmann populations at different relevant temperatures. While the MP2/cc-pVTZ energetics were chosen, the variability of the relative energies was explored using density functional theory and both Pople and Dunning basis sets (Section S2, ESI†). Previously, significant differences have been observed in the relative energetic order of deprotomers calculated with DFT, depending on the choice of functional.³² Overall, the relative energetic order of the protomers was consistent across all levels of theory used here, and while no significant geometric differences were found, we note that the choice of both functional and basis set in DFT can lead to quite significant variability in the relative energy and therefore the Boltzmann distribution.

Table 1 Calculated relative energies (zero-point energy (ZPE) corrected) and % Boltzmann populations for protomers of Z at the MP2/cc-pVTZ level of theory

Protomer	Relative E eV^−1	Boltzmann population %
		298.15 K	548.15 K
enol-N4	0.00	98.52	89.58
enol-N7O	+0.11	1.45	9.40
keto-N7O	+0.21	0.02	1.03

---

Irrespective of the level of theory, the enol-N4 protomer was the lowest-energy form of Z·H⁺, in which the N4 and O9 heteroatoms are protonated. An additional two protomers, the enol- and keto-N7O, were found to be close in energy and stable. In these two higher-energy protomers, the N7 NO₂ group is protonated in both forms, as well as either the O9 or N4 group for the enol and keto form, respectively. We note that the enol-form, in which the O9 group is protonated, corresponds to the lowest-energy protomeric forms of the Z-nucleobase, i.e. the nucleobase H-bonding interaction employs the protonated form that aligns with the intermolecular H-bond within the Z:P unnatural base pair.

3.2. Excited-state quantum chemistry calculations

Excited-state calculations were performed using TDDFT at the ωB97xd/cc-pVTZ level of theory to gain insight into the change in electronic structure in the different protomeric forms of Z. The modelled UV-vis spectra for the three protomers are shown in Fig. 3. Details of the performance of several different functionals and basis sets can be found in Section S4 (ESI†).

Fig. 3 TDDFT excitation energies for the enol-N4 (red), the enol-N7O (purple) and the keto-N7O (blue) protomer of Z, calculated using ωB97xd/cc-pVTZ. Oscillator strengths (Osc.) of individual transitions are given by the vertical bars, while the full line spectrum is a convolution of the calculated spectrum with a Gaussian function (0.25 eV FWHM). The excitation energies in the figure have been red shifted by 0.5 eV to account for the tendency of TDDFT to overestimate excitation energy.

For all protomers, two bright singlet states were found in the energetically accessed range of hv = 3–5 eV, as illustrated in Fig. 3. The detailed nature of these electronic transitions is discussed further in Section 3.5. Both enol protomers display a gap of ∼0.9 eV for the two ππ* states, while the keto-protomer has a much larger gap between the corresponding states of ∼1.5 eV. The 2ππ* transition of the keto form has a very low oscillator strength, and so is not expected to have a large effect on spectra. Full details of this state can be found in the ESI.†

3.3. Gas-phase absorption spectroscopy of Z·H⁺

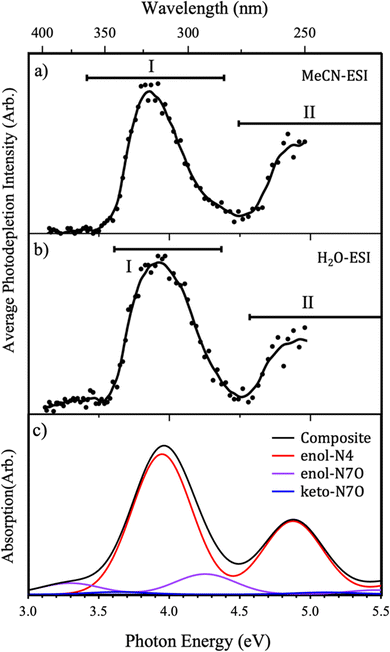
The gas-phase UV absorption (photodepletion) spectra of Z·H⁺ produced from ESI from solutions of acetonitrile (MeCN) and water, are shown in Fig. 4(a and b), respectively. Both spectra MeCN- and H₂O-ESI are notably similar, with two strong absorption regions (I and II) in the hv = 3–5 eV range. While the maxima of the band I features can be seen to differ slightly between the two different ESI solvent regimes, the same relative intensity of bands I and II is observed, with the lower-energy peak I at higher intensity.

Fig. 4 Gas-phase absorption (photodepletion) spectra for Z·H⁺ produced via (a) MeCN-ESI and (b) H₂O-ESI across the hv = 3.1–4.9 eV (400–229 nm) range. Solid lines are 5-point adjacent averages of data points. (c) Composite TDDFT curve for the enol-N4, enol-N7O and keto-N7O protomers calculated at the ωB97xd/cc-pVTZ level. All TDDFT curves are red-shifted by 0.5 eV and weighted according to the 548.15 K Boltzmann populations.

The photodepletion spectrum acquired following MeCN-ESI exhibits an onset in absorption from approximately 3.5 eV that develops into the strong absorption band (I) across the 3.5–4.5 eV range with a maximum at ∼3.85 eV. The second absorption feature (II) appears at high energies, as a rising absorption cross section with an onset of ∼4.5 eV. The absorption spectrum acquired following H₂O-ESI also exhibits a strong band (I) between approximately 3.5–4.5 eV, although it is broader and has a slightly blue-shifted band maximum (∼3.9 eV) than the corresponding feature from MeCN-ESI (Fig. 3(a)). The higher-energy absorption band (II) onset is also observed in the spectrum acquired from H₂O. Notably, Z·H⁺ ions electrosprayed from aqueous solutions show non-zero photodepletion at photon energies <3.5 eV, whereas the ions produced from an acetonitrile solution effectively display zero absorption in this low-energy region.

The differences observed between the two photodepletion spectra can be explained by considering the known variation in isomer distribution that can occur following ESI from protic or non-protic solvents.^28,42–44 To facilitate comparison, Fig. 4(c) shows the calculated TDDFT spectra for each of the low-energy Z·H⁺ protomers. In addition, this figure shows a composite TDDFT curve obtained by summing the individual Boltzmann-weighted TDDFT spectra to simulate the gas-phase absorption spectrum which is representative of the experimental population of protomers. The simulated pure enol-N4 spectrum has a very similar profile to the experimental photodepletion spectra, exhibiting a strong absorption feature in the band I region, as well as a lower-intensity absorption feature at higher energies (band II region). The similarities between the spectral shape of the modelled and experimental spectra confirm the assignment of the enol-N4 protomer as the dominant isomer in the experimental ion ensemble, regardless of ESI solvent. However, insight into the variations in the ESI-profiles as a function of changing solvent regime can be gained from the modelled composite spectra.

In the MeCN-ESI regime, there is very little variation seen between the experimental spectrum and the modelled enol-N4 protomer, shown in Fig. 4(a and c), respectively. Specifically, the enol-N4 protomer has no significant absorption in the low-energy spectral range (hv < 3.5 eV), consistent with the MeCN-ESI profile, and good agreement is seen in terms of band separations, peak widths, and onset energies for the absorption bands. This indicates that the Z·H⁺ ion ensemble produced via MeCN-ESI is dominated almost exclusively by the enol-N4 isomer. However, more significant deviations can be seen for the H₂O-ESI spectrum.

For the H₂O-ESI regime it is necessary to compare the experimental spectral shape with the modelled composite spectra (Fig. 4(b and c)), indicating the importance of the higher energy protomers in this gas-phase ion ensemble. The H₂O-ESI profile has two significant differences with respect to the MeCN-ESI profile: a non-zero absorption feature at hv < 3.5 eV and a slight blue-shifting and broadening of band I. Both features can be broadly understood to arise from the enol-N7O spectrum, in which the two bright ππ* states are red-shifted by ∼0.5 eV relative to the enol-N4 states, consistent with to the observed changes in the composite spectrum.

We conclude that the Z·H⁺ ion ensemble produced via H₂O-ESI is a mixture of the three lowest-energy protomers, whereas the spectrum obtained from MeCN-ESI can be attributed predominantly to the N4-enol protomer.

3.4. Photofragmentation of Z·H⁺

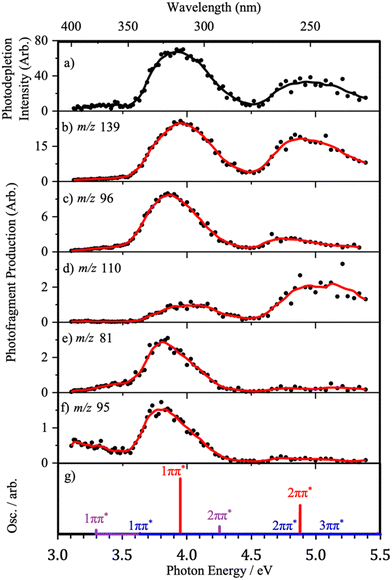
To gain further insight into the excited-state decay dynamics, it is instructive to inspect the photofragment production spectra. These are presented in Fig. 5 and 6, first as ion-yield plots and then as the individual photofragment production plots to provide further detail. Calculated TDDFT vertical excitation energies (VEEs) for each of the lowest-energy Z protomers are also presented in both figures to guide understanding and interpretation of the origin of relevant photofragments.

Fig. 5 Relative ion-yield plots for the major photofragments of Z·H⁺ (a and c) m/z 139, (b and d) m/z 81, 95, 96 and 110 across the 3.0–5.0 eV range produced via H₂O-ESI (a and b) and MeCN-ESI (c and d). Solid lines are 5-point adjacent averages of data points. (e) Calculated ωB97xd/cc-pVTZ VEEs for the enol-N4 protomer (red), the enol-N7O protomer (purple) and the keto-N7O protomer (blue), red-shifted by 0.5 eV. Oscillator strengths are scaled by relative intensities of the ion ensemble, weighted by the Boltzmann populations at 548.15 K.

Fig. 6 (a) Gas-phase absorption (photodepletion) spectrum for Z·H⁺ produced via H₂O-ESI, and photofragment production spectra of the following major photofragments: (b) m/z 139, (c) m/z 96, (d) m/z 110, (e) m/z 81 and (f) m/z 95, across the hv = 3.1–5.4 eV (400–229 nm) excitation-energy range. Solid lines are a 5-point adjacent average of data points. (g) Calculated ωB97xd/cc-pVTZ VEEs energies for the enol-N4 protomer (red), the enol-N7O protomer (purple) and the keto-N7O protomer (blue) where oscillator strengths (Osc.) are scaled according to ion population (Boltzmann calculations) and energies have been red-shifted by 0.5 eV.

Fig. 5 shows the relative ion-yield plots for the major photofragments arising from the mass-selected Z·H⁺ ion (m/z 156) following MeCN- and H₂O-ESI, alongside the calculated bright ππ* states of all three protomers. Regardless of solvent, broad similarities can be seen between the relative ion-yield plots.

In both solvent systems, the major photofragment is m/z 139, which exhibits greater relative production with increasing photon energy (Fig. 5(a and c)). The relative production of fragment m/z 96 is observed to increase from low photon energy to a maximum intensity of 25% at ∼3.6 eV before then decreasing as the photon energy increases further. Despite this decreasing yield, this remains a non-negligible ion loss channel across the experimental energy range. A similar production profile is seen for fragment m/z 81, albeit at much lower intensities and with a maximum relative yield of ∼3.4–3.6 eV in both solvents. It is notable that this fragment has a higher production in the H₂O-ESI regime. Given the discussion in Section 3.2, this suggests that the m/z 81 fragment may be predominantly produced from the N7O-enol protomer. Fragment m/z 95 shows a distinctive profile, initially displaying a greater relative yield than m/z 139 before then rapidly decreasing in intensity as the photon energy increases. The lowest relative intensity fragment, m/z 110, initially shows very low production intensity (<2.5%) before steadily increasing concurrent with photon energy.

Fig. 6 presents the full photofragment production spectra for the major photofragments along with the photodepletion spectrum and the calculated VEEs for the bright ππ* states for ease of comparison. We have chosen to only present the full photofragment production profiles for the ESI-H₂O conditions, since the multiple protomers are present under this regime. The production spectrum for the major photofragment, m/z 139 (Fig. 6(b)), shows two major production bands with maxima of approximately 3.95 eV and 4.85 eV, strongly resembling the H₂O-ESI gas-phase photodepletion spectrum (Fig. 6(a)).

The photofragment production profile for fragment m/z 96 exhibits two distinct absorption bands, again in broad agreement with the calculated enol-N4 VEEs (Fig. 6(c and g)). However, compared to the m/z 139 fragment, the maximum of the Band I is red-shifted by 0.1 eV and Band II has much lower relative intensity. The physical origin of the red-shifting is likely attributable to the presence of the higher-energy protomers, as both N7O-isomers have lower energy 1ππ* states.

The production profile for fragment m/z 81 (Fig. 6(c)) has one significant feature with a maximum at 3.80 eV, in addition to non-zero production intensity below 3.5 eV. Because the photofragment production spectrum is very different from the gas-phase photodepletion spectrum, it is likely that the pathway for producing this fragment does not involve the enol-N4 isomer. Instead, the red-shifting of the band relative to that observed for m/z 96, as well as the greater production intensity at low energies, indicates that the fragment is a product of (one or both of) the N7O higher-energy protomers. This is reflected by the TDDFT calculations where the maximum ion yield for this fragment is seen to lie between the 1ππ* VEEs for each of these protomers. Generally, the production profiles of fragments m/z 81 and m/z 95 (Fig. 6 and 7) resemble one another, and the arguments that apply to m/z 81 can therefore be similarly applied to m/z 95. However, at low hv, m/z 95 is unique in the distinct low-energy absorption which is seen to decrease between 3.0 eV and 3.5 eV. Considering the calculated VEEs, this feature can be attributed to photofragment production via the enol-N7O isomer alone, an observation that is supported by the shape of the ion-yield plot for this fragment below 3.5 eV, alongside the lower relative production intensity.

Fragment m/z 110 (Fig. 6d) exhibits two peaks in its production profile, with maxima at 4.03 eV and 5.03 eV. Unlike previous photofragment profiles, the higher-energy Band II has a much higher relative intensity than Band I. The inversion of the photofragmentation profile seen for m/z 110 compared to other photofragments indicates that the formation of m/z 110 is likely to be a product of photoexcitation of the 2ππ* state or a secondary fragmentation process.

3.5. Higher energy collisional dissociation of Z·H⁺

Fig. 7(a and b) display the HCD results for Z·H⁺, obtained from H₂O- and MeCN-ESI, respectively. To aid comparison of meaningful energy regimes between fragmentation methods (photo and HCD), we only plot the 0–40% HCD energy range.^29,45 The full 0–60% HCD energy probed can be found in Section S7 (ESI†). In both solvent systems similar HCD fragmentation profiles are seen. The major HCD fragment is m/z 139, mirroring the major photofragment, followed by m/z 96. Notably, all photofragments are also produced as HCD fragments, with the caveat that there are intensity variations between photofragments and HCD fragments across the different energy regimes. To facilitate direct comparison, the observed HCD and photofragments are provided together in Table 2. A more quantitative comparison of the intensities of the HCD and photofragments is provided in Section S8 of the ESI.†

Fig. 7 % Decay curve for mass selected [Z·H]⁺ ion (m/z 156) and associated % fragment production curves for major thermal fragments on high-energy CID over the range 0–40% HCD energy, in (a) H₂O-ESI and (b) MeCN-ESI. Data points are an average of five repeats and solid lines are a five-point adjacent average of data points. No CID fragments with a relative ion intensity of <5% are shown, further details of the full CID experiment are given in the ESI.†

Table 2 Proposed assignments of the major cationic photofragments and associated neutral losses observed upon hv = 3.1–4.9 eV and low-energy HCD (<24% energy) of Z·H⁺ (m/z 156)^ab

Photofragment (m/z)	Formula	Neutral/radical formula	Photofragment^c (H2O)	Low-energy HCD fragment^c
				MeCN	H2O
a Section S5 (ESI) gives the full fragment list. N.b. not all thermal fragments (<5% abundance) are not shown in Fig. 7. b Possible fragment structures are included in Section S5 (Table S2, ESI). c s, m, w, and vw refer to relative ion intensities >50% (s), 20–50% (m), 5–20% (w) and <5% (vw), respectively, with the relative ion intensities taken from Fig. 5 for the photofragments and Fig. 7 for the HCD fragments.
139	C5H5N3O2	OH	✓ (s)	✓(m)	✓(m)
138	C5H4N3O2	H2O	× □	✓(w)	✓(w)
110	C5H6N2O	NO2	✓(w)	✓(vw)	✓(vw)
109	C5H5N2O	NO2H	✓(vw)	✓(vw)	✓(vw)
96	C4H2NO2	CH4N2O	✓(m)	✓(m)	✓(m)
95	C4H3N2O	CH3NO2	✓(m)	✓(vw)	✓(vw)
82	C4H6N2	CNO3	✓(vw)	✓(vw)	✓(vw)
81	C4H5N2	CHNO3	✓(w)	✓(vw)	✓(vw)
54	C3H4N	C2H2NO3	✓(vw)	✓(vw)	✓(vw)

---

Overall, the fragmentation profiles appear to be unaffected by the ESI solvent system, with only minor notable differences. Following MeCN-ESI there is a greater abundance of fragments m/z 110, 109 and 82, while in H₂O-ESI we see more generation of fragments m/z 95 and 96. The former fragmentation pathways (where we believe the enol-N4 protomer is dominant) appear to be characterised by the loss of the NO₂ functional group, while in the latter (where three tautomers are believed to be present) the fragmentation is more complex, and indicates that the higher-energy tautomers fragment by pathways involving the cleavage of the heterocycle. The formation of the m/z 95 fragment occurs in higher proportions following photoexcitation, suggesting this may be a rearrangement or radical driven cleavage reaction, facilitated by an excited state.

3.6. Interpretation of the fragmentation patterns

A schematic showing the molecular orbitals involved in the calculated electronic transitions of the two bright lowest lying singlet excited states is shown in Fig. 8, annotated with red-shifted VEEs and oscillator strengths. These two states are ππ* character of roughly similar nodal character, differing in electron density distribution due to protonation site.

Fig. 8 A schematic showing the transitions involved in the two bright lowest lying singlet excited states, with the red-shifted VEEs, oscillator strengths and relevant molecular orbitals for each protomer.

The calculated VEEs for the ππ* states of the enol-N4 protomer (3.95 eV and 4.88 eV) correlate well with the production maxima for fragment m/z 139 (Fig. 6(b)), suggesting that this fragment is likely to derive from the enol-N4 protomer. This conclusion is consistent with the interpretation that the major photofragment results from the dominant protomer. The onset of photofragment production from this fragment is ∼3.25 eV. This suggests the beginning of this fragmentation pathway is concurrent with the 1ππ* state of the higher-energy protomers, with maxima in good agreement with the two ππ* states of the dominant enol-N4 protomer (Fig. 6(b and g)). The m/z 139 fragment corresponds to a loss of a neutral fragment with m/z 17, with respect to Z·H⁺, which is likely to correspond to a radical cation produced by homolytic cleavage of the C–OH bond of an enol protomer. Inspection of the occupied molecular orbitals of all protomers provides an insight into the physical origin of why both this specific fragmentation pathway is dominant, irrespective of fragmentation method, and the unusual relative ion-yield profile observed for its production. We have not seen such a gradually increasing ion production as a function of excitation energy previously.^10,31,46,47

For all of the protomers studied there is a node in the electron density between the C3–O9 atoms, weakening this bond even in the ground electronic state. The steady increase in production of this m/z 139 photofragment with increasing photon energy, Fig. 5(a and c), suggests this is indeed a facile fragmentation pathway. In the photofragmentation experiment, it appears that as the ππ* states of the protomers are populated, there is a route to the vibrationally hot ground state of the parent ion from which the OH group is ‘boiling off’ with increasing intensity as the internal energy increases. In the HCD experiment, the same statistical fragmentation pathway is accessed from the bottom-up through thermalisation. (The fall of this HCD channel at the highest HCD energies likely results in secondary fragmentation of m/z 139/138 into m/z 110/109.)

Further inspection of the electron density of the ππ* states may offer additional insight into other proposed photofragmentation pathways. Excitation of an electron from a π bonding molecular orbital to an anti-bonding π* molecular orbital can be understood to result in a weakening in specific bonding regions. If certain bonding regions weaken, then consequent geometric changes in the excited-state structure may lead to a minimum energy crossing point (MECP) with a dissociative potential energy surface, leading to fragmentation. This argument appears to offer good insight into the behaviour of the m/z 110 photofragment, which is understood to arise from loss of the NO₂ group. m/z 110 is produced in low relative intensity, from a broader band at 3.7–4.25 eV, switching on at the position of the 1ππ* state of N7O-keto and then switching back off after the 1ππ* state of N7O-enol. The fragmentation yield then increases with a maximum of ∼5 eV, in good agreement with the 3ππ* state of the N7O-keto. All the ππ* states of N7O-protomers result in a weakened C–NO₂ bond, relative to the ground state, suggesting that the increasing production of the m/z 110 photofragment is facilitated by these excited states.

The m/z 95 photofragment is also notable in this context since it is produced more strongly following photoexcitation than by HCD (Table 2). As outlined above, the production of this photofragment suggests a radical driven cleavage reaction facilitated by an excited state. This can be understood to be driven by the ππ* electron density redistribution that occurs upon photoexcitation.

4. Concluding remarks

The HCD (thermal) and photofragmentation experiments conducted on Z·H⁺ indicate that the dominant decay dynamics are consistent with statistical ultrafast decay, and facile loss of the Z molecule's OH group. The dominant fragmentation pathway is rationalised through inspection of the electron density of the occupied molecular orbitals, and a nodal pattern consistent with a weakened C3–O9 bond is proposed to be a physical origin of the prevalence of this fragment at all experimental photon energies. The “boil off” mechanism of OH loss is clear from the ion yield plots presented in this work and illustrates the value of such plots for providing insight into photochemical decay mechanisms. From a photochemical perspective, it should be noted that this decay pathway may be partially or fully quenched in a bulk solution where excess thermal energy can be lost to solvent. However, the decay pathways within an oligonucleotide are known to differ from those in bulk solution,⁴⁸ so that the OH loss pathway may still be important in a synthetic organism.

A number of minor non-statistical decay pathways have also been identified for Z·H⁺ in this work, evident in the production profiles of the m/z 110 and m/z 95 photofragments. The production of these fragments is enhanced by dynamics on the excited state surfaces, potentially due to triplet/repulsive surfaces. Our previous work on thiouracil and 2-phenylbenzimidazole-5-sulfonic acid (the cosmetic, PBSA) have demonstrated that the non-statistical photochemical decay pathways observed via LIMS correlate with long-lived excited states observed in solution-phase experiments.^11,25 This leads us to conclude that such long-lived excited states are likely to be present in the condensed-phase photodynamics of Z and its aggregates.

Although it is not certain that the photodynamics of protonated Z are the same as neutral Z, in other protonated nucleobase systems we have studied the protonated and neutral forms do exhibit similar photodynamics. For example, protonated uracil decays with statistical fragmentation following photoexcitation, indicating ultrafast excited-state decay which mirrors the ultrafast decay of the non-protonated uracil nucleobase.⁵ Similarly, 2-thiouracil has been shown to display longer-lived excited states (i.e. non-ultrafast excited-state decay) for both its neutral and protonated forms, so that the protonated system appears to closely mimic that of the neutral.²⁵ Therefore, it is not unreasonable to conclude that the predominately statistical decay dynamics, along with the minor non-statistical pathways, observed here for gas-phase Z·H⁺ ion will be matched by the Z neutral.

These results provide important fundamental information that can inform the design of future synthetic nucleobases. Previous photochemical studies on a very wide range of modestly modified natural nucleobases have revealed their unique nature in terms of their highly efficient excited-state decay pathways.^49–52 Mimicking and synthetically controlling these photodynamics has proven extremely challenging.^9,15 The loss of the OH group at the C3 position has implications for the design of synthetic nucleobases, as this group is directly involved in the hydrogen-bonding motif of the base pair. In addition to this dominant OH loss fragmentation pathway, we have also identified several dissociative photochemistry channels that are associated with intrinsic photoinstability. While such pathways are concerning if the desired design outcome is a robust, photostable synthetic nucleobase, the intrinsic instabilities found for the Z nucleobase have potential merit in applications where molecular photoinstability is desirable, e.g. next generation photodynamic therapies.⁵³

Author contributions

WW data collection and analysis and preliminary calculations under supervision of JAB and NGKW, KEM data collection and analysis, CSA electronic structure calculations, analysis and manuscript preparation, CEHD conceptualisation, resources, supervision and writing original draft.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank the University of York and the Department of Chemistry for provision of funds for the OPO laser system. The York Centre of Excellence in Mass Spectrometry, used for the higher-energy collisional dissociation (HCD) work, was created thanks to a major capital investment through Science City York, supported by Yorkshire Forward with funds from the Northern Way Initiative, and has more recently received additional support from the EPSRC and BBSRC. Finally, we thank Dr Ed Bergström for his assistance and guidance with the HCD experiments.

References

1. T. Chen, N. Hongdilokkul, Z. Liu, D. Thirunavukarasu and F. E. Romesberg, Curr. Opin. Chem. Biol., 2016, 34, 80–87.
2. A. Marx and K. Betz, Chem. – Eur. J., 2020, 26, 3446–3463.
3. P. Błażej, M. Wnetrzak, D. Mackiewicz and P. Mackiewicz, R. Soc. Open Sci., 2020, 7, 191384.
4. J. W. Chin, Nature, 2017, 550, 53–60.
5. M. Barbatti, A. J. A. Aquino, J. J. Szymczak, D. Nachtigallova, P. Hobza and H. Lischka, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 21453–21458.
6. A. A. Beckstead, Y. Zhang, M. S. de Vries and B. Kohler, Phys. Chem. Chem. Phys., 2016, 18, 24228–24238.
7. B. Ashwood, S. Jockusch and C. E. Crespo-Hernández, J. Phys. Chem. Lett., 2017, 8, 2387–2392.
8. W.-W. Guo, T.-S. Zhang, W.-H. Fang and G. Cui, Phys. Chem. Chem. Phys., 2018, 20, 5067–5073.
9. H. Wang, L. Wang, N. Ma, W. Zhu, B. Huo, A. Zhu and L. Li, ACS Synth. Biol., 2022, 11, 334–342.
10. N. G. K. Wong, C. Rhodes and C. E. H. Dessent, Molecules, 2021, 26, 6009.
11. N. G. K. Wong, J. A. Berenbeim and C. E. H. Dessent, ChemPhotoChem, 2019, 3, 1231–1237.
12. D. A. Malyshev, K. Dhami, T. Lavergne, T. Chen, N. Dai, J. M. Foster, I. R. Corrêa and F. E. Romesberg, Nature, 2014, 509, 385–388.
13. Y. Zhang, B. M. Lamb, A. W. Feldman, A. X. Zhou, T. Lavergne, L. Li and F. E. Romesberg, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 1317–1322.
14. D. A. Malyshev, K. Dhami, H. T. Quach, T. Lavergne, P. Ordoukhanian, A. Torkamani and F. E. Romesberg, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 12005–12010.
15. L. Li, M. Degardin, T. Lavergne, D. A. Malyshev, K. Dhami, P. Ordoukhanian and F. E. Romesberg, J. Am. Chem. Soc., 2014, 136, 826–829.
16. I. Hirao, M. Kimoto and R. Yamashige, Acc. Chem. Res., 2012, 45, 2055–2065.
17. N. Beiranvand, M. Freindorf and E. Kraka, Molecules, 2021, 26, 2268.
18. J. A. Piccirilli, S. A. Benner, T. Krauch, S. E. Moroney and S. A. Benner, Nature, 1990, 343, 33–37.
19. Z. Yang, D. Hutter, P. Sheng, A. M. Sismour and S. A. Benner, Nucleic Acids Res., 2006, 34, 6095–6101.
20. M. M. Georgiadis, I. Singh, W. F. Kellett, S. Hoshika, S. A. Benner and N. G. J. Richards, J. Am. Chem. Soc., 2015, 137, 6947–6955.
21. M. Chawla, R. Credendino, E. Chermak, R. Oliva and L. Cavallo, J. Phys. Chem. B, 2016, 120, 2216–2224.
22. R. Laos, C. Lampropoulos and S. A. Benner, Acta Crystallogr., Sect. C: Struct. Chem., 2019, 75, 22–28.
23. I. Singh, R. Laos, S. Hoshika, S. A. Benner and M. M. Georgiadis, Nucleic Acids Res., 2018, 46, 7977–7988.
24. N. G. J. Richards and M. M. Georgiadis, Acc. Chem. Res., 2017, 50, 1375–1382.
25. K. O. Uleanya, R. Cercola, M. Nikolova, E. Matthews, N. G. K. Wong and C. E. H. Dessent, Molecules, 2020, 25, 3157.
26. K. Kleinermanns, D. Nachtigallová and M. S. de Vries, Int. Rev. Phys. Chem., 2013, 32, 308–342.
27. E. Matthews and C. E. H. Dessent, J. Phys. Chem. A, 2016, 120, 9209–9216.
28. E. Matthews and C. E. H. Dessent, Phys. Chem. Chem. Phys., 2017, 19, 17434–17440.
29. R. Cercola, E. Matthews and C. E. H. Dessent, J. Phys. Chem. B, 2017, 121, 5553–5561.
30. B. Lucas, M. Barat, J. A. Fayeton, C. Jouvet, P. Çarçabal and G. Grégoire, Chem. Phys., 2008, 347, 324–330.
31. N. G. K. Wong, C. D. Rankine and C. E. H. Dessent, J. Phys. Chem. Lett., 2021, 12, 2831–2836.
32. N. G. K. Wong, C. D. Rankine and C. E. H. Dessent, J. Phys. Chem. A, 2021, 125, 6703–6714.
33. C. Marian, D. Nolting and R. Weinkauf, Phys. Chem. Chem. Phys., 2005, 7, 3306.
34. M. Grupe, P. Boden, P. Di Martino-Fumo, X. Gui, C. Bruschi, R. Israil, M. Schmitt, M. Nieger, M. Gerhards, W. Klopper, C. Riehn, C. Bizzarri and R. Diller, Chem. – Eur. J., 2021, 27, 15252–15271.
35. E. Matthews, A. Sen, N. Yoshikawa, E. Bergström and C. E. H. Dessent, Phys. Chem. Chem. Phys., 2016, 18, 15143–15152.
36. I. Compagnon, A.-R. Allouche, F. Bertorelle, R. Antoine and P. Dugourd, Phys. Chem. Chem. Phys., 2010, 12, 3399.
37. E. Matthews, Photodissociation Spectroscopy of Gaseous Bio-ions in a Commercial Quadrupole Ion Trap Mass Spectrometer, PhD thesis, University of York; 2018.
38. J. I. Brauman and K. C. Smyth, J. Am. Chem. Soc., 1969, 91, 7778–7780.
39. J. V. Olsen, B. Macek, O. Lange, A. Makarov, S. Horning and M. Mann, Nat. Methods, 2007, 4, 709–712.
40. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016.
41. A. Chantzis, A. D. Laurent, C. Adamo and D. Jacquemin, J. Chem. Theory Comput., 2013, 9, 4517–4525.
42. J. Schmidt, M. M. Meyer, I. Spector and S. R. Kass, J. Phys. Chem. A, 2011, 115, 7625–7632.
43. Z. Tian and S. R. Kass, Angew. Chem., Int. Ed., 2009, 48, 1321–1323.
44. J. D. Steill and J. Oomens, J. Am. Chem. Soc., 2009, 131, 13570–13571.
45. Y. Ho and P. Kebarle, Int. J. Mass Spectrom. Ion Processes, 1997, 165–166, 433–455.
46. R. Cercola, K. C. Fischer, S. L. Sherman, E. Garand, N. G. K. Wong, L. A. Hammerback, J. M. Lynam, I. J. S. Fairlamb and C. E. H. Dessent, Chem. – Eur. J., 2020, 26, 10297–10306.
47. J. A. Berenbeim, N. G. K. Wong, M. C. R. Cockett, G. Berden, J. Oomens, A. M. Rijs and C. E. H. Dessent, J. Phys. Chem. A, 2020, 124, 2919–2930.
48. B. Kohler, J. Phys. Chem. Lett., 2010, 1, 2047–2053.
49. C. E. Crespo-Hernández, B. Cohen, P. M. Hare and B. Kohler, Chem. Rev., 2004, 104, 1977–2020.
50. S. Ullrich, T. Schultz, M. Z. Zgierski and A. Stolow, Phys. Chem. Chem. Phys., 2004, 6, 2796.
51. S. Matsika, in Photoinduced Phenomena in Nucleic Acids I, ed. M. Barbatti, A. C. Borin and S. Ullrich, Springer International Publishing, Cham, 2014, vol. 355, pp. 209–243.
52. L. Martínez Fernández, F. Santoro and R. Improta, Acc. Chem. Res., 2022, 55, 2077–2087.
53. A. F. Dos Santos, D. R. Q. De Almeida, L. F. Terra, M. S. Baptista and L. Labriola, J. Cancer Metastasis Treat., 2019, 5, 25.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp03831e

---