Radiation effects, zero thermal expansion, and pressure-induced phase transition in CsMnCo(CN)₆

Abstract

The Prussian blue analogue CsMnCo(CN)₆ is studied using powder X-ray and neutron diffraction under variable temperature, pressure, and X-ray exposure. It retains cubic F4̄3m symmetry in the range 85–500 K with minimal thermal expansion, whereas a phase transition to P4̄n2 occurs at ∼2 GPa, driven by octahedral tilting. A small lattice contraction occurs upon increased X-ray dose. Comparisons with related systems indicate that the Cs^I ions decrease the thermal expansion and suppress the likelihood of phase transformations. The results improve the understanding of the stimuli-responsive behaviour of coordination polymers.

---

Understanding how external perturbations affect a material, in particular strain effects and the propensity for phase transitions, is a key research area in solid-state chemistry. Apart from the fundamental interest in stimuli-responsive behaviour, this is also critical to many applications. By way of example, a high resistance towards phase transitions is desirable for electrode materials during cation intercalation^1,2 or for pharmaceuticals during compression into tablets.³ Conversely, low mechanical stability allows for glass processing by pressure-induced amorphisation.^4,5 Moreover, the response to e.g. temperature or pressure fluctuations is an important consideration for materials exposed to changing conditions during operation or processing.⁶

Mechanical properties in framework materials are often linked to the amount of void space. For example, the thermal expansion and bulk modulus of the archetypal metal–organic framework UiO-66 can be tuned by introducing missing-cluster defects (vacancies),^7,8 whereas interstitial K^I ions in KMn[Ag(CN)₂]₃ increase the pressure range—but decrease the magnitude—of the negative linear compressibility.⁹ A family known for their large stoichiometric diversity—and thus variable void space—is the Prussian blue analogues (PBAs),^10,11 which exhibit versatile properties on account of the high tunability.^12–14 PBAs have the general formula A_xM[M′(CN)₆]_y·nH₂O (A = alkali metal and M/M′ = transition metals) and can be described as cyanide analogues of double perovskites. The behaviour of alkali-containing PBAs resembles that of oxides, in the sense that magnetic order and cation intercalation are possible.^12,13

Here we undertake an in-depth study of the stimuli-responsive behaviour of the PBA CsMnCo(CN)₆, using powder X-ray and neutron diffraction (XRD/ND) under variable temperature, pressure, and X-ray exposure. CsMnCo(CN)₆ resides at the dense end of the PBA stoichiometry spectrum and thus provides an insight into the limiting mechanical behaviour obtainable by inclusion of large cations. The Cs^I ions reduce the free space available for compression and transverse vibrations, and can thus be expected to enhance the rigidity. Many PBAs are explored as sorbents for radioactive Cs^I ions from nuclear waste,^15,16 which further motivates the study of Cs-containing PBAs. We find that CsMnCo(CN)₆ transitions to a tetragonal phase at 2 GPa, driven by octahedral tilting, but features no thermal phase transitions and a very low thermal expansion. Like certain other metal–cyanides, CsMnCo(CN)₆ is susceptible to X-ray radiation and contracts slightly as the exposure increases. The results are discussed in the context of other PBAs.

Polycrystalline CsMnCo(CN)₆ was prepared by direct combination of aqueous solutions of an appropriate Mn^II salt and K₃Co(CN)₆ in an excess of CsCl [see ESI† for details]. The large radius of Cs should prevent water from being included and hydration—which is integral to many other PBAs^17–19—is not expected to play a major role here. Powder X-ray diffraction (XRD) confirms that CsMnCo(CN)₆ adopts the non-centrosymmetric space group F4̄3m at ambient conditions [Fig. 1(a)]. This corresponds to the typical double perovskite structure with a rocksalt arrangement of Mn^II and Co^III ions linearly joined by cyanide ions. Each unit cell contains eight interstitial A-sites, half of which are occupied by Cs^I ions in an alternating arrangement, leading to the non-centrosymmetric symmetry. However, this order is not complete, as the lesser-occupied sites still show an occupancy of ca. 0.2 Cs^I ions, which leads to substantial broadening of reflections where h + k + l = 2n + 1 [Fig. S1, ESI†].

Fig. 1 The crystal structure of CsMnCo(CN)₆ at (left) ambient conditions in space group F4̄3m and (right) at 3.7 GPa in P4̄n2. Cs is coloured in teal; Mn and N in red; and Co and C in grey. The sizes of the Cs^I ions scale with the occupancies of the two sites.

Exposure to X-ray radiation can affect metal–cyanide frameworks, manifesting as changes in the lattice constants.^20–22 To investigate whether this occurs in CsMnCo(CN)₆, ten consecutive XRD patterns were collected on the same part of the sample at beamline I11, Diamond Light Source. This reveals a small, but significant and continuous, decrease in the lattice parameter as a function of increased radiation dose [Fig. S2–S4 and Table S2, ESI†], accompanied by a very slight decrease in the diffraction intensity. Radiation-induced unit cell contractions were recently named “negative X-ray expansion” (NXE),²² as this contrasts with the lattice expansion commonly seen as a sign of radiation damage in macromolecular and small-molecule crystallography.^23–25 As the dose was not monitored, the magnitude of NXE cannot be quantified, yet CsMnCo(CN)₆ belongs to the group of NXE materials—a group that is likely to grow as more systems are explored.

CsMnCo(CN)₆ was studied by variable-pressure X-ray diffraction up to ∼8 GPa and neutron diffraction up to ∼5 GPa. While reflections broaden slightly, the X-ray crystallinity is maintained within this pressure range [Fig. 2]. The ND patterns suffer more severe peak broadening upon increasing pressure, which is attributed to differences in the experimental set-up. As previously noted in an X-ray study,²⁶ CsMnCo(CN)₆ transitions to tetragonal symmetry around 2 GPa, with cell parameters related to that of the cubic parent (a_c) by 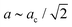and c ∼ a_c. This high-pressure phase could be fitted satisfactorily with either I4̄ or P4̄n2 symmetry, with a slight preference for the latter. Both space groups result from octahedral tilting,²⁷ but with different periodicity: I4̄ implies out-of-phase tilts (a⁰a⁰b⁻ in Glazer notation²⁸) and P4̄n2 from in-phase tilts (a⁰a⁰b⁺).²⁷ As these structures solely differ in the positions of the cyanide ions, they are not easily distinguished based on X-ray data alone. However, by refining against both X-ray and neutron data at 3.7 GPa, we here confirm that the correct space group is P4̄n2 [Fig. S5 and Table S3, ESI†]. The in-phase a⁰a⁰b⁺ octahedral tilt is relatively common in PBAs with large A-site cations²⁹ and is also prevalent in halide perovskites,³⁰ but rarely occurs in oxides.³¹

Fig. 2 The percentage change in (top) the lattice parameters, (middle) the local compressibilities (K_i), and (bottom) the tetragonality () of the high-pressure phase of CsMnCo(CN)₆ as a function of pressure found from XRD.

The tetragonal phase persists across the pressure range studied here, with anisotropic and pressure-dependent compressibilities (K_i) [Fig. 2 and Fig. S6, Table S4, ESI†]. Initially, the a axis is softer than the c axis by an order of magnitude, with K_a = 21.1(5) TPa⁻¹ and K_c = 1.8(3) TPa⁻¹. These values are considerably lower than the compressibilites of the tetragonal high-pressure phase of RbMnCo(CN)₆ (K_a = 36(2) TPa⁻¹, K_c = 5.3(6) TPa⁻¹),²⁶ which shows that the Cs^I ions decrease the flexibility of the framework. The large difference between K_a and K_c indicates that the compression mechanism after the phase transition mainly involves increasing tilting magnitude, which contracts the ab plane. As the pressure is raised, the a axis becomes increasingly stiff and the c axis softens slightly, such that K_a ∼ K_c above ∼6.5 GPa. Using a third-order Murnaghan equation of state to fit the volume–pressure data, the bulk modulus (B₀) is 4.4(4) GPa with a first pressure derivative of 7.08(8) [Fig. S7, ESI†]; hence, the high-pressure phase of CsMnCo(CN)₆ is initially very compressible, yet hardens rapidly as pressure increases.

As a result of the changes to the compressibility, the tetragonality —effectively a measure of the tilting amplitude—initially increases from unity and subsequently reaches a plateau at a value of ∼1.06 at higher pressures [Fig. 2]. This suggests that the contribution of the static tilting to the overall compression is reduced, and could potentially indicate the presence of an additional low-energy dynamic tilt mode affecting the c axis. The analogous RbMnCo(CN)₆ shows the same F4̄3m → P4̄n2 transition as the Cs compound, but has a further transition to the polar space group Pn, driven by a tilt along c (a⁻a⁻b⁺).²⁶ This tilt mode perhaps appears locally at CsMnCo(CN)₆ at these pressures, although no global, long-range phase transition was seen.

Variable-temperature X-ray diffraction was used to study CsMnCo(CN)₆ in the range 500–85 K upon cooling. To avoid the aforementioned X-ray effects, every XRD pattern was collected from a previously non-irradiated part of the sample. Due to the finite length of the capillary, this approach necessitated a change of capillary—with material from the same sample batch—between 300 and 260 K. CsMnCo(CN)₆ retains its cubic structure in the entire temperature range without noticeable changes to the XRD patterns [Fig. S8 and S9, ESI†].

Remarkably, the lattice parameters remain nearly unchanged [Fig. 3(a) and Table S5, ESI†] as a function of temperature, with the discontinuity between 300 and 260 K resulting from the capillary change. Given the extremely low overall expansivity, slight differences between different capillaries give changes in lattice parameter on the same scale as the expansion. The linear and volumetric coefficients of thermal expansion are 0.46(7) MK⁻¹ and 2.3(6) MK⁻¹, respectively. These values are very low and place CsMnCo(CN)₆ amongst the zero thermal expansion (ZTE) materials. Similarly low expansivities are also found for the closely related CsMnFe(CN)₆ and other Cs-containing PBAs.^32,33 The trend that Cs decreases the expansivitiy relative to Rb also appears to generally hold for thermal expansion, albeit the effect is smaller.³³ ZTE is of interest for many applications where the material is subjected to large temperature fluctuations, ranging from e.g. cookware to high-precision optics.³⁴

Fig. 3 Top: Cubic lattice parameter of CsMnCo(CN)₆ as a function of temperature with a line of best fit. Bottom: Linear coefficients of thermal expansion for cubic PBAs as a function of the studied temperature range, coloured according to the stoichiometry of the PBA.

For a given application, both the range and magnitude of the thermal expansion are important considerations.³⁵ Thus for context, the linear thermal expansion coefficients of numerous cubic PBAs are given in Fig. 3(b) as a function of the corresponding temperature range. An enlarged view is provided in Fig. S10 (ESI†). The entries are coloured according to stoichiometry: recalling the general formula of a PBA as A_xM[M′(CN)₆]_y·nH₂O, alkali-metal-containing compounds (teal) are defined as x > 0, stoichiometric (purple) as x = y = 0, and defective (grey) as y > 0.3. While this provides a useful categorisation for discussion of stoichiometrical effects on the thermal expansion behaviour, it should be remembered that the stoichiometry of PBAs is continuously variable, rather than discrete.³⁶

Stoichiometry clearly plays a role in dictating the thermal expansion of PBAs [Fig. 3(b)]. The defective PBAs show the largest spread of expansivities, and span large negative and positive values, depending on the framework metal ions.³⁷ This bears testament to the high structural flexibility resulting from the missing M′(CN)₆ clusters. However, this flexibility is also affected by guest species, typically water;³⁸ yet there are few studies on the interplay of hydration and thermal expansion in these materials. Stoichiometric and alkali metal-containing PBAs typically show thermal expansion coefficients closer to zero (|α_a| < 15 MK⁻¹), and many compounds in these two categories show ZTE. The introduction of alkali metals—or guest molecules—often leads to ZTE by inhibiting the low-energy transverse phonons responsible for NTE,^39,40 but this is evidently not a necessary condition. Several studies have shown a relationship between the lattice parameter and the thermal expansion in PBAs,^33,40,41 and so an appropriate choice of framework metal ions may also drive ZTE, e.g. FeCo(CN)₆.⁴² Taken together, vacancies exert a large influence on the thermal response of PBAs, and compositional factors play a key role for stoichiometric and alkali-metal-containing compounds. Similar effects have also been noted for the bulk moduli.²⁶

To conclude, the Prussian blue analogue CsMnCo(CN)₆ generally shows a low responsiveness to external temperature and pressure variation. This manifests as a lower propensity for pressure-induced phase transitions than the isostructural RbMnCo(CN)₆, and near-zero thermal expansion. We attribute this to the stabilising role of the large Cs^I ion, which will inhibit the transverse vibrations typically invoked to rationalise negative thermal expansion in PBAs,⁴³ and which presumably also drive the phase transitions under compression. Consequently, the incorporation of Cs^I ions may be useful in applications where low strain and large resistance to phase transitions are desirable, e.g. in electrodes.⁴⁴ Finally, CsMnCo(CN)₆ shows an X-ray-induced lattice contraction, where further studies are required for mechanistic insight.

We are grateful to Diamond Light Source and ISIS Neutron and Muon Source for the provision of beamtimes CY30164 and 2010048 (data DOI: https://doi.org/10.5286/ISIS.E.RB2010048), respectively. We thank S. J. Cassidy (Oxford) and the I11 beamline staff for assistance with the data collection. HLBB acknowledges financial support from the Alexander von Humboldt Foundation. B. V. Lotsch (MPI-FKF) is gratefully acknowledged for the use of lab space, M.-L. Schreiber (MPI-FKF) and D. Ojwang (Uppsala) for ICP measurements, and C. L. Bull (ISIS) for useful discussions. Open Access funding provided by the Max Planck Society.

Author contributions

H. L. B. B., conceptualisation, investigation, formal analysis, writing; A. B. C., investigation, formal analysis, writing—review and editing; N. P. F., investigation, formal analysis, writing—review and editing; D. D., investigation; M. C., investigation; C. J. R., investigation, writing—review and editing.

Conflicts of interest

There are no conflicts to declare.

References

1. K. Wang, P. Yan and M. Sui, Nano Energy, 2018, 54, 148–155.
2. J. Yang and Y. Xia, ACS Appl. Mater. Interfaces, 2016, 8, 1297–1308.
3. E. V. Boldyreva, V. Dmitriev and B. C. Hancock, Int. J. Pharm., 2006, 327, 51–57.
4. T. D. Bennett and A. K. Cheetham, Acc. Chem. Res., 2014, 47, 1555–1562.
5. K. W. Chapman, G. J. Halder and P. J. Chupas, J. Am. Chem. Soc., 2009, 131, 17546–17547.
6. S. C. McKellar and S. A. Moggach, Acta Crystallogr., Sect. B: Struct. Sci., 2015, B71, 587–607.
7. M. J. Cliffe, J. A. Hill, C. A. Murray, F.-X. Coudert and A. L. Goodwin, Phys. Chem. Chem. Phys., 2015, 17, 11586–11592.
8. S. Dissegna, P. Vervoorts, C. L. Hobday, T. Düren, D. Daisenberger, A. J. Smith, R. A. Fischer and G. Kieslich, J. Am. Chem. Soc., 2018, 140, 11581–11584.
9. A. B. Cairns, A. L. Thompson, M. G. Tucker, J. Haines and A. L. Goodwin, J. Am. Chem. Soc., 2012, 134, 4454–4456.
10. H. J. Buser, D. Schwarzenbach, W. Petter and A. Ludi, Inorg. Chem., 1977, 16, 2704–2710.
11. A. Ludi, H.-U. Güdel and M. Rüegg, Inorg. Chem., 1970, 9, 2224–2227.
12. G. Du and H. Pang, Energy Storage Mater., 2021, 36, 387–408.
13. M. Verdaguer, A. Bleuzen, V. Marvaud, J. Vaissermann, M. Seuleiman, C. Desplanches, A. Scuiller, C. Train, R. Garde, G. Gelly, C. Lomenech, I. Rosenman, P. Veillet, C. Cartier and F. Villain, Coord. Chem. Rev., 1999, 190–192, 1023–1047.
14. D. Aguilà, Y. Prado, E. S. Koumousi, C. Mathonière and R. Clérac, Chem. Soc. Rev., 2016, 45, 203–224.
15. S. Ayrault, B. Jimenez, E. Garnier, M. Fedoroff, D. J. Jones and C. Loos-Neskovic, J. Solid State Chem., 1998, 141, 475–485.
16. E. Ohara, T. Soejima and S. Ito, Inorg. Chim. Acta, 2021, 514, 120029.
17. J. Hu, H. Tao, M. Chen, Z. Zhang, S. Cao, Y. Shen, K. Jiang and M. Zhou, ACS Appl. Mater. Interfaces, 2022, 14, 12234–12242.
18. D. Wardecki, D. O. Ojwang, J. Grins and G. Svensson, Cryst. Growth Des., 2017, 17, 1285–1292.
19. V. K. Sharma, S. Mitra, A. Kumar, S. M. Yusuf, F. Juranyi and R. Mukhopadhyay, J. Phys.: Condens. Matter, 2011, 23, 446002.
20. S. H. Lapidus, G. J. Halder, P. J. Chupas and K. W. Chapman, J. Am. Chem. Soc., 2013, 135, 7621–7628.
21. H. L. B. Boström, A. B. Cairns, L. Liu, P. Lazor and I. E. Collings, Dalton Trans., 2020, 49, 12940–12944.
22. C. S. Coates, C. A. Murray, H. L. B. Boström, E. M. Reynolds and A. L. Goodwin, Mater. Horiz., 2021, 8, 1446–1453.
23. M. Gerstel, C. M. Deane and E. F. Garman, J. Synchrotron Radiat., 2015, 22, 201–212.
24. J. Christensen, P. N. Horton, C. S. Bury, J. L. Dickerson, H. Taberman, E. F. Garman and S. J. Coles, IUCrJ, 2019, 6, 703–713.
25. N. K. Fernando, A. B. Cairns, C. A. Murray, A. L. Thompson, J. L. Dickerson, E. F. Garman, N. Ahmed, L. E. Ratcliff and A. Regoutz, J. Phys. Chem. A, 2021, 125, 7473–7488.
26. H. L. B. Boström, I. E. Collings, D. Daisenberger, C. J. Ridley, N. P. Funnell and A. B. Cairns, J. Am. Chem. Soc., 2021, 143, 3544–3554.
27. C. J. Howard, B. J. Kennedy and P. M. Woodward, Acta Crystallogr., Sect. B: Struct. Sci., 2003, 59, 463–471.
28. A. M. Glazer, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1972, 28, 3384–3392.
29. H. L. B. Boström and W. R. Brant, J. Mater. Chem. C, 2022, 10, 13690–13699.
30. J. Young and J. M. Rondinelli, J. Phys. Chem. Lett., 2016, 7, 918–922.
31. S. Vasala and M. Karppinen, Prog. Solid State Chem., 2015, 43, 1–36.
32. T. Matsuda, H. Tokoro, K. Hashimoto and S.-I. Ohkoshi, Dalton Trans., 2006, 5046–5050.
33. T. Matsuda, J. E. Kim, K. Ohoyama and Y. Moritomo, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 172302.
34. J. S. O. Evans, J. Chem. Soc., Dalton Trans., 1999, 3317–3326.
35. C. S. Coates and A. L. Goodwin, Mater. Horiz., 2019, 6, 211–218.
36. S. Kjeldgaard, I. Dugulan, A. Mamakhel, M. Wagemaker, B. Brummerstedt Iversen and A. Bentien, R. Soc. Open Sci., 2021, 8, 201779.
37. S. Adak, L. L. Daemen, M. Hartl, D. Williams, J. Summerhill and H. Nakotte, J. Solid State Chem., 2011, 184, 2854–2861.
38. K. W. Chapman, K. A. Beyer, H. Zhao and P. J. Chupas, CrystEngComm, 2013, 15, 9377–9381.
39. Q. Gao, N. Shi, A. Sanson, Y. Sun, R. Milazzo, L. Olivi, H. Zhu, S. H. Lapidus, L. Zheng, J. Chen and X. Xing, Inorg. Chem., 2018, 57, 14027–14030.
40. Q. Gao, X. Shi, A. Venier, A. Carnera, Q. Huang, H. Wu, J. Chen, A. Sanson and E. Liang, Inorg. Chem., 2020, 59, 14852–14855.
41. K. W. Chapman, P. J. Chupas and C. J. Kepert, J. Am. Chem. Soc., 2006, 128, 7009–7014.
42. S. Margadonna, K. Prassides and A. N. Fitch, J. Am. Chem. Soc., 2004, 126, 15390–15391.
43. N. Shi, Q. Gao, A. Sanson, Q. Li, L. Fan, Y. Ren, L. Olivi, J. Chen and X. Xing, Dalton Trans., 2019, 48, 3658–3663.
44. D. Asakura, M. Okubo, Y. Mizuno, T. Kudo, H. Zhou, K. Ikedo, T. Mizokawa, A. Okazawa and N. Kojima, J. Phys. Chem. C, 2012, 116, 8364–8369.

---

Footnote

† Electronic supplementary information (ESI) available: Experimental methods; diffraction patterns and lattice parameters under variable pressure, temperature, and radiation; crystallographic data. See DOI: https://doi.org/10.1039/d2cp03754h

---