Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Role of fast dynamics in the complexation of G-quadruplexes with small molecules†
Luca
Bertini
a,
Valeria
Libera
ab,
Francesca
Ripanti
 a,
Tilo
Seydel
a,
Tilo
Seydel
 c,
Marco
Paolantoni
c,
Marco
Paolantoni
 d,
Andrea
Orecchini
a,
Caterina
Petrillo
a,
Lucia
Comez
d,
Andrea
Orecchini
a,
Caterina
Petrillo
a,
Lucia
Comez
 *b and
Alessandro
Paciaroni
*b and
Alessandro
Paciaroni
 *a
*a
aDepartment of Physics and Geology, University of Perugia, Via Alessandro Pascoli, 06123 Perugia, Italy. E-mail: alessandro.paciaroni@unipg.it
bIstituto Officina dei Materiali-IOM, National Research Council-CNR, Via Alessandro Pascoli, 06123 Perugia, Italy. E-mail: comez@iom.cnr.it
cInstitut Max von Laue – Paul Langevin (ILL) 71 avenue des Martyrs, 38042 Grenoble, France
dDepartment of Chemistry, Biology and Biotechnology, University of Perugia, Via Elce di Sotto, 6, 06123 Perugia, Italy
First published on 29th November 2022
Abstract
G-quadruplexes (G4s) formed by the human telomeric sequence AG3 (TTAG3)3 (Tel22) play a key role in cancer and aging. We combined elastic incoherent neutron scattering (EINS) and quasielastic incoherent neutron scattering (QENS) to characterize the internal dynamics of Tel22 G4s and to assess how it is affected by complexation with two standard ligands, Berberine and BRACO19. We show that the interaction with the two ligands induces an increase of the overall mobility of Tel22 as quantified by the mean squared displacements (MSD) of hydrogen atoms. At the same time, the complexes display a lower stiffness than G4 alone. Two different types of motion characterize the G4 nanosecond timescale dynamics. Upon complexation, an increasing fraction of G4 atomic groups participate in this fast dynamics, along with an increase in the relevant characteristic length scales. We suggest that the entropic contribution to the conformational free energy of these motions might be crucial for the complexation mechanisms.
1 Introduction
G4s are higher-order four-stranded DNA and RNA structures, resulting from the folding of guanine-rich sequences. These structures consist of the stacking of planar arrangements of four guanine bases linked via Hoogsteen hydrogen bonds, called G-tetrads, on top of each other.1–4 The sequence bases that are not involved in the tetrad formation are folded into loops. The presence of positive ions between the tetrads is essential to achieve stabilization.A prominent feature of G4s is their structural polymorphism, giving rise to a variety of topologies that can be assumed depending on several factors, like the diverse possible combinations of guanine run directions, variations in loop size and sequence, and the dependence on the type of ion that stabilizes the G4 structure.5,6 In addition, also the arrangement of the water network surrounding G4s may have a significant impact on their conformational properties.7 Because of their polymorphism, G4s display an elusive and transient character, which is also the main reason why they were discovered in vivo only very recently.8 A schematic representation of different architectures for intramolecular G4s is shown in Fig. 1.
The human telomere, the terminal part of chromosomes, is a key paradigmatic case where G4s play an important role for cancer and aging, thus making these structures promising targets for therapeutic purposes.9,10 In non-germ cells, the telomeric DNA consists of the repeated d(TTAGGG)n motif and ranges from 5 to 25 kb in length with a single-stranded overhang of a few hundred bases.11–13 The G4 structures formed in this single-stranded overhang have been proposed to inhibit the reverse-transcriptase enzyme telomerase,14 which is up-regulated in over 85% of cancer cells.15 Furthermore, small molecules interacting with G4s have been recognized to display anticancer activity by stabilizing G4 forming sequences found in many oncogene-related promoter regions.16,17
On these grounds, the development of small ligands that can stabilize G4 structures is a promising strategy to find new anticancer drugs and, to this aim, a thorough understanding of the G4–ligand interactions is required to properly modulate the G4 conformational and stability properties. Within this context, a considerable body of research has been carried out to investigate the structural properties of different G4-forming DNA sequences18–21 and how they are affected by small ligands.1,22–25 However, little is known about the dynamical features of G4s, an aspect that should play a relevant role given their transient nature. In the case of proteins and duplex DNA, the sub-nano- and nanosecond dynamics has been already linked to both structural and functional aspects.26 In particular, it has been shown that these fast motions are needed as precursors to trigger slower conformational changes occurring in the microsecond timescale and are also fundamental in the early stage of ligand recognition.27,28 Analogously, we expected a similar picture also in the case of G4s. We thus investigated the sub-nanosecond dynamics of a prototypical G4-forming sequence, the human telomeric repeat AG3 (TTAG3)3 (Tel22), by incoherent neutron scattering (INS), supported by Fourier-transform infrared spectroscopy (FTIR) to monitor G4 formation. The Tel22 structural fluctuations were also studied in the presence of two small molecules that are known to interact with G4s, to better understand the relationship between fast dynamics and ligand binding. To this purpose, we selected two standard G4 ligands: Berberine, a natural quaternary ammonium salt, from the group of benzylisoquinoline alkaloids, which has been shown to stabilize G4 structures,29 and BRACO19, a trisubstituted acridine G4-interacting compound that appears to inhibit telomerase activity.30 The systems were investigated in the powder state in the presence of deuterated solvent, so as to single out the internal dynamics of the biomolecule, with the possible smaller contribution from the ligand.
In order to fulfill their therapeutic task, ligands have to establish stable molecular bonds with the G4, so we would expect the overall mobility of Tel22 to decrease upon complexation. However, our INS results show that in the investigated timescale mobility increases upon complexation with both the selected ligands and that thermal stiffness decreases. We propose that this change in the fast dynamics contributes to the complexation free energy through an increase in the conformational entropy.
2 Materials and methods
2.1 Sample preparation
Lyophilized DNA oligonucleotide Tel22 sequence was purchased from Eurogentec (Seraing, Belgium). The lyophilized powder was dissolved in a 50 mM phosphate buffer at pH 7, 0.3 mM EDTA, and 150 mM KCl. The sample was lyophilized again, subsequently dissolved in D2O at a concentration of about 50 mg ml−1, and left at room temperature for 1 day to substitute all the exchangeable hydrogen atoms with deuterium ones. This diluted solution was then freeze-dried and further dehydrated under vacuum in the presence of P2O5 to obtain the lowest possible hydration level. The dried powder was subsequently hydrated with D2 O, until a hydration level 0.5 g D2O g−1 dried Tel22 was achieved. In analogy with double stranded DNA, where at least a hydration of 0.6 g D2O g−1 dried DNA corresponds to water molecules strongly coordinated by phosphate groups, we expect that at the present water content there is no free solvent. In the elastic intensities of the measured samples no Bragg peaks were observed at low temperature.Berberine and BRACO19 ligands were purchased from Merck KGaA (Missouri, USA); the oligonucleotide sample in phosphate buffer was complexed with the ligands in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 [DNA]
2 [DNA]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [ligand] stoichiometric molar ratio. Samples were left for two hours at room temperature in order to reach complexation. Finally, the same aforementioned procedure was followed to obtain hydrated powder samples with a water content of 0.5 g D2O g−1 dried Tel22. To perform FTIR measurements, samples were completely dehydrated.
[ligand] stoichiometric molar ratio. Samples were left for two hours at room temperature in order to reach complexation. Finally, the same aforementioned procedure was followed to obtain hydrated powder samples with a water content of 0.5 g D2O g−1 dried Tel22. To perform FTIR measurements, samples were completely dehydrated.
2.2 Incoherent neutron scattering experiment
In INS experiments, the fast biomolecular motions are studied by measuring the dynamic structure factor S(Q,E), which is proportional to the probability of an incident neutron being scattered with an energy transfer E and a momentum transfer ħQ.31,32 The total scattering cross-section is dominated by the incoherent contribution of hydrogen atoms (σinc = 79.90 b compared to σcoh = 1.76 b), which is by far larger than that of any other element and in particular of deuterium.31,32 As a consequence, in D2O hydrated samples, the detected signal is mainly due to non-exchangeable hydrogen atoms of the biomolecule. Since these atoms are abundant and almost uniformly distributed throughout biomolecules, their dynamics is representative of the motions arising from larger groups of atoms to which they are bound. In the case of complexes, we calculated the maximum incoherent contribution from BRACO19 and Berberine to the total signal to be 22% and 11% respectively, also accounting for the exchanged hydrogen atoms. By including also the coherent contribution to the signal, we found the total contribution to be equal to 19% and 10%, respectively. Then, we are confident that the signal of the ligand can be reasonably neglected compared to that of Tel22.In the present investigation, INS experiments were performed on the cold neutron back-scattering spectrometer IN16b at the Institut Laue-Langevin (ILL),33,34 with an energy resolution of ≈ 0.75 μeV FWHM (as estimated from the fit of the Vanadium standard in the range −1 μeV to 1 μeV), an energy-range of |E| ≤ 31 μeV, and a wavevector coverage of 0.19 Å−1 ≤ Q ≤ 1.9 Å−1. Si(1,1,1) crystals were used as monochromator and analyzers. Quasielastic scans were carried out on the uncomplexed Tel22 sample (T = 200 K, 219 K, 238 K, 257 K, 277 K, 294 K) and in the presence of either Berberine (T = 201 K, 240 K, 280 K) and BRACO19 (T = 200 K, 219 K, 239 K, 258 K, 280 K, 296 K) ligands. Elastic scans were performed for the uncomplexed Tel22 sample from 205 K to 295 K, and from 205 K to 280 K in the case of Tel22 with both complexes. Each sample, consisting of 100 mg of hydrogenated sample, was filled in sealed Al cans and kept in a cryofurnace during the acquisition. The initial reduction of the data was carried out using the Mantid Software.35
The samples were measured in the hydrated powder state. While the formation of G4 structures for human telomeric sequences in solution has been demonstrated,36 no evidence has been reported so far for their formation in the hydrated powder state, to the best of our knowledge. Hence, we performed ATR-FTIR measurements and confirmed the presence of G4 structures in our samples. Results of ATR-FTIR measurements are reported and discussed in the ESI.†
2.3 Theoretical models: EINS
EINS spectra carry important information on the dynamics of the investigated system, which is enclosed in the elastic scattering function S(![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) ,ω = 0). For a system consisting of N hydrogen atoms, each one following its own dynamics, this quantity can be related to the individual mean squared displacements 〈u2〉i using the Gaussian approximation:
,ω = 0). For a system consisting of N hydrogen atoms, each one following its own dynamics, this quantity can be related to the individual mean squared displacements 〈u2〉i using the Gaussian approximation: | (1) |
 | (2) |
 | (3) |
In this framework, the actual equation used to fit the elastic scattering data is:
 | (4) |
Within the framework of the conformational energy landscape, the thermal stiffness of the system can be assessed in a more quantitative way from the mean squared fluctuations (MSF) 〈r2〉 from the equilibrium position, which are half of the MSD.37 Scattering hydrogen atoms can be thought of as random walkers jumping among the available conformational substates in a confined potential. At lower temperatures the random walkers can explore a limited region of the energy landscape, contributing to the total MSF mainly with harmonic motions within the conformational substates; an onset of anharmonic motions at higher temperatures is observed as more conformational substates become available to the random walkers. If the confining potential is harmonic, we can write:26
 | (5) |
In the spirit of the hypothesis where the unfolding of biomolecules occurs just in correspondence to the melting of their solid-like core, we exploited the so-called Lindemann criterion42,43 to provide a tentative estimate of the conformational stiffness of the measured systems. This criterion, when applied to proteins, states that unfolding occurs in correspondence with the root of the MSF exceeding a universal fraction of the average characteristic distance L between non-bonded near-neighbor residues:42
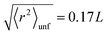 | (6) |
 | (7) |
Once 〈r2〉unf has been calculated, we estimated the force needed to mechanically unfold the G4 structures through the equation:
 | (8) |
2.4 Theoretical models: QENS
In analyzing QENS spectra, we were interested in quantifying the quasielastic broadening of the elastic peak, which contains the physical information on the diffusive motions and on the internal dynamics of atomic groups within the biomolecule. In our spectra we were able to distinguish a wide and a narrow broadening representative of a fast and a slow dynamics, respectively. Consequently, we developed a simple theoretical model to describe these two different dynamics inspired by the two-site jump model already used by Bee32 for both dynamical regimes. Within this model, the dynamic structure factor can be written as:| S(Q,ω) =A0(Q)δ(ω) + A1(Q)L(ω,Γ) | (9) |
 | (10) |
 | (11) |
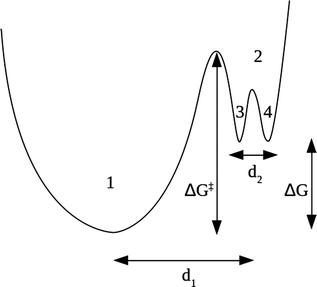
Our model combines the two regimes by means of an energy surface consisting of two non equivalent wells (1 and 2), the second one having its own substructure of two equivalent wells (3 and 4), as schematically shown in Fig. 2.
The slow dynamics corresponds to jumps among the two non equivalent wells 1 and 2, while the fast dynamics only involves the scatterers in well 2 jumping among the subwells 3 and 4. We remark that the complex dynamical features of biomolecules, mainly proteins, are often interpreted by introducing a multidimensional energy landscape, consisting of a large number of local minima.28,45 Here, the energy barriers between the minima define the characteristic timescales of the different dynamical processes, while at equilibrium conditions the relative populations of the minima are governed by basic thermodynamics. The model we propose in this work is a simplified unidimensional version of the aforementioned energy landscape, where we account for the timescales of just two dynamical processes.
Assuming that a fraction f of the scatterers participates to the fast dynamics (and hence a fraction 1 − f participates to the slow one), we can write the theoretical structure factor as:
| Sth(Q,ω) = (1 − f)S1(Q,ω) + fS2(Q,ω) | (12) |
Considering the experimental resolution described by the Gaussian response g(ω) derived from Vanadium standard spectra, the structure factor can be written as:
| S(Q,ω) = A(Q)g(ω) + B(Q)V1(ω,Γ1) + C(Q)V2(ω,Γ2) | (13) |
| A(Q) = (1 − f)A01(Q) + fA02(Q) | (14) |
| B(Q) = (1 − f)A11(Q) | (15) |
| C(Q) = fA12(Q) | (16) |
3 Results and discussion
3.1 EINS measurements
The MSF calculated through a Gaussian fit of the elastic intensity of Tel22, Tel22–Berberine, and Tel22–BRACO19 compounds are reported in Fig. 3 as a function of temperature along with the best fits using eqn (5). | ||
| Fig. 3 MSF as a function of temperature for Tel22 alone (black), Tel22–Berberine (blue), and Tel22–BRACO19 (red) complexes, along with the best fits to data (solid lines). | ||
Quite interestingly, the MSF of Tel22 show a dynamical transition at about 235 K, i.e. an increase of mobility above the low-temperature trend. This phenomenon has been already observed in hydrated proteins, where it has been related to the onset of anharmonic motions and to the activation of biological functionality.46 This dynamical transition seems to be shifted by about 10 K toward lower temperatures when Tel22 G4 is complexed with ligands. In Fig. S7 of ESI† we show the integrated elastic intensity as a function of temperature, which provides a model-independent evidence of the different dynamics of Tel22 in the complexed and uncomplexed states. As the coupling of fast biomolecular motions with solvent is well established,26 we speculate that the enhanced mobility of Tel22 is due to a different arrangement of the primary hydration shell in the presence of ligands. This finding may at first look counterintuitive, as both Berberine and BRACO19 are known to induce a stabilizing effect on G4.47,48 Besides, in some cases, the dynamics of biomolecules is known to be partially suppressed upon ligand binding, as it happens for aged Soman–hAChe complex.49 On the other hand, ligands may alter the arrangement of the water molecules around the biomolecular surface and increase their mobility, which in turn leads to a higher flexibility of biomolecules.49–51
We stress that, since in our experiments the solvent component was deuterated, the measured MSF refer only to the biomolecule or biomolecule-ligand hydrogen atoms. Therefore, these measurements only show how hydration water dynamics is reflected on the biomolecule dynamics, and not the water dynamics itself. The larger MSF values for complexes suggest that their conformational entropy is higher than that of Tel22 alone, thus supporting the picture where hydration water plays a crucial role in binding processes by means of the so-called enthalpy-entropy compensation phenomenon.52
As discussed above, from eqn (5) we obtained the force constants for each sample, as reported in Table 1. Tel22–Berberine and Tel22–BRACO19 complexes have force constants of kf = 0.26 N m−1 and kf = 0.29 N m−1, respectively, which are lower than that of Tel22 alone (kf = 0.37 N m−1), showing that complexation causes a slight decrease in stiffness. From these values, we estimated the resulting unfolding forces Fu by applying the Lindemann criterion (eqn (7) and (8)), as shown in Table 1. Quite interestingly, they are of the same order of magnitude of the unfolding forces determined from single-molecule pulling experiments,53,54 thus suggesting that the biomolecule hypersurface potential energy determines both the equilibrium G4 fast dynamics and the out-of-equilibrium mechanical unfolding experiments.
| Tel22 | Tel22–Berberine | Tel22–BRACO19 | |
|---|---|---|---|
| k f (N m−1) | 0.37 ± 0.02 | 0.26 ± 0.03 | 0.29 ± 0.02 |
| F u (pN) | 41 ± 3 | 29 ± 2 | 32 ± 2 |
| Tel22 | Tel22–Berberine | Tel22–BRACO19 | |
|---|---|---|---|
| d 1 (Å) | 5.2 ± 0.2 | 6.5 ± 0.3 | 6.3 ± 0.2 |
| d 2 (Å) | 2.1 ± 0.3 | 1.6 ± 0.4 | 2.4 ± 0.2 |
3.2 QENS measurements
QENS data were analyzed using the model shown in Fig. 2. All the fits were performed in the whole available energy range, i.e. from −30 μeV to 30 μeV. In Fig. S2 of the ESI† a representative example of this fit is shown along with a more detailed discussion of the whole fitting procedure. In Fig. 4 we report the measured QENS spectra (from −10 μeV to 10 μeV) of Tel22 alone, Tel22–Berberine, and Tel22–BRACO19 compounds acquired at T = 200 K, T = 240 K, and T = 280 K.In fitting the QENS spectra we were able to distinguish between a slow and a fast dynamical regime. This decomposition of the QENS signal into two terms is consistent with the findings from other biomolecules, such as proteins. Indeed, the fast protein dynamics has been already described in the past by means of two α-like and β-like relaxation processes.26
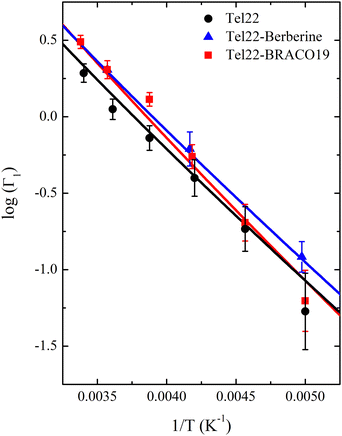
The comparison of the spectra of the three samples at a fixed temperature (T = 280 K) is reported in Fig. 5 along with the best fit using eqn (13): the narrow quasielastic broadening Γ1 clearly increases upon complexation, thus confirming the behavior observed from EINS data on the increasing mobility of Tel22–ligand complexes. On the other hand, we found a wide Lorentzian broadening Γ2 = 20 μeV common to all the three samples, which results to be independent on Q and T. Therefore, we fitted the spectra using eqn (13) with A, B, C, and Γ1 as independent parameters, while keeping Γ2 fixed to the value of 20 μeV. In the 0.70–1.75 Å−1Q range the slow dynamics broadening turns out to be constant, while for lower and higher values the quasielastic intensity was too small to provide reliable Γ1 values. An example of Q dependence of Γ1 at a fixed temperature is reported in Fig. S3 of the ESI.† The constant trend is consistent with confined random jump-like motions. The trend of the calculated Γ1 values as a function of temperature is shown in Fig. 6.
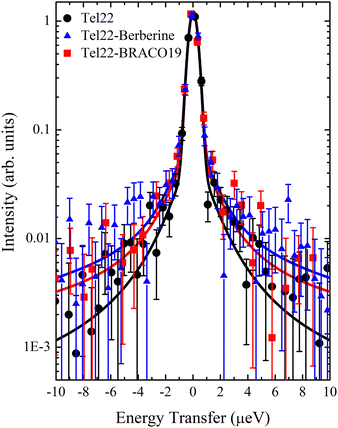 | ||
| Fig. 5 QENS spectra at T = 280 K from −10 μeV to 10 μeV for Tel22 alone (black), Tel22–Berberine (blue), and Tel22–BRACO19 (red) complexes, along with the best fits to data (solid lines). | ||
This thermal behavior can be exploited to calculate the free energy barrier ΔG‡ = ΔH‡ − TΔS‡ between the ground and the excited states, represented in Fig. 2, by using the Eyring equation:45
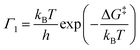 | (17) |
| Tel22 | Tel22–Berberine | Tel22–BRACO19 | |
|---|---|---|---|
| ΔH‡ (kJ mol−1) | 5.3 ± 0.4 | 5.3 ± 0.1 | 5.9 ± 0.6 |
| ΔS‡ (J mol−1 K−1) | −224 ± 1 | −223.0 ± 0.3 | −221 ± 2 |
| ΔH (kJ mol−1) | 16 ± 1 | 18.9 ± 0.7 | 17.7 ± 0.7 |
| ΔS (J mol−1 K−1) | 48 ± 6 | 64 ± 3 | 58 ± 3 |
Actually, by fitting the QENS spectra through the model described by eqn (13)–(16) (see Section 2 of ESI† for details), we easily obtained the populations  and p2′ corresponding to the ground and excited states of wells 1 and 2, i.e. we could quantify the fraction of moving G4 atomic groups, and the characteristic distances d1 and d2 corresponding to the two-regime dynamics. The
and p2′ corresponding to the ground and excited states of wells 1 and 2, i.e. we could quantify the fraction of moving G4 atomic groups, and the characteristic distances d1 and d2 corresponding to the two-regime dynamics. The  ratio can be expressed as a function of the free energy difference ΔG between the wells 1 and 2:38
ratio can be expressed as a function of the free energy difference ΔG between the wells 1 and 2:38
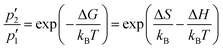 | (18) |
As for the distances between the wells, which are reported in Table 2, d2 does not significantly change upon complexation, which is in line with the behavior of the corresponding Lorentzian broadening Γ2, further confirming the small effect of the ligand on the fast dynamical regime. On the contrary, the distance d1 increases upon complexation, possibly contributing to the higher mobility mentioned before. Finally, both enthalpy and entropy differences between the two wells are higher in the presence of the ligands. However, due to their larger entropic term, the complexes are characterized by a lower free energy difference, which explains their increased mobility.
We remark that, thanks to the analysis of the QENS spectra, we may attribute the increase of complex mobility to two main factors: a larger spatial extent explored during the fast motions of the G4 atomic groups and an increased number of such moving groups. Both these factors contribute to the increase of the conformational entropy of the complexes. We may speculate that, due to the importance of the stacking bewteen Berberine/BRACO19 and Tel22 extremal tetrad for complexation,47,55 hydrophobic interactions may play an indirect role for the change in the hydration water network structure and the increase of the entropic component of the binding free energy.
4 Conclusions
In the present work we investigated the dynamical properties of the Tel22 G4 structure and the effect of complexation of the two standard ligands, Berberine and BRACO19, by combining QENS and EINS experiments. EINS measurements showed that the average MSD of the biomolecule hydrogen atoms, and hence the overall Tel22 mobility, increases upon complexation. At the same time a decrease in stiffness is observed. QENS data allowed us to understand the microscopic determinants at the origin of these dynamical changes. Particularly, we showed that a slow and a fast dynamical regimes contribute to the nanosecond dynamics. The former mainly contributes to the enhancement of the complex mobility, through the increase of both the fraction of moving Tel22 atomic groups and the spatial extent they can explore. We ascribed such an enhancement of fast dynamics to a larger conformational entropy of the complexes, which may play a significant role in the Tel22–ligand interaction. On the mechanistic point of view, we suggest that the binding of Tel22 to the ligands drives a substantial rearrangement of the hydration water network surrounding the biomolecule. This rearrangement, in turn, would lead to the aforementioned dynamical changes in G4–ligand complexes.Author contributions
Luca Bertini: investigation, data curation, writing – original draft; Valeria Libera: investigation, writing – review & editing; Francesca Ripanti: writing – review & editing; Tilo Seydel: investigation, writing – review & editing; Marco Paolantoni: investigation, visualization, writing – review & editing; Andrea Orecchini: writing – review & editing; Caterina Petrillo: writing – review & editing; Lucia Comez: investigation, visualization, writing – review & editing; Alessandro Paciaroni: investigation, supervision, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This publication was supported by the CarESS project, D.R.no. 597, from the University of Perugia. The authors really acknowledge the Institut Laue-Langevin (ILL) for providing beamtime allocation (https://doi.ill.fr/10.5291/ILL-DATA.8-04-880).References
- S. Neidle, Nat. Rev. Chem., 2017, 1, 1–10 CrossRef
.
- G. W. Collie and G. N. Parkinson, Chem. Soc. Rev., 2011, 40, 5867–5892 RSC
.
- S. Burge, G. N. Parkinson, P. Hazel, A. K. Todd and S. Neidle, Nucleic Acids Res., 2006, 34, 5402–5415 CrossRef CAS PubMed
.
- A. T. Phan, FEBS J., 2010, 277, 1107–1117 CrossRef CAS PubMed
.
- J. Kypr, I. Kejnovská, D. Renčiuk and M. Vorlisčková, Nucleic Acids Res., 2009, 37, 1713–1725 CrossRef CAS PubMed
.
- R. D. Gray, J. Li and J. B. Chaires, J. Phys. Chem. B, 2009, 113, 2676–2683 CrossRef CAS PubMed
.
- V. Libera, F. Bianchi, B. Rossi, F. D’Amico, C. Masciovecchio, C. Petrillo, F. Sacchetti, A. Paciaroni and L. Comez, Int. J. Mol. Sci., 2022, 23, 5123 CrossRef CAS PubMed
.
- G. Biffi, D. Tannahill, J. McCafferty and S. Balasubramanian, Nat. Chem., 2013, 5, 182–186 CrossRef CAS PubMed
.
- C. Sagne, V. Marcel, M. Bota, G. Martel-Planche, A. Nobrega, E. I. Palmero, L. Perriaud, M. Boniol, S. Vagner and D. G. Cox,
et al.
, Carcinogenesis, 2014, 35, 807–815 CrossRef CAS PubMed
.
- F.-Y. Teng, Z.-Z. Jiang, M. Guo, X.-Z. Tan, F. Chen, X.-G. Xi and Y. Xu, Cell. Mol. Life Sci., 2021, 78, 6557–6583 CrossRef CAS PubMed
.
- Q. Wang, J.-q Liu, Z. Chen, K.-w Zheng, C.-y Chen, Y.-h Hao and Z. Tan, Nucleic Acids Res., 2011, 39, 6229–6237 CrossRef CAS PubMed
.
- C. Testorelli, J. Exp. Clin. Cancer Res., 2003, 22, 165–169 CAS
.
- D. Hanahan and R. A. Weinberg, Cell, 2011, 144, 646–674 CrossRef CAS PubMed
.
- M. L. Bochman, K. Paeschke and V. A. Zakian, Nat. Rev. Genet., 2012, 13, 770–780 CrossRef CAS PubMed
.
- N. W. Kim, M. A. Piatyszek, K. R. Prowse, C. B. Harley, M. D. West, P. L. Ho, G. M. Coviello, W. E. Wright, S. L. Weinrich and J. W. Shay, Science, 1994, 266, 2011–2015 CrossRef CAS PubMed
.
- T. Lemarteleur, D. Gomez, R. Paterski, E. Mandine, P. Mailliet and J.-F. Riou, Biochem. Biophys. Res. Commun., 2004, 323, 802–808 CrossRef CAS PubMed
.
- A. Ambrus, D. Chen, J. Dai, R. A. Jones and D. Yang, Biochemistry, 2005, 44, 2048–2058 CrossRef CAS PubMed
.
- J. R. Williamson, M. Raghuraman and T. R. Cech, Cell, 1989, 59, 871–880 CrossRef CAS PubMed
.
- G. Biffi, D. Tannahill, J. McCafferty and S. Balasubramanian, Nat. Chem., 2013, 5(3), 182–186 CrossRef CAS PubMed
.
- S. A. Dvorkin, A. I. Karsisiotis and M. Webba da Silva, Sci. Adv., 2018, 4, eaat3007 CrossRef CAS PubMed
.
- R. C. Monsen, J. M. Maguire, L. W. DeLeeuw, J. B. Chaires and J. O. Trent, PLoS One, 2022, 17, e0270165 CrossRef CAS PubMed
.
- F. Bianchi, L. Comez, R. Biehl, F. D’Amico, A. Gessini, M. Longo, C. Masciovecchio, C. Petrillo, A. Radulescu and B. Rossi,
et al.
, Nucleic Acids Res., 2018, 46, 11927–11938 CrossRef CAS PubMed
.
- S. Di Fonzo, J. Amato, F. D’Aria, M. Caterino, F. D’Amico, A. Gessini, J. W. Brady, A. Cesàro, B. Pagano and C. Giancola, Phys. Chem. Chem. Phys., 2020, 22, 8128–8140 RSC
.
- L. Comez, F. Bianchi, V. Libera, M. Longo, C. Petrillo, F. Sacchetti, F. Sebastiani, F. D’Amico, B. Rossi and A. Gessini,
et al.
, Phys. Chem. Chem. Phys., 2020, 22, 11583–11592 RSC
.
- V. Libera, E. A. Andreeva, A. Martel, A. Thureau, M. Longo, C. Petrillo, A. Paciaroni, G. Schirò and L. Comez, J. Phys. Chem. Lett., 2021, 12, 8096–8102 CrossRef CAS PubMed
.
- P. W. Fenimore, H. Frauenfelder, B. McMahon and R. Young, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 14408–14413 CrossRef CAS PubMed
.
- J. R. Lewandowski, M. E. Halse, M. Blackledge and L. Emsley, Science, 2015, 348, 578–581 CrossRef CAS PubMed
.
- K. Henzler-Wildman and D. Kern, Nature, 2008, 450, 964–972 CrossRef PubMed
.
- X. Ji, H. Sun, H. Zhou, J. Xiang, Y. Tang and C. Zhao, Nucleic Acid Ther., 2012, 22, 127–136 CrossRef CAS PubMed
.
- D. Sun, B. Thompson, B. E. Cathers, M. Salazar, S. M. Kerwin, J. O. Trent, T. C. Jenkins, S. Neidle and L. H. Hurley, J. Med. Chem., 1997, 40, 2113–2116 CrossRef CAS PubMed
.
-
S. W. Lovesey, Theory of neutron scattering from condensed matter, Clarendon, Oxford, 1984 Search PubMed
.
-
M. Bée, Quasielastic neutron scattering, Adam & Hilger, 1988 Search PubMed
.
- B. Frick, J. Neutron Res., 2002, 13, 15–22 CrossRef
.
- B. Frick, E. Mamontov, L. Van Eijck and T. Seydel, Z. Phys. Chem., 2010, 224, 33–60 CrossRef CAS
.
- O. Arnold, J.-C. Bilheux, J. Borreguero, A. Buts, S. I. Campbell, L. Chapon, M. Doucet, N. Draper, R. F. Leal and M. Gigg,
et al.
, Nucl. Instrum. Methods Phys. Res., Sect. A, 2014, 764, 156–166 CrossRef CAS
.
- A. Ambrus, D. Chen, J. Dai, T. Bialis, R. A. Jones and D. Yang, Nucleic Acids Res., 2006, 34, 2723–2735 CrossRef CAS PubMed
.
- Z. Yi, Y. Miao, J. Baudry, N. Jain and J. C. Smith, J. Phys. Chem. B, 2012, 116, 5028–5036 CrossRef CAS PubMed
.
- F. Gabel, D. Bicout, U. Lehnert, M. Tehei, M. Weik and G. Zaccai, Q. Rev. Biophys., 2002, 35, 327–367 CrossRef CAS PubMed
.
- T. Becker and J. C. Smith, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 67, 021904 CrossRef PubMed
.
- T. Matsuo, A. De Francesco and J. Peters, Front. Mol. Biosci., 2022, 1283 Search PubMed
.
- D. Zeller, M. Telling, M. Zamponi, V. Garcia Sakai and J. Peters, J. Chem. Phys., 2018, 149, 234908 CrossRef CAS PubMed
.
- M. Katava, G. Stirnemann, M. Zanatta, S. Capaccioli, M. Pachetti, K. Ngai, F. Sterpone and A. Paciaroni, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 9361–9366 CrossRef CAS PubMed
.
- Y. Zhou, D. Vitkup and M. Karplus, J. Mol. Biol., 1999, 285, 1371–1375 CrossRef CAS PubMed
.
- A. E. Bergues-Pupo, I. Gutierrez, J. R. Arias-Gonzalez, F. Falo and A. Fiasconaro, Sci. Rep., 2017, 7, 1–13 CrossRef CAS PubMed
.
-
H. Frauenfelder, The physics of proteins: an introduction to biological physics and molecular biophysics, Springer Science & Business Media, 2010 Search PubMed
.
- W. Doster, S. Cusack and W. Petry, Nature, 1989, 337, 754–756 CrossRef CAS PubMed
.
- W.-J. Zhang, T.-M. Ou, Y.-J. Lu, Y.-Y. Huang, W.-B. Wu, Z.-S. Huang, J.-L. Zhou, K.-Y. Wong and L.-Q. Gu, Bioorg. Med. Chem., 2007, 15, 5493–5501 CrossRef CAS PubMed
.
- A. Awadasseid, X. Ma, Y. Wu and W. Zhang, Biomed. Pharmacother., 2021, 139, 111550 CrossRef CAS PubMed
.
- J. Peters, N. Martinez, M. Trovaslet, K. Scannapieco, M. M. Koza, P. Masson and F. Nachon, Phys. Chem. Chem. Phys., 2016, 18, 12992–13001 RSC
.
- C. Andersson, N. Martinez, D. Zeller, S. Rondahl, M. Koza, B. Frick, F. Ekström, J. Peters and A. Linusson, Phys. Chem. Chem. Phys., 2017, 19, 25369–25379 RSC
.
- A. L. B. de Carvalho, A. P. Mamede, A. Dopplapudi, V. G. Sakai, J. Doherty, M. Frogley, G. Cinque, P. Gardner, D. Gianolio and L. A. B. de Carvalho,
et al.
, Phys. Chem. Chem. Phys., 2019, 21, 4162–4175 RSC
.
- M. Maurer and C. Oostenbrink, J. Mol. Recognit., 2019, 32, e2810 CrossRef CAS PubMed
.
- Z. Yu, J. D. Schonhoft, S. Dhakal, R. Bajracharya, R. Hegde, S. Basu and H. Mao, J. Am. Chem. Soc., 2009, 131, 1876–1882 CrossRef CAS PubMed
.
- Y. Cheng, Y. Zhang and H. You, Biomolecules, 2021, 11, 1579 CrossRef CAS PubMed
.
- B. Machireddy, H.-J. Sullivan and C. Wu, Molecules, 2019, 24, 1010 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp03602a |
| This journal is © the Owner Societies 2022 |