From symmetry breaking in the bulk to phase transitions at the surface: a quantum-mechanical exploration of Li₆PS₅Cl argyrodite superionic conductor

Abstract

Lithium superionic conductor electrolytes may enable the safe use of metallic lithium anodes in all-solid-state batteries. The key to a successful application is a high Li conductivity in the electrolyte material, to be achieved through the maintenance of intimate contact with the electrodes and the knowledge of the chemical nature of that contact. In this manuscript, we tackle this issue by a theoretical ab initio approach. Focusing on the Li₆PS₅Cl, a thiophosphate with high ionic conductivity, we carry on thorough modeling of the surfaces together with the prediction of the thermal and elastic behaviour. Our investigation leads to some new findings: the bulk structure, as reported in the literature, appears to be metastable, with spontaneous symmetry breaking. Moreover, the relevant stoichiometric surfaces identified for stable and metastable crystal structures are not up-down symmetry related and they expose from one side Li₂S and LiCl. Surface reconstructions can be interpreted as local phase transitions. We also predict entirely ab initio the morphology of crystallites, charge, and electrostatic potential at surfaces, together with the effect of temperature on structural properties and the elastic behaviour of this material. Such findings may constitute the relevant groundwork for a better understanding of ionic transport in Li-ion conductors at the electrolyte/anode and electrolyte/cathode interfaces.

---

1 Introduction

Energy storage is a major global challenge today, and its importance grows with the increasing demand for energy-consuming devices and electric vehicles.^1,2 In this view, all solid-state batteries (ASSBs) – which adopt a solid electrolyte and lithium metal anode – are being watched with great expectations as they enable energy storage with higher energy densities and improved safety as compared to standard Li-ion cells based on liquid electrolytes.

The organic electrolytes used in modern lithium-ion batteries have shown certain technological issues such as their flammability, limited electrochemical stability, and the inability to block the Li-dendrite growth. Most frequent and recent incidents of Li-ion battery fires were caused by the ignition of the electrolyte.^3,4 Inorganic solid-state Li-ion conductors, on the other hand, benefit from many advantages such as superior electrochemical, mechanical, and thermal stability, absence of leakage, and the possibility of battery miniaturization.⁵ Indeed, solid-state batteries have been built that retain almost full storage capacity over thousands of cycles.^6,7 The main classes of solid-state electrolytes were recently reviewed by Ahniyaz et al.⁸ One open challenge, however, is the achievement of a Li⁺ conductivity comparable to the ones of liquid electrolytes (larger than 1 mS cm⁻¹).

Studies in the past decades have focused mainly on ionically conducting oxides such as LISICON,⁹ NASICON¹⁰ (e.g. Li_1.3Al_0.3Ti_1.7(PO₄)₃), perovskite¹¹ (e.g. La_0.5Li_0.5TiO₃), garnet¹² (e.g. Li₇La₃Zr₂O₁2) and LiPON¹³ (e.g. Li_2.88PO_3.73N_0.14). Significant progress has been made recently with the discovery of numerous sulfide-based compounds with higher ionic conductivities.^14–18 Argyrodites Li₆PS₅X with X = (Cl, Br, I) belong to this family of compounds,^19–21 they represent a class of crystalline Li-rich solids with an unusual high Li⁺ mobility.

In this work, we focus on the DFT investigation of the Li₆PS₅Cl Argyrodite compound. In the cubic structures, the polymorphs F4̄3m of Li₆PS₅X, Li⁺ ions are partially distributed over the tetrahedral interstices (48h and 24g Wyckoff sites).^22–25 However, a local monoclinic structure was found in the literature,²⁶ which indicates a possible distortion of the PS₄³⁻ tetrahedra. ⁶Li MAS NMR measurements have been also used to probe the local environment around the Li ions, showing large variations, i.e., a high degree of structural disorder. This might include different crystallinities, amorphous phase fractions, S/Cl anion disorder, and rotational PS₄³⁻ disorder²⁷ which all will be influenced by the details of the synthesis procedure (synthesis temperature, quenching rate, etc.). Synthesis methods for Li-argyrodite commonly involve, in the largest cases, the mechanical ball-milling and classical mechanical milling (followed by annealing); the direct solid-state sintering and the liquid phase route²⁸ can be also adopted. The morphology of submicron-sized (nano-sized) Li₆PS₅Cl particles becomes, then, an important feature to be kept under control. Hence a good knowledge of the surface formation and properties is instrumental not only to the understanding of Li-ion migration process between the nanocrystallites or at the interface with the electrode, but also to rationalizing and eventually controlling the particle size and shape.

In the present paper, we first unveil the symmetry breaking that results in the local distortions in the bulk mentioned above. We then simulate the thermal, structural, and elastic properties by adopting a quasi-harmonic approximation (QHA), that goes beyond the well-known limitations of the harmonic model^29,30 by introducing the missing volume dependence of phonon frequencies while retaining the harmonic expression for the Helmholtz free energy of the system.^31,32 Due to moisture, porosity, and sulfide chemistry the measurement of the mechanical behaviour of Li-argyrodite at variation with pressure is particularly challenging. In this view, our results represent a novelty and a useful reference for future experiments.

After the bulk characterization, we move to study the surface energy for different crystalline cuts of the bulk structure, characterizing the surface properties and structural reconstruction – a piece of information that is useful in view of understanding their behaviour at inter-phases with electrodes. Finally, we report the relative growth rate for the various surfaces which determines the equilibrium morphology of argyrodite crystals evaluated according to the Gibbs–Wulff theory, predicting that the equilibrium crystal shape should possess minimal total surface energy for a given volume.^33,34

2 Computational details

All calculations are based on the PBE0 global hybrid functional, as implemented in the CRYSTAL periodic program.^35,36 Ahlrichs split valence triple-zeta basis sets plus polarization (TZVP) have been adopted for all the elements (Li, Cl, P and S atoms).³⁷ The truncation criteria of the Coulomb and exchange infinite lattice series are controlled by five thresholds, T_i, which have been set to 8 (T₁–T₃), 16 (T₄) and 20 (T₅). The convergence threshold on energy for the self-consistent-field (SCF) procedure has been set to 10⁻⁸ hartree for structural optimizations and to 10⁻¹⁰ hartree for vibrational frequency calculations. A pruned Becke grid with 75 radial and 974 angular points was used. Reciprocal space sampling is based on a regular Pack–Monkhorst³⁸ grid centered at the Γ point, with shrinking factor 8 along each vector, which corresponds to 29 irreducible k-points the Brillouin zone for highly symmetric structures and to 260 k-points in the low symmetry P1 models.

Harmonic phonon frequencies at the Γ point are obtained from the diagonalization of the mass-weighted Hessian matrix of the second energy derivatives with respect to atomic displacements.^39–43 As mentioned in the introduction, the quasi-harmonic QHA model^31,32 has been adopted for thermal properties. QHA accounts for anharmonicity effects by giving a volume dependence to the phonon frequencies. With this assumption – together with the adiabatic approximation – we can express the Helmholtz free energy as a function of T and V:

where U(V) is the energy of the static lattice (electronic ground-state energy) with volume V, where k is Boltzmann's constant, and the ν_i(V) are the classical normal-mode frequencies of small-amplitude oscillations for the crystal with volume V. According to the QHA, the equilibrium volume, V(T), at any temperature T can then be deduced by minimizing the Helmholtz free energy F(V; T).

For a certain temperature and pressure range to be explored, the lattice dynamics has to be solved at few volumes in the expansion and compression regime, respectively. Concerning zero temperature, zero pressure equilibrium volume V₀, six equidistant volumes (corresponding to compressions and expansions in a volume range 92% to 108% of V₀) including V₀ have been considered. Thermal properties have been explored in the 100–400 K range of temperature and at 0.00 and 0.1 GPa, that is for values of pressure and temperature accessible for operating batteries. For the chosen set of values, full volume-constrained geometry optimization is performed and phonon frequencies computed. In the CRYSTAL code a direct-space approach to phonon calculation is adopted, and different super-cell dimensions have been considered in order to make the lattice dynamical description converge. The results mainly depend on two computational parameters: the number of K points and the size of the supercell (SC). Convergence of the thermal properties with respect to these parameters led to a 2 × 2 × 2 super-cell containing 104 atoms.

Elastic constants have been evaluated according to stress-strain relationships based on total energy calculation.⁴⁴

For more details on the methodology adopted for the calculation of the elastic tensor of a crystal under pressure, as well as the implementation of the calculation of the stiffness tensor B and its inverse, i.e. the compliance tensor, see ref. 45. We adopted the Voigt–Reuss–Hill (VRH) approximation for calculating the elastic moduli, assuming that the stress and strain are uniform throughout an aggregate. It has been proved that the Voigt moduli exceed the Reuss moduli, while the true value should lie in between.⁴⁶ In Hill's approximation, the arithmetic average of the Voigt and Reuss (B_H, G_H) boundary limits is provided.

For surface calculations, CRYSTAL adopts periodic slab models characterized by two infinite dimensions (x and y) and a finite thickness. For each termination, slabs of increasing thickness have been considered up to convergence of the corresponding surface energy. Surface energy has been computed according to the formula

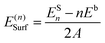where E^b is the energy of the bulk unit cell scaled to match the formula unit in a single layer, E^S_n the energy and A the surface area of the 2D unit cell in the n-layer slab.

3 Results and discussion

3.1 Bulk models

To create a model for the bulk structure of Li₆PS₅Cl, we started from the structures available in the literature, such as the F4̄3m space group with a lattice parameter of a = 9.8504 Å, from ref. 25. In such proposed models, a fully ordered arrangement was assumed for the halide on the Wyckoff 4a site (0,0,0), tetrahedral PS₄³⁻ ions on the 4b site (1/2, 1/2, 1/2), and S²⁻ ions on 4d. It was also observed²⁵ that the Li-ion might partially occupy either 48h (x, x, z) or 24g (1/4, 1/4, z) sites, opening up the possibility for a very large number of structures with different occupation patterns.

Let us consider the models with the highest local order, that is having Li ions occupying either only 24g sites or only 48h as in ref. 24. Tables 1 and 2 and Fig. 1a show the details of the first case, that we will call “Model 1” from now on. The optimized cell parameter is 10.254 Å, which is consistent with ref. 25. After vibrational analysis of model 1, however, we observed two three-fold degenerate modes one of F₁ symmetry and one of F₂ symmetry characterized by imaginary frequencies.

Fig. 1 (a) Model 1 with Li introduced in 24g site in cubic space group F4̄3m at PBE0/TZVP. Li atoms are in light gray color, Cl in magenta, P in green, and S in yellow color. (b) Model 2 with Li introduced in 24g site in space group P1 at PBE0/TZVP. Li atoms are in light gray color, Cl in magenta, P in green, and S in yellow color.

We conclude that the cubic structure of model 1 is therefore metastable. To search for the stable structure we performed a scan along a normal coordinate of the F₁ and F₂ modes, reported in Fig. 2. Two stationary points of lower symmetry are found, for which we have once again optimized the full structure and performed a vibrational analysis check, that resulted in no imaginary frequency. A similar process has been performed along all the normal coordinates associated with the three times degenerate F₁ and F₂ modes.

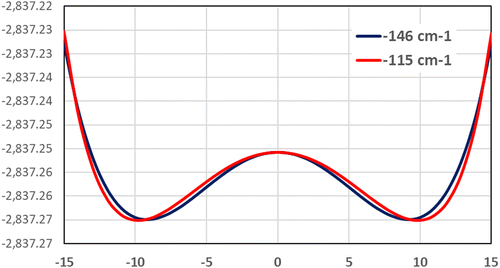Fig. 2 Scan modes (black, red lines) performed at PBE0/TZVP for both F₁ and F₂ modes having imaginary frequencies in model 1.

We obtained 24 pseudo-cubic structures of P1 symmetry that on average restore the cubic structure. The cell parameters of two structures among those obtained through this process are reported in Table 2 and one sketched in Fig. 1b. Such structures can be assumed to be isoenergetic (they differ by 10⁻⁵ eV per formula unit) and are more stable than the ideal cubic one by 0.831 eV per formula unit. It can be also noticed that in these structures Li⁺ ion coordinates are close to the 48h site. We will adopt these structures for further analysis and for constructing surfaces in the following of this paper, referring to it as “Model 2” (Table 2).

Table 1 Crystallographic details for bulk model 1

Site	Atom species	Wyckoff	Coordinates
Anion site 1	Cl^−	4a	0	0	0
Anion site 2	S^2−	4d	3/4	3/4	3/4
	P	4b	1/2	1/2	1/2
S linked to P	S^2−	16e	x	−x	z
Cation site 1	Li^+	24g	1/4	1/4	0

---

In a recent paper, Wang and Shao⁴⁷ also used the presence of imaginary frequencies in the phonon band structure as a criterion to prove the metastability of the F4̄3m cubic Li₆PS₅Cl. Breakdown of the symmetry led to the identification of a stable structure of P1 symmetry. Stable and metastable structures were localized by using the Universal Structure Predictor (USPEX) based on a materials genomic algorithm. According to their results, the fully relaxed P1 structure deviates only marginally from the high symmetry one (much less than 10%) and is more stable by 0.65 eV per formula unit (0.05 eV per atom); that is in very good agreement with our predictions. In addition, metastability of cubic Li₆PS₅Cl was briefly mentioned in the paper by Carrasco et al.⁴⁸

Instead of model 1, let us now consider cells with Li⁺ ion occupying the Wyckoff 48h site, we observe the following: upon optimization, the symmetry degradation leads to two stable minima, one monoclinic in a Pm space group (Model 4) and a structure with a P1 symmetry (Model 3). In the latter case, the crystalline positions of the atoms and the total energy are very close to our Model 2 just described. In the former case the monoclinic solution, already reported in the literature,²⁶ is characterized by a tiny distortion of the PS₄³⁻ tetrahedra and is less stable than model 2 by 0.310 eV for formula unit. The cell parameters for all models are reported in Table 2.

Table 2 Selected optimized crystallographic parameters for different models of Li₆PS₅Cl considered in this work. See text for details on the models

Model	a	b	c	Space group	α	β	γ	Li-coordinates
1	10.254	10.254	10.254	F4̄3m	90	90	90	1/4	1/4	1/4
2	9.963	10.051	10.013	P1	87.9	89.0	86.8	3/4	3/4	3/4
3	10.043	10.013	9.957	P148h	90.9	93.1	87.9	1/2	1/2	1/2
4	9.777	9.777	10.698	Pm	90.0	90.0	92.4	0.316	0.316	−0.0229

---

3.2 Thermal and elastic properties

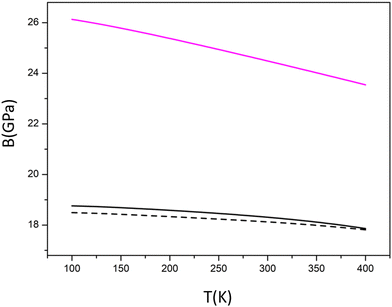
The mechanical response of the solid to temperature and pressure are important quantities from the technological point of view since the reliability and lifetime of the device might strongly depend on them. As mentioned in the Computational Details section, we have adopted a Quasi-Harmonic Approximation throughout.

3.2.1 Thermal expansion. In Fig. 3 we report thermal properties as derived from the Helmholtz free energy, in terms of α(T). We considered here the stable form of Model 2 that corresponds to the lowest energy minimum and the monoclinic structure (Model 4). For Model 2, we investigated two different values of pressure close to standard values, namely 0 GPa and 0.093 GPa. If we compare the computed values of α(T) with expansion coefficients of other materials in the same range of temperature of use we can notice that a typical perovskite has a value of ∼3.6 × 10⁻⁵ K⁻¹ whereas a typical fluorite has a value of ∼3.1 × 10⁻⁵ K⁻¹ and an oxide ion conductor La_0.8Sr_0.2Ga_0.9Mg_0.1O_3−x (LSGM-8291) ∼3.1 × 10⁻⁵ K⁻¹;⁴⁹ in all these cases we can notice smaller expansion of the lattice.

Fig. 3 Lattice expansion coefficient of pseudo-cubic model 2 (black line) at different pressures: 0 GPa (solid line), 0.093 GPa (dashed line); comparison with monoclinic structure at 0 GPa is reported in magenta.

The graphs reported in Fig. 3 show that: the value at T = 298.3 K is equal at 6.5481 × 10⁻⁵ K⁻¹ whereas at T = 400 K the value goes to 7.3877 × 10⁻⁵ K⁻¹ at P = 0 GPa, similarly at P = 0.093 GPa α(T) goes from 6.4698 × 10⁻⁵ K⁻¹ to 7.2401 × 10⁻⁵ K⁻¹. At both selected values of pressure, the ratio between the equilibrium volumes at T = 400 K and T = 298.3 K is 1.007; that will guarantee that at pressures close to the standard and in a range of temperature for operating batteries (also in case of misfunctioning), the expansion of solid electrolyte will be under control. The variation of lattice parameters is significantly smaller in the monoclinic case as evident in Fig. 3.

3.2.2 Elastic moduli. The trend of bulk modulus B for the pseudo-cubic in comparison with the monoclinic case (Model 4) as reported in Fig. 4 suggests that the monoclinic one has larger stiffness with respect to pseudo-cubic. Hence the monoclinic phase is expected to be less ductile and worst-matching electrode surfaces; we expect that an eventual transition to that phase during cycling could cause some fractures. Because of the absence of experimental data, we will refer (see Table 3 hereafter) to values of B at 0 K for structures of different solid electrolytes available in the literature.

Fig. 4 Bulk modulus vs. T as obtained from the QHA approximation for the pseudocubic Model 2 at different pressures (0 GPa black solid line, 0.093 GPa black dashed line) and for the monoclinic solution at P = 0 GPa (in magenta).

Table 3 Computed bulk modulus (B, in GPa), shear modulus (G, in GPa), Young's modulus (E, in GPa) and Poisson ratio (ν) for Model 2 and computed data reported in literature for Li₃PS₄ and Li₆PS₅Cl; results of calculations reported in ref. 50 are also reported for comparison

	Model 2	Li3PS4	Literature (ref. 50)
B R	16.05		—
B V	21.36		—
B H	18.71		—
B	18.71	23.3	28.7
G R	11.29		—
G V	13.69		—
G H	12.49		—
G	12.49	11.4	8.1
G/B	0.667	0.29	0.28
E	30.65	29.5	22.1
ν	0.227	0.49	0.37

---

The elastic moduli are often difficult to measure for superionic conductors, the values we get for these materials (which are mainly polycrystalline samples) are highly dependent on various factors such as moisture, porosity and microstructure, and the presence of secondary phases. Between them, some chemistries are also inherently more challenging to handle experimentally, such as sulfides which are very sensitive to moisture and air. The thiophosphates include a variety of materials, typically characterized by the presence of PS₄³⁻ tetrahedra. For these reasons modeling can represent the only easy route to get elastic behaviour.

In presence of an aggregate of crystals the relations expressing the stress in a single crystal in terms of the given strain has to be averaged over all possible lattice orientations or similarly the relations expressing the strain in terms of the given stress need to be averaged. To do that the elastic moduli, such as bulk modulus B, shear modulus G, and Young's modulus E were derived according to the Voigt–Reuss–Hill (VRH) approximation as already introduced in the computational section. The results are reported in Table 3 for pseudocubic Model 2 of argyrodite obtained from the cubic F4̄3m structure. Since experimental data are not available for our investigated polycrystalline material we compared our predictions of some parameters with previously computed elastic properties of both the cubic F4̄3m of Cl argyrodite and the orthorhombic Pnma polymorph of Li₃PS₄ using PBE0sol functional.⁵⁰ Compared to garnets or perovskites (t-Li₇La₃Zr₂O₁2, LLZO garnet and Li1/2La1/2TiO₃ LLTO) this sulfide (similarly to other sulfides) is predicted to have very small elastic moduli (E < 50 GPa, B < 40 GPa, G < 20 GPa). In terms of B and G, the behaviour of our model seems to be closer to the one of the parent Li₃PS₄. The Pugh's ratio,⁵¹G/B is commonly used to evaluate the brittleness of materials from elastic moduli. A larger G/B indicates that the material is more brittle. For most oxides, the G/B ratio lies between 0.5 and 0.6, while the high G/B ratio in antiperovskites (∼0.7) is an indication of their intrinsic brittle nature. Our prediction reveals that the stable form Model 2 is more brittle than other sulfides (G/B < 0.5) not so far from the antiperovskites ratio. At the same time, if we consider the data reported in the literature and Table 3 for the perfect face centered cubic structure, our pseudocubic structure appears more ductile.

After this compared analysis of elastic and thermal properties of the two main polymorphs of Cl-argyrodite, we wonder whether or not it would be possible to have a phase transition at ordinary P and in a range of temperature close to the conditions of usage of solid electrolytes. The Helmholtz free energy variation with temperature is reported in Fig. 5 for both the pseudocubic and the monoclinic Pm forms of argyrodite at P = 0. A similar trend was obtained at slightly higher values of pressures ∼0.1 GPa. Therefore, we found that in reasonable ranges of pressures and temperatures where the batteries work we cannot foresee any phase transition. A little variation of slope may be found at higher pressures for the F vs. T curve so we can guess a phase transition at very high pressures.

Fig. 5 Helmholtz free energy variation with temperature for pseudo-cubic Model 2 (black line) and monoclinic structure (magenta) of argyrodite at 0 GPa.

3.3 Surface properties

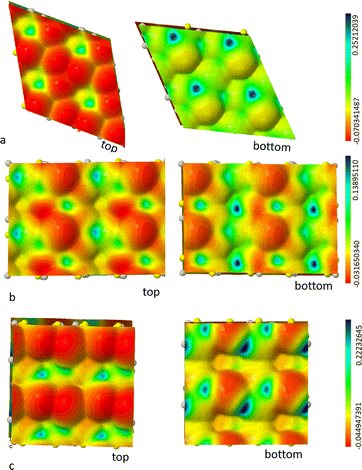
Our aim here is to find and characterize the crystalline surfaces that are more easily exposed, in order to (1) predict through a Wulff construction the possible form of crystallites and (2) prepare the ground for the study of interfaces between the solid electrolyte and other components of the battery.

3.3.1 Surface slab models. At 0 K the surface free energy is a close approximation of the surface energy as calculated by static lattice simulations, being that the entropy term is small. Hence we consider the surface electron energy, computed as reported in eqn (2). Our computational morphological analysis, performed on pseudocubic structures (Model 2), revealed that the most important crystallographic planes are the (111), (001) and (110) since they are characterized by the largest interplanar spacings, respectively 5.953, 5.156, 3.646 Å.

In Fig. 6 we report the geometry of the slabs as cut from the bulk Argyrodite after relaxation. It is clear that, out of a possible surface reconstruction, the (111) and (001) slabs are not symmetric, i.e. the top and bottom terminations are different. It turns out that, due to the structural features of the solid, no symmetric slab can be cut out from the bulk. At the same time, one can see that from chemical arguments not many terminations are possible: the solid should be looked at as an ionic crystal containing PS₄ indivisible subunits.

Fig. 6 PBE0/TZVP minima of slab models for most stable surfaces of model 2: 111 surface (panel a), 110 (panel b), 001 (panel c).

From the above reasoning we see that, even if we are bound to work with averaged surface formation energies (i.e. our values include both the formation of the upper and lower surface of the slab), this is still physically sensible as the surfaces we consider are the only possible ones. The only practical consequence, we believe, of working with averaged energies, is that we predict (see below) a symmetric crystallite, while in reality it might be asymmetric. As a side note, we remind that thanks to the local basis set adopted in crystal, these models are truly two-dimensional, that is they are nonperiodic along the z direction.

3.3.2 Surface stability and characterization. The averaged surface energy we computed (E_s) are reported in Table 4; the Basis Set Superposition Error (BSSE) is small – under 10% – so we believe it does not alter our conclusions, also considering that and since we are considering average values of energy. As shown in the Fig. 6, the bottom terminations of the (1 1 1) and (0 0 1) surfaces expose a mixed layer of Li₂S and LiCl and a single layer of Li₂S, respectively. On the contrary terminations of the (0 0 1) surface mainly exhibit PS₄ tetrahedra. Li₂S and LiCl precursors formed on a side of exposed surfaces are electronically insulating, ionically conducting phases and may work as potentially good passivating interfacial phases that act as a barrier against further decomposition of alkali superionic conductor electrolyte. Generally, those species are formed both below 1.7 V and above 2.3 V voltages.⁵² The interphases between argyrodite and some active materials (LCO, LMO, and NMC) have been chemically characterized in the pristine cases and after cycling, by X-ray photoelectron spectroscopy (XPS); the paper reports that an additional weak doublet at 160.5 eV is present in the pristine material already before cycling.⁵³ That can be attributed to Li₂S and that presence was also confirmed by X-ray diffraction data. Our pictures of surfaces reported in Fig. 6 may provide a further interpretation of that finding in addition to a claimed residue of reactant in samples of Li₆PS₅Cl.

Table 4 Argyrodite averaged surface stabilities

Surface	Averaged surface energy (J m^−2)
1 1 1	0.297
0 0 1	0.344
1 1 0	0.291

---

Table 4 shows that the surface energies are very close to each other whereas in absolute terms the very low values indicate high stability of all surfaces.

One point to consider is that different electric behaviour at the interface with the electrode can be obtained by exposing one side or the other of each surface to the electrode. Indeed, mixed Li₂S, LiCl and Li₂S layers characterizing one side termination of (1 1 1) and (0 0 1) surfaces can be conceived as a sort of incipient phase due to the surface decomposition of the material that can stabilize the solid electrolyte and essentially serve as solid-electrolyte-interphases in Li-ion ASSBs. The formation of the decomposition interphases plays an essential role in the stability of the solid electrolyte and should be considered in the design of solid electrolyte materials. In addition, properties of the interphases control the Li-ion diffusion between electrodes and argyrodite electrolytes as successfully investigated by exchange NMR spectroscopy.^54,55 It reveals that Li-ion diffusion across interfaces can be the main factor limiting the performance of Argyrodite electrolytes in the battery.

The 110-type surfaces of argyrodite, except for the presence of LiCl moieties, locally reproduce the (0 1 0) and (1 0 0) surfaces of, respectively, γ and β polymorphs of Li₃PS₄; in fact, in the orthorhombic lattices the stable surfaces expose PS₄³⁻ tetrahedra with Li⁺ counterions in nearby.⁵⁶ The same local arrangement is found in the case of argyrodite on the top surface of (1 1 1) and (0 0 1) surfaces reported in Fig. 6. From the energetic point of view, literature⁵⁶ reports for the most stable β phase (Pnma phase) of the parent structure Li₃PS₄ a (100) surface energy equal to 0.320 J m⁻². Even if in the cited literature, a certain variability is found for surface energy in dependence on the occupied Wyckoff site, the surface energies reported in the present paper (even averaged) seem to be perfectly in line with the available data for sulfide electrolytes.

A piece of useful information is then provided by the electrostatic potential mapped on top of an electron charge density isosurface in that it allows us to highlight positive and negative regions showing, in particular, the up-down asymmetry of slabs. Fig. 7 shows such a colour-coded iso-density surface for argyrodite surfaces. The discrepancy between top and bottom exposed surfaces is very clear in both the (111) and (001) cases. In the former case, the top section shows evident faces of PS₄³⁻ tetrahedra and the negative regions of potential due to sulfur contribution, whereas on the bottom side Li⁺ ions provide regions of blue positive electrostatic potential but also orange areas corresponding to Cl⁻ counterion are distinguishable. In the 001 case, the negative regions of the electrostatic potential (in red) are dominated by the sulfur counterions on the top side even with a different orientation of PS₄³⁻ tetrahedra. Fig. 7 shows on the bottom the presence of sulfur but in that case, the Li₂S moieties are evident. The electrostatic potential maps help us identifying nucleophilic regions on the top sides of surfaces reported in Fig. 7 (red areas), whereas the more or less electrophilic parts reside on the bottom surfaces (in blue and green, respectively). This variability justifies the reactivity typical of sulfide electrolytes.

Fig. 7 Electrostatic potential (in a.u.) as mapped on an electron charge density isosurface computed at a regular 3-dimensional grid of points for most stable surfaces of model 2: 111 surface (panel a) (mapped on 0.001 e bohr⁻³ charge density surface), 110 (panel b, mapped on 0.0003 e bohr⁻³ charge density surface), 001 (panel c, mapped on 0.0008 e bohr⁻³ charge density surface); both top and bottom views are reported. The blue colour codifies the regions in which the potential is positive while the red colour corresponds to negative values of potential; the green colour represents neutrality.

The morphological analysis allowed us to predict a reasonable shape for argyrodite crystals; Wulff's plot is reported in Fig. 8 in the assumption of its cubic crystalline habit. The analysis results in an area of (111), (001), and (110) surfaces respectively of 10.8%, 8.1%, and 81.1% of the total surface area of the crystal polyhedron, as visual inspection of Fig. 8 indicates. Since 110-type of surfaces also appears to be the less interesting one from the point of view of surface charge and electrostatic potential, the present modeling seems to suggest the necessity to maximize the occurrence of the less represented (111), (001) surfaces in the distribution of exposed surfaces by means of favorable preparation routes and reaction medium.

Fig. 8 Wulff's polar plot for cubic symmetry of argyrodite based on computed E_S at PBE0/TZVP, the corresponding families of planes are indicated on faces.

4 Conclusions

We presented a computational analysis of the structural, thermal, and elastic behaviour of a superionic conductor of sulfide nature – the Li₆PS₅Cl argyrodite. By means of vibrational analysis, we found the cubic F4̄3m structure – which was claimed to be the most stable polymorph at operating values of P and T state variables – to be metastable. A scan process along normal modes allowed us to identify 24 stable structures that returned on average a pseudocubic structure. In view of the challenges in the experimental determination of mechanical and elastic properties of this sulfide material, we provide our estimates according to a QHA approach, to be compared with future measurements. We predict for this material a relatively high value for the volumetric expansion coefficient with respect to other materials such as perovskites, and conductor oxides et al. The analysis of elastic properties – which are of relevance in studying the contact between the electrodes and the superionic conductor – reveals a higher value of bulk modulus B in the monoclinic case.

In presence of an aggregate of crystals typical of superionic conductors, by adopting the Voigt–Reuss–Hill approximation for polycrystalline materials, we observe relatively small elastic moduli with respect to garnets or perovskites. The low stiffness behaviour of our models seems to be closer to the one of the parent Li₃PS₄ material, while in terms of brittleness, the argyrodite seems very close to an anti-perovskite.

Lastly, we have investigated the most stable surfaces and terminations by means of 2D slab models. We found the most important crystallographic planes to be the (1 1 1), (0 0 1), and (1 1 0) planes, which we used to build a Wulff's polar plot. Almost none of the stoichiometric surfaces is up and down symmetric. The only exception is the (110) surface, which resembles the most stable terminations of the γ and β polymorphs of the parent Li₃PS₄ exposing PS₄³⁻ tetrahedra. The model (111) and (001) surfaces expose on the bottom side only the Li₂S, LiCl, and Li₂S precursors, respectively. Li₂S and LiCl precursors already present on a side of the exposed surfaces are electronically insulating, ionically conducting phases and may potentially work passivating interfacial phases that act as a barrier against further decomposition of the material.

The segregation occurring at (111) and (001) surfaces can be interpreted in terms of incipient phase separation that can be enhanced once a solid electrolyte is contacted to Li anode and it might pave the way to a real phase transition. That asymmetry and phase segregation would justify the electrostatic potential of surfaces determining the surface properties of materials and the interfaces at electrolyte/electrode contacts.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

MD thanks the HPC resources of CINECA i.e. Galileo 100 for Project ISCRA C, ‘ISc92: SEILIM’. The financial support by the MODALIS2 project, grant agreement no. 875193 of the European Union Horizon 2020 research and innovation program, is gratefully acknowledged.

Notes and references

1. V. Etacheri, R. Marom, R. Elazari, G. Salitra and D. Aurbach, Energy Environ. Sci., 2011, 4, 3243–3262.
2. B. Scrosati and J. Garche, J. Power Sources, 2010, 195, 2419–2430.
3. M. Henriksen, K. Vaagsaether, J. Lundberg, S. Forseth and D. Bjerketvedt, J. Hazard. Mater., 2019, 371, 1–7.
4. S. Hess, M. Wohlfahrt-Mehrens and M. Wachtler, J. Electrochem. Soc., 2015, 162, A3084–A3097.
5. P. Knauth, Solid State Ionics, 2009, 180, 911–916.
6. J. B. Bates, N. J. Dudney, B. Neudecker, A. Ueda and C. D. Evans, Solid State Ionics, 2000, 135, 33–45.
7. J. Li, C. Ma, M. Chi, C. Liang and N. J. Dudney, Adv. Energy Mater., 2015, 5, 1401408.
8. A. Ahniyaz, I. de Meatza, A. Kvasha, O. Garcia-Calvo, I. Ahmed, M. F. Sgroi, M. Giuliano, M. Dotoli, M.-A. Dumitrescu, M. Jahn and N. Zhang, Adv. Appl. Energy, 2021, 4, 100070.
9. P. G. Bruce, J. Electrochem. Soc., 1983, 130, 662–669.
10. H. Aono, J. Electrochem. Soc., 1990, 137, 1023–1027.
11. Y. Inaguma, Solid State Commun., 1993, 86, 689–693.
12. R. Murugan, V. Thangadurai and W. Weppner, Angew. Chem., Int. Ed., 2007, 46, 7778–7781.
13. X. Yu, J. B. Bates, G. E. J. Jellison and F. X. Hart, J. Electrochem. Soc., 1997, 144, 524–532.
14. R. Kanno and M. Murayama, J. Electrochem. Soc., 2001, 148, A742.
15. H. E. A. Yamane, Solid State Ionics, 2000, 178, 1163–1167.
16. Y. Seino, T. Ota, K. Takada, A. Hayashi and M. Tatsumisago, Energy Environ. Sci., 2014, 7, 627–631.
17. N. E. A. Kamaya, Nat. Mater., 2014, 10, 627–631.
18. A. Kuhn, V. Duppel and B. V. Lotsch, Energy Environ. Sci., 2013, 6, 3548–3552.
19. H.-J. Deiseroth, S.-T. Kong, H. Eckert, J. Vannahme, C. Reiner, T. Zaiß and M. Schlosser, Angew. Chem., Int. Ed., 2008, 47, 755–758.
20. R. P. Rao, N. Sharma, V. Peterson and S. Adams, Solid State Ionics, 2013, 230, 72–76.
21. H. M. Chen, C. Maohua and S. Adams, Phys. Chem. Chem. Phys., 2015, 17, 16494–16506.
22. M. A. Kraft, S. P. Culver, M. Calderon, F. Böcher, T. Krauskopf, A. Senyshyn, C. Dietrich, A. Zevalkink, J. Janek and W. G. Zeier, J. Am. Chem. Soc., 2017, 139, 10909–10918.
23. M. V. Reddy, C. M. Julien, A. Mauger and K. Zaghib, Nanomaterials, 2020, 10, 1606.
24. A. Baktash, J. Reid and T. E. A. Roman, npj Comput. Mater., 2020, 6, 162.
25. P. Rayavarapu, N. Sharma and V. E. A. Peterson, J. Solid State Electrochem., 2012, 16, 1807–1813.
26. R. Schlenker, A.-L. Hansen, A. Senyshyn, T. Zinkevich, M. Knapp, T. Hupfer, H. Ehrenberg and S. Indris, Chem. Mater., 2020, 32, 8420–8430.
27. M. A. Kraft, S. Ohno, T. Zinkevich, R. Koerver, S. P. Culver, T. Fuchs, A. Senyshyn, S. Indris, B. J. Morgan and W. G. Zeier, J. Am. Chem. Soc., 2018, 140, 16330–16339.
28. C. Yu, F. Zhao, J. Luo, L. Zhang and X. Sun, Nano Energy, 2021, 83, 105858.
29. S. Baroni, P. Giannozzi and E. Isaev, Rev. Mineral. Geochem., 2010, 71, 39.
30. N. Ashcroft and N. D. Mermin, Solid State Physics, Saunders College, Philadelphia, USA, New York, 1976, pp. 653–660.
31. L. L. Boyer, Phys. Rev. Lett., 1979, 42, 548–587.
32. R. E. Allen and F. W. De Wette, Phys. Rev., 1969, 179, 873.
33. G. Wulff, Z. Kristallogr. – Cryst. Mater., 1901, 34, 449–480.
34. J. W. Gibbs, The Collected Works, Longmans, New York, New York, 1928.
35. R. Dovesi, A. Erba, R. Orlando, C. M. Zicovich-Wilson, B. Civalleri, L. Maschio, M. Rérat, S. Casassa, J. Baima and S. Salustro, et al. , Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1360.
36. R. Dovesi, F. Pascale, B. Civalleri, K. Doll, N. M. Harrison, I. Bush, P. DArco, Y. Noël, M. Rérat and P. Carbonnière, et al. , J. Chem. Phys., 2020, 152, 204111.
37. A. Schaefer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829–5835.
38. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188.
39. F. Pascale, C. M. Zicovich-Wilson, F. L. Gejo, B. Civalleri, R. Orlando and R. Dovesi, J. Comput. Chem., 2004, 25, 888–897.
40. C. M. Zicovich-Wilson, F. Pascale, C. Roetti, V. R. Saunders, R. Orlando and R. Dovesi, J. Comput. Chem., 2004, 25, 1873–1881.
41. A. Erba, M. Ferrabone, R. Orlando and R. Dovesi, J. Comput. Chem., 2013, 34, 346–354.
42. C. Carteret, M. De La Pierre, M. Dossot, F. Pascale, A. Erba and R. Dovesi, J. Chem. Phys., 2013, 138, 014201.
43. J. Baima, M. Ferrabone, R. Orlando, A. Erba and R. Dovesi, Phys. Chem. Miner., 2016, 43, 137–149.
44. W. Perger, J. Criswell, B. Civalleri and R. Dovesi, Comput. Phys. Commun., 2009, 180, 1753–1759.
45. A. Mahmoud, A. Erba, K. Doll and R. Dovesi, J. Chem. Phys., 2014, 140, 234703.
46. R. Hill, Proc. Phys. Soc., London, Sect. A, 1952, 65, 349–354.
47. Z. Wang and G. Shao, J. Mater. Chem. A, 2017, 5, 21846–21857.
48. A. Golov and J. Carrasco, ACS Appl. Mater. Interfaces, 2021, 13, 43734–43745.
49. F. Tietz, Ionics, 1999, 5, 129–139.
50. Z. Deng, Z. Wang, I.-H. Chu and S. P. Ong, J. Electrochem. Soc., 2016, 163, A67–A74.
51. S. Pugh, London, Edinburgh Dublin Philos. Mag. J. Sci., 1954, 45, 823–843.
52. Z. Deng, Z. Zhu, I.-H. Chu and S. P. Ong, Chem. Mater., 2017, 29, 281–288.
53. J. Auvergniot, A. Cassel, J.-B. Ledeuil, V. Viallet, V. Seznec and R. Dedryvère, Chem. Mater., 2017, 29, 3883–3890.
54. H. Wang, C. Yu, S. Ganapathy, E. R. van Eck, L. van Eijck and M. Wagemaker, J. Power Sources, 2019, 412, 29–36.
55. T. K. Schwietert, V. A. Arszelewska, C. Wang, C. Yu, A. Vasileiadis, N. J. J. de Klerk, J. Hageman, T. Hupfer, I. Kerkamm, Y. Xu, E. van der Maas, E. M. Kelder, S. Ganapathy and M. Wagemaker, Nat. Mater., 2020, 19, 428–435.
56. N. D. Lepley, N. A. W. Holzwarth and Y. A. Du, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 104103.

---

Footnote

† Electronic supplementary information (ESI) available: Model 1–4: CIF files for main models reported in Table 2 of the mamuscript. See DOI: https://doi.org/10.1039/d2cp03599e

---