Velocity map images of desorbing oxygen from sub-surface states of Rh(111)

Abstract

We combine velocity map imaging (VMI) with temperature-programmed desorption (TPD) experiments to record the angular-resolved velocity distributions of recombinatively-desorbing oxygen from Rh(111). We assign the velocity distributions to desorption from specific surface and sub-surface states by matching the recorded distributions to the desorption temperature. These results provide insight into the recombinative desorption mechanisms and the availability of oxygen for surface-catalyzed reactions.

---

A Introduction

Surface-enhanced chemical reactivity is central for heterogeneously catalyzed processes that provide the foundation for the production of fine chemicals, materials, and pharmaceuticals.¹ In such processes, when gas-phase reactants adsorb onto a surface, this interaction with the surface leads to bond weakening, thus facilitating the reaction. When elucidating the elementary reactions in heterogeneous catalysis, we normally consider only surface bound species involved in processes such as adsorption, dissociation, diffusion, reaction, and desorption; however, recent advances indicate that sub-surface species, which are absorbed at the selvedge of the catalyst, may also exert a strong influence on catalysis.^2–5 These species not only provide an additional source of reactants, but they may also advantageously change the geometrical and electronic structure of the surface, or they even may provide altered reactivity due to the emergence of unique surface sites.^6–8 Consequently, theoretical models that describe the chemical reactivity of such systems need to take the dynamics of sub-surface species into account and experiments providing data to develop suitable models are necessary.

On many transition metal surfaces, oxygen molecules readily dissociate to form adsorbed oxygen atoms (O_ad) and create characteristic adsorbate structures or induce surface reconstruction.^9–11 At high O₂ dosages or with aggressive oxidants like NO₂ or gas-phase atomic oxygen (AO), sub-surface oxygen (O_sub) may also form in the selvedge of the metal.^12–15 In contrast to oxygen bound in metal oxides, O_sub is dissolved in the metal and mobile under many real-world conditions. In recent years, O/Rh(111) has established itself as a benchmark system for the study of sub-surface oxygen formation; hence, much is already known. On dosing Rh(111) with O₂ at room temperature, oxygen readily dissociates and saturates at an oxygen surface-coverage (θ_O) of 0.5 monolayers (ML, 1 ML = 1.6 × 10¹⁵ atoms cm⁻²)¹⁶ in a (2 × 1)-O adlayer.¹⁷ At these modest temperatures and low pressures, the rate of sub-surface oxygen formation is low. In contrast, when exposing Rh(111) to AO at elevated temperatures, sub-surface oxygen and single-layer RhO₂ surface oxide domains are created in addition to the (2 × 1)-O adlayer.¹⁸ Interestingly, dosing Rh(111) at room temperature with AO produces no RhO₂ surface oxide but results in the coexistence of the (2 × 2)-3O (θ_O = 0.75 ML) phase and the 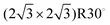(θ_O = 0.67 ML) phase along with O_sub.^19–21 When heating up such a prepared surface to 700 K, the high oxygen density phases transform to the (2 × 1)-O adlayer with some oxide growth at the step edges, while the originally formed O_sub remains below the surface. At an even higher temperature (∼800 K), sub-surface oxygen desorbs, which appears as a sharp desorption peak in the temperature-programmed desorption (TPD) experiment.¹⁸

Still little is known about the microscopic details of the sub-surface oxygen desorption process. In general, defect sites and step edges likely provide a highly reactive environment on the (111) surface, potentially facilitating the emergence of O_sub on the surface. However, a recent study on high index surfaces has shown that defects alone are not enough to explain the formation of O_sub.²² Instead, an indication was observed that O_sub emerges along the RhO₂-metallic boundary, which forms when heating up O-adlayers at Rh(111). When sufficient amounts of RhO₂ are formed, eruptive sub-surface oxygen desorption occurs.¹⁸ Once O_sub is depleted, the oxide decomposes and the resulting surface-bound oxygen recombinatively desorbs.

Velocity map imaging (VMI) has recently been implemented to surface science studies in velocity resolved kinetics (VRK) experiments. Here, a pulsed molecular beam of reactants adsorbs at the surface on a microsecond timescale and the product flux is measured in front of the surface by ion imaging after laser ionization.²⁴ This new technique has enabled a variety of studies resolving surface reaction kinetics with unprecedented resolution including CO oxidation on Pt, desorption kinetics of chiral molecules, H₂ oxidation on Pt, and CO₂ functionalization to formate on hydrogenated Pt.^25–28

In this paper, we present velocity distributions of recombinatively-desorbing oxygen from Rh(111) obtained during TPD experiments in combination with VMI. Such distributions are valuable dynamical fingerprints of the microscopic processes involved in the desorption of sub-surface oxygen. Such fingerprints are used to test and refine theory.²³ Specifically, we present results from a study combining VMI with TPD, allowing us to assign velocity distributions of desorption products to distinct peaks in the TPD spectrum with high temperature and velocity resolution. We observe hyperthermal velocity distributions for recombinatively-desorbing sub-surface oxygen as well as for recombinatively-desorbing surface oxygen from Rh(111) at T > 850 K. In contrast, O₂ surface desorption around T = 750 K occurs sub-thermally indicating different desorption dynamics.

B Experimental

We performed the experiments under ultra-high vacuum (UHV) conditions at a background pressure of 3 × 10⁻¹⁰ Torr. The Rh(111) crystal (MaTecK, 99.99%, ∅ 10 mm, 2 mm thickness, and <0.1° orientation accuracy) is mounted on a copper sample holder and can be temperature controlled by cryogenic He cooling (ARS Cryo CS-204AB) and resistive heating between 30 K and 1300 K. The surface is cleaned by Ar–ion sputtering at 2000 V (Staib instruments IG-5-C), and subsequent annealing in an oxygen atmosphere (1.0 × 10⁻⁶ Torr) at 1300 K. Cleanliness of the surface and oxygen adsorption is checked by Meitner–Auger electron spectroscopy (Staib Instruments ESA-150) and X-ray photoelectron spectroscopy (Staib PSP CTX400). We dose the surface at room temperature with AO that we produce by using a microcapillary array beam doser²⁹ and positioning the surface close to an Ir filament, through which we run (2.0–3.0) A at a chamber pressure of 1.0 × 10⁻⁶ Torr of O₂. We do not see any indication of Ir in the Meitner–Auger spectrum after the dosing procedure.

For VMI, we position the surface close to an ion-imaging detector as depicted in Fig. 1. While linearly increasing the temperature at the rate of 3 K s⁻¹, we ionize the desorbing molecules with the focused (f = 300 mm) output of a regeneratively amplified femtosecond laser (800 nm, 35 fs, Solstice, Spectra-Physics). We record 10 images s⁻¹ with 50 ionization events per image. The imaging detector consists of microchannel plates (MCPs, Topag MCP 56-15) and a phosphor screen (ProxiVision). Images are recorded with a CMOS camera (Basler ace acA1920-155 μm, (1920 × 1200) px). The MCPs are gated to the O₂ time-of-flight by increasing the MCPs voltage by 450 V for a 200 ns time window. We bias the repeller to +3000 V and achieve VMI mode when attaching +1200 V to the ion lens in the time of flight tube. In this mode, ions with the same velocity components in v_‖ and v_⊥ are mapped on the same position on the phosphor screen. Synchronization of the experiment and data acquisition during heating of the crystal is achieved by a homebuilt LabVIEW program. For calibration of the VMI detector, we backfill the chamber with argon and non-resonantly ionize with a femtosecond laser pulse. The VMI image is fitted with a thermal Maxwell–Boltzmann distribution providing the pixel to velocity scaling factor of the detector as explained in detail in a previous publication.²⁷ Additionally, we record conventional TPD spectra by linearly ramping up the sample temperature in front of a mass spectrometer (RGA-200, Stanford-Research-Systems).

Fig. 1 Experimental setup for temperature-programmed desorption experiments in combination with velocity map imaging. (a) Ionization region of the ion imaging detector. Desorbing oxygen is ionized between a repeller (+3000 V) and a grounded grid. A Nb shield with a 8 mm diameter hole biased at +60 V protects the imaging detector from heat radiation and emitted electrons from the resistively heated Ta wires. (b) Sectional view of the time-of-flight tube attached to the ionization region. Ionized oxygen is accelerated towards microchannel plates (MCPs) and a phosphor screen. Velocity map imaging is achieved when biasing the ion lens to 1445 V. The inset shows a typical raw image consisting of two parts: the symmetric signal around zero velocity is caused by background gas and is subtracted during data analysis. Desorbing molecules appear as a non-symmetric signal with velocity components parallel to the surface normal in the positive v_‖ direction.

C Results and discussion

Fig. 2 shows a conventional TPD spectrum of molecular oxygen desorption after dosing the surface with AO (with an Ir filament current of 2.0 A) for 300 s at T_surf = 400 K. In agreement with previous studies, we observe two distinct features: sub-surface oxygen desorption causes a sharp peak around 815 K (α), while surface oxygen desorption is detected as an overall lift of the baseline signal over a wide temperature range at T_surf > 850 K (β). Studies that combined scanning tunneling microscopy with TPD have shown that the β-peak corresponds to the decomposition of the (2 × 1)-O adlayer while the coverage decreases monotonically from 0.5 to 0. The α-peak corresponds to the desorption of subsurface oxygen accompanied by surface oxides and the (2 × 1)-O adlayer.¹⁸

Fig. 2 Temperature-programmed desorption (TPD) spectrum of oxygen molecules after dosing Rh(111) with atomic oxygen at T_surf = 400 K. We integrate the total ion signal for 32 amu while ramping up the surface temperature. We observe a distinct sharp desorption peak around 815 K (α) and a broad desorption feature at temperatures T > 850 K (β). The α-peak is caused by recombinatively-desorbing sub-surface oxygen atoms, and the β-peak by recombinatively-desorbing oxygen from the surface.¹⁸ The β-peak is broad and ranges up to 1300 K.²¹ Due to experimental limitations, we cannot detect ions up to this temperature.

When recording the TPD spectrum with the velocity map imaging detector, we position the surface in front of the ion detector, and detect O₂ desorption products by ionizing using a femtosecond laser (see Fig. 1). For mass resolution, we gate the ion time-of-flight to mass 32 amu while linearly ramping up the surface temperature at the rate of 3 K s⁻¹. At this mass, the phosphor screen records VMI images for desorbing oxygen molecules. We record 30 images per Kelvin of the temperature ramp, which provide velocity distributions in the TPD spectrum with significantly less than 1 K resolution. Summing up all images obtained during the desorption temperatures of a distinct peak allows us to assign velocity distributions to the chosen peaks. The shaded regions in Fig. 2 indicate the temperatures at which VMI images had been summed up to obtain the velocity distributions of recombinatively-desorbing oxygen during α-peak and β-peak desorption.

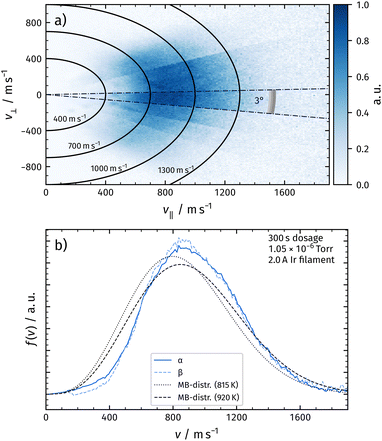
We obtain angular distributions of desorbing molecules by moving the surface relative to the ionization region. VMI allows the measurement of angular distribution of desorption products as the desorption angle appears directly in the image. However, the geometrical setup of the experiment limits the sensitivity for large desorption angles due to the distance between the ionization region and the surface (see Fig. 3). With the used ion imaging setup, we obtain velocity map imaging conditions within a circular region of 10 mm in diameter. Considering the distance between the surface and laser ionization of 30 mm, it is clear that desorbing molecules at large angles with respect to the surface normal will not be detected in this region. These molecules can only be detected if the relative position of the detector and surface is changed. We therefore systematically move the surface position with respect to the detector as shown in Fig. 3 and record velocity map images as described above. For each position, we obtain an image providing desorption velocities at larger angles.

Fig. 3 Top view of the ionization region. The dashed circle in the center illustrates the area from which ions are accelerated towards the detector. Outside of this area, no ions can be detected. We move the surface along the y-axis to detect desorption velocities at larger angles with respect to the surface normal.

Fig. 4a shows the corresponding flux of desorbing O₂ in the corresponding composite velocity map image for the α-peak. We extract the image from the raw data by subtracting the thermal background and converting density to flux by multiplying the signal with the corresponding velocity.²⁷

Fig. 4 Panel (a) shows the flux of recombinatively-desorbing oxygen for a wide angular range in a composite velocity map image. v_‖ denotes the velocity component parallel to the surface normal, v_⊥ denotes the component perpendicular to the normal. Panel (b) shows the velocity distributions at a certain angle by integrating the signal within the radial segments as indicated in panel (a). Velocity distributions for the α-peak and the β-peak are shown and do not exhibit significant differences. We do not observe significant changes of the distributions within one desorption peak. The velocity distributions of α-peak and β-peak are shifted towards higher velocities compared to a flux-weighted thermal distribution fixed to the surface temperature.

We deduce velocity distributions for a certain desorption angle by integrating velocity segments of the image as depicted in Fig. 4a. In Fig. 4b, we show velocity distributions of the α-peak and the β-peak for an angle of 3° with respect to the surface normal. We do not observe significant differences between the two distributions. Velocity distributions obtained from desorbing molecules at different temperatures within one desorption peak look identical. We also plot a flux-weighted thermal Maxwell–Boltzmann distribution as in eqn (1) with T_surf for comparison.

Here, v is the velocity, M_Ox the molar mass of oxygen molecules, and R the universal gas constant. We calculate T_surf of the desorption peak as the weighted average of the desorption peak using the total ion signal as a function of the temperature. The velocity distributions of the α-peak and β-peak are clearly shifted towards higher velocities and are narrower compared to a thermal distribution fixed to the surface temperatures of 815 K and 920 K.

From the integrated flux into a certain angular segment, we construct angular distributions from Fig. 4a, which can be fitted with a cos⁴(θ–4°) function. See Fig. 5, where we plot the results of the α-peak. We also calculate mean energies from the velocity distributions at various angles. The mean energy reduces at larger desorption angles. The dashed line indicates a cos²(θ–4°) function, which is expected for normal energy scaling.³⁰ Identical results are obtained for the β-peak.

Fig. 5 Dark blue circles: angular distribution of the flux density of recombinatively-desorbing oxygen from Rh(111) for the α-peak. The distribution is well-fitted with a cos⁴(θ–4°) function (solid line). The offset originates from a tilted mounting of the surface. Light blue triangles: mean energies of recombinatively-desorbing oxygen as a function of the desorption angle for the α-peak. The dashed line indicates a cos²(θ–4°) function, which is expected for normal energy scaling. The distributions look identical for the β-peak.

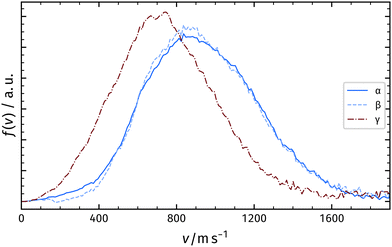
In a second experiment, we increased the atomic oxygen dosage by running 3.0 A instead of 2.0 A through the Ir filament. We again positioned the Rh crystal in front of the filament and dosed for 300 s. In Fig. 6a, we present the corresponding TPD spectrum. In addition to the desorption features observed with 2.0 A, we detect oxygen desorption at temperatures below the α-peak (γ).

Fig. 6 Panel (a) shows the TPD spectrum of molecular oxygen desorbing from Rh(111) after dosing for 300 s with 3.0 A at the Ir filament. In addition to the α- and β-peaks, we observe a third desorption peak at lower temperatures (γ). Also, the desorption feature of sub-surface oxygen is shifted towards higher temperatures. Panel (b) shows the TPD spectrum after dosing under the same conditions as shown in panel (a) and flash annealing at 815 K. This leads to the depletion of the γ-peak and a shift of the α-peak towards lower temperatures. The inset shows Meitner–Auger electron spectra (MAES) for both surfaces. We do not observe significant changes in the MAES.

Fig. 7 Velocity distributions for recombinatively-desorbing oxygen from Rh(111) at different desorption temperatures. The desorption of the γ-peak is significantly shifted towards lower velocities compared to the α-peak and the β-peak.

Previous studies using atomic oxygen as the oxidizing agent did not detect the γ-peak.^18,21 However, in contrast to those studies, the here employed experimental setup produces significantly higher AO fluxes towards the surface due to an elevated Ir filament temperature and the use of a microcapillary array beam doser. This probably leads to increased sub-surface oxygen generation. Fig. 6b shows the TPD spectrum after flash annealing the surface at 815 K, inducing the depletion of the γ-peak. The inset in Fig. 6 shows Meitner–Auger electron spectra before and after annealing at 815 K, indicating no significant change in the surface structure. We therefore exclude the formation of RhO₂ at temperatures around the γ-peak desorption. If the γ-peak was from a phase transition, we would expect a sharp peak (like α); however, it is a broad feature and could be the result of the leakage of metastable sub-surface oxygen accompanied by the transition of a high-density oxygen surface phase to the (2 × 1)-O adlayer.¹⁸ We will continue to investigate the origin of the γ-peak in our subsequent studies.

We record velocity map images from the α-, β-, and γ-peaks as explained above. The velocity distributions of the α-peak and the β-peak are identical to the measurements with a low Ir current as shown in Fig. 3. The γ-peak desorption occurs with a distribution significantly shifted towards lower velocities compared to the distributions of the α- and β-peaks.

Table 1 summarizes the characteristics of the velocity distribution of different recombinatively-desorbing oxygen features in the TPD spectrum. The velocity distributions corresponding to desorption after sub-surface emergence (α-peak) and desorption after surface recombination at elevated temperatures (β-peak) resemble each other and are both hyperthermal as shown in Fig. 4. This might indicate a common intermediate surface state prior to desorption involving for instance RhO₂ at the surface as suggested by Turano et al.¹⁸ In contrast, desorption of the γ-peak is sub-thermal and significantly shifted towards lower velocities indicating a different desorption mechanism.

Table 1 Mean desorption velocities and energies of the different recombinatively-desorbing oxygen features in the TPD spectrum deduced from the distributions shown in Fig. 7. Also shown are mean velocities v_Th for a flux-weighted velocity distribution of the respective desorption temperatures

Peak	T/K	Type	v/m s^−1	v Th/m s^−1	E/eV
α	815	Osub	940	865	0.131
β	910	Oad	955	914	0.136
γ	750	?	766	830	0.0813

---

The here presented results are in qualitative agreement with the previous work of Gibson et al., who measured the hyperthermal time-of-flight (ToF) of desorbing sub-surface oxygen from Rh(111) and discussed their results in the framework of detailed balance.³¹ Considering the principles of detailed balance, hyperthermal velocity distributions indicate an activated dissociative adsorption process, presuming an equilibrium between dissociated atoms at the surface and desorbed gas–phase molecules. A well-studied reaction of this kind is the H₂ dissociation on Cu(111), for which a large data set of ToF measurements exists after H atom permeation through the bulk.^30,32–36 For this system, permeated hydrogen atoms reach local equilibrium at the surface, recombine, and desorb. The reactivity is well described by the principle of detailed balance, which provides state sensitive energy barriers for dissociation. On first glance, the O/Rh experiments presented here look similar, as oxygen atoms recombine and desorb from the surface. However, one should note that the employed universal detection method does not allow deducing quantum state resolved velocity distributions (e.g., v, J). Hence, the distributions are averaged over all quantum states that are populated in desorbing molecules from the surface.

In Fig. 8, we analyze energy distributions of α- and γ-peak desorption following the concepts of detailed balance. Panel (a) shows the energy distribution of recombinatively-desorbing sub-surface oxygen during the eruptive α-peak. Also shown is a flux-weighted thermal energy distribution at 815 K, which is clearly shifted towards lower energies. We fit the experimental data using eqn (2) which is the product of the flux-weighted thermal energy distribution and the sticking function:³⁰

Here, K is a constant factor, E_tr is the translational energy of desorbing molecules, T_surf is the surface temperature and S(E_tr) is the sticking function. We plot the sticking function in Fig. 8 as dashed lines. For hyperthermal distributions as observed for the α-peak, the sticking function increases at elevated translational energies indicating an activated desorption process. In panel (a), we apply an error function to describe sticking as has been done in previous studies:^30,37–41Here, W represents the width and E₀ represents the inflection point. We can fit our data using E₀ = 0.045 eV and W = 0.1 eV. This leads to a non-zero sticking probability at E_tr = 0 eV. The presented sticking curve is deduced from an energy distribution obtained from desorbing molecules populating different quantum states. We therefore cannot assign energy barriers to O₂ dissociation on Rh(111) as these barriers are state dependent. For the vibrational ground state, theory predicts a dissociation barrier for O₂ on Rh(111) smaller than 200 meV.^42,43 The fact that we observe non-zero sticking at E_tr = 0 eV is indication that we produce significant amounts of vibrationally excited molecules when recombinatively desorbing from Rh(111). This vibrational energy might promote the dissociation reaction of O₂ on Rh(111) leading to reactivity at E_tr = 0 eV considering the O₂ frequency of 1580 cm⁻¹ (196 meV). State-resolved experiments on oxygen desorption from Rh(111) are necessary for a more detailed understanding. The results look identical for the β-peak, indicating a common intermediate surface state of adsorbed oxygen (β-peak) and absorbed oxygen (α-peak) prior to desorption.

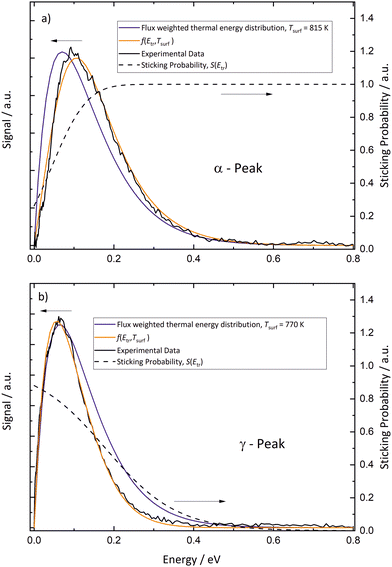Fig. 8 Panel (a) Energy distribution of recombinatively-desorbing sub-surface oxygen during the α-peak. Also displayed is a flux-weighted thermal energy distribution at 815 K. The measured distribution is clearly hyperthermal and can be modeled with the product of the flux-weighted thermal energy distribution and the sticking function (eqn (2), f(E_tr, T_surf)). Panel (b) The energy distribution of oxygen molecules desorbing during the γ-peak. The experimental data are clearly sub-thermal. The dashed lines show the sticking functions, which are fundamentally different for α-peak and γ-peak desorption.

In contrast, desorption of the γ-peak occurs with an energy distribution which is clearly sub-thermal as shown in Fig. 8b. Consequently, the sticking probability decreases at elevated energies, shown as dashed line. We again employ eqn (2) to fit the data, but using another sticking function following the lines developed by Rettner et al.:⁴⁴

We can model the data using a = 11 eV⁻¹ and ϕ = 2 eV as fitting parameters. The shape of the sticking function has the opposite trend to that of the α- and β-peaks, indicating that the desorption of the γ-peak occurs via an intermediate physisorbed molecular oxygen state. The sticking probability of such a precursor state would decrease at elevated incident energies as observed in the experiment. This is in qualitative agreement with TPD experiments on molecular oxygen physisorption on Rh(111), which appears at 140 K.⁴⁵ Based on the Polanyi–Wigner equation, one calculates for this temperature a desorption energy of E_A = 350 meV using ν₀ = 10¹³ s⁻¹ in a first order process. This corresponds to the energy, at which the sticking function shown in Fig. 8b approaches zero.

Conclusions

In this work, we have combined velocity map imaging (VMI) with temperature-programmed desorption (TPD) experiments to obtain velocity distributions of distinct peaks in the TPD spectrum of recombinatively-desorbing oxygen from Rh(111). The desorption of sub-surface oxygen after recombination at the surface (T = 815 K) exhibits a similar hyperthermal distribution to the desorption of surface oxygen at T > 900 K indicating a similar surface state prior to desorption. The velocity distribution of oxygen desorbing at T = 750 K is significantly shifted towards lower velocities and exhibits sub-thermal characteristics. We analyze the results using the principles of detailed balance to obtain energy dependent sticking functions. We identify different desorption dynamics on specific desorption peaks in the TPD spectrum. The α- and β-peak desorption occurs via activated recombination, while γ-peak desorption exhibits indication of an intermediate physisorbed molecular oxygen state prior to desorption. This study provides valuable data, on which models for sub-surface oxygen dynamics can be developed, tested, and refined, and also provides insight into the energetics of oxygen on metal surfaces relevant to heterogeneous catalysis.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

D. R. K wishes to acknowledge support from the National Science Foundation through awards CHE-1800291 and CHE-2155068 and ICASEC at University of Göttingen. T. S. acknowledges support from the Deutsche Forschungsgemeinschaft under Grant SCHA 1946/5-1 and INST 186/1302-1. Open Access funding provided by the Max Planck Society.

Notes and references

1. J. Ross, Heterogeneous Catalysis, Elsevier, Amsterdam, 2012.
2. M. Rebholz, R. Prins and N. Kruse, Surf. Sci., 1992, 269-270, 293–299.
3. A. von Oertzen, A. Mikhailov, H. H. Rotermund and G. Ertl, Surf. Sci., 1996, 350, 259–270.
4. N. M. H. Janssen, A. Schaak, B. E. Nieuwenhuys and R. Imbihl, Surf. Sci., 1996, 364, L555–L562.
5. J. Greeley and M. Mavrikakis, J. Phys. Chem. C, 2007, 111, 7992–7999.
6. Y. Xu, J. Greeley and M. Mavrikakis, J. Am. Chem. Soc., 2005, 127, 12823–12827.
7. S. T. Ceyer, Acc. Chem. Res., 2001, 34, 737–744.
8. K. D. Gibson, D. R. Killelea and S. J. Sibener, J. Phys. Chem. C, 2014, 118, 14977–14982.
9. C. Badan, R. G. Farber, Y. Heyrich, M. T. M. Koper, D. R. Killelea and L. B. F. Juurlink, J. Phys. Chem. C, 2016, 120, 22927–22935.
10. J. Derouin, R. G. Farber and D. R. Killelea, J. Phys. Chem. C, 2015, 119, 14748–14755.
11. D. H. Parker, M. E. Bartram and B. E. Koel, Surf. Sci., 1989, 217, 489–510.
12. J. Wider, T. Greber, E. Wetli, T. J. Kreutz, P. Schwaller and J. Osterwalder, Surf. Sci., 1998, 417, 301–310.
13. S. Schwegmann, H. Over, V. De Renzi and G. Ertl, Surf. Sci., 1997, 375, 91–106.
14. K. A. Peterlinz and S. J. Sibener, J. Phys. Chem., 1995, 99, 2817–2825.
15. K. D. Gibson, M. Viste, E. Sanchez and S. J. Sibener, J. Chem. Phys., 2000, 112, 2470–2478.
16. P. A. Thiel, J. T. Yates and W. H. Weinberg, Surf. Sci., 1979, 82, 22–44.
17. M. E. Turano, R. G. Farber, G. Hildebrandt and D. R. Killelea, Surf. Sci., 2020, 695, 121573.
18. M. E. Turano, E. A. Jamka, M. Z. Gillum, K. D. Gibson, R. G. Farber, W. Walkosz, S. J. Sibener, R. A. Rosenberg and D. R. Killelea, J. Phys. Chem. Lett., 2021, 12, 5844–5849.
19. J. Gustafson, A. Mikkelsen, M. Borg, E. Lundgren, L. Köhler, G. Kresse, M. Schmid, P. Varga, J. Yuhara, X. Torrelles, C. Quirós and J. N. Andersen, Phys. Rev. Lett., 2004, 92, 126102.
20. L. Köhler, G. Kresse, M. Schmid, E. Lundgren, J. Gustafson, A. Mikkelsen, M. Borg, J. Yuhara, J. N. Andersen, M. Marsman and P. Varga, Phys. Rev. Lett., 2004, 93, 266103.
21. R. G. Farber, M. E. Turano, E. C. N. Oskorep, N. T. Wands, E. V. Iski and D. R. Killelea, J. Phys. Chem. C, 2017, 121, 10470–10475.
22. R. G. Farber, M. E. Turano, E. C. N. Oskorep, N. T. Wands, L. B. F. Juurlink and D. R. Killelea, J. Phys.: Condens. Matter, 2017, 29, 164002.
23. D. J. Auerbach, J. C. Tully and A. M. Wodtke, Nat. Sci., 2021, 1, e10005.
24. D. J. Harding, J. Neugebohren, H. Hahn, D. J. Auerbach, T. N. Kitsopoulos and A. M. Wodtke, J. Chem. Phys., 2017, 147, 013939.
25. J. Neugebohren, D. Borodin, H. W. Hahn, J. Altschäffel, A. Kandratsenka, D. J. Auerbach, C. T. Campbell, D. Schwarzer, D. J. Harding, A. M. Wodtke and T. N. Kitsopoulos, Nature, 2018, 558, 280–283.
26. D. Borodin, M. Schwarzer, H. W. Hahn, J. Fingerhut, Y. Wang, D. J. Auerbach, H. Guo, J. Schroeder, T. N. Kitsopoulos and A. M. Wodtke, Mol. Phys., 2021, 119, e1966533.
27. J. Fingerhut, D. Borodin, M. Schwarzer, G. Skoulatakis, D. J. Auerbach, A. M. Wodtke and T. N. Kitsopoulos, J. Phys. Chem. A, 2021, 125, 7396–7405.
28. G. Westphal, J. Wega, R. E. A. Dissanayake and T. Schäfer, J. Chem. Phys., 2020, 153, 054707.
29. J. T. Yates Jr., Experimental Innovations in Surface Science, Springer, Cham, 2015.
30. H. A. Michelsen and D. J. Auerbach, J. Chem. Phys., 1991, 94, 7502–7520.
31. K. D. Gibson, J. I. Colonell and S. J. Sibener, Surf. Sci., 1995, 343, L1151–L1155.
32. G. Comsa and R. David, Surf. Sci., 1982, 117, 77–84.
33. H. A. Michelsen, C. T. Rettner and D. J. Auerbach, Surf. Sci., 1992, 272, 65–72.
34. C. T. Rettner, H. A. Michelsen, D. J. Auerbach and C. B. Mullins, J. Chem. Phys., 1991, 94, 7499–7501.
35. S. Kaufmann, Q. Shuai, D. J. Auerbach, D. Schwarzer and A. M. Wodtke, J. Chem. Phys., 2018, 148, 194703.
36. Q. Shuai, S. Kaufmann, D. J. Auerbach, D. Schwarzer and A. M. Wodtke, J. Phys. Chem. Lett., 2017, 8, 1657–1663.
37. H. A. Michelsen, C. T. Rettner and D. J. Auerbach, Phys. Rev. Lett., 1992, 69, 2678–2681.
38. H. A. Michelsen, C. T. Rettner, D. J. Auerbach and R. N. Zare, J. Chem. Phys., 1993, 98, 8294–8307.
39. C. T. Rettner, H. A. Michelsen and D. J. Auerbach, J. Chem. Phys., 1995, 102, 4625–4641.
40. D. R. Killelea and A. L. Utz, Phys. Chem. Chem. Phys., 2013, 15, 20545–20554.
41. A. C. Luntz, J. Chem. Phys., 2000, 113, 6901–6905.
42. M. Yan, Z.-Q. Huang, Y. Zhang and C.-R. Chang, Phys. Chem. Chem. Phys., 2017, 19, 2364–2371.
43. E. J. Walter, S. P. Lewis and A. M. Rappe, J. Chem. Phys., 2000, 113, 4388–4391.
44. C. T. Rettner, E. K. Schweizer and C. B. Mullins, J. Chem. Phys., 1989, 90, 3800–3813.
45. T. Matsushima, Surf. Sci., 1985, 157, 297–318.

---