The principal component analysis of the ring deformation in the nonadiabatic surface hopping dynamics†‡
Yifei
Zhu
 ab,
Jiawei
Peng
bc,
Xu
Kang
ab,
Chao
Xu
ab,
Jiawei
Peng
bc,
Xu
Kang
ab,
Chao
Xu
 ab and
Zhenggang
Lan
ab and
Zhenggang
Lan
 *ab
*ab
aSCNU Environmental Research Institute, Guangdong Provincial Key Laboratory of Chemical Pollution and Environmental Safety, School of Environment, South China Normal University, Guangzhou 510006, P. R. China. E-mail: zhenggang.lan@m.scnu.edu.cn
bMOE Key Laboratory of Environmental Theoretical Chemistry, South China Normal University, Guangzhou 510006, P. R. China
cSchool of Chemistry, South China Normal University, Guangzhou 510006, P. R. China
First published on 14th September 2022
Abstract
The analysis of the leading active molecular motions in the on-the-fly trajectory surface hopping simulation provides the essential information to understand the geometric evolution in nonadiabatic dynamics. When the ring deformation is involved, the identification of the key active coordinates becomes challenging. A “hierarchical” protocol based on the dimensionality reduction and clustering approaches is proposed for the automatic analysis of the ring deformation in the nonadiabatic molecular dynamics. The representative system keto isocytosine is taken as the prototype to illustrate this protocol. The results indicate that the current hierarchical analysis protocol is a powerful way to clearly clarify both the major and minor active molecular motions of the ring distortion in nonadiabatic dynamics.
I Introduction
Nonadiabatic dynamics plays a critical role in photophysics, photochemistry and photobiology.1–4 The simulation of nonadiabatic dynamics is always challenging because the strong-coupled electron–nucleus motion, i.e., the breakdown of the Born–Oppenheimer approximation, must be taken into account.3–5 With the increase of the complexity of systems under studies, it is also necessary to deal with a large number of degrees of freedom (DOFs) involved in nonadiabatic dynamics. In the last few decades, various efforts were contributed to develop nonadiabatic dynamics simulation approaches, which cover the full quantum dynamics,3,4,6–10 quantum dissipative dynamics based on the reduced density operator of the subsystem,3,9 mixed-quantum-classical and semiclassical approaches.3,10–14 Among them, trajectory surface hopping (TSH) approaches are widely employed due to their simplicity and accessibility in implementation.11,14–19 After the combination with the on-the-fly dynamics, TSH methods provide a feasible way to simulate the nonadiabatic dynamics of realistic polyatomic systems at the full-dimensional level, which gives a reasonable description of the photoreaction mechanism with affordable computational cost.12,14–17,20,21Within the trajectory-based on-the-fly nonadiabatic dynamics, numerous trajectories must be propagated until the statistical convergence is fulfilled. In principle, the statistical analysis of these trajectories gives important dynamics features, such as the excited-state lifetime, the branching ratio of reaction channels, the dominant molecular motions and so on. Moreover, for a direct view to understand the molecular evolution in the on-the-fly nonadiabatic dynamics, it is extremely crucial to identify a few key active coordinates that drive the photoinduced reactions. However, such analysis is not a simple and trivial task.22 In traditional analyses, several approaches were normally employed, for instance directly checking the differences between the hopping and initial geometries with human observation, examining the geometric evolution in the dynamics by eyes, and plotting the relevant internal coordinates as a function of time. The difficulty to perform such traditional analyses dramatically increases when the system size becomes larger, the complicated molecular motions are involved and a large number of trajectories are calculated. Alternatively, the normal mode analysis was used to analyse the geometric evolution of nonadiabatic dynamics.23–25 As a powerful tool, such analyses provide valuable physical insights into molecular vibrations when small-amplitude molecular motions are involved.
Actually it is difficult to extract the underlying structural evolution from extremely complex motions in the high-dimensional geometric space. But in the perspective of machine learning,26–28 it may be helpful to transform a high-dimensional data set to a low-dimensional reduced one, with the goal of preserving the main information contained in the original data set. Based on this reduced-dimensional space, it is preferable to employ clustering methods and other tools to obtain a transparent view of the data distribution patterns. Within this framework, in principle it is possible to introduce unsupervised machine learning algorithms into the analysis of the molecular dynamics, to effectively and accurately extract important dynamics features from the large amount of data given by trajectory simulations. Along this idea, considerable efforts were devoted to the analysis of the ground-state molecular dynamics results.27,29–38
In the meantime, the analysis of the simulation results of nonadiabatic dynamics with unsupervised learning algorithms is still challenging and only a few efforts were made in recent years.39 The diffusion map was used by Virshup et al. to perform the dimensionality reduction analyses of the photoisomerization dynamics with ab initio multiple spawning simulations.40 The same dimensionality reduction approach was used by Belyaev et al. to understand the geometric evolution in the TSH nonadiabatic dynamics.41 Li et al. employed two closely related dimensionality reduction approaches, classical multidimensional scaling (MDS) and isometric feature mapping (ISOMAP) methods, as well as the density-based spatial clustering of applications with noise (DBSCAN) clustering approach to analyse the geometric evolution in the nonadiabatic dynamics.42,43 Principal component analysis (PCA) was also used by Capano et al.44 and Peng et al.45 to analyse the photophysics of the Cu-complex in the TSH dynamics and the role of the bath motion in the symmetrical quasi-classical dynamics method based on Meyer–Miller mapping Hamiltonian, respectively. The combination of the normal mode and PCA was employed to understand the key motion of the nonadiabatic dynamics by González and coworkers.23 In addition, some efforts were also made to employ the unsupervised machine learning algorithms to analyse the nonadiabatic dynamics of solid state systems.46,47 Recently, the unsupervised machine learning algorithms were also applied by Choi et al. to understand and propagate the dynamics evolution of open quantum systems.48
The deformation of an aromatic ring widely exists in many nonadiabatic dynamics processes, including the photostability of the DNA bases,49–54 the internal conversion of the sunscreen molecules,55,56 the “channel-III” nonradiative process of benzene and its simple derivatives,57,58etc. Therefore, it is often necessary to find an appropriate way to characterize the ring deformation. Barbatti et al. once used the Cremer–Pople diagram59 to clarify the ring distortion in the TSH dynamics.52,60,61 The classification by Boeyens also provided a suitable description of the six-membered ring deformation.62 Certainly, it is fascinating to check how to employ the unsupervised machine learning algorithms to analyse the ring distortion. In fact, unsupervised learning methods were conducted by Cersonsky et al. to analyse the ring distortion of aliphatic cyclohexane in the metadynamics.63 The analysis of the ring deformation may not be straightforward, because we have to find a suitable way to obtain the balanced description of the major and minor active ring-part and side-group DOFs involved in the complicated molecular dynamics.
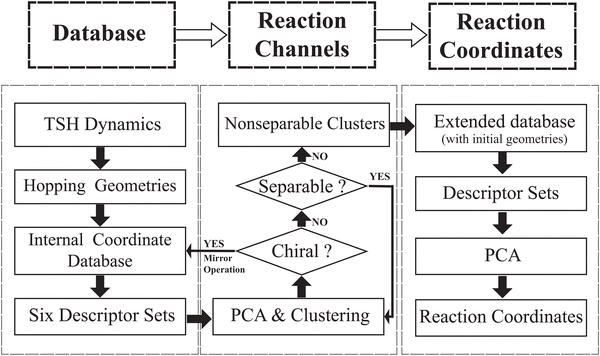
In the current work, we are committed to develop a hierarchical protocol based on unsupervised machine learning algorithms for automatically identifying different photoreaction channels and their corresponding critical molecular motions from the on-the-fly TSH dynamics simulations. As we expected, this hierarchical protocol can address the aforementioned difficulties to characterize the ring distortion. Here, the PCA27,29,30,44,45,64,65 and two clustering methods (DBSCAN66 and agglomerative clustering67,68) were used to perform analyses in the protocol. It is clear that the ring deformation may not be well captured by the Cartesian coordinates since such distortions generally display highly nonlinear features. To avoid the dilemma posed by Cartesian coordinates, we proposed to employ six descriptor sets constructed from different groups of redundant internal coordinates based on chemical meanings. The whole analysis protocol includes two stages. First, to identify the reaction channels, we analysed the DOFs belonging to the ring part and end groups successively by performing the PCA and clustering approaches of hopping geometries in the TSH dynamics in a hierarchical manner. In this step, several disjoint clusters were obtained, and in principle each cluster should represent a reaction channel. Second, to identify the major active coordinates of each channel, we compared the hopping geometries with the corresponding initial ones in each descriptor space by employing the PCA.
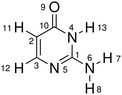
In this work, we selected the keto isocytosine (Table 1) as a prototype model to demonstrate the above proposed hierarchical protocol. As a tautomer of the cytosine (one of the DNA bases), the photoinduced processes of the keto isocytosine were widely studied in both experimental and theoretical works.69–77 These previous works indicated that several conical intersections (CIs) are involved in the nonadiabatic dynamics, which are governed by different ring deformation patterns.75,76 Therefore, the keto isocytosine is an ideal model to verify the performance of our hierarchical protocol in realistic systems. Through the analyses based on the proposed hierarchical protocol, six reaction channels and their main active coordinates relevant to the ring deformation were identified. At the same time, even the minor active molecular motions were noticed. All these channels were correlated with the optimized CIs and the further analysis provides the key physical insight into the nonadiabatic dynamics. This suggests that the current hierarchical protocol provides a powerful way to analyse the ring deformation in the nonadiabatic dynamics. Furthermore, although this work was performed on the basis of the TSH nonadiabatic molecular dynamics simulation, a similar idea can be generalized to understand other types of on-the-fly dynamics simulations.
| Molecular structure and atomic labels | ||||
|---|---|---|---|---|
| Descriptor sets | ||||
| D ring | D(4,1,5,3) | D(5,1,4,10) | D(10,2,3,5) | D(3,2,10,4) |
| D(2,3,5,1) | D(1,4,10,2) | |||
| A ring | A(4,1,5) | A(3,2,10) | A(2,3,5) | A(1,4,10) |
| A(1,5,3) | A(2,10,4) | |||
| R ring | R(1,4) | R(1,5) | R(2,3) | R(4,10) |
| R(3,5) | R(2,10) | |||
| D eg | D(6,1,5,3) | D(6,1,4,10) | D(1,4,10,9) | D(3,2,10,9) |
| A eg | A(4,1,6) | A(2,10,9) | A(5,1,6) | A(4,10,9) |
| R eg | R(1,6) | R(9,10) | ||
This paper is organized as follows. Section II focuses on theoretical methods, implementation and computational details. Section III provides the applications of the current proposed methods in the analysis of the nonadiabatic dynamics of keto isocytosine. Finally, Section IV gives the conclusion of this work.
II Theoretical methods and computational details
1 Theoretical methods
Although the Cartesian coordinates are used in the nuclear propagation in the on-the-fly simulation, this set of coordinates is not a good descriptor due to obvious limitations, i.e., the lack of translational and rotational symmetries and so on. Therefore, we need to transform the Cartesian coordinates into other sets of coordinates (commonly referred to as “descriptors” or “fingerprints”), which provide the appropriate description of the geometry evolution in the nonadiabatic dynamics.
The main purpose of this work is to analyse the ring deformation in the on-the-fly TSH nonadiabatic dynamics simulation. It is rather feasible to use internal coordinates to construct descriptors, since the bond lengths, bond angles and dihedral angles provide a rather compact and appropriate characterization of the ring deformation.
In this work, several points must be considered in the practical implementation:
(I) Different internal coordinates span in different numerical ranges; thus, they do not have the same scale. Furthermore, the internal coordinates form an over-completed and non-orthogonal space, in which different DOFs are correlated. For example, a simple out-the-plane motion of an end group may bring changes in both dihedral angles and bond angles. Here, we divided the bond lengths, bond angles and dihedral angles into different groups, and constructed several groups of descriptors.
(II) For each of the above three groups, we also divided all involved coordinates into two subgroups, which are either relevant to the motion of the ring part or the end-group part. Such a division is necessary, as the former and later sets give the reasonable descriptions on the ring distortion and the end-group motion, respectively. In this way, two types of motions are not mixed, and this way largely reduces the analysis difficulty.
(III) The H atoms generally display the large-amplitude motions owing to their lightness. In this case, it is easy to overestimate their contribution to the nonadiabatic dynamics. Because we mainly focus on the ring deformation, many internal coordinates associated with hydrogen-atom motions were not very essential. To avoid emphasizing the H-atom motions too much, we simply do not include them in the analysis.
We performed all analysis based on a special internal coordinate set, that is “redundant internal coordinates”.78,79 The basic rules to build these coordinate sets were discussed by previous studies in detail.78,79 Here, we only mention them briefly. The redundant internal coordinate set is composed of all pairwise bond distances, the appropriate bond angles and well-defined dihedral bond angles. The construction of the redundant internal coordinates can be realized as follows. First, all atomic distances are examined to determine whether two atoms are bonded to each other according to the clearly defined distance criteria.78,79 If yes, these two atoms are considered as bonded and their distance is considered as a valid bond distance. Second, the bond angles are assigned only when two atoms bonded to the same third atom. For example, A(C2,C3,N5) in Table 1 is defined as an appropriate bond angle when C2 is bonded to C3 and C3 is bonded to N5. Third, the valid dihedral angles are assigned to the situation that four atoms are bonded sequentially. For example, D(C1,N4,C10,O9) in Table 1 indicates that C1 is bonded to N4, N4 is bonded to C10 and C10 is bonded to O9. Following the above rules, a well-defined redundant internal coordinate set is obtained. In other words, this over-completed coordinate set does not change when the connectivity of a certain molecule remains unchanged. The chosen redundant internal coordinates are employed as default by the Gaussian package.79,80 The similar coordinate systems are used in the field of quantum chemistry.81–83 More discussions on the chosen redundant internal coordinates are given in the ESI.‡
In this work, the redundant internal coordinates are divided into either “ring” or “eg” group. If all related atoms are included in the ring, this internal coordinate is assigned to be in the “ring” group. For an internal coordinate, if some involved atoms are in the ring while others do not directly belong to the conjugated ring, it is labelled as the “eg”. For example, the molecular ring is formed by C1, N4, C10, C2, C3 and N5 in isocytosine; therefore, A(N4,C1,N5) and D(C1,N4,C10,C2) belong to the “ring” set, while R(O9,C10) and D(N6,C1,N4,C10) are divided into the “eg” group. Since only the ring deformation is mainly concerned, we did not consider the coordinates if all involved atoms are not in the ring moiety.
The current division strategy provides a basic idea rather than decisive division criteria, that is, we can divide the redundant internal coordinate space into different subspace according to different numerical ranges and chemical meanings. For example, in the current division, we may individually examine the different geometric evolution features in the ring parts and side groups connected to the ring moieties. If these two kinds of motions are decoupled or fall in different numerical ranges, the current analysis is very useful. Even if they are coupled, we still can treat them individually first and place them together at the end.
Nevertheless, the PCA can only be used in the linear data distribution. When the data are distributed on a manifold, the nonlinear dimension reduction methods, such as the diffusion map,40,84,85 ISOMAP27,29,42,86,87 and t-SNE (t-distributed stochastic neighbor embedding),88,89 become necessary. However, in many situations, the PCA is still among the first choices due to several advantages. For example, it provides a clear mathematical view of the data set distribution and explicitly generates the reduced coordinates. Thus, the PCA was chosen in the current work.
It is well known that the choice of the clustering approach strongly depends on the analysis purpose and the data distribution profile; thus, it is necessary to choose the suitable clustering method according to the data distribution patterns.27,28,90 When the data distribution clearly displays several distinct clusters and a few noise points, the DBSCAN method should be selected.91,92 If the data density in each cluster shows a large difference, the agglomerative clustering approach should work better.68,93,94 More detailed discussions on these clustering approaches are found in the ESI.‡
2 Implementation and computational details
In this work, we attempted to propose a useful protocol based on the PCA and clustering approaches to analyse the ring deformation in the on-the-fly trajectory-based nonadiabatic dynamics simulation, by following a hierarchical workflow as illustrated in Scheme 1. The whole analysis protocol is summarized as below.1. We performed on-the-fly Tully's TSH simulations. After collecting all geometries at hops, we built the database of the internal coordinate for these structures. We divided all internal coordinates into several descriptor groups and each represents a certain kind of geometric features.
2. We attempted to clarify how many reaction channels exist. Based on each descriptor set, the PCA and clustering analysis were performed for all hopping geometries. The iterative procedure is employed until each of the obtained cluster is non-separable, which should in principle represent a single reaction channel.
3. We attempted to identify the major active coordinates responsible for each nonadiabatic decay channel by comparing the initial structures and the hopping geometries in each channel. Such a comparison was performed based on the PCA.
Note that the above procedure is iterative and hierarchical, and more implementation details are discussed below.
The on-the-fly TSH dynamics simulation with Tully's fewest-switches surface hopping (FSSH) algorithm11 was performed at the SA3-CASSCF(12,9)/6-31G* level using the JADE code16,76,95 interfaced with the MOLPRO package.96 The decoherence correction proposed by Granucci et al.18 is introduced on top of the TSH algorithm with the correction parameter C = 0.1 hartree.97 All these calculation setups are very similar to our previous work.76 More details on the TSH simulations are given in the ESI.‡
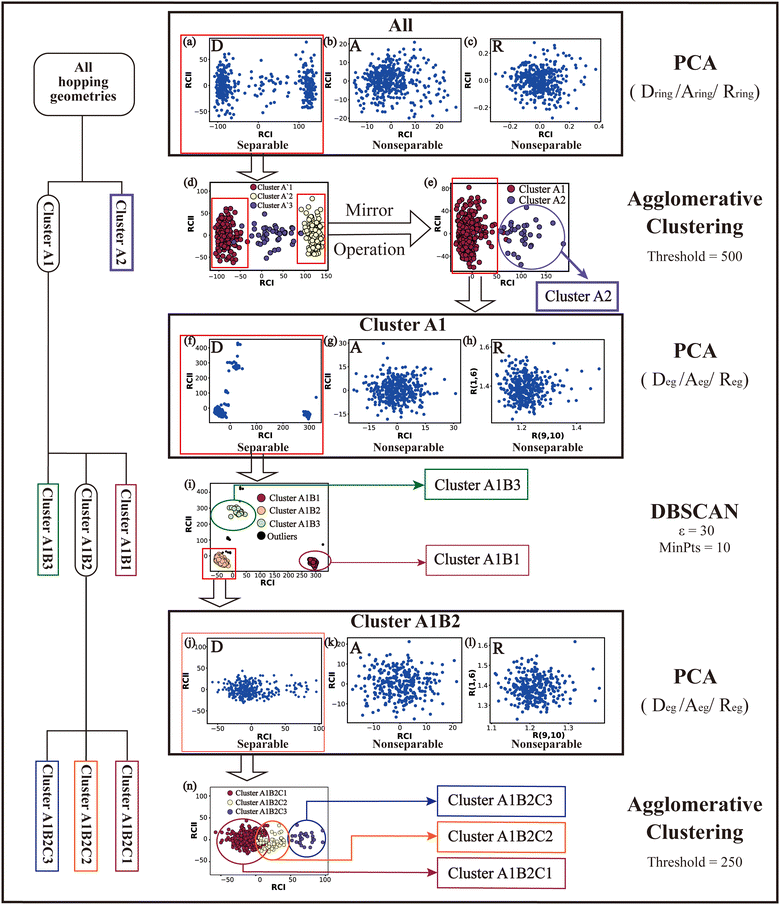
Firstly, we considered the DOFs in the ring moiety only and performed the PCA using three descriptor sets (Dring, Aring and Aring). This gives the data distribution patterns in three individual reduced spaces. For each of them, the clustering analysis was then conducted. In some cases, several clusters are obtained while in other cases we only obtain a single cluster. Sometimes, the symmetry property, that is, mirror symmetry, should be taken into account here.
For each individual cluster, we re-performed the PCA and applied the clustering analysis in the reduced space again, still based on the descriptor sets associated with the ring moiety. Such an iterative step was repeated until all clusters are non-separable. Here, if the separable clusters appear in two descriptor sets, we will take the case which gives the more clear cluster boundary. After this step, all hopping geometries were well analysed by the appropriate consideration of the DOFs in the ring moiety.
After the generation of several non-separable clusters by the analysis of the ring motion, we wished to separate the hopping geometries again based on the DOFs in the end groups. For each non-separable cluster obtained above, we performed the PCA again for each individual cluster based on the descriptor sets involving the end groups (Deg, Aeg and Aeg). After the PCA, the clustering analysis was applied to give some sub-clusters. After some iterations, several non-separable clusters were obtained. In principle, each cluster should correspond to a certain reaction channel.
In the above procedure, both DBSCAN and agglomerative clustering methods were employed according to the data distribution.
Starting from a single cluster, we collected the hopping geometries of this cluster together with their corresponding initial sampling structures. Next, the PCA was performed based on six descriptor sets, and the reduced low-dimensional space provided a direct view of data distribution patterns. Within the reduced spaces constructed from different molecular descriptors, we noticed that there are two types of data distribution patterns. In some situations, the initial geometries overlap with the hopping geometries, implying that the chosen descriptor set does not play the active part in the nonadiabatic dynamics. In other cases, the initial geometries are well separated from the hopping geometries, and at the same time, a few leading components contribute significantly to the variance of the data distribution. This indicates that the corresponding reduced coordinates can well capture the geometric difference between the initial and hopping geometries. In this way, the active coordinates for the chosen channel were identified. After the similar analysis procedure was applied for each reaction channel, all relevant active DOFs were found.
For each non-separable cluster, we attempted two approaches to obtain the representative hopping geometry. In the first one, the typical geometry was defined as the cluster center, which was obtained by the following approach. For a given cluster, we computed all pair-wise distances in the reduced space obtained from the PCA. For a data point, we calculated the summation of all inter-point distances of this point. If a data point gives the minimum of this summation, we chose it as the cluster center. In the second method, we calculated the average values of the internal coordinates for all geometries within the selected cluster to build an averaged molecular structure. These two ideas provide visible ways to capture the major geometric features of the given cluster.
All analysis codes were written with Python language, and some of them were developed based on Scikit-learn Python toolkit,99 for example, PCA, DBSCAN and agglomerative clustering.
III Results and discussion
1 The construction of geometric descriptors
In the current simulations, all calculation setups are very similar to those in our previous work,76 except that more trajectories were calculated and the longer simulation time duration was employed. As a consequence, the similar but more refined results were obtained.As shown in Fig. S1 (ESI‡), the population of the S2 state disappears very quickly, along with the accumulation of the S1 state in the early stage of the dynamics. Subsequently, the trajectories begin to jump back to the S0 state, and the population of the ground electronic state increases. Totally, we considered 1000 trajectories, of which 436 trajectories undergo S1–S0 “hops” within 1.5 ps. The overall population dynamics is similar to our previous work.76
We collected all geometries at the first S1–S0 hop events and constructed the descriptors to characterize their geometric features. The internal coordinates were built using the Gaussian package according to Table 1. Whereas the internal coordinates of seven hopping geometries are inconsistent with those of initial geometries, because the six-member ring breaks in the excited-state dynamics. We just discarded them in the further analysis because of their minor contribution (<2%). In this way, a database (DB) containing all hopping geometries was constructed, in which each geometry is represented by a group of geometric descriptors, i.e., Dring, Aring, Rring, Deg, Aeg and Reg, as discussed in Section II.2.3.
2 PCA and clustering analysis
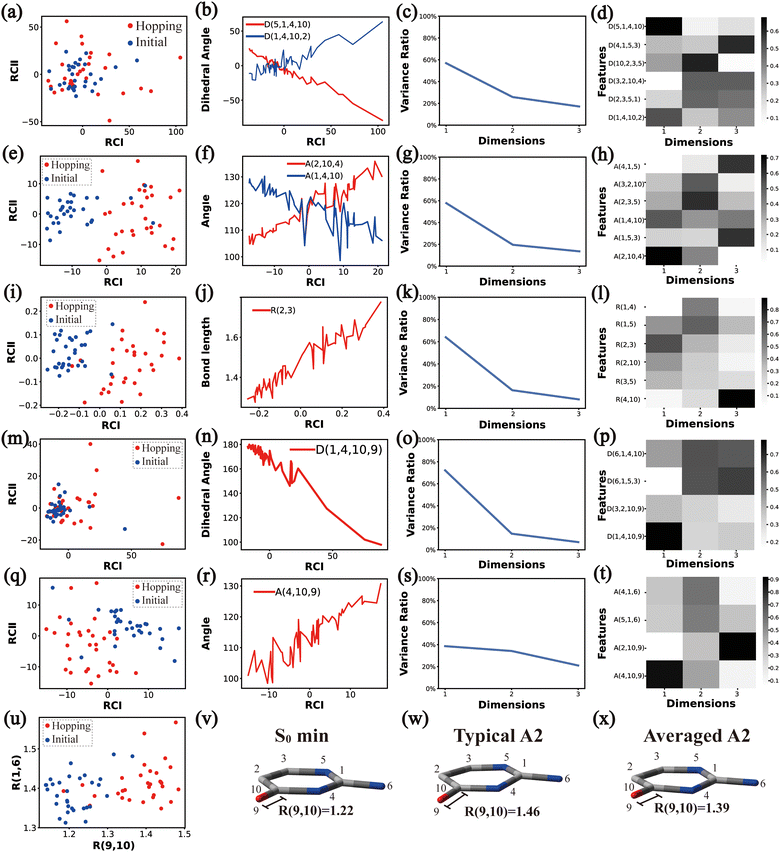
Based on all hopping geometries, we wanted to clarify how many excited-state reaction channels exit in the nonadiabatic dynamics evolution. For this purpose, we conducted the PCA and clustering analysis for these geometries. As discussed in Section II.2.4, the whole analysis process is composed of two steps: (1) the analysis of the ring-moiety motion and (2) the analysis of the end-group motion.Next, we performed the clustering analysis on top of the PCA results of the Dring coordinates, because of the existence of a few clearly separated clusters. As these three clusters have obviously different densities, we chose the agglomerative clustering method as discussed in Section II.1.1. Three clusters were identified, which are labeled as Clusters A′1, A′2 and A′3 in Fig. 1(d). The centers of these three clusters were taken to obtain a rough view of their typical geometric features. We noticed that the chiral symmetry may play some roles between the geometries of Cluster A′1 and Cluster A′3, because both upward and downward Dring puckering deformations may exist in the nonadiabatic dynamics starting from the initial planar structures. In order to eliminate the chiral effect, we simply reversed the signs of the z-coordinates of the geometries in Cluster A′3. After this mirror operation, we rebuilt the database DB and re-performed the PCA and clustering analysis. Now two clusters were obtained, which are labeled as Clusters A1 and A2 in Fig. 1(e).
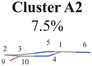
The next task is to clarify whether each individual cluster (Cluster A1 or A2) is separable by following the protocol in Section II.2.4. Since Cluster A2 contains 31 geometries (<15%), we considered that the Cluster A2 is non-separable. We only re-performed the PCA and clustering analysis for all geometries in Cluster A1 and found such a cluster to be not separable. Therefore, all hopping geometries were well separated into two groups, Clusters A1 and A2, by the PCA and clustering analysis of the ring-moiety motions.
As shown in Fig. 1(g) and (h), only one single data cluster is obtained in the cases when Aeg and Reg were considered. In contrast, three clusters with almost identical densities are clearly given in the PCA results based on Deg, beside a few outliers, as shown in Fig. 1(f). And the most important components of RCI and RCII are D(1,4,10,9) and D(3,2,10,9), respectively (see Fig. S6(A1)–(A4), ESI‡).
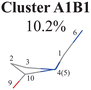
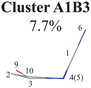
Next, we performed the further clustering analysis of all geometries in Cluster A1 on top of the Deg-based PCA results. The DBSCAN method was taken here because it works well when we want to separate several clusters with almost identical densities and to remove some outliers, as discussed in Section II.1.1. The clustering analysis gave three clear clusters and 16 noise points (<5%) in Fig. 1(i). Because all three clusters are sub-clusters of Cluster A1, they are reasonably labelled as Clusters A1B1, A1B2 and A1B3. They contain 308, 42 and 32 data points, respectively. To date, we have totally obtained four individual clusters (Cluster A1B1, Cluster A1B2, Cluster A1B3, and Cluster A2). Among them, only the number of hopping geometries in Cluster A1B2 is more than 15% of the total, and thus the other clusters are considered to be non-separable.
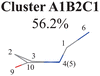
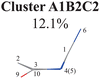
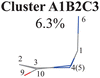
To further examine whether Cluster A1B2 is separable or not, we re-performed the PCA and clustering analysis of all hopping geometries in this group again. The results are given in Fig. 1(j)–(l). Among them, the PCA of Deg gives different results. The first leading reduced dimensional coordinate is extremely dominant, more than 70% variance, as shown in Fig. S6(B2) (ESI‡). In the reduced two-dimensional space given by the PCA of Deg, we still obtain three clusters. Although the boundaries of these clusters are not perfectly clear, it is enough to identify these clusters by their different densities. Thus, we attempted to perform the agglomerative clustering here, and three clusters were shown, namely Clusters A1B2C1, A1B2C2 and A1B2C3, in Fig. 1(n). Here, these groups contain 232, 50 and 26 hopping geometries, respectively. Therefore, the later two clusters (Clusters A1B2C2 and A1B2C3) are treated as the non-separable ones in our view.
We re-performed same the PCA and clustering analysis for all geometries in Cluster A1B2C1, while this cluster is no longer separable. Overall, when both the ring-moiety and end-group parts were considered, we finally obtained six groups, i.e., Clusters A1B1, A1B2C1, A1B2C2, A1B2C3, A1B3 and A2.
In the above analysis process, sometimes the unclear clusters may appear in the PCA of some descriptor sets, such as the situation in Fig. 1(b). In such cases, we always examined which descriptor set gives more clear separation of all clusters in the reduced space. If some DOFs show better performance, such as Dring in Fig. 1(a), we will simply take the corresponding descriptor set to conduct the further analysis.
3 Major active coordinates of each channel
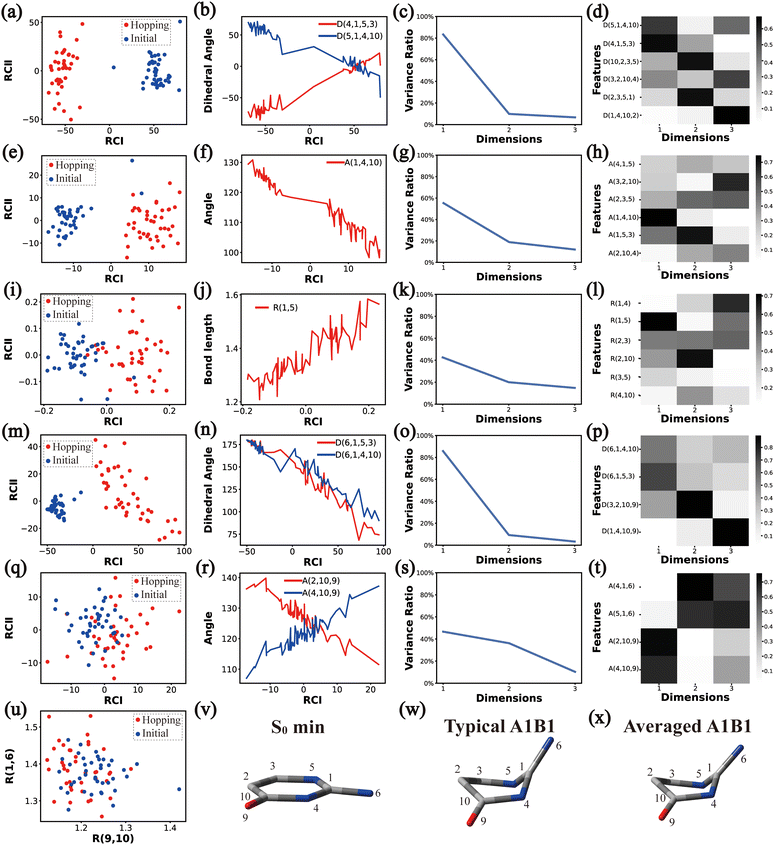
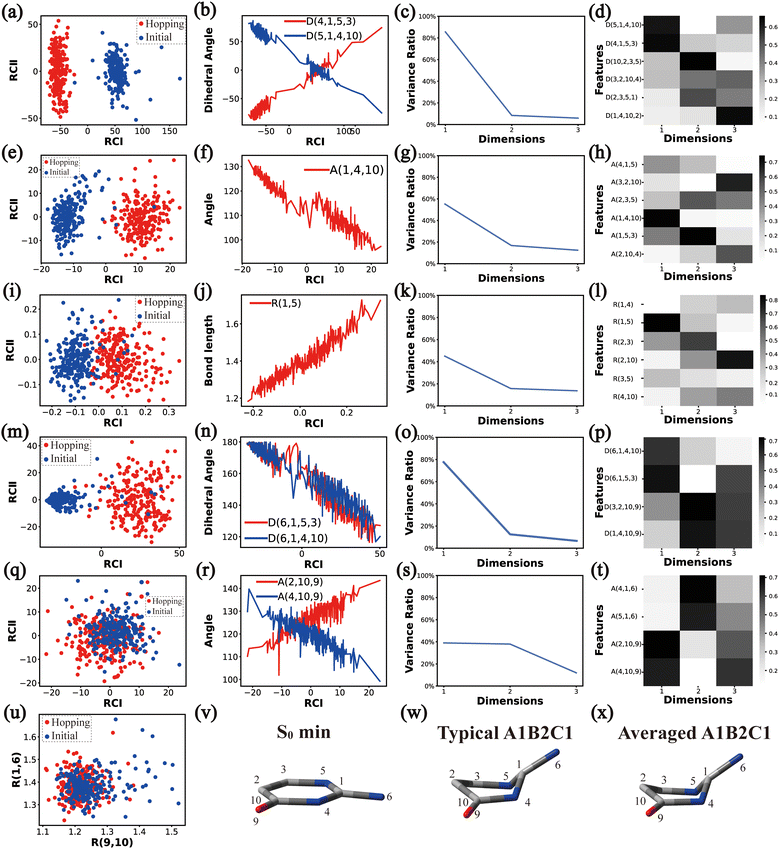
In principle, each of six individual non-separable clusters corresponds to a single reaction channel. We attempted to identify the key active coordinates of each channel by comparing the structures in each individual cluster with their corresponding initial geometries.For each cluster, we first collected all hopping structures and their corresponding initial sampling geometries to obtain an extended database. Each data point in the extended database is also represented by six descriptor sets given in Section III.2. Specially, here we took the absolute value of all dihedral angles in Deg to avoid the inherent numerical discontinuity. We performed the PCA based on these descriptor sets, except Reg that only includes two elements (R(9,10) and R(1,6)). All results are shown in Fig. 2–7 and each figure is composed of 24 subplots. Among them, the data distribution in the two-dimensional space spanned by two leading reduced coordinates, the relationship between RCI and a few most important internal coordinates, the variance ratio of each dimension and the components of a few leading reduced dimensions in the PCA are given in subplots (a)–(t). For Reg, we just directly analysed the space spanned by R(9,10) and R(1,6) in the subplot (u). In addition, the S0 minimum, the typical hopping structure and the averaged one in the corresponding cluster are shown in subplots (v)–(x) in each figure. In all cases, the latter two geometries give the roughly similar structural features.
By the analysis of the end-group motion, A(2,10,9) and A(4,10,9) play certain roles in the nonadiabatic dynamics. At the same time, D(6,1,4,10), D(6,1,5,3) and D(3,2,10,9) contribute to the separation of the hopping geometries from the initial structures.
In this channel, the puckering of the C1 atom and the puckering at the C10 site in opposite directions are the dominant molecular motion in the nonadiabatic dynamics. Overall, D(4,1,5,3), D(5,1,4,10), A(1,4,10), A(1,5,3), R(1,5), R(2,3) and R(2,10) in the ring part, and D(6,1,4,10), D(6,1,5,3), D(3,2,10,9), A(2,10,9) and A(4,10,9) relevant to end groups are the leading active coordinates for this channel. The variations of D(5,1,4,10), D(4,1,5,3) and several relevant angels indicate that ring puckering takes place near the C4–C1–C5 region. The changes of angles A(2,10,9) and A(4,10,9), bond lengths R(2,10) and others within conjugated part, as well as the relevant dihedral angles, imply the existence of the C10-puckering of the ring part and the out-of-plane motion of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond. These findings are consistent with the geometric features of the typical and averaged hopping structures given in Fig. 2(w) and (x).
O bond. These findings are consistent with the geometric features of the typical and averaged hopping structures given in Fig. 2(w) and (x).
Briefly, the main active coordinates in this A1B2C1 channel include D(5,1,4,10) and D(4,1,5,3), A(1,4,10), A(1,5,3) and A(4,1,5), R(1,5), R(2,3) and R(3,5), which indicate the C1-puckering motion, and D(6,1,4,10) and D(6,1,5,3) relevant to the downward out-of-plane motion of the C1–N6 bond.
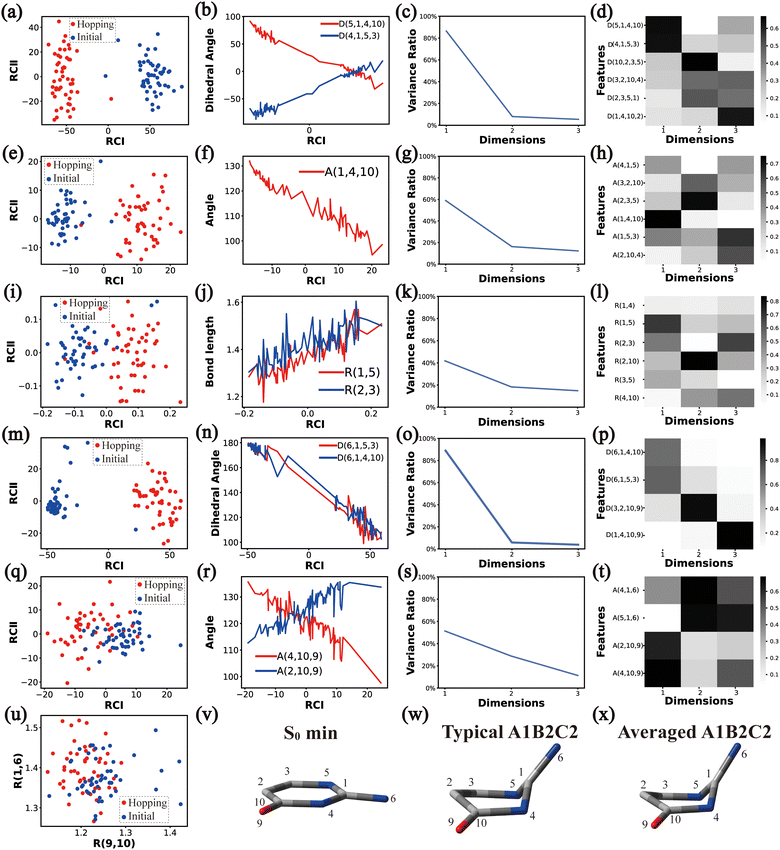
As a short summary, the dihedral angles D(5,1,4,10) and D(4,1,5,3), the bond angles A(1,4,10), A(1,5,3) and A(4,1,5), and the bond lengths R(1,5), R(2,3) and R(3,5) associated with the ring moiety, D(6,1,5,3), D(6,1,4,10), A(2,10,9) and A(4,10,9), in the end-group part are the major active coordinates of the A1B2C2 cluster. And the dominant motion of this channel is the C1-puckering motion.
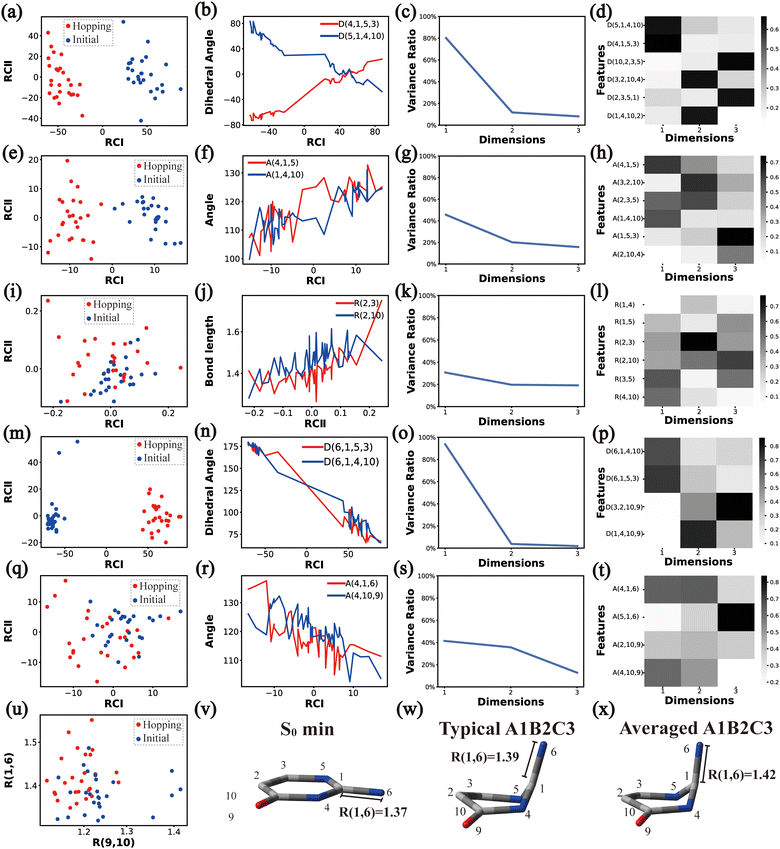
Overall, the C1 puckering motion and the out-of-plane motion of the amino group, accompanied by the CN bond stretching motion, are the important motions in this A1B2C3 channel. The dihedral angles D(5,1,4,10), D(4,1,5,3), D(6,1,4,10) and D(6,1,5,3), the angles A(1,4,10), A(2,3,5), A(4,1,5), A(4,1,6), A(4,10,9) and A(2,10,9), and the bond length R(1,6) contributing to these certain motions are important active coordinates.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O moiety is also observed.
O moiety is also observed.
Thus, the main active coordinates of this channel are the dihedral angles D(5,1,4,10), D(4,1,5,3), D(6,1,4,10), and D(6,1,5,3) and the bond angles A(1,4,10), A(4,1,5) and A(2,3,5). The C1-puckering and the out-of-plane motion of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O contribute mostly to this reaction channel, and these two motions follow the same orientation.
O contribute mostly to this reaction channel, and these two motions follow the same orientation.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond as shown in Fig. 7(u). This finding is consistent with the representative hopping geometries in Fig. 7(w) and (x). Along with it, the stretching and bending motions located in the six-membered ring also play visible roles. Compared to other channels, the whole molecular system remains a relatively planarity, but not complete planar due to the strong variations in the ring moiety.
O bond as shown in Fig. 7(u). This finding is consistent with the representative hopping geometries in Fig. 7(w) and (x). Along with it, the stretching and bending motions located in the six-membered ring also play visible roles. Compared to other channels, the whole molecular system remains a relatively planarity, but not complete planar due to the strong variations in the ring moiety.
| Channel | Important motion | Major active coordinates |
|---|---|---|
| a Taking the ring moiety as the reference and the direction of the C1-puckering motion as the upward one, [+] indicates an upward motion while [−] denotes a downward one. | ||
|
C1-puckering | Ring part: |
| C10-puckering | D(5,1,4,0) D(4,1,5,3) A(1,4,10) | |
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O out-of-plane motion[−]a O out-of-plane motion[−]a |
A(1,5,3) R(1,5) R(2,3) R(2,10) | |
| End-group part: | ||
| D(6,1,4,10) D(6,1,5,3) D(3,2,10,9) | ||
| A(2,10,9) A(4,10,9) | ||
|
C1-puckering | Ring part: |
| NH2 out-of-plane motion[−]a | D(5,1,4,0) D(4,1,5,3) | |
| A(1,4,10) A(1,5,3) A(4,1,5) | ||
| R(1,5) R(2,3) R(3,5) | ||
| End-group part: | ||
| D(6,1,4,10) D(6,1,5,3) | ||
|
C1-puckering | Ring part: |
| D(5,1,4,0) D(4,1,5,3) | ||
| A(1,4,10) A(1,5,3) A(4,1,5) | ||
| R(1,5) R(2,3) | ||
| End-group part: | ||
| D(6,1,4,10) D(6,1,5,3) | ||
| A(2,10,9) A(4,10,9) | ||
|
C1-puckering | Ring part: |
| NH2 out-of-plane motion[+]a | D(5,1,4,10) D(4,1,5,3) | |
| A(4,1,5) A(2,3,5) A(1,4,10) | ||
| C1–N6 bond stretching | End-group part: | |
| D(6,1,4,10) D(6,1,5,3) D(3,2,10,9) | ||
| A(4,1,6) A(4,10,9) A(2,10,8) R(1,6) | ||
|
C1-puckering | |
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O out-of-plane motion[+]a O out-of-plane motion[+]a |
Ring part: | |
| D(5,1,4,0) D(4,1,5,3) | ||
| A(1,4,10) A(4,1,5) A(2,3,5) | ||
| End-group part: | ||
| D(6,1,4,10) D(6,1,5,3) | ||
|
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching motion O stretching motion |
Ring part: |
| A(2,10,4) A(1,4,10) | ||
| R(2,3) | ||
| End-group part: | ||
| (4,10,9) R(9,10) | ||
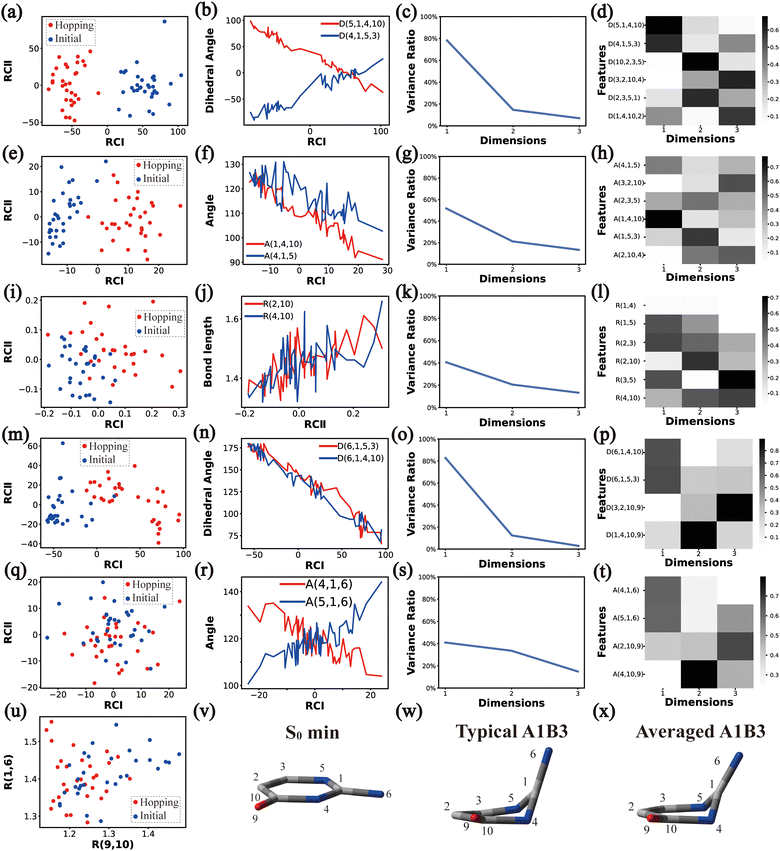
All clusters (Clusters A1B1, A1B2C1, A1B2C2, A1B2C3 and A1B3) belonging to Cluster A1 play the dominant roles (92.5% of all hops) in the TSH dynamics, which are mainly governed by the C1-puckering motion of the ring moiety. For illustration, we align all representative geometries of these channels by attributing the C1-puckering motion as the upward motion (Table 2), and discuss the other key molecular DOFs. All representative geometries in Cluster A1B1, A1B2 and A1B3 show many similar geometric features.
Here, we noticed that the representative geometries in Cluster A1B1, A1B2 and A1B3 are in fact distinctive by different statuses of the C10 atom in the ring and its associated C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O moiety. Their differences are clarified by examining two dihedral angles relevant to the O atom (D(1,4,10,9) and D(3,2,10,9)) (Fig. S6(A1)–(A4), ESI‡) and other relevant internal coordinates. We take the structure of Cluster A1B2 as the reference to illustrate. The downward and upward out-the-plane motions of the C
O moiety. Their differences are clarified by examining two dihedral angles relevant to the O atom (D(1,4,10,9) and D(3,2,10,9)) (Fig. S6(A1)–(A4), ESI‡) and other relevant internal coordinates. We take the structure of Cluster A1B2 as the reference to illustrate. The downward and upward out-the-plane motions of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O moiety are observed in the A1B1 and A1B3 decay channels, respectively, while the out-of-plane motion of the C
O moiety are observed in the A1B1 and A1B3 decay channels, respectively, while the out-of-plane motion of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O moiety is almost negligible in the A1B2 channel.
O moiety is almost negligible in the A1B2 channel.
Three sub-clusters (A1B2C1, A1B2C2 and A1B2C3) exist in Cluster A1B2, which are characterized by different combinations of the out-the-plane motions of the NH2 group and the pyramidalization motion at the C1 atom. When the pyramidalization motion at the C1 atom is not obvious, we obtained the A1B2C2 channel. When the strong pyramidalization motions are observed, different pyramidalization directions result in two channels, A1B2C1 and A1B2C3. Cluster A2 accounting for 7.5% was also clarified. The C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching motion and the relevant ring deformation contribute to this channel, while the aromatic ring remains nearly planar.
O stretching motion and the relevant ring deformation contribute to this channel, while the aromatic ring remains nearly planar.
In the analysis of the nonadiabatic dynamics reaction mechanism, it is meaningful to clarify the reaction channels and their corresponding major molecular motion. On top of these identifications, we can conduct the further analysis to obtain more physical-chemistry insight behind them.
We chose the typical geometries and five randomly selected hopping structures in each channel as initial guesses, and performed the CI optimization at the SA3-CASSCF(12,9)/6-31G* level with the MOLPRO package. As shown in Fig. 8, three CIs were obtained, which are Ethyl.I, Ethyl.II and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching CIs, consistent with the previous work.76 The first two CIs are characterized as the mixture between the ππ* and ground states, and the latter one displays the nπ*/GS character.
O stretching CIs, consistent with the previous work.76 The first two CIs are characterized as the mixture between the ππ* and ground states, and the latter one displays the nπ*/GS character.
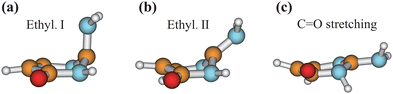 | ||
Fig. 8 Geometries of three CIs (Ethyl.I, Ethyl.II and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching) of keto isocytosine optimized at the SA3-CASSCF(12,9) level. O stretching) of keto isocytosine optimized at the SA3-CASSCF(12,9) level. | ||
When the initial geometries in the CI optimizations are chosen from the A1B1, A1B2C1 and A1B2C2 channels, the CI optimizations give Ethyl.II CI.75,76 If the channels A1B2C3 and A1B3 are chosen, Ethyl.I CI is obtained. These two CIs share some similarities in the presence of the C1 site puckering, but are distinguished by the different orientations of the out-the-plane motion. Here, Ethyl.II CI is preferred because the less NH2 torsion is required and no barrier exists.76 In addition, we also noticed that different conjugation statuses exist in the ring moieties at these two Ethyl CIs. The bond lengths in the ring moiety show larger changes in the A1B1, A1B2C1 and A1B2C2 channels (Ethyl.II CI) with respect to the S0 minimum, compared with the A1B2C3 and A1B3 channels (Ethyl.I CI). In one word, the latter channels experience less conjugation modification in the nonadiabatic decays. Therefore, the PCA results provide the additional possible reasons to explain that the Ethyl.II CI channels are preferred from the perspective of the conjugation alteration of the ring part.
In addition, the CI optimizations starting from the geometries of channel A2 give two CIs, Ethyl.II and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching CIs. As discussed in Section III.3.6, the geometries of channel A2 display quasi-planarity, which is close to the structure of the C
O stretching CIs. As discussed in Section III.3.6, the geometries of channel A2 display quasi-planarity, which is close to the structure of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching CI. Thus, the energy of this CI may be higher than the Ethyl.II CI. This again gives the additional supports in that the C
O stretching CI. Thus, the energy of this CI may be higher than the Ethyl.II CI. This again gives the additional supports in that the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching CI does not play the important role here. These findings are consistent with the previous work.76
O stretching CI does not play the important role here. These findings are consistent with the previous work.76
In principle, the CIs are not isolated points but continuous seams in the high dimensional space. The analysis of the role of the whole CI seam is also important. In the current protocol, we clearly demonstrate that different hopping channels may be associated with a single minimum-energy CI. For example, the A1B1, A1B2C1 and A1B2C2 channels are associated with Ethyl.II CI. Therefore, it is clear that different NH2 statuses may exist along this seam. More detailed analyses of the topology and branching space of the CI102 are given in the ESI.‡
In the previous work with fewer trajectories,75,76 aside from the major channel A1B2C1, two minor channels A1B2C3 and A2 were also found. The branching ratio given by the previous work is qualitatively consistent with the current findings, although some minor channels (A1B1 (10.2%), A1B2C2 (12.1%) and A1B3 (7.7%)) were not discussed. One of the possible reasons is that more trajectories and the long-time (1.5 ps) propagation were taken into account in the current work. Furthermore, the traditional analysis of the TSH dynamics may not identify the very minor and detailed distinctive differences of the ring distortion in the geometric evolution.
4 Discussion
The current analysis tool is user-friendly and applicable enough to analyse the ring deformation in the nonadiabatic dynamics. Let us consider that we want to perform such a task from scratch.First, we can choose the redundant internal coordinates as the geometric features to construct the descriptor sets. The redundant internal coordinates have the solid theoretical background.78,79 In the current work, since the ring breaks are rare in the nonadiabatic dynamics of the DNA bases as we demonstrated, that is, the current molecular connectivity remains unchanged, we choose the redundant internal coordinate set, and the construction details are well discussed in ref. 78 and 79. Since the chosen redundant internal coordinate system is used by default in the popular Gaussian 16 package, it is rather simple to use this package to generate the redundant internal coordinate set. This definitely improves the applicability of the current approach. If the molecular connectivity changes dramatically, different redundant internal coordinates for different geometries may be obtained. In this situation, we may need to set up a redundant internal coordinate set that is large enough to cover all involved internal coordinates and possible connectivity. Alternatively, it may be necessary to attempt other geometric descriptors such as the machine-learning based geometry descriptors.103–106 These are important research topics in the future. In addition, there are various sets of available internal coordinate systems, including the curvilinear natural internal coordinates81,82 and the delocalized internal coordinates by Baker et al.83 All these coordinate sets are easily generated by different quantum chemistry packages, which are also friendly choices in the similar analyses.
Second, we divided all internal coordinates into different descriptor sets. This division of internal coordinates gave us a more compact and suitable representation of the geometric evolution, and thus allowed us to obtain the better description of the geometric evolution in the relevant subspaces. When we want to analyse the similar systems, we may always follow the current division rules to make the preliminary analysis. In other situations, we may divide all redundant internal coordinates according to other suitable rules. For example, when dealing with other high conjugated systems with two rings, we may divide the redundant internal coordinates into three subgroups, the ring 1 part, the ring 2 part and their connectivity part. If the H atom should be considered, we may set a new subgroup containing the internal coordinates involving the H atom. Therefore, the current division strategy can be easily extended to other molecular systems for the analysis of ring deformation in the nonadiabatic dynamics. In addition, there is no “ground truth” in terms of the selection of geometric feature representations. Different specialized representations should be employed according to problems under study. Since each of these descriptors provides a data representation in the non-orthogonal space, the analysis on them may give different results. In other words, we should choose the problem-specific feature representations and suitable feature subspaces to give the appropriate description of the data distribution patterns. In the current analysis of the ring deformation in the nonadiabatic dynamics, we proposed such a simple division strategy, because that it can give the reasonable geometric features and appropriate subspaces to represent our data. For other similar problems, it is always possible to find the suitable division ways based on the current philosophy.
Thirdly, we performed the dimensionality reduction method first, and the resulting low-dimensional space provides a direct view on the data distributions, which guides the selection of clustering methods and the adjustment of corresponding parameters. Here, although our proposed analysis protocol is based on these “unsupervised” machine learning algorithms, it still requires additional human inventions to select methods and tune parameters.27,28 The PCA-then-clustering procedure give us the ideas on the appropriate selection of clustering approaches and corresponding parameters.
Finally, the unsupervised machine learning methods are available from many standard machine-learning libraries, such as Scikit-learn Python toolkit. Therefore, one may easily transfer our current work to analyse the aromatic ring deformation of other similar molecular systems.
Although the current protocol was mainly developed to analyse the Tully's FSSH dynamics simulation results, in principle it can certainly be used to understand the simulations by other trajectory-based or Gaussian-wavepacket based nonadiabatic methods.3,10,12,13,107 For example, for the Ehrenfest dynamics, we may directly extract the geometries when the trajectories experience the minimum energy gaps between different electronic states, and use them to compare with the starting geometries. In addition, the similar idea can be used to analyse the results obtained from the ab initio multiple spawning method10 by finding the geometries at the spawning events. After different reaction channels are identified, the further analysis can be performed to gain the chemical insight behind each of them.
IV Conclusions
We proposed a hierarchical protocol based on the PCA and clustering methods to analyse the ring deformation in the nonadiabatic molecular dynamics in a rather automatic manner. This protocol is composed of two steps, i.e., the first step is to identify how many reaction channels are involved in the nonadiabatic dynamics evolution, and the second one tries to clarify which molecular motion is responsible for each decay channel. First, the PCA and clustering approaches were hierarchically performed to analyse different sets of DOFs in the ring moiety and end-group part successively until several reaction channels were obtained. Next, to clarify the major active coordinates responsible for each channel, the hopping geometries are compared with the corresponding initial ones by the PCA.In practice, we collected the internal coordinates of hopping geometries from the TSH nonadiabatic molecular dynamics simulation. Then, we constructed six descriptor sets (Dring, Aring, Rring, Deg, Aeg and Reg). Three of them with a subscript ring only include DOFs in the ring moiety, while the other three contains end-group DOFs. Here, D, A and R denote the dihedral angles, bond angles and bond distances, respectively. Based on these descriptor sets, we hierarchically employed the PCA and clustering methods to analyse the DOFs involving the ring part and end groups successively, until each of the cluster we obtained is non-separable. In principle, each non-separable cluster corresponds to a single reaction channel. After clarifying how many decay channels exit in the current nonadiabatic dynamics, we wanted to identify the major active coordinates and other geometric features responsible for each decay channel. For each, we place the corresponding hopping geometries and their relevant initial structures together, and then performed the PCA with the above six descriptor sets again. If the hopping geometries and the initial ones are well-separated along some leading reduced coordinates, we considered their important components to be the key active coordinates of the corresponding channel.
The nonadiabatic molecular dynamics of the keto isocytosine model was used to examine this hierarchical protocol. Following the above procedure, we totally found six excited-state nonadiabatic decay channels, and their dominant molecular motions were also clarified. The current hierarchical method based on unsupervised machine learning algorithms can capture the major evolution features of the nonadiabatic dynamics of realistic systems, such as the reaction channels, the branching ratios and the corresponding dominant motions. Particularly, this protocol shows the strong ability to characterize both the major and minor active molecular motions and the important features of the ring distortion in detail. Thus, it is a powerful approach to analyse the ring deformation in the trajectory-based nonadiabatic molecular dynamics simulation.
With the development of the computational facilities and the advances of theoretical simulation approaches, the nonadiabatic dynamics under study may involve more and more complicated systems with a huge number of DOFs. In this case, the analysis of the mass amount of high-dimensional data produced by the nonadiabatic molecular dynamics simulations, such as on-the-fly TSH, becomes necessary. In this sense, it is highly preferable to develop the automated analysis protocol for this purpose. Along with this idea, the current work proposed a suitable way to perform the analysis of the ring motion in the nonadiabatic dynamics. In more complicated realistic systems, we expect that the employment of suitable geometric descriptors should be essential for such analyses. Therefore, the application of more advanced molecular descriptors103–106 should be rather critical and challenging in the future.
Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
The authors express sincere thanks to the National Natural Science Foundation of China (No. 21873112, 21933011 and 21903030) for financial support. Some calculations in this paper were performed on the SunRising-1 computing environment in the Supercomputing Center, Computer Network Information Center, CAS.References
- W. Domcke and D. R. Yarkony, Role of conical intersections in molecular spectroscopy and photoinduced chemical dynamics, Annu. Rev. Phys. Chem., 2012, 63, 325–352 CrossRef CAS.
- S. Matsika and P. Krause, Nonadiabatic events and conical intersections, Annu. Rev. Phys. Chem., 2011, 62, 621–643 CrossRef CAS PubMed.
- W. Domcke, D. Yarkony and H. Köppel, Conical intersections: electronic structure, dynamics & spectroscopy, World Scientific, 2004, vol. 15 Search PubMed.
- W. Domcke, D. R. Yarkony and H. Köppel, Conical intersections: theory, computation and experiment, World Scientific, 2011, vol. 17 Search PubMed.
- S. Matsika, Electronic structure methods for the description of nonadiabatic effects and conical intersections, Chem. Rev., 2021, 121, 9407–9449 CrossRef CAS PubMed.
- H. Wang and M. Thoss, Multilayer formulation of the multiconfiguration time-dependent Hartree theory, J. Chem. Phys., 2003, 119, 1289–1299 CrossRef CAS.
- S. Paeckel, T. Köhler, A. Swoboda, S. R. Manmana, U. Schollwöck and C. Hubig, Time-evolution methods for matrix-product states, Annu. Phys., 2019, 411, 167998 CrossRef CAS.
- H.-D. Meyer, F. Gatti and G. A. Worth, Multidimensional quantum dynamics: MCTDH theory and applications, John Wiley & Sons, 2009 Search PubMed.
- M. Schröter, S. D. Ivanov, J. Schulze, S. P. Polyutov, Y. Yan, T. Pullerits and O. Kühn, Exciton–vibrational coupling in the dynamics and spectroscopy of Frenkel excitons in molecular aggregates, Phys. Rep., 2015, 567, 1–78 CrossRef.
- B. F. Curchod and T. J. Martínez, Ab initio nonadiabatic quantum molecular dynamics, Chem. Rev., 2018, 118, 3305–3336 CrossRef CAS.
- J. C. Tully, Molecular dynamics with electronic transitions, J. Chem. Phys., 1990, 93, 1061–1071 CrossRef CAS.
- S. Mai, P. Marquetand and L. González, Nonadiabatic dynamics: the SHARC approach, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1370 Search PubMed.
- M. Thoss and H. Wang, Semiclassical description of molecular dynamics based on initialvalue representation methods, Annu. Rev. Phys. Chem., 2004, 55, 299 CrossRef CAS.
- R. Crespo-Otero and M. Barbatti, Recent advances and perspectives on nonadiabatic mixed quantum–classical dynamics, Chem. Rev., 2018, 118, 7026–7068 CrossRef CAS PubMed.
- A. V. Akimov, A. J. Neukirch and O. V. Prezhdo, Theoretical insights into photoinduced charge transfer and catalysis at oxide interfaces, Chem. Rev., 2013, 113, 4496–4565 CrossRef CAS PubMed.
- L. Du and Z. Lan, An on-the-fly surface-hopping program jade for nonadiabatic molecular dynamics of polyatomic systems: implementation and applications, J. Chem. Theory Comput., 2015, 11, 1360–1374 CrossRef CAS.
- E. Tapavicza, I. Tavernelli and U. Rothlisberger, Trajectory surface hopping within linear response time-dependent density-functional theory, Phys. Rev. Lett., 2007, 98, 023001 CrossRef PubMed.
- G. Granucci and M. Persico, Critical appraisal of the fewest switches algorithm for surface hopping, J. Chem. Phys., 2007, 126, 134114 CrossRef PubMed.
- L. Wang, A. Akimov and O. V. Prezhdo, Recent progress in surface hopping: 2011–2015, J. Phys. Chem. Lett., 2016, 7, 2100–2112 CrossRef CAS.
- T. Nelson, S. Fernandez-Alberti, A. E. Roitberg and S. Tretiak, Nonadiabatic excited state molecular dynamics: modeling photophysics in organic conjugated materials, Acc. Chem. Res., 2014, 47, 1155–1164 CrossRef CAS PubMed.
- T. R. Nelson, A. J. White, J. A. Bjorgaard, A. E. Sifain, Y. Zhang, B. Nebgen, S. Fernandez-Alberti, D. Mozyrsky, A. E. Roitberg and S. Tretiak, Non-adiabatic excited-state molecular dynamics: theory and applications for modeling photophysics in extended molecular materials, Chem. Rev., 2020, 120, 2215–2287 CrossRef CAS PubMed.
- J. C. Tully, Perspective: nonadiabatic dynamics theory, J. Chem. Phys., 2012, 137, 22A301 CrossRef PubMed.
- A. J. Atkins and L. González, Trajectory surface-hopping dynamics including intersystem crossing in [Ru(bpy)3]2+, J. Phys. Chem. Lett., 2017, 8, 3840–3845 CrossRef CAS.
- S. Mai and L. González, Identification of important normal modes in nonadiabatic dynamics simulations by coherence, correlation, and frequency analyses, J. Chem. Phys., 2019, 151, 244115 CrossRef PubMed.
- F. Plasser, M. Barbatti, A. J. Aquino and H. Lischka, Excited-state diproton transfer in [2,2′-Bipyridyl]-3,3′-diol: the mechanism is sequential, not Concerted, J. Phys. Chem. A, 2009, 113, 8490–8499 CrossRef CAS PubMed.
- I. Borg and P. J. Groenen, Modern multidimensional scaling: Theory and applications, Springer Science & Business Media, 2005 Search PubMed.
- A. Glielmo, B. E. Husic, A. Rodriguez, C. Clementi, F. Noé and A. Laio, Unsupervised learning methods for molecular simulation data, Chem. Rev., 2021, 121, 9722–9758 CrossRef CAS PubMed.
- M. Ceriotti, Unsupervised machine learning in atomistic simulations, between predictions and understanding, J. Chem. Phys., 2019, 150, 150901 CrossRef PubMed.
- M. A. Rohrdanz, W. Zheng and C. Clementi, Discovering mountain passes via torchlight: methods for the definition of reaction coordinates and pathways in complex macromolecular reactions, Annu. Rev. Phys. Chem., 2013, 64, 295–316 CrossRef CAS PubMed.
- A. Amadei, A. B. Linssen and H. J. Berendsen, Essential dynamics of proteins, Proteins: Struct., Funct., Genet., 1993, 17, 412–425 CrossRef CAS.
- S. Reiter, T. Schnappinger and R. D. Vivie-Riedle, Using an Autoencoder for Dimensionality Reduction in Quantum Dynamics. International Conference on Artificial Neural Networks. 2019, pp. 783–787.
- J. P. Zauleck, S. Thallmair, M. Loipersberger and R. de Vivie-Riedle, Two new methods to generate internal coordinates for molecular wave packet dynamics in reduced dimensions, J. Chem. Theory Comput., 2016, 12, 5698–5708 CrossRef CAS PubMed.
- S. R. Hare, L. A. Bratholm, D. R. Glowacki and B. K. Carpenter, Low dimensional representations along intrinsic reaction coordinates and molecular dynamics trajectories using interatomic distance matrices, Chem. Sci., 2019, 10, 9954–9968 RSC.
- P. Das, M. Moll, H. Stamati, L. E. Kavraki and C. Clementi, Low-dimensional, free energy landscapes of protein-folding reactions by nonlinear dimensionality reduction, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 9885–9890 CrossRef CAS.
- W. Shi, T. Jia and A. Li, Quasi-classical trajectory analysis with isometric feature mapping and locally linear embedding: deep insights into the multichannel reaction on an NH3+ (4A) potential energy surface, Phys. Chem. Chem. Phys., 2020, 22, 17460–17471 RSC.
- T. Tsutsumi, Y. Ono, Z. Arai and T. Taketsugu, Visualization of the Dynamics Effect: Projection of on-the-Fly Trajectories to the Subspace Spanned by the Static Reaction Path Network, J. Chem. Theory Comput., 2020, 16, 4029–4037 CrossRef CAS PubMed.
- J. P. Zauleck and R. de Vivie-Riedle, Constructing grids for molecular quantum dynamics using an autoencoder, J. Chem. Theory Comput., 2018, 14, 55–62 CrossRef CAS PubMed.
- F. Häse, I. F. Galván, A. Aspuru-Guzik, R. Lindh and M. Vacher, How machine learning can assist the interpretation of ab initio molecular dynamics simulations and conceptual understanding of chemistry, Chem. Sci., 2019, 10, 2298–2307 RSC.
- P. Marquetand, J. J. Nogueira, S. Mai, F. Plasser and L. González, Challenges in simulating light-induced processes in DNA, Molecules, 2016, 22, 49 CrossRef.
- A. M. Virshup, J. Chen and T. J. Martínez, Nonlinear dimensionality reduction for nonadiabatic dynamics: the influence of conical intersection topography on population transfer rates, J. Chem. Phys., 2012, 137, 22A519 CrossRef PubMed.
- A. K. Belyaev, W. Domcke, C. Lasser and G. Trigila, Nonadiabatic nuclear dynamics of the ammonia cation studied by surface hopping classical trajectory calculations, J. Chem. Phys., 2015, 142, 104307 CrossRef PubMed.
- X. Li, Y. Xie, D. Hu and Z. Lan, Analysis of the geometrical evolution in on-the-fly surface-hopping nonadiabatic dynamics with machine learning dimensionality reduction approaches: classical multidimensional scaling and isometric feature mapping, J. Chem. Theory Comput., 2017, 13, 4611–4623 CrossRef CAS PubMed.
- X. Li, D. Hu, Y. Xie and Z. Lan, Analysis of trajectory similarity and configuration similarity in on-the-fly surface-hopping simulation on multi-channel nonadiabatic photoisomerization dynamics, J. Chem. Phys., 2018, 149, 244104 CrossRef.
- G. Capano, T. Penfold, M. Chergui and I. Tavernelli, Photophysics of a copper phenanthroline elucidated by trajectory and wavepacket-based quantum dynamics: a synergetic approach, Phys. Chem. Chem. Phys., 2017, 19, 19590–19600 RSC.
- J. Peng, Y. Xie, D. Hu and Z. Lan, Analysis of bath motion in MM-SQC dynamics via dimensionality reduction approach: principal component analysis, J. Chem. Phys., 2021, 154, 094122 CrossRef CAS PubMed.
- W. B. How, B. Wang, W. Chu, A. Tkatchenko and O. V. Prezhdo, Significance of the Chemical Environment of an Element in Nonadiabatic Molecular Dynamics: Feature Selection and Dimensionality Reduction with Machine Learning, J. Phys. Chem. Lett., 2021, 12, 12026–12032 CrossRef CAS PubMed.
- S. M. Mangan, G. Zhou, W. Chu and O. V. Prezhdo, Dependence between Structural and Electronic Properties of CsPbI3: Unsupervised Machine Learning of Nonadiabatic Molecular Dynamics, J. Phys. Chem. Lett., 2021, 12, 8672–8678 CrossRef CAS PubMed.
- M. Choi, D. Flam-Shepherd, T. H. Kyaw and A. Aspuru-Guzik, Learning quantum dynamics with latent neural ordinary differential equations, Phys. Rev. A, 2022, 105, 042403 CrossRef CAS.
- S. Yamazaki, W. Domcke and A. L. Sobolewski, Nonradiative decay mechanisms of the biologically relevant tautomer of guanine, J. Phys. Chem. A, 2008, 112, 11965–11968 CrossRef CAS.
- Z. Lan, E. Fabiano and W. Thiel, Photoinduced nonadiabatic dynamics of pyrimidine nucleobases: on-the-fly surface-hopping study with semiempirical methods, J. Phys. Chem. B, 2009, 113, 3548–3555 CrossRef CAS PubMed.
- Z. Lan, Y. Lu, E. Fabiano and W. Thiel, QM/MM nonadiabatic decay dynamics of 9H-adenine in aqueous solution, ChemPhysChem, 2011, 12, 1989–1998 CrossRef CAS PubMed.
- M. Barbatti, J. J. Szymczak, A. J. Aquino, D. Nachtigallová and H. Lischka, The decay mechanism of photoexcited guanine- A nonadiabatic dynamics study, J. Chem. Phys., 2011, 134, 01B606 CrossRef PubMed.
- M. Barbatti, Z. Lan, R. Crespo-Otero, J. J. Szymczak, H. Lischka and W. Thiel, Critical appraisal of excited state nonadiabatic dynamics simulations of 9H-adenine, J. Chem. Phys., 2012, 137, 22A503 CrossRef PubMed.
- D. Tuna, A. L. Sobolewski and W. Domcke, Mechanisms of ultrafast excited-state deactivation in adenosine, J. Phys. Chem. A, 2014, 118, 122–127 CrossRef CAS PubMed.
- T. N. Karsili, B. Marchetti, M. N. Ashfold and W. Domcke, Ab initio study of potential ultrafast internal conversion routes in oxybenzone, caffeic acid, and ferulic acid: implications for sunscreens, J. Phys. Chem. A, 2014, 118, 11999–12010 CrossRef CAS PubMed.
- L. A. Baker, B. Marchetti, T. N. Karsili, V. G. Stavros and M. N. Ashfold, Photoprotection: extending lessons learned from studying natural sunscreens to the design of artificial sunscreen constituents, Chem. Soc. Rev., 2017, 46, 3770–3791 RSC.
- A. Sobolewski, An approach to the”channel three” phenomenon of benzene, J. Chem. Phys., 1990, 93, 6433–6439 CrossRef CAS.
- I. J. Palmer, I. N. Ragazos, F. Bernardi, M. Olivucci and M. A. Robb, An MC-SCF study of the S1 and S2 876 photochemical reactions of benzene, J. Am. Chem. Soc., 1993, 115, 673–682 CrossRef CAS.
- D. t Cremer and J. Pople, General definition of ring puckering coordinates, J. Am. Chem. Soc., 1975, 97, 1354–1358 CrossRef CAS.
- M. Barbatti and K. Sen, Effects of different initial condition samplings on photodynamics and spectrum of pyrrole, Int. J. Quantum Chem., 2016, 116, 762–771 CrossRef CAS.
- L. Stojanović, S. Bai, J. Nagesh, A. F. Izmaylov, R. Crespo-Otero, H. Lischka and M. Barbatti, New Insights into the State Trapping of UV-Excited Thymine, Molecules, 2016, 21, 1603 CrossRef PubMed.
- J. C. Boeyens, The conformation of six-membered rings, J. Cryst. Mol. Struct., 1978, 8, 317–320 CrossRef.
- R. K. Cersonsky and S. De, Unsupervised Learning, in Quantum Chemistry in the age of Machine Learning, ed. P. O. Dral, Elsevier, 2022, https://github.com/rosecers/unsupervised-ml Search PubMed.
- S. Wold, K. Esbensen and P. Geladi, Principal component analysis, Chemom. Intell. Lab. Syst., 1987, 2(1–3), 37–52 CrossRef CAS.
- H. Abdi and L. J. Williams, Principal component analysis, Wiley Interdiscip. Rev. Comput. Stat., 2010, 2, 433–459 CrossRef.
- M. Ester, H.-P. Kriegel, J. Sander and X. Xu, et al., A density-based algorithm for discovering clusters in large spatial databases with noise, KDD, 1996, 226–231 Search PubMed.
- J. H. Ward Jr, Hierarchical grouping to optimize an objective function, J. Am. Stat. Assoc., 1963, 58, 236–244 CrossRef.
- L. Kaufman and P. J. Rousseeuw, Finding groups in data: an introduction to cluster analysis, John Wiley & Sons, 2009 Search PubMed.
- L. Gorb, Y. Podolyan and J. Leszczynski, A theoretical investigation of tautomeric equilibria and proton transfer in isolated and monohydrated cytosine and isocytosine molecules, J. Mol. Struct., 1999, 487, 47–55 CrossRef CAS.
- T.-K. Ha, H. Keller, R. Gunde and H. Gunthard, Quantum chemical study of structure and stability of all 14 isomers of isocytosine, J. Mol. Struct., 1996, 376, 375–397 CrossRef CAS.
- J. S. Kwiatkowski and J. Leszczynski, Density functional theory study on molecular structure and vibrational IR spectra of isocytosine, Int. J. Quantum Chem., 1997, 61, 453–465 CrossRef CAS.
- H. Vranken, J. Smets, G. Maes, L. Lapinski, M. J. Nowak and L. Adamowicz, Infrared spectra and tautomerism of isocytosine; an ab initio and matrix isolation study, Spectrochim. Acta, Part A, 1994, 50, 875–889 CrossRef.
- M. K. Shukla and J. Leszczynski, Investigations of the excited-state properties of isocytosine: an ab initio approach, Int. J. Quantum Chem., 2000, 77, 240–254 CrossRef CAS.
- R. I. Bakalska and V. B. Delchev, Comparative study of the relaxation mechanisms of the excited states of cytosine and isocytosine, J. Mol. Model., 2012, 18, 5133–5146 CrossRef CAS PubMed.
- R. Szabla, R. W. Góra and J. Šponer, Ultrafast excited-state dynamics of isocytosine, Phys. Chem. Chem. Phys., 2016, 18, 20208–20218 RSC.
- D. Hu, Y. F. Liu, A. L. Sobolewski and Z. Lan, Nonadiabatic dynamics simulation of keto isocytosine: a comparison of dynamical performance of different electronic structure methods, Phys. Chem. Chem. Phys., 2017, 19, 19168–19177 RSC.
- J. Segarra-Martí and M. J. Bearpark, Modelling Photoionisation in Isocytosine: Potential Formation of Longer-Lived Excited State Cations in its Keto Form, ChemPhysChem, 2021, 22, 2172–2181 CrossRef PubMed.
- P. Pulay and G. Fogarasi, Geometry optimization in redundant internal coordinates, J. Chem. Phys., 1992, 96, 2856–2860 CrossRef CAS.
- C. Peng, P. Y. Ayala, H. B. Schlegel and M. J. Frisch, Using redundant internal coordinates to optimize equilibrium geometries and transition states, J. Comput. Chem., 1996, 17, 49–56 CrossRef CAS.
- M. J. Frisch et al. , Gaussian 16 Revision C.01, Gaussian Inc., Wallingford CT, 2016 Search PubMed.
- P. Pulay, G. Fogarasi, F. Pang and J. E. Boggs, Systematic ab initio gradient calculation of molecular geometries, force constants, and dipole moment derivatives, J. Am. Chem. Soc., 1979, 101, 2550–2560 CrossRef CAS.
- G. Fogarasi, X. Zhou, P. W. Taylor and P. Pulay, The calculation of ab initio molecular geometries: efficient optimization by natural internal coordinates and empirical correction by offset forces, J. Am. Chem. Soc., 1992, 114, 8191–8201 CrossRef CAS.
- J. Baker, A. Kessi and B. Delley, The generation and use of delocalized internal coordinates in geometry optimization, J. Chem. Phys., 1996, 105, 192–212 CrossRef CAS.
- R. R. Coifman, S. Lafon, A. B. Lee, M. Maggioni, B. Nadler, F. Warner and S. W. Zucker, Geometric diffusions as a tool for harmonic analysis and structure definition of data: diffusion maps, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 7426–7431 CrossRef CAS PubMed.
- R. R. Coifman and S. Lafon, Diffusion maps, Appl. Comput. Harmon. A, 2006, 21, 5–30 CrossRef.
- M. Balasubramanian and E. L. Schwartz, The isomap algorithm and topological stability, Science, 2002, 295, 7 CrossRef.
- J. B. Tenenbaum, V. D. Silva and J. C. Langford, A global geometric framework for nonlinear dimensionality reduction, Science, 2000, 290, 2319–2323 CrossRef CAS.
- G. Hinton, Stochastic neighbor embedding, Adv. Neural Inf. Process. Syst., 2003, 15, 857–864 Search PubMed.
- L. Van der Maaten and G. Hinton, Visualizing data using t-SNE, J. Mach. Learn. Res., 2008, 9, 2579–2605 Search PubMed.
- T. Hastie, R. Tibshirani, J. H. Friedman and J. H. Friedman, The elements of statistical learning: data mining, inference, and prediction, Springer, 2009, vol. 2 Search PubMed.
- H.-P. Kriegel, P. Kröger, J. Sander and A. Zimek, Density-based clustering, Wiley Interdiscip. Rev. Data Min. Knowl., 2011, 1, 231–240 CrossRef.
- E. Schubert, J. Sander, M. Ester, H. P. Kriegel and X. Xu, DBSCAN revisited, revisited: why and how you should (still) use DBSCAN, ACM T. Database Syst., 2017, 42, 1–21 CrossRef.
- A. D. Gordon, A review of hierarchical classification, J. R. Sata. Soc. A Stat., 1987, 150, 119–137 Search PubMed.
- S. Landau, M. Leese, D. Stahl and B. S. Everitt, Cluster analysis, John Wiley & Sons, 2011 Search PubMed.
- https://github.com/zglan/JADE-NAMD .
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schütz, P. Celani, T. Korona, R. Lindh, A. Mitrushenkov and G. Rauhut, et al., MOLPRO, version 2012.1, a package of ab initio programs, 2012, see https://www.molpro.net..
- C. Zhu, S. Nangia, A. W. Jasper and D. G. Truhlar, Coherent switching with decay of mixing: an improved treatment of electronic coherence for non-Born–Oppenheimer trajectories, J. Chem. Phys., 2004, 121, 7658–7670 CrossRef CAS.
- A. Zimek, E. Schubert and H.-P. Kriegel, A survey on unsupervised outlier detection in high-dimensional numerical data, Stat. Anal. Data Min., 2012, 5, 363–387 CrossRef.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss and V. Dubourg, et al., Scikit-learn: Machine learning in Python, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- B. Efron and R. J. Tibshirani, An introduction to the bootstrap, CRC Press, 1994 Search PubMed.
- H. Varian, Bootstrap tutorial, Mathematica J., 2005, 9, 768–775 Search PubMed.
- D. R. Yarkony, On the adiabatic to diabatic states transformation near intersections of conical intersections, J. Chem. Phys., 2000, 112, 2111–2120 CrossRef CAS.
- K. T. Schütt, H. E. Sauceda, P.-J. Kindermans, A. Tkatchenko and K.-R. Müller, Schnet–a deep learning architecture for molecules and materials, J. Chem. Phys., 2018, 148, 241722 CrossRef.
- L. Zhang, J. Han, H. Wang, W. Saidi and R. Car, et al., End-to-end symmetry preserving inter-atomic potential energy model for finite and extended systems, Adv. Neural Inf. Process. Syst., 2018, 31, 4436–4446 Search PubMed.
- Y. Zhang, C. Hu and B. Jiang, Embedded atom neural network potentials: efficient and accurate machine learning with a physically inspired representation, J. Phys. Chem. Lett., 2019, 10, 4962–4967 CrossRef CAS PubMed.
- Y. Zhang, J. Xia and B. Jiang, Physically motivated recursively embedded atom neural networks: incorporating local completeness and nonlocality, Phys. Rev. Lett., 2021, 127, 156002 CrossRef CAS PubMed.
- D. V. Makhov, C. Symonds, S. Fernandez-Alberti and D. V. Shalashilin, Ab initio quantum direct dynamics simulations of ultrafast photochemistry with multiconfigurational Ehrenfest approach, Chem. Phys., 2017, 493, 200–218 CrossRef CAS.
Footnotes |
| † The codes of the current work are also available on GitHub (https://github.com/Yifei-Zhu/PCA_ring.git). |
| ‡ Electronic supplementary information (ESI) available: More details of the theoretical methods and computational details; the time-dependent occupations of electronic states and related discussions; more additional PCA results; the statistical significance analysis of the PCA results; the structural information of the S0 minimum, as well as the averaged structure and the typical one of each channel; the optimized structure and the branching space of each CI. See DOI: https://doi.org/10.1039/d2cp03323b |
| This journal is © the Owner Societies 2022 |