Open Access Article
Open Access ArticleExploiting the “Lego brick” approach to predict accurate molecular structures of PAHs and PANHs†
Hexu
Ye
 a,
Silvia
Alessandrini
a,
Silvia
Alessandrini
 ab,
Mattia
Melosso
ab,
Mattia
Melosso
 ac and
Cristina
Puzzarini
ac and
Cristina
Puzzarini
 *a
*a
aDipartimento di Chimica “Giacomo Ciamician”, Università di Bologna, Via F. Selmi 2, 40126 Bologna, Italy. E-mail: cristina.puzzarini@unibo.it
bScuola Normale Superiore, Piazza dei Cavalieri 7, 56126 Pisa, Italy
cScuola Superiore Meridionale, Largo San Marcellino 10, 80138 Naples, Italy
First published on 31st August 2022
Abstract
Polycyclic aromatic hydrocarbons (PAHs) and polycyclic aromatic nitrogen heterocycles (PANHs) are important and ubiquitous species in space. However, their accurate structural and spectroscopic characterization is often missing. To fill this gap, we exploit the so-called “Lego brick” approach [Melli et al., J. Phys. Chem. A, 2021, 125, 9904] to evaluate accurate rotational constants of some astrochemically relevant PAHs and PANHs. This model is based on the assumption that a molecular system can be seen as formed by smaller fragments for which a very accurate equilibrium structure is available. Within this model, the “template molecule” (TM) approach is employed to account for the modifications occurring when going from the isolated fragment to the molecular system under investigation, with the “linear regression” model being exploited to correct the linkage between different fragments. In the present work, semi-experimental equilibrium structures are used within the TM model. The performance of the “Lego brick” approach has been first tested for a set of small PA(N)Hs for which experimental data are available, thus leading to the conclusion that it is able to provide rotational constants with a relative accuracy well within 0.1%. Subsequently, it has been extended to the accurate prediction of the rotational constants for systems lacking any spectroscopic characterization.
1 Introduction
Astronomical observations have led to the identification of more than 270 molecular species in the interstellar medium (ISM) and circumstellar shells.1,2 These span from simple hydrides (such as H2, H2O, and NH3) to the so-called “interstellar complex organic molecules” (i.e. C-containing molecular species with more than five atoms), to polycyclic aromatic hydrocarbons (PAHs).1–4 However, only a few molecules containing 12 atoms or more have been detected in the gas phase of the ISM. To give a few examples, simple aromatic species such as benzonitrile and cyanonaphthalene have been identified in the cold-core Taurus Molecular Cloud-1 (TMC-1).5,6 In addition, fullerenes (C60, C60+, and C70) have also been discovered in space and are thought to play a role in the chemistry and physics of the ISM and star-forming regions.7,8It is widely accepted that PAHs and polycyclic aromatic nitrogen heterocycles (PANHs) are wide spread throughout the universe, and they usually exist as medium-to-large-sized molecular systems.9 Their presence has been inferred from the prominent unidentified infrared (UIR) features, which are in good agreement with the characteristic stretching of the aromatic C–C and C–H bonds.10–13 However, the detection of specific carbonaceous molecules via infrared (IR) astronomical spectroscopy is extremely challenging because of its limited selectivity. In fact, the transition frequency of a given vibrational mode varies marginally when changing the molecular environment.
For gas-phase molecules, rotational transitions are often considered as “molecular fingerprints”. Indeed, most interstellar molecules (∼90%) have been discovered thanks to the observation of their rotational transitions via radioastronomy,4 and this technique can also be applied to the identification of PA(N)Hs. However, a major drawback is that PAHs are either nonpolar or weakly polar (i.e. a dipole moment of 0.5 D or smaller), and this might preclude not only their astronomical observation but also their laboratory characterisation.5,6,14 This shortcoming can be overcome by investigating the cyano-substituted derivatives (R–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N), which usually have large permanent dipole moments and thus intense rotational lines. Owing to the abundance of the CN radical in the ISM4 and its great reactivity,15,16 these species can be considered good proxies of PAHs, and the same applies to CCH-substituted and/or protonated species.5,6,17 Concerning PANHs, their pure rotational spectra are somewhat easier to observe because of the larger dipole moment due to the N atom. An example in this respect is provided by the experimental characterization of phenanthridine, acridine, and 1,10-phenanthroline.18 However, PA(N)Hs of small dimensions that could be present in the ISM are far from being well characterised.
N), which usually have large permanent dipole moments and thus intense rotational lines. Owing to the abundance of the CN radical in the ISM4 and its great reactivity,15,16 these species can be considered good proxies of PAHs, and the same applies to CCH-substituted and/or protonated species.5,6,17 Concerning PANHs, their pure rotational spectra are somewhat easier to observe because of the larger dipole moment due to the N atom. An example in this respect is provided by the experimental characterization of phenanthridine, acridine, and 1,10-phenanthroline.18 However, PA(N)Hs of small dimensions that could be present in the ISM are far from being well characterised.
The first step toward the identification of molecules in space is their spectroscopic characterization in laboratory, which often requires accurate predictions of the spectroscopic parameters involved. In rotational spectroscopy, the leading terms are the rotational constants, whose equilibrium values only depend on the equilibrium structure. Quantum-chemical (QC) calculations can provide accurate equilibrium structures whenever methodologies rooted in the coupled-cluster theory, at least accounting for extrapolation to the complete basis set (CBS) limit and core-correlation effects, are employed.19–23 In particular, highly accurate results are obtained by exploiting composite schemes. These account for the most important contributions evaluated at the best possible level (according to the dimension of the system) and then combined, thereby relying on additivity approximation.19,20,24–26 However, the sizes of PA(N)Hs and their functionalized forms prevent from the employment of any composite scheme. To obtain accurate equilibrium structures while retaining a feasible computational cost, a possible way-out is offered by the so-called “Lego brick” approach.27 This is based on the idea that medium-to-large systems can be seen as formed by different fragments (i.e., the “Lego bricks”), whose accurate equilibrium geometries are available. The template molecule (TM) approach28 is then used to account for the modifications occurring when moving from the isolated fragment to the molecular system under consideration. Furthermore, the linear regression (LR) model can be employed to correct the linkage between different fragments.29,30 While the composite schemes mentioned above can be exploited for the accurate determination of the equilibrium structure of the fragments, in this work, we resort to the so-called semi-experimental (SE) approach.31,32 In ref. 27, the resulting model has been denoted as the TM-SE_LR approach. Here, we refer to it simply as TM+LR (only TM if LR is not applied).
The reliability, robustness, and accuracy of this model have been demonstrated in ref. 27. In such an investigation, the SE structures of two fragments were used to template the geometrical parameters of larger systems obtained using a double-hybrid density functional in conjunction with a partially augmented triple-zeta basis set. To give an example, benzonitrile (C7H5N) can be considered formed by the benzene ring and the CN group from HCN, whose SE structures are available in the literature. While DFT provides equilibrium rotational constants that deviate on average by ∼0.4% with respect to the semi-experimental equilibrium values (that were obtained by subtracting computed vibrational corrections from experimental ground-state rotational constants), the TM+LR approach reduces the discrepancy to 0.02%. Furthermore, its application to 3-phenyl-2-propynenitrile and its isomers demonstrated that it can be successfully applied to systems containing more than two fragments.27
Based on the results obtained in ref. 27, in this work we apply the TM+LR approach to small PAHs and PANHs (and their cyano and ethynyl derivatives) of astrochemical relevance. After a detailed description of the methodology (see the next section), a data set of 18 small PAHs and PANHs for which experimental rotational constants are available has been used for validation. Then, a set of 13 species that have not been experimentally characterised yet has been considered and their accurate structure and rotational constants have been provided by exploiting the TM+LR approach. For this set of PA(N)Hs, the rotational spectra have also been simulated. Finally, in the concluding remarks, a particular emphasis is placed on the support to the field of high-resolution molecular spectroscopy as well as to the applicability of this approach to the characterisation of even larger systems. A critical discussion about the limitations of the TM(+LR) approach is also provided.
2 Methodology
As briefly explained in the Introduction, the “Lego brick” TM+LR approach is a cost-effective model to obtain accurate equilibrium structures. To summarize, it is based on identifying, within the molecule under investigation, fragments that belong to a smaller system for which a SE equilibrium geometry is available. The TM approach is employed to exploit these accurate data and apply them to the system under consideration, while corrections to the structural parameters linking the various fragments are obtained using the LR approach. In the following, a description of the three approaches involved, i.e. TM, LR and SE, is given.2.1 The template molecule (TM) approach
The TM approach combines low-level QC calculations with corrections from either high-level QC computations or SE equilibrium structures. As already mentioned, in the present study, we make use of the latter option. In the TM approach,28 the accurate structural parameters of the target molecule (rTe) are obtained via the following equation:| rTe = rDFT,Te + ΔrTM,Fe | (1) |
| ΔrTM,Fe = rSE,Fe − rDFT,Fe | (2) |
In this work, the DFT level considered is the double-hybrid rev-DSDPBEP86 (revDSD) functional33 in conjunction with the may-cc-pVTZ triple-ζ (mayTZ) basis set,34 which is equivalent to a minimally augmented triple-zeta basis set. DFT calculations also incorporate dispersion corrections by means of the Grimmes DFT-D3 scheme35 together with the Becke-Johnson damping function.36
2.2 The linear regression (LR) approach
In the TM approach, all parameters can be effectively adjusted except the bonds and angles connecting the fragments. These might be kept fixed at the corresponding DFT value. However, they can be improved by applying a LR correction taken from a purposely set up database.30 In such a case, the correction to the linkage between two fragments is computed as follows:| ΔrLRe = a × rDFTe + b. | (3) |
Consequently, the corrected linkage structural parameter of the target molecule is given by
| rTe = (1 + a) × rDFT,Te + b. | (4) |
In both equations, a and b are the linear regression parameters and depend on the DFT level chosen.30 In this work, we employ a corrective factor for the linkage C–C (a = −0.00184 and b = 0) and C–O (a = −0.00297 and b = 0) bonds.30
2.3 The semi-experimental (SE) approach
SE equilibrium structural parameters are determined by a linear least-squares fit of the SE equilibrium rotational constants (BSEe) of different isotopologues. The BSEe values are obtained by correcting the experimental ground-state rotational constants (Bexp0) with computed vibrational (ΔBcalcvib) corrections:31| BSEe = Bexp0 − ΔBcalcvib, | (5) |
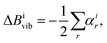 | (6) |
SE experimental structures have been collected from databases,28,29 such as the “SE100 database”.30
2.4 Benchmark for small PAHs and PANHs
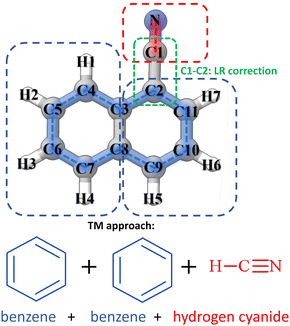
An overall graphical description of the TM+LR approach is provided in Fig. 1, where 1-cyanonaphthalene is used as an example. This molecule can be seen as containing three fragments, CN (from HCN) and two benzene rings, with only one linkage bond being present in the system. This is the C1–C2 distance, while none is required between the two benzene rings because the internal coordinates defining 1-cyanonaphthalene do not involve it (intrinsically defined as shown in Fig. 1, blue contour). According to what presented above, to apply the TM+LR approach, geometry optimizations are carried out at the revDSD/mayTZ level for 1-cyanonaphthalene, benzene and HCN. Then, the structural parameters of the CN group and the biphenyl ring fragment of 1-cyanonaphthalene are corrected using eqn (1) and (2) together with the SE data available in the “SE100 database”. The C2-C3 bond length is corrected using the LR coefficients provided above.To test the accuracy of the equilibrium structures obtained using the TM+LR approach, a benchmark study has been performed by comparing the corresponding rotational constants with the experimental counterparts. To have a meaningful comparison, the TM/TM+LR equilibrium rotational constants have been corrected for vibrational contributions computed using the hybrid B3LYP-D3BJ (hereafter B3) functional37,38 in conjunction with the jun-cc-pVDZ basis set (junDZ).34
The data set for the benchmark test contains small PA(N)Hs and derivatives, whose experimental data are available in the literature (ref. 18 and 39–49). They are shown in Fig. 2 and grouped according to their fragment composition. It is noted that they can be classified into three main groups:
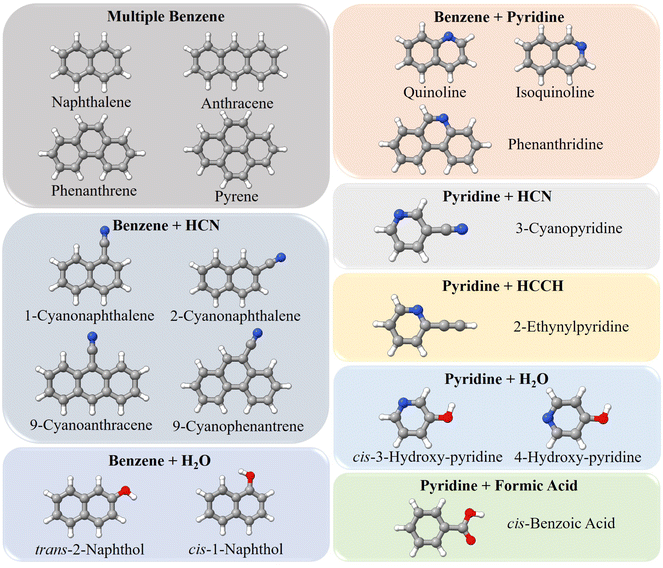 | ||
| Fig. 2 Molecules employed in the benchmark study: they are grouped according to their “Lego brick” fragments. | ||
• Molecules with benzene as the main fragment: naphthalene, anthracene, phenanthrene, 1-cyanonaphthalene, 2-cyanonaphthalene, 9-cyanoanthracene, 9-cyanophenantrene, cis-1-naphthol and trans-2-naphthol
• Molecules formed by benzene and pyridine: quinoline, isoquinoline, and phenanthridine;
• Molecules derived from pyridine: 3-cyanopyridine, 2-ethynylpyridine, cis-3-hydroxypyridine, 4-hydroxypyridine, and benzoic acid.
The SE equilibrium structural parameters of the fragments, i.e. benzene, pyridine, HCN, HCCH, and H2O as well as trans-formic acid (CH2O2), are taken from the “SE100 database”. All DFT calculations reported in this study have been carried out using the Gaussian 16 suite of programs.50
3 Results and discussion
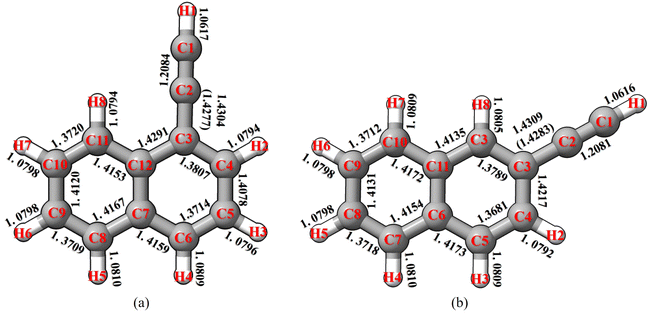
1-Cyanonaphthalene and 2-cyanonaphthalene have been selected as the first prototype models to test the TM/TM+LR approaches. For these species, the first point to clarify is that whether the CCN moiety is linear or slightly bent. To this aim, a non-covalent interaction (NCI) analysis,51,52 which provides an indication of the intramolecular non-covalent interactions on the basis of the electron density and its derivatives, has been carried for 1-cyanonaphthalene. The non-covalent interaction regions have been computed using the NCI plot program packages52 and the revDSD/mayTZ electronic density, and have been visualized using the VMD software.53 The results are shown in Fig. 3a, where a weak interaction between C1 and H1 is observed, thus pointing out the non-linearity of the CCN group. However, the revDSD/mayTZ structural parameters (see Fig. 3b) do not change noticeably when the angle is kept fixed at 180°, thereby stressing the weakness of such an interaction. The comparison of rotational constants for the two possible situations, namely the CCN angle fixed at 180° or unconstrained, is shown in Table 1. It is noted that the A rotational constant is the most affected by non-linearity. Indeed, changing the CCN angle by about 0.6° from linearity leads, at the revDSD/mayTZ level, to Ae varying from 1484.804 MHz (180°) to 1482.617 MHz, with the corresponding relative discrepancy with respect to the experimental ground-state value reducing from 0.40% to 0.25%. However, when considering all three rotational constants, the mean error remains very similar, i.e. it reduced from 0.19% (180°) to 0.18%. If one introduces the vibrational corrections at the B3/junDZ level, the overall discrepancy increases: 0.42% for the linear arrangement and 0.39% for the unconstrained one, but still they are very similar to each other and conclusions cannot be drawn about the non-linearity of the CCN group. Improving the equilibrium structure of 1-cyanonaphtalene using the TM approach leads to equilibrium values which are somewhat worse than the revDSD ones; however, once vibrational corrections are incorporated, the mean deviations from the experiment improve noticeably, namely 0.23% when considering the CCN frame as linear and 0.11% for the non-linear case. Above all, these discrepancies suggest that in 1-cyanonaphtalene the CCN moiety is non-linear. In detail, for the latter case, the deviations from the experiment are 0.04% for A, 0.18% for B, and 0.10% for C. When applying the LR correction to the C1–C2 bond while accounting for vibrational corrections, the results further improve, with an averaged deviation of 0.09% with respect to the experiment.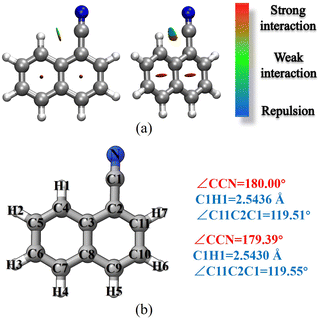 | ||
| Fig. 3 1-cyanonaphthalene: (a) non-covalent interactions; (b) atom labeling and selected revDSD/mayTZ structural parameters. | ||
| Parameter | Experimenta | B e (revDSD) | B e (revDSD) + ΔBvib | B e (TM) | B e (TM) + ΔBvib | B e (TM+LR) | B e (TM+LR) + ΔBvib |
|---|---|---|---|---|---|---|---|
| 1-Cyanonaphthalene | |||||||
| a Ref. 43. b Relative errors with respect to the experiment are provided in square brackets. c Mean absolute error (%) with respect to the experiment. | |||||||
| ∠CCN = 180° | |||||||
| A/MHz | 1478.848334(84) | 1484.804 [0.40]b | 1475.955 [−0.13] | 1489.540 [0.72] | 1481.691 [0.19] | 1490.180 [0.76] | 1482.331 [0.24] |
| B/MHz | 956.784207(37) | 956.248 [−0.06] | 950.460 [−0.66] | 959.184 [0.25] | 953.396 [−0.35] | 959.658 [0.30] | 953.870 [−0.30] |
| C/MHz | 580.9889759(74) | 581.651 [0.11] | 578.336 [−0.46] | 583.464 [0.43] | 580.149 [−0.14] | 583.738 [0.51] | 580.423 [−0.10] |
| MAEc | 0.19 | 0.42 | 0.47 | 0.23 | 0.51 | 0.21 | |
| ∠CCN ≠ 180° | |||||||
| A/MHz | 1482.617 [0.25] | 1474.790 [−0.27] | 1487.332 [0.57] | 1479.505 [0.04] | 1487.976 [0.62] | 1480.149 [0.09] | |
| B/MHz | 957.909 [0.12] | 952.098 [−0.49] | 960.853 [0.43] | 955.042 [−0.18] | 961.331 [0.48] | 955.520 [−0.13] | |
| C/MHz | 581.929 [0.16] | 578.609 [−0.41] | 583.742 [0.47] | 580.422 [−0.10] | 584.017 [0.52] | 580.697 [−0.05] | |
| MAEc | 0.18 | 0.39 | 0.49 | 0.11 | 0.54 | 0.09 | |
| 2-Cyanonaphthalene | |||||||
|---|---|---|---|---|---|---|---|
| A 0/MHz | 2707.009944 (102) | 2713.488 [0.24] | 2695.083 [−0.44] | 2722.767 [0.58] | 2704.362 [−0.10] | 2722.910 [0.59] | 2704.505 [−0.09] |
| B 0/MHz | 606.0955051 (134) | 607.067 [0.16] | 604.044 [−0.34] | 608.912 [0.46] | 605.889 [−0.03] | 609.263 [0.52] | 606.240 [0.02] |
| C 0/MHz | 495.2935210 (104) | 496.082 [0.16] | 493.505 [−0.36] | 497.625 [0.47] | 495.048 [−0.05] | 497.864 [0.52] | 495.287 [0.00] |
| MAE | 0.19 | 0.38 | 0.51 | 0.06 | 0.54 | 0.04 | |
It is interesting to note that 1- and 2-cyanonaphtalene can also be seen as formed by only two fragments: benzene and benzonitrile (C6H5CN), and the SE structure of the latter is available in ref. 54. This different approach is illustrated in Fig. S1 of the (ESI†), and the results are collected in Table S1 of the ESI.† In this case, the CCN moiety in 1-cyanonaphtalene is forced to be linear like in benzonitrile. The results for this different TM scheme seem to be slightly improved, and the MAEs are 0.08% and 0.05% for 1- and 2-cyanonaphthalene, respectively. This improvement is mainly due to the B and C rotational constants, while the A rotational constants worsen. Therefore, the conclusion drawn is that the TM approach benefits from the removal of the linking bond between C1 and C2, which is somewhat counterbalanced by considering the CCN group as linear.
As far as 2-cyanonaphtalene is concerned, the CCN group is undoubtedly linear and the trend for the models considered is very similar to what discussed above for 1-cyanonaphtalene. Indeed, the best results are obtained using the TM+LR approach, with a MAE of 0.04% and an error smaller than 0.01% for the C rotational constant, with the largest improvement being due to the introduction of the TM corrections.
3.1 The benchmark study: the “Lego brick” approach applied to small PAHs and PANHs
After the preliminary investigation on 1- and 2-cyanonaphtalene, we moved to the application of the TM/TM+LR approach to the benchmark data set introduced above. The results are summarized in Table 2, where computed rotational constants incorporating vibrational corrections are reported together with the deviations from the corresponding experimental ground-state rotational constants. Vibrational corrections (B3/junDZ level) are found in Table S2 of the ESI,† while the comparison between the experimental data and computed equilibrium values is provided in Table S3 (ESI†). In the case of naphthalene, anthracene, phenanthrene, pyrene, as well as quinoline, isoquinoline, and phenanthridine, the fragments chosen for the TM approach are benzene and/or pyridine. Hence, there is no linkage bond between the fragments. For all of them except phenanthrene, the average error of about 0.4% when revDSD/mayTZ is considered for equilibrium rotational constants. This error reduces by one order of magnitude when the TM approach is applied, i.e. it becomes about 0.04%. For example, for quinoline and isoquinoline, the TM approach leads to B and C rotational constants that show an error of 0.01% or smaller, while the largest error is associated with A and is 0.03%. This is a general outcome, and the discrepancy for A never exceeds 0.1% (anthracene). For phenantrene, the situation is different. We note a MAE of 0.13% at the revDSD/mayTZ level, which becomes 0.46% once the TM approach is applied. Since there is no reason why the TM approach should fail for this specific molecule while being successful for anthracene and pyrene, we expect that the experimental rotational constants are affected by some issues.41 However, the list of assigned transitions is not available and we were not able to further investigate such a discrepancy.| revDSD/mayTZ | TMb | TM+LR | revDSD/mayTZ | TMb | TM+LR | ||
|---|---|---|---|---|---|---|---|
| a Vibrational corrections at the B3/junDZ level of theory. b Naphthalene: two benzene molecules; anthracene: three benzene molecules; phenanthrene: three benzene molecules; pyrene: four benzene molecules; 9-cyanoanthracene: three benzene molecules and HCN; 9-cyanophenantrene: three benzene molecules and HCN; trans-2-naphthol: two benzene molecules and H2O; cis-1-naphthol: two benzene molecules and H2O; phenanthridine: two benzene molecules and pyridine; 3-cyanopyridine: pyridine and HCN; 2-ethynylpyridine: pyridine and HCN; cis-3-hydroxy-pyridine: pyridine and H2O; 4-hydroxy-pyridine: pyridine and H2O; benzoic acid: benzene and trans-formic acid. c Relative errors with respect to experimental ground-state rotational constants are provided in square brackets. d Mean absolute error (in %) with respect to the experiment. | |||||||
| Naphthalene | Anthracene | ||||||
| A 0/MHz | 3107.376 [−0.39]c | 3118.166 [−0.04] | A 0/MHz | 2136.777 [−0.44] | 2143.819 [−0.11] | ||
| B 0/MHz | 1228.749 [−0.34] | 1232.779 [−0.02] | B 0/MHz | 450.902 [−0.36] | 452.376 [−0.04] | ||
| C 0/MHz | 880.709 [−0.36] | 883.645 [−0.03] | C 0/MHz | 372.435 [−0.43] | 373.654 [−0.10] | ||
| MAEd | 0.36 | 0.03 | MAE | 0.41 | 0.08 | ||
| Phenanthrene | Pyrene | ||||||
| A 0/MHz | 1609.152 [0.15] | 1614.548 [0.48] | A 0/MHz | 1007.330 [−0.37] | 1010.590 [−0.05] | ||
| B 0/MHz | 550.233 [0.10] | 551.997 [0.42] | B 0/MHz | 554.594 [−0.31] | 556.387 [0.02] | ||
| C 0/MHz | 410.163 [0.15] | 411.493 [0.47] | C 0/MHz | 357.768 [−0.33] | 358.925 [−0.01] | ||
| MAE | 0.13 | 0.46 | MAE | 0.34 | 0.02 | ||
| 9-Cyanoanthracene | 9-Cyanophenantrene | ||||||
| A 0/MHz | 981.590 [−0.43] | 984.547 [−0.13] | 985.342 [−0.05] | A 0/MHz | 842.512 [−0.43] | 845.175 [−0.06] | 845.507 [−0.07] |
| B 0/MHz | 449.739 [−0.32] | 451.174 [−0.01] | 451.174 [−0.01] | B 0/MHz | 484.613 [−0.36] | 486.116 [−0.06] | 486.248 [−0.03] |
| C 0/MHz | 308.490 [−0.36] | 309.457 [−0.05] | 309.535 [−0.03] | C 0/MHz | 307.726 [−0.39] | 308.687 [−0.08] | 308.784 [−0.05] |
| MAE | 0.37 | 0.06 | 0.03 | MAE | 0.39 | 0.08 | 0.05 |
| trans-2-Naphthol | cis-1-Naphthol | ||||||
| A 0/MHz | 2834.666 [−0.38] | 2844.215 [−0.04] | 2844.763 [−0.02] | A 0/MHz | 1939.026 [−0.44] | 1944.532 [−0.15] | 1946.589 [−0.05] |
| B 0/MHz | 822.384 [−0.38] | 824.730 [−0.10] | 825.329 [−0.03] | B 0/MHz | 1120.756 [−0.32] | 1124.286 [0.002] | 1124.496 [0.02] |
| C 0/MHz | 637.619 [−0.39] | 639.512 [−0.09] | 639.900 [−0.03] | C 0/MHz | 710.552 [−0.36] | 712.709 [−0.05] | 713.068 [0.004] |
| MAE | 0.38 | 0.08 | 0.03 | MAE | 0.39 | 0.07 | 0.02 |
| Quinoline | Isoquinoline | ||||||
| A 0/MHz | 3134.015 [−0.37] | 3144.744 [−0.03] | A 0/MHz | 3186.754 [−0.38] | 3197.923 [−0.03] | ||
| B 0/MHz | 1267.000 [−0.36] | 1271.620 [0.003] | B 0/MHz | 1233.765 [−0.34] | 1237.959 [0.002] | ||
| C 0/MHz | 902.407 [−0.37] | 905.639 [−0.01] | C 0/MHz | 889.579 [−0.36] | 892.629 [−0.01] | ||
| MAE | 0.36 | 0.01 | MAE | 0.36 | 0.01 | ||
| Phenanthridine | 3-Cyanopyridine | ||||||
| A 0/MHz | 1637.168 [−0.32] | 1642.560 [0.01] | A 0/MHz | 5806.743 [−0.28] | 5828.346 [0.09] | 5828.349 [0.09] | |
| B 0/MHz | 555.417 [−0.42] | 557.319 [−0.07] | B 0/MHz | 1564.951 [−0.41] | 1569.544 [−0.12] | 1571.299 [−0.003] | |
| C 0/MHz | 414.855 [−0.40] | 416.261 [−0.06] | C 0/MHz | 1232.434 [−0.38] | 1236.256 [−0.07] | 1237.347 [0.01] | |
| MAE | 0.38 | 0.05 | MAE | 0.36 | 0.09 | 0.04 | |
| 2-Ethynylpyridine | cis-3-Hydroxy-pyridine | ||||||
| A 0/MHz | 5840.592 [−0.29] | 5861.682 [0.07] | 5861.683 [0.07] | A 0/MHz | 5799.384 [−0.30] | 5818.882 [0.03] | 5818.880 [0.03] |
| B 0/MHz | 1575.320 [−0.40] | 1579.432 [−0.14] | 1581.163 [−0.03] | B 0/MHz | 2677.827 [−0.44] | 2684.360 [−0.20] | 2688.875 [−0.03] |
| C 0/MHz | 1240.423 [−0.38] | 1243.924 [−0.10] | 1244.999 [−0.01] | C 0/MHz | 1831.952 [−0.41] | 1836.955 [−0.13] | 1839.069 [−0.02] |
| MAE | 0.35 | 0.10 | 0.04 | MAE | 0.38 | 0.12 | 0.03 |
| 4-Hydroxy-pyridine | cis-Benzoic acid | ||||||
| A 0/MHz | 5969.478 [−0.35] | 5990.387 [−0.001] | 5990.389 [−0.001] | A 0/MHz | 3855.244 [−0.44] | 3872.310 [0.001] | 3872.312 [0.001] |
| B 0/MHz | 2621.113 [−0.41] | 2627.396 [−0.17] | 2631.857 [0.001] | B 0/MHz | 1221.700 [−0.46] | 1224.776 [−0.21] | 1226.332 [−0.08] |
| C 0/MHz | 1821.369 [−0.40] | 1826.347 [−0.12] | 1828.504 [−0.01] | C 0/MHz | 928.230 [−0.46] | 930.991 [−0.17] | 931.889 [−0.07] |
| MAE | 0.38 | 0.10 | 0.003 | MAE | 0.45 | 0.13 | 0.05 |
In Table 2, the results for 9-cyanoanthracene, 9-cyanophenantrene, trans-2-naphthol, cis-1-naphthol, 3-cyanopyridine, 2-ethynylpyridine, cis-3-hydroxy-pyridine, 4-hydroxy-pyridine, and cis-benzoic acid are also given. Analogously to the set of molecules discussed above, the MAE for revDSD/mayTZ rotational constants is about 0.4% and the accuracy of the results is greatly improved when applying the TM approach, with the MAE reducing to 0.1% or less. The largest deviation observed is about 0.2% and it has been obtained for the B rotational constants of cis-3-hydroxy-pyridine, 4-hydroxy-pyridine, and benzoic acid. For 9-cyanoanthracene, 9-cyanophenantrene, 3-cyanopyridine, 2-ethynylpyridine, and benzoic acid, the LR correction can be introduced and leads to a further improvement, and the MAE is on average 0.06%. To give an example, the rotational constants of the benzoic acid are reproduced by the TM approach with a discrepancy of 0.13%, which reduces to 0.04% when TM+LR is employed.
As a sort of conclusion from the analysis of the benchmark data set results, we note that the TM approach greatly improves the agreement with the experimental data and the relative error on rotational constants is, on average, as low as 0.1%. Such a good agreement suggests that the TM structures are highly accurate, which means uncertainties smaller than 0.001 Å for bond lengths and 0.1° for angles. Therefore, the TM/TM+LR methodology is able to provide equilibrium structures with an accuracy similar to that of QC composite approaches entirely based on coupled-cluster techniques, which are not affordable for the systems under consideration.
3.2 The “application” study: structural prediction of small PAHs and PANHs
Based on the results discussed in the previous section, the TM/TM+LR approach is able to provide very accurate rotational constants. Therefore, we decided to extend its application to small PA(N)Hs for which the experimental information is still missing. Since 1- and 2-cyanonaphthalene have been recently detected in the ISM,6 we considered 1- and 2-ethynylnaphthalene (C10H7CCH) to be of particular interest. In fact, C10H7CCH and C10H7CN are somewhat chemically related because they share the C10H7 sub-unit, and only differ for the the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–H group which replaces the CN moiety. In ref. 55, it has been pointed out that, if a molecule containing the CN moiety is detected, then – very likely – the C
C–H group which replaces the CN moiety. In ref. 55, it has been pointed out that, if a molecule containing the CN moiety is detected, then – very likely – the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–H-containing analogue is also present. Several examples are indeed available, such as propargylimine56 and cyanomethanimine57 as well as HCSCN and HCSCCH.58 The molecular geometries of 1- and 2-ethynylnaphthalene (together with the atom labeling) are shown in Fig. 4. First of all, the linearity of the C3C2C1 and C2C1H1 groups in 1-ethynylnaphthalene has been investigated, but no intramolecular non-covalent interactions have been found affecting its structure, and thus the CCH moiety has been constrained to be linear. The TM/TM+LR bond lengths for 1- and 2-ethynylnaphthalene are reported in Fig. 4. Within the TM+LR approach, the LR correction has been applied to the C2–C3 linkage bond, while valence and dihedral angles were kept fixed at the revDSD/mayTZ values. The predicted equilibrium rotational constants are collected in Table 3, where the DFT values are also provided for comparison purposes. Analogously to the benchmark study, the DFT model employed is revDSD/mayTZ. Vibrational corrections have been calculated at the B3/junDZ level of theory and account for about 0.6% of the total ground-state rotational constants (see Table 3).
C–H-containing analogue is also present. Several examples are indeed available, such as propargylimine56 and cyanomethanimine57 as well as HCSCN and HCSCCH.58 The molecular geometries of 1- and 2-ethynylnaphthalene (together with the atom labeling) are shown in Fig. 4. First of all, the linearity of the C3C2C1 and C2C1H1 groups in 1-ethynylnaphthalene has been investigated, but no intramolecular non-covalent interactions have been found affecting its structure, and thus the CCH moiety has been constrained to be linear. The TM/TM+LR bond lengths for 1- and 2-ethynylnaphthalene are reported in Fig. 4. Within the TM+LR approach, the LR correction has been applied to the C2–C3 linkage bond, while valence and dihedral angles were kept fixed at the revDSD/mayTZ values. The predicted equilibrium rotational constants are collected in Table 3, where the DFT values are also provided for comparison purposes. Analogously to the benchmark study, the DFT model employed is revDSD/mayTZ. Vibrational corrections have been calculated at the B3/junDZ level of theory and account for about 0.6% of the total ground-state rotational constants (see Table 3).
| revDSD/mayTZ | TM | TM+LRa | ΔBvibb | |
|---|---|---|---|---|
| a C2–C3 bond length corrected using the LR approach. b Vibrational corrections at the B3/junDZ level of theory. | ||||
| 1-Ethynylnaphthalene | ||||
| A/MHz | 1478.122 | 1482.669 | 1483.260 | −7.944 |
| B/MHz | 955.578 | 958.430 | 958.894 | −5.637 |
| C/MHz | 580.376 | 582.129 | 582.391 | −3.269 |
| 2-Ethynylnaphthalene | ||||
| A/MHz | 2719.186 | 2728.401 | 2728.654 | −18.694 |
| B/MHz | 607.160 | 608.888 | 609.246 | −2.986 |
| C/MHz | 496.335 | 497.796 | 498.044 | −2.562 |
| 2-Quinolinecarbonitrile | ||||
| A/MHz | 2692.656 | 2701.698 | 2702.002 | −19.825 |
| B/MHz | 632.455 | 634.543 | 634.939 | −2.904 |
| C/MHz | 512.158 | 513.855 | 514.125 | −2.560 |
| 3-Quinolinecarbonitrile | ||||
| A/MHz | 2787.565 | 2796.948 | 2797.162 | −18.312 |
| B/MHz | 615.630 | 617.649 | 618.023 | −3.018 |
| C/MHz | 504.264 | 505.926 | 506.184 | −2.563 |
| 4-Quinolinecarbonitrile | ||||
| A/MHz | 1510.748 | 1515.858 | 1516.427 | −7.882 |
| B/MHz | 962.804 | 965.882 | 966.384 | −5.648 |
| C/MHz | 588.043 | 589.965 | 590.239 | −3.274 |
| 9-Ethynylanthracene | ||||
| A/MHz | 981.379 | 983.868 | 984.896 | −5.046 |
| B/MHz | 452.842 | 454.004 | 454.295 | −2.815 |
| C/MHz | 309.862 | 310.634 | 310.892 | −1.754 |
| 9-Ethynylphenanthrene | ||||
| A/MHz | 846.550 | 849.102 | 849.419 | −4.837 |
| B/MHz | 487.907 | 489.376 | 489.502 | −2.894 |
| C/MHz | 309.517 | 310.450 | 310.543 | −1.735 |
| 1-Pyrenecarbonitrile | ||||
| A/MHz | 845.840 | 848.544 | 848.678 | −5.282 |
| B/MHz | 372.917 | 374.072 | 374.201 | −2.125 |
| C/MHz | 258.812 | 259.621 | 259.695 | −1.462 |
| 2-Pyrenecarbonitrile | ||||
| A/MHz | 1012.394 | 1015.776 | 1015.776 | −7.197 |
| B/MHz | 313.586 | 314.543 | 314.674 | −1.592 |
| C/MHz | 239.425 | 240.172 | 240.249 | −1.280 |
| 4-Pyrenecarbonitrile | ||||
| A/MHz | 652.851 | 654.920 | 655.002 | −4.231 |
| B/MHz | 454.559 | 455.943 | 456.133 | −2.471 |
| C/MHz | 267.976 | 268.806 | 268.885 | −1.517 |
| 1-Ethynylpyrene | ||||
| A/MHz | 845.303 | 848.016 | 848.144 | −5.284 |
| B/MHz | 373.841 | 374.989 | 375.113 | −2.138 |
| C/MHz | 259.206 | 260.013 | 260.084 | −1.466 |
| 2-Ethynylpyrene | ||||
| A/MHz | 1013.966 | 1017.237 | 1017.237 | −7.270 |
| B/MHz | 314.766 | 315.726 | 315.855 | −1.592 |
| C/MHz | 240.200 | 240.943 | 241.018 | −1.284 |
| 4-Ethynylpyrene | ||||
| A/MHz | 653.048 | 655.096 | 655.174 | −4.051 |
| B/MHz | 455.145 | 456.551 | 456.733 | −2.551 |
| C/MHz | 268.212 | 269.047 | 269.123 | −1.513 |
The TM approach has also been employed to predict the structural parameters of a set of molecules containing either the CN group or the CCH group. This includes 2-quinolinecarbonitrile, 3-quinolinecarbonitrile, 4-quinolinecarbonitrile, 9-ethynylanthracene, 9-ethynylphenanthrene, 1-pyrenecarbonitrile, 2-pyrenecarbonitrile, 4-pyrenecarbonitrile, 1-ethynylpyrene, 2-ethynylpyrene, and 4-ethynylpyrene, whose geometries are shown in Fig. 5. The equilibrium rotational constants and vibrational corrections for these molecules are given in Table 3. It is noted that all rotational constants increase once the TM approach is applied, and the increase is within 3.5 MHz. As noted for 1- and 2-ethynylnaphthalene, the vibrational correction accounts for about 0.6% of the ground-state rotational constants. Based on the benchmark study, the TM/TM+LR ground-state rotational constants reported in Table 3 are expected to have an accuracy better than 0.1%. This means that they are probably sufficiently accurate to directly guide astronomical searches.
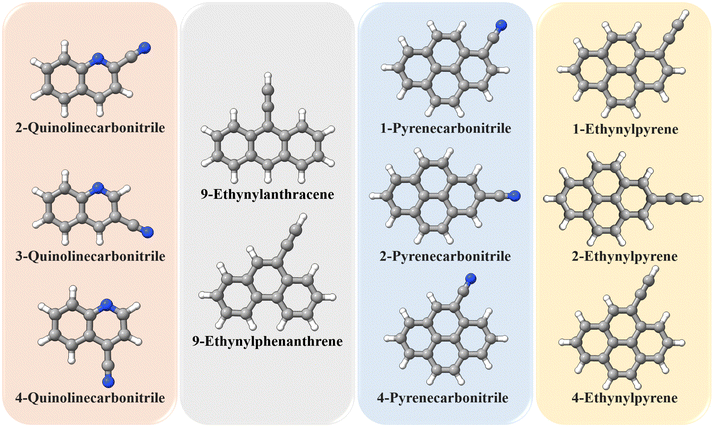 | ||
| Fig. 5 Molecules employed in the “application” study: they are grouped according to their “Lego brick” fragments (type and number). | ||
3.3 Small PAHs and PANHs: prediction of the rotational spectra
The rotational spectra of the set of molecules considered in our application study (see Fig. 4 and 5) have been predicted using the spectroscopic parameters computed in this work. In detail, we employed (i) the TM+LR equilibrium rotational constants augmented by vibrational corrections at the B3/junDZ level, together with (ii) the quartic centrifugal distortion terms and (iii) the vibrationally averaged dipole moment components (for transitions intensity), both at the B3/junDZ level of theory.The set of small PA(N)Hs mentioned above contains 13 molecules that are all planar and can be classified into two groups, depending on their symmetry. Three of them (namely, 9-ethynylanthracene, 2-pyrenecarbonitrile, and 2-ethynylpyrene) possess a C2v symmetry, while the remaining ten species belong to the Cs symmetry point group. The ab plane is the symmetry plane for all these molecules; therefore, the dipole moment component along the c-axis is null (μc = 0). From the spectroscopic point of view, all these 13 species are asymmetric-top rotors, with Ray's asymmetry parameter κ ranging from −0.9 to nearly 0. The spectral simulations have been performed using the standard semi-rigid Watson-type Hamiltonian in the S-reduction59 and the IIIr representation (x = a, y = b, and z = c).60
For the three species showing the C2v symmetry, spin-statistics effects have been considered in the simulation. For all of them, the rotation along the highest order rotational axis (Ĉ2 operation) exchanges four pairs of equivalent hydrogen nuclei. The exchange of a H pair must obey the Fermi–Dirac statistics; however, because there is an overall exchange of an even number of H pairs, the total wavefunction must be symmetric with respect to a 180° rotation. In total, there are 256 possible spin functions, 136 of which are symmetric (ortho state) and 120 anti-symmetric (para state). These can be reduced for simplicity to 17 and 15, respectively. Since we are considering the vibronic ground state of closed-shell molecules, the symmetric spin functions can only combine with symmetric rotational energy levels, whereas anti-symmetric spin functions only combine with anti-symmetric rotational energy levels. Therefore, all rotational lines present a relative intensity of 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15 between ortho and para states.
15 between ortho and para states.
The simulation of the rotational spectra of all 13 molecules has been carried out using PGOPHER, a versatile program for predicting and analyzing the electronic, vibrational, and rotational spectra.61 These simulations are provided in the ESI.† Given the large size of the molecules considered here, the simulation of the spectra has been truncated at J = 200, in order to speed up the diagonalization of the Hamiltonian matrix. For the same reason, the hyperfine structure of the rotational spectrum due to nitrogen quadrupole coupling (i.e. the coupling between the nitrogen electric quadrupole moment and the electric field gradient at the nucleus) has been ignored.
Since the rotational constants of these systems are small, all spectra are quite dense and contain several thousands of lines. At room temperature, the maximum intensity is typically observed around 100 GHz, a frequency-region covered by most millimeter-wave spectrometers. Given the high complexity of the spectra and the fact that, at 300 K, several vibrationally excited states are populated (each of which possesses its own rotational spectrum), our predictions are crucial for guiding future rotational spectroscopy experiments. As mentioned at the end of the previous section, the rotational constants used here are expected to have an accuracy better than 0.1%. The same precision can be roughly transferred on to the line position accuracy. Therefore, we expect to observe rotational transitions within a range of 0.1 GHz at 100 GHz.
4 Conclusions
In the present work, it has been demonstrated that the so-called “Lego brick” approach is able to provide, at a very limited computational cost, accurate results for the structure of rather rigid systems such as small PAHs and PANHs. This investigation further confirms and extends the results obtained in ref. 27: the “Lego brick” approach works extremely well for molecular species showing a relevant degree of rigidity. Ref. 27 suggested that flexibility might reduce the accuracy obtainable with the “Lego brick” approach; however, non-planar and very flexible systems such as amino acids have not been investigated yet. While these will be the focus of a subsequent study, we note that among the species investigated here there are some that incorporate the OH and COOH moieties (trans/cis-2-naphthol, cis-3-hydroxy-pyridine, 4-hydroxy-pyridine, and cis-benzoic acid), which show some flexibility. For them, no degradation in the accuracy is observed, with the TM+LR rotational constants deviating from the experiment by 0.02%, on average. The preliminary results indicate that a similar accuracy is obtainable for systems containing the NH2 group. In passing we note that the LR approach is proved to work well for flexible molecules,62 and the performance of the TM+LR approach requires a validation study.Since the equilibrium structure straightforwardly provides equilibrium rotational constants, the TM/TM+LR approach opens to the accurate spectroscopic characterization of small PAHs and PANHs that might be of astrochemical interest. Starting from the revDSD/mayTZ level of theory, the TM model and, whenever possible, LR corrections have been applied to a set of small PA(N)Hs whose rotational constants were experimentally determined. This allowed us to point out that the application of the TM/TM+LR approach reduces the discrepancy with respect to experiment from 0.4%, on average, at the revDSD/mayTZ level to less that 0.1%, with deviations as small as 0.01–0.03%. Such an accuracy can be reached only by QC composite schemes entirely based on coupled-cluster techniques that account for extrapolation to the complete basis set limit and excitations up to the full treatment of quadruples.22 However, these composite approaches are not affordable for the systems investigated here, even if the full treatment of triples and quadruples is avoided.
In view of the benchmark results, the TM/TM+LR approach has been applied to small PA(N)Hs not yet experimentally investigated. For a set of 13 molecules, accurate rotational constants have been obtained and used to accurately predict their rotational constants. This work also demonstrated that the “Lego brick” approach can be applied to systems of increasing dimensions without the deterioration of the accuracy; indeed, increasing the number of fragments does not affect its performance. This is an important result in the field of high-resolution molecular spectroscopy because quantitative spectroscopic characterization can be performed at a reduced computational cost.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the MUR (PRIN Grant Number 202082CE3T) and by the University of Bologna (RFO funds). H. Y. thanks the China Scholarship Council (CSC) for financial support.Notes and references
- Cologne Database for Molecular Spectroscopy (CDMS), https://cdms.astro.uni-koeln.de/.
- The Astrochymist, https://www.astrochymist.org/.
- K. I. Öberg and E. A. Bergin, Phys. Rep., 2021, 893, 1–48 CrossRef.
- B. A. McGuire, Astrophys. J., Suppl. Ser., 2022, 259, 30 CrossRef.
- B. A. McGuire, A. M. Burkhardt, S. Kalenskii, C. N. Shingledecker, A. J. Remijan, E. Herbst and M. C. McCarthy, Science, 2018, 359, 202–205 CrossRef CAS.
- B. A. McGuire, R. A. Loomis, A. M. Burkhardt, K. L. K. Lee, C. N. Shingledecker, S. B. Charnley, I. R. Cooke, M. A. Cordiner, E. Herbst and S. Kalenskii, et al. , Science, 2021, 371, 1265–1269 CrossRef CAS.
- E. K. Campbell, M. Holz, D. Gerlich and J. P. Maier, Nature, 2015, 523, 322–323 CrossRef CAS PubMed.
- J. Cami, J. Bernard-Salas, E. Peeters and S. E. Malek, Science, 2010, 329, 1180–1182 CrossRef CAS.
- A. Li, Nature Astronomy, 2020, 4, 339–351 CrossRef.
- A. G. G. M. Tielens, Annu. Rev. Astron. Astrophys., 2008, 46, 289–337 CrossRef CAS.
- L. J. Allamandola, A. G. G. M. Tielens and J. R. Barker, Astrophys. J., Suppl. Ser., 1989, 71, 733–775 CrossRef CAS PubMed.
- D. M. Hudgins, C. W. Bauschlicher Jr. and L. J. Allamandola, Astrophys. J., 2005, 632, 316 CrossRef CAS.
- J. E. Chiar, A. G. G. M. Tielens, A. J. Adamson and A. Ricca, Astrophys. J., 2013, 770, 78 CrossRef.
- S. Thorwirth, P. Theulé, C. Gottlieb, M. McCarthy and P. Thaddeus, Astrophys. J., 2007, 662, 1309 CrossRef CAS.
- K. L. K. Lee, B. A. McGuire and M. C. McCarthy, Phys. Chem. Chem. Phys., 2019, 21, 2946–2956 RSC.
- V. Barone and C. Puzzarini, Front. Astron. Space Sci., 2022, 8, 814384 CrossRef.
- I. R. Cooke, D. Gupta, J. P. Messinger and I. R. Sims, Astrophys. J. Let., 2020, 891, L41 CrossRef CAS.
- D. McNaughton, P. D. Godfrey, R. D. Brown, S. Thorwirth and J. Grabow, Astrophys. J., 2008, 678, 309 CrossRef CAS.
- M. Heckert, M. KÁllay and J. Gauss, Mol. Phys., 2005, 103, 2109–2115 CrossRef CAS.
- M. Heckert, M. Kállay, D. P. Tew, W. Klopper and J. Gauss, J. Chem. Phys., 2006, 125, 044108 CrossRef PubMed.
- C. Puzzarini, J. F. Stanton and J. Gauss, Int. Rev. Phys. Chem., 2010, 29, 273–367 Search PubMed.
- C. Puzzarini, M. Heckert and J. Gauss, J. Chem. Phys., 2008, 128, 194108 CrossRef PubMed.
- S. Alessandrini, J. Gauss and C. Puzzarini, J. Chem. Theory Comput., 2018, 14, 5360–5371 CrossRef CAS PubMed.
- W. D. Allen, A. L. L. East and A. G. Csaśzaŕ, in Structures and Conformations of Non-Rigid Molecules, ed. J. Laane, M. Dakkouri, B. van der Veken and H. Oberhammer, Kluwer, Dordrecht, 1993, p. 343 Search PubMed.
- C. Puzzarini and V. Barone, Phys. Chem. Chem. Phys., 2011, 13, 7189–7197 RSC.
- C. Puzzarini and V. Barone, Acc. Chem. Res., 2018, 51, 548–556 CrossRef CAS PubMed.
- A. Melli, F. Tonolo, V. Barone and C. Puzzarini, J. Phys. Chem. A, 2021, 125, 9904–9916 CrossRef CAS PubMed.
- M. Piccardo, E. Penocchio, C. Puzzarini, M. Biczysko and V. Barone, J. Phys. Chem. A, 2015, 119, 2058–2082 CrossRef CAS PubMed.
- E. Penocchio, M. Piccardo and V. Barone, J. Chem. Theory Comput., 2015, 11, 4689–4707 CrossRef CAS PubMed.
- G. Ceselin, V. Barone and N. Tasinato, J. Chem. Theory Comput., 2021, 17, 7290–7311 CrossRef CAS.
- P. Pulay, W. Meyer and J. E. Boggs, J. Chem. Phys., 1978, 68, 5077–5085 CrossRef CAS.
- J. Demaison, J. E. Boggs and A. G. Császár, Equilibrium molecular structures: from spectroscopy to quantum chemistry, CRC Press, 2016 Search PubMed.
- G. Santra, N. Sylvetsky and J. M. L. Martin, J. Phys. Chem. A, 2019, 123, 5129–5143 CrossRef CAS PubMed.
- E. Papajak, J. Zheng, X. Xu, H. R. Leverentz and D. G. Truhlar, J. Chem. Theory Comput., 2011, 7, 3027–3034 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098 CrossRef CAS PubMed.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS.
- O. Pirali, M. Goubet, T. Huet, R. Georges, P. Soulard, P. Asselin, J. Courbe, P. Roy and M. Vervloet, Phys. Chem. Chem. Phys., 2013, 15, 10141–10150 RSC.
- M. Baba, M. Saitoh, K. Taguma, K. Shinohara, K. Yoshida, Y. Semba, S. Kasahara, N. Nakayama, H. Goto and T. Ishimoto, et al. , J. Chem. Phys., 2009, 130, 134315 CrossRef PubMed.
- Y. Kowaka, T. Yamanaka and M. Baba, J. Chem. Phys., 2012, 136, 154301 CrossRef PubMed.
- B. E. Brumfield, J. T. Stewart and B. J. McCall, J. Phys. Chem. Lett., 2012, 3, 1985–1988 CrossRef CAS.
- D. McNaughton, M. K. Jahn, M. J. Travers, D. Wachsmuth, P. D. Godfrey and J.-U. Grabow, Mon. Not. R. Astron. Soc., 2018, 476, 5268–5273 CrossRef CAS.
- A. S. Hazrah, S. M. Nanayakkara, N. S. Seifert, E. Kraka and W. Jaeger, Phys. Chem. Chem. Phys., 2022 10.1039/D1CP05632H.
- P. M. Dorman, B. J. Esselman, R. C. Woods and R. J. McMahon, J. Mol. Spectrosc., 2020, 373, 111373 CrossRef CAS.
- X. Wang, S. Gao, J. Chen, W. Du, W. Cheng, X. Xu and Q. Gou, J. Phys. Chem. A, 2022 DOI:10.1021/acs.jpca.1c10013.
- R. Sanchez, B. M. Giuliano, S. Melandri and W. Caminati, Chem. Phys. Lett., 2007, 435, 10–13 CrossRef CAS.
- R. Sanchez, B. M. Giuliano, S. Melandri and W. Caminati, Chem. Phys. Lett., 2006, 425, 6–9 CrossRef CAS.
- M. Onda, M. Asai, K. Takise, K. Kuwae, K. Hayami, A. Kuroe, M. Mori, H. Miyazaki, N. Suzuki and I. Yamaguchi, J. Mol. Struct., 1999, 482, 301–303 CrossRef.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian-16 Revision B.01, Gaussian Inc., Wallingford CT, 2016 Search PubMed.
- E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-Garca, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506 CrossRef CAS PubMed.
- J. Contreras-Garca, E. R. Johnson, S. Keinan, R. Chaudret, J.-P. Piquemal, D. N. Beratan and W. Yang, J. Chem. Theory Comput., 2011, 7, 625–632 CrossRef PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS.
- H. D. Rudolph, J. Demaison and A. G. Császár, J. Phys. Chem. A, 2013, 117, 12969–12982 CrossRef CAS PubMed.
- J. Cernicharo, M. Agúndez, R. Kaiser, C. Cabezas, B. Tercero, N. Marcelino, J. Pardo and P. De Vicente, Astron. Astrophys., 2021, 655, L1 CrossRef CAS.
- L. Bizzocchi, D. Prudenzano, V. M. Rivilla, A. Pietropolli-Charmet, B. M. Giuliano, P. Caselli, J. Martn-Pintado, I. Jiménez-Serra, S. Martn and M. A. Requena-Torres, et al. , Astron. Astrophys., 2020, 640, A98 CrossRef CAS.
- V. M. Rivilla, J. Martín-Pintado, I. Jiménez-Serra, S. Zeng, S. Martín, J. Armijos-Abendaño, M. A. Requena-Torres, R. Aladro and D. Riquelme, Mon. Not. R. Astron. Soc., 2018, 483, L114–L119 CrossRef.
- J. Cernicharo, C. Cabezas, Y. Endo, M. Agúndez, B. Tercero, J. Pardo, N. Marcelino and P. de Vicente, Astron. Astrophys., 2021, 650, L14 CrossRef CAS PubMed.
- J. K. G. Watson, Vibrational Spectra and Structure, Elsevier, New York, NY, 1977, pp. 1–89 Search PubMed.
- W. Gordy and R. L. Cook, Microwave molecular spectra, Wiley, New York, 1984 Search PubMed.
- C. M. Western, J. Quant. Spectrosc. Ra., 2017, 186, 221–242 CrossRef CAS.
- I. León, M. Fusè, E. R. Alonso, S. Mata, G. Mancini, C. Puzzarini, J. L. Alonso and V. Barone, J. Chem. Phys., 2022, 157, 074107 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp03294e |
| This journal is © the Owner Societies 2022 |