Accurate computed singlet–triplet energy differences for cobalt systems: implication for two-state reactivity

Abstract

Accurate singlet–triplet energy differences for cobalt and rhodium complexes were calculated by using several wave function methods, such as MRCISD, CASPT2, CCSD(T) and BCCD(T). Relaxed energy differences were obtained by considering the singlet and triplet complexes, each at the minimum of their potential energy surfaces. Active spaces for multireference calculations were carefully checked to provide accurate results. The considered systems are built by increasing progressively the first coordination sphere around the metal. We included in our set two CpCoX complexes (Cp = cyclopentadienyl, X = alkenyl ligand), which have been suggested as intermediates in cycloaddition reactions. Indeed, cobalt systems have been used for more than a decade as active species in this kind of transformations, for which a two-state reactivity has been proposed. Most of the considered systems display a triplet ground state. However, in the case of a reaction intermediate, while a triplet ground state was predicted on the basis of Density Functional Theory results, our calculations suggest a singlet ground state. This stems from the competition between the exchange term (stabilising the triplet) and the accessibility of an intramolecular coordination (stabilising the singlet). This finding has an impact on the general mechanism of the cycloaddition reaction. Analogous rhodium systems were also studied and, as expected, they have a larger tendency to electron pairing than cobalt species.

---

1 Introduction

Transition metal complexes (TM), in particular those of the first-row, are versatile but challenging objects of study: they can exist under several oxidation and spin states, showing spin-crossover phenomena,^1–3 spin-forbidden reactivity’, or multistate reactivity.^4–7 They may undergo ‘spin-accelerated reactivity, when changes in spin states impact the kinetics of catalytic or metal-mediated transformations, in enzymatic or (bio)inorganic reactions.^8,9 All these phenomena are dictated by the shape and relative energetic positions of close-lying spin-state potential energy surfaces. Thus, if an accurate evaluation of spin-state energetics in transition-metal complexes is fundamental for the comprehension of their magnetic and optical properties, it is also essential for the description of their reactivity.

From a theoretical point of view, calculations of accurate energy differences between low-lying states of TM complexes are not trivial, as they need to take into account the effects of electron correlation, both dynamical and nondynamical. As well documented, Density Functional Theory (DFT) can be exploited for treating large systems, but the results strongly depend on the exchange-correlation functional.^10–13 Delocalisation error in semilocal density functionals can lead to an overstabilisation of low spin states, while the inclusion of some Hartree–Fock exchange can introduce a bias towards high spin ground states.^14–16 Several attempts have been made to compare DFT results with other ab initio computed energies differences.^17–23 In the framework of wave function theory, methods that provide strategies for systematic improvements of the results have been developed. Each approach has its advantages and drawbacks. The coupled-cluster CCSD(T) method is identified as the ‘golden standard’ for single-reference systems.^24–26 An alternative to CCSD(T) is the BCCD(T) approach.^27,28 This method is useful when the reference Hartree–Fock relaxes strongly in the presence of correlation, for instance for heavy atoms. It employs Brückner orbitals, directly incorporating orbital relaxation effects into the reference wave function, otherwise included indirectly by computing single excitations.²⁹ Besides their cost, these methods could present some deficiencies for systems with a non-negligible multireference character. In those cases, the use of multiconfigurational perturbation theory methods, such as CASPT2,³⁰ RASPT2,³¹ or NEVPT2,³² becomes relevant. A perturbation treatment is performed to recover the dynamical correlation on top of a reference wave function obtained at the CAS (complete active space) or RASSCF (restricted active space self-consistent field) level. The analysis of the multiconfigurational wave function can also offer the opportunity to gain valuable insights into the mechanisms leading to the stabilisation of a given spin state with respect to the others.^33,34 Multiconfigurational perturbation methods have been widely employed, however, the accuracy of the calculations depends dramatically on the choice of the active space. Moreover, Pierloot and coworkers have recently shown that CASPT2 treats correctly valence correlation effects, but tends to overstabilise high-spin states of first-row TM, as a consequence of the poor treatment of semicore 3s3p electron correlation.²⁴

In this work we propose a computational study of cobalt complexes relevant for reactivity. Although second- and third-row transition metals have been proven for several decades to be efficient and robust catalysts in several processes, first-row transition metals are more abundant and accessible, motivating the increasing interest towards their use.³⁶ Transition metal-catalysed [2+2+2] cycloaddition reactions exploiting CpCoL₂ complexes are well established methods for the synthesis of functionalised (hetero)aromatic polycyclic compounds.^37–39 Reaction mechanisms that have been proposed on the basis of DFT calculations suggest a two-state reactivity, presenting several crossings between singlet and triplet potential energy surfaces. A general catalytic cycle for a prototypical [2+2+2] cycloaddition reaction is proposed in Fig. 1, where possible crossing points between intermediates on singlet and triplet potential energy surfaces are indicated, as suggested in the literature.³⁵ The active species is a CpCo fragment, which is obtained from a CpCoL₂ complex. The compound CpCo(CO)₂ is often employed as a precursor, which requires a photochemical activation to promote the dissociation of the two CO molecules, leading to a triplet ³[CpCo]. The coordination of two unsaturated substrates (here two alkynes), occurs on the singlet potential energy surface. The oxidative coupling follows, leading to a singlet intermediate I, for which the triplet state is accessible. The coordination of a new unsaturated substrate (here an alkene) is possible on the singlet potential energy surface, where the insertion step takes place. It has been suggested that the final reductive elimination could imply again a crossing to the triplet potential energy surface from ¹II to ³II, and back to the singlet potential energy surface for the final step of the reaction. Although meta-GGA and GGA functionals have been employed to treat cobalt two-state reactivities,^9,40 many studies employ hybrid functionals, such as B3LYP,³⁵ which incorporate some Hartree–Fock exchange and may artificially destabilise singlet with respect to triplet states.

Fig. 1 General mechanism for a [2+2+2] cycloaddition reaction catalysed by a CpCoL₂ complex.³⁵ Hypothetical triplet species are indicated. The blue bonds show the C–C bonds formed in the mechanistic step.

As reaction intermediates are often short-living species, hard to isolate and characterise from an experimental point of view, it is difficult to obtain direct evidences to validate a proposed theoretical mechanism. Our computational study aims at evaluating how the singlet–triplet energy difference evolves in cobalt complexes. From the naked Co⁺ cation, its first coordination sphere is constructed block by block to reach the intermediates of the cycloaddition reaction preceding the final reductive elimination step. We are interested in comparing energies between the singlet complexes and the triplet complexes, each at the minimum of their potential energy surfaces. The singlet–triplet gaps relate to the electron-pairing energy that is expected to decrease from a lighter to a heavier atom in a group, due to the expansion of the valence shell. It is therefore predictable that analogous Rh complexes would systematically display smaller singlet–triplet energy differences. A comparison between cobalt and rhodium systems is valuable to verify and quantify this trend. Ab initio studies on closely related metallocenes demonstrated that cobalt complexes possess a certain degree of multiconfigurational character.^21,41,42 Thus, besides single reference coupled cluster approach CCSD(T) and BCCD(T), multireference CASSCF methods followed by a dynamical correlation treatment, CASPT2 or Multi-Reference Configuration Interaction with Single and Double excitations (MRCISD), are employed to gain a deeper understanding of the electronic structure of the cobalt systems involved in the cycloaddition mechanism. Finally, we compare our more reliable values with results obtained from some common DFT functionals. For comparison, Rh(I) systems have been also computed.

2 Systems and computational details

In the following, results are presented in terms of ΔE_ST, defined as:

ΔE_ST = E_S − E_T (1)

where E_S and E_T are the electronic energies computed on the optimised structures for the singlet and for the triplet states, respectively. Hence, ΔE_ST is not a vertical, but a relaxed energy difference.

2.1 Systems

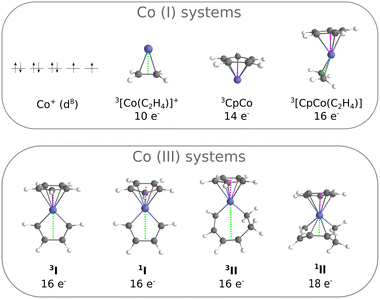
The systems considered in this work are presented in Fig. 2. The smallest is the experimentally characterised cobalt(I) ion, with a d⁸ external electronic configuration: the ground state is a ³F, with a higher lying ¹D with 8 electrons distributed over the 3d shell. From here, several complexes have been constructed by adding ligands and building progressively a complete coordination sphere around the metal: [Co(C₂H₄)]⁺, CpCo and [CpCo(C₂H₄)]. These systems, where the metal center is formally a Co(I), constitute our training set for comparing the performances of ab initio methods. The corresponding Rh(I) analogues (Rh⁺, [Rh(C₂H₄)]⁺, CpRh and [CpRh(C₂H₄)]) were also treated. Next, we build the systems I and II, where the metal center is formally a Co(III): they reproduce the key intermediates of the cycloaddition reaction following the oxidative coupling (I) and preceding the elimination step (II), Fig. 1. When going from [CpCo(C₂H₄)] to I, although the metal formally changes from Co(I) to Co(III), the electron counting leads again to a 16-electron complex. The triplet state of II is, as well, a 16-electron complex, while the singlet is a 18-electron complex.

Fig. 2 B3LYP-D3 structures of the cobalt systems treated in this work.

Geometry optimisations were performed at the DFT level, on singlet and triplet complexes, treated as a minimum on their potential energy surfaces. Calculations were carried out with some common functionals (geometries were re-optimised with each functional), using the TURBOMOLE program package:⁴³ TPSSh-D3,^44–48 PBE0-D3,^{44–46,49,50} B3LYP-D3,^{44,45,51–54} CAM-B3LYP,⁵⁵ TPSS-D3,^44–47 PBE-D3,^44–46,49 BP86-D3.^{44,45,51,52,56} and GAUSSIAN 09:⁵⁷ M06,⁵⁸ M06-L.⁵⁸ The D3 suffix denotes Grimme's dispersion corrections.⁵⁹ The basis set is of def2-TZVP quality for C and H, and of def2-QZVPP quality for the metal centers (Co and Rh), together with a relativistic effective core potential RECP for Rh.^60,61 As the RI-J technique was exploited,^62,63 the corresponding auxiliary basis functions were selected.⁶⁴

Selected geometry parameters are reported in Table 1, as computed at the B3LYP-D3 level of theory. In general, singlet and triplet systems have similar structures with Co–C distances that are slightly longer for triplet-state than for singlet-state complexes.⁶⁵ This behaviour is observed for the Co(I) systems and for I. However, complex II presents some peculiarities. Let us consider the Co–π distance between the metal and the middle of the C–C bond as indicated in Fig. 2 by the green line: at the B3LYP-D3 level, this distance is of 3.37 Å in the triplet and it reduces to 2.08 Å in the singlet. The same effect is found for geometries at the TPSS-D3 level (3.31 Å for the triplet and 1.97 Å for the singlet, Table 1). Thus, there exists an interaction between the cobalt and the alkene moiety of the ligand in the singlet, which is not found in the triplet system.

Table 1 Selected geometry parameters for cobalt complexes (Å). Co–π is the distance between the Co and the middle of a C–C bond in the ligand (see the green line in Fig. 2). Co–Cp is the distance between the Co and the centroid of the Cp ring (see the pink line in Fig. 2)

	Co–π		Co–Cp
	Singlet	Triplet	Singlet	Triplet
B3LYP-D3
[Co(C2H4)]^+	1.94	1.99	—	—
CpCo	—	—	1.68	1.75
[CpCo(C2H4)]	1.84	1.91	1.71	1.88
I	2.63	2.65	1.74	1.85
II	2.08	3.37	1.77	1.90
TPSS-D3
I	2.27	2.67	1.68	1.76
II	1.97	3.31	1.71	1.80

---

The same structural trends are observed with other functionals for all the systems. The only remarkable difference concerns I: singlet optimised structures obtained with GGA hybrid functionals (B3LYP-D3, PBE0-D3, CAM-B3LYP) and M06 are of C_s symmetry, while the other functionals (TPSSh-D3, TPSS-D3, PBE-D3, BP86-D3, M06-L) predict a C₁ geometry, even if the C_s structure is very close in energy (for TPSS-D3, the C_s structure is only 1.4 kcal mol⁻¹ higher in energy than the C₁).

For the wave function based methods, single-point energy calculations were performed on the B3LYP-D3 geometries. This choice is motivated by the fact that several studies on the cycloaddition reactions were performed at the B3LYP level of theory. However, in order to be exhaustive and to check that possible differences in structures do not impact sensitively the ΔE_ST values, calculations with the wave function based methods were performed also on the TPSS-D3 structures for our target systems I and II, for which we report some selected geometry parameters in Table 1. A full summary on the geometries is available in the ESI.†

2.2 Ab initio approaches

CASSCF/CASPT2 and RASSCF/RASPT2 treatments were carried out with OpenMolcas 21.02,^66,67 using the Cholesky decomposition (RICD) of the two-electron integrals with a threshold of 10⁻⁶ Hartree.^68,69 An IPEA shift, with the standard value of 0.25 Hartree,⁷⁰ and an imaginary level shift of 0.1 Hartree were systematically applied.⁷¹ We recall that the IPEA shift (IP for Ionisation Potential and EA for Electron Affinity) modifies the energies of active orbitals in the zeroth order Hamiltonian so that they are closer to either first ionisation energies or electron affinities of the corresponding excitations. In the following, active spaces are denoted as CAS(n_electrons, n_orbitals), where n_electrons indicates the number of treated electrons in n_orbitals orbitals. For restricted active spaces, the RAS(n,l,m;i,j,k) notation is used,⁷² with n the total number of active electrons, l the number of holes allowed in RAS1, and m the number of electrons allowed in RAS3. Labels i, j and k refer to the number of orbitals in RAS1, RAS2 and RAS3, respectively. MRCISD^73–76 (internally contracted) and CCSD(T)²⁵ calculations were performed with Molpro 2021.^77–79 Pople correction to the MRCISD energy for size-consistency was applied.⁸⁰ The CASSCF wave functions were recomputed with the Molpro program package,^81–84 with total energies not substantially differing from those obtained with OpenMolcas (deviations of about 10⁻⁴ Hartree). For the CCSD(T) calculations with Molpro 2021, triplet systems were treated using the spin-unrestricted UCCSD(T) formalism on a ROHF (restricted-open-shell) reference wave function, while closed-shell singlet systems were treated with the spin-restricted RCCSD(T) program. Core electrons (1s shell for carbon, 1s2s2p shells for cobalt) were kept frozen in all MRCISD, CASPT2 and coupled cluster calculations, while the possible impact of semicore electrons (3s3p for cobalt) in the dynamical correlation treatment has been considered. At the coupled cluster level, the nosp energies were obtained by freezing the core and semicore electrons, otherwise all but core electrons were correlated (sp calculations). At the CASPT2 or MRCISD level, energies were obtained by including into the post-CASSCF treatment either only active electrons (nosp calculations) or active and semicore electrons (see ESI†).

The orbital basis sets employed in this work are listed in Table 2. For cobalt systems, scalar relativistic effects were taken into account using a second order Douglas–Kroll–Hess Hamiltonian,^85–88 in combination with the appropriate all electron correlation-consistent basis set B1.^89–92 For systems I and II, due to their size, we reduced the basis quality to cc-pVTZ-DK on carbon atoms and will refer to it as B2. The non-relativistic counterpart of B1, B3, was also used to evaluate the influence of scalar relativistic effects, which turned out to be almost negligible, with an impact on the energy gaps of less than 1 kcal mol⁻¹ (see ESI,† Table S2) as expected for 3d-block transition metals. For rhodium systems, a 28-electron scalar Relativistic Effective Core Potential (RECP) was used at the metal center with the corresponding basis set, leading to B4, otherwise equivalent to B1.^93–96

Table 2 Summary of the basis sets used in this study

Basis set	Metal	C	H
B1	aug-cc-pwCVTZ-DK	cc-pwCVTZ-DK	cc-pVDZ-DK
B2	aug-cc-pwCVTZ-DK	cc-pVTZ-DK	cc-pVDZ-DK
B3	aug-cc-pwCVTZ	cc-pwCVTZ	cc-pVDZ
B4	aug-cc-pwCVTZ-PP	cc-pwCVTZ	cc-pVDZ
B5	def2-QZVP	def2-QZVP	def2-SVP

---

For comparison, explicitly correlated ^97,98 and ²⁹ calculations were also performed with Turbomole 7.5, using ROHF wave functions for the triplet states.^43,99 Explicitly correlated F12 methods allow to obtain values close to the basis set limit. For the open-shell systems, the UCCSD(T) formalism was employed, while a ROHF-BCCD(T) implementation was adopted. The B3 basis set was used in both cases as scalar relativistic effects were not taken into account. The same calculations were also performed with a basis set of split-valence quality denoted as B5. Associated auxiliary basis sets and correlation factors are reported in the ESI.† ^{60,61,89–92,100–104}

Full computational details, including a discussion on the choice of the basis set, are available in the ESI.†

2.2.1 Choice of the active space. Active spaces were selected according to well-established guidelines for transition metal complexes.^105–109 For the cobalt systems the complete 3d shell of the metal as well as the most important orbitals of the ligands in interaction with the metal were included. Ideally, for the unsaturated ligands, all the π and π* orbitals should be active. However, the totally bonding π orbital of cyclopentadienyl ligand is neglected because it is low in energy. For CASPT2 reference wave function, a second d-shell composed for cobalt of 4d orbitals was also included, introducing some dynamical correlation effects at the CASSCF level. This is not needed in MRCISD calculations.²⁴ We illustrate in Fig. 3 the process of selecting the active space with the example of [CpCo(C₂H₄)] in its triplet state. For the MRCISD calculations, the previous guidelines lead us to a CAS(14,11), formally built on the five 3d cobalt orbitals, the two orbitals of the ethylene and the four π/π* orbitals of the cyclopentadienyl. For CASPT2, the addition of a double shell leads to a CAS(14,16). As double-shell effects are small for second row transition metals, 5d orbitals are not included in the active spaces of the rhodium complexes.¹⁰⁵

Fig. 3 CASSCF natural orbital diagram of [CpCo(C₂H₄)] (triplet state) with partial occupation number, CAS(14,16).

Computational limitations prevent us from using CASSCF for larger cases (I and II), for which we turned to a RAS approach. First of all, we assessed the influence of treating the double shell effect in RAS3 on [CpCo(C₂H₄)]. This only results in a minor change in the ΔE_ST value, less than 1 kcal mol⁻¹ (ΔE_ST = 16.43 kcal mol⁻¹ and 15.72 kcal mol⁻¹ for CASPT2 on CAS(14,16) and RASPT2 on RAS(14,2,2;0,11,5), respectively). Secondly, the restricted active spaces for I and II were constructed and in both cases 18 electrons are kept in 21 orbitals, with the scheme RAS(18,2,2;3,10,8). The main difficulty associated with the choice of orbitals resides in keeping similar active spaces for singlet and triplet complexes, as their structures differ. Let us start from I. Orbitals that correspond mostly to the π and π* system of the ligands are included in the RAS1 and RAS3, respectively, as they are not strongly impacted by the changes in geometry between the singlet and triplet states: those accounts for the two cyclopentadienyl π orbitals and the totally bonding butadiene π orbital for the RAS1. All the five 3d-like orbitals in interaction with the ligands are included in the RAS2, as well as their antibonding counterparts. In the case of intermediate II, a very similar approach was used. Here, the alkenyl ligand also binds to the metal center with its central π orbital in the singlet whereas in the triplet case it is non-bonding, Fig. 2. Because of this, we chose to include all π-type orbitals of the alkenyl ligand into the RAS2 and a doubly-occupied 3d orbital is moved to the RAS1 instead. The rest of the active space is very similar to the one selected for intermediate I.

As geometries are not the same for the singlet and the triplet complexes, active spaces were accurately checked, so that the same typologies of orbitals are kept in the treatment of the two states. Active spaces for all the complexes, including comparisons between natural orbitals for triplets and singlets, are available in the ESI.†

3 Results and discussion

In this section we shall first present results obtained from the wave function methods for the training set and the target I and II systems. These results will provide reference values to benchmark a few DFT functionals, often employed in reactivity studies. A discussion is then proposed on the evolution of the ΔE_ST values.

3.1 Training set

Results for the training set are reported in Table 3 for the wave function based methods. As CASSCF wave functions were obtained to perform MRCISD and CASPT2 calculations, the weights of the leading configurations W₀, reported in Table 4 for the largest CAS, are available and give insights into the nature of the electronic structure for the treated systems. The Co⁺ and the [Co(C₂H₄)]⁺ systems possess high multireference character, due to the d⁸ electronic configuration of the bare cation. The addition of the ethylene ligand induces a splitting of the d orbitals of the metal center, leading to a well-defined ³A₂ ground state (C_2v symmetry, W₀ = 0.92); however, three leading configurations with significant weights (W₀ = 0.45, 0.21, 0.19) are necessary to describe the singlet state. For these two cases, coupled-cluster methods, which are based on mono-determinantal reference wave functions, are not adequate and results are not reported in Table 3. For the two complexes CpCo and [CpCo(C₂H₄)], which have a more complete coordination sphere, values of W₀ are larger than 0.8 and permit to identify the leading configurations, for both triplet and singlet states, but the weights remain lower than a threshold of 0.9 that identifies a system for which a coupled cluster calculation can clearly be taken as a reference. However, the remaining contributions to the CASSCF wave functions are numerous with weights of less than 0.04 (see ESI,† Section ‘Active Spaces for cobalt systems’ and ‘Active Spaces for rhodium systems’) and, despite the small multireference character, results in Table 3 for CpCo and [CpCo(C₂H₄)] show a nice agreement between MRCISD and CCSD(T) methods (less than 1 kcal mol⁻¹ difference).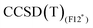 values obtained with the B3 basis, close to the infinite basis set limit, are essentially the same as those obtained with Molpro, thus confirming the good quality of the CCSD(T) results in terms of basis set. The method tends to stabilise the singlet with respect to the triplet by 1–2 kcal mol⁻¹, leading to slightly smaller ΔE_ST values compared to MRCISD (29.38 and 9.50 kcal mol⁻¹ at the level to compare to 30.33 and 11.43 at the MRCISD level, for CpCo and [CpCo(C₂H₄)], respectively). We recall that our F12 calculations do not include relativistic effects, but their impact on ΔE_ST is less than 1 kcal mol⁻¹ (see ESI†). Concerning the use of the split-valence basis set (B5), results are very close to those obtained with the B3 basis (within 0.5 kcal mol⁻¹). The effect is larger (2 kcal mol⁻¹) in the case of CpCo for 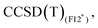as the ΔE_ST values vary from 30.26 kcal mol⁻¹ (B3 basis) to 32.29 kcal mol⁻¹ (B5 basis).

Table 3 ΔE_ST (kcal mol⁻¹, eqn (1)) for a series of cobalt and rhodium complexes. See Table 2 for basis set specifications. Semicore electrons are included in all methods treating dynamical correlation. Experimental values for Co⁺ and Rh⁺, based on a weighted average over J values (see ESI),¹¹⁰ are 31.32 and 28.56 kcal mol⁻¹, respectively^111–114

Co(I)	Basis set	Co^+	[Co(C2H4)]^+	CpCo	[CpCo(C2H4)]
CAS(i,j)MRCISD		(8,5)	(10,8)	(12,9)	(14,11)
MRCISD	B1	31.98	32.24	30.33	11.43
CAS(i,j)PT2;		(8,10)	(10,13)	(12,14)	(14,16)
CASSCF	B1	39.03	37.36	36.45	19.16
CASPT2	B1	30.16	31.03	30.50	16.43
HF	B1	—	—	60.84	56.62
CCSD	B1	—	—	37.09	19.53
CCSD(T)	B1	—	—	30.49	11.77
	B3	—	—	30.26	12.80
	B3	—	—	29.38	9.50
	B5	—	—	32.29	13.35
	B5	—	—	29.98	10.09

---

Rh(I)		Rh^+	[Rh(C2H4)]^+	CpRh	[CpRh(C2H4)]
CAS(i,j)		(8,5)	(10,8)	(14,11)	(14,11)
MRCISD	B4	24.61	11.43	12.68	−6.12
CASSCF	B4	32.28	21.07	17.80	−2.95
CASPT2	B4	22.65	11.42	10.94	−2.82
CCSD(T)	B4	—	—	13.16	−9.77

---

Table 4 Weight of the main configuration in the CASSCF wave function (W₀)

	CAS/RAS	Singlet	Triplet
[Co(C2H4)]^+	CAS(10,13)	0.45	0.92
CpCo	CAS(12,14)	0.81	0.87
[CpCo(C2H4)]	CAS(14,16)	0.82	0.85
I [TPSS-D3]	RAS(18,2,2;3,10,8)	0.73	0.76
II [TPSS-D3]	RAS(18,2,2;3,10,8)	0.76	0.77

---

A good agreement is observed between MRCISD (or CCSD(T)) and CASPT2 calculations, with deviations of about 1 kcal mol⁻¹ to 5 kcal mol⁻¹ for the [CpCo(C₂H₄)] system. Previous works on spin-state energetics for first-row transition metal complexes suggest that, in general, CASPT2 catches correctly valence correlation, but it may not describe in an accurate manner the metal 3s3p semicore correlation effects.²⁴ This would be partly responsible for an overstabilisation of high-spin with respect to low-spin states. We have then checked on our training system the effect of including the 3s3p correlation in the calculations by mean of the Δ_sp quantity, reported in Fig. 4 and defined as:

Δ_sp = ΔE^sp_ST − ΔE^nosp_ST (2)

where ΔE^sp_ST includes the 3s3p correlation contribution and ΔE^nosp_ST does not. Thus, a positive value of Δ_sp indicates that the 3s3p semicore correlation stabilises the triplet state with respect to the singlet at the given computational level and vice versa. For the Co⁺ and [Co(C₂H₄)]⁺ cases, the inclusion of the 3s3p effect tends to stabilise the singlet state with respect to the triplet in both the MRCISD and CASPT2 calculations. For the CpCo case, the effect is small for all the methods, but for the [CpCo(C₂H₄)] complex, where the coordination sphere has been increased, the triplet overstabilisation in the CASPT2 appears (positive Δ_sp), while the contributions evaluated at the MRCISD and CCSD(T) are slightly negative.

Fig. 4 Effect of 3s3p correlation, in terms of Δ_sp (eqn (2)).

Results at the Hartree–Fock (HF), CCSD and CASSCF levels are also reported in Table 3. As expected, at the HF level singlet states are much too high in energy compared to triplet states. At the CCSD level, ΔE_ST values dramatically drop, by about 20–25 kcal mol⁻¹, however, perturbative triples still account for about 7 kcal mol⁻¹. Their contribution can not be neglected to reach high accuracy.

Finally, we evaluated the singlet–triplet energy differences in the case of a similar set of rhodium complexes, by following a similar methodology. MRCISD and CASPT2 results are in agreement within 2 kcal mol⁻¹ for the Rh⁺, [Rh(C₂H₄)]⁺ and the deviations from MRCISD for CASPT2 and CCSD(T) are also in this range for the CpRh system. Deviations are somewhat larger for the [CpRh(C₂H₄)], although all methods predict this complex to be more stable in its singlet structure. Recently, the effect of size-inconsistency on spin-state relative energies was pointed out for MRCISD calculations.^20,21 The errors are expected to increase with the geometrical differences between the singlet and triplet, and with a larger number of correlated electrons. In the case of the [CpRh(C₂H₄)], the structures in the singlet and in the triplet differ by a 90° rotation of the ethylene group (see ESI,† for details on the structures); this might contribute to introduce a size-consistency error in the multireference calculation that affect the comparison between MRCISD and the coupled cluster results.

3.2 Complexes I and II

Results on systems I and II are collected in Table 5. MRCISD calculations were not performed for these systems, because they would be beyond our computing capacities and size-consistency errors may become significant.^20,21

Table 5 ΔE_ST (kcal mol⁻¹; 3s3p correlation included) for I and II (Co(III)). Basis sets B1 and B2 (Table 2) are employed for the RASPT2 and CCSD(T) calculations, respectively. RASPT2_corr is defined in Section 3.2

	I	I	II	II
	B3LYP-D3	TPSS-D3	B3LYP-D3	TPSS-D3
RASPT2	—	8.05	−3.07	−2.41
CCSD(T)	5.62	5.28	−9.37	−10.65
RASPT2/CC	—	6.01	−5.28	−6.44

---

Concerning I, we did not manage to have satisfyingly comparable active spaces for triplet and singlet with the B3LYP-D3 structures, thus we report only the TPSS-D3 results for RAS-based methods. Moreover, as two close-lying triplet states exist for I, state-averaged RASSCF on two roots were performed both for the triplet and singlet calculations. This allows to keep comparable active spaces for the two spin states. Concerning II, the structure of the singlet differs from that of the triplet because of the interaction between the metal and the alkene moiety of the ligand. In order to obtain a balanced description of the two states, the active space of the triplet contains all relevant orbitals for the corresponding singlet state and vice versa: importantly, the occupied π and virtual π* orbitals of the double bond interacting with the cobalt in the singlet are included in both RAS2 (see ESI,† Section ‘Active Spaces for cobalt systems’).

The computed ΔE_ST for I are all positive, indicating that the triplet is more stable. The CCSD(T) values are very similar for the two geometries, 5.62 and 5.28 kcal mol⁻¹ for B3LYP-D3 and TPSS-D3, respectively. The RASPT2 value (TPSS-D3 geometries, 8.05 kcal mol⁻¹) is slightly larger. The comparison between the results obtained with the two sets of geometries for II, show differences up to 1.3 kcal mol⁻¹ (CCSD(T) calculations); however, the computed ΔE_ST values are all negative, meaning that the singlet structure is more stable than the triplet. As for I, the RASPT2 values for II are larger than those at the CCSD(T) level (−3.07 and −2.41 to be compared to −9.37 and −10.65 kcal mol⁻¹, respectively for B3LYP-D3 and TPSS-D3 structures).

Since RASPT2 calculations including the 3s3p correlation tend to overstabilise a triplet with respect to a singlet, we propose RASPT2/CC corrected values by following Phung et al.:¹¹⁵ the Δ_sp contribution is evaluated at the coupled cluster level and used to correct the nosp RASPT2 energy. Despite some multireference character, the RASPT2/CC method gives an estimation of the Δ_sp errors: indeed, the leading configurations in the RASSCF wave functions for I and II are clearly identified, although their weights are less than 0.9, Table 4. We obtained in this way a ΔE_ST value of 6.01 kcal mol⁻¹ for I; for II we obtained −5.28 kcal mol⁻¹ (B3LYP-D3) and −6.44 kcal mol⁻¹ (TPSS-D3).

Finally, even without a unique reference ΔE_ST values for these two cases, all methods identify I as a triplet and II as a singlet.

3.3 Comparison with DFT results

ΔE_ST values computed with some DFT functionals are reported in Table 6 for M⁺, [M(C₂H₄)]⁺, CpM, and [CpM(C₂H₄)] (M = Co, Rh) training systems. The list of the tested functionals is clearly far from being exhaustive: we have considered only a few common methods among those in the DFT families (GGA, meta-GGA, hybrid or not). In this work we focus our attention on ΔE_ST: reproducing the right sign is essential to provide a correct picture in a two-state mechanism as it is proposed in the literature for the cobalt cycloaddition reaction.^35,39 However, we should keep in mind that if the aim is studying a reactivity at DFT level, the functional chosen should also provide correct relative energies along the whole reaction coordinate. Thus, tuning new DFT parameters for reproducing the singlet–triplet splitting on a few intermediates is not our target.

Table 6 ΔE_ST (kcal mol⁻¹) values computed with several DFT functionals for cobalt(I) and rhodium(I) systems

	Co^+	[Co(C2H4)]^+	CpCo	[CpCo(C2H4)]
M06	54.85	45.72	30.39	16.52
TPSSh-D3	64.73	52.08	33.68	14.22
PBE0-D3	64.61	55.44	39.83	22.92
B3LYP-D3	60.60	51.91	35.91	20.72
CAM-B3LYP	59.98	51.57	37.78	22.19
M06-L	—	—	30.86	13.87
TPSS-D3	—	—	28.36	7.15
PBE-D3	—	—	26.29	5.29
BP86-D3	—	—	26.60	5.75

---

	Rh^+	[Rh(C2H4)]^+	CpRh	[CpRh(C2H4)]
M06	41.14	10.84	12.64	−6.49
TPSSh-D3	50.42	22.20	15.74	−7.90
PBE0-D3	49.55	22.10	17.20	−6.46
B3LYP-D3	45.79	20.59	15.41	−5.36
CAM-B3LYP	45.15	21.33	17.10	−3.46
M06-L	—	—	14.72	−8.58
TPSS-D3	—	—	14.22	−9.10
PBE-D3	—	—	12.43	−9.66
BP86-D3	—	—	12.38	−8.80

---

Results with non-hybrid functionals for the M⁺ and [M(C₂H₄)]⁺ are not presented: we could not converge calculations with integer occupations of the Kohn–Sham orbitals, due to orbital degeneracy issues. Errors in ΔE_ST for the M⁺ and [M(C₂H₄)]⁺ are large, more than 20 kcal mol⁻¹, but this is not surprising due to the highly multireferential nature of these systems, notably for the singlet states, Table 4. All DFT methods predict the same sign as the MRCISD references for ΔE_ST values, with deviations that roughly vary according to the percentage of Hartree–Fock exchange, Fig. 5. Concerning the cobalt systems, PBE0-D3, B3LYP-D3 and CAM-B3LYP perform quite similarly and tend to overstabilise the triplet with respect to the singlet, with deviations up to 10 kcal mol⁻¹ for the [CpCo(C₂H₄)] system. The pure GGA functionals PBE-D3 and BP86-D3 show the opposite trend, predicting smaller ΔE_ST values, with deviations up to 6 kcal mol⁻¹. The meta-GGA functionals (hybrid or not) perform the best, with deviations up to 5 kcal mol⁻¹. Deviations from MRCISD values for CpRh and [CpRh(C₂H₄)] are smaller than those for the corresponding cobalt systems.

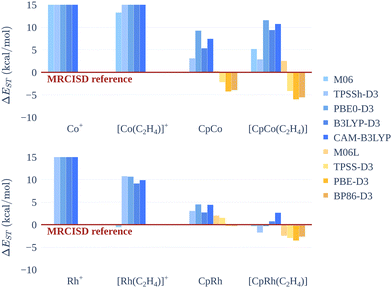Fig. 5 Deviations (kcal mol⁻¹) of ΔE_ST computed with several DFT functionals from MRCISD values for cobalt(I) and rhodium(I) systems.

DFT computed ΔE_ST values for I and II are reported in Table 7. The comparison with the CCSD(T) and RASPT2 results is shown in Fig. 6. For I, all the methods predict that the triplet is lower in energy. Non-hybrid GGA and non-hybrid meta-GGA functionals give values that are very close to those obtained with either the CCSD(T) or the RASPT2/CC methods, while deviations are somewhat larger for the other functionals. The case of II is more critical, as the hybrid PBE0-D3, B3LYP-D3 and CAM-B3LYP suggest that the triplet is more stable, whereas the CCSD(T) and RASPT2/CC calculations indicate that the singlet is preferred. In this case, we do not have a clear reference value, however pure GGA and meta-GGA functionals (hybrid or not) provide negative ΔE_ST values that are closer to either the CCSD(T) and RASPT2/CC results.

Table 7 ΔE_ST (kcal mol⁻¹) values computed with several DFT functionals for I and II (Co(III) systems)

	I	II
M06	11.73	−0.89
TPSSh-D3	11.10	−6.20
PBE0-D3	18.05	5.57
B3LYP-D3	15.83	8.13
CAM-B3LYP	16.55	8.53
M06-L	7.92	−3.78
TPSS-D3	6.17	−13.64
PBE-D3	5.04	−13.27
BP86-D3	5.50	−12.78

---

Fig. 6 Comparison between ΔE_ST (kcal mol⁻¹) computed with several DFT functionals, and CCSD(T) and RASPT2/CC values for target systems I and II (TPSS-D3 geometries, Co(III)).

3.4 Triplet or singlet ground state?

In the treated cobalt and rhodium triplet systems, the SOMO are essentially d orbitals, resulting in a spin density localised on the metal center, as depicted in Fig. 7 for either Co(I) or Co(III) complexes. The electron-pairing (from going from triplet to singlet) concerns mostly these d orbitals localised on the metal center in a similar way for all the treated systems. The larger tendency towards electron-pairing from 3d to 4d transition metals is verified for the Rh(I) systems: even if ΔE_ST values for Rh⁺, [Rh(C₂H₄)]⁺ and CpRh indicate that the triplet is still more stable for this systems than the singlet, these values are significantly lower than those for the corresponding cobalt systems. The [CpRh(C₂H₄)] is clearly a singlet. Concerning cobalt, all the systems of the training set and I have a triplet ground state: for Co⁺, [Co(C₂H₄)]⁺ and CpCo the triplet is more stable than the singlet by about 30 kcal mol⁻¹. Even if the ΔE_ST drops to about 12 to 5 kcal mol⁻¹, triplet states are clearly favored for [CpCo(C₂H₄)] and I. This is not surprising, as it has been already established that 16-electron cobalt complexes usually exhibit triplet ground states, while 18-electron systems should have a singlet state.^65,116 Notably, [CpM(L)] complexes with d⁸ metals are known to be triplets, whereas corresponding 18-electron [CpM(L)(L′)] systems display singlet ground state electronic configurations.

Fig. 7 Spin density plots generated from the CASSCF wave function of the cobalt systems treated in this work.

Concerning II, the coordination pattern of the cobalt in the triplet structure consists of the cyclopentadienyl ring and of an alkenyl moiety: formally, the metal has 16-electron as in ³I. In the singlet, the accessibility on the metallacycle of an unsatured moiety makes possible an interaction with the metal center, achieving a full 18-electron shell. There is therefore a competition between the stabilisation due to the exchange interaction operating in the triplet (Fig. 8a and b), and the energetic gain due to the ligand donation into an empty d orbital in the singlet (Fig. 8c). We have estimated that the loss in the exchange term is of 17 kcal mol⁻¹ (CCSD(T), TPSS-D3 geometries), by computing the energy difference between the singlet and the triplet in the triplet geometry of II, while the energy gain through the coordination of an alkene moiety is of about −36 kcal mol⁻¹ (CCSD(T) energy corresponding to the transformation: I + C₂H₄ = [(I)(C₂H₄)], TPSS geometries). Thus, the coordination energy can compensate the electron pairing and the structural constraints emerging in the intramolecular coordination in II.

Fig. 8 Schematic representation of some molecular orbitals that differ between the complexes ³II and ¹II. Co–π is the distance between the cobalt and the middle of the alkene moiety for the two structures optimised on either the triplet or the singlet potential energy surfaces.

Some methods could introduce an artificial preference towards high spin state and indeed some of the tested hybrid DFT functionals predict a reversed stability order for II. However and remarkably, all the wave function methods identify the singlet structure to be lower in energy for II, even at the RASPT2 level.

4 Conclusions

In this work, accurate computed singlet and triplet energy differences for several Co and Rh complexes are presented. The nice agreement between MRCISD and CCSD(T) for the training set, suggests that, for our specific problem, relevant correlation effects are efficiently recovered by the perturbative treatment of triple excitations and that CCSD(T) is well-behaving.

The systems Rh⁺, [Rh(C₂H₄)]⁺ and CpRh have a triplet ground state, while [CpRh(C₂H₄)] is a singlet. For the cobalt systems, Co⁺, [Co(C₂H₄)]⁺, CpCo, [CpCo(C₂H₄)] and I are triplets, while II is a singlet. Pure GGA and meta-GGA (hybrid or not) functionals predict the same sign for the ΔE_ST values as the wave function methods, while the PBE0-D3, B3LYP-D3, and CAM-B3LYP functionals overstabilise the triplet with respect to the singlet, notably for II.

The relative stability of the singlet vs. triplet for the cobalt system II has an impact on the general mechanism of the cycloaddition reaction: if the triplet were up to 10 kcal mol⁻¹ more stable than the singlet, as predicted with some DFT functionals, it would have been reasonable to assume that the reductive elimination step would occur on the triplet potential energy surface, as shown in Fig. 1. However, we show here that the singlet is more stable. Moreover, barriers for the reductive elimination step have been evaluated at less than 15 kcal mol⁻¹ (electronic energy).³⁵ They are therefore accessible at room temperature. We conclude that the preferred path for the reductive elimination step preferentially occurs on the singlet potential energy surface, as illustrated in Fig. 9.

Fig. 9 Revised general mechanism for a [2+2+2] cycloaddition reaction catalysed by a CpCoL₂ complex.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We wish to thank the French Research Ministry, Aix-Marseille University and CNRS for financial support and ‘Centre de Calcul Intensif d'Aix-Marseille’ for granting us access to its high performance computing resources. This work was also supported by the computing facilities of the CRCMM, ‘Centre Régional de Compétences en Modélisation Moléculaire de Marseille’.

Notes and references

1. P. Gütlich and H. A. Goodwin, Spin Crossover in Transition Metal Compounds III, Springer-Verlag, Heidelberg, 2004.
2. P. Gütlich and H. A. Goodwin, Spin Crossover in Transition Metal Compounds II, Springer-Verlag, Berlin, 2004.
3. P. Gütlich and H. A. Goodwin, Spin Crossover in Transition Metal Compounds I, Springer-Verlag, Heidelberg, 2004.
4. R. Poli and J. N. Harvey, Chem. Soc. Rev., 2003, 32, 1–8.
5. J. N. Harvey, R. Poli and K. M. Smith, Coord. Chem. Rev., 2003, 238-239, 347–361.
6. D. Schröder, S. Shaik and H. Schwarz, Acc. Chem. Res., 2000, 33, 139–145.
7. M. Swart and M. Costas Salgueiro, Spin states in biochemistry and inorganic chemistry: influence on structure and reactivity, John Wiley & Sons, Inc, Chichester, West Sussex, 2016.
8. K. M. Smith, R. Poli and J. N. Harvey, New J. Chem., 2000, 24, 77–80.
9. D. Kim, G. Pillon, D. J. DiPrimio and P. L. Holland, J. Am. Chem. Soc., 2021, 143, 3070–3074.
10. M. Swart, A. R. Groenhof, A. W. Ehlers and K. Lammertsma, J. Phys. Chem. A, 2004, 108, 5479–5483.
11. F. Furche and J. P. Perdew, J. Chem. Phys., 2006, 124, 044103.
12. J. N. Harvey, Annu. Rep. Prog. Chem., Sect. C: Phys. Chem., 2006, 102, 203–226.
13. D. N. Bowman and E. Jakubikova, Inorg. Chem., 2012, 51, 6011–6019.
14. G. Ganzenmüller, N. Berkaïne, A. Fouqueau, M. E. Casida and M. Reiher, J. Chem. Phys., 2005, 122, 234321.
15. J. Autschbach and M. Srebro, Acc. Chem. Res., 2014, 47, 2592–2602.
16. E. I. Ioannidis and H. J. Kulik, J. Chem. Phys., 2015, 143, 034104.
17. S. Vancoillie, H. Zhao, M. Radoń and K. Pierloot, J. Chem. Theory Comput., 2010, 6, 576–582.
18. L. M. Lawson Daku, F. Aquilante, T. W. Robinson and A. Hauser, J. Chem. Theory Comput., 2012, 8, 4216–4231.
19. S. E. Neale, D. A. Pantazis and S. A. Macgregor, Dalton Trans., 2020, 49, 6478–6487.
20. M. Radoń, Phys. Chem. Chem. Phys., 2019, 21, 4854–4870.
21. G. Drabik, J. Szklarzewicz and M. Radoń, Phys. Chem. Chem. Phys., 2021, 23, 151–172.
22. D. Zhang and D. G. Truhlar, J. Chem. Theory Comput., 2020, 16, 4416–4428.
23. S. Song, M.-C. Kim, E. Sim, A. Benali, O. Heinonen and K. Burke, J. Chem. Theory Comput., 2018, 14, 2304–2311.
24. K. Pierloot, Q. M. Phung and A. Domingo, J. Chem. Theory Comput., 2017, 13, 537–553.
25. P. J. Knowles, C. Hampel and H.-J. Werner, J. Chem. Phys., 1993, 99, 5219–5227.
26. J. D. Watts, J. Gauss and R. J. Bartlett, J. Chem. Phys., 1993, 98, 8718–8733.
27. J. F. Stanton, J. Gauss and R. J. Bartlett, J. Chem. Phys., 1992, 97, 5554–5559.
28. J. V. Ortiz, Int. J. Quantum Chem., 2004, 100, 1131–1135.
29. D. P. Tew, J. Chem. Phys., 2016, 145, 074103.
30. K. Andersson, P. Å. Malmqvist and B. O. Roos, J. Chem. Phys., 1992, 96, 1218–1226.
31. P. Å. Malmqvist, K. Pierloot, A. R. M. Shahi, C. J. Cramer and L. Gagliardi, J. Chem. Phys., 2008, 128, 204109.
32. C. Angeli, R. Cimiraglia, S. Evangelisti, T. Leininger and J.-P. Malrieu, J. Chem. Phys., 2001, 114, 10252–10264.
33. G. Li Manni and A. Alavi, J. Phys. Chem. A, 2018, 122, 4935–4947.
34. O. Weser, L. Freitag, K. Guther, A. Alavi and G. Li Manni, Int. J. Quantum Chem., 2021, 121, e26454.
35. V. Gandon, N. Agenet, K. P. C. Vollhardt, M. Malacria and C. Aubert, J. Am. Chem. Soc., 2006, 128, 8509–8520.
36. L. L. Schafer, P. Mountford and W. E. Piers, Dalton Trans., 2015, 44, 12027–12028.
37. A. A. Dahy, C. H. Suresh and N. Koga, Bull. Chem. Soc. Jpn., 2005, 78, 792–803.
38. A. A. Dahy and N. Koga, Bull. Chem. Soc. Jpn., 2005, 78, 781–791.
39. A. Roglans, A. Pla-Quintana and M. Solà, Chem. Rev., 2021, 121, 1894–1979.
40. M. Delorme, A. Punter, R. Oliveira, C. Aubert, Y. Carissan, J.-L. Parrain, M. Amatore, P. Nava and L. Commeiras, Dalton Trans., 2019, 48, 15767–15771.
41. Q. M. Phung, S. Vancoillie and K. Pierloot, J. Chem. Theory Comput., 2012, 8, 883–892.
42. Q. M. Phung, S. Vancoillie and K. Pierloot, J. Chem. Theory Comput., 2014, 10, 3681–3688.
43. TURBOMOLE V7.5 2020, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989-2007, TURBOMOLE GmbH, since 2007; available from https://www.turbomole.org.
44. P. A. M. Dirac and R. H. Fowler, Proc. Royal Soc., 1929, 123, 714–733.
45. J. C. Slater, Phys. Rev., 1951, 81, 385–390.
46. J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13244–13249.
47. J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401.
48. V. N. Staroverov, G. E. Scuseria, J. Tao and J. P. Perdew, J. Chem. Phys., 2003, 119, 12129–12137.
49. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
50. J. P. Perdew, M. Ernzerhof and K. Burke, J. Chem. Phys., 1996, 105, 9982–9985.
51. S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211.
52. A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100.
53. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
54. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
55. T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57.
56. J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824.
57. M. J. Frisch, G. W. Trucks, J. R. Cheeseman, G. Scalmani, M. Caricato, H. P. Hratchian, X. Li, V. Barone, J. Bloino, G. Zheng, T. Vreven, J. A. Montgomery, G. A. Petersson, G. E. Scuseria, H. B. Schlegel, H. Nakatsuji, A. F. Izmaylov, R. L. Martin, J. L. Sonnenberg, J. E. Peralta, J. J. Heyd, E. Brothers, F. Ogliaro, M. Bearpark, M. A. Robb, B. Mennucci, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, A. Rendell, R. Gomperts, V. G. Zakrzewski, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao and H. Nakai, Gaussian 09, Revision D.01.
58. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
59. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
60. F. Weigend, F. Furche and R. Ahlrichs, J. Chem. Phys., 2003, 119, 12753–12762.
61. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
62. K. Eichkorn, O. Treutler, H. Öhm, M. Häser and R. Ahlrichs, Chem. Phys. Lett., 1995, 240, 283–290.
63. K. Eichkorn, F. Weigend, O. Treutler and R. Ahlrichs, Theor. Chim. Acta, 1997, 97, 119–124.
64. F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065.
65. P. E. M. Siegbahn, J. Am. Chem. Soc., 1996, 118, 1487–1496.
66. I. Fdez. Galván, M. Vacher, A. Alavi, C. Angeli, F. Aquilante, J. Autschbach, J. J. Bao, S. I. Bokarev, N. A. Bogdanov, R. K. Carlson, L. F. Chibotaru, J. Creutzberg, N. Dattani, M. G. Delcey, S. S. Dong, A. Dreuw, L. Freitag, L. M. Frutos, L. Gagliardi, F. Gendron, A. Giussani, L. González, G. Grell, M. Guo, C. E. Hoyer, M. Johansson, S. Keller, S. Knecht, G. Kovăceví, E. Källman, G. Li Manni, M. Lundberg, Y. Ma, S. Mai, J. P. Malhado, P. Å. Malmqvist, P. Marquetand, S. A. Mewes, J. Norell, M. Olivucci, M. Oppel, Q. M. Phung, K. Pierloot, F. Plasser, M. Reiher, A. M. Sand, I. Schapiro, P. Sharma, C. J. Stein, L. K. Sørensen, D. G. Truhlar, M. Ugandi, L. Ungur, A. Valentini, S. Vancoillie, V. Veryazov, O. Weser, T. A. Wesołowski, P.-O. Widmark, S. Wouters, A. Zech, J. P. Zobel and R. Lindh, J. Chem. Theory Comput., 2019, 15, 5925–5964.
67. F. Aquilante, J. Autschbach, A. Baiardi, S. Battaglia, V. A. Borin, L. F. Chibotaru, I. Conti, L. De Vico, M. Delcey, I. F. Galván, N. Ferré, L. Freitag, M. Garavelli, X. Gong, S. Knecht, E. D. Larsson, R. Lindh, M. Lundberg, P. Å. Malmqvist, A. Nenov, J. Norell, M. Odelius, M. Olivucci, T. B. Pedersen, L. Pedraza-González, Q. M. Phung, K. Pierloot, M. Reiher, I. Schapiro, J. Segarra-Martí, F. Segatta, L. Seijo, S. Sen, D.-C. Sergentu, C. J. Stein, L. Ungur, M. Vacher, A. Valentini and V. Veryazov, J. Chem. Phys., 2020, 152, 214117.
68. F. Aquilante, P. Å. Malmqvist, T. B. Pedersen, A. Ghosh and B. O. Roos, J. Chem. Theory Comput., 2008, 4, 694–702.
69. F. Aquilante, L. Gagliardi, T. B. Pedersen and R. Lindh, J. Chem. Phys., 2009, 130, 154107.
70. G. Ghigo, B. O. Roos and P. Å. Malmqvist, Chem. Phys. Lett., 2004, 396, 142–149.
71. N. Forsberg and P. Å. Malmqvist, Chem. Phys. Lett., 1997, 274, 196–204.
72. V. Sauri, L. Serrano-Andrés, A. R. M. Shahi, L. Gagliardi, S. Vancoillie and K. Pierloot, J. Chem. Theory Comput., 2011, 7, 153–168.
73. H.-J. Werner and P. J. Knowles, J. Chem. Phys., 1988, 89, 5803–5814.
74. P. J. Knowles and H.-J. Werner, Chem. Phys. Lett., 1988, 145, 514–522.
75. P. J. Knowles and H.-J. Werner, Theor. Chim. Acta, 1992, 84, 95–103.
76. K. R. Shamasundar, G. Knizia and H.-J. Werner, J. Chem. Phys., 2011, 135, 054101.
77. H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 242–253.
78. H.-J. Werner, P. J. Knowles, F. R. Manby, J. A. Black, K. Doll, A. Heßelmann, D. Kats, A. Köhn, T. Korona, D. A. Kreplin, Q. Ma, T. F. Miller, A. Mitrushchenkov, K. A. Peterson, I. Polyak, G. Rauhut and M. Sibaev, J. Chem. Phys., 2020, 152, 144107.
79. H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schütz, P. Celani, W. Györffy, D. Kats, T. Korona, R. Lindh, A. Mitrushenkov, G. Rauhut, K. R. Shamasundar, T. B. Adler, R. D. Amos, S. J. Bennie, A. Bernhardsson, A. Berning, D. L. Cooper, M. J. O. Deegan, A. J. Dobbyn, F. Eckert, E. Goll, C. Hampel, A. Hesselmann, G. Hetzer, T. Hrenar, G. Jansen, C. Köppl, S. J. R. Lee, Y. Liu, A. W. Lloyd, Q. Ma, R. A. Mata, A. J. May, S. J. McNicholas, W. Meyer, T. F. Miller III, M. E. Mura, A. Nicklass, D. P. O'Neill, P. Palmieri, D. Peng, K. Pflüger, R. Pitzer, M. Reiher, T. Shiozaki, H. Stoll, A. J. Stone, R. Tarroni, T. Thorsteinsson, M. Wang and M. Welborn, MOLPRO, version 2021, a package of ab initio programs.
80. J. A. Pople, R. Seeger and R. Krishnan, Int. J. Quantum Chem., 1977, 12, 149–163.
81. H.-J. Werner and P. J. Knowles, J. Chem. Phys., 1985, 82, 5053.
82. P. J. Knowles and H.-J. Werner, Chem. Phys. Lett., 1985, 115, 259–267.
83. D. A. Kreplin, P. J. Knowles and H.-J. Werner, J. Chem. Phys., 2019, 150, 194106.
84. D. A. Kreplin, P. J. Knowles and H.-J. Werner, J. Chem. Phys., 2020, 152, 074102.
85. M. Douglas and N. M. Kroll, Ann. Phys., 1974, 82, 89–155.
86. B. A. Hess, Phys. Rev. A: At., Mol., Opt. Phys., 1986, 33, 3742–3748.
87. M. Reiher and A. Wolf, J. Chem. Phys., 2004, 121, 10945–10956.
88. M. Reiher and A. Wolf, J. Chem. Phys., 2004, 121, 2037–2047.
89. T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023.
90. K. A. Peterson and T. H. Dunning, J. Chem. Phys., 2002, 117, 10548–10560.
91. N. B. Balabanov and K. A. Peterson, J. Chem. Phys., 2005, 123, 064107.
92. W. A. de Jong, R. J. Harrison and D. A. Dixon, J. Chem. Phys., 2001, 114, 48–53.
93. K. A. Peterson, D. Figgen, M. Dolg and H. Stoll, J. Chem. Phys., 2007, 126, 124101.
94. B. P. Pritchard, D. Altarawy, B. Didier, T. D. Gibson and T. L. Windus, J. Chem. Inf. Model., 2019, 59, 4814–4820.
95. D. Feller, J. Comput. Chem., 1996, 17, 1571–1586.
96. K. L. Schuchardt, B. T. Didier, T. Elsethagen, L. Sun, V. Gurumoorthi, J. Chase, J. Li and T. L. Windus, J. Chem. Inf. Model., 2007, 47, 1045–1052.
97. R. A. Bachorz, F. A. Bischoff, A. Glöβ, C. Hättig, S. Höfener, W. Klopper and D. P. Tew, J. Comput. Chem., 2011, 32, 2492–2513.
98. C. Hättig, D. P. Tew and A. Köhn, J. Chem. Phys., 2010, 132, 231102.
99. S. G. Balasubramani, G. P. Chen, S. Coriani, M. Diedenhofen, M. S. Frank, Y. J. Franzke, F. Furche, R. Grotjahn, M. E. Harding, C. Hättig, A. Hellweg, B. Helmich-Paris, C. Holzer, U. Huniar, M. Kaupp, A. Marefat Khah, S. Karbalaei Khani, T. Müller, F. Mack, B. D. Nguyen, S. M. Parker, E. Perlt, D. Rappoport, K. Reiter, S. Roy, M. Rückert, G. Schmitz, M. Sierka, E. Tapavicza, D. P. Tew, C. van Wüllen, V. K. Voora, F. Weigend, A. Wodyński and J. M. Yu, J. Chem. Phys., 2020, 152, 184107.
100. C. Hättig, Phys. Chem. Chem. Phys., 2005, 7, 59–66.
101. F. Weigend, A. Köhn and C. Hättig, J. Chem. Phys., 2002, 116, 3175–3183.
102. F. Weigend, J. Comput. Chem., 2008, 29, 167–175.
103. F. Weigend, M. Häser, H. Patzelt and R. Ahlrichs, Chem. Phys. Lett., 1998, 294, 143–152.
104. J. G. Hill and J. A. Platts, J. Chem. Phys., 2008, 129, 134101.
105. K. Pierloot, in Computational Organometallic Chemistry, ed. T. R. Cundari, Marcel Dekker, Inc., New York, 2001, pp. 123–158.
106. K. Pierloot, Mol. Phys., 2003, 101, 2083–2094.
107. S. Vancoillie, H. Zhao, V. T. Tran, M. F. A. Hendrickx and K. Pierloot, J. Chem. Theory Comput., 2011, 7, 3961–3977.
108. K. Pierloot, Int. J. Quantum Chem., 2011, 111, 3291–3301.
109. V. Veryazov, P. Å. Malmqvist and B. O. Roos, Int. J. Quantum Chem., 2011, 111, 3329–3338.
110. A. Fouqueau, S. Mer, M. E. Casida, L. M. Lawson Daku, A. Hauser, T. Mineva and F. Neese, J. Chem. Phys., 2004, 120, 9473–9486.
111. J. C. Pickering, A. J. J. Raassen, P. H. M. Uylings and S. Johansson, Astrophys. J., Suppl. Ser., 1998, 117, 261–311.
112. J. Sugar and C. Corliss, J. Phys. Chem. Ref. Data, 1985, 14, 1–664.
113. F. J. Sancho, An. R. Soc. Esp. Fis. Quim., 1958, 54A, 41.
114. Y. Shadmi, Bull. Res. Counc. Isr., 1961, 9F, 141.
115. Q. M. Phung, M. Feldt, J. N. Harvey and K. Pierloot, J. Chem. Theory Comput., 2018, 14, 2446–2455.
116. P. Hofmann and M. Padmanabhan, Organometallics, 1983, 2, 1273–1284.

---

Footnote

† Electronic supplementary information (ESI) available: Complete computational details, basis sets, active spaces, structural parameters, energies and coordinates. See DOI: https://doi.org/10.1039/d2cp03291k

---