Impact of solvent interactions on ¹H and ¹³C chemical shifts investigated using DFT and a reference dataset recorded in CDCl₃ and CCl₄

Abstract

¹H and ¹³C chemical shifts of 35 small, rigid molecules were measured under standardized conditions in chloroform-d and in tetrachloromethane. The solvent change mainly affects carbon shifts of polar functional groups. This difference due to specific interactions with CDCl₃ cannot be adequately reproduced by DFT calculations in implicit solvent. The new dataset provides an accurate basis for the validation and calibration of shift calculations, especially with respect to improved solvent models.

---

Introduction

Structure elucidation by NMR and the determination of relative configuration are often assisted by comparison of experimental chemical shifts with shifts calculated using density functional theory (DFT).¹ With advances in computational resources and quantum chemical software, shielding constants can be obtained on a routine basis.² For comparison with experimental data, the shieldings (σ_calc) have to be converted into chemical shifts (δ_calc). Most simply, this is done using the shielding of tetramethylsilane (TMS), calculated at the same level of theory:

δ_calci = σ_calcTMS − σ_calci (1)

Instead of TMS, any chemical shift determined with respect to TMS can be used as reference, if the corresponding shielding calculation has been carried out at the same level of theory:

δ_calci = δ_expref + σ_calcref − σ_calci (2)

To compensate for shortcomings of the theoretical method in specific electronic environments, one can also employ multiple standards for different types of carbons (e.g. based on hybridization).³ In organic chemistry, the most popular way to convert shieldings into chemical shifts is to use a large set of reference data and perform a linear regression between calculated shieldings and experimental shifts:

If the calculation reproduced all shieldings perfectly, a slope of −1 would be obtained with the intercept being equivalent to σ_calcTMS. Chemical shifts are very sensitive to the chemical environment. They also depend on temperature, solute concentration,^4,5 protonation state and the presence of impurities.⁶ Therefore, control over the conditions at which the reference shifts are recorded is important for a consistent dataset. A popular reference set is the one from Tantillo et al.,⁷ which consists of ¹H and ¹³C shifts of 80 small and relatively rigid organic molecules. Scaling factors for numerous functional/basis set combinations can be found on the authors’ webpage.⁸ The chemical shifts, however, were collected from different sources and experimental conditions (i.e. temperature, concentration, and purity) are not indicated. In addition, the dataset contains multiple chlorinated compounds whose ¹³C chemical shifts are affected by relativistic effects that cannot be accounted for by standard DFT. Hehre et al.⁹ used a reference set of 2000 molecules to derive an elaborate empirical correction scheme for ¹³C chemical shifts calculated at the inexpensive ωB97X-D/6-31G* level of theory. Also here, no special attention was paid to solvent and concentration effects or standardized experimental conditions.

Given a high-quality reference set, there are different types of errors and approximations that impact the quality and reliability of the resulting shift prediction. One source of error is the chosen DFT method itself (functional and incomplete basis set). It is possible to go beyond DFT and perform e.g. a coupled-cluster calculation for improved accuracy, but such calculations are computationally extremely expensive and only feasible for very small systems. Numerous studies attempted to determine the best combination of functional and basis set for chemical shift calculations.^7,10–13 Presumably, some combinations are only better than others due to fortunate error compensation. In terms of the applied level of theory, a good compromise between accuracy and computational cost are double-hybrid functionals, giving mean absolute relative errors as low as 1.9% for the calculated shieldings compared to coupled-cluster calculations.¹⁴ Another potential source of error when comparing calculated shieldings with experimental chemical shifts are specific intermolecular interactions with impurities like water or the solvent itself (e.g. via hydrogen bonds), which are not trivial to account for in DFT calculations.^15–17 Also vibrational contributions to the chemical shift are usually neglected.

Experimental section

NMR measurements

The molecules included in the dataset are a selection of small, rigid organic compounds containing different functional groups and consisting of only H, C, N and O atoms. For each compound 10 mM solutions were prepared in chloroform-d (Apollo Scientific) and carbon tetrachloride (Sigma-Aldrich). Chloroform was previously filtered through a short column of aluminium oxide (EcoChrom, MP Alumina N, Akt. I) and stored over molecular sieve (3 Å, Dr Bender & Dr Hobein AG) in the fridge. TMS was added as internal standard. NMR spectra were recorded on a Bruker AVANCE III 600 MHz spectrometer equipped with a helium-cooled DCH cryogenic probe with z-gradients at 25.0 °C. For each compound, a ¹H (32 scans, sw 16.0 ppm, td 96 152, o1p 6.0 ppm, aq 5 s, d1 0.01 s) and a ¹³C spectrum (512 scans, sw 248.5 ppm, td 157 890, o1p 110 ppm, aq 2.1 s, d1 0.3 s) were recorded. The samples in tetrachloromethane were shimmed via the proton signal of TMS using the following TopSpin command:

topshim 1h rga lockoff o1p = 0.2 selwid = 0.5 durmax = 120

If peaks could not be assigned unambiguously, ¹³C-HSQC, ¹³C-HMBC, DQF-COSY, NOESY and PSYCHE¹⁸ spectra were recorded as needed. Processing of the spectra was done with Bruker TopSpin™ version 4.1 (Bruker Biospin AG) and MestreNova 14.1 (Mestrelab Research). A line broadening of 0.1 Hz for ¹H and 0.5 Hz for ¹³C spectra was used. The data points were extended by zero-filling to 64k data points for ¹H spectra and to 256k data points for ¹³C spectra.

All spectra were referenced to the signal of internal TMS set to 0 ppm in both solvents. 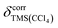, the susceptibility corrected chemical shift of TMS in CCl₄ referenced to external TMS in CDCl₃ was calculated using eqn (4).¹⁹

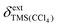Here, is the externally referenced chemical shift of TMS in CCl₄, [small alpha, Greek, macron] is a shape factor assumed to be 0.007,¹⁹ and κ and κ_ref are the volume magnetic susceptibilities of CCl₄ (−0.690) and CDCl₃ (−0.735),²⁰ respectively. On a Bruker spectrometer 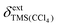can be obtained as follows: the spectrum of a dilute sample of TMS in CDCl₃ is recorded and the TMS signal is set to 0 ppm. The sample is exchanged with a dilute sample of TMS in CCl₄, and a second spectrum is recorded with the values of SR and FIELD kept fixed. The chemical shift of the TMS signal in the second spectrum corresponds to . At 25 °C, was determined to be 0.21 ppm for ¹H and 0.47 ppm for ¹³C (see Fig. S4 in the ESI†). Eqn (4) yielded values for of 0.02 ppm (¹H) and 0.28 ppm (¹³C).

Assigned NMR spectra in CDCl₃ and CCl₄ for compounds 1–35 are provided in the NMReData²¹ format as well as in separate MestreNova files together with the DFT optimized coordinates in vacuum. The data can be downloaded free of charge from https://doi.org/10.3929/ethz-b-000570841.

Computational details

Geometry optimization. 3D structures of the compounds were generated from SMILES strings using RDKit 2021.09.4.²² Atoms were reordered such that the hydrogen atoms directly follow the heavy atom they are bound to and such that magnetically equivalent groups have subsequent numbers. Hydrogens of CH₂ groups were ordered such that the proR hydrogen comes first. After a conformational search using ETKDG²³ in RDKit, each conformer was optimized with DFT in vacuum using Orca 5.0.1²⁴ at the BP86/def2-tzvp^25–27 level using the resolution of identity approximation with def2/J²⁸ as auxiliary basis set and Grimme's dispersion correction D3BJ.^29,30 Minima were verified by a frequency calculation at the same level of theory. In case of imaginary frequencies, the geometry at the most displaced point along the corresponding mode was taken as input for a new structure optimization. Only molecules with one dominant conformation were considered for the dataset.

Shielding calculation. ¹H and ¹³C shielding constants were computed with the gauge invariant atomic orbital (GIAO)³¹ approach using either the hybrid GGA functional PBE0³² with the cc-pVTZ basis set³³ and the cc-pVTZ/JK auxiliary basis set³⁴ or the 2013 version of the dispersion corrected, spin-component scaled double-hybrid functional PBEP86³⁵ with the pcSseg-3 basis set³⁶ and def2/J²⁸ and cc-pwCVQZ/C auxiliary basis sets.³⁷ The resolution of identity approximation for both Coulomb and HF exchange integrals (RIJK) was applied for the hybrid functional whereas for the double-hybrid functional resolution of identity was used for the Coulomb integrals and numerical chain-of-sphere integration was used for the HF exchange integrals (RIJCOSX). For both, D3BJ corrections were applied. Besides the calculation in vacuum, shieldings constants were also calculated using CPCM³⁸ as an implicit solvent for chloroform and tetrachloromethane with geometries reoptimized using CPCM. For comparison, shifts were also calculated with CPCM using geometries optimized in vacuum, and all calculations have also been performed with exchanged basis sets (see ESI†).

Chemical shifts. Calculated shielding constants were converted to chemical shifts using eqn (3). For comparison, the shielding constants were also converted to chemical shifts using eqn (1) (single reference with TMS) and eqn (2) (single reference with bridgehead CH of adamantane or the innermost CH pairs of anthracene).

Analysis of the data was done in a Jupyter Notebook³⁹ using Python 3.9.12.⁴⁰ The functionalities of the matplotlib 3.5.1,⁴¹ nglview 3.0.3,⁴² numpy 1.21.6,⁴³ openbabel 3.1.1,⁴⁴ and scipy 1.5.3⁴⁵ packages were used. DFT calculations were performed on the Euler cluster at ETH Zürich.

Results and discussion

In this study, we focus on solute–solvent interactions and how well these can be reproduced by DFT calculations with implicit solvent models. For this purpose, we measured a set of ¹H and ¹³C chemical shifts in two solvents, chloroform-d (CDCl₃) and tetrachloromethane (CCl₄). Although both can be considered apolar solvents, the solute–solvent interactions are stronger in CDCl₃ because CCl₄ cannot act as hydrogen-bond donor. This pair of solvents thus allows us to assess the impact of solute–solvent interactions on chemical shifts without solubility issues and very strong interactions. ¹H and ¹³C chemical shifts were measured in both solvents for a set of 35 small and rigid organic molecules, consisting only of H, C, N, and O atoms (Chart 1). The dataset was recorded under standardized conditions, referenced to internal TMS, and all chemical shifts were reassigned to eliminate potential incorrect assignments (see Experimental section). To make these measurements as reproducible as possible and to reduce unwanted intermolecular interactions between solute molecules as well as between solute and impurities, a concentration of 10 mM was chosen for all compounds with a maximum allowed impurity concentration (including water) of <2 mM. The temperature during the experiments was kept constant at 25.0 °C.

Chart 1 Chemical structures of the molecules in the dataset. Carbons are numbered according to their appearance in the coordinate files with identical labels for magnetically equivalent nuclei. Red dots: carbons with a difference in ¹³C chemical shift larger than 1 ppm between CDCl₃ and CCl₄. Blue circles: protons with a difference in ¹H chemical shift larger than 0.1 ppm between CDCl₃ and CCl₄.

After averaging magnetically equivalent nuclei, 141 ¹H and 170 ¹³C chemical shifts were obtained for the 35 molecules and unambiguously assigned in CDCl₃ (Table 1) and CCl₄ (Table 2). Exchangeable protons are listed but were not included in this study. First, we compared the chemical shifts in CDCl₃ with previously published data in the literature. Then, we investigated the chemical shift differences between the two solvents, followed by a detailed comparison with DFT calculated values.

Table 1 ¹H and ¹³C (every second row) chemical shifts for compounds 1–35 recorded in CDCl₃ under standardized conditions referenced to internal TMS. The atom numbering corresponds to Chart 1

Compound	1	2	3	4	5	6	7	8	9	10	11
a First value corresponds to cis-configured ^1H. b First value corresponds to ^1H on the same side as the nitrile group. c Exchangeable proton. d First value corresponds to proR ^1H. e First value corresponds to axial ^1H.
1	4.33
	62.5
2	1.59	4.42
	12.3	70.5
3	1.30	2.36
	10.5	10.9	120.7
4	2.03	6.87	6.15	9.50
	18.7	153.9	134.7	193.9
5	1.33	2.70
	20.0	19.8	123.8
6	4.83/4.92^a	5.85		1.01
	108.9	149.9	33.7	29.2
7	2.88			3.81
	74.8	74.5	153.1	53.0
8		1.34	1.08/1.01^b
	122.2	−3.5	7.1
9		2.50	2.27	4.35
	177.6	27.8	22.2	68.5
10		3.87	4.25	2.50
	215.0	70.6	66.9	37.1
11	1.98		3.82	4.23
	13.8	165.5	54.6	67.4
12		7.03
	164.1	136.5
13	3.78
	67.1
14		2.50	3.98
	206.5	42.9	67.9
15		8.24	7.56	7.70
	148.2	123.2	129.3	134.6
16	4.61^c	6.83	7.25	6.94
	155.4	115.3
17	3.81		6.91	7.30	6.95
	55.1	159.6	113.9	129.5	120.7
18	10.03		7.89	7.54	7.64
	192.4	136.4	129.8	129.0	134.5
19			7.67	7.48	7.61
	118.9	112.5	132.2	129.1	132.8
20	3.00		6.49	8.23
	39.0	154.2	106.6	149.9
21	9.25	8.76	7.34
	159.1	156.9	121.6
22		6.05		2.24
	180.2	113.8	165.4	19.8
23	2.85	1.31/1.08^d	5.99	0.95/1.61^e
	41.7	48.5	135.4	24.6
24		2.60	1.53/1.82^d	1.80/1.44^d	2.66	1.55/1.73^d	2.05/1.84^d
	218.3	49.9	24.2	27.2	35.3	37.7	45.3
25	1.03		1.03	2.14	1.53/1.79^d	1.71/1.79^d	1.39/1.56^d		1.14
	23.4	47.4	21.7	45.4	41.7	25.0	31.9	54.2	14.6	223.4
26		5.88		2.17		1.04	2.20	1.94
	199.9	125.6	160.3	45.3	33.6	28.3	50.8	24.6
27	10.10		8.00	7.85
	190.6	138.8	129.9	132.9	117.7	117.7
28	2.58		6.90		2.32		10.57
	20.5	141.5	130.5	143.8	21.5	130.0	193.0
29	0.91			2.35/1.85^d	2.09		0.84	0.96	1.95/1.34^d	1.68/1.41^d
	9.3	57.7	219.7	43.3	43.1	46.8	19.8	19.2	27.1	29.9
30		8.14^c	7.22	6.56	7.41	7.20	7.12	7.65
	127.9	135.8	124.1	102.7	111.0	122.0	119.8	120.7
31	1.88	1.75
	28.3	37.8
32	3.22	5.49	5.49	1.68/2.18^d	2.73	2.88	5.98	5.94	2.78	1.30/1.48^d
	54.8	132.0	132.1	34.7	41.2	46.2	132.4	136.0	45.2	50.4
33	2.70			8.00	7.52	7.48	7.85		7.71	7.37	7.32
	19.4	134.3	132.6	124.1	125.7	125.5	128.5	133.5	126.4	125.6	126.6
34				7.66	7.30	7.49	7.53
	193.9	134.2	144.5	124.4	129.1	134.7	120.3
35		8.01	7.46	8.43
	131.7	128.2	125.3	126.2

---

Table 2 ¹H and ¹³C (every second row) chemical shifts for compounds 1–35 recorded in CCl₄ under standardized conditions referenced to internal TMS. The atom numbering corresponds to Chart 1

Compound	1	2	3	4	5	6	7	8	9	10	11
a First value corresponds to cis-configured ^1H. b First value corresponds to ^1H on the same side as the nitrile group. c Exchangeable proton. d First value corresponds to proR ^1H. e First value corresponds to axial ^1H.
1	4.27
	61.6
2	1.59	4.34
	12.0	69.5
3	1.32	2.29
	10.4	10.5	118.1
4	2.03	6.72	6.07	9.43
	18.1	149.9	134.9	190.3
5	1.34	2.62
	19.9	19.4	121.3
6	4.78/4.86^a	5.77		1.01
	109.0	149.0	33.4	29.1
7	2.72			3.76
	73.4	74.6	151.6	51.9
8		1.27	1.07/0.96^b
	120.1	−3.1	6.9
9		2.36	2.22	4.25
	173.7	27.0	22.0	66.7
10		3.73	4.16	2.39
	211.2	69.7	66.0	36.4
11	1.88		3.70	4.11
	13.2	163.4	54.4	66.5
12		6.96
	162.7	135.7
13	3.57
	66.5
14		2.39	3.89
	202.1	42.5	67.3
15		8.23	7.53	7.64
	148.3	123.2	128.7	133.4
16	4.27^c	6.70	7.14	6.82
	155.2	114.9
17	3.76		6.78	7.17	6.83
	54.3	159.2	113.4	128.9	120.2
18	9.97		7.83	7.49	7.56
	189.3	136.6	129.2	128.5	133.4
19			7.63	7.45	7.55
	117.0	113.5	131.7	128.6	131.7
20	2.99		6.37	8.08
	38.8	153.4	106.1	149.5
21	9.11	8.65	7.23
	158.9	156.0	120.7
22		5.85		2.20
	176.7	113.8	162.9	19.3
23	2.83	1.31/1.06^d	5.92	0.95/1.59^e
	41.4	48.3	135.0	24.4
24		2.50	1.54/1.77^d	1.77/1.44^d	2.63	1.50/1.70^d	1.96/1.74^d
	212.4	48.8	23.8	27.2	35.0	37.3	44.5
25	1.00		0.99	2.09	1.47/1.75^d	1.68/1.79^d	1.37/1.50^d		1.10
	23.3	46.7	21.6	45.1	41.4	24.9	31.4	53.4	14.6	218.5
26		5.75		2.10		1.03	2.07	1.91
	195.5	125.8	155.7	45.1	33.2	28.3	50.3	24.1
27	10.05		7.96	7.82
	188.0	138.5	129.3	132.3	118.0	116.2
28	2.56		6.81		2.30		10.50
	20.7	141.1	130.6	142.6	21.7	130.5	190.5
29	0.86			2.25/1.75^d	2.03		0.83	0.95	1.93/1.34^d	1.62/1.39^d
	9.2	56.8	214.3	42.6	42.9	46.3	19.7	19.1	27.1	29.5
30		7.91^c	7.08	6.44	7.25	7.06	6.99	7.50
	127.6	135.5	122.8	102.9	110.3	121.7	119.6	120.5
31	1.88	1.75
	28.0	37.5
32	3.17	5.40	5.40	1.59/2.14^d	2.69	2.84	5.89	5.84	2.75	1.28/1.47^d
	54.5	131.5	131.7	34.7	41.0	45.9	131.9	135.7	44.9	50.1
33	2.68			7.90	7.42	7.39	7.74		7.60	7.27	7.22
	19.2	133.3	132.4	123.6	125.2	125.0	128.2	133.4	126.2	125.0	126.1
34				7.62	7.26	7.42	7.48
	191.2	134.2	144.0	124.1	128.6	133.6	119.6
35		7.92	7.38	8.34
	131.5	127.9	124.8	125.9

---

Comparison with experimental shifts in CDCl₃ from the literature

The chemical shifts measured in this study can be considered a highly homogeneous dataset, which presents a unique opportunity to assess the effect of variations in the experimental protocol by comparing to literature values from different sources. Also varying water content, although naturally limited in chloroform, may still impact the measured shifts. Fig. 1 shows a comparison between our ¹H and ¹³C chemical shifts in CDCl₃ and collected literature values (references given in the ESI†). A good agreement is observed, indicating that the effects of concentration, water content, other impurities, or slight variations in temperature are relatively small for the studied molecules in CDCl₃. Along with these effects, also proper referencing of the spectra and potential typos might be responsible for some of the variability. If we classify our data according to their association with a functional group, the largest deviations for the ¹³C chemical shifts were found for carbonyl carbons (RMSD of 0.43 ppm), which apparently are most affected by changes in sample or experiment conditions. The largest individual deviation from the values in our ¹³C dataset likely stems from a change in protonation state (see Table S1 in the ESI†).

Fig. 1 Comparison of experimental ¹H (left) and ¹³C (right) chemical shifts in CDCl₃ (this study) to literature values from various sources. A positive difference indicates that the literature value is larger.

While our shift data in CDCl₃ and the literature values do not differ much on average, the spread for some of the datapoints is still as high or higher as the accuracy one would like to achieve in a chemical shift calculation by DFT (≤1 ppm for ¹³C and ≤0.1 ppm for ¹H). Thus, the observed differences are still too large for the validation of computational approaches. Especially for the study of solute–solvent interactions or other weak effects, the use of compiled literature values is not optimal since their influence on the chemical shifts is expected to be on the same order of magnitude as the spread in experimental values. The homogeneous sets of chemical shifts measured in this study will therefore serve as valuable reference to both validate in silico methods and to investigate the influence of specific solvation effects.

Comparison of experimental shifts recorded in CDCl₃ and CCl₄

In general, one would expect that polar groups (i.e. carbons of carbonyls, nitriles, and other H-bond acceptors) exhibit the largest changes in chemical shift between CCl₄ and CDCl₃, which is a (weak) H-bond donor. Fig. 2 shows the chemical shift differences between CDCl₃ and CCl₄ (for evaluation metrics see Table S2 in the ESI†). For the ¹³C chemical shifts, a clear trend can be observed that correlates with the polarity of the functional groups. The largest difference is found for carbonyl carbons (cyan squares, RMSD of 3.82 ppm), followed by the nitrile carbons (violet diamonds, RMSD of 2.13 ppm), while the ¹³C chemical shifts of the sp³ carbons are similar in both solvents (green circles, RMSD of 0.54 ppm). An illustrative example is given for 26 in Fig. S1 in the ESI. † No such functional group associated trend was found for the ¹H shifts, although a general shift with a RMSD of 0.08 ppm is observed when going from CDCl₃ to CCl₄.

Fig. 2 Comparison of experimental ¹H (left) and ¹³C (right) chemical shifts measured under standardized conditions in CDCl₃ and CCl₄. The data points are colour and symbol coded with respect to the functional group of the carbon atom. The solid grey horizontal lines indicate , the susceptibility corrected chemical shift of TMS in CCl₄ referenced to external TMS in CDCl₃ (see main text).

To a minor extent, the change in chemical shift of TMS itself should also influence the observed chemical shift differences. We have experimentally determined this contribution which corresponds to the susceptibility corrected chemical shift of TMS in CCl₄ referenced to external TMS in CDCl₃. In Fig. 2, is indicated as horizontal line. Chemical shifts of positions that are only marginally affected by the solvent change should symmetrically scatter around this line. For the majority of the sp³-positions this is indeed the case.

To visualize in more detail which nuclei experience the largest solvent-induced change in chemical shift, we selected all ¹³C and ¹H chemical shifts which differ between the two solvents by more than 1.0 and 0.1 ppm, respectively (see Chart 1). For ¹³C, the marked nuclei agree with positions where – according to the general concepts used in organic chemistry – one would expect the largest change in partial charge upon protonation or interaction with a H-bond donor. Again, the trend is less clear for ¹H resonances.

Overall, inspection of the two datasets confirms that there is a clear effect of specific solvent–solute interactions on the chemical shifts – even for these relatively apolar solvents –, which is important to consider when comparing them with computed values.

Comparison of experimental shifts with vacuum DFT calculations

DFT calculations of chemical shifts have traditionally been performed in vacuum. To assess how large the effect of the vacuum condition is, we compared the experimental values with DFT calculations carried out in vacuum using the gauge invariant atomic orbital (GIAO)⁴⁶ approach in Orca 5.0.1²⁴ with either the hybrid GGA functional PBE0⁴⁷ with the cc-pVTZ basis set³³ (called PBE0 in the following) or the 2013 version of the double-hybrid functional PBEP86³⁵ together with the pcSseg-3 basis set³⁶ (called PBEP86 in the following). Both methods have been shown in the past to perform well in the calculation of chemical shifts.^14,48 Geometries were generated using RDKit²² and were optimized at the BP86/def2-tzvp^25–27 level of theory. As the solute–solvent interactions are weaker in CCl₄ than in CDCl₃, we expect the vacuum condition in the calculations to be more appropriate for the former solvent. Table 3 gives the RMSD values when comparing vacuum chemical shifts calculated using eqn (3) with experimental values in CDCl₃ or CCl₄. The graphical comparisons are provided in Fig. S5 and S6 in the ESI.†

Table 3 RMSD (ppm) between ¹H and ¹³C shifts calculated in vacuum and experimental values in CDCl₃ or CCl₄. Values are given for the complete set (all), for sp² carbons and attached protons (sp²), and for sp³ carbons and attached protons (sp³). Values in parentheses correspond to the reduced data set (see text)

DFT method	Exp. solvent	^1H			^13C
		All	sp^2	sp^3	All	sp^2	sp^3
PBE0	CCl4	0.11	0.10	0.09	1.37 (1.27)	1.47 (1.27)	1.05 (1.04)
PBEP86	CCl4	0.11	0.11	0.09	1.27 (1.05)	1.27 (0.86)	0.91 (0.88)
PBE0	CDCl3	0.12	0.11	0.10	1.50 (1.27)	1.69 (1.32)	1.12 (1.08)
PBEP86	CDCl3	0.12	0.11	0.10	1.78 (1.09)	1.75 (1.06)	0.97 (0.91)

---

For the ¹H shifts, only a very small change in RMSD (0.01 ppm) is observed when comparing to CDCl₃ or CCl₄ data. This might seem surprising as the experimental ¹H chemical shifts in the two solvents differed by a RMSD of 0.08 ppm. However, some of the offset between the two datasets can be compensated by changing the intercept in the linear regression (eqn (3)) without a significant increase in RMSD.

A large part of the potential shortcomings of the vacuum calculations can be masked by this mechanism. For the ¹³C chemical shifts, on the other hand, a clear increase in the deviation from experiment (0.13–0.51 ppm) can be seen when going from CCl₄ to CDCl₃ data. The sp² carbons are thereby more affected than the sp³ carbons (as expected from the results in Fig. 2). Again, the differences are not of the order of magnitude expected from the experimental comparison (RMSD of 1.40 ppm, see Table S2 in the ESI†). But here, the compensation by the regression procedure is not as efficient as for ¹H. Part of the reason for this might be that the differences in experimental ¹³C shifts between the two solvents systematically increase towards lower field. This is not the case for the ¹H shifts. The effect of the functional (PBE0 or PBEP86) is negligible for the ¹H shifts as also noted recently by Oliveira et al.⁴⁹ For ¹³C, PBEP86 performs better than PBE0 for the values recorded in CCl₄ and worse for the values recorded in CDCl₃. Mean absolute deviations (MAD) and maximum absolute deviations (max. AD) are given in Tables S3 and S4 (ESI†). Exchanging the basis sets (using PBE0/pcSseg-3 and PBEP86/cc-pVTZ) shows that PBE0 profits only marginally from the larger basis set. For PBEP86/cc-pVTZ, the ¹³C RMSD increases slightly by ca. 0.1 ppm (Table S31, ESI†).

To assess the baseline error of the DFT method, independent of the solvent, we can focus the analysis only on the ¹³C nuclei that showed no or a very small solvent effect in experiment (nuclei without mark in Chart 1, 135 ¹³C shifts). Table 3 shows that for this reduced set the deviation between calculation and experiment becomes similar for the two solvents, indicating a baseline error for PBEP86 of ca. 1 ppm for ¹³C chemical shifts (and 1.3 ppm with PBE0).

We have also calculated the vacuum chemical shifts using eqn (1) (TMS as single reference, Table S6, ESI†). The RMSDs from the experimental values are consistently larger than for the shifts obtained using eqn (3). The largest increase (up to five times) is seen for ¹³C shifts. RMSD values are only comparable for sp³ protons, i.e. for protons with shifts similar to the reference. The same trend can be seen if single resonances in adamantane (31) or anthracene (35) are used as reference (Table S9, ESI†). But for the latter compounds, ¹³C RMSDs are significantly smaller than for TMS. This behaviour is not surprising as eqn (1) assumes a linear relation with a fixed slope of −1 between chemical shift and calculated shielding and TMS lies at the edge of the sampled chemical shift range. With increasing distance from the reference, small deviations from the expected slope of −1 lead to large deviations between calculation and experiment. In this regard the peripheral position of TMS is far from ideal. Further, the difference between the results obtained with adamantane and TMS as reference points to an issue in the treatment of silicon, similar to the relativistic effects of chlorine that cannot be properly accounted for in standard DFT.¹³

If only closely related electronic environments are investigated, the use of eqn (1) or (2) is justified. But e.g. for the validation of constitution or configuration of a newly isolated, structurally diverse natural product, the use of eqn (3) is clearly preferable.

It is instructive in this respect, to use eqn (3) with m fixed at −1. This enforces the theoretically expected slope of −1 but is independent of a specific single reference. For ¹H, the RMSDs are about twice as large as in Table 3 but differences between the two datasets (CDCl₃ and CCl₄) and the different functional/basis set combinations are small. Combinations using the double hybrid functional perform slightly better. The ¹³C RMSDs for the reduced datasets vary between 1.11 and 3.80 ppm. Interestingly, changing the basis from cc-pVTZ to pcSseg-3 invariably leads to a doubling of the RMSD, irrespective of the functional. The best combination (PBEP86/cc-pVTZ) leads to values very close to the ones in Table 3 (1.11 ppm for CDCl₃ and 1.17 ppm for CCl₄). Inspection of the residual plots (see ESI†) shows that for calculations with pcSseg-3, the slope of σ_calcvs. δ_exp deviates more distinctly from −1 than for cc-pVTZ. Since this deviation cannot be compensated if m is fixed, cc-pVTZ performs significantly better.

Comparison of experimental shifts with DFT calculations using an implicit solvent model

We also performed geometry optimization and shielding calculation with an implicit solvent (conductor-like polarizable continuum model (CPCM)³⁸) to explore whether the agreement with the experimental data in solution can be improved. We directly compared the differences between the experimental shifts in the two solvents with the differences between the shielding values before conversion to chemical shifts (without using eqn (1)–(3)). Thus, specific effects only present for certain functional groups are not obscured by the regression procedure. Ideally, −Δσ_calc and Δδ_exp should only differ by (see above). But especially for ¹³C, it is observed that CPCM cannot fully account for the experimental changes in chemical shift between CDCl₃ and CCl₄ (Fig. 3). While the picture is less clear for protons, the largest differences between experimental and calculated differences for ¹³C can again be seen for carbonyl groups.

Fig. 3 Difference between the difference in experimental shifts in CDCl₃ and CCl₄ (Δδ_exp) and the difference in calculated PBE0 shielding with implicit CHCl₃ and CCl₄ (Δδ_calc = −Δσ_calc) plotted against the experimental shifts in CDCl₃. Note: since the experimental shift differences are mostly positive (see Fig. 2) a positive value for Δδ_exp − Δδ_calc typically corresponds to an underestimation of the absolute shift difference by the calculation. The solid grey horizontal lines indicate 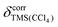, the susceptibility corrected chemical shift of TMS in CCl₄ referenced to external TMS in CDCl₃ (see main text).

After conversion to chemical shifts using eqn (3), the RMSDs from the experimental values in the two solvents were again investigated. While the agreement with experimental ¹H shifts improves slightly compared to the vacuum calculations (0.01–0.03 ppm), the use of an implicit solvent model only leads to an improvement for the CDCl₃¹³C shifts calculated with PBEP86. Table 4 summarizes the performance of the two DFT methods with the corresponding implicit solvents. The MAD and max. AD values are given in Tables S12 and S13 (ESI†). As the limitations of the CPCM model (lack of local H-bonding capacity) are expected to be more severe for chloroform than for CCl₄, it is surprising to see that the agreement with experimental data in CCl₄ is negatively affected by CPCM. Possible reasons for these findings are deficiencies in the CPCM implicit solvent model and/or more favourable error compensation in the vacuum calculations. For comparison, CPCM shieldings were also calculated for structures optimized in vacuum. Interestingly, lower RMSD values were obtained for the ¹³C shifts, whereas no difference was observed for the ¹H shifts (for evaluation metrics see ESI†). This suggests that – at least for the common procedure using eqn (3) – geometries optimized at the BP86/def2-tzvp level using CPCM provide no advantage compared to geometries optimized in vacuum.

Table 4 RMSD (ppm) between ¹H and ¹³C shifts calculated in the corresponding implicit solvent and experimental values in CDCl₃ or CCl₄. Values are given for the complete set (all), for sp² carbons and attached protons (sp²), and for sp³ carbons and attached protons (sp³)

DFT	Exp.	^1H			^13C
Method	Solvent	All	sp^2	sp^3	All	sp^2	sp^3
PBE0	CCl4	0.09	0.08	0.08	2.07	1.84	1.09
PBEP86	CCl4	0.10	0.11	0.07	1.53	1.21	0.99
PBE0	CDCl3	0.10	0.10	0.08	1.87	1.85	1.10
PBEP86	CDCl3	0.10	0.12	0.06	1.34	1.21	0.96

---

Conclusions

The presented dataset is intended for the calibration and assessment of chemical shift calculations in organic chemistry, particularly with respect to the treatment of solvent–solute interactions in CDCl₃.

Our experimental data show that specific interactions with the solute are present even in such apolar solvents. Especially the ¹³C shifts of carbonyl and nitrile groups are differentially affected by the two solvents. A direct comparison of calculated shieldings with chemical shifts recorded in CDCl₃ and CCl₄ implies that DFT in implicit solvent is not able to reproduce experimental values equally well for all functional groups. The likely reason are specific interactions with the solvent (e.g. H-bonds) that cannot be adequately described by implicit solvation. By converting the shieldings to chemical shifts using the common multi-standard regression (eqn (3)), the errors resulting from neglecting directed solvent-interactions are redistributed over the whole shift range, also affecting functional groups not engaging in interactions with the solvent. In the worst case, selective deficiencies of the solvation model can lead to higher inaccuracies in chemical shift prediction for all atoms. This effect may have added to the ambiguous outcome found in this study regarding the usefulness of implicit CHCl₃. For ¹H, there was no significant advantage from using an implicit solvent model. For ¹³C, the double-hybrid functional PBE86 with implicit solvent provided the best agreement with chemical shifts recorded in CDCl₃, while the implicit solvent was detrimental to the performance of PBE0. Importantly, our data also imply that the explicit treatment of solute–solvent interactions will be necessary for an even more accurate chemical shift prediction. Ignoring an incomplete representation of the solvent shell potentially obscures the direction to further improvement of DFT chemical shift prediction and hampers its fair assessment.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

S. R. gratefully acknowledges financial support by the Swiss National Science Foundation (grant number 200021-178762). The authors thank Dr Felix Pultar for providing some of the studied compounds and helpful discussions.

References

1. E. E. Kwan and R. Y. Liu, J. Chem. Theory Comput., 2015, 11, 5083–5089.
2. M. O. Marcarino, M. M. Zanardi, S. Cicetti and A. M. Sarotti, Acc. Chem. Res., 2020, 53, 1922–1932.
3. A. M. Sarotti and S. C. Pellegrinet, J. Org. Chem., 2009, 74, 7254–7260.
4. A. Mitra, P. J. Seaton, R. Ali Assarpour and T. Williamson, Tetrahedron, 1998, 54, 15489–15498.
5. F. C. Wermter, N. Mitschke, C. Bock and W. Dreher, Magn. Reson. Mater. Phys., Biol. Med., 2017, 30, 579–590.
6. S. Berger, Tetrahedron, 1981, 37, 1607–1611.
7. M. W. Lodewyk, M. R. Siebert and D. J. Tantillo, Chem. Rev., 2012, 112, 1839–1862.
8. CHESHIRE Chemical Shift Repository, https://cheshirenmr.info/, (accessed 27 May 2022).
9. W. Hehre, P. Klunzinger, B. Deppmeier, A. Driessen, N. Uchida, M. Hashimoto, E. Fukushi and Y. Takata, J. Nat. Prod., 2019, 82, 2299–2306.
10. P. R. Rablen, S. A. Pearlman and J. Finkbiner, J. Phys. Chem. A, 1999, 103, 7357–7363.
11. R. Jain, T. Bally and P. R. Rablen, J. Org. Chem., 2009, 74, 4017–4023.
12. M. A. Iron, J. Chem. Theory Comput., 2017, 13, 5798–5819.
13. L. B. Krivdin, Prog. Nucl. Magn. Reson. Spectrosc., 2019, 112–113, 103–156.
14. G. L. Stoychev, A. A. Auer and F. Neese, J. Chem. Theory Comput., 2018, 14, 4756–4771.
15. V. A. Semenov, D. O. Samultsev and L. B. Krivdin, Magn. Reson. Chem., 2014, 52, 686–693.
16. P. Cmoch, P. Krzeczyński and A. Leś, Molecules, 2018, 23, 161.
17. E. Artikis and C. L. Brooks, Biophys. J., 2019, 117, 258–268.
18. M. Foroozandeh, R. W. Adams, P. Kiraly, M. Nilsson and G. A. Morris, Chem. Commun., 2015, 51, 15410–15413.
19. R. K. Harris, E. D. Becker, S. M. C. De Menezes, P. Granger, R. E. Hoffman and K. W. Zilm, Magn. Reson. Chem., 2008, 46, 582–598.
20. J. Rumble, CRC Handbook of Chemistry and Physics, CRC Press/Taylor and Francis, Boca Raton, FL, 103rd edn, 2022.
21. M. Pupier, J.-M. Nuzillard, J. Wist, N. E. Schlörer, S. Kuhn, M. Erdelyi, C. Steinbeck, A. J. Williams, C. Butts, T. D. W. Claridge, B. Mikhova, W. Robien, H. Dashti, H. R. Eghbalnia, C. Farès, C. Adam, P. Kessler, F. Moriaud, M. Elyashberg, D. Argyropoulos, M. Pérez, P. Giraudeau, R. R. Gil, P. Trevorrow and D. Jeannerat, Magn. Reson. Chem., 2018, 56, 703–715.
22. G. A. Landrum, RDKit: Open-Source Cheminformatics Software, https://www.rdkit.org, (accessed 17 May 2022).
23. S. Riniker and G. A. Landrum, J. Chem. Inf. Model., 2015, 55, 2562–2574.
24. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, e1606.
25. A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100.
26. J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824.
27. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
28. F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065.
29. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
30. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
31. K. Wolinski, J. F. Hinton and P. Pulay, J. Am. Chem. Soc., 1990, 112, 8251–8260.
32. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170.
33. T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023.
34. Turbomole 7.0 basis set library.
35. S. Kozuch and J. M. L. Martin, J. Comput. Chem., 2013, 34, 2327–2344.
36. F. Jensen, J. Chem. Theory Comput., 2015, 11, 132–138.
37. C. Hättig, Phys. Chem. Chem. Phys., 2005, 7, 59–66.
38. V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995–2001.
39. T. Kluyver, B. Ragan-Kelley, F. Pérez, B. Granger, M. Bussonnier, J. Frederic, K. Kelley, J. Hamrick, J. Grout, S. Corlay, P. Ivanov, D. Avila, S. Abdalla and C. Willing, Jupyter development team, IOS Press, 2016, pp. 87–90.
40. G. van Rossum and F. L. Drake, Python 3 Reference Manual, 2009.
41. J. D. Hunter, Comput. Sci. Eng., 2007, 9, 90–95.
42. H. Nguyen, D. A. Case and A. S. Rose, Bioinformatics, 2018, 34, 1241–1242.
43. C. R. Harris, K. J. Millman, S. J. van der Walt, R. Gommers, P. Virtanen, D. Cournapeau, E. Wieser, J. Taylor, S. Berg, N. J. Smith, R. Kern, M. Picus, S. Hoyer, M. H. van Kerkwijk, M. Brett, A. Haldane, J. F. del Río, M. Wiebe, P. Peterson, P. Gérard-Marchant, K. Sheppard, T. Reddy, W. Weckesser, H. Abbasi, C. Gohlke and T. E. Oliphant, Nature, 2020, 585, 357–362.
44. N. M. O’Boyle, M. Banck, C. A. James, C. Morley, T. Vandermeersch and G. R. Hutchison, J. Cheminf., 2011, 3, 33.
45. P. Virtanen, R. Gommers, T. E. Oliphant, M. Haberland, T. Reddy, D. Cournapeau, E. Burovski, P. Peterson, W. Weckesser, J. Bright, S. J. van der Walt, M. Brett, J. Wilson, K. J. Millman, N. Mayorov, A. R. J. Nelson, E. Jones, R. Kern, E. Larson, C. J. Carey, İ. Polat, Y. Feng, E. W. Moore, J. VanderPlas, D. Laxalde, J. Perktold, R. Cimrman, I. Henriksen, E. A. Quintero, C. R. Harris, A. M. Archibald, A. H. Ribeiro, F. Pedregosa and P. van Mulbregt, Nat. Methods, 2020, 17, 261–272.
46. R. Ditchfield, Mol. Phys., 1974, 27, 789–807.
47. J. P. Perdew, M. Ernzerhof and K. Burke, J. Chem. Phys., 1996, 105, 9982–9985.
48. D. Flaig, M. Maurer, M. Hanni, K. Braunger, L. Kick, M. Thubauville and C. Ochsenfeld, J. Chem. Theory Comput., 2014, 10, 572–578.
49. M. T. de Oliveira, J. M. A. Alves, A. A. C. Braga, D. J. D. Wilson and C. A. Barboza, J. Chem. Theory Comput., 2021, 17, 6876–6885.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp03205h

---