 Open Access Article
Open Access ArticleThe quantum mean square displacement of thermalized CO on Cu(100) in the short time approximation
Roberto
Marquardt

Laboratoire de Chimie Quantique – Institut de Chimie – UMR 7177 CNRS/Université de Strasbourg, 4, rue Blaise Pascal – CS 90032, 67081 STRASBOURG CEDEX, France. E-mail: roberto.marquardt@unistra.fr
First published on 12th October 2022
Abstract
The mean square displacement 〈(x(t) − x(0))2〉 of the position x of a CO molecule adsorbed at thermal equilibrium on a Cu(100) substrate and moving along the 〈100〉 direction is evaluated quantum mechanically. The problem is treated in the independent particle formalism via the numerical solution of the time dependent Schrödinger equation with an initial thermal wave packet. The results are discussed in relation to observables from neutron scattering or helium-3 spin-echo experiments, and their interpretation in terms of classical or quantum mechanical expressions for the mean square displacement.
1 Introduction
The motion of adsorbed molecules along a substrate is an essential step in heterogeneous catalysis.1 Being essentially two-dimensional, it is apparently simple. Despite decades of investigations, in particular on particle diffusion,2–10 the surface dynamics of adsorbates is still far from being fully understood.Theoretically, diffusion has been understood as the result of randomized many-body interactions since more than a century11,12 in the framework of both classical and quantum mechanics.13,14 Experimentally, diffusion has been investigated by neutron scattering in liquids15 and, more specifically related to surface diffusion, by laser induced thermal desorption measurements,16 optical diffractometry,17 NMR spin-echo techniques,18,19 scanning tunneling microscopy (STM)20–22 and helium spin-echo spectroscopy at crystal surfaces (see ref. 9 and 23 for reviews). Helium spin-echo23,24 and more generally helium atom scattering have been central for the investigation of the surface structure also in the work of Wolfgang E. Ernst.25–30
Recently, it was shown that the quantum mechanical evaluation of the mean square displacement (MSD) of a single particle moving freely at thermal equilibrium inherently carries the characteristic elements of Brownian motion.31 Quite paradoxically, the assertion holds specifically for time intervals during which interactions with other particles can be neglected, i.e. in the absence of friction. Friction and random many-body interactions are connected via the fluctuation–dissipation theorem. The finding is related to the wave nature of a single adsorbate, the extreme delocalization of its thermal probability density and the ensuing uncertainty to find the particle at a specific position on the adsorption substrate.
Studying the MSD of thermalized quantum particles following ref. 31 is one possibility to approach quantum diffusion. Alternative quantum mechanical approaches were also proposed7,32–34 (see below). Quantum mechanical effects on the diffusion of particles have been observed in other theoretical works based on centroid35,36 and ring–polymer molecular dynamics,37,38 Monte Carlo39,40 and instanton path-integral techniques.41 In these approaches, quantum statistical properties are considered, whereas the actual particle dynamics is treated classically. Similarly, diffusion rates have also been calculated using transition state theories on the basis of the flux–flux correlation function42–44 and theories of thermally activated structures with the inclusion of quantum corrections.45–47 In this context, the work of Pollak and coworkers over the past three decades deserves particular attention, see ref. 6, 48 and 49 and references cited therein. Other authors solve the time independent Schrödinger equation to obtain transmission probabilities41 or rates by perturbation theory.50 In some of these works, potential energy functions were obtained from ab initio calculations. Truly time dependent quantum mechanical methods used to investigate diffusion are based on Bohmian dynamics,51,52 wave packet dynamics using a stochastic Schrödinger equation,53 or quantized forms of the generalized Langevin equation.54,55 None of these time dependent methods are ab initio, however, and many rely on coupling models with adjustable parameters. In ref. 56, a pseudo-thermal wave packet was studied, which describes a CO molecule initially localized in the Wigner-Seitz cell of a top adsorption site on the Cu(100) surface. The time evolution of the wave packet was obtained by the solution of the time dependent Schrödinger equation in a four-dimensional potential energy surface from ab initio calculations. The study rendered a time dependent escape probability and gave evidence of CO tunneling at 200 K in the picosecond time domain. However, this study, albeit multidimensional, did not infer directly on experimental observables. In particular, diffusion coefficients cannot be extracted from there. Methods to calculate diffusion coefficients in a time dependent approach from first principles, multidimensional quantum mechanical calculations are still needed.
One aim of the present study is therefore to work toward such a method. Although being grossly approximate, the independent particle approach is the simplest one to start with. The neglect of many-body interactions is a strong approximation and the present approach is correspondingly expected to yield realistic results in the short time dynamics, i.e. for time intervals smaller than the typical time parameter τ, to use the notation from ref. 11, in which the independent particle picture is valid. The values for τ can be estimated from collision rates or friction constants.
As an exemplary system, we shall focus on the quantum dynamics of a CO molecule moving at thermal equilibrium in a one-dimensional periodic potential representing the 〈100〉 direction along the Cu(100) surface. More specifically, we shall evaluate and analyze the mean square displacement (MSD) defined by eqn (1):
| δx2(t) = 〈(xθ(t) − xθ(0))2〉θ | (1) |
In ref. 7, 32–34, the alternative expression δx2(t) = Tr(![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (T)(
(T)(![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) (t) −
(t) − ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) (0))2) was used, where
(0))2) was used, where ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (T) is the ensemble averaged thermal density operator, and
(T) is the ensemble averaged thermal density operator, and ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) (t) is the Heisenberg representation of the position operator. This alternative definition is related to a quantum correlation function of the position operator14 and can be shown to yield, under particular conditions, the expression of the MSD expected in the classical limit. Nevertheless, this definition of the MSD cannot be given as the time dependent expectation value of a quantum mechanical operator in the Schrödinger representation, and is therefore somewhat problematic. In contrast, the definition in eqn (1) can be evaluated in both the Schrödinger and Heisenberg representations, but does not have a classical counterpart, as discussed in ref. 31. We shall consider eqn (1) exclusively in the present work. A thorough discussion of the alternative definitions of the MSD will be carried out elsewhere.
(t) is the Heisenberg representation of the position operator. This alternative definition is related to a quantum correlation function of the position operator14 and can be shown to yield, under particular conditions, the expression of the MSD expected in the classical limit. Nevertheless, this definition of the MSD cannot be given as the time dependent expectation value of a quantum mechanical operator in the Schrödinger representation, and is therefore somewhat problematic. In contrast, the definition in eqn (1) can be evaluated in both the Schrödinger and Heisenberg representations, but does not have a classical counterpart, as discussed in ref. 31. We shall consider eqn (1) exclusively in the present work. A thorough discussion of the alternative definitions of the MSD will be carried out elsewhere.
The MSD is connected to the self-part Gs(r,t) of the pair correlation function introduced by van Hove,57 more particularly to its space Fourier transformation, the intermediate scattering function (ISF). In ref. 31, it was suggested that, while the real part of the ISF can be related to the classical mechanical expression of the MSD, its imaginary part might possibly be related to the quantum mechanical expression eqn (1). This hypothesis could in principle be verified by the example of xenon atoms moving on a platinum substrate, which are essentially freely moving particles. It will be further elaborated in the present work using the example of CO molecules moving on a copper substrate.
This paper is an extension of the work presented in ref. 31. Here, a numerical protocol is proposed for the determination of diffusion coefficients from ab initio calculations. The free particle case treated before is reviewed here from the numerical perspective, by which the numerical approach can be validated. The numerical protocol is then applied to the specific case of a CO molecule moving on the copper surface Cu(100). The paper is structured as follows: in Section 2, theoretical and computational aspects of the treatment will be presented; these include the development of the aforementioned numerical protocol. In Section 3, the results are presented and analyzed. A discussion follows in Section 4 and the work is concluded in Section 5 with a discussion of its perspectives.
2 Theory and computational aspects
2.1 Theoretical frameworks
The mean square displacement (MSD) given by eqn (1) is evaluated quantum mechanically from the expectation value xθ(t) = 〈ψ(T)θ(t)|![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) |ψ(T)θ(t)〉 of the position of the particle at time t in a typical member state |ψ(T)θ(t)〉 of the thermal ensemble. Following Tolman,58 such a state is given as
|ψ(T)θ(t)〉 of the position of the particle at time t in a typical member state |ψ(T)θ(t)〉 of the thermal ensemble. Following Tolman,58 such a state is given as| |ψ(T)θ(t)〉 = e−iĤt/ħ|ψ(T)θ(0)〉 | (2) |
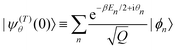 | (3) |
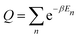 | (4) |
Quite obviously
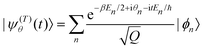 | (5) |
It is straightforward to show that xθ(t) = 〈ψ(T)θ(t)|![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) |ψ(T)θ(t)〉 is equivalent to xθ(t) = Tr(
|ψ(T)θ(t)〉 is equivalent to xθ(t) = Tr(![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (T)θ(t)
(T)θ(t) ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) ), where
), where ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (T)θ is the density operator of a typical member of the thermal ensemble.31 In eqn (5), the Schrödinger picture is used, but the same quantity xθ(t) is obtained in the Heisenberg picture, as Tr(
(T)θ is the density operator of a typical member of the thermal ensemble.31 In eqn (5), the Schrödinger picture is used, but the same quantity xθ(t) is obtained in the Heisenberg picture, as Tr(![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (T)θ(t)
(T)θ(t) ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) ) = Tr(
) = Tr(![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (T)θ
(T)θ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) (t)).
(t)).
In ref. 31, it was shown that eqn (1) and (5) lead to the following general expression of the MSD
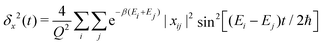 | (6) |
![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) |ϕj〉.
|ϕj〉.
The system considered is a particle of mass m moving in a one-dimensional potential, periodic in the lattice constant a: V(x) = V(x + a). Ĥ is the corresponding system Hamiltonian:
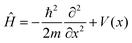 | (7) |
The system is cast in periodic super-cells of length L = N × a. The ratio a/L = 1/N can then be considered to be the coverage degree of the one dimensional lattice.
2.2 Computational methods
Instead of solving eqn (6), when the calculation of eigenstates becomes too involved, it is more convenient to evaluate eqn (1) fully numerically. This will be the main method used here.In practice, one first solves numerically the time dependent Schrödinger equation to propagate viaeqn (2) the initial thermal wave packet |ψ(T)θ(0)〉, given by eqn (3), in a finite representation space of basis states |χn〉, where n = −K,…,K (K∈ ![[Doublestruck N]](https://www.rsc.org/images/entities/char_e171.gif) ). The coordinate choice −L/2, ≤ x ≤ L/2 is made. Because of the periodic boundary conditions and the periodicity of the potential, it is always possible to label eigenstates with whole quantum numbers n∈
). The coordinate choice −L/2, ≤ x ≤ L/2 is made. Because of the periodic boundary conditions and the periodicity of the potential, it is always possible to label eigenstates with whole quantum numbers n∈ ![[Doublestruck Z]](https://www.rsc.org/images/entities/char_e17d.gif) , while granting En = E−n. While the individual matrix elements of the position operator may depend on the particular choice of the coordinate space, the overall result from eqn (1) or eqn (6) does not depend on this choice.
, while granting En = E−n. While the individual matrix elements of the position operator may depend on the particular choice of the coordinate space, the overall result from eqn (1) or eqn (6) does not depend on this choice.
The initial thermal wave packet, at a finite temperature T, is generated following ref. 60 from propagating a “white state” (at an infinite temperature), defined by
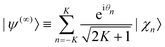 | (8) |
| |ψ(T)θ(0)〉 = e−Ĥτ/ħ |ψ(∞)〉 | (9) |
In eqn (8), individual phases θn are drawn from random number generators.
Statistical averages are computed on the basis of maximal 800 sets of random phases. This number was found to yield converged results with respect to the size of random sets. The results of the MSD from eqn (1) expectedly converge to those from eqn (6) for sufficiently large representation bases.
In the present work, for practical reasons, both imaginary (eqn (9)) and real time propagations (eqn (2)) are calculated using the Multiconfigurational Time-Dependent Hartree (MCTDH) program.62,63 To this end, an exponential discrete variable representation (DVR) is chosen to represent operators and wave functions. The corresponding finite basis functions are periodic plane waves 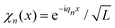 , qn = 2πn/L, i.e. the periodicity is L. The Schrödinger equation was integrated using the variable mean field integration scheme of MCTDH with a Runge–Kutta integrator of order 8, an error tolerance of 10−8 and a zero initial time step size. Using the MCTDH program to treat the present one-dimensional problem is not a necessity. It is convenient, however, in view of the prospective extension of this study to many dynamically coupled dimensions in the future. Routines to generate thermal wave packets were implemented64,65 and tested61 in MCTDH, but not used in the present work.
, qn = 2πn/L, i.e. the periodicity is L. The Schrödinger equation was integrated using the variable mean field integration scheme of MCTDH with a Runge–Kutta integrator of order 8, an error tolerance of 10−8 and a zero initial time step size. Using the MCTDH program to treat the present one-dimensional problem is not a necessity. It is convenient, however, in view of the prospective extension of this study to many dynamically coupled dimensions in the future. Routines to generate thermal wave packets were implemented64,65 and tested61 in MCTDH, but not used in the present work.
We should consider the specific potential function
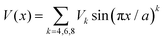 | (10) |
3 Results and analysis
3.1 CO molecules as ideal and quasi-ideal particles
We should first consider a hypothetical case where the CO molecule moves as a free particle in a zero (or constant) potential V(x) ≡ 0. In this case, En = ħqn2/(2m), the matrix elements xnn′ are given analytically and it is straightforward to carry out the sum in eqn (6) numerically. In ref. 31, it was shown that, for L → ∞, eqn (6) yields the simple analytical expression: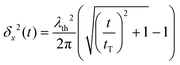 | (11) |
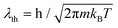 is the thermal de Broglie wavelength,68,69 and tT ≡ ħ/(kBT). In ref. 31, the natural unit λT = λth/2π was used to denote the thermal de Broglie wavelength.
is the thermal de Broglie wavelength,68,69 and tT ≡ ħ/(kBT). In ref. 31, the natural unit λT = λth/2π was used to denote the thermal de Broglie wavelength.
Eqn (11) was termed the MSD of an ideal particle in ref. 31. In contrast, a free particle bound to move in periodic super cells with finite cell lengths L was named quasi-ideal. The terminology is related to a stochastic collision model inferred in that work to rationalize the resulting MSD for varying values of L (see below).
The results from eqn (6) and (11) are shown in Fig. 1 at a temperature of 190 K. The mass is m ≈ 28 u. The length scale a ≈ 256 pm corresponds to the nearest neighbor distance along the 〈100〉 direction on a perfect Cu(100) substrate. This length scale is used here for the sake of comparison with the MSD obtained in the presence of the adsorption potential eqn (10), to be discussed later on.
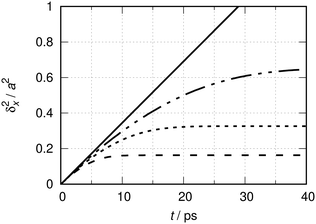 | ||
| Fig. 1 Quantum dynamical time evolution of the mean square displacement (MSD) δx2(t) of a CO molecule (m ≈ 28 u) moving on the hypothetically flat Cu(100) surface (a ≈ 256 pm) at a temperature T of 190 K. The interrupted lines show the MSD of quasi-ideal particles for finite values of L: L = 15a (–––), L = 30a (––––), L = 60a (—––—). The continuous black line is for L → ∞ (ideal particle). See ref. 31 for the definitions of ideal and quasi-ideal particles in the context of this study, and the corresponding Fig. 2 therein. | ||
The interrupted lines show the MSD of the quasi-ideal particle moving in super cells of lengths L = N × a, where N = 15, 30 and 60 (see caption). They correspond to 6.7, 3.3 and 1.7% coverage degrees, respectively. Bases contain K = 100 × N functions, i.e. a constant number of functions per elementary cell of length a, and the results are numerically converged. The continuous black line shows the MSD for the ideal particle, eqn (11), corresponding to a 0% coverage degree situation. Fig. 1 corresponds to Fig. 2 of ref. 31 in terms of the natural units λth ≈ 0.094a and tT ≈ 40 fs at T = 190 K.
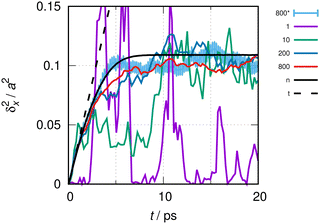 | ||
| Fig. 2 MSD of a freely moving CO molecule and conditions as in Fig. 1. The continuous lines show the MSD of the quasi-ideal particle with a super-cell length L = 10a. The black line, with a label “n”, results from the numerical evaluation of eqn (6). The dotted black line, labeled as “t”, is the result for the ideal particle from eqn (11). The colored lines result from the direct evaluation of eqn (1)via the numerical solution, eqn (2). Color codes relate to averages over different sizes of the statistical ensemble of random phases, as indicated by the key table (see text). The line labeled as 800* was calculated using 200 functions per elementary cell of length a and 800 sets (see the text); for this line, statistical error bars of ±1 standard deviation are also indicated as vertical bars. | ||
Initially, the MSDs of the quasi-ideal match those of the ideal particles. The larger L, the longer is the agreement. The very early evolution is quadratic in time,31δx2(t) ∝ t2 for t ≲ tT, which cannot be seen at the scale of the figure, but can analytically be concluded from both eqn (6) and (11).
For t → ∞, the MSD of the quasi-ideal particle stagnates asymptotically forming a plateau which is also its upper bound. The positions of the plateaus increase linearly with the super-cell length L. In the limit L → ∞, one reaches the situation of the thermalized particle that can be ideally treated as an independent particle. In this limit, the long time MSD increases linearly with time and the slope may be interpreted as a quantum diffusion coefficient Dq = ħ/2 mCO of the free CO particle.31
Strictly, the departure from the linear time evolution of the MSD at finite values for L is an artificial boundary effect in the first place. This effect can obviously be reduced by increasing L. Albeit being artificial, the asymptotic stagnation of the MSD has the characteristic behavior of a confined diffusion9 or of the diffusion in a Debye crystal.70 As explained in ref. 31, it can be interpreted within a stochastic collision model as being the consequence of random collisions that classical particles residing in neighboring cells would incur under the same thermal conditions. The average collision time inferred by that model increases linearly with L. This will be further exploited in the next section.
3.2 Initial slope method
The result unveiled by Fig. 1 has a methodological perspective. Quite obviously, the initial MSD of the quasi-ideal particle is a good approximation of the MSD of an ideal particle. Boundary effects deteriorate the ideal result for longer times. The larger the super-cell, the longer can the time window be made, in which boundary effects can be neglected within acceptable error limits in the numerical evaluation of the MSD.More specifically, the asymptotic slope of the MSD of the ideal particle may reliably be determined from a graphical or numerical evaluation of the slope of the MSD of the quasi-ideal particle during a certain initial time interval at the scale of the figure. This method is termed as the initial slope method.
The length of this initial time interval has an impact on the precision of the method. It must not be too short, in order to avoid the initial quadratic growth, nor must it be too long, in order to avoid the boundary effects. In appendix 1, the error made in the determination of the slope is investigated in detail as a function of the length of the initial time interval and L. We found, for instance, that, for L ≈ 40 a, the graphical determination of the slope entails a relative error of 10%, when restricted to the first 4 ps of the time evolution. Approximately, the length of the initial time interval needed for a reliable determination of the MSD from numerical evaluations of the free particle scales linearly with L.
To apply the initial slope method to a particle moving in a general potential, rather than using eqn (6), the procedure outlined in Section 2.2 to evaluate eqn (1) is to be used, as eigenvalues and eigenfunctions are not necessarily known. Hence, in addition to the systematic errors discussed above, statistical errors arise from the numerical integration of the Schrödinger equation with initial randomized thermal wave packets. Fig. 2 depicts the MSD of a quasi-ideal CO molecule in a super-cell of length L = 10a, otherwise under identical conditions as in Fig. 1. Almost all lines were obtained with 100 basis functions per elementary cell. The magenta line shows the result for a single set of random numbers, i.e. a single quantum trajectory. The green line is the result of the average over 10, the dark blue line is over 200 and the red line is over 800 trajectories. The light blue line is the result for the average over 800 trajectories and 200 basis functions per elementary cell, i.e. twice as many basis functions as for the red line. The drawing of this line includes error bars of ±1 standard deviation to show an example of the statistical uncertainty. The solid black line is the result from eqn (6), and the interrupted black line is the analytical result from eqn (11) (valid for L → ∞).
Up to about 1 ps, at the beginning of the evolution depicted in Fig. 2, δx2(t) obtained from the evaluation of eqn (1) agrees well with the evaluations from eqn (6) and (11) within acceptable errors of maximal 10%. Statistical errors are vanishingly small in this interval, when more than 200 quantum trajectories are run. For times beyond about 2 ps, δx2(t) from eqn (1) and (6) still differs even after averaging over 800 trajectories. Differences can be reduced, however, if the basis is increased.
Boundary effects are one aspect determining the accuracy of the initial slope method. They are obviously related to the degree of coverage a/L of the substrate. Hence, the coverage degree must be small, in order to reduce the boundary effects. Being formally related to the aforementioned stochastic collision model, the average collision times must be long enough to obtain accurate results.
A second aspect is the independent particle picture. The reliability of the calculation is limited to times smaller than the time parameter τ, beyond which interactions between particles must not be neglected. In the low coverage limit, the actual average collision time between CO molecules is expected to be long and insignificant. τ may then be estimated as the reciprocal of the friction constant. In the case of CO moving on the Cu(100) surface, coupling to substrate phonons is believed to be the major source for friction.71 The friction constant is estimated experimentally72 to be γ ≈ 0.12 ps−1, such that τ ≈ 8 ps. Consequently, the minimal super-cell length for the evaluation of the MSD of CO on Cu(100) with the initial slope method should be about L ≈ 80a.
The initial slope method outlined in this section will be used in the following section to investigate the MSD of the surface bound, but otherwise independent CO molecules.
3.3 CO along the 〈100〉 direction on Cu(100)
In this section, eqn (1) is evaluated following the method presented in Section 2.2 to simulate quantum dynamically the MSD of a CO molecule along the 〈100〉 direction of the Cu(100) crystal. The potential function is given in eqn (10). As discussed above for the free particle case, the numerical evaluation of eqn (1) is subjected to boundary effects, basis sizes and the number of random phase samples, which are examined in detail in Appendix 2. The resulting MSD is depicted as a black continuous line in Fig. 3.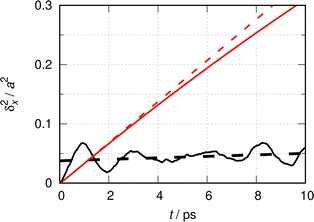 | ||
| Fig. 3 One dimensional quantum simulation of the MSD δx2(t) of a CO molecule moving along the 〈100〉 direction on the Cu(100) crystal surface at T = 190 K according to eqn (1) (continuous black line). The method described in Section 2.2 and the potential function of eqn (10) were used with 800 random phase sets, 100 states per elementary cell and a super-cell size N = L/a = 80. The time resolution of the drawing is 10 fs. The interrupted black line is a linear fit to δx2(t) (see the text). The red lines describe the free CO particle in the absence of any potential function (as discussed in Fig. 1): the continuous red line is a direct numerical evaluation of eqn (6), and the dotted red line is the analytical result from eqn (11) with Dq = ħ/2mCO ≈ 113 Å2 ns−1. | ||
The red continuous line in this figure yields the MSD of the freely moving CO molecule (constant potential) as a quasi-ideal particle from eqn (6). In test calculations not reproduced here, the potential barrier of eqn (10) was gradually reduced from ∼34 meV to zero. In this way, it was verified that the red line is the limiting MSD when the potential becomes completely flat. Clearly, the surface corrugation resulting from the potential barrier leads to a significant reduction of the MSD, when compared with the freely moving molecule. The interrupted red line is the MSD of an ideal CO molecule. The difference between the two red lines allows us to assess quantitatively the deviation from the independent particle picture induced by the finite value of the super-cell length. This picture looses anyway its physical validity for times beyond τ ∼ 8 ps, as discussed above.
The black continuous line features a nearly periodic behavior of the MSD and a slight, more or less linear ascension of the base line. The nearly periodic behavior of the MSD is more pronounced initially. In the following, we show that it can be related to a CO molecule bouncing forth and back in a harmonic potential representing the confinement in an elementary cell of length a. The MSD for a classical harmonic oscillator has a periodic variation of δx2(t) with a period of tvib = 2π/ω, where ω is the angular frequency of the oscillator.73 The same result holds for the quantum mechanical MSD from the evaluation of eqn (6) (see eqn (5) in the appendix). The fundamental transition of CO moving in the potential of eqn (10) is ∼14.6 cm−1.67 If this value is assumed to be the harmonic wave number of a CO molecule moving in a harmonic potential, one gets tvib = 1/![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) c ≈ 2.3 ps. The evolution of the MSD is not perfectly periodic, because the potential is quite anharmonic.
c ≈ 2.3 ps. The evolution of the MSD is not perfectly periodic, because the potential is quite anharmonic.
As a guide of the eye for the linear increase of the MSD in Fig. 3, a linear function c1 × t + c0 is fitted to δx2(t), with equal weights to the 1000 points used in Fig. 3 to draw the MSD. This linear function is shown there as an interrupted black line. It describes the evolution of the base line or the median of the MSD. This median is defined as the average of the MSD over one period of intra-cell diffusion. For a statistically relevant fit, it is interesting to include many periods. The time interval of 10 ps includes about 5 periods of length ∼2 ps. The relevant value resulting from the fit is the slope c1 ≈ (1.2 ± 0.4) 10−3a2/ps.
4 Discussion
It is interesting to note that the general form of the MSD given by the black continuous line in Fig. 3 resembles the typical results obtained from neutron scattering experiments in liquids. Fig. 3 in ref. 15 and Fig. 1 in ref. 70 show for instance the time evolution of the width of the main peak of the self-part of the pair-correlation function obtained in the classical approximation from incoherent neutron scattering in liquid lead. Some similarity of the behavior with Fig. 3 from the present work is clearly apparent, both regarding the qualitative aspects of the functions and, rather fortuitously, the order of length and time scales. Chudley and Elliott70 analyzed the neutron scattering data using a jump diffusion model.The evolution of the MSD depicted in Fig. 3 reflects such discrete jumps with “some slight increases at large t”, see ref. 70, p. 358. In their work, Chudley and Elliot considered a time beyond a few multiples of the characteristic jump time to be large. In Fig. 3, a large time is considerably longer than the vibrational period tvib, but smaller than τ ∼ γ−1, the time beyond which the independent particle picture becomes invalid; here, γ is the friction constant. Continuous diffusion sets in at times longer than γ−1.
The analysis suggests that the quantum mechanical MSD of a thermalized particle moving in a periodic potential may be interpreted, following Chudley and Elliot, as being the consequence of two convoluted processes: an intra-cell diffusion, characterized by the approximately periodic motion confined to one elementary cell – this process was termed as “vibrational dephasing” in ref. 9; and an inter-cell diffusion, characterized by the monotonically increasing median of the MSD for times larger than a few multiples of the vibrational period. In the limiting case of a flat potential, the former disappears and the latter becomes a Brownian type motion with a nearly to linear increase of the MSD. The interpretation is meaningful for times shorter than τ and, in this sense, the inter-cell diffusion would more appropriately correspond to an intermediate jump-diffusion from ref. 70 before continuous diffusion sets in.
In this spirit, the slope c1 of the linear function describing the median of the MSD over a few vibrational periods in Fig. 3 may be interpreted as a quantum mechanical result for the inter-cell diffusion coefficient D(inter) = c1/2 ≈ 4.1 Å2 ns−1. The uncertainty of this value is estimated to be at least ±1 Å2 ns−1 because of the limited precision of the initial slope method. Calculations can be carried out at different temperatures and for other crystallographic directions along the substrate. For instance, D(inter) decreases to about 1 Å2 ns−1 at 150 K. Because of the large errors, however, it is unreasonable to give a quantitative account of these studies at this stage.
An experimental value of the unidirectional diffusion coefficient of the CO molecule on Cu(100) along the 〈100〉 crystallographic direction can be determined from the broadening of the dynamical structure factor (DSF) S(ΔK,ω) in the quasi-elastic helium-3 scattering experiments.74 The width of the DSF at ω ≈ 0 in the long wave length limit (ΔK = 0) increases quadratically with ΔK, and its curvature is four times the diffusion coefficient.4,70 The evaluation of Fig. 1 of ref. 74, at T = 190 K, yields D(DSF) ≈ (0.6 ± 0.2) Å2 ns−1.
D (inter) is about one order of magnitude larger than D(DSF). A few remarks are in place here:
1. D(DSF) is the diffusion coefficient corresponding to continuous diffusion in the long time limit t ≫ τ, i.e. after friction will have largely influenced the dynamics. D(inter) reflects an intermediate diffusion coefficient for inter-cell diffusion determined in the short time limit t ≲ τ, before friction can effectively take place. It should be noted that the neutron scattering data in liquid lead could only be modeled satisfactorily for intermediate times. Chudley and Elliott argued70 that the jump diffusion model was lacking a further source of broadening. Here, we can only speculate about the further evolution of the MSD in Fig. 3 beyond the independent particle approximation including realistically collisions with other particles. Collisions hamper the motion of a molecule and hence decrease the diffusion coefficient in the course of time. The inclusion of friction would presumably lead to an additional flattening of the line at longer times. The statistical collision model inferred in ref. 31 to interpret the asymptotic flattening of the MSD for a quasi-ideal particle supports this view.
2. D(DSF) was obtained from experiments at a coverage degree of 10% (0.1 ML); D(inter) was obtained in the present work at a coverage degree of only about 1% and is hence not necessarily comparable with the experimental result because of the different conditions. Such a low coverage degree was necessary in the theoretical treatment to reduce the boundary effects and thus ensure accuracy in the relevant time window of the calculation. If the coverage degree is to be increased, to reach a similarly accurate theoretical treatment, the inclusion of explicit many-body interactions becomes mandatory anyway.
3. The first peak of the MSD in Fig. 3 has an amplitude of about 0.07a2. Assuming that the oscillations in that figure are loosely related to the oscillations of one particle in one well with a harmonic wave number of ∼15 cm−1, at the temperature of the simulation in the figure, the amplitude of the first peak should be about 0.013a2, from eqn (5). At this temperature, βħω ≈ 0.1, and the classical limit is essentially reached. The amplitude of the MSD of the classical oscillator is 4/(βmω2) ≈ 0.49a2. As discussed in ref. 31, the MSD from eqn (1) does not have any classical counterpart, however, and the comparison of the results from Fig. 3 with classical mechanics is not relevant in this sense. It would be interesting to evaluate the MSD using alternative definitions which, as mentioned before, yield the classically expected results under given conditions. Such a work is in preparation and will be published separately.
4. As discussed in ref. 31, the broadening of the DSF reflects the evolution of the MSD from within a classical mechanical interpretation of the motion, whereas the quantum mechanical MSD is related to the recoil energy or to the phase ϕISF(q,t) of the intermediate scattering function (ISF). These correspondences are theoretical conjectures and valid in the case of the ideal particle and in the long time limit. They could in principle be verified experimentally by the example of the Xe/Pt(111) system, which mimics an ideal, two dimensional gas.75 If these correspondences can be generalized to other systems, D(inter) and D(DSF) would not be directly comparable anyway. It would therefore be interesting to verify experimentally the result depicted in Fig. 3 by the inspection of ϕISF(q,t) from the measurement of the real and imaginary parts of the ISF of CO/Cu(100). Because the width of the DSF for CO/Cu(100) is much smaller than that for Xe/Pt(111), the ISF of the former system decays much slower than that of the latter, and the analysis might work out to be easier.
5. The value for D(inter) relies on the quality of the underlying potential energy surfaces obtained from ab initio calculations. In the present case, any discrepancy to experimental results could as well be related to a wrong potential barrier obtained from the calculations in ref. 66.
5 Conclusions
In the present work, the mean square displacement (MSD) δx2(t) of a thermalized CO molecule moving in a one dimensional, periodic potential V(x) describing its interaction with copper atoms of a Cu(100) substrate was calculated quantum mechanically within an independent particle formalism. The potential function was obtained from ab initio calculations.66 A key aspect of the formalism is that a thermal state of the particle is described by a typical member of the thermal ensemble, rather than by its statistical average.31 As a consequence, the probability density shows fluctuations which are essential to obtain quantum mechanically a time dependent MSD.Different approaches were analyzed leading to three in principle equivalent equations for the MSD: the first one, eqn (1), is evaluated by the numerical integration of the time dependent Schrödinger equation for randomized initial thermal states; the other by numerically evaluating the MSD while avoiding the explicit numerical integration step (eqn (6)), and an analytical result (eqn (11)), valid in the case V ≡ 0 for an ideal quantum particle. Solving eqn (6) is particularly suitable when the energies En and wave functions ϕn(x) of the eigenstates of the particle and the matrix elements xnn′ = 〈ϕn|![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) |ϕn′〉 are accessible analytically.
|ϕn′〉 are accessible analytically.
Eqn (11) reveals an interesting behavior: while initially of ballistic character, the MSD of the ideal quantum particle of mass m moving in an unrestrained manner at a temperature T gains the character of a Brownian diffusion after a time of order tT ≡ ħ/(kBT). The temperature independent slope of the MSD obtained at long times is given by Dq = ħ/(2 dm), where d is the dimensionality of the particle. While this quantity cannot be directly related to a diffusion coefficient in the classical sense, due to the absence of friction in the theoretical framework that led to it, several arguments are presented in ref. 31 indicating that it might hypothetically be a finite limit of the diffusion coefficient of a free particle, which would be imposed by quantum mechanics in the limit of zero friction.
A numerical method, termed the initial slope method, was developed on the basis of the solution of the time dependent Schrödinger equation and initial thermal wave packets. The essential aspect of this method is that the MSD can be reliably obtained from the numerical evaluation at least during a certain initial time interval, as long as interactions perturbing the independent particle formalism can be neglected.
The initial slope method was used to calculate the quantum mechanical MSD of a CO molecule adsorbed at 190 K on the Cu(100) surface. The careful analysis of the basis size convergence and statistical errors leads us to conclude that δx2(t) is approximately given by the convolution of two processes: an approximately periodic variation with time and a linear increase of the base line. While the periodic variation can be related to intra-cell diffusion, the steady increase of the base line possibly reveals the inter-cell diffusion of the Brownian type in the presence of the periodic potential. This interpretation is based on the Chudley–Elliott model for jump diffusion.70 While the jump-diffusion model is entirely classical, the inter-cell diffusion inferred in the present work is the consequence of the quantum nature of the adsorbed particle, which can tunnel under the potential barriers,56 and the fluctuations inherent to its thermal state.
In the case of CO on Cu(100) at 190 K, the slope of the base line leads to a value of about 4 Å2 ns−1 for the inter-cell diffusion coefficient. This is about one order of magnitude larger than the experimental value of ∼0.6 Å2 ns−1 derived from ref. 74 in the classical approximation of the pair correlation function. Several aspects of this comparison were discussed. The experimental value results from the broadening of the dynamical structure factor which gives the coefficient typical for the diffusion at times much longer than the inverse friction constant, whereas the theoretical result reflects a quantum mechanical diffusion coefficient valid for intermediate times. To compare the two values more appropriately, theory must be extended beyond the independent particle approximation, i.e. by the explicit inclusion of friction.
Another aspect is that the quantum mechanical MSD of an ideal particle, as defined by eqn (1), is related to the phase ϕISF of the intermediate scattering function (ISF), whereas the classical MSD is related to the width of the dynamical structure factor (DSF). In this context, it would be interesting to determine ϕISF for the CO/Cu(100) system from the experimental values related to the real and imaginary parts of the ISF, but also to evaluate the MSD from alternative definitions, as discussed in the Introduction section. Such a work is in progress.
Despite the lack of quantitative agreement between theoretical and experimental results, the method proposed in this work is promising. It should be understood as a first step toward the determination of diffusion coefficients from first principle calculations. It will next be extended to a full dimensional treatment of the dynamics of the CO molecule on Cu(100) using the MCTDH program on the global potential energy surface calculated from ref. 66, first within a rigid substrate model. By gradually inserting mobile copper atoms, such as in ref. 76, we then plan to address the role of friction. Other possibilities include using a hierarchical effective mode approach,77 or stochastic operators.78,79 The theoretical results should then become fully quantitative which would allow us to ultimately verify the method and to assess the quality of the potential energy surfaces calculated ab initio.
Conflicts of interest
There are no conflicts to declare.Appendices
A. Free particle, graphical determination of the slope
Fig. 4 depicts the relative slope sr in the initial 20 tT of the evolution of the MSD (tT = ħ/(kBT) is a natural time unit, here). This quantity is defined by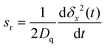 | (A1) |
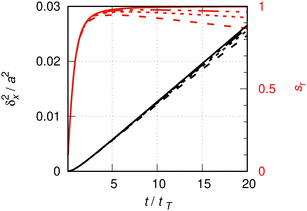 | ||
| Fig. 4 Details of Fig. 1, see the caption of that figure for the definition of line labels. The lines drawn in red are relative slopes (ordinate on the right hand side), according to eqn (A1). In all cases, for t ≲ tT, δx2(t) ∼ t2. | ||
s r rapidly increases from zero to a maximal value slightly below one. The maximum marks an inflection point, beyond which the slope of the quasi-ideal particle slowly but steadily decreases. The inflection points are approximately at 5, 7 and 9 tT, respectively, for L = 10, 20 and 40a. The corresponding maximal relative slopes of 0.95, 0.97 and 0.98 are good approximations of the ideal one. Alternatively, one might take the average relative slope say, between the inflection point and some upper time limits. For the duration shown in Fig. 4 (20 tT), the average slope determined this way for the L = 10a calculation is 0.91. In doing so, one commits a systematic error of about 10%. For the L = 40a calculation, this average slope is 0.975 with a systematic error of about 2%. Let an acceptable upper limit for this error to be of order 10%. Then the initial time interval must not exceed ∼20 tT for the L = 10a calculation and ∼80 tT for L = 40a. The inspection of Fig. 1 suggests an initial time interval of about this length to be considered for the determination of the average slope from the L = 40a line. Indeed, the slope may even be determined graphically, with an error of 10%, in the full initial interval [ 0, 100 tT], as the initial, fast increase of the slope due to the quadratic increase of the MSD can be neglected in the low resolution of the figure. At t = 100 tT, the square root of the MSD is δx ≈ 0.4a, which is comparable with the thermal de Broglie wave length of CO at 190 K, λth ≈ 0.1a.
B. Convergence tests for the MSD of CO/Cu(100)
Fig. 5 shows the MSD in a super-cell of length L = 80 × a for different basis sizes. At this super-cell length, the critical time for the onset of boundary effects in the case of the free particle under similar conditions is 200 tT. One might expect that this critical time is similar for the particle moving under the influence of an external potential, so that for the duration of the evolution shown in this figure boundary conditions should not severely affect the dynamics.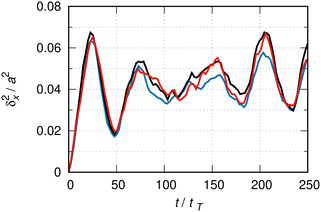 | ||
| Fig. 5 δ x 2(t) as in Fig. 3. The color codes relate to different numbers of basis functions: blue to 75, black to 100 and red to 125 functions per elementary cell. The average over 800 sets of random phases. The statistical error from the ensemble average is maximal 6% toward t ∼ 250 tT. The super-cell of length L = 80 × a, where a = 255.6 pm is the crystal lattice constant. tT ≈ 40 fs, as in Fig. 1. | ||
The evolution is not perfectly converged in this figure. For instance, the relative difference between the black (100) and red (125 functions per elementary cell) lines at t ≈ 180 tT is about 20%. For the remainder of this study, we fix the basis size to 100 functions per elementary cell and estimate the maximal relative error due to the lack of basis size convergence to be of the order of 20%.
We next discuss the convergence of the MSD with respect to the size of the super-cell. Fig. 6 shows the MSD for different super-cell lengths L = N × a and 100 functions per elementary cell. Again, the evolution is not perfectly converged in the first 250 tT of the evolution. Very clearly, however, a super-cell with N = 20 readily drops off after 100 tT. Similarly to the free moving particle case, this drop off is understood as an indicator for the onset of boundary effects, which visibly takes place later than that for the free particle (∼40 tT). The N = 80 (black) and N = 120 (green) lines in this figure match well, while the N = 100 line (red line) clearly deviates from both. In the remainder of this study, a super-cell containing 80 elementary cells will be considered. From the relative difference between the black and red lines in Fig. 6 at t ≈ 180 tT, a maximal error related to boundary effects of about 15% is estimated.
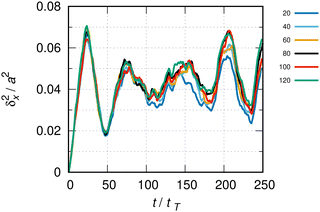 | ||
| Fig. 6 δ x 2(t) as in Fig. 5, using 100 states per elementary cell and super-cell sizes; the numbers N = L/a are indicated in the color key table. | ||
C Harmonic oscillator
For a harmonic oscillator with a mass m and a harmonic frequency ω, En = ħωn (n = 0,1,2,…), and the position matrix elements become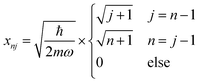 | (C1) |
Insertion into eqn (6) yields
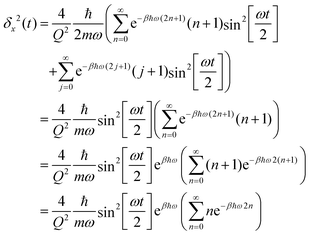 | (C2) |
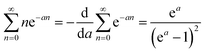 | (C3) |
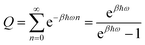 | (C4) |
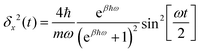 | (C5) |
Acknowledgements
The author thanks Peter Saalfrank for bringing to his attention the question about the quantum mechanical time evolution of the MSD; very helpful discussions with him and with Salvador Miret-Artés, Jörn Manz, Fabien Gatti, Jean-Christophe Tremblay and Lorenz Cederbaum are gratefully acknowledged. This work benefits from the ANR grant under project QDDA.Notes and references
- G. Ertl, Angew. Chem., Int. Ed. Engl., 1990, 29, 1219–1227 CrossRef.
- Y. Kagan and M. I. Klinger, J. Phys. C: Solid State Phys., 1974, 7, 2791–2807 CrossRef CAS.
- P. Hänggi, P. Talkner and M. Borkovec, Rev. Mod. Phys., 1990, 62, 251–341 CrossRef.
- R. Gomer, Rep. Prog. Phys., 1990, 53, 917–1002 CrossRef CAS.
- S. J. Lombardo and A. T. Bell, Surf. Sci. Rep., 1991, 13, 3–72 CrossRef.
- G. R. Haynes, G. A. Voth and E. Pollak, J. Chem. Phys., 1994, 101, 7811–7822 CrossRef CAS.
- C. W. Gardiner and P. Zoller, Quantum Noise, Springer, Berlin, Heidelberg, New York, 2004 Search PubMed.
- J. Bisquert, Phys. Chem. Chem. Phys., 2008, 10, 49–72 RSC.
- A. P. Jardine, H. Hedgeland, G. Alexandrowicz, W. Allison and J. Ellis, Prog. Surf. Sci., 2009, 84, 323–379 CrossRef CAS.
- D. L. Price and F. Fernandez-Alonso, Neutron Scattering – Fundamentals, Academic Press, 2013, vol. 44, pp. 1–136 Search PubMed.
- A. Einstein, Ann. Phys., 1905, 322, 549–560 CrossRef.
- M. V. Smoluchowski, Ann. Phys., 1916, 353, 1103–1112 CrossRef.
- S. Chandrasekhar, Rev. Mod. Phys., 1943, 15, 1–89 CrossRef.
- R. Kubo, M. Toda and N. Hashitsume, Statistical Physics II, Nonequilibrium Statistical Mechanics, Springer, Heidelberg, 2nd edn, 1992 Search PubMed.
- B. N. Brockhouse and N. K. Pope, Phys. Rev. Lett., 1959, 3, 259–262 CrossRef CAS.
- D. Meixner and S. M. George, Surf. Sci., 1993, 297, 27–39 CrossRef CAS.
- X. Wang, Y. Fei and X. Zhu, Chem. Phys. Lett., 2009, 481, 58–61 CrossRef CAS.
- K. R. Harris and L. A. Woolf, J. Chem. Soc., Faraday Trans. 1, 1980, 76, 377–385 RSC.
- M. Holz, R. Haselmeier, R. K. Mazitov and H. Weingaertner, J. Am. Chem. Soc., 1994, 116, 801–802 CrossRef CAS.
- B. G. Briner, M. Doering, H.-P. Rust and A. M. Bradshaw, Science, 1997, 278, 257–260 CrossRef CAS.
- L. J. Lauhon and W. Ho, Phys. Rev. Lett., 2002, 89, 079901 CrossRef.
- L. Bartels, F. Wang, D. Möller, E. Knoesel and T. F. Heinz, Science, 2004, 305, 648–651 CrossRef CAS PubMed.
- B. Holst, G. Alexandrowicz, N. Avidor, G. Benedek, G. Bracco, W. E. Ernst, D. Faras, A. P. Jardine, K. Lefmann, J. R. Manson, R. Marquardt, S. M. Artés, S. J. Sibener, J. W. Wells, A. Tamtögl and W. Allison, Phys. Chem. Chem. Phys., 2021, 23, 7653–7672 RSC.
- A. Tamtögl, M. Pusterhofer, M. Bremholm, E. M. Hedegaard, B. B. Iversen, P. Hofmann, J. Ellis, W. Allison, S. Miret-Artés and W. E. Ernst, Surf. Sci., 2018, 678, 25–31 CrossRef.
- W. E. Ernst, Microsc. Microanal., 2020, 26, 182 CrossRef.
- W. Steurer, A. Apfolter, M. Koch, W. E. Ernst, E. Søndergård, J. R. Manson and B. Holst, Phys. Rev. Lett., 2008, 100, 135504 CrossRef CAS PubMed.
- A. Tamtögl, M. Mayrhofer-Reinhartshuber, N. Balak, W. E. Ernst and K. H. Rieder, J. Phys.: Condens. Matter, 2010, 22, 304019 CrossRef.
- A. Tamtögl, P. Kraus, M. Mayrhofer-Reinhartshuber, D. Campi, M. Bernasconi, G. Benedek and W. E. Ernst, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 035410 CrossRef.
- A. Tamtögl, P. Kraus, N. Avidor, M. Bremholm, E. M. J. Hedegaard, B. B. Iversen, M. Bianchi, P. Hofmann, J. Ellis, W. Allison, G. Benedek and W. E. Ernst, Phys. Rev. B, 2017, 95, 195401 CrossRef.
- G. Benedek, S. Miret-Artés, J. R. Manson, A. Ruckhofer, W. E. Ernst and A. Tamtögl, J. Phys. Chem. Lett., 2020, 11, 1927–1933 CrossRef CAS.
- R. Marquardt, Mol. Phys., 2021, 119, e1971315 CrossRef.
- G. W. Ford, J. T. Lewis and R. F. O'Connell, Phys. Rev. A, 2001, 64, 032101 CrossRef.
- G. Ford and R. O'Connell, Phys. Lett. A, 2001, 286, 87–90 CrossRef CAS.
- D. K. Wójcik and J. R. Dorfman, Phys. Rev. Lett., 2003, 90, 230602 CrossRef PubMed.
- S. W. Rick, D. L. Lynch and J. D. Doll, J. Chem. Phys., 1993, 99, 8183–8193 CrossRef CAS.
- A. Calhoun, M. Pavese and G. A. Voth, Chem. Phys. Lett., 1996, 262, 415–420 CrossRef CAS.
- T. F. Miller and D. E. Manolopoulos, J. Chem. Phys., 2005, 123, 154504 CrossRef PubMed.
- Y. V. Suleimanov, J. Phys. Chem. C, 2012, 116, 11141–11153 CrossRef CAS.
- T. R. Mattsson, U. Engberg and G. Wahnström, Phys. Rev. Lett., 1993, 71, 2615–2618 CrossRef CAS PubMed.
- L. Y. Chen and S. C. Ying, Phys. Rev. Lett., 1994, 73, 700–703 CrossRef CAS PubMed.
- W. Fang, J. O. Richardson, J. Chen, X.-Z. Li and A. Michaelides, Phys. Rev. Lett., 2017, 119, 126001 CrossRef PubMed.
- K. Haug and H. Metiu, J. Chem. Phys., 1991, 94, 3251–3267 CrossRef CAS.
- P. Saalfrank and W. H. Miller, Surf. Sci., 1994, 303, 206–230 CrossRef CAS.
- D. H. Zhang, J. C. Light and S.-Y. Lee, J. Chem. Phys., 1999, 111, 5741–5753 CrossRef CAS.
- X. D. Zhu, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 11279–11282 CrossRef CAS PubMed.
- J. Kua, L. J. Lauhon, W. Ho and W. A. Goddard, J. Chem. Phys., 2001, 115, 5620–5624 CrossRef CAS.
- P. G. Sundell and G. Wahnström, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 081403 CrossRef.
- I. Rips and E. Pollak, Phys. Rev. A, 1990, 41, 5366–5382 CrossRef CAS PubMed.
- R. Ianconescu and E. Pollak, J. Chem. Phys., 2019, 151, 024703 CrossRef PubMed.
- T. R. Mattsson, G. Wahnström, L. Bengtsson and B. Hammer, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 2258–2266 CrossRef CAS.
- A. B. Nassar and S. Miret-Artés, Phys. Rev. Lett., 2013, 111, 150401 CrossRef PubMed.
- S. V. Mousavi and S. Miret-Artés, Eur. Phys. J. Plus, 2019, 134, 311 CrossRef.
- X. Zhong and Y. Zhao, J. Chem. Phys., 2013, 138, 014111 CrossRef PubMed.
- Z.-W. Bai, J.-D. Bao and Y.-L. Song, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 061105 CrossRef PubMed.
- S. S. Sinha, D. Mondal, B. C. Bag and D. S. Ray, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 051125 CrossRef PubMed.
- D. Zanuttini, F. Gatti and R. Marquardt, Chem. Phys., 2018, 509, 3–12 CrossRef CAS.
- L. van Hove, Phys. Rev., 1954, 95, 249–262 CrossRef CAS.
- R. C. Tolman, The principles of statistical mechanics, Oxford University Press, Oxford (UK), 1938 Search PubMed.
- M. Quack, Adv. Chem. Phys., 1982, 50, 395–473 CAS.
- D. Gelman and R. Kosloff, Chem. Phys. Lett., 2003, 381, 129–138 CrossRef CAS.
- U. Lorenz and P. Saalfrank, J. Chem. Phys., 2014, 140, 044106 CrossRef CAS PubMed.
- H.-D. Meyer, U. Manthe and L. S. Cederbaum, Chem. Phys. Lett., 1990, 165, 73 CrossRef CAS.
- G. A. Worth, M. H. Beck, A. Jäckle and H.-D. Meyer, The MCTDH Package, Version 8.2, (2000). H.-D. Meyer, Version 8.3 (2002), Version 8.4 (2007), Revision 8 (2012). See https://mctdh.uni-hd.de/, 2012.
- U. Manthe and F. Huarte-Larrañaga, Chem. Phys. Lett., 2001, 349, 321–328 CrossRef CAS.
- M. Nest and R. Kosloff, J. Chem. Phys., 2007, 127, 134711 CrossRef CAS PubMed.
- R. Marquardt, F. Cuvelier, R. A. Olsen, E. J. Baerends, J. C. Tremblay and P. Saalfrank, J. Chem. Phys., 2010, 132, 074108 CrossRef PubMed.
- T. Firmino, R. Marquardt, F. Gatti, D. Zanuttini and W. Dong, Frontiers in Quantum Methods and Applications in Chemistry and Physics: Selected and Edited Proceedings of QSCP-XVIII (Paraty, Brazil, December 2013), 2015.
- C. Kittel and H. Krömer, Thermal physics, Freeman, San Francisco, 2nd edn, 1980 Search PubMed.
- B. Vacchini and K. Hornberger, Phys. Rep., 2009, 478, 71–120 CrossRef CAS.
- C. T. Chudley and R. J. Elliot, Proc. Phys. Soc., 1961, 77, 353–361 CrossRef.
- M. Head-Gordon and J. C. Tully, J. Chem. Phys., 1992, 96, 3939–3949 CrossRef CAS.
- A. P. Jardine, J. Ellis and W. Allison, J. Chem. Phys., 2004, 120, 8724–8733 CrossRef CAS PubMed.
- G. H. Vineyard, Phys. Rev., 1958, 110, 999–1010 CrossRef CAS.
- G. Alexandrowicz, A. P. Jardine, P. Fouquet, S. Dworski, W. Allison and J. Ellis, Phys. Rev. Lett., 2004, 93, 156103 CrossRef CAS PubMed.
- J. Ellis, A. P. Graham and J. P. Toennies, Phys. Rev. Lett., 1999, 82, 5072–5075 CrossRef CAS.
- Q. Meng and H.-D. Meyer, J. Chem. Phys., 2017, 146, 184305 CrossRef.
- I. Burghardt, R. Martinazzo and K. H. Hughes, J. Chem. Phys., 2012, 137, 144107 CrossRef PubMed.
- T. Serwatka and J. C. Tremblay, J. Chem. Phys., 2019, 150, 184105 CrossRef CAS PubMed.
- S. Mandal, F. Gatti, O. Bindech, R. Marquardt and J.-C. Tremblay, J. Chem. Phys., 2022, 156, 094109 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2022 |
