Influence of intermolecular interactions on the infrared complex indices of refraction for binary liquid mixtures

Abstract

This paper investigates the accuracy of deriving the composite optical constants of binary mixtures from only the complex indices of refraction of the neat materials. These optical constants enable the reflectance spectra of the binary mixtures to be modeled for multiple scenarios (e.g., different substrates, thicknesses, volume ratios), which is important for contact and standoff chemical detection. Using volume fractions, each mixture's complex index of refraction was approximated via three different mixing rules. To explore the impact of intermolecular interactions, these predictions are tested by experimental measurements for two representative sets of binary mixtures: (1) tributyl phosphate combined with n-dodecane, a non-polar medium, to represent mixtures which primarily interact via dispersion forces and (2) tributyl phosphate and 1-butanol to represent mixtures with polar functional groups that can also interact via dipole–dipole interactions, including hydrogen bonding. The residuals and the root-mean-square error between the experimental and calculated index values are computed and demonstrate that for miscible liquids in which the average geometry of the cross-interactions can be considered isotropic (e.g., dispersion), the refractive indices of the mixtures can be modeled using composite n and k values derived from volume fractions of the neat liquids. Conversely, in spectral regions where the geometry of the cross-interactions is more restricted and anisotropic (e.g., hydrogen bonding), the calculated n and k values vary from the measured values. The impact of these interactions on the reflectance spectra are then compared by modeling a thin film of the binary mixtures on an aluminum substrate using both the measured and the mathematically computed indices of refraction.

---

I. Introduction

Detection of solids, liquids and gases is important for a wide range of environmental, industrial and national security applications, including extraterrestrial exploration,^1–3 pollution monitoring^4,5 and hazardous chemical detection.⁶ Spectroscopic methods⁷ are often used and typically involve applying detection (or spectral matching) algorithms^8–10 that rely on a set of library spectra containing both target and background materials for material identification. For gases, databases of absorbance spectra allow identification of unknown gases in plumes¹¹ and can be used along with other methods to estimate plume temperature and path length. For solid materials, databases of reflectance spectra are often employed^12–17 whereas transmittance (absorbance) data are more commonly used for liquids.^18,19 Liquids, however, are seldom observed in the environment in pure bulk form except for bodies of water, and only seldom for most solids. Thus, for both solid- and liquid-phases, there has been an ever-increasing need to model, rather than measure, the reflectance (or emittance) spectra that can account for the sundry morphological forms that may exist in natural and industrial environments, including thin vs. thick layers, mixtures, particles, droplets, etc.^16,20–23 Such modeling can be undertaken by knowing or anticipating the suspected geometry (e.g. liquid layer thickness), and then ray tracing using the Beer Lambert Law, Snell's Law and the Fresnel equations.¹⁹ The real, n(ν), and imaginary, k(ν), components of the complex refractive index, however, are a prerequisite to such calculations, which can be used to simulate the reflectance spectra and account for the multiple phenomena (reflection, refraction and absorption) that affect the spectral content of the light reflected from condensed phase materials deposited on different substrates.²⁴

To this end, work has been undertaken in our laboratory to catalog the complex index of refraction for numerous liquids¹⁸ that can provide an alternative approach to identifying unknown liquid substances. In the event of chemical spills, for example, liquids are more likely encountered as thin films (submicron to 100's of microns) on metallic or dielectric substrates whereby both the substrate as well as the liquid contribute to the composite reflectance signature. By knowing the complex index of refraction of a liquid (as well as the substrate) the arrangement can thus be modeled (by varying liquid thickness, substrate type, angle of incidence, polarization) using methods such as ray tracing or thin film modeling along with the transfer matrix method (TMM)²⁵ until a match is obtained for the previously unknown acquired signature. For the present purposes, the complex index of refraction is defined as below in eqn (1) where n(λ) governs the refraction and reflection of light, and k(λ) is concerned with attenuation and the reflectance of light, especially in metals.

ñ(λ) = n(λ) + ik(λ) (1)

Most modeling efforts have focused on a single material deposited on a substrate even though mixtures are more likely to be encountered in the environment and are more challenging for spectral identification compared to their neat liquid counterparts. Generation of reference spectra for liquid mixtures²⁶ using simply the experimentally determined complex index of refraction data for the neat liquids along with the ratio of each component is appealing since preparing and measuring all possible combinations of mixtures that may be present is impractical. Other approaches involve post-processing using spectral unmixing algorithms to estimate the abundances of each of the constituents from the neat end-member spectra.²⁷ These methods, however, are only effective if the individual components of the mixture do not interact strongly with one another and often require a priori knowledge of the materials in the scene.

Many prior studies have investigated the optical and thermodynamic properties of binary liquid mixtures due to their relevance for solvation and extraction chemistries.^28–36 The earlier studies mostly focused on predicting the real part of the refractive index in non-absorbing spectral regions, e.g., in the visible region at select wavelengths such as 589 nm,^28,29 546 nm and 436 nm.^30,31 This study examines the complex refractive index in absorbing regions from 1 to 25 μm (10 000 to 400 cm⁻¹) as this spectral region is most important for chemical detection, containing both the fundamental absorption bands as well as weaker overtone and combination bands.

Different van der Waals forces, including London dispersion, dipole–induced dipole, and dipole–dipole interactions have the potential to influence the various functional groups within the mixtures and can therefore perturb the resulting spectra. Specifically, for dipole–dipole interactions, including hydrogen-bonding, the interaction is determined by the relative orientation of the two dipoles and therefore tends to be localized to specific functional groups within the pair of molecules. In the limit of two interacting molecules, the distribution of energetically favorable dipole–dipole interactions is not randomly distributed (i.e., there is a preferred orientation). Consequently, dipole–dipole interactions should have a greater tendency to influence the spectral responses of the functional groups involved in the interaction. Conversely, dispersion interactions simply involve transient perturbations to the electron clouds of the interacting molecules. Unlike dipole–dipole, the distribution of dispersion interactions is reasonably isotropic (i.e., there is not a preferred orientation since the geometry of the interaction is not limited to a specific functional group, and the two molecules can adopt any orientation relative to one another). As a result, dispersion interactions should have comparatively little influence on spectral properties, especially if both molecules exhibit comparable dispersion interactions. Thus, to gain a better quantitative understanding of the role of intermolecular interactions on the optical constants of mixtures, we examine two representative cases: (1) a binary mixture capable of interacting predominantly through dispersion interactions (and therefore exhibiting well-behaved spectral responses, characteristic of a linear combination of the neat spectra) and (2) a binary mixture that is also capable of hydrogen bonding (dipole–dipole) interactions which are more likely to impact the infrared spectral features. Specifically, the first case combines tributyl phosphate (TBP), [(CH₃CH₂CH₂CH₂O)₃P=O], a polar organophosphate compound, with n-dodecane, [CH₃(CH₂)₁₀CH₃], a long non-polar hydrocarbon chain. The P=O functional group in TBP leads to dipole–dipole interactions for neat TBP, whereas n-dodecane experiences stronger dispersion forces due to its long, linear hydrocarbon chain.³⁷ These intermolecular interactions in the neat liquids are quite strong as evidenced by the high boiling points (i.e., TBP = 289 °C and n-dodecane = 216 °C).³⁸ In addition to dispersion, dipole–induced dipole interactions can also occur between these two liquids. Prior studies have shown, however, that n-dodecane does not interact significantly with TBP;³⁹ thus, it is expected that these binary mixtures should lead to more ideal spectral responses. The second case mixes TBP with 1-butanol, [CH₃(CH₂)₃OH], a polar protic solvent with an OH moiety capable of hydrogen-bonding. Similar to the TBP:n-dodecane mixtures, TBP:1-butanol is capable of both dispersion and dipole–induced dipole interactions. However, due to the presence of the OH and PO moieties, the TBP:1-butanol mixtures are also capable of hydrogen bonding (dipole–dipole) interactions. Consequently, it is expected that these binary mixtures should lead to non-ideal spectral responses, particularly in regions associated with functional groups involved in the interaction.

A series of binary mixtures is prepared for both TBP:n-dodecane and TBP:1-butanol with different volume percentages to experimentally derive the composite index of refraction for both sample cases and investigate its impact on the resulting quality of the predicted spectra. The complex refractive indices of the binary mixtures are computed using three different mixing rules along with the measured optical constants of the neat liquids.^30,40–42 The experimentally derived and computed optical constants of the mixtures are compared to assess the impact of the various intermolecular interactions. Finally, to investigate the efficacy of using the predicted optical constants for modeling reflectance spectra, thin liquid layers of the binary mixtures are modeled on an aluminum substrate using both sets of index values.

II. Methods

A. Experimental

The measurement of the complex index of refraction of the liquid mixtures was performed as described in detail in a previous publication for neat species.¹⁸ These vetted protocols are readily applied to the binary mix measurements: a wide range of cell path lengths are used to determine the k-vector spectrum as a single sample cell cannot usually yield a complete k-vector, because strong bands saturate in the long path cells, while weak bands are often obscured by noise in the short path cell data. From the multiple cell spectra, the resulting k-vectors are baseline corrected and then spliced together using selected bands over their linear domains to form a composite k-vector that is valid for both weak and strong bands, extending across the full spectral range of the instrument. This k-vector is smoothed (in select regions) if necessary and the associated n-vector is determined by application of the Kramers–Kronig relations.⁴³ The final calculation of the n-vector is a key product of the analysis; all the intermediate n-vectors calculated for individual cells (which are not valid across entire spectral range) are discarded.

B. Data acquisition

The following chemicals were used either as neat materials or mixtures in selected proportions: tributyl phosphate (Sigma-Aldrich, >99%), n-dodecane (Alfa Aesar, >99%) and 1-butanol (Sigma-Aldrich, 99.8%). Mixtures were prepared by carefully combining appropriate mass amounts of the two chemicals. The scalar refractive indices of the samples were measured using an Abbe refractometer at fixed wavelengths in the near-infrared and visible domain. As suggested by Bertie, the refractive index at the highest wavenumber is determined from a fit of n to the measured values.^44,45

Commercially prepared optical cells (International Crystal Laboratories) with either potassium bromide (KBr) or potassium chloride (KCl) windows were used with path lengths of approximately 3000, 1000, 500, 200, 100, 50 or 25 micrometer (μm). In addition, cells of shorter path length, e.g., approximately 15, 10, 5, 2 and 1 μm, were prepared by compressing the 25 μm commercial cells with a hydraulic press. Prior to analyzing the liquid chemicals, a survey IR spectrum was recorded, and the path length of the empty cell was estimated from the fringe spacing using the equation d = (2 × n × Δv)⁻¹ where n refers to the refractive index of air (n = 1) and Δv is the fringe spacing. The liquid sample was loaded into the optical cell using a syringe.

The optical cells were placed in sample holders in both Bruker Tensor 37 and Bruker Vertex 70 instruments for mid-infrared (MIR) and near-infrared (NIR) measurements, respectively. Cell path lengths of approximately 3000, 1000, 500, 200 and 100 μm were analyzed using the (NIR) Vertex 70 and cell path lengths of approximately 500, 200, 100, 50, 20, 10, 5, 2, and 1 μm were analyzed using the (MIR) Tensor 37. Typically, for the 500, 200 and 100 μm path lengths, the same cell with the same liquid fill was used for both systems. The spectrometer sample compartment was continuously purged with ultra-high purity N₂ during data collection. The FTIR experimental parameters are provided in Table S1 of the ESI.†

A daily calibration was conducted for both the MIR and NIR systems to ensure consistent optimal performance. The x-axis (frequency) was calibrated by comparing an absorbance spectrum of air (obtained by opening the sample chamber) to reference CO₂ and H₂O lines from the PNNL gas-phase database.⁴⁶ The y-axis (transmission) was calibrated with an MRC Infrared Linearity Standard (MRC-910-NG11 S/N 0108) where known transmission values were compared to measured values at various wavelengths across the spectrum. A signal-to-noise test was also performed to check for drift or reduction in the IR signal.

C. Experimentally-derived optical constants

Typically, six spectra of each cell path length were recorded. Replicate spectra of a single sample were evaluated for consistency and an average spectrum calculated in OPUS,⁴⁷ excluding any outlier spectra. The measured cell path lengths were adjusted using Beer–Lambert Law plots in which the NIR and MIR data were analyzed independently. The imaginary part of the refractive index, or k vector, was determined for each absorbance file as per Bertie's program “RNJ46A”^45,48 which takes into account the reflective losses due to the KCl or KBr cell windows. The k vectors were created via a classical, weighted, linear, least squares fit using the output files of program “RNJ46A” in which individual absorbance values were weighted by T² (transmission squared) and all absorbance values ≥2.5 were given zero weight to ensure linearity across the entire spectral range. The individual k vectors for each cell path length were baseline-corrected prior to creating composite k vectors using data from appropriate cell path lengths and spanning appropriate wavenumber ranges.^18,49 Finally, a single composite k vector was prepared for each of the MIR and NIR data. The two composite k vectors representing the MIR and NIR data were then merged over a narrow spectral range (typically of 100–500 cm⁻¹ width, near 3300 cm⁻¹) in the overlap region where both MIR and NIR data were collected with few absorption features, i.e. near the baseline.⁵⁰

The real part of the complex index of refraction (n) was determined by first measuring the n-values for the binary mixtures at 480, 486, 546, 589, 644, 656 and 1550 nm using an ATAGO refractometer. A modified-Sellmeier equation was then used to interpolate n at 10 000 cm⁻¹.⁵¹ The final n vector for each point mixture was calculated using the composite k vector and the refractive index at 10 000 cm⁻¹ per Bertie's “LZZKTB” program with the Kramers–Kronig relation. The real and imaginary parts of the complex index of refraction are provided for the neat substances in Fig. S1 and S2 of the ESI.†

D. Binary sample preparation and measurement

Two sample series based on binary mixtures of TBP with either n-dodecane or 1-butanol were prepared. Each chemical was prepared and analyzed in its original form, and in mixtures in select proportions to yield a 7-point mixing line: 100/0%, 90/10%, 70/30%, 50/50%, 30/70%, 10/90% and 0/100% based on mole percentages. These mixtures were prepared by carefully combining appropriate mass amounts of the two chemicals to obtain the desired mole percentages. As the mixing rules are based on volume fraction (ϕ), the volume percentages (ϕ × 100%) were calculated using the reported densities³⁸ and are summarized in Table 1 for both series of mixtures.

Table 1 Summary of the parameters for the TBP:n-dodecane and TBP:1-butanol mixtures

TBP^a mass (g)	Mole percent (%)	Volume percent (%)	n-dodecane^b mass (g)	Mole percent (%)	Volume percent (%)
a TBP properties: M = 266.32 g mol^−1, ρ = 0.9727 g cm^−3. b n-Dodecane properties: M = 170.33 g mol^−1, ρ = 0.7495 g cm^−3. c 1-Butanol properties: M = 74.121 g mol^−1, ρ = 0.8095 g cm^−3, Vm = 91.6 cm^3 mol^−1. d Mixture excluded from analysis since it is predominantly TBP.
13.1898	91	92	0.8750	9	8
11.7638	70	74	3.2448	30	26
9.1543	50	55	5.8678	50	45
6.0559	30	34	8.9859	70	66
2.2163	9	10	15.0088	91	90

---

TBP mass (g)	Mole percent (%)	Volume percent (%)	1-Butanol^c mass (g)	Mole percent (%)	Volume percent (%)
1.7677	4	10	13.2375	96	90
4.3186	10	25	10.8129	90	75
9.0966	30	56	5.9073	70	44
11.7396	50	75	3.2715	50	25
13.4146	70	88	1.5923	30	12
14.9555^d	90	96	0.4479	10	4

---

The calculated volume percentages for the TBP:n-dodecane mixtures (Table 1) are almost equivalent to the mole percentages since the two species have similar molar volumes (V_m) whereas the calculated volume percentages for TBP:1-butanol mixtures (Table 1) are significantly different than the mole percentages. (The reported densities and molar masses can be used to calculate the molar volumes: V_m is equal to 273.8 cm³ mol⁻¹ for TBP, 227.3 cm³ mol⁻¹ for n-dodecane and 91.6 cm³ mol⁻¹ for 1-butanol, respectively). To provide similar proportions for the volume percentages for the TBP–1-butanol mixtures, an additional mixture was prepared to include a 10 : 90 volume percent ratio, and the 90 : 10 mole percent mixture was excluded from the analysis since it was mostly TBP, i.e. 96% TBP by volume.

E. Computational

Three different mixing rules of varying complexity were used to compute the composite optical constants of the binary mixtures. Each of these expressions use the n and k values of the neat materials, which were experimentally derived (Section II.C). The simplest approach for calculating the complex refractive index for mixtures is that of Dale–Gladstone and Arago–Biot⁴⁰ that takes the form shown below in eqn (2) and is referred to as the Arago–Biot (AB) method. Here ñ_mix is reported as a function of wavelength (λ) and is defined as the complex index of refraction previously defined in eqn (1), in which ϕ_a and ϕ_b are proportionality constants based on volume fraction.

ñ_mix(λ) = ϕ_añ_a(λ) + ϕ_bñ_b(λ) (2)

Another variation referred to as the Newton method,³⁰ is shown in eqn (3). This method is based on the relative permittivity,⁴¹ where ε signifies the relative permittivity of the liquid and is defined as ε = (ñ)².

ñ_mix²(λ) = ϕ_añ_a²(λ) + ϕ_bñ_b²(λ) (3)

Finally, the Lorentz–Lorenz (L–L) equation⁴² as detailed in eqn (4) is similar to the Newton method with some additional factors:These three methods are all predicated on the following assumptions:

1. The liquids are assumed to be non-reacting with each other.

2. The total volume or mass of the mixture is equal to the sum volume or mass of the two liquids being mixed.

3. All measurements and analyses are assumed at a fixed temperature, e.g., 27 °C.

III. Results and analysis

A. Passive influence of dispersion interactions: mixtures of tributyl phosphate and n-dodecane

The neat liquids of TBP and n-dodecane provide a case study for mixtures that primarily interact through the dispersion forces between the alkyl chains present in both liquids (though dipole–induced dipole interactions may also occur due to the polar P=O group in TBP, see S3 in ESI†). Specifically, due to the isotropic nature of dispersion interactions (i.e., the interaction is not localized to a specific functional group/molecular orientation), these mixtures are predicted to demonstrate more ideal behavior in which the calculated n and k spectra are expected to better match the measured spectra. As indicated in Table 1, volume percent ratios of 100 : 0, 92 : 08, 74 : 26, 55 : 45, 34 : 66, 10 : 90 and 0 : 100 were prepared and measured for TBP and n-dodecane mixtures. The first number refers to the TBP volume percent, the second to the n-dodecane volume percent. Fig. 1 presents the experimental progression of both the real (n) and imaginary part (k) of the index as the volume mixture percentage varies from 100% TBP (black trace in Fig. 1) to 100% n-dodecane (purple trace in Fig. 1). The strongest absorption features for TBP include the triplet peak centered at 1029 cm⁻¹ (9.72 μm) assigned to the P–O–C group, the peak located at 1282 cm⁻¹ (7.8 μm) assigned to the P=O stretch and a band centered around 2961 cm⁻¹ (3.38 μm) corresponding to the C–H stretching modes.⁵² For n-dodecane, the dominant peaks are the C–H stretching modes centered around 2924 cm⁻¹ (3.42 μm).

Fig. 1 The measured (a) real part of the index of refraction n and (b) imaginary part of the index of refraction k as the percent volume mixture ratio progresses from 100 : 0 to 0 : 100 for TBP:n-dodecane. The spectra are offset for clarity.

For each of the TBP:n-dodecane mixtures, the composite n and k values were also calculated from the expressions in eqn (2) through eqn (4). These predicted n and k values were compared to the measured n and k values presented in Fig. 1, and the residuals determined by subtracting the calculated index of refraction from the values derived from the measurements of the binary mixtures. As an example, the results for the n and k spectra of the 55 : 45 mixture of TBP:n-dodecane along with its residuals are shown in Fig. 2. Inspection of the residuals show that the differences are not randomly distributed but rather centered around spectral features. These residuals can also be referred to as the excess spectrum, similar to the excess molar volume and excess molar enthalpies described by other researchers.^28,35,53 The differences for the n-values (Fig. 2a) range from −0.011 to 0.015 and show the model mostly overpredicts the n-values as indicated by the negative offset ca. −0.002. The root-mean square error (RMSE) between the modeled and measured refractive index of the mixtures is 0.002. For comparison, the standard measurement error (2σ) for the measured n-value at 1550 nm is 0.001. The measured and modeled n-values at 10 000 cm⁻¹ for the five mixtures and the neat components are also provided in Fig. S4 of the ESI.† Similarly, as seen in Fig. 2b, the model mostly overpredicts the k-values, and the residuals vary from −0.16 to 0.008 in which the largest differences occur at 1280 and 2924 cm⁻¹ corresponding to the P=O and C–H stretching regions, respectively. The RMSE between the calculated and measured k-values is 0.001. Note that the mixing rules require the use of volume fractions vs. mole fractions; using mole fractions with eqn (2) through eqn (4) leads to slightly higher errors in the calculated spectra since the mole fractions are slightly different than the volume fractions (see Table 1).

Fig. 2 Plots showing (a) the real part (n) and (b) imaginary part (k) of the complex refractive index for both the experimentally measured and calculated values (using eqn (2)) for a 55 : 45 mixture of TBP and n-dodecane. Bottom panels show the residual error between the experimental and calculated index values.

An expanded view of the measured (solid lines) and computed k-values (dashed lines) centered in spectral regions corresponding to the C–H and P=O stretching regions is seen in Fig. 3 for all five binary mixtures of TBP:n-dodecane as well as neat TBP and n-dodecane. Fig. 3a is plotted from 1310–1220 cm⁻¹ (7.6–8.2 μm) and highlights the P=O stretching region. Three peaks in the P=O stretching region are observed and have been previously attributed to different distributions of conformers.⁵⁴ However, an ab initio calculation of the fundamental vibrational modes of TBP predicts three distinct P=O modes in this region: ν₆₆ (1250 cm⁻¹) and ν₆₉ (1265 cm⁻¹), both assignable to the P=O stretch plus different CH₂ wags, as well as ν₇₁ (1280 cm⁻¹) which is assignable to the P=O stretch plus CH₂ rocking motions (see S3 in ESI† for more detail). In this spectral region, the residuals for the k-values in the 55 : 45 mixture are primarily negative (Fig. 2b) indicating the mixtures of TBP and n-dodecane are interacting (if only slightly). The deviation from ideal behavior provides a measure of the degree of interaction between the two liquids. In addition, a slight blue-shift for the P=O peak for TBP at 1282 cm⁻¹ is observed as the fraction of n-dodecane increases, e.g., the P=O peak is shifted to 1287 cm⁻¹ for the 10 : 90 mixture. For TBP:n-dodecane, the mixture with the largest concentration of TBP (92 : 08) has the smallest errors. Fig. 3b is plotted from 3000–2817 cm⁻¹ (3.3–3.55 μm) and highlights the C–H stretching region. In this spectral region, the residuals are also negative for most of the mixtures, particularly for the band located at 2924 cm⁻¹, which is assigned to the CH₂ antisymmetric stretch for n-dodecane.⁵⁵ Note that the deviation between measured and computed k-values for this mode increases with the n-dodecane concentration and is largest for the 10 : 90 mixture. Slightly lower k-values at 2924 cm⁻¹ are observed for the three mixtures with the highest concentration of n-dodecane (i.e., 55 : 45, 34 : 66 and 10 : 90) compared to the computed k-values. The alkyl chains in TBP and n-dodecane will interact via London dispersion forces and these are predicted to be the strongest cross-interactions (see Fig. S3 of the ESI†). However, dipole–induced dipole interactions between the P=O and CH₂ moieties may also occur. These cross-interactions might explain the slight blue-shift of the P=O mode and the reduced amplitude of the CH₂ stretch.

Fig. 3 The k-spectra for the binary mixtures of TBP:n-dodecane in the region of the (a) P=O stretching region from 1310–1220 cm⁻¹ (7.6–8.2 μm) and (b) C–H stretching region from 3000–2817 cm⁻¹ (3.3–3.55 μm). The experimental data are plotted as solid lines, and the theoretical predictions (based on eqn (2)) are plotted as dashed lines.

B. Perturbing influence of dipole–dipole interactions: mixtures of tributyl phosphate and 1-butanol

The neat liquids of TPB and 1-butanol provide opportunities to examine systems of increased complexity. In addition to the dispersion and dipole–induced dipole interactions present in the TBP:n-dodecane mixtures examined above, TBP:1-butanol is also capable of hydrogen bonding (dipole–dipole) interactions and is thus expected to demonstrate a greater propensity for non-ideal spectral behavior. Specifically, due to the anisotropic nature of dipole–dipole interactions (i.e., the interaction preferentially involves specific functional groups in each molecule), the predicted n and k spectra are expected to deviate from the measured spectra in these mixtures (particularly in the O–H and P=O stretching modes). Volume mixture ratios of 100 : 0, 88 : 12, 75 : 25, 56 : 44, 25 : 75, 10 : 90 and 0 : 100 were prepared and measured for mixtures of TBP:1-butanol. The real and imaginary parts of the refractive index are stack-plotted in Fig. 4 in which the mixture ratio varies from neat TBP (black trace) to neat 1-butanol (purple trace). For 1-butanol, the strongest absorption features correspond to the broad O–H stretching band centered at 3329 cm⁻¹ (3.0 μm), multiple bands in the 2950–2850 cm⁻¹ (3.4–3.5 μm) domain assigned to C–H stretching modes, and multiple bands around 1080–1025 cm⁻¹ (9.3–9.8 μm) assigned to C–C and C–O stretching modes along with CH₃ rocking motion.^56,57

Fig. 4 The measured (a) real part of the index of refraction n and (b) imaginary part of the index of refraction k as the percent volume mixture ratio progresses from 100 : 0 to 0 : 100 for TBP : 1-butanol mixtures. The spectra are offset for clarity.

For each of the mixtures, the n and k values were also computed using the expressions in eqn (2) through eqn (4) and compared to the measured n and k values presented in Fig. 4. Fig. 5 shows the measured and computed values for the 56 : 44 mixture of TBP : 1-butanol along with the residuals for both n and k values, respectively. The model mostly overpredicts the n-values and a negative offset of −0.01 is observed. The residuals for the n-values (Fig. 5a) vary from −0.077 to 0.042, and the RMSE between the measured and calculated n-values is 0.012, which is a factor of six larger than the RMSE of 0.002 observed for 55 : 45 mixture of TBP : n-dodecane and well outside of the measurement variability (2σ < 0.001). The measured and modeled n-values at 10 000 cm⁻¹ for the five mixtures and the neat components are also provided in Fig. S4 of the ESI.†Fig. 5b shows the model both over and under-predicts the k-values, and the residuals range from −0.066 to 0.057 with an RMSE of 0.005, compared to an RMSE of 0.001 for the 55 : 45 mixture of TBP : n-dodecane. The largest differences in Fig. 5b occur at 1283 cm⁻¹ (7.8 μm) and 1246 cm⁻¹ (8.0 μm), i.e., the P=O stretching region. Similar to the TBP:n-dodecane mixtures, using molar fractions in eqn (2) through eqn (4) leads to higher errors in the calculated spectra due to the differences between molar and volume fractions (see Table 1).

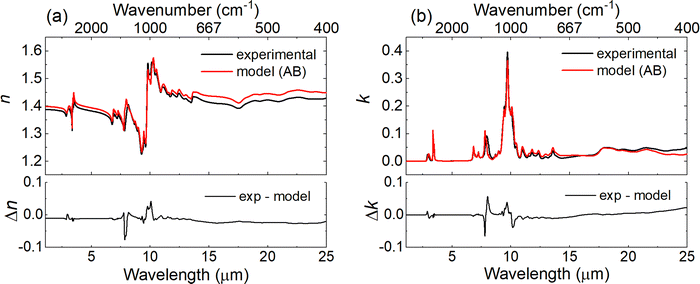Fig. 5 Plots showing (a) the real part (n) and (b) imaginary part (k) of the complex refractive index for both the experimentally measured and calculated values (using eqn (2)) for a 56 : 44 mixture of TBP and 1-butanol. Bottom panels show the residual error between the experimental and calculated index values.

While the TBP and 1-butanol are quite miscible, there is not a linear correlation between simply adding the k vectors of the two neat liquids in ratios corresponding to the volume fractions for all spectral regions in the infrared. The OH moiety in 1-butanol enables H-bonding with the phosphoryl oxygen in TBP²⁸ causing non-ideal behavior that is not captured by the mixing rules. This behavior can be better understood by inspection of Fig. 6 which plots the experimentally derived k values (solid lines) and calculated k values (dashed lines) using eqn (2). Fig. 6a highlights the P=O stretching region from 1310–1220 cm⁻¹ (7.6–8.2 μm). With increasing fraction of 1-butanol, the P=O (phosphoryl) peak for TBP at 1282 cm⁻¹ (7.8 μm) shows a reduction in predicted amplitude whereas an increase in amplitude and broadening is observed around the two peaks at 1262 cm⁻¹ (7.9 μm) and 1236 cm⁻¹ (8.1 μm). The change in the measured spectra indicates an increase in the number of chemical environments for the P=O moiety, suggesting some of the TBP molecules continue to interact with itself, but some also interact with the 1-butanol molecules via hydrogen bonding between the phosphoryl oxygen and the hydroxyl group (see Section III.D). To further assess if hydrogen-bonding is indeed occurring, Fig. 6b is expanded from 3600–3030 cm⁻¹ (2.8–3.3 μm) and includes the broad band for the O–H stretching frequency at 3333 cm⁻¹ for 1-butanol. As the volume percentage of TBP increases, the broad OH peak changes to a doublet and shifts to higher wavenumber (e.g., shifts to 3446 cm⁻¹ for the 88 : 12 mixture), with the O–H band vanishing entirely as the volume fraction moves to that of 100% TBP. The doublet nature of the peak is seen most clearly in the spectrum for the 56% by volume TBP mixture (light green trace in Fig. 6b). The peak shift to higher wavenumber is attributed to hydrogen bonding of the P=O oxygen atom with the OH moiety in 1-butanol.⁵⁸ It is blue-shifted from the OH peak in neat 1-butanol indicating that some of the OH groups begin to associate with the P=O group of TBP versus other OH groups in 1-butanol. The blue-shift may indicate the strength of the interaction is weaker as steric effects from the bulky butyl groups are forcing the interactions between the OH and P=O groups over larger distances. Both proton-NMR (Fig. S5 in the ESI†) and phosphorus-31 NMR (Fig. S6 in the ESI†) data support the notion that the OH and P=O groups are interacting and causing electron density perturbations as the ¹H NMR data indicate an upfield chemical shift for the OH proton⁵⁸ with increasing TBP concentration, and, in contrast, the ³¹P NMR data show a downfield chemical shift for the ³¹P with increasing TBP concentration.^59,60

Fig. 6 The k-spectra for the binary mixtures of TPB:1-butanol in the region of the (a) P=O stretching region from 1310–1220 cm⁻¹ (7.6–8.2 μm) and (b) O–H stretching region from 3600–3030 cm⁻¹ (2.8–3.3 μm). The experimental data are plotted as solid lines, and the theoretical predictions (based on eqn (2)) are plotted as dashed lines.

C. Comparison of the mixing rules

To assess if any of the three mixing rules yield better predictive capabilities for the n and k values for the binary mixtures, the root mean square error (RMSE) between the modeled and measured data was calculated⁶¹ and is plotted in Fig. 7. The dashed lines show the RMSE values for mixtures of TBP:n-dodecane, and the solid lines represent the values for TBP:1-butanol. A lower RMSE indicates better agreement between the simulated and measured data, i.e. better accuracy.

Fig. 7 The RMSE values between the measured and calculated index values using the three methods for binary mixtures of TBP:n-dodecane (dashed lines) and TBP:1-butanol (solid lines) are shown as a function of volume percent for the (a) n-values and (b) k-values.

For both binary mixtures, all three approaches show similar agreement although Fig. 7b shows a slight edge in accuracy for the k-values using the L–L method for TBP:1-butanol and the Arago–Biot method for TBP:n-dodecane (except for the 92 : 8 mixture). As seen in Fig. 7, the RMSEs for n and k are lower for TBP:n-dodecane with RMSE values below 0.003 and 0.002, respectively, for all mixtures except for the mixture with the highest percentage of n-dodecane. The RMSE generally increases as the volume percentage of dodecane increases. On the other hand, for TBP:1-butanol mixtures, the RMSE for both n and k is highest for the 56 : 44 mixture peaking at 0.012 and 0.005 for n and k, respectively.

D. Spectral deconvolution of the isolated and interacting components in a binary mixture

In this section, we seek to quantify the influence of intermolecular interactions on the measured k-spectra of the various binary mixtures considered in this study. Such interactions can influence a variety of molecular properties (e.g., bond lengths, reduced masses, effective charges, force constants),⁶² which can manifest in the measured spectra as variations in transition frequencies and absorption intensities. In order to quantify these interactions, the observed spectral bands were partitioned into discrete populations assignable as either isolated or interacting liquids. The utility of this approach is that the population of isolated liquids represents the fraction of the measured spectra most consistent with the simulations generated by the three models (eqn (2)–(4)), which do not explicitly account for intermolecular interactions. Conversely, the population of interacting liquids represents the portion of the measured spectra that should deviate from model predictions. To simplify this process, the analysis was limited to bands unique to either of the two binary components (i.e., present in the neat spectra of one but not the other). The ratio of each population can then be deduced as a function of the volume fraction of the reference component (i.e., the component producing the absorption band). To undertake this approach, we first develop a simple physical model.

A binary mixture of liquids, composed of components x₁ and x₂, can be modeled by a simple equilibrium expression, x₁ + x₂ ⇋ x₁::x₂. This modest description suggests that there exist discrete populations of each component that can be assigned as being effectively isolated (i.e., x₁ and x₂, which behave like the neat liquid samples), as well as a population for which the two components are interacting with one another (i.e., x₁::x₂). Note that this simple model ignores self-interactions (i.e., consisting of two or more of the same molecules interacting with each other), as the primary interest here is in distinguishing binary mixtures from neat samples. This is not to suggest that self-interactions are not occurring in these mixtures. Rather, for the interacting population, we are solely concerned with cross-component interactions as these lead to spectral perturbations relative to the neat samples. Self-interactions, on the other hand, are already contained within the neat spectra and are hence already accounted for in each of the three models. We first consider the hydrogen bonding interaction in the P=O stretch of TBP for binary mixtures with 1-butanol. Based upon the above equilibrium model, the k-spectra depicted in Fig. 6a can be described as a convolution of two distinct vibrational bands: (1) a band resembling the P=O stretch of neat TBP and (2) a frequency and intensity perturbed band that is characteristic of the intermolecular interactions between TBP and 1-butanol. Note that neat 1-butanol (Fig. 6a, purple trace) does not exhibit measurable vibrational transitions over this wavelength range. Consequently, the TBP::1-butanol intermolecular interaction band can be deduced as a perturbation to the P=O spectrum of neat TBP.

Specifically, it is feasible to deconvolute the measured k-spectra and isolate the individual components by subtracting out an intensity scaled copy of the neat TBP P=O stretch band. This analysis was done iteratively with the constraints that the scaled TBP fraction is maximized, and the intensity profile of the resulting difference spectrum remains positive over the entire wavelength range. The rationale for maximizing the TBP fraction is two-fold: (1) the spectral band predominantly originates from TBP (i.e., it is not present in the neat 1-butanol spectrum) and (2) without some constraint, there exists an infinite combination of band shapes which could sum together to produce the measured signal. The remaining spectral features can then be assigned as the vibrational band of the TBP::1-butanol intermolecular interaction complex. Fig. 8a depicts a representative deconvolution of the measured k-spectrum for the 75 : 25 mixture of TBP : 1-butanol (solid orange line) into an isolated TBP band (dashed black line) and a TBP::1-butanol complex band (dashed green line).

Fig. 8 Spectral deconvolution of measured k-spectra into separate populations assignable to either isolated or interacting liquids. The insets depict the relative fraction of the deconvoluted populations plotted as a function of the volume fraction of the reference component. (a) P=O stretch of TBP in a 75 : 25 TBP : 1-butanol mixture. (b) O–H stretch of 1-butanol in a 56 : 44 TBP : 1-butanol mixture. (c) P=O stretch of TBP in a 55 : 45 TBP : n-dodecane mixture. (See Fig. S3 in ESI† for plots of the other volume fractions.)

The deconvoluted spectral bands (Fig. 8a) are useful in that they permit an assessment of the concentration dependence (volume fraction) for which the deduced populations transition between isolated (neat) liquids and interacting liquids. Specifically, deconvolution analysis was performed for each of the binary mixtures in Fig. 6a (Fig. S3a in ESI†) and the relative fractions of the isolated (black dots) and interacting populations (green dots) were plotted as a function of the TBP volume fraction (Fig. 8a, inset). These trends were then fit to power functions in order to estimate continuous trends. As a basis for comparison, we then defined the quantity Γ₅₀ as the volume fraction of the reference component for which the intensity of the measured absorption band is composed of equal parts of the isolated and interacting populations. For mixture ratios above Γ₅₀, the absorption band is dominated by the isolated population and should be reasonably well described by the three mixing rules. Conversely, for mixture ratios below Γ₅₀, the absorption band will be dominated by the interacting population and will have a greater propensity to deviate from model predictions. As depicted in the inset of Fig. 8a, for the binary mixture of TBP:1-butanol, the P=O stretch of TBP can be characterized with a Γ₅₀ of 78%. This suggests that, except for high volume ratios of TBP (≥78%), the measured TBP P=O stretch absorption will be dominated by the hydrogen bonding interaction and will therefore tend to deviate from model predictions.

Similar analysis was performed on the O–H stretch of 1-butanol for the TBP:1-butanol mixtures depicted in Fig. 6b. Whereas the P=O stretch acts as a reporter for TBP, the O–H stretch provides a complementary measure of the hydrogen bonding interaction from the perspective of 1-butanol. As stipulated above, neat TBP (Fig. 6b, black line) does not exhibit measurable vibrational transitions over this wavelength range. Consequently, the TBP::1-butanol intermolecular interaction band can likewise be deduced as a perturbation to the O–H band of neat 1-butanol. Fig. 8b depicts a representative deconvolution of the O–H stretch of 1-butanol in the 56 : 44 mixture of TBP:1-butanol (solid green line) into an isolated 1-butanol band (dashed black line) and a TBP::1-butanol complex band (dashed blue line). Similar deconvolution analysis was performed for each of the binary mixtures in Fig. 6b (see Fig. S3b in ESI†). The relative fractions of the isolated (black dots) and interacting populations (blue dots) were then plotted as a function of the 1-butanol volume fraction (Fig. 8b, inset). The trends were fit to power functions and Γ₅₀ for the O–H stretch of 1-butanol (in a TBP:1-butanol binary mixture) was deduced as 47%. As noted above, this suggests that, except for high volume ratios of 1-butanol (≥47%), the O–H stretch absorption is dominated by the hydrogen bonding interaction with the P=O group in TBP. Given the complementary nature of these interactions (i.e., both TBP and 1-butanol contribute to the intermolecular interaction), it is initially surprising that the Γ₅₀ values are not more similar. This disparity could stem from several possibilities, including differences in hydrogen bonding-induced changes in absorption cross sections (which may well differ for phosphates and hydroxyl groups) or even different stoichiometric ratios of the components involved in the interaction. Thermodynamically, this could result from the fact that unlike TBP, 1-butanol is capable of self-hydrogen bonding. Consequently, while mixing of TBP and 1-butanol is certainly going to be entropically favorable, the process of breaking 1-butanol hydrogen bonds and forming TBP:1-butanol hydrogen bonds may be enthalpically hindered. We plan to further explore this possibility in future temperature dependent studies. In general, this observation suggests that the influence of hydrogen bonding on an absorption feature is likely dependent upon the specifics of the intermolecular interaction, including the strength of the interaction and the fraction of molecules involved in the interaction complex. Further, it is worth emphasizing that both TBP and 1-butanol exhibit reasonably high Γ₅₀ values (≥47%), indicating that hydrogen bonding significantly alters absorption bands that are susceptible to these types of interactions.

Finally, in addition to hydrogen bonding, other van der Waals based interactions in binary mixtures of TBP and n-dodecane were also analyzed. Due to the concurrent presence of C–H bonds in both TBP and n-dodecane, we chose not to analyze the C–H stretch bands (Fig. 3b) and instead focused on the P=O stretch of TBP (Fig. 3a). Similar to the hydrogen bonding interaction discussed above, the k-spectra depicted in Fig. 3a can be described as a convolution of vibrational bands: (1) a band resembling the P=O stretch of neat TBP and (2) a perturbed band that is characteristic of the various van der Waals interactions between TBP and n-dodecane. Similar to 1-butanol, n-dodecane (Fig. 3a, purple line) does not exhibit measurable vibrational transitions over this wavelength range. Consequently, the TBP::n-dodecane intermolecular interaction band can be deduced as a perturbation to the P=O spectrum of neat TBP. Fig. 8c depicts a representative deconvolution of the P=O stretch of TBP in the 55 : 45 mixture of TBP : n-dodecane (solid green line) into an isolated TBP band (dashed black line) and a TBP::n-dodecane complex band (dashed blue line). Deconvolution analysis was performed for each of the binary mixtures in Fig. 3a (see Fig. S3c in ESI†). The relative fractions of the isolated (black dots) and interacting populations (blue dots) were then plotted as a function of the TBP volume fraction (Fig. 8c, inset). The trends were fit to power functions and Γ₅₀ for the P=O stretch of TBP (in the TBP:n-dodecane binary mixture) was deduced as 1.5%. As detailed above, this suggests that the P=O stretch of TBP will almost always resemble the neat liquid. It is only for extremely low volume ratios of TBP (≤1.5%) that van der Waals interactions between the binary components dominate the absorption band. This is in stark contrast to the influence of the hydrogen bonding interactions (Fig. 8a and b), for which the intermolecular interaction complex dominates the measured spectra for TBP (1-butanol) volume fractions below ca. 50%. These observations nicely account for the fact that the three mixing rules (eqn (2)–(4)) do an excellent job of predicting the k-spectra of binary mixtures exhibiting only isotropic interactions (e.g., dispersion), but a less satisfactory job for binary mixtures capable of anisotropic interactions (e.g., hydrogen bonding) as they have a greater propensity to perturb the spectra.

E. Modeling the reflectance spectra using calculated index values of mixtures

In situations where liquid layers are optically thin enough that light interacts with both the liquid layer and substrate, the complex index of refraction data along with accurate optical models to describe the phenomena can be used to successfully identify unknown liquids on various substrates. Using the derived n and k vectors, for example, the reflectance spectra of thin films of liquids on a substrate such as aluminum can be computed.¹⁹ In this section, we have made initial attempts at modeling more complex systems such as binary mixtures in which these synthetic spectra could be used to populate the members of a spectral library using a range of mixing ratios, layer thicknesses and substrates to account for various combinations that may be present in the experimental data.

To examine how the differences in the computed optical constants will impact the synthetic reflectance spectra, ray tracing models of both binary mixtures were constructed and reflectance versus wavelength (wavenumber) computed using the simplest model, i.e., eqn (2) (Arago–Biot). These computed results were compared to reflectance spectra generated using the experimentally measured n and k values for the binary mixture, and the RMSE was calculated to determine the predictive capability for the computed spectra using just the optical constants for the neat liquids. For this work, TracePro⁶³ was used to model the mixture(s) on a substrate of aluminum. A profile view of a 1 μm layer of a binary liquid mixture is given below in Fig. 9 to illustrate the cumulative effect of absorption in the thin film as well as reflective losses at each film interface.

Fig. 9 Side view of the model illustrating light propagation through a 1 μm layer of a binary mixture atop an aluminum substrate illuminated at 30° angle of incidence at a wavelength of 10 μm. The ray colors denote relative intensity of the light as it traverses the thin film structure, with red symbolizing the most intense, green, intermediate intensity, and blue, the weakest intensity. The arrows denote the direction of light propagation.

The reflectance spectra were modeled for both (a) a 55 : 45 mixture of TBP : n-dodecane and (b) a 56 : 44 mixture of TBP : 1-butanol applied to an aluminum substrate with a 1 μm layer thickness. Fig. 10 shows the results of the modeled reflectance spectra using the complex index of refraction values that were either measured (black trace) or mathematically computed using the Arago–Biot method of eqn (2) (red trace). As illustrated by the residuals in the bottom panels of Fig. 10a, excellent agreement is observed for the thin film of TBP:n-dodecane using calculated n and k values when compared to measured index of refraction values (RMSE is 0.004). On the other hand, Fig. 10b shows higher residuals for the modeled reflectance for the thin film of TBP:1-butanol on aluminum. The RMSE increases by a factor of six to 0.024 due to the cross-interactions between TBP and 1-butanol, which impact the optical constants as seen in Fig. 5. As expected, the largest errors for TBP:1-butanol appear in the OH stretching region at 3449 and 3264 cm⁻¹ and the P=O stretching region at 1283 and 1246 cm⁻¹ due to frequency shifts induced by the interaction between the TBP and 1-butanol molecules.

Fig. 10 Results of modeling a 1 μm layer on an aluminum substrate of a (a) 55 : 45 mixture of TBP : n-dodecane and a (b) 56 : 44 mixture of TBP : 1-butanol. Bottom panels show the residual error between the modeled spectra using measured n and k values (black trace) vs. using n and k values computed (red trace) by the method of Arago–Biot (eqn (2)).

IV. Discussion

This paper examined the influence of intermolecular interactions on the complex refractive index of binary mixtures in the infrared spectral region. Specifically, two representative sets of binary mixtures were considered: (1) TBP and n-dodecane, for which only dispersion and dipole–induced dipole intermolecular interactions were possible between the two components and (2) TBP and 1-butanol, for which dipole–dipole interactions, including hydrogen bonding, were also feasible. In addition to measured spectral components, the binary mixtures were simulated using three established mixing models (eqn (2)–(4)). It was reasoned that intermolecular interactions such as hydrogen-bonding, in which the geometry of the interaction is restricted by the orientation of the permanent dipoles in the two components, should result in significant perturbations in the measured spectra (particularly for the functional groups involved in the interaction) and hence deviations from the predicted spectra. Conversely, the geometry of intermolecular interactions resulting from an induced dipole (i.e., dispersion forces) is not limited and were predicted to have little to no influence on either the measured or modeled spectra.

Indeed, as evidenced by lower residuals (Fig. 2 and 5) and lower RMSE values (Fig. 7), overall better agreement with the three models was achieved with TBP:n-dodecane compared to TBP:1-butanol. For example, the RMSE of the k-values for all TBP:n-dodecane mixtures and methods was consistently below 0.002 (Fig. 7b). This low RMSE was only achieved for the TBP:1-butanol mixture with the highest percentage of TBP (i.e., 88 : 12, Fig. 7b), indicating that TBP and 1-butanol have intermolecular interactions that lead to larger deviations, including frequency shifts. Further, it is worth noting that all three models (eqn (2)–(4)) produced remarkably similar results (Fig. 7), with only slight differences, indicating that any of the three expressions could be used, as long as intermolecular interactions do not lead to significant perturbations.

It is also of interest to note the characteristic trends of the deduced errors at higher TBP concentrations. For the TBP:n-dodecane mixtures (no cross dipole–dipole interactions), the RMSE values were shown to increase almost monotonically as the percentage of TBP decreased (Fig. 7). In general, this appears to suggest that each of the three methods is better at simulating TBP spectra compared to n-dodecane (i.e., the errors increased as the spectra became more characteristic of n-dodecane). Lower RMSE values were also observed for the TBP:1-butanol mixtures preferentially enriched with TBP. If we consider the specific self-intermolecular interactions at play in these systems, n-dodecane which is a non-polar molecule, exhibits dispersion interactions (i.e., no dipole–dipole) whereas 1-butanol is polar and capable of hydrogen bonding (dipole–dipole). Tributyl phosphate is capable of both dipole–dipole and dispersion interactions and has the highest boiling point of the three liquids, indicating it has the strongest intermolecular forces. Since higher concentrations of both n-dodecane and 1-butanol lead to larger errors from the models, the addition of TBP appears to have a bigger impact on the mixture properties (and hence the cross-intermolecular interactions) than either the addition of n-dodecane or 1-butanol. Due to the strong intermolecular interactions in neat TBP, a larger concentration of 1-butanol is required before most of these interactions are disrupted. Perhaps more interesting, however, is the behavior of the 56 : 44 mixture of TBP:1-butanol. For this mixture, which corresponds to when the sample is roughly equal parts (by volume) TBP and 1-butanol (Fig. 7), the maximum RMSE between the measured and computed n and k spectra is observed. Importantly, for this specific mixture ratio, hydrogen bonding should significantly influence both components in the sample (i.e., the P=O stretch of TBP and the O–H stretch of 1-butanol). Conceptually, as the mixture ratio is decreased in either direction, there should be an increased propensity for the remaining dominant component to behave as an isolated (rather than interacting) liquid. Given that none of the three models explicitly considers intermolecular interactions between the two components, it is therefore reasonable that the approximately 50 : 50 mixture (i.e., for which cross-component H-bonding should be maximally occurring) should exhibit the greatest RMSE.

As depicted in Fig. 2 and 5, intermolecular interactions are shown to measurably influence the spectra of binary mixtures. Dispersion forces were shown to have minimal impact on the spectra of binary mixtures (Fig. 3), whereas dipole–dipole interactions (e.g., hydrogen-bonding) resulted in significant perturbations in the spectral regions that are impacted by these forces (Fig. 6). For example, in TBP, the phosphoryl oxygen (P=O) is a H-acceptor, so the addition of 1-butanol can lead to H-bonding between the phosphoryl oxygen and the hydroxyl group. Since the OH moiety in 1-butanol can be either a H-donor or H-acceptor, self-association via H-bonding also occurs in neat 1-butanol. Due to disruption of the H-bonding between 1-butanol molecules from the addition of TBP, a blue-shift is observed for the O–H band at 3300 cm⁻¹ (Fig. 6b). This blue-shift may also indicate the interactions between the O–H and P=O bond occur over larger distances due to steric hindrance from the bulky butyl chains. Investigating smaller alcohols with TBP would help determine if steric hindrance is a contributing factor. In the same way, the introduction of H-bonding between the OH and P=O groups leads to a broad peak that is red-shifted for the P=O band at 1282 cm⁻¹ (Fig. 6a). The change in intermolecular interactions upon mixing causes much more significant spectral alteration for the binary mixtures of TBP and 1-butanol (Fig. 5) compared to mixtures of TBP and n-dodecane (Fig. 3). For binary mixtures of TBP and n-dodecane, only a small blue-shift (up to 5 cm⁻¹ for the 10 : 90 mixture) is observed for the P=O band (Fig. 3a), likely due to dispersion (and possibly dipole–induced dipole) interactions between TBP and dodecane molecules disrupting some of the self-interactions in the neat liquids. These results were supported by the spectral deconvolution analysis presented in Section III.C, which quantified the influence of cross-component intermolecular interactions on the resulting spectra. Specifically, as depicted in Fig. 8, hydrogen bonding between TBP and 1-butanol was shown to dominate the measured spectra for all volume ratios consisting of less than 78% TBP. This is in stark contrast to the binary mixtures of TBP and dodecane which only began to show the influence of cross-component van der Waals interactions (e.g., dispersion or dipole–induced dipole) for extremely dilute volume ratios of TBP (i.e., below 1.5%).

Finally, Section III.D showed that spectral modeling using the three mixing rules is a viable approach for materials that are dominated by dispersion (and weak dipole–induced dipole) forces as these interactions only induce minimal perturbations in the spectra of liquid mixtures. For example, spectral modeling of a thin layer of a 55 : 45 TBP : n-dodecane mixture yielded excellent agreement between the reflectance spectrum calculated using either measured or computed n and k values (Fig. 10a). Larger perturbations were observed for mixtures of TBP:1-butanol, particularly in spectral regions where hydrogen-bonding occurs (Fig. 10b). These results demonstrate the need for improved mixing models which implicitly incorporate intermolecular interactions between the binary components. In the meantime, one potentially viable approach is to simply exclude spectral regions which are strongly influenced by such interactions from modeled spectra. For example, for stand-off chemical detection, excluding the OH bands is reasonable as this spectral region is notoriously problematic due to the presence of atmospheric water which hinders detection efforts. As a result, this spectral region is routinely ignored in such analysis. However, such an approach is largely impractical for other spectral regions that are characteristic of the distinct functional groups present in the mixture components and are therefore necessary to help with material identification, such as the P=O bands. For these samples, the only viable path forward is improved models which consider intermolecular interactions between the mixture components.

V. Conclusion

This paper evaluated the validity of computing the optical constants of binary mixtures by using the measured optical constants of the neat constituents along with the volume ratio for the various mixtures. By computing the optical constants of the mixtures, laboratory reference measurements can be drastically reduced by using the computed optical constants to model the synthetic reference spectra of binary mixtures for populating into a spectral library. In particular, three methods of calculating the complex refractive index for binary mixtures were investigated: the method of Arago–Biot (eqn (2)),⁴⁰ the Newton method using relative permittivity (eqn (3))³⁰ and the L–L method (eqn (4)).⁴² Each method was evaluated by calculating the difference between the measured values and the predicted values for both the real and imaginary parts of the index. Using linear combinations of the n and k vectors of the neat substances, the three methods provided similar approximations of the resulting complex index of refraction when compared with measured values of the same mixture ratios using volume fractions to determine both n and k. Additionally, the RMSE between the measured and calculated index values using the three methods for binary mixtures was calculated and plotted for each mixture and no method was found to provide superior results; the simplest method of Arago–Biot defined in eqn (2) appears to be adequate to estimate the complex index of refraction of binary liquid mixtures as long as the interactions between the two liquids are dominated by isotropic forces (e.g., dispersion) rather than anisotropic (dipole–dipole) interactions.

The largest differences between the calculated and measured spectra were seen in regions where cross-intermolecular interactions, particularly H-bonding, occur. Good agreement is achieved for both mixtures in regions with ideal mixing behavior, but regions that are affected by dipole–dipole interactions, particularly H-bonding, need to be accounted for in the modeling. Modeling these interactions using e.g., effective medium models,⁶⁴ will be a future area of study.

Author contributions

The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank our sponsors for support of this work. Pacific Northwest National Laboratory (PNNL) is operated by Battelle Memorial Institute for the Department of Energy (DOE) under Contract DE-AC05-76RL01830.

References

1. K. Kitazato, R. E. Milliken, T. Iwata, M. Abe, M. Ohtake, S. Matsuura, T. Arai, Y. Nakauchi, T. Nakamura, M. Matsuoka, H. Senshu, N. Hirata, T. Hiroi, C. Pilorget, R. Brunetto, F. Poulet, L. Riu, J.-P. Bibring, D. Takir, D. L. Domingue, F. Vilas, M. A. Barucci, D. Perna, E. Palomba, A. Galiano, K. Tsumura, T. Osawa, M. Komatsu, A. Nakato, T. Arai, N. Takato, T. Matsunaga, Y. Takagi, K. Matsumoto, T. Kouyama, Y. Yokota, E. Tatsumi, N. Sakatani, Y. Yamamoto, T. Okada, S. Sugita, R. Honda, T. Morota, S. Kameda, H. Sawada, C. Honda, M. Yamada, H. Suzuki, K. Yoshioka, M. Hayakawa, K. Ogawa, Y. Cho, K. Shirai, Y. Shimaki, N. Hirata, A. Yamaguchi, N. Ogawa, F. Terui, T. Yamaguchi, Y. Takei, T. Saiki, S. Nakazawa, S. Tanaka, M. Yoshikawa, S. Watanabe and Y. Tsuda, The Surface Composition of Asteroid 162173 Ryugu from Hayabusa2 Near-Infrared Spectroscopy, Science, 2019, 364(6437), 272–275.
2. B. H. N. Horgan, R. Anderson, G. Dromart, E. S. Amador and M. S. Rice, The Mineral Diversity of Jezero Crater: Evidence for Possible Lacustrine Carbonates on Mars, Icarus, 2020, 339, 113526.
3. T. D. Brandt and D. S. Spiegel, Prospects for Detecting Oxygen, Water, and Chlorophyll on an Exo-Earth, Proc. Natl. Acad. Sci. U. S. A., 2014, 111(37), 13278–13283.
4. Y. Huang, C. K. C. Lee, Y.-S. Yam, W.-C. Mok, J. L. Zhou, Y. Zhuang, N. C. Surawski, B. Organ and E. F. C. Chan, Rapid Detection of High-Emitting Vehicles by On-Road Remote Sensing Technology Improves Urban Air Quality, Sci. Adv., 2022, 8(5), eabl7575.
5. R. E. C. Pabón, C. R. de Souza Filho and W. J. d de Oliveira, Reflectance and Imaging Spectroscopy Applied to Detection of Petroleum Hydrocarbon Pollution in Bare Soils, Sci. Total Environ., 2019, 649, 1224–1236.
6. T. Rasheed, M. Bilal, F. Nabeel, M. Adeel and H. M. N. Iqbal, Environmentally-Related Contaminants of High Concern: Potential Sources and Analytical Modalities for Detection, Quantification, and Treatment, Environ. Int., 2019, 122, 52–66.
7. J. Li, Z. Yu, Z. Du, Y. Ji and C. Liu, Standoff Chemical Detection Using Laser Absorption Spectroscopy: A Review, Remote Sens., 2020, 12(17), 2771.
8. R. Lowry, D. A. Huppler and C. R. Anderson, Data Base Development and Search Algorithms for Automated Infrared Spectral Identification, J. Chem. Inf. Comput. Sci., 1985, 25(3), 235–241.
9. J. B. Loudermilk, D. S. Himmelsbach, F. E. Barton and J. A. Haseth, Novel Search Algorithms for a Mid-Infrared Spectral Library of Cotton Contaminants, Appl. Spectrosc., 2008, 62(6), 661–670.
10. O.-W. Lau, P.-K. Hon and T. Bai, A New Approach to a Coding and Retrieval System for Infrared Spectral Data: The ‘Effective Peaks Matching’ Method, Vibr. Spectrosc., 2000, 23(1), 23–30.
11. T. J. Johnson, L. T. M. Profeta, R. L. Sams, D. W. T. Griffith and R. L. Yokelson, Infrared Spectral Database for Detection of Gases Emitted by Biomass Burning, Vib. Spectrosc., 2010, 53(1), 97–102.
12. A. M. Baldridge, S. J. Hook, C. I. Grove and G. Rivera, The ASTER Spectral Library Version 2.0, Remote Sens. Environ., 2009, 113(4), 711–715.
13. R. F. Kokaly, R. N. Clark, G. A. Swayze, K. E. Livo, T. M. Hoefen, N. C. Pearson, R. A. Wise, W. M. Benzel, H. A. Lowers, R. L. Driscoll and A. J. Klein, USGS Spectral Library Version 7; 1035, Reston, VA, 2017, p. 68.
14. T. N. Beiswenger, N. B. Gallagher, T. L. Myers, J. E. Szecsody, R. G. Tonkyn, Y. F. Su, L. E. Sweet, T. A. Lewallen and T. J. Johnson, Identification of Uranium Minerals in Natural U-Bearing Rocks Using Infrared Reflectance Spectroscopy, Appl. Spectrosc., 2018, 72(2), 209–224.
15. T. L. Myers, T. J. Johnson, N. B. Gallagher, B. E. Bernacki, T. N. Beiswenger, J. E. Szecsody, R. G. Tonkyn, A. M. Bradley, Y.-F. Su and T. O. Danby, Hyperspectral Imaging of Minerals in the Longwave Infrared: The Use of Laboratory Directional-Hemispherical Reference Measurements for Field Exploration Data, J. Appl. Remote Sens., 2019, 13(3), 034527.
16. J. F. Mustard and J. E. Hays, Effects of Hyperfine Particles on Reflectance Spectra from 0.3 to 25 μm, Icarus, 1997, 125, 145–163.
17. J. E. Moersch and P. R. Christensen, Thermal Emission from Particulate Surfaces: A Comparison of Scattering models with Measured Spectra, J. Geophys. Res.-Planet., 1995, 100(E4), 7465–7477.
18. T. L. Myers, R. G. Tonkyn, T. O. Danby, M. S. Taubman, B. E. Bernacki, J. C. Birnbaum, S. W. Sharpe and T. J. Johnson, Accurate Measurement of the Optical Constants n and k for a Series of 57 Inorganic and Organic Liquids for Optical Modeling and Detection, Appl. Spectrosc., 2018, 72(4), 535–550.
19. B. E. Bernacki, T. J. Johnson and T. L. Myers, Modeling Thin Layers of Analytes on Substrates for Spectral Analysis: Use of Solid/Liquid n and k Values to Model Reflectance Spectra, Opt. Eng., 2020, 59(9), 092005.
20. R. Furstenberg, A. Shabaev, C. Kendziora and R. A. McGill, Measurements and Modeling of Infrared Reflectance Signatures of Microparticle Traces on Surfaces, Opt. Eng., 2020, 59(9), 092010.
21. M. D. Lane, Midinfrared Optical Constants of Calcite and Their Relationship to Particle Size Effects in Thermal Emission Spectra of Granular Calcite, J. Geophys. Res.-Planet., 1999, 104(E6), 14099–14108.
22. T. L. Myers, C. S. Brauer, Y.-F. Su, T. A. Blake, R. G. Tonkyn, A. B. Ertel, T. J. Johnson and R. L. Richardson, Quantitative Reflectance Spectra of Solid Powders as a Function of Particle Size, Appl. Opt., 2015, 54(15), 4863–4875.
23. J. L. Lansford and D. G. Vlachos, Infrared Spectroscopy Data- and Physics-Driven Machine Learning for Characterizing Surface Microstructure of Complex Materials, Nat. Commun., 2020, 11(1), 1513.
24. O. S. Heavens, Optical Properties of Thin Films, Rep. Prog. Phys., 1960, 23(1), 1–65.
25. H. A. Macleod, Thin-Film Optical Filters, Institute of Physics, Bristol, 3rd edn, 2001.
26. C.-S. Chen, Y. Li and C. W. Brown, Searching a Mid-Infrared Spectral Library of Solids and Liquids with Spectra of Mixtures, Vib. Spectrosc., 1997, 14(1), 9–17.
27. F. Grillini, J.-B. Thomas and S. George, Comparison of Imaging Models for Spectral Unmixing in Oil Painting, Sensors, 2021, 21(7), 2471.
28. M. N. Hossain, M. M. H. Rocky and S. Akhtar, Density, Refractive Index, and Sound Velocity for the Binary Mixtures of Tri-n-Butyl Phosphate and n-Butanol Between 303.15 K and 323.15 K, J. Chem. Eng. Data, 2016, 61(1), 124–131.
29. N. An, B. Zhuang, M. Li, Y. Lu and Z.-G. Wang, Combined Theoretical and Experimental Study of Refractive Indices of Water–Acetonitrile–Salt Systems, J. Phys. Chem. B, 2015, 119(33), 10701–10709.
30. T. M. Aminabhavi, L. Manjeshwar, R. Balundagi and S. Halligudi, Thermodynamic & Optical Studies on Binary Liquid Mixtures, Indian J. Chem. A, 1988, 27A(9), 303–307.
31. T. M. Aminabhavi, Use of Mixing Rules in the Analysis of Data for Binary Liquid Mixtures, J. Chem. Eng. Data, 1984, 29(1), 54–55.
32. G. Baranović, Refractive Index Mixing Rules and Excess Infrared Spectra of Binary Mixtures, Appl. Spectrosc., 2017, 71(5), 1039–1049.
33. J. E. Bertie and Z. Lan, Liquid Water−Acetonitrile Mixtures at 25 °C:  The Hydrogen-Bonded Structure Studied through Infrared Absolute Integrated Absorption Intensities, J. Phys. Chem. B, 1997, 101(20), 4111–4119.
34. M. Basu, T. Samanta and D. Das, Volumetric and Acoustic Properties of Binary Mixtures of Tri-n-Butyl Phosphate with n-Hexane, Cyclohexane, and n-Heptane from T = (298.15 to 323.15)K, J. Chem. Thermodyn., 2013, 57, 335–343.
35. H. L. Liu, S. J. Liu, Z. L. Xiao, Q. Y. Chen and D. W. Yang, Excess Molar Enthalpies of Binary Mixtures for (Tributyl Phosphate + Methanol/Ethanol) at 298.15 K, J. Therm. Anal. Calorim., 2006, 85(3), 541–544.
36. T. G. Mayerhöfer and J. Popp, Beyond Beer's Law: Spectral Mixing Rules, Appl. Spectrosc., 2020, 74(10), 1287–1294.
37. M. A. Strauss and H. A. Wegner, London Dispersion in Alkane Solvents, Angew. Chem., Int. Ed., 2021, 60(2), 779–786.
38. Physical Constants of Organic Compounds, in CRC Handbook of Chemistry and Physics, ed. Haynes, W. M., CRC Press, Boca Raton, FL, 96th edn, 2015, pp. 3–78, 3-236, and 3-518.
39. S. Cui, V. F. de Almeida and B. Khomami, Molecular Dynamics Simulations of Tri-n-butyl-phosphate/n-N-dodecane Mixture: Thermophysical Properties and Molecular Structure, J. Phys. Chem. B, 2014, 118(36), 10750–10760.
40. J. C. R. Reis, I. M. S. Lampreia, Â. F. S. Santos, M. L. C. J. Moita and G. Douhéret, Refractive Index of Liquid Mixtures: Theory and Experiment, ChemPhysChem, 2010, 11(17), 3722–3733.
41. J. C. R. Reis, T. P. Iglesias, G. Douhéret and M. I. Davis, The Permittivity of Thermodynamically Ideal Liquid Mixtures and the Excess Relative Permittivity of Binary Dielectrics, Phys. Chem. Chem. Phys., 2009, 11(20), 3977–3986.
42. W. Heller, Remarks on Refractive Index Mixture Rules, J. Phys. Chem., 1965, 69(4), 1123–1129.
43. J. E. Bertie and S. L. Zhang, Infrared Intensities of Liquids. IX. The Kramers–Kronig Transform, and Its Approximation by the Finite Hilbert Transform via Fast Fourier Transforms, Can. J. Chem., 1992, 70(2), 520–531.
44. J. E. Bertie and H. H. Eysel, Infrared Intensities of Liquids I: Determination of Infrared Optical and Dielectric Constants by FT-IR Using the CIRCLE ATR Cell, Appl. Spectrosc., 1985, 39(3), 392–401.
45. J. E. Bertie, S. L. Zhang and C. D. Keefe, Measurement and Use of Absolute Infrared Absorption Intensities of Neat Liquids, Vib. Spectrosc., 1995, 8(2), 215–229.
46. S. W. Sharpe, T. J. Johnson, R. L. Sams, P. M. Chu, G. C. Rhoderick and P. A. Johnson, Gas-Phase Databases for Quantitative Infrared Spectroscopy, Appl. Spectrosc., 2004, 58(12), 1452–1461.
47. OPUS, Version 5.5, Bruker Optik GmbH, Ettlingen, 2004.
48. J. E. Bertie, John Bertie's Download Sitehttps://sites.ualberta.ca/~jbertie/JBDownload.HTM (downloaded 6 Nov 2020).
49. J. E. Bertie, C. D. Keefe and R. N. Jones, Infrared Intensities of Liquids VIII. Accurate Baseline Correction of Transmission Spectra of Liquids for Computation of Absolute Intensities, and the 1036 cm^-1 Band of Benzene as a Potential Intensity Standard, Can. J. Chem., 1991, 69(11), 1609–1618.
50. T. L. Myers, R. G. Tonkyn, J. S. Loring, A. M. Oeck, C. A. Banach, R. M. Francis, Y.-F. Su and T. J. Johnson, Accurate Optical Constants for Liquids in the Near-infrared: Improved Methods for Obtaining the n and k Constants from 1 to 4 μm, Proc. SPIE, 2019, 11010, 110100O.
51. B. Tatian, Fitting Refractive-Index Data with the Sellmeier Dispersion Formula, Appl. Opt., 1984, 23(24), 4477–4485.
52. K. Nukada, N. Keiji and M. Utako, On the Mechanism of the Extraction of Uranyl Nitrate by Tributyl Phosphate II. Infrared Study, Bull. Chem. Soc. Jpn., 1960, 33(7), 894–898.
53. Q. Li, N. Wang, Q. Zhou, S. Sun and Z. Yu, Excess Infrared Absorption Spectroscopy and its Applications in the Studies of Hydrogen Bonds in Alcohol-Containing Binary Mixtures, Appl. Spectrosc., 2008, 62(2), 166–170.
54. L. George, K. Sankaran, K. S. Viswanatha and C. K. Mathews, Matrix-Isolation Infrared Spectroscopy of Organic Phosphates, Appl. Spectrosc., 1994, 48(1), 801–807.
55. K. K. Gorai, A. Shastri, P. J. Singh and S. N. Jha, Experimental and Theoretical Studies On the Absorption Spectra of n-Dodecane in the IR and VUV Regions, J. Quant. Spectrosc. Radiat. Transf., 2019, 236, 106582.
56. G. A. Crowder and M. J. Townsend, Vibrational Spectra of 1-Butanol, J. Mol. Struct., 1977, 42, 27–30.
57. K. Ohno, H. Yoshida, H. Watanabe, T. Fujita and H. Matsuura, Conformational Study of 1-Butanol by the Combined Use of Vibrational Spectroscopy and ab Initio Molecular Orbital Calculations, J. Phys. Chem., 1994, 98(28), 6924–6930.
58. R. Joshi and S. P. Pasilis, The Effect of Tributylphosphate and Tributyl Phosphine Oxide on Hydrogen Bonding Interactions Between Water and the 1-Ethyl-3-methylimidazolium Cation in 1-Ethyl-3-methylimidazolium bis(Trifluoromethylsulfonyl)imide, J. Mol. Liq., 2015, 209, 381–386.
59. R. Streck and A. J. Barnes, Solvent Effects on Infrared, ¹³C and ³¹P NMR Spectra of Trimethyl Phosphate, Spectrochim. Acta, Part A, 1999, 55(5), 1059–1076.
60. V. I. S. Giba, V. V. Mulloyarova, G. S. Denisov and P. M. Tolstoy, Sensitivity of ³¹P NMR Chemical Shifts to Hydrogen Bond Geometry and Molecular Conformation for Complexes of Phosphinic Acids with Pyridines, MRC, 2021, 59(4), 465–477.
61. Mathematica, ver. 12.2, Wolfram Research Inc., Champaign, IL, 2020.
62. D. J. Skrovanek, S. E. Howe, P. C. Painter, M. Michael and M. M. Coleman, Hydrogen Bonding in Polymers: Infrared Temperature Studies of an Amorphous Polyamide, Macromolecules, 1986, 18, 1676–1683,  DOI:10.1021/ma00151a006.
63. TracePro, Lambda Research Corporation, Littleton, MA, 2020.
64. J. W. Zhou and M. H. Arbab, Effective Debye Relaxation Models for Binary Solutions of Polar Liquids at Terahertz Frequencies, Phys. Chem. Chem. Phys., 2021, 23(7), 4426–4436.

---

Footnote

† Electronic supplementary information (ESI) available: FTIR data collection parameters, the n(λ) and k(λ) spectra for neat TBP, n-dodecane and 1-butanol, the calculated intermolecular interactions, the measured and modeled n-values for mixtures of TBP with n-dodecane and 1-butanol at 10 000 cm⁻¹, ¹H NMR spectra and ³¹P NMR spectra for the TBP:n-butanol mixtures and the spectral deconvolution plots (PDF). See DOI: https://doi.org/10.1039/d2cp02920k

---