Investigating the efficiency of silica materials with wall-embedded nitroxide radicals for dynamic nuclear polarisation NMR

Abstract

Dynamic nuclear polarisation (DNP) can significantly enhance the sensitivity of solid-state nuclear magnetic resonance (SSNMR) experiments by transferring the electron spin polarisation of paramagnetic species to nuclei through microwave irradiation of the sample at cryogenic temperatures. Paramagnetic species required for DNP can be provided in the form of mesoporous silica materials containing nitroxide radicals either located on the porous surface or embedded in the pore walls. The present study focuses specifically on porous materials with wall-embedded radicals that were synthesised using conventional molecular imprinting protocols. More remarkably, by changing the molecular structure of the TEMPO precursor, the theoretical distance between the oxygen atoms in a pair of wall-embedded face-to-face TEMPO radicals was increased stepwise (0.7, 0.9, 1.1, 1.3 and 1.5 nm). The thermal activation of these five series of materials led to 37 TEMPO-functionalised silica materials with different radical concentrations. Their efficiency as DNP polarising agents was subsequently investigated at 9.4 T and ∼110 K under magic-angle spinning conditions (10 kHz) after impregnating them at room temperature with an aqueous solution of isotopically enriched proline. Our results show that the highest DNP efficiency was obtained for the silica materials that exhibited the shortest theoretical oxygen-oxygen distance between the TEMPO rings, suggesting that the design rules accepted for soluble DNP polarising agents may not be transposed to these materials with wall-embedded pairs of nitroxides.

---

Introduction

Dynamic nuclear polarisation (DNP) has become a technique of choice to enhance the sensitivity of NMR experiments.^1,2 In particular, when combined with magic-angle spinning (MAS), DNP can tremendously improve the sensitivity of high-field solid-state NMR (SSNMR) experiments,^3–7 and this has allowed for the detailed structural characterisation of a very broad range of samples, from biomolecular compounds^8–14 to inorganic^15–20 or hybrid materials,^21–24 organic crystals^25–29 and polymers.^30–37 More precisely, DNP enhances nuclear magnetisation through the microwave-driven transfer (usually at cryogenic temperatures) of electron spin polarisation to nuclei via exogenous paramagnetic centres referred to as polarising agents (PA). These polarising agents are stable paramagnetic species (e.g. stable radicals, metal complexes…) used for doping diamagnetic samples in order to provide the source of electron polarisation required for DNP.^38–50 At moderately high magnetic fields (∼10 T) and a temperature of 100 K, the most efficient DNP mechanism so far is the cross-effect (CE).^4,7,51 Briefly, CE DNP is a 3-spin process that involves two coupled electron spins in hyperfine interaction with one nuclear spin. Extensive research efforts over the last few years have led to the design of tailored bisnitroxides with optimised geometry (e.g. electron–electron distance, relative electron g-tensors orientation…) and molecular weight, providing ¹H DNP signal enhancements of >200 in some cases (the maximum theoretical value being ∼660, which is the ratio of the electron to the proton gyromagnetic ratios). The rational design of increasingly efficient PA currently remains an active field of research, especially for targeting higher magnetic fields and higher operating temperatures.^52–59 In all cases, key to the success of any DNP SSNMR experiment is the ability to introduce PA homogeneously in the sample of interest. This is usually performed with a PA-containing solvent that is used to solubilise or to impregnate the sample at room temperature, and which acts as a good glass former at the cryogenic temperatures where DNP SSNMR experiments are subsequently conducted. This is critical to avoid radical aggregation upon freezing, which has a knowingly deleterious effect on DNP efficiency.⁶⁰

In 2013, Copéret and coworkers proposed an inspiring alternative by (post)grafting radicals onto the pores of mesoporous silica materials.⁶¹ Although the homogeneous dispersion of the radicals onto the porous surface was difficult to ensure, and the average electron–electron distances hardly controllable, the so-obtained solid phase matrices were shown to polarise efficiently impregnated molecules without the use of any glass forming solvent, yielding DNP signal enhancements of ∼25 at 9.4 T and ∼100 K. These materials were also shown to provide great perspectives for dissolution DNP in vivo applications.^62,63 Since then, several interesting materials have been introduced in order to homogenously disperse the PA required for the DNP experiments, including covalent organic frameworks,⁶⁴ which allowed DNP signal enhancements of ∼40 to be recorded in ¹H → ¹³C CP MAS experiments at 9.4 T and ∼100 K, or even porous polymers, which proved to have exceptional potential for dissolution DNP applications.⁶⁵ Alternatively, hybrid mesoporous silica materials with wall-embedded 2,2,6,6-tetramethylpiperidine-1-oxyl (TEMPO) precursors have also been proposed.^66,67 The resulting silica materials with wall-embedded nitroxides proved to be reliable polarisation matrices for DNP SSNMR experiments performed on impregnating solutes at 9.4 T and 105 K, both in water and in 1,1,2,2-tetrachloroethane (TCE), overall, this approach has 2 main advantages. First, all radicals are exclusively located in the walls of the silica framework, ensuring that the analytes are not in physical contact with the PA. Second, this approach allows the average theoretical distance between the two TEMPO moieties of a given pair of radicals to be controlled. This property allows us to vary both the total radical concentration in the materials and the inter-radical distance independently, and this remarkable feature forms the basis of the present study. In fact, in our first work, we used a benzylic derivative as the anchorable TEMPO precursor, leading eventually to silica materials with wall-embedded TEMPO radicals exhibiting a theoretical distance between the oxygen atoms of the TEMPO rings of about 0.7 nm.

In this contribution, a range of silica materials with wall-embedded TEMPO radicals have been designed through the use of tailored TEMPO precursors with specific molecular structures. Interestingly, the resulting pairs of wall-embedded, presumably face-to-face TEMPO radicals exhibited theoretical oxygen-oxygen distances ranging from 0.7 to 1.5 nm. Moreover, the total electron concentration in the silica materials varied from 15 to 600 μmol g⁻¹, offering a large set of materials with distinct structural features that were used to carry out DNP MAS experiments with substantial DNP signal enhancement at 9.4 T.

Material and methods

Synthesis

Precursors 1 to 5 were straightforwardly prepared in 3 steps from 5 different benzylic bromides (Scheme 1). After trapping of the benzylic radicals with TEMPOL, the hydroxyl functions were allylated. Finally, a hydrosilylation of the double bonds enabled the introduction of the two triethoxysilyl groups indispensable for the implementation of the sol–gel process by direct synthesis.

Scheme 1 Synthesis of precursors 1 to 5.

2D hexagonal SBA type silicas were prepared by co-condensation of bridged organotriethoxysilanes 1 to 5 with tetraethyl orthosilicate (TEOS) in the presence of P123 (PEO₂₀PPO₇₀PEO₂₀) as structure directing agent (Fig. 1a). The sol–gel process by direct synthesis led to 5 nanostructured silicas with a radical precursor in their framework (SBA₆₃-1, SBA₅₆-2, SBA₅₅-3, SBA₆₀-4, and SBA₆₀-5, where the index n indicates the TEMPO precursor/TEOS molar ratio 1/n determined after the characterization of the hybrid silicas with the thermogravimetric analysis).

Fig. 1 (a) Synthesis of SBA_n-1 to SBA_n-5 and SBA_m-A to SBA_m-E materials. The molecular structures of the 5 distinct spacers considered in this study are reported in (b), together with an estimation of the theoretical distance between the oxygen atoms of the TEMPO rings after thermolysis.

All these silicas were characterized by standard methods (nitrogen adsorption/desorption analysis, SAXS, NMR, thermogravimetric analysis (TGA) (see ESI†)). The main characteristics of these materials are gathered in Table 1. In spite of the size difference between the organic precursors, an excellent homogeneity in the structural features of the functionalized silicas was obtained overall. In fact, only weak differences were observed between pore diameters, surfaces, and pore volumes, which ranged for the whole set of materials from 6.8 to 7.2 nm, 651 to 842 m² g⁻¹, and 1.01 to 1.44 cm³ g⁻¹, respectively. The 2D hexagonal structure of the silicas were evidenced with the XRD patterns of the powders which exhibited three well-resolved diffraction peaks indexed as (100), (110) and (200) reflections.

Table 1 Physico-chemical characteristics of SBA₆₃-1, SBA₅₆-2, SBA₅₅-3, SBA₆₀-4, and SBA₆₀-5

	Precursor (μmol g^−1)	D p (nm)	S BET (m^2 g^−1)	V p (cm^3 g^−1)	d 100 (nm)	a 0 (nm)	Wall thickness (nm)
SBA63-1	454	7.2	651	1.01	11.5	13.3	6.2
SBA56-2	509	6.9	842	1.31	10.4	12.0	5.1
SBA55-3	511	7.1	831	1.44	10.7	12.3	5.2
SBA60-4	472	6.8	657	1.10	10.4	12.0	5.2
SBA60-5	400	7.2	759	1.25	10.4	12.0	4.8

---

The preservation of the carbon skeleton of the radical precursors during the sol–gel process as well as the presence of T₃ sites in the silica materials (proving the covalent bonding of the organic moieties to silica with a Si–C bond) were verified by ¹H → ¹³C and ¹H → ²⁹Si CP MAS NMR experiments.

A 130 °C thermolysis of these starting materials gave rise to 5 main families of silica materials with wall-embedded TEMPO radicals (SBA_m-A, SBA_m-B, SBA_m-C, SBA_m-D, and SBA_m-E, with m the concentration in TEMPO radicals in μmol g⁻¹). The radical concentration of these silica materials was controlled by adjusting the thermolysis time using decomposition kinetics data preliminary established by EPR (see ESI†). The elimination of the spacer through the microporosities of the silica was indirectly evidenced by analysing the materials with the highest loadings by ¹³C SSNMR, which highlighted the disappearance of Csp² signals from the corresponding ¹³C spectra after thermolysis (see ESI†). The radical concentrations of the silica materials after thermolysis were estimated by comparing their EPR signal double integral to that of an analogous SBA silica material whose pores had been functionalised with TEMPO radicals and for which the TEMPO loading was known from thermogravimetric analysis.⁶⁸

DNP MAS SSNMR experiments

All DNP SSNMR spectra were recorded on a Bruker 9.4 T wide-bore magnet (Larmor frequencies: ¹H, 400 MHz; ¹³C, 100 MHz) operated by an AVANCE-III NMR spectrometer and equipped with a Bruker 3.2 mm DNP low-temperature double-resonance ¹H/{²⁹Si–¹³C} MAS probe. In all experiments, the MAS frequency was 10 kHz. Microwave irradiation was applied using a gyrotron connected to the NMR probe (frequency, 263 GHz; power, 4 W). Samples for DNP SSNMR analysis were prepared by impregnating ca. 20 mg of each of the SBA_m silica materials with 40 μL of a 0.2 M H₂O solution of U-¹³C/¹⁵N proline. ¹³C cross-polarisation magic-angle spinning (CPMAS) spectra were recorded on these samples at ca. 105 K with or without microwave field irradiation, and the intensities of the proline NMR signals in the resulting ¹³C CPMAS spectra (I_ON and I_OFF, respectively) were used to calculate the so-called ¹³C CP DNP enhancement (ε_C,CP = I_ON/I_OFF).

EPR experiments

Continuous wave (CW) EPR spectra were recorded on a Bruker Elexsys E500 spectrometer and pulsed EPR spectra were recorded on a Bruker Elexsys E580 spectrometer equipped with a dielectric ring resonator (ER4118X-MD5) and a helium flow cryostat (Oxford CF935). All EPR experiments were either conducted at room temperature on the samples available as powders, or at low temperature (110 K) on the samples impregnated with 1,1,2,2-tretrachlorethane (TCE) in order to be comparable with both DNP operating conditions and literature data. Full details of the EPR experiments are given in ESI.†

Results and discussion

Besides their ability to generate a pair of face-to-face TEMPO moieties, a family of radical precursors was designed to increase in a stepwise fashion the distance between the oxygen atoms of the masked TEMPO rings. Specifically, molecular dynamics simulations were used to select 5 rigid polyaromatic spacers that ultimately led through the use of conventional molecular imprinting techniques to the synthesis of silica materials with wall-embedded nitroxides exhibiting a pairwise oxygen-oxygen distance ranging from ∼0.7 nm to 1.5 nm, with a regular increment of 0.2 nm (Fig. 1a and b). These distances globally encompass the range of electron–electron distances typically found for the most effective bisnitroxides in CE MAS DNP at 9.4 T.

All SBA_m materials were first analyzed by CW EPR (9.4 GHz) at 110 K in the presence of TCE (see Experimental section). In particular, Fig. 2 shows the X-band CW EPR spectrum recorded on SBA₄₃₄-A impregnated with TCE at 110 K. This spectrum displays a typical rigid-limit powder pattern that is characteristic of nitroxides immobilized in a rigid matrix. Interestingly, for all the families of SBA materials, half-field EPR signals of substantial intensity were detected for the samples with high nitroxide concentrations (see ESI†), with a maximum relative value observed for the SBA_m-A samples.

Fig. 2 X-band EPR spectrum of SBA₄₃₄-A impregnated with TCE at 110 K.

Moreover, Fig. 3a shows the DNP enhancement ε_C,CP measured for the 0.2 M water solution of U-¹³C/¹⁵N proline as a function of the radical concentration. It should be noted that no glycerol was added to this proline solution. Overall, the observed trends were essentially equivalent for all the series, showing a DNP efficiency (as expressed herein by ε_C,CP) that globally increased with the radical concentration. Fig. 3a does not indicate, however, any remarkable influence on DNP efficiency of the theoretical distance (upon thermolysis) between the oxygen atoms of the TEMPO rings.

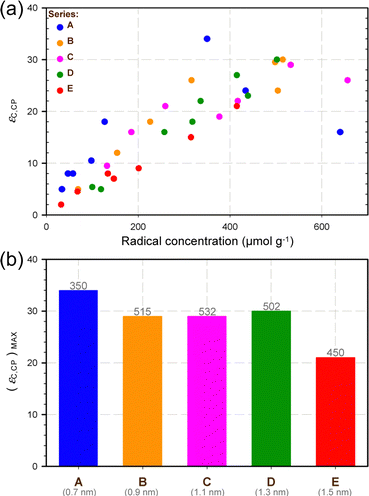Fig. 3 (a) Evolution of the ¹³C CP DNP signal enhancement (ε_C,CP) as a function of the radical concentration for several SBA_m-x samples, where x is A, B, C, D, or E (see Fig. 1). ε_C,CP was measured on the ¹³C resonances of a CPMAS spectrum recorded at ∼105 K on a 0.2 M water solution of U-¹³C/¹⁵N proline. (b) Maximum ε_C,CP value obtained for each of the 5 series of samples considered in this study. The grey numbers reported on top of the coloured bars are the corresponding radical concentrations (expressed in μmol g⁻¹) whereas those reported below the letters indicate the theoretical distances between the oxygen atoms of the TEMPO rings upon thermolysis.

Interestingly, the observation of an approximate bell shape for the curve of the SBA_m-A samples suggests that the shape of all the curves could well be bell-like as well, as is typically observed for these types of optimisations. The range of radical concentrations explored herein, however, was most likely insufficiently large to observe the second (and declining) half of the expected bell-like curves for some of these samples. This is best illustrated by inspecting the trend observed for the SBA_m-E samples with respect to that observed for SBA_m-A samples. We also observed experimentally that the radical concentrations obtained in some cases for the longest thermolysis times were systematically lower than expected (see ESI†). We tentatively attributed this discrepancy to the possible coupling between nitroxide radicals at high concentrations, which artificially decreased the apparent radical concentration measured by EPR (possibly due to magnetic extinction effects). Altogether, the maximum DNP efficiencies observed for the investigated families of samples were somewhat similar (Fig. 3b), except for the SBA_m-E samples (which show a significantly lower maximum ¹³C CP DNP signal enhancement). Precisely, the highest maximum DNP efficiency was observed for the SBA_m-A samples, but the corresponding value (34) remained comparable to those obtained for the SBA_m-B, SBA_m-C, SBA_m-D series (29, 29, and 30, respectively).

In parallel, because DNP efficiency has also been shown to correlate with electron magnetic relaxation properties, pulsed EPR experiments were performed to estimate the electron mean recovery time 〈T_1e〉 of these samples impregnated with TCE at 110 K. 〈T_1e〉 refers to the first moment of the electron T₁ relaxation distribution and describes a mean recovery time (see ESI†).

The data reported in Fig. 4 indicate that the evolution of 〈T_1e〉 as a function of the radical concentration was comparable for all 5 families of samples, with a steep reduction observed between 0 and ∼200 μmol g⁻¹, followed by a rather flat decay for higher concentrations. This graph would suggest a 2-phase behaviour corresponding approximately to radical concentrations between 0 and 200 μmol g⁻¹, and between 200 and 600 μmol g⁻¹. We hypothesized that this could be related to the presence of different types of electron–electron interactions. In fact, because radicals are necessarily generated in a pairwise and presumably face-to-face fashion owing to the synthesis protocol employed herein (i.e. molecular imprinting), one could reasonably assume that the electron–electron interactions that prevail at the lowest radical concentrations are those involving the electrons within a single pair of TEMPO radicals. In contrast, as the radical concentration in the materials increases, the total number of pairs of TEMPO radicals increases as well, and hence the probability that the electrons from different pairs of TEMPO radicals interact with one another becomes more significant. For simplicity, we will hereafter refer to these two possible main regimes of electron–electron interactions as intra-pair and inter-pair regimes, respectively, although it is likely that intra-pair electron–electron interactions may still play a role within the so-called inter-pair regime (as both types of electron–electron interactions can hardly be disentangled from one another). In other words, if one is interested in looking at the effect of the electron–electron distance on DNP efficiency, one should rather focus on the former regime (intra-pair) by inspecting the evolution of the ¹³C CP DNP signal enhancement for all SBA_m samples but restraining the analysis to the lowest radical concentrations (<200 μmol g⁻¹). In that case, as shown in Fig. 5, one can see that, for a given nitroxide concentration, ε_C,CP roughly scales inversely with the electron–electron distance.

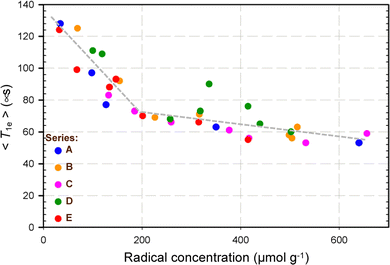Fig. 4 Evolution of the electron mean recovery time 〈T_1e〉 as a function of the radical concentration for several SBA_m-x samples, where x is A, B, C, D, or E (see Fig. 1). 〈T_1e〉 were measured by pulsed EPR at 9.4 GHz on TCE-impregnated samples at 110 K. The dark-grey, short-dashed linear curves of different slopes between 0 and ∼200 μmol g⁻¹, and between ∼200 and ∼600 μmol g⁻¹, respectively, are provided as guides to the eye only.

Fig. 5 Zoom in on the evolution of the ¹³C CP DNP signal enhancement (ε_C,CP) as a function of the radical concentration for several SBA_m-x samples, where x is A, B, C, D, or E (see Fig. 1). The coloured short-dashed curves are linear fits of the corresponding data points and are provided as guides to the eye only.

For instance, at a concentration of about 130 μmol g⁻¹, the ¹³C CP DNP signal enhancement was increased by a factor 3 when the theoretical intra-pair electron–electron distance was divided by 2. Overall, at all radical concentrations, SBA_m-A samples are clearly the most effective, indicating that the shortest theoretical electron–electron distance is key for these types of materials to achieve the highest DNP efficiency. Noteworthily, short electron–electron distances give rise to a strong electron dipolar interaction, which has long been recognised as a key parameter for CE DNP. A simplistic calculation using the theoretical intra-pair electron–electron distances of the herein selected samples yields approximate electron dipolar couplings of 150 MHz, 70 MHz, 40 MHz, 25 MHz, and 15 MHz for the SBA_m-A, SBA_m-B, SBA_m-C, SBA_m-D, and SBA_m-E families, respectively. These values are to be compared with those of rigid bisnitroxides such as AMUPol and TEKPol (ca. 35 MHz and 30 MHz, respectively), some of the best DNP polarising agents to date at 9.4 T and ∼100 K. Such a wide range of theoretical dipolar couplings should have an impact on the EPR spectra of the corresponding samples, especially on the width of the central EPR line that is the most sensitive to the dipolar broadening because it is least broadened by the g-tensor and hyperfine anisotropies. Experimentally, however, we observed that the width of the central line for EPR spectra recorded at 110 K on all TCE-impregnated SBA_m samples displayed a globally similar average broadening of ∼12 G. According to Coperet and co-workers, for isolated radicals on the surface of mesoporous materials, this is consistent with an average inter-radical distance larger than 1.3 nm. This estimate does not match the inter radical distance that can be expected from our SBA_m materials (especially SBA_m-A and SBA_m-B). We do not have any reasonable explanation to this observation at this point. Clearly, we cannot a priori exclude that there could be distributions of electron–electron distances owing to the relative flexibility of the TEMPO radicals tethered to the silica walls, which could in turn give rise to distributions of electron dipolar couplings (the medians of those distributions being invariably lower than the above-mentioned theoretical values). However, because no information is available yet regarding the actual size of the cavities within the silica matrix where the pairs of TEMPO radicals are embedded, it is impossible at this point to estimate their actual relative mobility after thermolysis (once the spacer has been removed), which could be helpful to estimate the amplitude of their respective movements and hence evaluate the corresponding electron–electron distances that would effectively result from these motions. Nevertheless, it still seems rather unlikely that the medians of these distributions would lie very far from the theoretical electron–electron distances predicted by molecular modelling (before thermolysis)

We also recorded the 9.4 GHz CW EPR spectra on the non-impregnated samples at room temperature. Results reported in Fig. 6 show comparable trends for all the SBA_m samples with a linewidth going from ∼6.5 G to ∼11.9 G for the least and the most concentrated samples, respectively. In particular, SBA_m-A samples exhibited the lowest linewidths, especially at radical concentrations lower than 200 μmol g⁻¹ where intra-pair electron–electron interactions supposedly prevail, which is somehow counterintuitive considering that these samples should theoretically display the largest dipolar electron interaction. One possibility to explain these observations could be the presence in these systems of an exchange interaction of significant magnitude, which could contribute to narrow down the measured EPR linewidths. This assumption is somehow coherent with the observation in the EPR CW spectra of these materials of half-field EPR transitions of substantial amplitude, which decrease with increasing e–e distance (see ESI†). Overall, our data suggest that the design rules accepted for soluble PA may not be transposed to these solid, molecular imprinted systems.

Fig. 6 Evolution of the EPR linewidths (Δν_1/2) at room temperature as a function of the radical concentration for several non-impregnated SBA_m-x samples where x corresponds to A, B, C, D, or E. The EPR spectra were recorded at 9.4 GHz. The black dashed line is a guide to the eye.

Conclusion

This study aimed to evaluate a wide range of nanostructured materials as polarising agents for DNP MAS SSNMR. The use of well-established molecular imprinting protocols enabled to modulate the distance between the wall-embedded nitroxides as well as their concentrations in the silica materials. All in all, 37 functionalized mesoporous silicas were tested. The effect of precursor structures was observable on enhancement factors at low radical concentrations. The results showed that the highest DNP efficiency was achieved for the family of materials obtained from the TEMPO precursor with the benzylic derivative, which is expected to yield the shortest distance between the oxygen atoms of the TEMPO rings (with correspondingly strong electron–electron interactions). This would indicate that the design rules accepted for soluble PA might not be transposable to these solid systems. The unexpected EPR observations might be directly related to the polyradical nature of the silicas and the resulting complex electron–electron interactions. Importantly, these silica matrices are useful tools to perform DNP experiments. First, their optimal signal enhancement factors (∼30) allow them to be used for targeted DNP applications, especially for those in aqueous media as no glass forming agent is required here to achieve good DNP signal enhancements.⁶⁹ Second, they could be considered as a platform for studying radical-radical interactions. This, however, requires more in-depth investigations that are underway.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This study has received funding from the Excellence Initiative of Aix-Marseille University – A*Midex, a French “Investissements d’Avenir” programme supported of the A*MIDEX project (no. ANR-11-IDEX-0001-02) funded by the “Investissements d’Avenir”. The authors acknowledge the Agence Nationale de la Recherche for funding (ANR-18-CE29-007). The authors are grateful to the EPRMRS facility of the French Research Infrastructure INFRANALYTICS (FR2054) and the Aix-Marseille University EPR center.

Notes and references

1. A. W. Overhauser, Phys. Rev., 1953, 92, 411–415.
2. T. R. Carver and C. P. Slichter, Phys. Rev., 1953, 92, 212–213.
3. D. A. Hall, D. C. Maus, G. J. Gerfen, S. J. Inati, L. R. Becerra, F. W. Dahlquist and R. G. Griffin, Science, 1997, 276, 930–932.
4. Q. Z. Ni, E. Daviso, T. V. Can, E. Markhasin, S. K. Jawla, T. M. Swager, R. J. Temkin, J. Herzfeld and R. G. Griffin, Acc. Chem. Res., 2013, 46, 1933–1941.
5. A. J. Rossini, A. Zagdoun, M. Lelli, A. Lesage, C. Copéret and L. Emsley, Acc. Chem. Res., 2013, 46, 1942–1951.
6. D. Lee, S. Hediger and G. De Paëpe, Solid State Nucl. Magn. Reson., 2015, 66-67, 6–20.
7. A. S. Lilly Thankamony, J. J. Wittmann, M. Kaushik and B. Corzilius, Prog. Nucl. Magn. Reson. Spectrosc., 2017, 102-103, 120–195.
8. A. N. Smith and J. R. Long, Anal. Chem., 2016, 88, 122–132.
9. M. Kaushik, T. Bahrenberg, T. V. Can, M. A. Caporini, R. Silvers, J. Heiliger, A. A. Smith, H. Schwalbe, R. G. Griffin and B. Corzilius, Phys. Chem. Chem. Phys., 2016, 18, 27205–27218.
10. M. Mehler, C. E. Eckert, A. J. Leeder, J. Kaur, T. Fischer, N. Kubatova, L. J. Brown, R. C. D. Brown, J. Becker-Baldus, J. Wachtveitl and C. Glaubitz, J. Am. Chem. Soc., 2017, 139, 16143–16153.
11. A. N. Smith, K. Märker, T. Piretra, J. C. Boatz, I. Matlahov, R. Kodali, S. Hediger, P. C. A. van der Wel and G. De Paëpe, J. Am. Chem. Soc., 2018, 140, 14576–14580.
12. K. Jaudzems, A. Bertarello, S. R. Chaudhari, A. Pica, D. Cala-De Paepe, E. Barbet-Massin, A. J. Pell, I. Akopjana, S. Kotelovica, D. Gajan, O. Ouari, K. Tars, G. Pintacuda and A. Lesage, Angew. Chem., Int. Ed., 2018, 57, 7458–7462.
13. K. K. Frederick, V. K. Michaelis, M. A. Caporini, L. B. Andreas, G. T. Debelouchina, R. G. Griffin and S. Lindquist, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 3642–3647.
14. K. Jaudzems, T. Polenova, G. Pintacuda, H. Oschkinat and A. Lesage, J. Struct. Biol., 2019, 206, 90–98.
15. D. Lee, C. Leroy, C. Crevant, L. Bonhomme-Coury, F. Babonneau, D. Laurencin, C. Bonhomme and G. De Paëpe, Nat. Commun., 2017, 8, 14104.
16. C. Leroy, F. Aussenac, L. Bonhomme-Coury, A. Osaka, S. Hayakawa, F. Babonneau, C. Coelho-Diogo and C. Bonhomme, Anal. Chem., 2017, 89, 10201–10207.
17. F. A. Perras, J. D. Padmos, R. L. Johnson, L.-L. Wang, T. J. Schwartz, T. Kobayashi, J. H. Horton, J. A. Dumesic, B. H. Shanks, D. D. Johnson and M. Pruski, J. Am. Chem. Soc., 2017, 139, 2702–2709.
18. T. Wolf, S. Kumar, H. Singh, T. Chakrabarty, F. Aussenac, A. I. Frenkel, D. T. Major and M. Leskes, J. Am. Chem. Soc., 2019, 141, 451–462.
19. D. Xiao, S. Xu, N. J. Brownbill, S. Paul, L.-H. Chen, S. Pawsey, F. Aussenac, B.-L. Su, X. Han, X. Bao, Z. Liu and F. Blanc, Chem. Sci., 2018, 9, 8184–8193.
20. T. Segal-Peretz, J. P. Jahnke, A. Berenson, L. Neeman, D. Oron, A. J. Rossini, B. F. Chmelka and G. L. Frey, J. Phys. Chem. C, 2014, 118, 25374–25391.
21. A. S. Lilly-Thankamony, C. Lion, F. Pourpoint, B. Singh, A. J. Perez-Linde, D. Carnevale, G. Bodenhausen, H. Vezin, O. Lafon and V. Polshettiwar, Angew. Chem., Int. Ed., 2015, 54, 2190–2193.
22. P. Berruyer, L. Emsley and A. Lesage, eMagRes, 2018, pp. 93–104 DOI:10.1002/9780470034590.emrstm1554.
23. A. J. Rossini, J. Phys. Chem. Lett., 2018, 9, 5150–5159.
24. A. G. M. Rankin, J. Trébosc, F. Pourpoint, J.-P. Amoureux and O. Lafon, Solid State Nucl. Magn. Reson., 2019, 101, 116–143.
25. A. J. Rossini, A. Zagdoun, F. Hegner, M. Schwarzwälder, D. Gajan, C. Copéret, A. Lesage and L. Emsley, J. Am. Chem. Soc., 2012, 134, 16899–16908.
26. A. J. Rossini, C. M. Widdifield, A. Zagdoun, M. Lelli, M. Schwarzwälder, C. Copéret, A. Lesage and L. Emsley, J. Am. Chem. Soc., 2014, 136, 2324–2334.
27. G. Mollica, M. Dekhil, F. Ziarelli, P. Thureau and S. Viel, Angew. Chem., Int. Ed., 2015, 54, 6028–6031.
28. K. Märker, S. Paul, C. Fernández-de-Alba, D. Lee, J.-M. Mouesca, S. Hediger and G. De Paëpe, Chem. Sci., 2017, 8, 974–987.
29. P. C. Vioglio, P. Thureau, M. Juramy, F. Ziarelli, S. Viel, P. A. Williams, C. E. Hughes, K. D. M. Harris and G. Mollica, J. Phys. Chem. Lett., 2019, 10, 1505–1510.
30. O. Ouari, T. Phan, F. Ziarelli, G. Casano, F. Aussenac, P. Thureau, D. Gigmes, P. Tordo and S. Viel, ACS Macro Lett., 2013, 2, 715–719.
31. F. Blanc, S. Y. Chong, T. O. McDonald, D. J. Adams, S. Pawsey, M. A. Caporini and A. I. Cooper, J. Am. Chem. Soc., 2013, 135, 15290–15293.
32. D. Le, G. Casano, T. N. T. Phan, F. Ziarelli, O. Ouari, F. Aussenac, P. Thureau, G. Mollica, D. Gigmes, P. Tordo and S. Viel, Macromolecules, 2014, 47, 3909–3916.
33. G. Mollica, D. Le, F. Ziarelli, G. Casano, O. Ouari, T. N. T. Phan, F. Aussenac, P. Thureau, D. Gigmes, P. Tordo and S. Viel, ACS Macro Lett., 2014, 3, 922–925.
34. N. J. Brownbill, R. S. Sprick, B. Bonillo, S. Pawsey, F. Aussenac, A. J. Fielding, A. I. Cooper and F. Blanc, Macromolecules, 2018, 51, 3088–3096.
35. E. Verde-Sesto, N. Goujon, H. Sardon, P. Ruiz, T. V. Huynh, F. Elizalde, D. Mecerreyes, M. Forsyth and L. A. O’Dell, Macromolecules, 2018, 51, 8046–8053.
36. G. Mollica, F. Ziarelli, P. Thureau and S. Viel, NMR Methods for Characterization of Synthetic and Natural Polymers, The Royal Society of Chemistry, 2019, pp. 533–554 10.1039/9781788016483-00533.
37. S. Tanaka, W.-C. Liao, A. Ogawa, K. Sato and C. Copéret, Phys. Chem. Chem. Phys., 2020, 22, 3184–3190.
38. C. Song, K.-N. Hu, C.-G. Joo, T. M. Swager and R. G. Griffin, J. Am. Chem. Soc., 2006, 128, 11385–11390.
39. M. K. Kiesewetter, B. Corzilius, A. A. Smith, R. G. Griffin and T. M. Swager, J. Am. Chem. Soc., 2012, 134, 4537–4540.
40. A. Zagdoun, G. Casano, O. Ouari, M. Schwarzwälder, A. J. Rossini, F. Aussenac, M. Yulikov, G. Jeschke, C. Copéret, A. Lesage, P. Tordo and L. Emsley, J. Am. Chem. Soc., 2013, 135, 12790–12797.
41. C. Sauvée, M. Rosay, G. Casano, F. Aussenac, R. T. Weber, O. Ouari and P. Tordo, Angew. Chem., Int. Ed., 2013, 52, 10858–10861.
42. B. Corzilius, V. K. Michaelis, S. A. Penzel, E. Ravera, A. A. Smith, C. Luchinat and R. G. Griffin, J. Am. Chem. Soc., 2014, 136, 11716–11727.
43. G. Mathies, M. A. Caporini, V. K. Michaelis, Y. Liu, K.-N. Hu, D. Mance, J. L. Zweier, M. Rosay, M. Baldus and R. G. Griffin, Angew. Chem., Int. Ed., 2015, 54, 11770–11774.
44. B. Corzilius, Phys. Chem. Chem. Phys., 2016, 18, 27190–27204.
45. M.-A. Geiger, A. P. Jagtap, M. Kaushik, H. Sun, D. Stöppler, S. T. Sigurdsson, B. Corzilius and H. Oschkinat, Chem. – Eur. J., 2018, 24, 13485–13494.
46. D. Wisser, G. Karthikeyan, A. Lund, G. Casano, H. Karoui, M. Yulikov, G. Menzildjian, A. C. Pinon, A. Purea, F. Engelke, S. R. Chaudhari, D. Kubicki, A. J. Rossini, I. B. Moroz, D. Gajan, C. Copéret, G. Jeschke, M. Lelli, L. Emsley, A. Lesage and O. Ouari, J. Am. Chem. Soc., 2018, 140, 13340–13349.
47. F. Mentink-Vigier, I. Marin-Montesinos, A. P. Jagtap, T. Halbritter, J. van Tol, S. Hediger, D. Lee, S. T. Sigurdsson and G. De Paëpe, J. Am. Chem. Soc., 2018, 140, 11013–11019.
48. S. Bothe, J. Nowag, V. Klimavičius, M. Hoffmann, T. I. Troitskaya, E. V. Amosov, V. M. Tormyshev, I. Kirilyuk, A. Taratayko, A. Kuzhelev, D. Parkhomenko, E. Bagryanskaya, T. Gutmann and G. Buntkowsky, J. Phys. Chem. C, 2018, 122, 11422–11432.
49. G. Stevanato, D. J. Kubicki, G. Menzildjian, A.-S. Chauvin, K. Keller, M. Yulikov, G. Jeschke, M. Mazzanti and L. Emsley, J. Am. Chem. Soc., 2019, 141, 8746–8751.
50. A. Lund, G. Casano, G. Menzildjian, M. Kaushik, G. Stevanato, M. Yulikov, R. Jabbour, D. Wisser, M. Renom-Carrasco, C. Thieuleux, F. Bernada, H. Karoui, D. Siri, M. Rosay, I. V. Sergeyev, D. Gajan, M. Lelli, L. Emsley, O. Ouari and A. Lesage, Chem. Sci., 2020, 11, 2810–2818.
51. A. Equbal, K. Tagami and S. Han, J. Phys. Chem. Lett., 2019, 10, 7781–7788.
52. D. Mance, P. Gast, M. Huber, M. Baldus and K. L. Ivanov, J. Chem. Phys., 2015, 142, 234201.
53. D. J. Kubicki, G. Casano, M. Schwarzwalder, S. Abel, C. Sauvee, K. Ganesan, M. Yulikov, A. J. Rossini, G. Jeschke, C. Copéret, A. Lesage, P. Tordo, O. Ouari and L. Emsley, Chem. Sci., 2016, 7, 550–558.
54. A. P. Jagtap, M.-A. Geiger, D. Stöppler, M. Orwick-Rydmark, H. Oschkinat and S. T. Sigurdsson, Chem. Commun., 2016, 52, 7020–7023.
55. F. A. Perras, A. Sadow and M. Pruski, Chem. Phys. Chem., 2017, 18, 2279–2287.
56. W. Zhai, Y. Feng, H. Liu, A. Rockenbauer, D. Mance, S. Li, Y. Song, M. Baldus and Y. Liu, Chem. Sci., 2018, 9, 4381–4391.
57. K. Sato, R. Hirao, I. Timofeev, O. Krumkacheva, E. Zaytseva, O. Rogozhnikova, V. M. Tormyshev, D. Trukhin, E. Bagryanskaya, T. Gutmann, V. Klimavicius, G. Buntkowsky, K. Sugisaki, S. Nakazawa, H. Matsuoka, K. Toyota, D. Shiomi and T. Takui, J. Phys. Chem. A, 2019, 123, 7507–7517.
58. F. Mentink-Vigier, Phys. Chem. Chem. Phys., 2020, 22, 3643–3652.
59. F. A. Perras, M. Raju, S. L. Carnahan, D. Akbarian, A. C. T. van Duin, A. J. Rossini and M. Pruski, J. Phys. Chem. Lett., 2020, 11, 5655–5660.
60. G. J. Gerfen, L. R. Becerra, D. A. Hall, R. G. Griffin, R. J. Temkin and D. J. Singel, J. Chem. Phys., 1995, 102, 9494–9497.
61. D. Gajan, M. Schwarzwälder, M. P. Conley, W. R. Grüning, A. J. Rossini, A. Zagdoun, M. Lelli, M. Yulikov, G. Jeschke, C. Sauvée, O. Ouari, P. Tordo, L. Veyre, A. Lesage, C. Thieuleux, L. Emsley and C. Copéret, J. Am. Chem. Soc., 2013, 135, 15459–15466.
62. D. Gajan, A. Bornet, B. Vuichoud, J. Milani, R. Melzi, H. A. van Kalkeren, L. Veyre, C. Thieuleux, M. P. Conley, W. R. Gruning, M. Schwarzwalder, A. Lesage, C. Copéret, G. Bodenhausen, L. Emsley and S. Jannin, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 14693–14697.
63. M. Cavaillès, A. Bornet, X. Jaurand, B. Vuichoud, D. Baudouin, M. Baudin, L. Veyre, G. Bodenhausen, J.-N. Dumez, S. Jannin, C. Copéret and C. Thieuleux, Angew. Chem., Int. Ed., 2018, 57, 7453–7457.
64. W. Cao, W. D. Wang, H.-S. Xu, I. V. Sergeyev, J. Struppe, X. Wang, F. Mentink-Vigier, Z. Gan, M.-X. Xiao, L.-Y. Wang, G.-P. Chen, S.-Y. Ding, S. Bai and W. Wang, J. Am. Chem. Soc., 2018, 140, 6969–6977.
65. T. El Daraï, S. F. Cousin, Q. Stern, M. Ceillier, J. Kempf, D. Eshchenko, R. Melzi, M. Schnell, L. Gremillard, A. Bornet, J. Milani, B. Vuichoud, O. Cala, D. Montarnal and S. Jannin, Nat. Commun., 2021, 12, 4695.
66. E. Besson, F. Ziarelli, E. Bloch, G. Gerbaud, S. Queyroy, S. Viel and S. Gastaldi, Chem. Commun., 2016, 52, 5531–5533.
67. D. L. Silverio, H. A. van Kalkeren, T.-C. Ong, M. Baudin, M. Yulikov, L. Veyre, P. Berruyer, S. Chaudhari, D. Gajan, D. Baudouin, M. Cavaillès, B. Vuichoud, A. Bornet, G. Jeschke, G. Bodenhausen, A. Lesage, L. Emsley, S. Jannin, C. Thieuleux and C. Copéret, Helv. Chim. Acta, 2017, 100, e1700101.
68. P. Nabokoff, S. Gastaldi and E. Besson, Microporous Mesoporous Mater., 2021, 311, 110674.
69. M. Juramy, R. Chèvre, P. Cerreia Vioglio, F. Ziarelli, E. Besson, S. Gastaldi, S. Viel, P. Thureau, K. D. M. Harris and G. Mollica, J. Am. Chem. Soc., 2021, 143, 6095–6103.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp02872g

---