 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Molecular dynamics simulations and solid-state nuclear magnetic resonance spectroscopy measurements of C–H bond order parameters and effective correlation times in a POPC-GM3 bilayer†
Simon
Fridolf
 *a,
Mona Koder
Hamid
b,
Leo
Svenningsson
a,
Marie
Skepö
*a,
Mona Koder
Hamid
b,
Leo
Svenningsson
a,
Marie
Skepö
 b,
Emma
Sparr
b,
Emma
Sparr
 a and
Daniel
Topgaard
a
a and
Daniel
Topgaard
a
aDivision of Physical Chemistry, Lund University, Lund, Sweden. E-mail: simon.fridolf@fkem1.lu.se
bDivision of Theoretical Chemistry, Lund University, Lund, Sweden
First published on 7th October 2022
Abstract
Glycolipids such as gangliosides affect the properties of lipid membranes and in extension the interactions between membranes and other biomolecules like proteins. To better understand how the properties of individual lipid molecules can contribute to shape the functional aspects of a membrane, the spatial restriction and dynamics of C–H bond segments can be measured using nuclear magnetic resonance (NMR) spectroscopy. We combine solid-state NMR spectroscopy with all-atom molecular dynamics (MD) simulations to investigate how ganglioside GM3 affects the bilayer structure and dynamics of C–H bond segments. These two methods yield reorientational correlation functions, molecular profiles of C–H bond order parameters |SCH| and effective correlation times τe, which we compare for lipids in POPC bilayers with and without 30 mol% GM3. Our results revealed that all C–H segments of POPC reorient slower in the presence of GM3 and that the defining features of the GM3-POPC bilayer lie in the GM3 headgroup; it gives the bilayer an extended headgroup layer with high order (|SCH| up to 0.3–0.4) and slow dynamics (τe up to 100 ns), a character that may be mechanistically important in ganglioside interactions with other biomolecules.
Introduction
Cell membranes are very complex biological assemblies composed of a large variety of lipids, proteins and carbohydrates. Both composition and structure vary largely between different cellular organelles and even between the inner and outer leaflets of the cellular membranes.1 With respect to the lipid components, the evolution has led to a great chemical diversity of the major lipid classes in mammals cells, including glycerophospholipids, glycolipids and sterols, each of them promoting different membrane structures and targets for interactions with biomolecules in the membrane environment. Glycolipids are lipids with carbohydrate headgroups (Fig. 1) that typically contain glucose (Glc) and galactose (Gal) residues with different linkages and substitutions. The chemical properties of lipids such as headgroup size and charge, hydrophobic chain length and degree of unsaturation affect lipid self-assembly2 and may have consequences for the function of integral membrane proteins3 and how peripheral membrane proteins interface with the membrane surface.4 The headgroup structure of glycolipids enables strong inter-headgroup interactions,5 which can lead to the formation of clusters with in-plane dimensions on the 10–100 nm length scale.6 The formation of such clusters may in turn be crucial for the interactions between the membrane and macromolecules in the membrane surroundings. As an example, glycolipid-containing membranes have previously been shown to interfere with the process of amyloid formation for different amyloid-forming proteins.7,8Gangliosides are glycosphingolipids that contain sialic acid, most commonly N-acetylneuraminic acid (NeuAc) in humans9 and ceramide (Cer) as their hydrophobic part. These types of lipids are mainly located in the outer leaflet of the plasma membrane and are particularly concentrated (up to 10 wt%) in neurons,10 where they have been suggested to have important roles in neuronal development and function,11 modulation of cell-surface interactions and cell signalling.12–15 Ganglioside GM3 is one of the simpler gangliosides, from which the major brain gangliosides GM1, GD1a, GD1b and GT1b are biosynthesized.15 The headgroup of GM3 is a three sugar-units long oligosaccharide, including a negatively charged NeuAc residue (Fig. 1). It is the major ganglioside type in mammalian heart, skeletal muscle, kidney, liver and adipose tissue14,16 and has been linked to insulin resistance,17 diabetes,18 cancer19 and neuronal cell death.20
The composition of lipid membranes affects their self-assembly behavior with implications for dynamics, structure and lateral heterogeneity. Lipid membranes exhibit a range of dynamics on different time scales,21 such as librations, trans-gauche isomerism and rotational and lateral diffusion. For lipids like phosphatidylcholines the gradients in dynamic properties along the molecular segments of the acyl chains and the headgroup are relatively well characterized,22,23 whereas mixtures including gangliosides are far less investigated. For a simple phosphatidylcholine bilayer, the choline headgroup and the ends of the hydrophobic tails display much faster dynamics than the parts of the molecules positioned at the hydrophilic–hydrophobic interface.24 The presence of a double bond in the hydrophobic tails has only a minor effect on the rate of motions but rather decreases the C–H order parameter |SCH|,25 which describes the amplitude of motions. When the bilayer composition increases in complexity, one can expect that the lipid dynamics at different positions of the bilayer may be affected. Some characteristic properties of glycolipids are related to the dynamics of the large and bulky hydrophilic carbohydrate headgroup region, which is inflexible due to a high energy barrier for conformational change of the pyranose rings. These bulky and inflexible sugar headgroups will thus likely influence the membrane dynamics in a different way compared to small and flexible phosphocholine headgroups, long and flexible synthetic polyethylene glycol (PEG) lipids commonly used for pharmaceutical applications, or lipids with a very small hydrophilic part like cholesterol. Differences in lipid headgroups will also impact the lipid phase behavior. As an example, different lipids with large hydrophilic headgroups may affect the phase behavior in different ways depending on the chemical nature of the headgroup, where the response in lipid phase behavior to temperature changes appears much stronger for PEG-based lipids as compared to glycolipids.5,26 These observations could be related to differences in the dynamics of the large hydrophilic headgroups.
In this study, we raised the question of how lipid dynamics are affected by the presence of a glycolipid. We chose a model system composed of a common phospholipid, 1-palmitoyl-2-oleoyl-phosphatidylcholine (POPC) in the presence and absence of ganglioside GM3. These model systems are sufficiently complex to display the expected dynamical properties, while being simple enough for atomically resolved studies using molecular dynamics (MD) simulations and NMR experiments.27
We present an atomic-resolution description of the dynamics and order in the POPC-GM3 bilayer based on solid-state NMR experiments and all-atom MD simulations. Solid-state NMR spectroscopy can directly measure |SCH| from dipolar splittings,28 and dynamics in the form of relaxation constants. Separated local field (SLF) is a class of NMR methods that allows for the measurement of powder-pattern type dipolar splittings for all chemical shift-resolved segments simultaneously in a 2D-experiment under magic-angle spinning (MAS), or without MAS on oriented samples.29 Measurements of the set of 13C R1 and R1ρ relaxation constants, which are sensitive to motions in liquid crystalline lipid membranes on different time scales, together with |SCH| can be expressed as an effective correlation time, τe. The value of τe is appropriate for describing nanosecond dynamics in anisotropic lipid bilayers.30–32 The physical interpretation of relaxation data is however not straightforward and depends on the choice of a motional model, which may lead to bias.33 To resolve the ambiguity surrounding relaxation constants, NMR measurements can be combined with MD simulations, which have a direct physical interpretation on timescales probed by NMR R1 and R1ρ measurements.34 The C–H reorientation autocorrelation function g(τ) can be directly calculated from the MD trajectory and be related with relaxation rate constants via the spectral density.35 Using the methods above, a quantitative and atomically-resolved picture of the dynamics in a lipid membrane is obtained, which can be used to investigate the effect of the presence of GM3.
The obtained MD trajectories and NMR observables were analyzed in terms of τe, describing molecular segment reorientation on timescales below microseconds. Fully hydrated POPC bilayers display a gradient in τe along the different lipid segments, ranging from around 5 ns for the hydrophilic–hydrophobic interface to 0.1 ns at the ends of the acyl chains and the phosphocholine headgroup.30,31 Our results highlight the different behaviors in the hydrophilic surface of the POPC and POPC-GM3 bilayers, where the GM3 headgroup forms a carbohydrate layer at the bilayer surface with effective correlation times up to 100 ns in the sugar residues of the GM3 headgroup, which is 10 times slower than the slowest segments in POPC. As the headgroups of glycolipids, such as gangliosides, are the most exposed moieties on membrane surfaces, their structural and dynamical behavior could be essential for biological functions that takes place via membrane interactions with other biomacromolecules.
Materials and methods
Materials and sample preparation
POPC and ganglioside GM3 were purchased from Avanti Polar Lipids (Alabaster, AL). Chloroform and methanol were purchased from Sigma-Aldrich. Homogeneous mixing of POPC and GM3 was ensured by dissolving the freeze-dried powders in chloroform:methanol 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The solvent was gently evaporated under a stream of N2 and further dried at reduced pressure overnight. Lamellar phases of lipids were prepared by adding 50% (wt/wt) water to the lipid films followed by equilibration for 24 h before transferring the samples to 4 mm NMR rotors with disposable inserts.
1. The solvent was gently evaporated under a stream of N2 and further dried at reduced pressure overnight. Lamellar phases of lipids were prepared by adding 50% (wt/wt) water to the lipid films followed by equilibration for 24 h before transferring the samples to 4 mm NMR rotors with disposable inserts.
MD simulations
All-atom MD simulations were performed for a pure POPC bilayer and a bilayer containing 30 mol% GM3, with 64 water molecules per lipid. The CHARMM3636 force field was used with TIP3P37,38 water. The initial bilayers were constructed with the CHARMM-GUI Membrane Builder39 and the simulations were performed using the GROMACS package (version 2021).40 Following equilibration, production runs were performed for a duration of 1 μs with a time step of 2 fs and saved every 100 ps in the NPT ensemble, maintaining 303 K temperature with the Nose–Hoover thermostat41,42 and 1 bar pressure with the Parrinello–Rahman barostat.43 Further simulations were done for a minimum of 1 ns where frames were saved more frequently, down to the limit of 2 fs, and used in the calculation of correlation functions. Correlation functions from the different trajectories were plotted together and cropped when necessary to obtain continuous data in Fig. 2(B). Further details of the simulations are presented in the ESI.† Snapshots with motion blur in Fig. 2(A) and Fig. S5 (ESI†) were produced using the POV-Ray software44 from the average of 500 snapshots calculated in Matlab45 using equally spaced times between t = 0 and the exposure time (0 ps, 50 ps, 0.5 ns or 5 ns). | ||
| Fig. 2 MD simulations of POPC in the absence and presence of 30 mol% GM3 at 303 K. (A) MD simulation snapshots of POPC and POPC with 30 mol% GM3 at varying expoure times (motion blur), illustrating the timescale of segmental motions. The colors identify different molecular segments: blue (water), red (headgroups) and yellow (hydrophobic tails). White labels and arrows annotate water, the POPC headgroup, the central acyl chain carbons and terminal methyl groups on the acyl chains. The view scale for all snapshots is the same and the length of the white scale bar represents 1 nm. The field of view is 1.1 times the box sizes in the x and y directions and 0.7 in the z-direction. Periodic boundry conditions were applied in all directions. (B) Autocorrelation functions g(τ) for selected C–H bonds of a 30 mol% GM3 bilayer calculated with eqn (1). Cyan lines show segments of POPC in the absence of GM3. For lipid bilayers, g(τ) typically decays to a plateau value equal to the square of the order parameter |SCH| due to anisotropic molecular motions at time scales below ms. The black lines are fits to eqn (3) and the dotted points at the end of each g(τ) correspond to |SCH| calculated with eqn (2). | ||
The autocorrelation function g(τ) is expressed as the time-averaged reorientation of the C–H bond unitary vector μ at the time t for a given correlation time τ
 | (1) |
 | (2) |
 | (3) |
 | (4) |
The R1 and R1ρ relaxation rates are calculated from g(τ) obtained in MD simulations via the reduced spectral density, which is the Fourier transform of eqn (1) and can be written as
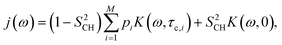 | (5) |
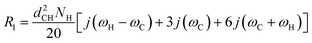 | (6) |
 | (7) |
NMR spectroscopy
The measurements were performed using a Bruker Avance NEO-500 NMR spectrometer operating at a 13C frequency of 125 MHz equipped with a standard bore E-free CP-MAS 4 mm (13C/31P/1H) probe. All experiments used a MAS frequency of 5 kHz at a temperature of 303 K. Measurements with INEPT52 or CP53 for 1H–13C polarization transfer used the following settings: refocused INEPT with τ1 and τ2 of 1.79 ms and 1.20 ms respectively, CP contact time equal to 1000 μs, radiofrequency pulses set to give the nutation frequencies 81 kHz (13C and 1H 90° and 180° pulses) and 68 kHz SPINAL6454 decoupling of protons. 13C dimensions were sampled using a spectral width of 250 ppm during an acquisition time of 100 ms and a 2 s recycle delay.In 1H–13C heteronuclear chemical shift correlation (HETCOR)55 and R-PDLF experiments, the indirect dimension was sampled with t1 increments of 200 μs and 400 μs in 128 or 32 steps respectively. The R-PDLF technique56 is used to measure high-resolution dipolar splittings for unoriented liquid crystals under MAS via recoupling of heteronuclear 1H–13C dipolar couplings at natural isotopic abundance. The R-PDLF R1871 recoupling pulses were set to a nutation frequency of 45 kHz. The 13C R1 values were measured with polarization transfer by INEPT or CP, followed by a 90° pulse applied to the resulting 13C transverse magnetization, a waiting time t1 defining the indirect dimension and a subsequent 90° pulse prior to acquisition. A phase cycling scheme for the sequence was used as described by Torchia.57 The 13C R1ρ values were measured by performing a sequence with a subsequent spin lock of the 13C magnetization at spin lock frequencies of 24.0, 28.8, 33.6, 38.4, 43.2 and 48.0 kHz. 8 points were used for the indirect dimension of R1 experiments from 0.1 to 2 s with logarithmic spacing, while for R1ρ measurements, 8 points were used from 0.1 to 100 ms with linear spacing.
The 13C dimensions were processed with a line broadening of 10 Hz, zero-filling from 6250 to 16384 time-domain points, Fourier transform and phase- and baseline corrected with an in-house Matlab45 script, partly derived from MatNMR.58 In the dipolar dimension of R-PDLF experiments a sine-square apodization and zero filling were applied to the time-domain signal before the final Fourier transform. The values of |SCH| were determined directly from the dipolar splittings using the relation
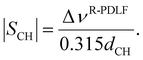 | (8) |
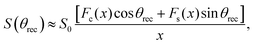 | (9) |
 . The approximation sign originates from a truncation of the infinite sum interpretation of the powder pattern signal integral while ignoring weak heteronuclear contributions. The functions Fc(x), Fs(x) are the corresponding Fresnel equations
. The approximation sign originates from a truncation of the infinite sum interpretation of the powder pattern signal integral while ignoring weak heteronuclear contributions. The functions Fc(x), Fs(x) are the corresponding Fresnel equations | (10) |
and
 | (11) |
| f(t1) = k + (1 − k)S(θrec)e−a1t1, | (12) |
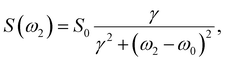 | (13) |
| S(t1) = S0e−t1R1/1ρ, | (14) |
With the modest assumption that g(τ) can be separated into fast gf(τ) and slow gs(τ) motion regimes for frequencies ω/2π > 1 MHz and ω/2π < 100 kHz, respectively, it is possible to express an effective correlation time τe which can be estimated from experimental measurements of R1, R1ρ, S2CH as30,31
 | (15) |
Results
MD simulations
To investigate the effect of ganglioside GM3 on the structure and dynamics of a POPC bilayer, we performed all-atom MD simulations for POPC with and without 30 mol% GM3 using the CHARMM36 force field and the TIP3P water model. Snapshots for the two systems are shown in Fig. 2(A), where the GM3 headgroup sugars form an additional layer at the hydrophilic surface that extends into the water. We calculated the head-to-head (DHH), hydrophobic (DC) and bilayer thickness (DB) from the electron densities and volume probabilities (Fig. S1–S4, ESI†). All the distances increase when GM3 is present in the bilayer (Table 1).The vectors defined by the I1–I4, II1–II4 and III2–III5 carbons in the Glc, Gal and NeuAc residues (Fig. 1) of the ganglioside molecules report on the overall orientation of the respective residues. In the simulations the I1–I4 and II1–II4 vectors are orientated parallel to the bilayer normal while the III2–III5 vector is often tilted. Fig. 2(A) illustrates the timescales of segmental motions in the bilayers by “motion blur” pictures obtained by averaging hundreds of simulation snapshots over increasingly longer time intervals. While all molecules appear sharp at an exposure time of 0 ns, corresponding to a conventional snapshot, motions that are fast on the scale of the exposure time will introduce blurring of the involved segments due to averaging of the atomic positions. Fig. 2(A) shows that the estimated order-of-magnitude hierarchy of timescales for different segments is as follows, from fast to slow; water (<50 ps), terminal methyl groups and phosphocholine (<0.5 ns) and hydrophobic tails (<5 ns). The motions of the GM3 headgroups are still slow compared to the rest of the bilayer on these time scales. The blurring in Fig. 2(A) is caused by translational motion, which is most strongly coupled to the rotational motion that we quantify at short time scales. More side- and top view images at additional exposure times are available in Fig. S5 in the ESI.† The full motion pictures are available for the POPC bilayer (M1 and M2) and POPC with GM3 bilayer (M3 and M4) in the ESI.†
The reorientational autocorrelation function g(τ) and the order parameter |SCH| for each C–H bond vector was calculated from the MD trajectory using eqn (1) and (2), respectively. Fast internal motions normally causes decay of g(τ) on the ps–ns time scale and approaches a plateau value of S2CH related to anisotropic reorientation. The dynamical hierarchy illustrated by the snapshots in Fig. 2(A) is expressed quantitatively using g(τ) and |SCH| in Fig. 2(B) for selected segments of GM3 and POPC. The plots of g(τ) show a gradient in dynamics and order throughout the molecules, where faster reorientation corresponds to more rapidly decaying g(τ) and shorter effective correlation time τe. The value of τe described by eqn (4) is defined as the area under g(τ) scaled by (1 − S2CH)−1,25 and roughly corresponds to the exposure time at the sharp–blur transition in Fig. 2(A).
The most rapidly decaying g(τ) is from the terminal methyl groups (18, 16′, R18 and R16′) on the hydrophobic tails (0.1 ns), followed by the γ groups in the POPC headgroup (1 ns). The order of these segments is low, with |SCH| close to zero because of methyl group rotation. Compared to the other methyl groups, g(τ) for the N-acetyl methyl moiety (III11) in the GM3 headgroup decays in an additional distinct step related to the rotation barrier associated with the amide bond, where the first step is from unrestricted methyl group rotation. Carbon atoms representative of the hydrophobic tails (10′, R9′) have more slowly decaying g(τ) (10 ns), which is mainly associated with trans-gauche isomerization but also whole-molecule rotational diffusion and wobble.60,61 The value |SCH| ≈ 0.2 for the hydrophobic tails is greater than for the methyl groups. There is a pronounced gradient in |SCH| which increases towards the hydrophilic–hydrophobic interface where the headgroup is anchored,22 limiting the amplitude of motions. The segments in the hydrophilic–hydrophobic interface of POPC have slower dynamics than the tail region, with g(τ) for the g2 carbon extending into 100 ns due to the inflexibility of the interface region.
The GM3 headgroup stands out with exceptionally slow dynamics and high order compared to the rest of GM3 and POPC; g(τ) for segments in the Gal and Glc residues and the interface region of GM3 (III5, II3, I3 and R2) do not plateau on the time scale of the simulation analysis (ca. 500 ns of the 1000 ns trajectory) and give |SCH| up to around 0.35. The internal dynamics in the GM3 headgroup should be slow considering high energy barriers for conversion between different conformations of the pyranose rings. The I1–I4 and II1–II4 vectors of the Glc and Gal residues are oriented approximately parallel to the bilayer normal, which leads to high |SCH| for the equatorial C–H bonds because |SCH| has a local maximum at an angle of 90° as described by eqn (2). A gradient in dynamics exists for the GM3 headgroup that is similar but smaller than the corresponding gradient along the hydrophobic region, where the sugar residue closest to the hydrophobic–hydrophilic interface region is slowest (Fig. 2(B), GM3 oligosaccharide panel). Comparing the simulated bilayers with and without GM3 (cyan lines in Fig. 2(B)) shows that the presence of GM3 leads to a slower decay rate of g(τ) for segments in the headgroup (β) and interface region (g2) of POPC. Other segments of POPC, like the hydrophobic tails and methyl groups, are less affected but are also slightly slowed down. The presence of GM3 also causes small increases of |SCH| for the interface region and hydrophobic tails.
Chemical shift assignments
Fig. 3(A) and (B) shows the assigned chemical shifts of GM3 and POPC from 1D 13C and 2D 1H–13C spectra with CP and INEPT for polarization transfer. All carbons from POPC are resolved except for the CH2 carbons of the hydrophobic tails in the crowded 30 ppm region. The following descriptions use the labels shown in Fig. 1 for GM3 carbon atoms. GM3 peaks that are well-resolved in 1D spectra are: III8, I6, III5, III3, R2′ and III11. Several more peaks that overlap in 1D spectra are resolved in the HETCOR spectrum: R1, I2, III6, III7, II3, II5, I3, I5, II4 and II6. GM3 peaks that remain unresolved are: R3 overlapping with R6, I1 with II1 and III4 with III7/II4. Peaks from the hydrophobic tails of GM3 overlap with those from similar carbons on POPC. In the presence of 30 mol% GM3, the crowded CH2 30 ppm region extends towards higher chemical shift values because of a higher fraction of all-trans conformations,62 also suggested by the increased |SCH| in Fig. 2(B). More detailed assignments of this region are shown in Fig. S6, ESI.† Peaks from carbons in the GM3 headgroup and interface are distributed across the spectrum except for some carbons belonging to the pyranose rings, which are concentrated in the 68–79 ppm region. The III1, III2 and III10 carbons are not connected to a proton, which cuts off signal enhancement by INEPT or short CP. Not all peaks in Fig. 3(A)–(C) could be assigned to POPC or GM3; there are peaks of unknown origin at 71.8, 70, 68, 60.2, 34 (side of 2,2′ peak) and 33 ppm with amplitudes similar to the smallest GM3 peaks. Because of the similarities in chemical shift and dipolar splitting between the peaks assigned to GM3 and the unidentified ones, it is possible that the latter stem from chemically modified or isomerized forms of GM3. | ||
| Fig. 3 13C MAS NMR spectra of a fully hydrated lamellar phase of POPC in the presence of 30 mol% GM3, recorded at 303 K, a 13C Larmor frequency of 125 MHz, 5 kHz MAS and 68 kHz SPINAL64 1H-decoupling during 13C acquisition. All experiments were done using both INEPT (red) and CP (blue) for 1H–13C polarisation transfer. (A) 1D CP and INEPT 13C spectra with POPC peak assignments from Ferreira et al.63 (B) 2D 1H–13C HETCOR55 spectra with chemical shift correlations used for GM3 peak assignments together with reported values from Sillerud et al.64 (C) 2D 1H–13C R-PDLF28 spectra, where the CP data is an overlay of two separate measurements with 2.5 and 7.5 kHz spectral width in the dipolar dimension. The experimental C–H order parameters are proportional to the splittings in the dipolar dimension according to eqn (8). The label n.a. means “not assigned”. | ||
Measurements of dipolar coupling
To investigate how GM3 affects the structure of a POPC membrane, we determined |SCH| experimentally with R-PDLF NMR spectroscopy. These data can be directly compared with |SCH| calculated from bond orientations relative to the bilayer normal in the MD trajectory. The 2D R-PDLF spectrum of POPC with 30 mol% GM3 is shown in Fig. 3(C). The peak splittings in the dipolar dimension are directly proportional to |SCH| on the time scale of <10 μs described by eqn (8) and decrease in magnitude with the amplitude of anisotropic motions according to eqn (2). Several well-resolved dipolar splittings are shown for POPC and GM3 segments in Fig. 3(C), except for the phosphocholine methyl groups, which can reorient isotropically. While not immediately apparent in Fig. 3(C), the terminal methyl groups on the hydrophobic tails yield a finite splitting of 0.027 kHz as deduced from the dipolar modulation minimum that is observable in the indirect time domain of the R-PDLF experiment (Fig. S7, ESI†). The N-acetyl methyl group (III11) in the GM3 headgroup, however, shows a distinct splitting of around 0.50 kHz. Protruding groups like α and β on POPC and III7–III9 on GM3 are relatively unrestricted by neighboring molecules and have splittings in the range 0.15–0.40 kHz.The dipolar dimension of the R-PDLF experiments in Fig. 3(C) provides additional resolution of carbons in the hydrophobic tails compared to the 1D and HETCOR experiments in Fig. 3(A) and (B). These give splittings in the range of 0.60–1.6 kHz, in a gradient of order that decreases from the hydrophobic–hydrophilic interface region towards the terminal methyl groups in the hydrophobic tails. The hydrophilic–hydrophobic interface region in both lipids has high order and gives splittings up to 1.4 kHz for the glycerol part in POPC and 1.7 kHz in the Cer–Glc interface of GM3. While the values for the NeuAc residue of the GM3 headgroup are relatively small (0.1–0.3 kHz), the Gal and Glc residues give large splittings of up to 1.9 kHz caused by ordering of ring C–H bonds perpendicular to the bilayer normal and low amplitudes of motion in the rigid pyranose rings. Comparing the values with and without GM3 (Fig. S8, ESI†) reveals that the presence of GM3 leads to changes in splittings for some segments in POPC on the order of 0.15 kHz. Increased splittings are observed in the middle of the hydrophobic tails, while decreased values are observed for the g1 and g3 segments in the POPC glycerol region.
Molecular profiles of |SCH|, τe, R1 and R1ρ
The values of τe calculated from MD using eqn (4) and NMR using eqn (15) are shown in Fig. 4–6 together with values of |SCH|, R1ρ and R1 for the headgroup and glycerol segments, ceramide and POPC tails respectively. All values are available in Tables S2–S5 in the ESI.† The τe profiles from MD and NMR produce consistent patterns that show the expected dynamics gradient going from fast (methyl groups, phosphocholine) to intermediate (hydrophobic tails) to slow (interface region), where the presence of 30 mol% GM3 introduces a new region with slow dynamics (GM3 interface-headgroup). The effect of GM3 to decrease POPC dynamics is also consistent between experiments and simulation, while this is less clear for the hydrophobic tail from NMR because of spectral overlap in the 30 ppm region. In contrast to conventional R1 measurements, changes in the quantity τe, obtained by combining R1, R1ρ and |SCH| according to eqn (15) always represent slowdown or acceleration of C–H bond reorientation in lipid bilayers when the following assumptions are met:31 (i) g(τ) decays to the value of. S2CH in less than 1 μs, (ii) slow isotropic motions related to diffusion between bilayers with different orientations do not affect the spectral density on time scales below μs, (iii) R1 and R1ρ measurements are carried out using B0 fields above 1 MHz and spin lock frequencies between 10–100 kHz, respectively. | ||
| Fig. 4 Experimental NMR and simulated MD molecular profiles of order parameters |SCH|, effective correlation times τe and R1ρ and R1 relaxation rates for the GM3 NeuAc, Gal and Glc carbons and the POPC choline and glycerol carbons in a fully hydrated lamellar phase of POPC with and without 30 mol% GM3 at 303 K. In the frequency-domain analysis, ΔνR-PDLF was manually measured in the 2D spectrum, while the fitted values were obtained viaeqn (9). All experiments were performed using both INEPT and CP for 1H–13C polarisation transfer. The panels show the values of |SCH| calculated with eqn (2) and (8), τe calculated with eqn (4) and (15) and measured values of the 13C R1 and R1ρ relaxation rates for the respective POPC and GM3 carbons. Values of R1 and R1ρ were calculated from MD simulations with eqn (6) and (7). | ||
 | ||
| Fig. 5 Experimental NMR and simulated MD molecular profiles of order parameters |SCH|, effective correlation times τe and R1ρ and R1 relaxation rates for the ceramide carbons in a fully hydrated lamellar phase of POPC with 30 mol% GM3 at 303 K. All the values correspond to carbons in the ceramide chains of GM3. See Fig. 4 caption for details. The arrows annotate carbons that were assigned the same values because their signals could not be individually resolved in the NMR experiments. | ||
 | ||
| Fig. 6 Experimental NMR and simulated MD molecular profiles of order parameters |SCH|, effective correlation times τe and R1ρ and R1 relaxation rates for the POPC acyl chain carbons in a fully hydrated lamellar phase of POPC with and without 30 mol% GM3 at 303 K. All the values correspond to carbons in the palmitoyl and oleyl chains of POPC. See Fig. 4 caption for details. The arrows annotate carbons that were assigned the same values because their signals could not be individually resolved in the NMR experiments. | ||
The pyranose ring C–H bonds in the GM3 headgroup (Fig. 4) have τe in the range 20–100 ns (MD) and 2–15 ns (NMR). The hydroxymethyl groups that extend from the rings rotate about a single bond (e.g., I5–I6), analogous to terminal methyl groups, which gives a lower τe of 15–20 ns in the simulations. This detailed information is more difficult to extract from the NMR results because of the larger uncertainty in the individual τe values for the GM3 headgroup. However these CH2 segments (I6, II6) have the shortest τe of the respective sugar residue which means that they reorient faster than the C–H bonds fixed to the pyranose rings. However, the I6 and II6 carbons suffer from poor resolution in the 1D spectrum, which complicates the interpretation of τe. The segments at the interface of Cer and the GM3 headgroup (Fig. 5) have long τe values around 40 ns in the simulations and some of the longest τe values of around 10 ns in the NMR results.
The carbons in the central part of the ceramide tails (Fig. 5) have τe of approximately 0.3–7 ns (MD) and 0.5–3 ns (NMR), illustrating the gradient in order and dynamics from the end of the hydrophobic tails near the terminal methyl group (small |SCH|, fast dynamics) to the interface with the hydrophilic headgroups (high |SCH|, slow dynamics). The corresponding values for the POPC palmitoyl and oleyl chains (Fig. 6) are 0.2–1 ns. The central carbons in the tails have no experimental points due to low 1D resolution in the 30 ppm region, which prevents extraction of atom-specific information from the pseudo-2D relaxation measurements. The interface region of GM3 has τe of 30–40 ns (MD) and 1.5–10 ns (NMR), while for POPC the value of τe for this region is 2–5 ns (MD) and 2–4 ns (NMR) in our results at 303 K. This can be compared with 2–3 ns and 1.5–3 ns reported for glycerol segments in POPC bilayers without GM3 at a lower temperature of 298 K,30,31 which in general leads to longer τe.
The methyl segments follow a trend in the MD-values of τe: hydrophobic tails (0.02 ns) < phosphocholine (0.2 ns) < N-acetyl moiety on GM3 (10 ns). The NMR values of τe for these segments are close to 0.1 ns for both the tails and phosphocholine and not determined for the N-acetyl group because of overlap with the peak from the 17, 15′, R17 and R15′ carbons. Values of τe for the terminal methyl groups in the tails and phosphocholine segments have been reported as close to zero and 0.1 ns respectively from previous NMR experiments.30,31 The lower detection limit of τe is determined by the need to avoid excessive heating from radio-frequency irradiation, which gives a maximum spin lock duration of around 100 ms corresponding to τe = 0.1 ns.
While the GM3 headgroup-interface region forms an extended headgroup layer with exceptionally slow dynamics and high order, we also observe an effect on POPC in the bilayer in the presence of GM3. When POPC is in the presence of 30 mol% GM3, the hydrophobic tails have increased τe and |SCH| values from MD simulations and increased dipolar splittings from NMR (Fig. S8, ESI†). The MD τe values for these segments are then increased by up to a factor of two. More specifically, the MD values of τe are increased in the glycerol (2 ns to 5–10 ns), α-, β- (0.3 ns to 2 ns) and γ-segments (0.07 ns to 0.15 ns). The NMR results for these segments confirm an increase in the headgroup-interface τe values, but the effect is smaller than indicated by MD. This increase in τe values suggests that the presence of GM3 decreases the rate of POPC headgroup axial rotation and tumbling that occurs on the time scale of several ns.
Discussion
The extended GM3 headgroup layer
Our combined experimental and MD simulation results show that there exists a distinct hierarchy of molecular motions on the ps–ns time scale in the POPC-GM3 bilayer. The GM3 oligosaccharide groups form an extended headgroup layer structure, which is reflected in the head-to-head distance (DHH) that increases from 3.91 nm without GM3 to 5.68 nm for the furthest maxima in the total density with GM3 (Table 1 and Fig. S2, ESI†). The GM3 headgroup segments have high order parameters with |SCH| = <0.35 and long effective correlation times τe up to 100 ns, compared to POPC. Our results show that the dynamics in the GM3 headgroup is slower than for other lipid segments, including the POPC headgroup. The hydrophilic layer of the membrane is also extended (protrudes further into the bulk water) in the presence of GM3. Together these two effects can give a membrane containing GM3 or other gangliosides profoundly different properties compared with other membranes, which can in turn affect interactions with other macromolecules.| Lipid system | D HH (nm) | D C (nm) | D B (nm) |
|---|---|---|---|
| POPC | 3.91 | 2.65 | 3.90 |
| POPC with 30 mol% GM3 | 5.68, 4.24 | 2.85 | 4.62 |
The extended headgroup layer observed in MD simulations includes the GM3 Gal and NeuAc residues, whereas the Glc residue is approximately level with the phosphocholine on POPC. The values of |SCH| are high for Gal where the C–H bonds are oriented approximately perpendicular to the bilayer normal, while NeuAc gives smaller values due to a tilted orientation of the III2–III5 vector relative to the bilayer normal. The bilayer properties at the hydrophilic–hydrophobic interface will be significantly affected by changing the lipid composition and by an increased thickness of the hydrophilic layer when GM3 is present, which may promote interactions with peripheral proteins. The presence of bulky GM3 headgroups may also limit the access to hydrophobic parts of the membrane, which can affect proteins with exposed hydrophobic patches.
From Fig. 2(A) it is inferred that the Gal and NeuAc are more accessible to water molecules than Glc, which is the closest GM3 headgroup residue to the hydrophilic–hydrophobic interface of the bilayer. The time-dependent position of the GM3 headgroup relative to the bilayer surface in a DMPC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) GM3 47
GM3 47![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 bilayer has previously been investigated using all-atom MD simulations using the GLYCAM0665 force field and validated with 3J-coupling constants and NOE distances from NMR together with crystallographic data.27 It was shown that the Lee–Richards molecular surface66 is around 25% for Glc, 75% for Gal and close to 100% for NeuAc, where solvent exposure of residues increases with distance from the bilayer. In the same study it was also found that the glycosidic torsion angle for Gal–Glc pair is smaller than for the NeuAc–Gal pair. This is consistent with the values of |SCH| we obtained, which are smaller for NeuAc. The |SCH| values in this report are directly related to the angle of C–H bonds relative to the bilayer normal and are complementary to values of J-coupling and NOE that give information on dihedral torsion angles and internuclear distances, respectively.
1 bilayer has previously been investigated using all-atom MD simulations using the GLYCAM0665 force field and validated with 3J-coupling constants and NOE distances from NMR together with crystallographic data.27 It was shown that the Lee–Richards molecular surface66 is around 25% for Glc, 75% for Gal and close to 100% for NeuAc, where solvent exposure of residues increases with distance from the bilayer. In the same study it was also found that the glycosidic torsion angle for Gal–Glc pair is smaller than for the NeuAc–Gal pair. This is consistent with the values of |SCH| we obtained, which are smaller for NeuAc. The |SCH| values in this report are directly related to the angle of C–H bonds relative to the bilayer normal and are complementary to values of J-coupling and NOE that give information on dihedral torsion angles and internuclear distances, respectively.
The present data can be compared to previous studies of the properties of the headgroup layer in ganglioside containing bilayers. The position and orientation relative to the membrane surface of ganglioside GM1 in DMPC bicelles has previously been investigated using NMR paramagnetic relaxation enhancement (PRE) together with all-atom MD simulations.67 In these systems, GM1 showed similar behavior with respect to solvent exposure as what is here shown for GM3 in Fig. 2 and in both cases the residues closest to the membrane surface are shielded from the solvent by phosphocholine groups. It is here important to point out that the headgroup of GM1 is branched and contains two more sugar residues than GM3. Because of averaging of the molecular positions on the time scale of an NMR experiment, the variance in calculated PREs using an ensemble of GM1 structures also showed that there is a large conformational heterogeneity in the glycosidic linkages of the terminal Gal and NeuAc residues of the GM1 headgroup. This effect coincides with the small values of |SCH| for the terminal NeuAc residue of our system in Fig. 4, which shows that the amplitude of C–H reorientations is relatively large for these segments.
Slow dynamics in the GM3 headgroup
We observed the following hierarchy of motional rates in the POPC-GM3 bilayer on the τe scale: methyl groups and phosphocholine < hydrophobic tails < POPC hydrophilic–hydrophobic interface < GM3 headgroup and interface. Values of τe were especially large for the GM3 headgroup and hydrophilic–hydrophobic interface regions compared to the rest of the bilayer. While there are no other reported τe values for gangliosides in the literature, studies on the branched, six-residue long and doubly negatively charged GD1a in detergent (dodecylphosphocholine, DPC) micelles showed that the corresponding R1 values for the headgroup are similar to our results (approximately 2 s−1 on average throughout the headgroup in both cases) while R1ρ values are up to five-fold smaller (compare 8.9 s−1 to our result 10–50 s−1).68 The latter discrepancy is explained by the fast tumbling time (5 ns) of the DPC micelles, whereas the time scale of motions that contribute to isotropic reorientation are many orders of magnitude longer for the bilayers in our experiments.We observed a longer τe and greater R1ρ values for almost all POPC segments in the presence of 30 mol% GM3 in the bilayer as compared to the bilayer composed of only POPC. From the MD simulations it is inferred that the effects of GM3 are strongest for the hydrophilic–hydrophobic interface region. This can be compared to the effects of other additives on phosphocholine molecular dynamics. It has been shown that addition of cholesterol to a POPC bilayer leads to a rough doubling of R1ρ-values for segments in the interface and hydrophobic tails region of POPC, which was interpreted as a slowdown of the whole-lipid rotational diffusion rather than of the internal motions.30 Interestingly the POPC headgroup dynamics observed by Antila et al. was unaffected by the addition of cholesterol, which indicated that the dynamics of the phosphocholine is decoupled from the main body of the lipid. In our experiments, the POPC headgroup is affected on a similar scale as other segments in the presence of the large GM3 headgroup. It is finally noted that the present results for the phosphocholine headgroups in the bilayer composed of only POPC are consistent with previous reports for similar systems.30,31
Ordering of GM3 headgroups and implications for lateral heterogeneity in bilayers
The orientation and interactions between the GM3 headgroups at the bilayer interface can strongly impact the overall lipid organization in the bilayer. Gangliosides have been reported to distribute heterogeneously in a POPC membrane,69 which may be driven by favorable ganglioside–ganglioside headgroup interactions.70 Early MD simulations of an all-atom GM3 bilayer using a force field derived from GROMOS8771 was validated using wide-angle X-ray experiments and showed that, as opposed to phosphocholines, there is a strong headgroup–headgroup correlation on the scale of 0.4 nm for GM3 that depends on the branched nature and asphericity of the sugar rings.72 No clear correlations on such a scale are visible in our simulation snapshots in Fig. 2(A).More recently, it was shown from all-atom MD simulations that in a POPC membrane GM3 may form clusters that are more ordered and larger than in the corresponding membrane with GM1.70 In these simulations GM3 lipids are packed tightly and almost parallel to each other, where the headgroups adopt planar structures with extensive hydrogen bonding between neighboring molecules. This tight packing of the headgroups and the parallel orientations of the Gal and Glc residues are consistent with our experimental |SCH| values, that are highest in the headgroup Gal–Glc residues and interface regions of GM3. This means that the I1–I4 and II1–II4 vectors in the GM3 headgroup are oriented parallel to the bilayer normal and that the amplitudes of C–H reorientations are small. In analogy with the mechanism for cellulose insolubility in water,73 stacking of carbohydrate groups in adjacent molecules may be driven by hydrophobic interactions between the faces of the pyranose ring planes.74 However, our high |SCH| values are observed in the absence of tight packing or clusters in the MD simulations, which indicates that the high order is rather related to the conformational rigidity of the pyranose rings.
Quantitative comparisons between the MD and NMR results
MD simulations and NMR spectroscopy are synergistic methods since they both, in principle, offer atomic resolution information on the lipid molecular dynamics. It is possible to directly calculate and compare |SCH| and τe from the MD trajectory (via the correlation function and spectral density) with values obtained from NMR measurements on lipid bilayers. The CHARMM36 force field with TIP3P water can reproduce τe values within experimental uncertainty for a POPC bilayer and capture the qualitative changes when cholesterol is present in the bilayer.30 In those simulations, τe values are often underestimated for the hydrophobic tails while overestimated for the hydrophobic–hydrophilic interface.From the comparisons in Fig. 4–6 we conclude an overall good agreement between the MD and NMR data, but that there are also some clear discrepancies. In line with the previous observations, |SCH| was overestimated for almost all segments of GM3 and POPC while τe values were overestimated for the GM3 headgroup and interface segments. Overestimation of |SCH| has been discussed in terms of incorrect dihedral angle parameters in the MD model or lateral heterogeneity in the bilayer.63 MD simulations are carried out with a small periodic set of molecules on a short time scale compared to NMR experiments. As such, it is difficult to capture the influence of slow motions that are responsible for the behavior of g(τ) beyond the initial fast decay due to rotational diffusion of single molecules and bonds. A relatively small MD system compared to an experimental sample can also have problems with capturing the effect of collective or concerted motions about several bonds or different/neighboring chains. The parameterization of the force field can also be tuned to reduce the mismatch between experiment and simulation to reproduce experimental results more accurately.
When peaks overlap in the NMR spectra, atomic resolution is lost and direct comparison with MD results becomes difficult; the low resolution of the 30 ppm region with signals from the hydrophobic tails (Fig. 3) led to missing τe values for these segments in Fig. 4–6. From peak overlap in the 1D spectrum some peaks will have less reliable relaxation values, for example the I1 and II1 segments of the GM3 headgroup. In the case of complete overlap only an average can be measured, while for partial overlap deconvolution can be attempted. The good qualitative agreement between our MD and NMR results allows the use of the simulation data to interpret the gaps in the experimental results. The MD results for multiple atoms with the same chemical shift could also be combined for a more direct comparison with NMR results. This approach would however also require estimation of the CP and INEPT efficiency.
Conclusions
The atomic-resolution behavior of specific lipids like gangliosides in lipid membranes are useful for understanding their effects on the physical properties of the membrane and how they may modulate membrane interactions with other biomolecules. Our all-atom MD simulation results on a POPC bilayer with and without 30 mol% ganglioside GM3 are compared to experimental NMR results that include measurements of residual dipolar couplings, R1 and R1ρ relaxation rates in terms of molecular profiles of C–H order parameters |SCH| and effective correlation times τe. The results can be summarized in two main observations:(I) The most prominent feature of the GM3-POPC bilayer is the high values of |SCH| and τe obtained for molecular segments in the headgroup and hydrophilic–hydrophobic interface of GM3. Because of the role of gangliosides as surface-recognition molecules, a detailed view of the structure of the GM3 headgroup residues is important for understanding how GM3 is presented to binding partners in the headgroup layer at the membrane. Values of τe for headgroup segments can be used to gain atomically resolved mechanistic information on interaction with other molecules, for example in the presence of a protein that binds selectively to GM3 in membranes.
(II) The presence of 30 mol% GM3 in the bilayer leads to increased |SCH| and τe for basically all molecular segments of POPC. This type of information can be used to understand how the atomic-scale properties of individual C–H bonds are connected to the physical properties of lipid membranes and how these properties are affected by the presence of specific lipids like gangliosides.
The main relevance of this work is to reveal atomic-resolution structural and dynamic behavior of GM3 in a lipid membrane. We believe that the results presented here may be an important contribution to the underlying mechanisms of how gangliosides in lipid membranes interact with other biomolecules.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Knut and Alice Wallenberg foundation (E. S. and D. T.). The simulations were enabled by resources provided by the Swedish National Infrastructure for Computing (SNIC) at the Center for Scientific and Technical Computing at Lund University (LUNARC).References
- O. G. Mouritsen and L. A. Bagatolli, Life-as a matter of fat: lipids in a membrane biophysics perspective, Springer, 2015 Search PubMed.
- J. N. Israelachvili, D. J. Mitchell and B. W. Ninham, J. Chem. Soc., Faraday Trans. 2, 1976, 72, 1525–1568 RSC.
- A. G. Lee, Biochim. Biophys. Acta, Biomembr., 2004, 1666, 62–87 CrossRef CAS PubMed.
- A. Whited and A. Johs, Chem. Phys. Lipids, 2015, 192, 51–59 CrossRef CAS PubMed.
- M. Hato, H. Minamikawa, K. Tamada, T. Baba and Y. Tanabe, Adv. Colloid Interface Sci., 1999, 80, 233–270 CrossRef CAS PubMed.
- A. Fujita, J. Cheng, M. Hirakawa, K. Furukawa, S. Kusunoki and T. Fujimoto, Mol. Biol. Cell, 2007, 18, 2112–2122 CrossRef CAS PubMed.
- R. Gaspar, J. Pallbo, U. Weininger, S. Linse and E. Sparr, Biochim. Biophys. Acta, Proteins Proteomics, 2018, 1866, 1062–1072 CrossRef CAS PubMed.
- T. Hoshino, M. I. Mahmood, K. Mori and K. Matsuzaki, J. Phys. Chem. B, 2013, 117, 8085–8094 CrossRef CAS PubMed.
- T. Kolter, Int. Scholarly Res. Not., 2012, 2012, 506160 Search PubMed.
- K. Palmano, A. Rowan, R. Guillermo, J. Guan and P. McJarrow, Nutrients, 2015, 7, 3891–3913 CrossRef CAS PubMed.
- C.-L. Schengrund, Trends Biochem. Sci., 2015, 40, 397–406 CrossRef CAS PubMed.
- M. L. Allende and R. L. Proia, Curr. Opin. Struct. Biol., 2002, 12, 587–592 CrossRef CAS PubMed.
- P. H. Lopez and R. L. Schnaar, Curr. Opin. Struct. Biol., 2009, 19, 549–557 CrossRef CAS PubMed.
- N. Prokazova, N. Samovilova, E. Gracheva and N. Golovanova, Biochem., 2009, 74, 235–249 CAS.
- R. L. Schnaar, Adv. Carbohydr. Chem. Biochem., 2019, 76, 113–148 CrossRef PubMed.
- J.-i Inokuchi, K.-i Inamori, K. Kabayama, M. Nagafuku, S. Uemura, S. Go, A. Suzuki, I. Ohno, H. Kanoh and F. Shishido, Prog. Mol. Biol. Transl. Sci., 2018, 156, 151–195 CAS.
- T. Yamashita, A. Hashiramoto, M. Haluzik, H. Mizukami, S. Beck, A. Norton, M. Kono, S. Tsuji, J. L. Daniotti and N. Werth, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 3445–3449 CrossRef CAS PubMed.
- J.-i Inokuchi, Glycoconjugate J., 2014, 31, 193–197 CrossRef CAS PubMed.
- C. Zheng, M. Terreni, M. Sollogoub and Y. Zhang, Curr. Med. Chem., 2019, 26, 2933–2947 CrossRef CAS PubMed.
- H. Sohn, Y.-S. Kim, H.-T. Kim, C.-H. Kim, E.-W. Cho, H.-Y. Kang, N.-S. Kim, C.-H. Kim, S. E. Ryu and J.-H. Lee, FASEB J., 2006, 20, 1248–1250 CrossRef CAS PubMed.
- A. Leftin and M. F. Brown, Biochim. Biophys. Acta, Biomembr., 2011, 1808, 818–839 CrossRef CAS PubMed.
- H. Walderhaug, O. Soederman and P. Stilbs, J. Phys. Chem., 1984, 88, 1655–1662 CrossRef CAS.
- H. Wennerström and B. Lindman, Phys. Rep., 1979, 52, 1–86 CrossRef.
- J. B. Klauda, N. V. Eldho, K. Gawrisch, B. R. Brooks and R. W. Pastor, J. Phys. Chem. B, 2008, 112, 5924–5929 CrossRef CAS PubMed.
- G. Lipari and A. Szabo, J. Am. Chem. Soc., 1982, 104, 4546–4559 CrossRef CAS.
- M. Pappalardo, D. Milardi, D. Grasso and C. La Rosa, J. Therm. Anal. Calorim., 2005, 80, 413–418 CrossRef CAS.
- M. L. DeMarco and R. J. Woods, Glycobiology, 2009, 19, 344–355 CrossRef CAS PubMed.
- S. V. Dvinskikh, V. Castro and D. Sandström, Phys. Chem. Chem. Phys., 2005, 7, 607–613 RSC.
- P. Schanda and M. Ernst, Prog. Nucl. Magn. Reson. Spectrosc., 2016, 96, 1–46 CrossRef CAS PubMed.
- H. S. Antila, A. Wurl, O. S. Ollila, M. S. Miettinen and T. M. Ferreira, Biophys. J., 2022, 121, 68–78 CrossRef CAS PubMed.
- T. M. Ferreira, O. S. Ollila, R. Pigliapochi, A. P. Dabkowska and D. Topgaard, J. Chem. Phys., 2015, 142, 044905 CrossRef PubMed.
- Q. D. Pham, D. Topgaard and E. Sparr, Langmuir, 2015, 31, 11067–11077 CrossRef CAS PubMed.
- A. A. Smith, M. Ernst and B. H. Meier, Angew. Chem., 2017, 129, 13778–13783 CrossRef.
- O. Fisette, P. Lagüe, S. Gagné and S. Morin, J. Biotechnol. Biomed., 2012, 2012, 254208 Search PubMed.
- J. Kowalewski and L. Mäler, Nuclear Spin Relaxation in Liquids: Theory, Experiments, and Applications, 2006 Search PubMed.
- J. B. Klauda, R. M. Venable, J. A. Freites, J. W. O’Connor, D. J. Tobias, C. Mondragon-Ramirez, I. Vorobyov, A. D. MacKerell Jr and R. W. Pastor, J. Phys. Chem. B, 2010, 114, 7830–7843 CrossRef CAS PubMed.
- W. Jorgensen, J. Chandrasekhar, J. Madura, R. Impey and M. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- A. D. MacKerell Jr, D. Bashford, M. Bellott, R. L. Dunbrack Jr, J. D. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo and S. Ha, J. Phys. Chem. B, 1998, 102, 3586–3616 CrossRef PubMed.
- J. Lee, D. S. Patel, J. Ståhle, S.-J. Park, N. R. Kern, S. Kim, J. Lee, X. Cheng, M. A. Valvano and O. Holst, J. Chem. Theory Comput., 2018, 15, 775–786 CrossRef PubMed.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1, 19–25 CrossRef.
- W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695 CrossRef PubMed.
- S. Nosé, Mol. Phys., 1984, 52, 255–268 CrossRef.
- M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef CAS.
- Persistence of Vision Raytracer (Version 3.6), Persistence of Vision Pty. Ltd., 2004 Search PubMed.
- MATLAB. 9.8.0.1451342 (R2020a), The MathWorks Inc., 2020 Search PubMed.
- The NMRlipids project, http://nmrlipids.blogspot.com, (accessed May, 2022).
- NMRlipids GitHub respository, https://github.com/NMRLipids/nmrlipids.blogspot.fi, (accessed May, 2022).
- A. Botan, F. Favela-Rosales, P. F. Fuchs, M. Javanainen, M. Kanduč, W. Kulig, A. Lamberg, C. Loison, A. Lyubartsev and M. S. Miettinen, J. Phys. Chem. B, 2015, 119, 15075–15088 CrossRef CAS PubMed.
- A. Nowacka, N. Bongartz, O. Ollila, T. Nylander and D. Topgaard, J. Magn. Reson., 2013, 230, 165–175 CrossRef CAS PubMed.
- R. K. Harris, Nuclear Magnetic Resonance Spectroscopy, Wiley, Cambridge, 1987 Search PubMed.
- J. Becker, A. Comotti, R. Simonutti, P. Sozzani and K. Saalwächter, J. Phys. Chem. B, 2005, 109, 23285–23294 CrossRef CAS PubMed.
- G. A. Morris, J. Am. Chem. Soc., 1980, 102, 428–429 CrossRef CAS.
- A. Pines, M. G. Gibby and J. Waugh, J. Chem. Phys., 1973, 59, 569–590 CrossRef CAS.
- B. Fung, A. Khitrin and K. Ermolaev, J. Magn. Reson., 2000, 142, 97–101 CrossRef CAS PubMed.
- A. Bax, D. G. Davis and S. K. Sarkar, J. Magn. Reson., 1985, 63, 230–234 CAS.
- S. V. Dvinskikh, H. Zimmermann, A. Maliniak and D. Sandström, J. Magn. Reson., 2004, 168, 194–201 CrossRef CAS PubMed.
- D. A. Torchia, J. Magn. Reson., 1978, 30, 613–616 CAS.
- J. D. van Beek, J. Magn. Reson., 2007, 187, 19–26 CrossRef CAS PubMed.
- A. Gansmüller, J.-P. Simorre and S. Hediger, J. Magn. Reson., 2013, 234, 154–164 CrossRef PubMed.
- J. Charvolin and A. Tardieu, Solid State Phys., 1978, 14, 209–257 CAS.
- V. Luzzati and F. Husson, J. Cell Biol., 1962, 12, 207–219 CrossRef CAS PubMed.
- W. L. Earl and D. VanderHart, Macromolecules, 1979, 12, 762–767 CrossRef CAS.
- T. M. Ferreira, F. Coreta-Gomes, O. S. Ollila, M. J. Moreno, W. L. Vaz and D. Topgaard, Phys. Chem. Chem. Phys., 2013, 15, 1976–1989 RSC.
- L. O. Sillerud, R. K. Yu and D. E. Schafer, Biochemistry, 1982, 21, 1260–1271 CrossRef CAS PubMed.
- K. N. Kirschner, A. B. Yongye, S. M. Tschampel, J. González-Outeiriño, C. R. Daniels, B. L. Foley and R. J. Woods, J. Comput. Chem., 2008, 29, 622–655 CrossRef CAS PubMed.
- B. Lee and F. M. Richards, J. Mol. Biol., 1971, 55, 379–IN374 CrossRef CAS PubMed.
- M. L. DeMarco, R. J. Woods, J. H. Prestegard and F. Tian, J. Am. Chem. Soc., 2010, 132, 1334–1338 CrossRef CAS PubMed.
- L. Poppe, H. Van Halbeek, D. Acquotti and S. Sonnino, Biophys. J., 1994, 66, 1642–1652 CrossRef CAS PubMed.
- C. Yuan, J. Furlong, P. Burgos and L. J. Johnston, Biophys. J., 2002, 82, 2526–2535 CrossRef CAS PubMed.
- R.-X. Gu, H. I. Ingólfsson, A. H. De Vries, S. J. Marrink and D. P. Tieleman, J. Phys. Chem. B, 2017, 121, 3262–3275 CrossRef CAS PubMed.
- W. F. van Gunsteren and H. J. Berendsen, Groningen molecular simulation (GROMOS) library manual, Biomos, Groningen, 1987, vol. 24, p. 13 Search PubMed.
- M. Sega, R. Vallauri, P. Brocca, L. Cantù and S. Melchionna, J. Phys. Chem. B, 2007, 111, 10965–10969 CrossRef CAS PubMed.
- B. Medronho, A. Romano, M. G. Miguel, L. Stigsson and B. Lindman, Cellulose, 2012, 19, 581–587 CrossRef CAS.
- C. Yamane, T. Aoyagi, M. Ago, K. Sato, K. Okajima and T. Takahashi, Polym. J., 2006, 38, 819–826 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp02860c |
| This journal is © the Owner Societies 2022 |

