Quantum and quasi-classical dynamics of the C(³P) + O₂(³Σ⁻_g) → CO(¹Σ⁺) + O(¹D) reaction on its electronic ground state

Abstract

The dynamics of the C(³P) + O₂(³Σ⁻_g) → CO(¹Σ⁺) + O(¹D) reaction on its electronic ground state is investigated by using time-dependent wave packet propagation (TDWP) and quasi-classical trajectory (QCT) simulations. For the moderate collision energies considered (E_c = 0.001 to 0.4 eV, corresponding to a range from 10 K to 4600 K) the total reaction probabilities from the two different treatments of the nuclear dynamics agree very favourably. The undulations present in P(E) from the quantum mechanical treatment can be related to stabilization of the intermediate CO₂ complex with lifetimes on the 0.05 ps time scale. This is also confirmed from direct analysis of the TDWP simulations and QCT trajectories. Product diatom vibrational and rotational level resolved state-to-state reaction probabilities from TDWP and QCT simulations agree well except for the highest product vibrational states (v′ ≥ 15) and for the lowest product rotational states (j′ ≤ 10). Opening of the product vibrational level CO(v′ = 17) requires ∼0.2 eV from QCT and TDWP simulations with O₂(j = 0) and decreases to 0.04 eV if all initial rotational states are included in the QCT analysis, compared with E_c > 0.04 eV obtained from experiments. It is thus concluded that QCT simulations are suitable for investigating and realistically describe the C(³P) + O₂(³Σ⁻_g) → CO(¹Σ⁺) + O(¹D) reaction down to low collision energies when compared with results from a quantum mechanical treatment using TDWPs.

---

1 Introduction

Reactions involving carbon and oxygen atoms play a vital role in the atmosphere, in combustion, and in hypersonic flow.¹ Among all, the C(³P) + O₂(³Σ⁻_g) ↔ CO(¹Σ⁺) + O(¹D)/O(³P) reaction involving the CO₂ intermediate and several electronic states is particularly important and has, therefore, been investigated both, experimentally and through computations.^2–21 The electronic ground and excited state potential energy surfaces (PESs) were studied computationally in detail at different levels of theory^12,21–27 and various dynamics simulations were also carried out for this system.^{13,15,21,28,29}

One of the latest investigations for the entire C(³P) + O₂(³Σ⁻_g) ↔ CO₂ ↔ CO(¹Σ⁺) + O(¹D)/O(³P) reaction was carried out using quasi-classical trajectory (QCT) simulations with kernel-represented PESs based on extensive multi reference configuration interaction (MRCI) calculations.²¹ The focus was more on the high-temperature regime of the reaction also because experimental and computational data from shock tube experiments for the C + O₂ → CO + O reaction between 1500–4200 K was available.^9,13 The latest QCT simulations reported the forward and backward thermal rates for the lowest five electronic states together with vibrational relaxation times.²¹ However, the state-to-state dynamics was not considered and the question remains whether a classical framework is suitable when compared with results from a quantum mechanical treatment of the nuclear dynamics.

One recurrent theme for atom + diatom reactions concerns the range of applicability of quasi-classical-based dynamics approaches for computing thermal rates and final state distributions. Cross sections and thermal rates are averaged over initial and/or final ro-vibrational resolved state-to-state information. Thus, although more or less heavily averaged quantities may favourably agree between different approaches, it is possible that such agreement arises from the averaging process. Hence, it is also relevant to compare properties at the state-to-state level. All such quantities are essential as input to more coarse-grained investigations of reaction networks as they appear in hypersonics, combustion, atmospheric and astrophysical chemistry.³⁰ Because QCT simulations are computationally more efficient, they are often used instead of and also along with more time-consuming quantum nuclear dynamics simulations.^31–35

Quantum mechanical and QCT approaches were used to evaluate reaction probabilities and rates for the C + OH reaction and were found to be in fairly good agreement.^36–38 For the S + OH reaction quantum mechanical and QCT simulations produced excellent agreement for cross sections but only fair agreement for the total reaction probabilities and thermal rates.^32,39 Comprehensive QCT and QM dynamics investigations for the Br + H₂ and O + HCl reactions reported favourable agreement between QM and QCT results for properties such as reaction probabilities, integral and differential cross sections.^40,41 Similar to the S + OH reaction, for N + H₂ results from QM and QCT simulations agree favourably for cross sections but not so well for reaction probabilities.⁴²

For the S + OH reaction it has been specifically reported that for reactive collisions a more general relationship between the mechanistic details of the dynamics and the ensuing rates can be difficult to obtain.³² Nonetheless, it is generally believed that the dynamical features of an exoergic and barrierless reaction primarily depend on the masses of the participating atoms, the exoergicity and the topographical details of the underlying PES.^32,43,44 To better understand the origins of the observed dynamics systematic investigations have been carried out for different systems.^38,43–47 As an example, for the C + OH reactive collisions^38,43,44 it was found that reagent vibrational excitation decreased reactivity on the first electronically excited PES and enhances reactivity on the second excited state. The excess vibrational energy is transferred into product translational energy for the first excited PES whereas for the second excited state it is transferred into product vibration and rotation. These dynamical effects on the final states are caused by the topology of the underlying PESs which have no barrier to products for the first electronically excited state but involve a late barrier for the second excited state.

The reaction C(³P) + O₂(³Σ⁻_g) → CO(¹Σ⁺) + O(¹D)/O(³P) using its five lowest lying states (¹A′, ³A′, ³A′′, ¹A′′ and (2)¹A′) is a particularly suitable system for such an investigation due to the availability of high-quality, full-dimensional PESs which were recently validated vis-a-vis experiment.²¹ The exoergicity of the three singlet and two triplet states are ∼3.8 eV and ∼5.9 eV, respectively.²¹ Therefore, the difference in the dynamical attributes on the singlet and triplet states is expected to arise solely from the topographical details of the underlying surfaces.³²

Quantum mechanics-based dynamics approaches can become computationally expensive for barrierless exoergic reactions with deep wells.^{32,38,43,44,48,49} Thus, QCT approaches are an attractive alternative, at least at the qualitative level. In the present work the initial state-selected and state-to-state reaction probabilities for the C(³P) + O₂(³Σ⁻_g) → CO(¹Σ⁺) + O(¹D) reaction on the electronic ground (¹A′) state are determined for low to moderate collision energies (E_c ≤ 0.4 eV) by TDWP and QCT approaches. Total reaction probabilities and final state distributions are determined for a range of collision energies and allow to compare the two dynamics methods in terms of their findings and with experiment. The work is organized as follows. First the methods used are described. Then, the convergence of the TDWP simulations is assessed, followed by results for the total reaction probabilities and the product vibrational resolved reaction probabilities from TDWP and QCT simulations. Next, product vibrational and rotational state distributions are determined and compared. Finally, the computational results are discussed in the context of experiments and in a broader sense.

2 Methods

2.1 Time dependent wavepacket calculations

State-to-state quantum dynamics was investigated using the modified DIFFREALWAVE code which is based on propagating real wave packets (RWP).^50,51 Here only a summary of the method employed is given as the theory has been described extensively elsewhere.^44,50–53 The RWP approach is advantageous from a computational perspective as the formalism requires only the real part of the wave packet (WP) to be propagated for obtaining the state-to-state S-matrix elements. An initial WP, q_A(R_A, r_A, γ_A, t = 0) is prepared in the asymptotic reactant channel with the geometry described in a Jacobi coordinate system (R_A: distance of atom A from the center-of-mass of BC, r_A: BC internuclear distance and γ_A: approach angle of A to the center-of-mass of BC), see Fig. 1. The real part of such a WP in this coordinate system takes the form^44,52,53The parameters α and β_s define the width and the smoothness of the WP, respectively,⁵⁴k₀ is the initial momentum of the WP centered at R₀, ϕ^BC_vj and P^Ω_j (cos γ_a) represent the ro-vibrational eigenfunction of BC and the associated Legendre polynomials, respectively, and v and j are the initial vibrational and rotational levels of the reactant diatom.

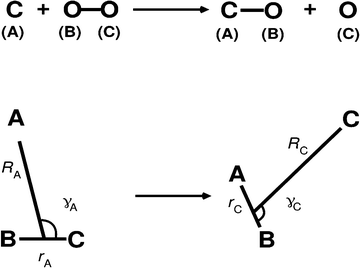Fig. 1 Reactant (left) and product (right) collision geometries in body-fixed Jacobi coordinates for the present TDWP simulations.

The initial WP (eqn (1)) is subsequently transformed to product state Jacobi coordinates (R_C, r_C, γ_C) with C as atom and AB as diatom, see right-bottom part of Fig. 1, according to⁵²

Here N, , β and Ω′ are normalization, the reduced Wigner matrix, the angle between the two vectors, R_C and R_A, and the projection of the total angular momentum J on the body-fixed Z-axis of the product Jacobi coordinates, respectively.

The action of the nuclear Hamiltonian Ĥ_nuc, formulated in product Jacobi coordinates, Ĥ_nuc, on the WP is^52,55

Here and in what follows, the coordinate dependence of the WPs, , and is omitted for clarity. The terms and represent the three body and product diatom reduced masses, respectively. The action of the radial kinetic energy part of the Hamiltonian is carried out using fast Fourier transformation techniques.⁵⁶ For the action of the angular kinetic energy part a discrete variable representation based on Gauss–Legendre quadrature is used.^57–59 The effect of the potential energy operator, V̂(R_C,r_C,γ_C), on the WP is multiplicative on the coordinate grid and the last two terms of eqn (3) denote the Coriolis coupling and lead to mixing of the WP, 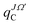with other WPs, and as shown in the eqn (3).

The propagated WP at the first time step, τ₁, is evaluated according to

where denotes the imaginary part of the initial WP (see eqn (1) and (2)). For the subsequent time propagation a three term recursion is usedwhere τ is the discrete time step. In eqn (4) and (5), Ĥ_nuc,s represents the scaled and shifted Hamiltonian whose minimum and maximum eigenvalues lie between −1 and +1.⁵¹

As is customary for TDWP simulations, spurious reflections of the WP components from the finite sized grid edges at longer propagation time need to be damped. This is done by multiplying the wavepacket with a double exponential damping function⁵²a(y) along coordinates y = R_c, r_c

a(y) = exp[−c_absexp(−2(y_max − y_abs)/(y − y_abs))] (6)

according to , where c_abs and y_abs represent the strength and the starting point of the absorption, respectively. The absorption is applicable for y > y_abs and the value of the function is equal to 1 elsewhere.

The propagated WP is projected on ro-vibrational levels of the product diatom at the product asymptote (R = R_∞) to obtain the time-dependent coefficients⁵²

The term, in eqn (7) represents the (v′, j′) state of the product diatom AB. The time-dependent coefficients are Fourier transformed to obtain energy dependent coefficients, in the body fixed frame and then are transformed to the space fixed frame from which the scattering matrix (S-matrix) elements, are obtained. These S-matrix elements are finally transferred back to the body-fixed frame to yield from which energy dependent state-to-state reaction probabilities are obtained according toTotal reaction and product internal level resolved probabilities are calculated by summing up the probabilities of eqn (8) over relevant quantum numbers. Summation over all three quantum numbers, (Ω′, j′, v′) yields the energy resolved total reaction probabilities. For further details, see ref. 52.

2.2 Quasi classical trajectory simulations

The QCT simulations in the present investigation were carried out following earlier work²¹ and based on established procedures.^60–63 Therefore, only specific technical aspects are briefly summarized here.

Hamilton's equations of motion were solved using a fourth order Runge–Kutta method. The initial conditions for initiating the trajectories were sampled by using standard Monte Carlo methods⁶³ and the ro-vibrational levels of reactant and product diatoms are calculated using semiclassical quantization. The simulations are run at several collision energies with a time step of Δt = 0.05 fs which guarantees the conservation of total energy and angular momentum. At each collision energy, 5 × 10⁵ trajectories are run for converged results, except at the two lowest energies, 0.0055 and 0.001022 eV for which 10⁶ trajectories are run for convergence of the total reaction probability for O₂(v = 0, j = 0). It is found that the difference between the total reaction probabilities at these two energies obtained from 5 × 10⁵ and 10⁶ trajectories appears at the fourth decimal place and therefore all remaining calculations are carried out with 5 × 10⁵ trajectory simulations. As the associated quantum numbers are real-valued, their necessary assignment to integer values was made either by using Gaussian binning (GB)^61,64,65 which centers Gaussian weights around the integer values and has a full width at half maximum of 0.1 or from Histogram binning (HB) which rounds to the nearest integer.

The reaction probability at collision energy E_col is obtained as

where N_r(E_col) is the number of reactive trajectories and N_tot(E_col) is the total number of trajectories at a give E_col.

3 Results and discussion

3.1 Convergence of the TDWP approach

The TDWP approach is a grid-based method and the results depend on the parameters characterizing the wavepacket and the underlying grids. In a first step, convergence of the total reaction probability was sought for each parameter. For a particular parameter considered (see Table 1) its value was changed until the total reaction probability remained unchanged, see also Fig. S1 (ESI†). The convergence runs for C + O₂(v = 0, j = 0) were initialized from arbitrary guesses for the parameters and the wave packet propagation was carried out for fewer time steps (25 000 in the present case) than for the final production runs. If convergence was not achieved, the WP was propagated for longer times.

Table 1 Parameters characterizing the TDWP simulations for J = 0 and the wavepacket itself for the C + O₂(v = 0–2, j = 0) → CO + O reaction on its electronic ground (¹A′) state. Simulations for parameter selection for C + O₂(v = 0, j = 0) were initialized from arbitrary guesses for the parameters and the wave packet was propagated for 25 000 time steps or until convergence of the total reaction probability. To determine simulation parameters for initial C + O₂(v = 1–2, j = 0) exploration of parameter space started from the converged values for C + O₂(v = 0, j = 0) and explored parameters in their vicinity. Additional runs were also performed at values more distant from the converged values to confirm convergence. The parameters for O₂(v = 1–2, j = 0) were found to be converged at the converged values of O₂(v = 0, j = 0), see also Fig. S1 (ESI)

Parameter	Value	Description
N R/Nr/Nγ	499/419/240	Number of grid points for product Jacobi coordinates (RC, rC, γC)
R min/Rmax (a0)	2.2/22.0	Extension of the grid along RC
r min/rmax (a0)	1.5/17.9902	Extension of the grid along rC
R ∞ (a0)	12.5	Location of the dividing surface in the product channel
R abs/rabs (a0)	14.0/14.75	Starting point of the absorption function along RC and rC
C abs/cabs	30.0/30.0	Strength of the absorption along RC and rC
R 0 (a0)	13.2	Center of the initial wave packet in reactant Jacobi coordinate
E trans (eV)	0.115	Initial translational energy in eV
α	12.0	Width of the initial wave packet
β s	0.5	Smoothing of the initial wave packet

---

Convergence runs for all parameters were carried out for J = 0 and for reactant O₂(v = 0, 1, 2, j = 0). The converged parameters are summarized in Table 1 and demonstrate that extensive grids along the three product Jacobi coordinates are required resulting in computationally expensive calculations. The requirement for such large grids is the result of the heavy masses of the interacting atoms and the presence of the deep potential well.²¹ The large number of grid points required along the angular Jacobi coordinate reflects the pronounced angular anisotropy of the underlying PES.

Two-dimensional (2-D) contours of the underlying PES are shown in Fig. 2. The top row reports the PES in reactant Jacobi coordinates for R_OO = r_A = 3.40 a₀, i.e. a stretched geometry of the reactant diatom before C-insertion occurs to form O–C–O (minimum at 90°). Because after formation of the triatom the system only spends little time in this state (typically <0.5 ps, see Discussion section) to move towards the product, it is also of interest to provide a representation of the reactant PES in terms of product Jacobi coordinates (R_C,γ_C) which is shown in the top right panel in Fig. 2. Comparison of the two representations clarifies that spatial symmetry is lost for the product state coordinates and the anisotropy of the PES differs considerably. Similarly, the bottom row reports the PES in product state coordinates for R_CO = r_C = 3.0 a₀, i.e. for the system on its way to form products (left panel) and the same PES represented in reactant state coordinates (R_A,γ_A) in the right hand lower panel of Fig. 2. In addition, representative structures for CO₂ are reported and their location on the PES are indicated by arrows. Two geometries (see black and purple crosses in the top row panels) are chosen to show their positions in the reactant and equivalent product Jacobi coordinates.

Fig. 2 Two-dimensional contour diagrams of the ¹A′ PES for CO₂ for both Jacobi coordinate systems (reactant: R_A,γ_A) and (product: R_C,γ_C). Top: r_OO ∼ 3.4 a₀ for reactant (left) and product (right) coordinates. Bottom: r_CO = 3.0a₀ for product (left) and reactant (right) coordinates. Contours are drawn at −2.0 eV (violet), −3.0 eV (black), −4.0 eV (red), −5.0 eV (blue), −6.0 eV (yellow), −7.0 eV (orange), −8.0 eV (cyan), −9.0 eV (green) which are with respect to the total atomization energy C(³P) + O(³P) + O(³P). In each panel, a representative structure for CO₂ is shown in terms of the respective Jacobi coordinates. Structures for CO₂ (carbon atom grey and oxygen atoms red spheres) near the minima are schematically shown and their position on the PES is indicated with arrows. The black and purple crosses indicate equivalent geometries in the two different Jacobi coordinates.

In the production runs, for O₂(v = 0, j = 0) the number of product vibrational levels included v′ = 0–18 which was suitably increased to v′ = 19 and v′ = 20 with the reactant in its two vibrationally excited states. The WP was propagated for up to 70 000 time steps (corresponding to ∼1.4 ps) in order to obtain converged reaction probabilities for J = 0 and the potential and/or centrifugal cut-off was 0.57E_h.

3.2 Total reaction probabilities

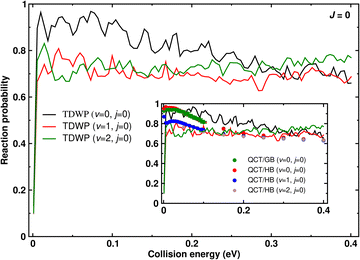
Initial state-selected and energy resolved total reaction probabilities of the C(³P) + O₂(³Σ⁻_g, v = 0–2, j = 0) → CO(¹Σ⁺, ∑v′, ∑j′) + O(¹D) reaction on its electronic ground state (¹A′) are shown as function of collision energy in Fig. 3. These probabilities are calculated for total angular momentum J = 0. The inset compares the TDWP results (solid lines) with the QCT results (solid circles), respectively.

Fig. 3 Initial state-selected and energy resolved total reaction probabilities of the C(³P) + O₂(³Σ⁻_g, v = 0–2, j = 0) → CO(¹Σ⁺, ∑v′, ∑j′) + O(¹D) reaction on its electronic ground state as a function of collision energy for J = 0. The TDWP and QCT probabilities are shown by solid lines and circles, respectively. The red and green circles represent the QCT results obtained by using Histogram and Gaussian binning, respectively, for O₂(v = 0, j = 0). The probabilities at the two lowest collision energies are calculated by running 10⁶ trajectories whereas 5 × 10⁵ trajectories are used for the other energies. The QCT probabilities for O₂(v = 1–2, j = 0) are shown in the inset by blue and brown solid circles. For the interval between 0.01 and 0.1 eV a much denser grid was used for the QCT simulations to probe whether or not undulations appear in the classical simulations.

Fig. 3 shows that starting at low collision energy (E_col = 0.001 eV ≈ 10 K) the TDWP probability for O₂(v = 0, j = 0) rises sharply and oscillates around 0.95 up to E_col ∼ 0.1 eV. Afterwards, the total reaction probability decreases slowly with undulations and reaches P ∼ 0.7 at E_col ∼ 0.4 eV. The non-zero probability for E_col ∼ 10⁻³ eV (Fig. 3) reflects the barrierless nature of this exoergic reaction.²¹ The barrierless and exoergic features of this reaction along with the deep potential well (formation of CO₂) on the underlying PES (cf., Fig. 1 of ref. 21) and the large masses of the participating atoms make the quantum dynamical calculation computationally challenging. The undulations in the total reaction probability (see Fig. 3) are indicative of formation of intermediate collision complexes inside the deep potential well.⁶⁶ However, the higher exoergicity of the reaction facilitates breakup of these complexes and thus shortens their lifetimes. Despite a deeper well on the underlying PES, lower exoergicity could change these undulations into sharp and intense resonance oscillations which was found for the S + OH, C + OH, C + H₂, and S + H₂/D₂/HD reactions.^{32,43,44,67,68}

The reaction probabilities from the wavepacket simulations in Fig. 3 reveal that reactant vibrational excitation decreases the reactivity at low and intermediate collision energies, whereas the reactivity is enhanced for O₂(v = 2, j = 0) at the highest collision energies considered. Undulations for the total reaction probability are also observed for vibrationally excited reactants and analyzed further below.

Next, the reaction probabilities from the QCT simulations are considered and compared with the TDWP results. QCT reaction probabilities are largest for O₂(v = 0, j = 0) and decay with increasing collision energy, see green (GB) and red (HB) circles in the inset of Fig. 3. For O₂(v = 1, j = 0) (blue circles) at low E_col the reaction probability is smaller than for O₂(v = 0, j = 0) but approaches it with increasing collision energy. Interestingly, for O₂(v = 2, j = 0) (brown circles) the QCT reaction probability starts low at low E_col, increases – similar to TDWP – and then also decays towards a comparable amplitude as for v = 1 and v = 0. Compared with the results from TDWP simulations the QCT simulations are in excellent overall agreement except for the lowest collision energies considered. In contrast to TDWP, the QCT results decay monotonically for higher collision energies also for O₂(v = 0, j = 0), (see inset of Fig. 3). With increasing collision energy the QCT probability for all initial v-states converges to the same value (reaction probability ∼0.6). This is also apparently found for the TDWP simulations except for O₂(v = 2). This possibly happens as the opening of energetically higher product (CO) internal levels for vibrationally excited reagent becomes easier at higher collision energies which enhances the reaction probability as a result. Increase of reaction probability (with oscillations) with collision energy is also seen in TDWP investigation of C + OH reaction on its first and second excited states.⁴⁴ The C + OH reaction on its first (barrierless) and second (small barrier at the exit channel) excited states is also exoergic and proceeds through potential wells on the underlying potential energy surface.

The effect of initial translational/collision energy and vibrational energy on reactivity depending on the shape of the underlying PES has been discussed from the perspective of Polanyi's rules: Translational energy is more effective to promote the reactivity for an early barrier reaction, whereas the effect of reactant vibrational energy is more relevant for a reaction with a late barrier.⁴⁵ Furthermore, a more recent investigation of a number of atom + diatom reactions⁴⁶ reveals the importance of a cross over point for the effects of reagent vibrational and translational/collision energy on the reactivity. Therefore, the interplay between initial translational and vibrational energy can play a significant role in reaction dynamics. The present TDWP simulations suggest that with increasing reactant vibrational excitation the reaction probability slightly increases above E_col ∼ 0.3 eV (which approximately corresponds to the energy of the O₂(v = 1) state), also due to the more delocalized nature of the wavepacket which allows for some coupling between translation and vibration. For the QCT simulations such an effect is not observed which is probably due to the short contact time (∼50 fs, see below) which essentially precludes transfer between vibrational and translational degrees of freedom.

3.3 Product vibrational state resolved reaction probabilities

Product vibrational level resolved reaction probabilities for CO(v′ = 0–17) and for J = 0 are shown in Fig. 4 as a function of collision energy. The TDWP probabilities are the solid (black) lines and the QCT(HB) probabilities are the red circles. For comparison, probabilities are also determined from GB for v′ = 16–17 (solid green circles) in Fig. 4. Similar to the total reaction probabilities, undulations are also found in product vibrational level resolved TDWP probabilities, see Fig. 3 and 4. The sharp increase of probability at the low collision energies is not found for low v′. Conversely, the TDWP probabilities for v′ = 9–13 possess significant qualitative similarity with the total reaction probability.

Fig. 4 Product diatom vibrational level resolved state-to-state reaction probabilities for the C(³P) + O₂(³Σ⁻_g, v = 0, j = 0) → CO(¹Σ⁺, v′, Σj′) + O(¹D) reaction on its electronic ground state and for J = 0 as function of collision energy. The probabilities calculated from the TDWP approach and QCT(HB) method are shown by solid (black) lines and solid (red) circles, respectively. Probabilities are also calculated by using QCT(GB) method for v′ = 16–17 and the results are shown by solid green circles. A higher density of points from the QCT simulations is provided for 0.05 < E_col < 0.1 eV in particular to clarify which features from the TDWP simulations are or are not captured, see e.g. v′ = 16. On the other hand it is remarkable that the slopes of the black lines are well captured by the red circles, see e.g. the change for v′ = 9, v′ = 11, and v′ = 14.

A comparison of the state-to-state TDWP and QCT reaction probabilities in Fig. 4 shows that the results are in excellent agreement with each other at all collision energies considered for v′ = 0–8, which is remarkable. However, differences at low collision energies (E_col < 0.05 eV) appear for v′ = [9, 10, 12–14] in that the TDWP results find reaction probabilities that decay to close to zero for the lowest collision energies followed by a pronounced peak whereas for the QCT simulations the reaction probability does not decay to zero for the lowest collision energy considered. A second observation concerns the reaction probability for v′ = 16 for which the quantum results feature a maximum in the reaction probability between E_col = 0.05 and 0.1 eV which is not present in the results from QCT simulations. However, this is expected as QCT simulations are unable to capture features related to resonances due to the neglect of coherences.

The two panels of Fig. 4 for CO(v′ = 16, 17) reveal that TDWP find energy thresholds for product formation for E_col ∼ 0.014 and ∼0.22 eV, respectively. This is in quite good agreement with a value of 0.19 eV for v′ = 17 from recent QCT simulations.²¹ With histogram binning for analyzing the QCT results there is no threshold for CO(v′ = 16) but generating CO(v′ = 17) requires collision energy. Analyzing the same data with GB finds thresholds for CO(v′ = 16, 17), see Fig. 4. For the reaction with vibrational energy in the reactant state C + O₂(v = 1, j = 0), see Fig. S2 (ESI†) the product diatom vibrational level-resolved reaction probabilities from TDWP and QCT simulations compare as well as for O₂(v = 0, j = 0). It can also be seen that reactant vibrational excitation has an insignificant effect on product vibrational level resolved reaction probabilities.

3.4 Product vibrational state distributions

The product (CO) diatom vibrational level distributions P(v′) at five different collision energies for the C + O₂(v = 0–2, j = 0) reaction and with J = 0 are shown in Fig. 5 from TDWP (open circles) and QCT (red circles) simulations. Overall, the final state distributions from the two approaches agree favourably although P(v′) from QCT simulations are smoother than those from the TDWP simulations. This is particularly prevalent for low collision energies and for initial v = 0. With increasing vibrational excitation in the reactant P(v′) from the TDWP simulations also become smoother and the results from QCT overlap closely with them. Compared with earlier work on the C + OH reaction the present results indicate somewhat closer agreement between the TDWP and QCT approaches, in particular with regards to pronounced minima and maxima at intermediate values of v′ in P(v′) from the TDWP simulations.⁶⁹ It is also noteworthy to mention here that although the TDWP and QCT total reaction probabilities for O₂(v = 2, j = 0) differ at higher energies (Fig. 3), the vibrational distributions at E_col ∼ 0.3 eV and 0.4 eV agree reasonably well except for high v′ ≥ 15, see Fig. 5.

Fig. 5 Product diatom vibrational level distributions at five different collision energies (E_col) for the C + O₂(v = 0–2, j = 0) reaction, by means of reaction probabilities of J = 0. The results calculated by employing the TDWP and QCT approaches are shown by black lines with open circle and solid red circles, respectively. The QCT probabilities from using the HB and GB methods are the red and green spheres, respectively.

The feature that agrees most closely between the TDWP and QCT approaches is the value for v′ beyond which the final state probability P(v′) decays to zero. Also, for low collision energy and most of the distributions emerging from O₂(v = 0, j = 0) the TDWP and QCT results for low v′ agree favourably. On the other hand there are also differences in P(v′) from the two approaches which concern P(v′) for low vibrational quantum numbers, see e.g. all initial v-states for E_col = 0.4 eV or most of the distributions for O₂(v = 2, j = 0). In addition, there are features such as the increase in P(v′) for O₂(v = 0, j = 0) at E_col = 0.3 eV around v′ = 10 which are present in the TDWP simulations but absent in the QCT simulations.

It can also be seen from Fig. 5 that with increasing vibrational excitation of the reactant diatom the number of product vibrational state increases. The energy supplied to reactant vibration enhances the total energy of the system and makes the opening of vibrationally excited product channels possible. This suggests that part of the reactant internal energy is transferred/disposed into product vibration. However, a careful look at Fig. 5 reveals that the collision energy and reactant vibrational excitation hardly have any effect on the overall pattern of the distribution and thus it becomes very difficult to find a general/regular trend for the variation of the distribution with these two types of energy.

3.5 Product rotational level distributions

The product diatom rotational level distributions P(j′) of the C + O₂(v = 0–1, j = 0) → CO(∑v′, j′) + O reaction at three different collision energies (E_col ∼ 0.05 eV, 0.3 eV and 0.4 eV) are shown from TDWP (black bars) and QCT simulations (green lines) in Fig. 6a–f. A five-point average (red) for the TDWP distribution in each panel allows for easier comparison with the QCT results. Fig. 6 shows that the agreement of the TDWP and QCT rotational distributions is excellent for moderate and high j′ and also improves with increasing collision energy. Disagreement between the results from the two approaches is found for low j′. The TDWP results predict a peak at low j′ which is missing in the QCT results. A possible explanation for this is the fact that low j′ from QCT simulation is typically associated with separation of the two fragments from a near-collinear geometry which is unlikely to occur given the anisotropy of the PES. On the other hand, due to its spatial extent, the wavepacket samples such regions. Given the small rotational constant of the product, even small rotational energies can lead to appreciable population of low-j′ states.

Fig. 6 Product diatom rotational level distributions of the C + O₂(v = 0–1, j = 0) → CO(∑v′, j′) + O reaction at three different collision energies (E_col) as function of product diatom rotational quantum number j′. The TDWP and QCT results are shown in black bars and green line types, respectively. The red line in each panel represents a 5-point average of the TDWP distributions. The distributions for O₂(v = 0, j = 0) and O₂(v = 1, j = 0) are shown in panels a–c and d–f, respectively.

It can also be seen from each row of Fig. 6 that reactant vibrational excitation does not change the pattern of the distributions. This is observed in both TDWP and QCT results. Thus, similar to the vibrational distributions (Fig. 5), the overall pattern of the rotational distributions is also unaffected by reactant vibrational excitation. However, the peak height of the TDWP distributions at the low j′ gets lowered and the distribution becomes flatter at E_col ∼ 0.4 eV. This is more prominent when the reactant is in its ground ro-vibrational level. Therefore, at higher collision energies the diatom is formed with lower and moderate j′ with almost equal possibility.

4 Discussion and conclusion

The dynamics of the C + O₂(³Σ⁻_g, v = 0–2, j = 0) → CO(¹Σ⁺, v′, j′) + O(¹D) reaction is investigated from TDWP and QCT calculations for J = 0 considering the ¹A′ electronic ground state. The energy resolved total reaction probabilities calculated by these two approaches are in overall excellent agreement with each other except for the lowest collision energies and for reactant O₂(v = 2, j = 0) at higher energies. Enhancement of the reactivity for O₂(v = 2, j = 0) at higher energies is obtained from the WP calculations whereas reactivity predicted by QCT remains insensitive to reactant vibrational excitation. The binning employed in the QCT simulations (Gaussian vs. Histogram binning) is unlikely to affect this as the total reaction probability and the product diatom vibrational distribution from using the two binning schemes is virtually identical, see Fig. 3 and 5.

In addition to the forward C + O₂ reaction, which was the topic up to this point, the thermoneutral atom-exchange, CO_A + O_B → CO_B + O_A, and the endoergic backward CO_A + O_B → C + O_AO_B reactions also take place on the ¹A′ PES. To complete the picture, total reaction probabilities from QCT simulations for these two reactions were calculated up to 6.5 eV collision energy and the results are shown in Fig. 7 as function of collision energy. It can be seen from Fig. 7 that the CO_A (v = 0, j = 0) + O_B → C + O_AO_B reaction has a high energy threshold whereas the atom-exchange reaction is barrierless. Comparison of probabilities shown in Fig. 3 and 7 reveals that the reactivity is highest for the exoergic C + O₂→ CO + O reaction, followed by the atom-exchange reaction. The TDWP approach can also be applied here, however, the parameters shown in Table 1 need to be converged separately for the atom-exchange and endoergic backward reactions which is outside the scope of the present work. Given the good agreement between TDWP and QCT simulations it is, however, expected that the results from Fig. 7 are representative.

Fig. 7 Energy resolved total reaction probabilities of the, CO_A (v = 0, j = 0) + O_B → C + O_AO_B and CO_B + O_A, reaction as function of collision energy and for J = 0, calculated by employing the QCT approach.

The thermoneutral atom-exchange reaction (CO_A + O_B → CO_B + O_A) has already been considered in the context of stabilizing CO₂ on amorphous solid water (ASW) to better understand molecule formation at astrophysical conditions.^70,71 For this process it was found that for bulk temperatures of ∼50 K formation and stabilization of CO₂ is very likely (60% of the trajectories stabilize). Together with the present results this suggests that quantum effects will only marginally affect this conclusion. This is also consistent with results from QCT and TDWP simulations for O(³P) + O(³P) recombination for which quantum mechanical effects were also found to be far less important than effects of ASW surface roughness on the diffusivity and recombination dynamics.^72,73

The undulations in the total reaction probabilities from TDWP simulations (Fig. 3, 4 and Fig. S2, ESI†) are attributed to formation and transient stabilization of the CO₂ intermediate inside the potential well. These are largely unaffected by reactant vibrational excitation, and merit some further discussion. Previous work on the N + OH reaction⁶⁶ has associated a dense pattern of resonances between 0.41 and 0.43 eV with formation of long-lived intermediates in the deep HON well together with a pronounced exoergicity of 1.99 eV of the reaction without, however, providing further support for this interpretation. In the present case the undulations in the total reaction probability are considerably more pronounced and regular and the reaction has an exoergicity of ∼3.8 eV which warrants further exploration. The black-solid curve in Fig. 3 features 19 prominent peaks across the entire range of collision energies considered. Peak separations range from ∼0.009 eV to ∼0.036 eV with an average of ∼0.021 eV. Using the energy/time uncertainty relationship ΔE × Δt = ħ, corresponding lifetimes range from ∼0.018 ps to ∼0.073 ps with an average of ∼0.038 ps.

The three internuclear separations from representative QCT simulations for E_col = 0.05 eV and E_col = 0.40 eV are shown in Fig. 8 and the corresponding collision time distributions P(τ_c) are reported in Fig. S3 (ESI†). Here, τ_c is defined as the time for which the sum of the three internuclear distances is smaller than 14a₀ or 12a₀, respectively. The distribution P(τ_c) was determined from 22 000 reactive trajectories at each of the collision energies. The time series in Fig. 8a and d represent trajectories with short collision time τ_c ∼ 0.03 ps and ∼0.04 ps, respectively, whereas Fig. 8b and e show trajectories with longer τ_c (∼1.0 ps and ∼1.02 ps, respectively). The results of panels b and e clearly indicate the formation of triatomic intermediate complexes whereas the findings of panels c and f suggest the formation of weakly bound triatomic complexes with short contact times, reminiscent of roaming.

Fig. 8 Time evolution of the inter nuclear distances from QCT simulations of the three diatoms, O₂ (red), CO_A (blue) and CO_B (black) as function of time for E_col = 0.05 eV (left column) and E_col = 0.40 eV (right column). Collision times are ∼0.03, ∼1.0, ∼3.8, ∼0.04, ∼1.02 and ∼3.9 ps.

Formation of the collision complex is found from both, TDWP (panel A) and QCT simulations (panels C and D). For this, the deviation Δ_A of the C–O_A separation from the equilibrium bond length in CO₂(O_A–C–O_B), which is²¹ 2.20 a₀, was considered, and similarly for C–O_B. From this, the difference Δ_A + Δ_B was determined and is shown in Fig. 9A for TDWP and in panels C and D for QCT simulations. For small Δ_A + Δ_B or values close to zero the structure is that of the CO₂ intermediate, whereas for large values of Δ_A + Δ_B the system is in its two asymptotic states CO_A + O_B or CO_B + O_A. The asymptotic region corresponds to Δ_A + Δ_B ∼ 15a₀ whereas Δ_A + Δ_B ∼ 5 a₀ is indicative of CO₂ formation.

Fig. 9 Formation of the collision complex is found from both, TDWP (panels A and B) and QCT simulations (panels C and D). Data extraction and preparation are discussed in the text. In panel A the instantaneous values for Δ_A + Δ_B (black) together with a running average over 50 fs (red) is reported. Panel B shows the values for R and γ in product coordinates at which the WP has its maximum as a function of simulation time. In panels C and D the average of Δ_A + Δ_B over 100 independent QCT simulations for collision energies 0.05 eV (panel C) and 0.25 eV (panel D) is reported.

For the analysis of the quantum simulations the position of the maximum of the wavepacket was extracted. Every 100 time step of the propagation the position (R^(m), r^(m), γ^(m)) of the maximum of the wavepacket in product state Jacobi coordinates was determined from which separations C–O_A and C–O_B are obtained. For the QCT simulations a total of 100 reactive trajectories with final states CO_A + O_B (50 trajectories) and CO_B + O_A (50 trajectories) were run. Because the reaction time for each trajectory differs, all time series for Δ_A + Δ_B were first synchronized in time by shifting the time to zero when they reach Δ_A + Δ_B = 15.0 a₀. Then, histograms as a function of time were generated, see Fig. S4 (ESI†), and their centers of gravity of the distributions are reported in Fig. 9C and D.

Fig. 9A shows that the sum of deviations from the CO₂ equilibrium structure flattens out between ∼200 fs and 300 fs after launching the TDWP. During this time the van der Waals separation R (lower panel in Fig. 9B) first decreases to 3.5a₀ and stabilizes there for the next 75 fs. This is accompanied by a change in the angle to γ ∼ 15° indicative of linear CO₂. This linearity is established between 190 fs and 265 fs after launching the wavepacket. From all this data an approximate lifetime of ∼75 fs is assigned to the intermediate from TDWP.

From QCT simulations (Fig. 9C and D) it is first found that with increasing collision energy the collision complex forms more rapidly. Secondly, a collision complex as seen in Fig. 8, corresponds to values of Δ_A + Δ_B ≲ 5 a₀ or shorter. This further confirms that the signatures for R ∼ 3.5 a₀ in the TDWP simulations indeed correspond to the collision complex. Due to the large energy (11.22 eV) released upon formation of CO₂ from C + O₂ the system is formed in a highly non-equilibrium state which is unlikely to sample the CO₂ minimum energy structure. Hence, sampling values Δ_A + Δ_B ∼ 0 is very unlikely. This is found for both, TDWP and QCT simulations. Finally, when comparing results from TDWP and QCT simulations it should be remembered that QCT simulations are always run for one specific value of the collision energy whereas in a TDWP all collision energies considered are propagated together. Hence, only the superposition of results from QCT simulations for a range of collision energies can be expected to give information comparable to that from a TDWP.

The collision time distributions from QCT simulations are strongly peaked with their maxima at τ_c ∼ 0.07 ps and ∼0.056 ps for E_col = 0.05 eV and 0.40 eV, respectively, see inset of Fig. S3 (ESI†). The probability for finding such short collision times is 20% and 30%, respectively, for the two collision energies considered. If a shorter distance cutoff of 12a₀ is used the maxima of P(τ_c) are at τ_c = 0.056 ps whereas the longest lifetimes are 4.5 ps and 3.2 ps for the two collision energies. Hence, the analysis of the lifetimes is only moderately affected by the choice of the cutoff value for the sum of the three interatomic distances.

Collision times of the order of 0.06 ps are in quite good qualitative agreement with the analysis of the recurrences in the reaction probabilities from TDWP simulations which yielded lifetimes of around ∼0.04 ps, see above. On the other hand, the QCT simulations also find a long tail in the collision time distributions extending out to ∼4.8 ps and ∼5.3 ps for the longest collision times for the two simulation conditions considered. Overall, it is found that the implied time scales of the undulations in the TDWP reaction probabilities, which have previously been linked to formation of a collisionally stabilized intermediate,⁶⁶ are consistent with the collision times from the QCT simulations, and that they constitute an inherent characteristic of the reaction considered.

The present results can also be compared with results from pulsed, crossed, supersonic molecular beams, at relative translational energies between 4.4 and 90 meV.⁷⁴ Such experiments found that collision energy E_c > 0.04 eV is required to open the product CO(v′ = 17) channel. For CO(v′ = 17), the present QCT investigation shows a threshold of ∼0.15 eV from analysis based on histogram and ∼0.25 eV from Gaussian binning, respectively. An earlier QCT investigation²¹ on a finer grid for E_c showed that for (v = 0, j < 10) the threshold is 0.18 eV which changes to 0.25 eV if the same data is analyzed for (v = 0, j = 0). This is also consistent with ∼0.22 eV from the TDWP simulations. Including higher rotational states for the reactant progressively shift the threshold to 0.04 eV when all reactant j-states are included which agrees well with the experiments.^21,74

In summary, this work provides a stringent comparison for total and product diatom vibrational state resolved reaction probabilities and product state vibrational and rotational distributions from TDWP and QCT simulations for the C + O₂ → O + CO reaction on its ground electronic state. Overall, the agreement of a quasi-classical description with results from wavepacket simulations is encouraging except for the lowest collision energies or lowest product rotational states. Expected quantum effects such as undulations in the total reaction probability P(E_c) can be rationalized from analysis of the TDWP and the QCT trajectories. Given the ease with which QCT simulations can be carried out the present work suggests that they are a meaningful approach for understanding the dynamics of atom plus diatom reactions and for larger systems as well. QCT-based approaches have also been used for the reaction of H₂ on platinum surfaces,⁷⁵ the formation of CO₂ on amorphous solid water,^70,71 CO adsorbed on NaCl,⁷⁶ and for investigating photodissociation reactions of larger molecules such as acetaldehyde or the syn-Criegee intermediate.^77,78

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Support from the AFOSR (Air Force Office for Scientific Research), by the Swiss National Science Foundation through grants 200020_188724, the NCCR MUST (to MM), and the University of Basel is acknowledged. This project has also received funding from the European Union Horizon 2020 funding scheme under MCSA Grant No 801459, FP-RESOMUS.

References

1. M. Sharma, A. B. Swantek, W. Flaherty, J. M. Austin, S. Doraiswamy and G. V. Candler, Experimental and Numerical Investigation of Hypervelocity Carbon Dioxide Flow over Blunt Bodies, J. Thermophys. Heat Transfer, 2010, 24, 673–683.
2. D. Husain and A. N. Young, Kinetic investigation of ground state carbon atoms, C(2³ P), J. Chem. Soc., Faraday Trans. 2, 1975, 71, 525–531.
3. A. Bergeat, T. Calvo, G. Dorthe and J. Loison, Fast-flow study of the C + NO and C + O₂ reactions, Chem. Phys. Lett., 1999, 308, 7–12.
4. W. D. Geppert, D. Reignier, T. Stoecklin, C. Naulin, M. Costes, D. Chastaing, S. D. Le Picard, I. R. Sims and I. W. M. Smith, Comparison of the cross-sections and thermal rate constants for the reactions of C(³P) atoms with O₂ and NO, Phys. Chem. Chem. Phys., 2000, 2, 2873–2881.
5. K. H. Becker, K. J. Brockmann and P. Weisen, Spectroscopic identification of C(³P) atoms in halogenomethane + H flame systems and measurements of C(³P) reaction rate constants by two-photon laser-induced fluorescence, J. Chem. Soc., Faraday Trans. 2, 1988, 84, 455–461.
6. G. Dorthe, P. Caubet, T. Vias, B. Barrere and J. Marchais, Fast flow studies of atomic carbon kinetics at room temperature, J. Phys. Chem., 1991, 95, 5109–5116.
7. D. Chastaing, P. L. James, I. R. Sims and I. W. M. Smith, Neutral–neutral reactions at the temperatures of interstellar clouds: Rate coefficients for reactions of atomic carbon, C(³P), with O₂, C₂H₂, C₂H₄ and C₃H₆ down to 15 K, Phys. Chem. Chem. Phys., 1999, 1, 2247–2256.
8. D. Chastaing, S. D. Le Picard and I. R. Sims, Direct kinetic measurements on reactions of atomic carbon, C(³P), with O₂ and NO at temperatures down to 15 K, J. Chem. Phys., 2000, 112, 8466–8469.
9. A. J. Dean, D. F. Davidson and R. K. Hanson, A shock tube study of reactions of C atoms with H₂ and O₂ using excimer photolysis of C₃O₂ and C atom atomic resonance absorption spectroscopy, J. Phys. Chem., 1991, 95, 183–191.
10. E. Ogryzlo, J. Reilly and B. Thrush, Vibrational excitation of CO from the reaction C+ O₂, Chem. Phys. Lett., 1973, 23, 37–39.
11. J. Dubrin, C. MacKay, M. Pandow and R. Wolfgang, Reactions of atomic carbon with π -bonded inorganic molecules, J. Inorg. Nucl. Chem., 1964, 26, 2113–2122.
12. S. S. Xantheas and K. Ruedenberg, Potential energy surfaces of carbon dioxide, Int. J. Quantum Chem., 1994, 49, 409–427.
13. A. W. Jasper and R. Dawes, Non-Born–Oppenheimer molecular dynamics of the spin-forbidden reaction O(³P) + CO(X¹Σ⁺) → CO₂(X¹Σ_g⁺), J. Chem. Phys., 2013, 139, 154313.
14. J. Troe, Thermal dissociation and recombination of polyatomic molecules, Fifth Symp. (Int.) Combust., 1975, 15, 667–679.
15. M. Braunstein and J. W. Duff, Electronic structure and dynamics of O(³P) + CO(¹Σ⁺) collisions, J. Chem. Phys., 2000, 112, 2736–2745.
16. P. Kozlov, V. Makarov, V. Pavlov and O. Shatalov, Experimental investigation of CO vibrational deactivation in a supersonic cooling gas flow, Shock Waves, 2000, 10, 191–195.
17. R. E. Center, Vibrational relaxation of CO by O atoms, J. Chem. Phys., 1973, 58, 5230–5236.
18. J. D. Kelley and R. L. Thommarson, Vibrational deactivation and atom exchange in O(³P) + CO(X¹Σ⁺) collisions, J. Chem. Phys., 1977, 66, 1953–1959.
19. J. A. Davidson, H. I. Schiff, T. J. Brown and C. J. Howard, Temperature dependence of the deactivation of O(¹ D) by CO from 113-333 K, J. Chem. Phys., 1978, 69, 1216–1217.
20. J. C. Tully, Reactions of O(¹ D) with atmospheric molecules, J. Chem. Phys., 1975, 62, 1893–1898.
21. J. C. San Vicente Veliz, D. Koner, M. Schwilk, R. J. Bemish and M. Meuwly, The C(³P) + O₂(3Σ_g⁻) ↔ CO₂ ↔ CO(¹Σ⁺) + O(¹D)/O(³P) reaction: thermal and vibrational relaxation rates from 15 K to 20000 K, Phys. Chem. Chem. Phys., 2021, 23, 11251–11263.
22. N. W. Winter, C. F. Bender and W. A. Goddard III, Theoretical assignments of the low-lying electronic states of carbon dioxide, Chem. Phys. Lett., 1973, 20, 489–492.
23. S. Y. Grebenshchikov and R. Borrelli, Crossing Electronic States in the Franck-Condon Zone of Carbon Dioxide: A Five-Fold Closed Seam of Conical and Glancing Intersections, J. Phys. Chem. Lett., 2012, 3, 3223–3227.
24. S. Y. Grebenshchikov, Photodissociation of carbon dioxide in singlet valence electronic states. II. Five state absorption spectrum and vibronic assignment, J. Chem. Phys., 2013, 138, 224107.
25. S. Y. Grebenshchikov, Photodissociation of carbon dioxide in singlet valence electronic states. I. Six multiply intersecting ab initio potential energy surfaces, J. Chem. Phys., 2013, 138, 224106.
26. J. A. Schmidt, M. S. Johnson and R. Schinke, Carbon dioxide photolysis from 150 to 210 nm: Singlet and triplet channel dynamics, UV-spectrum, and isotope effects, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 17691–17696.
27. B. Zhou, C. Zhu, Z. Wen, Z. Jiang, J. Yu, Y.-P. Lee and S. H. Lin, Topology of conical/surface intersections among five low-lying electronic states of CO₂: Multireference configuration interaction calculations, J. Chem. Phys., 2013, 139, 154302.
28. S. Kinnersly and J. Murrell, A classical dynamical study of the reaction between C(³P) and O₂(³Σ_g⁻), Mol. Phys., 1977, 33, 1479–1494.
29. A. L. Brunsvold, H. P. Upadhyaya, J. Zhang, R. Cooper, T. K. Minton, M. Braunstein and J. W. Duff, Dynamics of Hyperthermal Collisions of O(³P) with CO, J. Phys. Chem. A, 2008, 112, 2192–2205.
30. D. Koner, R. J. Bemish and M. Meuwly, Dynamics on multiple potential energy surfaces: quantitative studies of elementary processes relevant to hypersonics, J. Phys. Chem. A, 2020, 124, 6255–6269.
31. A. Zanchet, B. Bussery-Honvault, M. Jorfi and P. Honvault, Study of the C(³P) + OH(X²Π)→ CO(a³Π) + H(² S) reaction: fully global ab initio potential energy surfaces of the 1²A′ and 1⁴A′ excited states and non adiabatic couplings, Phys. Chem. Chem. Phys., 2009, 11, 6182–6191.
32. S. Goswami, T. R. Rao, S. Mahapatra, B. Bussery-Honvault and P. Honvault, Time-dependent quantum wave packet dynamics of S + OH reaction on its electronic ground state, J. Phys. Chem. A, 2014, 118, 5915–5926.
33. M. Jorfi, P. Honvault and P. Halvick, Quasi-classical determination of integral cross-sections and rate constants for the N + OH → NO + H reaction, Chem. Phys. Lett., 2009, 471, 65–70.
34. M. Jorfi, P. Honvault and P. Halvick, Quasiclassical trajectory calculations of differential cross sections and product energy distributions for the N + OH → NO + H reaction, J. Chem. Phys., 2009, 131, 094302.
35. M. Jorfi, P. Honvault, P. Bargueño, T. González-Lezana, P. Larrégaray, L. Bonnet and P. Halvick, On the statistical behavior of the O + OH → H + O₂ reaction: A comparison between quasiclassical trajectory, quantum scattering, and statistical calculations, J. Chem. Phys., 2009, 130, 184301.
36. M. Jorfi and P. Honvault, Quantum dynamics at the state-to-state level of the C + OH reaction on the first excited potential energy surface, J. Phys. Chem. A, 2010, 114, 4742–4747.
37. M. Jorfi and P. Honvault, State-to-state quantum dynamics calculations of the C + OH reaction on the second excited potential energy surface, J. Phys. Chem. A, 2011, 115, 8791–8796.
38. T. R. Rao, S. Goswami, S. Mahapatra, B. Bussery-Honvault and P. Honvault, Time-dependent quantum wave packet dynamics of the C + OH reaction on the excited electronic state, J. Chem. Phys., 2013, 138, 094318.
39. M. Jorfi and P. Honvault, Quasi-classical trajectory study of the S + OH → SO + H reaction: from reaction probability to thermal rate constant, Phys. Chem. Chem. Phys., 2011, 13, 8414–8421.
40. A. N. Panda, D. Herráez-Aguilar, P. G. Jambrina, J. Aldegunde, S. C. Althorpe and F. J. Aoiz, A state-to-state dynamical study of the Br + H₂ reaction: comparison of quantum and classical trajectory results, Phys. Chem. Chem. Phys., 2012, 14, 13067–13075.
41. P. Bargueño, P. Jambrina, J. M. Alvariño, M. Menéndez, E. Verdasco, M. Hankel, S. Smith, F. J. Aoiz and T. González-Lezana, Energy dependent dynamics of the O(¹ D) + HCl reaction: A quantum, quasiclassical and statistical study, Phys. Chem. Chem. Phys., 2011, 13, 8502–8514.
42. M. Hankel and X.-F. Yue, Quantum dynamics study of the N(² D) + H₂ reaction and the effects of the potential energy surface on the propagation time, Comput. Theor. Chem., 2012, 990, 23–29.
43. S. Goswami, B. Bussery-Honvault, P. Honvault and S. Mahapatra, Effect of internal excitations of reagent diatom on initial state-selected dynamics of C + OH reaction on its second excited (1⁴A′′) electronic state, Mol. Phys., 2017, 115, 2658–2672.
44. S. Goswami, J. Sahoo, T. R. Rao, B. Bussery-Honvault, P. Honvault and S. Mahapatra, A theoretical study on the C + OH reaction dynamics and product energy disposal with vibrationally excited reagent, Eur. Phys. J. D, 2018, 72, 1–19.
45. J. Polanyi, Some concepts in reaction dynamics, Acc. Chem. Res., 1972, 5, 161.
46. B. Jiang and H. Guo, Relative efficacy of vibrational vs. translational excitation in promoting atom-diatom reactivity: Rigorous examination of Polanyi's rules and proposition of sudden vector projection (SVP) model, J. Chem. Phys., 2013, 138, 234104.
47. J. C. Polanyi, Some concepts in reaction dynamics, Science, 1987, 236, 680–690.
48. N. Bulut, O. Roncero, M. Jorfi and P. Honvault, Accurate time dependent wave packet calculations for the N + OH reaction, J. Chem. Phys., 2011, 135, 104307.
49. S. Y. Lin, H. Guo, P. Honvault, C. Xu and D. Xie, Accurate quantum mechanical calculations of differential and integral cross sections and rate constant for the O+ OH reaction using an ab initio potential energy surface, J. Chem. Phys., 2008, 128, 014303.
50. M. Hankel, S. C. Smith, S. K. Gray and G. G. Balint-Kurti, DIFFREALWAVE: A parallel real wavepacket code for the quantum mechanical calculation of reactive state-to-state differential cross sections in atom plus diatom collisions, Comput. Phys. Commun., 2008, 179, 569–578.
51. S. K. Gray and G. G. Balint-Kurti, Quantum dynamics with real wave packets, including application to three-dimensional (J = 0) D + H₂→ HD + H reactive scattering, J. Chem. Phys., 1998, 108, 950–962.
52. M. Hankel, S. C. Smith, R. J. Allan, S. K. Gray and G. G. Balint-Kurti, State-to-state reactive differential cross sections for the H + H₂→ H₂ + H reaction on five different potential energy surfaces employing a new quantum wavepacket computer code: DIFFREALWAVE, J. Chem. Phys., 2006, 125, 164303.
53. S. Goswami, J. Sahoo, S. K. Paul, T. R. Rao and S. Mahapatra, Effect of Reagent Vibration and Rotation on the State-to-State Dynamics of the Hydrogen Exchange Reaction, H + H₂→ H₂ + H, J. Phys. Chem. A, 2020, 124, 9343–9359.
54. M. Hankel, G. G. Balint-Kurti and S. K. Gray, Sinc wave packets: New form of wave packet for time-dependent quantum mechanical reactive scattering calculations, Int. J. Quantum Chem., 2003, 92, 205–211.
55. A. R. Offer and G. G. Balint-Kurti, Time-dependent quantum mechanical study of the photodissociation of HOCl and DOCl, J. Chem. Phys., 1994, 101, 10416–10428.
56. D. Kosloff and R. Kosloff, A Fourier method solution for the time dependent Schrödinger equation as a tool in molecular dynamics, J. Comput. Phys., 1983, 52, 35–53.
57. J. Light, I. Hamilton and J. Lill, Generalized discrete variable approximation in quantum mechanics, J. Chem. Phys., 1985, 82, 1400–1409.
58. J. Lill, G. Parker and J. Light, Discrete variable representations and sudden models in quantum scattering theory, Chem. Phys. Lett., 1982, 89, 483–489.
59. I. Hamilton and J. Light, On distributed Gaussian bases for simple model multidimensional vibrational problems, J. Chem. Phys., 1986, 84, 306–317.
60. N. E. Henriksen and F. Y. Hansen, Theories of Molecular Reaction Dynamics, Oxford, 2011.
61. D. Koner, L. Barrios, T. González-Lezana and A. N. Panda, State-to-State Dynamics of the Ne + HeH⁺(v = 0, j = 0)→ NeH⁺(v′, j′) + He Reaction, J. Phys. Chem. A, 2016, 120, 4731–4741.
62. D. Koner, R. J. Bemish and M. Meuwly, The C(³P) + NO(X²Π) → O(³P) + CN(X²Σ⁺), N(² D)/N(⁴ S) + CO(X¹Σ⁺) reaction: Rates, branching ratios, and final states from 15 K to 20 000 K, J. Chem. Phys., 2018, 149, 094305.
63. D. G. Truhlar and J. T. Muckerman, in Atom-Molecule Collision Theory, ed. R. B. Bernstein, Springer, US, 1979, pp. 505–566.
64. L. Bonnet and J.-C. Rayez, Quasiclassical Trajectory Method for Molecular Scattering Processes: Necessity of a Weighted Binning Approach, Chem. Phys. Lett., 1997, 277, 183–190.
65. L. Bonnet and J.-C. Rayez, Gaussian Weighting in the Quasiclassical Trajectory Method, Chem. Phys. Lett., 2004, 397, 106–109.
66. M. Jorfi and P. Honvault, State-to-state quantum dynamical study of the N + OH → NO + H reaction, J. Phys. Chem. A, 2009, 113, 2316–2322.
67. L. Bañares, F. Aoiz, P. Honvault, B. Bussery-Honvault and J.-M. Launay, Quantum mechanical and quasi-classical trajectory study of the C(¹ D) + H₂ reaction dynamics, J. Chem. Phys., 2003, 118, 565–568.
68. L. Banares, J. Castillo, P. Honvault and J.-M. Launay, Quantum mechanical and quasi-classical trajectory reaction probabilities and cross sections for the S(¹D) + H₂, D₂, HD insertion reactions, Phys. Chem. Chem. Phys., 2005, 7, 627–634.
69. N. Bulut, A. Zanchet, P. Honvault, B. Bussery-Honvault and L. Bañares, Time-dependent wave packet and quasiclassical trajectory study of the C(³P) + OH(X²Π)→ CO(X¹Σ⁺) + H(² S) reaction at the state-to-state level, J. Chem. Phys., 2009, 130, 194303.
70. M. Upadhyay, M. Pezzella and M. Meuwly, Genesis of Polyatomic Molecules in Dark Clouds: CO2 Formation on Cold Amorphous Solid Water, J. Phys. Chem. Lett., 2021, 12, 6781–6787.
71. M. Upadhyay and M. Meuwly, Energy Redistribution Following CO2 Formation on Cold Amorphous Solid Water, Front. Chem., 2021, 9, 827085.
72. M. Pezzella, O. T. Unke and M. Meuwly, Molecular Oxygen Formation in Interstellar Ices Does Not Require Tunneling, J. Phys. Chem. Lett., 2018, 9, 1822–1826.
73. M. Pezzella, D. Koner and M. Meuwly, Formation and Stabilization of Ground and Excited-State Singlet O₂ upon Recombination of ³ P Oxygen on Amorphous Solid Water, J. Phys. Chem. Lett., 2020, 11, 2171–2176.
74. M. Costes and C. Naulin, State-to-state cross sections for the C(³P_J) + O₂(X³Σ_g⁻) → CO(X¹Σ⁺) + O(¹D₂) reaction at kinetic energies between 4.4 and 90 meV, C. R. Acad. Sci., Ser. IIC: Chem., 1998, 1, 771–775.
75. N. Gerrits, Accurate Simulations of the Reaction of H2 on a Curved Pt Crystal through Machine Learning, J. Phys. Chem. Lett., 2021, 12, 12157–12164.
76. A. Nandi, P. Zhang, J. Chen, H. Guo and J. M. Bowman, Quasiclassical simulations based on cluster models reveal vibration-facilitated roaming in the isomerization of CO adsorbed on NaCl, Nat. Chem., 2021, 13, 249–254.
77. B. R. Heazlewood, M. J. Jordan, S. H. Kable, T. M. Selby, D. L. Osborn, B. C. Shepler, B. J. Braams and J. M. Bowman, Roaming is the dominant mechanism for molecular products in acetaldehyde photodissociation, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 12719–12724.
78. M. Upadhyay and M. Meuwly, Thermal and Vibrationally Activated Decomposition of the syn-CH₃ CHOO Criegee Intermediate, ACS Earth Space Chem., 2021, 5, 3396–3406.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp02840a

---