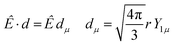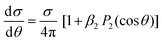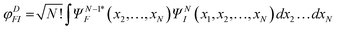Open Access Article
Open Access ArticleTrends in angle-resolved molecular photoelectron spectroscopy
Danielle
Dowek
*a and
Piero
Decleva
 *b
*b
aUniversité Paris-Saclay, CNRS, Institut des Sciences Moléculaires d’Orsay, 91405 Orsay, France. E-mail: danielle.dowek@universite-paris-saclay.fr
bCNR IOM and Dipartimento DSCF, Università di Trieste, Trieste, Italy. E-mail: decleva@units.it
First published on 7th October 2022
Abstract
The field of angle-resolved molecular photoelectron spectroscopy is reviewed, with emphasis on foundations and most recent applications in different regimes of light–matter interaction. The basic formalism underlying one-photon electron angular distributions is presented, from the primary molecular frame (MF) photoemission i.e. emission from fully oriented molecules to laboratory frame (LF) observables produced from randomly oriented targets, extensions to multiphoton and strong field processes being briefly described, followed by a survey of current quantum mechanical computational approaches. The description of experimental developments is focused on the advancements in two major instrumentation fields for angle-resolved PES of molecules in the last two decades, namely charged-particle imaging spectrometers and adiabatically or impulsively laser-induced molecular alignment, together with their interplay with the remarkable characteristics achieved nowadays by the ionizing light sources and the challenging control of complex molecules in the gas phase. Aspects and applications of LF angular observables from unoriented targets are presented, with contemporary applications, especially as probes of the target electronic structure, including higher angular observables, in particular photoelectron circular dichroism (PECD) from chiral molecules, which is confirmed as a powerful chiral technique, and higher terms arising from multiphoton or non-dipole terms. Molecular frame photoelectron angular distributions (MFPADs), which stand out as the most complete observables of molecular photoionization stereodynamics in different excitation regimes, now broadly extended to characterize molecular structure and dynamics, are then discussed stemming from fully oriented molecules tackled by electron–ion momentum coincidence techniques, or from laser aligned samples. Finally, novel developments and challenging perspectives, notably the implementation of PAD in time-resolved schemes at ultrashort time scales, high energy, and high intensity regimes are drawn.
Introduction
Over a century has passed since the discovery of the photoelectron effect by Hertz and Lenard, and the explanation by Einstein in terms of photons, alternating periods of slow developments and quantum leaps. These were basically determined by the emergence of new light sources and new spectrometers and detectors. The modern era of photoelectron spectroscopy was ushered by Siegbahn and Turner, with the introduction of bright fixed wavelength sources in the X-ray and VUV regions, and high resolution electron spectrometers. A second step was the developments of dedicated synchrotrons, and widespread use of coincidence detection. The current one is marked by the advent of powerful lasers, and free electron lasers (FEL), and further improvement of detectors able to collect the full 4π emission. This has allowed probing the photoionization process in amazing detail, in the three directions of photon energy, field intensity and time resolution. This perspective will be focused on angularly resolved molecular photoionization studies, that is photoelectron angular distributions (PADs), and especially studies with fixed in space molecules molecular frame PADs (MFPADs), in the one photon, multiphoton and strong field regimes, but we only briefly touch the time domain aspects, which are addressed in a companion paper.1 The lack of spherical symmetry of the molecular potential generates a large number of partial waves in the continuum, whose interference is reflected in the MFPADS, but gets averaged for random orientation. There are several motivations for the continuing intense study of these processes. The basic one is the detailed understanding of light–matter interaction at energies above ionization. It is worth recalling that the largest part of the total oscillator strength for electronic excitation generally lies in the continuum. While the basic theory of molecular PADS was fully developed,2 and later expanded to cover nondipole effects at higher energies, the description of the interaction with molecular electronic structure, especially the continuum, and the nuclear degrees of freedom is a big challenge which is still advancing. Correlation and relativistic effects, multichannel scattering and resonances, vibrational excitation and dissociation, and the coupling of electronic and nuclear motions are all topics of current research, for which photoionization has been the most powerful probe. At the most basic level quantum interference and entanglement are still generating surprising effects. As an instrument for studying properties of molecular targets, photoionization continues to give ever finer details of the structure and the dynamics, thanks to the availability of ultrafast pulses in time resolved studies, for which photoionization is one of the most effective probes. Coincidence detection of fragment ions adds a further dimension. Also the range of targets is expanding, from prototypical small molecules to large systems of chemical or biological interests, clusters, and nanoparticles, thanks to the development of powerful methods to bring intact molecules in the gas phase, now extending to adsorbates and liquids.The combination of selection of orbital ionization, photon energy dependence and angular information, already for randomly oriented molecules up to the MFPADS, offers an enormous amount of information which is becoming available even for complex targets, relying on many current developments extending the technique of molecular alignment and orientation via laser pulses and external fields.
This perspective will start with a review of the formalism of PADS, and of the theoretical tools for their simulation by electronic structure calculations. Some current experimental methods will be then described. Present capabilities will be illustrated through a discussion of selected latest studies, first relative to PADS from randomly oriented molecules and the information that can be gained, focusing in particular on chiral systems and high energy experiments, and then from full MFPADS or molecular alignment. Finally a glimpse of near future developments will be given.
Formalism
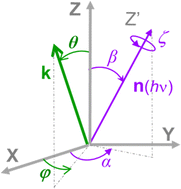
The formulation of angular distribution in all generality is relatively involved, so we shall follow the simplest path and indicate generalizations. It was first derived by Dill2 and further considered by many authors.3–8 One needs to define a molecular frame (MF) fixed with the molecule, with axis (X,Y,Z) (in general unprimed quantities), and a laboratory frame (LF) (X′,Y′,Z′) (primed quantities).Light propagation and polarization are defined in LF, molecular quantities in MF. The Euler angles Ω ≡ α, β, ζ define the rotation MF → LF, and the photoelectron momentum is k with emission angles θ,φ in MF as shown in Fig. 1, with corresponding θ′, φ′ in LF. In the simple case of linear (LP) or circular (CP) polarization, the field is defined by a single vector (electric polarization with LP, propagation direction for CP) generally chosen as Z′ axis in LF, and therefore on (β, α) as polar and azimuthal angles in MF. For a general polarization, expressed via Stokes parameters or other parametrization, or nondipole terms, the full Ω is required.
Let us consider single photon ionization in the dipole approximation. It is a transition from an initial bound state ΨI to a final state characterized asymptotically by an ion in state ΨF (with N − 1 electrons) and a continuum electron with momentum k, described by a full wavefunction Ψ(−)Fk with appropriate incoming wave boundary conditions. Atomic units (a.u.) will be used.
In MF the differential cross section is given by
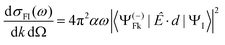 | (1) |
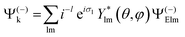 | (2) |
with μ = +1, −1 for left and right CP (LCP, RCP), and μ = 0 for linear polarization. A proper linear combination,8 or a photon density matrix7 describes the most general polarization.
The dipole is rotated in MF, with a rotation matrix D1γμ
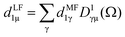 | (3) |
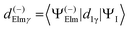 | (4) |
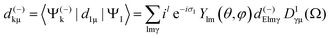 | (5) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ,
θ,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ,
φ,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ω) of the complex dipole d(−)kμ, the one-photon time delay is expressed by its energy derivative
Ω) of the complex dipole d(−)kμ, the one-photon time delay is expressed by its energy derivative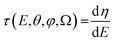 | (6) |
From here, introducing in (1), one arrives at an expression for the differential cross section in MF as a series of angular terms
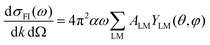 | (7) |
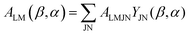 | (8) |
The coefficients can be analyzed in detail for specific cases, in particular LP and CP cases, linear molecules, core 1s ionizations, other point group symmetries,3 which simplify the full expression, and in particular reduce the number of independent symmetry adapted dipole transition matrix elements. Direct formulas for circular (CDAD) or linear (LDAD) dichroism in photoelectron angular distributions, i.e. difference in differential emission probabilities relative to left and right CP or to two perpendicular LP light have been derived.6,7 The functions may be directly determined by four independent polarization experiments, and allow to reduce the full MFPAD information, as the cross section dependence on the other angles is expressed through low order trigonometric functions.
An alternative general expression of the MFPAD I(θ,φ,Ω) was proposed15,16 which emphasizes its dependence in terms of low-order trigonometric functions of the electron emission azimuthal angle φ on the one hand, and Ω on the other hand. In the case of single photon ionization of a linear molecule induced by circularly polarized light (CPL), it takes the remarkably simple form
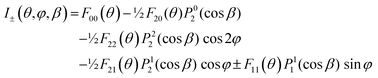 | (9) |
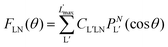 | (10) |
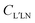 are expressed in terms of the dipole matrix elements15 and L′ runs from 0 up to twice the maximum orbital angular momentum carried away by the photoelectron. It is noteworthy that except for the F11 function which is specific to circularly (or elliptically17) polarized light, the four other FLN functions are identical to those obtained from an experiment with linearly polarized light.15 Therefore a single measurement using circularly polarized light provides the complete accessible information. CDAD (or LDAD) is expressed simply in terms of the FLNs.17 The expansion of the MFPAD in eqn (9) is particularly relevant when studying dissociative photoionization of an assembly of randomly oriented molecules with a 4π angle collection of photoelectrons and photoions, and it subtends the extraction of FLN(θ) functions by performing a (β,φ) Legendre–Fourier analysis of the I(θ,φ,Ω) measured angular distribution,15,16,18 also extended to electron frame EFPADs.19 It is worth noting that the complete set of emission directions and molecular orientations thereby contributes to the FLN(θ) determination, obtained with an optimal statistical quality. Eqn (9) (or the related one for linear polarization) then enables to reconstruct specific MFPADs for any polarization geometry at a similar statistical level. This methodology has been applied for several photoionization schemes, involving linear or non-linear molecules of different symmetry, MFPADs and recoil frame RFPADs, one-photon or multi-photon ionization.8,20
are expressed in terms of the dipole matrix elements15 and L′ runs from 0 up to twice the maximum orbital angular momentum carried away by the photoelectron. It is noteworthy that except for the F11 function which is specific to circularly (or elliptically17) polarized light, the four other FLN functions are identical to those obtained from an experiment with linearly polarized light.15 Therefore a single measurement using circularly polarized light provides the complete accessible information. CDAD (or LDAD) is expressed simply in terms of the FLNs.17 The expansion of the MFPAD in eqn (9) is particularly relevant when studying dissociative photoionization of an assembly of randomly oriented molecules with a 4π angle collection of photoelectrons and photoions, and it subtends the extraction of FLN(θ) functions by performing a (β,φ) Legendre–Fourier analysis of the I(θ,φ,Ω) measured angular distribution,15,16,18 also extended to electron frame EFPADs.19 It is worth noting that the complete set of emission directions and molecular orientations thereby contributes to the FLN(θ) determination, obtained with an optimal statistical quality. Eqn (9) (or the related one for linear polarization) then enables to reconstruct specific MFPADs for any polarization geometry at a similar statistical level. This methodology has been applied for several photoionization schemes, involving linear or non-linear molecules of different symmetry, MFPADs and recoil frame RFPADs, one-photon or multi-photon ionization.8,20
Here we stress that the coefficients ALM in eqn (7), or 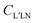 in eqn (10), depend on the dipole matrix elements through the products
in eqn (10), depend on the dipole matrix elements through the products 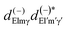 . So
. So 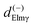 defined in MF are the basic quantities that connect the wavefunctions to the angular distribution and theoretical calculations to experimental results. From the computed
defined in MF are the basic quantities that connect the wavefunctions to the angular distribution and theoretical calculations to experimental results. From the computed 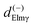 one can derive a theoretical MFPAD, and compare to the experiment, or from the experiment one can derive ALM or equivalent parametrizations, and with sufficient data reconstruct complex dipole matrix elements, up to a so-called complete experiment.17,21–24 In principle the (lm) expansion goes to infinity, in practice it converges fast at low kinetic energies. The quadratic nature of the correspondence may give spurious solutions, but generally physical arguments, or even a comparison with theoretical values provides a unique answer. It is also important to remark that the dependence of the ALM on the molecular orientation is linear in a rotation matrix DKγμ(Ω), with K = 0, 1, 2 limited by the recoupling of two angular momenta of the photon spin. The so-called polarization averaged (PA) MFPAD,25 corresponding to averaging the MFPAD over all orientations of the radiation, is simply obtained integrating over Ω, which lets surviving the single term relative to D000 = 1.
one can derive a theoretical MFPAD, and compare to the experiment, or from the experiment one can derive ALM or equivalent parametrizations, and with sufficient data reconstruct complex dipole matrix elements, up to a so-called complete experiment.17,21–24 In principle the (lm) expansion goes to infinity, in practice it converges fast at low kinetic energies. The quadratic nature of the correspondence may give spurious solutions, but generally physical arguments, or even a comparison with theoretical values provides a unique answer. It is also important to remark that the dependence of the ALM on the molecular orientation is linear in a rotation matrix DKγμ(Ω), with K = 0, 1, 2 limited by the recoupling of two angular momenta of the photon spin. The so-called polarization averaged (PA) MFPAD,25 corresponding to averaging the MFPAD over all orientations of the radiation, is simply obtained integrating over Ω, which lets surviving the single term relative to D000 = 1.
If complete orientation is not achieved, averages over the distribution of molecular axes have to be performed. A typical situation occurs in two-body dissociation of polyatomic molecules, giving a so called (recoil frame) RFPAD. Then an average of the MFPAD around the recoil axis has to be performed.26 If the axis coincides with the MF Z axis, this requires just an integration over (α,ζ). The RF axis is often assumed to coincide with a molecular bond which breaks, but fast nuclear relaxation may change the direction of recoil. In any case the cylindrical symmetry gives a RFPAD of the same structure as that for a linear molecule.
In general it will be necessary to rotate the MFPAD result to a new reference system before the average, giving
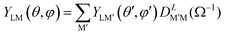 | (11) |
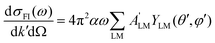 | (12) |
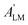 depend linearly on a rotation matrix DKPQ. The same logic applies to rotation back of MF to LF. Averages over molecular orientations are now possible.27 In general the molecular orientation in the sample can be described by a distribution function P(Ω), which we assume normalized
depend linearly on a rotation matrix DKPQ. The same logic applies to rotation back of MF to LF. Averages over molecular orientations are now possible.27 In general the molecular orientation in the sample can be described by a distribution function P(Ω), which we assume normalized 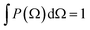 , that can be expressed as a series of rotation matrices, with expansion coefficients (multipole moments)
, that can be expressed as a series of rotation matrices, with expansion coefficients (multipole moments)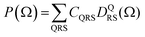 | (13) |
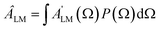 | (14) |
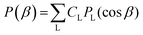 . In the latter case also the LFPAD will be a function of the single θ′ angle (from now on we shall omit the primes for LF angles, understood from the context)
. In the latter case also the LFPAD will be a function of the single θ′ angle (from now on we shall omit the primes for LF angles, understood from the context)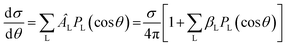 | (15) |
Often the distribution P(Ω) is generated by a laser pulse.28,29 For instance, in the most common pump–probe experiment a random molecular sample is excited with a pump pulse to an excited state, whose dynamic will be further followed. In this case the pump generates a molecular alignment with a simple distribution cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χ where χ is the angle between the LF polarization axis of the pump and the molecular axis defined by the dipole transition moment of the excitation. Alignment or even orientation with laser pulses has become increasingly effective.30 In particular the creation of rotational wavepackets by tailored pulses generates a time dependent distribution P(t,Ω) and related CQRS(t) coefficients which induces a time dependent PAD with ÂLM(t) coefficients.31 The distribution can be computed by solving the time dependent Schrödinger equation (TDSE) for a rigid rotor in an appropriate resonant pulse, or can be experimentally characterized, e.g. via Coulomb explosion. As the ÂLM(t) depend linearly on the products
χ where χ is the angle between the LF polarization axis of the pump and the molecular axis defined by the dipole transition moment of the excitation. Alignment or even orientation with laser pulses has become increasingly effective.30 In particular the creation of rotational wavepackets by tailored pulses generates a time dependent distribution P(t,Ω) and related CQRS(t) coefficients which induces a time dependent PAD with ÂLM(t) coefficients.31 The distribution can be computed by solving the time dependent Schrödinger equation (TDSE) for a rigid rotor in an appropriate resonant pulse, or can be experimentally characterized, e.g. via Coulomb explosion. As the ÂLM(t) depend linearly on the products 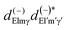 that gives a large set of data which in principle allow the determination of the dipole matrix elements, with the limitations mentioned.
that gives a large set of data which in principle allow the determination of the dipole matrix elements, with the limitations mentioned.
Finally in the case of completely random orientation the integration over Ω produces the well known result
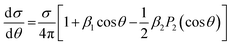 | (16) |
Generally MFPADS and related averages are sensitive to the nature of the ionized orbital, that is both to its composition in terms of atomic orbitals and to the geometrical structure of the molecule, which makes difficult to disentangle the two contributions. A particularly simple case is for core ionization, where the initial orbital reduces essentially to a single atomic orbital localized on the relevant center (or equivalent centers if more than one chemically equivalent atoms are present). Especially at relatively high kinetic energies (some hundreds of eV) also the final wavefunction becomes simpler, and can be approximated by a single scattering by the neighboring atoms in a multiple scattering approach (vide infra). This photoelectron diffraction limit enhances the geometrical content of the PADs and is better suited for geometry determination. Also the use of PA MFPADs has been claimed to enhance geometry determination, as the typically large forward peaks towards neighboring atoms are averaged out, maximizing contrast of the interference fringes. Ideally one would like to invert the photoelectron patterns to get real space images.32,33 At very high energies Fourier transforms could be used, and proposals for improvement have been put forward.34 As a matter of fact, these are hardly quantitative, and best results are obtained by trial and error fitting to full wavefunction calculated MFPADS.
When more complex mechanisms are responsible for the ionization, most of the discussion remains unaltered, with the substitution of an appropriate operator in place of the dipole interaction. For the higher multipoles of the radiation they can be just added to E·d, in particular the magnetic moment (M1) and electric quadrupole (E2). For randomly oriented molecules the corresponding first order PAD (with LP) has been derived,35 involving two additional parameters, usually denoted as γ and δ,
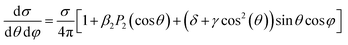 | (17) |
In the case of very high energies it is probably easier to work directly with the full plane wave form of the photon field and compute the transition matrix and the cross section as a function of the kγ vector of the radiation. The PAD can be always expressed as a series of spherical harmonics, but the coefficients have to be evaluated separately for each orientation of kγ.
The case of multiphoton ionization (MPI) has recently attracted great interest. While a nonresonant ionization can be treated via lowest order perturbation theory (LOPT), much used in the atomic case, the most common situation is resonant, especially REMPI(n + 1), also because of the high density of states in molecules. The simplest treatment assumes a sequential ionization step from the previously reached excited state, and the PAD can be then described considering the molecular alignment of the excited state, like in the (1 + 1) pump–probe scheme already considered. In any case, for randomly oriented initial system, the PAD will be a series28,29
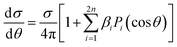 | (18) |
A powerful technique, that can deal also with arbitrary complex pulses, which are at the forefront of current research, is the numerical solution of the TDSE for the pulse.37–40 At the end T of the pulse, the initial state ΨI(0) is transformed into ΨI(T) = U(T,0)ΨI(0) and the final probability amplitude of observing the final state is given by the scalar product
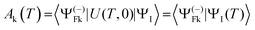 | (19) |
We may finally mention Auger decay. It is actually a double (or multiple) electron ionization, which is a large topic outside our present scope. In most situations it is however well described as a two-step process, i.e. the decay of an isolated resonance (the core hole state) in the continuum, caused by the interelectronic coulomb term. At this level Auger intensities are obtained by Fermi golden rule, or Wentzel ansatz43
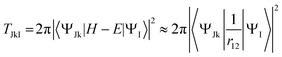 | (20) |
The description of electronic states
The description of electronic states in photoionization involves many-electron bound and continuum states. For the latter an essential ingredient is the calculation of single electron continuum wavefunctions in the nonspherical molecular potential.The calculation of bound states is a central theme of quantum chemistry,47–49 highly developed, and dominated by the treatment of electron correlation, or many-body effects, that is deviations from the predictions based on the mean field Hartree–Fock (HF) approach. Bound states are important per se, as initial, intermediate or final ionic states of the system, and for the calculation of transition amplitudes. Moreover they enter in the formulation of the final continuum, together with the photoelectron wavefunction. The reference point is the HF single determinant (configuration) description of the ground state (GS), with optimum orbitals variationally determined (by the self consistent field, SCF procedure). Orbitals are efficiently obtained by basis set expansion, employing a set of functions (atomic orbitals, AOs, mostly built from Gaussian type functions, GTOs) centered on the various atoms. These provide the occupied orbitals as well as a complementary set of excited state molecular orbitals (MOs). From the full set of occupied and excited orbitals, excited configurations can be constructed, and linear combinations (configuration interaction, CI) may be determined by diagonalizing the Hamiltonian, to describe both excited states and introducing correlation. Taking all configurations into account, so called full CI, is prohibitive except for the smallest orbital spaces, and truncations have to be introduced, which strongly affect the quality of the results. The simplest is truncation on the order of excitation, like Singles (S), doubles (D) and so on (T, Q). Going beyond the singles and doubles (SD) excitation level is very expensive, but an accurate choice is to generate SD excitations starting from a selected set of strongly interacting configurations, called multireference CI (MRCI). If in addition orbitals are optimized then multiconfigurational SCF (MCSCF) wavefunctions are obtained, the most common variant being CASSCF (complete active space, i.e. full CI over a restricted orbital space) or RASSCF (restricted active space, i.e. one or two electrons outside the CAS space). Corrections due to configuration mixing can be obtained by perturbation theory (PT), and often PT is included on top of CI, to correct for the next layer of configurations omitted (MRCI-PT, CAS PT2, RAS PT2).50,51 A different expansion based on an excitation operator in exponential form generates the coupled cluster (CC) expansion like CCSD, CC3, which includes products of lower order excitations, via nonlinear optimization, satisfying important formal requirements (size extensivity) and a more complete treatment of correlation. A different approach is based on the response (linear, quadratic, etc.) of the system to an external perturbation, or to the calculation of propagators (or closely related green functions (GF) or equation of motion (EOM)), which directly approach the excited (ionized) states and the relevant transition amplitudes without explicitly computing excited state wavefunctions. The lowest order approach is random phase approximation (RPA) for excitation. Widely used are OVGF (outer valence Greens function)52,53 and the algebraic diagrammatic construction (ADC(n)),54–56 where n is the order of PT employed, which has been recently reformulated as a wavefunction approach (note that different formalisms are required for excitation, ionization, etc.) and the LR or EOM approaches based on the CC ground state (EOM-CC)57 at different excitation levels.58,59 A similar approach is the SAC CI wavefunction, specifically designed for excitation and ionization.60 These approaches are very effective for a balanced treatment of correlation, but suffer when a multireference treatment is required. Finally a different theoretical approach is density functional theory (DFT),61,62 although most common implementations, based on the Kohn–Sham (KS) approach are formally similar to HF, differing in practice for the HF exchange potential substituted by an exchange–correlation potential VXC, partly theoretically derived, which includes some correlation. In practice DFT works quite well, and in case of local VXC potentials it is also computationally easier. It is difficult however to treat multiconfigurational states. Also fully time dependent DFT equations are computationally viable and often employed. The linear response approximation, TDDFT,63 formally identical to RPA, is widely employed for the treatment of excited states, as well as for continuum calculations.64
It must be recognized however that the ability to use a very accurate approach is often restricted to rather small systems because of the computational demands, and that may still represent a limitation in the case of molecules with complex electronic structures where correlation effects play a prominent role, like systems with open shells, excited multiconfigurational states, or with transition metal atoms.65,66 Correlation effects appear very clearly in photoelectron spectra by the presence of final states (satellites) relative to multiple electronic excitations, forbidden at the HF level.67,68
The situation is significantly more complex for the final continuum states. The final state has to obey scattering boundary conditions which pose significant problems both for the description of the photoelectron and the structure of the many electron wavefunction. The current strong interest in the description of ionization processes, both in the few photon and strong-field regimes, and the time resolved processes that can be addressed by the ultrashort pulses available with new laser/FEL sources have prompted several groups to propose new algorithms and computer codes.69–74
In principle a very accurate representation of the continuum states can be achieved by the so-called close-coupling form of the wavefunction
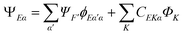 | (21) |
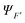 strongly interacting times a corresponding continuum orbital
strongly interacting times a corresponding continuum orbital 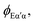 and a sum over bound state wavefunctions ΦK to describe short range correlations and possibly autoionizing states, although there is some freedom to move bound state components between the two expansions, and special constraints are needed to ensure a unique solution. Many specific approximations are possible depending on the type of target states employed and the quality of their description. The single channel (SC) approach limits the expansion to a single term
and a sum over bound state wavefunctions ΦK to describe short range correlations and possibly autoionizing states, although there is some freedom to move bound state components between the two expansions, and special constraints are needed to ensure a unique solution. Many specific approximations are possible depending on the type of target states employed and the quality of their description. The single channel (SC) approach limits the expansion to a single term| ΨEα = ΨFϕEα | (22) |
which is readily calculated from the bound wavefunctions ΨF and ΨI, relative to the ion and the initial state,51,58,59,75 the transition dipole moment (4) reduces to a good approximation as a single particle transition moment between the Dyson and the continuum orbitals
In the simplest approach, with bound states described by single Slater determinants, Dyson orbital reduces to the orbital in the initial state which is ionized, i.e. removed in the ionic state. So in the static exchange approximation (SE), the continuum is calculated in the frozen HF potential of the ion, and the dipole transition between the latter and the corresponding HF orbital. In the similar static DFT approach the same procedure is applied with orbitals solutions of a frozen DFT (also called Kohn–Sham) Hamiltonian describing the ground state. These are the most commonly used approximations employed for larger systems, or for large scale calculations. They can be generalized to a linear response theory, which includes interchannel coupling, giving the random phase approximation (RPA) in the ab initio framework or time dependent DFT (TDDFT) approaches, the latter more commonly employed in molecules.64 It is however easy to include a highly correlated target state, if correlation within the bound states is important. It is also viable to couple via Dyson orbital a continuum electron wavefunction separately obtained, at a simpler level, e.g. analytical,58 or DFT (TDDFT).59
In any case the most important issue is the calculation of the continuum orbitals, which lie outside the Hilbert space and are solutions of an (integro)differential equation with appropriate boundary conditions. Simple approximations like plane waves (PW) or Coulomb waves (CW) and orthogonalized variants (OPW, OCW) are often quite poor at low to moderate electron energies, especially for angular distributions. In the atomic case the problem reduces to a set of, possibly coupled, ordinary differential equations (ODE) in the radial variable, that can be efficiently solved by finite difference techniques. In the case of nonspherical molecular potential the situation is more difficult. A one (single) centre expansion (OCE or SCE) can be employed with finite differences, still giving coupled ODEs which are reasonably good for small molecules, but converge very slowly in the case of heavy atoms far from the expansion centre. Alternatively cartesian grids have been employed, especially for time dependent problems via TDSE, but again rather restricted grids can be employed, and pseudopotentials have to be used to describe the inner cores. A grid approach is computationally very efficient employing the so called Muffin-Tin (MT) approximation to the potential,76 which divides space into atom centered spheres plus an outer sphere encompassing the whole molecule, where a spherical approximation to the potential within each sphere is invoked, and an interstitial region in between, with constant potential. The Multiple Scattering (MS) approach76,77 allows then to join solution across the various boundaries. This approach has been abandoned for the evaluation of bound states, being rather inaccurate, but is still quite useful for continuum states. A so called full potential MS approach, eliminating the MT by employing cells filling the whole space has been implemented, but it becomes computationally much more demanding.78 A completely different alternative if the use of basis sets to expand the continuum orbitals, following the very successful approach for bound state orbitals employed in Quantum Chemistry. However both new basis functions (GTOs have met limited success at low energies) and different solution algorithms have to be employed. A long range OCE basis is typically supplemented by additional atom centered (LCAO) functions. For the OCE B-splines or finite elements are mostly employed, while for the LCAO part either GTOs or again B-splines are common. Different choices and hybrid combinations are employed in actual codes. For the determination of continuum states, also in the CC multielectron case, different algorithms are employed, like variational principles for the continuum (Schwinger,79 Kohn80), the R-matrix approach,81,82 or the Galerkin method.83,84 In practice all lead to an accurate solution of the relevant equations.
Returning to the complete treatment of photoionization, at the DFT level, one of the first general molecular approaches has been the widely used MS-Xα approach based on the MT and the Xα VXC potential.77 A full potential MS approach has been implemented more recently and used in this context.78 Note that in the literature Multiple Scattering is referred both to the computational scheme which originates from the MT approximation, and to the development based on a Born series for the scattering amplitudes, especially appealing in the case of core ionization, where a primary photoelectron wave is emitted by a strictly localized centre, and then interferes with secondary waves scattered by the neighbouring centres. It is mostly useful at relatively high kinetic energies, where the series converges very rapidly, so that the sum of the zero and first order terms is already sufficiently accurate.85 A full potential multicentre implementation using B-splines has been widely used, employing both DFT and TDDFT hamiltonians, and extended also to SC formulations via the Dyson orbital formalism.74 DFT and real time TDDFT (TDSE) are implemented with a cartesian grid in the Octopus code.40 In the ab initio framework one of the first widely used full close coupling implementation is the Schwinger Iterative approach,69,79 limited to linear molecules. A number of other programs have been implemented very recently,71–73,86,87 most with still rather limited applications. One may note that the R-matrix approach was one of the oldest available for the atomic case, later extended to molecules, but only recently generalized.73 The bound state components ΨF, ΦK, are taken from Quantum Chemistry approaches, often of the CASSCF type. It may be noted that the close-coupling structure eqn (21), needed to satisfy boundary conditions, is not trivial to implement, and that makes it difficult to generalize to propagator like approaches, except to the lowest order RPA, which has prevented their application to this problem. The same applies to MCSCF implementations, which have been successfully developed but restricted to solving the TDSE with short pulses.88 Besides the solution of the coupled equations for the continuum orbitals, also the evaluation of the Hamiltonian matrix elements, if a basis set is employed for the continuum,72,89 or the reduction to the set of coupled equations, are complex and computationally demanding with complex correlated target states. This has restricted the full close-coupling approach to rather small systems. For larger systems often the wavefunction is restricted to the pure SE approach, or to the SCI form, which includes interchannel coupling at the lowest level.
A brief summary of the current close coupling approaches for accurate photoionization calculations are the Schwinger variational approach, either static-exchange (ePolyScat)90,91 or multichannel Schwinger configuration interaction (MCSCI),69 with the molecular R-matrix73 and XCHEM72 more recently developed. Also the TREX code71 belongs to this family, but has been mostly employed for strong field applications. Some capabilities are available also in the OCE codes.70,86 All are employed at the lower static exchange level for larger systems. At the SC level the B-spline Tiresia code74 and the MS-Xα approach77,92–94 are the most used, the former also offering TDDFT and Dyson capabilities. All calculations on chiral molecules, of current interest, have employed the latter two approaches, or the OCE(SCE) code,70,87 with large angular momentum expansion. The single channel proves reasonably accurate except for the first few eV close to threshold, as for very slow electrons correlation (polarization) of the ionic core is generally important. Most of the approaches can also be used in the TDSE context to describe strong field and ultrafast electronic processes.
This quick overview has considered only single point, fixed geometry calculations. To take into account nuclear motion, one of the present challenges, entails repeating calculations, up to some order of magnitude more times, for the description of vibrational states, nonadiabatic couplings, large amplitude motions involved in the dynamics of excited states, like in the current pump–probe processes as described in the companion paper on time dependent processes.1 This is why an array of approaches, offering reasonable compromise between accuracy and computational cost, is going to be in use also in the near future. The joining of current electronic continuum algorithms and computer codes with those currently developed for the description of the nuclear motion is a pressing issue which is just being developed. Initial steps towards implementation of the description of vibrationally resolved spectra in large polyatomics beyond the Franck–Condon (FC) approximation have been undertaken95 as well as the calculation of time resolved spectra in pump–probe experiments with the surface hopping dynamical approach,96,97 or the multiple spawning approach98 or Multiconfigurational Time Dependent Hartree (MCTDH).99 For more details see the companion perspective.1
Improvements both in algorithms and computer implementations also exploiting hardware development and massive parallelism, is certain to take place, to improve accuracy and increase speed, and make them available to a wider community, like is the present case with highly developed Quantum Chemistry programs for bound states.
In conclusion there is a tight dialogue between theory and experiment. Experiment is a constant challenge to theory, to refine formulations and approximations, both to devise a correct description of novel processes and to push for increased accuracy. Theory helps experiment by building bridges between observables and the underlying structure of the systems studied, by deepening understanding and by providing some missing data.
Experimental methods and tools
In this section we focus on two major directions characterizing the instrumental methods which value angle-resolved studies of molecular photoionization in the laboratory and in the molecular frame, namely the continuous advancement in electron (and ion) momentum imaging spectrometers of large angular acceptance, and the flourishing laser-induced molecular alignment and orientation techniques. At the core of photoelectron science naturally stands the impressive development of advanced light sources, new generations of free electron laser and synchrotron radiation facilities, table-top femtosecond lasers at infrared (IR) and mid-infrared (mid-IR) wavelengths, high-order harmonic generation (HHG) laser based sources of attosecond XUV pulses: their key role and their adequacy for the research projects covering different light–matter interaction regimes and employing different techniques are addressed and referenced in relation with the experiments evoked in this perspective and related publications. Another aspect, underlying the extending field of photoelectron studies towards molecular systems of increasing complexity, is the chemical and physical handling of the samples. While supersonic expansion and seeded molecular beams, continuous or pulsed using mostly an Even–Lavie valve,100 are central for setting a localized, rotationally cold sample of molecules, a number of challenging issues are at play to bring large molecules e.g. organic or biomolecules from liquid or solid to the gas phase, control their quantum state, discriminate isomers, conformers, clusters, etc., involving a variety of sophisticated methods. For these aspects, complementing recent reviews and results,101–105 we refer as well to the relevant publications.Momentum imaging spectrometers
Nowadays, most of the experiments aiming at the measurement of angular distributions of photoelectrons in a broad kinetic energy range (from hundreds of meV to hundreds of eV) rely on efficient momentum imaging spectrometers where charged particles emitted at the crossing of the light beam and the molecular beam are driven from the interaction region towards multidimensional position sensitive detectors (PSDs) by electrostatic fields ensuring a 4π angular collection. Two main approaches form the basis of the flourishing developments observed within the past 30 years, which may be selected according to the targeted scientific needs, and the characteristics of the light sources used. We first describe briefly the main features of electron–ion coincidence 3D momentum spectrometers, referred to under the generic name of reaction microscopes, at the core of many experiments addressing molecular frame or recoil frame photoelectron angular distributions (MFPADs or RFPADs) of diatomic and small polyatomic molecules, now extending to larger molecular systems, of the order of 10 atoms. We then consider devices relying on Velocity Map Imaging mostly used in photoelectron spectroscopy to measure LFPADs for an assembly of randomly oriented molecules, described by a set of β asymmetry parameters, or reaching molecular frame angular features in presence of laser aligned molecules. Both approaches are combined in recent “hybrid” spectrometers or end stations to achieve optimal performance according to the light source and scientific context, as sketched below.Building on photoelectron–photoion coincidence detection methods (PEPICO),106–108 and pioneering measurements of PADs in the molecular frame,4,109–111 double particle imaging spectrometers encountered a large development since the late nineties,111,112 driven in part by the experimental determination of MFPADs in dissociative photoionization processes. Electron–ion coincidence 3D momentum spectrometers measuring both the impact position (x,y) and the arrival time (t) for each particle arising from photoionization of a single molecule and guided to the relevant electron or ion PSD using uniform electrostatic fields,113–115 or parallel electrostatic and magnetic fields in COLd Target Recoil Ion Momentum Spectroscopy (COLTRIMS) set-ups,116–119 provide event-by-event acquisition of the correlated 3D initial momenta of all emitted charged particles, featuring a kinematically complete description of each ionization event. For dissociative photoionization which prevails for inner-valence and inner-shell ionization of molecules, the measured correlated photoelectron and photoion velocity vectors (or momenta) from initially randomly oriented molecules provide MFPADs when dissociation of the molecular ion is rapid compared to molecular rotation i.e. within the axial recoil approximation.120,121 As defined in the formalism section, for each DPI process characterized by a set of photoelectron energy and kinetic energy release (KER) of the fragments, the fourfold MFPAD stands here for the (θ,φ) photoemission diagram in the MF, for any orientation (β,γ) of the molecular axis relative to the field frame in the general case of elliptical polarization. PSDs used in these coincidence 3D momentum spectrometers consist of a set of multichannel plates (MCPs) of currently 80 mm or 120 mm (up to 150 mm) diameter and an anode which relies mostly on delay-line fast timing technology.122,123 The latter is made of two or three copper coils coupled with a multichannel time-to-digital converter (TDC), providing the impact position and the arrival time for each particle with typically a time precision of 100 ps and a spatial resolution up to 45 μm,124 and few particle multihit capabilities. The ion time-of-flights (TOF) are typically in the range of several microseconds (μs), with backward–forward (BW–FW) extension of few hundreds of nanoseconds (ns) corresponding to the pz momentum distribution, while the corresponding values for electrons lie typically in the range of tens of ns for the TOF, with BW-FW extension of few ns which often motivates a dedicated time-stamping exploiting the MCP signal. The detection efficiency, which plays a major role when performing (multi) coincidence measurements, has been quite significantly improved recently by the use of “funnel” MCPs, i.e. MCPs designed with tapered pores increasing the open area ratio up to 90%.125,126
With the additional magnetic field parallel to the extraction field in COLTRIMS, electron trajectories are constrained to a spiral motion within the radial dimension of the detector, thereby using a significantly lower extraction field to achieve a 4π collection angle than required without magnetic field.116–118 This scheme enables detection and momentum measurement of photoelectrons up to few hundreds of eV, including specific designs for dedicated purposes such as Auger electron momentum studies.127
In order to improve the resolution of coincidence 3D momentum spectrometers, extra electrostatic focusing lenses have in several cases been implemented, to reduce the blurring effect due to the source volume and to allow working with lower extraction fields.115,116,128–130 The relationship that thereby connects in particular the pz component to both the measured arrival time and position is obtained by e.g. raytracing simulations of the particle trajectories experiencing inhomogeneous extraction fields, or by means of detailed calibrations. Discussion of the ultimate energy and angular resolution achieved in different set-ups and documented with their description, depending also on the characteristics of the light sources and the studied electron kinetic energy range, is out of the scope of this brief description.
Since valid electron–ion coincidence detection imposes that less than one ionization event occurs per shot of a pulsed light source, electron–ion coincidence momentum spectrometers have been mostly deployed at third generation synchrotron radiation facilities, taking advantage of the MHz repetition rate and of the few bunch mode temporal structure where two pulses of typically 50 ps width are separated by a duration of few tens of ns, larger than the typical flight time of photoelectrons from the interaction center to the PSD, as well as of spectral resolution, extended tunability, availability of exotic polarization states.
Meanwhile coincidence experiments providing MFPADs (or RFPADs) were achieved using 1–5 kHz femtosecond laser sources at typically 400 nm or 266 nm wavelengths, in pioneering time-resolved photo-dissociation of molecular excited states probed by photoionization,114,131,132 or e.g. multi-photon ionization.133 Electron–ion reaction microscopes have later on been combined with attosecond XUV pulses134 generated by 10 kHz NIR driving lasers, mostly based on Ti:Sapphire technology, to investigate angularly resolved photoionization dynamics at the femtosecond to attosecond time scale. Most recent breakthroughs fostering coincidence experiments rely on fiber and optical parametric chirped pulse amplification (OPCPA) based laser developments providing intense femtosecond NIR or mid-IR pulses, and further attosecond pulses at extended photon energies with repetition rates in the 100 kHz range,135–140 together with the remarkable increase up to MHz repetition rates achieved by intense femtosecond XFEL pulses.141–144 The XFELs characterized by an unmatched brightness compared to other XUV or X-ray sources, with up to 1014 photons per pulse i.e. a gain of several orders of magnitude, give rise to nonlinear multi-photon processes leading to sequential emission of electrons, as outlined below.
On the other hand, a number of imaging spectrometers mostly dedicated to LFPADs (or LFPIADs) rely on standard Velocity Map Imaging (VMI) and related advanced particle imaging.145 In VMI the primary observable is the projection of the 3D Newton sphere onto a (x,y) 2D detector, achieved under the action of a customized inhomogeneous electrostatic field map based on open electrodes (repeller–extractor) producing a lensing effect in the extraction region.146 Inversion methods such as Abel transform or Basex147,148 allow to retrieve the 3D momentum distribution of emitted photoelectrons or photoions from the 2D recorded image, provided that the experiment possesses an axis of cylindrical symmetry in the plane of the detector, leading to the respective multiplex kinetic energy and angular distributions expanded in Legendre polynomials. The great impact of VMIs in molecular dynamics research originates from its “deblurring” capacity, enabling a quasi-suppression of the effect of the finite spatial extension of the interaction volume, therefore resulting in both excellent energy and PAD's angle resolution. Standard VMI set-ups make use of 2D detectors based on a set of MCPs, and a fluorescent (phosphor) screen anode which is read by a pixelated CCD (charge-coupled device) or CMOS (complementary metal–oxide semiconductor) camera with fast readout.149,150 When the cylindrical symmetry condition is not valid, alternative methods have been implemented to access the 3D distribution such as slice imaging techniques,151 or tomographic reconstruction of 3D photoelectron distributions based on the record of 2D images for a number of polarization angles.152,153
The standard VMI configuration enabling high count rates is widely used for its efficacy and relative simplicity by the PES community using pulsed laser sources145 or FELs of rather low repetition rates (from 10 Hz to 1 kHz)154,155 producing a large number of ionization events per shot, in an extended photoelectron energy range, from low energy (100 meV–5 eV) to high energy (few hundreds of eV) relying on additional electrostatic lenses.130,156,157 When combined with efficient molecular alignment techniques, the measured PADs give access to MFPADs, although the retrieved angular distribution, being intrinsically averaged on the azimuthal angle φ by the 2D projection, is generally restricted to the θ polar angle dependence for specific polarization geometries. Well adapted to e.g. XFEL experiments involving hundreds of events per shot, double sided VMI spectrometers were implemented to record PADs and MFPADs while monitoring simultaneously the degree of molecular alignment158,159 in real time through 2D Coulomb explosion ion imaging.160
In the last decade, beyond standard VMI spectrometers, an increasing number of applications of VMI electrostatic lensing have taken as well advantage of time-and-position sensitive anodes, such as delay-line detectors (DLDs) outlined above,129 or discrete imaging anodes, such as TimePix, PImMS or Tpx3Cam, where fast CMOS sensors enable to detect arrival times of few particles at the pixel level up to a few ns to 1 ns temporal resolution,150,161,162 with enhanced multi-hit capabilities. Combining the arrival time sensitivity with the VMI spatial resolution and high count rate ability is highly valuable, enabling e.g. strategies to measure 3D momenta distributions of photoions, or potentially photoelectrons if the required temporal resolution is achieved, up to 3D momentum of individual particles in coincidence in relevant event rate conditions.163–165
Another valuable consequence of the arrival time sensitivity for PAD applications is to take advantage of photoelectron VMI in coincidence with a tandem detection of photoions. The latter can stand e.g. as a simple TOF analyzer providing fragment-mass resolved PADs,166,167 a 2D,112,168 or 3D photoion momentum spectrometer130,169 where PADs are assigned to fully resolved parent or ionic fragment momenta. Such hybrid double imaging electron–ion coincidence spectrometers are well adapted for operating in the quasi-continuous multi-bunch mode of synchrotron radiation, precluding measurement of the electron TOF.130,169 VMI coincidence spectrometers realizing 3D momentum imaging of ions and electrons produced by femtosecond lasers with high temporal resolution were developed relying on two DLD detectors,129 evolving towards a simpler spectrometer based on a single DLD of comparable performance.170 Other recent examples of coincidence electron–ion VMI spectrometers based on a single detector employ a fast CMOS sensor together with a waveform digitizer coupled to the MCPs,171 or novel time-stamping fast optical camera, such as Tpx3Cam.164 Likewise, recording position and arrival time information with sensitive multi-hit CMOS-type sensors in high count rate per shot conditions which preclude real coincidence experiments, frequently met using intense lasers or XFELs, enables a post-analysis of the data based on statistical covariance mapping enlightening correlations between photoelectrons and photoions.172
Laser-induced molecular alignment
There have been remarkable developments in the last two decades to achieve efficient photo-induced alignment and orientation of molecules with a number of applications in gas phase stereodynamics.30,173,174 In the perspective of photoionization, preparing an assembly of fixed-in-space molecules in the laboratory frame (LF) with a controlled alignment and/or orientation, i.e. a well defined confinement of molecular axes in the LF, is a route to molecular frame photoelectron angular distributions, since the measured LFPADs then tend toward MFPADs.175 This approach has a strong potential in particular for the study of non-dissociative processes, or photoionization of molecular systems of increasing complexity, and more generally when the overall conditions do not lend themselves to the use of coincidence techniques, e.g. for intense light sources of low repetition rates.Molecular alignment/orientation induced by an optical field results from the interaction of the light field with the anisotropic polarizability of rotationally cold molecules. It relies on the use of polarized moderately intense non-resonant laser pulses (≤1013 W cm−2) in two distinct regimes characterized by their long (τlaser (ns) ≫ τrot) or short (τlaser (fs-to-ps) ≪ τrot) temporal width relative to the period of the molecular rotational motion τrot, responsible for adiabatic176 or impulsive177 (non-adiabatic) alignment of molecules, respectively. In the adiabatic regime irradiated molecules are aligned during the nanosecond laser pulse and the alignment is highest at the peak maximum. On the other hand, impulsive alignment follows the sudden building up of a rotational wave packet launched by the interaction of a linearly polarized femtosecond laser pulse with the molecular beam. This generates revivals, i.e. samples of molecules transiently aligned parallel or perpendicular (anti-aligned) to the driving laser polarization, after well-defined time-intervals of few picoseconds, corresponding to the rotational period(s) of the target, lasting in a narrow time-window limited to about 1 ps due to fast rotational dispersion of freely-rotating molecules. Most experiments use either Nd:YAG ns lasers (λ = 1064 nm), or fs–ps laser pulses originating from amplified Ti-Sapphire femtosecond laser systems with a 800 nm central wavelength, shaped by stretchers or compressors. Seeding molecules in a high pressure He supersonic expansion strongly lowers their rotational temperature which typically reaches values close to 1 K.101
One-dimensional (1D) laser-induced alignment, where the most polarizable molecular axis is fixed in the laboratory frame, and three-dimensional (3D) alignment, where three principal molecular axes are confined in space, can be achieved using an aligning laser field linearly or elliptically polarized,176 respectively. It applies to all molecules characterized by an anisotropic polarizability and has been demonstrated from diatomic to polyatomic molecules such as substituted biphenyls, including chiral molecules.178 The degrees of alignment and orientation are usually quantified by 〈cos2(θ)〉 (or related 〈cos2(θ2D)〉 when 2D distributions are measured) and 〈cos(θ)〉 coefficients, respectively, where θ is the angle between the molecular axis and the light quantization axis.30 They are currently probed by photoion imaging induced by dissociative ionization, Coulomb explosion by intense near infrared (NIR) femtosecond laser (×1014 W cm−2),179 or X-ray free electron laser pulse,159,180–182 synchronized relative to the aligning pulses, taking advantage of coincidence momentum spectroscopy,183 or VMI covariance mapping.172 Adiabatic alignment provides higher alignment degrees than non-adiabatic methods, and therefore enables a closer determination of MFPADs.175 A disadvantage is that it lasts only in presence of the aligning laser field, which can create perturbations in the studied processes,184 while impulsive alignment allows for generally preferred field-free conditions. Both schemes have led to significant applications (see MFPADs). For polar molecules, where the orientation additionally refers to the direction of the permanent dipole moment, laser pulses can be efficiently combined with a weak static uniform or inhomogeneous electric field allowing for quantum-state selection prior to the laser-interaction,101,104 creating conditions for higher degrees of alignment and orientation, in adiabatic (e.g. 〈cos2(θ2D)〉 ≈ 0.97 for iodobenzene)185,186 or impulsive (e.g. 〈cos2(θ)〉 ≈ 0.82 for NO) alignment.187
Most recent developments aim to gather the advantages of both approaches, the focus being to create samples of sharply aligned molecules preferentially under field-free conditions. Combining quantum-state selection with specific pulse shaping of the aligning laser pulse has recently demonstrated unprecedented degrees of field-free alignment (1D) for the linear OCS molecule 〈cos2(θ2D)〉 ≈ 0.96,188 and (3D) for generic asymmetric-top molecules such as indole C8H7N with a 3D metric degree 〈cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ〉 ≈ 0.89.189
δ〉 ≈ 0.89.189
Moreover, the limitation of impulsive field-free laser alignment time-windows to about 1 ps within the revivals, demonstrated for small and linear molecules and appropriate for time-resolved investigations using MFPADs as probes of ultra-fast electronic and nuclear dynamics processes, e.g. chemical reactions at conical intersection, charge migration, dissociation, fragmentation…, motivates new developments where field-free alignment can last for several ps in the perspective of studying time-resolved molecular dynamics in an extended time-scale.
One recent progress is the design of moderately-long (100 ps) rapidly-truncated (few ps) pulses, where after a slow adiabatic turn-on of the alignment laser pulse up to the peak, realizing optimal alignment, a sharp non-adiabatic cut-off is applied which drops the intensity to less than one per cent using a single passive optics,190 ensuring high repetition rates and very good contrast. Such spectrally truncated chirped pulses based on a longpass optical filter generating switched wave packets with few rotational states were used to demonstrate field-free alignment of linear (OCS) and asymmetric top molecules such as iodobenzene, with alignment coefficients at the observed revivals close to those reached by adiabatic alignment.190
Another remarkable achievement is the demonstration of laser-induced 1D191 and 3D192 alignment of molecules dissolved in He nanodroplets, in both the adiabatic and non-adiabatic limits, which significantly extends the range of applications of structural and dynamical investigations.193 This relies on two main properties: on the one hand, the 0.4 K temperature of the He droplets, shared with the embedded molecules, leads to quite high degrees of alignment (0.96); on the other hand, when using sharply truncated laser pulses, the impeding effect of the He environment on molecular rotation increases up to about 10 ps the time-window of field-free strong alignment, occurring right after extinction of the laser field at the peak of the pulse. This powerful technique opens new perspectives for molecular frame experiments, including ultrafast excited state dynamics, on a variety of large molecules and complexes as demonstrated by 3D alignment of e.g. dibromothiophene oligomers194 or bromobenzene dimers.165
Finally, we note that all-optical schemes employing intense non-resonant two-color pulses,195 or based on terahertz pulses,196,197 have been proposed to control molecular orientation. A high degree of orientation was recently achieved in e.g. OCS with two-color nanosecond pulses,198 and 3D orientation of polyatomic and asymmetric top molecules demonstrated with two-color femtosecond laser pulses.199,200
Laboratory frame PADs
Photoionization dynamics
The simplest angular distribution in laboratory frame photoionization is that described by the β2 parameter followed by β4,…, β2n in the case of multiphoton absorption. It can convey important information on the nature of the target, notably the character of the ionized orbitals. It has been used in the past as a support for the assignment of close-lying ionizations, e.g. to distinguish between outer valence σ and π ionizations, or from nonbonding orbitals, in aromatic compounds,201,202 where generally π ionizations show a much steeper β2 increase after threshold. It is clearly sensitive to the AO composition of molecular orbitals. As it depends on the ratios and interference among contributions of different partial waves, it can be more sensitive to some typical continuum structures, like shape resonances or Cooper minima than is found for cross sections. For instance a deep minimum in β2 at a well defined energy is a clear signature of third row or heavier atoms np orbital participation to the ionized orbital.203 An interesting case has been recently observed in epichlorohydrine, which presents an outermost composite ionization band, which is found to comprise four ionizations, two of which show a pronounced β2 well, of different depth, due to Cl 3p AO participation.204 Theoretical calculations employing DFT or HF initial orbitals significantly disagreed with the observed β2 profiles, and only employing a highly correlated Dyson orbital together with a TDDFT continuum a very satisfactory agreement is reached. This is the first experimental evidence of hole-mixing, or orbital rotation upon ionization, a correlation effect predicted long ago,205,206 and typically expected in low symmetry systems with closely spaced ionizations. Recent probes of the orbital character or the role of resonances where emphasized in e.g. experimental and theoretical study of β2 for outer valence ionization of OsO4 and RuO4.207 Also characterization of spin–orbit and ligand field split 4d orbitals ionization in XeF2 compared with that of Xe was studied.208 A subsequent investigation addressed angular distributions in Auger and resonant Auger from the Xe 3d and F 1s shells.209Another recent application is in the photodetachment of anions,210–213 to characterize the nature of the loosely bound electron, e.g. in dipole bound anions. At very low kinetic energies often a single partial wave, s or p, dominates, and is easily recognised by its β2 behavior. The effect of molecular conformation in a series of substituted phenolate anions was probed through β2 measurements in different channels, with different sensitivities.214 Vibrationally resolved β2 was observed in the SO3− anion, showing unexpected behavior still to be understood. A combined experimental and theoretical study of CN− close to threshold showed the importance of the contribution of the molecular dipole moment and the improvement over a pure plane wave description.215 Effect of correlation and basis set were also investigated.216 Not unexpectedly diffuse functions proved essential for a correct description, while DFT orbitals proved close to Dyson ones, but HF significantly worse. The vinilydene–acetylene isomerization was studied through photodetachment of the H2CC− anion,217 with characteristic β2 values splitting into two different groups, reflecting the presence of Franck–Condon forbidden bands activated through vibronic coupling.
Angular resolved PES allows to scrutinize resonances in the ionization continuum of molecules. A study of angular distributions in the two-photon non-resonant ionization in N2 employing 9.3 eV photons from HHG and a COLTRIMS set-up, measuring β2 and β4, uncovered sharp variations in angular distributions.218 The latter have been attributed to dipole forbidden autoionization resonances in the final continuum, supported by an initial theoretical study that treated the ionization as a two step (resonant) process.218 Fano resonances with femtosecond lifetime in the same Hopfield continuum were characterized by angle resolved HHG-pump-IR-probe VMI experiments.219 Sub-picosecond time-dependent oscillations in the photoelectron yields and angular distributions, and their decay was assigned to interactions within a complex group of resonances close to the N2+(X) ionization threshold at the FERMI FEL.220 Another example is the determination of the photoemission time delay due to a shape resonance in the N2+(X) state using HHG-second harmonic attosecond stereo-photoionization interferometry.221
Photoelectron spectra are one of the most informative probes of quantum states in pump–probe experiments, e.g. studies aimed to disentangle the detailed mechanism of nonadiabatic dynamics in photon induced processes.1 Often the pure ionization energies (TRPES) are insufficient to unambiguously pinpoint the evolution of electronic states, as they reflect also the changing nuclear geometry. Angular distribution (time resolved PE imaging, TRPEI) may give very valuable information on the nature of the excited states as they are more sensitive to the structure of the relevant orbitals. The ideal goal of fully oriented results is rarely attained,222,223 but already β2 and β4 are very informative. After some pioneering studies, like excited state dynamics in pyrazine,224,225 very few pump–probe experiments include measurements of angular distributions, due to the complexity of the experimental setup. Examples from a study of the dynamics in aniline and some derivatives are reported.226 A comprehensive discussion of TRPES of pyrazine including calculation of time dependent angular parameters at the DFT level,96 is shown to disentangle the contributions due to different channels. It was found that β4 is very small close to threshold, in agreement with experimental data227 but increases significantly at higher energies. A clear evolution in such studies has been the development of sufficiently intense sources of higher photon energy. Initial studies employed low photon energy lasers and multiphoton ionization, that were fine for revealing the underlying kinetics, but generally too complex to follow the excited states. An example is the study of acetylacetone dynamics.228 The development of higher energy laser pulses finally enabled single photon ionization, which is much cleaner to follow and easier to interpret, as in the work on pyrazine.225 Further developments of FELS, like the seeded Fermi source, allowing the use of still higher energy photons, produce even cleaner photoelectron spectra, avoiding the threshold region, ideally amenable to detailed theoretical investigations, like that of acetylacetone.229 Still uncertainties in the nature and the evolution of excited states are present, that cannot be disentangled from the pure photoelectron spectrum. The specific situation in acetylacetone is rather challenging, as the four excited states all involve a single excited orbital, π*, coupled either singlet or triplet to initial vacancy n (HOMO) or π (HOMO−1), so that ionization always involves the same π* orbital, and only electron correlation can affect its nature and the relevant photoionization observables. In a recent study of the same dynamics ionized by VUV laser (166 nm) probe230β2 and β4 were obtained and showed weak but distinct anisotropy, but were not analysed beyond providing independent tests of the timescales. Expanding angular detection in TRPEI experiments is a clear goal for the immediate future.
As mentioned initial multiphoton ionization often provided spectra very difficult to understand. A very large number of studies have flourished thanks to the new experimental facilities available both in the multiphoton and strong field regimes, both employing techniques already available from classical laser studies applied to the new energy domain, and generalizing to new situations possible by the development of precise control over time and phase in multicolor pulses, and structured light. This is a very rapidly developing field, that is not possible to adequately represent in this review, and we shall limit to a few ref. 231–236. Others will be devoted to the special section on chirality and photoelectron circular dichroism (PECD).
Finally LFPADS give additional insights in photoionization studies of more complex species, or targets often problematic to bring in the gas phase. Among these are typically large biomolecules, clusters and nanoparticles,237,238 areosols, and systems at the boundary of condensed phases. Recent activity is on the study of liquids, in particular water and solutions, like droplets or liquid jets,239,240 or surfactant layer structure at liquid–vapor interface.241
Photoelectron circular dichroism
Photoelectron circular dichroism in single photon ionization of chiral molecules with CP light was theoretically predicted in 1976,242 and realistically calculated by Powis in 2000,92,93 which spurred a first experimental confirmation soon after,243 and a flurry of subsequent work. It consists in a forward–backward asymmetry in photoelectron emission by CP light in randomly oriented molecules, which reverses for different R and S enantiomers, quantified by the β1 parameter (sometimes G = (I+1(0) − I−1(π))/Itot = 2β1), originating by the mixing of partial waves of different parity. As this is generated by the chiral molecular potential, the effect is quite strong at low KE, but decays fast and is generally negligible after a few tens of eV.Recent studies detect LFPADs in coincidence with one ionic molecular fragment from a specific dissociation channel, taking advantage of synchrotron radiation extended capabilities (see Experimental Section). This improves the resolving power of the technique, and affords deciphering between different fragmentation channels and/or a specific molecule in a mixture for analytical purposes.103 Advances in electron–ion coincidence 3D momentum spectroscopy have allowed full MFPAD experiments, highlighting for each channel different contributions to the overall measured PECD (vide infra).
Furthermore the strong development of laser technology (ns or ps, repetition rate, XUV photon HHG, FELs, strong field) has afforded PECD experiments both in the single photon and multiphoton (especially resonant, REMPI) domains as well as in the strong field regime.244,245
Single photon PECD is now a well established technique that can be used to investigate chemical properties of selected targets. It is essentially a gas-phase technique, due to the ultrahigh vacuum needed to detect electrons, although a first experiment on liquid jets has just appeared.246 In this sense it can be considered complementary to established chiral techniques like CD in absorption, very weak and hard to detect with dilute samples, which is therefore most employed with solutions. Gas phase CD measurements can nevertheless be achieved with special techniques,247,248 and have notably been recently demonstrated in mass selected photodetachment of DNA strands.249
While PECD may require special techniques to bring delicate samples in the gas phase, it may probe systems, like anions or cations that cannot survive in solution, or in typical ultrahigh vacuum environments, like the study of surfaces and adsorbates. The absence of solvent interactions also avoids cutoff due to solvent absorption and the process may be easier to simulate theoretically. We shall concentrate on very recent work since many examples are reported in the two most recent reviews.102,103 Examples include determination of absolute configuration, molecular conformation, electronic and vibrational structure, and very recent extension to complex biological samples, nanoparticles and liquids. Let us remind that absolute configuration assignment of chiral molecules still presents difficult cases, with relatively few techniques available,250 and PECD stands as a very powerful technique in this respect.251
Many details of molecular structure can be analyzed. At variance with IP, σ or β2, PECD, like other chiral techniques, is generally very sensitive to molecular conformation, as has been highlighted by theoretical simulations.252 The power of PECD to reveal conformational changes in the gas phase has been highlighted in a study of 1-indanol, where supersonic expansion of the molecule in He and Ar produce a mixture of conformers in the former, but the pure equatorial one in the latter. Despite the superimposable photoelectron spectra and β2 parameter, PECD showed a clearly distinct behaviour.253 The conformational dependence is generally hidden as averages in the experimental results, but has been recently investigated in one photon ionization of amino acid proline254 which presents two pairs of stable conformers. It is a rare case where conformers can be discerned by rather different IP's, which allowed to gain detailed information on the dependence of PECD on conformation, as well as of the fragmentation patterns.
A possible link of PECD of amino acids such as alanine and proline with the origin of life's homochirality along with other processes is discussed in the context of astrobiology.255
Another chemically driven investigation is PECD of the organometallic complex Ru(acac)3 (acac = acetylacetonate).256 It is an example of a class of chiral metal trischelates, of D3 symmetry. The PES spectrum is very rich, with several well resolved bands, that afford a wealth of experimental data. It proved however very difficult to study theoretically, both for the size of the molecule and the presence of a metal atom, plus the open shell electronic structure which gives rise to multiplets in the PES spectrum, preventing a definite assignment of the spectrum. Actually an older study of the simpler Co(acac)3, which is closed shell, showed quite satisfactory agreement with theoretical calculations for the HOMO band,257 but very poor for the following ones.258 The problem probably lies in the poor description of ionic states, as is suggested by the bad reproduction of the PES spectrum by the OVGF approach, which is generally very accurate for organic molecules. Typically very strong correlation effects appear in transition metal compounds, and PECD can be a powerful tool also for a correct assignment of the spectrum.
The influence of vibrational excitation on the β1 parameter has been analyzed,95 exploiting the large vibrational envelope of the HOMO ionization in 3-carene, which is a rigid molecule, well separated from the following HOMO−1 band. An excellent reproduction of the experimental points by the MS-Xα approach is obtained for the mostly adiabatic low energy side of the HOMO band. Scanning the whole band a large variation of β1 is observed, and comparing measurements along the band at identical electron KE shows conclusively that KE variations are of minor importance for the changes observed. A calculation of FC factors, with harmonic wavefunctions and including Duschinski rotations shows a myriad of vibrationally excited components, overtones and combination bands, although the main peaks visible in the spectrum are associated with the stretching of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bond, and to a puckering vibration. More insight is obtained by theoretical simulations involving a single vibration at a time. It remains clear however that the overwhelming complexity of the vibrational spectrum precludes a detailed explanation of the observed experimental trends, and call for a full non FC simulation including the majority of the normal modes along with the associated change of the transition dipole moment, still to be developed. A similar study was performed on methyloxirane and the trifluromethyl derivative.259,260
C double bond, and to a puckering vibration. More insight is obtained by theoretical simulations involving a single vibration at a time. It remains clear however that the overwhelming complexity of the vibrational spectrum precludes a detailed explanation of the observed experimental trends, and call for a full non FC simulation including the majority of the normal modes along with the associated change of the transition dipole moment, still to be developed. A similar study was performed on methyloxirane and the trifluromethyl derivative.259,260
Investigation of PECD for larger molecules e.g. of biological relevance often requires special sample preparation to handle them in the gas phase. Measurements of PECD in photodetachment of amino acid anions261 have been performed employing circularly polarized laser beams and electrospray techniques for the preparation of the gas phase samples. Although these are initial results, the potential for the study of complex biological systems is clearly demonstrated. A theoretical simulation on a model anion system by the SCE approach has confirmed the sensitivity of the technique.262 A further extension to the study of PECD in condensed phases, relative to aerosols of the amino acid serine, has been undertaken.263 Unexpectedly PECD, although reduced in absolute value with respect to the isolated monomer, survives in the nanoparticle, at variance with the β2 parameter which is totally quenched. Detailed interpretation proves very difficult in such complex systems, and will have probably to rely on phenomenological arguments, but again a clear indication of the potential of the technique in this area is achieved.
At the more fundamental level is the study of autoionization resonances, effect of molecular orientation, or pump–probe experiments. The behavior of the Fano resonance in β1 around the first O 1s resonant absorption in methyloxirane was investigated recently.264 While the direct channel is computed to show a negligible β1, as expected since β1 goes quickly to zero at high electron KE, a hundredfold increase due to the interference with the resonance is predicted, with an effect of the order of 2%, which is clearly measurable, and a characteristic dispersion profile across the resonance, in fair agreement with the experimental result. This shows the opportunity of measuring β1 in resonant Auger spectra, an interesting new possibility. Actually a similar Fano resonance was observed,257 associated with the 3p → 3d excitation in Co(acac)3, but at much lower energy, with a typical Fano shape profile.
A two-color pump–probe study involving X-ray femtosecond pulses at the linac coherent light source (LCLS)-XFEL at SLAC National Accelerator Laboratory, the first photon (LP) ionizing a F 1s core in enantiomerically pure trifluoromethyloxirane followed by Auger decay, the second one (CP) probing the PECD temporal evolution for F 1s ionization of the chiral mother-ion in the (C3H3F2O+–F+) dissociation channel within few hundreds of fs, was reported recently.265 This experiment, supported by the theoretical prediction of a significant PECD dependence upon the internuclear distance between the ejected F+ and chiral ionic fragments and the position of the emitter-site, shows the feasibility of XFEL dynamical PECD studies, as a probe of molecular dynamics at distances of the two ions largely exceeding chemical interaction.265
The possibility of employing table top instruments relying on laser technology, even if highly sophisticated presently, is now expanding the availability of the PECD technique to many laboratories. A first experiment producing highly elliptically polarized light from high harmonic generation, has shown the potential to address single photon PECD.266 Most studies have addressed PECD in multiphoton ionization (REMPI). The variety of situations is quite large and we shall limit to a few recent papers, but tracing the first experiments.
More conventional, and practical multiphoton experiments (MP-PECD) carried out few years ago, showed great promise of widespread application, beyond the analysis of higher order processes.267–270 Recent developments include the use of a nanosecond laser,271 which is found to yield very similar PECD compared to femtosecond, but with large differences in the photoionization rates relative to the intermediate states reached in the 2 + 1 REMPI ionization subsequent to improved resolution capabilities. This was followed by a high resolution study pinpointing the specific vibronic levels reached through the narrow bandwidth laser.272 A substantial insensitivity of the PECD to the specific vibrational level reached in the resonant excitation was found, which gives confidence in the robustness of the technique for the identification of the molecule and the analytical possibility to identify several compounds in a mixture by selectively tuning to specific resonances. A further study however showed a more complex situation, suggesting vibronic coupling between close Rydberg intermediate excited states, and a reversal of the PECD for some vibronic state.273 A similar study has been performed on α-pinene and 3-carene,274 where all individual βj, up to j = 6 have been measured. Those studies highlight the richness, but also the complexity, given the high density of states in the resonant region, of REMPI studies of chirality, and the challenge posed by a detailed interpretation of the results. A recent study illustrated in Fig. 2 employed the same technique to provide detection of absolute configuration in a mixture of chiral molecules, in this case camphor and fenchone.275 By tuning to the 3s intermediate state resonance, which is separated by about 8 nm (114 meV) in the two compounds, almost pure signals from each molecule could be achieved, and PECD was able to differentiate accurately among the four possible enantiomer mixtures, which may become a feasible tool for chiral analysis of mixtures.
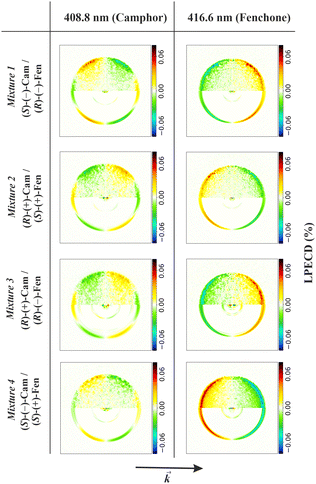 | ||
| Fig. 2 PECD images extracted from mixtures of camphor and fenchone, relative to the 4 combinations of R/S enantiomers, REMPI results relative to excitation at 408.8 nm and 416.6 nm wavelengths, the first resonant for camphor, the second for fenchone.275 Signals from the two molecules can be clearly distinguished, as well as the specific R/S combination. Figure reproduced from Fig. 2 of ref. 275 from Physical Chemistry Chemical Physics under Creative Commons Attribution 3.0 International license (http://creativecommons.org/licenses/by/3.0/). | ||
Full angular distribution of photoelectrons emitted in (3 + 1) REMPI with elliptically polarized light shows a very complex pattern, with nonlinear dependence on the increasing ellipticity towards CP276 associated with the change in molecular orientation distribution reached in the intermediate resonant excitation. From the full PAD relative to the RCP and LCP, taking sum and difference, PAD and PEELD (Photoelectron Elliptical Dichroism) are defined, the latter showing very strong signatures of the chirality. Also reduced PEELD by suitable averaging prove sufficient to characterize the species and determine the enatiomeric excess with high accuracy. The technique has been expanded as an analytical tool, capable of real time (∼1 s) determination of enantiomeric excesses of several chiral molecules at the same time by scanning the ellipticity of the light.276,277
The possibility offered by MP-PECD as an analytic tool for chirality detection has been exploited to study surface desorption of fenchone on Ag(111).278 It demonstrates the potential for enantiomer-specific detection of surface reaction products on heterogeneous catalysts in asymmetric synthesis. Another experiment looked at the coincident PECD and PICD,279 where the latter is the dichroism in fragment ion production. In methyloxirane comparable asymmetries were observed for both dichroic effects, which may be coincidental, and it was proposed that a joint measurement can better discriminate between different molecules. Circular Dichroism (CD) in strong field ionization of chiral molecules such as CHFClBr has been characterized by Coulomb explosion subsequent to fourfold ionization.280 The experiment considered a pure racemic mixture, and the results for each enantiomer were selected by orientation of three coincident ion momenta, F+, Cl+, Br+. CD was measured for both the total ionization intensity, and the Br+ ion production chosen as observable, as well as for the fully differential ionization which displays a CD enhanced by two orders of magnitude reaching 10%. A second experiment focused on strong field single ionization in methyloxirane, with results strongly different from the predicted one photon case, still to be fully understood.280 A different scheme was studied, where PECD is detected in two photon excitation, the first with circularly polarized light to a set of Rydberg orbitals in fenchone and camphor followed by ionization with a second linearly polarized pulse,281 based on a theoretical development.282 Further recent studies address the effect of time control of the field chirality at the subcycle level,283 and the influence of chirality on tunnel-ionization dynamics.284 Finally a very intense development is taking place on the possibilities offered by the use of structured light, with specifically designed pulses, mostly at the theoretical level.285
At the theoretical level, the one photon PECD is well understood, but development towards increasing accuracy of the continuum description, accurate treatment of the nuclear motion and description of floppy molecules, and computational efficiency are still in progress. The situation is less developed for the multiphoton, especially the REMPI case. Initial approaches have been considered already in the first experiments,267 then a more elaborate perturbative description,231,286 and a TDSE treatment245 were presented. Although giving qualitative agreement with measured asymmetries, experience is too limited and more work has to be done before reaching a well established methodology. At a more theoretical level, a deeper analysis based on the underlying symmetries has been presented in a series of papers.287–290 This allows to predict the type of chiral signal expected from any specific arrangement of the external fields.
Non dipole parameters
The study of non-dipole effects in the molecular PADs started quite some time ago291 but proved to be very delicate, and some results reported were not verified.292,293 The additional parameters γ and δ characterizing the PAD (eqn (17)) are typically rather small, but quite structured. Recently renewed interest has been spurred by the advent of new light sources in the tender and hard X-ray regime,294–296 probably beyond the first order effects that have been hitherto considered, but molecular nondipole effects have been barely investigated. A number of theoretical papers have appeared,297–299 including the full photon plane wave, and a review, also covering the strong field regime.300Exploring the hard X-ray region, new results have been reported for K-shell ionization of N2 at 40 keV,301 where one Auger electron and the two N+ ions are detected in coincidence using a COLTRIMS set-up, providing momentum vectors of four particles including the energetic photoelectron. Strong modifications of the KER pattern from low energy photoexcitation are observed, where direct photoionization and Compton effect can be clearly separated. The main result is that recoil of the parent ion is imparted by both photoelectron and photon momenta on the same footing. An interesting issue relates to core hole localization, since this experiment shows that the photon is entirely absorbed by one of the equivalent atoms, and not delocalized between the two. Remarkable photoemission features are identified in the molecular frame as reported below. The transfer of photon momentum from about 0.1 to 10. atomic units was observed in photoionization of He and N2 in the 300 eV–40 keV energy range,302 verifying the prediction of momentum sharing between electron and ions, the latter being shifted backwards with respect to the light propagation vector. The γ parameter for He measured over the full energy range was found in excellent agreement with theoretical calculations. Finally a study of nondipole effects on the angular distribution in xenon induced by strong field ionization (SFI) with CP light303 emphasized an asymmetry with respect to the polarization plane, due to both the magnetic and electric nondipole components, a fingerprint that should also affect SFI of molecules.
Molecular frame and recoil frame PADs
The range of experiments addressing photoelectron angular distributions in the molecular frame is continuously expanding whether they address the intrinsic photoionization processes for molecules of increasing complexity and different regimes of light–matter interactions, or they use photoionization as a probe of alternative photoinduced electronic and nuclear dynamics.29,142,304 The molecular frame is rigidly attached to the molecule. For simple systems it is based on symmetry axes in the molecule, selecting the principal symmetry axis as reference, while the laboratory frame identifies with the light field frame, referred to the polarization axis or the propagation axis for linearly or circularly (elliptically) polarized light, respectively.In this section we present some current issues of MFPAD studies, according to the two major ways to establish the molecular frame, presented in the experimental section, i.e. (i) working with randomly oriented molecules and determine the effective molecular frame a posteriori for each dissociative photoionization event, by means of electron–ion coincidence momentum spectroscopy, or (ii) preparing assemblies of molecules well aligned and/or oriented relative to the field frame, and repeat the measurements for all relevant polarization geometries. Until recently, these two approaches were generally implying different light sources (see Experimental Section): the use of synchrotron radiation facilities well adapted to the conditions of coincidence experiments in therefore weak field conditions, and that of lasers, or free electron lasers, in different field strength regimes, for studies involving aligned targets. However, advancing in the field it is often quite relevant to gather advantages provided by both techniques, which is also supported by the remarkable evolution of the light sources including e.g. the increased repetition rate of mid-IR lasers and related XUV HHG sources, and XFELs.
A. MFPADs from randomly oriented molecules: electron–ion coincidence 3D momentum spectroscopy
In single-photon ionization, experiments taking advantage of electron–ion coincidence techniques mostly apply to inner-valence or inner-shell ionization of molecules where the produced cationic states often fragment rapidly, leading to the production of one photoelectron and one or several ionic fragments (if subsequent Auger decay occurs), and for which the validity of the axial recoil approximation can be controlled.120,121 Dissociation of the ionic states is either a consequence of steep repulsive potential curves in the Franck Condon region, or, in the case of quasi-bound ionic states due to predissociation subsequent to coupling with a repulsive state. Depending on the associated life-time compared to the rotational period of the cation state, dissociation may be prompt or involve some rotation which must be accounted for in the data analysis. Thus, in the simplest case where a molecular ion dissociates rapidly in two fragments, measuring in coincidence the momentum of the ionic fragment(s) which features the molecular bond at the instant of photoionization, and the ejected electron momentum, provides the photoelectron angular distribution in the molecular frame, for each orientation of the light polarization relative to the molecular axis. Most of the experiments in this section rely on the use of reaction microscopes ensuring a 4π collection angle of electrons and ions as described in the Exp. section.Here we present selected recent examples illustrating contributions of MFPAD studies to the description of (i) photoionization dynamics, (ii) characterization of molecular structure and dynamics or (iii) fundamental questions in quantum mechanics and light–matter interactions.
Photoionization dynamics
Building on the pioneering expression of MFPADs (Section Formalism)2 reflecting the interference of a number of partial waves in the ionization continuum, the goal to access the partial wave resolved complex dipole matrix elements (DMEs), i.e. the dynamical parameters providing a complete description of a photoionization transition from the initial ionized molecular orbital to the ionization continuum for each photon energy was well recognized (see Formalism). It was addressed in the earlier AR-PEPICO studies reported for inner-valence ionization of diatomic and small polyatomic molecules,4,110,111,305 and in the first measured MFPADs for K-shell ionization of N2.109 Both inner-valence and inner-shell ionization processes were further on scrutinized in the molecular frame.Inner-valence photoionization of molecules leads to the production of excited molecular ionic states which involve electronic correlation and play an important role in photochemistry resulting from the interaction of XUV radiation with dilute matter. It gives rise to a number of competing dissociative photoionization (DPI) channels, for which MFPADs stand as fingerprints deciphering the symmetry of the initial neutral ground state and final excited electronic states. Such studies were first carried out for single ionization of linear or small polyatomic molecules using electron–ion coincidence momentum spectroscopy in the axial recoil approximation,16,20,113,306,307 although some deviations have also been investigated and exploited to determine a predissociation time or a bending angle in e.g. excited states of N2O+.308,309 Here we point out briefly some of these results relevant for current studies, most of which were obtained relying on the general description of MFPADs in terms of FLN functions (Section Formalism). An example of the five FLN(θ) extracted from the measured MFPAD I(θ,φ,β) for PI of the NO molecule into the NO+(c 3Π) ionic state induced by circularly polarized light (see eqn (9)) is displayed in Fig. 3(A), together with the result of MCSCI calculations.310 Based on the measured FLNs, Fig. 3(B) displays a complete set of four MFPADs featuring the parallel (a) and perpendicular (b) transitions, as well as MFPADs for a molecule oriented at 45° relative to linearly polarized light (c) or at 90° relative to the propagation axis of circularly polarized light (d) which both result from different coherent superposition of parallel and perpendicular transitions.
 | ||
| Fig. 3 (A) Measured (red) and computed (blue) FLN functions (see text) and CDAD parameter for ionization of NO into the NO+(c 3Π 4σ−1) at hν = 26.35 eV photon energy,310 experiment and theory are normalized such that the total cross-section is identical. (B) Polar and azimuthal dependence of the corresponding measured MFPADs for a linear polarization of the ionizing light parallel (a), perpendicular (b) or tilted at 45° (c) relative to the molecular axis as shown, or for RHC polarized light propagating perpendicular to the molecular axis (d). | ||
Magnitudes and signed phases of the partial wave resolved DMEs were determined for selected processes such as PI of the NO molecule into the NO+(c 3Π) state in the region of the 4σ → kσ* shape resonance.15,17,23,310,311 The DME dynamical parameters were extracted through a non-linear least-squares fit of the 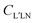 coefficients obtained via the Legendre polynomial expansion of the measured FLN functions and compared with ab initio calculations.17 A recent highlight illustrating the photoionization dynamics in terms of MF angle resolved photoionization time-delays (see eqn (6)), relying on the derivation of DMEs from measured MFPADs, is presented below.311 It is noteworthy that the temporal dynamics of this PI process is also addressed in a recent study312 relying on the XUV-IR RABBITT (Reconstruction of attosecond beating by two-photon transitions313) interference scheme resolved in the molecular frame.314
coefficients obtained via the Legendre polynomial expansion of the measured FLN functions and compared with ab initio calculations.17 A recent highlight illustrating the photoionization dynamics in terms of MF angle resolved photoionization time-delays (see eqn (6)), relying on the derivation of DMEs from measured MFPADs, is presented below.311 It is noteworthy that the temporal dynamics of this PI process is also addressed in a recent study312 relying on the XUV-IR RABBITT (Reconstruction of attosecond beating by two-photon transitions313) interference scheme resolved in the molecular frame.314
Another outcome of complete MFPAD measurements is the direct evidence of the CDAD which measures the different MFPAD response of a molecule when exposed to left or right CPL,315,316 as predicted and observed in earlier investigations.17,317–320 Governed by the F11 function in eqn (9), the CDAD is a signature of the signed relative phase between the photoionization amplitudes for the parallel and perpendicular transitions, and a sensitive probe of autoionizing resonances.316,321 In PI of non-chiral molecules, the CDAD enabled by non-coplanarity of the electron momentum k, the molecular axis and the light propagation axis, quantifies the subsequent right-left anisotropy in the MF described by the azimuthal dependence in sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ in eqn (9). The latter is maximal for electron emission in the polarization plane when the molecular axis is perpendicular to the light propagation axis. It contributes as well to the emission anisotropies observed for chiral molecules as illustrated below, but is distinct from PECD effects.322,323
φ in eqn (9). The latter is maximal for electron emission in the polarization plane when the molecular axis is perpendicular to the light propagation axis. It contributes as well to the emission anisotropies observed for chiral molecules as illustrated below, but is distinct from PECD effects.322,323
It is pointed out that when PI is induced by elliptical polarization, the MFPAD general expression encodes the complete polarization state of the ionizing light in terms of e.g. the three Stokes parameters.17,324 This property has been recently exploited to probe the polarization state of high order harmonics generated in SF6 molecules by an elliptically polarized IR field,325 or driven by intense ultrashort bichromatic circularly polarized fields in Ar.326
For dissociative ionization of non-linear molecules, the observable consists of the recoil frame photoelectron angular distribution (RFPAD), obtained from the MFPAD by a rotation (αR, βR, γR) of the MF into the recoil frame (RF) attached to the recoil direction (αR, βR) of the ionic fragment, and average of the MFPAD over the azimuthal angle γR. For single photon ionization of a molecule of C2v symmetry breaking in two fragments, such as NO2 where ionization of the (1a2) and (4a1) MOs was studied,26 it was shown that the RFPAD I(θ,φ,β) takes the same functional form as that of MFPADs for linear molecules, after averaging on the unknown spatial orientation of the molecular fragment, enabling a detailed comparison of measured and computed observables. This method was extended to characterize MPI of e.g. NO2 induced by 400 nm femtosecond pulses, accounting for the partial molecular alignment subsequent to (n − 1) photon absorption.133,327
Structured RFPADs have been reported for single photon ionization of the (1t1,4t2,1e) outer MOs of the CF4 molecule dissociating into CF3+ + F, for a recoil axis parallel to the polarization.328 For e.g. (4t2) ionization, a striking flip of the RFPAD anisotropy with electron energy is assigned to a strong intra-channel coupling between overlapping shape resonances of a1 and t2 symmetry supported by ab initio calculations.328 The PI dynamics underlying the role of these shape resonances is also investigated in two recent time-resolved studies of RFPADs for photoionization of CF4, decaying to the (CF3+ + F) channel, using the XUV-IR RABBITT interference scheme.329,330 The latter reveal significant variations of the measured recoil-frame angle-resolved photoionization time delays in the range of a few hundred of attoseconds, in particular asymmetries along the recoil frame axis at the lowest explored energies.329 The question to which extent the one-photon (XUV) ionization delays can be extracted from the measured MF angle resolved two-photon PI delays is considered.329,330 While the single photon ionization delay is well defined and computed as the energy derivative of the phase of the photoionization amplitude (eqn (6)) as illustrated below, that obtained in two-photon XUV/IR RABBITT experiments are more complex to disentangle, as they comprise additional phases, in particular that intrinsically part of the two-photon matrix element involving continuum–continuum transitions.10,11,14 In the example outlined here, two theoretical formulations were employed, via second order perturbation theory, based on the approximate evaluation of the continuum–continuum transition delay,329 or via a simulation based on the solution of the TDSE with the two colour pulse, which in principle includes exactly all contributions.330 Both are limited by the treatment of correlation effects, at the Hartree–Fock and Density Functional levels respectively. They show that although following qualitatively the one-photon delays the additional terms are not constant and do not cancel out in taking differences relative to one reference.
For inner-valence ionization of weakly bound systems such as atomic or molecular dimers, an important class of non-local electronic decay mechanisms is described as Interatomic Coulombic Decay (ICD).331,332 In ICD, following ionization of one atom of a dimer, a valence electron fills the vacancy, while the de-excitation energy is transferred to the second atom, causing ionization of a valence electron from that atom. Subsequent Coulomb explosion enables determination of ICD-electron angular distributions in the dimer-fixed frame, as recently illustrated for resonant ICD, following inner-valence Rydberg excitation of [Ne*(2s−1np)Ne] dimers.333
Core–shell photoionization of molecules is followed by Auger decay occurring within a few femtoseconds and subsequent Coulomb explosion of the multiply-charged cation leading to the emission of two (or more) ionic fragments, together with the photoelectron and Auger electrons. This provides a vast opportunity for MF characterization of photoionization dynamics of linear and polyatomic molecules, as well as for electronic relaxation and fragmentation dynamics of cationic states. Complete photoionization experiments combining linear and circular (elliptical) polarization states were demonstrated e.g. for K-shell ionization of CO and N2,320 and (2σg) ionization of N2.334 When using CPL, a large CDAD in the molecular frame was demonstrated for K-shell ionization and identified as a sensitive probe of theory.320 The photon (or photoelectron) energy dependence of the MFPADs, and that of the magnitude and phases of the DMEs when extracted, provided the orbital angular momentum composition of the electron wave function temporarily trapped in a shape resonance.109,334 In this context, K-shell ionization of CO recently led to the extraction of MF angle resolved photoionization time-delays.335
Molecular frame Auger electron angular distributions (MFAADs) for decay channels stamped by the KER of the ionic fragments allowed to scrutinize the validity of a two-step model, where core-level photoionization and subsequent Auger decay are described as independent steps. While this framework was supported by the dependence of MFAADs on the symmetry of the Auger transition, independent on the orientation of the polarization axis,127 small asymmetries of MFPADs correlated with Auger decay channels in e.g. C(1s) and O(1s) ionization of CO2,336,337 were interpreted as a partial breakdown of the two-step model. MFAADs were shown to disentangle fragmentation pathways of dications, such as symmetric fragmentation, isomerization, or deprotonation in K-shell ionization of acetylene,338 involving curve crossings and conical intersections, or fragmentation channels subsequent to 1σg and 1σu core ionization of N2, resolved by additional coincident angle resolved detection of photoelectrons.339,340
Resonant excitation of a core–shell electron to an antibonding molecular orbital leads to ultrafast dissociation, which may occur on a few femtosecond time-scale comparable to that of Auger decay. There the KER of the fragments encodes the internuclear distance at which ionization occurs, providing an internal clock of the molecular breakup. MFAADs resulting e.g. from Cl(2p) excitation of HCl to the 6σ lowest unoccupied MO, corresponding to different KERs, were shown to map the evolution of the ionized orbital from a σ-type MO to an atomic p orbital oriented perpendicular to the molecular bond,341 tracing the electron density temporal evolution during molecular breakup. This strategy is at work in ongoing studies.
With the advent of XFELs, double core hole (DCH) angle resolved Auger electron spectroscopy has emerged as a novel source of information probing the local valence structure of molecules, with first partial MFAADs measured at LCLS on impulsively aligned N2 molecules.342 Recent experiments characterizing sequential two-photon ionization of O2 into DCH states based on MFPADs were carried out at the EUXFEL as presented below.343
For small polyatomic molecules, recording 3D MFPADs is enabled by the coincident detection of the photoelectron with that of three or more ionic fragments subsequent to Auger decay. 3D mapping of photoemission from H2O was e.g. reported measuring 3D momenta of the (H+, O+, H+) ions in coincidence with photoelectron 2D detection, providing MFPADs for the three a1 → a1, a1 → b2, and a1 → b1, ionization channels assigned to well defined polarization geometries, in very good agreement with TDDFT calculations.344 Exploring 3D MFPADs for K-shell ionization of more complex molecules using 3D momentum spectroscopy of both electron and ion fragments is pursued: recent applications address in particular PECD for space-fixed chiral molecules.323,345,346
We illustrate below two recent results addressing MF photoionization time delays, and PAD analysis for core–shell ionization of space fixed chiral molecules.
On the other hand, as outlined above, photoionization delays with complete angular resolution in the molecular frame were recently derived from single-photon MFPADs measured using synchrotron radiation (BESSY and SOLEIL) at a series of spectrally-resolved photon energies across a shape resonance, providing benchmark references for two well characterized prototype reactions, namely K-shell ionization of CO,335 and inner-valence ionization of NO(X2Π) into the NO+(c 3Π 4σ−1) ionic state,311 and compared with ab initio calculations. The magnitudes dlm and relative phases ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) lm of the partial-wave dipole matrix elements were extracted from the measured MFPADs, providing the complex valued photoionization amplitude and subsequently the time delays for any MF emission direction
lm of the partial-wave dipole matrix elements were extracted from the measured MFPADs, providing the complex valued photoionization amplitude and subsequently the time delays for any MF emission direction ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) , or orientation of the molecule
, or orientation of the molecule  . The relative phases of the partial wave DMEs were based on a common reference not coupled to the resonance,311 or deduced from theoretical modelling.335 MFPADs measured for C(1s) ionization of CO in the range of the first 20 eV above threshold led to the determination of angle-dependent Wigner delays for both ionization into the continua of Σ and Π symmetry, showing evidence of larger delays in the Σ case assigned to the influence of a shape resonance.335 Results displayed in Fig. 4 correspond to inner-valence ionization of NO in the region of the (4σ → kσ*) shape resonance up to 20 eV above the NO+(c3Π) ionization threshold, as described in Fig. 3 for a given photon energy, selecting an orientation parallel to the polarization axis. Together with the strong variation of MFPADs, the measured and computed photoemission delays varying within a few hundreds of attoseconds reveal comparable strong anisotropies as function of electron energy and MF electron emission polar angle. The observed angular dependence of the MF-resolved time delays is interpreted as a signature of the interference between the resonant and non-resonant components of the photoionization amplitude described by a multichannel Fano formalism, where the ionization delay of the resonant component is angle-independent.311 These results are coherent with those extracted from measured two-photon delays reported recently for the same reaction.312
. The relative phases of the partial wave DMEs were based on a common reference not coupled to the resonance,311 or deduced from theoretical modelling.335 MFPADs measured for C(1s) ionization of CO in the range of the first 20 eV above threshold led to the determination of angle-dependent Wigner delays for both ionization into the continua of Σ and Π symmetry, showing evidence of larger delays in the Σ case assigned to the influence of a shape resonance.335 Results displayed in Fig. 4 correspond to inner-valence ionization of NO in the region of the (4σ → kσ*) shape resonance up to 20 eV above the NO+(c3Π) ionization threshold, as described in Fig. 3 for a given photon energy, selecting an orientation parallel to the polarization axis. Together with the strong variation of MFPADs, the measured and computed photoemission delays varying within a few hundreds of attoseconds reveal comparable strong anisotropies as function of electron energy and MF electron emission polar angle. The observed angular dependence of the MF-resolved time delays is interpreted as a signature of the interference between the resonant and non-resonant components of the photoionization amplitude described by a multichannel Fano formalism, where the ionization delay of the resonant component is angle-independent.311 These results are coherent with those extracted from measured two-photon delays reported recently for the same reaction.312
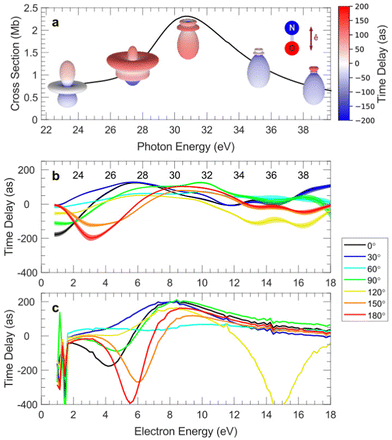 | ||
| Fig. 4 MFPADs measured at selected photon energies for ionization of NO across the NO+(c 3Π 4σ−1) shape resonance, for a molecule oriented parallel to the polarization as shown: the color of the 3D plots features the emission time-delay (a); 1D plots of measured (b) and computed (MCSCI) (c) time-delays, for selected emission angles in the MF.311 | ||
Selecting further e.g. a three fragment breakup channel such as CH2+–C2H2,3+ and OH1,2, after O(1s) ionization of methyloxirane, fixes the molecular frame (close to the fragment recoil frame) in three spatial dimensions, and gives access to MFPADs for each orientation of the light propagation axis relative to the molecular frame.347 These fourfold differential angular distributions, where both the electron emission direction and the propagation axis are defined by a set of polar and azimuthal angles (θ,φ) in the MF, measured for both helicities and enantiomers, can then be interpreted in terms of a PECD(θ,φ) parameter for each orientation of the molecule relative to the light propagation axis, revealing maximum values larger than 50%. A similar analysis in the trifluoromethyloxirane has been further conducted for four initial ionization bands, the two unresolved carbon atoms of the ring, the CF3 carbon, and the three unresolved fluorine atoms, in addition to oxygen.346 The PECD of space fixed oriented chiral molecules may then stand as a sensitive structural and analytical technique for the enantiomeric excess determination, at the cost however of a more complex experiment. Rationalizing the influence of spatial alignment of molecules photoionized by CPL is as well relevant for the interpretation of PECD studies relying on REMPI which induces partial alignment of the molecule.231 It also supports the interpretation of the strong fragmentation channel dependence of PECD in strong field ionization of methyloxirane348 as attributed to the selection of specific molecular orientations for each fragmentation channel.
On top of the description of photoionization dynamics, core-level ionization 3D MFPAD (or RFPAD) studies have focused on imaging the molecular structure in three dimensions, relying on the localized character of the emission source, spotlighting different perspectives depending on the photoelectron energy.
Molecular structure: photoelectron “diffraction from within”
For carbon K-shell ionization of polyatomic molecules such as methane,349 ethane, carbon tetrafluoride or difluoroethylene,350 3D MFPADs measured few eV above threshold at the Advanced Light Source (ALS, Lawrence Berkeley National Laboratory) by 3D momentum spectroscopy of both electron and ion fragments with a COLTRIMS end station, revealed that the maxima in the 3D emission pattern point either along the directions of the molecular bonds (CH4, C2H6), or away from (bisecting) these directions (CF4). This striking observation, well predicted by ab initio complex Kohn variational calculations, was emphasized when considering polarization averaged MFPADs (PA-MFPADs),25,349,350i.e. MFPADs averaged with respect to the light polarization direction, providing a direct imaging of the molecular geometry, or its “opposite”. The generality of these statements has been examined in a theoretical study considering molecules with different atomic centers and symmetries, in an extended electron energy range, where the propensity for direct imaging of molecular geometry by means of K-shell PA-MFPADs was only observed for simple hydrides at very low or selected high kinetic energies.351 Still, it was found that this observable can be informative on the three-dimensional arrangement of the system in correlating the anisotropies in PA-MFPADs with partial accumulation of the electron density in the region surrounded by the peripheral atoms. Other investigations fostering quantitative information extractable from PA-MFPADs (or PA-RFPADs), measured using electron–ion 3D momentum spectroscopy at Spring 8, have been reported probing e.g. molecular bond-length in O(1s) ionization of CO2 and C(1s) ionization of CH3I, relying on the FLN description of MF and RFPADs.352,353 The results obtained at different electron energies compare well with MCSCI or TDDFT calculations, respectively, which shed light on diffraction features predicted at higher energies. The interpretation of such PA core-level MFPADs focusing on molecular structure is supported by a full-potential multiple scattering theory for photoelectron energies in the 100 eV range.354,355 Further comparative studies of 3D MFPADs measured for e.g. O(1s) ionization of methanol with SC calculations,356 and with earlier results for carbon monoxide MFPADs for similar polarization geometries of the CO central bond,118 elucidate the influence of both bond lengths and presence of H additional atoms.Along with scattering and diffraction of X rays and electrons providing well identified tools for exploration of the structure and properties of matter, it was suggested about two decades ago that MFPADs for site and element specific inner-shell ionization may be interpreted as X-ray photoelectron diffraction (XPD) mapping.357 This representation is supported by the multiple scattering picture of the ionization process, where the emission intensity in a given direction in the molecular frame results from the coherent superposition of a direct wave arising from the K shell of the ionized atom, with those scattered one or more times from the other atoms in the molecule (see Section Formalism). Noting that an electron energy of 150 eV corresponds to a de Broglie wavelength of 1 Å, it is expected that MFPADs including different polarization geometries constitute thereby unique fingerprints of the molecular potential, increasingly informative on the geometry of the molecule for photon energies far from the ionization threshold, supporting the concept of “electron diffraction from within”. This concept supports e.g. the interpretation of recent studies aiming at imaging of a molecular breakup using an XFEL illustrated below, and further examples are discussed later in the different contexts of Femtosecond photoelectron diffraction, and Laser Induced Electron Diffraction (LIED) giving rise to another type of “scattering from within”.
Fundamental studies of light–matter interactions
Fundamental questions in light–matter interactions addressed in the last two decades, relying on coincidence techniques and subsequent characterization of MFPADs, unveiled new quantum phenomena at the molecular scale as illustrated by few examples such as interferences in molecular double-slit or multislit arrangements.358–360 Symmetry breaking in resonant one-photon dissociative ionization of H2 through doubly excited states autoionizing on a few femtosecond time scale comparable to the dissociation time was demonstrated through the anisotropies of MFPADs induced by linearly361 and circularly316 polarized EUV photons, reflecting interferences between channels involving ionic states of different u and g symmetry subsequent to autoionization. Through their fundamental quantum nature, these questions overlap with that of the localized or non-localized character of single-holes in transient short-lived electronic states formed by one-photon K-shell ionization of symmetric molecules with two chemically equivalent atoms. The quantum entanglement of the photoelectron-Auger electron pair in K-shell ionization of N2 was unveiled by the correlation between MFPADs and MFAADs.339 Core–hole localization was further characterized by MFPAD or RFPAD asymmetries in K-shell ionization of polyatomic molecules e.g. O(1s) CO2 or F(1s) CF4.337,362 In S(1s) ionization of CS2 the localized/delocalized character of the S(1s) hole in the (SCS)4+ cationic intermediate states formed after Auger decay, was observed in measured and computed MFPADs for selected KERs in the S+ + C+ + S2+ DPI channel, featuring different relaxation pathways.363 Another twist of symmetry versus localization/delocalization occurs in presence of double well molecular potentials, as featured by a recent theoretical study of angularly and vibrationally resolved valence photoionization of NH3, involving the umbrella inversion mode.364 For linearly polarized light parallel to the C3 symmetry axis, MFPADs show a quite distinct behavior according to the even/odd symmetry of the initial vibrational wavefunction and their incoherent or coherent superposition.At high electron kinetic energies the continuum wavefunction becomes close to a plane wave, and the transition dipole moment from an initial bound state targeted by a given MO proportional to its Fourier transform. In an experiment on H2 at 400 eV photon energy with CP light propagating perpendicular to the molecular axis, MFPADS in the polarization plane were measured for the final 1σg ground state of H2+, as well as for the 1σu and 2σg excited states (satellites) resolved via the measured kinetic energy release KER of the reaction.365 As the latter ionic states are fully dissociative, the measured KER also led to MFPADs for different internuclear distances within the Franck–Condon region. MFPADs assigned to each excited ionic state provide an image of the corresponding component of the correlated initial state of H2. Actually they feature an image of the Dyson orbitals relative to the corresponding final states of H2+. This work of general application highlights the interest in measuring MFPADs of satellite states, which convey important information on the electronic correlation within the neutral molecule.366
Building on the remarkable developments of advanced light sources based on third generation synchrotron radiation, free electron lasers and lasers, more extreme regimes of the light–matter interaction are being explored accessing new ionization mechanisms and dynamics.
In the follow-up of LF characterization of non-dipole and recoil effects outlined earlier, full MFPADS were measured for N2(1s) ionized with an excitation energy of 40 keV through the coincident detection of two N+ fragments and one Auger electron, the fast photoelectron momentum being deduced by momentum conservation, and compared with SCE calculations.369 A remarkable two-fold emission anisotropy is observed in the MF. On the one hand a forward–backward asymmetry with respect to the photon momentum, favoring FW emission, is found for any orientation of the molecular axis, resulting in the anisotropy measured in the LF, well predicted at the MF level by theoretical calculations including the full photon plane wave  . On the other hand, an additional MFPAD strong asymmetry along the light polarization axis is noted when the molecular axis is neither parallel nor perpendicular to the photon momentum (or the polarization axis), favoring emission in the direction of the FW nitrogen atom: in the calculations a very weak dependence of the MFPADs relative to the molecular axis alignment was obtained, unless the combined impact of the sum of the recoil momentum of the fast photoelectron and the linear momentum of the high energy photon on the nuclei was properly taken into account, leading to a very good description of the newly observed symmetry breaking of MFPADs relative to the light polarization axis. Such effects will influence the interpretation of high energy experiments scheduled at XFELs.
. On the other hand, an additional MFPAD strong asymmetry along the light polarization axis is noted when the molecular axis is neither parallel nor perpendicular to the photon momentum (or the polarization axis), favoring emission in the direction of the FW nitrogen atom: in the calculations a very weak dependence of the MFPADs relative to the molecular axis alignment was obtained, unless the combined impact of the sum of the recoil momentum of the fast photoelectron and the linear momentum of the high energy photon on the nuclei was properly taken into account, leading to a very good description of the newly observed symmetry breaking of MFPADs relative to the light polarization axis. Such effects will influence the interpretation of high energy experiments scheduled at XFELs.
Another manifestation of nondipole effects was highlighted in a recent study aimed at quantifying the time delay relative to photoionization by different parts of an extended molecular orbital.370 The experiment considered double ionization of H2 by 800 eV photons with coincident measurement of the momenta of the H+ ions and the slow photoelectron, providing MFPADs of the fast photoelectron, in conditions where double-slit interference effects are met and the MFPADs are analyzed as fringe patterns. Recording the position of the fringes as a function of the light propagation direction with respect to the molecular axis, a displacement of the fringe pattern is observed, which is maximal when both axes coincide. This phase shift of the photoionization amplitude is assigned to a variation of the electron birth time delay and can be interpreted as the time the light takes to move from one proton to the other, that is estimated as 247 zeptoseconds, coherent with the average internuclear distance and the velocity of light.
This result can be clearly interpreted as a non-dipole effect, which takes into account the spatial variation of the field, neglected in the dipole approximation. It generated a flurry of theoretical work, employing a real time dependent description through TDSE, which included retardation in the field description.371–373 An alternative approach, based on the use of a high intensity 100 eV pulse, has been studied theoretically solving the TDSE including first-order nondipole effects, and interpreting the results via a simplified analytic model, showing the ability to detect the expected sub-as delays.374
Multiphoton processes in the X-ray regime have been explored theoretically, e.g. Stimulated Compton scattering (SCS).375 Significant asymmetries in the MFPADS of the low energy electrons are calculated, which also depend on the orientations of both light propagation and polarization directions in the MF.
 | ||
| Fig. 5 Schematic of the PAP two-photon K-shell ionization of O2 leading to the (O+ + O3+) channel377 based on typical potential energy curves, featuring the internuclear distance R2 and delay t for the second photon absorption (a); measured (dots) and computed (red line) PA-MFPADs for three KERs assigned to (R,t) parameters, assuming a second photon absorption by the K orbital of the right-hand O ion (labeled “3” in the inset) (b). Figure adapted from Fig. 2 and Fig. 6 of ref. 377 with permission from Physical Review X under Creative Commons Attribution 4.0 International license (http://creativecommons.org/licenses/by/4.0/). | ||
Supported by theoretical modeling using the single center method within the relaxed-core Hartree–Fock approximation, these MFPADs are interpreted as photoelectron diffraction patterns imaging the increase of the internuclear distance during the X-ray induced breakup of the O2 molecule. Thereby the internuclear distances and times where the second photon is absorbed within the 25 fs pulse can be inferred, revealing a first molecular movie of sequential core–hole ionization.377 The experimental and computed angular distributions in qualitative agreement support the feasibility of making molecular movies using upcoming two-pulse pump–probe schemes at high repetition rate XFELs. On the other hand, inspection of the coincidence maps correlating electron energies, or the ion fragment KER and electron energy, for (O2+ + O2+) channels, demonstrates the generation of double core–hole (DCH) ionic states,343 produced in an ionization sequence where ultrafast ejection of the two photoelectrons, occurring typically within less than 5 fs, precedes Auger decay. These energy maps allow to identify single-site (SS) and two-site (TS) DCH states, corresponding to emission of the two K-shell electrons from the same atom, or from different atoms. MFPADs for these processes have been obtained for the first time and constitute sensitive probes of the inherently different charge distribution of both channels.
MF photoemission resulting from tunneling ionization of randomly oriented H2,378 or HCl379 molecules was studied using a COLTRIMS set-up and an intense femtosecond IR circularly polarized laser (1014 W cm−2, 40 fs 800 nm) with the intent to image electronic structure fingerprints. In this case, although the highest occupied molecular orbital (HOMO) is primarily ionized populating bound ionic states, dissociative ionization occurs due to bond softening and their coupling with a higher dissociative state, providing access to correlated electron and ion fragment momenta detected about the polarization plane. The anisotropy of the subsequent MFPADs highlighted a favored tunnel ionization parallel to the molecular axis of H2, and the effective participation of the HOMO−1 lower valence MO in tunneling from HCl, reflecting many-electron effects and the formation of a correlated ion. For HCl, the observed asymmetry of the ionization probability along the molecular axis can be assigned to the dipole moment of the molecule. Such observables have stimulated theoretical modelling of strong field ionization in molecules.
Combining angular streaking with electron–ion coincidence 3D momentum spectroscopy of strong field multielectron dynamics is further illustrated in recent experiments carried out using 3D coincidence VMIs.162 RFPADs measured in the polarization plane of intense circularly polarized IR femtosecond pulses for dissociative ionization of polyatomic molecules such as methyl iodide CH3I were reported for single and double ionization featuring as well angle-dependent ionization yields reflecting contributions of both HOMO and HOMO−1 orbitals.380
Beyond setting electron tunneling as a tool for imaging the electronic structure of single molecules, further research investigates the detailed dynamics of tunnel ionization and its characterization by Wigner time-delays τW, defined as the energy derivative of the phase of the electron's wavefunction in momentum space. Most recent results address the dependence of τW(E,β) Wigner delays on the electron energy and emission angle β with respect to the molecular axis, here H2, within the polarization plane of circularly polarized laser light.381 To access the phase information carried by the detected electron wavepacket, an interferometric method termed holographic angular streaking of electrons (HASE) has been developed,382 where ionization is triggered by a co-rotating two-color (2ω,ω) laser field, formed by superposition of two circularly polarized femtosecond laser pulses. The observed Wigner time delays, extracted from the MFPADs obtained using a COLTRIMS reaction microscope, are assigned to spatial shifts of the electron birth positions when emerging from the potential barrier.
B. MFPADs from laser aligned molecules
Other strategies to measure MFPADs are dictated by the different means to establish the molecular frame experimentally, or by extracting the relevant MF information from LFPAD experiments controlling the rotational degree of freedom in simple molecules. Mostly relevant for photoionization studies of non-dissociative processes, of complex molecules, or using light sources operating at low repetition rates (<1 kHz) unfavorable for coincidence techniques, molecular frame photoelectron angular distributions can be obtained from samples of aligned molecules.Building on the study of rotationally state-resolved LFPADs for resonance-enhanced two-photon ionization by linearly and circularly polarized light, featured by the NO A2Σ+(v,N) → NO+ X1Σ+(v′,N′) + e(l,λ) transition,21 providing a complete description of the PI reaction and a demonstration of MF circular dichroism,383,384 REMPI of isotropically distributed gas-phase molecules represents one direction to bridge the gap between the LF and the MF.27 It has been extended to characterize the valence PI dynamics of light polyatomic molecules such as acetylene385 or ammonia386 carried into a partially aligned electronic state by the absorption of n pump photons, and ionized close to the ionization threshold by m probe photons, taking advantage of different polarization geometries.29 While the achievable alignment increases with the number of photons involved in the excitation process, the degree of alignment established for ionization of those excited molecular states remains limited requesting an extensive data processing, and as a purely optical scheme it does not allow for selection of molecular orientation.
Alternative techniques rely on laser induced molecular alignment and orientation. Whether one considers adiabatic or nonadiabatic laser molecular alignment (see Exp. section), setting a photoionization experiment from aligned molecules requires a pump–probe scheme where the alignment laser and the ionizing “probe” laser pulses are temporally resolved. The latter may consist of an XUV femtosecond pulse, e.g. produced by HHG leading to single photon ionization in weak field conditions (perturbative regime) or by free electron lasers (FEL) for which high fluxes allow for multiphoton processes still in the perturbative regime, a pico-to-femtosecond UV pulse initiating a REMPI process (perturbative multiphoton), or an IR or mid-IR intense laser involving strong field ionization. All these situations are indeed met and exploited in the ongoing research as briefly sketched in this section. The dependence of ionization yields measured at aligned or anti-aligned revivals, with reduced information with respect to MFPADS but still quite informative, remains attractive with the advantage of a simpler experimental setup: it was e.g. recently used at FERMI, combined with photoelectron spectra, as a control variable of the dissociation pattern for single photon inner-valence ionization of acetylene in the XUV photon energy range.387 It serves as well as a probe of strong field ionization as outlined below.
First demonstrations of MFPADs measured from impulsively aligned molecules were achieved in femtosecond time-resolved studies, where photoionization acted as a probe of electronic–vibrational dynamics in photodissociation of CS2 excited states.222,223
Valence-shell ionization of aligned molecules
MF photoemission for valence-shell ionization of CO2, N2, O2, CO molecules into bound ionic states was highlighted in the last decade combining impulsive alignment by a moderately strong femto-second laser and ionization by an HHG XUV source.388–390 Photoelectron momentum distributions recorded with a VMI in field-free conditions, around aligned and anti-aligned revivals of a rotational wavepacket, provided MFPADs for ionization of HOMO, HOMO−1, up to HOMO−4 molecular orbitals, resolved within congested energy spectra in an extended photoelectron energy range (0–30 eV). Different polarization geometries led to MFPADs for parallel and perpendicular transitions (averaged on the MF azimuthal emission angle). The latter, well predicted by MCSCI388,389 and multi-channel R-matrix390 calculations imprint information on the electronic structure of valence MOs.PADs for valence ionization of excited states of naphthalene and aniline polyatomic molecules, 1D or 3D adiabatically aligned with 100 ps IR laser temporally truncated pulses, were reported recently for various polarization geometries, in a two-photon resonant scheme using low intensity UV ionizing pulses of few ps duration.184 For both molecules, the two-photon process is resonant at the one-photon level with the S1 electronically excited state. For the naphthalene molecule, the structured PADs recorded with a VMI set-up displayed in Fig. 6 show an enhanced anisotropy in presence of the alignment laser. They compare well with numerical simulations of the 2D PADs based on ePolyScat ab initio calculations of MFPADs for ionization of the S1 state (averaged on the MF azimuthal emission angle), demonstrating also that a high degree of alignment was achieved. The situation is however different for aniline, which points to the contribution of additional ionization channels, subsequent to the perturbing presence of the alignment laser. This flaw can be avoided to achieve MFPADs for the electronic ground state using VUV single-photon ionization. More generally, these results support the use of field-free molecular alignment relying on the recent achievements (see Exp. section) combining spectrally truncated chirped laser pulses,190 and long-lasting field-free alignment of molecules imbedded in He nanodroplets.194 Although imaging of photoions resulting from Coulomb explosion is currently used to characterize their degree of alignment,165,194,391 work is still in progress to demonstrate PADs for molecules in He droplets.
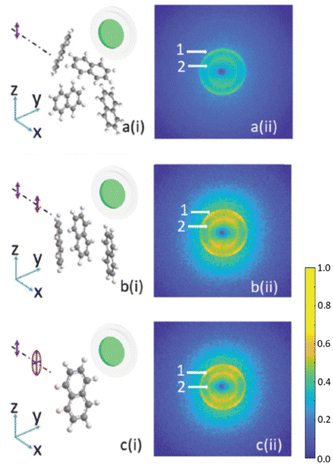 | ||
| Fig. 6 Photoelectron VMI raw images for two-photon linearly polarized REMPI (293.53 nm) of naphthalene (vertical purple arrow) for: an isotropic distribution of molecules (a), a linearly polarized alignment pulse (red arrow) providing 1D alignment (b), an elliptically polarized alignment pulse (red ellipse) providing 3D alignment of naphthalene.184 Reprinted with permission by Taylor and Francis, http://www.tandfonline.com, from J. Arlt et al., Photoelectron angular distributions from resonant two-photon ionisation of adiabatically aligned naphthalene and aniline molecules, Molecular Physics, 2021, 119, e1836411.184 | ||
Molecular frame reconstruction using time-domain photoionization interferometry
The complete retrieval of dynamical dipole matrix elements by time-resolved TRPADs measurements in LF was demonstrated in (1 + 1′) two-photon ionization of rotationally cold NO via the NO(A2Σ+) state, using a pump–probe scheme based on femtosecond UV lasers with variable wavelength of the probe corresponding to 0–1.33 eV photoelectron kinetic energy.392 The observables consisting of (t,E) time-energy maps of LFPADs are described by the time dependent β2(t) and β4(t) asymmetry parameters (together with the cross section), which expand for each energy in terms of the dynamical parameters CLMKQ and the AKQ(t) moments characterizing the evolution of the molecular axis alignment. The latter being theoretically predicted based on molecular constants, rotational temperature and pump pulse characteristics, the dynamical parameters CLMKQ were extracted from the measured β2(t) and β4(t) parameters, leading via a nonlinear regression to the dipole moments magnitude and phases for l = 0–3 partial waves, in total 6 moduli and 5 phases (relative values) (see Formalism). The missing phase connecting σ and π channels, which would require circularly polarized light, was computed. The retrieved complex valued dipole moments were found in fair agreement with those obtained from previous calculations393 and from rotationally resolved studies,383 the sensitivity of the (t,E) time-energy maps enabling to discriminate between the two previous sets of data. Crucial is the very accurate, low noise primary data for the TRPADs.Impulsive laser alignment, avoiding resonant conditions, was pushed to its limit to allow the full determination of complex dipole matrix elements, and to reconstruct MFPADs for ionization of N2 in the X, A and B channels, by recording LFPADs from a broad rotational wavepacket.31 High harmonics of a 267 nm driving field, H5 at 23.3 eV and H7 at 32.6 eV, were employed to record PADs for the three channels by sampling the delay relative to the alignment pulse in 150 time steps of 67 fs covering 10 ps. The large amount of data was used initially to reconstruct the time dependent moments describing the axis alignment P(θ,t) from the βL(t) measured parameters of the PADs, S(θ,t) = ΣLMβLM(t)YLM(θ,0), L = 0, 2, 4, 6. From
| P(θ,t)= ΣKQAK,-Q(t)YKQ(θ,0) βLM(t) = ΣKQCLMKQAK,Q(t) |
 (see formalism), and once the CLMKQ have been extracted in LF one can retrieve the corresponding coefficients in MF, and express the full MFPAD through them, bypassing the determination of the individual dipole matrix elements, by solving systems of linear equations (with generalized inverses in case of singularities) instead of quadratic regressions. This was demonstrated for N2 and C2H4, making explicit use of molecular symmetry.394
(see formalism), and once the CLMKQ have been extracted in LF one can retrieve the corresponding coefficients in MF, and express the full MFPAD through them, bypassing the determination of the individual dipole matrix elements, by solving systems of linear equations (with generalized inverses in case of singularities) instead of quadratic regressions. This was demonstrated for N2 and C2H4, making explicit use of molecular symmetry.394
Momentum analysis of LFPAD anisotropies relying on ultrafast time-energy-angle resolved observables, when an electron wave-packet launched by a pump pulse is probed by valence ionization, was recently proposed as a new method to access molecular frame electronic coherences, as demonstrated for dissociation of excited states of the NH3 molecule.1,395
Inner-shell ionization of aligned molecules: Femtosecond photoelectron diffraction
The availability of ultra-intense X-ray femtosecond pulses at XFEL facilities motivated the implementation of experiments extending the previously described “photoelectron diffraction from within” scheme, aiming at following time-dependent structural changes in molecules with femtosecond time and Angström spatial resolution,32 as an alternative to X-ray photon diffraction or ultra-fast photoelectron diffraction based on electron guns. At XFELs, the method benefits from the extended photon energy range accessible to induce inner-shell localized photoionization processes up to few hundreds of eV above ionization thresholds, and relies on their comparatively large cross sections of the order of 10−20 cm2. The optimal strategy to take advantage of the huge intensity available (1013 ph per pulse) resulting in hundreds of electrons per pulse, and account for the low repetition rate of the order of 100 Hz in the FEL context e.g. at LCLS,396 was to work with an assembly of aligned and/or oriented molecules and use a dedicated double sided VMI spectrometer such as the CAMP endstation (see Exp. section).158 The latter was designed to measure simultaneously both high-energy electrons and ion fragments, thereby taking the electron diffraction data extracted from the PADs while continuously monitoring the degree of alignment of the molecules, as well as identifying the fragmentation channels. First experiments were performed at LCLS on rotationally cold adiabatically aligned and mixed-field oriented polyatomic molecules such as 1-ethynyl-4-fluorobenzene (C8H5F) or 1,4-dibromobenzene (C6H4Br2),397,398 and the PADs for core–shell ionization of the halogen atom interpreted based on comparison with DFT calculations, taking into account a degree of alignment up to 〈cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ2D〉 = 0.89. They demonstrated the feasibility of photoelectron diffraction at XFELs for femtosecond time-resolved molecular structure imaging provided that some issues are achieved, such as e.g. an excellent degree of molecular alignment (larger than 0.95) preferably in field-free conditions to avoid the influence of the alignment laser on the studied processes, or the control of contamination of the target by molecular clusters.181
θ2D〉 = 0.89. They demonstrated the feasibility of photoelectron diffraction at XFELs for femtosecond time-resolved molecular structure imaging provided that some issues are achieved, such as e.g. an excellent degree of molecular alignment (larger than 0.95) preferably in field-free conditions to avoid the influence of the alignment laser on the studied processes, or the control of contamination of the target by molecular clusters.181
A similar project aiming at X-ray photoelectron diffraction (XPD) was pursued at the SPring-8 Ångström Compact free-electron Laser (SACLA).399 In an experiment analyzing XPD PADs recorded for adiabatically aligned I2 molecules ionized by the SACLA XFEL 140 eV above threshold of the I 2p3/2 inner-shell (IP = 4.557 keV) an I–I internuclear distance elongated by about 10% of its equilibrium value of 2.66 Å was revealed400 and interpreted as bond length softening due to multi-photon excitation of the I2 molecule in presence of the moderately intense alignment Nd:YAG laser. The need for field free conditions and for a degree of alignment significantly larger than those reported (〈cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ2D〉 = 0.734) was as well underlined in order to achieve precise XPD studies.
θ2D〉 = 0.734) was as well underlined in order to achieve precise XPD studies.
The situation has evolved recently with the advent of high repetition rates in the MHz range at the European XFEL,143 and becoming soon available at LCLS-II,144 opening access to coincidence experiments and related diagnostics as illustrated above.
Strong field ionization in the molecular frame
Within the development of attosecond science, strong field ionization of molecules is a topic of widespread interest. The complex photoelectron angular distribution resulting from the interaction of an intense IR femtosecond laser field with a molecule can be assigned to contributions of the ionization process as described by the well-known three step model:401,402 within a period of the driving femtosecond optical field, a valence electron wavepacket is extracted from the target through tunnel ionization or above threshold ionization, accelerated in vacuum by the laser field, and partly driven back to the parent ion, where it encounters rescattering or radiative recombination.The dependence of strong field ionization yields on the angle between the principal molecular axis, or the most polarizable axis, and the ionizing field is a more restricted observable, however pursued in different contexts to improve the description of molecular tunneling ionization based on a detailed comparison with theoretical models.410–414 It was as well considered to unveil multiple electronic SFI channels for above-threshold ionization (ATI) of e.g. 1,3-butadiene molecules.415
Beyond the molecular frame dependence of the nascent photoelectron momentum distribution probing tunnel ionization, the imprints of the emitted photoelectron wavepacket onto laser-driven electron recollision,416 photoelectron holography417 or laser-induced electron diffraction418–420 are further scrutinized in recent studies involving small molecules, as well as more complex polyatomic molecules such as 1–3 butadiene (C4H6)416 or the prototypical biomolecule indole (C8H7N), a major ultraviolet-absorbing chromophore of proteins.421
A first quantitative LIED application to molecular dynamics for a sample of randomly aligned N2 and O2 molecules was demonstrated by varying the wavelength of the 1 kHz mid-IR ionizing laser (1.7–2–2.3 μm), which is equivalent to taking snapshots of the molecular structure at different recollision times (variation of few fs) within an intrapulse pump–probe scheme, probing a bond length contraction of 0.1 Å with a sensitivity of 5 picometre (pm) for the O2 case due to the vibrational motion subsequent to tunnel ionization.427 After extraction of the field-free DCS from the measured PMDs based on the quantitative rescattering theory (QRS),424,428,429 bond lengths (R) were retrieved from the comparison of measured molecular contrast factors ∼(sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) qR)/qR, reflecting the molecular interference term of the rescattered electron momentum distribution, as a function of the momentum transfer q = 2prsin(θr/2), with computed ones based on the independent-atom model (IAM).429 Geometrical structure and bond lengths were also obtained for unaligned polyatomic molecules such as benzene430 and ethylene431 using a similar approach. It is worth noting that for randomly oriented neutral small molecules the ionization step generally induces partial alignment, though the contrast of the diffraction features after rescattering is improved for prepared laser aligned molecules, thereby relating each step of the process resulting in the studied PAD or PMD to the molecular frame.
qR)/qR, reflecting the molecular interference term of the rescattered electron momentum distribution, as a function of the momentum transfer q = 2prsin(θr/2), with computed ones based on the independent-atom model (IAM).429 Geometrical structure and bond lengths were also obtained for unaligned polyatomic molecules such as benzene430 and ethylene431 using a similar approach. It is worth noting that for randomly oriented neutral small molecules the ionization step generally induces partial alignment, though the contrast of the diffraction features after rescattering is improved for prepared laser aligned molecules, thereby relating each step of the process resulting in the studied PAD or PMD to the molecular frame.
Combining a 160 kHz mid-IR (3.1 μm) source with a reaction microscope,136 LIED was exploited e.g. to retrieve multiple bond lengths in impulsively aligned acetylene,432 image bond breaking in di-ionized acetylene,433 or non-adiabatic Renner–Teller effects in the neutral CS2(B1B2) excited state of carbonyl disulfide,434 relying on the electron–ion coincidence to decipher between different reaction pathways. Unlike the case of CS2 where vibronic excitation induced by the driving field prior to ionization was inferred,434 as illustrated in Fig. 7, LIED of randomly oriented molecules carbonyl sulfide OCS using mid-IR (2 μm) around a comparable 1014 W cm−2 intensity and a high energy VMI imaging electrons up to 500 eV, the geometry and bond distances of the OCS molecule extracted with a precision better than ±5 pm were found in good agreement with the known structure of ground-state OCS.435 Additionally, the classical rescattering model can also be invoked to associate a specific returning time to the measured electron rescattering energy, reaching a sub-femtosecond temporal resolution for the geometrical structure.432,434
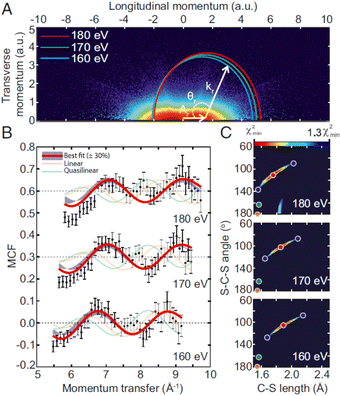 | ||
| Fig. 7 LIED imaging of laser-induced vibronic excitation in CS2:434 (A) measured photoelectron momentum distribution providing field free DCSs for different electron returning energies ER using the QRS theory, (B) molecular contrast factors for ER = 160, 170, 180 eV: (dots) experimental, and (red line) computed for the geometric structure leading to the MCF closest to the experiment, (C) (red dots) retrieved most probable symmetrically stretched and bent geometry of CS2+. Figure reproduced from Fig. 1 of ref. 434 with permission from Proc. Natl. Acad. Sci. USA under Creative Commons Attribution 4.0 International license (http://creativecommons.org/licenses/by/4.0/). | ||
Through these examples LIED demonstrates its ability for probing photoinduced molecular dynamics in the MF with femto-to-attosecond temporal and sub-Å spatial resolutions. A careful account of the influence of the three ionization, propagation and rescattering steps, in particular the MF orientation relative to the polarization436 or the multielectron character419 governing the properties of the released electron wavepacket is to be considered for the interpretation of the recorded 3D PMDs. For more complex molecules, structure information retrieval requires extending the tractability of the QRS theory and IAM model algorithms based on the θr dependence of PMDs at fixed kr. The measured PMDs can alternatively be analyzed through a Fourier transform variant of LIED based on energy spectra of back-scattered electrons (θr = 180°): FT-LIED,418,437,438i.e. fixed-angle broadband laser driven electron scattering (FABLES),439 or through implementation of more general retrieval methods,440 as recently demonstrated combining LIED with machine learning to image molecules such as Fenchone.441
If pump–probe femtosecond experiments where LIED acts as a probe of ultrafast dynamics launched by a coherent pump pulse has not been yet fully demonstrated, recent time-resolved results in the picosecond range have been reported based on the analysis of PMDs acquired with a VMI spectrometer.442,443 LIED and photoelectron holography were investigated simultaneously through the PMDs for SFI of nitrogen monoxide NO, recorded at different delays after launching a rotational wave packet in NO, tracking the coupling between valence-shell electronic and rotational dynamics.442 The measured and computed field-free DCSs extracted from laser induced electron recollision PADs for SFI of Iodine I2 weakly bound excited state in the regime of low-energy electron scattering were shown to display comparable features evolving with the time-delay relative to the prompt excitation of a vibrational wave packet, assigned to the role of a shape resonance and its energy dependence to the molecular internuclear distance.443
Perspective
As illustrated through the range of experiments addressed in this perspective, the scope of angle resolved molecular photoelectron spectroscopy has broadly expanded in the last two decades, uncovering light–matter interactions in different field strength regimes and involving targets of increasing complexity as illustrated e.g. by the characterization of chiral objects. Access to these new regimes challenges as well theoretical descriptions. The richness of the PAD observables, and in particular MFPADs, emerges from the quantum interference imprint carried by the photoelectron scattering states and unveiled in angular distributions. They provide highly valuable information on the electronic structure of stationary molecular states and photoionization dynamics influenced by electronic correlation, resonances or fundamental symmetries, accessing the final continuum partial wave phases and transition amplitudes of the relevant operator (electric dipole in the simplest case), ideally up to so-called complete experiment where all matrix elements up to a given final angular momentum are reconstructed. MFPADs, PA-MFPADs, or PMDs are also currently interpreted as diffraction patterns of the scattered electron wave revealing molecular geometrical structures, in particular when emission occurs from a localized atomic orbital subsequent to X-ray ionization, or results from strong field tunnel ionization in LIED. This methodological corpus builds up a strong potential for future studies of molecular structure and dynamics in real time.1,444From the experimental side, new challenges are driven by the impressive achievements of light sources, both at large-scale XFEL facilities and based on advanced table-top laser sources, pushing to higher intensity and higher energy photons, ever shorter pulse duration, with increasing repetition rates in the range of several hundreds of kHz up to MHz, but also ever more complex pulses and nonclassical light, characterized by fields structured in the four-dimensional space-time, with strong inhomogeneity of all light parameters.234,236 Angular distributions from ionization with specially tailored fields are mostly untouched. Beside HHG attosecond XUV pulses, X-ray laser-enhanced attosecond pulses are in progress at LCLS and European XFEL, as characterized using photoelectron angular streaking spectroscopy.445 Concurrently, the continuous progress in large solid angle acceptance, efficient position and time sensitive detectors will benefit multicoincidence experiments, in general allowing the study of low cross section minority channels. It includes e.g. extensions to electron–ion–photon coincidences, favoured by enhanced photon detection efficiency combined with the time and position capabilities,161,446 foreseen in particular in the hard X-ray domain where radiative decay contributes to the relaxation of core–hole excited states.295 Moreover the sharpening alignment and orientation techniques for gas phase molecules combined with VMI based detection will render MFPADS much more routinely available for complex systems.
This instrumental context will extend significantly the range and the achievements of temporally resolved studies aiming at characterizing in real time molecular structure and intramolecular dynamics triggered by photoabsorption and probed by photoionization,1i.e. featuring a so-called “molecular movie”. Such processes involve the relaxation dynamics of excited molecular states to lower potential energy surfaces via nonadiabatic couplings, and to vibrational motion giving rise to bond stretching/opening, isomerization, and dissociation, generally underlying chemical bond making and breaking, or even electronic wavepacket motion or charge migration.447–449 Despite the popularity of challenging pump–probe experiments, quite few probe the dynamics beyond the simple photoelectron spectra, often leading to a limited characterization of the internal dynamics, with remaining ambiguities. The rich information embodied in angularly resolved studies from oriented molecules will be greatly beneficial to fully characterize the electronic states involved, their coupling with nuclear motion,450 and the electron wavepacket coherences395,451,452 and bifurcations, up to now quite elusive, both in valence excitation and ionization with broad pulses.
Recent results obtained at the European XFEL for single-pulse two-photon sequential core ionization pave the way for MF angle-resolved X-ray pump X-ray probe experiments temporally resolved at the femtosecond time scale, with perspectives to observe e.g. coherent electron–hole dynamics on the attosecond scale. In strong field ionization, implementing LIED, which also features an intrapulse pump–probe scheme, as an effective pump–probe tool to characterize molecular structure in real time is in progress.
Probing the photoionization dynamics in the MF in real time with attosecond accuracy, involving the overlap of an XUV attosecond pulse and a phase-locked NIR femtosecond pulse e.g. in the RABBITT interference scheme, fostered by recent developments, should be further investigated. The achievement of coherent XUV pulses, e.g. at the fundamental ω and second harmonic 2ω as demonstrated at the FERMI seeded FEL,453 enables recording interferences between one-photon and two-photon quantum paths,454 revealing LF angle resolved phase differences of the corresponding photoionization amplitudes, opening new perspectives for molecules.290
Meanwhile, the complementarity between ultrafast time domain studies and high resolution energy domain achieved at synchrotrons remains quite relevant and attractive, as illustrated e.g. by the recent developments of MF angle resolved photoionization time delays.
Another direction is the push to multiphoton effects in the high energy domains with XFELS. Double (multiple) core holes and decays will be studied, including time delays for sequential process, exploiting photoelectron and Auger in coincidence. The hard X-ray region, where a number of unexplored issues are anticipated,455 has been barely explored in molecules. A number of new effects, like non dipole, nuclear recoil and Compton scattering,456 although individually understood in basic terms, contribute together and will open a new window in molecular interactions. Compton scattering from individual orbitals in oriented molecules can provide a new and direct way of orbital imaging.457,458 Nonlinear process like stimulated Compton scattering will become available.375 Other double ionization studies will be extended into the high kinetic energy domain, where the two electron continuum simplifies and new windows may be opened to the imaging of the electronic wavefunction.
One obvious fostered perspective is the extension of LF or MF angle resolved PES studies to more complex molecules (finite systems), supported by both recent advances in Coulomb explosion imaging,459 and the fast improvement of alignment/orientation protocols.193 This direction also implies specialized methods to produce gas phase targets from different species as mentioned earlier, such as fragile molecules, radicals, positive and negative ions, clusters, nanoparticles, high temperature vapors, and further selection of conformers.104 Further developments exploring the boundary between gas phase and condensed systems are e.g. aqueous solutions in droplets or liquid jets, surfactant layer structure at liquid–vapor interface, and molecules adsorbed on surfaces.
Besides characterization of the electronic structure of the target, like orbital composition and imaging, a deeper insight into many-body effects, both in the bound and continuum states, will be pursued, through precise experiments on multielectron effects in ionization, in particular multiply excited initial and final states with different excitation mechanisms. Their understanding is a fundamental problem of current electronic structure theory, which is very directly linked to these observables. A direct imaging of two electron wavefunction is a long sought goal that may become accessible. New observables like time delays in different excitation mechanisms may explore another dimension. One may recall the enormous contribution to the understanding of the electronic structure in molecules generated by the close dialog between photoionization experiments and electronic structure theory, a two-way challenge that will be brought to an upper stage. A frontier in the theoretical understanding is the detailed description of coupled electron–nuclear dynamics, and the study of coherent electron–nuclear wavepackets, for which the pump–probe experiments already mentioned may give details hitherto unavailable. Also the accurate description of ionization processes with complex pulses, non perturbative fields and structured light is another challenge to be met by theoretical development.
Finally, although barely touched in this paper, applications of PADs as for example PECD will offer a rich potential as tools for analytical purposes, for the characterization of complex molecules and processes, including chemical reactions and catalysis, and merging into molecular studies of adsorbates on surfaces, as well as for quantitative determinations. In the latter case also theoretical simulation may require a more quantitative refinement.
Acronyms
| BW-FW | backward–forward |
| CC | Close coupling expansion |
| CCD | Charge-coupled device |
| CMOS | Complementary metal-oxide semi-conductor |
| CDAD | Circular dichroism in photoelectron angular distribution |
| CD | Circular dichroism |
| CI | Configuration interaction |
| COLTRIMS | Cold target recoil ion momentum spectrometer |
| CP | Circular polarization |
| DFT | Density functional theory |
| DLD | Delay line detector |
| DME | Dipole matrix element |
| DPI | Dissociative photon ionization |
| FC | Franck–Condon |
| FEL | Free electron laser |
| HF | Hartree–Fock |
| HHG | High order harmonic generation |
| HOMO | Highest occupied molecular orbital |
| ICD | Interatomic Coulombic Decay |
| IE | Ionization energy |
| IP | Ionization potential (same as IE) |
| KER | Kinetic energy release |
| LCLS | Linac coherent light source |
| LCP | Left circular polarization |
| LDAD | Linear dichroism in photoelectron angular distribution |
| LF | Laboratory frame |
| LFPAD | Laboratory frame photoelectron angular distribution |
| LIED | Laser induced electron diffraction |
| LP | Linear polarization |
| MCP | Multichannel plate |
| MFAAD | Molecular frame Auger electron angular distribution |
| MF | Molecular frame |
| MFPAD | Molecular frame photoelectron angular distribution |
| MO | Molecular orbital |
| MP | Multiphoton |
| ND | Non dipole |
| NIR | Near infrared |
| OCE | One center expansion (also SCE single center) |
| OPCPA | Optical parametric chirped pulse amplification |
| OVGF | Outer valence green function |
| PAD | Photoelectron angular distribution |
| PA MFPAD | Polarized averaged MFPAD |
| PECD | Photoelectron circular dichroism |
| PEPICO | Photoelectron–photoion coincidence |
| PES | Photoelectron spectroscopy (also photoelectron spectra) |
| PICD | Photoion circular dichroism |
| PI | Photoionization |
| PMD | Photoelectron momentum distribution |
| PSD | Position sensitive detector |
| RCP | Right circular polarization |
| REMPI | Resonant enhanced multi photon ionization |
| RFPAD | Recoil frame photoelectron angular distribution |
| RPA | Random phase approximation |
| SC | Single channel |
| SF | Strong field |
| TDC | Time to digital converter |
| TDDFT | Time dependent density functional theory |
| TDSE | Time dependent Schrödinger equation |
| TOF | Time-of-flight |
| TRPEI | Time resolved photoelectron imaging |
| TRPES | Time resolved photoelectron spectroscopy |
| VMI | Velocity map imaging |
| VUV | Vacuum ultraviolet |
| XFEL | X-ray free electron laser |
| XUV | Extreme ultraviolet |
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We are very grateful to Reinhard Dörner, Kiyoshi Ueda, Katharine Reid, Robert Lucchese, Kevin Prince, Thomas Baumert, Henrik Stapelfeldt, Michael Meyer, Till Jahnke, Jens Biegert, Marc Simon, Ottmar Jagutzki and Fabian Holzmeier for fruitful scientific exchanges within the preparation of this perspective.References
- M. S. Schuurman and V. Blanchet, Phys. Chem. Chem. Phys., 2022 10.1039/D1CP05885A.
- D. Dill, J. Chem. Phys., 1976, 65, 1130–1133 CrossRef CAS.
- N. Chandra, J. Phys. B: At. Mol. Phys., 1987, 20, 3405–3415 CrossRef CAS.
- A. V. Golovin, N. A. Cherepkov and V. V. Kuznetsov, Z. Phys. D - Atoms Molec. Clusters, 1992, 24, 371–375 CrossRef CAS.
- H. Park and R. N. Zare, J. Chem. Phys., 1996, 104, 4554–4567 CrossRef CAS.
- S. K. Semenov and N. A. Cherepkov, J. Phys. B: At., Mol. Opt. Phys., 2009, 42, 085101 CrossRef.
- V. V. Kuznetsov, S. K. Semenov and N. A. Cherepkov, J. Chem. Phys., 2011, 134, 134301 CrossRef CAS PubMed.
- R. R. Lucchese and D. Dowek, Attosecond and XUV Physics: Ultrafast Dynamics and Spectroscopy, ed. T. Schultz and M. Vrakking, Wiley Online Library, 2014, 293–320 Search PubMed.
- E. P. Wigner, Phys. Rev., 1955, 98, 145–147 CrossRef CAS.
- J. M. Dahlström, A. L’Huillier and A. Maquet, J. Phys. B: At., Mol. Opt. Phys., 2012, 45, 183001 CrossRef.
- J. M. Dahlström, D. Guénot, K. Klünder, M. Gisselbrecht, J. Mauritsson, A. L’Huillier, A. Maquet and R. Taïeb, Chem. Phys., 2013, 414, 53–64 CrossRef.
- R. Pazourek, S. Nagele and J. Burgdörfer, Rev. Mod. Phys., 2015, 87, 765–802 CrossRef CAS.
- P. Hockett, E. Frumker, D. M. Villeneuve and P. B. Corkum, J. Phys. B: At., Mol. Opt. Phys., 2016, 49, 095602 CrossRef.
- D. Baykusheva and H. J. Wörner, J. Chem. Phys., 2017, 146, 124306 CrossRef PubMed.
- R. R. Lucchese, A. Lafosse, J. C. Brenot, P. M. Guyon, J. C. Houver, M. Lebech, G. Raseev and D. Dowek, Phys. Rev. A, 2002, 65, 020702 CrossRef.
- A. Lafosse, J. C. Brenot, P. M. Guyon, J. C. Houver, A. V. Golovin, M. Lebech, D. Dowek, P. Lin and R. R. Lucchese, J. Chem. Phys., 2002, 117, 8368–8384 CrossRef CAS.
- M. Lebech, J. C. Houver, A. Lafosse, D. Dowek, C. Alcaraz, L. Nahon and R. R. Lucchese, J. Chem. Phys., 2003, 118, 9653–9663 CrossRef CAS.
- X.-J. Liu, R. R. Lucchese, A. N. Grum-Grzhimailo, Y. Morishita, N. Saito, G. Prümper and K. Ueda, J. Phys. B: At., Mol. Opt. Phys., 2007, 40, 485–496 CrossRef CAS.
- R. R. Lucchese, R. Montuoro, A. N. Grum-Grzhimailo, X.-J. Liu, G. Prümper, Y. Morishita, N. Saito and K. Ueda, J. Electron Spectrosc. Relat. Phenom., 2007, 155, 95–99 CrossRef CAS.
- D. Dowek and R. R. Lucchese, Dynamical Processes in Atomic and Molecular Physics, Bentham Bussum The Netherlands, 2012, vol. 39, pp. 57–95 Search PubMed.
- K. L. Reid, D. J. Leahy and R. N. Zare, Phys. Rev. Lett., 1992, 68, 3527–3530 CrossRef CAS PubMed.
- N. A. Cherepkov, G. Raseev, J. Adachi, Y. Hikosaka, K. Ito, S. Motoki, M. Sano, K. Soejima and A. Yagishita, J. Phys. B: At., Mol. Opt. Phys., 2000, 33, 4213–4236 CrossRef CAS.
- O. Geßner, Y. Hikosaka, B. Zimmermann, A. Hempelmann, R. R. Lucchese, J. H. D. Eland, P.-M. Guyon and U. Becker, Phys. Rev. Lett., 2002, 88, 193002 CrossRef PubMed.
- P. Hockett, M. Wollenhaupt, C. Lux and T. Baumert, Phys. Rev. Lett., 2014, 112, 223001 CrossRef CAS PubMed.
- C. S. Trevisan, C. W. McCurdy and T. N. Rescigno, J. Phys. B: At., Mol. Opt. Phys., 2012, 45, 194002 CrossRef.
- D. Toffoli, R. R. Lucchese, M. Lebech, J. C. Houver and D. Dowek, J. Chem. Phys., 2007, 126, 054307 CrossRef PubMed.
- J. G. Underwood and K. L. Reid, J. Chem. Phys., 2000, 113, 1067–1074 CrossRef CAS.
- K. L. Reid, Annu. Rev. Phys. Chem., 2003, 54, 397–424 CrossRef CAS PubMed.
- K. L. Reid, Mol. Phys., 2012, 110, 131–147 CrossRef CAS.
- H. Stapelfeldt and T. Seideman, Rev. Mod. Phys., 2003, 75, 543–557 CrossRef CAS.
- C. Marceau, V. Makhija, D. Platzer, A. Y. Naumov, P. B. Corkum, A. Stolow, D. M. Villeneuve and P. Hockett, Phys. Rev. Lett., 2017, 119, 083401 CrossRef PubMed.
- F. Krasniqi, B. Najjari, L. Strüder, D. Rolles, A. Voitkiv and J. Ullrich, Phys. Rev. A, 2010, 81, 033411 CrossRef.
- M. Kazama, T. Fujikawa, N. Kishimoto, T. Mizuno, J. Adachi and A. Yagishita, Phys. Rev. A, 2013, 87, 063417 CrossRef.
- C. Yu and X. Wang, Phys. Rev. A, 2019, 100, 063422 CrossRef CAS.
- J. W. Cooper, Phys. Rev. A, 1990, 42, 6942–6945 CrossRef CAS PubMed.
- A. N. Grum-Grzhimailo, J. Phys. B: At., Mol. Opt. Phys., 2003, 36, 2385–2407 CrossRef CAS.
- R. Kosloff, J. Phys. Chem., 1988, 92, 2087–2100 CrossRef CAS.
- A. Castro, M. A. L. Marques and A. Rubio, J. Chem. Phys., 2004, 121, 9 CrossRef PubMed.
- A. C. Brown, G. S. J. Armstrong, J. Benda, D. D. A. Clarke, J. Wragg, K. R. Hamilton, Z. Mašín, J. D. Gorfinkiel and H. W. van der Hart, Comput. Phys. Commun., 2020, 250, 107062 CrossRef CAS.
- N. Tancogne-Dejean, M. J. T. Oliveira, X. Andrade, H. Appel, C. H. Borca, G. Le Breton, F. Buchholz, A. Castro, S. Corni, A. A. Correa, U. De Giovannini, A. Delgado, F. G. Eich, J. Flick, G. Gil, A. Gomez, N. Helbig, H. Hübener, R. Jestädt, J. Jornet-Somoza, A. H. Larsen, I. V. Lebedeva, M. Lüders, M. A. L. Marques, S. T. Ohlmann, S. Pipolo, M. Rampp, C. A. Rozzi, D. A. Strubbe, S. A. Sato, C. Schäfer, I. Theophilou, A. Welden and A. Rubio, J. Chem. Phys., 2020, 152, 124119 CrossRef CAS PubMed.
- L. B. Madsen, L. A. A. Nikolopoulos and P. Lambropoulos, Eur. Phys. J. D, 2000, 10, 67–79 CrossRef CAS.
- A. Palacios, C. W. McCurdy and T. N. Rescigno, Phys. Rev. A, 2007, 76, 043420 CrossRef.
- G. Grell, O. Kühn and S. I. Bokarev, Phys. Rev. A, 2019, 100, 042512 CrossRef CAS.
- N. Chandra and M. Chakraborty, J. Chem. Phys., 1992, 97, 236–244 CrossRef CAS.
- N. Chandra and M. Chakraborty, J. Chem. Phys., 1993, 99, 7314–7330 CrossRef CAS.
- S. K. Semenov, V. V. Kuznetsov, N. A. Cherepkov, P. Bolognesi, V. Feyer, A. Lahmam-Bennani, M. E. S. Casagrande and L. Avaldi, Phys. Rev. A, 2007, 75, 032707 CrossRef.
- A. Szabo and N. S. Ostlund, Modern quantum chemistry: introduction to advanced electronic structure theory, Courier Corporation, 2012 Search PubMed.
- T. Helgaker, P. Jorgensen and J. Olsen, Molecular electronic-structure theory, John Wiley & Sons, 2014 Search PubMed.
- B. O. Roos, R. Lindh, P. Malmqvist, V. Veryazov and P. O. Widmark, Multiconfigurational Quantum Chemistry, Wiley-Blackwell, 2016 Search PubMed.
- F. Aquilante, J. Autschbach, A. Baiardi, S. Battaglia, V. A. Borin, L. F. Chibotaru, I. Conti, L. De Vico, M. Delcey, I. F. Galván, N. Ferré, L. Freitag, M. Garavelli, X. Gong, S. Knecht, E. D. Larsson, R. Lindh, M. Lundberg, P. Å. Malmqvist, A. Nenov, J. Norell, M. Odelius, M. Olivucci, T. B. Pedersen, L. Pedraza-González, Q. M. Phung, K. Pierloot, M. Reiher, I. Schapiro, J. Segarra-Martí, F. Segatta, L. Seijo, S. Sen, D.-C. Sergentu, C. J. Stein, L. Ungur, M. Vacher, A. Valentini and V. Veryazov, J. Chem. Phys., 2020, 152, 214117 CrossRef CAS PubMed.
- B. N. C. Tenorio, A. Ponzi, S. Coriani and P. Decleva, Molecules, 2022, 27, 1203 CrossRef CAS PubMed.
- L. S. Cederbaum and W. Domcke, in Advances in Chemical Physics, ed. I. Prigogine and S. A. Rice, John Wiley & Sons, Inc., Hoboken, NJ, USA, 1977, pp. 205–344 Search PubMed.
- J. V. Ortiz, J. Chem. Phys., 2020, 153, 070902 CrossRef CAS PubMed.
- J. Schirmer and A. B. Trofimov, J. Chem. Phys., 2004, 120, 11449–11464 CrossRef CAS PubMed.
- S. Banerjee and A. Y. Sokolov, J. Chem. Phys., 2019, 151, 224112 CrossRef PubMed.
- A. L. Dempwolff, M. Hodecker and A. Dreuw, J. Chem. Phys., 2022, 156, 054114 CrossRef CAS PubMed.
- J. F. Stanton and R. J. Bartlett, J. Chem. Phys., 1993, 98, 7029–7039 CrossRef CAS.
- C. Melania Oana and A. I. Krylov, J. Chem. Phys., 2007, 127, 234106 CrossRef PubMed.
- T. Moitra, A. C. Paul, P. Decleva, H. Koch and S. Coriani, Phys. Chem. Chem. Phys., 2022, 24, 8329–8343 RSC.
- M. Ehara, J. Hasegawa and H. Nakatsuji, in Theory and Applications of Computational Chemistry, ed. C. E. Dykstra, G. Frenking, K. S. Kim and G. E. Scuseria, Elsevier, Amsterdam, 2005, pp. 1099–1141 Search PubMed.
- R. Parr and W. Yang, Density Functional Theory of Atoms and Molecules, New York, Oxford Univ. Press, 1989 Search PubMed.
- K. Burke and L. O. Wagner, Int. J. Quantum Chem., 2013, 113, 96–101 CrossRef CAS.
- K. Burke, J. Werschnik and E. K. U. Gross, J. Chem. Phys., 2005, 123, 062206 CrossRef PubMed.
- M. Stener, G. Fronzoni and P. Decleva, J. Chem. Phys., 2005, 122, 234301 CrossRef CAS PubMed.
- S. I. Bokarev and O. Kühn, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020, 10, e1433 CAS.
- C. Daniel, L. González and F. Neese, Phys. Chem. Chem. Phys., 2021, 23, 2533–2534 RSC.
- L. S. Cederbaum, W. Domcke, J. Schirmer and W. V. Niessen, in Advances in Chemical Physics, ed. I. Prigogine and S. A. Rice, John Wiley & Sons, Inc., Hoboken, NJ, USA, 1986, pp. 115–159 Search PubMed.
- A. D. O. Bawagan and E. R. Davidson, Advances in Chemical Physics, John Wiley & Sons, Ltd, 1999, pp. 215–266 Search PubMed.
- R. E. Stratmann and R. R. Lucchese, J. Chem. Phys., 1995, 102, 8493–8505 CrossRef CAS.
- P. V. Demekhin, A. Ehresmann and V. L. Sukhorukov, J. Chem. Phys., 2011, 134, 024113 CrossRef PubMed.
- V. P. Majety, A. Zielinski and A. Scrinzi, New J. Phys., 2015, 17, 063002 CrossRef.
- C. Marante, M. Klinker, I. Corral, J. González-Vázquez, L. Argenti and F. Martín, J. Chem. Theory Comput., 2017, 13, 499–514 CrossRef CAS PubMed.
- Z. Mašín, J. Benda, J. D. Gorfinkiel, A. G. Harvey and J. Tennyson, Comput. Phys. Commun., 2020, 249, 107092 CrossRef.
- P. Decleva, M. Stener and D. Toffoli, Molecules, 2022, 27, 2026 CrossRef CAS PubMed.
- A. Ponzi, C. Angeli, R. Cimiraglia, S. Coriani and P. Decleva, J. Chem. Phys., 2014, 140, 204304 CrossRef PubMed.
- K. H. Johnson, in Advances in Quantum Chemistry, ed. P.-O. Löwdin, Academic Press, 1973, vol. 7, pp. 143–185 Search PubMed.
- D. Dill and J. L. Dehmer, J. Chem. Phys., 1974, 61, 692–699 CrossRef CAS.
- K. Hatada, K. Hayakawa, M. Benfatto and C. R. Natoli, J. Phys.: Condens. Matter, 2010, 22, 185501 CrossRef PubMed.
- R. R. Lucchese, K. Takatsuka and V. McKoy, Phys. Rep., 1986, 131, 147–221 CrossRef.
- T. N. Rescigno, C. W. McCurdy, A. E. Orel and B. H. Lengsfield, in Computational Methods for Electron-Molecule Collisions, ed. W. M. Huo and F. A. Gianturco, Plenum Press, New York, 1995, pp. 1–44 Search PubMed.
- P. G. Burke, R-matrix theory of atomic collisions: Application to atomic, molecular and optical processes, Springer Science & Business Media, 2011, vol. 61 Search PubMed.
- P. Descouvemont and D. Baye, Rep. Prog. Phys., 2010, 73, 036301 CrossRef.
- C. Froese Fischer and M. Idrees, Comput. Phys., 1989, 3, 53 CrossRef.
- M. Brosolo and P. Decleva, Chem. Phys., 1992, 159, 185–196 CrossRef CAS.
- M. Kazama, T. Fujikawa, N. Kishimoto, T. Mizuno, J. Adachi and A. Yagishita, Phys. Rev. A, 2013, 87, 063417 CrossRef.
- D. Toffoli and P. Decleva, J. Chem. Theory Comput., 2016, 12, 4996–5008 CrossRef CAS PubMed.
- N. M. Novikovskiy, A. N. Artemyev, D. V. Rezvan, B. M. Lagutin and P. V. Demekhin, J. Phys. B: At., Mol. Opt. Phys., 2022, 55, 175001 CrossRef.
- T. Sato and K. L. Ishikawa, Phys. Rev. A, 2013, 88, 023402 CrossRef.
- A. F. Al-Refaie and J. Tennyson, Comput. Phys. Commun., 2017, 221, 53–62 CrossRef CAS.
- F. A. Gianturco, R. R. Lucchese and N. Sanna, J. Chem. Phys., 1994, 100, 6464–6471 CrossRef CAS.
- A. P. Natalense and R. R. Lucchese, J. Chem. Phys., 1999, 111, 5344–5348 CrossRef CAS.
- I. Powis, J. Chem. Phys., 2000, 112, 301–310 CrossRef CAS.
- I. Powis, J. Phys. Chem. A, 2000, 104, 878–882 CrossRef CAS.
- Y. Suzuki and T. Suzuki, J. Phys. Chem. A, 2008, 112, 402–411 CrossRef CAS PubMed.
- H. Ganjitabar, G. A. Garcia, L. Nahon and I. Powis, J. Chem. Phys., 2020, 153, 034302 CrossRef CAS PubMed.
- T. Piteša, M. Sapunar, A. Ponzi, M. F. Gelin, N. Došlić, W. Domcke and P. Decleva, J. Chem. Theory Comput., 2021, 17, 5098–5109 CrossRef PubMed.
- F. Ota, S. Abe, K. Hatada, K. Ueda, S. Díaz-Tendero and F. Martín, Phys. Chem. Chem. Phys., 2021, 23, 20174–20182 RSC.
- M. Williams, R. Forbes, H. Weir, K. Veyrinas, R. J. MacDonell, A. E. Boguslavskiy, M. S. Schuurman, A. Stolow and T. J. Martinez, J. Phys. Chem. Lett., 2021, 12, 6363–6369 CrossRef CAS PubMed.
- R. Forbes, S. P. Neville, M. A. B. Larsen, A. Röder, A. E. Boguslavskiy, R. Lausten, M. S. Schuurman and A. Stolow, J. Phys. Chem. Lett., 2021, 12, 8541–8547 CrossRef CAS PubMed.
- U. Even, EPJ tech. instrum., 2015, 2, 17 CrossRef.
- F. Filsinger, G. Meijer, H. Stapelfeldt, H. N. Chapman and J. Küpper, Phys. Chem. Chem. Phys., 2011, 13, 2076–2087 RSC.
- M. H. M. Janssen and I. Powis, Phys. Chem. Chem. Phys., 2014, 16, 856–871 RSC.
- L. Nahon, G. A. Garcia and I. Powis, J. Electron Spectrosc. Relat. Phenom., 2015, 204, 322–334 CrossRef CAS.
- Y.-P. Chang, D. A. Horke, S. Trippel and J. Küpper, Int. Rev. Phys. Chem., 2015, 34, 557–590 Search PubMed.
- M. Shaikh, X. Liu, K. Amini, T. Steinle and J. Biegert, Rev. Sci. Instrum., 2021, 92, 104103 CrossRef CAS PubMed.
- J. Eland, Int. J. Mass Spectrom. Ion Phys., 1972, 8, 143–151 CrossRef CAS.
- C. J. Danby and J. H. D. Eland, Int. J. Mass Spectrom. Ion Phys., 1972, 8, 153–161 CrossRef CAS.
- J. Eland, J. Chem. Phys., 1979, 70, 2926–2933 CrossRef CAS.
- E. Shigemasa, J. Adachi, M. Oura and A. Yagishita, Phys. Rev. Lett., 1995, 74, 359–362 CrossRef CAS PubMed.
- J. Eland and E. Duerr, Chem. Phys., 1998, 229, 1–11 CrossRef CAS.
- P. Downie and I. Powis, Phys. Rev. Lett., 1999, 82, 2864 CrossRef CAS.
- M. Takahashi, J. P. Cave and J. H. D. Eland, Rev. Sci. Instrum., 2000, 71, 1337–1344 CrossRef CAS.
- A. Lafosse, M. Lebech, J. C. Brenot, P. M. Guyon, O. Jagutzki, L. Spielberger, M. Vervloet, J. C. Houver and D. Dowek, Phys. Rev. Lett., 2000, 84, 5987–5990 CrossRef CAS PubMed.
- J. A. Davies, R. E. Continetti, D. W. Chandler and C. C. Hayden, Phys. Rev. Lett., 2000, 84, 5983–5986 CrossRef CAS PubMed.
- C. Bomme, R. Guillemin, T. Marin, L. Journel, T. Marchenko, D. Dowek, N. Trcera, B. Pilette, A. Avila, H. Ringuenet, R. K. Kushawaha and M. Simon, Rev. Sci. Instrum., 2013, 84, 103104 CrossRef CAS PubMed.
- R. Dörner, V. Mergel, O. Jagutzki, L. Spielberger, J. Ullrich, R. Moshammer and H. Schmidt-Böcking, Phys. Rep., 2000, 330, 95–192 CrossRef.
- J. Ullrich, R. Moshammer, A. Dorn, R. Dörner, L. P. H. Schmidt and H. Schmidt-Böcking, Rep. Prog. Phys., 2003, 66, 1463–1545 CrossRef CAS.
- T. Jahnke, Th Weber, T. Osipov, A. L. Landers, O. Jagutzki, L. P. H. Schmidt, C. L. Cocke, M. H. Prior, H. Schmidt-Böcking and R. Dörner, J. Electron Spectrosc. Relat. Phenom., 2004, 141, 229–238 CrossRef CAS.
- M. Gisselbrecht, A. Huetz, M. Lavollée, T. Reddish and D. Seccombe, Rev. Sci. Instrum., 2005, 76, 013105 CrossRef.
- R. N. Zare, Mol. Photochem., 1972, 4, 1–37 CAS.
- J. A. Beswick and R. N. Zare, J. Chem. Phys., 2008, 129, 164315 CrossRef PubMed.
- O. Jagutzki, V. Mergel, K. Ullmann-Pfleger, L. Spielberger, U. Spillmann, R. Dörner and H. Schmidt-Böcking, Nucl. Instrum. Methods Phys. Res., Sect. A, 2002, 477, 244–249 CrossRef CAS.
- O. Jagutzki, A. Cerezo, A. Czasch, R. Dorner, M. Hattas, M. Huang, V. Mergel, U. Spillmann, K. Ullmann-Pfleger and T. Weber, IEEE Trans. Nucl. Sci., 2002, 49, 2477–2483 Search PubMed.
- RoentDek Handels GmbH, http://www.roentdek.com.
- S. Matoba, R. Takahashi, C. Io, T. Koizumi and H. Shiromaru, Jpn. J. Appl. Phys., 2011, 50, 112201 CrossRef.
- K. Fehre, D. Trojanowskaja, J. Gatzke, M. Kunitski, F. Trinter, S. Zeller, L. P. H. Schmidt, J. Stohner, R. Berger and A. Czasch, Rev. Sci. Instrum., 2018, 89, 045112 CrossRef CAS PubMed.
- T. Weber, M. Weckenbrock, M. Balser, L. Schmidt, O. Jagutzki, W. Arnold, O. Hohn, M. Schöffler, E. Arenholz, T. Young, T. Osipov, L. Foucar, A. D. Fanis, R. Díez Muiño, H. Schmidt-Böcking, C. L. Cocke, M. H. Prior and R. Dörner, Phys. Rev. Lett., 2003, 90, 153003 CrossRef PubMed.
- M. Lebech, J. C. Houver and D. Dowek, Rev. Sci. Instrum., 2002, 73, 1866–1874 CrossRef CAS.
- A. Vredenborg, W. G. Roeterdink and M. H. M. Janssen, Rev. Sci. Instrum., 2008, 79, 063108 CrossRef PubMed.
- U. Ablikim, C. Bomme, T. Osipov, H. Xiong, R. Obaid, R. C. Bilodeau, N. G. Kling, I. Dumitriu, S. Augustin, S. Pathak, K. Schnorr, D. Kilcoyne, N. Berrah and D. Rolles, Rev. Sci. Instrum., 2019, 90, 055103 CrossRef PubMed.
- O. Gessner, A. Lee, J. P. Shaffer, H. Reisler, S. V. Levchenko, A. I. Krylov, J. G. Underwood, H. Shi, A. L. East and D. Wardlaw, Science, 2006, 311, 219–222 CrossRef CAS PubMed.
- A. Vredenborg, W. G. Roeterdink and M. H. M. Janssen, J. Chem. Phys., 2008, 128, 204311 CrossRef PubMed.
- S. Marggi Poullain, C. Elkharrat, W. B. Li, K. Veyrinas, J. C. Houver, C. Cornaggia, T. N. Rescigno, R. R. Lucchese and D. Dowek, J. Phys. B: At. Mol. Phys., 2014, 47, 124024 CrossRef.
- M. Sabbar, S. Heuser, R. Boge, M. Lucchini, L. Gallmann, C. Cirelli and U. Keller, Rev. Sci. Instrum., 2014, 85, 103113 CrossRef CAS PubMed.
- J. Biegert, F. Calegari, N. Dudovich, F. Quéré and M. Vrakking, J. Phys. B: At. Mol. Phys., 2021, 54, 070201 CrossRef.
- B. Wolter, M. G. Pullen, M. Baudisch, M. Sclafani, M. Hemmer, A. Senftleben, C. D. Schröter, J. Ullrich, R. Moshammer and J. Biegert, Phys. Rev. X, 2015, 5, 021034 Search PubMed.
- D. Hammerland, P. Zhang, S. Kühn, P. Jojart, I. Seres, V. Zuba, Z. Varallyay, D. Charalambidis, K. Osvay and T. T. Luu, J. Phys. B: At. Mol. Phys., 2019, 52, 23LT01 CrossRef CAS.
- M. Osolodkov, F. J. Furch, F. Schell, P. Šušnjar, F. Cavalcante, C. S. Menoni, C. P. Schulz, T. Witting and M. J. Vrakking, J. Phys. B: At. Mol. Phys., 2020, 53, 194003 CrossRef CAS.
- T. Witting, M. Osolodkov, F. Schell, F. Morales, S. Patchkovskii, P. Šušnjar, F. H. M. Cavalcante, C. S. Menoni, C. P. Schulz, F. J. Furch and M. J. J. Vrakking, Optica, 2022, 9, 145–151 CrossRef CAS.
- S. Mikaelsson, J. Vogelsang, C. Guo, I. Sytcevich, A.-L. Viotti, F. Langer, Y.-C. Cheng, S. Nandi, W. Jin, A. Olofsson, R. Weissenbilder, J. Mauritsson, A. L’Huillier, M. Gisselbrecht and C. L. Arnold, Nanophotonics, 2021, 10, 117–128 CAS.
- L. Young, K. Ueda, M. Gühr, P. H. Bucksbaum, M. Simon, S. Mukamel, N. Rohringer, K. C. Prince, C. Masciovecchio, M. Meyer, A. Rudenko, D. Rolles, C. Bostedt, M. Fuchs, D. A. Reis, R. Santra, H. Kapteyn, M. Murnane, H. Ibrahim, F. Légaré, M. Vrakking, M. Isinger, D. Kroon, M. Gisselbrecht, A. L’Huillier, H. J. Wörner and S. R. Leone, J. Phys. B: At. Mol. Phys., 2018, 51, 032003 CrossRef.
- K. Ueda, E. Sokell, S. Schippers, F. Aumayr, H. Sadeghpour, J. Burgdörfer, C. Lemell, X.-M. Tong, T. Pfeifer, F. Calegari, A. Palacios, F. Martin, P. Corkum, G. Sansone, E. V. Gryzlova, A. N. Grum-Grzhimailo, M. N. Piancastelli, P. M. Weber, T. Steinle, K. Amini, J. Biegert, N. Berrah, E. Kukk, R. Santra, A. Müller, D. Dowek, R. R. Lucchese, C. W. McCurdy, P. Bolognesi, L. Avaldi, T. Jahnke, M. S. Schöffler, R. Dörner, Y. Mairesse, L. Nahon, O. Smirnova, T. Schlathölter, E. E. B. Campbell, J.-M. Rost, M. Meyer and K. A. Tanaka, J. Phys. B: At. Mol. Phys., 2019, 52, 171001 CrossRef CAS.
- W. Decking, S. Abeghyan, P. Abramian, A. Abramsky, A. Aguirre, C. Albrecht, P. Alou, M. Altarelli, P. Altmann, K. Amyan, V. Anashin, E. Apostolov, K. Appel, D. Auguste, V. Ayvazyan, S. Baark, F. Babies, N. Baboi, P. Bak, V. Balandin, R. Baldinger, B. Baranasic, S. Barbanotti, O. Belikov, V. Belokurov, L. Belova, V. Belyakov, S. Berry, M. Bertucci, B. Beutner, A. Block, M. Blöcher, T. Böckmann, C. Bohm, M. Böhnert, V. Bondar, E. Bondarchuk, M. Bonezzi, P. Borowiec, C. Bösch, U. Bösenberg, A. Bosotti, R. Böspflug, M. Bousonville, E. Boyd, Y. Bozhko, A. Brand, J. Branlard, S. Briechle, F. Brinker, S. Brinker, R. Brinkmann, S. Brockhauser, O. Brovko, H. Brück, A. Brüdgam, L. Butkowski, T. Büttner, J. Calero, E. Castro-Carballo, G. Cattalanotto, J. Charrier, J. Chen, A. Cherepenko, V. Cheskidov, M. Chiodini, A. Chong, S. Choroba, M. Chorowski, D. Churanov, W. Cichalewski, M. Clausen, W. Clement, C. Cloué, J. A. Cobos, N. Coppola, S. Cunis, K. Czuba, M. Czwalinna, B. D’Almagne, J. Dammann, H. Danared, A. de Zubiaurre Wagner, A. Delfs, T. Delfs, F. Dietrich, T. Dietrich, M. Dohlus, M. Dommach, A. Donat, X. Dong, N. Doynikov, M. Dressel, M. Duda, P. Duda, H. Eckoldt, W. Ehsan, J. Eidam, F. Eints, C. Engling, U. Englisch, A. Ermakov, K. Escherich, J. Eschke, E. Saldin, M. Faesing, A. Fallou, M. Felber, M. Fenner, B. Fernandes, J. M. Fernández, S. Feuker, K. Filippakopoulos, K. Floettmann, V. Fogel, M. Fontaine, A. Francés, I. F. Martin, W. Freund, T. Freyermuth, M. Friedland, L. Fröhlich, M. Fusetti, J. Fydrych, A. Gallas, O. García, L. Garcia-Tabares, G. Geloni, N. Gerasimova, C. Gerth, P. Geßler, V. Gharibyan, M. Gloor, J. Głowinkowski, A. Goessel, Z. Gołębiewski, N. Golubeva, W. Grabowski, W. Graeff, A. Grebentsov, M. Grecki, T. Grevsmuehl, M. Gross, U. Grosse-Wortmann, J. Grünert, S. Grunewald, P. Grzegory, G. Feng, H. Guler, G. Gusev, J. L. Gutierrez, L. Hagge, M. Hamberg, R. Hanneken, E. Harms, I. Hartl, A. Hauberg, S. Hauf, J. Hauschildt, J. Hauser, J. Havlicek, A. Hedqvist, N. Heidbrook, F. Hellberg, D. Henning, O. Hensler, T. Hermann, A. Hidvégi, M. Hierholzer, H. Hintz, F. Hoffmann, M. Hoffmann, M. Hoffmann, Y. Holler, M. Hüning, A. Ignatenko, M. Ilchen, A. Iluk, J. Iversen, J. Iversen, M. Izquierdo, L. Jachmann, N. Jardon, U. Jastrow, K. Jensch, J. Jensen, M. Jeżabek, M. Jidda, H. Jin, N. Johansson, R. Jonas, W. Kaabi, D. Kaefer, R. Kammering, H. Kapitza, S. Karabekyan, S. Karstensen, K. Kasprzak, V. Katalev, D. Keese, B. Keil, M. Kholopov, M. Killenberger, B. Kitaev, Y. Klimchenko, R. Klos, L. Knebel, A. Koch, M. Koepke, S. Köhler, W. Köhler, N. Kohlstrunk, Z. Konopkova, A. Konstantinov, W. Kook, W. Koprek, M. Körfer, O. Korth, A. Kosarev, K. Kosiński, D. Kostin, Y. Kot, A. Kotarba, T. Kozak, V. Kozak, R. Kramert, M. Krasilnikov, A. Krasnov, B. Krause, L. Kravchuk, O. Krebs, R. Kretschmer, J. Kreutzkamp, O. Kröplin, K. Krzysik, G. Kube, H. Kuehn, N. Kujala, V. Kulikov, V. Kuzminych, D. La Civita, M. Lacroix, T. Lamb, A. Lancetov, M. Larsson, D. Le Pinvidic, S. Lederer, T. Lensch, D. Lenz, A. Leuschner, F. Levenhagen, Y. Li, J. Liebing, L. Lilje, T. Limberg, D. Lipka, B. List, J. Liu, S. Liu, B. Lorbeer, J. Lorkiewicz, H. H. Lu, F. Ludwig, K. Machau, W. Maciocha, C. Madec, C. Magueur, C. Maiano, I. Maksimova, K. Malcher, T. Maltezopoulos, E. Mamoshkina, B. Manschwetus, F. Marcellini, G. Marinkovic, T. Martinez, H. Martirosyan, W. Maschmann, M. Maslov, A. Matheisen, U. Mavric, J. Meißner, K. Meissner, M. Messerschmidt, N. Meyners, G. Michalski, P. Michelato, N. Mildner, M. Moe, F. Moglia, C. Mohr, S. Mohr, W. Möller, M. Mommerz, L. Monaco, C. Montiel, M. Moretti, I. Morozov, P. Morozov, D. Mross, J. Mueller, C. Müller, J. Müller, K. Müller, J. Munilla, A. Münnich, V. Muratov, O. Napoly, B. Näser, N. Nefedov, R. Neumann, R. Neumann, N. Ngada, D. Noelle, F. Obier, I. Okunev, J. A. Oliver, M. Omet, A. Oppelt, A. Ottmar, M. Oublaid, C. Pagani, R. Paparella, V. Paramonov, C. Peitzmann, J. Penning, A. Perus, F. Peters, B. Petersen, A. Petrov, I. Petrov, S. Pfeiffer, J. Pflüger, S. Philipp, Y. Pienaud, P. Pierini, S. Pivovarov, M. Planas, E. Pławski, M. Pohl, J. Polinski, V. Popov, S. Prat, J. Prenting, G. Priebe, H. Pryschelski, K. Przygoda, E. Pyata, B. Racky, A. Rathjen, W. Ratuschni, S. Regnaud-Campderros, K. Rehlich, D. Reschke, C. Robson, J. Roever, M. Roggli, J. Rothenburg, E. Rusiński, R. Rybaniec, H. Sahling, M. Salmani, L. Samoylova, D. Sanzone, F. Saretzki, O. Sawlanski, J. Schaffran, H. Schlarb, M. Schlösser, V. Schlott, C. Schmidt, F. Schmidt-Foehre, M. Schmitz, M. Schmökel, T. Schnautz, E. Schneidmiller, M. Scholz, B. Schöneburg, J. Schultze, C. Schulz, A. Schwarz, J. Sekutowicz, D. Sellmann, E. Semenov, S. Serkez, D. Sertore, N. Shehzad, P. Shemarykin, L. Shi, M. Sienkiewicz, D. Sikora, M. Sikorski, A. Silenzi, C. Simon, W. Singer, X. Singer, H. Sinn, K. Sinram, N. Skvorodnev, P. Smirnow, T. Sommer, A. Sorokin, M. Stadler, M. Steckel, B. Steffen, N. Steinhau-Kühl, F. Stephan, M. Stodulski, M. Stolper, A. Sulimov, R. Susen, J. Świerblewski, C. Sydlo, E. Syresin, V. Sytchev, J. Szuba, N. Tesch, J. Thie, A. Thiebault, K. Tiedtke, D. Tischhauser, J. Tolkiehn, S. Tomin, F. Tonisch, F. Toral, I. Torbin, A. Trapp, D. Treyer, G. Trowitzsch, T. Trublet, T. Tschentscher, F. Ullrich, M. Vannoni, P. Varela, G. Varghese, G. Vashchenko, M. Vasic, C. Vazquez-Velez, A. Verguet, S. Vilcins-Czvitkovits, R. Villanueva, B. Visentin, M. Viti, E. Vogel, E. Volobuev, R. Wagner, N. Walker, T. Wamsat, H. Weddig, G. Weichert, H. Weise, R. Wenndorf, M. Werner, R. Wichmann, C. Wiebers, M. Wiencek, T. Wilksen, I. Will, L. Winkelmann, M. Winkowski, K. Wittenburg, A. Witzig, P. Wlk, T. Wohlenberg, M. Wojciechowski, F. Wolff-Fabris, G. Wrochna, K. Wrona, M. Yakopov, B. Yang, F. Yang, M. Yurkov, I. Zagorodnov, P. Zalden, A. Zavadtsev, D. Zavadtsev, A. Zhirnov, A. Zhukov, V. Ziemann, A. Zolotov, N. Zolotukhina, F. Zummack and D. Zybin, Nat. Photonics, 2020, 14, 391–397 CrossRef CAS.
- J. N. Galayda, The LCLS-II: A high power upgrade to the LCLS, SLAC National Accelerator Lab., Menlo Park, CA (United States), 2018 Search PubMed.
- D. W. Chandler, P. L. Houston and D. H. Parker, J. Chem. Phys., 2017, 147, 013601 CrossRef PubMed.
- A. T. J. B. Eppink and D. H. Parker, Rev. Sci. Instrum., 1997, 68, 3477–3484 CrossRef CAS.
- V. Dribinski, A. Ossadtchi, V. A. Mandelshtam and H. Reisler, Rev. Sci. Instrum., 2002, 73, 2634–2642 CrossRef CAS.
- G. A. Garcia, L. Nahon and I. Powis, Rev. Sci. Instrum., 2004, 75, 4989–4996 CrossRef CAS.
- T. Horio and T. Suzuki, Rev. Sci. Instrum., 2009, 80, 013706 CrossRef PubMed.
- C. Vallance, M. Brouard, A. Lauer, C. S. Slater, E. Halford, B. Winter, S. J. King, J. W. L. Lee, D. E. Pooley, I. Sedgwick, R. Turchetta, A. Nomerotski, J. J. John and L. Hill, Phys. Chem. Chem. Phys., 2014, 16, 383–395 RSC.
- S. K. Lee, Y. F. Lin, S. Lingenfelter, L. Fan, A. H. Winney and W. Li, J. Chem. Phys., 2014, 141, 221101 CrossRef PubMed.
- M. Wollenhaupt, M. Krug, J. Köhler, T. Bayer, C. Sarpe-Tudoran and T. Baumert, Appl. Phys. B, 2009, 95, 245–259 CrossRef CAS.
- J. Maurer, D. Dimitrovski, L. Christensen, L. B. Madsen and H. Stapelfeldt, Phys. Rev. Lett., 2012, 109, 123001 CrossRef PubMed.
- P. Johnsson, W. Siu, A. Gijsbertsen, J. Verhoeven, A. S. Meijer, W. van der Zande and M. J. J. Vrakking, J. Mod. Opt., 2008, 55, 2693–2709 CrossRef CAS.
- P. O’Keeffe, V. Feyer, P. Bolognesi, M. Coreno, C. Callegari, G. Cautero, A. Moise, K. C. Prince, R. Richter, R. Sergo, M. Alagia, M. de Simone, A. Kivimäki, M. Devetta, T. Mazza, P. Piseri, V. Lyamayev, R. Katzy, F. Stienkemeier, Y. Ovcharenko, T. Möller and L. Avaldi, Nucl. Instrum. Methods Phys. Res., Sect. B, 2012, 284, 69–73 CrossRef.
- G. A. Garcia, L. Nahon, C. J. Harding, E. A. Mikajlo and I. Powis, Rev. Sci. Instrum., 2005, 76, 053302 CrossRef.
- N. G. Kling, D. Paul, A. Gura, G. Laurent, S. De, H. Li, Z. Wang, B. Ahn, C. H. Kim, T. K. Kim, I. V. Litvinyuk, C. L. Cocke, I. Ben-Itzhak, D. Kim and M. F. Kling, J. Inst., 2014, 9, P05005 Search PubMed.
- L. Strüder, S. Epp, D. Rolles, R. Hartmann, P. Holl, G. Lutz, H. Soltau, R. Eckart, C. Reich, K. Heinzinger, C. Thamm, A. Rudenko, F. Krasniqi, K.-U. Kühnel, C. Bauer, C.-D. Schröter, R. Moshammer, S. Techert, D. Miessner, M. Porro, O. Hälker, N. Meidinger, N. Kimmel, R. Andritschke, F. Schopper, G. Weidenspointner, A. Ziegler, D. Pietschner, S. Herrmann, U. Pietsch, A. Walenta, W. Leitenberger, C. Bostedt, T. Möller, D. Rupp, M. Adolph, H. Graafsma, H. Hirsemann, K. Gärtner, R. Richter, L. Foucar, R. L. Shoeman, I. Schlichting and J. Ullrich, Nucl. Instrum. Methods Phys. Res., Sect. A, 2010, 614, 483–496 CrossRef.
- K. Nakajima, T. Teramoto, H. Akagi, T. Fujikawa, T. Majima, S. Minemoto, K. Ogawa, H. Sakai, T. Togashi, K. Tono, S. Tsuru, K. Wada, M. Yabashi and A. Yagishita, Sci. Rep., 2015, 5, 14065 CrossRef CAS PubMed.
- Z. Vager, R. Naaman and E. Kanter, Science, 1989, 244, 426–431 CrossRef CAS PubMed.
- A. Tremsin and J. Vallerga, Radiat. Meas., 2020, 130, 106228 CrossRef CAS.
- G. Basnayake, Y. Ranathunga, S. K. Lee and W. Li, J. Phys. B: At., Mol. Opt. Phys., 2022, 55, 023001 CrossRef CAS.
- J. Long, F. J. Furch, J. Durá, A. S. Tremsin, J. Vallerga, C. P. Schulz, A. Rouzée and M. J. Vrakking, J. Chem. Phys., 2017, 147, 013919 CrossRef PubMed.
- A. Zhao, M. van Beuzekom, B. Bouwens, D. Byelov, I. Chakaberia, C. Cheng, E. Maddox, A. Nomerotski, P. Svihra, J. Visser, V. Vrba and T. Weinacht, Rev. Sci. Instrum., 2017, 88, 113104 CrossRef PubMed.
- C. Schouder, A. S. Chatterley, M. Johny, F. Hübschmann, A. F. Al-Refaie, F. Calvo, J. Küpper and H. Stapelfeldt, J. Phys. B: At. Mol. Phys., 2021, 54, 184001 CrossRef CAS.
- G. A. Garcia, H. Soldi-Lose and L. Nahon, Rev. Sci. Instrum., 2009, 80, 023102 CrossRef PubMed.
- A. Bodi, M. Johnson, T. Gerber, Z. Gengeliczki, B. Sztáray and T. Baer, Rev. Sci. Instrum., 2009, 80, 034101 CrossRef PubMed.
- A. Bodi, P. Hemberger, T. Gerber and B. Sztáray, Rev. Sci. Instrum., 2012, 83, 083105 CrossRef PubMed.
- G. A. Garcia, B. K. Cunha de Miranda, M. Tia, S. Daly and L. Nahon, Rev. Sci. Instrum., 2013, 84, 053112 CrossRef CAS PubMed.
- C. S. Lehmann, N. B. Ram and M. H. M. Janssen, Rev. Sci. Instrum., 2012, 83, 093103 CrossRef PubMed.
- L. Fan, S. K. Lee, Y.-J. Tu, B. Mignolet, D. Couch, K. Dorney, Q. Nguyen, L. Wooldridge, M. Murnane, F. Remacle, H. B. Schlegel and W. Li, J. Chem. Phys., 2017, 147, 013920 CrossRef PubMed.
- L. J. Frasinski, J. Phys. B: At., Mol. Opt. Phys., 2016, 49, 152004 CrossRef.
- C. P. Koch, M. Lemeshko and D. Sugny, Rev. Mod. Phys., 2019, 91, 035005 CrossRef CAS.
- K. Lin, I. Tutunnikov, J. Ma, J. Qiang, L. Zhou, O. Faucher, Y. Prior, I. S. Averbukh and J. Wu, Adv. Photonics, 2020, 2, 024002 CAS.
- K. L. Reid, Philos. Trans. R. Soc., A, 2018, 376, 20170158 CrossRef PubMed.
- J. J. Larsen, K. Hald, N. Bjerre, H. Stapelfeldt and T. Seideman, Phys. Rev. Lett., 2000, 85, 2470–2473 CrossRef CAS PubMed.
- F. Rosca-Pruna and M. Vrakking, Phys. Rev. Lett., 2001, 87, 153902 CrossRef CAS PubMed.
- J. L. Hansen, J. H. Nielsen, C. B. Madsen, A. T. Lindhardt, M. P. Johansson, T. Skrydstrup, L. B. Madsen and H. Stapelfeldt, J. Chem. Phys., 2012, 136, 204310 CrossRef PubMed.
- K. Amini, R. Boll, A. Lauer, M. Burt, J. W. L. Lee, L. Christensen, F. Brauβe, T. Mullins, E. Savelyev, U. Ablikim, N. Berrah, C. Bomme, S. Düsterer, B. Erk, H. Höppner, P. Johnsson, T. Kierspel, F. Krecinic, J. Küpper, M. Müller, E. Müller, H. Redlin, A. Rouzée, N. Schirmel, J. Thøgersen, S. Techert, S. Toleikis, R. Treusch, S. Trippel, A. Ulmer, J. Wiese, C. Vallance, A. Rudenko, H. Stapelfeldt, M. Brouard and D. Rolles, J. Chem. Phys., 2017, 147, 013933 CrossRef PubMed.
- P. Johnsson, A. Rouzée, W. Siu, Y. Huismans, F. Lépine, T. Marchenko, S. Düsterer, F. Tavella, N. Stojanovic, A. Azima, R. Treusch, M. F. Kling and M. J. J. Vrakking, J. Phys. B: At., Mol. Opt. Phys., 2009, 42, 134017 CrossRef.
- R. Boll, A. Rouzée, M. Adolph, D. Anielski, A. Aquila, S. Bari, C. Bomme, C. Bostedt, J. D. Bozek, H. N. Chapman, L. Christensen, R. Coffee, N. Coppola, S. De, P. Decleva, S. W. Epp, B. Erk, F. Filsinger, L. Foucar, T. Gorkhover, L. Gumprecht, A. Hömke, L. Holmegaard, P. Johnsson, J. S. Kienitz, T. Kierspel, F. Krasniqi, K.-U. Kühnel, J. Maurer, M. Messerschmidt, R. Moshammer, N. L. M. Müller, B. Rudek, E. Savelyev, I. Schlichting, C. Schmidt, F. Scholz, S. Schorb, J. Schulz, J. Seltmann, M. Stener, S. Stern, S. Techert, J. Thøgersen, S. Trippel, J. Viefhaus, M. Vrakking, H. Stapelfeldt, J. Küpper, J. Ullrich, A. Rudenko and D. Rolles, Faraday Discuss., 2014, 171, 57–80 RSC.
- M. Di Fraia, P. Finetti, R. Richter, K. C. Prince, J. Wiese, M. Devetta, M. Negro, C. Vozzi, A. G. Ciriolo, A. Pusala, A. Demidovich, M. B. Danailov, E. T. Karamatskos, S. Trippel, J. Küpper and C. Callegari, Phys. Chem. Chem. Phys., 2017, 19, 19733–19739 RSC.
- M. Pitzer, M. Kunitski, A. S. Johnson, T. Jahnke, H. Sann, F. Sturm, L. P. H. Schmidt, H. Schmidt-Böcking, R. Dörner, J. Stohner, J. Kiedrowski, M. Reggelin, S. Marquardt, A. Schießer, R. Berger and M. S. Schöffler, Science, 2013, 341, 1096–1100 Search PubMed.
- J. Arlt, D. P. Singh, J. O. F. Thompson, A. S. Chatterley, P. Hockett, H. Stapelfeldt and K. L. Reid, Mol. Phys., 2021, 119, e1836411 CrossRef.
- F. Filsinger, J. Küpper, G. Meijer, L. Holmegaard, J. H. Nielsen, I. Nevo, J. L. Hansen and H. Stapelfeldt, J. Chem. Phys., 2009, 131, 064309 CrossRef PubMed.
- L. Holmegaard, J. H. Nielsen, I. Nevo, H. Stapelfeldt, F. Filsinger, J. Küpper and G. Meijer, Phys. Rev. Lett., 2009, 102, 023001 CrossRef PubMed.
- O. Ghafur, A. Rouzée, A. Gijsbertsen, W. K. Siu, S. Stolte and M. J. J. Vrakking, Nat. Phys., 2009, 5, 289–293 Search PubMed.
- E. T. Karamatskos, S. Raabe, T. Mullins, A. Trabattoni, P. Stammer, G. Goldsztejn, R. R. Johansen, K. Długołecki, H. Stapelfeldt, M. J. J. Vrakking, S. Trippel, A. Rouzée and J. Küpper, Nat. Commun., 2019, 10, 3364 Search PubMed.
- T. Mullins, E. T. Karamatskos, J. Wiese, J. Onvlee, A. Rouzée, A. Yachmenev, S. Trippel and J. Küpper, Nat. Commun., 2022, 13, 1–7 Search PubMed.
- A. S. Chatterley, E. T. Karamatskos, C. Schouder, L. Christiansen, A. V. Jørgensen, T. Mullins, J. Küpper and H. Stapelfeldt, J. Chem. Phys., 2018, 148, 221105 CrossRef PubMed.
- B. Shepperson, A. S. Chatterley, A. A. Søndergaard, L. Christiansen, M. Lemeshko and H. Stapelfeldt, J. Chem. Phys., 2017, 147, 013946 CrossRef PubMed.
- A. S. Chatterley, B. Shepperson and H. Stapelfeldt, Phys. Rev. Lett., 2017, 119, 073202 CrossRef PubMed.
- J. H. Nielsen, D. Pentlehner, L. Christiansen, B. Shepperson, A. A. Sondergaard, A. S. Chatterley, J. D. Pickering, C. Schouder, A. Vinas Munoz, L. Kranabetter and H. Stapelfeldt, in Molecules in Superfluid Helium Droplets – Spectroscopy, Structure and Dynamics, ed. A. Slenczka and J. P. Toennies, Springer, Berlin, 2022, vol. 145 Search PubMed.
- A. S. Chatterley, C. Schouder, L. Christiansen, B. Shepperson, M. H. Rasmussen and H. Stapelfeldt, Nat. Commun., 2019, 10, 133 CrossRef PubMed.
- K. Oda, M. Hita, S. Minemoto and H. Sakai, Phys. Rev. Lett., 2010, 104, 213901 CrossRef PubMed.
- L. H. Coudert, J. Chem. Phys., 2018, 148, 094306 CrossRef.
- I. Tutunnikov, L. Xu, R. W. Field, K. A. Nelson, Y. Prior and I. S. Averbukh, Phys. Rev. Res., 2021, 3, 013249 CrossRef CAS.
- Md. M. Hossain, X. Zhang, S. Minemoto and H. Sakai, J. Chem. Phys., 2022, 156, 041101 CrossRef CAS PubMed.
- K. Lin, I. Tutunnikov, J. Qiang, J. Ma, Q. Song, Q. Ji, W. Zhang, H. Li, F. Sun, X. Gong, H. Li, P. Lu, H. Zeng, Y. Prior, I. S. Averbukh and J. Wu, Nat. Commun., 2018, 9, 5134 CrossRef PubMed.
- L. Xu, I. Tutunnikov, Y. Prior and I. S. Averbukh, J. Phys. B: At., Mol. Opt. Phys., 2021, 54, 164003 CrossRef CAS.
- M. Piancastelli, P. Keller and J. Taylor, J. Am. Chem. Soc., 1983, 105, 4235–4239 CrossRef CAS.
- P. Baltzer, L. Karlsson, B. Wannberg, G. Öhrwall, D. Holland, M. MacDonald, M. Hayes and W. Von Niessen, Chem. Phys., 1997, 224, 95–119 CrossRef CAS.
- I. Powis, M. Patanen, E. Antonsson, C. Nicolas, C. Miron and D. M. P. Holland, Phys. Rev. A, 2017, 96, 013413 CrossRef.
- L. Schio et al. , to be published, 2022.
- W. Von Niessen, G. Bieri, J. Schirmer and L. Cederbaum, Chem. Phys., 1982, 65, 157–176 CrossRef CAS.
- A. I. Kuleff and L. S. Cederbaum, J. Phys. B: At., Mol. Opt. Phys., 2014, 47, 124002 CrossRef.
- L. Schio, M. Alagia, D. Toffoli, P. Decleva, R. Richter, O. Schalk, R. D. Thomas, M. Mucke, F. Salvador, P. Bertoch, D. Benedetti, C. Dri, G. Cautero, R. Sergo, L. Stebel, D. Vivoda and S. Stranges, Inorg. Chem., 2020, 59, 7274–7282 CrossRef CAS PubMed.
- R. Forbes, P. Hockett, I. Powis, J. D. Bozek, D. M. P. Holland and S. T. Pratt, J. Chem. Phys., 2021, 155, 194301 CrossRef CAS PubMed.
- R. Forbes, P. Hockett, I. Powis, J. D. Bozek, S. T. Pratt and D. M. P. Holland, Phys. Chem. Chem. Phys., 2022, 24, 1367–1379 RSC.
- R. Mabbs, E. R. Grumbling, K. Pichugin and A. Sanov, Chem. Soc. Rev., 2009, 38, 2169 RSC.
- A. Sanov, Annu. Rev. Phys. Chem., 2014, 65, 341–363 CrossRef CAS PubMed.
- R. E. Continetti and H. Guo, Chem. Soc. Rev., 2017, 46, 7650–7667 RSC.
- C. C. Blackstone, A. A. Wallace and A. Sanov, Mol. Phys., 2021, 119, e1831636 CrossRef.
- C. S. Anstöter, C. R. Dean and J. R. R. Verlet, J. Phys. Chem. Lett., 2017, 8, 2268–2273 CrossRef PubMed.
- C. A. Hart, J. Lyle, J. Spellberg, A. I. Krylov and R. Mabbs, J. Phys. Chem. Lett., 2021, 12, 10086–10092 CrossRef CAS PubMed.
- C. S. Anstöter and J. R. R. Verlet, J. Phys. Chem. A, 2021, 125, 4888–4895 CrossRef PubMed.
- J. A. DeVine, M. L. Weichman, B. Laws, J. Chang, M. C. Babin, G. Balerdi, C. Xie, C. L. Malbon, W. C. Lineberger, D. R. Yarkony, R. W. Field, S. T. Gibson, J. Ma, H. Guo and D. M. Neumark, Science, 2017, 358, 336–339 CrossRef CAS PubMed.
- K. A. Larsen, R. Y. Bello, R. R. Lucchese, T. N. Rescigno, C. W. McCurdy, D. S. Slaughter and T. Weber, Phys. Rev. A, 2020, 102, 063118 CrossRef CAS.
- M. Eckstein, C.-H. Yang, F. Frassetto, L. Poletto, G. Sansone, M. J. J. Vrakking and O. Kornilov, Phys. Rev. Lett., 2016, 116, 163003 CrossRef PubMed.
- M. Fushitani, S. T. Pratt, D. You, S. Saito, Y. Luo, K. Ueda, H. Fujise, A. Hishikawa, H. Ibrahim, F. Légaré, P. Johnsson, J. Peschel, E. R. Simpson, A. Olofsson, J. Mauritsson, P. A. Carpeggiani, P. K. Maroju, M. Moioli, D. Ertel, R. Shah, G. Sansone, T. Csizmadia, M. Dumergue, N. G. Harshitha, S. Kühn, C. Callegari, O. Plekan, M. Di Fraia, M. B. Danailov, A. Demidovich, L. Giannessi, L. Raimondi, M. Zangrando, G. De Ninno, P. R. Ribič and K. C. Prince, J. Chem. Phys., 2021, 154, 144305 CrossRef CAS PubMed.
- V. Loriot, A. Marciniak, S. Nandi, G. Karras, M. Hervé, E. Constant, E. Plésiat, A. Palacios, F. Martín and F. Lépine, J. Phys. Photonics, 2020, 2, 024003 CrossRef CAS.
- C. Z. Bisgaard, O. J. Clarkin, G. Wu, A. M. D. Lee, O. Geßner, C. C. Hayden and A. Stolow, Science, 2009, 323, 1464 CrossRef CAS PubMed.
- P. Hockett, C. Z. Bisgaard, O. J. Clarkin and A. Stolow, Nat. Phys., 2011, 7, 612–615 Search PubMed.
- Y.-I. Suzuki and T. Suzuki, J. Chem. Phys., 2012, 137, 194314 CrossRef PubMed.
- T. Horio, R. Spesyvtsev, K. Nagashima, R. A. Ingle, Y. Suzuki and T. Suzuki, J. Chem. Phys., 2016, 145, 044306 CrossRef PubMed.
- J. O. F. Thompson, L. Saalbach, S. W. Crane, M. J. Paterson and D. Townsend, J. Chem. Phys., 2015, 142, 114309 CrossRef PubMed.
- T. Suzuki, private communication.
- L. Poisson, P. Roubin, S. Coussan, B. Soep and J.-M. Mestdagh, J. Am. Chem. Soc., 2008, 130, 2974–2983 CrossRef CAS PubMed.
- R. J. Squibb, M. Sapunar, A. Ponzi, R. Richter, A. Kivimäki, O. Plekan, P. Finetti, N. Sisourat, V. Zhaunerchyk, T. Marchenko, L. Journel, R. Guillemin, R. Cucini, M. Coreno, C. Grazioli, M. Di Fraia, C. Callegari, K. C. Prince, P. Decleva, M. Simon, J. H. D. Eland, N. Došlić, R. Feifel and M. N. Piancastelli, Nat. Commun., 2018, 9, 63 CrossRef CAS PubMed.
- N. Kotsina, M. Candelaresi, L. Saalbach, M. M. Zawadzki, S. W. Crane, C. Sparling and D. Townsend, Phys. Chem. Chem. Phys., 2020, 22, 4647–4658 RSC.
- R. E. Goetz, T. A. Isaev, B. Nikoobakht, R. Berger and C. P. Koch, J. Chem. Phys., 2017, 146, 024306 CrossRef CAS PubMed.
- C. Rosales-Guzmán, B. Ndagano and A. Forbes, J. Opt., 2018, 20, 123001 CrossRef.
- H. Kang, A. S. Maxwell, D. Trabert, X. Lai, S. Eckart, M. Kunitski, M. Schöffler, T. Jahnke, X. Bian, R. Dörner and C. F. M. de Faria, Phys. Rev. A, 2020, 102, 013109 CrossRef CAS.
- O. V. Angelsky, A. Y. Bekshaev, S. G. Hanson, C. Y. Zenkova, I. I. Mokhun and Z. Jun, Front. Phys., 2020, 8, 114 CrossRef.
- C. Figueira de Morisson Faria and A. S. Maxwell, Rep. Prog. Phys., 2020, 83, 034401 CrossRef CAS PubMed.
- A. Forbes, M. de Oliveira and M. R. Dennis, Nat. Photonics, 2021, 15, 253–262 CrossRef CAS.
- S. Hartweg, B. L. Yoder, G. A. Garcia, L. Nahon and R. Signorell, Phys. Rev. Lett., 2017, 118, 103402 CrossRef PubMed.
- D. K. Božanić, G. A. Garcia, O. Sublemontier, J. Pajović, V. Djoković and L. Nahon, J. Phys. Chem. C, 2020, 124, 24500–24512 CrossRef.
- T. Suzuki, J. Chem. Phys., 2019, 151, 090901 CrossRef PubMed.
- R. Signorell and B. Winter, Phys. Chem. Chem. Phys., 2022, 24, 13438–13460 RSC.
- R. Dupuy, J. Filser, C. Richter, R. Seidel, F. Trinter, T. Buttersack, C. Nicolas, J. Bozek, U. Hergenhahn and H. Oberhofer, Phys. Chem. Chem. Phys., 2022, 24, 4796–4808 RSC.
- B. Ritchie, Phys. Rev. A, 1976, 13, 1411–1415 CrossRef.
- N. Böwering, T. Lischke, B. Schmidtke, N. Müller, T. Khalil and U. Heinzmann, Phys. Rev. Lett., 2001, 86, 1187–1190 CrossRef PubMed.
- S. Beaulieu, A. Ferré, R. Géneaux, R. Canonge, D. Descamps, B. Fabre, N. Fedorov, F. Légaré, S. Petit and T. Ruchon, New J. Phys., 2016, 18, 102002 CrossRef.
- A. D. Müller, E. Kutscher, A. N. Artemyev and P. V. Demekhin, J. Chem. Phys., 2020, 152, 044302 CrossRef PubMed.
- M. N. Pohl, S. Malerz, F. Trinter, C. Lee, C. Kolbeck, I. Wilkinson, S. Thürmer, D. M. Neumark, L. Nahon, I. Powis, G. Meijer, B. Winter and U. Hergenhahn, Phys. Chem. Chem. Phys., 2022, 24, 8081–8092 RSC.
- T. Müller, K. B. Wiberg and P. H. Vaccaro, J. Phys. Chem. A, 2000, 104, 5959–5968 CrossRef.
- C. Meinert, A. D. Garcia, J. Topin, N. C. Jones, M. Diekmann, R. Berger, L. Nahon, S. V. Hoffmann and U. J. Meierhenrich, Nat. Commun., 2022, 13, 502 CrossRef CAS PubMed.
- S. Daly, F. Rosu and V. Gabelica, Science, 2020, 368, 1465–1468 CrossRef CAS PubMed.
- F. Saito and P. R. Schreiner, Eur. J. Org. Chem., 2020, 6328–6339 CrossRef CAS.
- P. Decleva, Chemistry, 2022, 4, 31–41 CrossRef CAS.
- D. Di Tommaso, M. Stener, G. Fronzoni and P. Decleva, ChemPhysChem, 2006, 7, 924–934 CrossRef CAS PubMed.
- J. Dupont, V. Lepère, A. Zehnacker, S. Hartweg, G. A. Garcia and L. Nahon, J. Phys. Chem. Lett., 2022, 13, 2313–2320 CrossRef CAS PubMed.
- R. Hadidi, D. K. Božanić, H. Ganjitabar, G. A. Garcia, I. Powis and L. Nahon, Commun. Chem., 2021, 4, 72 CrossRef CAS.
- R. Hadidi, D. K. Bozanic, G. A. Garcia and L. Nahon, Adv. Phys.: X, 2018, 3, 1477530 Search PubMed.
- B. Darquié, N. Saleh, S. K. Tokunaga, M. Srebro-Hooper, A. Ponzi, J. Autschbach, P. Decleva, G. A. Garcia, J. Crassous and L. Nahon, Phys. Chem. Chem. Phys., 2021, 23, 24140–24153 RSC.
- D. Catone, M. Stener, P. Decleva, G. Contini, N. Zema, T. Prosperi, V. Feyer, K. C. Prince and S. Turchini, Phys. Rev. Lett., 2012, 108, 083001 CrossRef CAS PubMed.
- D. Catone, S. Turchini, M. Stener, P. Decleva, G. Contini, T. Prosperi, V. Feyer, K. C. Prince and N. Zema, Rend. Fis. Acc. Lincei, 2013, 24, 269–275 CrossRef.
- G. A. Garcia, L. Nahon, S. Daly and I. Powis, Nat. Commun., 2013, 4, 2132 CrossRef PubMed.
- G. A. Garcia, H. Dossmann, L. Nahon, S. Daly and I. Powis, ChemPhysChem, 2017, 18, 500–512 CrossRef CAS PubMed.
- P. Krüger and K. Weitzel, Angew. Chem., Int. Ed., 2021, 60, 17861–17865 CrossRef PubMed.
- A. N. Artemyev, E. Kutscher and P. V. Demekhin, J. Chem. Phys., 2022, 156, 031101 CrossRef CAS PubMed.
- S. Hartweg, G. A. Garcia, D. K. Božanić and L. Nahon, J. Phys. Chem. Lett., 2021, 12, 2385–2393 CrossRef CAS PubMed.
- G. Hartmann, M. Ilchen, P. Schmidt, C. Küstner-Wetekam, C. Ozga, F. Scholz, J. Buck, F. Trinter, J. Viefhaus, A. Ehresmann, M. S. Schöffler, A. Knie and P. V. Demekhin, Phys. Rev. Lett., 2019, 123, 043202 CrossRef CAS PubMed.
- M. Ilchen, P. Schmidt, N. M. Novikovskiy, G. Hartmann, P. Rupprecht, R. N. Coffee, A. Ehresmann, A. Galler, N. Hartmann and W. Helml, Commun. Chem., 2021, 4, 1–9 CrossRef.
- A. Ferré, C. Handschin, M. Dumergue, F. Burgy, A. Comby, D. Descamps, B. Fabre, G. A. Garcia, R. Géneaux, L. Merceron, E. Mével, L. Nahon, S. Petit, B. Pons, D. Staedter, S. Weber, T. Ruchon, V. Blanchet and Y. Mairesse, Nat. Photonics, 2015, 9, 93–98 CrossRef.
- M. M. Rafiee Fanood, I. Powis and M. H. M. Janssen, J. Phys. Chem. A, 2014, 118, 11541–11546 CrossRef CAS PubMed.
- C. S. Lehmann, N. B. Ram, I. Powis and M. H. M. Janssen, J. Chem. Phys., 2013, 139, 234307 CrossRef PubMed.
- C. Lux, M. Wollenhaupt, T. Bolze, Q. Liang, J. Köhler, C. Sarpe and T. Baumert, Angew. Chem., Int. Ed., 2012, 51, 5001–5005 CrossRef CAS PubMed.
- C. Lux, M. Wollenhaupt, C. Sarpe and T. Baumert, ChemPhysChem, 2015, 16, 115–137 CrossRef CAS PubMed.
- A. Kastner, T. Ring, H. Braun, A. Senftleben and T. Baumert, ChemPhysChem, 2019, 20, 1416 CAS.
- A. Kastner, G. Koumarianou, P. Glodic, P. C. Samartzis, N. Ladda, S. T. Ranecky, T. Ring, S. Vasudevan, C. Witte, H. Braun, H.-G. Lee, A. Senftleben, R. Berger, G. B. Park, T. Schäfer and T. Baumert, Phys. Chem. Chem. Phys., 2020, 22, 7404–7411 RSC.
- D. P. Singh, J. O. F. Thompson, K. L. Reid and I. Powis, J. Phys. Chem. Lett., 2021, 12, 11438–11443 CrossRef CAS PubMed.
- H. Ganjitabar, D. P. Singh, R. Chapman, A. Gardner, R. S. Minns, I. Powis, K. L. Reid and A. Vredenborg, Mol. Phys., 2021, 119, e1808907 CrossRef.
- S. T. Ranecky, G. B. Park, P. C. Samartzis, I. C. Giannakidis, D. Schwarzer, A. Senftleben, T. Baumert and T. Schäfer, Phys. Chem. Chem. Phys., 2022, 24, 2758–2761 RSC.
- A. Comby, E. Bloch, C. M. M. Bond, D. Descamps, J. Miles, S. Petit, S. Rozen, J. B. Greenwood, V. Blanchet and Y. Mairesse, Nat. Commun., 2018, 9, 5212 CrossRef CAS PubMed.
- A. Comby, C. M. M. Bond, E. Bloch, D. Descamps, B. Fabre, S. Petit, Y. Mairesse, J. B. Greenwood and V. Blanchet, Chirality, 2020, 32, 1225–1233 CrossRef CAS PubMed.
- G. Westphal, J. Wega, R. E. A. Dissanayake and T. Schäfer, J. Chem. Phys., 2020, 153, 054707 CrossRef CAS PubMed.
- C. S. Lehmann and K.-M. Weitzel, Phys. Chem. Chem. Phys., 2020, 22, 13707–13712 RSC.
- K. Fehre, S. Eckart, M. Kunitski, C. Janke, D. Trabert, M. Hofmann, J. Rist, M. Weller, A. Hartung, L. P. H. Schmidt, T. Jahnke, H. Braun, T. Baumert, J. Stohner, P. V. Demekhin, M. S. Schöffler and R. Dörner, Phys. Rev. Lett., 2021, 126, 083201 CrossRef CAS PubMed.
- S. Beaulieu, A. Comby, D. Descamps, B. Fabre, G. A. Garcia, R. Géneaux, A. G. Harvey, F. Légaré, Z. Mašín, L. Nahon, A. F. Ordonez, S. Petit, B. Pons, Y. Mairesse, O. Smirnova and V. Blanchet, Nat. Phys., 2018, 14, 484–489 Search PubMed.
- A. G. Harvey, Z. Mašín and O. Smirnova, J. Chem. Phys., 2018, 149, 064104 CrossRef PubMed.
- S. Rozen, A. Comby, E. Bloch, S. Beauvarlet, D. Descamps, B. Fabre, S. Petit, V. Blanchet, B. Pons, N. Dudovich and Y. Mairesse, Phys. Rev. X, 2019, 9, 031004 CAS.
- E. Bloch, S. Larroque, S. Rozen, S. Beaulieu, A. Comby, S. Beauvarlet, D. Descamps, B. Fabre, S. Petit, R. Taïeb, A. J. Uzan, V. Blanchet, N. Dudovich, B. Pons and Y. Mairesse, Phys. Rev. X, 2021, 11, 041056 CAS.
- O. Neufeld, H. Hübener, A. Rubio and U. De Giovannini, Phys. Rev. Res., 2021, 3, L032006 CrossRef CAS.
- M. Mondelo-Martell, D. Basilewitsch, H. Braun, C. P. Koch and D. M. Reich, Phys. Chem. Chem. Phys., 2022, 24, 9286–9297 RSC.
- A. F. Ordonez and O. Smirnova, Phys. Rev. A, 2018, 98, 063428 CrossRef CAS.
- A. F. Ordonez and O. Smirnova, Phys. Rev. A, 2019, 99, 043417 CrossRef CAS.
- A. F. Ordonez and O. Smirnova, Phys. Chem. Chem. Phys., 2022, 24, 5720–5728 RSC.
- A. F. Ordonez and O. Smirnova, Phys. Chem. Chem. Phys., 2022, 24, 7264–7273 RSC.
- R. Guillemin, O. Hemmers, D. W. Lindle and S. T. Manson, Radiat. Phys. Chem., 2006, 75, 2258–2274 CrossRef CAS.
- K. Hosaka, J. Adachi, A. V. Golovin, M. Takahashi, T. Teramoto, N. Watanabe, A. Yagishita, S. K. Semenov and N. A. Cherepkov, J. Phys. B: At., Mol. Opt. Phys., 2006, 39, L25–L34 CrossRef CAS.
- D. Toffoli and P. Decleva, J. Phys. B: At. Mol. Phys., 2006, 39, 2681–2691 CrossRef CAS.
- M. Oura, T. Gejo, K. Nagaya, Y. Kohmura, K. Tamasaku, L. Journel, M. N. Piancastelli and M. Simon, New J. Phys., 2019, 21, 043015 CrossRef CAS.
- M. N. Piancastelli, T. Marchenko, R. Guillemin, L. Journel, O. Travnikova, I. Ismail and M. Simon, Rep. Prog. Phys., 2020, 83, 016401 CrossRef CAS PubMed.
- C. Kalha, N. K. Fernando, P. Bhatt, F. O. L. Johansson, A. Lindblad, H. Rensmo, L. Z. Medina, R. Lindblad, S. Siol, L. P. H. Jeurgens, C. Cancellieri, K. Rossnagel, K. Medjanik, G. Schönhense, M. Simon, A. X. Gray, S. Nemšák, P. Lömker, C. Schlueter and A. Regoutz, J. Phys.: Condens. Matter, 2021, 33, 233001 CrossRef CAS PubMed.
- I. E. Brumboiu, O. Eriksson and P. Norman, J. Chem. Theory Comput., 2019, 15, 5483–5494 CrossRef CAS PubMed.
- N. H. List, T. R. L. Melin, M. van Horn and T. Saue, J. Chem. Phys., 2020, 152, 184110 CrossRef CAS PubMed.
- Y.-I. Suzuki, J. Phys. B: At., Mol. Opt. Phys., 2020, 53, 215202 CrossRef.
- M.-X. Wang, S.-G. Chen, H. Liang and L.-Y. Peng, Chin. Phys. B, 2020, 29, 013302 CrossRef CAS.
- M. Kircher, J. Rist, F. Trinter, S. Grundmann, M. Waitz, N. Melzer, I. Vela-Perez, T. Mletzko, A. Pier, N. Strenger, J. Siebert, R. Janssen, V. Honkimäki, J. Drnec, P. V. Demekhin, L. P. H. Schmidt, M. S. Schöffler, T. Jahnke and R. Dörner, Phys. Rev. Lett., 2019, 123, 193001 CrossRef CAS PubMed.
- S. Grundmann, M. Kircher, I. Vela-Perez, G. Nalin, D. Trabert, N. Anders, N. Melzer, J. Rist, A. Pier, N. Strenger, J. Siebert, P. V. Demekhin, L. P. H. Schmidt, F. Trinter, M. S. Schöffler, T. Jahnke and R. Dörner, Phys. Rev. Lett., 2020, 124, 233201 CrossRef CAS PubMed.
- A. Hartung, S. Brennecke, K. Lin, D. Trabert, K. Fehre, J. Rist, M. S. Schöffler, T. Jahnke, L. P. H. Schmidt, M. Kunitski, M. Lein, R. Dörner and S. Eckart, Phys. Rev. Lett., 2021, 126, 053202 CrossRef CAS PubMed.
- R. R. Lucchese and A. Stolow, J. Phys. B: At. Mol. Phys., 2012, 45, 190201 CrossRef.
- A. V. Golovin, F. Heiser, C. J. K. Quayle, P. Morin, M. Simon, O. Gessner, P.-M. Guyon and U. Becker, Phys. Rev. Lett., 1997, 79, 4554–4557 CrossRef CAS.
- A. Lafosse, M. Lebech, J. C. Brenot, P. M. Guyon, L. Spielberger, O. Jagutzki, J. C. Houver and D. Dowek, J. Phys. B: At. Mol. Phys., 2003, 36, 4683–4702 CrossRef CAS.
- D. Dowek, M. Lebech, J. C. Houver and R. R. Lucchese, J. Electron Spectrosc. Relat. Phenom., 2004, 141, 211–227 CrossRef CAS.
- M. Lebech, J. C. Houver, D. Dowek and R. R. Lucchese, J. Chem. Phys., 2002, 117, 9248–9257 CrossRef CAS.
- M. Lebech, J. C. Houver, D. Dowek and R. R. Lucchese, J. Chem. Phys., 2004, 120, 8226–8240 CrossRef CAS PubMed.
- K. Veyrinas, N. Saquet, S. Marggi Poullain, M. Lebech, J.-C. Houver, R. R. Lucchese and D. Dowek, J. Chem. Phys., 2019, 151, 174305 CrossRef CAS PubMed.
- F. Holzmeier, J. Joseph, J. C. Houver, M. Lebech, D. Dowek and R. R. Lucchese, Nat. Commun., 2021, 12, 7343 CrossRef CAS PubMed.
- X. Gong, W. Jiang, J. Tong, J. Qiang, P. Lu, H. Ni, R. Lucchese, K. Ueda and J. Wu, Phys. Rev. X, 2022, 12, 011002 CAS.
- P.-M. Paul, E. S. Toma, P. Breger, G. Mullot, F. Augé, P. Balcou, H. G. Muller and P. Agostini, Science, 2001, 292, 1689–1692 CrossRef CAS PubMed.
- J. Vos, L. Cattaneo, S. Patchkovskii, T. Zimmermann, C. Cirelli, M. Lucchini, A. Kheifets, A. S. Landsman and U. Keller, Science, 2018, 360, 1326 CrossRef CAS PubMed.
- D. Dowek, M. Lebech, J. C. Houver and R. R. Lucchese, Mol. Phys., 2007, 105, 1757–1768 CrossRef CAS.
- D. Dowek, J. F. Pérez-Torres, Y. J. Picard, P. Billaud, C. Elkharrat, J. C. Houver, J. L. Sanz-Vicario and F. Martín, Phys. Rev. Lett., 2010, 104, 233003 CrossRef CAS PubMed.
- N. Cherepkov, Chem. Phys. Lett., 1982, 87, 344–348 CrossRef CAS.
- R. L. Dubs, S. N. Dixit and V. McKoy, Phys. Rev. Lett., 1985, 54, 1249–1251 CrossRef CAS PubMed.
- C. Westphal, J. Bansmann, M. Getzlaff and G. Schönhense, Phys. Rev. Lett., 1989, 63, 151–154 CrossRef CAS PubMed.
- T. Jahnke, T. Weber, A. L. Landers, A. Knapp, S. Schössler, J. Nickles, S. Kammer, O. Jagutzki, L. Schmidt, A. Czasch, T. Osipov, E. Arenholz, A. T. Young, R. Díez Muiño, D. Rolles, F. J. García de Abajo, C. S. Fadley, M. A. Van Hove, S. K. Semenov, N. A. Cherepkov, J. Rösch, M. H. Prior, H. Schmidt-Böcking, C. L. Cocke and R. Dörner, Phys. Rev. Lett., 2002, 88, 073002 CrossRef CAS PubMed.
- M. Lebech, J. C. Houver, D. Dowek and R. R. Lucchese, Phys. Rev. Lett., 2006, 96, 073001 CrossRef CAS PubMed.
- G. Schönhense and J. Hormes, VUV and Soft X-Ray Photoionization, Springer Science & Business Media, 2012, pp. 607–652 Search PubMed.
- M. Tia, M. Pitzer, G. Kastirke, J. Gatzke, H.-K. Kim, F. Trinter, J. Rist, A. Hartung, D. Trabert, J. Siebert, K. Henrichs, J. Becht, S. Zeller, H. Gassert, F. Wiegandt, R. Wallauer, A. Kuhlins, C. Schober, T. Bauer, N. Wechselberger, P. Burzynski, J. Neff, M. Weller, D. Metz, M. Kircher, M. Waitz, J. B. Williams, L. P. H. Schmidt, A. D. Müller, A. Knie, A. Hans, L. Ben Ltaief, A. Ehresmann, R. Berger, H. Fukuzawa, K. Ueda, H. Schmidt-Böcking, R. Dörner, T. Jahnke, P. V. Demekhin and M. Schöffler, J. Phys. Chem. Lett., 2017, 8, 2780–2786 CrossRef CAS PubMed.
- K. Veyrinas, C. Elkharrat, S. Marggi Poullain, N. Saquet, D. Dowek, R. R. Lucchese, G. A. Garcia and L. Nahon, Phys. Rev. A, 2013, 88, 063411 CrossRef.
- K. Veyrinas, V. Gruson, S. J. Weber, L. Barreau, T. Ruchon, J.-F. Hergott, J.-C. Houver, R. R. Lucchese, P. Salières and D. Dowek, Faraday Discuss., 2016, 194, 161–183 RSC.
- L. Barreau, K. Veyrinas, V. Gruson, S. J. Weber, T. Auguste, J.-F. Hergott, F. Lepetit, B. Carré, J.-C. Houver, D. Dowek and P. Salières, Nat. Commun., 2018, 9, 4727 CrossRef PubMed.
- S. M. Poullain, R. Cireasa, C. Cornaggia, M. Simon, T. Marin, R. Guillemin, J. C. Houver, R. R. Lucchese and D. Dowek, Phys. Chem. Chem. Phys., 2017, 19, 21996–22007 RSC.
- K. A. Larsen, C. S. Trevisan, R. R. Lucchese, S. Heck, W. Iskandar, E. Champenois, A. Gatton, R. Moshammer, R. Strom, T. Severt, B. Jochim, D. Reedy, M. Weller, A. L. Landers, J. B. Williams, I. Ben-Itzhak, R. Dörner, D. Slaughter, C. W. McCurdy, T. Weber and T. N. Rescigno, Phys. Chem. Chem. Phys., 2018, 20, 21075–21084 RSC.
- S. Heck, D. Baykusheva, H. Meng, J. Jia-Bao, P. Conaill, X. Gong and H. J. Woerner, Sci. Adv., 2022, 7, eabj8121 CrossRef PubMed.
- H. Ahmadi, E. Plésiat, M. Moioli, F. Frassetto, L. Poletto, P. Decleva, C. D. Schröter, T. Pfeifer, R. Moshammer, A. Palacios, F. Martin and G. Sansone, Nat. Commun., 2022, 13, 1242 CrossRef CAS PubMed.
- L. S. Cederbaum, J. Zobeley and F. Tarantelli, Phys. Rev. Lett., 1997, 79, 4778–4781 CrossRef CAS.
- T. Jahnke, J. Phys. B: At., Mol. Opt. Phys., 2015, 48, 082001 CrossRef.
- A. Mhamdi, J. Rist, D. Aslitürk, M. Weller, N. Melzer, D. Trabert, M. Kircher, I. Vela-Pérez, J. Siebert, S. Eckart, S. Grundmann, G. Kastirke, M. Waitz, A. Khan, M. S. Schöffler, F. Trinter, R. Dörner, T. Jahnke and P. V. Demekhin, Phys. Rev. Lett., 2018, 121, 243002 CrossRef CAS PubMed.
- S. Motoki, J. Adachi, K. Ito, K. Ishii, K. Soejima, A. Yagishita, S. K. Semenov and N. A. Cherepkov, J. Phys. B: At., Mol. Opt. Phys., 2002, 35, 3801–3819 CrossRef CAS.
- J. Rist, K. Klyssek, N. M. Novikovskiy, M. Kircher, I. Vela-Pérez, D. Trabert, S. Grundmann, D. Tsitsonis, J. Siebert, A. Geyer, N. Melzer, C. Schwarz, N. Anders, L. Kaiser, K. Fehre, A. Hartung, S. Eckart, L. P. H. Schmidt, M. S. Schöffler, V. T. Davis, J. B. Williams, F. Trinter, R. Dörner, P. V. Demekhin and T. Jahnke, Nat. Commun., 2021, 12, 6657 CrossRef CAS PubMed.
- X.-J. Liu, H. Fukuzawa, T. Teranishi, A. De Fanis, M. Takahashi, H. Yoshida, A. Cassimi, A. Czasch, L. Schmidt, R. Dörner, K. Wang, B. Zimmermann, V. McKoy, I. Koyano, N. Saito and K. Ueda, Phys. Rev. Lett., 2008, 101, 083001 CrossRef PubMed.
- R. R. Lucchese, H. Fukuzawa, X.-J. Liu, T. Teranishi, N. Saito and K. Ueda, J. Phys. B: At., Mol. Opt. Phys., 2012, 45, 194014 CrossRef.
- T. Osipov, T. N. Rescigno, T. Weber, S. Miyabe, T. Jahnke, A. S. Alnaser, M. P. Hertlein, O. Jagutzki, L. P. H. Schmidt, M. Schöffler, L. Foucar, S. Schössler, T. Havermeier, M. Odenweller, S. Voss, B. Feinberg, A. L. Landers, M. H. Prior, R. Dörner, C. L. Cocke and A. Belkacem, J. Phys. B: At., Mol. Opt. Phys., 2008, 41, 091001 CrossRef.
- M. S. Schöffler, J. Titze, N. Petridis, T. Jahnke, K. Cole, L. P. H. Schmidt, A. Czasch, D. Akoury, O. Jagutzki, J. B. Williams, N. A. Cherepkov, S. K. Semenov, C. W. McCurdy, T. N. Rescigno, C. L. Cocke, T. Osipov, S. Lee, M. H. Prior, A. Belkacem, A. L. Landers, H. Schmidt-Böcking, T. Weber and R. Dörner, Science, 2008, 320, 920–923 CrossRef PubMed.
- S. K. Semenov, M. S. Schöffler, J. Titze, N. Petridis, T. Jahnke, K. Cole, L. P. H. Schmidt, A. Czasch, D. Akoury, O. Jagutzki, J. B. Williams, T. Osipov, S. Lee, M. H. Prior, A. Belkacem, A. L. Landers, H. Schmidt-Böcking, T. Weber, N. A. Cherepkov and R. Dörner, Phys. Rev. A, 2010, 81, 043426 CrossRef.
- H. Sann, T. Havermeier, C. Müller, H.-K. Kim, F. Trinter, M. Waitz, J. Voigtsberger, F. Sturm, T. Bauer, R. Wallauer, D. Schneider, M. Weller, C. Goihl, J. Tross, K. Cole, J. Wu, M. S. Schöffler, H. Schmidt-Böcking, T. Jahnke, M. Simon and R. Dörner, Phys. Rev. Lett., 2016, 117, 243002 CrossRef CAS PubMed.
- J. P. Cryan, J. M. Glownia, J. Andreasson, A. Belkacem, N. Berrah, C. I. Blaga, C. Bostedt, J. Bozek, C. Buth, L. F. DiMauro, L. Fang, O. Gessner, M. Guehr, J. Hajdu, M. P. Hertlein, M. Hoener, O. Kornilov, J. P. Marangos, A. M. March, B. K. McFarland, H. Merdji, V. S. Petrović, C. Raman, D. Ray, D. Reis, F. Tarantelli, M. Trigo, J. L. White, W. White, L. Young, P. H. Bucksbaum and R. N. Coffee, Phys. Rev. Lett., 2010, 105, 083004 CrossRef PubMed.
- G. Kastirke, M. S. Schöffler, M. Weller, J. Rist, R. Boll, N. Anders, T. M. Baumann, S. Eckart, B. Erk, A. De Fanis, K. Fehre, A. Gatton, S. Grundmann, P. Grychtol, A. Hartung, M. Hofmann, M. Ilchen, C. Janke, M. Kircher, M. Kunitski, X. Li, T. Mazza, N. Melzer, J. Montano, V. Music, G. Nalin, Y. Ovcharenko, A. Pier, N. Rennhack, D. E. Rivas, R. Dörner, D. Rolles, A. Rudenko, P. Schmidt, J. Siebert, N. Strenger, D. Trabert, I. Vela-Perez, R. Wagner, T. Weber, J. B. Williams, P. Ziolkowski, L. P. H. Schmidt, A. Czasch, K. Ueda, F. Trinter, M. Meyer, P. V. Demekhin and T. Jahnke, Phys. Rev. Lett., 2020, 125, 163201 CrossRef CAS PubMed.
- M. Yamazaki, J. Adachi, T. Teramoto, A. Yagishita, M. Stener and P. Decleva, J. Phys. B: At., Mol. Opt. Phys., 2009, 42, 051001 CrossRef.
- G. Nalin, K. Fehre, F. Trinter, N. M. Novikovskiy, N. Anders, D. Trabert, S. Grundmann, M. Kircher, A. Khan, R. Tomar, M. Hofmann, M. Waitz, I. Vela-Pérez, G. Kastirke, J. Siebert, D. Tsitsonis, H. Fukuzawa, K. Ueda, J. B. Williams, D. Kargin, M. Maurer, C. Küstner-Wetekam, L. Marder, J. Viehmann, A. Knie, T. Jahnke, M. Ilchen, R. Dörner, R. Pietschnig, P. V. Demekhin and M. S. Schöffler, Phys. Chem. Chem. Phys., 2021, 23, 17248–17258 RSC.
- K. Fehre, F. Trinter, N. M. Novikovskiy, S. Grundmann, D. Tsitsonis, S. Eckart, L. Bauer, M. Hilzinger, T. Jahnke, R. Dörner, P. V. Demekhin and M. S. Schöffler, Phys. Chem. Chem. Phys., 2022, 24, 13597–13604 RSC.
- K. Fehre, N. M. Novikovskiy, S. Grundmann, G. Kastirke, S. Eckart, F. Trinter, J. Rist, A. Hartung, D. Trabert, C. Janke, G. Nalin, M. Pitzer, S. Zeller, F. Wiegandt, M. Weller, M. Kircher, M. Hofmann, L. P. H. Schmidt, A. Knie, A. Hans, L. B. Ltaief, A. Ehresmann, R. Berger, H. Fukuzawa, K. Ueda, H. Schmidt-Böcking, J. B. Williams, T. Jahnke, R. Dörner, M. S. Schöffler and P. V. Demekhin, Phys. Rev. Lett., 2021, 127, 103201 CrossRef CAS PubMed.
- K. Fehre, S. Eckart, M. Kunitski, C. Janke, D. Trabert, J. Rist, M. Weller, A. Hartung, L. P. H. Schmidt and T. Jahnke, J. Phys. Chem. A, 2019, 123, 6491–6495 CrossRef CAS PubMed.
- J. B. Williams, C. S. Trevisan, M. S. Schöffler, T. Jahnke, I. Bocharova, H. Kim, B. Ulrich, R. Wallauer, F. Sturm, T. N. Rescigno, A. Belkacem, R. Dörner, T. Weber, C. W. McCurdy and A. L. Landers, Phys. Rev. Lett., 2012, 108, 233002 CrossRef CAS PubMed.
- A. Menssen, C. S. Trevisan, M. S. Schöffler, T. Jahnke, I. Bocharova, F. Sturm, N. Gehrken, B. Gaire, H. Gassert, S. Zeller, J. Voigtsberger, A. Kuhlins, F. Trinter, A. Gatton, J. Sartor, D. Reedy, C. Nook, B. Berry, M. Zohrabi, A. Kalinin, I. Ben-Itzhak, A. Belkacem, R. Dörner, T. Weber, A. L. Landers, T. N. Rescigno, C. W. McCurdy and J. B. Williams, J. Phys. B: At., Mol. Opt. Phys., 2016, 49, 055203 CrossRef.
- E. Plésiat, P. Decleva and F. Martín, Phys. Rev. A, 2013, 88, 063409 CrossRef.
- H. Fukuzawa, R. R. Lucchese, X.-J. Liu, K. Sakai, H. Iwayama, K. Nagaya, K. Kreidi, M. S. Schöffler, J. R. Harries, Y. Tamenori, Y. Morishita, I. H. Suzuki, N. Saito and K. Ueda, J. Chem. Phys., 2019, 150, 174306 CrossRef PubMed.
- H. Fukuzawa, S. Yamada, Y. Sakakibara, T. Tachibana, Y. Ito, T. Takanashi, T. Nishiyama, T. Sakai, K. Nagaya, N. Saito, M. Oura, M. Stener, P. Decleva and K. Ueda, J. Chem. Phys., 2019, 151, 104302 CrossRef PubMed.
- F. Ota, K. Hatada, D. Sébilleau, K. Ueda and K. Yamazaki, J. Phys. B: At., Mol. Opt. Phys., 2021, 54, 084001 CrossRef CAS.
- F. Ota, K. Yamazaki, D. Sébilleau, K. Ueda and K. Hatada, J. Phys. B: At., Mol. Opt. Phys., 2021, 54, 024003 CrossRef CAS.
- L. Kaiser, K. Fehre, N. M. Novikovskiy, J. Stindl, D. Tsitsonis, G. Gopakumar, I. Unger, J. Söderström, O. Björneholm, M. Schöffler, T. Jahnke, R. Dörner, F. Trinter and P. V. Demekhin, J. Phys. B: At., Mol. Opt. Phys., 2020, 53, 194002 CrossRef CAS.
- A. Landers, Th Weber, I. Ali, A. Cassimi, M. Hattass, O. Jagutzki, A. Nauert, T. Osipov, A. Staudte, M. H. Prior, H. Schmidt-Böcking, C. L. Cocke and R. Dörner, Phys. Rev. Lett., 2001, 87, 013002 CrossRef CAS PubMed.
- D. Rolles, M. Braune, S. Cvejanović, O. Geßner, R. Hentges, S. Korica, B. Langer, T. Lischke, G. Prümper, A. Reinköster, J. Viefhaus, B. Zimmermann, V. McKoy and U. Becker, Nature, 2005, 437, 711–715 CrossRef CAS PubMed.
- D. Akoury, K. Kreidi, T. Jahnke, T. Weber, A. Staudte, M. Schöffler, N. Neumann, J. Titze, L. P. H. Schmidt, A. Czasch, O. Jagutzki, R. A. C. Fraga, R. E. Grisenti, R. D. Muiño, N. A. Cherepkov, S. K. Semenov, P. Ranitovic, C. L. Cocke, T. Osipov, H. Adaniya, J. C. Thompson, M. H. Prior, A. Belkacem, A. L. Landers, H. Schmidt-Böcking and R. Dörner, Science, 2007, 318, 949–952 CrossRef CAS PubMed.
- B. Zimmermann, D. Rolles, B. Langer, R. Hentges, M. Braune, S. Cvejanovic, O. Geßner, F. Heiser, S. Korica, T. Lischke, A. Reinköster, J. Viefhaus, R. Dörner, V. McKoy and U. Becker, Nat. Phys., 2008, 4, 649–655 Search PubMed.
- F. Martín, J. Fernández, T. Havermeier, L. Foucar, T. Weber, K. Kreidi, M. Schöffler, L. Schmidt, T. Jahnke, O. Jagutzki, A. Czasch, E. P. Benis, T. Osipov, A. L. Landers, A. Belkacem, M. H. Prior, H. Schmidt-Böcking, C. L. Cocke and R. Dörner, Science, 2007, 315, 629–633 CrossRef PubMed.
- C. W. McCurdy, T. N. Rescigno, C. S. Trevisan, R. R. Lucchese, B. Gaire, A. Menssen, M. S. Schöffler, A. Gatton, J. Neff, P. M. Stammer, J. Rist, S. Eckart, B. Berry, T. Severt, J. Sartor, A. Moradmand, T. Jahnke, A. L. Landers, J. B. Williams, I. Ben-Itzhak, R. Dörner, A. Belkacem and T. Weber, Phys. Rev. A, 2017, 95, 011401 CrossRef.
- R. Guillemin, P. Decleva, M. Stener, C. Bomme, T. Marin, L. Journel, T. Marchenko, R. K. Kushawaha, K. Jänkälä, N. Trcera, K. P. Bowen, D. W. Lindle, M. N. Piancastelli and M. Simon, Nat. Commun., 2015, 6, 6166 CrossRef CAS PubMed.
- C. M. González-Collado, E. Plésiat, P. Decleva, A. Palacios and F. Martín, Phys. Chem. Chem. Phys., 2022, 24, 7700–7712 RSC.
- M. Waitz, R. Y. Bello, D. Metz, J. Lower, F. Trinter, C. Schober, M. Keiling, U. Lenz, M. Pitzer, K. Mertens, M. Martins, J. Viefhaus, S. Klumpp, T. Weber, L. P. H. Schmidt, J. B. Williams, M. S. Schöffler, V. V. Serov, A. S. Kheifets, L. Argenti, A. Palacios, F. Martín, T. Jahnke and R. Dörner, Nat. Commun., 2017, 8, 2266 CrossRef CAS PubMed.
- M. Lebech, J. C. Houver, G. Raseev, A. S. dos Santos, D. Dowek and R. R. Lucchese, J. Chem. Phys., 2012, 136, 094303 CrossRef CAS PubMed.
- E. Kukk, T. D. Thomas, D. Céolin, S. Granroth, O. Travnikova, M. Berholts, T. Marchenko, R. Guillemin, L. Journel, I. Ismail, R. Püttner, M. N. Piancastelli, K. Ueda and M. Simon, Phys. Rev. Lett., 2018, 121, 073002 CrossRef CAS PubMed.
- R. Guillemin, L. Gerchikov, S. Sheinerman, M. Zmerli, T. Marin, L. Journel, O. Travnikova, T. Marchenko, B. Lassalle-Kaiser, M. N. Piancastelli and M. Simon, Phys. Rev. A, 2019, 99, 063409 CrossRef CAS.
- M. Kircher, J. Rist, F. Trinter, S. Grundmann, M. Waitz, N. Melzer, I. Vela-Pérez, T. Mletzko, A. Pier, N. Strenger, J. Siebert, R. Janssen, L. P. H. Schmidt, A. N. Artemyev, M. S. Schöffler, T. Jahnke, R. Dörner and P. V. Demekhin, Phys. Rev. Lett., 2019, 123, 243201 CrossRef CAS PubMed.
- S. Grundmann, D. Trabert, K. Fehre, N. Strenger, A. Pier, L. Kaiser, M. Kircher, M. Weller, S. Eckart, L. P. H. Schmidt, F. Trinter, T. Jahnke, M. S. Schöffler and R. Dörner, Science, 2020, 370, 339–341 CrossRef CAS PubMed.
- Z.-H. Zhang and F. He, Phys. Rev. A, 2021, 103, 033112 CrossRef CAS.
- H. Liang, S. Grundmann, Y.-K. Fang, L. Geng, Q. Gong and L.-Y. Peng, Phys. Rev. A, 2021, 104, L021101 CrossRef CAS.
- X. Lai, S. Xu, S. Yu, M. Shi, W. Quan and X. Liu, Phys. Rev. A, 2021, 104, 043105 CrossRef CAS.
- I. A. Ivanov, A. S. Kheifets and K. T. Kim, Sci. Rep., 2021, 11, 21457 CrossRef CAS PubMed.
- A. Sopena, F. Catoire, A. Palacios, F. Martín and H. Bachau, Phys. Rev. A, 2022, 105, 033104 CrossRef CAS.
- T. Tschentscher, C. Bressler, J. Grünert, A. Madsen, A. P. Mancuso, M. Meyer, A. Scherz, H. Sinn and U. Zastrau, Appl. Sci., 2017, 7, 592 CrossRef.
- G. Kastirke, M. S. Schöffler, M. Weller, J. Rist, R. Boll, N. Anders, T. M. Baumann, S. Eckart, B. Erk, A. De Fanis, K. Fehre, A. Gatton, S. Grundmann, P. Grychtol, A. Hartung, M. Hofmann, M. Ilchen, C. Janke, M. Kircher, M. Kunitski, X. Li, T. Mazza, N. Melzer, J. Montano, V. Music, G. Nalin, Y. Ovcharenko, A. Pier, N. Rennhack, D. E. Rivas, R. Dörner, D. Rolles, A. Rudenko, P. Schmidt, J. Siebert, N. Strenger, D. Trabert, I. Vela-Perez, R. Wagner, T. Weber, J. B. Williams, P. Ziolkowski, L. P. H. Schmidt, A. Czasch, F. Trinter, M. Meyer, K. Ueda, P. V. Demekhin and T. Jahnke, Phys. Rev. X, 2020, 10, 021052, DOI:10.1103/PhysRevX.10.021052.
- A. Staudte, S. Patchkovskii, D. Pavičić, H. Akagi, O. Smirnova, D. Zeidler, M. Meckel, D. M. Villeneuve, R. Dörner, M. Y. Ivanov and P. B. Corkum, Phys. Rev. Lett., 2009, 102, 033004 CrossRef CAS PubMed.
- H. Akagi, T. Otobe, A. Staudte, A. Shiner, F. Turner, R. Dörner, D. M. Villeneuve and P. B. Corkum, Science, 2009, 325, 1364–1367 CrossRef CAS PubMed.
- A. H. Winney, G. Basnayake, D. A. Debrah, Y. F. Lin, S. K. Lee, P. Hoerner, Q. Liao, H. B. Schlegel and W. Li, J. Phys. Chem. Lett., 2018, 9, 2539–2545 CrossRef CAS PubMed.
- D. Trabert, S. Brennecke, K. Fehre, N. Anders, A. Geyer, S. Grundmann, M. S. Schöffler, L. P. H. Schmidt, T. Jahnke, R. Dörner, M. Kunitski and S. Eckart, Nat. Commun., 2021, 12, 1697 CrossRef CAS PubMed.
- S. Eckart, Phys. Rev. Res., 2020, 2, 033248 CrossRef CAS.
- D. J. Leahy, K. L. Reid, H. Park and R. N. Zare, J. Chem. Phys., 1992, 97, 4948–4957 CrossRef CAS.
- A. Sen, S. T. Pratt and K. L. Reid, J. Chem. Phys., 2017, 147, 013927 CrossRef PubMed.
- P. Hockett, A. K. King, I. Powis and K. L. Reid, J. Chem. Phys., 2007, 127, 154307 CrossRef PubMed.
- P. Hockett, M. Staniforth, K. L. Reid and D. Townsend, Phys. Rev. Lett., 2009, 4 Search PubMed.
- L. Varvarezos and et al., to be submitted, 2022.
- F. Kelkensberg, A. Rouzée, W. Siu, G. Gademann, P. Johnsson, M. Lucchini, R. R. Lucchese and M. J. J. Vrakking, Phys. Rev. A, 2011, 84, 051404 CrossRef.
- A. Rouzée, F. Kelkensberg, W. K. Siu, G. Gademann, R. R. Lucchese and M. J. J. Vrakking, J. Phys. B: At., Mol. Opt. Phys., 2012, 45, 074016 CrossRef.
- A. Rouzée, A. G. Harvey, F. Kelkensberg, D. Brambila, W. K. Siu, G. Gademann, O. Smirnova and M. J. J. Vrakking, J. Phys. B: At., Mol. Opt. Phys., 2014, 47, 124017 CrossRef.
- C. A. Schouder, A. S. Chatterley, J. D. Pickering and H. Stapelfeldt, Annu. Rev. Phys. Chem., 2022, 73, 323–347 CrossRef PubMed.
- Y. Tang, Y.-I. Suzuki, T. Horio and T. Suzuki, Phys. Rev. Lett., 2010, 104, 073002 CrossRef PubMed.
- H. Rudolph and V. McKoy, J. Chem. Phys., 1989, 91, 2235–2238 CrossRef CAS.
- M. Gregory, P. Hockett, A. Stolow and V. Makhija, J. Phys. B: At., Mol. Opt. Phys., 2021, 54, 145601 CrossRef CAS.
- V. Makhija, K. Veyrinas, A. E. Boguslavskiy, R. Forbes, I. Wilkinson, R. Lausten, S. P. Neville, S. T. Pratt, M. S. Schuurman and A. Stolow, J. Phys. B: At., Mol. Opt. Phys., 2020, 53, 114001 CrossRef CAS.
- P. Emma, R. Akre, J. Arthur, R. Bionta, C. Bostedt, J. Bozek, A. Brachmann, P. Bucksbaum, R. Coffee and F.-J. Decker, Nat. Photonics, 2010, 4, 641–647 CrossRef CAS.
- R. Boll, D. Anielski, C. Bostedt, J. D. Bozek, L. Christensen, R. Coffee, S. De, P. Decleva, S. W. Epp, B. Erk, L. Foucar, F. Krasniqi, J. Küpper, A. Rouzée, B. Rudek, A. Rudenko, S. Schorb, H. Stapelfeldt, M. Stener, S. Stern, S. Techert, S. Trippel, M. J. J. Vrakking, J. Ullrich and D. Rolles, Phys. Rev. A, 2013, 88, 061402 CrossRef.
- D. Rolles, R. Boll, M. Adolph, A. Aquila, C. Bostedt, J. D. Bozek, H. N. Chapman, R. Coffee, N. Coppola, P. Decleva, T. Delmas, S. W. Epp, B. Erk, F. Filsinger, L. Foucar, L. Gumprecht, A. Hömke, T. Gorkhover, L. Holmegaard, P. Johnsson, C. Kaiser, F. Krasniqi, K.-U. Kühnel, J. Maurer, M. Messerschmidt, R. Moshammer, W. Quevedo, I. Rajkovic, A. Rouzée, B. Rudek, I. Schlichting, C. Schmidt, S. Schorb, C. D. Schröter, J. Schulz, H. Stapelfeldt, M. Stener, S. Stern, S. Techert, J. Thøgersen, M. J. J. Vrakking, A. Rudenko, J. Küpper and J. Ullrich, J. Phys. B: At., Mol. Opt. Phys., 2014, 47, 124035 CrossRef.
- A. Yagishita, J. Electron Spectrosc. Relat. Phenom., 2015, 200, 247–256 CrossRef CAS.
- S. Minemoto, T. Teramoto, H. Akagi, T. Fujikawa, T. Majima, K. Nakajima, K. Niki, S. Owada, H. Sakai, T. Togashi, K. Tono, S. Tsuru, K. Wada, M. Yabashi, S. Yoshida and A. Yagishita, Sci. Rep., 2016, 6, 38654 CrossRef CAS PubMed.
- P. B. Corkum, Phys. Rev. Lett., 1993, 71, 1994–1997 CrossRef CAS PubMed.
- K. J. Schafer, B. Yang, L. F. DiMauro and K. C. Kulander, Phys. Rev. Lett., 1993, 70, 1599–1602 CrossRef CAS PubMed.
- V. Kumarappan, L. Holmegaard, C. Martiny, C. B. Madsen, T. K. Kjeldsen, S. S. Viftrup, L. B. Madsen and H. Stapelfeldt, Phys. Rev. Lett., 2008, 100, 093006 CrossRef PubMed.
- M. Meckel, D. Comtois, D. Zeidler, A. Staudte, D. Pavičić, H. C. Bandulet, H. Pépin, J. C. Kieffer, R. Dörner, D. M. Villeneuve and P. B. Corkum, Science, 2008, 320, 1478–1482 CrossRef CAS PubMed.
- L. Holmegaard, J. L. Hansen, L. Kalhøj, S. Louise Kragh, H. Stapelfeldt, F. Filsinger, J. Küpper, G. Meijer, D. Dimitrovski, M. Abu-samha, C. P. J. Martiny and L. Bojer Madsen, Nat. Phys., 2010, 6, 428–432 Search PubMed.
- J. L. Hansen, L. Holmegaard, L. Kalhøj, S. L. Kragh, H. Stapelfeldt, F. Filsinger, G. Meijer, J. Küpper, D. Dimitrovski, M. Abu-samha, C. P. J. Martiny and L. B. Madsen, Phys. Rev. A, 2011, 83, 023406 CrossRef.
- D. Dimitrovski, M. Abu-samha, L. B. Madsen, F. Filsinger, G. Meijer, J. Küpper, L. Holmegaard, L. Kalhøj, J. H. Nielsen and H. Stapelfeldt, Phys. Rev. A, 2011, 83, 023405 CrossRef.
- M. V. Ammosov, N. B. Delone and V. P. Krainov, J. Exp. Theor. Phys., 1986, 64, 1191 Search PubMed.
- J. Maurer, D. Dimitrovski, L. Christensen, L. B. Madsen and H. Stapelfeldt, Phys. Rev. Lett., 2012, 109, 123001 CrossRef PubMed.
- D. Pavičić, K. F. Lee, D. M. Rayner, P. B. Corkum and D. M. Villeneuve, Phys. Rev. Lett., 2007, 98, 243001 CrossRef PubMed.
- S. Petretti, Y. V. Vanne, A. Saenz, A. Castro and P. Decleva, Phys. Rev. Lett., 2010, 104, 223001 CrossRef PubMed.
- R. Johansen, K. G. Bay, L. Christensen, J. Thøgersen, D. Dimitrovski, L. B. Madsen and H. Stapelfeldt, J. Phys. B: At., Mol. Opt. Phys., 2016, 49, 205601 CrossRef.
- P. Sándor, A. Sissay, F. Mauger, M. W. Gordon, T. T. Gorman, T. D. Scarborough, M. B. Gaarde, K. Lopata, K. J. Schafer and R. R. Jones, J. Chem. Phys., 2019, 151, 194308 CrossRef PubMed.
- H. V. S. Lam, S. Yarlagadda, A. Venkatachalam, T. N. Wangjam, R. K. Kushawaha, C. Cheng, P. Svihra, A. Nomerotski, T. Weinacht, D. Rolles and V. Kumarappan, Phys. Rev. A, 2020, 102, 043119 CrossRef CAS.
- J. Mikosch, A. E. Boguslavskiy, I. Wilkinson, M. Spanner, S. Patchkovskii and A. Stolow, Phys. Rev. Lett., 2013, 110, 023004 CrossRef PubMed.
- F. Schell, T. Bredtmann, C. P. Schulz, S. Patchkovskii, M. J. J. Vrakking and J. Mikosch, Sci. Adv., 2018, 4, eaap8148 CrossRef PubMed.
- M. Meckel, A. Staudte, S. Patchkovskii, D. M. Villeneuve, P. B. Corkum, R. Dörner and M. Spanner, Nat. Phys., 2014, 10, 594–600 Search PubMed.
- M. G. Pullen, B. Wolter, A.-T. Le, M. Baudisch, M. Sclafani, H. Pires, C. D. Schröter, J. Ullrich, R. Moshammer, T. Pfeifer, C. D. Lin and J. Biegert, Nat. Commun., 2016, 7, 11922 Search PubMed.
- F. Krečinić, P. Wopperer, B. Frusteri, F. Brauße, J.-G. Brisset, U. De Giovannini, A. Rubio, A. Rouzée and M. J. J. Vrakking, Phys. Rev. A, 2018, 98, 041401 CrossRef.
- A. Trabattoni, J. Wiese, U. De Giovannini, J.-F. Olivieri, T. Mullins, J. Onvlee, S.-K. Son, B. Frusteri, A. Rubio, S. Trippel and J. Küpper, Nat. Commun., 2020, 11, 2546 CrossRef CAS PubMed.
- J. Wiese, J. Onvlee, S. Trippel and J. Küpper, Phys. Rev. Res., 2021, 3, 013089 CrossRef CAS.
- T. Zuo, A. Bandrauk and P. B. Corkum, Chem. Phys. Lett., 1996, 259, 313–320 CrossRef CAS.
- M. Lein, J. P. Marangos and P. L. Knight, Phys. Rev. A, 2002, 66, 051404 CrossRef.
- J. Xu, Z. Chen, A.-T. Le and C. D. Lin, Phys. Rev. A, 2010, 82, 033403 CrossRef.
- M. Peters, T. T. Nguyen-Dang, C. Cornaggia, S. Saugout, E. Charron, A. Keller and O. Atabek, Phys. Rev. A, 2011, 83, 051403 CrossRef.
- T. Morishita, A.-T. Le, Z. Chen and C. D. Lin, Phys. Rev. Lett., 2008, 100, 013903 CrossRef PubMed.
- C. I. Blaga, J. Xu, A. D. DiChiara, E. Sistrunk, K. Zhang, P. Agostini, T. A. Miller, L. F. DiMauro and C. D. Lin, Nature, 2012, 483, 194–197 CrossRef CAS PubMed.
- Z. Chen, A.-T. Le, T. Morishita and C. D. Lin, J. Phys. B: At., Mol. Opt. Phys., 2009, 42, 061001 CrossRef.
- C. D. Lin, A.-T. Le, Z. Chen, T. Morishita and R. Lucchese, J. Phys. B: At., Mol. Opt. Phys., 2010, 43, 122001 CrossRef.
- Y. Ito, C. Wang, A.-T. Le, M. Okunishi, D. Ding, C. D. Lin and K. Ueda, Struct. Dyn., 2016, 3, 034303 CrossRef PubMed.
- Y. Ito, R. Carranza, M. Okunishi, R. R. Lucchese and K. Ueda, Phys. Rev. A, 2017, 96, 053414 CrossRef.
- M. G. Pullen, B. Wolter, A.-T. Le, M. Baudisch, M. Hemmer, A. Senftleben, C. D. Schröter, J. Ullrich, R. Moshammer, C. D. Lin and J. Biegert, Nat. Commun., 2015, 6, 7262 CrossRef CAS PubMed.
- B. Wolter, M. G. Pullen, A.-T. Le, M. Baudisch, K. Doblhoff-Dier, A. Senftleben, M. Hemmer, C. D. Schröter, J. Ullrich and T. Pfeifer, Science, 2016, 354, 308–312 CrossRef CAS PubMed.
- K. Amini, M. Sclafani, T. Steinle, A.-T. Le, A. Sanchez, C. Müller, J. Steinmetzer, L. Yue, J. R. Martínez Saavedra, M. Hemmer, M. Lewenstein, R. Moshammer, T. Pfeifer, M. G. Pullen, J. Ullrich, B. Wolter, R. Moszynski, F. J. García de Abajo, C. D. Lin, S. Gräfe and J. Biegert, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 8173–8177, DOI:10.1073/pnas.1817465116.
- E. T. Karamatskos, G. Goldsztejn, S. Raabe, P. Stammer, T. Mullins, A. Trabattoni, R. R. Johansen, H. Stapelfeldt, S. Trippel, M. J. J. Vrakking, J. Küpper and A. Rouzée, J. Chem. Phys., 2019, 150, 244301 CrossRef PubMed.
- W. Xie, J. Yan, M. Li, C. Cao, K. Guo, Y. Zhou and P. Lu, Phys. Rev. Lett., 2021, 127, 263202 CrossRef CAS PubMed.
- X. Liu, K. Amini, T. Steinle, A. Sanchez, M. Shaikh, B. Belsa, J. Steinmetzer, A.-T. Le, R. Moshammer and T. Pfeifer, J. Chem. Phys., 2019, 151, 024306 CrossRef PubMed.
- B. Belsa, K. Amini, X. Liu, A. Sanchez, T. Steinle, J. Steinmetzer, A. T. Le, R. Moshammer, T. Pfeifer, J. Ullrich, R. Moszynski, C. D. Lin, S. Gräfe and J. Biegert, Struct. Dyn., 2021, 8, 014301 CrossRef CAS PubMed.
- J. Xu, C. I. Blaga, K. Zhang, Y. H. Lai, C. Lin, T. A. Miller, P. Agostini and L. F. DiMauro, Nat. Commun., 2014, 5, 1–6 CAS.
- A. Sanchez, K. Amini, S.-J. Wang, T. Steinle, B. Belsa, J. Danek, A. T. Le, X. Liu, R. Moshammer, T. Pfeifer, M. Richter, J. Ullrich, S. Gräfe, C. D. Lin and J. Biegert, Nat. Commun., 2021, 12, 1520 CrossRef CAS PubMed.
- X. Liu, K. Amini, A. Sanchez, B. Belsa, T. Steinle and J. Biegert, Commun. Chem., 2021, 4, 154 CrossRef CAS.
- S. G. Walt, N. Bhargava Ram, M. Atala, N. I. Shvetsov-Shilovski, A. von Conta, D. Baykusheva, M. Lein and H. J. Wörner, Nat. Commun., 2017, 8, 15651 CrossRef CAS PubMed.
- F. Brausse, F. Bach, F. Krečinić, M. J. J. Vrakking and A. Rouzée, Phys. Rev. Lett., 2020, 125, 123001 CrossRef CAS PubMed.
- N. Kotsina and D. Townsend, Phys. Chem. Chem. Phys., 2021, 23, 10736–10755 RSC.
- N. Hartmann, G. Hartmann, R. Heider, M. Wagner, M. Ilchen, J. Buck, A. Lindahl, C. Benko, J. Grünert and J. Krzywinski, Nat. Photonics, 2018, 12, 215–220 CrossRef CAS.
- I. Ismail, L. Journel, R. Vacheresse, J. Palaudoux, T. Marin, F. Penent and M. Simon, Rev. Sci. Instrum., 2018, 89, 113101 CrossRef PubMed.
- B. Mignolet, R. D. Levine and F. Remacle, J. Phys. B: At. Mol. Phys., 2014, 47, 124011 CrossRef.
- E. Plésiat, M. Lara-Astiaso, P. Decleva, A. Palacios and F. Martín, Chem. – Eur. J., 2018, 24, 12061–12070 CrossRef PubMed.
- E. P. Månsson, S. Latini, F. Covito, V. Wanie, M. Galli, E. Perfetto, G. Stefanucci, H. Hübener, U. De Giovannini, M. C. Castrovilli, A. Trabattoni, F. Frassetto, L. Poletto, J. B. Greenwood, F. Légaré, M. Nisoli, A. Rubio and F. Calegari, Commun. Chem., 2021, 4, 73 CrossRef.
- L. Cattaneo, L. Pedrelli, R. Y. Bello, A. Palacios, P. D. Keathley, F. Martín and U. Keller, Phys. Rev. Lett., 2022, 128, 063001 CrossRef CAS PubMed.
- S. M. Cavaletto, D. Keefer and S. Mukamel, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2121383119 CrossRef CAS PubMed.
- L.-M. Koll, L. Maikowski, L. Drescher, T. Witting and M. J. J. Vrakking, Phys. Rev. Lett., 2022, 128, 043201 CrossRef CAS PubMed.
- K. Prince, E. Allaria, C. Callegari, R. Cucini, G. De Ninno, S. Di Mitri, B. Diviacco, E. Ferrari, P. Finetti and D. Gauthier, Nat. Photonics, 2016, 10, 176–179 CrossRef CAS.
- D. You, K. Ueda, E. V. Gryzlova, A. N. Grum-Grzhimailo, M. M. Popova, E. I. Staroselskaya, O. Tugs, Y. Orimo, T. Sato, K. L. Ishikawa, P. A. Carpeggiani, T. Csizmadia, M. Füle, G. Sansone, P. K. Maroju, A. D’Elia, T. Mazza, M. Meyer, C. Callegari, M. Di Fraia, O. Plekan, R. Richter, L. Giannessi, E. Allaria, G. De Ninno, M. Trovò, L. Badano, B. Diviacco, G. Gaio, D. Gauthier, N. Mirian, G. Penco, P. R. Ribič, S. Spampinati, C. Spezzani and K. C. Prince, Phys. Rev. X, 2020, 10, 031070 CAS.
- R. H. Pratt, Radiat. Phys. Chem., 2014, 95, 4–13 CrossRef CAS.
- M. Kircher, F. Trinter, S. Grundmann, I. Vela-Perez, S. Brennecke, N. Eicke, J. Rist, S. Eckart, S. Houamer, O. Chuluunbaatar, Y. V. Popov, I. P. Volobuev, K. Bagschik, M. N. Piancastelli, M. Lein, T. Jahnke, M. S. Schöffler and R. Dörner, Nat. Phys., 2020, 16, 756–760 Search PubMed.
- O. Chuluunbaatar, S. Houamer, Yu. V. Popov, I. P. Volobuev, M. Kircher and R. Dörner, J. Quant. Spectrosc. Radiat. Transfer, 2021, 272, 107820 CrossRef CAS.
- O. Chuluunbaatar, S. Houamer, Yu. V. Popov, I. P. Volobuev, M. Kircher and R. Dörner, J. Quant. Spectrosc. Radiat. Transfer, 2022, 278, 108020 CrossRef CAS.
- R. Boll, J. M. Schäfer, B. Richard, K. Fehre, G. Kastirke, Z. Jurek, M. S. Schöffler, M. M. Abdullah, N. Anders, T. M. Baumann, S. Eckart, B. Erk, A. De Fanis, R. Dörner, S. Grundmann, P. Grychtol, A. Hartung, M. Hofmann, M. Ilchen, L. Inhester, C. Janke, R. Jin, M. Kircher, K. Kubicek, M. Kunitski, X. Li, T. Mazza, S. Meister, N. Melzer, J. Montano, V. Music, G. Nalin, Y. Ovcharenko, C. Passow, A. Pier, N. Rennhack, J. Rist, D. E. Rivas, D. Rolles, I. Schlichting, L. P. H. Schmidt, P. Schmidt, J. Siebert, N. Strenger, D. Trabert, F. Trinter, I. Vela-Perez, R. Wagner, P. Walter, M. Weller, P. Ziolkowski, S.-K. Son, A. Rudenko, M. Meyer, R. Santra and T. Jahnke, Nat. Phys., 2022, 18, 423–428 Search PubMed.
| This journal is © the Owner Societies 2022 |