Thermodynamics of supercritical carbon dioxide mixtures across the Widom line

Abstract

Supercritical carbon dioxide (scCO₂) mixtures are essential for many industrial applications. However, the knowledge of their thermophysical properties in the extended critical region is insufficient. Here, supercritical liquid- and gas-like regions dominated by distinct dynamics and thermodynamics exist and are demarcated by the so-called Widom line. The nature of the anomalies observed for several thermophysical properties at the crossover between these two regions is the subject of a lively debate. Hence, the extended critical region of scCO₂ and seven of its binary mixtures with hydrogen, methane, ethane, isobutane, benzene, toluene or naphthalene is studied with respect to thermodynamic, transport and structural properties on the basis of molecular dynamics simulations and equation of state calculations. The Widom line is evaluated employing five criteria and a new empirical equation is proposed for its prediction. Further, the crossover anomalies are investigated in the light of pseudo-boiling theory, diffusion and viscosity as well as structural characteristics given by the radial distribution function.

---

1 Introduction

Supercritical carbon dioxide (scCO₂) plays a crucial role in technologies to mitigate global warming,¹ efficiently generate power² or replace traditional organic solvents.^3,4 Further, scCO₂ is an efficient and environmentally friendly alternative to water for shale gas recovery,⁵ being a potential bridging fuel in the transition from coal to renewable energy sources.⁶

These technologies exploit the unique properties of CO₂: its chemical stability, wide availability at low cost and good accessibility of its supercritical region due to a critical point (T_c = 304.13 K, p_c = 7.38 MPa) that is near the ambient temperature. Furthermore, CO₂ is non-toxic, not combustible and has a high solubility for a wide range of solutes. Hence, it is also applied in many industrial separation and extraction processes.⁷ However, the compression of CO₂ into supercritical states and its transportation is energy and cost intensive.⁸ These costs can be reduced by operating supercritical fluid (SCF) technologies within an optimal range of thermodynamic conditions. In fact, the most attractive region of operation for SCF technologies is close to the critical point of the fluid, i.e., 1 < T/T_c < 1.1 and 1 < p/p_c < 1.5.⁹ Therefore, a solid knowledge of the thermophysical properties of the working fluid is required. In practice, scCO₂ is not likely to be found in its pure form in industrial applications since impurities are inevitable.¹⁰ The presence of other components can significantly affect its thermophysical properties,^11,12 and consequently, the design and material requirements of SCF industrial units.¹³ However, despite recent efforts,^14–16 experimental data for mixtures in the extended critical region are rather rare.^17,18

Due to the rapid development of experimental and molecular simulation techniques in the last decade, unique features of SCF have been revealed. Near the critical point, distinct regions where SCF exhibit liquid-like or gas-like structures and a characteristic behavior have been observed by experiment^19–22 and molecular simulation.^{17,20,22–26}

The transition between the liquid-like and gas-like SCF regions occurs at a supercritical crossover line, whose nature and definition is the topic of an ongoing scientific debate.^27–32 Across the so-called Widom line, which can be considered as a continuation of the vapor pressure curve, SCF properties like density or enthalpy change continuously from liquid-like to gas-like values over a narrow temperature range.³³ The Widom line, that can be observed up to about 10·p_c,³⁴ is also termed pseudo-critical, pseudo-spinodal or pseudo-boiling line.³⁵

The interpretation of the Widom line is still the subject of controversy³³ so that several definitions can be found in the literature.^20,24,30,31 It has been approximated by the locus of maxima of different thermodynamic response functions that originate at the critical point.^13,33 In fact, different response functions give rise to distinct lines that diverge from each other when moving away from the critical point.^13,23,36 Due to these differences, the concepts of Widom region or Widom delta have also been introduced.^24,37,38 The Widom region represents a temperature range at a given supercritical pressure where different Widom lines can be evaluated, e.g., by means of the maximum of the correlation length³⁹ or, most commonly, by the maximum of the isobaric heat capacity.^40,41

Criteria resting on transport properties can also be used to determine the delimiting line between liquid- and gas-like regions, e.g., the minimum of the kinematic viscosity⁴² or the equality between the kinetic and potential contributions to the shear viscosity.⁴³ In the Widom region, transport properties can drastically change over just a few Kelvin. Further, in case of mixtures, inflection points of the intra-diffusion coefficients or the average coordination number have also been found around the Widom line temperature.⁴⁴

Another, not less controversial, theory proposes that by crossing the Widom line, under isobaric conditions up to about 3·p_c, a SCF undergoes a supercritical phase evolution over a finite temperature interval akin to subcritical boiling, which is called pseudo-boiling. The middle temperature of the pseudo-boiling transition corresponds to the Widom line temperature. This concept, originally introduced by Ackerman⁴⁵ half a century ago, has been employed recently to quantitatively analyze the liquid- to gas-like transition of several pure fluids, such as argon,⁴⁶ nitrogen,⁴⁷ carbon dioxide⁴⁸ and water.^22,49

Another definition in this context is that of the Frenkel line, where the transition between liquid- and gas-like molecular diffusion mechanisms^27,50–53 in SCF occurs. This line does not touch the critical point and extends to arbitrarily high temperatures and pressures.^51,52 However, because most industrial applications of SCF operate at near-critical or transcritical conditions,^31,54 only the thermodynamic behavior of SCF across the Widom line was regarded in this work.

The distinct behavior of the thermodynamic properties observed in the Widom region can be considered as reminiscent of the critical anomalies of subcritical fluids.³⁵ Here, just a small variation of temperature or pressure may cause the density of scCO₂ mixtures to halve, the enthalpy to double and the isobaric heat capacity to peak by a factor of three or more. As the pressure increases further away from its critical value, the distinction between liquid- and gas-like regions⁵⁵ as well as the extrema of the thermodynamic response functions fade.³⁵ This behavior is schematically illustrated in Fig. 1.

Fig. 1 Density, enthalpy and isobaric heat capacity of the scCO₂ mixture with 1 mol% of hydrogen along the isobars p = 9 MPa and 12 MPa (inset). Solid lines represent the GERG-2008 EOS⁵⁶ and the dotted line indicates the Widom line temperature. The isobaric heat capacity was scaled up by a factor of ten. The temperature range in which these properties strongly change is delimited by dashed lines.

This work builds on previous molecular simulation studies of binary scCO₂ mixtures with diluted methane⁵⁷ or ethanol⁴⁴ in the extended critical region. The aim of the present work was to gain a better understanding of the changes of thermodynamic, transport and structural properties of dilute scCO₂ mixtures upon the near-critical crossover between liquid- and gas-like SCF regions, also known as Widom line. To examine the influence of the solute on these properties, seven diluted mixtures of scCO₂ with hydrogen or different hydrocarbons ranging from methane to naphthalene were studied. For this purpose, molecular simulation tools and equations of state (EOS) were employed.

Binary mixtures of hydrogen, ethane, isobutane, benzene, toluene or naphthalene diluted in sCO₂ were considered. All mixtures were studied at three solute mole fractions near the infinite dilution limit (mostly 0.5, 1.0 and 1.5 mol%) in the temperature range from T = 290 K to 350 K along the isobar p = 9 MPa. Further, the three scCO₂ mixtures with aromatic compounds (benzene, toluene or naphthalene) were studied along two additional isobars, i.e., p = 10 MPa and 12 MPa. Moreover, the binary mixture of sCO₂ with methane was studied in the entire composition range in order to compare the observations made for diluted mixtures with mixtures having higher solute concentrations.

This paper is organized as follows: first, theoretical background and methodology are described. Second, simulation results for different thermodynamic properties are shown together with EOS-based calculations. Subsequently, the limits of the Widom region, based on pseudo-boiling theory, are given for all regarded mixtures and an equation for the determination of the Widom line is proposed. Transport properties, i.e. diffusion coefficient and shear viscosity, are discussed with an emphasis on the dynamic definitions of the Widom line. Radial distribution function and the excess number of solvent molecules are interpreted in the light of the microscopic structure, leading to the observed characteristics of the Widom region. Finally, conclusions are drawn. Computational details and additional results are supplied in the ESI.†

2 Methods

2.1 Force fields

Molecular models that adequately mimic the intermolecular interactions are the primary requirement for the sampling of thermophysical properties by molecular simulation techniques. In this work, rigid and non-polarizable force fields of united-atom type were employed, which account for intermolecular interactions by a set of Lennard-Jones sites and, if required, point dipoles or point quadrupoles. The molecular models for CO₂,⁵⁸ hydrogen,⁵⁹ methane,⁶⁰ ethane,⁶⁰ isobutane,⁶¹ benzene,⁶² toluene⁶² and naphthalene⁶³ were parameterized with an optimization procedure based on quantum chemical calculations and fitting to experimental vapor–liquid equilibrium (VLE) data in previous work of our group.^61,64,65 The molecular models for benzene and toluene were additionally fitted to self-diffusion coefficient data.⁶² The parameters of the employed force fields are listed in the MolMod database.⁶³ A visual representation of the molecular models for the seven binary scCO₂ mixtures studied in this work is shown in Fig. 2.

Fig. 2 Visual representation of the molecular models that form the seven scCO₂ mixtures that were investigated in this study.

To define a molecular model for a mixture on the basis of pairwise additive pure substance models, only the unlike interactions have to be specified. The unlike electrostatic interactions can be determined by the laws of electrostatics. However, unlike Lennard-Jones parameters are treated by combining rules, as no physically sound alternative exists.⁶⁶ The simple Lorentz–Berthelot combining rules were chosen as a starting point, but a binary interaction parameter ξ was employed to adjust the unlike Lennard-Jones energy parameter

σ_ab = (σ_aa + σ_bb)/2 (1)

andwhere σ_ab and ε_ab are the Lennard-Jones parameters for size and energy of the unlike interaction, respectively. The optimal binary interaction parameter ξ for a given mixture was fitted to experimental VLE data with a procedure described in preceding work,⁶⁷cf. Table S1 of the ESI.†

The isothermal VLE of the studied mixtures show an excellent agreement between simulation data on the one side and experimental and EOS data on the other side, cf.Fig. 3 and Fig. S1–S3 of the ESI.† VLE of all mixtures considered in this work, except for CO₂ + toluene and CO₂ + hydrogen, were studied along three isotherms near the critical temperature of the solute. For instance, CO₂ + methane was considered along three isotherms that are well above the critical temperature of the solute, cf. Fig. S2 of the ESI.†Fig. 3 shows the isothermal VLE of CO₂ mixtures with ethane or benzene. CO₂ + ethane has a low boiling azeotropic behavior since the critical temperature of CO₂ and of ethane are similar. In contrast, the remaining CO₂ mixtures exhibit a zeotropic phase behavior.

Fig. 3 Vapor–liquid equilibria of CO₂ mixtures with ethane (bottom) or benzene (top) along three isotherms. Solid lines for CO₂ + ethane denote data from the GERG-2008 EOS⁵⁶ and for CO₂ + benzene from the Peng–Robinson EOS (k_ij = 0.096).⁶⁸ Crosses represent experimental data for CO₂ + ethane⁶⁹ and CO₂ + benzene,^68,70,71 whereas circles depict present molecular simulation results. Red vertical marks on the very right stand for the supercritical states of interest.

2.2 Thermodynamic properties

Two subsequent equilibrium molecular dynamics simulations were carried out with the ms2⁷² code to sample thermodynamic, transport and structural properties of scCO₂ mixtures. In the first run, a simulation in the isobaric–isothermal (NpT) ensemble was performed at specified conditions of temperature, pressure and composition to obtain the mixture density. This density was subsequently specified for the second simulation run in the canonical (NVT) ensemble to determine the thermodynamic, transport and structural properties of interest.

Six thermodynamic properties were studied due to their anomalous behavior in the supercritical state:³⁵ density ρ, enthalpy h, isobaric heat capacity c_p, isothermal compressibility β_T, volume expansivity α and speed of sound w. These properties were calculated from the derivatives of the Helmholtz energy obtained with the Lustig formalism^72–74 in the NVT ensemble. For the enthalpy, isobaric heat capacity and speed of sound, ideal contributions from the reference EOS (see Section 2.5) were added to the residual contributions sampled by simulation. The superposition of the ideal contribution from EOS with the residual simulation data may be questioned due to the missing internal degrees of freedom of the employed molecular models.⁷⁵ However, the comparison of the residual isobaric heat capacity from simulation and EOS shows good agreement, suggesting a small influence of the internal degrees of freedom on the studied properties.

The relations between the Helmholtz energy derivatives and the remaining thermodynamic properties are straightforward, cf. Thol et al.⁷⁶ For instance, the speed of sound was determined by

where A^r_mn represents the residual Helmholtz derivatives with respect to the reduced inverse temperature and reduced density and A^o₂₀ = −c^o_v expresses the isochoric heat capacity of the ideal gas.⁷⁶

2.3 Kirkwood–Buff integrals

Kirkwood–Buff integrals (KBI) G_ij were calculated to gain insight into the microscopic fluid behavior of the studied mixtures. KBI are defined as⁷⁷where g_ij(r) is the radial distribution function. Because eqn (4) is defined for the grand canonical ensemble, corrections are required when the canonical ensemble is employed.⁷⁸ Thus, the truncation method by Krüger et al.⁷⁹ was applied here. Moreover, corrections of the radial distribution function based on the method by Ganguly and van der Vegt⁸⁰ were employed. The partial molar volume v_i of the binary mixture of components i and j can be calculated employing the sampled KBI withwhere ρ_i and ρ_j are the molar densities with ρ_i = ρx_i. Cluster formation can be characterized by the excess number of solvent molecules surrounding a solute one with respect to the bulk.⁸¹ The so-called excess coordination number is given by⁸²where is the density of pure CO₂ and G_ij denotes the KBI between CO₂ and a solute.

2.4 Transport properties

Transport properties were sampled with equilibrium molecular dynamics and the Green–Kubo formalism.^83,84 Diffusion coefficients and shear viscosity can be obtained concurrently with this approach so that it was preferred over non-equilibrium molecular dynamics. Here, self-diffusion coefficients, more specifically termed intra-diffusion coefficients in case of mixtures, were sampled on the basis of the individual molecular velocity autocorrelation functions byTherein, N_a is the number of molecules of component a and v^a_i(t) is the center of mass velocity vector of the i-th molecule of component a at time t. The brackets 〈⋯〉 denote the NVT ensemble average.

The shear viscosity η is associated with the off-diagonal elements of the microscopic stress tensor J^xy_p

where V stands for the volume andHere, i and j denote different molecules of any species that interact with the potential u. The upper indices x and y stand for the spatial vector components, e.g., for velocity v^x_i or site–site distance r^x_ij. The first and second terms of eqn (9) represent the kinetic and configurational (potential) energy contribution to the shear viscosity, respectively. Consequently, the Green–Kubo integral (8) can be decomposed into kinetic, configurational and kinetic-configurational energy contributions. The mathematical expressions of these contributions to the shear viscosity are given in the ESI.† To improve statistics of the simulation data, five independent terms of the stress tensor J^xy_p, J^xz_p, J^yz_p, (J^xx_p − J^yy_p)/2 and (J^yy_p − J^zz_p)/2 were considered.⁸⁵

Two approaches to correct the finite-size effects of the sampled intra-diffusion coefficients were studied. The correction methods by Yeh and Hummer⁸⁶ and Leverant et al.⁸⁷ were assessed by looking at four mixtures for systems containing different numbers of molecules (500, 1000, 2500 and 5000). Three state points were considered per mixture. The results from both approaches are similar for the scCO₂ mixtures with 1.5 mol% of benzene or toluene sampled at three pressures, cf. Fig. S4 and S5 of the ESI.† The approach by Leverant et al. yields marginally better results for the scCO₂ mixtures with ethane and isobutane for three compositions along the isobar p = 9 MPa, cf. Fig. S6 and S7 of the ESI.† Finite-size corrections based on the approach by Yeh and Hummer were thus used in this work. They amount between 5.0% and 6.8% for the intra-diffusion coefficients of benzene and toluene, and between 1.0% and 4.3% for ethane and isobutane.

2.5 Equations of state

Molecular simulation data were compared to empirical reference models implemented in the NIST REFPROP 10.0⁸⁸ and TREND 5.0⁸⁹ databases. Experimental data for CO₂ mixtures at the supercritical states of interest are hardly available in the Dortmund Data Bank (DDBST).¹⁸ Thus, the Helmholtz energy EOS from Span and Wagner⁹⁰ was used for pure CO₂ and the highly accurate GERG-2008 EOS⁵⁶ was used to predict the thermodynamic properties of scCO₂ mixtures with hydrogen, methane, ethane or isobutane. The data for the mixtures CO₂ + benzene and CO₂ + toluene were calculated with REFPROP on the basis of the mixture models from Blackham and Lemmon.⁸⁸ It is important to note that the accuracy of the predictions of the empirical mixture models cannot be completely assured because of possible data extrapolation into the supercritical region.

The shear viscosity of scCO₂ was evaluated with the reference correlation by Laesecke et al.⁹¹ The prediction of the shear viscosity of binary scCO₂ mixtures is based on a modified one-fluid, extended corresponding states approach,⁹² which is also implemented in REFPROP. Due to the lack of experimental shear viscosity data for binary scCO₂ mixtures, these predictions have to be taken with caution.

3 Results and discussion

Pure scCO₂ and seven of its binary mixtures with hydrogen (H₂), methane (CH₄), ethane (C₂H₆), isobutane (C₄H₁₀), benzene (C₆H₆), toluene (C₇H₈) or naphthalene (C₁₀H₈) were studied in this work. The supercritical states of interest were specified to have a composition close to the infinite dilution limit (0.5, 1.0 or 1.5 mol% of solute) in the temperature range from T = 290 K (0.95·T_c,CO2) to 350 K (1.15·T_c,CO2) along the isobar p = 9 MPa (1.22·p_c,CO2). The aromatics benzene and toluene were additionally studied along the isobars p = 10 MPa and 12 MPa. As an exception, CO₂ + naphthalene was studied at solute mole fractions of 0.3, 0.5 and 0.6 mol% to obtain adequate statistics. On average, 23 simulations per mixture were performed at the supercritical states of interest, which are exemplarily indicated by red vertical marks in Fig. 3.

The Widom line, defined as the locus of the maxima of a given thermodynamic response function, can be easily obtained from an EOS. In this context, several distinct Widom line types, which depend on the selected response function, e.g., the isobaric heat capacity, can be defined, cf.Fig. 4. These lines are enclosed in the Widom region, which contains a set of Widom temperatures at a given supercritical pressure. In the following discussion on thermodynamic properties, the Widom line temperature is referred to as the temperature where the isobaric heat capacity exhibits a maximum at a given pressure, cf.Fig. 5.

Fig. 4 Different Widom line types of pure CO₂ determined by the maxima of c_p (red), α (dark red), β_T (dark green) or the minimum of w (pink) from the EOS by Span and Wagner.⁹⁰ Symbols show the present molecular simulation results. Circles represent the Widom line temperature determined by the isobaric heat capacity maximum. Triangles indicate the crossover temperature from the equality of the configurational and kinetic contributions to the shear viscosity. The critical point of CO₂ is represented by a cross and the dotted lines (red) delimit the pressure range of interest.

Fig. 5 Temperature dependence of the thermodynamic properties of scCO₂ (black) and its mixtures with 1.5 mol% of hydrogen (blue) or benzene (red) at p = 9 MPa. Symbols show the present molecular simulation results. Density (circles) and enthalpy (triangles up) are shown at the top, isobaric heat capacity (triangles down) and speed of sound (squares) in the center, isothermal compressibility (diamonds) and volume expansivity (hexagons) at the bottom. Dashed and solid lines represent the EOS by Span and Wagner for CO₂,⁹⁰ the GERG-2008 EOS⁵⁶ for CO₂ + hydrogen and the mixture model by Blackham and Lemmon⁸⁸ for CO₂ + benzene. Dotted lines indicate the Widom line temperature determined by the maximum of the isobaric heat capacity. Statistical uncertainties were omitted when they are either within symbol size or lead to visual clutter.

Criteria resting on transport properties, e.g., the minimum of kinematic viscosity⁴² or the equality of the configurational and kinetic contributions to the shear viscosity,⁴³ have also been used to determine the position of the crossover line between liquid- and gas-like regions of SCF. Both criteria have been shown to be consistent with the Widom line obtained from the maximum of the isobaric heat capacity criterion for simple model fluids.⁴² This correspondence was also observed in this work employing molecular simulation data, as shown in Fig. 4 for pure scCO₂.

An overview of the criteria that have been proposed in the literature for the determination of the Widom line from thermodynamic, dynamic and structural points of view is given in Table 1.

Table 1 Thermodynamic, dynamic and structural criteria for the determination of the Widom line based on different properties

	Criterion	Ref.
Thermodynamics
Density ρ	Inflection	13 and 35
Enthalpy h	Inflection	13 and 44
Isobaric heat capacity cp	Maximum	35
Isothermal compressibility βT	Maximum	35
Volume expansivity α	Maximum	35
Speed of sound w	Minimum	35
Thermodynamic factor Γ	Minimum	44
Dynamics
Configurational shear viscosity ηcc, kinetic shear viscosity ηkk	Equality	43
Kinematic viscosity ν	Minimum	42
Thermal diffusivity DT	Minimum	42
Intra-diffusion coefficient Di	Inflection	17 and 44
Structure
Average coordination number NA–B	Inflection	44

---

3.1 Thermodynamic properties

The mole fraction dependence of different thermodynamic properties of all seven scCO₂ mixtures along the isobar p = 9 MPa is given in Fig. 5 and Fig. S8–S18 of the ESI.† The pressure dependence of these properties for scCO₂ mixtures at a constant mole fraction is given in Fig. 6 and Fig. S19–S23 of the ESI.†

Fig. 6 Temperature dependence of the thermodynamic properties of scCO₂ (black) and its mixture with 1.5 mol% benzene at p = 10 MPa (red) as well as scCO₂ (blue) and its mixture with 1.5 mol% benzene at p = 12 MPa (green). Symbols show the present molecular simulation results. Density (circles) and enthalpy (triangles up) are shown at the top, isobaric heat capacity (triangles down) and speed of sound (squares) in the center, isothermal compressibility (diamonds) and volume expansivity (hexagons) at the bottom. Dashed and solid lines represent the EOS by Span and Wagner for CO₂⁹⁰ and the mixture model by Blackham and Lemmon⁸⁸ for CO₂ + benzene. Dotted lines indicate the Widom line temperature determined by the maximum of the isobaric heat capacity. Statistical uncertainties were omitted when they are either within symbol size or lead to visual clutter.

Simulation results and EOS data follow the same qualitative trends for all scCO₂ mixtures and compositions studied along the isobar p = 9 MPa, cf.Fig. 5 and Fig. S8–S15 of the ESI.† Data from molecular simulation exhibit a relatively large scatter near the Widom line, which can be traced back to strong density fluctuations relative to the system size that are inherent to this region. Nonetheless, molecular simulation results predict the location of the maximum or minimum of the observed thermodynamic properties well. Both density and enthalpy curves have a symmetrical sigmoidal shape with respect to the temperature. Isobaric heat capacity c_p, isothermal compressibility β_T and volume expansivity α peak by approximately one order of magnitude within this temperature range. The speed of sound exhibits a minimum as the slope of its temperature dependence changes from negative, characteristic for liquids, to positive, which is normal for gases. As the pressure increases, the peaks of the thermodynamic response functions concurrently lose amplitude, widen and shift to higher temperatures, cf.Fig. 6. In addition, density and enthalpy curves gradually change from a sigmoidal to a more linear course, as illustrated in Fig. 1. Thus, the distinction between the liquid- and gas-like supercritical regions disappears as the SCF shifts away from the critical point.

The average relative deviation (ARD) between simulation and EOS data for density, enthalpy and speed of sound for all mixtures along the isobar p = 9 MPa is 3.6%, 6.1% and 6.0%, respectively. However, these deviations depend strongly on temperature. For example, the ARD of density between simulation and the reference EOS for CO₂⁹⁰ in the temperature range from T = 312 K to 333.15 K amounts to 7.6%. Hence, the employed molecular model for CO₂ is slightly less accurate in this temperature range. The density of diluted scCO₂ mixtures from present simulation work is nonetheless consistent with the EOS. The sampled thermodynamic properties c_p, β_T and α of all CO₂ mixtures show ARD to EOS data of 12.0%, 15.1% and 13.6%, respectively.

The strongest changes of the time-independent thermodynamic properties occur between T = 305 K and 320 K for all mixtures and compositions studied along the isobar p = 9 MPa. Depending on the solute, density and enthalpy of these mixtures decrease by a factor of ∼2 to 2.7 and ∼1.7 to 2.2, respectively. More than two thirds of these changes take place in a narrow band around the Widom line temperature (T_w ± 2.5 K).

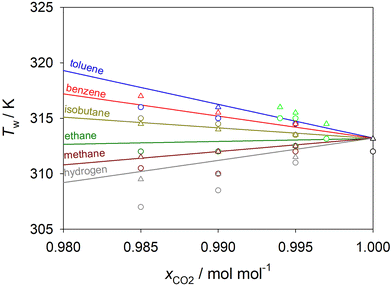
Simulation results show that the Widom line temperature of scCO₂ decreases upon the addition of 1.5 mol% hydrogen by ΔT ∼ 5 K and increases upon the addition of 1.5 mol% benzene by ΔT ∼ 4 K, respectively. Empirical EOS models predict a shift of the Widom line temperature in the same direction by ΔT ∼ 3 K for each mixture. This shift of the Widom line temperature corresponds, e.g., to a modification of the pressure for pure scCO₂ by ∼0.55 MPa.

The shift of the Widom line temperature at a given pressure varies strongly with the solute added and becomes weaker with decreasing solute mole fraction, cf.Fig. 8. As expected, the less solute in the scCO₂ mixture, the closer is its Widom line temperature to that of pure scCO₂. However, as it can be inferred from molecular simulation data, even a small amount of solute, e.g., 0.1 mol%, can shift this temperature by ΔT = −0.33 K for CO₂ + hydrogen, by ΔT = +0.20 K for CO₂ + isobutane and by ΔT = +0.50 K for CO₂ + naphthalene. Minor impurities present in scCO₂, e.g., with a few hundred ppm, would shift the Widom line temperature by just a few mK.

The observed shift of the Widom line can be linked to the displacement of the critical point of the binary mixture caused by the addition of solute.⁹³ To visualize this link, the Widom line temperature of the scCO₂ mixtures calculated by simulation and EOS was plotted against the critical temperature of the solute in Fig. S24 of the ESI.† In fact, experimental critical point data from DDBST¹⁸ support that the critical temperature shifts to lower temperatures for CO₂ mixtures with hydrogen, methane or ethane, while it shifts to higher temperatures for CO₂ mixtures with isobutane, benzene, toluene or naphthalene. Thus, a solute with a lower critical temperature than that of pure CO₂ decreases the critical temperature and consequently the Widom line temperature of the mixture and vice versa. Benzene and toluene have similar critical properties so that the Widom line temperature of their mixtures with scCO₂ hardly changes.

The pressure dependence of the Widom line temperature of scCO₂ and its binary mixtures with benzene, toluene or naphthalene sampled with molecular simulation is shown in Fig. S25 of the ESI.† An increase of the pressure from p = 9 MPa to 12 MPa rises the Widom line temperature of these scCO₂ mixtures at a constant composition by about ΔT ∼ 15 K. Thus, the Widom line temperature of these three mixtures increases linearly by ΔT ∼ 0.5 K for a pressure shift of Δp = +0.1 MPa independent on the solute mole fraction.

Note that for the studied mixtures and thermodynamic conditions only one Widom region was observed. The presence of two Widom regions, as described by Raju et al.¹⁷ for mixtures having strongly different critical points, was not found for the regarded mixtures, which can be traced back to the small amount of the solute present and the limited range of studied thermodynamic conditions. This intriguing behavior was also not found in this work for the mixture of scCO₂ with CH₄, which was analysed over the entire composition range. Only one Widom region was observed along the isobar 9 MPa and temperatures between 208 K and 335 K, cf. Fig. S26 and S27 of the ESI.† Further studies are required to shed light into the thermodynamic behavior of concentrated mixtures of scCO₂ during their liquid- to gas-like transition.

3.2 Limits of the extended Widom region

Separating out the Widom region, where thermodynamic and transport properties change dramatically over a small temperature range, can simplify the analysis of SCF, since fluids outside of this region can be regarded as normal gases or liquids.⁵⁴ In this work, the methodology proposed by Banuti⁹⁴ based on pseudo-boiling theory was used to analyse the limits of the Widom region for the regarded scCO₂ mixtures, cf.Fig. 7 and Fig. S28–S30 of the ESI.† In this theory, the phase evolution from liquid- to gas-like SCF is compared to isobaric boiling of a subcritical liquid. Both processes require a structural enthalpy contribution to overcome the intermolecular attraction during the transition from liquid- to gas-like regions. However, the supercritical phase evolution needs additional enthalpy to overcome the temperature interval associated with pseudo-boiling.⁹⁴ All thermodynamic quantities related to pseudo-boiling were calculated with the asymptotes of the ideal gas, liquid and pseudo-boiling enthalpy^47,94 on the basis of EOS data, as demonstrated in Fig. S28 of the ESI.† The numerical results are listed in Table S2 of the ESI.† The mixture scCO₂ + naphthalene was not considered due to the lack of EOS data.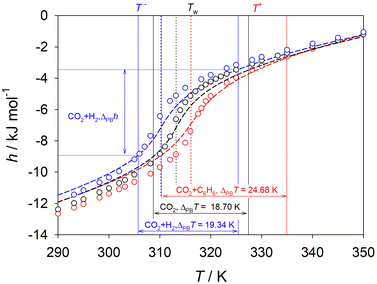

Fig. 7 Pseudo-boiling analysis of scCO₂ (black) and its mixtures with 1.5 mol% of hydrogen (blue) or benzene (red) along the isobar p = 9 MPa. Circles represent simulation data. Dashed lines represent the EOS by Span and Wagner for CO₂,⁹⁰ the GERG-2008 EOS⁵⁶ for CO₂ + hydrogen and the mixture model by Blackham and Lemmon⁸⁸ for CO₂ + benzene. The Widom line temperature is indicated by the dotted lines. The pseudo-boiling start T⁻ and end T⁺ temperatures enclose the extended Widom region as depicted by solid lines.

Fig. 8 Mole fraction dependence of the Widom line temperature along the isobar p = 9 MPa employing two criteria: (1) maximum of the isobaric heat capacity, (2) equality of the kinetic and configurational contributions to the shear viscosity. The Widom line temperature calculated with criterion (1) on the basis of EOS is represented by solid lines. Circles and triangles indicate the Widom line temperature calculated from simulation data with criterion (1) and (2), respectively.

Fig. 7 shows the pseudo-boiling analysis of the scCO₂ mixtures with 1.5 mol% of hydrogen or benzene along the isobar p = 9 MPa. The transition between liquid- and gas-like SCF begins at the denominated pseudo-boiling start temperature (T⁻), crosses the Widom line (T_W) and terminates at the end temperature (T⁺). A fluid is considered to have indistinguishable liquid-like characteristics at temperatures below T⁻ and gas-like characteristics for temperatures above T⁺.⁹⁵ The extended Widom region is delimited by T⁻ and T⁺. Thus, anomalous behavior of time-independent and transport properties of the SCF is expected to be found only therein. The knowledge of the limits of the extended Widom region is important for process design in near-critical regions either to avoid or to benefit from the strong changes of the thermodynamic properties of SCF.

The temperature interval delimiting the extended Widom region Δ_PBT = T⁺ − T⁻ varies, depending on the solute present in the scCO₂ mixture. For instance, this temperature interval for scCO₂ mixed with 1.5 mol% benzene Δ_PBT = 24.7 K differs strongly from the temperature interval of pure scCO₂ Δ_PBT = 18.7 K. In the extended Widom region, the mixture of scCO₂ + benzene is associated with an enthalpy change that is ∼12% larger than that of pure scCO₂. All scCO₂ mixtures experience a reduction of density by a factor of ∼2.5 to 2.9 and an increase of enthalpy by a factor of ∼2.1 to 2.5 within the extended Widom region. The structural enthalpy, defined by pseudo-boiling theory, is 2.2 to 2.6 times larger than the thermal enthalpy for all mixtures and compositions studied along the isobar p = 9 MPa.

In terms of pressure dependence, the calculated temperature interval of the extended Widom region for pure scCO₂ at p = 12 MPa is three times larger than at p = 9 MPa. Consequently, the pseudo-boiling enthalpy of pure scCO₂ is 50% larger at the higher isobar because a larger temperature interval Δ_PBT = 56.7 K has to be overcome. Hence, the thermal enthalpy increases and the ratio of the structural to thermal enthalpy contributions decreases with increasing pressure. It should be noticed that the structural enthalpy along the isobar p = 12 MPa is still 10% larger than the thermal enthalpy.

3.3 Widom line temperature

The Widom line temperature was assessed for all studied mixtures employing five different criteria, i.e. two thermodynamic and three dynamic, as listed in Table 1. Numerical results are presented in Table S3 of the ESI.† Simulation and EOS data show the same qualitative trends for the Widom line temperature with respect to the solute mole fraction along the isobar p = 9 MPa. The quantitative shift of the Widom line temperature differs slightly, depending on the employed criterion. Exemplarily, Fig. 8 shows the comparison of the Widom line temperature assessed from simulation data with that calculated from EOS data on the basis of one thermodynamic and one dynamic criterion. The Widom temperature calculated from the maximum of the isobaric heat capacity and EOS data agrees well with the one obtained employing the same criterion and simulation data, having an ARD of 0.3%. Further, there is a good agreement with the Widom temperature calculated from the equality between the kinetic and configurational contributions to the shear viscosity (see Section 3.5), with an ARD of 0.2%. Hence, these two criteria are comparable. Furthermore, the temperature at the kinematic viscosity minimum corresponds largely to the temperature obtained with the shear viscosity criterion with an ARD of 0.2%. In contrast, the Widom line temperature determined from the inflection point of the intra-diffusion coefficient deviates by about 1% from the reference Widom temperature.

A simple equation for the prediction of the Widom line temperature of scCO₂ mixtures was developed, cf.eqn (10). For this purpose, the Widom line of the scCO₂ mixtures was fitted with respect to the pressure p, solute mole fraction x_i and critical properties of both mixture components

where T_c,i is the critical temperature of the solute, while T_c,CO2 = 304.13 K and p_c,CO2 = 7.3773 MPa are the critical properties of CO₂. The results obtained from eqn (10) for nine scCO₂ mixtures along three isobars were compared to EOS and simulation data in Fig. S31 of the ESI.† The change of the Widom line temperature with solute mole fraction in dependence of the solute added was reproduced well with this equation. It should be pointed out that the proposed empirical equation is expected to be accurate for scCO₂ mixtures near the infinite dilution limit in the regarded temperature and pressure ranges.

3.4 Intra-diffusion

Transport and thermodynamic properties of fluids are strongly connected.⁴³ In fact, the inflection point of the shear viscosity and the self-diffusion coefficient have been used before to identify the crossover between the liquid- and gas-like regions of scH₂O, which was shown to coincide with the Widom line.²³ Consequently, the behavior of transport properties close to the Widom line was closely examined for the studied scCO₂ mixtures.

The intra-diffusion coefficients of scCO₂ and the given solute were analyzed. It was observed that both intra-diffusion coefficients exhibit a sigmoidal course with respect to the temperature for all mixtures along the isobar p = 9 MPa, cf.Fig. 9 and Fig. S32, S33 of the ESI.† These curves show a linear behavior at low temperatures, experience a strong increase in the temperature range from T = 305 K to 320 K, i.e., the Widom region, and become progressively linear at higher temperatures. Thus, they show a similar behavior as previously observed for the enthalpy. Across the extended Widom region, the intra-diffusion coefficient of scCO₂ increases by approximately one order of magnitude and that of the solute by a factor of ∼3.5. These data point out the existence of distinct regions with a liquid-like low diffusivity and a gas-like high diffusivity of the SCF.

Fig. 9 Temperature dependence of the intra-diffusion coefficients of binary mixtures of scCO₂ (black) with 0.5 mol% of ethane (dark green), isobutane (dark yellow), benzene (red), toluene (blue) or naphthalene (green) along the isobar p = 9 MPa. Circles represent the intra-diffusion coefficient of the solute and solid lines represent the intra-diffusion coefficient of scCO₂. The inset shows the results for hydrogen (grey) and methane (dark red) over a larger intra-diffusion coefficient range.

Consistent with the differences observed in the Widom region for time-independent properties, the strong change of the temperature dependence of the intra-diffusion coefficients starts at different temperatures, depending on the solute, demonstrating a shift of the Widom line for mixtures. The intra-diffusion coefficients of CO₂ and ethane behave similarly with increasing temperature. Hence, the Widom line of this mixture is expected to be similar as for pure CO₂ at the same pressure. In fact, this observation was also made with respect to time-independent properties.

Diffusion of molecular species is affected by the thermodynamic conditions, but also by their weight and size. For instance, lighter molecules propagate faster, which is reflected by a larger intra-diffusion coefficient, e.g., for hydrogen diluted in scCO₂. The intra-diffusion coefficient of hydrogen increases by at least one order of magnitude over the studied temperature range. Heavier molecules, such as naphthalene, propagate significantly slower and their intra-diffusion coefficient curves are smoother, cf.Fig. 9.

3.5 Shear viscosity

Recently, Bell et al.⁴³ introduced a methodology to determine the crossover between liquid- and gas-like regions of SCF. The authors showed the crossover to be consistent with that observed at the kinematic viscosity minimum⁴³ and hence with the Widom line defined by the maximum of the isobaric heat capacity.⁴² Bell et al.⁴³ found for some model and real fluids that this crossover occurs where the shear viscosity kinetic contribution η_kk (eqn (S2) of the ESI†), that dominates the gas phase, and the configurational contribution η_cc (eqn (S3) of the ESI†), that dominates the liquid phase, are equal. These contributions to the shear viscosity can be sampled only by means of molecular dynamics simulation. Thus, both contributions were assessed here to analyze the seven scCO₂ mixtures along the isobar p = 9 MPa.

Fig. 10 shows the temperature dependence of the kinetic, configurational and kinetic-configurational contributions to the shear viscosity of scCO₂ + hydrogen along the isobar p = 9 MPa. As can be seen, the shear viscosity kinetic and configurational contributions have opposing trends with respect to the temperature. At lower temperatures, the configurational contribution is dominant, which is characteristic for dense fluids with a liquid-like behavior. As expected, the kinetic contribution increases with temperature, while the configurational contribution decreases as the intermolecular interactions become weaker. With further temperature rise, the kinetic contribution prevails, which is typical for low-density fluids and gases.⁴³ Similar trends of the individual contributions to the shear viscosity were confirmed for scCO₂ along three isobars and scCO₂ + naphthalene at two compositions along the isobar p = 9 MPa, cf. Fig. S34 and S35 of the ESI.†

Fig. 10 Temperature dependence of the kinetic η_kk (brown triangles), configurational η_cc (green triangles) and kinetic-configurational η_kc (grey squares) contributions to the shear viscosity of scCO₂ mixtures with 0.5 (top), 1 (center) and 1.5 mol% (bottom) of hydrogen along the isobar p = 9 MPa. The dotted line indicates the Widom line temperature calculated with the criterion of Bell et al.⁴³ The inset shows the temperature dependence of the shear viscosity of binary mixtures of scCO₂ (red) with 0.5 (top), 1 (center) and 1.5 mol% (bottom) of hydrogen (blue) or benzene (red) along the isobar p = 9 MPa. Here, circles show simulation data and solid lines EOS data. The reference correlation for the shear viscosity by Laesecke et al.⁹¹ was used for scCO₂. An extended corresponding states approach⁹² was used for the mixtures.

The observed behavior of both contributions is in line with the assessed shear viscosity of the studied scCO₂ mixtures, since it changes from high, liquid-like values, to low, gas-like values with rising temperature. Across the Widom region, the shear viscosity changes on average by a factor of ∼1.8 for all studied mixtures. Interestingly, the addition of 0.5 to 1.5 mol% of solute has a minor influence on the shear viscosity of the mixture. Exemplarily, the inset of Fig. 10 shows the shear viscosity of scCO₂ mixed with 0.5 to 1.5 mol% of hydrogen or benzene as a function of temperature along the isobar p = 9 MPa. Analogous graphs for the remaining mixtures are depicted in Fig. S34 and S35 of the ESI.† In general, simulation results agree within their statistical uncertainties for temperatures well below and above the Widom region. In this region, simulation data show a rather strong scatter mainly due to density fluctuations. Nevertheless, simulation data follow throughout the qualitative trends specified by the predictive equations.

3.6 Structural analysis

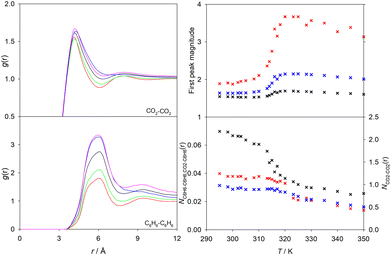
The anomalous behavior of the thermodynamic and transport properties observed in the Widom region is considered to be reminiscent of the singular behavior of fluids at the critical point.³⁵ The divergence of these properties at the critical point is related to the divergent correlation length and the presence of critical fluctuations, whose magnitude and effects decrease when moving away from the critical point.^54,96 The correlation length, which describes the inner relation between fluctuations,⁵⁴ was calculated for all studied mixtures with the method recommended by Sengers et al.⁹⁷ The required susceptibility was obtained from simulation data, while the remaining parameters are either constant or calculated from critical data. A maximum of the correlation length was observed in the Widom region, indicating that fluctuations become larger when the Widom line is approached, cf. Fig. S36 of the ESI.† Thus, the strong changes of the studied thermodynamic properties can be traced back to this phenomenon. Further, the correlation length of near-critical fluctuations⁹⁸ was smaller than half of the simulation box length for all explored conditions.

The radial distribution functions (RDF) is usually employed to gain insight on the microscopic structure of fluids. Here, the RDF of all scCO₂ mixtures with 1 mol% of the solute was studied. Exemplarily, the solvent–solvent RDF and the solute-solute RDF, the magnitude of the first peak and the average coordination number are shown in Fig. 11 for scCO₂ + benzene at selected temperatures in the extended Widom region. Similar plots for the remaining mixtures are given in Fig. S37–S42 of the ESI.†

Fig. 11 Microscopic structure of the scCO₂ mixture with 1.0 mol% of benzene at p = 9 MPa. Center-of-mass radial distribution functions g(r) for CO₂–CO₂ (top left) and C₆H₆–C₆H₆ (bottom left) are shown for five temperatures: 300 K (red), 310 K (green), 315 K (black), 317 K (pink) and 340 K (blue). The magnitude of the first peak (top right) and the average coordination number (bottom right) for CO₂–CO₂ (black), C₆H₆–C₆H₆ (red) and CO₂–C₆H₆ (blue) as a function of temperature are depicted by crosses.

A clearly pronounced first peak of both RDF is present for all studied scCO₂ mixtures. However, magnitude, shape and position of the peak depend on the solute and the state point. In general, the position of the nearest neighbor shell peak of the solvent–solvent interaction g_CO2–CO2(r) does not change significantly with temperature. It is located at ∼4.2 Å, which is consistent with neutron-diffraction experiments with pure scCO₂.⁹⁹ However, the peak becomes broader with rising temperature, indicating thermally induced weakening of the fluid structure of the first coordination shell. At lower temperatures (T < 310 K), the presence of a second peak can be clearly observed, which indicates a well-structured second coordination shell. With rising temperature, the second peak becomes broader and eventually subsides at T = 340 K. This weakening of the second peak indicates the progressive reduction of the molecular order in the fluid structure, which is consistent with the transition from a liquid- to a gas-like structure, where a second coordination shell cannot be distinguished anymore. Similarly, the first peak position of the solute-solute RDF remains nearly constant with varying temperature, but the peak magnitude and shape noticeably change, which can also be considered as a result of the thermal weakening of the structure. However, a stronger change of the peak suggests that the solute-solute structure is more easily disturbed by rising temperature than the solvent–solvent structure. Further, the flattening of the second coordination shell peak within the extended Widom region was also observed for the solute-solute RDF. It should be noticed that the presence of a shoulder in the first peak of g_C6H6–C6H6(r) that can be seen in Fig. 11 is related to the different orientations that can be adopted by benzene molecules. Furthermore, on the same basis, similar observations were made for the scCO₂ mixture with toluene as a solute.

To gain a better insight, the magnitude of the first peak and the average coordination number of the RDF for solvent–solvent, solute-solute and solvent–solute were plotted over temperature, cf. Fig. S37–S42 of the ESI.† Exemplarily, results for scCO₂ + benzene are shown in Fig. 11. In general, the temperature dependence of the first peak magnitude resembles the sigmoidal shape observed for the density and enthalpy, i.e., a relatively strong change of the peak magnitude occurs over a small temperature range. This fact and the increase of the peak magnitude with rising temperature can be explained by the normalization of the RDF with the average bulk density. An exception to this behavior was found for scCO₂ + hydrogen, where g_H2–H2(r) and g_CO2–H2(r) fall with rising temperature. For this mixture, it can be assumed that the normalization effect of the density does not override the stronger H₂–H₂ interactions present at lower temperatures in the liquid-like region. On the other hand, the RDF g_C6H6–C6H6(r) and g_C7H8–C7H8(r) experience a similar shift of the position and of the peak magnitude with rising temperature. This may be attributed to the similar molecular structure of these aromatics. Both show a ∼1.8 times larger first peak amplitude at the highest than at the lowest temperature along the isobar p = 9 MPa.

In analogy to the density, the average coordination number up to the first shell decreases sigmoidally with respect to temperature for all studied mixtures. The steepest change of the average coordination number occurs around the Widom line temperature. As expected, the average coordination number of g_CO2–CO2(r) is higher than that between the solute molecules because of their large surplus in the mixture. In general, the average coordination number of solute-solute and solvent–solute also decreases with rising temperature. However, for most of the studied mixtures, at temperatures above ∼320 K, the solute-solute and mixed coordination number have approximately the same value, which can be explained by a weakening of intermolecular solvent–solvent interactions observed in the gas-like region.

Furthermore, the “clustering” effect,⁸² where many solvent molecules collapse around a single solute molecule in the high compressibility region, was also studied in this work. This effect leads to a negative partial molar volume of the solute component at infinite dilution and can be quantified by the excess coordination number of CO₂ molecules surrounding the solute molecule regarding a uniform distribution at bulk density.⁸¹Fig. 12 shows the calculated excess coordination number and the partial molar volume of the studied aromatics infinitely diluted in scCO₂, whereas the remaining mixtures are discussed in Fig. S43 of the ESI.† Both properties exhibit values close to zero at lower temperatures (T < 305 K) and increase rapidly near the Widom line, where a maximum is observed, before approaching zero again at higher temperatures. These observations suggest that during the transition between liquid- and gas-like regions, the clustering effects together with large fluctuations can, as a reminiscence of criticality, explain the behavior of static and dynamic thermodynamic properties observed in the Widom region.

Fig. 12 Excess coordination number (open symbols) and partial molar volume of the solute component at infinite dilution (solid symbols) for scCO₂ mixed with benzene (top), toluene (center) and naphthalene (bottom) along the isobar p = 9 MPa. Both properties were calculated from Kirkwood–Buff integrals¹⁰⁰ corrected with the procedure by Ganguly and van der Vegt.⁸⁰ Dashed lines indicate the zero values of the two vertical axes.

Snapshots of molecular configurations represent only one microstate. However, a single microstate may well represent all possible microstates being permutations of the fluid structure patterns.¹⁰¹ Therefore, snapshots of the mixtures at different temperatures were analyzed. Exemplarily, snapshots of simulation volumes of scCO₂ mixed with 1.0 mol% benzene at three temperatures are shown in Fig. S44 of the ESI.† At the lowest temperature, where the mixture is clearly in liquid-like region, the solute molecules appear in more organized structures than at the highest depicted temperature, which is consistent with the previous observations. Thus, across the Widom region, the liquid-like ordering of the solute molecules gives way to a random structure characteristic of the gas-like region.

4 Conclusions

Molecular dynamics simulation was extensively applied to scCO₂ and seven of its binary mixtures with hydrogen, methane, ethane, isobutane, benzene, toluene or naphthalene and, where possible, compared to the most accurate EOS models. A thorough analysis of these scCO₂ mixtures was performed to characterize the anomalies observed in the Widom region.

It was shown that the density, intra-diffusion coefficients and shear viscosity of scCO₂ mixtures vary at least by a factor of two when the Widom region is crossed at the studied conditions. Thermodynamic response functions peak significantly and structural properties, i.e., the magnitude of the first peak of the RDF and the average coordination number, show strong sigmoidal changes with rising temperature. Further examination of the structure of scCO₂ mixtures indicates a progressive reduction of the molecular order and thus a transition from liquid- to gas-like structures. For instance, the second coordination shell becomes indistinguishable and eventually disappears with rising temperature.

Additional molecular simulation analysis shows a maximum of the correlation length and the excess coordination number at the Widom line, which indicate the presence of clustering effects in this region, which might explain the anomalous behavior of the studied thermodynamic properties and the observed negative partial molar volumes. To sum up, the existence of distinct liquid-like regions (high density, high viscosity and low diffusivity) and gas-like regions (low density, low viscosity and high diffusivity) in the extended critical region was confirmed in this work, together with the crossover between these regions. This crossover occurs in the Widom region, where anomalies of thermodynamic response functions and transport properties are observed and suggested to be the result of the presence of fluctuations and clustering, which are a reminiscence of criticality.

Five criteria for the determination of the Widom line were compared for all studied mixtures. The criterion of the equality of the kinetic and configurational contributions to the shear viscosity, which can only be assessed by molecular dynamics simulation, was applied for the first time to real mixtures. The line where these contributions are equal was shown to closely match the Widom line defined by the maximum of the isobaric heat capacity.

Further, a simple equation to predict the Widom line of dilute scCO₂ mixtures as a function of pressure, solute mole fraction and critical properties of the mixture components was proposed. It was shown that the liquid- to gas-like crossover line exhibits a non-negligible variation upon the addition of even small amounts of solute to pure scCO₂. These changes of the Widom line arise from modifications in both the critical point and the slope of the coexistence line of mixtures.

Finally, the region where the transition between liquid- and gas-like regions occurs was delimited based on pseudo-boiling theory and advanced EOS. It was shown that this extended Widom region varies with the type and amount of the solute.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

D. Saric gratefully acknowledges the support by the Konrad-Adenauer-Stiftung e.V. This work was funded by the Deutsche Forschungsgemeinschaft (DFG) under the grant VR 6/11 and conducted under the auspices of the Boltzmann-Zuse Society of Computational Molecular Engineering (BZS). Molecular dynamics simulations were performed either on the Cray's CS500 system Noctua at the Paderborn Center for Parallel Computing (PC²) or on the HPE Apollo system Hawk at the High-Performance Computing Center Stuttgart (HLRS) contributing to the project MMHBF2.

Notes and references

1. A. Imre, C. Ramboz, U. Deiters and T. Kraska, Environ. Earth Sci., 2015, 73, 4373–4384.
2. E. I. Koytsoumpa, C. Bergins and E. Kakaras, J. Supercrit. Fluids, 2018, 132, 3–16.
3. M. Sihvonen, E. Järvenpää, V. Hietaniemi and R. Huopalahti, Trends Food Sci. Technol., 1999, 10, 217–222.
4. F. M. Baena-Moreno, M. Rodrguez-Galán, F. Vega, B. Alonso-Fariñas, L. F. Vilches Arenas and B. Navarrete, Energy Sources, Part A, 2019, 41, 1403–1433.
5. Q. Yuan, X. Zhu, K. Lin and Y.-P. Zhao, Phys. Chem. Chem. Phys., 2015, 17, 31887–31893.
6. Q. Lyu, J. Tan, L. Li, Y. Ju, A. Busch, D. A. Wood, P. G. Ranjith, R. Middleton, B. Shu, C. Hu, Z. Wang and R. Hu, Energy Environ. Sci., 2021, 14, 4203–4227.
7. G. Brunner, Annu. Rev. Chem. Biomol. Eng., 2010, 1, 321–342.
8. Z. Zhang, S.-Y. Pan, H. Li, J. Cai, A. G. Olabi, E. J. Anthony and V. Manovic, Renewable Sustainable Energy Rev., 2020, 125, 109799.
9. J. F. Brennecke and C. A. Eckert, AIChE J., 1989, 35, 1409–1427.
10. A. Yu, W. Su, X. Lin and N. Zhou, Nucl. Eng. Technol., 2021, 53, 699–714.
11. B. Wetenhall, H. Aghajani, H. Chalmers, S. Benson, M. Ferrari, J. Li, J. Race, P. Singh and J. Davison, Energy Procedia, 2014, 63, 2764–2778.
12. M. Bui, C. S. Adjiman, A. Bardow, E. J. Anthony, A. Boston, S. Brown, P. S. Fennell, S. Fuss, A. Galindo, L. A. Hackett, J. P. Hallett, H. J. Herzog, G. Jackson, J. Kemper, S. Krevor, G. C. Maitland, M. Matuszewski, I. S. Metcalfe, C. Petit, G. Puxty, J. Reimer, D. M. Reiner, E. S. Rubin, S. A. Scott, N. Shah, B. Smit, J. P. M. Trusler, P. Webley, J. Wilcox and N. Mac Dowell, Energy Environ. Sci., 2018, 11, 1062–1176.
13. A. Imre, U. Deiters, T. Kraska and I. Tiselj, Nucl. Eng. Des., 2012, 252, 179–183.
14. J.-P. Bazile, D. Nasri, A. W. S. Hamani, G. Galliero and J.-L. Daridon, J. Supercrit. Fluids, 2018, 140, 218–232.
15. J.-P. Bazile, D. Nasri, A. W. Saley Hamani, G. Galliero and J.-L. Daridon, J. Chem. Eng. Data, 2019, 64, 3187–3204.
16. J.-P. Bazile, D. Nasri, G. Galliero and J.-L. Daridon, J. Chem. Eng. Data, 2021, 66, 3245–3257.
17. M. Raju, D. T. Banuti, P. C. Ma and M. Ihme, Sci. Rep., 2017, 7, 1–10.
18. Dortmund Data Bank, 2019, accessed on December 15, 2021, http://www.ddbst.com.
19. K. Nishikawa and I. Tanaka, Chem. Phys. Lett., 1995, 244, 149–152.
20. G. Simeoni, T. Bryk, F. Gorelli, M. Krisch, G. Ruocco, M. Santoro and T. Scopigno, Nat. Phys., 2010, 6, 503–507.
21. P. F. McMillan and H. E. Stanley, Nat. Phys., 2010, 6, 479–480.
22. F. Maxim, C. Contescu, P. Boillat, B. Niceno, K. Karalis, A. Testino and C. Ludwig, Nat. Commun., 2019, 10, 1–11.
23. P. Gallo, D. Corradini and M. Rovere, Nat. Commun., 2014, 5, 1–6.
24. M. Y. Ha, T. J. Yoon, T. Tlusty, Y. Jho and W. B. Lee, J. Phys. Chem. Lett., 2018, 9, 1734–1738.
25. A. S. Raman, H. Li and Y. Chiew, J. Chem. Phys., 2018, 148, 014502.
26. K. Karalis, C. Ludwig and B. Niceno, Sci. Rep., 2019, 9, 1–10.
27. Y. D. Fomin, V. Ryzhov, E. Tsiok and V. Brazhkin, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 022111.
28. T. Bryk, F. Gorelli, I. Mryglod, G. Ruocco, M. Santoro and T. Scopigno, J. Phys. Chem. Lett., 2017, 8, 4995–5001.
29. V. V. Brazhkin, C. Prescher, Y. D. Fomin, E. N. Tsiok, A. G. Lyapin, V. N. Ryzhov, V. B. Prakapenka, J. Stefanski, K. Trachenko and A. Sapelkin, J. Phys. Chem. B, 2018, 122, 6124–6128.
30. E. A. Ploetz and P. E. Smith, J. Phys. Chem. B, 2019, 123, 6554–6563.
31. J. Proctor, C. Pruteanu, I. Morrison, I. Crowe and J. Loveday, J. Phys. Chem. Lett., 2019, 10, 6584–6589.
32. E. de Jesús, J. Torres-Arenas and A. Benavides, J. Mol. Liq., 2021, 322, 114529.
33. D. Banuti, M. Raju and M. Ihme, Phys. Rev. E, 2017, 95, 052120.
34. D. Banuti, M. Raju and M. Ihme, J. Supercrit. Fluids, 2020, 165, 104895.
35. A. R. Imre, A. Groniewsky, G. Györke, A. Katona and D. Velmovszki, Period. Polytech., Chem. Eng., 2019, 63, 276–285.
36. P. Schienbein and D. Marx, Phys. Rev. E, 2018, 98, 022104.
37. T. J. Yoon, M. Y. Ha, W. B. Lee and Y.-W. Lee, J. Chem. Phys., 2019, 150, 154503.
38. E. I. Mareev, A. P. Sviridov and V. M. Gordienko, Int. J. Mol. Sci., 2021, 22, 9813.
39. G. Franzese and H. E. Stanley, J. Phys.: Condens. Matter, 2007, 19, 205126.
40. L. Xu, P. Kumar, S. V. Buldyrev, S.-H. Chen, P. H. Poole, F. Sciortino and H. E. Stanley, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 16558–16562.
41. D. Corradini, M. Rovere and P. Gallo, J. Chem. Phys., 2015, 143, 114502.
42. I. H. Bell, G. Galliero, S. Delage-Santacreu and L. Costigliola, J. Chem. Phys., 2020, 152, 191102.
43. I. H. Bell, S. Delage-Santacreu, H. Hoang and G. Galliero, J. Phys. Chem. Lett., 2021, 12, 6411–6417.
44. R. S. Chatwell, G. Guevara-Carrion, Y. Gaponenko, V. Shevtsova and J. Vrabec, Phys. Chem. Chem. Phys., 2021, 23, 3106–3115.
45. J. W. Ackerman, J. Heat Transfer, 1970, 92, 490–497.
46. D. Banuti, Period. Polytech., Chem. Eng., 2019, 63, 270–275.
47. P. E. Lapenna, Phys. Fluids, 2018, 30, 077106.
48. B. Zhu, J. Xu, C. Yan and J. Xie, Int. J. Heat Mass Transfer, 2020, 148, 119080.
49. F. Maxim, K. Karalis, P. Boillat, D. T. Banuti, J. I. Marquez Damian, B. Niceno and C. Ludwig, Adv. Sci., 2021, 8, 2002312.
50. V. V. Brazhkin, A. G. Lyapin, V. N. Ryzhov, K. Trachenko, Y. D. Fomin and E. N. Tsiok, Physics, 2012, 55, 1061–1079.
51. V. Brazhkin, Y. D. Fomin, A. Lyapin, V. Ryzhov and K. Trachenko, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 031203.
52. V. Brazhkin, Y. D. Fomin, A. Lyapin, V. Ryzhov, E. Tsiok and K. Trachenko, Phys. Rev. Lett., 2013, 111, 145901.
53. T. J. Yoon, L. A. Patel, T. Ju, M. J. Vigil, A. T. Findikoglu, R. P. Currier and K. A. Maerzke, Phys. Chem. Chem. Phys., 2020, 22, 16051–16062.
54. M. Liu, J. Tang, S. Liu, D. Xi, L. Min, J. Zang, G. Liu, J. Wang, S. Huang and Y. Huang, J. Supercrit. Fluids, 2022, 183, 105554.
55. J. Xu, Y. Wang and X. Ma, Phys. Rev. E, 2021, 104, 014142.
56. O. Kunz and W. Wagner, J. Chem. Eng. Data, 2012, 57, 3032–3091.
57. G. Guevara-Carrion, S. Ancherbak, A. Mialdun, J. Vrabec and V. Shevtsova, Sci. Rep., 2019, 9, 1–14.
58. T. Merker, C. Engin, J. Vrabec and H. Hasse, J. Chem. Phys., 2010, 132, 234512.
59. A. Köster, M. Thol and J. Vrabec, J. Chem. Eng. Data, 2018, 63, 305–320.
60. J. Vrabec, J. Stoll and H. Hasse, J. Phys. Chem. B, 2001, 105, 12126–12133.
61. B. Eckl, J. Vrabec and H. Hasse, J. Phys. Chem. B, 2008, 112, 12710–12721.
62. G. Guevara-Carrion, T. Janzen, Y. M. Muñoz-Muñoz and J. Vrabec, J. Chem. Phys., 2016, 144, 124501.
63. S. Stephan, M. T. Horsch, J. Vrabec and H. Hasse, Mol. Simul., 2019, 45, 806–814.
64. T. Merker, J. Vrabec and H. Hasse, Soft Mater., 2012, 10, 3–25.
65. Y. M. Muñoz-Muñoz, C.-M. Hsieh and J. Vrabec, J. Phys. Chem. B, 2017, 121, 5374–5384.
66. T. Schnabel, J. Vrabec and H. Hasse, J. Mol. Liq., 2007, 135, 170–178.
67. J. Vrabec, Y.-L. Huang and H. Hasse, Fluid Phase Equilib., 2009, 279, 120–135.
68. C.-H. Kim, P. Vimalchand and M. D. Donohue, Fluid Phase Equilib., 1986, 31, 299–311.
69. M. S.-W. Wei, T. S. Brown, A. J. Kidnay and E. D. Sloan, J. Chem. Eng. Data, 1995, 40, 726–731.
70. M. K. Gupta, Y. H. Li, B. J. Hulsey and R. L. Robinson Jr, J. Chem. Eng. Data, 1982, 27, 55–57.
71. H. Inomata, K. Arai and S. Saito, Fluid Phase Equilib., 1987, 36, 107–119.
72. R. Fingerhut, G. Guevara-Carrion, I. Nitzke, D. Saric, J. Marx, K. Langenbach, S. Prokopev, D. Celný, M. Bernreuther and S. Stephan, et al. , Comput. Phys. Commun., 2021, 262, 107860.
73. R. Lustig, Mol. Simul., 2011, 37, 457–465.
74. R. Lustig, Mol. Phys., 2012, 110, 3041–3052.
75. Á. Madarász, A. Hamza, D. Ferenc and I. Bakó, J. Chem. Theory Comput., 2021, 17, 7187–7194.
76. M. Thol, G. Rutkai, A. Köster, R. Lustig, R. Span and J. Vrabec, J. Phys. Chem. Ref. Data, 2016, 45, 023101.
77. J. G. Kirkwood and F. P. Buff, J. Chem. Phys., 1951, 19, 774–777.
78. J. Milzetti, D. Nayar and N. F. van der Vegt, J. Phys. Chem. B, 2018, 122, 5515–5526.
79. P. Krüger, S. K. Schnell, D. Bedeaux, S. Kjelstrup, T. J. H. Vlugt and J.-M. Simon, J. Phys. Chem. Lett., 2013, 4, 235–238.
80. P. Ganguly and N. F. A. van der Vegt, J. Chem. Theory Comput., 2013, 9, 1347–1355.
81. A. W. S. Hamani, H. Hoang, T. Q. Q. Viet, J.-L. Daridon and G. Galliero, J. Supercrit. Fluids, 2020, 164, 104890.
82. P. G. Debenedetti, Chem. Eng. Sci., 1987, 42, 2203–2212.
83. M. S. Green, J. Chem. Phys., 1954, 22, 398–414.
84. R. Kubo, J. Phys. Soc. Jpn., 1957, 12, 570–586.
85. D. Alfe and M. J. Gillan, Phys. Rev. Lett., 1988, 81, 5161–5164.
86. I. C. Yeh and G. Hummer, J. Phys. Chem. B, 2004, 108, 15873–15879.
87. C. J. Leverant, J. A. Harvey and T. M. Alam, J. Phys. Chem. Lett., 2020, 11, 10375–10381.
88. E. Lemmon, I. H. Bell, M. Huber and M. McLinden, NIST Standard Reference Database 23: Reference Fluid Thermodynamic and Transport Properties-REFPROP, Version 10.0, National Institute of Standards and Technology, Gaithersburg, Maryland 20899, 2018.
89. R. Span, R. Beckmüller, S. Hielscher, A. Jäger, E. Mickoleit, T. Neumann, B. Pohl, S. M. Semrau and M. Thol, TREND. Thermodynamic Reference and Engineering Data 5.0, Lehrstuhl für Thermodynamik, Ruhr-Universität Bochum, 2021.
90. R. Span and W. Wagner, J. Phys. Chem. Ref. Data, 1996, 25, 1509–1596.
91. A. Laesecke and C. D. Muzny, J. Phys. Chem. Ref. Data, 2017, 46, 013107.
92. J. C. Chichester and M. L. Huber, NISTIR 6650: Documentation and assessment of the transport property model for mixtures implemented in NIST REFPROP (Version 8.0), US Department of Commerce, National Institute of Standards and Technology, 2008.
93. S. Artemenko, V. Mazur and P. Krijgsman, Near-critical and Supercritical Water and Their Applications for Biorefineries, Springer, Netherlands, Dordrecht, 2014, pp. 41–68.
94. D. Banuti, J. Supercrit. Fluids, 2015, 98, 12–16.
95. C. Yan, J. Xu, B. Zhu, X. He and G. Liu, Sci. China Technol., 2021, 64, 995–1006.
96. P. Carlès, J. Supercrit. Fluids, 2010, 53, 2–11.
97. J. Sengers and R. Perkins, Transport Properties of Fluids near Critical Points, Royal Society of Chemistry (RSC) Publishing, Cambridge, 2014.
98. R. A. Perkins and J. V. Sengers, Int. J. Thermophys., 2013, 34, 2046–2052.
99. P. Cipriani, M. Nardone and F. Ricci, Phys. B, 1997, 241, 940–946.
100. R. Fingerhut and J. Vrabec, Fluid Phase Equilib., 2019, 485, 270–281.
101. M. Požar, B. Lovrinčević, L. Zoranić, T. Primorac, F. Sokolić and A. Perera, Phys. Chem. Chem. Phys., 2016, 18, 23971–23979.

---

Footnote

† Electronic supplementary information (ESI) available: It includes technical details of the molecular dynamics simulations, finite size corrections as well as thermodynamic properties of the remaining scCO₂ mixtures. Numerical data of the pseudo-boiling analysis as well as the Widom line temperature of the scCO₂ mixtures are also given. Furthermore, transport and structural properties of the remaining scCO₂ mixtures are presented. See DOI: https://doi.org/10.1039/d2cp02701a

---