In-depth theoretical understanding of the chemical interaction of aromatic compounds with a gold nanoparticle

Abstract

Gold Nanoparticles (GNPs), owing to their unique properties and versatile preparation strategy, have been demonstrated to exhibit promising applications in diverse fields, which include bio-sensors, catalysts, nanomedicines and radiotherapy. Yet, the nature of the interfacial interaction of GNPs with their chemical environment remains elusive. Experimental vibrational spectroscopy can reveal different interactions of aromatic biological molecules absorbed on GNPs, that may result from changes in the orientation of the molecule. However, the presence of multiple functional groups and the aqueous solvent introduces competition, and complexifies the spectral interpretations. Therefore, our objective is to theoretically investigate the adsorption of aromatic molecules containing various functional groups on the surface of GNPs to comparatively study their preferred adsorption modes. The interaction between Au₃₂, as a model of GNPs, and a series of substituted aromatic compounds that includes benzene, aniline, phenol, toluene, benzoic acid, acetophenone, methyl benzoate, and thiophenol, is investigated. Our computed interaction energies highlight the preference of the aromatic ring to lie flat on the surface. The orientations of the molecules can be distinguished using infrared spectroscopy along with strong changes in intensity and significant shifts of some vibrational modes when the molecule interacts with the GNP. The interaction energy and the electron transfer between the nanoparticle and the aromatic molecule are not found to correlate, possibly because of significant back donation of electrons from GNPs to organic molecules as revealed by charge decomposition analysis. A thorough quantum topological analysis identifies multiple non-covalent interactions and assigns the nature of the interaction mostly to dative interactions between the aromatic ring and the GNP as well as dispersive interaction. Finally, energy decomposition analyses point out the role of the charge transfer energy contribution in the subtle balance of the different physical components.

---

1 Introduction

The interest in understanding the interaction between gold nanoparticles (GNPs) and their surroundings, which includes surface ligands and solvent, has recently increased significantly, owing to their tunability allowing the design and synthesis of materials with desired physical, chemical, and optical properties. These materials have a broad range of application, such as catalysis, nanomedicine, imaging, biosensors, etc.^1–6 The different orientation of ligands on the surface, as spectroscopically identified, depends on various factors such as coverage, surface charge, etc. and can affect significantly their physical and chemical properties.

With the development of surface sensitive spectroscopy techniques, such as surface enhanced Raman spectroscopy (SERS), Surface Plasmon Resonance (SPR), attenuated total reflection Fourier transform infrared (ATR-FTIR) and sum frequency generation (SFG), it is now possible to obtain structural information of the compounds interacting at the surface of nanoparticles.^7–14 The spectroscopic signatures provide information on the way biomolecules (proteins, lipids, and others) interact with nanoparticles, revealing whether the structural integrity is maintained or disrupted as they interact.^7,15–17 Nevertheless, interpretation of experimental data is often difficult as illustrated with infrared (IR) spectra that exhibit considerable vibrations along with band broadening. Also, the presence of solvent molecules can additionally induce an important difference between spectra of isolated or adsorbed molecules, making interpretation uncertain.

Also, there is still limited understanding on the underlying forces governing the interaction energy. Several computational studies investigate the interaction at the interface of nanoparticles with various molecules, such as oxygen, carbon monoxide, amino acids, etc.^18–23 However, these efforts have faced several challenges that include the complexity of nanoparticles in terms of size and shape, which result in different reactivity sites.

In this context, computational chemistry can provide insights at the atomistic scale. Within the quantum chemistry framework, there is still a size limitation for the systems under evaluation, despite the rapid development in the computational power. To mitigate this limitation, there are different computational methodologies available to enable the simulation of gold nanoparticles, such as the semi-empirical DFTB method,^24–26 classical force fields^22,27,28 and coarse grained models,^29,30 with increasing level of approximations introduced respectively. Therefore, these methodologies are generally developed relying on more accurate methods acting as a reference to ensure their reliability. Here, an in-depth DFT level investigation is performed to study the interaction between gold nanoparticles with aromatic organic molecules, including the dominant physical origins of the interaction energies. The achieved understanding might help the development of simplified, empirical methods: the strength and physical origin of the interactions are valuable guides for choosing the most appropriate approaches between (polarized) force fields, tight-binding methods and machine-learning potentials.

Our previous work on the interaction with a series of small organic molecules has indicated that benzene prefers to adopt a flat configuration (with the aromatic plane interacting parallel to the surface of GNP).³¹ This could be attributed to the optimized interaction between the HOMO of benzene and LUMO of GNP, as well as the maximization of dispersion interactions. However, previous studies of aromatic containing compounds deposited on metal surfaces have indicated that the aromatic plane is not always adsorbed in a parallel configuration.^8,12,13,32 They could adopt either a perpendicular configuration or a tilted orientation with respect to the plane of the surface. Contributing factors include, among others, the presence of functional groups, that either alter the electron density of the aromatic compound, introduce steric effects or lead to stronger “direct” interactions because of high ligand affinity for gold. Considering the extensive presence of aromatic containing systems across diverse fields, i.e. materials science, enzyme design, etc., it is important to understand the interactions between GNPs and aromatic compounds, in particular the substituent effect on the preferred adsorption geometries.

In this work, we are systematically investigating the interaction of a series of substituted aromatic compounds, i.e. benzene, benzoic acid, acetophenone, ethyl benzoate, toluene, phenol, aniline, and thiophenol, on Au₃₂, which is taken as the GNP model (Fig. 1). As the study is performed in the gas phase, benzoic acid and thiophenol are protonated whereas aniline is not protonated (NH₂ group). These forms are not the ones usually present in experimental conditions in solution. The icosahedral strucutre of Au₃₂ has been taken from the literature without further change.³³ Initially, the aromatic compounds are placed in at least two different configurations, called “flat” and “perpendicular” (see Fig. 1). The complexes are then optimized without constraints and subsequently, the IR spectra are computed. The effect of the interaction with GNP is studied in detail by examining the modification of the vibrational modes of the aromatic molecule. Finally, different topological and energy decomposition analyses are performed to probe the nature of the interactions. The comparison between the different approaches leads to a more precise description of the equilibrium of the terms that compose the chemical interaction.

Fig. 1 (a) Schematic representation of aromatic compounds adsorbed on Au₃₂ adopting flat configuration “F” (left) or perpendicular configuration “P” (right). (b) Aromatic molecules and their abbreviations.

2 Methodology

2.1 DFT calculations

DFT calculations have been performed with the GGA/PBE functional associated with the D3 dispersion correction³⁴ using deMon2k,^35,36 unless otherwise mentioned. Gold atoms are described with a relativistic effective core potential (RECP), either with small core (SC), i.e. 60 core electrons, or with large core (LC), i.e. 68 core electrons, and their associated valence basis sets. The organic atoms are described with DZVP basis set. The deMon2k code, which is based on variational fitting of Coulomb potential, uses an auxiliary density to calculate the exchange-correlation contributions, resulting in significant acceleration in computation time. The criteria for SCF and auxiliary density convergences are set to 1.0 × 10⁻⁹ a.u and 1.0 × 10⁻⁷ a.u, respectively. The geometry optimizations of each of the complexes have been performed without constraints, with the convergence criterion for RMS gradient set to be 1.0 × 10⁻⁵ a.u. Since the LC-RECP optimized geometry of Au₃₂ interacting with benzene is similar to the one obtained with SC-RECP, (Au–benzene distance differs by 0.06 Å), the LC-RECP has been used for the optimization of all the other complexes, with a significant reduction in the computational cost.

The interaction energy, E_int, was obtained for the optimized geometries via:

E_int = E_sys − E_GNP,sys − E_org,sys (1)

with E_sys the energy of the global system, E_GNP,sys the electronic energy of Au₃₂, and E_org,sys the electronic energy of the respective organic molecule at the geometry of the full system. The adsorption energies of the complexes, which take into account the deformation energy, are provided in ESI† and differ by 3 kcal mol⁻¹ in average compared to the interaction energies (GNP contributes to 80% of the deformation energy). The charge transfer (CT) was obtained by subtracting the total charge of Au₃₂ with and without the adsorbate using different population schemes. Vibrational frequencies have been computed analytically for each of the optimized complexes with the LC-RECP/DZVP basis sets to obtain the IR spectra, which have been plotted with a Lorentzian line shape and half-width value of 1 cm⁻¹.³⁷

Due to convergence issues in deMon2k, the impact of the basis set superposition error (BSSE) has been estimated with the counterpoise method with Orca package.³⁸ The Au atom is described by the SC-RECP and its associated valence basis set, while the other atoms are described by def2-SVP or def2-TZVP basis set. The calculated BSSE values are reported in Table S2 and Fig. S2 in ESI.† The calculated BSSE using the TZ basis set is small and regular (∼2.5 kcal mol⁻¹), so the interaction energies have not been corrected from here onwards. While the impact of the basis set for the adsorbate geometry and the interaction energy is small (DZVP vs. TZVP), the interaction energies computed with LC-RECP are significantly overestimated as compared to SC-RECP, as well as the results from Orca (see Table S2 and Fig. 2).

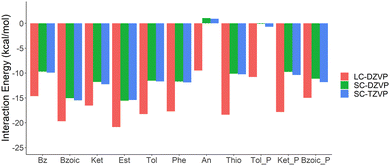Fig. 2 Uncorrected interaction energy calculated with LC-RECP/DZVP, SC-RECP/DZVP, and SC-RECP/TZVP for the various organic compounds. “P” stands for perpendicular.

2.1.1 Condensed Fukui analysis of Au₃₂. Au₃₂, as shown in Fig. S1 (ESI†), is an icosahedral fullerene-like nanostructure, first computationally predicted to be stable by Johansson et al.³³ Since then, several works have been done with Au₃₂ as the starting model to study the interaction between GNP with amino acids²⁰ and small molecules (CO, H₂, O₂).^39,40 To assess the reactivity of Au₃₂, the condensed Fukui function has been computed using an analytical approach, as implemented in deMon2k.³⁶ It allows to localize the electrophilic and nucleophilic sites at the surface, and the results are shown in Table S1 (ESI†).^41,42 Due to the high symmetry, this nanoparticle contains 20 six-coordinated and 12 five-coordinated gold atoms. The condensed Fukui value of all the five-coordinated gold atoms is greater than 0, which means that they are electrophilic sites and susceptible to interact with nucleophilic species. On the other hand, the six-coordinated gold atoms are mostly nucleophilic sites, susceptible to interact with electrophilic species. This assessment agrees with previous molecular electrostatic potential study by Wang et al.⁴³

2.2 Topological analyses

All of the topological analyses have been carried out within Multiwfn code,⁴⁴ except for the quantification of non-covalent interaction (NCI) basins, which has been performed with NCIplot4.⁴⁵

Quantum Theories of Atoms in Molecule (QTAIM). The QTAIM approach, developed by Bader and coworkers,^46,47 provides a robust way to study chemical bonding, based on partitioning of electron density in terms of the basins of attractors of the density gradient field. Within this framework, we can search for bond critical points and their associated bond paths, that are representative of the interaction. The characterization of this interaction is then made possible by calculating the local properties, such as electron density, Laplacian of the electron density, and energy density, according to the classification reported by Bianchi and coworkers.⁴⁸

Non-covalent interaction analysis (NCI). With the NCI analysis, developed by Johnson et al.,⁴⁹ the intermolecular non-covalent interactions can be identified based on the reduced density gradient, while the strength of the interaction is characterized by the multiplication of the sign of the second eigenvalues of the Hessian matrix with the electron density. This analysis results in qualitative visualization of the interaction basins, color coded based on the strength of the interaction. Furthermore, with the recent implementation in NCIplot4,⁴⁵ the interaction basins can be further decomposed into different types of interactions, and they are then integrated to produce quantitative results.

2.3 Energy and charge decomposition analyses

The energy decomposition analysis (EDA) has been performed based on two different approaches, which are the Block-Localized Wavefunction energy decomposition analysis (BLW-EDA), as implemented in CP2K,^50,51 and Symmetry Adapted Perturbation Theory (SAPT) at HF level with density fitting, as implemented in PSI4 and named SAPT0.^52–54 For the sake of simplicity, the SAPT0 results will be referred to as SAPT in the following text.

BLW-EDA is based on the absolutely localized molecular orbitals (ALMO) and defines molecules in terms of “blocks” of basis functions, inhibiting any exchange or sharing of electrons between blocks. The interaction energy calculated with BLW-EDA is defined in the eqn (2), and it can be decomposed into polarization (pol), charge transfer (CT), and frozen terms. The sum of frozen and polarization terms is called BLW. E_GNP,sys and E_org,sys correspond to the energy of the GNP and organic fragment in their final geometry adopted in the presence of the other fragment. E_guess is the systems energy obtained by a superposition of the fragment density matrices. E_BSSE corresponds to basis set superposition error estimated in the counterpoise procedure.

E_int = E_frozen + E_pol + E_CT = E_BLW + E_CT

E_frozen = E_guess − E_GNP,sys − E_org,sys

E_pol = E_BLW − E_guess

E_CT = E_sys − E_BLW − E_BSSE (2)

Here, we define two blocks, one for the GNP and one for the aromatic adsorbate. Since the polarization of each block in the presence of the other is computed variationally, this method allows rigorous separation between polarization and charge transfer contributions.⁵⁰ The frozen term describes the interaction between isolated fragment densities, which encompasses electrostatic, repulsive, and dispersive contributions.⁵⁵ For this calculation, we applied PBE-D3 level of theory, using the MOLOPT-DZVP basis set for valence electrons and Goedecker, Teter, and Hutter (GTH) pseudopotentials. For Au atoms, the 11 valence electron potential is used. The electron smearing was approximated at 300 K by Fermi–Dirac distribution. Note that this setup closely follows a previous publication, where it has been shown to yield analogous results to plane-wave basis set computations using VASP.⁵⁶

SAPT, on the other hand, treats the interaction energy as the perturbation introduced to the Hamiltonian of the isolated monomer, as it interacts in a dimer. The simplest SAPT method, is SAPT0, whose interaction energy can be defined as:

E^SAPT0_int = E⁽¹⁾_elec + E⁽¹⁾_exch + E⁽²⁾_ind + E⁽²⁾_disp (3)

This interaction can be decomposed into meaningful physical components, which are electrostatic (E_elec), exchange (E_exch), induction (E_ind) and dispersion (E_disp). In eqn (3), superscripts (1) and (2) indicate the first and second order terms, respectively. The electrostatic component contains both the interpenetration of the charge clouds and Coulombic interactions. The exchange interaction arises from the overlap of the monomer wave functions and the requirement of a fermionic antisymmetric wave function in the dimer. The induction includes both the polarization response and charge transfer. Dispersion results from the dynamical correlation of electrons between the two monomers. Being the simplest method, SAPT0 has the largest mean absolute error as compared to the other SAPT methods. But, considering the relatively low computational cost, this method has been applied. The SAPT analysis has been performed with density fitting, frozen core, and def2-TZVP basis set. Gold atom has been described with SC-RECP and its associated valence basis set.

Lastly, the charge decomposition analysis (CDA), as developed by Dapprich and Frenking and implemented in Multiwfn,⁵⁷ constructs the molecular orbital of complexes by linear combinations of the fragment orbitals. This approach allows the quantification of charge transfer between donor and acceptor (donation, back donation, and polarization term). Furthermore, it also gives insight into which molecular orbitals of the isolated fragments play significant role in the formation of the complex.

3 Results and discussion

3.1 Geometry and electronic structure analysis

3.1.1 Flat configuration. The optimized structures of the complexes adopting flat configurations at the DFT level are shown in Fig. 3 in the order of increasing interaction energy. In overall, there is an increase of the interaction energy with the addition of functional groups on benzene. An increase of the interaction energy in the dimer of substituted benzene has been previously observed and rationalized.^58,59 Thus, the observed increase for the complexes studied here could similarly be attributed to the additional direct dispersive and electrostatic interactions between the substituent groups and Au₃₂. A closer look at the orientation of the aromatic compounds on the surface of Au₃₂ reveals quite different orientations depending on the substituent groups (see Fig. S3, ESI†). Benzene, phenol, toluene, and aniline are showed to adopt a slightly tilted orientation. Meanwhile, benzoic acid and thiophenol are revealed to adopt a more flat configuration, where the aromatic plane is almost parallel to the surface of Au₃₂. This could arise due to the stronger interaction between their respective functional groups (–COOH and –SH) with the gold surface atoms. Acetophenone, on the other hand, is tilted away from the surface of GNP, to favor the interaction between carbonyl group with the gold surface atoms. Ethyl benzoate is planar in gas phase but it rearranges itself in favor of interactions with the –CH₂–CH₃ group. This rearrangement results in the phenyl group to be tilted away from the surface of GNP. Moreover, other higher-energy conformations have been obtained and are provided in ESI† (see Fig. S4).

Fig. 3 Interaction of substituted aromatic compounds with Au₃₂ adopting a flat configuration of the aromatic ring, along with the interaction energy (in kcal mol⁻¹, black color) and the charge transfer with ADCH scheme (in e⁻, blue color).

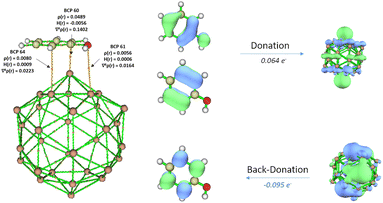
The CT has subsequently been obtained from the atomic dipole moment corrected Hirshfeld (ADCH) population scheme and is provided in Fig. 3. In general, there is a net electron transfer from the organic compound to the GNP, which demonstrated the electrophilicity of GNP. However, there seems to be a weak correlation between the interaction energy and CT (R² of 0.68, see Fig. S5, ESI†). In particular, the CT calculated for acetophenone and ethyl benzoate are smaller compared to the one for benzoic acid, despite their stronger interaction energy. We have additionally performed population analysis with different schemes for comparison (see Fig. S6 and S7 in ESI†). All schemes produce consistent result in regards to the electrophilicity of GNP, but the different schemes result in different amount of CT, in line with the non-uniqueness of the definition of atomic charges.⁶⁰ Reassuringly, regardless of the population schemes a weak correlation is found between the interaction energy and CT.

We have also performed charge decomposition analysis (CDA) to decompose the electron donation and back donation, as well as for the identification of the interacting molecular orbitals (see Table S4 and Fig. 4, Fig. S8–S15 in ESI†). Firstly, the molecular orbitals of the aromatic molecules are in general delocalized throughout the ring and the functional groups. They tend to overlap with the unoccupied molecular orbitals of GNP, leading to a favorable flat orientation (see Fig. S8, ESI†). Secondly, the analysis shows a small contribution of electron back donation the HOMO of GNP to the LUMO of the aromatic molecule. The synergy between donation and back donation eventually results in stronger interaction energy. However, the interpretation of the charge transfer becomes less straightforward.

Fig. 4 BCPs calculated within the QTAIM framework, along with the values of local properties, for flat configuration of phenol (left). The interacting molecular orbitals of phenol and GNP, as obtained within CDA framework (right).

3.1.2 Perpendicular configuration. The optimized geometries of the complexes adopting perpendicular configuration are shown in Fig. 5. Most of the compounds relaxed back to the flat orientation during the optimization but some of them have a local minimum with perpendicular orientation. In this adsorption mode, the interactions are formed with the substituents, and not with the phenyl ring. The interaction mode through the phenyl ring, with hydrogen pointing towards the GNP surface, also relaxes back to the flat configuration. In the cases of toluene and acetophenone, the perpendicular mode results in a much weaker interaction compared to the flat counterpart. On the other hand, the interaction between GNP and the –COOH functional group is shown to be more favorable compared to the flat counterpart. This implies the stronger interaction between carboxylic functional groups in comparison to benzene. The amount of CT for this interaction mode is also shown in Fig. 5 and is smaller in quantity as compared to that of the flat counterpart, in line with our earlier observation that CT and interaction energy are not correlated.

Fig. 5 Interaction of substituted aromatic compounds with Au₃₂ adopting perpendicular configuration of the aromatic ring, along with the interaction energy (in kcal mol⁻¹, black color) and the charge transfer with ADCH scheme (in e⁻, blue color).

The charge decomposition analysis shows that the molecular orbital of organic molecule participating in the complex formation is localized on the functional groups (see Fig. S9, S10, and S12 in ESI†). Although electron donation is dominating, back donation also participates to the stabilization of adsorption modes.

3.2 Vibrational analysis

Greenler, et al. previously proposed the surface selection rule of molecules adsorbed on small metal particles for IR spectra.⁶¹ Furthermore, Schunke et al. investigated the influence of the adsorption orientation of halobenzene on copper surfaces via infrared spectroscopy experiments.³² In this work, frequency calculations have been performed to simulate the vibrational IR spectra of the isolated molecules and the complexes, and to investigate how the interaction with GNP affects the IR spectra. This insight would be helpful to structural identification in experimental IR spectra.

Our general observation is that firstly, some IR inactive vibrational modes for the isolated molecule have become active. This can be seen clearly in the IR spectrum of benzene adsorbed on GNP in Fig. 6. Due to its high symmetry, only few vibrational modes are IR active in the free molecule. Upon interacting with GNP, several modes between 750 cm⁻¹ and 1000 cm⁻¹, assigned to C–H aromatic bending modes, have become IR active due to symmetry breaking. Secondly, it is interesting to observe that the intensity of C–H aromatic stretching modes of benzene (at ca. 3100 cm⁻¹) have been significantly reduced, as compared to the isolated one (37 km mol⁻¹ for isolated benzene vs. <5 km mol⁻¹ for adsorbed benzene). Such observation has consistently been made for all the aromatic compounds adopting flat configurations. Thirdly, the functional groups that interact closely with GNP, or acting as the anchor, undergo quite significant frequency shifts, as can be seen in the case of most of the complexes under study. In the case of toluene, for example, the –CH₃ moiety interacts closely with GNP, for both flat and perpendicular configurations. As such, the frequency corresponding to the –CH₃ stretching (see Fig. 6) has been considerably red shifted, i.e. from 2981 cm⁻¹ in isolated toluene to 2942 cm⁻¹ in the flat complex and 2936 cm⁻¹ in the perpendicular complex. In the case for thiophenol, where –SH interacts strongly with GNP, the frequency corresponding to the –SH stretching mode has red shifted as well, from 2634 cm⁻¹ in isolated to 2627 cm⁻¹ in the complex (see Fig. 6). Similar observations have been made for acetophenone and benzoic acid (see Fig. S19 and S20 in ESI†), where the C=O stretching mode has considerably shifted due to its relatively strong interaction with GNP, i.e. from 1694 cm⁻¹ in isolation to 1640 cm⁻¹ in flat complex and 1705 cm⁻¹ in perpendicular complex in acetophenone, and from 1741 cm⁻¹ in isolation to 1678 cm⁻¹ in flat complex and to 1664 cm⁻¹ in perpendicular complex in benzoic acid.

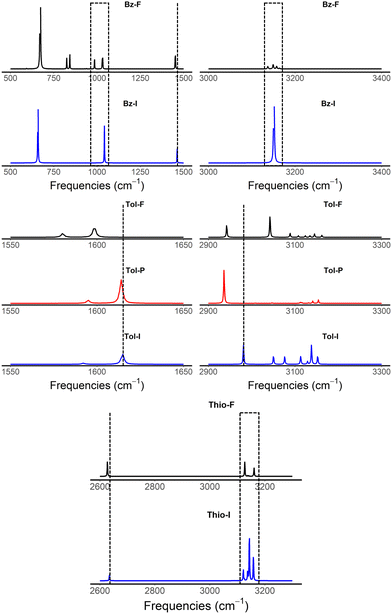Fig. 6 IR computed spectra of benzene, toluene and thiophenol isolated (I in blue) and adsorbed on Au₃₂ (A). “F” (in black) and “P” (in red) stand for flat and perpendicular, respectively.

Moreover, a published FTIR experiment on thiophenol functionalized gold nanoparticles found CH stretching vibration modes (the strongest of which was at 3057 cm⁻¹) in reasonably well agreement with our unscaled calculated frequencies in the region of 3100–3200 cm⁻¹.⁶² These peaks were not detectable in thiophenol solutions when the gold nanoparticles were absent, hence demonstrating that thiophenol interacts with gold nanoparticles.

3.3 Topological analysis

3.3.1 Quantum theory of atoms in molecule. Within the QTAIM framework, bond critical points (BCPs) and their associated bond paths have been identified for each of the optimized complexes. The local properties, i.e. the electron density, the Laplacian, and the energy density, calculated at the respective BCPs, are shown in Fig. 4, Fig. S16 and S17, and tabulated in Table S5 in ESI.†

Flat configuration. When aromatic compounds adopt the flat configuration, multiple BCPs have been found. For benzene, two BCPs are found, one classified as dative and the other as dispersive interactions. The addition of functional groups subsequently results in an increased number of BCPs, associated to stronger interaction energies. This observation is in agreement with general observations of substituent effects on interaction energies and for adsorption energies on metal surfaces, and can be rationalized by the direct interaction between the functional groups and the GNP surface.^58,63 In the cases of toluene, phenol, and aniline, one BCP is found in between the –CH₃, –OH, and –NH₂, respectively, and the interaction is classified as dispersion. In the cases of benzoic acid and thiophenol, the –COOH and –SH functional groups both form strong dative interactions with GNP. Meanwhile, in the cases of both acetophenone and ethyl benzoate, as discussed earlier, the aromatic ring does not lie flat on the surface of GNP and only one BCP corresponding to the interaction between aromatic moiety and GNP has been found. The functional groups, on the other hand, form rather strong interaction with the surface, according to the local properties of the BCP. Furthermore, it can be deduced from this analysis that the carbonyl and thiol functional groups form stronger interaction with the surface, as compared to the hydroxyl and amine functional groups.

Perpendicular configuration. For the molecules adsorbed in a perpendicular configuration, only a few BCPs exist. In the cases of toluene and acetophenone, only one BCP has been found, between GNP and –CH₃ and –COCH₃, respectively. Based on the essentially zero interaction energy and basic chemical principles, they correspond to a very weak dispersion interaction between the adsorbate and the GNP. As for benzoic acid, two BCPs have been found for both C=O and O–H, with the interaction classified as dative with the one formed with C=O being stronger than O–H, an expected result based on the availability of oxygen electron lone-pairs to interact with the GNP.

3.3.2 Non-covalent interaction analysis. Since QTAIM analysis has indicated the non-covalent nature of the interactions, NCI analysis⁴⁹ is used to obtain a visualization and spatial understanding of these non-covalent interactions. Fig. 7 and 8 show the intermolecular NCI results of the optimized complexes, with the basins color-coded to represent the strength and the nature of the interaction (red representing repulsive interactions, green representing dispersion interactions, and blue representing dative interactions). By construction, the position of the basins found in NCI corresponds the calculated BCPs.

Fig. 7 NCI analysis of the aromatic molecules adsorbed on Au₃₂ in a flat configuration, and the associated color code: from left to right, benzene, benzoic acid, acetophenone, ethylbenzoate, toluene, phenol, aniline, and thiophenol.

Flat configuration. For the complexes adopting a flat configuration, multiple delocalized interaction basins have been found. For benzene, there are two delocalized basins, with one stronger dative interaction and the other a dispersive interaction. Similarly, by adding substituents, these two delocalized basins are still generally present in the flat configuration. In addition to these two delocalized basins, there are additional interactions formed between the functional groups and the GNP. The –OH, –NH₂, –CH₃ in phenol, aniline and toluene form dispersive interaction with GNP. On the other hand, the –COOH and –SH functional groups in benzoic acid and thiolbenzene form a rather strong dative interaction. As for ethyl benzoate and acetophenone, ester and ketone functional groups form multiple non-covalent interactions that caused the phenyl ring to form only one interaction with the GNP.

Perpendicular configuration. For the perpendicular configuration, and similar to QTAIM analysis, lesser number of interaction basins have been found (see Fig. 8). The non-covalent basins are present for the CH₃ moiety for both toluene and acetophenone. For benzoic acid, two interaction basins are found between the carboxylic acid functional groups and the GNP, i.e. one for the C=O and one for –OH.

Fig. 8 NCI analysis of the aromatic molecules adsorbed on Au₃₂ in a perpendicular configuration, see Fig. 7 for the color code: toluene, acetophenone, and benzoic acid.

Quantification of NCI basins. The NCI basins have been integrated for quantitative analysis and tabulated in Table S6 in (ESI†). Fig. 9 shows the integrated volumes based on the decomposition terms: dative interaction (in blue), dispersive interaction (in green), and repulsive interaction (in red) for each system. Based on this analysis, the total interaction is a subtle interplay between the three terms. Since Fig. 9 shows largest volume integral for the dispersive basins, the interaction between aromatic system and Au₃₂ is driven by dispersive interactions. Additionally, the dative interaction is increasing for all of the substituted benzene, as compared to that of benzene. In some cases, it can be attributed to the additional blue basins formed by the functional groups (i.e. –C=O of benzoic acid, –C=O of acetophenone, –CH₃ of ethylbenzoate, and –SH of thiophenol) as seen in Fig. 7. In the cases of toluene, phenol, and aniline, however, the dative interaction is only observed for the interaction with the phenyl ring. This can then be related to the electron donating nature of these functional groups, that results in increased electron density of the phenyl ring, leading to an increase of dative interaction.

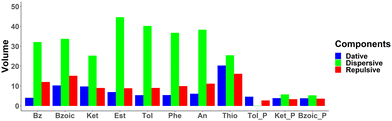Fig. 9 Integrated volumes of the NCI basins for the aromatic molecules for flat and perpendicular geometries adsorbed on Au₃₂.

The integrated total volume of NCI basins (summation of the volumes of all constituting basins), which could represent the strength of the interaction energy, is found to be moderately correlated with the interaction energy calculated above (see Fig. S23, R² = 0.60). In particular, the total volumes of NCI basins for benzoic acid in flat and perpendicular configurations (102.70 and 24.78, respectively) clearly do not reflect the change in the interaction energy (−9.8 vs. −11.1 kcal mol⁻¹). This qualitative disagreement might be due to an inaccurate description of the electrostatic interactions by the NCI basins. Interestingly, a strong correlation is, however, found between the volumes of the NCI basins and the CT (obtained with the ADCH scheme, see Fig. S23 in ESI,†R² = 0.91). This can be rationalized by the general observation of the distance dependence of charge transfer: the more contact there is between the two fragments at the equilibrium distance, the higher the charge transfer is expected to be, with the volumes of the NCI basins being a convenient measure for the contact volume. This is further corroborated by the correlation between the repulsive NCI basin volumes with the total NCI basin volumes (R² > 0.9, see Fig. S24), even though it is the smallest component (the volume corresponding to dispersion interactions are about twice as large).

3.4 Energy decomposition analysis (EDA)

To further understand the underlying contributing factors to the interaction from an energetic point of view, EDA has also been performed using two different approaches, i.e. BLW-EDA and SAPT. The total energies from BLW-EDA and SAPT correlate well with the interaction energy obtained previously (R² = 0.96 and 0.81, see Fig. 10).

Fig. 10 The correlation between the total interaction energy obtained with SAPT (top), BLW-EDA (bottom) with the interaction energy obtained with molecular approach.

BLW-EDA. Fig. 11 shows the contributing energy terms calculated with the BLW-EDA approach, i.e. frozen, polarization, and charge transfer, for each system. The frozen term is positive highlighting the dominant role of the Pauli repulsion contribution compared to electrostatic and dispersion contributions. This term is nearly constant across the series and, therefore, uncorrelated to the total interaction energy (see Fig. 11, R² = 0.54). This repulsive energy is only partially compensated by the favorable polarization and it is the charge transfer term that provides the actual stabilization. The functional groups generally increase the weight of polarization in the interaction, with –CO functional groups leading to the highest polarization as shown in the case of acetophenone and benzoic acid in a perpendicular configuration (see Fig. S26, ESI†). Similarly, the functional groups also affect the charge transfer energy, taking benzene as the reference. Except for –SH functional group, the effect is similar to that observed for polarization energy. Sulfur has a high tendency to form bonds with Au,⁶⁴ which rationalizes that the charge transfer contribution of the interaction between thiophenol and GNP is found to be the strongest.

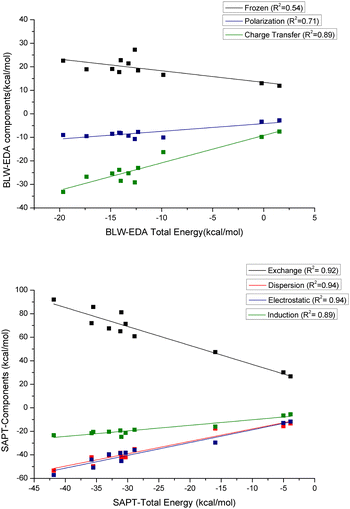Fig. 11 The correlation of the respective energy decomposition terms with respect to the total energy for the various complexes: (top) BLW-EDA, and (bottom) SAPT.

According to Fig. 11 and Fig. S28 (ESI†), and in contrast to our observations for water add-layers,⁵⁶ the polarization energy is neither sufficiently strong to off-set the Pauli repulsion, nor to induce a significant correlation between FRZ + POL (called BLW interaction energy) and the total interaction energy (R² = 0.14). For the GNP-aromatics interaction, it is the correlation between the charge transfer energy and the BLW-EDA energy that is found to be strong (R² = 0.89, see Fig. 11). This demonstrates the relative importance of charge transfer energy term as compared to polarization term for these systems. This is reminiscent of the correlation between the interaction energy and the ADCH analysis and indeed the two completely independent measures for CT are well correlated (R² = 0.80, see Fig. S27). In contrast, the correlation between CT and the dative NCI basins, which should describe a similar physics, is weak (R² = 0.41, see Fig. S29).

SAPT. Fig. 11 shows the energy terms calculated with SAPT approach, i.e. exchange energy, electrostatic energy, dispersion energy, and induction energy. As compared to DFT, the interaction energy obtained with SAPT is significantly (factor 2.85) more stabilizing. Our hypothesis is that the perturbative treatment of the dispersion energy is to blame for this overestimation: for metallic systems (small band-gap) low-order perturbation theory can be expected to lead to overestimations. The exchange energy represents the repulsion contribution, which is necessarily positive. According to SAPT both electrostatic and dispersion energies give a significant contribution to the total interaction energy, while induction energy is smaller in magnitude. As could have been expected, the sum of electrostatic and exchange energies from SAPT is well correlated with the frozen term of BLW-EDA (R² = 0.87, see Fig. S29, ESI†), even though the later also includes the dispersion-correction components of the DFT interaction energy. Given that all SAPT components correlate well (R² > 0.8) with the total interaction energy, it is difficult to distinguish which physical effects lead to increased interaction energy. Based on the above analysis (ADCH, BLW), one could have expected induction to be dominating, but according to the slopes with respect to the total interaction energy, dispersion is found to be much more significant. However, this has to be taken with caution, as the total interaction energy obtained with SAPT is significantly overestimated compared to the DFT results. This later originates probably in the perturbative treatment of dispersion. Note that in contrast to dispersion, the induction energy contains an “infinite order” correction terms, δ_HF, which leads to a near perfect (R² = 0.98) correlation with the sum of polarization and charge-transfer interactions as obtained by BLW-EDA. According to Fig. S29 in ESI,† the correlation between the repulsion energy from SAPT and the corresponding NCI basins is strong (R² = 0.80), while the agreement for the dispersive interaction energies is significantly lower (R² = 0.66). This highlights the difficulty to capture dispersion interactions solely based on the (reduced) density (gradient).

4 Conclusion

We have systematically and quantitatively investigated the chemical interaction between substituted aromatic compounds and Au₃₂ as a model of gold nanoparticles. These interactions mainly consist of multiple non-covalent interactions, with dative, dispersive, and repulsive nature. In general, the substituted aromatic compounds prefer to adopt a relatively flat configuration, where the aromatic ring lies almost parallel to the surface of Au₃₂, except for benzoic acid, where the interaction with the –COOH group is stronger than the interaction with the phenyl ring, resulting in a favorable perpendicular orientation. These flat and perpendicular orientations can be distinguished using vibrational spectroscopy, where the CH aromatic stretching modes are less IR active for the flat configuration. The interactions have further been quantitatively decomposed using NCI, BLW-EDA and SAPT analyses. Though these three methods adopt different approaches in the energy decomposition, we found strong agreement among them, and the results of this analysis could help in designing accurate force fields for gold nanoparticles based materials. In particular, our analysis has evidenced the importance of charge transfer, both in terms of interaction energy and in terms of transferred electrons, which impacts the medium-range electrostatic interactions with the environment (e.g., solvent).

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Dr Dominik Domin for his valuable technical assistance. This collaborative work was supported by GDR 2035 SolvATE, funded by CNRS. This work was performed using HPC resources from the GENCI (CINES/IDRIS, Grant no. 2021-A0100806830).

Notes and references

1. G. Li and R. Jin, Nanotechnol. Rev., 2013, 2, 529–545.
2. G. Han, P. Ghosh and V. M. Rotello, Nanomedicine, 2007, 2, 113–123.
3. S. Her, D. A. Jaffray and C. Allen, Adv. Drug Delivery Rev., 2017, 109, 84–101.
4. A. Corma and H. Garcia, Chem. Soc. Rev., 2008, 37, 2096–2126.
5. X. Hu, Y. Zhang, T. Ding, J. Liu and H. Zhao, Front. Bioeng. Biotechnol., 2020, 8, 1–17.
6. L. Pasquato, P. Pengo and P. Scrimin, J. Mater. Chem., 2004, 14, 3481–3487.
7. M. Iosin, F. Toderas, P. L. Baldeck and S. Astilean, J. Mol. Struct., 2009, 924–926, 196–200.
8. J. Gao, Y. Hu, S. Li, Y. Zhang and X. Chen, Spectrochim. Acta, Part A, 2013, 104, 41–47.
9. S. Hussain and Y. Pang, J. Mol. Struct., 2015, 1096, 121–128.
10. G. P. Szekeres and J. Kneipp, Analyst, 2018, 143, 6061–6068.
11. G. P. Szekeres and J. Kneipp, Front. Chem., 2019, 7, 30.
12. F. Madzharova, Z. Heiner and J. Kneipp, J. Phys. Chem. C, 2020, 124, 6233–6241.
13. F. Madzharova, Z. Heiner and J. Kneipp, J. Phys. Chem. C, 2017, 121, 1235–1242.
14. M. Moskovits, J. Chem. Phys., 1982, 77, 4408–4416.
15. I. Lynch and K. A. Dawson, Nano Today, 2008, 3, 40–47.
16. X. Toledo-Fuentes, D. Lis and F. Cecchet, J. Phys. Chem. C, 2016, 120, 21399–21409.
17. A. M. Engstrom, R. A. Faase, G. W. Marquart, J. E. Baio, M. R. Mackiewicz and S. L. Harper, Int. J. Nanomed., 2020, 15, 4091–4104.
18. X. Cheng, F. Li and C. Wang, Comput. Theor. Chem., 2016, 1097, 1–7.
19. G.-J. Kang, Z.-X. Chen and Z. Li, J. Chem. Phys., 2009, 131, 034710.
20. M. Darvish Ganji, H. Tavassoli Larijani, R. Alamol-hoda and M. Mehdizadeh, Sci. Rep., 2018, 8, 11400.
21. H. R. Abd El-Mageed and M. Taha, J. Mol. Liq., 2019, 296, 111903.
22. Q. Shao and C. K. Hall, Langmuir, 2016, 32, 7888–7896.
23. G. Yao and Q. Huang, J. Phys. Chem. C, 2018, 122, 15241–15251.
24. A. Fihey, C. Hettich, J. Touzeau, F. Maurel, A. Perrier, C. Köhler, B. Aradi and T. Frauenheim, J. Comput. Chem., 2015, 36, 2075–2087.
25. A. Domnguez-Castro, D. Hernández and F. Guzmán, Theor. Chem. Acc., 2017, 136, 84.
26. G. Fazio, G. Seifert, M. Rapacioli, N. Tarrat and J.-O. Joswig, Z. Phys. Chem., 2018, 232, 1583–1592.
27. O. A. Perfilieva, D. V. Pyshnyi and A. A. Lomzov, J. Chem. Theory Comput., 2019, 15, 1278–1292.
28. H. Heinz, K. C. Jha, J. Luettmer-Strathmann, B. L. Farmer and R. R. Naik, J. R. Soc., Interface, 2011, 8, 220–232.
29. M. S. Jahan Sajib, P. Sarker, Y. Wei, X. Tao and T. Wei, Langmuir, 2020, 36, 13356–13363.
30. F. Tavanti and M. C. Menziani, Int. J. Mol. Sci., 2021, 22, 8722.
31. R. Tandiana, N.-T. Van-Oanh and C. Clavaguéra, Theor. Chem. Acc., 2021, 140, 118.
32. C. Schunke, D. P. Miller, E. Zurek and K. Morgenstern, Phys. Chem. Chem. Phys., 2022, 24, 4485–4492.
33. M. P. Johansson, D. Sundholm and J. Vaara, Angew. Chem., Int. Ed., 2004, 116, 2732–2735.
34. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
35. G. Geudtner, P. Calaminici, J. Carmona-Espndola, J. M. d Campo, V. D. Domnguez-Soria, R. F. Moreno, G. U. Gamboa, A. Goursot, A. M. Köster, J. U. Reveles, T. Mineva, J. M. Vásquez-Pérez, A. Vela, B. Zúñinga-Gutierrez and D. R. Salahub, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 548–555.
36. R. Flores-Moreno, J. Melin, J. V. Ortiz and G. Merino, J. Chem. Phys., 2008, 129, 224105.
37. R. I. Delgado-Venegas, D. Meja-Rodrguez, R. Flores-Moreno, P. Calaminici and A. M. Köster, J. Chem. Phys., 2016, 145, 224103.
38. F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108.
39. Y. Wang and X. G. Gong, J. Chem. Phys., 2006, 125, 124703.
40. L. Fang, T. Chen, Y. Meng, Y. Wang, J. Xue, Z. Ni and S. Xia, Mol. Catal., 2020, 483, 110757.
41. C. Morell, A. Grand and A. Toro-Labbé, Chem. Phys. Lett., 2006, 425, 342–346.
42. T. C. Allison and Y. J. Tong, Phys. Chem. Chem. Phys., 2011, 13, 12858–12864.
43. D.-L. Wang, X.-P. Sun, H.-T. Shen, D.-Y. Hou and Y.-C. Zhai, Chem. Phys. Lett., 2008, 457, 366–370.
44. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
45. R. A. Boto, F. Peccati, R. Laplaza, C. Quan, A. Carbone, J.-P. Piquemal, Y. Maday and J. Contreras-Garcia, J. Chem. Theory Comput., 2020, 16, 4150–4158.
46. R. F. W. Bader, P. J. MacDougall and C. D. H. Lau, J. Am. Chem. Soc., 1984, 106, 1594–1605.
47. R. F. W. Bader, J. Phys. Chem. A, 1998, 102, 7314–7323.
48. R. Bianchi, G. Gervasio and D. Marabello, Inorg. Chem., 2000, 39, 2360–2366.
49. E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-Garcia, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506.
50. R. Staub, M. Iannuzzi, R. Z. Khaliullin and S. N. Steinmann, J. Chem. Theory Comput., 2019, 15, 265–275.
51. T. D. Kühne, M. Iannuzzi, M. Del Ben, V. V. Rybkin, P. Seewald, F. Stein, T. Laino, R. Z. Khaliullin, O. Schütt, F. Schiffmann, D. Golze, J. Wilhelm, S. Chulkov, M. H. Bani-Hashemian, V. Weber, U. Borštnik, M. Taillefumier, A. S. Jakobovits, A. Lazzaro, H. Pabst, T. Müller, R. Schade, M. Guidon, S. Andermatt, N. Holmberg, G. K. Schenter, A. Hehn, A. Bussy, F. Belleflamme, G. Tabacchi, A. Glöβ, M. Lass, I. Bethune, C. J. Mundy, C. Plessl, M. Watkins, J. VandeVondele, M. Krack and J. Hutter, J. Chem. Phys., 2020, 152, 194103.
52. D. G. A. Smith, L. A. Burns, A. C. Simmonett, R. M. Parrish, M. C. Schieber, R. Galvelis, P. Kraus, H. Kruse, R. Di Remigio, A. Alenaizan, A. M. James, S. Lehtola, J. P. Misiewicz, M. Scheurer, R. A. Shaw, J. B. Schriber, Y. Xie, Z. L. Glick, D. A. Sirianni, J. S. O'Brien, J. M. Waldrop, A. Kumar, E. G. Hohenstein, B. P. Pritchard, B. R. Brooks, H. F. Schaefer, A. Y. Sokolov, K. Patkowski, A. E. DePrince, U. Bozkaya, R. A. King, F. A. Evangelista, J. M. Turney, T. D. Crawford and C. D. Sherrill, J. Chem. Phys., 2020, 152, 184108.
53. B. Jeziorski, R. Moszynski and K. Szalewicz, Chem. Rev., 1994, 94, 1887–1930.
54. E. G. Hohenstein and C. D. Sherrill, J. Chem. Phys., 2010, 132, 184111.
55. S. N. Steinmann, C. Corminboeuf, W. Wu and Y. Mo, J. Phys. Chem. A, 2011, 115, 5467–5477.
56. P. Clabaut, R. Staub, J. Galiana, E. Antonetti and S. N. Steinmann, J. Chem. Phys., 2020, 153, 054703.
57. S. Dapprich and G. Frenking, J. Phys. Chem., 1995, 99, 9352–9362.
58. S. E. Wheeler and K. N. Houk, J. Am. Chem. Soc., 2008, 130, 10854–10855.
59. M. O. Sinnokrot and C. D. Sherrill, J. Am. Chem. Soc., 2004, 126, 7690–7697.
60. J. F. Gonthier, S. N. Steinmann, M. D. Wodrich and C. Corminboeuf, Chem. Soc. Rev., 2012, 41, 4671–4687.
61. R. G. Greenler, D. R. Snider, D. Witt and R. S. Sorbello, Surf. Sci., 1982, 118, 415–428.
62. C. Humbert, O. Pluchery, E. Lacaze, A. Tadjeddine and B. Busson, Gold Bull., 2013, 46, 299–309.
63. R. Réocreux, M. Huynh, C. Michel and P. Sautet, J. Phys. Chem. Lett., 2016, 7, 2074–2079.
64. H. Hakkinen, Nat. Chem., 2012, 4, 443–455.

---

Footnote

† Electronic supplementary information (ESI) available: Detailed results for Fukui calculations, BSSE effects, interaction energies, geometries, charge transfer from different populations schemes, CDA and QTAIM analysis, IR calculated spectra, NCI analysis, and SAPT and BLW energy decomposition analysis are provided in Supplementary Information. Separate files for the coordinates of the entire series of compound. See DOI: https://doi.org/10.1039/d2cp02654f

---