Analysis of the orientation of cholesterol in high-density lipoprotein nanodiscs using solid-state NMR

Abstract

Cholesterol is an essential component of eukaryotic cellular membranes that regulates the order and phase behaviour of dynamic lipid bilayers. Although cholesterol performs many vital physiological roles, hypercholesterolaemia and the accumulation of cholesterol in atherosclerotic plaques can increase the risk of coronary heart disease morbidity. The risk is mitigated by the transportation of cholesterol from peripheral tissue to the liver by high-density lipoprotein (HDL), 6–20 nm-diameter particles of lipid bilayers constrained by an annular belt of the protein apolipoprotein A-I (apoA-I). Information on the dynamics and orientation of cholesterol in HDL is pertinent to the essential role of HDL in cholesterol cycling. This work investigates whether the molecular orientation of cholesterol in HDL differs from that in the unconstrained lipid bilayers of multilamellar vesicles (MLVs). Solid-state NMR (ssNMR) measurements of dynamically-averaged ¹³C–¹³C and ¹³C–¹H dipolar couplings were used to determine the average orientation of triple ¹³C-labelled cholesterol in palmitoyloleoylphosphatidylcholine (POPC) lipid bilayers in reconstituted HDL (rHDL) nanodiscs and in MLVs. Individual ¹³C–¹³C dipolar couplings were measured from [2,3,4-¹³C₃]cholesterol in a one-dimensional NMR experiment, by using a novel application of a method to excite double quantum coherence at rotational resonance. The measured dipolar couplings were compared with average values calculated from orientational distributions of cholesterol generated using a Gaussian probability density function. The data were consistent with small differences in the average orientation of cholesterol in rHDL and MLVs, which may reflect the effects of the constrained and unconstrained lipid bilayers in the two environments. The calculated distributions of cholesterol in rHDL and MLVs that were consistent with the NMR data also agreed well with orientational distributions extracted from previous molecular dynamics simulations of HDL nanodiscs and planar POPC bilayers.

---

1. Introduction

Cholesterol is an important and fascinating building block of mammalian cell membranes that performs the essential roles of reinforcing membrane integrity and controlling membrane fluidity under physiological conditions and temperature.¹ In plasma membranes, cholesterol represents 30–50% of total lipid content,² but excessive accumulation in the vasculature in the form of atherosclerotic plaques can increase the risk of coronary artery disease and heart attacks. Consequently, cholesterol levels are subject to tight and complex physiological regulatory mechanisms.³ One important component of the regulatory toolkit is high-density lipoprotein (HDL), a heterogeneous ensemble of discoidal and spheroidal nanoparticles composed of bilayer phospholipids, triglycerides and cholesterol/cholesteryl esters surrounded by a belt of α-helical proteins, chiefly apolipoprotein A-I (apoA-I).

Nascent, lipid-poor discoidal (pre-β) HDL particles are formed when the ATP-binding cassette transporter A1 (ABCA1) facilitates the transfer of cholesterol and lipids from peripheral tissue to circulating apoA-I. Mature spherical HDL particles bind to the hepatocyte scavenger receptor SR-B1 and transfer cholesterol and its esters to the liver for excretion.⁴ Whilst the behaviour of cholesterol in model phospholipid membrane systems has been studied in depth, little is known about the properties of cholesterol in HDL particles. The morphological plasticity of HDL influences their lipid-binding properties and metabolism, and the surface curvature of the lipid cargo regulates interactions with cholesterol-handling enzymes.^5–8 Consequently, information on the dynamics and orientation of cholesterol in HDL is pertinent to its essential role in cholesterol cycling.⁴

A wealth of information on the physical properties of cholesterol and its effect on phospholipid bilayers has been gained by using solid-state NMR (ssNMR) spectroscopy with model membrane systems such as multilamellar vesicles (MLVs).^9–12 Wide-line and oriented ²H NMR of deuterated cholesterol has been used extensively to study the effects of cholesterol on membrane ordering,¹³ membrane deformation⁹ and dynamics.^14,15 Additionally, natural-abundance ¹³C–¹H NMR and ³¹P NMR have been used to study the segmental motions of cholesterol and phospholipids¹⁶ and the effects of cholesterol on the phase behaviour of lipid bilayers.^17,18 Cholesterol adopts, on average, an upright orientation approximately parallel with the lipid bilayer normal with the 3-OH group situated in the vicinity of the phospholipid glyceryl backbone and pointing toward the interface between the bilayer surface and the aqueous phase.^19–21 The molecule undergoes fast axial rotation in lipid bilayers and the amplitude of motions are described by a molecular order parameter, S_mol, which takes values from zero, indicating isotropic reorientation, to 1.0, indicating rotation about a single axis. NMR studies on cholesterol in model membranes typically report S_mol values of between 0.80 and 0.95,^11,12 dependent on temperature and physicochemical properties of the phospholipids. These values are consistent with limited random motional excursions from an average orientation.

In contrast to the detailed level of understanding of cholesterol gained from model membrane systems, there is a scarcity of information on the orientation and order of cholesterol in the lipid bilayer environment of HDL-like particles. Structural studies of discoidal, reconstituted HDL (rHDL) composed of lipids, cholesterol and apoA-I have focused largely on the topology and registration of the apoA-I double belt,^22,23 but the behaviour of cholesterol in the particles has been neglected. Molecular dynamics simulations of assemblies representing nascent, discoidal HDL have been reported,²⁴ including an atomistic simulation over a 20 μs trajectory,²⁵ but the orientation and distribution of cholesterol in the simulations lack experimental verification. Considering the fundamental role of HDL in facilitating cholesterol uptake and recycling, it would be useful to know if the annular protein belt that surrounds the lipids in HDL, and constrains the size and shape of the particles, influences the orientational distribution of cholesterol as compared to when it diffuses freely in unconstrained lipid vesicles.

Here, we use ssNMR to examine the orientation of cholesterol in discoidal rHDL resembling nascent pre-β particles, and in MLVs. Deuterium ssNMR is a powerful tool for probing molecular orientations in lipid bilayers, and has been used study the cholesterol analogue estradiol in rHDL particles,²⁶ but the ²H nucleus has low sensitivity and ambiguities can occur in spectral assignments of multiple-labelled molecules. We therefore use ¹³C cross-polarisation magic-angle spinning (CP-MAS) ssNMR methods to observe [2,3,4-¹³C₃]cholesterol (Fig. 1a) in the rHDL and MLV preparations. Whilst the relative insensitivity of ²H NMR or ¹³C at natural abundance can be challenging at low sample concentrations, ¹³C NMR peaks for ¹³C-enriched cholesterol are detected rapidly and assigned unambiguously.²⁷ Selective measurements of dynamically-averaged, residual dipolar couplings between C3 and the three bonded nuclei, C2, C4 and H3, are used to estimate the average orientation of cholesterol about the bilayer normal. The ¹³C–¹³C dipolar couplings are measured selectively in a novel application of a one-dimensional experiment that observes the mechanical excitation of zero-quantum coherence at rotational resonance.^28,29

Fig. 1 Morphological analysis of rHDL containing [2,3,4-¹³C₃]cholesterol. (a) The chemical structure of cholesterol indicating the ¹³C-labelled sites, C2, C3 and C4. (b) Negatively-stained TEM image of rHDL. (c) Size distribution of the rHDL nanodiscs measured from the TEM image.

2. Results and discussion

2.1 Initial characterisation of rHDL

Nanoparticles of rHDL were prepared by detergent dialysis³⁰ from a mixture of palmitoyloleoylphosphatidylcholine (POPC), [2,3,4-¹³C₃]cholesterol and recombinant apoA-I in a molar ratio of 200 : 20 : 2 (these proportions denote the average ratio of lipid, cholesterol and protein per particle). For NMR analysis, the particles were precipitated from aqueous solution by polyethylene glycol (PEG) as described previously.³¹ Visualisation by transmission electron microscopy (TEM) confirmed the expected rHDL discoidal morphology with a mean diameter of 12.6 nm (2.3 nm SD) (Fig. 1b and c). Proton-decoupled ¹³C CP-MAS NMR spectra of rHDL revealed peaks for the three enriched carbon sites, C2 (32.6 ppm), C3 (72.5 ppm) and C4 (43.4 ppm), distinct from the background peaks from the lipid/cholesterol ¹³C nuclei at natural abundance (Fig. 2a). Rapid anisotropic motions of cholesterol, combined with MAS at 9 kHz, render the peaks narrow enough to measure one-bond ¹³C–¹³C J-coupling constants of 33 Hz.

Fig. 2 ¹³C CP-MAS NMR analysis of rHDL and MLVs containing POPC and 10 mol% [2,3,4-¹³C₃]cholesterol. (a) Spectrum of rHDL at a MAS frequency (ν_r) of 9000 Hz overlaid with a simulated spectrum (red) with ¹³C–¹³C J-coupling constants of 33 Hz and a line broadening factor of 30 Hz. (b) Spectrum of rHDL at ν_r = 5113 Hz, which corresponds to the n = 1 rotational resonance condition with respect to the frequencies of C3 and C4 at the applied magnetic field of 16.3 T. (c) Spectrum of rHDL at ν_r = 7010 Hz, which corresponds to the n = 1 rotational resonance condition with respect to the C2 and C3 frequencies. The red lines in (b) and (c) are simulated spectra for ¹³C–¹³C dipolar coupling constants b²³_av = b³⁴_av = 250 Hz at the two rotational resonance conditions.

2.2 Calculation of average dipolar couplings for cholesterol in rHDL and in MLVs

The well-known rotational resonance condition³² was exploited to observe ¹³C–¹³C dipolar couplings between C2 and C3, and C3 and C4. When the MAS frequency ν_R matches the difference of the C2 and C3 resonance frequencies (7010 Hz), the peaks for C2 and C3 broaden selectively; similar broadening of the peaks for C3 and C4 is observed when ν_R matches the frequency difference of C3 and C4 (5113 Hz) (Fig. 2b and c). This broadening occurs because the n = 1 rotational resonance conditions with respect to C2–C3 and C3–C4 are satisfied at the two MAS frequencies, whereupon the dipolar interactions between the pairs ¹³C nuclei are re-introduced selectively. The peak broadening is considerably less than would be expected for the rigid limit ¹³C–¹³C dipolar coupling constants of 2250 Hz calculated from the crystal structure because of scaling by the anisotropic motions of cholesterol in the bilayer. The dipolar coupling constants are therefore defined as dynamically-averaged values: b²³_av for C2–C3 and b³⁴_av for C3–C4. Peak fitting to the spectra at rotational resonance obtained reasonable agreement for residual ¹³C–¹³C dipolar coupling constants of |b²³_av| = |b³⁴_av| = 250 Hz (Fig. 2b and c). Note that absolute values are given because the sign of the averaged couplings cannot be determined experimentally.

Rotational diffusion of cholesterol in lipid bilayers scales the dipolar couplings in a defined way and the observed values may be used to determine the average orientation of cholesterol in the bilayer. Although values of |b²³_av| and |b³⁴_av| were estimated from the NMR lineshapes at rotational resonance, measurements of weak dipolar couplings directly from NMR peaks can be prone to errors, particularly in the presence of ¹³C–¹³C J-coupling. A novel approach was therefore used for verification of the estimated values, using an experiment that mechanically (i.e., through sample rotation) excites zero quantum (ZQ) coherence between C2–C3 and C3–C4 spin pairs at n = 1 rotational resonance. The pulse sequence converts ZQ coherence to double quantum (DQ) coherence and then back to ZQ coherence, and finally observable magnetization is recovered by reversing the ZQ excitation process^28,29,33 (Fig. 3a and Fig. S1a, ESI†). A series of DQ-filtered spectra was collected at different excitation intervals, τ, and the summed integrated peak intensities for the selectively recoupled spins initially increase and reach a maximum at an optimal interval given approximately by ,²⁸ where b^ij_av is expressed in Hertz. The data were compared with curves simulated for different values of b^ij_av and the zero quantum relaxation term, T_ZQ, to find the values in closest agreement. The simulated curves fit both sets of data closely when |b²³_av| = |b³⁴_av| = 230 ± 50 Hz and T_ZQ = 11.5 ms (Fig. 3b, left, and Table 1). These values are close to those determined by NMR line shape analysis. The build-up of DQ coherence for [2,3,4-¹³C₃]cholesterol in POPC MLVs are consistent with |b²³_av| = |b³⁴_av| = 320 ± 50 Hz and T_ZQ = 5.5 ms (Fig. 3b, right, and Table 2). The different extent of scaling of the ¹³C–¹³C dipolar couplings in rHDL and MLVs suggest differences in the dynamic behaviour of cholesterol in the two lipid bilayer environments. This conclusion was supported by measurements of residual C3–H3 dipolar couplings using the ¹H–¹³C DIPSHIFT NMR experiment,³⁴ which yielded values of b³³_av of 3500 ± 100 Hz for cholesterol in rHDL and 4300 ± 100 Hz for cholesterol in MLVs (Fig. 3c and Tables 1, 2). In Fig. 3c it can be seen that the ¹³C transverse magnetization refocuses fully over one rotor period, implying that cholesterol does not undergo intermediate motions that interfere with MAS time dependence that disrupt the coherence of the time domain signal.³⁵

Fig. 3 Measurements of ¹³C–¹³C and ¹³C–¹H dipolar couplings for cholesterol in rHDL and MLVs determined by CP-MAS ssNMR. (a) Selective excitation of C2–C3 and C3–C4 ¹³C–¹³C ZQ coherences at the n = 1 rotational conditions for both spin pairs, detected by conversion of ZQ to DQ coherence and reconversion to observable magnetization. (b) Build-up and decay of C2–C3 (black circles) and C3–C4 (red circles) ¹³C difference intensities as a function of the ZQ excitation period τ of the NMR pulse sequence (given in the Fig. S1a, ESI†). Solid lines are the best fitting simulated ZQ build-up curves corresponding to the values of dipolar coupling constants b²³_av and b³⁴_av and zero-quantum relaxation time, T^ZQ₂, given in the main text. The error bars indicate the level of the noise. (c) Evolution of the ¹³C transverse magnetisation of C3 over one cycle of sample rotation in the presence of C3–H3 dipolar coupling, measured using the DIPSHIFT experiment (Fig. S1b, ESI†).

Table 1 Summary of the dynamically averaged dipolar couplings for cholesterol in rHDL measured experimentally by ssNMR (Fig. 2 and 3), calculated using the Gaussian distribution procedure (Fig. 4) and extracted from MD simulations of 200 : 20 : 2 POPC : cholesterol : apoA-I nanodiscs (Fig. 6)²⁵

Nuclear spin pair ij	|b^ijav| (Hz)
	Experimental	Gaussian distribution^a	MD simulation^b
a Gaussian distribution generated from αMR = 90°, αMR = 155°, αMR = 34°. b From ref. 21 and DOI: https://doi.org/10.5281/zenodo.897027. The simulations were run on the Anton 2 supercomputer, and converted to CHARMM readable files. The trajectories consisted of frames at every 4.8 ns and 10 frames were selected at random from the late stages of the 2 ms simulation.
^13C2–^13C3	230 ± 50	233	257
^13C3–^13C4	230 ± 50	245	288
^13C3–^1H3	3500 ± 100	3511	3412

---

Table 2 Summary of the dynamically-averaged dipolar couplings for cholesterol measured experimentally in 10 : 1 POPC : cholesterol MLVs (Fig. 3), calculated using the Gaussian distribution procedure (Fig. 4) and extracted from MD simulations of 200 : 22 POPC : cholesterol bilayers (Fig. 6)³⁶

Nuclear spin pair ij	|b^ijav| (Hz)
	Experimental	Gaussian distribution^a	MD simulation^b
a Gaussian distribution generated from αMR = 91°, αMR = 163°, αMR = 28°. b From DOI: https://doi.org/10.5281/zenodo.3243328. Cholesterol orientations were extracted from 10 frames of a 100 ns simulation of a POPC bilayer consisting of 200 lipids (100 per leaflet) in the presence of 10% (22 molecules) cholesterol. The Slipids model (force field parameters downloaded from https://mmkluster.fos.su.se/slipids) was employed for lipids, and the tip3p model for water.
^13C2–^13C3	320 ± 50	327	405
^13C3–^13C4	320 ± 50	326	426
^13C3–^1H3	4300 ± 100	4284	4185

---

2.3 Analysis of the average dipolar couplings to determine the orientation of cholesterol

The dynamic behaviour of cholesterol in lipid bilayers involves rapid reorientation about a principal rotational axis, R. The experimentally-determined values of b²³_av, b³⁴_av and b³³_av hold information about the average orientation of cholesterol in the rHDL and MLV lipid bilayers, relative to R and to the bilayer normal, N. The dynamically-averaged dipolar couplings, b^ij_av, depend on the maximum, rigid-limit couplings, b^ij_max, according to:where θ^ij_DR are the angles between the ij internuclear vectors and the rotational axis; these angles are assumed here to be invariant in the rigid ring system of cholesterol. θ_RN is the angle between the rotational axis R and N. The term in brackets 〈⋯〉, which is equivalent to the molecular order parameter, S_mol, is averaged over a distribution of angles because the rotational axis undergoes random angular excursions from its average orientation along the bilayer normal.

It is convenient to specify a molecular axis system within which the orientation of R can be specified by azimuthal angle α_MR and polar angle β_MR (Fig. 4, Steps 1 and 2). For cholesterol, we chose a molecular frame with the z-axis directed along the C3–O3 bond and y-axis in the O3–C3–H3 plane. In this molecular frame, the orientation of each internuclear vector ij, defined by angles θ^ij_DR, can be calculated for any values of α_MR and β_MR using equations of the form

cos θ^ij_DR = x^ij cos α_MR sin β_MR + y^ij sin α_MR sin β_MR +z^ij cos β_MR (2)

where x^ij, y^ij and z^ij are the Cartesian coordinates in the molecular frame of the internuclear unit vectors passing through the origin at C3 (C3 being common to all three couplings measured).

Fig. 4 Schematic of the procedure for calculating the orientation of cholesterol relative to the rotational axis. Step 1: a molecular axis system is defined, based on the geometry of cholesterol (see main text for details). Step 2: angles α_MR and β_MR specify the orientation of the principal rotational axis R of cholesterol in the molecular axis system. Step 3: cholesterol and its rotational axis undergo random fluctuations from the average position of R along the bilayer normal N by angle θ_RN. The amplitude of deviation from N is defined by a Gaussian distribution with standard deviation σ_RN. Step 4: the cholesterol molecule in each orientation undergoes rotation about R by angle ψ_RN to generate a set of molecular rotamers. Step 5: from each cholesterol orientation are calculated the angles between the ij internuclear vectors and N (θ²³_DR, θ³⁴_DR and θ³³_DR), from which the average values of the dipolar coupling constants are obtained according to eqn (4). Step 6: the orientational distribution of cholesterol molecules generated by Steps 3 and 4 is represented by the distribution of angles α_MN and β_MN. Steps 2 to 6 are carried out iteratively to find he values of α_MR and β_MR that are consistent with the experimentally determined values of b^ij_av.

We assessed whether combinations of angles α_MR and β_MR could be found that are consistent with the measured values of b²³_av, b³⁴_av and b³³_av for cholesterol in rHDL and MLVs. To do so, an initial state was established in which the rotational axis R is parallel with the bilayer normal N and one particular orientation of cholesterol relative to R was specified by a pair of [α_MR, β_MR] angles, where each angle can take a value of 0° to 180° (Fig. 4, Step 2). A distribution function was then selected to represent the spread of orientations of R about N, defined by angles θ_RN. The cholesterol molecular coordinates and rotational axis R were rotated away from N by a set of n randomly-generated angles, [small straight theta, Greek, circumflex]_RN, weighted as a Gaussian distribution with [small theta, Greek, macron]_RN = 0° as the fixed mean and σ_RN as a variable standard deviation (Fig. 4, Step 3). For each new orientation of R, a series of cholesterol rotamers was generated by revolving the molecule about R in equal increments by angle ψ_R, where 0° ≤ ψ_R < 360° (Fig. 4, Step 4). The three variables in the simulation were therefore α_MR, β_MR and σ_DR and a distribution of 5 × 10⁵ cholesterol orientations was generated for different combinations of these variables. The values of b²³_av, b³⁴_av and b³³_av were then calculated from each distribution generated (Fig. 4, Step 5). This was done by first determining the orientations of the ij internuclear vectors with respect to the bilayer normal, given by angles θ^ij_DN, for each cholesterol orientation, where

The average dipolar couplings over the distribution of θ^ij_DN values according to

b^ij_av = 〈(3 cos² θ^ij_DN(θⁿ_RN) − 1)/2〉 (4)

where 〈⋯〉 indicates a weighted average over all the possible values of θ^ij_DN. The distributions of individual dipolar couplings measured from each cholesterol orientation are given in Fig. S2 (ESI†). The distribution of cholesterol orientations generated by this procedure is represented by angles, a_MN and β_MN, which define the orientation of each cholesterol molecular axis frame relative to the bilayer normal N (Fig. 4, Step 6).

An iterative process was used to calculate the values of b²³_av, b³⁴_av and b³³_av corresponding to different orientational distributions of cholesterol generated from the three variables according to Fig. 4 (see Section 5.2 for further details). Steps 2 to 6 in Fig. 4 were repeated for different combinations of α_MR and β_MR values within their allowed ranges (0–180°), and for σ_DR values of 0° to 40° in 1° increments, and values of b²³_av, b³⁴_av and b³³_av were calculated for each set of [α_MR, β_MR, σ_DR] values. Combinations of the three variables that yielded dipolar couplings that were all within the experimentally-determined ranges were captured. These experimentally-consistent values of α_MR and β_MR are represented by the contoured regions in Fig. 5(a and b). The [α_MR, β_MR] combinations are confined to only a limited range of values in both cases, being [90 ± 3°, 155 ± 3°] for cholesterol in rHDL and [91 ± 4°, 163 ± 3°] for cholesterol in MLVs. The value of ∼90° for α_MR is a consequence of the near degeneracy of the dipolar couplings b²³_av and b³⁴_av. No other combinations of angles satisfied all three measured dipolar coupling values. For rHDL, values of α_MR and β_MR that were consistent with the data were only found when σ_RN assumed values of 34 ± 3°; for MLVs the spread of orientations was slightly lower at σ_RN = 28 ± 2°. Hence, the dipolar couplings measured from cholesterol in rHDL and MLVs are consistent with slightly different orientations of cholesterol relative to the principal rotational axis and suggest that the distribution of cholesterol orientations is different in the two environment.

Fig. 5 Average orientation in HDL and MLVs of the rigid ring system of cholesterol relative to the principal rotation axis R. (a and b) Contour plots showing the combinations of α_MR and β_MR that are consistent with the three measured dipolar coupling values. Full details of the calculation are given in the Experimental section 5.2. (c and d) Orientations of cholesterol (and the molecular axis system) relative to the rotational axis R, as specified by the values of α_MR and β_MR corresponding to the red central region of the contour plots. The tables give the ranges of possible angles and standard deviation σ_RN consistent with the data. The average orientation of the flexible hydrocarbon tail (circled) cannot be determined from the dipolar couplings.

2.4 Comparison of the experimental data with molecular dynamics simulations

To validate the interpretation of the NMR-determined dipolar coupling values, we analysed previously published atomistic molecular dynamics (MD) simulations of a 200 : 20 : 2 (mol : mol : mol) POPC : cholesterol : apoA-I discoidal assembly²⁵ (analogous in composition to the rHDL formulations here) and of 200 : 22 (mol : mol) POPC : cholesterol in square planar bilayers of surface area ∼56 nm² (Fig. 6a and b).³⁶ The planar bilayers were considered to be a satisfactory approximation of MLVs, which are typically >500 nm in diameter and therefore have <5° curvature over the simulation dimensions in the outermost lamellae. We selected 10 frames at random from the later stages of the simulation trajectories (20 μs for POPC:cholesterol:apoA-I and 100 ns for POPC:cholesterol) and from these snapshots determined the distribution of cholesterol orientations relative to the bilayer normal N, defined by angles α_MN and β_MN (Fig. 6b and c, discrete bars). The mean α_MN and β_MN values and standard deviations for cholesterol in the two MD simulation environments are summarised in Table 3, and indicate that cholesterol adopts slightly different distributions of orientations in the two environments. The ¹³C2–¹³C3, ¹³C3–¹³C4 and ¹³C3–¹H3 dipolar couplings were calculated for each cholesterol molecule in the distributions (Fig. S3, ESI†) and averaged across the ensemble of cholesterol molecules. The experimentally-determined average dipolar couplings are in excellent agreement with the values measured from cholesterol in both simulation environments (Tables 1 and 2). The different average coupling values measured from the POPC:cholesterol:apoA-I and POPC:cholesterol simulations originates from the slightly different distribution profiles of cholesterol in the two bilayer environments. Finally, we compared the cholesterol orientations in the two environments as determined from the MD simulations and as generated by the Gaussian distribution function described in Fig. 4, using the mean parameters tabulated in Fig. 5 (Fig. 6b and c, solid lines). The distribution profiles generated by the Gaussian function agree very well with the histograms calculated from the MD snapshots, with the mean values, [small alpha, Greek, macron]_MN and [small beta, Greek, macron]_MN and standard deviations σ_RN, being very similar for the two approaches (Table 3).

Fig. 6 Analysis of the orientational distribution of cholesterol in MD simulations of rHDL nanodiscs (200 : 20 : 2 POPC : cholesterol : apoA-I) and planar lipid bilayers (200 : 22 POPC : cholesterol). (a and b) Single frame snapshots taken from the late stages of the simulation trajectories (2 μs for (a) and 100 ns for (b)). (c and d) Histograms of angles α_MN (red) and β_MN (blue) defining the distribution of orientations of the cholesterol molecular frame relative to the bilayer normal N. Solid lines represent the distribution of angles calculated using the Gaussian distribution method (step 6 in Fig. 4). The means and standard deviations of the distributions are summarised in Table 3.

Table 3 Summary of distribution parameters (means and standard deviations) for cholesterol in rHDL and MLVs determined from MD simulations and by generation of a Gaussian distribution of orientations according to the procedure outlined in Fig. 4

	MD simulations		Gaussian distribution
	[small alpha, Greek, macron] MN (σMN)	[small beta, Greek, macron] MN (σMN)	[small alpha, Greek, macron] MN (σMN)	[small beta, Greek, macron] MN (σMN)
a Gaussian distribution generated from αMR = 90°, αMR = 155°, αMR = 34°. b Gaussian distribution generated from αMR = 91°, αMR = 163°, αMR = 28°.
rHDL^a	89° (19°)	150° (16°)	90° (19°)	148° (16°)
MLV^b	94° (17°)	157° (15°)	90° (18°)	154° (15°)

---

3. Conclusion

With the aid of ¹³C CP-MAS ssNMR methods, new insights have been gained into the orientation of cholesterol in rHDL nanoparticles approximating the discoidal morphology of nascent pre-β HDL. By exploiting dynamically-averaged ¹³C–¹³C and ¹H–¹³C dipolar coupling measurements, it is shown that the average orientation of cholesterol in rHDL is slightly different from that in MLV bilayers. The NMR data are also consistent with a slightly larger spread of orientations in rHDL than in MLVs. These differences in the orientational behaviour of cholesterol likely arise from the lateral and rotational diffusion of the lipid components being constrained by the diameter of the apoA-I double belt, which forces the bilayer to distort and ripple to accommodate the internal strain on the lipid components. As cholesterol is added, the overall shape and size of the cross section of the disk remains constant, but to accommodate the cholesterol the lipid bilayer core swells and this may influence the orientation of cholesterol.³⁷ Such constraints are more relaxed in MLVs because the lipids and cholesterol molecules are free to diffuse laterally unhindered. Wide-line ²H ssNMR studies of phospholipid chain order in nanodiscs prepared with MSPΔH5, a truncated apoA-I variant, concluded that the restricted area in the nanodiscs reduce the cooperativity of lipid assembly during the gel-to-liquid crystalline phase transition and increase lipid fluidity above the transition.³⁸ Interestingly, the same study reported an ordering effect of cholesterol, although the order/disorder of cholesterol itself was not examined. The higher orientational disorder of cholesterol presented here could contribute to the HDL particle plasticity observed in atomistic simulations.²⁵ The particle plasticity could be required to enable the particles to interact with multiple enzymes and cell receptors in reverse cholesterol transport.^4,5,39 An important outcome of this work is that the dipolar coupling measurements agree well with values calculated for cholesterol in MD simulations of HDL-like nanodiscs and in planar lipid bilayers, thereby providing hitherto unavailable experimental validation of the simulations. Unexpectedly, the cholesterol distributions generated by a Gaussian function with variables α_MR, β_MR and σ_RN, that are consistent with the NMR measurements, also agree well with the distributions extracted from the MD simulations.

The methodology presented here paves the way for further investigation of cholesterol orientational order and dynamics in rHDL particles of different lipid composition and cholesterol concentration, as well as in spherical HDL in which cholesteryl esters penetrate deeper into the lipid core of the particles. In such particles, which approximate “mature” HDL, it should be possible in principle to determine the orientation of cholesterol relative to its axis of rotation.

4. Experimental procedures

4.1 Materials

[2,3,4-¹³C₃]Cholesterol was obtained from Merck. Palmitoyloleoylphosphatidylcholine (POPC) was obtained from Avanti® Polar Lipids (Merck).

4.2 Preparation of multilamellar vesicles

Aliquots of POPC (328.9 mM) and [2,3,4-¹³C₃]cholesterol (25.7 mM) stocks in CHCl₃ were combined in a round-bottom flask to a final molar ratio of POPC : [2,3,4-¹³C₃]cholesterol of 10 : 1 (mol/mol). The CHCl₃ was evaporated under a stream of N₂, and the thin film was placed under vacuum for ≥4 hours. The film was resuspended in 0.5 mL rHDL buffer (10 mM tris base, 1 mM EDTA) pH 7.4, to form MLVs with a final POPC : [2,3,4-¹³C₃]cholesterol molar ratio of 26.3 : 2.63 mM. The MLVs were homogenised with 10 freeze–thaw cycles, pelleted by bench-top centrifugation (10 minutes, 13.4k rpm), and transferred into a 3.2 mm diameter MAS rotor.

4.3 Production of rHDL particles

The rHDL particles were prepared as described previously³¹ using the widely established detergent mediated sodium cholate dialysis method.³⁰ Briefly, a thin film of POPC : [2,3,4-¹³C₃]cholesterol at a 10 : 1 (M/M) molar ratio was prepared as above. An aliquot of sodium cholate (232.2 mM) stock in rHDL buffer, pH 7.4, was added to a final molar ratio of lipid : detergent of 1 : 1–2 (M/M). The solution was stirred at 4 °C until clear. Recombinant WT apoA-I (2-243)⁴⁰ was added to a final molar ratio of lipid : protein of 200 : 2 (M/M) and the sample was stirred at 4 °C for ≥12 hours. The detergent was removed by dialysis against a 500-fold excess volume of rHDL buffer, pH 7.4, over 3 days at 4 °C, with at least 5 buffer changes. The dialysis tubing MWCO was 12–14 kDa (Merck).

For ¹³C CP-MAS ssNMR the rHDL particles were spin concentrated using an Amicon Ultra-4 device (10 kDa MWCO, Merck). The rHDL particles were precipitated in a ≥48 hour incubation at 4 °C with 24% (w/v) PEG-6000 in rHDL buffer, pH 7.4.^31,41 The precipitated particles were pelleted at 4 °C by ultracentrifugation at 41k rpm for 2 hours in an SW55 Ti rotor (Beckman Coulter). The PEG-precipitated rHDL was transferred to a 3.2 mm diameter MAS rotor and stored at 4 °C. The lipid and cholesterol concentration were measured in duplicate using 96-well plate colorimetric quantification assay kits (CS0001 and MAK043, Sigma-Aldrich®). A Nanodrop™ 2000 spectrophotometer (ThermoFisher Scientific) was used to measure the protein concentration (n = 9).

4.4 Transmission electron microscopy

The rHDL particles were imaged on formvar/carbon coated 300 mesh Cu grids (agar scientific). To increase sample adhesion 10 μL of 0.1% (w/v) poly-L-lysine in dH₂O was incubated on the grid for 1 minute.⁴² The sample (10 μL, 36 μM protein) was incubated on the grid for 2 minutes, followed by negative staining with 10 μL of 2% (w/v) PTA, pH 7.0, incubated for 1 minute. Between each step the liquid was blotted with filter paper. The reagents were kindly provided by Papatziamou. The sample grid was imaged using a JEOL JEM-1010 microscope (BLS, Lancaster University) with an 80 kV tungsten filament electron source and an AMT CCD camera at 120k× magnification. The images were processed using FIJI software.⁴³ A total of 100 particles per window (n = 3) were measured on the TEM grid to determine the average particle diameter.

4.5 NMR experiments

The ¹³C cross-polarization magic-angle-spinning (CP-MAS) NMR measurements were conducted on a Bruker Avance III 700 spectrometer (operating at resonance frequency 700.1 MHz for ¹H and 175.9 MHz for ¹³C). A triple resonance (HXY) 3.2 mm MAS probe was used for all measurements, at a calibrated temperature of 298 K. In all experiments, the cross-polarization Hartmann–Hahn contact time was 2 ms at a proton field of 66 kHz, with 90° pulse lengths of 4 μs for ¹³C and 3 μs for ¹H. To measure ¹H–¹³C dipolar couplings, a constant-time DIPSHIFT experiment³⁴ was used in which frequency-switched Lee Goldberg was used for homonuclear decoupling (at a field of 51 kHz) over periods τ of up to one rotor cycle (i.e., 0 ≤ τ ≤ 2π/ω_r), followed by a 180° pulse and a further period of heteronuclear decoupling (t_HC = 4π/ω_r − t_HH) to refocus the ¹³C chemical shifts. The spinning frequency ω_r/2π was 4400 Hz. A series of free induction decays were obtained with proton decoupling for incremented periods of τ. After Fourier transformation of the FIDs, the evolution of ¹³C magnetisation was measured from the peak intensities for C3 at the different τ periods.

For the double quantum (DQ) experiments an adaptation of the pulse sequences described by Karlsson et al. was used.^28,29 This method was chosen because, unlike other one-dimensional dipolar recoupling methods, it allows for selective measurements of the C2–C3 and C3–C4 couplings at rotational resonance and so avoids ambiguities arising from multiple spin couplings involving C3. Although double quantum coherence is observed in the spectra, the rates of signal build-up (Fig. 3b) actually represent the rate of mechanical excitation of zero quantum (ZQ) coherence. The initial rate of excitation at rotational resonance is proportional to the magnitude of the dipolar coupling and hence is expected to be slower in dynamically averaged systems than in rigid solids. The experiment proceeds as follows. After cross-polarization, the transverse magnetization for the ¹³C–¹³C spin pairs of interest, S₁ and S₂, are converted to longitudinal difference magnetization, S_1Z − S_2Z. At the n = 1 rotational resonance condition the dipolar coupling between the spin pair is reintroduced and mechanically-driven excitation of ZQ coherence occurs from the initial S_1Z − S_2Z state over a variable interval τ. The ZQ coherence is then converted to DQ coherence and immediately back to ZQ coherence and a second τ interval regenerates the longitudinal difference magnetization. A final readout 90° pulse creates transverse magnetization with the two ¹³C spins having opposite phase. The receiver phase cycle selects only the magnetization that has passed through the ZQ–DQ–ZQ filter, and the Fourier transformed spectrum exhibits positive and negative peaks only from the two coupled ¹³C spins. The sum of the absolute values of the integrated intensities of the two peaks are plotted as a function of τ to visualise the rates of excitation and relaxation of the ZQ coherence.

5. Computational procedures

5.1 NMR simulations

Simulations of the ZQ evolution and ¹³C magnetization evolution under ¹H dipolar coupling measured in the DIPSHIFT experiment were carried out to find the values of dynamically-averaged dipolar coupling constants providing the closest fit to the data. Simulations were carried out in the SIMPSON environment.⁴⁴ Fixed parameters used in the simulations were the ¹³C–¹³C J-coupling constants (33 Hz for C2–C3 and C3–C4) and ¹³C chemical shift anisotropy (CSA) parameters measured from ¹³C NMR spectra of non-spinning samples to be approximately 1.1 kHz. The extensive scaling of the ¹³C CSA values meant that they had little effect on the shapes of the simulated curves. For the DIPSHIFT simulations, a series of time-domain curves representing the evolution of ¹³C transverse magnetization over one rotor cycle (at a MAS frequency ω_r/2π = 4400 Hz) were calculated for different values of the ¹³C–¹H dipolar coupling constant and compared with the data to find the best fit. The proton isotropic chemical shifts and chemical shift anisotropy were set to zero.

For simulations of the ZQ excitation at n = 1 rotational resonance, the MAS frequency was set to the difference in the isotropic chemical shifts of the appropriate ¹³C spins (C2 and C3, or C3 and C4). An initial condition of ¹³C difference magnetization (S_1z − S_2z) was established and the read-out was ZQ coherence (S₁⁺S₂⁻ + S₁⁻S₂⁺) as a function of excitation time. The curves generated for different ¹³C–¹³C dipolar coupling constants, b^av_ij, were multiplied by an exponential zero-quantum relaxation term and normalised to the maximum intensity. The maximum intensity (in the absence of relaxation) occurs at close to an excitation time 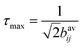,²⁸ where b^av_ij is in Hertz. This relationship was verified here from measurements on standard ¹³C labelled compounds for which the ¹³C–¹³C distances are known.

5.2 Calculation of cholesterol orientations

The values of the angles α_MR and β_MR, defining the allowed orientations of the principal rotation axis R in the pre-defined molecular frame of cholesterol were calculated by generating a Gaussian distribution of R about the bilayer normal N, as described in the main text, and computing the average dipolar couplings b^ij_av across the distribution. For a given value of σ_RN, representing the spread of orientations of R relative to N, angles α_MR and β_MR were each varied through 180° and for every [α_MR, β_MR] pair were calculated angles, θ^ij_DR, defining the orientation of each internuclear vector of interest relative to R (eqn (2)). The values of θ^ij_DR were substituted into eqn (3) and (4) to calculate θ^ij_DN and the average dipolar coupling constants b^ij_av for the entire distribution. The allowed orientations of R were those for which α_MR and β_MR yielded b^ij_av values within all three of the experimentally-measured ranges. These [α_MR, β_MR] pairs were saved and added to subsequent [α_MR, β_MR] pairs that were consistent with the measured b^ij_av values after each incrementation of σ_RN. The contoured regions in the plots in Fig. 5(a and b) represent the frequency with which each captured α_MR and β_MR values occur across all values of σ_RN from 5° to 40°, with the red areas corresponding to the highest frequency. For each distribution, the individual cholesterol orientations were defined by angles α_MN and β_MN. By representing the bilayer normal as a unit vector N̂^T = (0, 0, 1) and the x- and z-axes of the cholesterol molecular frame as unit vectors x̂ and ẑ, the orientation of each cholesterol molecule relative to the bilayer normal may be expressed as

α_MN = cos[−x₁z₁z₃ − x₂z₂z₃ + x₃(1 − z₃²)] (5)

and

β_MN = a cos z₃ (6)

Eqn (5) and (6) were also used to calculate the cholesterol orientations in the MD simulations after, where necessary, rotating the lipid bilayer into a coordinate system with N directed along the z-axis. All calculations were performed by a C program written for the purpose.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The work was funded by the British Heart Foundation Project Grant PG/21/10498. We greatly appreciate Dr Elisabeth Shaw's help in providing technical assistance with the TEM imaging and manuscript preparation. We are grateful to Dimitra Papatziamou for advice and reagents in preparing the TEM samples.

References

1. P. L. Yeagle, Biochim. Biophys. Acta, 1985, 822, 267–287.
2. E. Sackmann, in Structure and Dynamics of Membranes, ed. R. Lipowsky and E. Sackmann, Elsevier, Amsterdam, 1995, pp. 1–64.
3. A. V. Khera, M. Cuchel, M. de la Llera-Moya, A. Rodrigues, M. F. Burke, K. Jafri, B. C. French, J. A. Phillips, M. L. Mucksavage, R. L. Wilensky, E. R. Mohler, G. H. Rothblat and D. J. Rader, N. Engl. J. Med., 2011, 364, 127–135.
4. M. Ouimet, T. J. Barrett and E. A. Fisher, Circ. Res., 2019, 124, 1505–1518.
5. M. Zhang, R. Charles, H. Tong, L. Zhang, M. Patel, F. Wang, M. J. Rames, A. Ren, K.-A. Rye, X. Qiu, D. G. Johns, M. A. Charles and G. Ren, Sci. Rep., 2015, 5, 8741.
6. X. Y. Qiu, A. Mistry, M. J. Ammirati, B. A. Chrunyk, R. W. Clark, Y. Cong, J. S. Culp, D. E. Danley, T. B. Freeman, K. F. Geoghegan, M. C. Griffor, S. J. Hawrylik, C. M. Hayward, P. Hensley, L. R. Hoth, G. A. Karam, M. E. Lira, D. B. Lloyd, K. M. McGrath, K. J. Stutzman-Engwall, A. K. Subashi, T. A. Subashi, J. F. Thompson, I. K. Wang, H. L. Zhao and A. P. Seddon, Nat. Struct. Mol. Biol., 2007, 14, 106–113.
7. T. Laurenzi, C. Parravicini, L. Palazzolo, U. Guerrini, E. Gianazza, L. Calabresi and I. Eberini, J. Lipid Res., 2021, 62, 100006.
8. L. Chen, Z.-W. Zhao, P.-H. Zeng, Y.-J. Zhou and W.-J. Yin, Cell Cycle, 2022, 1–19,  DOI:10.1080/15384101.2022.2042777.
9. T. R. Molugu, K. J. Mallikarjunaiah, J. J. Kinnun, H. I. Petrache, M. Doktorova, G. Khelashvili, R. Ashkar and M. F. Brown, Biophys. J., 2021, 120, 41A.
10. T. R. Molugu and M. F. Brown, in Cholesterol Modulation of Protein Function: Sterol Specificity and Indirect Mechanisms, ed. A. Rosenhouse-Dantsker and A. N. Bukiya, 2019, vol. 1115, pp. 99–133.
11. M. P. Marsan, I. Muller, C. Ramos, F. Rodriguez, E. J. Dufourc, J. Czaplicki and A. Milon, Biophys. J., 1999, 76, 351–359.
12. E. J. Dufourc, E. J. Parish, S. Chitrakorn and I. C. P. Smith, Biochemistry, 1984, 23, 6062–6071.
13. T. Rog, M. Pasenkiewicz-Gierula, I. Vattulainen and M. Karttunen, Biochim. Biophys. Acta, Biomembr., 2009, 1788, 97–121.
14. F. Aussenac, M. Tavares and E. J. Dufourc, Biochemistry, 2003, 42, 1383–1390.
15. E. K. Tiburu, P. C. Dave and G. A. Lorigan, Magn. Reson. Chem., 2004, 42, 132–138.
16. T. M. Ferreira, F. Coreta-Gomes, O. H. S. Ollila, M. J. Moreno, W. L. C. Vaz and D. Topgaard, Phys. Chem. Chem. Phys., 2013, 15, 1976–1989.
17. J. A. Clarke, J. M. Seddon and R. V. Law, Soft Matter, 2009, 5, 369–378.
18. J. A. Clarke, A. J. Heron, J. M. Seddon and R. V. Law, Biophys. J., 2006, 90, 2383–2393.
19. N. P. Franks, J. Mol. Biol., 1976, 100, 345–358.
20. D. L. Worcester and N. P. Franks, J. Mol. Biol., 1976, 100, 359–378.
21. S. Waldie, M. Moulin, L. Porcar, H. Pichler, G. A. Strohmeier, M. Skoda, V. T. Forsyth, M. Haertlein, S. Maric and M. Cardenas, Sci. Rep., 2019, 9, 5118.
22. Z. Wu, M. A. Wagner, L. Zheng, J. S. Parks, J. M. Shy, J. D. Smith, V. Gogonea and S. L. Hazen, Nat. Struct. Mol. Biol., 2007, 14, 861–868.
23. R. Silva, G. M. Hilliard, L. Li, J. P. Segrest and W. S. Davidson, Biochemistry, 2005, 44, 8600–8607.
24. M. Pourmousa and R. W. Pastor, Biochim. Biophys. Acta, Biomembr., 2018, 1860, 2094–2107.
25. M. Pourmousa, H. D. Song, Y. He, J. W. Heinecke, J. P. Segrest and R. W. Pastor, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 5163–5168.
26. A. Vogel, H. A. Scheidt, S. E. Feller, J. Metso, R. M. Badeau, M. J. Tikkanen, K. Wahala, M. Jauhiainen and D. Huster, Biophys. J., 2014, 107, 114–125.
27. L. A. Della Ripa, Z. A. Petros, A. G. Cioffi, D. W. Piehl, J. M. Courtney, M. D. Burke and C. M. Rienstra, Methods, 2018, 138, 47–53.
28. T. Karlsson, M. Eden, H. Luthman and M. H. Levitt, J. Magn. Reson., 2000, 145, 95–107.
29. T. Karlsson, C. E. Hughes, J. Gunne and M. H. Levitt, J. Magn. Reson., 2001, 148, 238–247.
30. A. Jonas, Methods Enzymol., 1986, 128, 553–582.
31. S. Lau and D. A. Middleton, Angew. Chem., Int. Ed., 2020, 59, 18126–18130.
32. S. Dusold and A. Sebald, in Annual Reports on Nmr Spectroscopy, ed. G. A. Webb, 2000, vol. 41, pp. 185–264.
33. T. Karlsson, A. Brinkmann, P. J. E. Verdegem, J. Lugtenburg and M. H. Levitt, Solid State Nucl. Magn. Reson., 1999, 14, 43–58.
34. M. G. Munowitz, R. G. Griffin, G. Bodenhausen and T. H. Huang, J. Am. Chem. Soc., 1981, 103, 2529–2533.
35. E. R. Deazevedo, K. Saalwachter, O. Pascui, A. A. De Souza, T. J. Bonagamba and D. Reichert, J. Chem. Phys., 2008, 128, 104505.
36. M. Javanainan  DOI:10.5281/zenodo.640085 .
37. S. R. Midtgaard, M. C. Pedersen and L. Arleth, Biophys. J., 2015, 109, 308–318.
38. D. Martinez, M. Decossas, J. Kowal, L. Frey, H. Stahlberg, E. J. Dufourc, R. Riek, B. Habenstein, S. Bibow and A. Loquet, Chem. Phys. Chem., 2017, 18, 2651–2657.
39. D. Sahoo, T. C. Trischuk, T. Chan, V. A. B. Drover, S. Ho, G. Chimini, L. B. Agellon, R. Agnihotri, G. A. Francis and R. Lehner, J. Lipid Res., 2004, 45, 1122–1131.
40. D. Townsend, E. Hughes, R. Hussain, G. Siligardi, S. Baldock, J. Madine and D. A. Middleton, Biochemistry, 2017, 56, 1632–1644.
41. K. Mors, C. Roos, F. Scholz, J. Wachtveitl, V. Dotsch, F. Bernhard and C. Glaubitz, Biochim. Biophys. Acta, Biomembr., 2013, 1828, 1222–1229.
42. R. S. Anjum, S. M. Bray, J. K. Blackwood, M. L. Kilkenny, M. A. Coelho, B. M. Foster, S. R. Li, J. A. Howard, L. Pellegrini, S. V. Albers, M. J. Deery and N. P. Robinson, Nat. Commun., 2015, 6, 8163.
43. J. Schindelin, I. Arganda-Carreras, E. Frise, V. Kaynig, M. Longair, T. Pietzsch, S. Preibisch, C. Rueden, S. Saalfeld, B. Schmid, J. Y. Tinevez, D. J. White, V. Hartenstein, K. Eliceiri, P. Tomancak and A. Cardona, Nat. Methods, 2012, 9, 676–682.
44. M. Bak, J. T. Rasmussen and N. C. Nielsen, J. Magn. Reson., 2000, 147, 296–330.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp02393h

---