 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Nontrivial spectral band progressions in electronic circular dichroism spectra of carbohelicenes revealed by linear response calculations†
Manuel
Brand
 * and
Patrick
Norman
* and
Patrick
Norman
 *
*
Department of Theoretical Chemistry and Biology, School of Engineering Sciences in Chemistry, Biotechnology and Health, KTH Royal Institute of Technology, SE-106 91 Stockholm, Sweden. E-mail: manuelbr@kth.se; panor@kth.se
First published on 1st August 2022
Abstract
We demonstrate that contemporary computational resources allow for accurate theoretical studies of systems matching recent advances in experimental helicene chemistry. Concerned with first-principles calculations of carbohelicenes, our work surpasses CH[12] as the largest system investigated to date and unravels trends in the electronic structure of the low-lying states of the homologous series. Utilizing a highly efficient implementation of linear response algorithms, we present electronic circular dichroism (CD) spectra of carbohelicenes ranging from CH[5] to CH[30] at the level of Kohn–Sham density-functional theory. Our results for a systematic increase in system size show the emergence of new CD bands that subsequently rise to intensities dominating the spectrum. The spectral band progressions exhibit a periodicity directly linked to the number of overlapping layers of conjugation. While our findings rectify the current understanding of the electronic structure of carbohelicenes, they also serve as a general call for caution regarding the extrapolation of trends from small system ranges.
1 Introduction
The compound class of helicenes comprises nonplanar screw-shaped molecules formed by angularly ortho-annulated aromatic rings.1,2 While the building blocks of the helical backbone in the subgroup of carbo[n]helicenes (CH[n]) are confined to be (n) benzene rings, introduction of heteroatoms into the skeletal framework manifoldly increases the variety and hence functionality of helicenes. Their helical structure manifests a unique chirality and gives rise to a variety of exceptional properties making them interesting for applications in asymmetric catalysis,3–5 organic light-emitting diodes (OLEDs),6–8 organic field-effect transistors (OFETs),9,10 molecular recognition, and supramolecular chemistry.11,12 Although the first reported characterization of a member of the helicene family goes back to 1903,13 they were of little interest until the 1950s, since when helicene chemistry advanced remarkably. Besides the synthesis of novel functionalized compounds, the aim to synthesize longer multi-layered helicenes has been of interest ever since. The long-held record of Martin et al.14 of CH[14] as the longest homologue was not broken until the characterization of CH[16] in 2015.15 More recent synthesis of a single-strain backbone of 19 aromatic rings, but including 2H-pyran units16 and polyhelicene frameworks with an end-to-end length of up to 24 benzene rings17 show that this quest is nowhere near to an end.The developments in helicene chemistry are naturally supported by a large number of computational studies, that almost exclusively address the chiroptical properties of helicenes.18–27 These studies include electronic structure calculations at different levels of theory, with the computationally expensive coupled-cluster singles and doubles scheme employing the resolution of identity (RI-CC2) being limited to system sizes up to CH[10].18 Overall, with the exception of spectrum calculations of CH[16]27 and up to CH[36]23 using a simplified time-dependent density-functional theory approach (sTD-DFT)28 and the semi-empirical intermediate neglect of differential overlap for spectroscopy (INDO/S) method,29 respectively, computationally treated helicenes do not exceed a backbone length of 12 benzene rings.21 In light of the aforementioned experimental advances, it becomes evident that computational studies lag behind. Instead of investigating larger systems explicitly, trends of non-representative size ranges are used to extrapolate properties, such as excitation wavelengths and electronic circular dichroism (CD) band intensities18—a practice that needs to stand up to scrutiny.
As one of the standard techniques to investigate chiroptical properties, electronic CD spectroscopy measures differences in the absorption of left- and right-circularly polarized light. The scope of its application exceeds merely assigning enantiomeres, but covers a wide range including reaction mechanism elucidation and protein binding site identification.30–34 The combination with theoretical calculations gives rise to complementary transition properties, such as dipole moments, enhancing the utility of CD significantly.35,36 Reviews on the calculation of chiroptical properties with first-principles methods are available.37,38
The growing importance of comprehensive theoretical studies of CD and related chiroptical properties faces the challenge of heavy computational costs for the treatment of the often large systems of interest. With the computing capacity of contemporary supercomputers at hand, that challenge translates to the development of quantum chemical software suited for harnessing these vast computational resources.
Our contribution to this work brought forth the VeloxChem program—a modern, object-oriented software written in Python/C++, enabling the simulation of spectroscopic properties at the DFT level of theory in high-performance computing (HPC) environments.39 Included features crucial for carrying out the calculations for this study are numerical solvers for the linear response eigenvalue equation and evaluation of multiple damped response equations, employing the complex polarization propagator (CPP) approach.40–43 Both of them utilize the highly efficient hybrid open multi-processing (OpenMP)/message passing interface (MPI) parallel Fock-matrix construction implemented in VeloxChem.
As we have previously demonstrated the capability of VeloxChem to push the limits of first-principles computational chemistry,44 we investigate the homologous series of carbohelicenes up to a system size of CH[30] (Fig. 1) that goes far beyond any previous ab initio treatment. By means of linear response theory, we perform CD spectrum calculations, obtaining electric and magnetic transition dipole moments along the way. Based on a favorable assessment comparison with experimental and theoretical reference data for CH[5]–CH[9], our methodology is deemed to be accurate and reveals complex CD band progressions for carbohelicenes of increasing size.
2 Methodology
The processes of one-photon absorption (OPA) and its chiroptical analogue CD are linear responses of molecular systems to the perturbation by an external electromagnetic field. The defining observable quantity for CD, namely the anisotropy of the decadic molar extinction coefficient Δε can therefore be addressed computationally by means of linear response theory, as outlined below.The excitation energies for every electronic transition ħωn0 can be found as poles of the sum-over-states expression of a general linear response function
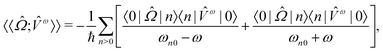 | (1) |
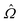 is a general property operator,
is a general property operator, ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) ω a general perturbation operator, and |0〉 and |n〉 are the electronic ground and excited states, respectively. Subsequently, the transition amplitudes can be obtained by performing a residue analysis for the resolved excitation.45 When introducing a single determinant approximation, such as in the Hartree–Fock (HF) or Kohn–Sham DFT methods, the problem of determining the excitation energies reduces to solving the generalized eigenvalue equation
ω a general perturbation operator, and |0〉 and |n〉 are the electronic ground and excited states, respectively. Subsequently, the transition amplitudes can be obtained by performing a residue analysis for the resolved excitation.45 When introducing a single determinant approximation, such as in the Hartree–Fock (HF) or Kohn–Sham DFT methods, the problem of determining the excitation energies reduces to solving the generalized eigenvalue equation| [E[2] − ħωn0S[2]]Xn = 0, | (2) |
μ[1]†Xn = 〈0|![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) |n〉, X†nm[1] = 〈n| |n〉, X†nm[1] = 〈n|![[m with combining circumflex]](https://www.rsc.org/images/entities/i_char_006d_0302.gif) |0〉 |0〉 | (3) |
 | (4) |
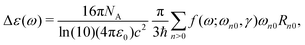 | (5) |
 | (6) |
 | (7) |
![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) is presented as the right-hand side. Finally, the relation between Δε and β is given in atomic units as
is presented as the right-hand side. Finally, the relation between Δε and β is given in atomic units as | (8) |
Employing reduced space algorithms, an hybrid OpenMP/MPI implementation for both solving the generalized eigenvalue equation and effective multifrequency/gradient evaluation of complex linear response functions has been reported recently.39
3 Computational details
The helicene geometries were optimized at the DFT level of theory using the B3LYP exchange-correlation functional47 in combination with the def2-TZVP basis set.48 The molecular structure optimizations were carried out with use of the Gaussian program.49 For comparison, a smaller range of systems was additionally optimized with the semi-empirical density functional tight-binding (DFTB)50 method using the approximate normal coordinate rational function optimization (ANCOPT) scheme. The DFTB calculations were carried out with the xtb program (version 6.2.3) applying the GFN2-xTB parameterization.51 All molecular response properties were calculated at the DFT level of theory, employing the B3LYP exchange-correlation functional in combination with the augmented def2-SVPD basis set.52 The contained contraction schemes of [4s2p|2s2p] and [8s4p2d|4s2p2d] for the primitive basis functions of hydrogen and carbon atoms, respectively, lead to a total number of 2952 contracted basis functions for the largest system investigated in this study. The spectra were obtained from the calculation of the 40 lowest excited states and evaluation of complex response functions between 0.07 and 0.15 a.u. in steps of 0.0025 a.u. for the eigenvalue equation and CPP approach, respectively. The convergence threshold for the relative residual norm in the subspace procedures for the eigenvalue and complex response solver was set to 10−4. The VeloxChem program (modified version 1.0)39 was used for all property calculations.4 Results and discussion
4.1 Computational protocol validation
Theoretically obtained molecular properties can only be as accurate as the underlying nuclear coordinates representing the molecular structure. The calculations of OPA and CD spectra are no exception to this rule, with the latter being especially sensitive to structural deviations.31 Experimentally obtained crystallographic structures are often distorted due to packing forces and not well suited as a starting point for computational studies. Especially in the case of carbohelicenes, the strong deviation from a C2 symmetry for reported structures and occurrence of several geometries for CH[5] and CH[7] discourage their usage.53–55 However, even a perfect structure is not sufficient to guarantee a reliable spectrum calculation. Also depending on the method applied for obtaining the excited state properties of interest, the challenge often lies within finding a balance between different levels of theory for both steps. Therefore, a computational protocol of obtaining geometries for carbohelicenes and subsequently calculating molecular properties is established in the following by comparison between theoretically and experimentally obtained CD spectra of CH[5]–CH[9].Adapting to an approach for obtaining optimized geometries used in a comprehensive study for smaller carbohelicenes,18 the DFT functional B3LYP in combination with a triple-zeta basis set (def2-TZVP) was chosen for initial testing. As it represents a rather conventional way for geometry optimizations, expected to yield highly accurate structures, it also allows for direct comparison of our methodology with the reported spectra obtained at the RI-CC2 level of theory. In an attempt to reduce the overall computational cost limiting the scope of our investigation, the relatively cheap DFTB method was used in addition. This choice was encouraged by its successful employment in a previous study on fullerenes44 and increasing popularity in the community.50 The CD spectra of CH[5] up to CH[9] were calculated for geometries optimized with both approaches by means of linear response theory at the DFT level of theory. The B3LYP functional was employed together with the def2-SVPD basis set containing diffuse basis functions. The spectral lineshape is obtained by convolution of the excitation energies and rotatory strengths of the 40 lowest excited states with a Lorentzian line broadening function. The first row of panels in Fig. 2 shows the calculated CD spectra of CH[5], CH[6], and CH[7] alongside the experimental and RI-CC2 reference spectra.
 | ||
| Fig. 2 CD spectra of CH[5]–CH[9] and selected systems of the investigated range. CH[5]–CH[9]: red and blue lines represent spectra calculated at the DFT level from geometries obtained with DFTB and standard DFT, respectively. Bars indicate the rotatory strengths of the 40 lowest excited states. RI-CC2 reference spectra, taken from ref. 18, based on the same DFT optimized geometries are shown in dotted dark grey, experimental spectra18,56 in dashed light grey. CH[n], n > 9: Arrows indicate the excited states contributing to CD bands dominant in the investigated range. States contributing to bands A, B, and C are shown in blue, orange, and green, respectively. | ||
Comparison of the calculated spectra of the DFTB and DFT optimized geometries reveals their structural sensitivity. For CH[5] and CH[6] the convoluted curves are in good agreement, each differing only by 9% in intensity and 0.04 eV in excitation energy for the positive spectral band maximum lowest in energy. Moving up in system size to CH[7], however, the corresponding discrepancies increase to 37% and 0.15 eV. This trend is confirmed to continue for the larger systems CH[8]/CH[9] (56%/64%, 0.14/0.15 eV; second row of Fig. 2) and identifies the need for an accurate geometry optimization method. Closer examination of the obtained structures indicate a deficiency of the semi-empirical DFTB method to accurately describe dihedral angles. This is expressed in an average dihedral angle of the helicene backbone of 23.5° and 22.4° for the DFT and DFTB optimized structures of CH[9], respectively. The deviation becomes even larger when the two outer dihedral angles are not considered (26.9° vs. 24.1°). The expected amplification of the resulting error with growing length of the helicene backbone is in line with the observed trend.
Based on the DFT optimized geometries, the applied methodology for the calculation of spectra was then to be assessed by a comparison with experimental data as well as with the generally accurate RI-CC2 approach reported in the literature, using the identical geometry optimization method. For the lowest-energy spectral band, our calculations for CH[5]–CH[7] exhibit a discrepancy in intensity from the experimentally obtained spectrum by 11%, 5%, and 1%, respectively, which, in the light of the deviations of 21%, 1%, and 9% of the RI-CC2 intensities, is deemed to be in excellent agreement. Whereas there is no coherent behaviour regarding an under- or overestimation of the intensities, a different picture is observed for the corresponding excitation energies. Our calculations underestimate the energies of the band maxima for CH[5], CH[6], and CH[7] by 0.15, 0.15, and 0.21 eV. This accuracy cannot quite compete with the CC2 reference, which shows an overestimation for CH[5]/CH[6] by 0.15/0.07 eV and underestimation by 0.01 eV for CH[7], but is still considered to be in very good agreement. This assessment is supported by the fact, that the spectral features higher in energy appear to be described sufficiently well by the applied LR-DFT approach, with arguably even better agreement than the CC2 reference.
The ability to qualitatively describe CD spectra independent of the length of the helicene backbone is crucial for the calculations carried out within this work. Confidence in a steady accuracy for larger system sizes is strengthened by comparison to experimental data for CH[8]/CH[9]. Similar deviations are observed for the intensity and excitation energy of the first spectral band (9%/1%, 0.14/0.10 eV).
The computational protocol employing DFT for geometry optimization and the linear response formalism at the DFT level of theory for spectrum calculations is used in the following after assessment over a range of system sizes that is comparable to the full investigated range in previous state-of-the-art studies.18,21
4.2 System size-depenency of the lowest-energy CD band
The calculated/experimental CD spectra of carbohelicenes CH[5]–CH[9] exhibit several noteworthy features and trends. All spectra show a positive molar circular dichroism Δε as their lowest-energy band, satisfying an a priori rule of thumb for right-handed helices,30 such as the probed (P)-carbohelicenes. For each system this band rapidly descends into a negative band with increasing excitation energy, a characteristic also known as positive Cotton effect. The intensity of the positive band (referred to as band A in the following and further categorized in Section 4.3) does not vary significantly for different system sizes apart from an increase with the completion of one helical turn (CH[6]), whereas the negative band intensity does not seem to follow any pattern. The most striking trend, however, is the change in excitation energy of band A. With every added benzene ring, a red-shift in the calculated (experimental) band energy varying from 0.13 (0.18) to 0.33 (0.27) eV can be observed, accounting for a total shift of 0.79 (0.84) eV over the full range. This alteration has been addressed by previous studies18,23 and has—based on the tendency of the shift to decrease on the larger end of the investigated ranges—led to the conclusion that the excitation energy reaches convergence towards an effective conjugation length for carbohelicenes. This behaviour, for which the corresponding energy shift shows linear dependence on the reciprocal number of building blocks 1/n, is common for CD and absorption bands in many π-conjugated oligomers with planar backbones57 and was also found for the linear and hence planar carbohelicene-analogue of acenes.58While we fully support the prediction of a convergence for that particular spectral band, we argue that neither the range of systems calculated above for comparison with experiments, nor the slightly larger range (CH[4]–CH[10]) used in ref. 18 are sufficient to accurately estimate the convergence limit. Moreover, the overlap of the conjugated system with itself as introduced by the helical structure constitutes a fundamental difference to planar analogues that potentially prevents a straightforward extrapolation of CD/absorption spectra of systems with significantly longer backbone chains altogether. Not least the predicted inversion of the Cotton effect as a result of the calculated convergence limits of the positive and negative CD bands prompted us to explicitly examine larger systems. With the computational resources, as well as the software tools to harness those at hand, we therefore calculated the CD spectra of carbohelicenes up to CH[30] employing the established computational protocol (see Fig. S1 and S2 in the ESI,† for all spectra).
In order to ensure that the spectral region of interest is sufficiently well described by calculation of the lowest 40 excited states even on the larger end of the investigated range of systems, the CD spectra of CH[12], CH[18], CH[24], and CH[30] were additionally calculated with the CPP approach (Fig. S3 in the ESI†). In contrast to the convoluted spectrum, evaluation of complex response functions gives rise to values of the observable that are exact within the methodological framework for given frequencies. The convoluted spectra of CH[12], CH[18], and CH[24] are confirmed to represent all spectral bands of interest with only marginal deviations. The largest system CH[30] shows minor discrepancies that do not affect the following discussion.
The calculated CD spectra of the next larger systems CH[10] to CH[12] show a further decreasing red-shift of band A slowly revealing the convergence in excitation energy. The negative spectral band next higher in energy, however, vanishes for CH[11] for the first time in the homologous series due to the dominance of the high energy region of the spectra by excited states assigned with positive rotatory strengths. This effect is amplified by the emergence of an excited state close in energy to band A that rapidly gains rotatory strength while experiencing a red-shift larger than the lowest-energy band (Fig. 2). After it first appears in the CD spectrum of CH[13] with seemingly negligible impact, its contribution alters the spectral shape for CH[15] significantly, leading to the formation of a new CD band (denoted band B, and analyzed in Section 4.3) that exceeds the intensity of band A for CH[17] and larger systems. The further increase of the intensity of band B causes the incorporation of band A. However, the rotatory strengths of the excited states contributing to the latter experience a decrease for longer backbone lengths, with CH[23] being the largest system showing a noticeable contribution.
A very similar behaviour can be observed for another band, for which a contributing excited state can first be detected in the CD spectrum of CH[19]. Analogously, the corresponding contributing excited states undergo an increase in rotatory strength with growing backbone length along with a red-shift in excitation energy larger than that of the spectrum-dominating states, leading to the formation of a distinct spectral band (denoted band C, and analyzed in Section 4.3). Deviating from the first merge of CD bands, the gain in intensity of band C with system size is not large enough to significantly dominate band B by the time the shift in energy causes the bands to coalesce for CH[24]–CH[26], suggesting that band B remains dominant. Yet, the contributing rotatory strengths and the observed acceleration of the increase in intensity of the band reveal the switch in band-dominance finalized at CH[27]. Again, the progression of states is accompanied by a decrease in the contribution of the priorly dominating band B.
Fig. 3 shows a schematic overview of the isolated spectral bands A, B, and C, resolved for the range of system sizes CH[n] with n = 13–30. For a proportionate representation, the shown spectra were obtained by Lorentzian line-broadening considering only the contributing excited states for each band. This choice enables a direct comparison of the progression of the bands, emphasizing the large differences in intensity clearly dominating the previous one. The respective maxima of those intensities are reached at different excitation energies, decreasing from A to B to C.
 | ||
| Fig. 3 Isolated CD spectra of bands A, B, and C for systems CH[13]–CH[30]. Curves were obtained by Lorentzian line-broadening of the contributing rotatory strengths for each band. | ||
In order to gain further insights in the system size-dependency, the excitation energies and molar circular dichroism of the isolated band maxima were plotted over the the number of benzene rings n of the homologous series (Fig. 4).
Along with those for the band maxima, the excitation energies of the contributing states are included in the upper panel. Whereas the intensities of bands A and B can be mapped to rotatory strengths of one or two excited states, band C arises from a more complex pattern with contributions of up to three excited states, sometimes largely separated in excitation energy. This complexity makes an assignment of contributing states more difficult, while reducing the error introduced by wrongfully assigned states at the same time.
The progression in excitation energy shows a similar pattern for all spectral bands. The described red-shift with respect to an increase of n is strongest in the first steps following the emergence of the band, but weakens continuously, seemingly approaching a convergence limit. However, the increasing overlap between bands A and B along with the decrease in intensity of the former to a point at which it vanishes, makes an extrapolation of this limit for band A and the corresponding effective conjugation length obsolete. In the light of this observation, the similar progression of band B within the investigated range of system sizes strongly suggests that the same assumption can be made for this band. Moreover, one specific aspect about the progressions of bands A, B, and C indicate a periodic recurrence of newly emerging CD bands: With the completion of one helical turn (to a good approximation) every six benzene rings (Fig. 1), the systems CH[13] and CH[19] not only mark the starting point of the progressions of bands B and C, respectively, but also introduce an additional overlapping layer in the helix. This correlation becomes more evident after a closer inspection of the smaller end of the system range. The band maxima for CH[5] and CH[6] appear to slightly deviate in both, excitation energy and Δε from the progression described by systems CH[7]–CH[23]. Additionally, from a structural point of view, these carbohelicenes constitute an exception, as the respective ends of the helical chains are in close proximity, enabling a unique direct interaction. Following this logic, the true origin of the progression is represented by CH[7], fitting exactly into the sequence of systems mentioned above. As a consequence, the emergence of a fourth CD band is expected to fall into the investigated range at CH[25]. In fact, the convoluted spectra of CH[25]–CH[30] exhibit a positive feature higher in energy than band C. However, the underlying electronic structure appears to be more complex than for bands A to C and an assignment of contributing excited states, that potentially rank close to the limit of 40 computed excitations, becomes speculative. Missing this assignment, which is particularly difficult in the onset of the progression, the visualization of a fourth CD band was omitted in Fig. 3 and 4.
The progressions of the band maximum intensities emphasize the similarities between the different spectral bands. The rapid increase in intensity with respect to the number of benzene rings for all bands is followed by a decrease with a similar rate for bands A and B in the investigated range. The maximum intensity of the CD signal is rising from bands A to B and C, although a maximum for band C is not observed up to the largest system CH[30]. The step-wise growth in intensity maxima combined with a similar increase rate for all bands leads to a “delayed” dominance of the spectrum with respect to the emergence of bands B and C. While the bands first appear for CH[13] and CH[19]—a difference of one helical turn, as outlined above—they become the most dominant band in the spectrum of CH[17] and CH[26], respectively, differing by nine benzene rings. The resulting overall buildup of the lowest-energy CD band is therefore not expected to follow the same periodicity of helical turns. This behaviour also explains why a fourth CD band is nowhere close to a dominance of the spectrum of CH[30].
Despite not being periodic, the increase in intensity strongly deviates from a linear scaling with respect to the number of benzene rings, as predicted in ref. 23 based on semi-empirical calculations at the INDO/S level of theory. Supported by the fact that a linear behavior also contradicts experimental findings for CH[5]–CH[9], we argue that our first-principles approach provides the most accurate description of this size-dependency to date. The general trend, however, is confirmed and even though an amplification of the CD signal, desirable for many applications, is usually achieved by functionalization,6,17,20 the observed intensity-size relation opens up new perspectives, as experimental techniques advance.
4.3 Characterization of CD bands
So far, the three spectral bands and the contributing states that are subject to the discussion above were denoted A, B, and C for simplicity. Based on their distinctive nature, several classifications of electronic states in polycyclic aromatic systems have been suggested and applied to hexahelicene CH[6],59 out of which the nomenclature by Platt for cata-condensed hydrocarbons60 has been established in the decades to come and is commonly used in recent publications. Besides the multiplicity and symmetry considerations, the main feature for classification is the so-called ring quantum number q, originating in Hückel theory,61 defined by the molecular orbitals involved in the excitation. Owing to the high density of states and complexity of the transitions in the carbohelicenes towards the larger end of the investigated range, especially for bands B and C, an adaption of this nomenclature is nontrivial and beyond the scope of this work. Although the notation chosen instead (A/B/C) is sufficient for describing the observed progressions, it is worthwhile to have a closer look at some of the characteristic features.The near C2 symmetry of the geometry-optimized carbohelicenes enables a categorization of electronic states according to their polarization with respect to the rotational axis. Excitations polarizing along the C2-axis or perpendicular to it are assigned to symmetries A or B, respectively. The direction of polarization can be directly seen from the electric transition dipole moment μ. The electric transition dipole moments of the contributing transitions to bands A, B, and C are shown in Fig. 1 along with the corresponding magnetic transition dipole moments. In the chosen orientation the x-axis corresponds to the rotational C2-axis, whereas the helical axis is aligned with the z-axis. The transition dipole moment vectors are represented by their projection onto the yz-plane, justified by negligible out-of-plane components of less than 1% of the shown projection for the electric and magnetic moments.
The orientation of the electric transition dipole moments reveals, that all CD bands exhibit B symmetry, as previously reported for band A.18 Moreover, since the rotatory strength is determined by their scalar product, the relative orientation of the electric and magnetic moment gives further insight in the progression of each band. Thus, the rise in intensity following the emergence of each band is linked to a decrease in the angle between the two moment vectors with the chosen gauge origin. In the case of bands B and C this trend is amplified by an increase of the magnitudes of the transition moments, whereas the largest magnitudes for band A are already present in the smallest investigated system CH[5], emphasizing the uniqueness of the beginning of the progression of band A. As the moment vectors become more parallel with larger system sizes, they also align with the helical axis. The observed decrease in intensity for bands A and B is connected to the decline in magnitudes of the corresponding transition dipole moments. Hereby, the decrease of the electric moment sets in at smaller system sizes, to then be followed by the magnetic moment.
It should be mentioned that each spectral band is represented by the dipole transition moments of one (the most dominant) excited state per carbohelicene in Fig. 1. While the orientations of vectors contributing to the same band are alike, their magnitudes differ corresponding to the amount of the contribution. As a consequence, it is not possible to quantify the described trends. Regarding the contribution of several excited states to the intensity of CD bands, a well-behaved trend was found for bands A and B: For carbohelicenes with an even number of benzene rings, both bands A and B arise solely from one excited state. However, for odd values of n the band highest in intensity experiences a split into contributions from two separate excited states (see Fig. 4 or Fig. S1 and S2 in the ESI†). Investigation of the orbitals involved in the transition shows, that the split originates from excitations resulting in two different electron-density distributions—with a localization on benzene rings 2k and 2k + 1 (k = 0, 1, 2,…), respectively. The absence of this split for systems with even numbers of aromatic rings can be explained with the symmetry-caused degeneracy of the same effect. The only exception of this trend is marked by CH[5], again, indicating an inconsistency with the progression. For band C no such trend is recognized, potentially hidden by the complexity of the underlying electronic structure.
In order to obtain a more detailed description of the electronic transitions leading to the formation of the spectral bands, the involved orbitals were examined in the form of natural transition orbitals (NTOs).62 The latter provide a more compact representation of transitions with significant contributions from more than one molecular orbital to the ground and excited state electron density. These more descriptive particle and hole densities are obtained by means of unitary transformations. The NTOs of the transitions contributing to bands A–C display localization effects varying for every band. As two-dimensional orbital representations can often be ambiguous or even misleading, the analysis tool ElecTrans63,64 was used to achieve a clearer picture. For an illustration of localization effects, a division of the system into subsystems is obligatory. Due to their symmetry a minimum of three continuous subgroups is needed in the case of carbohelicenes and a partitioning into three parts approximately equal in size has been proven to capture the observed effects in the best way possible. The differences in the hole and particle densities of the respective subunits give rise to the net transfer of electron density resulting from the corresponding excitation. Thereby, ElecTrans does not consider linear combinations of atomic orbital densities, but is solely based on a Voronoi segmentation of the grid points for the hole and particle densities provided by VeloxChem. The electronic transitions for different bands are summarized in Fig. 5 using exemplary systems.
 | ||
| Fig. 5 Net electron density transfer in natural transition orbitals (NTOs) for electronic excitations contributing to bands A, B, and C. The analysis tool ElecTrans63,64 was used after selection of suitable subunits for each system. | ||
The only contributing state to band A in the CD spectrum of CH[12] exhibits a relatively small transfer of electron density from the outer eight rings to the inner four. The division into subunits for this particular system is therefore rather arbitrary and the electronic excitation can be identified as a local excitation (LE). However, the hole and particle densities are not delocalized over the full length of the helical chain, with vanishing values positioned on the exterior two benzene rings on both ends. This causes an disproportional fraction of around 50% to be found on the inner third of the molecule. As band B arises from a single excited state in the spectrum of CH[18] with a strong rotatory strength and well separated from other states, this transition was chosen for analysis with ElecTrans. The resulting picture after separation into subunits of six benzene rings each shows a localization on both outer subunits of the hole density. Excitation is accompanied by an electron transfer to the inner subunit of 40.1% in total, indicating a charge-transfer (CT) character. The strongest contributing excited state in the spectrum of CH[28] and a division into subunits of eight inner and ten outer benzene rings were chosen for the representation of band C. The corresponding analysis displays an almost reversed pattern with respect to band B. The hole density is just slightly localized on the inner subunit (35.0% of the density localized on 26.4% of the atoms), but the substantial transfer of 26.8% of the density to the outer subunits through the excitation causes a strong localization of the particle density on the latter. From the transfer of electron density it becomes evident, that there are fundamental differences in the nature of the electronic transitions underlying to the spectral bands. The CT character of bands B and C naturally raises the suspicion that their occurrence is merely an artifact of the applied method, as DFT is known for deficiencies in describing CT states without consideration of long-range corrections.65 However, calculations at the HF level that do inherently not suffer from the same deficiencies showed equivalent CD band progressions to those presented herein. Therefore, we are confident to provide an accurate description of the electronic structure.
5 Summary
Enabled by recent advances in the utilization of large-scale high-performance computing resources for quantum chemical simulations, we calculated the electronic CD spectra of carbohelicenes in the range of CH[5]–CH[30] at the LR-DFT/B3LYP level of theory, including the by far largest members of the homologous series treated with an ab initio approach to date.The chosen computational protocol was assessed by comparison with reference data for CH[5]–CH[9]. Discrepancies from experimentally obtained spectra in intensities and excitation energies of the lowest-energy spectral band are no larger than 11% and 0.21 eV, similar in accuracy to reported state-of-the-art benchmark calculations. Together with a good qualitative description of spectral features higher in energy, these values establish reliability of the results obtained for larger systems.
The calculated CD spectra show the emergence of two new bands that rapidly gain intensity and undergo a strong, but decreasing red-shift with increasing system size. These progressions cause each band to dominate the priorly prevalent band, leading to a step-wise intensity-buildup of the lowest-energy band. In contrast to linear analogues, this behavior makes the estimation of an effective conjugation length obsolete—a consequence of the unique helical structure that allows the conjugated system to interact with itself. A series of characteristics of the band progressions, such as the onset system sizes (CH[7], CH[13], CH[19]), growing rate of intensity, relative orientation of transition dipole moments and symmetry of the contributing states indicate a periodic recurrence of the emergence of new spectral bands, that is directly linked to the number of helical turns and hence overlapping layers of conjugation.
Further analysis revealed the fundamentally different nature of the electronic transitions leading to the formation of the observed CD bands. Accordingly, the initially observed band was identified as LE, whereas the emerged bands show CT character with electron density transfer between outer and inner subunits of 40.1% and 26.8%, but reversed direction.
While the provided in-depth description of the system size-dependency of the electronic structure of carbohelicenes confirms the previously reported enhancement of the CD signal strength, it dissents from the linearity of this relation and the prediction of an effective conjugation length. With previous studies being limited by the accuracy of the applied methods23 or range of systems,18,21 we are confident that our fully analytical approach overhauls the current conception. Moreover, the revealed complexity of the CD band progressions generally encourages to exercise caution when extrapolating trends from a small range of systems for seemingly straightforward size extensions.
Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Acknowledgements
Financial support is acknowledged from the European Commission in the form of the ITN titled ‘Computational Spectroscopy in Natural Sciences and Engineering’ (COSINE) (Grant No. 765739), the Swedish e-Science Research Centre (SeRC), and the Swedish Research Council (Grant No. 2018–4343). Computational resources are provided by the Swedish National Infrastructure for Computing (SNIC). The authors thank Mathieu Linares for useful discussions and assistance in the analysis with ElecTrans.References
- A. D. McNaught and A. Wilkinson, IUPAC. Compendium of Chemical Terminology, Blackwell Scientific Publications, Oxford, 2nd edn, 1997 Search PubMed.
- Y. Shen and C.-F. Chen, Chem. Rev., 2012, 112, 1463–1535 CrossRef CAS PubMed.
- K. Yamamoto, T. Shimizu, K. Igawa, K. Tomooka, G. Hirai, H. Suemune and K. Usui, Sci. Rep., 2016, 6, 36211 CrossRef PubMed.
- N. Takenaka, J. Chen, B. Captain, R. S. Sarangthem and A. Chandrakumar, J. Am. Chem. Soc., 2010, 132, 4536–4537 CrossRef CAS PubMed.
- P. Aillard, A. Voituriez and A. Marinetti, Dalton Trans., 2014, 43, 15263–15278 RSC.
- W. Hua, Z. Liu, L. Duan, G. Dong, Y. Qiu, B. Zhang, D. Cui, X. Tao, N. Cheng and Y. Liu, RSC Adv., 2015, 5, 75–84 RSC.
- J. OuYang and J. Crassous, Coord. Chem. Rev., 2018, 376, 533–547 CrossRef CAS.
- J. R. Brandt, X. Wang, Y. Yang, A. J. Campbell and M. J. Fuchter, J. Am. Chem. Soc., 2016, 138, 9743–9746 CrossRef CAS PubMed.
- Y. Yang, R. C. Da Costa, M. J. Fuchter and A. J. Campbell, Nat. Photonics, 2013, 7, 634–638 CrossRef CAS.
- Y. Yang, B. Rice, X. Shi, J. R. Brandt, R. Correa da Costa, G. J. Hedley, D.-M. Smilgies, J. M. Frost, I. D. W. Samuel, A. Otero-de-la Roza, E. R. Johnson, K. E. Jelfs, J. Nelson, A. J. Campbell and M. J. Fuchter, ACS Nano, 2017, 11, 8329–8338 CrossRef CAS PubMed.
- K. Nakano, H. Oyama, Y. Nishimura, S. Nakasako and K. Nozaki, Angew. Chem., Int. Ed., 2012, 51, 695–699 CrossRef CAS PubMed.
- R. Rodrguez, C. Naranjo, A. Kumar, P. Matozzo, T. K. Das, Q. Zhu, N. Vanthuyne, R. Gómez, R. Naaman and L. Sánchez, et al. , J. Am. Chem. Soc., 2022, 144, 7709–7719 CrossRef PubMed.
- J. Meisenheimer and K. Witte, Ber. Dtsch. Chem. Ges., 1903, 36, 4153–4164 CrossRef CAS.
- R. Martin and M. Baes, Tetrahedron, 1975, 31, 2135–2137 CrossRef CAS.
- K. Mori, T. Murase and M. Fujita, Angew. Chem., Int. Ed., 2015, 54, 6847–6851 CrossRef CAS PubMed.
- J. Nejedly, M. Šámal, J. Rybáček, M. Tobrmanová, F. Szydlo, C. Coudret, M. Neumeier, J. Vacek, J. Vacek Chocholoušová, M. Buděšìnsky, D. Šaman, L. Bednárová, L. Sieger, I. G. Stará and I. Stary, Angew. Chem., Int. Ed., 2017, 56, 5839–5843 CrossRef CAS PubMed.
- X. Xiao, S. K. Pedersen, D. Aranda, J. Yang, R. A. Wiscons, M. Pittelkow, M. L. Steigerwald, F. Santoro, N. J. Schuster and C. Nuckolls, J. Am. Chem. Soc., 2021, 143, 983–991 CrossRef CAS PubMed.
- Y. Nakai, T. Mori and Y. Inoue, J. Phys. Chem. A, 2012, 116, 7372–7385 CrossRef CAS PubMed.
- Y. Nakai, T. Mori, K. Sato and Y. Inoue, J. Phys. Chem. A, 2013, 117, 5082–5092 CrossRef CAS PubMed.
- Y. Nakai, T. Mori and Y. Inoue, J. Phys. Chem. A, 2013, 117, 83–93 CrossRef CAS PubMed.
- F. Furche, R. Ahlrichs, C. Wachsmann, E. Weber, A. Sobanski, F. Vögtle and S. Grimme, J. Am. Chem. Soc., 2000, 122, 1717–1724 CrossRef CAS.
- J. Autschbach, T. Ziegler, S. J. van Gisbergen and E. J. Baerends, J. Chem. Phys., 2002, 116, 6930–6940 CrossRef CAS.
- E. Botek and B. Champagne, J. Chem. Phys., 2007, 127, 204101 CrossRef PubMed.
- E. Cherni, B. Champagne, S. Ayadi and V. Liégeois, Phys. Chem. Chem. Phys., 2019, 21, 14678–14691 RSC.
- B. Champagne, J.-M. André, E. Botek, E. Licandro, S. Maiorana, A. Bossi, K. Clays and A. Persoons, ChemPhysChem, 2004, 5, 1438–1442 CrossRef CAS PubMed.
- T. B. Demissie, M. S. Sundar, K. Thangavel, V. Andrushchenko, A. V. Bedekar and P. Bour, ACS Omega, 2021, 6, 2420–2428 CrossRef CAS PubMed.
- C. Bannwarth, J. Seibert and S. Grimme, Chirality, 2016, 28, 365–369 CrossRef CAS PubMed.
- C. Bannwarth and S. Grimme, Comput. Theor. Chem., 2014, 1040, 45–53 CrossRef.
- J. Ridley and M. Zerner, Theor. Chem. Acc., 1973, 32, 111–134 Search PubMed.
- N. Berova, K. Nakanishi and R. W. Woody, Circular Dichroism: Principles and Applications, John Wiley & Sons, Ltd, New York, 2000 Search PubMed.
- G. Pescitelli, L. Di Bari and N. Berova, Chem. Soc. Rev., 2011, 40, 4603–4625 RSC.
- S. Grimme, J. Harren, A. Sobanski and F. Vögtle, Eur. J. Org. Chem., 1998, 1491–1509 CrossRef CAS.
- T. Wu, X. P. Zhang, C. H. Li, P. Bour, Y. Z. Li and X. Z. You, Chirality, 2012, 24, 451–458 CrossRef CAS PubMed.
- F. Zsila, Z. Bikádi and M. Simonyi, Biochem. Pharmacol., 2003, 65, 447–456 CrossRef CAS PubMed.
- I. Warnke and F. Furche, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 150–166 CAS.
- P. L. Polavarapu, Chem. Rec., 2007, 7, 125–136 CrossRef CAS PubMed.
- J. Autschbach, Chirality, 2009, 21, E116–E152 CrossRef CAS PubMed.
- M. Srebro-Hooper and J. Autschbach, Annu. Rev. Phys. Chem., 2017, 68, 399–420 CrossRef CAS PubMed.
- Z. Rinkevicius, X. Li, O. Vahtras, K. Ahmadzadeh, M. Brand, M. Ringholm, N. H. List, M. Scheurer, M. Scott, A. Dreuw and P. Norman, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020, 10, e1457 CAS.
- P. Norman, D. M. Bishop, H. J. A. Jensen and J. Oddershede, J. Chem. Phys., 2001, 115, 10323–10334 CrossRef CAS.
- P. Norman, D. M. Bishop, H. J. A. Jensen and J. Oddershede, J. Chem. Phys., 2005, 123, 1–18 Search PubMed.
- J. Kauczor, P. Jørgensen and P. Norman, J. Chem. Theory Comput., 2011, 7, 1610–1630 CrossRef CAS PubMed.
- J. Kauczor and P. Norman, J. Chem. Theory Comput., 2014, 10, 2449 CrossRef CAS PubMed.
- M. Brand, K. Ahmadzadeh, X. Li, Z. Rinkevicius, W. A. Saidi and P. Norman, J. Chem. Phys., 2021, 154, 074304 CrossRef CAS PubMed.
- P. Norman, K. Ruud and T. Saue, Principles and practices of molecular properties, John Wiley & Sons, Ltd, Chichester, UK, 2018 Search PubMed.
- J. Oddershede, P. Jørgensen and D. L. Yeager, Comput. Phys. Rep., 1984, 2, 33–92 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian-16 Revision C.01, 2019, Gaussian Inc., Wallingford CT Search PubMed.
- C. Bannwarth, E. Caldeweyher, S. Ehlert, A. Hansen, P. Pracht, J. Seibert, S. Spicher and S. Grimme, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11, e1493 CAS.
- C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652–1671 CrossRef CAS PubMed.
- D. Rappoport and F. Furche, J. Chem. Phys., 2010, 133, 134105 CrossRef PubMed.
- R. Kuroda, J. Chem. Soc., Perkin Trans. 2, 1982, 789–794 RSC.
- P. T. Beurskens, G. Beurskens and T. E. M. Van, den Hark, Cryst. Struct. Commun., 1976, 5, 241–246 CAS.
- M. Joly, N. Defay, R. H. Martin, J. P. Declerq, G. Germain, B. Soubrier-Payen and M. Van Meerssche, Helv. Chim. Acta, 1977, 60, 537–560 CrossRef CAS.
- R. Martin and M. Marchant, Tetrahedron, 1974, 30, 343–345 CrossRef CAS.
- R. E. Martin and F. Diederich, Angew. Chem., Int. Ed., 1999, 38, 1350–1377 CrossRef PubMed.
- B. Shen, J. Tatchen, E. Sanchez-Garcia and H. F. Bettinger, Angew. Chem., Int. Ed., 2018, 57, 10506–10509 CrossRef CAS PubMed.
- O. E. Weigang, J. A. Turner and P. A. Trouard, J. Chem. Phys., 1966, 45, 1126–1134 CrossRef CAS.
- J. R. Platt, J. Chem. Phys., 1949, 17, 484–495 CrossRef CAS.
- E. Hückel, Z. Phys., 1931, 70, 204 CrossRef.
- R. L. Martin, J. Chem. Phys., 2003, 118, 4775–4777 CrossRef CAS.
- T. B. Masood, ElecTrans, https://github.com/tbmasood/ElecTrans, 2022.
- T. B. Masood, S. Thygesen, M. Linares, A. I. Abrikosov, V. Natarajan and I. Hotz, Comput. Graph. Forum, 2021, 40, 287–298 CrossRef.
- A. Dreuw, J. L. Weisman and M. Head-Gordon, J. Chem. Phys., 2003, 119, 2943–2946 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: All CD spectra of CH[5]-CH[30] and comparison to calculations with the CPP approach for CH[12], CH[18], CH[24], and CH[30]. See DOI: https://doi.org/10.1039/d2cp02371g |
| This journal is © the Owner Societies 2022 |


