On the origin of the inverted singlet–triplet gap of the 5th generation light-emitting molecules

Abstract

Excitation energies of the lowest singlet and triplet state of molecules whose first excited singlet state lies energetically below the first triplet state have been studied computationally at (time-dependent) density functional theory, coupled-cluster, and second-order multiconfiguration perturbation theory levels. The calculations at the ab initio levels show that the singlet–triplet gap is inverted as compared to the one expected from Hund's rule, whereas all density functionals yield the triplet state as the lowest excited state. Double excitations responsible for the inverted singlet–triplet gap have been identified. Employing the spin-flip and ΔSCF methods, singlet–triplet inversion was obtained at the density functional theory level for some of the studied molecules.

---

1 Introduction

Molecules violating Hund's first rule¹ have become a hot research topic, studied in many recent articles.^2–10 Some nitrogen- and boron-substituted π-conjugated systems exhibit an inverted energy order of the lowest excited singlet and triplet states; the S₁ state is energetically below the T₁ state. Results obtained in experimental studies on chemical derivatives of this class of molecules agree with the theoretically predicted reverse order of the lowest singlet and triplet states.^3,6,11 The inverted singlet–triplet gap, often abbreviated INVEST, makes these molecules interesting not only from fundamental research point of view, but also as promising candidate molecules for use in photophysical applications.

The most recent organic light-emitting diodes (OLEDs) function on the principle of thermally activated delayed fluorescence (TADF).^12–20 As excitons injected into OLEDs recombine in a singlet–triplet ratio of 1 : 3, the internal quantum efficiency (IQE) cannot theoretically exceed 25% without using triplet excitons. In TADF, the reverse intersystem crossing (RISC) is enabled at room temperature due to a small energy gap between the lowest singlet and triplet states (ΔE_ST) and a non-vanishing spin–orbit (SO) coupling between the first excited singlet and triplet states, leading to a thermal up-conversion of triplet excitons to the singlet state, which results in a high IQE of up to 100%.^14,15

The ΔE_ST value is to the first order proportional to the exchange interaction that can be minimized by a spatial separation of the molecular orbitals involved in the excitation-related transitions, which usually are the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO).^2,21 Long-ranged spatial separation of the HOMO and LUMO leads to systems with considerable charge-transfer (CT) character and nearly degenerate excited singlet and triplet states.¹⁴ Minimizing the singlet–triplet gap by a large spatial separation of the frontier orbitals on donor and acceptor groups may also result in a large Stokes shift and a broad luminescence peak.¹⁹ Recent studies suggest that long-ranged HOMO–LUMO separations are only one of the determining factors in the design of molecules with a small (or negative) singlet–triplet gap.^2,19 The small HOMO–LUMO gap that is necessary for TADF emitters can also be obtained by using molecules with a significant multiple resonance effect (MRE).^19,22,23 The same mechanism may also be responsible for the inverted singlet–triplet gap of INVEST molecules.²

Several recent studies have concluded that molecules with inverted singlet–triplet excitation energies, which are thus violating Hund's first rule, have a good chance of becoming a new class of efficient OLED molecules that are called the fifth (5th) generation OLED molecules.^2–8 The triplet excitons are expected to favor the SO-induced intersystem crossing (ISC) de-excitation pathway without any need for thermal activation as the transfer is exothermic. Although the first reported INVEST molecule dates back to 1980,²⁴ the interest in discovering new molecules exhibiting the INVEST property was apparently sparked by two independent publications in 2019.^2,3 The first presented systems were N-substituted phenalenes cyclazine and heptazine and their derivatives. These molecules were soon accompanied by many other INVEST molecules.^4–6,10

Recent computational studies have shown that time-dependent density functional theory (TDDFT) methods fail to predict an inverted S₁–T₁ energy separation.^2–5,8,25 The reason for this is proposed to be the inability of conventional TDDFT methods to include double excitation contributions,^26,27 which seems to be the prerequisite for the description of an inverted singlet–triplet gap.^2–4,25

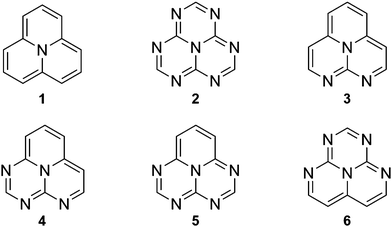
In this work, we computationally study electronic excited states of the INVEST molecules shown in Fig. 1 with the aim to understand the underlying reasons for the inverted singlet–triplet gap, and to determine which computational methods are suitable for correct recognition of the INVEST property. The examined systems have been chosen among the set of new molecules exhibiting the INVEST property discovered in a recent extensive virtual screening study by Pollice et al.⁶

Fig. 1 The chemical structures of the studied molecules.

In the following sections, the inability of TDDFT to predict the INVEST property is addressed by a computational benchmark. Results of the benchmark study are compared with results obtained in ab initio and density functional theory (DFT) calculations using the spin-flip DFT (SFDFT) and the ΔSCF (self-consistent-field) approaches. Density-difference and spin-density plots obtained using various methods are discussed. We show that the SFDFT and the ΔSCF methods may provide viable DFT approaches for studies of the INVEST systems. Approximate second-order coupled-cluster methods are appropriate ab initio computational levels for studies of the large INVEST molecules, since they yield similar results as obtained at computationally expensive multireference ab initio levels of theory.

2 Methods

Density functional theory (DFT) optimizations of the molecular structure of the ground state (S₀) of molecules 1–6 were carried out at the B3LYP/def2-TZVPD^28–31 level using the m5 integration grid³² and the D3–BJ dispersion correction.^33,34 The excited state geometries were optimized at the same level of theory using time-dependent DFT (TDDFT).²¹ Vertical excitation energies of the lowest excited singlet (S₁) and triplet (T₁) states were calculated for the DFT optimized S₀ geometry at the ab initio second-order algebraic diagrammatic construction (ADC(2))^35,36 level, the approximate second-order coupled cluster (CC2) level^37,38 and at TDDFT levels using the def2-TZVPD basis set.³¹ We employed the S-VWN^39–41 local density approximation (LDA) functional; BP86^28,41,42 and PBE^43,44 functionals at the generalized gradient approximation (GGA) level; the TPSS^43,45 meta-GGA functional; the PBE0,^43,46,47 TPSSh,^43,45,48 B3LYP,^28–30 and BHLYP^28,29,49 hybrid functionals; the CAM-B3LYP,⁵⁰ tuned-CAM-B3LYP,⁵¹ ωB97X-D,⁵² and MN15⁵³ range-separated functionals; and the LH14t-calPBE⁵⁴ local hybrid functional.

The ground-state geometries were also optimized at the second-order Møller–Plesset (MP2) perturbation theory level using the def2-TZVP basis set.⁵⁵ The excited state geometries were optimized at the ab initio level using the ADC(2) method employing the same basis set. The transition energies i.e., excitation energies from S₀ to S₁ and T₁ and de-excitation energies from S₁ and T₁ to S₀ were computed using ADC(2) and CC2 with the def2-TZVP basis set.

The Turbomole 7.5.1 program package^56,57 was used for the DFT, MP2, ADC(2), and CC2 calculations. Molecules 1, 2, 3, 5 and 6 were studied at the DFT level using the C_2v point group, whereas the point group of molecule 4 is C_s. The excited state structures were also optimized without symmetry constraints, since they may have a lower symmetry than the ground state. No symmetry was considered in the ab initio calculations. The molecular structure of the excited states belong to the same point group as the ground state. In the resolution-of-identity (RI) approximation^36–38 of the DFT calculations, we used the universal auxiliary basis sets.⁵⁸ In the ab initio calculations employing the RI approximation, we used the corresponding auxiliary basis sets.⁵⁹ Vibrational frequencies for the ground state were calculated using the aoforce module of Turbomole.^60,61 The vibrational frequencies of the excited states were calculated with the NumForce module of Turbomole. Calculations of the vibrational frequencies showed that the optimized molecular structures are minima on the potential energy surface. Zero point vibrational energies (ZPVE) for the 0–0 excitation energies were calculated with NumForce at the CC2 and ADC(2) level using the ab initio optimized structures.

Molecular structure optimization of the ground state of all molecules was also performed at the extended multi-configuration quasi-degenerate perturbation theory at the second order (XMC-QDPT2) level⁶² using the def2-TZVP basis set. Optimizations of the molecular structures of the S₁ and T₁ states were carried out at the same level of theory. The active space of the complete active space self-consistent field (CASSCF) calculations includes 12 electrons in 9 molecular orbitals. For molecule 1, we also performed similar calculations with 14 electrons in 14 orbitals. The XMC-QDPT2 calculations were performed using the Firefly QC package,⁶³ which is partially based on the GAMESS (US) source code.⁶⁴ The commonly used abbreviation CASPT2 (complete active space perturbation theory of second order) is used instead of XMC-QDPT2 in discussion of the results.

The spin-flip DFT (SFDFT) calculations were performed at the Tamm–Dancoff LDA level using Turbomole⁶⁵ employing the S-VWN functional and the def2-TZVPD basis set. The non-aufbau SCF solutions of the S₁ and T₁ states of five of the six molecules were optimized at the unrestricted DFT level with one electron in the LUMO belonging to the b₂ irreducible representation of the C_2v point group and only one electron in the HOMO of the a₂ irreducible representation. The energy difference between the total energy of S₁ and T₁ states (ΔSCF energies) were calculated with the B3LYP and ωB97X-D functionals.

3 Results and discussion

3.1 Evaluation of TDDFT performance

TDDFT is often the method of choice for computational characterization of excited states. A recent extensive study evaluating the performance of TDDFT calculations with 43 functionals on a large benchmark set suggested that TDDFT generally provides data with rather high accuracy at reasonable computational costs.⁶⁶ However, the inability of TDDFT to correctly predict the singlet–triplet inversion of the INVEST molecules has been shown previously.^2–4,8 In this work, we perform a computational benchmark study employing different types of functionals showing that all employed TDDFT functionals are indeed unable to provide an inverted singlet–triplet gap for the studied molecules. The employed functionals represent most functional classes because they include local density approximation (LDA), generalized gradient approximation (GGA), meta-GGA, hybrid, meta-hybrid, range-separated hybrid functionals, and a local hybrid functional.

The data in Table 1 show that none of the functionals employed at the TDDFT level predicts a singlet–triplet inversion unlike the employed ab initio methods. The singlet–triplet gaps (ΔE_ST) predicted by TDDFT calculations are positive in the range of [0.143,0.457] eV for the studied molecules, where positive means that the first triplet state is energetically below the first excited singlet state. The pure functionals yield smaller ΔE_ST values, whereas incorporation of exact exchange in the hybrid functionals apparently leads to an increase in the singlet–triplet energy separation; ΔE_ST increases with the amount of exact exchange included in the functional, except for the range-separated functionals. The increase in the ΔE_ST gap can be explained by the fact that high-spin states are generally stabilized relatively to low-spin states by the inclusion of exact exchange. The dependence of ΔE_ST values on exact exchange is illustrated in Fig. 2.

Table 1 The singlet–triplet gaps (ΔE_ST in eV) of the vertical excitation energies calculated using different electronic structure methods. The molecular structures were optimized at the B3LYP/def2-TZVPD level

Method	1	2	3	4	5	6
a The tuned-CAM-B3LYP functional. b The spin-flip DFT approach. c The ΔSCF approach.
S-VWN	0.143	0.225	0.182	0.203	0.191	0.199
BP86		0.188	0.223	0.250	0.234	0.243
PBE	0.174	0.183	0.217	0.243	0.227	0.236
TPSS	0.186	0.195	0.234	0.264	0.246	0.256
TPSSh	0.208	0.219	0.265	0.303	0.281	0.294
B3LYP	0.200	0.218	0.261	0.301	0.281	0.295
PBE0	0.235	0.251	0.303	0.350	0.325	0.342
BHLYP	0.288	0.308	0.389	0.469	0.434	0.457
MN15	0.152	0.172	0.218	0.267	0.244	0.256
CAM-B3LYP	0.255	0.264	0.333	0.391	0.362	0.382
t-CAM-B3LYP^a	0.193	0.208	0.251	0.287	0.267	0.282
ωB97X-D	0.233	0.246	0.312	0.367	0.340	0.361
LH14t-calPBE	0.208	0.223	0.261	0.316	0.294	0.311
S-VWN^b	−0.039	−0.349	−0.008	0.019	0.005	0.008
B3LYP^c	−0.115	−0.154	−0.094		−0.097	−0.088
ωB97X-D^c	−0.280	−0.331	−0.221		−0.215	−0.186
ADC(2)	−0.132	−0.247	−0.117	−0.095	−0.142	−0.130
CC2	−0.139	−0.240	−0.109	−0.085	−0.134	−0.121

---

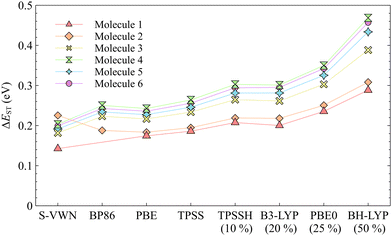Fig. 2 The singlet–triplet gap (ΔE_ST) as a function of exact-exchange admixture. For the hybrid functionals, the percentage of the Hartree–Fock (HF) exchange is given within parentheses.

Among the range-separated hybrid functionals, the smallest ΔE_ST was obtained using MN15, followed by the tuned-CAM-B3LYP, ωB97X-D, and finally CAM-B3LYP. However, the sign of ΔE_ST is wrong at all employed TDDFT levels. The ωB97X-D functional, which was found to be the most accurate functional in a recent benchmark study,⁶⁶ does not provide the most accurate excitation energies of the INVEST molecules at the TDDFT level. The employed local hybrid functional yields a positive ΔE_ST gap as well. Vertical excitation energies of each molecule computed at the TDDFT levels can be found in Table S1 of the ESI.† The calculations show that the employed TDDFT functionals are not able to accurately describe the lowest excited states of the studied molecules, which has been suggested to be due to lacking treatment of double excitations in current DFT functionals.^2–6,8,25

3.2 Ab initio methods

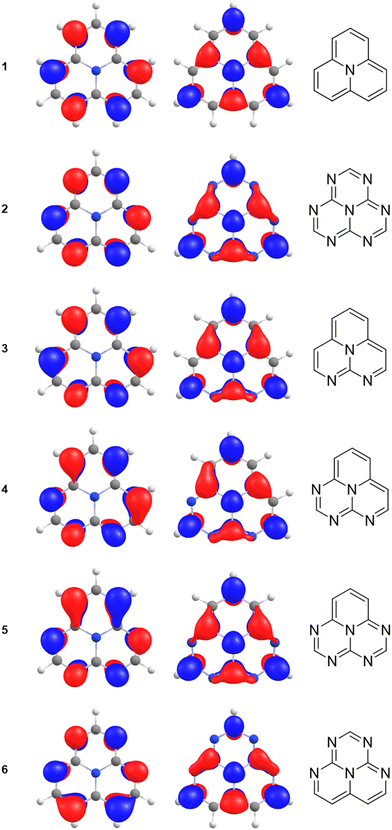
The studied molecules exhibit an unusual spatial separation of the HOMO and LUMO (see Fig. 3), resulting in a very small HOMO–LUMO overlap. The weight of the HOMO–LUMO configurations based on the ab initio calculations is for the molecules in the range of 89.3–97.9% for S₁ and 95.6–98.5% for T₁. The weights are reported in Table S2 of the ESI.† The S₁ and T₁ states are thus accurately described by the HOMO → LUMO transition. The small overlap leads to a small energy contribution from the exchange interaction. It also indicates a short-range intramolecular CT character of the excitations leading to a small energy difference between the lowest excited singlet and triplet states.

Fig. 3 The highest occupied (HOMO) and the lowest unoccupied (LUMO) molecular orbitals of the ground states of 1 to 6 calculated at the B3LYP/def2-TZVPD level show the inner charge transfer character of excited states of the INVEST molecules.

The electron correlation contributions originating from higher-order excitations may affect the energy ordering of the lowest excited states. In the studied molecules, the S₁ state is stabilized relatively to the T₁ state by doubly excited configurations,² resulting in the S₁ and T₁ inversion. The contributions of double excitations calculated at the CC2 level of theory (see Table 2) show that the S₁ state indeed comprises slightly higher amount of double excited configurations than the T₁ state. The influence of doubly excited configurations seems to be significant for both S₁ and T₁. They contribute by ∼10% to the wave function of the S₁ and T₁ states at the CC2 level. No clear correlation between the amount of double excitation character and ΔE_ST is observed in Table 2, however.

Table 2 Contributions from doubly excited configurations to the wave function of the S₁ and T₁ states (in %) and the difference in the double excitation character (ΔD in %) calculated at the CC2 level. The corresponding ΔE_ST (in eV) are also reported. The molecular structures of ground states were optimized at the MP2/def2-TZVP level

	1	2	3	4	5	6
S1 (CC2)	11.47	12.40	11.87	11.92	12.04	12.13
T1 (CC2)	10.25	11.17	10.46	10.33	10.53	10.55
ΔD	0.22	1.23	1.41	1.59	1.51	1.58
ΔEST	−0.133	−0.242	−0.110	−0.076	−0.135	−0.123

---

Analysis of the CC2 calculations shows that the inverted singlet–triplet gap of 1 mainly originates from single excitations involving the HOMO belonging to the a₂ irreducible representation coupled to single excitations from the three highest occupied b₂ orbitals. The planar molecule in the xz plane is assumed to belong to the C_2v point group. The orbitals are shown in Fig. 4. The single excitation from HOMO (3a₂) to LUMO (5b₂) is the dominating contribution to the S₁ and T₁ states belonging to the b₁ irreducible representation, whereas the simultaneous excitation from the highest occupied (b₂) orbitals is necessary for obtaining the inverted singlet–triplet gap. The b₂ → b₂ excitations also contribute to the inner charge transfer, since the occupied b₂ orbitals are delocalized over two to four carbons, whereas the virtual ones are localized on every second carbon atom.

Fig. 4 The highest occupied and the lowest virtual b₂ orbitals of 1 calculated at the B3LYP/def2-TZVPD level. The HOMO is 3a₂ and the LUMO is 5b₂.

The gap is inverted when at least two of the occupied b₂ orbitals and the four lowest virtual b₂ orbitals are included in the correlated orbital (active) space of the CC2 calculation. The excitation energies and ΔE_ST for various sizes of the active space of the CC2 calculations are reported in Table 3. The slightly larger admixture of double excitations in the S₁ state as compared to the T₁ state stabilizes the singlet relatively to the triplet. Even though the double excitation character is very small, it has a significant effect on the energy difference between the lowest singlet and triplet states. The double excitations are implicitly considered at the CC2 and ADC(2) levels of theory, whereas they are not accounted for in the TDDFT calculations with today's functionals.²⁶

Table 3 The excitation energy to the lowest excited singlet state (E(S₁) in eV) and to the lowest triplet state (E(T₁) in eV) of 1 and the energy difference between them (ΔE_ST in eV) as a function of the size of the active space in the CC2 calculation. In the notation, we use the number of occupied orbitals in the four irreducible representations (a₁a₂b₁b₂)/the number of virtual orbitals in the four irreducible representations

Active space	E(S1)	E(T1)	ΔEST
0 1 0 1/0 0 0 4	1.793	1.769	0.024
0 1 0 1/0 0 0 9	1.801	1.771	0.029
0 1 0 1/0 0 0 30	1.777	1.758	0.019
0 1 0 2/0 0 0 2	2.132	1.899	0.233
0 1 0 2/0 0 0 3	1.892	1.834	0.058
0 1 0 2/0 0 0 4	1.751	1.779	−0.028
0 1 0 2/0 0 0 9	1.738	1.765	−0.027
0 1 0 2/0 0 0 19	1.689	1.726	−0.037
0 1 0 2/0 0 0 30	1.683	1.720	−0.037
0 1 0 3/0 0 0 4	1.707	1.784	−0.077
0 1 0 3/0 0 0 30	1.599	1.691	−0.092

---

The employed ab initio methods predict the correct energy order of the two lowest excited singlet and triplet states, i.e., the singlet–triplet inversion is obtained for the studied molecules. Since high-order ab initio calculations are computationally demanding, low-order ab initio levels such as the ADC(2) and CC2 methods seem to be well suited for studies of this class of INVEST molecules because they are computationally much cheaper than many other ab initio approaches, especially when aiming at optimized molecular structures and vibrational frequencies of the excited states.

The computational costs of the CC2 calculations are found to be about a factor of two to three higher than when employing the ADC(2) method. Excitation energies calculated at the CC2 level are generally slightly more accurate than those obtained at the ADC(2) level. However, the energy differences are not large.^67,68 One can also speed up the ADC(2) and CC2 calculations by using the reduced virtual space (RVS) approach.^69,70 The CC2 calculations are then almost as fast as TDDFT calculations without significantly affecting the accuracy of the obtained excitation energies when using an RVS cut-off threshold of 50–60 eV.⁷¹ Vertical, adiabatic, and 0–0 excitation energies calculated at the CC2 are given in Table 4 and the corresponding excitation energies calculated at the ADC(2) level are reported in Table S3 of the ESI.† ZPVE corrections do not affect the inverted energy order of S₁ and T₁ states of the studied molecules.

Table 4 Vertical, adiabatic, and 0–0 excitation energies (in eV) calculated at the CC2 level of theory. The molecular structures of ground states were optimized at the MP2/def2-TZVP level of theory, whereas excited state geometries were optimized at the ADC(2)/def2-TZVP level of theory

	Vertical		Adiabatic		0–0
Molecule	S1	T1	S1	T1	S1	T1
1	1.047	1.180	0.976	1.117	0.992	1.068
2	2.756	2.998	2.640	2.894	2.512	2.618
3	1.608	1.718	1.520	1.637	1.474	1.550
4	1.987	2.063	1.822	1.943	1.747	1.817
5	2.231	2.365	2.066	2.197	1.971	2.056
6	2.168	2.291	2.063	2.196	1.973	2.068

---

The excitation energies calculated at the ADC(2) and CC2 levels agree well with values obtained using computationally more expensive ab initio levels of theory.^2–8,25 Correlated ab initio methods (SCS-CC2, SCS-ADC(2), SA-CASSCF, and SC-NEVPT2, RASSCF, ADC(2) and EOM-CCSD) employed in previous studies^2–6,25 and here yielded consistently inverted singlet–triplet gaps in the range of [−0.66, −0.03] eV for molecule 1 and 2. Literature values are collected in Table S4 of the ESI.†

According to a recent study,⁹ the intersystem crossing (ISC) rate between S₁ and T₁ is larger when the ΔE_ST value is small, whereas larger ΔE_ST values are accompanied by a smaller ISC rate constants. Thus, especially 4 belonging to the C_s point group should be considered as the best candidate for subsequent studies on 5th generation luminescent molecules.

Calculations at the CASSCF level using an active space with 12 electrons in 9 orbitals (12,9) showed that molecules 1, 2, and 3 are INVEST molecules, whereas 4, 5, and 6 are not. However, increasing the active space to 14 electrons in 14 orbitals (14,14) yielded an inverted singlet–triplet gap for all six molecules. Considering the dynamic correlation at the CASPT2 level on top of the (12,9) CASSCF calculations also led to the exhibition of the INVEST property in all the studied molecules. CASPT2 calculation with a (14,14) reference on molecule 1 yielded almost the same singlet–triplet gap as obtained in the (12,9) CASPT2 calculation suggesting that the energy gaps obtained in the CASPT2 (9,12) calculations are accurate. The obtained ΔE_ST are summarized in Table 5. Since the CASPT2 (14,14) calculations are computationally expensive, we did not perform such calculations on the rest of the molecules. The largest CASSCF and CASPT2 calculations yielded inverted singlet–triplet gaps as also obtained at the CC2 and ADC(2) levels. However, the energy gaps obtained at the CASSCF and CASPT2 level are more scattered than the ones calculated at the CC2 and ADC(2) levels suggesting that considering dynamic correlation is more important than a multireference treatment. Vertical excitation energies of each molecule computed at the CASSCF and CASPT2 levels with various sizes of the active space can be found in Table S5 of the ESI.†

Table 5 The singlet–triplet gaps (ΔE_ST in eV) of the vertical excitation energies calculated using different multireference electronic structure methods. The molecular structures were optimized at the XMC-QDPT2 level (12 electrons in 9 orbitals)

Method	1	2	3	4	5	6
a The active space is 12 electrons in 9 orbitals. b The active space is 14 electrons in 14 orbitals. c XMC-QDPT2 calculations with 12 electrons in 9 orbitals. d XMC-QDPT2 calculation with 14 electrons in 14 orbitals.
CASSCF^a	−0.163	−0.226	−0.074	0.166	0.260	0.165
CASSCF^b	−0.373	−0.641	−0.431	−0.083	−0.413	−0.571
CASPT2^c	−0.148	−0.018	−0.055	−0.219	−0.654	−0.160
CASPT2^d	−0.106

---

3.3 Spin-flip calculations

Since double excitations are needed for obtaining the correct sign of the singlet–triplet gap, we also employed the spin-flip method at the DFT level (SFDFT) for calculating the T₁ excitation energies (see Table S6 of the ESI†). The resulting ΔE_ST values are compared to values obtained with other methods in Fig. 5. Previous studies have shown that SFDFT methods generally provide a rather accurate description of excited states with a significant double excitation character.⁷² Spin-flip calculations have also previously been performed on INVEST molecules.⁶ The DFT based SFDFT method yielded the correct sign of ΔE_ST for some of the studied molecules. Even though the ΔE_ST values calculated at the SFDFT level are positive for 4–6, they are closer to the ab initio results than the ones obtained using standard TDDFT.

Fig. 5 Comparison of singlet–triplet gap of vertical excitation energies calculated at ab initio, ΔSCF, SFDFT, and TDDFT levels of theory.

3.4 ΔSCF calculations

The ΔE_ST values were also estimated at the B3LYP and ωB97X-D levels using the ΔSCF approach.^73–77 We do not discuss any details of the ΔSCF method since its history has recently been reviewed in ref. 77. The orthogonality of the non-aufbau SCF solutions can be easily introduced for five of the six studied molecules because the HOMO and the LUMO belong to different irreducible representations of the C_2v point group. Molecule 4 belongs to the C_s point group with the HOMO and LUMO in the same irreducible representation (a′′) implying that more advanced optimization approaches must be employed in the ΔSCF calculations.^73,77–79 The ΔSCF solutions may be used as reference wave functions for ab initio correlation approaches.⁷⁷ However, the ΔSCF calculations at the HF level on the present molecules led to significant spin contamination hampering its use as reference wave function in ab initio correlation calculations.

The ΔSCF calculations at the B3LYP and ωB97X-D level on the S₁ state also suffered from spin contamination. However, the spin contamination was not as severe as at the HF level. The expectation values of ŝ² are given in Table S7 of the ESI.† ΔSCF calculations using the B3LYP functional yielded negative energy differences in close agreement with values obtained at the CC2 level, whereas the ΔE_ST values calculated at the ωB97X-D ΔSCF level are about a factor of two larger than those obtained at the B3LYP ΔSCF level. The ΔE_ST values calculated at the DFT ΔSCF levels are compared to CC2 data in Table 1 and in Fig. 5. The ΔE_ST values calculated at the DFT ΔSCF level correlate with those calculated at the CC2 and ADC(2) level. The excitation energies calculated employing the ΔSCF method can be found in Table S8 of the ESI.†

3.5 Density plots analysis

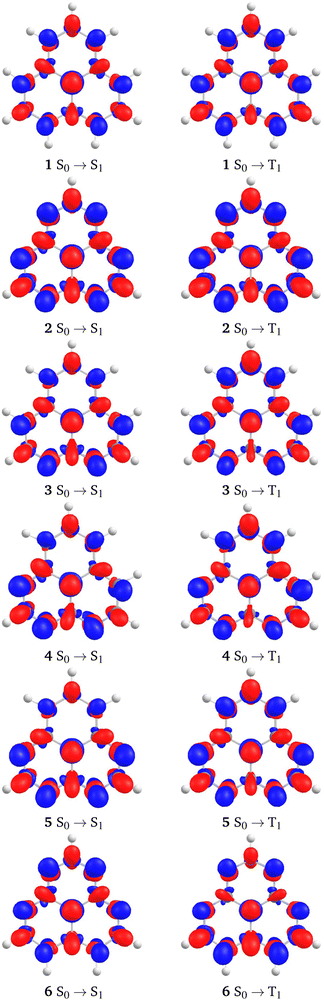
The difference in the electron densities of the S₀ and S₁ states as well as the density difference between the S₀ and the T₁ states calculated at the CC2 level are shown in Fig. 6. Similar plots calculated at the TDDFT level using the B3LYP and ωB97XD functionals are shown in Fig. S1 and S2 of the ESI.† Unlike the authors of ref. 8, we did not obtain any significant dissimilarities between density differences calculated at ab initio and TDDFT levels. Since the lowest singlet and triplet states are completely dominated by the HOMO → LUMO transition, it is expected that the density differences are very similar regardless of the employed computational level. The inner charge-transfer character of the excitations is clearly seen in the density differences (Fig. 6).

Fig. 6 Density differences for the S₀ → S₁ and S₀ → T₁ excitations calculated at the CC2/def2-TZVP level. Regions of decreasing electron density are in blue, red color denotes regions of increasing density. The used isosurface is 0.004.

The spin densities of the lowest T₁ state calculated at the CC2 level and at the DFT level using the B3LYP functional differ. The spin-polarization is more pronounced at the CC2 level, whereas the shape of the spin density obtained in the DFT calculation is very similar to the electron density of the HOMO and LUMO orbitals. The spin densities in Fig. S3 of the ESI† show that the spin density is alternating at the CC2 level, whereas it is more evenly distributed at the DFT level. Judged from the spin density, one may conclude that a more pronounced MRE is obtained at the CC2 level as compared to the DFT calculations.

4 Conclusions

We have calculated excitation energies of the first excited singlet and triplet states of a series of INVEST molecules in the search for suitable computational levels for studies of such molecules. The present study confirms the results of previous studies that calculations at TDDFT levels yield the wrong sign of the energy difference between the lowest singlet and triplet states (ΔE_ST). Wrong sign of ΔE_ST was obtained with all employed functionals, i.e., using LDA, GGA, meta-GGA, hybrid, meta-hybrid, range-separated hybrid, and local hybrid functionals. Calculations using SFDFT yielded smaller ΔE_ST values than ordinary TDDFT calculations. The correct sign of ΔE_ST was obtained for some of the studied molecules at the SFDFT level. DFT calculations using the ΔSCF approach yielded negative ΔE_ST values in close agreement with those calculates at the CC2 level, especially when using the B3LYP functional.

The INVEST property is found to originate from simultaneous excitations from occupied frontier orbitals to low-lying virtual ones. Even though the double-excitation character is relatively small, these excitations, that are considered in the ab initio models contribute to the MRE leading to the inverse singlet–triplet splitting.

Calculations employing second-order coupled-cluster methods such as CC2 and ADC(2) yielded accurate ΔE_ST values, because the S₁ and T₁ states are dominated by a single replacement of the electron density from HOMO to LUMO. CC2 and ADC(2) calculations can be performed on large molecules that can be of interest in OLED devices, especially when using the RVS approach to speed up the calculations.

Since static correlation and near-degeneration effects play a minor role and dynamic correlation is mainly responsible for the INVEST property, large active spaces must be used in multireference calculations such as at the CASSCF level. The CASPT2 (XMC-QDPT2) calculations are computationally expensive levels of theory that also yield inverted singlet–triplet splittings since they account for the important dynamic correlation contribution of the INVEST property.

Author contributions

LT did calculations at DFT and CC levels. RRV did the multireference calculations. LT and DS wrote the first version of the manuscript. All authors contributed to the writing of the final version of the article.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The work has been performed under the Project HPC-EUROPA3 (INFRAIA-2016-1-730897), with the support of the EC Research Innovation Action under the H2020 Programme. It has also been supported by the Academy of Finland through project numbers 314821, 340582 and 340583, by the Magnus Ehrnrooth Foundation, and the Swedish Cultural Foundation in Finland. We acknowledge computational resources from the Finnish Grid and Cloud Infrastructure (persistent identifier urn:nbn:fi:research-infras-2016072533). LT gratefully acknowledges the support of the computer resources and technical support provided by CSC – IT Center for Science, Finland. MS and LT were supported by Czech Science Foundation Grant No. 21-23261S.

Notes and references

1. F. Hund, Z. Phys., 1925, 33, 345–371.
2. P. de Silva, J. Phys. Chem. Lett., 2019, 10, 5674–5679.
3. J. Ehrmaier, E. J. Rabe, S. R. Pristash, K. L. Corp, C. W. Schlenker, A. L. Sobolewski and W. Domcke, J. Phys. Chem. A, 2019, 123, 8099–8108.
4. G. Ricci, E. San-Fabián, Y. Olivier and J. C. Sancho-García, ChemPhysChem, 2021, 22, 553–560.
5. J. Sanz-Rodrigo, G. Ricci, Y. Olivier and J. C. Sancho-García, J. Phys. Chem. A, 2021, 125, 513–522.
6. R. Pollice, P. Friederich, C. Lavigne, G. dos Passos Gomes and A. Aspuru-Guzik, Matter, 2021, 4, 1654–1682.
7. A. L. Sobolewski and W. Domcke, J. Phys. Chem. Lett., 2021, 12, 6852–6860.
8. K. Bhattacharyya, Chem. Phys. Lett., 2021, 779, 138827.
9. F. Dinkelbach, M. Bracker, M. Kleinschmidt and C. M. Marian, J. Phys. Chem. A, 2021, 125, 10044–10051.
10. S. Pios, X. Huang, A. L. Sobolewski and W. Domcke, Phys. Chem. Chem. Phys., 2021, 23, 12968–12975.
11. D. Miyajima, N. Aizawa, Y.-J. Pu, A. Nihonyanagi, R. Ibuka, H. Inuzuka, B. Dhara, Y. Koyama and F. Araoka, 2021 DOI:10.21203/rs.3.rs-478258/v1, preprint.
12. A. Endo, M. Ogasawara, A. Takahashi, D. Yokoyama, Y. Kato and C. Adachi, Adv. Mater., 2009, 21, 4802–4806.
13. A. Endo, K. Sato, K. Yoshimura, T. Kai, A. Kawada, H. Miyazaki and C. Adachi, Appl. Phys. Lett., 2011, 98, 42.
14. H. Uoyama, K. Goushi, K. Shizu, H. Nomura and C. Adachi, Nature, 2012, 492, 234–238.
15. K. Goushi, K. Yoshida, K. Sato and C. Adachi, Nat. Photonics, 2012, 6, 253–258.
16. J. Li, T. Nakagawa, J. MacDonald, Q. Zhang, H. Nomura, H. Miyazaki and C. Adachi, Adv. Mater., 2013, 25, 3319–3323.
17. J. Li, H. Nomura, H. Miyazaki and C. Adachi, Chem. Commun., 2014, 50, 6174–6176.
18. J. Li, Q. Zhang, H. Nomura, H. Miyazaki and C. Adachi, Appl. Phys. Lett., 2014, 105, 013301.
19. T. Hatakeyama, K. Shiren, K. Nakajima, S. Nomura, S. Nakatsuka, K. Kinoshita, J. Ni, Y. Ono and T. Ikuta, Adv. Mater., 2016, 28, 2777–2781.
20. P. de Silva, C. A. Kim, T. Zhu and T. Van Voorhis, Chem. Mater., 2019, 31, 6995–7006.
21. M. E. Casida and M. Huix-Rotllant, Annu. Rev. Phys. Chem., 2012, 63, 287–323.
22. S. Oda, B. Kawakami, R. Kawasumi, R. Okita and T. Hatakeyama, Org. Lett., 2019, 21, 9311–9314.
23. K. Shizu and H. Kaji, Commun. Chem., 2022, 5, 53.
24. W. Leupin and J. Wirz, J. Am. Chem. Soc., 1980, 102, 6068–6075.
25. S. Ghosh and K. Bhattacharyya, J. Phys. Chem. A, 2022, 126, 1378–1385.
26. N. T. Maitra, F. Zhang, R. J. Cave and K. Burke, J. Chem. Phys., 2004, 120, 5932–5937.
27. P. Elliott, S. Goldson, C. Canahui and N. T. Maitra, Chem. Phys., 2011, 391, 110–119.
28. A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100.
29. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
30. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
31. D. Rappoport and F. Furche, J. Chem. Phys., 2010, 133, 134105.
32. K. Eichkorn, F. Weigend, O. Treutler and R. Ahlrichs, Theor. Chem. Acc., 1997, 97, 119–124.
33. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
34. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
35. J. Schirmer, Phys. Rev. A: At., Mol., Opt. Phys., 1982, 26, 2395.
36. C. Hättig, Adv. Quantum Chem., 2005, 50, 37–60.
37. C. Hättig and F. Weigend, J. Chem. Phys., 2000, 113, 5154–5161.
38. C. Hättig and K. Hald, Phys. Chem. Chem. Phys., 2002, 4, 2111–2118.
39. P. A. M. Dirac, Proc. R. Soc. London, Ser. A, 1929, 123, 714–733.
40. J. C. Slater, Phys. Rev., 1951, 81, 385.
41. S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211.
42. J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824.
43. J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13244.
44. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
45. J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401.
46. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 78, 1396.
47. J. P. Perdew, M. Ernzerhof and K. Burke, J. Chem. Phys., 1996, 105, 9982–9985.
48. V. N. Staroverov, G. E. Scuseria, J. Tao and J. P. Perdew, J. Chem. Phys., 2003, 119, 12129–12137.
49. A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377.
50. T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57.
51. K. Okuno, Y. Shigeta, R. Kishi, H. Miyasaka and M. Nakano, J. Photochem. Photobiol., A, 2012, 235, 29–34.
52. J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620.
53. S. Y. Haoyu, X. He, S. L. Li and D. G. Truhlar, Chem. Sci., 2016, 7, 5032–5051.
54. A. V. Arbuznikov and M. Kaupp, J. Chem. Phys., 2014, 141, 204101.
55. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
56. TURBOMOLE V7.5.1 2021, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989-2007, TURBOMOLE GmbH, since 2007; available from https://www.turbomole.org.
57. S. G. Balasubramani, G. P. Chen, S. Coriani, M. Diedenhofen, M. S. Frank, Y. J. Franzke, F. Furche, R. Grotjahn, M. E. Harding, C. Hättig, A. Hellweg, B. Helmich-Paris, C. Holzer, U. Huniar, M. Kaupp, A. Marefat Khah, S. Karbalaei Khani, T. Müller, F. Mack, B. D. Nguyen, S. M. Parker, E. Perlt, D. Rappoport, K. Reiter, S. Roy, M. Rückert, G. Schmitz, M. Sierka, E. Tapavicza, D. P. Tew, C. van Wüllen, V. K. Voora, F. Weigend, A. Wodynski and J. M. Yu, J. Chem. Phys., 2020, 152, 184107.
58. F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065.
59. F. Weigend, M. Häser, H. Patzelt and R. Ahlrichs, Chem. Phys. Lett., 1998, 294, 143–152.
60. P. Deglmann and F. Furche, Chem. Phys. Lett., 2002, 362, 511–518.
61. F. Furche and R. Ahlrichs, J. Chem. Phys., 2002, 117, 7433–7447.
62. A. A. Granovsky, J. Chem. Phys., 2011, 134, 214113.
63. A. A. Granovsky, Firefly version 8.0.0, https://classic.chem.msu.su/gran/firefly/index.html.
64. G. M. J. Barca, C. Bertoni, L. Carrington, D. Datta, N. De Silva, J. E. Deustua, D. G. Fedorov, J. R. Gour, A. O. Gunina, E. Guidez, T. Harville, S. Irle, J. Ivanic, K. Kowalski, S. S. Leang, H. Li, W. Li, J. J. Lutz, I. Magoulas, J. Mato, V. Mironov, H. Nakata, B. Q. Pham, P. Piecuch, D. Poole, S. R. Pruitt, A. P. Rendell, L. B. Roskop, K. Ruedenberg, T. Sattasathuchana, M. W. Schmidt, J. Shen, L. Slipchenko, M. Sosonkina, V. Sundriyal, A. Tiwari, J. L. Galvez Vallejo, B. Westheimer, M. Wloch, P. Xu, F. Zahariev and M. S. Gordon, J. Chem. Phys., 2020, 152, 154102.
65. M. Kühn and F. Weigend, ChemPhysChem, 2011, 12, 3331–3336.
66. J. Liang, X. Feng, D. Hait and M. Head-Gordon, J. Chem. Theory Comput., 2022, 18, 3460–3473.
67. N. O. C. Winter, N. K. Graf, S. Leutwyler and C. Hättig, Phys. Chem. Chem. Phys., 2013, 15, 6623–6630.
68. C.-M. Suomivuori, H. Fliegl, E. B. Starikov, T. S. Balaban, V. R. I. Kaila and D. Sundholm, Phys. Chem. Chem. Phys., 2019, 21, 6851–6858.
69. R. Send, V. R. I. Kaila and D. Sundholm, J. Chem. Phys., 2011, 134, 214114.
70. R. Send, C. M. Suomivuori, V. R. I. Kaila and D. Sundholm, J. Phys. Chem. B, 2015, 119, 2933–2945.
71. C.-M. Suomivuori, N. O. C. Winter, C. Hättig, D. Sundholm and V. R. I. Kaila, J. Chem. Theory Comput., 2016, 12, 2644–2651.
72. Y. Shao, M. Head-Gordon and A. I. Krylov, J. Chem. Phys., 2003, 118, 4807–4818.
73. A. T. B. Gilbert, N. A. Besley and P. M. W. Gill, J. Phys. Chem. A, 2008, 112, 13164–13171.
74. T. Kowalczyk, S. R. Yost and T. V. Voorhis, J. Chem. Phys., 2011, 134, 054128.
75. G. M. J. Barca, A. T. B. Gilbert and P. M. W. Gill, J. Chem. Phys., 2014, 141, 111104.
76. J. A. R. Shea and E. Neuscamman, J. Chem. Phys., 2018, 149, 081101.
77. G. David, T. J. P. Irons, A. E. A. Fouda, J. W. Furness and A. M. Teale, J. Chem. Theory Comput., 2021, 17, 5492–5508.
78. R. Colle, A. Fortunelli and O. Salvetti, Theor. Chim. Acta, 1987, 71, 467–478.
79. D. Hait and M. Head-Gordon, J. Chem. Theory Comput., 2020, 16, 1699–1710.

---

Footnote

† Electronic supplementary information (ESI) available: Vertical excitation energies calculated at the TDDFT level; percentage of HOMO–LUMO configuration calculated at ab initio levels of theory; excitation energies calculated at the ADC(2) level; collected calculated excitation energies found in the literature; excitation energies calculated at various ab initio levels of theory; triplet excitation energies calculated using the spin-flip approach; spin contamination of the ΔSCF calculations; excitation energies calculated using the ΔSCF method; density difference calculated at TDDFT levels; spin densities calculated at DFT and CC2 levels. See DOI: https://doi.org/10.1039/d2cp02364d

---