A multiscale free energy method reveals an unprecedented photoactivation of a bimetallic Os(II)–Pt(II) dual anticancer agent

Abstract

The photoreactivity of relatively large transition metal complexes is often limited to the description of the static potential energy surfaces of the involved electronic states. While useful to grasp some physical grounds of the photoinduced molecular responses, this approach does not statistically sample the multiple molecular degrees of freedom of the systems under investigation, which grow significantly if we consider the explicit coupling with the environment, and does not consider dynamic effects. The problem is even more complex if the reactivity takes place in the excited state. The present work uses state-of-the-art multiscale QM/MM dynamics to describe the photoactivation of a Pt(II)-unit of an in silico designed two-component Os(II)–Pt(II) assembly proposed for a dual anticancer approach, by explicitly accounting for both dynamic and environmental effects. We clearly identify a transition state region with partial metal-to-metal charge transfer (³MMCT) character with no precedents in the scarce Ru(II)–Pt(II) analogues, indicative of a large synergistic effect between the Os(II) and Pt(II) metals and crucial in the photolabilization process of the Pt(II)–Cl bond. This is the first evidence of the ability of Os(II) to promote photoactivation of the Pt(II)-moiety, a contingency that would open new perspectives in this emerging field. The designed complex is therefore able to combine the traditional activity in photodynamic therapy (PDT) with the photoactivated chemotherapy (PCT) exerted by the Pt(II) unit, representing a new paradigm for a combined PDT/PCT anticancer approach while providing an advance in the methodology used to describe the photochemistry of transition-metal complexes in solution.

---

Introduction

The search for more selective therapies against cancer, able to overcome the occurrence of serious side effects produced by traditional treatments, has led to the development of new light-driven approaches, among which photodynamic therapy (PDT) is the most advanced one.^1,2 PDT exploits light irradiation to trigger the toxicity of a drug in a spatially and time-resolved manner. Its minimal invasiveness, simplicity, and selective destruction of neoplastic tissue through direct cellular damage, also invoking immune responses, promoted the global acceptance and continuous growth of this strategy.^3,4

The efficacy of conventional PDT is strictly dependent on the availability of a sufficient oxygenated environment as the cytotoxic agent is the singlet oxygen ¹O₂ species produced in situ as a result of the photodynamic process. The latter is triggered by the photosensitizer's (PS) T₁ quenching mechanism involving a direct energy transfer to ground-state molecular oxygen, via the so-called Type II photoreactions. Alternatively, other reactive oxygen species (ROS) such as superoxide anions (O₂˙⁻) and hydroxyl radicals (HO˙) can be produced in the case of Type I photoreactions in which the excited PS reacts through hydrogen/electron transfer with oxygen or biological substrates.

Unfortunately, some of the most aggressive and drug-resistant tumors are characterized by acute hypoxia conditions that hamper the treatment outcome.⁵ Even under normoxic conditions, ROS production can deplete the tumor oxygenation, creating local hypoxia and decreasing PDT performances. Besides this, PDT still faces the poor light penetration of common photosensitizers and a nonhomogeneous distribution of the PS within the tumor which often precludes a complete eradication. All these factors actually hinder the PDT from reaching the status of “standard cure”, emphasizing the need to propose new strategies for achieving better therapeutic results while developing improved PS with desirable properties.^6,7

In recent years, remarkable advances have been made toward the design of next-generation PSs (sometimes referred to as fourth-generation) able to display multiple reactivity against cancer and conceived with the aim to tackle the current limitations of PDT in the clinic.⁸ In this field, Ru(II)-polypyridyl complexes^9–12 are receiving growing attention especially since McFarland's first Ru(II)-complex TLD-1433 entered phase II clinical trials for the treatment of non-muscle invasive bladder cancer.^13,14 This compound also displays a promising Type I/Type II dual photoreactivity, exerting its phototoxicity at different oxygen tension levels.¹⁵ More recently, unprecedented phototoxicities in a hypoxia environment have been reported in joint experimental and theoretical investigations for other similar Ru(II) families¹² and for analogues bearing a Os(II)-metal centre.^16,17 The normoxic and hypoxic activities for the latter are the largest reported to date, demonstrating the utility of osmium for phototherapy applications. Indeed, although relatively unexplored in medicinal chemistry when compared to their analogous group 8 counterparts, osmium complexes have the advantage of an extended absorption window and definitely open new challenging perspectives in their use in PDT.¹⁸ Ru(II)-Polypyridyl also represents a promising and extensively studied family of complexes for application in photochemotherapy (PCT, otherwise known as photoactivated cancer therapy, PACT) in which, the phototoxicity of the metal scaffold arises from the population of dissociative ³MC states leading to photosubstitution mechanisms and light-driven DNA-binding.^13,19,20

The search for new-generation PSs with multimodal activity also includes another inspiring strategy, which is still in its infancy, based on the coupling of an active PS to a platinum center. These two-component assemblies have emerged as a promising class of potential drugs whose activity exceeds that of initial precursors benefiting from interesting synergistic effects. The Pt(II)-bioactive site offers the potential of steering the ROS generator directly to the DNA target thereby achieving a better distribution of the PS within the tumor, combining the oxygen-independent cytostatic activity of the Pt(II) center with the photodynamic effect of PSs.^21–24 Even in this approach, Ru(II)-chromophores appeared to be, from the outset, especially suitable to reach a dual activity and a handful of examples of Ru(II)/Ru(III) coupled with Pt(II)/Pt(IV) complexes already exist in the literature.²⁵

Among them, photoactive complexes containing bidentate terminal ligands and communicative bridging ligands developed by Brewer and coworkers deserve special attention. They first proposed monometallic Ru- and Os-[(Ph₂phen)₂M(dpp)]²⁺ (Ph₂phen = 4,7-diphenyl-1,10-phenanthroline; dpp = 2,3-bis(2-pyridyl)pyrazine; M = Ru/Os) polyazine complexes 1 and 3 (Chart 1) showing light-promoted cytotoxicity in rat malignant glioma F98 cells.^26,27 Coupled with a PtCl₂ subunit via the rigid dpp bridging ligand, the mixed Ru–Pt complex 4 [(Ph₂phen)₂Ru(dpp)PtCl₂]²⁺ (Chart 1), proposed by the same research group, enables multiple toxicity pathways leading to enhanced cytotoxicity through a combination of DNA platination mechanism and oxidative stress induced by the Ru polypyridil chromophore.^28,29 Compared with cis-Pt, superior cellular uptake and antiproliferative activity were found towards F98 malignant glioma cells using visible light irradiation. In vitro tests that revealed selective DNA cleavage compared to other cleavage proteins such as bovine serum albumin (BSA) suggest less off-target binding in vivo and less side effects than other platinum-based drugs.²⁹ Moreover, our previous theoretical exploration on the Ru–Pt complex 4 revealed an outstanding synergistic effect between the two metal centers that makes the assembly more effective than initial monometallic precursor.³⁰ Besides improving the photophysical properties of the chromophore, the supramolecular architecture was established to promote an alternative and unique means of photoactivation of the Pt(II) moiety through the photorelease of the Cl⁻ leaving group.

Chart 1 (a) Chemical structures of the Ru and Os polypyridyl PSs and of their bimetallic assemblies with the Pt(II)-moiety; (b) optimized ground-state geometries of the Os complexes 1 and 2 herein investigated, in water at the M06/6-31+G(d,p)/SDD level of theory.

Despite the higher photocytotoxicity of the monometallic Os complex 1 compared with the Ru congener 3 under both blue (470 nm) and red light (625 nm) irradiation (IC₅₀ values of 50.7 ± 2.9 μM and 86.1 ± 8.5 μM, respectively),²⁷ its coupling with platinum has not been investigated until now. Our recent exciting outcomes on Os(II)-application in PDT^16,17 strongly encourage further studies to finally break the barrier on the use of osmium complexes in medicinal chemistry. As a consequence, drawing also inspiration from the promising activity of the analogue Ru–Pt assembly 4,³⁰ we decided to undertake a careful theoretical exploration aimed at comparing the properties of the mono- and bi-metallic Os 1 and Os–Pt 2 (see Chart 1) and employ quantum mechanics/molecular mechanics (QM/MM) dynamics to describe the photoreactivity of 2. To the best of our knowledge, no investigation already exists on similar bimetallic complexes bearing osmium for a combined PDT/PCT approach. As shall be discussed in the following, our exploration reveals improved photophysical properties of the two-component conjugate 2 compared with the monometallic 1 and an unprecedented favorable mechanism for the photolabilization of the Pt–Cl bond. As revealed by the QM/MM excited-state dynamics, the latter process occurs through the population of the triplet metal-to-ligand charge transfer (³MLCT) state followed by the population of a metal-to-metal (Os → Pt) charge transfer (³MMCT) state in the transition state (TS) region.

Computational methods

Geometry optimizations and excited-state determinations

Singlet and triplet geometry optimizations were obtained at the density functional theory (DFT) method in water and without any structural constraints, employing the M06 exchange–correlation functional³¹ together with the 6-31G(d,p) basis set^32,33 for all atoms except metals, described with the quasi-relativistic Stuttgart–Dresden pseudopotential (SDD).³⁴ The SMD variation of the integral equation formalism polarizable continuum model (IEFPCM) was used to account for the solvent environment (water). UV-Vis absorption spectra were obtained in water as vertical electronic excitations on the ground-state structures, using the time-dependent (TD)-DFT formulation,³⁵ at the same level of theory as for the optimizations (M06/6-31G(d,p)/SDD). The used protocol has been extensively validated previously.^{12,15–17,36} All the calculations were performed by using the Gaussian 16 program.³⁷

Spin–orbit coupling computations

Spin–orbit couplings (SOCs) between the six lowest-lying singlet and triplet excited states were computed on top of the S₀, S₁, and T₁ equilibrium geometries of 1 and 2. Relativistic effects were treated with the zeroth-order regular approximation (ZORA)³⁸ as implemented in the ORCA 5.0 software.³⁹ The ZORA-Def2-TZVP basis set was used for all elements except Os and Pt, which were treated with the SARC-ZORA-TZVP basis set. The auxiliary basis set Def2-TZVP/C was used throughout, and the SOC operator was treated with RI-SOMF(1×). Solvent effects (water) were described by using the CPCM method with the ORCA 5.0 default settings. The possible influence of the basis set and the PCM settings between Gaussian and ORCA is evaluated in Tables S1 and S2 (ESI†). The comparison reveals negligible differences.

QM/MM simulations and excited-state potential of mean force

The ground-state structure of Os–Pt 2 optimized in the gas phase was initially placed in the center of a water cubic box of at least 15 Å of separation between the chromophore and any box edge. In total, 3464 water molecules were added. Two Cl⁻ ions were required to neutralize the +2 charge of the Os–Pt complex, giving rise to a total number of 10 504 atoms. These atoms remain far from the OsPt complex, thus not participating in the photoreaction (Fig. S1, ESI†). All QM/MM simulations were performed with the Amber 20/ORCA 5.0 interface making use of the electrostatic embedding implementation in Amber.^39,40 QM energies and gradients were computed by ORCA, while energies and gradients of the classical partition, QM-MM interactions (cutoff = 9.0 Å) and Newton's equations of motion were solved by Amber. The QM partition was treated throughout with the M06 functional in combination with the 6-31G basis set for all atoms except the heavy metals Os and Pt, that were treated with the def2-TZVP basis set including an SDD pseudopotential. The ground state was described with restricted DFT/M06, and the first triplet state, T₁, was computed with the unrestricted DFT/M06 ansatz. This level of theory provides a very satisfactory description of the Cl⁻ photorelease, as benchmarked in Fig. S2 (ESI†). Moreover, no spin contamination is observed in the QM/MM dynamics (Table S3, ESI†), thus validating the uM06/MM method used to describe the T₁ state free-energy path.

The QM partition (Fig. 1) includes the OsPt chromophore and a nearby water molecule. The benzene substituents attached to the phenanthroline ligands of Os–Pt were excluded from the QM partition.

Fig. 1 Os–Pt system 2 solvated inside a cubic water box (left) and QM partition composed of the Os–Pt system and a nearby water molecule (right). The snapshot corresponds to a representative transition state structure of the Cl⁻ photo-hydrolysis in the triplet state. The four benzene rings represented as grey licorice bars were treated with a MM force field.

The bonded parameters for the benzene moieties were parameterized from the general amber force field (GAFF),⁴¹ while point charges were obtained from the fitting of the electrostatic potential calculated with the restrained electrostatic potential (RESP) protocol.⁴² The link atom method was used to saturate the QM subsystem with hydrogen atoms. Water molecules and Cl⁻ counterions were treated with the TIP3P force field.⁴³

The water box was initially relaxed for 6000 steps of classical MD freezing only the atoms of the Os–Pt chromophore 2. The whole system was further relaxed for 1000 steps of QM/MM minimization in S₀ without any restriction. Later, a QM/MM relaxed scan in T₁ was performed on the Pt–O coordinate by adding a harmonic restraint V as implemented in Amber, with the form:

V = k(x − x₀)²

where x stands for the actual Pt–O distance (in Å), x₀ is the equilibrium Pt–O distance at which the spring is centered (x₀ = 4.4, 4.3,…,2.8 Å), and k is the force constant (initially set to 3000 kcal mol⁻¹ Å⁻² to ensure the desired Pt–O distance is maintained, this value is relaxed in posterior simulations). 150 minimization cycles were applied to each scan step.

14 windows with x₀ values 2.0, 2.2, 2.4, 2.6, 2.8, 2.9, 3.0, 3.2, 3.4, 3.6, 3.8, 4.0, 4.2, and 4.4 Å were prepared to compute the free energy profile of the hydration of the Pt center in the triplet excited state. The initial coordinates for the windows from 4.4 to 2.8 Å were the final structures of the QM/MM T₁ scan. These were further minimized individually through 500 minimization cycles biasing the potential now with a force constant k = 1000 kcal mol⁻¹ Å⁻². To ensure that the product structures connect with those of the TS, the final structure after minimization with the spring centered at x₀ = 2.8 Å (TS area) was used for the individual minimizations of x₀ = 2.6, 2.4, 2.2 and 2.0 Å. The additional window defined by x₀ = 2.9 Å was included to increase the sampling of the TS area. The individually minimized structures were slowly heated from 0 to 310.15 K in 2.5 ps of QM/MM dynamics in the NVT ensemble using k = 50 kcal mol⁻¹ Å⁻², followed by 1 ps of pre-production and by 7–14 ps of production runs in the NPT ensemble (see Table S4, ESI,† for the specific simulation times) with the same k = 50 kcal mol⁻¹ Å⁻². The Pt–O distances were collected for each simulation step. The PMF was integrated from the set of Pt–O bond distances collected for each simulation window by means of the weighted histogram analysis method (WHAM) developed by the Grossfield lab.⁴⁴ The Pt–O distances show an excellent overlap between all simulation windows (Fig. S3, ESI†). A sensitivity study of the PMF to the integration limits evidences the robustness of the computed free energy path (Fig. S4, ESI†).

All QM/MM minimizations and dynamics were performed using the Particle Mesh-Ewald method⁴⁵ with a non-bonded cutoff of 9.0 Å and under periodic boundary conditions. The timestep for all QM/MM dynamics was 1 fs. The pressure was set to 1 atm and kept constant using the Monte Carlo barostat with a time constant of 1 ps, whereas temperature conservation (310.15 K) was achieved through Langevin dynamics with a collision frequency γ = 1 ps⁻¹. No SHAKE algorithm was applied to hydrogen bond distances neither in the QM nor MM partitions.

No force-field parameterization has been conducted in this work. All biased dynamics have been performed with the QM/MM method in the T₁ state, allowing structural solvent (water) relaxation around the electronically excited chromophore.

Results and discussion

Absorption properties of the mono- and bi-metallic complexes

The computed absorption spectra for 1 and 2 are reported in Fig. 2. Both are efficient light absorbers throughout the UV-Vis region. The presence of the Pt(II) moiety significantly influences the spectral behavior of the Os chromophore making the bimetallic assembly more suitable for PDT application thanks to a bathochromic shift from ∼450 to ∼520 nm of the lowest energy band with therapeutic relevance. A careful inspection of each band allows a full characterization of the spectra providing valuable and further information compared to the experimental data available for complex 1.²⁷ As the bimetallic conjugate 2 is designed herein, experimental spectral data are obviously lacking. Nevertheless, the good agreement between computed and experimental values obtained for 1 confirms the accuracy of the chosen protocol and therefore validates the predictions for 2.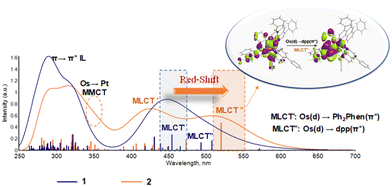

Fig. 2 Absorption spectra of 1 and 2 in water computed with the M06/6-31G(d,p)/SDD method. Vertical bars indicate the vertical absorptions that were phenomenologically convoluted to simulate the absorption spectra. Picture inset: Natural transition orbitals (NTOs)^46,47 describing the lowest-energy Os(d) → dpp π* (MLCT′′) band, computed with the software Chemissian.⁴⁸

Experimentally, the Os complex 1 shows bands at 279 and 320 nm.^26,27 They were previously associated with Ph₂phen and dpp π → π* intra-ligand (IL) absorptions, respectively. Computations confirm the presence of bands centred at 292 nm and 322 nm, in good agreement with the above-mentioned values, nevertheless, they are both ascribed to a Ph₂phen IL charge transfer, as clearly demonstrated by the natural transition orbitals (NTOs) related to them (see Tables S5 and S6, ESI†). The nature of both these bands is further supported by inspecting the spectrum generated by the single Ph₂phen fragment, which is characterized by bands in those regions (see Fig. S5, ESI†). The dpp IL bands are computed at 305 nm and 326 nm, the latter having a mixed dpp π → π* and dpp π → Ph₂phen π* ligand-to-ligand (LLCT) nature. Indeed, such a band is not present in the single dpp fragment spectrum, confirming the involvement of the second ligand. At longer wavelengths, two bands centred at 444 and 494 nm were experimentally assigned to metal-to-ligand charge transfer (MLCT) transitions from Os(d) to Ph₂phen π* and dpp π*, respectively. According to our computational analysis, the broad Os(d) → Ph₂phen π* is generated by several transitions located between 431 nm and 493 nm, with the most intense one centered at 455 nm. Visual inspection of the involved NTOs confirms the assigned MLCT nature of those set of transitions. A less intense transition is computed at lower energy (508 nm) whose nature is univocally assigned to Os(d) → dpp π*, in agreement with experimental interpretations.

The Os–Pt complex 2 shows an intense lowest-energy Os(d) → dpp π* (MLCT′′) band at 521 nm which dominates the visible region of the spectrum (Fig. 2). As an effect of the platination, the Os-based HOMOs and the dpp π*-based LUMOs in the bimetallic assembly are significantly stabilized, leading to a decrease of the HOMO–LUMO gap directly connected with the red-shift of the lowest energy band compared to 1 (Fig. S6 and Table S7, ESI†). The separation between the MLCT′ and MLCT′′ bands at long wavelengths is more pronounced for 2 as compared to the monometallic complex 1. In the case of 2, the Os(d) → Ph₂phen π* (MLCT′) absorption appears as a broad band centered at 431 nm and generated by several transitions with lower intensity from 407 nm and 473 nm of the same nature. In this case, the Ph₂Phen acceptor orbitals do not experience the same stabilization effect observed for the Os-based HOMO upon platination and the energy gap between the donor and acceptor orbitals increases in the bimetallic assembly compared with the Os complex 1. Such an increase in the energy difference between the involved orbitals leads to a blue shift of the MLCT′ band (Fig. S6, ESI†).

Peculiar bands are predicted at 346 nm and 325 nm, both involving the platinum subsystem. The first transition is characterized by a net charge transfer toward the dpp ligand and Pt metal center from the Os(d) orbital mixed with a Ph₂phen π orbital. On the other hand, the band at 325 has a clear Pt(d) → dpp(π*) character with a mixing dpp IL contribution. Such a band is reminiscent of the same one detected by us in the analogue Ru–Pt complex 4,³⁰ not previously assigned in experiments. Strikingly, and as a direct consequence of the Ru → Os replacement from 4 to 2, the MMCT predicted at 346 nm for Os–Pt 2 is absent in the Ru–Pt 4 analogue,³⁰ indicating a higher degree of synergy between the two metals in complex 2. This excitation is likely stabilized by the smaller atomic ionization energy of Os as compared to Ru, which increases the electron donor capacities of the Os. This improved property stabilizes the excited states in which the electronic density reorganization takes place from the Os center to other molecular subsystems, i.e. MLCT′, MLCT′′, and MMCT, as clearly displayed in Fig. 2. In contrast, the lowest part of the UV region remains almost identical for all complexes 1–4 since the excitations located in this region are mostly of IL nature (π → π*).

Triplet states and feasibility of Type II photodynamic therapy mechanism

As shown in Fig. 3 diagram, the lowest-lying triplet state (T₁) of both 1 and 2 compounds lies at sufficient energy to promote the generation of the cytotoxic singlet dioxygen ¹O₂ through triplet–triplet energy transfer (PDT Type II photoreaction).

Fig. 3 Jablonski diagram for complexes 1 and 2 showing the lowest-lying singlet and triplet states and the singlet dioxygen energy.

Note that the energy of the latter species was previously computed to be 0.90 eV (20.75 kcal mol⁻¹) (vs. 0.98 eV/20.60 kcal mol⁻¹, exp).⁴⁹ In both 1 and 2 cases, the T₁ state is of the same MLCT nature, namely Os(d) → dpp(π*), as shown in Fig. 4. The drop in the T₁ energy going from 1 to 2, also observed when comparing 3 and 4,³⁰ is a consequence of the platination. The presence of Pt(II) likely increases the electron acceptor capabilities of the dpp fragment. As a matter of fact, it slightly participates in the ³MLCT excitation (Fig. 4).

Fig. 4 NTOs^46,47 for the T₁ states of (a) 1 and (b) 2 complexes, computed with the software Chemissian.⁴⁸

After photoexcitation to the singlet manifold, triplet states are accessed through readily operative ultrafast intersystem crossing (ISC) process characteristic of complexes based on heavy metals.^50–54 Typically, the excited-state cooling (occurring in a few hundreds of fs) relaxes the chromophore to its lowest-lying excited states, which ultimately govern the photophysical and photochemical decay routes.^55–60 Therefore, the ISC will be dictated by the interplay between the lowest-lying singlet excited states and the energetically close triplet states. To ascertain the impact of the platination of complex 1 on the ISC dynamics, Table 1 compares the singlet–triplet SOCs for the two Os– and Os–Pt complexes 1 and 2 (see benchmarks in Tables S1 and S2, ESI†). Overall, in the FC region, the bimetallic assembly 2 has slightly larger SOC values with respect to 1, with some exceptions involving the S₁–T₂ and S₂–T₃ couplings. No significant changes are observed for the SOCs computed at the S₁ min and T₁ min structures with respect to the FC region (Table 1), except the S₁–T₁ and S₁–T₂ evident exchange of values for 1, indicative of strong T₁–T₂ mixing causing an energy order inversion when optimizing the S₁ and T₁ states.

Table 1 SOC values between the lowest-lying singlet and triplet states of 1 and 2 computed in a water solution with the TD-M06 method within the ZORA³⁸ as implemented in ORCA 5.0³⁹

Geometry	S0 min		S1 min		T1 min
SOC (cm^−1)	1	2	1	2	1	2
S1–T1	1310	1429	666	1449	975	1383
S1–T2	707	384	1419	554	1257	693
S1–T3	1226	1420	1442	1500	1426	1489
S2–T2	1154	1401	950	1463	1031	1436
S2–T3	566	355	219	180	258	196

---

From the computed data emerge that the platination of 1 has much less impact than the platination of Ru-monometallic complex 3 documented in a previous work.³⁰ This is likely due to the already extremely large SOCs values displayed by the Os-based complex 1, that is much heavier than Ru, so that the introduction of the second metal in the Os-scaffold does not produce a significant enhancement of the SOC values. Intersystem crossing dynamics are governed to a great extent by the singlet–triplet SOCs between the states partaking in the excited-state relaxation, however, it shall be mentioned that other factors contribute to the triplet population kinetics. Among these factors one can find the potential energy surface shapes, vibronic coupling,⁶¹ and/or the presence of alternative intersystem crossing routes not considered in Table 1.

Free energy profile for the light-induced Pt(II) activation

The possibility to propose such kinds of conjugates for a dual anticancer approach lies in the well-known recognized ability of Pt(II) moiety to covalently bind DNA, thus combining the singlet oxygen production promoted by the Os(II)-chromophore with the cytostatic activity of Pt(II). The formation of active aqua-species is a key step preceding the binding to the biological target, as largely accepted in the literature.⁶² Interestingly, for the analogue Ru–Pt mixed metals complex, it was suggested a low-energy light-induced photolabilization of the Pt–Cl bond from an ³MLCT state,^28,30 a mechanism far from being usual for Pt(II). Anyway, the influence of Ru(II) was demonstrated to be crucial for triggering the substitution mechanism.³⁰ No evidence exists, instead, on the ability of Os(II) to promote a photoactivation of the Pt(II)-moiety, a contingency that would open new perspectives in this emerging field. Accordingly, the Cl⁻ ligand-exchange mechanism in the excited state has been herein explored in detail.

To simultaneously account for both dynamical and environmental effects, the photorelease of Cl⁻ in explicit water solution has been studied by means of biased QM/MM dynamics using the Amber 20/ORCA 5.0 interface.^39,40 The free energy path of the process has been computed through the umbrella sampling method, imposing a series of harmonic restraints on the Pt–O reaction coordinate. This advanced methodology provides the free energy path of the process simultaneously accounting for both dynamical and environmental effects.^63–65 The Os–Pt photosensitizer 2 was initially solvated inside a cubic water box (Fig. 1). The QM partition includes the photosensitizer and a nearby water molecule, except the benzene substituents linked to the phenantroline ligands, which were treated with a classical force field. The QM level of theory was validated by benchmarking different functionals and basis sets for the elongation of a Pt–Cl bond in a gas-phase model (Fig. S2, ESI†), using the M06/6-31G(d,p)/SDD level of theory as reference. The system was first minimized in the ground state, followed by a forward and backward QM/MM scan along the Pt–O reaction coordinate (between the Pt center and the oxygen of a nearby water molecule) in the T₁ state. The minimization, equilibration, and the production runs at 310.15 K of each simulation window were performed as documented in detail in the Computational Methods section and the ESI.†

Fig. 5a schematizes the Pt–Cl hydrolysis in the excited state studied in this work, while Fig. 5b shows the free energy path (potential of mean force, PMF) for this process. The energy barrier associated with the de-coordination of a Cl⁻ leaving group and the coordination of a water molecule is about 3.4 kcal mol⁻¹, indicative of a kinetically fast process and compatible with the experimental photolabilization observed for the closely related Ru–Pt system 4.²⁸ In this particular case, ΔG^‡ is the difference in the free energy between the transition state and the pre-reactive (reactants) complex. By assuming that the concentration of the activated complex only depends on the reactive 2, since water is in great excess solvating the chromophore, it is reasonable to expect that the rate-limiting step is the formation of the Pt–O bond (coupled with the Cl⁻ release), and not the formation of the pre-reactive complex with water. Eyring's equation provides an estimated rate constant k:

where k_b is the Boltzmann constant, h refers to the Planck constant, T is the temperature (310.15 K), and R stands for the ideal gas constant. The half-life t_1/2 is given by the equation:
The estimated half-life for the Pt–O bond formation and Cl⁻ photorelease is 26.5 ps, faster than the non-radiative excited-state decay taking place from tens of picoseconds to hundreds of nanoseconds measured for other octahedral Ru- and Os-based complexes,¹⁶ including the archetypal complex [Ru(bpy₃)]²⁺.^58,66,67

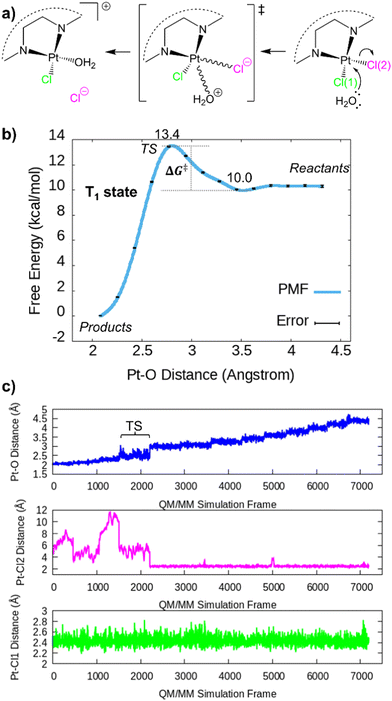Fig. 5 (a) Schematic representation of the products (left), transition state (middle), and reactants (right). (b) Potential of mean force (PMF) for the formation of the Pt–O bond and the synchronous release of an anion chloride leaving group obtained with the umbrella sampling method from biased QM/MM simulations in the first triplet state. The PMF has been computed with the weighted histogram analysis method (WHAM) developed by the Grossfield lab.⁴⁴ (c) Pt–O and Pt–Cl distances obtained from the QM/MM simulation windows. The biasing potential was applied to the Pt–O coordinate. Simulation frames for this analysis were stored with a frequency of 20 fs.

To the best of our knowledge, the spectroscopic transients associated with the excited state dynamics of 2 have not been measured so far. Nevertheless, it is reasonable to expect that the triplet lifetime will resemble those of other octahedral Os(II) complexes, likely exceeding the nanosecond time scale. Therefore, the present computational data indicate that the triplet state will live enough to activate the photohydrolysis of the Pt(II) center in the bimetallic unit 2. Pastore and co-workers⁶⁸ have experimentally and computationally⁶⁹ characterized the solvent relaxation around an electronically excited Ru(II) octahedral complex. For this related molecule, the transient spectroscopy spectrum (absorption from T₁) at t = 20 ps shows a red shift of the broadband from ∼625 to ∼650 nm (0.076 eV, 1.75 kcal mol⁻¹) with respect to the spectrum at t = 0 ps.⁶⁸ Even though the electrostatic QM/MM embedding employed in this work does not describe the polarization of the water molecules due to the chromophore excitation, the long QM/MM simulations performed herein (Table S4, ESI†) do capture the short-range solvent reorganization around 2 in the triplet excited state. The solvent relaxation at the time scale at hand is expected to be rather small (similarly to other structurally related complexes^68,69) and will equally affect the reactants, TS, and products, barely altering the free energies reported in Fig. 5a.

The transition state (TS) area corresponds to the Pt–O distance of ∼2.8 Å. The small energy barrier suggests that it should be kinetically competitive with the triplet decay to the singlet ground state S₀. Both PESs show a crossing at long Pt–Cl distances (Fig. S2a, ESI†), where the Cl⁻ release seems the most probable outcome. The formation of the products, i.e. [N₂PtClOH₂]⁺ + Cl⁻, is clearly exergonic, releasing ca. 10 kcal mol⁻¹ with respect to the initial reactants (Fig. 5b). Analysis of the Pt–O and the two Pt–Cl interatomic distances along the QM/MM simulations reveal that the cleavage of the Pt–Cl2 bond takes place at the TS area defined at Pt–O distances of 2.8 Å, indicating that the H₂O coordination and the Pt–Cl2 bond breaking are indeed coupled (Fig. 5c). In contrast, the bond Pt–Cl1 remains unaltered throughout the simulations. The free energy path shape along the Pt–O reaction coordinate (Fig. 5b) obeys the statistical distribution of the Pt–O distances collected for the 14 simulation windows (Fig. S3, ESI†). The energy penalty associated with Pt–O distances around 2.8 Å (TS zone) decreases the probability of remaining in this area during the QM/MM simulations. In fact, the system tends to fall to the reactant region despite the active harmonic restraint. Therefore, the small statistical abundance of Pt–O distances around 2.7–2.8 Å correlates very well with the higher free energy integrated for the TS region. The nature of the triplet state active in the simulations was investigated by randomly extracting snapshots from the reactants, TS, and products simulation windows, i.e. x₀(Pt–O) = 4.4, 2.8, and 2.0 Å, respectively (Fig. 6 and Fig. S7, ESI†). The ³MLCT configuration clearly dominates the reactants and the product regions (Fig. S7a and b, respectively, ESI†), characterized by a spin density of Os close to 1 and that of Pt close to 0. In contrast, the Pt center accumulates spin density (>0.5) in 6 out of 50 snapshots of the TS area (12%, Fig. 6), where it has a partially empty coordination site that facilitates the population of antibonding orbitals in part centered over Pt. This electronic structure is not prevalent, coherent with the fact that the TS area is less visited in the QM/MM dynamics, as compared to other regions (see histogram distances, Fig. S3, ESI†). The ³MMCT state results in a net Os(phen) → Pt electron transfer (with partial involvement of the phen ligands). Strikingly, this ³MMCT configuration has been also detected at the FC geometry of 2 in Fig. 1. Other higher triplet states with significant antibonding character over Pt will be also stabilized by the relatively large Pt–O and Pt–Cl bond distances characteristic of the TS area, however, in this work we focus on the description of T₁, the most relevant state for the photodynamics. The facile PCT photoactivation of 2 may imply a significant therapeutic advantage by increasing the alkylating capabilities and therefore the anticancer potency of the compound.

Fig. 6 Os and Pt Mulliken spin densities in some snapshots sampled from the TS zone QM/MM dynamics (harmonic restraint centered at a Pt–O distance of 2.8 Å). Computed with the uM06/6-31G/SDD method through the Amber 20/Gaussian interface. The singly occupied molecular orbitals showing the ³MMCT electronic state for one representative snapshot are also shown.

Conclusion and perspectives

This work proposes for the first time the association of Os(II) and Pt(II) in a dual PDT/PCT anticancer compound. We have analyzed in detail the absorption properties of the osmium-based polypyridyl complex 1 and its platinated assembly Os–Pt 2 showing that the inclusion of the Pt unit increases the light absorption capabilities of the monometallic Os compound, making the assembly much more attractive for light-driven therapies. Innovative biased QM/MM simulations have allowed the determination of an unprecedented mechanism for the photoexcited hydrolysis of a Pt–Cl bond in a bimetallic complex occurring in the triplet state, a crucial process in the activation of the PCT capacities. Results show that the Pt–Cl bond breaking and the Pt–O bond formation with a nearby water molecule are coupled. The process is overall very favorable (energy barrier ∼3.4 kcal mol⁻¹) and is mostly driven by the lowest-lying ³MLCT state, except in the TS region. In the latter zone, some net Os → Pt charge transfer is observed due to the partial de-coordination of Pt, which decreases the energy of antibonding orbitals centered on Pt. The higher ionization potential of Os (as compared to Ru) also clearly points to a stabilization of this elusive ³MMCT state, greatly increasing the attractiveness and potential of the Os–Pt assembly as a non-canonical anticancer drug activatable by visible light. This is the first evidence of the photolabilization of a Pt(II)–Cl bond promoted by an Os(II) scaffold in the excited state.

The current multiscale QM/MM dynamics represent a step further in the study of the photochemistry of transition-metal complexes in solution and could allow more realistic descriptions of their photobiological events in the presence of biological macromolecules (such as proteins and DNA). Our research group is currently working in this challenging direction. Moreover, the outcomes of our investigation are expected to open new perspectives on the use of coupled osmium–platinum complexes strengthening the premises for the development of an effective multifunctional agent able to combine PDT and a light-resolved drug-delivery through a photosubstitution mechanism.

Author contributions

M. E. A. and A. F.-M. contributed equally to this work.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

M. E. A. acknowledges the CINECA award under the ISCRA initiative “PS-Dual” project, for the availability of HPC resources. A. F.-M. is grateful to the Juan de la Cierva program of the Ministerio de Ciencia e Innovación (contract IJC2019-039297-I) for financial support. Both authors thank the Servei d’Informàtica (Universitat de València, Spain) for the computational resources at the LluisVives v2 supercluster.

References

1. (a) G. M. Cramer, K. A. Cengel and T. M. Busch, Forging Forward in Photodynamic Therapy, Cancer Res., 2022, 82, 534–536; (b) S. Yano, S. Hirohara, M. Obata, Y. Haguya, S.-I. Ogura, A. Ikeda, H. Kataoka, M. Tanaka and T. Joh, Current states and future views in photodynamic therapy, J. Photochem. Photobiol., C, 2011, 12, 46–67 and references therein.
2. (a) D. Kessel, Photodynamic Therapy: Critical PDT Theory, Photochem. Photobiol., 2022 DOI:10.1111/php.13616; (b) I. J. Macdonald and T. J. Dougherty, Basic principles of photodynamic therapy, J. Porphyrins Phthalocyanines, 2001, 5, 105–129.
3. S. O. Gollnick and C. M. Brackett, Enhancement of Anti-Tumor Immunity by Photodynamic Therapy, Immunol. Res., 2010, 46, 216–226.
4. R. Falk-Mahapatra and S. O. Gollnick, Photodynamic Therapy and Immunity: An Update, Photochem. Photobiol., 2020, 96, 550–559.
5. (a) Y. Wan, L.-H. Fu, C. Li, J. Lin and P. Huang, Conquering the hypoxia limitation for photodynamic therapy, Adv. Mater., 2021, 33, 2103978; (b) L. Larue, B. Myrzakhmetov, A. Ben-Mihoub, A. Moussaron, N. Thomas, P. Arnoux, F. Baros, R. Vanderesse, S. Acherar and C. Frochot, Fighting hypoxia to improve PDT, Pharmaceuticals, 2019, 12, 163; (c) X. Li, N. Kwon, T. Guo, Z. Liu and J. Yoon, Innovative strategies for hypoxic-tumor photodynamic therapy, Angew. Chem., Int. Ed., 2018, 57, 11522; (d) J. Du, T. Shi, S. Long, P. Chen, W. Sun, J. Fan and X. Peng, Enhanced photodynamic therapy for overcoming tumor hypoxia: From microenvironment regulation to photosensitizer innovation, Coord. Chem. Rev., 2021, 427, 213604.
6. G. Gunaydin, M. E. Gedik and A. Seylan, Photodynamic Therapy—Current Limitations and Novel Approaches, Front. Chem., 2021, 9, 691697.
7. (a) X. Zhao, J. Liu, J. Fan, H. Chao and X. Peng, Recent progress in photosensitizers for overcoming the challenges of photodynamic therapy: from molecular design to application, Chem. Soc. Rev., 2021, 50, 4185–4219; (b) D. Lee, S. Kwon, S.-y Jang, E. Park, Y. Lee and H. Koo, Overcoming the obstacles of current photodynamic therapy in tumors using nanoparticles, Bioact. Mater., 2022, 8, 20–34.
8. R. Paprocka, M. Wiese-Szadkowska, S. Janciauskiene, T. Kosmalski, M. Kulik and A. Helmin-Basa, Latest developments in metal complexes as anticancer agents, Coord. Chem. Rev., 2022, 452, 214307.
9. (a) C. Mari, V. Pierroz, S. Ferrari and G. Gasser, Chem. Sci., 2015, 6, 2660–2686; (b) F. Heinemann, J. Karges and G. Gasser, Critical Overview of the Use of Ru(II) Polypyridyl Complexes as Photosensitizers in One-Photon and Two-Photon Photodynamic Therapy, Acc. Chem. Res., 2017, 50, 2727–2736.
10. Y. Wu, S. Li, Y. Chen, W. He and Z. Guo, Recent advances in noble metal complex based photodynamic therapy, Chem. Sci., 2022, 13, 5085–5106.
11. L. Conti, E. Macedi, C. Giorgi, B. Valtancoli and V. Fusi, Combination of light and Ru(II) polypyridyl complexes: Recent advances in the development of new anticancer drugs, Coord. Chem. Rev., 2022, 469, 214656.
12. J. Roque III, H. Cole, P. Barrett, L. Lifshits, R. Hodges, S. Kim, A. Francés-Monerris, M. E. Alberto, C. G. Cameron and S. A. McFarland, Intraligand Excited States Turn a Ruthenium Oligothiophene Complex into a Light-Triggered Ubertoxin with Anticancer Effects in Extreme Hypoxia, J. Am. Chem. Soc., 2022, 144, 8317–8336.
13. S. Monro, K. L. Colón, H. Yin, J. Roque, P. Konda, S. Gujar, R. P. Thummel, L. Lilge, C. G. Cameron and S. A. McFarland, Transition Metal Complexes and Photodynamic Therapy from a Tumor-Centered Approach: Challenges, Opportunities, and Highlights from the Development of TLD1433, Chem. Rev., 2019, 119, 797–828.
14. G. Shi, S. Monro, R. Hennigar, J. Colpitts, J. Fong, K. Kasimova, H. Yin, R. DeCoste, C. Spencer, L. Chamberlain, A. Mandel, L. Lilge and S. A. McFarland, Ru(II) dyads derived from α-oligothiophenes: A new class of potent and versatile photosensitizers for PDT, Coord. Chem. Rev., 2015, 282–283, 127–138.
15. M. E. Alberto, J. Pirillo, N. Russo and C. Adamo, Theoretical Exploration of Type I/Type II Dual Photoreactivity of Promising Ru(II) Dyads for PDT Approach, Inorg. Chem., 2016, 55, 11185–11192.
16. J. A. Roque III, P. C. Barrett, H. D. Cole, L. M. Lifshits, G. Shi, S. Monro, D. von Dohlen, S. Kim, N. Russo, G. Deep, C. G. Cameron, M. E. Alberto and S. A. McFarland, Breaking the Barrier: An Osmium Photosensitizer with Unprecedented Hypoxic Phototoxicity for Real World Photodynamic Therapy, Chem. Sci., 2020, 11, 9784–9806.
17. J. A. Roque III, P. C. Barrett, H. D. Cole, L. M. Lifshits, E. Bradner, G. Shi, D. von Dohlen, S. Kim, N. Russo, G. Deep, C. G. Cameron, M. E. Alberto and S. A. McFarland, Os(II) Oligothienyl Complexes as a Hypoxia-Active Photosensitizer Class for Photodynamic Therapy, Inorg. Chem., 2020, 59, 16341–16360.
18. C. B. Smith, L. C. Days, D. R. Alajroush, K. Faye, Y. Khodour, S. J. Beebe and A. A. Holder, Photodynamic Therapy of Inorganic Complexes for the Treatment of Cancer, Photochem. Photobiol., 2022, 98, 17–41.
19. L. M. Loftus, A. Li, K. L. Fillman, P. D. Martin, J. J. Kodanko and C. Turro, Unusual Role of Excited State Mixing in the Enhancement of Photoinduced Ligand Exchange in Ru(II) Complexes, J. Am. Chem. Soc., 2017, 139, 18295–18306.
20. C. Imberti, P. Zhang, H. Huang and P. J. Sadler, New Designs for Phototherapeutic Transition Metal Complexes, Angew. Chem., Int. Ed., 2020, 59, 61.
21. A. Naik, R. Rubbiani, G. Gasser and B. Spingler, Angew. Chem., Int. Ed., 2014, 53, 6938–6941.
22. C. Lottner, K. C. Bart, G. Bernhardt and H. Brunner, J. Med. Chem., 2002, 45, 2079–2089.
23. M. E. Alberto and C. Adamo, Chem. – Eur. J., 2017, 23, 15124–15132.
24. F. Ponte, M. E. Alberto, B. C. De Simone, N. Russo and E. Sicilia, Inorg. Chem., 2019, 58, 9882–9889.
25. A. Jain, Multifunctional, Heterometallic Ruthenium-Platinum Complexes with Medicinal Applications, Coord. Chem. Rev., 2019, 401, 213067.
26. S. L. H. Higgins, T. A. White, B. S. J. Winkel and K. J. Brewer, Inorg. Chem., 2011, 50, 463–470.
27. J. Zhu, A. Dominijanni, J. A. Rodríguez-Corrales, R. Prussin, Z. Zhao, T. Li, J. L. Robertson and K. J. Brewer, Visible light-induced cytotoxicity of Ru,Os–polyazine complexes towards rat malignant glioma, Inorg. Chim. Acta, 2017, 454, 155–161.
28. S. L. H. Higgins, A. J. Tucker, B. S. J. Winkel and K. J. Brewer, Chem. Commun., 2012, 48, 67–69.
29. J. Zhu, J. A. Rodríguez-Corrales, R. Prussin, Z. Zhao, A. Dominijanni, S. L. Hopkins, B. S. J. Winkel, J. L. Robertson and K. J. Brewer, Exploring the activity of a polyazine bridged Ru(II)–Pt(II) supramolecule in F98 rat malignant glioma cells, Chem. Commun., 2017, 53, 145–148.
30. M. E. Alberto, N. Russo and C. Adamo, Synergistic Effects of Metals in a Promising Ru(II)−Pt(II) Assembly for a Combined Anticancer Approach: Theoretical Exploration of the Photophysical Properties, Chem. – Eur. J., 2016, 22, 9162–9168.
31. Y. Zhao and D. G. Truhlar, The M06 Suite of Density Functionals for Main Group Thermochemistry, Thermochemical Kinetics, Noncovalent Interactions, Excited States, and Transition Elements: Two New Functionals and Systematic Testing of Four M06-Class Functionals and 12 Other Function, Theor. Chem. Acc., 2008, 120, 215–241.
32. W. J. Hehre, R. F. Stewart and J. A. Pople, Self-consistent molecular-orbital methods.i. use of gaussian expansions of slater-type atomic orbitals, J. Chem. Phys., 1969, 51, 2657.
33. M. M. Francl, W. J. Pietro, W. J. Hehre, J. S. Binkley, M. S. Gordon, D. J. DeFrees and J. A. Pople, Self-consistent Molecular Orbital Methods. XXIII. A Polarization-type Basis Set for Second-row Elements, J. Chem. Phys., 1982, 77, 3654–3665.
34. D. Andrae, U. Häußermann, M. Dolg, H. Stoll and H. Preuß, Energy-Adjusted Ab Initio Pseudopotentials for the Second and Third Row Transition Elements, Theor. Chim. Acta, 1990, 77, 123–141.
35. M. E. Casida, Time-Dependent Density Functional Response Theory for Molecules, in Recent Advances in Density Functional Methods (Part I), ed. D. P. Chong, World Scientific, Sin, 1995, pp. 155–192.
36. M. E. Alberto, T. Marino, N. Russo, E. Sicilia and M. Toscano, Phys. Chem. Chem. Phys., 2012, 14, 14943–14953.
37. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016.
38. E. van Lenthe, E. J. Baerends and J. G. Snijders, Relativistic Regular Two-component Hamiltonians, J. Chem. Phys., 1993, 99, 4597–4610.
39. F. Neese, F. Wennmohs, U. Becker and C. Riplinger, The ORCA Quantum Chemistry Program Package, J. Chem. Phys., 2020, 152, 224108.
40. D. A. Case, H. M. Aktulga, K. Belfon, I. Y. Ben-Shalom, S. R. Brozell, D. S. Cerutti, T. E. Cheatham III, G. A. Cisneros, V. W. D. vCruzeiro and T. A. Dardenet al., Amber 20, San Francisco, 2021.
41. J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, Development and testing of a general amber force field, J. Comput. Chem., 2004, 25, 1157–1174.
42. J. Wang, P. Cieplak and P. A. Kollman, How well does a restrained electrostatic potential (RESP) model perform in calculating conformational energies of organic and biological molecules?, J. Comput. Chem., 2000, 21, 1049–1074.
43. W. L. Jorgensen, J. Chandrasekhar and J. D. Madura, Comparison of simple potential functions for simulating liquid water, J. Chem. Phys., 1983, 79, 926–935.
44. A. Grossfield, WHAM: An Implementation of the Weighted Histogram Analysis Method, Version 2.0.9. https://membrane.urmc.rochester.edu/content/wham/.
45. T. Darden, D. York and L. Pedersen, Particle mesh Ewald: An Nlog(N) method for Ewald sums in large systems, J. Chem. Phys., 1993, 98, 10089.
46. T. Etienne, X. Assfeld and A. Monari, New Insight into the Topology of Excited States through Detachment/Attachment Density Matrices-Based Centroids of Charge, J. Chem. Theory Comput., 2014, 10, 3906–3914.
47. T. Etienne, X. Assfeld and A. Monari, Toward a Quantitative Assessment of Electronic Transitions’ Charge-Transfer Character, J. Chem. Theory Comput., 2014, 10, 3896–3905.
48. L. Skripnikov, Chemissian 4.67, 2020, https://www.chemissian.com.
49. M. E. Alberto, B. C. De Simone, G. Mazzone, E. Sicilia and N. Russo, Phys. Chem. Chem. Phys., 2015, 17, 23595–23601.
50. A. Francés-Monerris, K. Magra, M. Darari, C. Cebrián, M. Beley, E. Domenichini, S. Haacke, M. Pastore, X. Assfeld and P. C. Gros, et al., Synthesis and Computational Study of a Pyridylcarbene Fe(II) Complex: Unexpected Effects of Fac/Mer Isomerism in Metal-to-Ligand Triplet Potential Energy Surfaces, Inorg. Chem., 2018, 57, 10431–10441.
51. K. Magra, E. Domenichini, A. Francés-Monerris, C. Cebrián, M. Beley, M. Darari, M. Pastore, A. Monari, X. Assfeld and S. Haacke, et al., Impact of the Fac/Mer Isomerism on the Excited-State Dynamics of Pyridyl-Carbene Fe(II) Complexes, Inorg. Chem., 2019, 58, 5069–5081.
52. T. J. Penfold, E. Gindensperger, C. Daniel and C. M. Marian, Spin-Vibronic Mechanism for Intersystem Crossing, Chem. Rev., 2018, 118, 6975–7025.
53. M. Heindl and L. González, Taming Disulfide Bonds with Laser Fields. Nonadiabatic Surface-Hopping Simulations in a Ruthenium Complex, J. Phys. Chem. Lett., 2022, 13, 1894–1900.
54. K. Magra, A. Francés-Monerris, C. Cebrián, A. Monari, S. Haacke and P. C. Bidentate, Pyridyl-NHC Ligands: Synthesis, Ground and Excited State Properties of Their Iron(II) Complexes and the Role of the Fac/Mer Isomerism, Eur. J. Inorg. Chem., 2022, e202100818.
55. A. Soupart, F. Alary, J.-L. Heully, P. I. P. Elliott and I. M. Dixon, Recent Progress in Ligand Photorelease Reaction Mechanisms: Theoretical Insights Focusing on Ru(II) ³MC States, Coord. Chem. Rev., 2020, 408, 213184.
56. A. Francés-Monerris, P. C. Gros, X. Assfeld, A. Monari and M. Pastore, Toward Luminescent Iron Complexes: Unravelling the Photophysics by Computing Potential Energy Surfaces, ChemPhotoChem, 2019, 3, 666–683.
57. I. M. Dixon, F. Alary, M. Boggio-Pasqua and J.-L. Heully, Reversing the Relative ³MLCT–³MC Order in Fe(II) Complexes Using Cyclometallating Ligands: A Computational Study Aiming at Luminescent Fe(II) Complexes, Dalton Trans., 2015, 44, 13498–13503.
58. Q. Sun, B. Dereka, E. Vauthey, L. M. Lawson Daku and A. Hauser, Ultrafast Transient IR Spectroscopy and DFT Calculations of Ruthenium(II) Polypyridyl Complexes, Chem. Sci., 2017, 8, 223–230.
59. K. Morgan, S. Lidin, S. Styring, S. Essén, P. Persson, A. Honarfar, J. Uhlig, T. Ericsson, J. Bendix and E. Thyrhaug, et al., A Low-Spin Fe(III) Complex with 100-Ps Ligand-to-Metal Charge Transfer Photoluminescence, Nature, 2017, 543, 695–699.
60. K. S. Kjær, N. Kaul, O. Prakash, P. Chábera, N. W. Rosemann, A. Honarfar, O. Gordivska, L. A. Fredin, K. E. Bergquist and L. Häggström, et al., Luminescence and Reactivity of a Charge-Transfer Excited Iron Complex with Nanosecond Lifetime, Science, 2019, 363, 249–253.
61. T. J. Penfold, E. Gindensperger, C. Daniel and C. M. Marian, Spin-Vibronic Mechanism for Intersystem Crossing, Chem. Rev., 2018, 118, 6975–7025.
62. D. Wang and S. Lippard, Cellular processing of platinum anticancer drugs, Nat. Rev. Drug Discovery, 2005, 4, 307–320.
63. A. Francés-Monerris, M. Marazzi, V. Besancenot, S. Grandemange, X. Assfeld and A. Monari, Computational Spectroscopy and Photophysics in Complex Biological Systems: Towards an In Silico Photobiology, in Computational Techniques for Analytical Chemistry and Bioanalysis, The Royal Society of Chemistry, 2021, pp. 202–246.
64. A. Francés-Monerris, C. Hognon, T. Douki and A. Monari, Photoinduced DNA Lesions in Dormant Bacteria. The Peculiar Route Leading to Spore Photoproduct Characterized by Multiscale Molecular Dynamics, Chem. – Eur. J., 2020, 26, 14236–14241.
65. (a) J. Aranda, A. Francés-Monerris, I. Tuñón and D. Roca-Sanjuán, Regioselectivity of the OH Radical Addition to Uracil in Nucleic Acids. A Theoretical Approach Based on QM/MM Simulations, J. Chem. Theory Comput., 2017, 13, 5089–5096; (b) A. Francés-Monerris, I. Tuñón and A. Monari, Hypoxia-Selective Dissociation Mechanism of a Nitroimidazole Nucleoside in a DNA Environment, J. Phys. Chem. Lett., 2019, 10, 6750–6754.
66. P. Müller and K. Brettel, Ru(bpy)₃]²⁺ as a reference in transient absorption spectroscopy: differential absorption coefficients for formation of the long-lived ³MLCT excited state, Photochem. Photobiol. Sci., 2012, 11, 632–636.
67. A. Cannizzo, F. van Mourik, W. Gawelda, G. Zgrablic, C. Bressler and M. Chergui, Broadband Femtosecond Fluorescence Spectroscopy of [Ru(bpy)₃]²⁺, Angew. Chem., 2006, 118, 3246–3248.
68. N. Azzaroli, M. Lobello, A. Lapini, A. Iagatti, L. Bussotti, M. Di Donato, G. Calogero, M. Pastore, F. De Angelis and P. Foggi, Monitoring the intramolecular charge transfer process in the Z907 solar cell sensitizer: a transient Vis and IR spectroscopy and ab initio investigation, Phys. Chem. Chem. Phys., 2015, 17, 21594–21604.
69. (a) G. Prampolini, F. Ingrosso, J. Cerezo, A. Iagatti, P. Foggi and M. Pastore, Short- and Long-Range Solvation Effects on the Transient UV-Vis Absorption Spectra of a Ru(II)–Polypyridine Complex Disentangled by Nonequilibrium Molecular Dynamics, J. Phys. Chem. Lett., 2019, 10, 2885–2891; (b) G. Prampolini, F. Ingrosso, A. Segalina, S. Caramori, P. Foggi and M. Pastore, Dynamical and Environmental Effects on the Optical Properties of an Heteroleptic Ru(II)–Polypyridine Complex: A Multilevel Approach Combining Accurate Ground and Excited State QM-Derived Force Fields, MD and TD-DFT, J. Chem. Theory Comput., 2019, 15, 529–545.

---

Footnote

† Electronic supplementary information (ESI) available: NTOs for the singlet states, HOMO and LUMO, square of the total spin operator expectation values, M06 and ZORA-M06 excitation energies, a benchmark for the Pt–Cl bond breaking, QM/MM Mulliken spin densities, a sensitivity analysis of the PMF integration limits, a histogram of the Pt–O distances collected in the umbrella sampling technique, umbrella sampling windows and complete simulation times, and Cartesian coordinates for complexes 1 and 2. See DOI: https://doi.org/10.1039/d2cp02128e

---