Open Access Article
Open Access ArticleConcentration dependent interfacial chemistry of the NaOH(aq): gibbsite interface†
Wei
Liu‡
a,
Maxime
Pouvreau‡
 b,
Andrew G.
Stack
b,
Andrew G.
Stack
 c,
Xiaoning
Yang
c,
Xiaoning
Yang
 *a and
Aurora E.
Clark
*a and
Aurora E.
Clark
 *b
*b
aState Key Laboratory of Materials-Oriented Chemical Engineering, College of Chemical Engineering, Nanjing Tech University, Nanjing 211816, P. R. China. E-mail: yangxia@njtech.edu.cn
bDepartment of Chemistry, Washington State University, Pullman, Washington 99164, USA. E-mail: maxime.pouvreau@pnnl.gov; aurora.clark@utah.edu
cOak Ridge National Laboratory, Oak Ridge, TN 37831, USA
First published on 17th August 2022
Abstract
Caustic conditions are often employed for dissolution of a wide variety of minerals, where ion sorption, surface diffusion, and interfacial organization impact surface reactivity. In the case of gibbsite, γ-Al(OH)3, the chemistry at the NaOH(aq) interface is deeply intertwined with industrial processing of aluminum, including metal production and the disposition of Al-containing wastes. To date, little is known about the structure, speciation, and dynamic behavior of gibbsite interfaces (and that of many other minerals) with NaOH(aq)—particularly as a function of ionic strength. Yet concentration-dependent interfacial organization and dynamics are a critical starting point to develop a fundamental understanding of the factors that influence dissolution. This work reports equilibrium molecular dynamics simulations of the γ-Al(OH)3:NaOH(aq) interface, revealing the sorption behavior and speciation of ions from 0.5–10 M [NaOH]. As inner-sphere complexes, Na+ primarily coordinates to the side of the gibbsite hexagonal cavities, while OH− accepts hydrogen-bonding from the surface-OH groups. The mobility of inner-sphere Na+ and OH− ions is significantly reduced due to a strong surface affinity in comparison to previous reports of NaCl, CaCl2, or BaCl2 electrolytes. At high [NaOH], contact ion pairing that is observed in the bulk solution is partially disrupted upon sorption to the gibbsite surface by the individual ion–surface interactions. The molecular-scale changes to surface speciation and competition between ion–surface vs. ion–ion interactions influence surface characterization of gibbsite and potential dissolution processes, providing a valuable baseline for starting conditions needed within future reactive molecular simulations.
1. Introduction
Gibbsite (γ-Al(OH)3) is the most abundant aluminum hydroxide polymorph.1–3 It consists of octahedral Al-atoms coordinated by three hydroxyl O-atoms each above and below the Al sheet4,5 that form hexagonal cavities in the basal plane (001) (Fig. 1); its basal surface is terminated by hydroxyls coordinated to two Al3+ (Al2OH), while the (100) and (110) edge surfaces consist of both AlOH and Al2OH terminated by –OH and –OH2 groups.6,7 The dissolution of gibbsite from bauxite ores (which contain gibbsite) followed by its re-precipitation in highly concentrated NaOH(aq) are the two critical steps of the Bayer process for aluminum and alumina production.8–10 The caustic chemistry of gibbsite is relevant to other industrial settings, for example to the treatment and disposal of highly radioactive wastes such as those at the Hanford nuclear reservation. Therein, tank sludge, primarily composed of gibbsite and boehmite, is leached by highly concentrated NaOH solutions.11The nature of the sorption of Na+ and OH− from highly concentrated NaOH(aq) on gibbsite surfaces has not been comprehensively studied, with prior work focusing upon the development of a macroscopic or mesoscopic understanding of gibbsite dissolution by NaOH(aq)9,12–23 Yet the availability of these ions to participate within interfacial reactions could be intrinsically dependent upon their surface speciation and adsorption characteristics. Understanding the physical sorption of Na+ and OH− from aqueous solution to the gibbsite basal surface is a critical first step toward characterizing the full surface chemistry behavior, as it provides relevant reference configurations for exploring the large phase space of potential dissolution reactions. Given that in alkaline conditions, the dissolution rate increases with [NaOH],13 there must be a catalytic effect of OH− on the Al-O bond breaking that will need to be investigated by computation. Of course, this catalysis cannot be approached without understanding of the structure and dynamics of the interface prior to dissolution, i.e. the concentration-dependent interfacial organization, speciation, and diffusive behavior of Na+, OH− and Na+·OH−. With this aim in mind, molecular dynamics (MD) simulations have been used in this work to study the speciation and characteristics of NaOH(aq) at the (001) basal surface of gibbsite (from 0.5 M to 10 M). As inner-sphere (IS) complexes, Na+ primarily adsorbs to the side of the gibbsite hexagonal cavities, while OH− accepts hydrogen-bonding from the surface hydroxyls. The ion mobility along the perpendicular direction is greatly inhibited due to the strong surface adsorption interaction and the mobility of Na+ and OH− ions in the inner-sphere region is clearly reduced.
2. Computational methods
Simulation model
The structural model of the gibbsite interface is illustrated in Fig. 1 and consists of a 4 × 6 × 2 supercell created from the monoclinic gibbsite unit cell of dimensions a = 8.68 Å, b = 5.08 Å, and c = 9.74 Å, with α = γ = 90°, and β = 94.54° and where the unit cell was cleaved along the (001) plane to form a gibbsite slab of dimensions 34.7 × 30.4 × 38.8 Å3. The slab was put in contact with an aqueous NaOH solution, and five different NaOH concentrations were examined: 0.5, 1.0, 2.0, 5.0, and 10 M (molecular compositions and densities presented in Table S1, ESI†). Since a perfect cleavage of the basal surface was considered in the current work and that the maximum NaOH concentration is 10 M (pH = 15) the surface oxygens of the basal surface are all considered singly protonated. These are consistent with first-principles MD calculations of the pKa using the vertical energy gap method,24 that predict a surface pKa value of 22 and are within 1–2 pKa units of experiment.24,25 As such a perfect basal surface cannot be proton active in the common pH range. Yet results from potentiometric and AFM measurements provide contradicting conclusions concerning the proton activity of basal Al2OH groups.6,26–30 Importantly, features that could give rise to a surface charge interpreted as proton activity28 include ion pairs,26,27 as well as the presence of defects (including steps and kinks) that reveal proton-active groups.26,31 As such, it is important to examine and compare the concentrations of adsorbed ions as well as adsorbed contact ion pairs (CIP) and to understand their impact upon interfacial organization. The variation in ion speciation at the surface was compared to simulations of bulk NaOH solutions at the same concentrations.Force field implementation and benchmarking
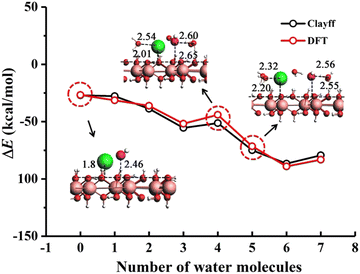
The ClayFF suite of interatomic potentials is essentially based on a nonbonded description of the metal–oxygen interactions associated with hydrated phases, which allows good transferability of the force field parameters while maintaining full flexibility of the simulation system. Furthermore, the use of a simple nonbonded interaction potential to describe metal–oxygen bonds and harmonic terms provides an efficient and accurate basis for simulating large systems.32 Here, the ClayFF potential was employed to describe the gibbsite mineral interactions, including an Al–O–H bending term33 along with a harmonic O–H bond term and the flexible water SPC model.34 ClayFF with the addition of the metal–O–H term has been fully validated for the gibbsite/water interface against AIMD,33 and to our knowledge such validation has not been done for other force fields able to model gibbsite interfaces, such as INTERFACE FF.35 As the metal–O–H term was initially associated with a Morse O–H potential but occurrences of unphysical bond breaking were observed at 10 M NaOH concentration, the original harmonic ClayFF O–H bond term was modified by selecting r0(O–H) = 0.9572 Å instead of r0(O–H) = 1.0 Å, resulting in a virtually identical surface Hhydroxyl–Owater RDF (related to hydrogen-bonding) compared to the Morse O–H bond term by Greathouse et al.36 The Na+ Lennard-Jones parameters were taken from Joung et al.37 and the OH− parameters from Balbuena et al.38 The Lorentz–Berthelot mixing rules were applied for the Lennard-Jones interactions of unlike particles. Combined with the flexible SPC model, the Na+ model predicts a Na+-Owater coordination number (CN) of 5.8 in water, within the margin of error of the experimental value obtained in dilute conditions.39 The HO−⋯HW coordination number of 5.8 predicted by the hydroxide model is an overestimation relative to the experimental value of 4.1,40 however this is a common feature of 2-site point charge models.41 Although explicit polarization can improve the OH− coordination number42,43 it does not necessarily improve the general NaOH solution structure obtained from X-ray or neutron scattering44 and is of course incompatible with the nonpolarizable ClayFF model employed for the gibbsite slab. The nonpolarizable model by Ufimtsev et al.41 is further computationally impractical because of the large number of sites involved. The electrostatic continuum correction was subsequently examined as a means to improve the OH− CN. Test calculations indicated that although the H2O⋯OH− binding energies in the gas phase and HO−⋯Hwater coordination numbers in solution were improved by scaling the charges by 75%, the Na+·OH− CIP interaction energy and ion–surface interactions were significantly underestimated – a feature that could not be recovered by a modification of the Lennard-Jones terms. Given these observations, the original nonpolarizable OH− potential was employed. Finally, the particle–particle particle–mesh (PPPM) method45 was employed to compute the long-range electrostatic interaction with a tolerance of 10−5.DFT calculations were performed to validate the ability of the force field to correctly describe the interactions of the Na+·OH− CIP with the surface of gibbsite. A 3 × 4 gibbsite supercell (26.05 × 20.31 Å2) with the basal (001) surface exposed was constructed. Geometry optimization was performed on hydrated NaOH clusters of the form NaOH-(H2O)n (n = 0–7) placed on the (001) surface using the BAND module of AMS (Amsterdam Modeling Suite 2019) under periodic boundary conditions.46 The PBE functional47 with a dispersion correction through the Grimme approach48,49 and a triple zeta basis set plus polarization (TZP) basis set us was employed. The DFT-optimized structures were then utilized to compute the binding interaction energies (ΔE) between the adsorbed NaOH(H2O)n hydrated complexes on the gibbsite surface. The (ΔE) is defined as:
| ΔE = Egibbsite/NaOH–(H2O)n − Egibbsite − ENaOH–(H2O)n | (1) |
Simulation and equilibration protocol
All simulations were performed using LAMMPS50 with a time step of 1 fs. The volume of the aqueous phase was first equilibrated using the NPT ensemble according to the equations of Shinoda et al.51 at 300 K and 1 atm along the z-axis, resulting in a slit pore of length ∼70 Å along this dimension, ensuring the absence of confinement. Within this stage of the equilibration, the integrity of the mineral slab was preserved by constraining the velocity of its Al- and O-atoms to zero, which still allowed fluctuations of the volume of the aqueous phase. In the subsequent NVT run, two 1 ns temperature cycles from 300 K to 500 K and back were performed. At the final temperature of 300 K the mineral slab constraint was released; during this phase, the radial distribution functions (RDFs) for all O–H and Na–O pairs were monitored and the system was considered equilibrated when they reached convergence (after 30–40 ns). A final 1 ns equilibration of the density was done in the NPT ensemble at 300 K. All the properties of the system were computed based on a subsequent 40 ns production phase in the NVT ensemble.Umbrella sampling
Umbrella sampling was employed to investigate the free energy profiles of ion adsorption to the basal gibbsite surface. Note that the inclusion of multiple ions would requires tens of ns of ensemble averaging over 75 umbrella sampling windows. Separate MD simulations were performed using the gibbsite slab, water, and a single ion present (either Na+ or OH−). The collective variable was defined as the z-coordinate of the ion relative to the plane formed by the outermost mineral O-atoms (set to z = 0). One hundred ps umbrella sampling windows were separated by 0.1 Å with k = 125 kcal mol Å−2 for 1 Å < z < 6 Å and 0.2 Å with k = 30 kcal mol Å−2 for 6 Å < z < 11 Å. To prevent the Na+ from moving laterally across the hexagonal surface cavity, the distance between the ion and the line orthogonal to the surface and passing through the site was constrained to zero. However, the force constant of the restraint k = 1 kcal mol Å−2, was much weaker than the restraint of the biasing collective variable, ensuring that this secondary, lateral restraint had a negligible influence on the potential of mean force (PMF). As the gibbsite surface is neutral, the electrostatic interaction between every ion and the surface is zero and the interaction at z = 10 Å is close to zero.3. Results and discussion
Adsorption characteristics
We first consider the general adsorption characteristics of NaOH(aq) moving from the bulk solution to the surface of gibbsite, as shown in Fig. 3via the number density profiles for Na+, OH− and the contact ion pairs (CIP) between Na+ and OH−, abbreviated Na+·OH−. Contact ion pairs are defined as those ion pairs with a direct ion–ion interaction and no intervening solvent molecules between them. In the trajectory analysis, one CIP is counted every time the Na+-OH− distance is less than 2.85 Å (distance corresponding to the minimum after the first Na-O(OH−) RDF peak). For clarification, a single ion can have multiple direct contacts with an ion of opposite charge, i.e. several CIPs can be associated with a single ion. The coordinates of the Na+·OH− CIP are chosen as the center of the Na-O axis.The density profiles further allow the definition of inner-sphere (IS) sorbed ions as those whose distance is z < 3.3 Å, meaning their direct interaction with surface-atoms, while outer-sphere (OS) sorbed ions reside within 3.3 < z < 5.3 Å (having intervening H2O between the ion and the surface atoms). Even if a third, less structured ion layer exists (visible for both ions at 10 M in Fig. 3e), the z > 5.3 Å portion of the solution is considered “bulk” for the sake of convenience. The density profiles clearly show the IS and OS species as two distinct layers from z = 0 Å, respectively. The distribution of Na+ within the IS layer consists of three peaks at 1.4 Å, 1.8 Å and 2.3 Å that correspond to different adsorption sites (vide infra). The distribution of OH− within the IS layer consists of one peak at 2.6 Å. The Na+·OH− CIPs are mostly located within the IS layer at a distance of 2.2 Å. The OW and HW number density profiles are shown in Fig. S1 (ESI†). The most prominent effect therein is the decrease of the height of the first HW peak (z < 2 Å) associated with HWO–HW⋯Ogibbsite) hydrogen bonding, presumably caused by hindrance due to the increased number of Na+ coordinated to the surface O-atoms.
From 0.5 M to 2 M [NaOH] the surface coverages of Na+ and OH− continuously increase, and saturation is reached 5 M with a coverage of ∼7–8 ions nm−2. Interesting comparisons can be made to a similar study of NaCl(aq) sorption by Ho et al.7 within the same concentration range and using similar quality force fields. Although the current work reports a surface coverage of Na+ and OH− at 1 M that is greater than 2 per nm2, in the case of Na+ and Cl− from NaCl(aq) surface coverage values of 0.4 and 0.7 ions nm−2 were observed, respectively. At 2 M NaCl(aq), 1.1 Na+ nm−2 were observed to be sorbed to the basal surface of gibbsite as compared to our 4 Na+ nm−2 from 2 M NaOH(aq) (note that the Cl− surface coverage was not mentioned by the authors at this concentration). Excluding the possible effects of the box size, the force field, and the equilibration procedure, which are likely minor, these data indicate a likely smaller affinity of Cl− for the surface than OH−, which results in less Na+ adsorbed due to charge compensation. Ho et al. found even smaller adsorption values for Ca2+ (in CaCl2(aq)) and Ba2+ (in BaCl2(aq)), where 0.8–0.9 ions nm−2 were sorbed from 2 M electrolyte solutions. The surface coverage of Na+ in the IS layer is systematically larger than that of the OS layer, in agreement with observations regarding NaCl(aq) on the gibbsite basal surface. However, the IS/OS ratio for Na+ decreases with increasing concentration.
Very different trends are observed for OH− sorption, as similar amounts of anions are found in the IS and the OS layers irrespective of [NaOH]. The lower degree of adsorption of OH− in the IS layer compared to Na+ indicates a cumulatively weaker interaction of OH− with the hydroxyls caused by hydrogen-bonding and coulombic forces than the coulombic interaction of Na+ with surface O-atoms. At higher concentrations, the balance between Na+ and OH− in the inner sphere tends to equalize as a result of saturation being reached, even if a slight imbalance in favor of Na+ remains. Interestingly, the number of OH− in the OS slightly overcompensates this imbalance at 5 M and 10 M, though an approximately neutral net charge is obtained when the third layer is accounted for (not shown here). Finally, H2O surface coverage is very modestly affected by ion sorption, with a decrease in surface coverage of ∼1 H2O nm−2 (or a 10% decrease) between 0.5 M and 10 M in the first water layer, and virtually no change in the second layer (Fig. 4). Note that the coordinate perpendicular to the surface was allowed to relax during the equilibration, and thus the small decrease of the number of H2O at the interface compared to the large increase in the number of sorbed ions between 0.5 M and 10 M may be explained by the overall contraction of the H2O⋯H2O distances in the volume unoccupied by the ions.
As indicated from Fig. 5a, between 0.5 and 2 M NaOH the overall Na+·OH− contact ion pairing is slightly increased at the gibbsite surface relative to bulk NaOH(aq) simulations, suggesting that the surface facilitates ion pairing at moderate concentrations. In contrast, under higher [NaOH] contact ion pairing is strongly reduced at the solid/liquid interface where the IS and OS layers are saturated (Fig. 4, 5 and 10 M). Across the concentration range, there is competition amongst the inter-particle interactions associated with adsorption of individual ions vs. contact ion pairing. Fig. 5b shows the number of CIPs between an ion in the IS and an ion of opposite charge either in the IS (IS–IS) or in the OS (IS–OS), divided by the total number of Na+ in the solution. This increases up to 2 M NaOH, then decreases with higher concentrations, indicating that ion saturation at the surface causes an energetic penalty for CIP interactions of sorbed species.
Ion adsorption sites
The planar (xy) density distributions were then examined to elucidate the adsorption sites of Na+ and OH−. Fig. 6 depicts the preferential adsorption sites along the xy plane for inner-sphere adsorbed Na+ and OH−. Two adsorption sites are observed for Na+ (Fig. 6a): #1 above the center of a hexagonal cavity formed by the Al-atoms and coordinating with three surface O-atoms; #2 above the Al-atoms and coordinated by three surface O-atoms. On average, 0.76 Na+ and 0.60 OH− per hexagonal cavity are adsorbed as IS complexes at saturation (5 M). For OH−, the surface adsorption site is primarily located near the surface H-atoms belonging to the surface hydroxyls that point toward the solution (Fig. 6b) through a hydrogen bond (HB) interaction. Fig. 6c shows the planar density distributions of H2O in the 5 M NaOH(aq). It is clear that most H2O are distributed on the edge of the hexagonal cavities on the surface (001), just like the inner-sphere bound OH−. The anticipated effect this may have upon an estimated surface charge is discussed in the ESI.†Ion hydration and interfacial hydrogen-bonding
RDFs were used to characterize the structure of the ion hydration shells where IS complexation significantly decreases hydration numbers in the first coordination shell (Fig. 7). For example, at 2 M [NaOH] the ion-OW coordination number (CN) in the IS region is reduced by 1.8 and 2.0 for OH− and Na+, respectively, compared to the bulk. We note that the bulk CN(Na+–OW) of 5.1 is smaller than the value mentioned in the Methods section as a result of significant ion-pairing with OH− that obviously does not occur at high dilution.As in the bulk, the gibbsite basal surface features intralayer hydrogen-bonding between hydroxyl groups in the basal plane and out of the basal plane,52 the latter representing 58% of the OH groups (Fig. S2, ESI†). Hydroxyl groups also form HBs with adsorbed H2O (both as HB donors and acceptors) and OH− (only donated). The evolution of the average number of HBs as a function of concentration is represented in Fig. 8c. The corresponding HB autocorrelation function53 is defined as
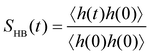 | (2) |
It is interesting to consider whether the observed modifications to interfacial water structure would be detectable by experiment, for example in atomic force microscopy (AFM). Nakouzi et al.54 recently utilized fast force mapping AFM, complemented by classical molecular dynamics rare event simulations, to observe the molecular structure of the interface of boehmite (γ-AlO(OH)) with pH 11 water, a surface related to the α-Al(OH)3:water studied here. That work found that the molecular structure of the interface measured by AFM was strongly sensitive to the local interfacial water density, which likely reflects a templating effect of the mineral surface structure upon that of interfacial water. If true, it suggests that surface charge at even more elevated pH would not affect the average interfacial water structure until the surface charge density is sufficiently high to affect a comprehensive change in the mineral–water interface structure (e.g., several charged sites per nm2). This in turn might create an unstable surface, leading to dissolution. Regardless, since interfacial water density is not significantly modified by ion sorption at saturation, and given that an ideal gibbsite basal surface site is not proton active,55 the aforementioned data on boehmite indicates that the basal gibbsite interface structure measured by AFM spectroscopy would not vary significantly at high pH as long as the density of step edges remains small.
Adsorption energetics
As shown in the Fig. 9, the free energy profiles for ion sorption (obtained from potential of mean force simulations) feature two separated free energy minima, corresponding to the IS and OS adsorption positions in the corresponding density profiles (Fig. 3). In Fig. 9a, the Na+ on site #2 (side of the hexagonal cavity) has a smaller energy minimum in IS, which agrees with the density profiles. For Na+ and OH− the first PMF minimum (corresponding to IS adsorption) is respectively at 1.9 Å and at 2.7 Å, consistent with the observation that the first adsorption layer of Na+ is closer to the gibbsite surface (001) than OH−. In the PMF profiles, the first free energy minimum of the Na+ on site #2 is approximately 2.3 kcal mol−1 lower in energy than that of the OH− (−2.0 kcal mol−1), demonstrating that Na+ has a stronger adsorption stability. The PMF in Fig. 9a reveals that Na+ adsorption to the side of the hexagonal cavity consists of three sites that correspond to three minima observed at z-values between 1.9 and 2.4 Å depending on whether Na+ is directly above the Al-atom or slightly offset (Table 1).| Na+ | OH− | ||
|---|---|---|---|
| IS → OS | K = [OS]/[IS] | 0.21 | 0.34 |
| OS → bulk | K = [dissolved]/[OS] | 0.88 | 0.83 |
However, the difference in stability and the energy barriers between those sites is less than kT (0.6 kcal mol−1) and thus inter-site hops are not rare events and thermodynamic distinction between these sites is not meaningful. Less importantly, for the PMF to site #1, near z = 2.4 Å (the third IS minimum) some incursions near the center of the cavity occur due to the weak lateral restraint.
The adsorption equilibrium constants (K) for the NaOH near the gibbsite surface, were calculated according to:
 | (3) |
Dynamic behavior of adsorbed ions
In order to elucidate the dynamic behavior of the Na+ and OH− ions within the interfacial region, their in-plane mean square displacement along the xy plane (MSDxy) and the out-of-plane mean square displacement along the z-direction (MSDz) have been computed. The MSDs are defined as:| MSDxy = 〈Δx(t)2〉 + Δy(t)2〉 ∝ tk | (4) |
The simulated MSDxy and MSDz for both ions at 1 M NaOH within the interfacial IS and OS regions are shown in Fig. 10 and those for other concentrations in Fig. S5 (ESI†). In general, Na+ and OH− ions show identical concentration dependent trends in diffusion behavior. In the IS, the slopes of all the logarithmic MSD curve are nearly 0.5 in the period of 1–100 ps. Beyond that, the diffusion of ions exhibits Fickian diffusion (k ≈ 1). The ion mobility it evaluated using the self-diffusion coefficient Ds with the Einstein relation.60 The in-plane two-dimensional diffusion coefficient Ds can be calculated from the slope of the in-plane mean squared displacements (MSDxy) as,
 | (5) |
4. Conclusions
MD simulations have been employed to investigate the concentration dependent interfacial organization and ion adsorption behavior of NaOH(aq) on the (001) basal surface of gibbsite. Both Na+ and OH− are observed to adsorb primarily as inner-sphere species, with Na+ residing either within or on the edge of a hexagonal cavity of the surface O-atoms. For OH−, the surface adsorption sites are located above the gibbsite hydroxyls from which they accept hydrogen bonds. The adsorption capacity of Na+ and OH− ions on the gibbsite surface is higher than those previously reported for aqueous NaCl, CaCl2, or BaCl2 electrolytes. This behavior could be attributed to the enhanced affinity of OH− ions with the gibbsite surface (and consequently Na+ due to contact ion pairing). Up to 2 M NaOH, the surface is found to enhance contact ion pairing within the IS region, however it strongly disrupts the formation of interfacially bound CIPs above 2 M NaOH. The interfacial diffusion properties of the ions indicate that ion mobility is greatly inhibited in the inner-sphere region, while the motion of ions in the outer-sphere region is more unrestrained due to the weaker surface interaction.Note that although dissolution may occur primarily at edges (including step edges), at very high pH (typically pH > 13) the (100) surface (which is a predominant edge surface according to Hiemstra et al.6) only consist of OH groups,55 as in the basal (001) surface considered in this work. Such edges may be quantitatively modulated by the O–Al coordination, surface charge, among other aspects, yet the concentration dependent behavior of ion sorption on the (001) including the modulation of contact ion paired species at the surface, in combination with the changes to surface diffusion, provide valuable new insight toward ongoing and future studies of gibbsite dissolution under NaOH(aq) conditions relevant to Al industrial processing and metal production.6 More generally, this work expands a fundamental understanding of ion-sorption under highly caustic conditions, which is relevant to a wide variety of processes that leverage NaOH (or other hydroxide electrolytes) for dissolution.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was supported by the Interfacial Dynamics in Radioactive Environments and Materials (IDREAM), an Energy Frontier Research Center funded by the U.S. Department of Energy, Office of Science, Basic Energy Sciences. Molecular simulations used resources from the Center for Institutional Research Computing at Washington State University.References
- R. Demichelis, Y. Noel, P. Ugliengo, C. M. Zicovich-Wilson and R. Dovesi, J. Phys. Chem. C, 2011, 115, 13107–13134 CrossRef CAS.
- S. Nagendran, G. Periyasamy and P. V. Kamath, Z. Anorg. Allg. Chem., 2015, 641, 2396–2403 CrossRef CAS.
- M. F. Peintinger, M. J. Kratz and T. Bredow, J. Mater. Chem. A, 2014, 2, 13143–13158 RSC.
- J. T. Kloprogge, L. V. Duong, B. J. Wood and R. L. Frost, J. Colloid Interface Sci., 2006, 296, 572–576 CrossRef CAS PubMed.
- S.-L. Wang and C. T. Johnston, Am. Miner., 2000, 85, 739–744 CrossRef CAS.
- T. Hiemstra, H. Yong and W. H. Van Riemsdijk, Langmuir, 1999, 15, 5942–5955 CrossRef CAS.
- T. A. Ho, J. A. Greathouse, A. S. Lee and L. J. Criscenti, Langmuir, 2018, 34, 5926–5934 CrossRef CAS PubMed.
- A. R. Hind, S. K. Bhargava and S. C. Grocott, Colloids Surf., A, 1999, 146, 359–374 CrossRef CAS.
- J. A. M. Pereira, M. Schwaab, E. Dell’Oro, J. C. Pinto, J. L. F. Monteiro and C. A. Henriques, Hydrometallurgy, 2009, 96, 6–13 CrossRef CAS.
- H. B. Yang, X. L. Pan, H. Y. Yu, G. F. Tu and J. M. Sun, Nonferrous Met. Soc., 2015, 25, 4151–4159 CrossRef CAS.
- J. G. Reynolds, J. K. McCoskey and D. L. Herting, Ind. Eng. Chem. Res., 2016, 55, 5465–5473 CrossRef CAS.
- R. F. Scotford and J. R. Glastonbury, J. Chem. Eng., 1971, 49, 611–616 CAS.
- R. F. Scotford and J. R. Glastonbury, Can. J. Chem. Eng., 1972, 50, 754–758 CrossRef CAS.
- A. Bauer and G. Berger, Appl. Geochem., 1998, 13, 905–916 CrossRef CAS.
- P. Benezeth, D. A. Palmer and D. J. Wesolowski, Geochim. Cosmochim. Acta, 2008, 72, 2429–2453 CrossRef CAS.
- J. A. Chermak, Miner, 1992, 40, 650–658 CAS.
- J. A. Chermak, Miner, 1993, 41, 365–372 CAS.
- T. R. Graham, M. Dembowski, E. Martinez-Baez, X. Zhang, N. R. Jaegers, J. Hu, M. S. Gruszkiewicz, H.-W. Wang, A. G. Stack, M. E. Bowden, C. H. Delegard, G. K. Schenter, A. E. Clark, S. B. Clark, A. R. Felmy, K. M. Rosso and C. I. Pearce, Inorg. Chem., 2018, 57, 11864–11873 CrossRef CAS PubMed.
- H. Grenman, T. Salmi, D. Y. Murzin and J. Addai-Mensah, Eng. Chem. Res., 2010, 49, 2600–2607 CrossRef CAS.
- C. D. Peskleway, G. S. Henderson and F. J. Wicks, Am. Mineral., 2003, 88, 18–26 CrossRef CAS.
- N. Brown, J. Cryst. Grow., 1972, 12, 39–45 CrossRef CAS.
- Z. Shen, S. N. Kerisit, A. G. Stack and K. M. Rosso, J. Phys. Chem. Lett., 2018, 9, 1809–1814 CrossRef CAS PubMed.
- R. Schliemann and S. V. Churakov, Geochim. Cosmochim. Acta, 2021, 293, 438–460 CrossRef CAS.
- M. Sulpizi and M. Sprik, Phys. Chem. Chem. Phys., 2008, 10, 5238–5249 RSC.
- T. De Meyer, B. Ensing, S. M. J. Rogge, K. De Clerck, E. J. Meijer and V. Van Speybroeck, ChemPhysChem, 2016, 17, 3447–3459 CrossRef CAS PubMed.
- J. Rosenqvist, P. Persson and S. Sjöberg, Langmuir, 2002, 18, 4598–4604 CrossRef CAS.
- M.-C. Jodin, F. Gaboriaud and B. Humbert, J. Colloid Interface Sci., 2005, 287, 581 CrossRef CAS PubMed.
- Y. Gan and G. V. Franks, 6.
- S. Mitchell, Theses and Dissertations.
- B. R. Bickmore, C. J. Tadanier, K. M. Rosso, W. D. Monn and D. L. Eggett, Geochim. Cosmochim. Acta, 2004, 68, 2025–2042 CrossRef CAS.
- A. Klaassen, F. Liu, D. van den Ende, F. Mugele and I. Siretanu, Nanoscale, 2017, 9, 4721–4729 RSC.
- R. T. Cygan, J.-J. Liang and A. G. Kalinichev, J. Phys. Chem. B, 2004, 108, 1255–1266 CrossRef CAS.
- M. Pouvreau, J. A. Greathouse, R. T. Cygan and A. G. Kalinichev, J. Phys. Chem. C, 2017, 121, 14757–14771 CrossRef CAS.
- O. Teleman, B. Jönsson and S. Engström, Mol. Phys., 1987, 60, 193–203 CrossRef CAS.
- H. Heinz, T.-J. Lin, R. Kishore Mishra and F. S. Emami, Langmuir, 2013, 29, 1754–1765 CrossRef CAS PubMed.
- J. A. Greathouse, J. S. Durkin, J. P. Larentzos and R. T. Cygan, J. Chem. Phys., 2009, 130, 134713 CrossRef PubMed.
- I. S. Joung and T. E. Cheatham, J. Phys. Chem. B, 2008, 112, 9020–9041 CrossRef CAS PubMed.
- P. B. Balbuena, K. P. Johnston and P. J. Rossky, J. Phys. Chem., 1996, 100, 2706–2715 CrossRef CAS.
- M. Galib, M. D. Baer, L. B. Skinner, C. J. Mundy, T. Huthwelker, G. K. Schenter, C. J. Benmore, N. Govind and J. L. Fulton, J. Chem. Phys., 2017, 146, 084504 CrossRef CAS PubMed.
- S. E. McLain, S. Imberti, A. K. Soper, A. Botti, F. Bruni and M. A. Ricci, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 094201 CrossRef.
- I. S. Ufimtsev, A. G. Kalinichev, T. J. Martinez and R. J. Kirkpatrick, Chem. Phys. Lett., 2007, 442, 128–133 CrossRef CAS.
- R. Vácha, T. Megyes, I. Bakó, L. Pusztai and P. Jungwirth, J. Phys. Chem. A, 2009, 113, 4022–4027 CrossRef PubMed.
- J. S. Hub, M. G. Wolf, C. Caleman, P. J. van Maaren, G. Groenhof and D. van der Spoel, Chem. Sci., 2014, 5, 1745 RSC.
- D. Semrouni, H.-W. Wang, S. B. Clark, C. I. Pearce, K. Page, G. Schenter, D. J. Wesolowski, A. G. Stack and A. E. Clark, Phys. Chem. Chem. Phys., 2019, 21, 6828–6838 RSC.
- J. W. Eastwood, R. W. Hockney and D. N. Lawrence, Comput. Phys. Commun., 1980, 19, 215–261 CrossRef CAS.
- G. Velde, F. M. Bickelhaupt, E. J. Baerends, C. F. Guerra, S. J. A. V. Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- W. Shinoda, M. Shiga and M. Mikami, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 134103 CrossRef.
- R. Demichelis, B. Civalleri, Y. Noel, A. Meyer and R. Dovesi, Chem. Phys. Lett., 2008, 465, 220–225 CrossRef CAS.
- A. Chandra, J. Phys. Chem. B, 2003, 107, 3899–3906 CrossRef CAS.
- E. Nakouzi, A. G. Stack, S. Kerisit, B. A. Legg, C. J. Mundy, G. K. Schenter, J. Chun and J. J. De Yoreo, J. Phys. Chem. C, 2021, 125, 1282–1291 CrossRef CAS.
- X. Liu, J. Cheng, M. Sprik, X. Lu and R. Wang, Geochim. Cosmochim. Acta, 2013, 120, 487–495 CrossRef CAS.
- R. Weerasooriya, H. J. Tobschall, H. K. D. K. Wijesekara, E. K. I. A. U. K. Arachchige and K. A. S. Pathirathne, Adsorp. Gibbsite, Chemosp., 2003, 51, 1001–1013 CAS.
- A. Striolo, Nano Lett., 2006, 6, 633–639 CrossRef CAS PubMed.
- J. P. Bouchaud, A. Georges, J. Koplik, A. Provata and S. Redner, Phys. Rev. Lett., 1990, 64, 2503–2506 CrossRef PubMed.
- H. F. Ye, H. W. Zhang, Y. G. Zheng and Z. Q. Zhang, Nanofluid, 2011, 10, 1359–1364 CrossRef CAS.
- E. H. P. Liu and B. Berne, J. Phys. Chem. B, 2004, 108, 6595 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp01997c |
| ‡ These authors contributed equally to this work. |
| This journal is © the Owner Societies 2022 |