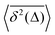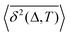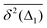Anomalous diffusion, aging, and nonergodicity of scaled Brownian motion with fractional Gaussian noise: overview of related experimental observations and models
Received
14th April 2022
, Accepted 7th June 2022
First published on 7th June 2022
Abstract
How does a systematic time-dependence of the diffusion coefficient D(t) affect the ergodic and statistical characteristics of fractional Brownian motion (FBM)? Here, we answer this question via studying the characteristics of a set of standard statistical quantifiers relevant to single-particle-tracking (SPT) experiments. We examine, for instance, how the behavior of the ensemble- and time-averaged mean-squared displacements—denoted as the standard MSD 〈x2(Δ)〉 and TAMSD 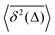 quantifiers—of FBM featuring
quantifiers—of FBM featuring 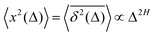 (where H is the Hurst exponent and Δ is the [lag] time) changes in the presence of a power-law deterministically varying diffusivity Dα(t) ∝ tα−1—germane to the process of scaled Brownian motion (SBM)—determining the strength of fractional Gaussian noise. The resulting compound “scaled-fractional” Brownian motion or FBM–SBM is found to be nonergodic, with 〈x2(Δ)〉 ∝ Δα+2H−1 and
(where H is the Hurst exponent and Δ is the [lag] time) changes in the presence of a power-law deterministically varying diffusivity Dα(t) ∝ tα−1—germane to the process of scaled Brownian motion (SBM)—determining the strength of fractional Gaussian noise. The resulting compound “scaled-fractional” Brownian motion or FBM–SBM is found to be nonergodic, with 〈x2(Δ)〉 ∝ Δα+2H−1 and 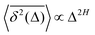 . We also detect a stalling behavior of the MSDs for very subdiffusive SBM and FBM, when α + 2H − 1 < 0. The distribution of particle displacements for FBM–SBM remains Gaussian, as that for the parent processes of FBM and SBM, in the entire region of scaling exponents (0 < α < 2 and 0 < H < 1). The FBM–SBM process is aging in a manner similar to SBM. The velocity autocorrelation function (ACF) of particle increments of FBM–SBM exhibits a dip when the parent FBM process is subdiffusive. Both for sub- and superdiffusive FBM contributions to the FBM–SBM process, the SBM exponent affects the long-time decay exponent of the ACF. Applications of the FBM–SBM-amalgamated process to the analysis of SPT data are discussed. A comparative tabulated overview of recent experimental (mainly SPT) and computational datasets amenable for interpretation in terms of FBM-, SBM-, and FBM–SBM-like models of diffusion culminates the presentation. The statistical aspects of the dynamics of a wide range of biological systems is compared in the table, from nanosized beads in living cells, to chromosomal loci, to water diffusion in the brain, and, finally, to patterns of animal movements.
. We also detect a stalling behavior of the MSDs for very subdiffusive SBM and FBM, when α + 2H − 1 < 0. The distribution of particle displacements for FBM–SBM remains Gaussian, as that for the parent processes of FBM and SBM, in the entire region of scaling exponents (0 < α < 2 and 0 < H < 1). The FBM–SBM process is aging in a manner similar to SBM. The velocity autocorrelation function (ACF) of particle increments of FBM–SBM exhibits a dip when the parent FBM process is subdiffusive. Both for sub- and superdiffusive FBM contributions to the FBM–SBM process, the SBM exponent affects the long-time decay exponent of the ACF. Applications of the FBM–SBM-amalgamated process to the analysis of SPT data are discussed. A comparative tabulated overview of recent experimental (mainly SPT) and computational datasets amenable for interpretation in terms of FBM-, SBM-, and FBM–SBM-like models of diffusion culminates the presentation. The statistical aspects of the dynamics of a wide range of biological systems is compared in the table, from nanosized beads in living cells, to chromosomal loci, to water diffusion in the brain, and, finally, to patterns of animal movements.
I Introduction
The flurry of new single-particle-tracking (SPT) datasets reporting on and novel theoretical-analysis tools assessing the properties of anomalous diffusion1–27 has established an unprecedented need for novel theoretical models of diffusion and transport. Such models should desirably embody certain characteristic features of different “standard” anomalous-diffusion processes28–33 such as, i.e., conventional Brownian motion (BM),34–41 fractional BM (FBM)42–48 governed by fractional Gaussian noise, scaled BM (SBM)49–61 and ultraslow SBM62,63 with a power-law time-dependent diffusivity D(t) ∝ tα−1, continuous-time random walks (CTRWs),31,64,65 Lévy walks and flights,66 heterogeneous diffusion processes (HDPs)52,53,67–69 with a power-law position-dependent diffusivity, D(x) ∝ |x|![[small alpha, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c2.gif) , etc.
, etc.
In recent years, certain combinations of models were proposed, including switching-diffusivity11,13,70–77 and annealed-transient-time models (ATTM),78 BM with fluctuating or diffusing diffusivity (DD),70,79–85 BM- and anomalous-diffusion-models with “superstatistically” distributed model parameters,86–89 compound diffusion processes of SBM-DD,84 SBM–HDPs,90,91 FBM-DD,92 FBM–HDPs,19,93 SBM with exponentially and logarithmically varying D(t),94 CTRWs with random walks on fractal (RWFs),95 CTRW–FBM,16,96–98 as well as several other models,74,99–113 including fractional-Langevin-equation (FLE) motion. Renewal processes involving alternation of different types of motions were proposed as well [with, e.g., switching between different diffusion processes,20,100,114,115 processes with intermittent mobility states,13 or with different anomalous scaling exponents12,103,116–119]. For some recent examples, we refer the reader to, e.g., the hybrid models of alternating Lévy walks with BMs120,121 and Lévy walks with CTRWs.122 Multifractional FBM-based processes with a Hurst exponent varying in time49,123,124 were also considered recently.125–127 Such processes were used, e.g., in mathematical-finance models with (multi-)fractional stochastic volatility.128,129
This multifaceted picture of diffusion scenarios potentially realizable for SPT datasets is, however, far from being complete, and we develop here one more useful model of FBM–SBM. The main objective is to examine how the temporal correlations of fractional Gaussian noise—featuring persistent displacements for superdiffusive and antipersistent displacements of a particle for subdiffusive Hurst exponents H of FBM—“interfere” with a power-law deterministic D(t)-dependence of SBM.
The rest of the paper is organized as follows. In Section II we introduce the concepts of ensemble- and time-averaging and discuss ergodicity130 of FBM and SBM. Some details of simulations are given in Section III A. The main results of the theoretical analysis and of computer simulations for the FBM–SBM model are presented in Section III. Specifically, the properties of the ensemble-averaged mean-squared displacement (MSD) and of the time-averaged MSD (TAMSD), the aging characteristics of the TAMSD, the probability-density function (PDF), and increment/velocity autocorrelation function (ACF) are considered in Section III B, III C, III D, and III E, respectively. The discussion and conclusions are presented in Section IV. The list of applications of FBM and SBM is overviewed in Section IV A. The main features of experimental SPT datasets and FBM-, SBM-, and FBM–SBM-related theoretical models are summarized in Table 1, while several additional figures are listed in Appendix A.
Table 1 Comparative overview of several recent (last decade) experimental SPT and simulations-based datasets, with their typical MSD and TAMSD scaling relations (at short and long time), the aging dependence of the TAMSD on the trajectory length, the observed scatter/dispersion of individual TAMSD realizations computed at short lag times, the degree of polydispersity of the tracer particles, the general form of the ACF, and the tentative mathematical model(s) of diffusion. These quantities are organized in the columns of the table. The entries are ordered in blocks [separated by delimiters] reporting the FBM-like experimental, SBM-like experimental, SBM-like simulational, and, finally, FBM–SBM-mixed studies as well as hybrid-model-based dynamics. A system with weak ergodicity breaking features MSD(Δ) ≠ TAMSD(Δ) at short lag times
| Dataset |
MSD, 〈x2(Δ)〉 |
TAMSD, 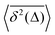
|
Aging of 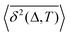
|
Scatter of 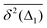
|
Polydispersity of tracers |
Form of the ACF |
Model of diffusion |
Dataset on nonergodic subdiffusion of chromosomal loci in live bacterial cells.
With distributed p(Kβ) and p(β) in the short-lag-time fit (4).
Diffusion of a fictitious zipping fork along a polymer chain undergoing a Rouse dynamics, as studied by computer simulations.
The decay of the negative part of the ACF for the subdiffusive dynamics, with the tail scaling ∝t2H−2 = t−1.12, observed in these simulations is consistent with the FBM-based exponents of the MSD growth as well as with the growth of the variance σ2 of the detected PDF, namely σ2(t) ∝ t2H ∝ MSD(t).
The SPT-microscopy dataset on and the statistical analysis of diffusion of lipid granules in fission-yeast cells.
Telomere diffusion in mammalian U2OS cancer cells.
Ergodic model of polymer dynamics; with the observed irreproducibilities of the TAMSD diffusion coefficients (with ca. 20 times variation) attributable to inhomogeneities of the diffusion environment and to variabilities of local chromosome organization.
SPT dataset on the dynamics of telomeres in the nucleus of mammalian U2OS osteosarcoma cells.
A typical size of telomeres is 50 to 100 nm.197
See also ref. 198 for an independent confirmation of the FBM model for this dataset based on the statistics of tracer increments and the generalized p-variation test.
Statistical analysis and SPT in vivo measurements of diffusion of telomere in 3T3 mouse embryonic fibroblast cells.
After the correction terms due to the effects of measurement noise were taken into account. This has improved the initial assessment of the TAMSD growth with ∝Δ0.24 at short and ∝Δ0.65 at long lag times (in a heterogeneous population of tracers and noisy original data).
SPT dataset on subdiffusion of fluorescent beads (50 nm in diameter) in artificial crowded fluids, such as sucrose and dextran.
M. Weiss, personal communication, 2022.
Dataset on tracking of avian predators to study the statistics of their slow-dynamics area-restricted search patterns and of directed, nearly ballistic commuting paths.
M. Assaf, personal communication, 2022.
Note that fitting the MSD growth at short times (typical for the SPT-data analysis) would yield significantly smaller MSD and TAMSD scaling exponents of this mode.
Heterogeneities in the size distribution of tracked animals, in specific terrestrial Beschaffenheiten, as well as in individual behavioral traits can affect the degree of the TAMSD spread observed25,200,201 in each mode of the spreading dynamics.
Note, however, the change in the detected MSD scaling behavior.
Molecular-dynamics-based large-scale computer simulations of diffusion of lipids and proteins in pure/noncrowded lipid membranes.
The MSD behavior was not reported in ref. 203 and 204, mainly employing sliding averaging (TAMSDs and mean TAMSDs). For the case of a homogeneous system in the liquid-disordered state the MSD-to-(mean TAMSD) equality in scaling and magnitude was confirmed by computer simulations at short-to-intermediate times (0.01…10 ns, where the results of ensemble averaging were still reliable) [J.-H. Jeon, personal communication, 2022]. For diffusion of cholesterol in lipid membranes as well as for the lipid dynamics in the gel-phase lipid systems—where the spread of the TAMSDs becomes significant, see Fig. S8 and S12 (ESI) in ref. 203—the MSD-to-TAMSD equivalence—being a prerequisite of the FBM- and FLE-based model descriptions—was not confirmed in simulations.
Although for diffusion in noncrowded membranes no aging was observed, under the crowded conditions some diffusing lipids did rarely display trapping events on their entire trajectories. This fact not only produced a significantly larger individual-TAMSD spread, but also resulted in aging of the TAMSDs and a slower than expected31,44 EB ∼ 1/T decay of the ergodicity breaking parameter with the trace length T (see Fig. 8 in ref. 204). No aging was however observed after averaging over all diffusing particles [M. Javanainen, personal communication, 2022].
Large-scale computer simulations of lateral diffusion of lipids in lipid membranes.
Purely ballistic initial diffusion with the exponent β = 2 was not observed at short times in simulations [M. Javanainen, personal communication, 2022].
Large-scale computer simulations of lipid diffusion in membranes.
Two-dimensional SPT dataset of diffusion of insulin granules in live MIN6 cells.
The granules are ca. 250…350 nm in diameter.
FBM subordinated to CTRW [responsible for distributed waiting times of binding-unbinding events of the granules] is described in the supplement of ref. 96, see also ref. 95 for CTRW and RWF.
SPT dataset of both ergodic and nonergodic anomalous-diffusion dynamics of Kv2.1 potassium channels in the plasma membrane.
Examination of the SPT dataset on diffusion of chromosomal loci in the presence of particle-localization uncertainties.
After both static and dynamical errors were taken into account, see Fig. S3 in ref. 142.
Examined both in terms of the minimum of and the overall form of the ACF, for H in close agreement with the inferred MSD exponents.
Static SPT-localization errors206 due to photon statistics and the dynamical errors due to finite exposure times [motion blur] were examined i.e. in ref. 142 in their effects onto the short-time MSD behavior and the ACF features for subdiffusive FBM-like motion. The minimum of the ACF becomes shallower at larger time shifts δ for static errors contributing to the data, corroborating a less subdiffusive MSD exponent at later times [and the up-shift of short-time MSD]. In the presence of dynamical localization errors, in contrast, the ACF minimum goes down for larger δ shifts, consistent with a more subdiffusive MSD exponent at later times [with the short-time MSD acquiring a downward shift] for FBM-like diffusion. For a confined diffusion, the same downward shift of the ACF negative peak at later time-lags is found, see ref. 207. Reexamination of the conclusions on the inferred anomalous exponents and the extent of the region of subdiffusion for a number already studied SPT datasets [i.e., some from this table] regarding the effects of localization errors—either unknown, considered not important, or neglected in the original studies—would thus be informative/compelling, especially for the datasets yielding low magnitudes of the short-time TAMSDs, time-varying TAMSD scaling exponent from a transiently subdiffusive to a more “normal” behavior, or featuring confined/adsorbed states with the internal dynamics of the tracers to be inferred.
SPT experiments of QDs in the cytoplasm of living mammalian HeLa cells.
With the precise form of the ACF, including the depth of its minimum due to subdiffusion, being in full correspondence with the theoretical FBM-based prediction for the exponent 2H as determined from the TAMSD-evolution data.
Intermittent and heterogeneous FBM—with alternations between the two states characterized by different tracer mobilities—describes the data. Such dichotomous switching also gets reflected in the two states visible in the PDF (as, e.g., in ref. 163).
SPT dataset on motor-driven highly superdiffusive active motion of endogenous intracellular particles in the amoeboid cells of Acanthamoeba castellanii.
SPT dataset of diffusion of transmembrane parts of the HIV-spike proteins in the plasma membrane of immune T-cells.
The mean over the TAMSD-aging exponents in each of 30 T-cells in the dataset is computed here, see ref. 27 for the detailed statistical analysis [complementary to that presented in ref. 1].
With transient and permanent clusters of the traced proteins being possible.
The computed ACF1 is reminiscent of that of subdiffusive FBM. Note, however, that for slow- and medium-mobility subpopulations the depth of the initial dip [indicative of the degree of anticorrelations for FBM and RWF] does not change with the time shift, whereas for the fast subpopulation this minimum becomes deeper at later times (compare to the opposite trend observed in ref. 16).
SPT dataset and the analysis of anomalous diffusion of network elements of the endoplasmic reticulum.
With the depth of the ACF minimum increasing measurably as longer time-intervals δt are being used in the ACF analysis.
With the distributed diffusivities p(Kβ) and skewed Rayleigh-like distribution of the TAMSD exponents, p(β).
SPT dataset and the statistical analysis of the nonergodic dynamics of membrane proteins on the somatic surface of hippocampal neurons.
Approximately, in magnitude and exponent [for the entire length of the recorded traces]. A nearly ergodic dynamics was observed after the removal of immobilized segments of the trajectories, whereas prior to that the strongly subdiffusive periods of motion yielded MSD ≫ TAMSD and also disparate anomalous scaling exponents.103
These mean scaling exponents were computed after removing strongly subdiffusive parts of the trajectories (bound tracers), based on the evaluated time-local TAMSD exponents.
With a transient formation of nanoclusters by the tracer molecules.
FBM or RWF were proposed (but not confirmed) as the mathematical models of diffusion. Widely distributed and strongly positively correlated Kβ and β were experimentally detected [being computed for the full trajectories].
SPT dataset of nanosized-tracers diffusion in the cytoplasm of mammalian cells and the statistical analysis of particle-medium interactions and medium heterogeneities.
See the detailed discussion in ref. 8 on implications of various preset conditions for a SPT dataset, specifically, for the effects of [distributed, minimal/maximal, etc.] trajectory lengths, the number of fitting points used for assessing the TAMSD exponents for individual SPT time series (see also ref. 142, 199 and 208–210), polydisperse tracer particles and heterogeneous environments (see also ref. 211), etc.
For NPs and QDs, thoroughly controlled; with a tracer-size dependent polydispersity.
With a power-law distribution of the tracer-environment immobilization times, ψ(τ) ∼ 1/τγ+1, with large variabilities of the particle mobilities realized for 0 < γ < 1.
Tracking of membraneless organelles (p-granules) in single-cell state of Caenorhabditis elegans embryos.
For subdiffusive, nearly normal, and superdiffusive subpopulations of p-granules, respectively.
With the characteristic ACF features expected for the respective values of FBM exponents of tracer subpopulations, see footnote bc.
Broadly distributed and strongly positively correlated trajectory-specific generalized TAMSD transport coefficients with the distribution p(Kβ) and TAMSD scaling exponents with the distribution p(β) were observed,140 alike in ref. 8.
SPT trajectories and statistical analysis of diffusion of endosomes in a heterogeneous media inside living eukaryotic cells, with the tracers displaying switching between persistent and anti-persistent modes of motion.
In magnitude and exponent at intermediate times, whereas at short times a levelling off of the MSD and TAMSD curves is observed [see also footnote ag].
For slow subpopulation, all tracers, and fast tracers, respectively.
But not studied in detail in ref. 19. The short-time values of the MSDs and TAMSDs for the trajectories with T > 2 s are larger than those for a subset of traces with T > 8 s.
Dependent on the number of fitting points used to extract the generalized diffusivities and scaling exponents from the source data [N. Korabel, personal communication, 2022], see also the discussion in ref. 6 and 8. The transport coefficients and scaling exponents were found to be strongly positively correlated.19
With a pronounced negative peak for a slow subpopulations of the tracers.
The heterogeneity was observed in experiments and achieved in the accompanying computer simulations of a subdiffusive FBM in terms of particular distributions of trace lengths ϕ(T) ∝ T−1.85 and diffusion coefficients D(T) ∝ T−0.6 among the trajectories. These distributions can, e.g., yield the MSD function surprisingly decreasing with diffusion time, see Fig. 2a and 4 in ref. 19 [N. Korabel, personal communication, 2022]. How much bias such hard-to-control—but SPT-experimental-conditions-predisposed and thus inevitable (see also the discussion in ref. 8)—distributions of the trace lengths, particle mobilities, medium heterogeneities, etc. have on the results, conclusions, and interpretation of numerous existing/published SPT datasets regarding, first and foremost, the temporal duration and actual degree of anomalous diffusion remains to be understood via a thorough and comparative analysis of the effects of systematically varied “preparatory” conditions in and the data-analysis parameters of various SPT datasets.
SPT dataset of diffusion of polystyrene colloids (0.25 and 0.75 micron in radius) in the polymerized solutions of G-actin polymers.
SPT-data on and the statistical analysis of the two-dimensional spreading dynamics of shape-heterogeneous amoeboid cells of Dictyostelium discoideum.
With distributed and negatively correlated Kβ and β values.
Tracking and statistical analysis of self-propelled metastatic glioblastoma U87-MG brain-cancer cells invading a three-dimensional extracellular matrix.
For gradient-containing and gradient-free migration assay, correspondingly; 2D projections of 3D migration patterns in Matrigel™ were recorded.
Heterogeneous distributions of the TAMSD trajectories were observed, with distributed trace-specific persistence times and propulsion speeds in terms of the underlying persistent random walk (PRW). With the cells moving radially and superdiffusively outward in the spheroid-induced gradient, the individual TAMSDs were fitted by the Fürth-Ornstein formula for PRWs,212–214 to extract these individual diffusion parameters.
As other statistical properties—such as TAMSD aging or ACF—were not studied, an interpretation of these data in terms of FBM-SBM model cannot be excluded too.
The same system as for ref. 111.
Variable MSD scaling exponents, depending on the concentrations of the extracellular matrix.
A large spread of the TAMSDs for individual trajectories is detected, reflecting rather broad distributions of times of persistent motion and of migration speeds of the cells [L. Jauffred, personal communication, 2022].
A double-exponential decay of the observed ACF was proposed (rather than a single-exponent decay, as for standard PRWs216), with the characteristic decay times varying
with the penetrability of the diffusion matrix. Fitting the ACF with superdiffusive-FBM-like functional form might also be a plausible alternative.
With different persistent times along the main and auxiliary direction of cell motion. Distinct subpopulations of the cancer cells—with the persistent time of about 15 minutes and a much more persistent subpopulation (superspreaders)—were detected, underlying a heterogeneity of the cells' proliferation properties.
SPT dataset reporting transient superdiffusion of polydisperse vacuoles in motile amoeboid cells of Acanthamoeba castellanii.
The mean TAMSD is somewhat subdiffusive at short times (see footnotes ag and eb for possible reasons) and it turns superdiffusive at intermediate lag times, closely matching the MSD in these time domains.
With broad distributions of p(Kβ) and p(β). The trajectory-specific diffusivities and scaling exponents are strongly positively correlated at the start of the TAMSDs of vacuoles and (surprisingly, see also footnote bl) reverting this behavior into pronounced anticorrelations of Kβ and β at the late stages of vacuole diffusion.10
With a division of the time series into subpopulations corresponding to small, medium, and large vacuoles being performed in the analysis.
With the FBM-commensurate behavior of the velocity-ACF in the region of short-time subdiffusion and intermediate-time superdiffusion of vacuoles.
SPT dataset on diffusion of histone-like nucleoid-structuring H-NS proteins in living cells of Escherichia coli.
With power-law distributed diffusivities of the trajectories, with p(Kβ) ∝ Kβ−(1.94±0.07), see also footnote bl and ref. 89. The measured diffusivities and scaling exponents increase as the length of bacteria grows for older cells (being divided into 3 cell-length subpopulations in the analysis), being supported by the measurements of their more fluidized cytoplasm.
With the measured distribution of the number of proteins per protein cluster being P(n) ∝ pn, with p ≈ 0.95.
With widely distributed tracer sizes and mobility parameters.
SPT dataset and the statistical analysis of tracer diffusion in mucin hydrogels at varying pH.
The physical age of samples was not precisely controlled and the trajectory-length-variations of the computed TAMSD magnitudes were not measured.
Depending on the pH values, the ACFs are, respectively, BM-, subdiffusive-FBM-, and BM-like.
FBM was shown to dominate the results of the Bayesian model-assessment analysis at all pH values used in the experiments,8,163 with the distributed p(Kβ) and p(β) among the trajectories of the tracers.
SPT dataset of nonergodic diffusion of receptor molecules on living-cell membranes.
The diffusion model based on the overdamped Langevin equation with diffusion coefficients distributed along each trajectory according to a Gamma-distribution pD(D) ∼ Dσ−1e−D/D0 and with the exponentially distributed transit times was used to rationalize the experimental data.
All-atom supercomputer simulations and the statistical analysis of diffusion of doxorubicin drug molecules in silica nanoslits.
But with the dip of the ACF becoming shallower for longer time shifts δ, see Fig. 14 in ref. 16, as compared to the constant depth (10) for FBM.
SPT dataset of diffusion of rhodamine molecules in water nanofilms on hydrated silica surfaces at varying humidity levels.
Apart from a relatively small TAMSD decrease/aging present for very short trajectories, irrespective of the degree of subdiffusion.
The heterogeneities of the diffusion environment in terms of the strength of the adsorption sites were however pronounced.
The depth of the ACF negative peak decreases measurably at higher humidities (see Fig. S2 of ref. 218) corroborating the accompanying transition from subdiffusion to nearly normal diffusion observed for the MSD and TAMSD.
Molecular-dynamics simulations of laterally diffusing M2-receptor proteins (at infinite dilution) in a hydrated mixed lipid membranes (with up to 50 percent of cholesterol).
The velocity-ACF reflected the MSD behavior, with a region of negative correlations at ∼10…50 ps for diffusing proteins. The velocity-ACF- and the MSD-behaviors for lipids were also similar, with the respective regions of the dynamics shifted earlier by about one order of time.
A model of this equation with specific memory kernels was used to described the crossovers in protein diffusion from the short-time ballistic, to the intermediate-time strongly subdiffusive, and, ultimately, to the long-time Brownian behavior of the MSD.
Particle-collisions and events-based large-scale computer simulations of the dynamics in a free-cooling granular gas.
Particles of the same size were used in simulations [A. Bodrova, personal communication, 2022].
With the MSD scaling exponent being α = 1/6 and time-dependence of the temperature being T(t) ∝ 1/t2×5/6, as recently confirmed experimentally.190 The MSD and TAMSD for the data190 regarding the applicability of the SBM model were not analyzed, as the tracers were not tagged rendering a time-series-based analysis impossible [M. Sperl, personal communication, 2022].
Water diffusion and D(t) time-dependent diffusion coefficients in the brain tissues.
Possibly, SBM-like short-time diffusion is realized. In diffusion-magnetic-resonance imaging, the diffusion coefficient is measured and commonly reported as D(t) = 〈x2(t)〉/(2t). If one defines the instantaneous diffusion coefficient as Dinst(t) = ∂〈x2(t)〉/∂(2t), then at long times Dinst(t) = D∞ + Const × t−ϑ, where ϑ = (p + d)/2 is the exponent of temporal correlations (here p is the structural exponent and d is the system dimensionality).168 This SBM-like dependence of Dinst(t) − D∞ describes a correction to the asymptotically normal, Gaussian diffusion with the bulk diffusivity D∞ [D. Novikov, personal communication, 2022].
Theory and computer simulations of the overdamped Langevin equation with the diffusivity D(t) ∼ 1/(1 + t/τ0).
Expected to be SBM-like.
Theory and simulations of the underdamped Langevin equation with the time-varying temperature T(t) ∼ (1 + t/τ0)2α−2, the damping coefficient 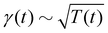 , and the diffusivity given by the time-dependent Einstein relation, D(t) ∼ T(t)/γ(t).
Expected to be small and SBM-like.
SBM for massive particles in the case α = 0.
Stochastic computer simulations of both massless and massive particles with exponentially time-varying diffusivity, , and the diffusivity given by the time-dependent Einstein relation, D(t) ∼ T(t)/γ(t).
Expected to be small and SBM-like.
SBM for massive particles in the case α = 0.
Stochastic computer simulations of both massless and massive particles with exponentially time-varying diffusivity, 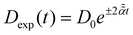 .
For massless particles with .
For massless particles with 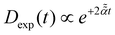 , see eqn (A27) in ref. 94.
For massless particles with , see eqn (A27) in ref. 94.
For massless particles with 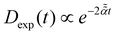 , see eqn (B22) in ref. 94.
As in footnote dg, but for the diffusion coefficient
varying logarithmically in time, Dlog(t) = D0 , see eqn (B22) in ref. 94.
As in footnote dg, but for the diffusion coefficient
varying logarithmically in time, Dlog(t) = D0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log[t/ log[t/![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) 0].
For massless particles, see eqn (C36) in ref. 94.
Computer simulations and the theoretical analysis of SBM confined in a parabolic potential, U(x) = kx2/2.
Theory and computer simulations of renewal Poissonian-reset SBM with exponentially distributed waiting times between the reset events ψ(t) = re−rt in the model of overdamped Langevin equation [here r is the reset rate].
Stochastic computer simulations of the FBM-DD system of equations in the overdamped limit.
ACF was not shown in ref. 92, but checked by us later via computer simulations [results not shown].
Simulations of the underdamped Langevin equation (particle mass m) driven by fractional Gaussian noise.
The dispersion of individual TAMSDs for massive FBM decreases with T as for standard FBM, see footnote ds. In addition, for the particles of small-to-intermediate masses at short lag times48 EB(m) ∝ m1 for 0 < H < 3/4 and EB(m) ∝ m4−4H for 1 > H > 3/4.
Simulations of the overdamped Langevin equation driven by fractional Gaussian noise and confined to an interval [−L, L]. We refer the reader also to ref. 137, 138 and 221 where non-Gaussian PDFs of boundary-reflected FBM were observed, with depletion and accumulation of particles near the wall for reflected sub- and superdiffusive FBM, respectively.
With the spread of the short-lag-time TAMSDs decreasing dramatically for smaller confining intervals. The ergodicity-breaking parameter EB31 at short lag times decreases with the trace length T as EB(T) ∝ 1/T for 0 < H < 3/4 and as EB(T) ∝ 1/T4−4H for 1 > H > 3/4.
The same as in ref. 220, but for Poisson-reset FBM.
For strongly subdiffusive initial FBM the spread of TAMSDs of reset FBM is very small (FBM-like), while for strongly superdiffusive reset FBM it can reach 1–2 decades, see Fig. 2 and 13 of ref. 222. The TAMSD dispersion of frequently reset superdiffusive FBM, in addition, depends reciprocally on the reset rate: the respective ergodicity-breaking parameter31 computed at short lag times decreases as EB(r) ∝ 1/r, see Fig. 4 and 5, and of ref. 222.
The same as in ref. 222, but with Poisson-reset FBM considered in the stationary regime.
The increment-MSD222 computed in the nonequilibrium steady state equals the mean TAMSD at short times (both for sub- and superdiffusive FBM exponents) as well as at long times in the TAMSD-plateau region, restoring the ergodicity, as compared to the results of ref. 222.
Provided the reset process is stationary and the trajectory length is much longer that the relaxation time.
Theory and simulations of heavy-tailed subdiffusive CTRWs as subordinated walks on fractal structures (CTRW and RWF). The PDF of waiting times is ψ(τ) ∼ 1/τ1+β, the MSD is 〈x2(Δ)〉 ∝ Δ2Hβ, and the short-lag-time TAMSD growth is 0].
For massless particles, see eqn (C36) in ref. 94.
Computer simulations and the theoretical analysis of SBM confined in a parabolic potential, U(x) = kx2/2.
Theory and computer simulations of renewal Poissonian-reset SBM with exponentially distributed waiting times between the reset events ψ(t) = re−rt in the model of overdamped Langevin equation [here r is the reset rate].
Stochastic computer simulations of the FBM-DD system of equations in the overdamped limit.
ACF was not shown in ref. 92, but checked by us later via computer simulations [results not shown].
Simulations of the underdamped Langevin equation (particle mass m) driven by fractional Gaussian noise.
The dispersion of individual TAMSDs for massive FBM decreases with T as for standard FBM, see footnote ds. In addition, for the particles of small-to-intermediate masses at short lag times48 EB(m) ∝ m1 for 0 < H < 3/4 and EB(m) ∝ m4−4H for 1 > H > 3/4.
Simulations of the overdamped Langevin equation driven by fractional Gaussian noise and confined to an interval [−L, L]. We refer the reader also to ref. 137, 138 and 221 where non-Gaussian PDFs of boundary-reflected FBM were observed, with depletion and accumulation of particles near the wall for reflected sub- and superdiffusive FBM, respectively.
With the spread of the short-lag-time TAMSDs decreasing dramatically for smaller confining intervals. The ergodicity-breaking parameter EB31 at short lag times decreases with the trace length T as EB(T) ∝ 1/T for 0 < H < 3/4 and as EB(T) ∝ 1/T4−4H for 1 > H > 3/4.
The same as in ref. 220, but for Poisson-reset FBM.
For strongly subdiffusive initial FBM the spread of TAMSDs of reset FBM is very small (FBM-like), while for strongly superdiffusive reset FBM it can reach 1–2 decades, see Fig. 2 and 13 of ref. 222. The TAMSD dispersion of frequently reset superdiffusive FBM, in addition, depends reciprocally on the reset rate: the respective ergodicity-breaking parameter31 computed at short lag times decreases as EB(r) ∝ 1/r, see Fig. 4 and 5, and of ref. 222.
The same as in ref. 222, but with Poisson-reset FBM considered in the stationary regime.
The increment-MSD222 computed in the nonequilibrium steady state equals the mean TAMSD at short times (both for sub- and superdiffusive FBM exponents) as well as at long times in the TAMSD-plateau region, restoring the ergodicity, as compared to the results of ref. 222.
Provided the reset process is stationary and the trajectory length is much longer that the relaxation time.
Theory and simulations of heavy-tailed subdiffusive CTRWs as subordinated walks on fractal structures (CTRW and RWF). The PDF of waiting times is ψ(τ) ∼ 1/τ1+β, the MSD is 〈x2(Δ)〉 ∝ Δ2Hβ, and the short-lag-time TAMSD growth is 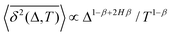 . The TAMSD thus resembles that of FBM–SBM, being nonlinear in Δ and featuring a CTRW-like aging behavior for varying T, with the exponents of the source processes of CTRW and RWF entering the exponent of the MSD of the resulting process also multiplicatively, as in SBM–HDP91 and FBM–HDP.93
Diffusion of the massless particles with the diffusivity varying exponentially in space, . The TAMSD thus resembles that of FBM–SBM, being nonlinear in Δ and featuring a CTRW-like aging behavior for varying T, with the exponents of the source processes of CTRW and RWF entering the exponent of the MSD of the resulting process also multiplicatively, as in SBM–HDP91 and FBM–HDP.93
Diffusion of the massless particles with the diffusivity varying exponentially in space, 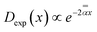 .
At long times, after the relaxation of the initial conditions, x0 = x(0).
Splitting of the entire ensemble of trajectories into two subpopulations with distinctly different growth of the TAMSDs with the lag time Δ. Scalings are valid both at short and long lag times.
Large scatter of the TAMSDs of 2…3 decades for large negative x0 values (in the region of exponentially high diffusivity) and vanishing scatter of the TAMSDs (with very low overall magnitudes) for large positive x0 values.
The same as in footnote dz, but for logarithmically varying diffusivity, Dlog(x) ∝ log[(x/ .
At long times, after the relaxation of the initial conditions, x0 = x(0).
Splitting of the entire ensemble of trajectories into two subpopulations with distinctly different growth of the TAMSDs with the lag time Δ. Scalings are valid both at short and long lag times.
Large scatter of the TAMSDs of 2…3 decades for large negative x0 values (in the region of exponentially high diffusivity) and vanishing scatter of the TAMSDs (with very low overall magnitudes) for large positive x0 values.
The same as in footnote dz, but for logarithmically varying diffusivity, Dlog(x) ∝ log[(x/![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) )2 + 1].
The scatter of 1…4 decades decreases for larger initial positions x0, where the space-variation of the diffusivity Dlog(x) is progressively smaller.
Stochastic simulations of the SBM–HDP-related overdamped Langevin equation.
A HDP-like ACF is expected, which itself is reminiscent of the ACF of FBM, see Fig. C1 in ref. 67, with the HDP subdiffusive exponent of the MSD 2/(2 − )2 + 1].
The scatter of 1…4 decades decreases for larger initial positions x0, where the space-variation of the diffusivity Dlog(x) is progressively smaller.
Stochastic simulations of the SBM–HDP-related overdamped Langevin equation.
A HDP-like ACF is expected, which itself is reminiscent of the ACF of FBM, see Fig. C1 in ref. 67, with the HDP subdiffusive exponent of the MSD 2/(2 − ![[small alpha, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c2.gif) ) < 1 corresponding to the Hurst exponent 2H < 1.
With the space-time dependence of the diffusivity of the form D(x, t) ∝ |x| ) < 1 corresponding to the Hurst exponent 2H < 1.
With the space-time dependence of the diffusivity of the form D(x, t) ∝ |x|![[small alpha, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c2.gif) tα−1 and p( tα−1 and p(![[small alpha, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c2.gif) ) = 2/(2 − ) = 2/(2 − ![[small alpha, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c2.gif) ). Note that such power-law D(x, t) were proposed, e.g., to rationalize data on diffusion laws in turbulence,90,224 that is one of the first examples of a non-Fickian and anomalously fast 〈x2(t)〉 ∝ t3 relative dispersion for a pair of molecules.225,226 Power-law-like D(x) were also employed to describe animal dynamics.227
Stochastic simulations of the overdamped FBM–HDP Langevin equation.
Stochastic simulations of the FBM-SBM-related overdamped Langevin equation. ). Note that such power-law D(x, t) were proposed, e.g., to rationalize data on diffusion laws in turbulence,90,224 that is one of the first examples of a non-Fickian and anomalously fast 〈x2(t)〉 ∝ t3 relative dispersion for a pair of molecules.225,226 Power-law-like D(x) were also employed to describe animal dynamics.227
Stochastic simulations of the overdamped FBM–HDP Langevin equation.
Stochastic simulations of the FBM-SBM-related overdamped Langevin equation.
|
| Ref. 156, exper.a |
∝Δ0.4 (short times) |
∝Δ0.4 (short times) |
Unknown |
Large (≈1.5 decades) |
Medium to large |
FBM-like |
FBMb |
| Ref. 195, simul.c |
∝t2/2.26 ∝ t0.88 |
Not studied |
Not studied |
Not studied |
None |
FBM-liked |
FBM |
| Ref. 157, exper.e |
∝Δ0.80…0.85 (short times) |
∝Δ1 (short times), ∝Δ0.1…0.2 (long times) |
None, ∝1/T0 |
Medium (≈0.5 decades) |
Present, not specified |
Confined-FBM- or confined-CTRW-like |
CTRW (short), FBM (long times) |
| Ref. 196, exper.f |
Not shown |
∝Δ0.32±0.12 (short times, 10−2…100 s) ∝Δ1.15±0.44 (long times, 3 × 102…104 s) |
None, ∝1/T0 |
Medium (≈1 decade) |
Medium to large |
Not studied |
Polymer reptationg |
| Ref. 197, exper.h |
Not shown |
∝Δ0.31±0.11 (short times, 10−2…101 s) |
∝1/T0 |
Not presented |
Medium to largei |
Not studied |
FBM,j FLE |
| Ref. 199, exper.k |
Not presented |
∝Δ0.4±0.04 (all times)l |
Not shown |
Not shown |
Medium to large |
Not computed |
FBM or obstructed diffusion |
| Ref. 161 and 162, exper.m |
∝Δ0.82, ∝Δ0.98 (short times) |
∝Δ0.82, ∝Δ0.98 (short times) |
None, ∝1/T0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) n n |
Not presented |
Small, controlled |
FBM-like |
FBM |
| Ref. 200 and 201, exper.o |
∝Δ0.6 (short times) |
∝Δ0.35…0.5 (short times) |
∝1/T0.26…0.28 |
Medium |
Moderater |
Not computed |
Confined143,202 |
|
|
∝Δ0.11 (long times)p |
∝Δ0.35…0.5 (long times) |
(Slow dynamics) |
(≈1…1.5 decades) |
|
|
subdiff. CTRWss |
|
|
Slow dynamics [nesting periods] |
Slow dynamics |
Unknown |
(Slow dynamics) |
|
|
(Slow dynamics) |
|
|
∝Δ1.52…1.69 (all times) |
∝Δ1.6…1.8 (all times)q |
(Fast dynamics) |
Not computed |
|
|
Not examined |
|
|
Fast dynamics [commuting periods] |
Fast dynamics |
|
(Fast dynamics) |
|
|
(Fast dynamics) |
| Ref. 203, simul.t |
Not reportedu |
∝Δ0.63…0.67 (short times, 0.01…1 ns) ∝Δ0.94…0.97 (long times, 10…100 ns) |
None, ∝1/T0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) v v |
Very small, BM-like |
Small to none |
FLE-like |
FBM and FLE |
| Ref. 205, simul.w |
Not reported |
∝Δ≈1.5…1.7x (short times, 1…100 fs), ∝Δ≈0.3…0.7 (interm. times, 0.01…10 ns), ∝Δ≈0.8…1.0 (long times, 0.1…10 µs) |
Not presented |
Small (≈0.5 decade) |
Small to none |
Not presented |
FBM and FLE |
| Ref. 204, simul.y |
Not reported |
∝Δ0.8…0.9 (short/interm. times) |
None, ∝1/T0 |
Medium (≈0.5…1.5 decades) |
Small |
FLE-like |
FBM, FLE |
| Ref. 96, exper.z |
Not presented |
∝Δ0.76…0.84 (short times) |
∝1/T0.2…0.28 |
Large (≈1…1.5 decades) |
Moderateaa |
Not examined |
FBM-CTRWab |
| Ref. 167, exper.ac |
∝Δ0.9 (short times) |
∝Δ0.8 (short times) |
∝1/T0.1 |
Large (≈1.5 decades) |
High, with clusters |
Not presented |
CTRW + fractal BM |
| Ref. 142, exper.ad |
Not studied |
∝Δ0.74±0.26 (0.1…1 s)ae |
Not studied |
Medium (≈1 decade) |
Moderate to large |
FBMaf |
FBMag |
| Ref. 13, exper.ah |
Not presented |
∝Δ0.59 (short times) |
Not studied |
Small-medium (≈0.5 decade) |
Small |
FBM-likeai |
FBMaj |
|
|
|
∝Δ0.46 (short times) |
|
|
|
|
|
|
|
|
(Nocodazole-treated cells) |
|
|
|
|
|
| Ref. 164, exper.ak |
Not specified |
∝Δ≈1.4…2 |
Not specified |
Medium (≈1 decade) |
Medium-large |
Not presented |
FBM with drift |
| Ref. 1, exper.al |
∝Δ0.61, ∝Δ0.63, ∝Δ0.81 |
∝Δ0.63, ∝Δ0.50, ∝Δ0.72 |
∝1/T0.39±0…08![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) am am |
Very large (≈3…4 decades) |
Medium to highan |
FBM-likeao |
FBM and RWF1; FBM, BM, SBM, BM-DD, and HDPs27 |
|
|
Slow, medium, and fast diffusion “states” (short times) |
3 diffusion “states” (short times) |
|
|
|
|
|
| Ref. 165, exper.ap |
Not presented |
∝Δ0.48±0.01 (0.1…10 s) (Polymerized microtubules) ∝Δ0.3 (nocodazole-treated cells) |
Not studied |
Medium (≈1 decade) |
Moderate to large |
FBM-likeaq |
FBMar |
| Ref. 103, exper.as |
MSD(Δ) ≈ TAMSD(Δ)at |
{∝Δ0.90, ∝Δ0.86, ∝Δ0.92}au |
Not studied |
Medium {≈1, ≈1.5, ≈1} decades for {Nav1.6, Kv1.4, CD4} |
Medium to largeav |
Not studied |
FBM or RWFaw |
|
|
|
for {Nav1.6, Kv1.4, CD4} (short times) |
|
|
|
|
|
| Ref. 4, exper.ax |
Not specified |
∝Δ0.92 (fast 25 nm Rho-NPs), |
Not specified |
Medium (≈1 decades) |
Smallaz |
Not analyzed |
CTRWba |
|
|
Not specified |
∝Δ0.18 (slow 25 nm Rho-NPs); |
Not specified |
Large (≈2 decades) |
|
|
|
|
|
Not specified |
∝Δ0.56 (75 nm Rho-NPs); |
Not specified |
Not specified |
|
|
|
|
|
Not specified |
∝Δ1 (20 nm QDs, short times [10 ms]), |
∝1/T0.3 undefined |
Large (≈1.5 decades) |
|
|
|
|
|
Not specified |
∝Δ0.7 (20 nm QDs, long times [1 s]) |
∝1/T0.3 |
Not well defined |
|
|
|
|
|
Not specified |
∝Δ0.82 (20 nm QDs, all times, T > T*)ay |
|
Large (≈2 decades) |
|
|
|
| Ref. 140, exper.bb |
Not shown |
{∝Δ0.1…0.9, ∝Δ0.9…1.1, ∝Δ1.1…1.6}bc (short times) |
Not studied |
Medium (≈1.5 decades) |
Moderate |
FBM-likebd |
FBMbe |
| Ref. 19, exper.bf |
MSD(Δ) ≈ TAMSD(Δ)bg |
{∝Δ1/2, ∝Δ1, ∝Δ1.26}bh (interm. times) |
Presentbi |
Very large (≈1.5…2 decades)bj |
Large |
FBM-likebk |
“Heterogeneous” FBMbl |
| Ref. 97, exper.bm |
{∝Δ1, ∝Δ0.5, ∝Δ0.6} |
{∝Δ1, ∝Δ0.7, ∝Δ0.6} |
Unknown |
Very small |
Small, controlled size |
Not studied |
{BM, CTRW, FBM} 3 tracer sizes |
|
|
3 tracer sizes (short times) |
3 tracer sizes (short times) |
|
|
|
|
|
| Ref. 6, exper.bn |
∝Δ1.28 (short times) |
∝Δ1.37 (short times) |
∝1/T0.3 |
Large (≈1.5 decades)bo |
Medium-high |
Not computed |
Not examined |
| Ref. 111, exper.bp |
∝t1.38…1.41 and ∝t1.30…1.33 (short times, ≲100 min)bq |
Not presented |
Not studied |
Mediumbr |
Medium-to-large |
Not shown |
Biased random walk or PRWbs |
| Ref. 215, exper.bt |
∝t1.44…1.53 (short times, ≲100 min)bu |
Not shown |
Not studied |
Not shown |
Medium-to-largebv |
Always positive, decayingbw |
PRW, anisotropic PRWbx |
| Ref. 10, exper.by |
MSD(Δ) ≈ TAMSD(Δ) |
∝Δ1.2…1.4 (interm. times)bz |
Not examined |
Medium (≈1 decade)ca |
Largecb |
FBM-likecc |
Parameter-distributed FBM |
| Ref. 217, exper.cd |
Not shown |
∝Δ0.57±0.02 |
Not studied |
Very largece (≈2.5…3 decades) |
Largecf |
Subdiffusive-FBM-like |
FBMcg |
| Ref. 8, exper.ch |
{∝Δ0.46, ∝Δ0.28, ∝Δ0.36} 3 pH values (short times) |
{∝Δ1.09, ∝Δ0.75, ∝Δ0.94} 3 pH values (short times) |
Unknownci |
{Very large (≈3 decades), medium (≈1.5 decades), small (≈0.5 decades)} 3 pH values |
Small, controlled |
FBM-likecj |
FBM,ck also BM and BM-DD |
| Ref. 70, exper.cl |
∝Δ0.84±0.05 (all times) |
∝Δ0.95±0.05 (all times) |
∝1/T0.17±0.05 |
Medium-large (≈1.5 decades) |
Small |
Not presented |
BM with pD(D)cm |
| Ref. 16, simul.cn |
∝Δ1 (short times), ∝Δ0.2…0.4 (long times) |
∝Δ0.48 (short times), ∝Δ0.9 (long times) |
∝1/T0.34 |
Medium (≈0.5 decades) |
None or controlled |
FBM-likeco |
FBM-CTRW hybrid |
| Ref. 218, exper.cp |
{∝Δ0.44, ∝Δ0.62, ∝Δ0.82, ∝Δ0.92} 4 humidity values (short times) |
{∝Δ0.49, ∝Δ0.66, ∝Δ0.84, ∝Δ0.95} 4 humidity values (short times) |
∝1/T0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cq cq |
Not presented |
Smallcr |
FBM-likecs |
FBM, FBM subordinated to CTRW |
| Ref. 219, simul.ct |
∝Δ2 (short times, 1 ps) |
Not studied |
Not studied |
Not studied |
Small |
With a negative dipcu |
Generalized Langevin equationcv |
|
|
∝Δ0.3…0.6 |
|
|
|
|
|
|
|
|
(interm. times, ∼101…104 ps) |
|
|
|
|
|
|
|
|
∝Δ1 (long times, 400 ns) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Ref. 57, simul.cw |
∝Δ1/6 (short times) |
∝Δ7/6, ∝Δ1 |
∝1/T5/6, ∝1/T1 |
Very small, SBM-like |
Nonecx |
Not analyzed |
SBMcy |
| Ref. 168 and 169, exper.cz |
∝Δ1−ϑ (short times, 0 < ϑ < 1) |
Not measured |
Not measured |
Not measured |
Small or none |
Not studied |
Not examinedda |
|
|
∝Δ1 (long times) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Ref. 62, simul.db |
∝Δ1 (short times, Δ ≪ τ0) |
∝Δ1 (short times, τ0 ≪ Δ ≪ T) |
∝1/T |
Very small, SBM-like |
None |
Not showndc |
Ultraslow SBM |
|
|
∝log[Δ] (long times, τ0 ≪ Δ ≪ T) |
∝(Δ/T)log[T/Δ] (long times, Δ ≫ τ0) |
|
|
|
|
|
| Ref. 58 and 63, simul.dd |
∝Δ2 (short times, Δ ≪ 1/γ0) |
∝Δ2 (short times, Δ ≪ 1/γ0) ∝ Δ1+α (interm. times, Δ ≪ Δ* ≪ T) ∝ Δ1 (interm. times, Δ ≫ Δ* ≫ τ0) |
∝1/T1−α (interm. times) |
Not presentedde |
None |
Not analyzed |
Underdamped SBM |
|
|
∝Δ1 (interm. times, 1/γ0 ≪ Δ ≪ τ0) |
|
|
|
|
|
|
|
|
∝Δα (long times, Δ ≫ τ0, α > 0) |
|
|
|
|
|
|
| Ref. 58, simul.df |
∝Δ2 (short times, Δ ≪ 1/γ0) |
∝Δ2 (short times, Δ ≪ 1/γ0) |
∝1/T (short and interm. times) |
Very small, SBM-like |
None |
Not shown |
Ultraslow underdamped SBM |
|
|
∝Δ1 (interm. times, 1/γ0 ≪ Δ ≪ τ0) |
∝Δ1 (interm. times, Δ ≪ Δ*) |
|
|
|
|
|
|
|
∝log[Δ] (long times, Δ ≫ τ0) |
∝(Δ/T)log[T/Δ] (long times, Δ* ≪ Δ ≪ T) |
|
|
|
|
|
| Ref. 94, simul.dg |
See Table 1 in ref. 94 |
See Table 1 in ref. 94 |
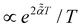 ∝1/Tdi
∝1/Tdi |
Small-to-moderate, 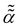 -dependent -dependent |
None |
Not studied |
Exponential SBM |
| Ref. 94, simul.dj |
See Table 1 in ref. 94 |
See Table 1 in ref. 94 |
∝log[T/![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) 0]dk 0]dk |
Small |
None |
Not studied |
Logarithmic SBM |
| Ref. 55, simul.dl |
∝Δα (short times, Δ ≪ 1/k) |
∝Δ1 (short times) |
Not studied |
Not presented |
None |
Not studied |
Confined SBM |
|
|
∝Δα−1 (long times, Δ ≫ 1/k) |
∝Δ0 (long times) |
|
|
|
|
|
| Ref. 220, simul.dm |
∝Δα (short times, Δ ≪ 1/r) |
Not studied |
Not studied |
Not studied |
None |
Not studied |
Reset SBM |
|
|
∝1/rα (long times, Δ ≫ 1/r) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Ref. 92, simul.dn |
∝Δ2H (short times) |
∝Δ2H (short times) |
None, ∝1/T0 |
Small-medium (≈0.5 decades) |
None |
FBM-likedo |
FBM-DD |
|
|
∝Δ2H (long times, 1/2 < H) |
∝Δ2H (long times, 1/2 < H) |
|
|
|
|
|
|
|
∝Δ1 (long times, H < 1/2) |
∝Δ1 (long times, H < 1/2) |
|
|
|
|
|
| Ref. 48, simul.dp |
∝Δ2H+2 (short times) |
∝Δ2 (short times) |
Not studied |
FBM-likedq |
None |
Not studied |
Underdamped FBM |
|
|
∝Δ2H (long times) |
∝Δ2H (long times) |
|
|
|
|
|
| Ref. 45 and 46, simul.dr |
MSD(Δ) = TAMSD(Δ) |
∝Δ2H (short times) |
Not studied |
FBM-likeds |
None |
Not studied |
Confined FBM |
|
|
|
∝Δ0 × L2/3 (long times, 2K2HΔ2H ≫ L2) |
|
|
|
|
|
| Ref. 222, simul.dt |
∝Δ2H (short times, Δ ≪ 1/r) |
∝Δ2H (short times, 0 < H < 1/2) |
Not studied |
Small to mediumdu |
None |
Not studied |
Reset FBM |
|
|
∝1/r2H (long times, Δ ≫ 1/r) |
∝Δ1 (short times, 1 > H > 1/2) |
|
|
|
|
|
|
|
|
∝2/r2H (long times) |
|
|
|
|
|
| Ref. 154, simul.dv |
iMSD(Δ) = TAMSD(Δ)dw |
∝Δ2H (short times, Δ ≪ 1/r) |
None, ∝1/T0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) dx dx |
Small to medium |
None |
Not studied |
Stationary reset FBM |
|
|
|
for 0 < H < 1/2 |
|
|
|
|
|
|
|
|
∝Δ1 (short times, Δ ≪ 1/r) |
|
|
|
|
|
|
|
|
for 1/2 < H < 1 |
|
|
|
|
|
|
|
|
∝1/r2H (long times, Δ ≫ 1/r) |
|
|
|
|
|
| Ref. 95, simul.dy |
∝Δ2Hβ |
Δ
1−β+2Hβ
|
1/T1−β |
Not reported |
None |
Not reported |
CTRW with RWF |
| Ref. 223, simul.dz |
∝log2(t)ea |
∝Δ1, for large positive x0 |
Present, not studied |
Dependent on x0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ec ec |
None |
Not studied |
Exponential HDP |
|
|
|
∝Δ1 and ∝Δ1/2, for x (0) ≈ 5eb |
|
|
|
|
|
|
|
|
∝Δ1/2, for large negative x0 |
|
|
|
|
|
| Ref. 223, simul.ed |
∝x02 + 2Dlog(x0) × t1 |
∝2Dlog(x0) × Δ1 |
Present, not studied |
Medium-to-largeee |
None |
Not studied |
Logarithmic HDP |
| Ref. 91, simul.ef |
∝Δα×2/(2−![[small alpha, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c2.gif) ) ) |
∝Δ1 |
∝1/T1−α × 2/(2−![[small alpha, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c2.gif) ) ) |
Large, HDP-like, ![[small alpha, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c2.gif) -dependent -dependent |
None |
Not computedeg |
SBM–HDPeh |
| Ref. 93, simul.ei |
∝Δ2H×2/(2−![[small alpha, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c2.gif) ) ) |
∝Δ2H |
∝1/T(1−2/(2−![[small alpha, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c2.gif) ))2H ))2H |
Large, HDP-like, ![[small alpha, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c2.gif) -dependent -dependent |
None |
Not computed |
FBM–HDP |
| This study, simul.ej |
∝Δ2H+α−1 |
∝Δ2H |
∝1/T1−α |
Small, SBM- and FBM-like |
None |
FBM-like |
FBM–SBM |
II Statistical properties of FBM and SBM
FBM and SBM are formulated based on the Langevin equation,131| | 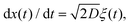 | (1) |
driven by fractional Gaussian noise ξH(t) for a constant diffusion coefficient D for FBM and by white Gaussian noise ξ(t) for a time-dependent diffusion coefficient Dα(t) for SBM, see below.
A FBM
The parental process of FBM—as introduced in ref. 42 and 43 and developed in some of our recent studies,45,46,48,92 see eqn (16) (below)—is stationary in increments and nearly as ergodic31,44 as BM. For FBM, the exponent and magnitude of the power-law anomalous28,31,132–135 growth of the MSD| | 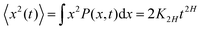 | (2) |
and TAMSD| | 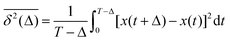 | (3) |
are equal at short lag times, Δ ≪ T, where| | 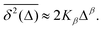 | (4) |
Here, the exponent β = 2H is twice the Hurst exponent136 and K2H is the generalized diffusion coefficient. The exponent H = 1/2 demarcates the situations of persistent (positive) and antipersistent (negative) correlations of particle displacements realized for FBM at 1 > H > 1/2 and 0 < H < 1/2, correspondingly, see ref. 45, 46, 48 and 92 and Section III A below. These two regimes yield super- and subdiffusion respectively. The discrete version of expression (3), used to rationalize various SPT datasets, is| | 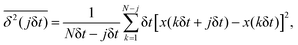 | (5) |
where δt is the discretization step of a time series with N points.
For FBM, all individual TAMSD trajectories, being highly reproducible,45,46,48,92 are equal to the MSD in the limit of long measurement times T,
| | 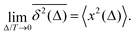 | (6) |
The mean TAMSD for an ensemble of
N independent [and statistically identical] trajectories for a given lag time
Δ and measurement time
T is computed as the arithmetic mean,
| | 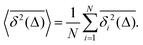 | (7) |
The magnitude of the TAMSDs is insensitive to the trajectory length and thus FBM does not feature aging, see ref.
31 and
44–46.
The PDF of FBM is Gaussian and the distribution of particle displacement at time t has the form
| | 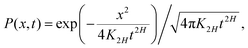 | (8) |
provided the initial PDF is
P(
x,
t = 0) =
δ(
x). We consider below the free-space spreading dynamics, but emphasize that implementing a physically self-consistent scheme for FBM in the presence of confinement
45,46 and reflecting boundaries
137–139 is a nontrivial task due to the nonlocality of FBM and possibly variable degree of memory loss upon a reflection from a planar boundary [depending,
e.g., on the angle of incidence of the jump to be reflected].
The ACF computed from the increments of particle positions, normalized to the initial value at time t = 0, is
| | 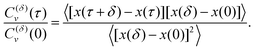 | (9) |
Here,
δ is the period of increment measurement. This ACF for subdiffusive FBM starts with unity at the initial time
τ = 0, exhibits a dip at short time lags with the depth
13,140| | | C(δ)v (τ = δ)/C(δ)v (0) = 22H−1 − 1, | (10) |
and relaxes to zero from below in a power-law manner at
n ≫ 1 as,
67,141,142| | | C(δ)v (τ = nδt) ∝ n2H−2. | (11) |
Here
n is the number of elementary time-intervals δ
t used in the analysis. The depth of this dip reflects the degree of antipersistence of successive displacements for FBM with 0 < 2
H < 1. For superdiffusive FBM, with 1 < 2
H < 2, the velocity ACF drops from unity at the initial time
τ = 0 to the same value
(10) which is now positive, indicative of persistence in displacement correlations. At longer times the ACF approaches zero from above, again as a power law
(11).
B SBM
The inherently nonstationary process of SBM—as introduced in ref. 51, 54 and 55 and developed recently, i.e., in ref. 56–58—features the diffusion coefficient of the form,with 0 < α < 2. SBM is a nonergodic process in the sense of MSD-to-TAMSD nonequivalence.31,55,57 SBM, like FBM, is an athermal process that can additionally be considered as a “mean field” over CTRWs.54 For subdiffusive SBM, for instance, we observe a power-law-like MSD growth,while at short lag times Δ/T ≪ 1 the mean TAMSD is linear in lag time,| | | TAMSD(Δ, T) ∝ Δ1/T1−α. | (14) |
Note that the argument of the MSD is real physical time (even if Δ is used for it below), while the argument of the TAMSD [per definition] is the lag time. The decay of the TAMSD with the trajectory length T for α < 1—underlying a slower dynamics of subdiffusive SBM at later times—is a conspicuous feature of SBM aging. The functional dependence of this decay on T as a function of α is similar to that of subdiffusive CTRWs65,143–147 and subdiffusive HDPs.68,69,91
In contrast to CTRWs and HDPs, for SBM, the distribution of TAMSDs is, however, narrow and the respective EB parameter,28,31
| | 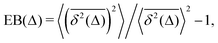 | (15) |
characterizing this small irreproducibility of the TAMSDs from one realization to the next behaves often similar to that for BM, see ref.
54,
56 and
91.
The process of SBM is Markovian and it features the same PDF as FBM, with a trivial substitution 2H → α.
The ACF of SBM for sub- and superdiffusive realizations is the same as that of BM for disjoint time intervals. Namely, the ACF—normalized to the ACF at zero time shift—starts at unity, drops within one step δ = δt to zero, and—due to the absence of temporal noise correlations on later stages—stays zero at longer lag times τ (see, e.g., Fig. 2 in ref. 60).
III Results for FBM–SBM
A Model and simulations
We examine the overdamped Langevin equation featuring the power-law SBM-like diffusion coefficient (12) and FBM-associated external fractional Gaussian noise ξH(t),| | 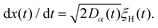 | (16) |
Here, noise ξH(t) for time instances |t1 − t2| ≫ 0 features the correlation function| | | 〈ξH(t1)ξH(t2)〉 ∝ K2H2H(2H − 1)|t1 − t2|2H−2. | (17) |
These long-range temporal correlations for non-Markovian FBM are contrasting memoryless white Gaussian noise giving rise to BM. The diffusion coefficient in eqn (16)—stemming from a subdiffusive source process of SBM—describes the particle dynamics slowing down with time.
We emphasize that the underdamped Langevin equation131 and FBM for massive particles were considered recently too48 (see also ref. 148). The consideration of massive particles with both a power-law SBM-like time-varying diffusivity Dα(t) as well as with the exponential and logarithmic dependencies D(t) were recently presented, see ref. 57, 58, 62, 63 and 94, respectively. For exponential-SBM, for instance, the MSD grows with time as for a multiplicative process of geometric BM,149,150 see also ref. 151.
For numerical simulation of eqn (16) we employ the same standard forward-running Ito-like152,153 discrete iterative scheme with a variable time-step δt, see the detailed description in our previous studies for the simulations of HDPs,68,69 SBM–HDPs,91 and, particularly, of FBM–HDPs93 and FBM-DD92 processes.
B MSD and TAMSD
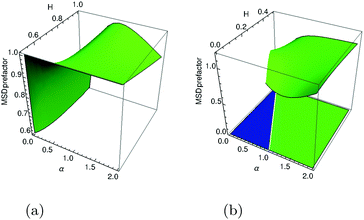
The compound FBM–SBM process is weakly nonergodic. Specifically, the ergodic FBM behavior with the equivalent MSD (2) and TAMSD (3) for FBM–SBM with 2 > α > 1 changes toandFBM–SBM with 0 < α < 1 is also nonergodic. For a growing-in-time SBM diffusivity realized at 2 > α > 1 and for superdiffusive FBM the MSD of FBM–SBM is considerably lower than its TAMSD. The situation is the opposite for 0 < α < 1 when the MSD at short times is much larger than the TAMSD of FBM–SBM, see Fig. 1a and b, respectively. Naturally, as the Hurst exponent approaches the BM limit H = 1/2, the MSD exponent of FBM–SBM is 2H and its MSD–TAMSD behavior turns into that of pure SBM.† The process of FBM–SBM, as its parental processes, is free of a typical time scale.
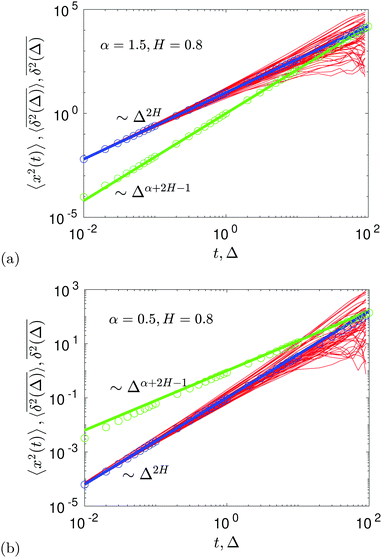 |
| | Fig. 1 MSD and TAMSD of FBM–SBM as function of time t and lag time Δ, respectively. Superdiffusive parental FBM is considered, with H = 0.8. The diffusion scenarios of super- and subdiffusive parental SBM correspond to panels (a) and (b), respectively. The SBM exponents are provided in the legend. Thick green and blue curves are the theoretical asymptotes (18) of the MSD and (19) of the TAMSD (plotted with the unit prefactors (see also eqn (21) and Fig. 3)), while the respective symbols are the results of simulations. The red curves are the individual TAMSDs from simulations. Other parameters are as follows: the initial position of the particles is chosen at x0 = 0, the total length of the diffusion trajectory is T = 102, the time-step in the simulations is δt = 10−2, and ensemble averaging is performed over N = 103in silico-generated time series. For all plots, the noise strength is set at K2H = 1/2 in eqn (17) and we use Kα = 1/2 in eqn (12). For this, and all other plots expect Fig. 9, the time-step is δt = 0.01. | |
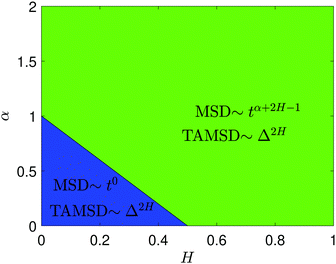 |
| | Fig. 2 Variation of the MSD scaling exponent of FBM–SBM from expression (18). The region of the MSD plateau 2H + α − 1 < 0 is indicated in the blue color, while the green color designates the domain of growing-in-time MSDs. | |
The derivation of the MSD (18) and TAMSD (19) of FBM–SBM is as follows. Starting from (16), we get
| | 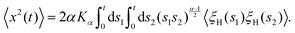 | (20) |
At
H = 1/2 the fractional noise reduces to the white Gaussian noise and one arrives at pure SBM with 〈
x2(
t)〉 ∼
tα. At
H > 1/2, using the approximate expression
(17) for the noise correlations, the MSD reads
| | 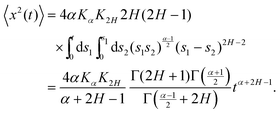 | (21) |
The prefactor of this MSD as a function of exponents
α and
H of the two parental processes is shown in
Fig. 3a to demonstrate the simulations
vs. theory agreement. We find that in a large region of exponents the MSD prefactor is of order unity, corroborating the unit asymptotics used in
Fig. 1. In special cases of pure SBM (2
H = 1 and
K2H = 1/2) or pure FBM (
α = 1 and
Kα = 1/2) the general MSD expression
(21) for FBM–SBM yields, respectively, the expected dependencies 〈
x2(
t)〉 = 2
αKαtα for SBM and 〈
x2(
t)〉 = 2
K2Ht2H for superdiffusive FBM.
 |
| | Fig. 3 Visualization of the MSD prefactors in eqn (21) for superdiffusive (panel a) and in eqn (23) for subdiffusive (panel b, after n = 25 steps) parental FBM process, both yielding a growing-in-time MSDs of FBM–SBM (2H + α − 1 > 0). The color scheme for the respective regions of exponents is as in Fig. 2. | |
At H < 1/2, using the exact correlator of the noise,
| | 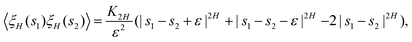 | (22) |
within the discretized scheme (see ref.
154), for the time step δ
t and with
ε = δ
t the MSD after
n steps and
t =
n × δ
t becomes
| | | 〈x2(t)〉 = 4αKαK2HC(α, H, n) × (n × δt)α+2H−1, | (23) |
where the coefficient
| | 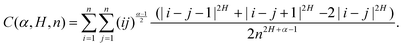 | (24) |
The MSD prefactor in
eqn (23) for the power law ∝
tα+2H−1 is shown in
Fig. 3b. If
α + 2
H − 1 > 0, the
C (
α,
H,
n) ∼ 1 and thus 〈
x2(
t)〉 ∼
tα+2H−1.
In contrast, for the region of exponents α + 2H − 1 < 0—shown as the blue domain in Fig. 3b—the MSD is almost a constant, see Fig. 7. The explicit dependence of the MSD (23) on the time step δt—reciprocal in this regime of the parental exponents—is a rationale for the time-step-dependent plateaus of the MSD shown in Fig. 8.
Regarding the TAMSD, based on the intuition we gained studying similarly constructed hybrid processes of SBM–HDP and FBM–HDP with the TAMSD-to-MSD ratios (28) and (29) provided below, respectively, the anticipated TAMSD-to-MSD ratio for FBM–SBM given by (30) is fully supported by the results of our computer simulations. We thus do not derive here the explicit TAMSD expression analytically.
As FBM and SBM reveal a narrow amplitude spread of their TAMSD trajectories, a similar behavior is also observed for their combination FBM–SBM, see Fig. 1.
For FBM–SBM this “independence” of the parental processes (characteristic, e.g., for FBM–HDP93 and SBM–HDP91) is no longer present. The temporal correlations of fractional Gaussian noise do interfere with the temporal decay or increase of the SBM-related diffusion coefficient. The respective FBM and SBM exponents in the MSD of FBM–SBM are, thus, being summed instead of being multiplied, see the green domain in the diagram of Fig. 2. For the TAMSD of FBM–SBM, rather non-surprisingly, the same scaling exponent as for FBM is observed.
We observe, however, a less obvious behavior for the situations of subdiffusive SBM and strongly subdiffusive FBM, see the blue domain in Fig. 2. The TAMSD of the combined FBM–SBM process still exhibits FBM-like scaling ∝Δ2H, whereas the MSD very quickly stalls or stagnates at a plateau, see Fig. 7 and 8. The smaller the simulation step, the higher is the observed MSD plateau, with the MSD-plateau level being reached in the simulations within first couple of time-steps, Fig. 8. The MSD quickly jumps to a plateau because the (effective) diffusivity of the particles decays very quickly at longer times.‡
As the exponents for subdiffusive SBM and subdiffusive FBM decrease, the crossover time—beyond which the stalling MSD behavior is detected in the simulations—increases. As the parental FBM process turns less subdiffusive, the MSD of FBM–SBM in the limit of long times starts approaching the asymptote (18), see Fig. 9. It is essential that the MSD exponent of FBM–SBM is positive in this regime, α − 1 + 2H > 0. In the limit of short times, however, the MSD still reveals a dependence on the step-size in simulations.
C Aging of the TAMSD
The aging behavior of FBM–SBM is consistent with our physical intuition. Namely, as FBM is a nonaging process, aging of FBM–SBM stems solely from that of SBM, yielding for the mean TAMSD at short lag times (Δ ≪ T) the relation| | 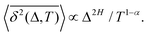 | (25) |
Therefore, for subdiffusive SBM with 0 < α < 1 the magnitude of the observed TAMSD of FBM–SBM decreases with the trace length T, indicating a dynamics slowing down with time. The scaling behavior (25) is supported by our computer simulations for both sub- and superdiffusive parental SBM, see Fig. 4. The TAMSD amplitude at short lag times is considered as the most representative and statistically robust characteristics.31,94
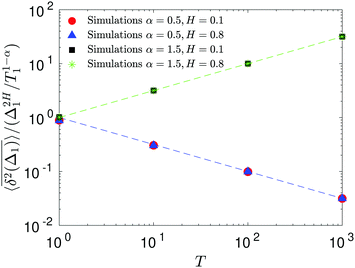 |
| | Fig. 4 Variation of the TAMSD magnitude at short lag times with the length of the trajectory, with the relation (25) shown as the asymptotes (here, the “normalization” trace-length is T1 = 1). The values of FBM and SBM exponents are provided in the legend. Due to the TAMSD “normalization” employed here, the two different SBM exponents used define the two aging exponents of FBM–SBM in the computer-simulation results. | |
We also stress that—similarly to subdiffusive HDPs and subdiffusive CTRWs—pure SBM features a peculiar aging property. Namely, the ratio of the aged mean TAMSD31
| | 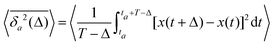 | (26) |
to the nonaged mean TAMSD
(3) is given for SBM by
63,91| | | Λα(ta/T) = (1 + ta/T)α − (ta/T)α. | (27) |
Here, the aging time is denoted by
ta. The same law is observed for SBM–FBM, see
Fig. 5, because FBM is a nonaging process. Note also that expression
(27) is valid for the aging behavior of the TAMSD for subdiffusive HDPs and subdiffusive CTRWs too, see
eqn (15) in ref.
68 and eqn (39) in ref.
145, respectively.
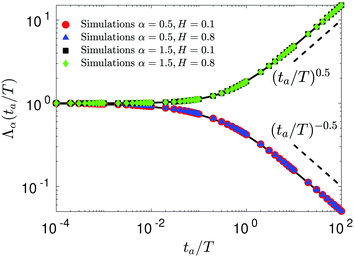 |
| | Fig. 5 Dependence of the normalized TAMSD magnitude on aging time  , with the relation (27) shown as the solid curves. The scaling relations at long aging times are given by the dashed lines. Parental FBM and SBM exponents are provided in the legend. , with the relation (27) shown as the solid curves. The scaling relations at long aging times are given by the dashed lines. Parental FBM and SBM exponents are provided in the legend. | |
There exist close similarities in scaling relations for the MSD-to-TAMSD ratios for the compound processes of SBM–HDP, FBM–HDP, and FBM–SBM. For SBM–HDP with D(x, t) ∝ |x|![[small alpha, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c2.gif) tα−1 we found that91 the MSD grows as 〈x2(Δ)〉 ∝ Δαp, the TAMSD increases [at short lag times] as
tα−1 we found that91 the MSD grows as 〈x2(Δ)〉 ∝ Δαp, the TAMSD increases [at short lag times] as 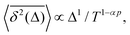 and their ratio is
and their ratio is
| | 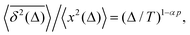 | (28) |
where
p = 2/(2 −
![[small alpha, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c2.gif)
) is the MSD exponent of pure HDPs.
67,69 For FBM–HDP we demonstrated that
93 〈
x2(
Δ)〉 ∝
Δ2Hp,
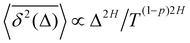
, and
| | 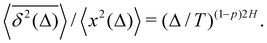 | (29) |
For FBM–SBM [considered here] we observe that at short times 〈
x2(
Δ)〉 ∝
Δ2H+α−1,
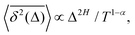
and
| | 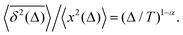 | (30) |
These relations are valid for the MSD and TAMSD growing with (lag) time.
§ The scaling relations of this paragraph embody the main characteristics of a family of SBM–HDP, FBM–HDP, and FBM–SBM hybrid processes, see
Table 1.
D PDF
For FBM–SBM with a nonstalling MSD behavior we always observe PDFs of a Gaussian shape. This finding is intuitive (results not shown) because the parental processes of FBM and SBM are also Gaussian, eqn (8). The width of the PDFs characterizing the dispersion of the particles grows in time in full correspondence to the observed MSD-growth law, see Fig. 11. What is more surprising is that the Gaussian PDFs are also detected for situations with a stalling-MSD behavior of FBM–SBM. The integration of the fitted PDFs of particle displacements, eqn (2), in the stagnating/stalling regime of the MSD yields for the second moment the plateau values in full agreement with the simulations, as illustrated in Fig. 8.
E ACF
For FBM–SBM the ACF C(δ)v(τ)/C(δ)v(0) behaves similarly to that of FBM, see Fig. 12. Quantitatively, for subdiffusive FBM contributing to FBM–SBM the depth of the minimal value of the ACF shifts upwards for sub- and downwards for superdiffusive SBM contributions. For superdiffusive FBM in FBM–SBM the ACF curve shifts downwards and upwards for sub- and superdiffusive SBM in FBM–FBM, respectively. The decay law for the long-time tail of the ACF of FBM–SBM gets modified as compared to (11) for FBM. Namely, using the discretely defined ACF (9), we get| | | C(δ)v(τ = nδt)/C(δ)v(0) ∝ n2H−2+(α−1)/2, | (31) |
as illustrated in Fig. 13.
In terms of the MSD exponent (18), for FBM–SBM with subdiffusive FBM and subdiffusive SBM the resulting process is more subdiffusive than original FBM. For superdiffusive FBM, the superdiffusive SBM contribution makes the resulting FBM–SBM more superdiffusive. The behavior of the ACF minimum, being computed naively as in Fig. 12 and described above, therefore, does not agree with these trends of the MSD exponents. This inconsistency gets “repaired/fixed” by a time-dependent normalization of the ACF, namely
| | 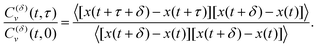 | (32) |
Namely, as FBM–SBM is a nonstationary process, the time-dependence of the instantaneous mean-squared displacement-increments, scaling from
eqn (16) as
| | | 〈(dx(t)/dt)2〉 ∝ D(t) ∝ tα−1, | (33) |
should enter the ACF normalization (see,
e.g., ref.
155 for the consideration of nonstationary ACFs). From
eqn (16) for FBM–SBM it follows that
| |  | (34) |
The ACF of FBM–SBM normalized this way, that accounts for the nonstationarity of SBM, is (nearly) the same as that of its parental FBM, see the results of simulations shown in
Fig. 6. This is expected because the displacement-ACF of SBM—being similar to that of BM, Section II B—is zero at long lag times. SBM, therefore, does not affect the long-time tails of the properly-normalized ACF of FBM–SBM
(34): it renders the scaling behavior
(31) equal to
(11) for pure FBM, as confirmed by the results of simulations presented in
Fig. 14.
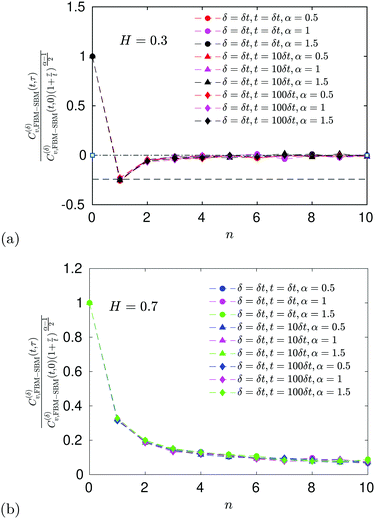 |
| | Fig. 6 ACF of FBM–SBM after the time-dependent renormalization (34) due to the nonstationarity of SBM was taken into account (see the legend for the parameter values). The results of pure FBM for different times t are included as the FBM–SBM results with α = 1. The dashed and dot-dashed lines in panel (a) indicate, respectively, the minimum (9) for pure FBM and the ACF = 0 level. | |
IV Discussion and conclusions
A Applications of FBM and SBM
Some recently observed mainly biophysical phenomena describable (at least partially) by FBM and SBM are as follows.
The model of antipersistent subdiffusive FBM—including the situations with ensemble-distributed values of 2H and K2H—has been successfully applied to the description of the spreading characteristics of tracers of various nature in living biological cells13,140,156–159 as well as in various prototypical in vitro crowded environments8,160–163 (sucrose, dextran, mucin, etc.) mimicking the macromolecularly crowded cyto- and nucleoplasm of a cell. The list of endogenous and “introduced” tracers includes micron-sized beads (both inert and interacting with the medium), quantum dots (QDs), granules, polymer segments (mRNA, chromosomal loci and telomeres,156etc.), vacuoles and particles,164 p-granules and organelles.12,140,165 Note that experimental studies of non-equilibrium cytoskeleton-induced forces impacting the subdiffusion of telomeres also exist.166
Some concrete biophysical examples of FBM-type motions are as follows. The physical mechanisms potentially underlying the anomalous dynamics of (i) potassium channels in the plasma membrane,167 (ii) intracellular transport of insulin granules,96 (iii) envelope glycoprotein gp41 transmembrane proteins of human-immunodeficiency virus in the T-cell plasma membranes,1 (iv) subdiffusion of chromosomal loci in bacterial cells,156 (v) subdiffusion of endogenous lipid granules in the living cells of fission yeast,157 (vi) lysosome and endosome intracellular movements [describable by FBM with a stochastic Hurst exponent],12,19 to name a few, see Table 1.
As to SBM, one example concerns the in vivo observations and physical interpretations of time-dependent diffusion of water in white- and gray-matter tissues of the [human] brain. The respective diffusion process features an SBM-like variation of the time-dependent part of the diffusion coefficient on time, as thoroughly studied recently168–175 [see also ref. 176 and our recent coverage;94 we refer here to Table 1]. The experimentally measured finite long-time diffusion coefficients—in nonconfining compartments, such as in the extra-cellular space, with long-time diffusivity D∞ > 0—are strongly supportive of the picture of normal macroscopic water diffusion in the brain tissues, with often Gaussian distribution of displacements.168,169,171,172 The detailed features of possible transient anomalous diffusion of water in neural tissues were discussed in ref. 177. For some earlier studies of time-dependent diffusion—with the diffusivities D(t) often decreasing with time—in barrier- or obstacle-containing, compartmentalized, and labyrinthine tissue environments we refer to ref. 168 and 178–185 for, D(t) in neural tissues, muscle tissues, and prostate cancer. These diffusion-MRI studies aim at unravelling the detailed microstructure of the respective tissues.
The second example of a physical system amenable for the SBM description is nonergodic diffusion of particles57 in free-cooling granular gases,186–190 see Table 1. Nonelastic collisions of particles/constituents in such gases lead to energy dissipation and, as a result, the effective temperature of the environments decreases in accord with (12), along with the particle diffusivity. Note, however, that for a cooling gas of rapidly aggregating particles the standard Haffs191 temperature law57,190T(t) ∝ 1/t2 can be inverted yielding an increasing—rather than decreasing—energy of an aggregate particle in time, as advocated recently.189
Lastly, for the experiments on fluorescence recovery after photobleaching in the presence of passive and active particle motion the effective diffusion coefficient has, e.g., a time-dependent correction192D(t) = D(1 + v2t/(4D)) to yield the MSD 〈x2(t)〉 = 4D(t) × t = 4Dt + v2t2. Diffusion of BM-tracers in expanding or contracting media (like our Universe) produces a time-space-rescaled stochastic process similar to SBM (in terms of its long-time MSD).193 Generally, the spreading kinetics slowing down in time—as, e.g., in the polymerization or aggregation reactions of polymers194—where the diffusivity drops with the typical particle size [e.g., in a Stockesian ∝1/size fashion] and with diffusion time—can potentially be considered as SBM with a power-law (or more complicated) functional forms for D(t).
B FBM–SBM
The FBM–SBM process introduced here enriches the armamentarium of anomalous-diffusion processes applicable to the description of SPT datasets. Some “paradoxical”55 features of nonstationary SBM coupled to a power-law decaying memory of FBM yields a so-called scaled-fractional process of FBM–SBM, certain characteristics of which are unveiled in the present study. The combination of SBM and FBM yields a nonlinear-in-lag-time FBM-like growth of the TAMSD and the presence of aging for FBM–SBM is reflected in the SBM-like dependence of the TAMSD magnitude [at short lag times] on the trajectory length, eqn (25). The MSD exponent for FBM–SBM is the “sum” of the SBM and FBM scaling exponents. The magnitude and scaling relation of the MSD are disparate from those of the TAMSD and, thus, FBM–SBM features weak ergodicity breaking.
These two essential attributes—nonequal scaling exponents of the MSD and TAMSD as well as a pronounced aging of the TAMSD—are particularly useful (indispensable) when selecting for or envisaging the most appropriate models of anomalous and nonergodic diffusion in a statistical analysis of SPT datasets. For instance, the TAMSD dependencies nonlinear in lag time and TAMSD aging with the trace length as in (25) were observed for diffusion of micron-sized beads in hydrogels of mucin polymers,8 propulsive chemotaxis-free dynamics of amoeboid cells,6 diffusion of doxorubicin drug molecules in silica nanoslits,16 as well as diffusion of gp41 transmembrane proteins in the plasma membranes of surface-adhered immune T-cells.1,27 The process of FBM–SBM is thus applicable to nonstationary physical systems with power-law-like varying SBM-like diffusion coefficient and FBM-like memory-containing correlations of particle displacements in successive time steps.
To conclude, paraphrasing the classics, “knowing is not enough, we must apply” the mathematical models of anomalous diffusion to real experimental data to check if really “all models are wrong, but some are useful”. We hope that Table 1—targeting primarily the experimental SPT community—unveils the usefulness of some pure and hybrid mathematical models of anomalous diffusion as examination tools for rationalizing, understanding, and categorizing some relevant and measurable attributes of natural physical phenomena, as gained from the experimental SPT observations as well as from (toy-)model-based in silico studies.
Abbreviations
| PDF | Probability-density function |
| MSD | Mean-squared displacement |
| TAMSD | Time-averaged MSD |
| SPT | Single-particle tracking |
| BM | Brownian motion |
| SBM | Scaled BM |
| FBM | Fractional Brownian motion |
| FLE motion | Fractional-Langevin-equation motion |
| HDPs | Heterogeneous diffusion processes |
| CTRW | Continuous-time random walk |
| ATTM | Annealed transient-time model |
| RWF | Random walk on a fractal |
| PRW | Persistent random walk |
| DD model | Diffusing-diffusivity model |
| QDs | Quantum dots |
| NPs | Nanoparticles |
Conflicts of interest
There are no conflicts to declare.
Appendix A: Auxiliary figures
Here, we present some supplementary plots supporting the claims of the main text.
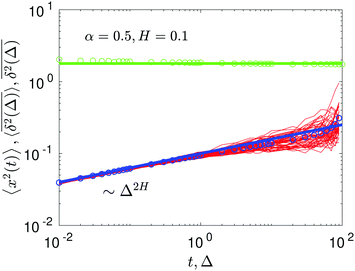 |
| | Fig. 7 The plateau behavior of the MSD for subdiffusive SBM and very subdiffusive FBM exponents such that α − 1 + 2H < 0 (see the legend for the values). The notations and colors for the curves and symbols are the same as in Fig. 1. | |
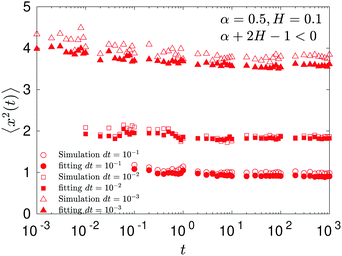 |
| | Fig. 8 The plateau behavior of the MSD for subdiffusive SBM and very subdiffusive FBM exponents such that α − 1 + 2H < 0, shown for the scaling exponents used in Fig. 7 for varying values of the time-step (see the legend). | |
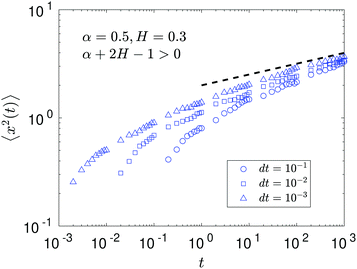 |
| | Fig. 9 The same as in Fig. 8 but for somewhat larger Hurst exponent, plotted for different time-steps used in the simulations. The long-time MSD asymptote (18) is shown as the dashed line. | |
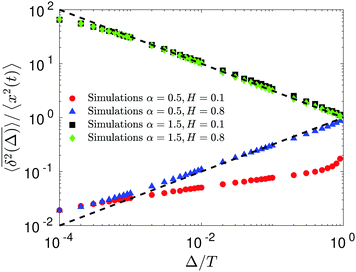 |
| | Fig. 10 Ratio of the TAMSD to MSD for FBM–SBM, with the asymptote (30) shown as the dashed line. Parameters are provided in the legend. At the last point, we find MSD(T) = TAMSD(T), as expected for the MSDs growing in time. For the model parameters in the blue region of Fig. 2 and for a stagnating MSD this statement regarding the last-point MSD-to-TAMSD equality is no longer valid, see also Fig. 7.31 | |
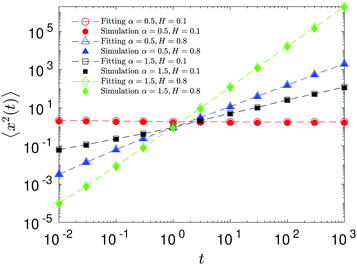 |
| | Fig. 11 MSD growth in the simulations (solid symbols) as compared to the fitted MSDs, obtained via integrating the Gaussian PDFs extracted as a fit of the actual distributions of particle displacements (empty symbols connected by the lines). FBM and SBM parental exponents are given in the legend. The laws of the MSD growth are also consistent with (18). | |
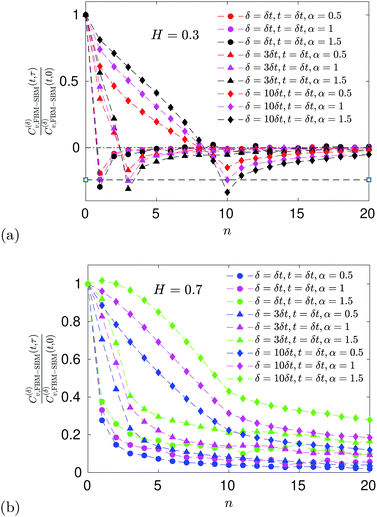 |
| | Fig. 12 ACF of FBM–SBM for subdiffusive (panel a) and superdiffusive (panel b) parental FBM process, with the results being plotted for varying SBM scaling exponent and variable time shifts used in the computation. The legends report the values of the model parameters; t = 1 × δt. | |
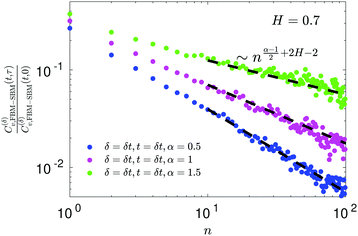 |
| | Fig. 13 Scaling of the ACF tail of FBM–SBM for superdiffusive FBM (see the legend for actual parameters, t = 1 × δt), with expression (31) presented as the asymptote. | |
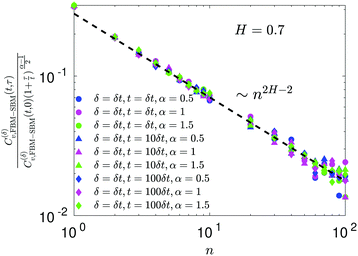 |
| | Fig. 14 The same as in Fig. 13 after the time-dependent ACF renormalization, shown for varying times t. | |
Acknowledgements
W. W. acknowledges the computational resources provided by the MPI-PKS in Dresden. A. G. C. thanks M. Assaf, M. Balcerek, A. Bodrova, N. Brilliantov, M. Javanainen, J.-H. Jeon, N. Korabel, L. Jauffred, D. Novikov, F. Spahn, M. Sperl, and M. Weiss for scientific correspondence. R. M. acknowledges support from the Deutsche Forschungsgemeinschaft (DFG Grant ME 1535/12-1).
References
- Y. Golan and E. Sherman, Resolving mixed mechanisms of protein subdiffusion at the T cell plasma membrane, Nat. Commun., 2017, 8(1), 15851 CrossRef CAS PubMed.
- T. Sungkaworn, M.-L. Jobin, K. Burnecki, A. Weron, M. J. Lohse and D. Calebiro, Single-molecule imaging reveals receptor-G protein interactions at cell surface hot spots, Nature, 2017, 550(7677), 543–547 CrossRef CAS PubMed.
- M. Yanagawa, M. Hiroshima, Y. Togashi, M. Abe, T. Yamashita, Y. Shichida, M. Murata, M. Ueda and Y. Sako, Single-molecule diffusion-based estimation of ligand effects on G protein-coupled receptors, Sci. Signaling, 2018, 11(548), eaao1917 CrossRef PubMed.
- F. Etoc, E. Balloul, C. Vicario, D. Normanno, D. Liße, A. Sittner, J. Piehler, M. Dahan and M. Coppey, Non-specific interactions govern cytosolic diffusion of nanosized objects in mammalian cells, Nat. Mater., 2018, 17(8), 740–746 CrossRef CAS PubMed.
- M. A. Tucker,
et al., Moving in the Anthropocene: Global reductions in terrestrial mammalian movements, Science, 2018, 359(6374), 466–469 CrossRef CAS PubMed.
- A. G. Cherstvy, O. Nagel, C. Beta and R. Metzler, Non-Gaussianity, population heterogeneity, and transient superdiffusion in the spreading dynamics of amoeboid cells, Phys. Chem. Chem. Phys., 2018, 20(35), 23034–23054 RSC.
- S. Thapa, M. A. Lomholt, J. Krog, A. G. Cherstvy and R. Metzler, Bayesian analysis of single-particle tracking data using the nested-sampling algorithm: maximum-likelihood model selection applied to stochastic-diffusivity data, Phys. Chem. Chem. Phys., 2018, 20(46), 29018–29037 RSC.
- A. G. Cherstvy, S. Thapa, C. E. Wagner and R. Metzler, Non-Gaussian, non-ergodic, and non-Fickian diffusion of tracers in mucin hydrogels, Soft Matter, 2019, 15(12), 2526–2551 RSC.
- K. Joly, E. Gurarie, M. S. Sorum, P. Kaczensky, M. D. Cameron, A. F. Jakes, B. L. Borg, D. Nandintsetseg, J. G. C. Hopcraft, B. Buuveibaatar, P. F. Jones, T. Mueller, C. Walzer, K. A. Olson, J. C. Payne, A. Yadamsuren and M. Hebblewhite, Longest terrestrial migrations and movements around the world, Sci. Rep., 2019, 9(1), 15333 CrossRef PubMed.
- S. Thapa, N. Lukat, C. Selhuber-Unkel, A. G. Cherstvy and R. Metzler, Transient superdiffusion of polydisperse vacuoles in highly motile amoeboid cells, J. Chem. Phys., 2019, 150(14), 144901 CrossRef PubMed.
- G. Muñoz-Gil, M. A. Garcia-March, C. Manzo, J. D. Martn-Guerrero and M. Lewenstein, Single trajectory characterization via machine learning, New J. Phys., 2020, 22(1), 013010 CrossRef.
- D. Han, N. Korabel, R. Chen, M. Johnston, A. Gavrilova, V. J. Allan, S. Fedotov and T. A. Waigh, Deciphering anomalous heterogeneous intracellular transport with neural networks, eLife, 2020, 9, e52224 CrossRef PubMed.
- A. Sabri, X. Xu, D. Krapf and M. Weiss, Elucidating the origin of heterogeneous anomalous diffusion in the cytoplasm of mammalian cells, Phys. Rev. Lett., 2020, 125(5), 058101 CrossRef CAS PubMed.
- J. Janczura, P. Kowalek, H. Loch-Olszewska, J. Szwabiński and A. Weron, Classification of particle trajectories in living cells: Machine learning versus statistical testing hypothesis for fractional anomalous diffusion, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2020, 102(3), 032402 CrossRef CAS PubMed.
- H. Loch-Olszewska and J. Szwabiski, Impact of feature choice on machine learning classification of fractional anomalous diffusion, Entropy, 2020, 22(12), 1436 CrossRef PubMed.
- A. D. Fernandez, P. Charchar, A. G. Cherstvy, R. Metzler and M. W. Finnis, The diffusion of doxorubicin drug molecules in silica nanoslits is non-Gaussian, intermittent and anticorrelated, Phys. Chem. Chem. Phys., 2020, 22(48), 27955–27965 RSC.
- N. Granik, L. E. Weiss, E. Nehme, M. Levin, M. Chein, E. Perlson, Y. Roichman and Y. Shechtman, Single-particle diffusion characterization by deep learning, Biophys. J., 2019, 117(2), 185–192 CrossRef CAS PubMed.
- G. Muñoz-Gil, G. Volpe, M. A. Garcia-March, E. Aghion, A. Argun, C. B. Hong, T. Bland, S. Bo, J. Alberto Conejero, N. Firbas, Ò. Garibo i Orts, A. Gentili, Z. Huang, J.-H. Jeon, H. Kabbech, Y. Kim, P. Kowalek, D. Krapf, H. Loch-Olszewska, M. A. Lomholt, J.-B. Masson, P. G. Meyer, S. Park, B. Requena, I. Smal, T. Song, J. Szwabiński, S. Thapa, H. Verdier, G. Volpe, A. Widera, M. Lewenstein, R. Metzler and C. Manzo, Objective comparison of methods to decode anomalous diffusion, Nat. Commun., 2021, 12(1), 6253 CrossRef PubMed.
- N. Korabel, D. Han, A. Taloni, G. Pagnini, S. Fedotov, V. Allan and T. A. Waigh, Local analysis of heterogeneous intracellular transport: Slow and fast moving endosomes, Entropy, 2021, 23(8), 958 CrossRef PubMed.
- A. Argun, G. Volpe and S. Bo, Classification, inference and segmentation of anomalous diffusion with recurrent neural networks, J. Phys. A: Math. Theor., 2021, 54(29), 294003 CrossRef.
- H. D. Pinholt, S. S.-R. Bohr, J. F. Iversen, W. Boomsma and N. S. Hatzakis, Single-particle diffusional fingerprinting: A machine-learning framework for quantitative analysis of heterogeneous diffusion, Proc. Natl. Acad. Sci. U. S. A., 2021, 118(31), e2104624118 CrossRef CAS PubMed.
- D. S. W. Lee, N. S. Wingreen and C. P. Brangwynne, Chromatin mechanics dictates subdiffusion and coarsening dynamics of embedded condensates, Nat. Phys., 2021, 17(4), 531–538 Search PubMed.
- M. Gajowczyk and J. Szwabinski, Detection of anomalous diffusion with deep residual networks, Entropy, 2021, 23(6), 649 CrossRef PubMed.
- F. Reina, J. M. A. Wigg, M. Dmitrieva, J. Lefebvre, J. Rittscher and C. Eggeling, Trait2d: a software for quantitative qnalysis of single particle diffusion data, F1000Research, 2021, 10, 838 Search PubMed.
- R. Nathan, C. T. Monk, R. Arlinghaus, T. Adam, J. Alos, M. Assaf, H. Baktoft, C. E. Beardsworth, M. G. Bertram, A. I. Bijleveld, T. Brodin, J. L. Brooks, A. Campos-Candela, S. J. Cooke, K. O. Gjelland, P. R. Gupte, R. Harel, G. Hellström, F. Jeltsch, S. S. Killen, T. Klefoth, R. Langrock, R. J. Lennox, E. Lourie, J. R. Madden, Y. Orchan, I. S. Pauwels, M. Ríha, M. Roeleke, U. E. Schlägel, D. Shohami, J. Signer, S. Toledo, O. Vilk, S. Westrelin, M. A. Whiteside and I. Jaric, Big-data approaches lead to an increased understanding of the ecology of animal movement, Science, 2022, 375(6582), eabg1780 CrossRef CAS PubMed.
- M. Mytiliniou, J. A. J. Wondergem, T. Schmidt and D. Heinrich, Impact of neurite alignment on organelle motion, J. R. Soc., Interface, 2022, 19(187), 20210617 CrossRef CAS PubMed.
-
A. G. Cherstvy, S. Thapa, R. Metzler and E. Sherman, Cell-to-cell variability of anomalous, multistate, nonergodic, and aging diffusion of gp41 transmembrane proteins on plasma membranes of immune T-cells, work in preparation, 2022.
- S. Burov, J.-H. Jeon, R. Metzler and E. Barkai, Single particle tracking in systems showing anomalous diffusion: the role of weak ergodicity breaking, Phys. Chem. Chem. Phys., 2011, 13(5), 1800–1812 RSC.
- I. M. Sokolov, Models of anomalous diffusion in crowded environments, Soft Matter, 2012, 8(35), 9043–9052 RSC.
- F. Höfling and T. Franosch, Anomalous transport in the crowded world of biological cells, Rep. Prog. Phys., 2013, 76(4), 046602 CrossRef PubMed.
- R. Metzler, J.-H. Jeon, A. G. Cherstvy and E. Barkai, Anomalous diffusion models and their properties: non-stationarity, non-ergodicity, and ageing at the centenary of single particle tracking, Phys. Chem. Chem. Phys., 2014, 16(44), 24128–24164 RSC.
- C. Manzo and M. F. Garcia-Parajo, A review of progress in single particle tracking: from methods to biophysical insights, Rep. Prog. Phys., 2015, 78(12), 124601 CrossRef PubMed.
- F. A. Oliveira, R. M. S. Ferreira, L. C. Lapas and M. H. Vainstein, Anomalous diffusion: A basic mechanism for the evolution of inhomogeneous systems, Front. Phys., 2019, 7, 18 CrossRef.
- R. Brown, A brief account of microscopical observations made in the months of June, July and August 1827, on the particles contained in the pollen of plants; and on the general existence of active molecules in organic and inorganic bodies, Philos. Mag., 1828, 4(21), 161–173 CrossRef.
- A. Fick, Über Diffusion, Ann. Phys., 1855, 170(1), 59–86 CrossRef.
- L. Bachelier, Théorie de la spéculation, Ann. Sci. Éc. Norm. Supér., 1900, 17, 21–86 CrossRef.
- A. Einstein, Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen, Ann. Phys., 1905, 322(8), 549–560 CrossRef.
- E. Frey and K. Kroy, Brownian motion: a paradigm of soft matter and biological physics, Ann. Phys., 2005, 14(1-3), 20–50 CrossRef CAS.
- T. Li, S. Kheifets, D. Medellin and M. G. Raizen, Measurement of the instantaneous velocity of a Brownian particle, Science, 2010, 328(5986), 1673–1675 CrossRef CAS PubMed.
- T. Franosch, M. Grimm, M. Belushkin, F. M. Mor, G. Foffi, L. Forró and S. Jeney, Resonances arising from hydrodynamic memory in Brownian motion, Nature, 2011, 478(7367), 85–88 CrossRef CAS PubMed.
- S. Kheifets, A. Simha, K. Melin, T. Li and M. G. Raizen, Observation of Brownian motion in liquids at short times: Instantaneous velocity and memory loss, Science, 2014, 343(6178), 1493–1496 CrossRef CAS PubMed.
- A. N. Kolmogorov, Wienersche Spiralen und einige andere interessante Kurven im Hilbertschen Raum, CR (Doklady) Acad. Sci. URSS (NS), 1940, 26, 115 Search PubMed.
- B. B. Mandelbrot and J. W. van Ness, Fractional Brownian motions, fractional noises and applications, SIAM Rev., 1968, 10(4), 422–437 CrossRef.
- W. Deng and E. Barkai, Ergodic properties of fractional Brownian-Langevin motion, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79(1), 011112 CrossRef PubMed.
- J.-H. Jeon and R. Metzler, Fractional Brownian motion and motion governed by the fractional Langevin equation in confined geometries, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81(2), 021103 CrossRef PubMed.
- J.-H. Jeon and R. Metzler, Inequivalence of time and ensemble averages in ergodic systems: Exponential versus power-law relaxation in confinement, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85(2), 021147 CrossRef PubMed.
- A. Fuliński, Fractional Brownian motions: memory, diffusion velocity, and correlation functions, J. Phys. A: Math. Theor., 2017, 50(5), 054002 CrossRef.
- A. G. Cherstvy, W. Wang, R. Metzler and I. M. Sokolov, Inertia triggers nonergodicity of fractional Brownian motion, Phys. Rev. E: Stat., Nonlinear, Soft Matter, 2021, 104(2), 024115 CrossRef CAS PubMed.
- S. C. Lim and S. V. Muniandy, On some possible generalizations of fractional Brownian motion, Phys. Lett. A, 2000, 266(2), 140–145 CrossRef CAS.
- V. M. Muniandy and S. C. Lim, Modeling of locally self-similar processes using multifractional Brownian motion of Riemann-Liouville type, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 63(4), 046104 CrossRef PubMed.
- S. C. Lim and S. V. Muniandy, Self-similar Gaussian processes for modeling anomalous diffusion, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66(2), 021114 CrossRef CAS PubMed.
- A. Fulinski, Communication: How to generate and measure anomalous diffusion in simple systems, J. Chem. Phys., 2013, 138(2), 021101 CrossRef CAS PubMed.
- A. Fulinski, Anomalous weakly nonergodic Brownian motions in nonuniform temperatures, Acta Phys. Pol., B, 2013, 44(5), 1137 CrossRef CAS.
- F. Thiel and I. M. Sokolov, Scaled Brownian motion as a mean-field model for continuous-time random walks, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89(1), 012115 CrossRef PubMed.
- J.-H. Jeon, A. V. Chechkin and R. Metzler, Scaled Brownian motion: a paradoxical process with a time dependent diffusivity for the description of anomalous diffusion, Phys. Chem. Chem. Phys., 2014, 16(30), 15811–15817 RSC.
- H. Safdari, A. G. Cherstvy, A. V. Chechkin, F. Thiel, I. M. Sokolov and R. Metzler, Quantifying the non-ergodicity of scaled Brownian motion, J. Phys. A: Math. Theor., 2015, 48(37), 375002 CrossRef.
- A. Bodrova, A. V. Chechkin, A. G. Cherstvy and R. Metzler, Quantifying non-ergodic dynamics of force-free granular gases, Phys. Chem. Chem. Phys., 2015, 17(34), 21791–21798 RSC.
- A. S. Bodrova, A. V. Chechkin, A. G. Cherstvy, H. Safdari, I. M. Sokolov and R. Metzler, Underdamped scaled Brownian motion: (non-)existence of the overdamped limit in anomalous diffusion, Sci. Rep., 2016, 6(1), 30520 CrossRef CAS PubMed.
- V. Sposini, R. Metzler and G. Oshanin, Single-trajectory spectral analysis of scaled Brownian motion, New J. Phys., 2019, 21(7), 073043 CrossRef.
- M. Balcerek, K. Burnecki, G. Sikora and A. Wylomanska, Discriminating Gaussian processes via quadratic form statistics, Chaos, 2021, 31(6), 063101 CrossRef PubMed.
- S. Thapa, S. Park, Y. Kim, J.-H. Jeon, R. Metzler and M. A. Lomholt, Bayesian inference of scaled versus fractional Brownian motion, J. Phys. A: Math. Theor., 2022, 55(19), 194003 CrossRef.
- A. S. Bodrova, A. V. Chechkin, A. G. Cherstvy and R. Metzler, Ultraslow scaled Brownian motion, New J. Phys., 2015, 17(6), 063038 CrossRef.
- H. Safdari, A. G. Cherstvy, A. V. Chechkin, A. Bodrova and R. Metzler, Aging underdamped scaled Brownian motion: Ensemble- and time-averaged particle displacements, nonergodicity, and the failure of the overdamping approximation, Phys. Rev. E: Stat., Nonlinear, Soft Matter, 2017, 95(1), 012120 CrossRef PubMed.
- T. Akimoto, A. G. Cherstvy and R. Metzler, Ergodicity, rejuvenation, enhancement, and slow relaxation of diffusion in biased continuous-time random walks, Phys. Rev. E: Stat., Nonlinear, Soft Matter, 2018, 98(2), 022105 CrossRef CAS PubMed.
- R. Hou, A. G. Cherstvy, R. Metzler and T. Akimoto, Biased continuous-time random walks for ordinary and equilibrium cases: facilitation of diffusion, ergodicity breaking and ageing, Phys. Chem. Chem. Phys., 2018, 20(32), 20827–20848 RSC.
- V. Zaburdaev, S. Denisov and J. Klafter, Lévy walks, Rev. Mod. Phys., 2015, 87(2), 483–530 CrossRef CAS.
- A. G. Cherstvy, A. V. Chechkin and R. Metzler, Anomalous
diffusion and ergodicity breaking in heterogeneous diffusion processes, New J. Phys., 2013, 15(8), 083039 CrossRef.
- A. G. Cherstvy, A. V. Chechkin and R. Metzler, Ageing and confinement in non-ergodic heterogeneous diffusion processes, J. Phys. A: Math. Theor., 2014, 47(48), 485002 CrossRef.
- A. G. Cherstvy and R. Metzler, Nonergodicity, fluctuations, and criticality in heterogeneous diffusion processes, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90(1), 012134 CrossRef CAS PubMed.
- C. Manzo, J. A. Torreno-Pina, P. Massignan, G. J. Lapeyre, M. Lewenstein and M. F. Garcia Parajo, Weak ergodicity breaking of receptor motion in living cells stemming from random diffusivity, Phys. Rev. X, 2015, 5(1), 011021 Search PubMed.
- T. Akimoto and E. Yamamoto, Distributional behavior of diffusion coefficients obtained by single trajectories in annealed transit time model, J. Stat. Mech.: Theory Exp., 2016, 2016(12), 123201 CrossRef.
- T. Miyaguchi, T. Akimoto and E. Yamamoto, Langevin equation with fluctuating diffusivity: A two-state model, Phys. Rev. E: Stat., Nonlinear, Soft Matter, 2016, 94(1), 012109 CrossRef PubMed.
- T. Miyaguchi, T. Uneyama and T. Akimoto, Brownian motion with alternately fluctuating diffusivity: Stretched-exponential and power-law relaxation, Phys. Rev. E: Stat., Nonlinear, Soft Matter, 2019, 100(1), 012116 CrossRef CAS PubMed.
- Y. Lanoiselée and D. S. Grebenkov, A model of non-Gaussian diffusion in heterogeneous media, J. Phys. A: Math. Theor., 2018, 51(14), 145602 CrossRef.
- D. S. Grebenkov, Time-averaged mean square displacement for switching diffusion, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2019, 99(3), 032133 CrossRef CAS PubMed.
- M. Hidalgo-Soria, E. Barkai and S. Burov, Cusp of non-Gaussian density of particles for a diffusing diffusivity model, Entropy, 2021, 23(2), 231 CrossRef PubMed.
- J. Janczura, M. Balcerek, K. Burnecki, A. Sabri, M. Weiss and D. Krapf, Identifying heterogeneous diffusion states in the cytoplasm by a hidden Markov model, New J. Phys., 2021, 23(5), 053018 CrossRef.
- P. Massignan, C. Manzo, J. A. Torreno-Pina, M. F. Garca-Parajo, M. Lewenstein and G. J. Lapeyre, Nonergodic subdiffusion from Brownian motion in an inhomogeneous medium, Phys. Rev. Lett., 2014, 112(15), 150603 CrossRef CAS PubMed.
- M. V. Chubynsky and G. W. Slater, Diffusing diffusivity: A model for anomalous, yet Brownian, diffusion, Phys. Rev. Lett., 2014, 113(9), 098302 CrossRef PubMed.
-
J. Masoliver and J. Perello, First-passage and extremes in socio-economic systems, First-Passage Phenomena and Their Applications, ed. R. Metzler, G. Oshanin and S. Redner, World Scientific, 2014, ch. 1, pp. 477–501 Search PubMed.
- T. Uneyama, T. Miyaguchi and T. Akimoto, Fluctuation analysis of time-averaged mean-square displacement for the Langevin equation with time-dependent and fluctuating diffusivity, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92(3), 032140 CrossRef PubMed.
- T. Akimoto and E. Yamamoto, Distributional behaviors of time-averaged observables in the Langevin equation with fluctuating diffusivity: Normal diffusion but anomalous fluctuations, Phys. Rev. E: Stat., Nonlinear, Soft Matter, 2016, 93(6), 062109 CrossRef PubMed.
- T. J. Lampo, S. Stylianidou, M. P. Backlund, P. A. Wiggins and A. J. Spakowitz, Cytoplasmic RNA-protein particles exhibit non-Gaussian subdiffusive behavior, Biophys. J., 2017, 112(3), 532–542 CrossRef CAS PubMed.
- A. G. Cherstvy and R. Metzler, Anomalous diffusion in time-fluctuating non-stationary diffusivity landscapes, Phys. Chem. Chem. Phys., 2016, 18(34), 23840–23852 RSC.
- A. V. Chechkin, F. Seno, R. Metzler and I. M. Sokolov, Brownian yet non-Gaussian diffusion: From superstatistics to subordination of diffusing diffusivities, Phys. Rev. X, 2017, 7(2), 021002 Search PubMed.
- C. Metzner, C. Mark, J. Steinwachs, L. Lautscham, F. Stadler and B. Fabry, Superstatistical analysis and modelling of heterogeneous random walks, Nat. Commun., 2015, 6(1), 7516 CrossRef CAS PubMed.
- E. B. Postnikov, A. V. Chechkin and I. M. Sokolov, Brownian yet non-Gaussian diffusion in heterogeneous media: from superstatistics to homogenization, New J. Phys., 2020, 22(6), 063046 CrossRef.
-
M. A. F. dos Santos, L. Menon Junior and D. Cius, Superstatistical approach of the anomalous exponent for scaled Brownian motion, arXiv: 2206.07820.
- Y. Itto and C. Beck, Superstatistical modelling of protein diffusion dynamics in bacteria, J. R. Soc., Interface, 2021, 18(176), 20200927 CrossRef CAS PubMed.
- H. George., E. Hentschel and I. Procaccia, Relative diffusion in turbulent media: The fractal dimension of clouds, Phys. Rev. A: At., Mol., Opt. Phys., 1984, 29(3), 1461–1470 CrossRef.
- A. G. Cherstvy and R. Metzler, Ergodicity breaking, ageing, and confinement in generalized diffusion processes with position and time dependent diffusivity, J. Stat. Mech.: Theory Exp., 2015, 5, P05010 CrossRef.
- W. Wang, A. G. Cherstvy, A. V. Chechkin, S. Thapa, F. Seno, X. Liu and R. Metzler, Fractional Brownian motion with random diffusivity: emerging residual nonergodicity below the correlation time, J. Phys. A: Math. Theor., 2020, 53(47), 474001 CrossRef.
- W. Wang, A. G. Cherstvy, X. Liu and R. Metzler, Anomalous diffusion and nonergodicity for heterogeneous diffusion processes with fractional Gaussian noise, Phys. Rev. E: Stat., Nonlinear, Soft Matter, 2020, 102(1), 012146 CrossRef CAS PubMed.
- A. G. Cherstvy, H. Safdari and R. Metzler, Anomalous diffusion, nonergodicity, and ageing for exponentially and logarithmically time-dependent diffusivity: striking differences for massive versus massless particles, J. Phys. D: Appl. Phys., 2021, 54(19), 195401 CrossRef CAS.
- Y. Meroz, I. M. Sokolov and J. Klafter, Subdiffusion of mixed origins: When ergodicity and nonergodicity coexist, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81(1), 010101 CrossRef PubMed.
- S. M. Ali Tabei, S. Burov, H. Y. Kim, A. Kuznetsov, T. Huynh, J. Jureller, L. H. Philipson, A. R. Dinner and N. F. Scherer, Intracellular transport of insulin granules is a subordinated random walk, Proc. Natl. Acad. Sci. U. S. A., 2013, 110(13), 4911–4916 CrossRef CAS PubMed.
- M. Levin, G. Bel and Y. Roichman, Measurements and characterization of the dynamics of tracer particles in an actin network, J. Chem. Phys., 2021, 154(14), 144901 CrossRef CAS PubMed.
- Z. R. Fox, E. Barkai and D. Krapf, Aging power spectrum of membrane protein transport and other subordinated random walks, Nat. Commun., 2021, 12(1), 6162 CrossRef CAS PubMed.
- A. W. C. Lau and T. C. Lubensky, State-dependent diffusion: Thermodynamic consistency and its path integral formulation, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76(1), 011123 CrossRef CAS PubMed.
- E. Gurarie, R. D. Andrews and K. L. Laidre, A novel method for identifying behavioural changes in animal movement data, Ecol. Lett., 2009, 12(5), 395–408 CrossRef PubMed.
- I. Goychuk, Viscoelastic subdiffusion: Generalized Langevin equation approach, Adv. Chem. Phys., 2012, 150, 187–253 CrossRef CAS.
- F. Thiel and I. M. Sokolov, Weak ergodicity breaking in an anomalous diffusion process of mixed origins, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89(1), 012136 CrossRef PubMed.
- A. Weron, K. Burnecki, E. J. Akin, L. Solé, M. Balcerek, M. M. Tamkun and D. Krapf, Ergodicity breaking on the neuronal surface emerges from random switching between diffusive states, Sci. Rep., 2017, 7(1), 5404 CrossRef PubMed.
- Y. Liang, S. Wang, W. Chen, Z. Zhou and R. L. Magin, A survey of models of ultraslow diffusion in heterogeneous materials, Appl. Mech. Rev., 2019, 71(4), 040802 CrossRef.
- Y. Chen and X. Wang, Novel anomalous diffusion phenomena of underdamped Langevin equation with random parameters, New J. Phys., 2021, 23(12), 123024 CrossRef.
- I. Goychuk and T. Pöschel, Fingerprints of viscoelastic subdiffusion in random environments: Revisiting some experimental data and their interpretations, Phys. Rev. E: Stat., Nonlinear, Soft Matter, 2021, 104(3), 034125 CrossRef CAS PubMed.
- M. A. F. dos Santos, E. H. Colombo and C. Anteneodo, Random diffusivity scenarios behind anomalous non-Gaussian diffusion, Chaos, Solitons Fractals, 2021, 152, 111422 CrossRef.
- H. Watanabe, Relations between anomalous diffusion and fluctuation scaling: the case of ultraslow diffusion and time-scale-independent fluctuation scaling in language, Eur. Phys. J. B, 2021, 94(11), 227 CrossRef CAS.
- I. I. Eliazar and T. Kachman, Anomalous diffusion: Fractional Brownian motion vs. fractional Ito motion, J. Phys. A: Math. Theor., 2022, 55(11), 115002 CrossRef.
- H.-D. Shi, L.-C. Du, F.-J. Huang and W. Guo, Collective topological active particles: Non-ergodic superdiffusion and ageing in complex environments, Chaos, Solitons Fractals, 2022, 157, 111935 CrossRef.
-
M. Audoin, M. T. Søgaard and L. Jauffred, Tumor spheroids accelerate persistently invading cancer cells, bioRxiv, 2022 DOI:10.1101/2022.04.04.486939.
-
A. Pacheco-Pozo and I. M. Sokolov, Universal fluctuations and ergodicity of generalized diffusivity on critical percolation clusters, 2022, arXiv:2203.10919.
-
D. G. Kelty-Stephen and M. Mangalam, Fractal and multifractal descriptors restore ergodicity broken by non-Gaussianity in time series, arXiv:2204.00572.
- A. I. Shushin, Anomalous two-state model for anomalous diffusion, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 64(5), 051108 CrossRef CAS PubMed.
- T. Sandev, W. Deng and P. Xu, Models for characterizing the transition among anomalous diffusions with different diffusion exponents, J. Phys. A: Math. Theor., 2018, 51(40), 405002 CrossRef.
- C. H. Eab and S. C. Lim, Fractional Langevin equations of distributed order, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83(3), 031136 CrossRef CAS PubMed.
- T. Sandev, A. V. Chechkin, N. Korabel, H. Kantz, I. M. Sokolov and R. Metzler, Distributed-order diffusion equations and multifractality: models and solutions, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92(4), 042117 CrossRef PubMed.
- A. Stanislavsky and A. Weron, Control of the transient subdiffusion exponent at short and long times, Phys. Rev. Res., 2019, 1(2), 023006 CrossRef CAS.
- A. Stanislavsky and A. Weron, Accelerating and retarding anomalous diffusion: A Bernstein function approach, Phys. Rev. E: Stat., Nonlinear, Soft Matter, 2020, 101(5), 052119 CrossRef CAS PubMed.
- K. Chen, B. Wang and S. Granick, Memoryless self-reinforcing directionality in endosomal active transport within living cells, Nat. Mater., 2015, 14(6), 589–593 CrossRef CAS PubMed.
- X. Wang, Y. Chen and W. Deng, Strong anomalous diffusion in two-state process with Lévy walk and Brownian motion, Phys. Rev. Res., 2020, 2(1), 013102 CrossRef CAS.
- J. Liu, P. Zhu, J.-D. Bao and X. Chen, Strong anomalous diffusive behaviors of the two-state random walk process, Phys. Rev. E: Stat., Nonlinear, Soft Matter, 2022, 105(1), 014122 CrossRef CAS PubMed.
-
M. Li, S. C. Lim, B.-J. Hu and H. Feng, Towards describing multi-fractality of traffic using local Hurst function, in Computational Science - ICCS 2007, ed. Y. Shi, G. D. van Albada, J. Dongarra and P. M. A. Sloot, Springer Berlin Heidelberg, Berlin, Heidelberg, 2007, pp. 1012–1020 Search PubMed.
- C. H. Eab and S. C. Lim, Accelerating and retarding anomalous diffusion, J. Phys. A: Math. Theor., 2012, 45(14), 145001 CrossRef.
- M. Balcerek and K. Burnecki, Testing of multifractional Brownian motion, Entropy, 2020, 22(12), 1403 CrossRef PubMed.
- M. Li, Modified multifractional Gaussian noise and its application, Phys. Scr., 2021, 96(12), 125002 CrossRef.
- R. Mattera and F. D. Sciorio, Option pricing under multifractional process and long-range dependence, Fluct. Noise Lett., 2021, 20(01), 2150008 CrossRef.
-
E. Ghysels, A. C. Harvey and E. Renault, Stochastic Volatility, Statistical Methods in Finance, Handbook of Statistics, Elsevier Science B.V., 1996, vol. 14, pp. 119–191 Search PubMed.
- S. Corlay, J. Lebovits and J. L. Vehel, Multifractional stochastic volatility models, Math. Finance, 2014, 24(2), 364–402 CrossRef.
- L. Boltzmann, Ueber die Eigenschaften monocyclischer und anderer damit verwandter Systeme, J. Pure Appl. Math., 1885, 98, 68–94 Search PubMed.
- P. Langevin, Sur la théorie du mouvement brownien, Rep. Acad. Sci., 1908, 146, 530–533 CAS.
- J.-P. Bouchaud and A. Georges, Anomalous diffusion in disordered media: Statistical mechanisms, models and physical applications, Phys. Rep., 1990, 195(4), 127–293 CrossRef.
- R. Metzler and J. Klafter., The random walk's guide to anomalous diffusion: a fractional dynamics approach, Phys. Rep., 2000, 339(1), 1–77 CrossRef CAS.
- G. M. Zaslavsky, Chaos, fractional kinetics, and anomalous transport, Phys. Rep., 2002, 371(6), 461–580 CrossRef.
- R. Metzler and J. Klafter., The restaurant at the end of the random walk: recent developments in the description of anomalous transport by fractional dynamics, J. Phys. A: Math. Theor., 2004, 37(31), R161–R208 CrossRef.
- H. E. Hurst, Long-term storage capacity of reservoirs, Trans. Am. Soc. Civ. Eng., 1951, 116(1), 770–799 CrossRef.
- A. H. O. Wada and T. Vojta, Fractional Brownian motion with a reflecting wall, Phys. Rev. E: Stat., Nonlinear, Soft Matter, 2018, 97(2), 020102 CrossRef CAS PubMed.
- T. Vojta, S. Skinner and R. Metzler, Probability density of the fractional Langevin equation with reflecting walls, Phys. Rev. E: Stat., Nonlinear, Soft Matter, 2019, 100(4), 042142 CrossRef CAS PubMed.
- T. Vojta, S. Halladay, S. Skinner, S. Janusonis, T. Guggenberger and R. Metzler, Reflected fractional Brownian motion in one and higher dimensions, Phys. Rev. E: Stat., Nonlinear, Soft Matter, 2020, 102(3), 032108 CrossRef CAS PubMed.
- R. Benelli and M. Weiss, From sub- to superdiffusion: fractional Brownian motion of membraneless organelles in early C. elegans embryos, New J. Phys., 2021, 23(6), 063072 CrossRef.
- J.-H. Jeon, N. Leijnse, L. B. Oddershede and R. Metzler, Anomalous diffusion and power-law relaxation of the time averaged mean squared displacement in worm-like micellar solutions, New J. Phys., 2013, 15(4), 045011 CrossRef CAS.
- M. P. Backlund, R. Joyner and W. E. Moerner, Chromosomal locus tracking with proper accounting of static and dynamic errors, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91(6), 062716 CrossRef PubMed.
- T. Neusius, I. M. Sokolov and J. C. Smith, Subdiffusion in time-averaged, confined random walks, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80(1), 011109 CrossRef PubMed.
- J. H. P. Schulz, E. Barkai and R. Metzler, Aging effects and population splitting in single-particle trajectory averages, Phys. Rev. Lett., 2013, 110(2), 020602 CrossRef PubMed.
- J. H. P. Schulz, E. Barkai and R. Metzler, Aging renewal theory and application to random walks, Phys. Rev. X, 2014, 4(1), 011028 Search PubMed.
- F. Thiel and I. M. Sokolov, Time averages in continuous-time random walks, Phys. Rev. E: Stat., Nonlinear, Soft Matter, 2017, 95(2), 022108 CrossRef PubMed.
- R. Kutner and J. Masoliver, The continuous time random walk, still trendy: fifty-year history, state of art and outlook, Eur. Phys. J. B, 2017, 90, 50 CrossRef.
- I. Goychuk and T. Pöschel, Finite-range viscoelastic subdiffusion in disordered systems with inclusion of inertial effects, New J. Phys., 2020, 22(11), 113018 CrossRef CAS.
- S. Ritschel, A. G. Cherstvy and R. Metzler, Universality of delay-time averages for financial time series: analytical results, computer simulations, and analysis of historical stock-market prices, J. Phys.: Complex., 2021, 4(2), 045003 Search PubMed.
- A. G. Cherstvy, D. Vinod, E. Aghion, I. M. Sokolov and R. Metzler, Scaled geometric Brownian motion features sub- or superexponential ensemble-averaged, but linear time-averaged mean-squared displacements, Phys. Rev. E: Stat., Nonlinear, Soft Matter, 2021, 103(6), 062127 CrossRef CAS PubMed.
- L. Lv, C. Zheng and L. Wang, Option pricing under the subordinated market models, Discrete Dyn. Nat. Soc., 2022, 2022, 6213803 Search PubMed.
- I. M. Sokolov, Ito, Stratonovich, Hänggi and all the rest: The thermodynamics of interpretation, Chem. Phys., 2010, 375(2), 359–363 CrossRef CAS.
- I. Goychuk, Resonance-like enhancement of forced nonlinear diffusion as a nonequilibrium phase transition, New J. Phys., 2022, 24, 04318 CrossRef.
- W. Wang, A. G. Cherstvy, R. Metzler and I. M. Sokolov, Restoring ergodicity of stochastically reset anomalous-diffusion processes, Phys. Rev. Res., 2022, 4(1), 013161 CrossRef CAS.
- A. Dechant, E. Lutz, D. A. Kessler and E. Barkai, Scaling Green-Kubo relation and application to three aging systems, Phys. Rev. X, 2014, 4(1), 011022 Search PubMed.
- S. C. Weber, A. J. Spakowitz and J. A. Theriot, Bacterial chromosomal loci move subdiffusively through a viscoelastic cytoplasm, Phys. Rev. Lett., 2010, 104(23), 238102 CrossRef PubMed.
- J.-H. Jeon, V. Tejedor, S. Burov, E. Barkai, C. Selhuber-Unkel, K. Berg-Sørensen, L. Oddershede and R. Metzler,
In vivo anomalous diffusion and weak ergodicity breaking of lipid granules, Phys. Rev. Lett., 2011, 106(4), 048103 CrossRef PubMed.
- K. Speckner and M. Weiss, Single-particle tracking reveals anti-persistent subdiffusion in cell extracts, Entropy, 2021, 23(7), 892 CrossRef PubMed.
-
R. Benelli and M. Weiss, Probing local chromatin dynamics by tracking telomeres. bioRxiv, 2022 DOI:10.1101/2022.02.15.480529.
- J. Szymanski and M. Weiss, Elucidating the origin of anomalous diffusion in crowded fluids, Phys. Rev. Lett., 2009, 103(3), 038102 CrossRef PubMed.
- D. Ernst, M. Hellmann, J. Köhler and M. Weiss, Fractional Brownian motion in crowded fluids, Soft Matter, 2012, 8(18), 4886–4889 RSC.
- M. Weiss, Single-particle tracking data reveal anticorrelated fractional Brownian motion in crowded fluids, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88(1), 010101(R) CrossRef PubMed.
- C. E. Wagner, B. S. Turner, M. Rubinstein, G. H. McKinley and K. Ribbeck, A rheological study of the association and dynamics of MUC5AC gels, Biomacromolecules, 2017, 18(11), 3654–3664 CrossRef CAS PubMed.
- J. F. Reverey, J.-H. Jeon, H. Bao, M. Leippe, R. Metzler and C. Selhuber-Unkel, Superdiffusion dominates intracellular particle motion in the supercrowded cytoplasm of pathogenic Acanthamoeba castellanii, Sci. Rep., 2015, 5(1), 11690 CrossRef PubMed.
- K. Speckner, L. Stadler and M. Weiss, Anomalous dynamics of the endoplasmic reticulum network, Phys. Rev. E: Stat., Nonlinear, Soft Matter, 2018, 98(1), 012406 CrossRef CAS PubMed.
- L. Stadler and M. Weiss, Non-equilibrium forces drive the anomalous diffusion of telomeres in the nucleus of mammalian cells, New J. Phys., 2017, 19(11), 113048 CrossRef.
- A. V. Weigel, B. Simon, M. M. Tamkun and D. Krapf, Ergodic and nonergodic processes coexist in the plasma membrane as observed by single-molecule tracking, Proc. Natl. Acad. Sci. U. S. A., 2011, 108(16), 6438–6443 CrossRef CAS PubMed.
- D. S. Novikov, J. H. Jensen, J. A. Helpern and E. Fieremans, Revealing mesoscopic structural universality with diffusion, Proc. Natl. Acad. Sci. U. S. A., 2014, 111(14), 5088–5093 CrossRef CAS PubMed.
- E. Fieremans, L. M. Burcaw, H.-H. Lee, G. Lemberskiy, J. Veraart and D. S. Novikov,
In vivo observation and biophysical interpretation of time-dependent diffusion in human white matter, NeuroImage, 2016, 129, 414–427 CrossRef PubMed.
- V. G. Kiselev, Fundamentals of diffusion MRI physics, NMR Biomed., 2017, 30(3), e3602 CrossRef PubMed.
- D. S. Novikov, V. G. Kiselev and S. N. Jespersen, On modeling, Magn. Reson. Med., 2018, 79(6), 3172–3193 CrossRef PubMed.
- D. S. Novikov, E. Fieremans, S. N. Jespersen and V. G. Kiselev, Quantifying brain microstructure with diffusion MRI: Theory and parameter estimation, NMR Biomed., 2019, 32(4), e3998 CrossRef PubMed.
- H.-H. Lee, A. Papaioannou, S.-L. Kim, D. S. Novikov and E. Fieremans, A time-dependent diffusion MRI signature of axon caliber variations and beading, Commun. Biol., 2020, 3(1), 354 CrossRef CAS PubMed.
- H.-H. Lee, A. Papaioannou, D. S. Novikov and E. Fieremans,
In vivo observation and biophysical interpretation of time-dependent diffusion in human cortical gray matter, NeuroImage, 2020, 222, 117054 CrossRef PubMed.
- D. S. Novikov, The present and the future of microstructure MRI: From a paradigm shift to normal science, J. Neurosci. Methods, 2021, 351, 108947 CrossRef PubMed.
- S. Capuani and M. Palombo, Mini review on anomalous diffusion by MRI: Potential advantages, pitfalls, limitations, nomenclature, and correct interpretation of literature, Front. Phys., 2020, 7, 248 CrossRef.
- A. Caporale, G. B. Bonomo, G. T. Raffaelli, A. M. Tata, B. Avallone, F. W. Wehrli and S. Capuani, Transient anomalous diffusion MRI in excised mouse spinal cord: Comparison among different diffusion metrics and validation with histology, Front. Neurosci., 2022, 15, 79764 Search PubMed.
- L. L. Latour, K. Svoboda, P. P. Mitra and C. H. Sotak, Time-dependent diffusion of water in a biological model system, Proc. Natl. Acad. Sci. U. S. A., 1994, 91(4), 1229–1233 CrossRef CAS PubMed.
- P. N. Sen, Time-dependent diffusion coefficient as a probe of geometry, Concepts Magn. Reson., Part A, 2004, 23A(1), 1–21 CrossRef.
- J. H. Jensen and J. A. Helpern, MRI quantification of non-Gaussian water diffusion by kurtosis analysis, NMR Biomed., 2010, 23(7), 698–710 CrossRef PubMed.
- D. S. Novikov, E. Fieremans, J. H. Jensen and J. A. Helpern, Random walks with barriers, Nat. Phys., 2011, 7(6), 508–514 Search PubMed.
- S. Kim, G. Chi-Fishman, A. S. Barnett and C. Pierpaoli, Dependence on diffusion time of apparent diffusion tensor of ex vivo calf tongue and heart, Magn. Reson. Med., 2005, 54(6), 1387–1396 CrossRef PubMed.
- E. E. Sigmund, D. S. Novikov, D. Sui, O. Ukpebor, S. Baete, J. S. Babb, K. Liu, T. Feiweier, J. Kwon, K. A. McGorty, J. Bencardino and E. Fieremans, Time-dependent diffusion in skeletal muscle with the random permeable barrier model (RPBM): application to normal controls and chronic exertional compartment syndrome patients, NMR Biomed., 2014, 27(5), 519–528 CrossRef PubMed.
- G. Lemberskiy, A. B. Rosenkrantz, J. Veraart, S. S. Taneja, D. S. Novikov and E. Fieremans, Time-dependent diffusion in prostate cancer, Invest. Radiol., 2017, 52(7), 405–411 CrossRef PubMed.
- G. Lemberskiy, E. Fieremans, J. Veraart, F.-M. Deng, A. B. Rosenkrantz and D. S. Novikov, Characterization of prostate microstructure using water diffusion and NMR relaxation, Front. Phys., 2018, 6, 91 CrossRef PubMed.
- N. V. Brilliantov, F. Spahn, J.-M. Hertzsch and T. Pöschel, Model for collisions in granular gases, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1996, 53(5), 5382–5392 CrossRef CAS PubMed.
- N. V. Brilliantov and T. Pöschel, Self-diffusion in granular gases, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2000, 61(2), 1716–1721 CrossRef CAS PubMed.
- N. V. Brilliantov, T. Pöschel, W. T. Kranz and A. Zippelius, Translations and rotations are correlated in granular gases, Phys. Rev. Lett., 2007, 98(12), 128001 CrossRef CAS PubMed.
- N. V. Brilliantov, A. Formella and T. Pöschel, Increasing temperature of cooling granular gases, Nat. Commun., 2018, 9(1), 797 CrossRef PubMed.
- P. Yu, M. Schröter and M. Sperl, Velocity distribution of a homogeneously cooling granular gas, Phys. Rev. Lett., 2020, 124(20), 208007 CrossRef CAS PubMed.
- P. K. Haff, Grain flow as a fluid-mechanical phenomenon, J. Fluid Mech., 1983, 134, 401–430 CrossRef.
- N. Periasamy and A. S. Verkman, Analysis of fluorophore diffusion by continuous distributions of diffusion coefficients: Application to photobleaching measurements of multicomponent and anomalous diffusion, Biophys. J., 1998, 75(1), 557–567 CrossRef CAS PubMed.
- S. B. Yuste, E. Abad and C. Escudero, Diffusion in an expanding medium: Fokker-Planck equation, Green's function, and first-passage properties, Phys. Rev. E: Stat., Nonlinear, Soft Matter, 2016, 94(3), 032118 CrossRef CAS PubMed.
- G. Oshanin and M. Moreau, Influence of transport limitations on the kinetics of homopolymerization reactions, J. Chem. Phys., 1995, 102(7), 2977–2985 CrossRef CAS.
- J.-C. Walter, A. Ferrantini, E. Carlon and C. Vanderzande, Fractional Brownian motion and the critical dynamics of zipping polymers, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85(3), 031120 CrossRef PubMed.
- I. Bronstein, Y. Israel, E. Kepten, S. Mai, Y. Shav-Tal, E. Barkai and Y. Garini, Transient anomalous diffusion of telomeres in the nucleus of mammalian cells, Phys. Rev. Lett., 2009, 103(1), 018102 CrossRef CAS PubMed.
- E. Kepten, I. Bronshtein and Y. Garini, Ergodicity convergence test suggests telomere motion obeys fractional dynamics, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83(4), 041919 CrossRef CAS PubMed.
- K. Burnecki, E. Kepten, J. Janczura, I. Bronshtein, Y. Garini and A. Weron, Universal algorithm for identification of fractional Brownian motion. a case of telomere subdiffusion, Biophys. J., 2012, 103(9), 1839–1847 CrossRef CAS PubMed.
- E. Kepten, I. Bronshtein and Y. Garini, Improved estimation of anomalous diffusion exponents in single-particle tracking experiments, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87(5), 052713 CrossRef PubMed.
-
O. Vilk, Y. Orchan, M. Charter, N. Ganot, S. Toledo, R. Nathan and M. Assaf, Ergodicity breaking and lack of a typical waiting time in area-restricted search of avian predators, 2022, arXiv:2101.11527.
-
O. Vilk, E. Aghion, T. Avgar, C. Beta, O. Nagel, A. Sabri, R. Sarfati, D. K. Schwartz, M. Weiss, D. Krapf, R. Nathan, R. Metzler and M. Assaf, Unravelling the origins of anomalous diffusion: from molecules to migrating storks, 2022, arXiv:2109.04309.
- J.-H. Jeon and R. Metzler, Analysis of short subdiffusive time series: scatter of the time-averaged mean-squared displacement, J. Phys. A: Math. Theor., 2010, 43(25), 252001 CrossRef.
- J.-H. Jeon, H. M.-S. Monne, M. Javanainen and R. Metzler, Anomalous diffusion of phospholipids and cholesterols in a lipid bilayer and its origins, Phys. Rev. Lett., 2012, 109(18), 188103 CrossRef PubMed.
- J.-H. Jeon, M. Javanainen, H. Martinez-Seara, R. Metzler and I. Vattulainen, Protein crowding in lipid bilayers gives rise to non-Gaussian anomalous lateral diffusion of phospholipids and proteins, Phys. Rev. X, 2016, 6(2), 021006 Search PubMed.
- M. Javanainen, H. Hammaren, L. Monticelli, J.-H. Jeon, M. S. Miettinen, H. Martinez-Seara, R. Metzler and I. Vattulainen, Anomalous and normal diffusion of proteins and lipids in crowded lipid membranes, Faraday Discuss., 2013, 161, 397–417 RSC.
- T. Savin and P. S. Doyle, Static and dynamic errors in particle tracking microrheology, Biophys. J., 2005, 88(1), 623–638 CrossRef CAS PubMed.
- S. C. Weber, M. A. Thompson, W. E. Moerner, A. J. Spakowitz and J. A. Theriot, Analytical tools to distinguish the effects of localization error, confinement, and medium elasticity on the velocity autocorrelation function, Biophys. J., 2012, 102(11), 2443–2450 CrossRef CAS PubMed.
- X. Michalet, Mean square displacement analysis of single-particle trajectories with localization error: Brownian motion in an isotropic medium, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82(4), 041914 CrossRef PubMed.
- X. Michalet and A. J. Berglund, Optimal diffusion coefficient estimation in single-particle tracking, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85(6), 061916 CrossRef PubMed.
- M. Weiss, Resampling single-particle tracking data eliminates localization errors and reveals proper diffusion anomalies, Phys. Rev. E: Stat., Nonlinear, Soft Matter, 2019, 100(4), 042125 CrossRef CAS PubMed.
- M. T. Valentine, P. D. Kaplan, D. Thota, J. C. Crocker, T. Gisler, R. K. Prud'homme, M. Beck and D. A. Weitz, Investigating the microenvironments of inhomogeneous soft materials with multiple particle tracking, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 64(6), 061506 CrossRef CAS PubMed.
- R. Fürth, Die Brownsche Bewegung bei Berücksichtigung einer Persistenz der Bewegungsrichtung. Mit Anwendungen auf die Bewegung lebender Infusorien, Z. Phys., 1920, 2(3), 244–256 CrossRef.
- L. S. Ornstein, On the Brownian motion, Proc. R. Acad. Amsterdam, 1917, 21, 96108 Search PubMed.
-
K. R. Naqvi, The origin of the Langevin equation and the calculation of the mean squared displacement: Let's set the record straight, 2005, arXiv: 0502141.
- A. Nousi, M. T. Søgaard, M. Audoin and L. Jauffred, Single-cell tracking reveals super-spreading brain cancer cells with high persistence, Biochem. Biophys. Rep., 2021, 28, 101120 Search PubMed.
- P.-H. Wu, A. Giri, S. X. Sun and D. Wirtz, Three-dimensional cell migration does not follow a random walk, Proc. Natl. Acad. Sci. U. S. A., 2014, 111(11), 3949–3954 CrossRef CAS PubMed.
- A. A. Sadoon and Y. Wang, Anomalous, non-Gaussian, viscoelastic, and age-dependent dynamics of histonelike nucleoid-structuring proteins in live Escherichia coli, Phys. Rev. E: Stat., Nonlinear, Soft Matter, 2018, 98(4), 042411 CrossRef CAS.
- R. Sarfati and D. K. Schwartz, Temporally anticorrelated subdiffusion in water nanofilms on silica suggests near-surface viscoelasticity, ACS Nano, 2020, 14(3), 3041–3047 CrossRef CAS PubMed.
- L. D. Cairano, B. Stamm and V. Calandrini, Subdiffusive-Brownian crossover in membrane proteins: a generalized Langevin equation-based approach, Biophys. J., 2021, 120(21), 4722–4737 CrossRef PubMed.
- A. S. Bodrova, A. V. Chechkin and I. M. Sokolov, Scaled Brownian motion with renewal resetting, Phys. Rev. E: Stat., Nonlinear, Soft Matter, 2019, 100(1), 012120 CrossRef CAS PubMed.
- S. Janusonis, N. Detering, R. Metzler and T. Vojta, Serotonergic axons as fractional Brownian motion paths: Insights into the self-organization of regional densities, Front. Comput. Neurosci., 2020, 14, 56 CrossRef PubMed.
- W. Wang, A. G. Cherstvy, H. Kantz, R. Metzler and I. M. Sokolov, Time averaging and emerging nonergodicity upon resetting of fractional Brownian motion and heterogeneous diffusion processes, Phys. Rev. E: Stat., Nonlinear, Soft Matter, 2021, 104(2), 024105 CrossRef CAS PubMed.
- A. G. Cherstvy and R. Metzler, Population splitting, trapping, and non-ergodicity in heterogeneous diffusion processes, Phys. Chem. Chem. Phys., 2013, 15(46), 20220–20235 RSC.
- I. Procaccia, Fractal structures in turbulence, J. Stat. Phys., 1984, 36(5), 649–663 CrossRef.
- L. F. Richardson, Atmospheric diffusion shown on a distance-neighbour graph, Proc. R. Soc. London, Ser. A, 1926, 110(756), 709–737 Search PubMed.
- G. K. Batchelor, Diffusion in a field of homogeneous turbulence: Ii. the relative motion of particles, Math. Proc. Cambridge Philos. Soc., 1952, 48(2), 345362 Search PubMed.
- A. Okubo, Dynamical aspects of animal grouping: Swarms, schools, flocks, and herds, Adv. Biophys., 1986, 22, 1–94 CrossRef CAS PubMed.
Footnotes |
† We remind the reader here that for FBM–HDP and SBM–HDP the scaling exponents of the MSD were found to be the products of the respective scaling exponents of the parental processes (see eqn (35) in ref. 93 and eqn (20) in ref. 91, correspondingly; see also Table 1). The position-dependent diffusion coefficient in these processes did not “interfere” with the properties of FBM-related noise and with the time-dependence of the SBM Dα(t). For FBM-SBM, the MSD exponent is the sum of the respective SBM and FBM exponents because both processes “mix” along the time axis introducing temporal changes of the diffusivity and temporal correlation of noise. We note also that for the combination FBM-HDP the TAMSDs scales always as 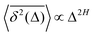 [because the TAMSD of HDPs per se is always linear in Δ], while for SBM-HDP the TAMSD is always linear, [because the TAMSD of HDPs per se is always linear in Δ], while for SBM-HDP the TAMSD is always linear, 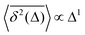 [as the TAMSDs of SBM and HDPs are linear in Δ]. We refer the reader to eqn (36) in ref. 93 and eqn (22) in ref. 91 for these relations, respectively. [as the TAMSDs of SBM and HDPs are linear in Δ]. We refer the reader to eqn (36) in ref. 93 and eqn (22) in ref. 91 for these relations, respectively. |
| ‡ The divergence of the respective MSD integral, as follows from eqn (16) for the displacement increments, is the reason for this. These MSD plateaus indicate a stalling dynamics of the particles: the subdiffusive SBM part progressively slows down the diffusivity and—in addition to that—the anticorrelated successive increments of the particle from parental subdiffusive FBM lead to nearly zero net displacement. The plateaus are realized in the region of FBM and SBM exponents where the cumulative MSD exponent of FBM–SBM is negative. Note also that for pure SBM, e.g., negative MSD exponents are outside of the region of allowed model parameters so that such stalling MSD situations were not observed.55 Technically, however, the simulations of FBM–SBM in this parameter region presents no complications. |
§ The prefactors in the MSDs and TAMSDs above are rather complicated, but the MSD-to-TAMSD ratio—characterizing the respective degree of ergodicity 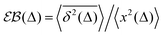 of a given process in this list—contains no prefactors. This ratio is thus a valuable tool to assess the nonergodicity of an unknown dataset of time-series, see Table 1. The absence of coefficients in these TAMSD-to-MSD ratios—proven in Fig. 10 for several values of the exponents of parental SBM and FBM processes—also renders the often tedious analytical calculations of the MSD and [especially] of the TAMSD as separate quantities less important. of a given process in this list—contains no prefactors. This ratio is thus a valuable tool to assess the nonergodicity of an unknown dataset of time-series, see Table 1. The absence of coefficients in these TAMSD-to-MSD ratios—proven in Fig. 10 for several values of the exponents of parental SBM and FBM processes—also renders the often tedious analytical calculations of the MSD and [especially] of the TAMSD as separate quantities less important. |
|
| This journal is © the Owner Societies 2022 |
Click here to see how this site uses Cookies. View our privacy policy here.  ab,
Ralf
Metzler
ab,
Ralf
Metzler
 a and
Andrey G.
Cherstvy
a and
Andrey G.
Cherstvy
 a
a
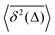 quantifiers—of FBM featuring
quantifiers—of FBM featuring 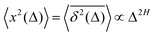 (where H is the Hurst exponent and Δ is the [lag] time) changes in the presence of a power-law deterministically varying diffusivity Dα(t) ∝ tα−1—germane to the process of scaled Brownian motion (SBM)—determining the strength of fractional Gaussian noise. The resulting compound “scaled-fractional” Brownian motion or FBM–SBM is found to be nonergodic, with 〈x2(Δ)〉 ∝ Δα+2H−1 and
(where H is the Hurst exponent and Δ is the [lag] time) changes in the presence of a power-law deterministically varying diffusivity Dα(t) ∝ tα−1—germane to the process of scaled Brownian motion (SBM)—determining the strength of fractional Gaussian noise. The resulting compound “scaled-fractional” Brownian motion or FBM–SBM is found to be nonergodic, with 〈x2(Δ)〉 ∝ Δα+2H−1 and 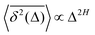 . We also detect a stalling behavior of the MSDs for very subdiffusive SBM and FBM, when α + 2H − 1 < 0. The distribution of particle displacements for FBM–SBM remains Gaussian, as that for the parent processes of FBM and SBM, in the entire region of scaling exponents (0 < α < 2 and 0 < H < 1). The FBM–SBM process is aging in a manner similar to SBM. The velocity autocorrelation function (ACF) of particle increments of FBM–SBM exhibits a dip when the parent FBM process is subdiffusive. Both for sub- and superdiffusive FBM contributions to the FBM–SBM process, the SBM exponent affects the long-time decay exponent of the ACF. Applications of the FBM–SBM-amalgamated process to the analysis of SPT data are discussed. A comparative tabulated overview of recent experimental (mainly SPT) and computational datasets amenable for interpretation in terms of FBM-, SBM-, and FBM–SBM-like models of diffusion culminates the presentation. The statistical aspects of the dynamics of a wide range of biological systems is compared in the table, from nanosized beads in living cells, to chromosomal loci, to water diffusion in the brain, and, finally, to patterns of animal movements.
. We also detect a stalling behavior of the MSDs for very subdiffusive SBM and FBM, when α + 2H − 1 < 0. The distribution of particle displacements for FBM–SBM remains Gaussian, as that for the parent processes of FBM and SBM, in the entire region of scaling exponents (0 < α < 2 and 0 < H < 1). The FBM–SBM process is aging in a manner similar to SBM. The velocity autocorrelation function (ACF) of particle increments of FBM–SBM exhibits a dip when the parent FBM process is subdiffusive. Both for sub- and superdiffusive FBM contributions to the FBM–SBM process, the SBM exponent affects the long-time decay exponent of the ACF. Applications of the FBM–SBM-amalgamated process to the analysis of SPT data are discussed. A comparative tabulated overview of recent experimental (mainly SPT) and computational datasets amenable for interpretation in terms of FBM-, SBM-, and FBM–SBM-like models of diffusion culminates the presentation. The statistical aspects of the dynamics of a wide range of biological systems is compared in the table, from nanosized beads in living cells, to chromosomal loci, to water diffusion in the brain, and, finally, to patterns of animal movements.![[small alpha, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c2.gif) , etc.
, etc.
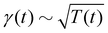 , and the diffusivity given by the time-dependent Einstein relation, D(t) ∼ T(t)/γ(t).
de Expected to be small and SBM-like.
df SBM for massive particles in the case α = 0.
dg Stochastic computer simulations of both massless and massive particles with exponentially time-varying diffusivity,
, and the diffusivity given by the time-dependent Einstein relation, D(t) ∼ T(t)/γ(t).
de Expected to be small and SBM-like.
df SBM for massive particles in the case α = 0.
dg Stochastic computer simulations of both massless and massive particles with exponentially time-varying diffusivity, 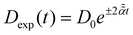 .
dh For massless particles with
.
dh For massless particles with 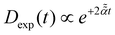 , see eqn (A27) in ref. 94.
di For massless particles with
, see eqn (A27) in ref. 94.
di For massless particles with 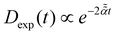 , see eqn (B22) in ref. 94.
dj As in footnote dg, but for the diffusion coefficient
varying logarithmically in time, Dlog(t) = D0
, see eqn (B22) in ref. 94.
dj As in footnote dg, but for the diffusion coefficient
varying logarithmically in time, Dlog(t) = D0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log[t/
log[t/![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) 0].
dk For massless particles, see eqn (C36) in ref. 94.
dl Computer simulations and the theoretical analysis of SBM confined in a parabolic potential, U(x) = kx2/2.
dm Theory and computer simulations of renewal Poissonian-reset SBM with exponentially distributed waiting times between the reset events ψ(t) = re−rt in the model of overdamped Langevin equation [here r is the reset rate].
dn Stochastic computer simulations of the FBM-DD system of equations in the overdamped limit.
do ACF was not shown in ref. 92, but checked by us later via computer simulations [results not shown].
dp Simulations of the underdamped Langevin equation (particle mass m) driven by fractional Gaussian noise.
dq The dispersion of individual TAMSDs for massive FBM decreases with T as for standard FBM, see footnote ds. In addition, for the particles of small-to-intermediate masses at short lag times48 EB(m) ∝ m1 for 0 < H < 3/4 and EB(m) ∝ m4−4H for 1 > H > 3/4.
dr Simulations of the overdamped Langevin equation driven by fractional Gaussian noise and confined to an interval [−L, L]. We refer the reader also to ref. 137, 138 and 221 where non-Gaussian PDFs of boundary-reflected FBM were observed, with depletion and accumulation of particles near the wall for reflected sub- and superdiffusive FBM, respectively.
ds With the spread of the short-lag-time TAMSDs decreasing dramatically for smaller confining intervals. The ergodicity-breaking parameter EB31 at short lag times decreases with the trace length T as EB(T) ∝ 1/T for 0 < H < 3/4 and as EB(T) ∝ 1/T4−4H for 1 > H > 3/4.
dt The same as in ref. 220, but for Poisson-reset FBM.
du For strongly subdiffusive initial FBM the spread of TAMSDs of reset FBM is very small (FBM-like), while for strongly superdiffusive reset FBM it can reach 1–2 decades, see Fig. 2 and 13 of ref. 222. The TAMSD dispersion of frequently reset superdiffusive FBM, in addition, depends reciprocally on the reset rate: the respective ergodicity-breaking parameter31 computed at short lag times decreases as EB(r) ∝ 1/r, see Fig. 4 and 5, and of ref. 222.
dv The same as in ref. 222, but with Poisson-reset FBM considered in the stationary regime.
dw The increment-MSD222 computed in the nonequilibrium steady state equals the mean TAMSD at short times (both for sub- and superdiffusive FBM exponents) as well as at long times in the TAMSD-plateau region, restoring the ergodicity, as compared to the results of ref. 222.
dx Provided the reset process is stationary and the trajectory length is much longer that the relaxation time.
dy Theory and simulations of heavy-tailed subdiffusive CTRWs as subordinated walks on fractal structures (CTRW and RWF). The PDF of waiting times is ψ(τ) ∼ 1/τ1+β, the MSD is 〈x2(Δ)〉 ∝ Δ2Hβ, and the short-lag-time TAMSD growth is
0].
dk For massless particles, see eqn (C36) in ref. 94.
dl Computer simulations and the theoretical analysis of SBM confined in a parabolic potential, U(x) = kx2/2.
dm Theory and computer simulations of renewal Poissonian-reset SBM with exponentially distributed waiting times between the reset events ψ(t) = re−rt in the model of overdamped Langevin equation [here r is the reset rate].
dn Stochastic computer simulations of the FBM-DD system of equations in the overdamped limit.
do ACF was not shown in ref. 92, but checked by us later via computer simulations [results not shown].
dp Simulations of the underdamped Langevin equation (particle mass m) driven by fractional Gaussian noise.
dq The dispersion of individual TAMSDs for massive FBM decreases with T as for standard FBM, see footnote ds. In addition, for the particles of small-to-intermediate masses at short lag times48 EB(m) ∝ m1 for 0 < H < 3/4 and EB(m) ∝ m4−4H for 1 > H > 3/4.
dr Simulations of the overdamped Langevin equation driven by fractional Gaussian noise and confined to an interval [−L, L]. We refer the reader also to ref. 137, 138 and 221 where non-Gaussian PDFs of boundary-reflected FBM were observed, with depletion and accumulation of particles near the wall for reflected sub- and superdiffusive FBM, respectively.
ds With the spread of the short-lag-time TAMSDs decreasing dramatically for smaller confining intervals. The ergodicity-breaking parameter EB31 at short lag times decreases with the trace length T as EB(T) ∝ 1/T for 0 < H < 3/4 and as EB(T) ∝ 1/T4−4H for 1 > H > 3/4.
dt The same as in ref. 220, but for Poisson-reset FBM.
du For strongly subdiffusive initial FBM the spread of TAMSDs of reset FBM is very small (FBM-like), while for strongly superdiffusive reset FBM it can reach 1–2 decades, see Fig. 2 and 13 of ref. 222. The TAMSD dispersion of frequently reset superdiffusive FBM, in addition, depends reciprocally on the reset rate: the respective ergodicity-breaking parameter31 computed at short lag times decreases as EB(r) ∝ 1/r, see Fig. 4 and 5, and of ref. 222.
dv The same as in ref. 222, but with Poisson-reset FBM considered in the stationary regime.
dw The increment-MSD222 computed in the nonequilibrium steady state equals the mean TAMSD at short times (both for sub- and superdiffusive FBM exponents) as well as at long times in the TAMSD-plateau region, restoring the ergodicity, as compared to the results of ref. 222.
dx Provided the reset process is stationary and the trajectory length is much longer that the relaxation time.
dy Theory and simulations of heavy-tailed subdiffusive CTRWs as subordinated walks on fractal structures (CTRW and RWF). The PDF of waiting times is ψ(τ) ∼ 1/τ1+β, the MSD is 〈x2(Δ)〉 ∝ Δ2Hβ, and the short-lag-time TAMSD growth is 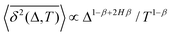 . The TAMSD thus resembles that of FBM–SBM, being nonlinear in Δ and featuring a CTRW-like aging behavior for varying T, with the exponents of the source processes of CTRW and RWF entering the exponent of the MSD of the resulting process also multiplicatively, as in SBM–HDP91 and FBM–HDP.93
dz Diffusion of the massless particles with the diffusivity varying exponentially in space,
. The TAMSD thus resembles that of FBM–SBM, being nonlinear in Δ and featuring a CTRW-like aging behavior for varying T, with the exponents of the source processes of CTRW and RWF entering the exponent of the MSD of the resulting process also multiplicatively, as in SBM–HDP91 and FBM–HDP.93
dz Diffusion of the massless particles with the diffusivity varying exponentially in space, 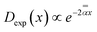 .
ea At long times, after the relaxation of the initial conditions, x0 = x(0).
eb Splitting of the entire ensemble of trajectories into two subpopulations with distinctly different growth of the TAMSDs with the lag time Δ. Scalings are valid both at short and long lag times.
ec Large scatter of the TAMSDs of 2…3 decades for large negative x0 values (in the region of exponentially high diffusivity) and vanishing scatter of the TAMSDs (with very low overall magnitudes) for large positive x0 values.
ed The same as in footnote dz, but for logarithmically varying diffusivity, Dlog(x) ∝ log[(x/
.
ea At long times, after the relaxation of the initial conditions, x0 = x(0).
eb Splitting of the entire ensemble of trajectories into two subpopulations with distinctly different growth of the TAMSDs with the lag time Δ. Scalings are valid both at short and long lag times.
ec Large scatter of the TAMSDs of 2…3 decades for large negative x0 values (in the region of exponentially high diffusivity) and vanishing scatter of the TAMSDs (with very low overall magnitudes) for large positive x0 values.
ed The same as in footnote dz, but for logarithmically varying diffusivity, Dlog(x) ∝ log[(x/![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) )2 + 1].
ee The scatter of 1…4 decades decreases for larger initial positions x0, where the space-variation of the diffusivity Dlog(x) is progressively smaller.
ef Stochastic simulations of the SBM–HDP-related overdamped Langevin equation.
eg A HDP-like ACF is expected, which itself is reminiscent of the ACF of FBM, see Fig. C1 in ref. 67, with the HDP subdiffusive exponent of the MSD 2/(2 −
)2 + 1].
ee The scatter of 1…4 decades decreases for larger initial positions x0, where the space-variation of the diffusivity Dlog(x) is progressively smaller.
ef Stochastic simulations of the SBM–HDP-related overdamped Langevin equation.
eg A HDP-like ACF is expected, which itself is reminiscent of the ACF of FBM, see Fig. C1 in ref. 67, with the HDP subdiffusive exponent of the MSD 2/(2 − ![[small alpha, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c2.gif) ) < 1 corresponding to the Hurst exponent 2H < 1.
eh With the space-time dependence of the diffusivity of the form D(x, t) ∝ |x|
) < 1 corresponding to the Hurst exponent 2H < 1.
eh With the space-time dependence of the diffusivity of the form D(x, t) ∝ |x|![[small alpha, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c2.gif) tα−1 and p(
tα−1 and p(![[small alpha, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c2.gif) ) = 2/(2 −
) = 2/(2 − ![[small alpha, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c2.gif) ). Note that such power-law D(x, t) were proposed, e.g., to rationalize data on diffusion laws in turbulence,90,224 that is one of the first examples of a non-Fickian and anomalously fast 〈x2(t)〉 ∝ t3 relative dispersion for a pair of molecules.225,226 Power-law-like D(x) were also employed to describe animal dynamics.227
ei Stochastic simulations of the overdamped FBM–HDP Langevin equation.
ej Stochastic simulations of the FBM-SBM-related overdamped Langevin equation.
). Note that such power-law D(x, t) were proposed, e.g., to rationalize data on diffusion laws in turbulence,90,224 that is one of the first examples of a non-Fickian and anomalously fast 〈x2(t)〉 ∝ t3 relative dispersion for a pair of molecules.225,226 Power-law-like D(x) were also employed to describe animal dynamics.227
ei Stochastic simulations of the overdamped FBM–HDP Langevin equation.
ej Stochastic simulations of the FBM-SBM-related overdamped Langevin equation.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) n
n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) v
v![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) am
am![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cq
cq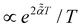 ∝1/Tdi
∝1/Tdi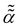 -dependent
-dependent![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) 0]dk
0]dk![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) dx
dx![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ec
ec![[small alpha, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c2.gif) )
)![[small alpha, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c2.gif) )
)![[small alpha, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c2.gif) -dependent
-dependent![[small alpha, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c2.gif) )
)![[small alpha, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c2.gif) ))2H
))2H![[small alpha, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c2.gif) -dependent
-dependent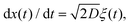
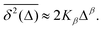
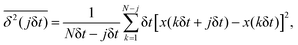
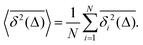
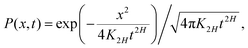
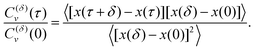
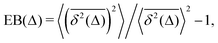


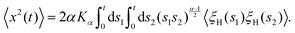
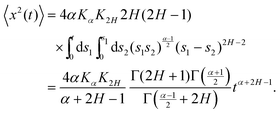

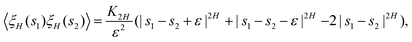
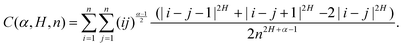
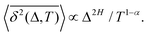

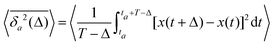

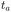 , with the relation (27) shown as the solid curves. The scaling relations at long aging times are given by the dashed lines. Parental FBM and SBM exponents are provided in the legend.
, with the relation (27) shown as the solid curves. The scaling relations at long aging times are given by the dashed lines. Parental FBM and SBM exponents are provided in the legend.![[small alpha, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c2.gif) tα−1 we found that91 the MSD grows as 〈x2(Δ)〉 ∝ Δαp, the TAMSD increases [at short lag times] as
tα−1 we found that91 the MSD grows as 〈x2(Δ)〉 ∝ Δαp, the TAMSD increases [at short lag times] as 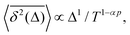 and their ratio is
and their ratio is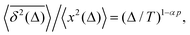
![[small alpha, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c2.gif) ) is the MSD exponent of pure HDPs.67,69 For FBM–HDP we demonstrated that93 〈x2(Δ)〉 ∝ Δ2Hp,
) is the MSD exponent of pure HDPs.67,69 For FBM–HDP we demonstrated that93 〈x2(Δ)〉 ∝ Δ2Hp, 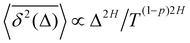 , and
, and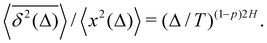
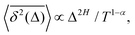 and
and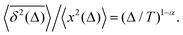
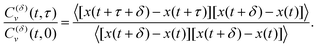









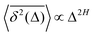 [because the TAMSD of HDPs per se is always linear in Δ], while for SBM-HDP the TAMSD is always linear,
[because the TAMSD of HDPs per se is always linear in Δ], while for SBM-HDP the TAMSD is always linear, 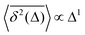 [as the TAMSDs of SBM and HDPs are linear in Δ]. We refer the reader to eqn (36) in ref. 93 and eqn (22) in ref. 91 for these relations, respectively.
[as the TAMSDs of SBM and HDPs are linear in Δ]. We refer the reader to eqn (36) in ref. 93 and eqn (22) in ref. 91 for these relations, respectively.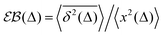 of a given process in this list—contains no prefactors. This ratio is thus a valuable tool to assess the nonergodicity of an unknown dataset of time-series, see Table 1. The absence of coefficients in these TAMSD-to-MSD ratios—proven in Fig. 10 for several values of the exponents of parental SBM and FBM processes—also renders the often tedious analytical calculations of the MSD and [especially] of the TAMSD as separate quantities less important.
of a given process in this list—contains no prefactors. This ratio is thus a valuable tool to assess the nonergodicity of an unknown dataset of time-series, see Table 1. The absence of coefficients in these TAMSD-to-MSD ratios—proven in Fig. 10 for several values of the exponents of parental SBM and FBM processes—also renders the often tedious analytical calculations of the MSD and [especially] of the TAMSD as separate quantities less important.