Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Charge transfer and electrical double layer of an amphiphilic protic ionic liquid in bulk and when confined in nanochannels†
Szilvia
Vavra
 *a,
Elisabet
Ahlberg
*a,
Elisabet
Ahlberg
 b and
Anna
Martinelli
b and
Anna
Martinelli
 a
a
aDepartment of Chemistry and Chemical engineering, Chalmers University of Technology, 412 96 Gothenburg, Sweden. E-mail: anna.martinelli@chalmers.se; Tel: +46 772 3002
bProfessor Emerita: Department of Chemistry and Molecular Biology, University of Gothenburg, Sweden
First published on 23rd September 2022
Abstract
We report the behavior of the protic and surface active ionic liquid octylimidazolium bis(trifluoromethylsulfonyl)imide, [HC8Im][TFSI], in bulk and inside silica nanochannels, at the interface with the conductive substrate indium tin oxide (ITO) upon applied potential. The two distinct cases of the ionic liquid being in contact with a bare ITO substrate and an ITO substrate covered with a thin film of mesoporous silica containing vertically-aligned channel-like pores have been investigated. These correspond to the behavior of the bulk ionic liquid and the ionic liquid confined within nanochannels (approximately 3.5 nm wide and 65 nm long). Broadband dielectric spectroscopy (BDS) and electrochemical impedance spectroscopy (EIS) have been used as the experimental methods, while modelling with equivalent circuits has been applied to evaluate the experimental results. Thus, this study does not only show a functional ionic liquid/silica hybrid material, but also presents an in-depth electrochemical characterization revealing an enhanced specific capacitance at the confined-IL/ITO interface (∼16 μF cm−2) as compared to the case of bulk IL/ITO (∼6 μF cm−2). This suggests that local structure and ion ordering inside the nanochannels of silica are different from that of the bulk ionic liquid, favoring denser ionic packing and a higher specific capacitance at the metal interface.
1 Introduction
Ionic liquids (ILs) are well-known and highly researched for their potential use as electrolytes in various electrochemical and energy relevant devices.1,2 Initially there was a clear distinction between aprotic ionic liquids, studied mainly as electrolytes for capacitors and batteries, and protic ionic liquids (PILs), primarily of interest for fuel cell applications.1 This distinction derived from the larger electrochemical window of aprotic ionic liquids compared to PILs, originating from a fundamental difference in their chemical structure. Notably, PILs possess an acidic proton typically on the cation, which can be reduced at a less negative cathodic potential than the cathodic limit of the aprotic analogues.1,3 Despite this, PILs have recently also attracted interest for use as electrolytes in capacitors, because they are typically cheaper than aprotic ionic liquids, safer than organic solvent-based electrolytes and still provide wider electrochemical windows than aqueous electrolytes.1,3 In addition, it is generally considered that PILs are relatively easy to synthesize.4Thus far, a number of protic and aprotic non-amphiphilic ionic liquids (NAILs) have been investigated for use in supercapacitors, including pure ionic liquids, eutectic ionic liquids and mixtures of ionic liquids and organic solvents. A common asset of ionic liquids is the possibility to operate at high temperatures, given their outstanding thermostability. At low temperatures, on the other hand, ionic liquid based electrolytes suffer from high viscosity and poor contact to the electrodes, a limitation that can be addressed by using eutectic mixtures.5 Among all the ILs available, those based on the imidazolium cation have been considered by a larger extent because of their high ionic conductivity, while pyrrolidinium based ionic liquids bring the advantage of wider, electrochemically stable windows. In general, the high charge density of ILs make them unique among ion-conductive electrolytes but also leads to electrical double layers that can not be described by classical models because ion-ion interactions are not negligible (in fact, they fundamentally determine the physico-chemical properties of ILs) and the ions can not be treated as point charges.1,6–8 Instead, to determine the structure of the double layer theoretical modelling and surface-sensitive methods, such as scanning tunneling microscopy (STM), atomic force microscopy (AFM) and neutron reflectometry (NR), are used.6,8–11 Ionic liquids can show overscreening effects at low potentials, meaning that the first layer of counter-ion contains more counter-charge than is on the electrode, leading to a double layer structure that consists in an alternation of counter-ion-rich and co-ion-rich layers until the bulk structure is recovered. The overscreening effect is more dominant at lower potentials and the alternating structure disappears at higher potentials when the first adsorbed layer can not contain enough counter-ions to balance the electrode charge and further accumulation of the counter-ions proceeds, which is also known as the crowding regime.6–8
The interest in surface-active ionic liquids (SAILs) for use in supercapacitors is very recent, by date covering only a few aprotic ionic liquids studied for their distinct ion distribution at the electrode/electrolyte interface which is, however, not fully understood yet. SAILs are attractive electrolytes also because they do not absorb moisture, as many NAILs that display a high ionic conductivity do. Even though there is a very limited number of publications, it has already been proven for different SAIL-based systems that the capacitance can depend on applied voltage, temperature, and geometry of the electrochemical cell.7,8,10,12 Su et al. have shown experimentally that the differential capacitance measured as a function of the applied voltage shows a ‘bell’-shaped curve in the case of ionic liquids with relatively short chains (PMIPF4 and BMIPF4) and a ‘camel’-shaped curve in the case of an ionic liquid with a longer chain (OMIPF4).10 The authors discuss that these capacitance maxima are associated to changes in the ions’ structuration at the electrode surface. The first maximum appears at around −0.6 V [vs. Pt] for ionic liquids with both shorter and longer alkyl chains, which is associated to the formation of stripe-like double-row adsorbates of assembled imidazolium cations showing polar/apolar nanosegregation with the alkyl chains pointing towards each other. By increasing the voltage, only OMIPF4 shows a second maximum at −1.6 V [vs. Pt] that has been assigned to the order-disorder structure transformation.10 In the study published by Mao et al.,12 a distinct temperature dependence of capacitance measured with SAIL electrolytes is revealed, suggesting that SAILs can outperform NAILs as capacitor electrolytes at elevated temperatures. In this particular case, the apolar group was attached to the anion of the ionic liquid, [C4C1Im][AOT] and [C4C1Im][CnSO4] (n = 8, 10, 12) showing a higher capacitance than [C4C1Im][BF4] at temperatures above 130 °C.
With respect to the geometry of the electrochemical setup in the case of SAILs, the effect of confinement on capacitance has been studied only by computational approaches using classical density functional theory.13 In this study by Yang et al.,13 the capacitance was predicted for nanoporous electrodes having 4 nm wide pores coupled with imidazolium ionic liquids with different chain lengths as the electrolyte, i.e. [CnC1Im][TFSI] with n = 2, 4, 6. The results revealed that the ionic liquids with a longer chain showed a higher differential capacitance at low potentials (i.e. smaller than ±0.5 V). With respect to confinement effects, experimental studies have been done only on NAILs, investigating mainly carbon derived porous electrodes since they enable an efficient use of the high specific surface area during reversible ion adsorption.14,15 For conventional electrolytes (i.e. salts in water or organic solvents), it has been shown that the pore size of the porous electrode plays an important role in the resulting capacitance, an effect that was explained by a sieving effect at pore sizes close to that of the adsorbed ions. This behaviour was later also confirmed for the ionic liquid [EMIM][TFSI] that, in association with a carbide-derived carbon electrode, displayed capacitances between 7 and 13 μF cm−2, with a maximum at a pore size of 0.7 nm. This value coincides with the size of the ionic liquid's both ions, i.e. the EMIM cation and the TFSI anion.14 This very important work illustrates that, for maximizing the capacitance of supercapacitors, the electrode/electrolyte couple must be chosen with attention to the size of both ions and pores. A general concept valid for all types of porous electrodes is that their structure should promote facile ion diffusion, ideally enabling unobstructed ion transport for high power density and providing extremely high, ion-accessible surface areas for high capacity and thus energy density.6,15 With this insight, mesoporous carbon nanospheres have been prepared that, in association with the neat ionic liquid [EMIM][BF4], could achieve a specific areal capacitance of 9 μF cm−2 in the case of 3.5 nm wide pores.16
IL/silica hybrid materials have primarily been considered as model systems for studying the ionic motion within nanoscaled domains, since mesoporous silica is a versatile material that can be prepared to result in particles or thin films with a wide range of well-defined pore sizes. In addition, these silica structures can be chemically functionalized to suit diverse purposes. From a practical point of view, the confinement of ionic liquids in the pores of an inorganic matrix can be exploited to prevent leakage of the ionic liquid when used in a device. Indeed, the practical use of ionic liquid-based organic-inorganic hybrid materials in electrochemical devices relies on a profound understanding of how an unrestricted or even enhanced ion diffusion can be achieved under confinement. In particular, the pore morphology of silica thin films with vertically-aligned and straight nanochannels with a well-defined pore size is an interesting strategy to achieve thinner membranes with reduced ohmic losses.‡
In this work, we present the electrochemical behavior of an amphiphilic protic ionic liquid, as a bulk liquid and when confined in the nanochannels of a mesoporous silica film. More specifically, we have studied the protic ionic liquid octylimidazolium-bistriflimide, [HC8Im][TFSI], in direct contact with an ITO (indium titanium oxide) electrode. We have also investigated how this protic ionic liquid behaves in proximity to the ITO electrode in the case of a deposited thin film of mesoporous silica containing vertical nanochannels approximately 65 nm long and about 3.5 nm wide. The absolute and specific capacitances measured are discussed with reference to the available literature, with emphasis on nanoscale effects. Broadband dielectric spectroscopy (BDS) and electrochemical impedance spectroscopy (EIS) have been used as complementary experimental methods while equivalent circuit modelling has been used to evaluate the experimental results. The ionic liquid octylimidazolium-bistriflimide has been selected for two main reasons; the first is that it has a relatively long tail (octyl) and hence provides an opportunity to better understand the role of amphiphillicity at electrode interfaces while the second is that it is protic and as such it is considered to be a safe and cheaper alternative to aprotic analogues. The TFSI anion is simply already known to contribute to a lower viscosity, compared to other conventional anions.
2 Experimental
2.1 Materials
The studied protic ionic liquid, [HC8Im][TFSI], was custom made and provided by IoLiTec (Ionic Liquids Technologies GmbH) (>97% of purity; less than 0.03% of H2O content). [HC8Im][TFSI] is an amphiphilic ionic liquid, in particular the [HC8Im] cation carries an octyl group as the side chain and has a protic NH site on the imidazolium head, while the TFSI anion contributes to hydrophobicity. For the study of [HC8Im][TFSI] in the confined state, a nanoporous silica thin film – containing permeable, distinct, and vertically aligned channels – was prepared and used. The detailed description of the synthesis procedure based on the work of Despas et al.17 and the characterization18 of the film using IR (Infrared spectroscopy), GISAXS (grazing-incidence small-angle X-ray scattering) and CV (cyclic voltammetry) are presented in Section SI of the ESI† (Fig. S1–S5). More precisely, from this characterization we can conclude that the synthesis, based on the EASA (electrochemically assisted self assembly) method, resulted in an intact and insoluble mesoporous film, which covered the entire area of the electrode. In addition, based on the work of Goux et al.19 the thickness of the film was estimated to be 65 nm. Since the nanochannels result from a templating procedure using CTAB (followed by extraction), the diameter of the nanochannels was estimated to be 3.5 nm, based on the work of Gibaud et al.20 Finally, from pure geometrical considerations, the porosity was estimated to be 0.57 (more details are available in Section SI of the ESI†).2.2 Broadband dielectric spectroscopy
Broadband dielectric spectroscopy (BDS) was employed to measure dielectric and conductive properties of the protic ionic liquid in its neat, bulk state. A Broadband Dielectric Spectrometer from Novocontrol GmbH was used. The protic ionic liquid was placed between two gold-plated brass electrodes with a diameter of 5 mm and a thickness of 3 mm. The thickness of each sample was controlled to be 1 mm using a spacer of silica. Measurements were conducted in the frequency range between 10−1 and 107 Hz, whereas the temperature was varied between 168 and 428, during both heating and cooling scans (more precisely from 293 K to 173 K on first cooling, from 168 K to 428 K on subsequent heating, and back to 298 K on final cooling, at temperature steps of 5 K). The temperature was controlled using a nitrogen gas cryostat with a stability of ±0.5 °C.2.3 Cyclic voltammetry
To identify the electrochemically stable potential window of the ionic liquid [HC8Im][TFSI], a cyclic voltammetric (CV) measurement was performed using a three-electrode cell. This cell was based on a platinum coil as the counter electrode, an Ag wire as the pseudo-reference electrode, and a bare ITO plate as the working electrode that was in contact with the ionic liquid over a circular area of 0.196 cm2. The voltammetric curves were recorded with a Gamry Interface 1000E potentiostat between −1.3 V and 2.1 V (vs. Ag) at a scan rate of 100 mV s−1.2.4 Electrochemical impedance spectroscopy
Electrochemical impedance spectroscopy (EIS) measurements were conducted in a similar three-electrode cell as the one used for CV measurements. The counter electrode was a platinum coil and a Ag wire was used as the pseudo-reference electrode, while two different working electrodes were used to be in contact with the ionic liquid over the circular area of 0.196 cm2. These were; (i) “ITO + film”, i.e. an ITO substrate with a thin film of mesoporous silica deposited on it (to investigate the electrochemical behaviour of the ionic liquid confined within nanochannels) and (ii) “ITO”, i.e. a bare and neat ITO electrode used as a reference (to study the behavior of the bulk ionic liquid). The impedance spectra were recorded covering the frequency range from 10−2 Hz to 106 Hz, at room temperature and using a Gamry Interface 1000E potentiostat. The sinusoidal potential perturbation had an amplitude of 10 mV (rms), which is much smaller than the potential window of electrochemical stability recorded for the ionic liquid investigated (see Fig. 1). The impedance measurements were made at the open circuit voltage, which was measured prior to performing the EIS measurements and was found to be −60 mV for the ITO + film electrode and +40 mV for the bare ITO electrode (Fig. S6, ESI†). Equivalent circuit modelling was used to fit the obtained Bode and Nyquist plots and thus estimate the electrochemical properties of the studied materials. The goodness of the fit model is reflected by the value of χ2, which was lower than 0.02. | ||
| Fig. 1 Cyclic voltammetric curve recorded for the protic ionic liquid [HC8Im][TFSI] over the potential range from −1.3 V to 2.1 V, at a scan rate of 100 mV s−1. | ||
3 Results and discussion
3.1 Potential window of electrochemical stability
In view of the electrochemical studies intended to be performed on the protic ionic liquid [HC8Im][TFSI], cyclic voltammetry was first used to identify a potential window with no contributions from faradaic currents. The recorded CV curve shown in Fig. 1 covers the potential range from −1.3 V to +2.1 V and reveals a stability range of ca. 2.7 V. The cathodic reaction with an onset at ca. −1.0 V is attributed to the reduction of the imidazolium cation, while the anodic reaction starting at ca. 1.75 V results from the oxidation of the TFSI anion. No other faradaic currents are captured within the whole investigated window. In general, protic ionic liquids display a slightly narrower window of electrochemical stability than their aprotic counterparts; a distinction recently presented and discussed for a series of new imidazolium based protic ionic liquids of the [TFSI]− and [TFI]− anions.43.2 Ionic conductivity in the bulk ionic liquid
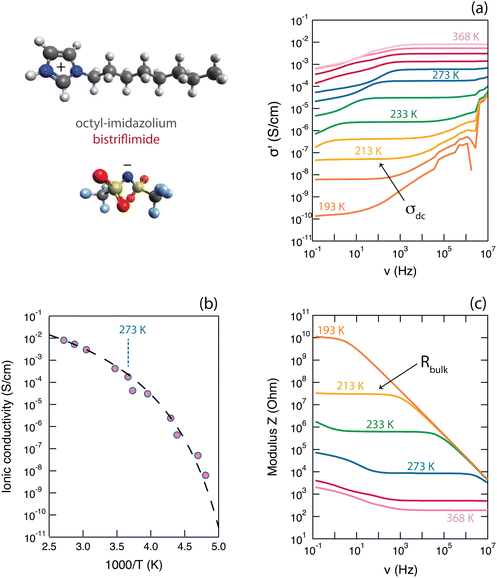
The ionic conductivity of the protic ionic liquid [HC8Im][TFSI] in the bulk state was investigated by use of broadband dielectric spectroscopy (BDS), which allows measuring over wide temperature windows. As a note, this ionic liquid does not show first-order phase transitions, i.e. melting/crystallization, during the temperature scans by differential scanning calorimetry (DSC), but rather behaves as a glass forming liquid with a glass transition temperature, Tg, around −81 °C.21Fig. 2 shows selected properties of [HC8Im][TFSI], captured during BDS measurements, as a function of temperature.The real part of the ionic conductivity, σ′(ν) (which is related to the dielectric function through σ*(ω) = iωε0ε*(ω), where ε = ε′ − iε′′ and ω is the angular frequency), is given in Fig. 2a. This property shows a strong frequency dependence, with plateau values (σdc) that increase with temperature and cover wide frequency ranges (for the temperature of 233 K, a whole three decades of frequency). The fact that these plateau values do represent phenomena of ionic conduction is supported by the behaviour of the phase angle, Φ(ν), being zero in the corresponding frequency range (see Fig. S7a, ESI†). It is interesting to observe that, as can be better seen for temperatures well above 273 K, the values of σ′(ν) tend to smear out towards the lowest frequencies, which is a direct effect of the upturn of ε′(ν),22i.e. the real part of permittivity shown in an own plot in Fig. S7b (ESI†) (further details on the behavior of ε′(ν) are presented in Section SII of the ESI†). This can be associated to the occurrence of an additional mechanism other than the conductive motion in the bulk, which is also manifested by a deviation from zero of the phase angle (Fig. S7a, ESI†). At higher frequencies, the real part of the ionic conductivity, σ′(ν), takes values greater than those of the plateau showing, again, a strong frequency dependence; see e.g. the σ′(ν) curves in Fig. 2a for temperatures of 233 K or lower. An upturn of σ′(ν) here corresponds to constant values in ε′′(ν) and ε′(ν) (Fig. S7b, ESI†) and is normally associated to relaxational processes; for the case of ionic liquids, these may be the reorientational motions of dipolar ions.23
The increase with temperature of the σdc values, is summarized in Fig. 2b in the representation of an Arrhenius plot. The increase of σdc with T is as expected for samples in which the transport of ions is thermally activated, while the curved trend followed by the experimental data is typical for liquid electrolytes, including ionic liquids, in which ions move primarily by the vehicular mechanism. In such liquids, charges move mainly as ionic molecular species at a rate that is determined by the diffusivity of the molecules, hence by the viscosity of the liquid.23 In these cases, the empirical VFT (Vogel–Fulcher–Tamman) equation σdc = σ0·e−(B)/(T−T0) can be used to fit the experimental data, which can generate an estimation of the ionic conductivity at infinite temperatures (σ∞, for T → ∞) as well as a pseudo-activation energy, Ea, for ionic conduction (where Ea = kB·B). The σdc(T) data shown in Fig. 2b have been fitted using the VFT relation, imposing that at Tg (Tg = −81 °C, as found from previous DSC experiments21) the ionic conductivity is 10−15 S cm−1.23 This approach returned the following fitting parameters: a value for T0 equal to 168 K, Ea equal to 0.07 eV (associated to a B value of 812 K) and a σ∞ value of 0.43 S cm−1. These values for the fitting parameters are in good agreement with those previously reported in the literature for other imidazolium based ionic liquids,23,24 even though these previous works focused on aprotic cationic structures rather than on protic ones. Moreover, in one of our recent works focused on a series of protic ionic liquids of the imidazolium cation, we could show that the activation energy, Ea, increases with the length of the alkyl chain attached to the cation, reaching a maximum value around the length of an octyl.21
The modulus of impedance, |Z|(ν), a direct output property of the BDS experiment that is derived from the relation Z*(ν) = U*(ν)/I*(ν), also shows a strong frequency dependence, with the plateau values (when observed within the detected frequency window) representing the resistance of the bulk liquid phase. This value decreases with increasing temperature, as expected, and is shown in Fig. 2c. The overall trend, with a plateau region followed by increasing values as frequency is decreased, is typical of a system showing a capacitive behaviour at lower frequencies and primarily resistivity at higher frequencies. In support for the latter, is the fact that the plateau values of |Z|(ν) are observed in frequency ranges of constant σ′(ν) values, thus representing the resistance to ionic motion in the bulk ionic liquid. For the temperature of 293 K (i.e. 20 °C), |Z| takes the value of 2.6 kΩ.
3.3 Enhanced capacitance in nanoconfinement
After having characterized the conductive properties of the bulk protic ionic liquid [HC8Im][TFSI], we had interest in investigating its behaviour when confined within the space of nanochannels. With this purpose, electrochemical impedance spectroscopy (EIS) experiments were performed with the bulk ionic liquid in direct contact with (i) a bare ITO surface, acting as the working electrode, and (ii) an ITO surface on which a thin film of mesoporous silica had been deposited, containing vertically aligned channel-like pores with an estimated diameter of 3.5 nm, as illustrated in Fig. 3. The EIS measurements were performed using a conventional three-electrodes cell, as described in the experimental section. These experiments were also repeated using two electrodes only, by connecting the reference and the counter electrodes together, which however showed no differences at all (see Fig. S8 in Section SIII of the ESI†). Hence, for simplicity and conciseness, only the results from the three-electrodes cell, obtained at room temperature, are shown and discussed.Within the frequency window 10−2–106 Hz, the Nyquist plot of Z′′ versus Z′ does not show full semi-circles, and the values obtained for the ITO covered with the thin silica film are lower, Fig. 4a. The frequency dependence of the modulus of Z, |Z|(ν), is shown in Fig. 4b in a log(|Z|)–log(ν) plot, revealing a linear behaviour below 101 Hz and constant values above 102 Hz. As in the case of the BDS results, the plateau in the high-frequency region corresponds to the resistance in the bulk phase of the ionic liquid,§ while the slope is associated to phenomena occurring at the electrode/liquid interface. The phase angle recorded for the two cases investigated (which are bare ITO and ITO + film) is shown in Fig. 4c, also as a function of frequency. The dependence of |Z| on frequency has been modelled using equivalent circuits, illustrated in Fig. 5, and the fitted parameters are presented in Table 1. Using equivalent circuit modelling to describe the dielectric properties of ionic liquids, has been a recent subject of debate. In fact, depending on the specific response measured, but also the frequency range investigated, a constant phase element circuit (CPE) or a distributed RC equivalent circuit may be used.22,23,25
| Method | Working electrode | R bulk [kΩ] | R pore [kΩ] | Q pore [Ω−1 s] (α) | R dl [MΩ] | Q dl [Ω−1 s] (α) | C sdl [μF cm−2] |
|---|---|---|---|---|---|---|---|
| EIS | ITO | 6.80 ± 0.022 | 89.0 ± 17 | 1.89 ± 0.008 × 10−6 | ∼6 | ||
| (0.91 ± 0.002) | |||||||
| EIS | ITO + film | 4.50 ± 0.008 | 94.43 ± 8 | 5.59 ± 0.16 × 10−6 | 8.33 ± 0.32 | 3.96 ± 0.007 × 10−6 | ∼16 |
| (0.90 ± 0.014) | (0.84 ± 0.007) |
The equivalent circuit describing the bare ITO surface in contact with the protic ionic liquid [HC8Im][TFSI], can be simplified to only include a bulk resistance Rbulk of 6.8 kΩ, and a constant phase element Qdl (1.89 × 10−6 Ω−1 sα; α = 0.91) in parallel with a polarization resistance Rdl of 89 MΩ (see also the values reported in Table 1). Then, based on the treatment of the surface distribution of time constants as presented by Hirschorn et al.,26 the effective capacitance Cdl could be estimated using the relation
 | (1) |
| Cdl = Q1/αdl·(Rbulk)(1−α)/α | (2) |
This is comparable to other values reported in the literature. For example, Jitvisate et al.27 have directly measured the electrical double layer capacitance of a series of ionic liquids in contact with a working electrode of polycrystalline platinum, obtaining values between 6 and 7.5 μF cm−2 for potential values very close to the open circuit voltage. Also, a comprehensive investigation of the electrochemical properties of a series of protic ionic liquids has been reported by Lu et al.,28 albeit these were based on cations and anions different from [HC8Im]+ and [TFSI]−. In that work, the authors report a double layer capacitance of 15.3 μF cm−2, using a glassy carbon (GC) working electrode, for the protic ionic liquid (Et2NH)((BuO)2POOH)) which has a relatively high viscosity (200 cP). For comparison, the protic ionic liquid [HC8Im][TFSI] at focus in this work has a viscosity of 155 cP.21 Another relevant study is the one proofing the use of a (PET)ITO–ionic liquid–ITO(PET) system for sensing changes in mechanical pressure (PET is polyethylene terephthalate).29 In this study, the ionic liquid used was 1-butyl-3-methylimidazolium bistriflimide (more precisely, a filter paper imbibed with this ionic liquid) and the measured capacitance varied between ca. 4 × 10−7 F for an applied pressure of 10 kPa and ca. 3 × 10−6 F for an applied pressure of 20 kPa. One should consider, however, that the maximum surface area reported in this work was of 1 cm2, while only a fraction of this total area was in fact active during the application of mechanical pressure. As an example, if one third of the total area is considered to be in contact with the ITO surface at sensing mechanical pressures (see Fig. 1 in ref. 29) a specific capacitance of ca. 3 μF cm−2 is roughly estimated.
Furthermore, by assuming the value of 12.16 for the dielectric constant (εPIL) of the protic ionic liquid [HC8Im][TFSI],¶ as predicted in the extensive work of Rybinska-Fryca et al.,32 the electrostatic screening length d (i.e. a characteristic length scale defined in the classical theory as the Debye length, λD) of the electric double layer at the ITO interface can be estimated using the relation
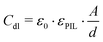 | (3) |
During the evaluation of the EIS spectra obtained with the ITO electrode covered by a film of mesoporous silica, it was found that additional elements had to be included in the modelling equivalent circuit to get fits of good quality. The need of including additional elements in the equivalent circuit, and thus of time constants, is also visible in the frequency dependence of the phase angle, Fig. 4c, which only for the case of ITO with the deposited thin mesoporous film shows a deviation from the angle of −80°. First, an equivalent circuit was considered that based on the work of Hirschorn et al.26 could model the surface and normal distribution of time-constants. In our material, this distribution originates from the presence of the thin film covering the whole electrode surface and its channel-like pores normally oriented with respect to the flat surface of the electrode; this first equivalent circuit and the corresponding fitting parameters are presented in Fig. S9 (Section SIV of the ESI†). More precisely, two capacitive elements were set in parallel to each other to describe the additive contribution of silica (labelled “oxide” in Fig. S9, ESI†) and of the in-pore ionic liquid phase (labelled “pore” in Fig. S9, ESI,† and in Fig. 5) that together constitute the IL-filled porous film of silica; see also the bottom scheme in Fig. 5. From the viewpoint of the ionic liquid, the bulk phase, the in-pore phase and the phase at closest proximity to the ITO interface (labelled “dl” in Fig. S9, ESI,† and in Fig. 5) are considered to be in series. Such a distinction is reasonable given that the electric double layer has dimensions much smaller than the full length of the nanochannels (ca. 65 nm). In addition, we find that the capacitive contribution of the bulk silica is extremely low (0.0046 μF)|| and its resistance extremely high (7.5 GΩ; see also the additional information in the ESI,† Section SIV)** indicating that the ‘oxide’ component can be neglected and the equivalent circuit reduced to the one shown in the bottom scheme of Fig. 5. The goodness of the fitting can be appreciated from Fig. S10 of the ESI.† Hence, in the following discussion only the label “pore” will be used while the label “oxide” will be left behind. By modelling |Z|(ν) with such an equivalent circuit, the following fitting parameters were found: a bulk resistance Rbulk of 4.5 kΩ, a pore resistance Rpore of 94 kΩ in parallel with the CPE element Qpore (5.59 × 10−6 Ω−1 sα; α = 0.90), and a polarization resistance Rdl of 8.3 MΩ in parallel with the CPE element Qdl (3.96 × 10−6 Ω−1 sα; α = 0.84). These values are also reported in Table 1.
The lower value for Rdl in the ITO + film case is not clear to us at this stage but is unlikely associated to a more facile reduction of the imidazolium cation, because the amplitude of the potential used during the EIS experiment (10 mV) is much smaller than the potential window of electrochemical stability measured for this ionic liquid (Fig. 1). The high value for the in-pore resistance (Rpore = 94 kΩ), on the other hand, can be rationalized considering that it describes all the ions inside the nanochannels, including those at the core of the channel and those (the cations) interacting with the negatively charged silica walls. Several studies have demonstrated decreased mobility of ionic liquids in the confining space of hydrophilic silica pores, which has been explained to be a consequence of strong interactions between the pore wall and the ions, in addition to tortuosity effects.36–38††
For example, for the ionic liquid [C6mim][TFSI] confined in the 10 nm wide pores of mesoporous silica particles, the molar conductivity was about one order of magnitude lower than for the bulk liquid. However, by functionalization of the silica pore walls with tributyl groups, a high ionic conductivity was recovered.40 In that work, it was also verified that the type of surface effects and thus of molecular orientation at the silica interface, was the same for protic and aprotic ionic liquids, since this is driven by electrostatic interactions albeit hydrogen bonds may also contribute. These results, that is the strong effect of surface modification on the mobility of a nanoconfined ionic liquid, are in perfect agreement with those presented by Bou-Malham et al.,41 who have measured a tenfold increase in viscosity (as compared to the bulk liquid) for [C4 mim]-based ionic liquids confined in 3.5 nm wide channels of mica. By contrast, methyl-functionalized mica resulted in bulk-like viscosity despite the nanoconfinement.
Based on the results presented in this work, and on those already available in the literature, the ionic organization at the entrance of, and inside, the nanochannels grown over ITO might be as illustrated in Fig. 6. Since the silica pore walls are slightly negatively charged (by having surface –O− and –OH groups) it is expected that an interfacial layer of immobile ions is formed, that consists of imidazolium cations with their aromatic head flatly oriented towards the silica wall and their alkyl chain pointing towards the center of the pores (interfacial, immobile cations). Compared to these cations, the anions are located further away from the silica surface.37,42 This is analogous to the local structure demonstrated by solid state NMR spectroscopy in ionogels prepared with the ionic liquid 1-hexyl-3-methylimidazolium-TFSI42 as well as to the local structure revealed by MD simulations for 1-butyl-3-methylimidazolium-TFSI at close proximity to silica walls.43
Since protic ionic liquids are promising candidates for use in proton conducting membranes and their confinement in porous matrices is crucial to bring them in the solid state for an easier use in electrochemical devices, it is worth mentioning that there are means to decrease the high in-pore resistance that we find. As discussed above, a straightforward method is the hydrophobization of the silica walls, since it is known that the ionic species of an ionic liquid close to a hydrophobic surface (like modified silica or carbon based tubes) experience weaker interactions and display higher mobility.36,37,40,44 Furthermore, the thin films with straight, vertically aligned channel-like pores with a narrow pore-distribution that we discuss in this work are of high scientific interest since they enable studying the dynamics of truly and exclusively in-pore ionic species (unlike the case of ionogels or IL-filled mesoporous silica particles for which it can be difficult to experimentally discriminate between ions residing inside and outside the pores).45
The effective double layer capacitance Cdl at the in-pore IL/ITO interface has been determined to be 1.87 μF, from the CPE element Qdl and by applying eqn (1) with the obtained fitting parameters.26 This can in turn be expressed as a specific capacitance considering that only 57% of the total ITO area is exposed to the ionic liquid phase during the EIS measurement, leading to a value of 16 μF cm−2.‡‡ This result is notable, since it indicates that in the case of the mesoporous thin film deposited over the ITO substrate the specific capacitance is higher than for the case of the bare ITO surface. To the best of our knowledge, this is the first time that a specific capacitance is experimentally measured for a surface active ionic liquid in nanoconfinement. Nevertheless, we report an empirical observation, which requires further dedicated studies to be fully understood. However, assuming the molecular organization within the pores described above (which is supported by multiple congruent studies),36–38 it is possible that the reduced pore width and the presence of proximate oriented and immobile octyl chains induce the ions to adopt a more vertical orientation at the ITO interface, with a consequent increase in ion density. Alternatively, the in-pore pressure that is likely different from the one experienced in the bulk liquid phase may squeeze the first layer of adsorbed ions resulting in enhanced double layer capacitance.
Capacitance increases for ionic liquids in a confined space (mainly non-amphiphilic and aprotic ionic liquids) have been reported by several authors, for porous electrodes with unimodal and well-defined pore widths.14,16,46,47 In general, the capacitance values that we obtain are in fair agreement with those measured for other more conventional ionic liquids; for instance the ionic liquid ethyl-methylimidazolium-TFSI that, when residing within carbon nanopores about 1 nm wide, results in an areal capacitance of ca. 7 μF cm−2.14 In yet another work, reporting the synthesis of mesoporous carbon nanospheres, the specific capacitance in the case of the ionic liquid ethyl-metylimidazolium-BF4 was measured to be 9 μF cm−2, when mesopores with a diameter of 3 nm were considered.16 In this context, it must be mentioned that studying the behaviour of ionic liquids in the nano-space of electrodes, for applications in supercapacitors, is a current hot topic of research. On one hand, ionic liquids offer wider windows of electrochemical stability than conventional organic electrolytes, hence greater values of energy density (E = 0.5·CV2)1 and, on the other hand, the size effect of nanopores in which the ionic liquid resides is yet not completely understood.48 As for the latter issue, experimental results have shown that when the size between two flat capacitive electrodes is decreased in the nanometer range, the specific capacitance can increase;14 while DFT calculations performed to follow up on this result have evidenced an oscillating effect of the specific capacitance when the spacing between the electrodes approaches the size of the ions.48 However, compared to these previous computational and experimental works, that have exclusively considered flat nano-domains orthogonal to the applied electric field, our system differs by having the nano-channels vertically oriented with respect to the polarized electrode (ITO) as well as by considering a protic ionic liquid whose [HC8Im]+ cation is bulkier than, for instance, the ethyl-methylimidazolium cation previously and commonly investigated. In any case, these precedent studies have reported ion-exclusion effects as well as denser ionic packing at the electrode interface for the case of ionic liquids in nanodomains, which may have similarities to our observation of an increased specific capacitance.
4 Conclusions
In this work, the electrochemical properties of the protic and surface active ionic liquid [HC8Im][TFSI] have been investigated in bulk and inside silica nanochannels. Cyclic voltammetric results show that [HC8Im][TFSI] has a sufficiently wide window of electrochemical stability, i.e. 2.7 V, while broadband dielectric spectroscopy reveals that ion conduction is dominated by the vehicular mechanism. The behaviours of bulk and nano-confined [HC8Im][TFSI] have been compared by impedance spectroscopic measurements using a three-electrode cell. The ionic liquid was either in direct contact with a flat, neat ITO electrode or with an ITO electrode covered with a thin film of mesoporous silica containing vertically-aligned channel-like pores that run through the entire thickness of the film. The equivalent circuit modelling of the EIS results shows a higher resistance of the ionic liquid inside the hydrophilic silica nanochannels, which reflects hindered diffusion due to a strong interaction of cations with the negatively charged silica wall. However, an enhanced specific capacitance is observed at the in-pore IL/ITO interface, which could possibly be explained by an orientational change that favors ion packing or a more compact first ionic layer. This positive effect is attributed to the nanoscale of the pores concomitant to the ability of this ionic liquid to self-assemble. More studies are desired to better understand our observations. In particular, it will be very interesting to verify the potential dependence of the specific capacitance for the ITO + film system, extending to higher voltages where SAILs are expected to outperform non-amphiphilic ionic liquids.12Author contributions
The authors have contributed to this article in the following way. Szilvia Vavra has synthesized the thin films grown over the ITO substrate, and performed experiments to confirm their mesoporous structure with vertically aligned nanochannels. She has performed all impedance spectroscopic measurements, and reported the results. Elisabet Ahlberg has modeled the experimental data with appropriate equivalent circuits. Anna Martinelli has supervised the whole project from idea to realization and finalized the layout of the figures. All authors have contributed actively to the discussion of the results and to the writing of the entire article.Conflicts of interest
The authors state that there are no conflicts to declare.Acknowledgements
The authors acknowledge the financial support from the Swedish Foundation for Strategic Research (SSF, FFL-16 0092 grant). The Chalmers Materials Analysis Laboratory (CMAL) is also acknowledged for providing instrumental time to perform GISAXS measurements. The authors thank Dr Iqbaal Abdurrokhman for helping with the setup of the BDS measurements.References
- S. Pan, M. Yao, J. Zhang, B. Li, C. Xing, X. Song, P. Su and H. Zhang, Front. Chem., 2020, 8, 1–18 CrossRef PubMed.
- A. S. Amarasekara, Chem. Rev., 2016, 116, 6133–6183 CrossRef CAS PubMed.
- T. Stettner and A. Balducci, Energy Storage Mater., 2021, 40, 402–414 CrossRef.
- T. Stettner, F. C. Walter and A. Balducci, Batteries Supercaps, 2019, 2, 55–59 CrossRef CAS.
- B. Lin, S. Cheng, L. Qiu, F. Yan, S. Shang and J. Lu, Chem. Mater., 2010, 22, 1807–1813 CrossRef CAS.
- M. Salanne, Top. Curr. Chem., 2017, 375, 1–25 CrossRef CAS PubMed.
- M. V. Fedorov and A. A. Kornyshev, Chem. Rev., 2014, 114, 2978–3036 CrossRef CAS.
- M. Z. Bazant, B. D. Storey and A. A. Kornyshev, Phys. Rev. Lett., 2011, 106, 6–9 CrossRef.
- C. Rodenbucher, Y. Chen, K. Wippermann, P. M. Kowalski, M. Giesen, D. Mayer, F. Hausen and C. Korte, Int. J. Mol. Sci., 2021, 22, 12653 CrossRef.
- Y. Su, J. Yan, M. Li, M. Zhang and B. Mao, J. Phys. Chem. C, 2013, 117, 205–212 CrossRef CAS.
- K. Akutsu-Suyama, M. Cagnes, K. Tamura, T. Kanaya and T. Darwish, Phys. Chem. Chem. Phys., 2019, 21, 17512–17516 RSC.
- X. Mao, P. Brown, C. Červinka, G. Hazell, H. Li, Y. Ren, D. Chen, R. Atkin, J. Eastoe, I. Grillo, A. A. Padua, M. F. Costa Gomes and T. A. Hatton, Nat. Mater., 2019, 18, 1350–1357 CrossRef CAS PubMed.
- J. Yang, C. Lian and H. Liu, Chem. Eng. Sci., 2020, 227, 115927 CrossRef CAS.
- C. Largeot, C. Portet, J. Chmiola, P. L. Taberna, Y. Gogotsi and P. Simon, J. Am. Chem. Soc., 2008, 130, 2730–2731 CrossRef CAS PubMed.
- H. Zhong, F. Xu, Z. Li, R. Fu and D. Wu, Nanoscale, 2013, 5, 4678–4682 RSC.
- X. Q. Zhang, A. H. Lu, Q. Sun, X. F. Yu, J. Y. Chen and W. C. Li, ACS Appl. Energy Mater., 2018, 1, 5999–6005 CrossRef.
- C. Despas, N. A. Vodolazkaya, J. Ghanbaja and A. Walcarius, J. Solid State Electrochem., 2015, 19, 2075–2085 CrossRef CAS.
- S. Vavra, N. Vilà, A. Lotsari, A. Walcarius and A. Martinelli, Microporous Mesoporous Mater., 2020, 110407 CrossRef.
- A. Goux, M. Etienne, C. Emmanuel Aubert, E. Lecomte, J. Ghanbaja and A. Walcarius, Chem. Mater., 2009, 731–741 CrossRef CAS.
- A. Gibaud, A. Baptiste, D. A. Doshi, C. J. Brinker, L. Yang and B. Ocko, Europhys. Lett., 2003, 63, 833–839 CrossRef CAS.
- I. Abdurrokhman, K. Elamin, O. Danyliv, M. Hasani, J. Swenson and A. Martinelli, J. Phys. Chem. B, 2019, 123, 4044–4054 CrossRef CAS PubMed.
- S. Emmert, M. Wolf, R. Gulich, S. Krohns, S. Kastner, P. Lunkenheimer and A. Loidl, Eur. Phys. J. B, 2011, 83, 157–165 CrossRef CAS.
- P. Sippel, P. Lunkenheimer, S. Krohns, E. Thoms and A. Loidl, Sci. Rep., 2015, 5, 1–8 Search PubMed.
- J. Leys, M. Wübbenhorst, C. Preethy Menon, R. Rajesh, J. Thoen, C. Glorieux, P. Nockemann, B. Thijs, K. Binnemans and S. Longuemart, J. Chem. Phys., 2008, 128, 064509 CrossRef.
- I. N. Jiya, N. Gurusinghe and R. Gouws, Electronics, 2018, 7, 268 CrossRef CAS.
- B. Hirschorn, M. E. Orazem, B. Tribollet, V. Vivier, I. Frateur and M. Musiani, Electrochim. Acta, 2010, 55, 6218–6227 CrossRef CAS.
- M. Jitsivate and J. Seddon, J. Phys. Chem. Lett., 2018, 9, 126–131 CrossRef PubMed.
- X. Lu, G. Burrell, F. Separovic and C. Zhao, J. Phys. Chem. B, 2012, 116, 9160–9170 CrossRef CAS PubMed.
- Q. Yang, Z. Zhang, X. G. Sun, Y. S. Hu, H. Xing and S. Dai, Chem. Soc. Rev., 2018, 47, 2020–2064 RSC.
- H. Weingartner, J. Mol. Liq., 2014, 192, 185–190 CrossRef CAS.
- C. Wakai, A. Oleinkova, M. Ott and H. Weingarten, J. Phys. Chem. B, 2005, 109, 17028–17030 CrossRef CAS PubMed.
- A. Rybinska-Fryca, A. Sosnowska and T. Puzyn, J. Mol. Liq., 2018, 260, 57–64 CrossRef CAS.
- A. Smith, A. Lee and S. Perkin, J. Phys. Chem. Lett., 2016, 7, 2157–2163 CrossRef CAS PubMed.
- L. Nichols and J. Thorp, Trans. Faraday Soc., 1970, 66, 1741–1747 RSC.
- J. Anderson and G. Parks, J. Phys. Chem., 1968, 72, 3662–3668 CrossRef CAS.
- C. Iacob, J. R. Sangoro, P. Papadopoulos, T. Schubert, S. Naumov, R. Valiullin, J. Kärger and F. Kremer, Phys. Chem. Chem. Phys., 2010, 12, 13798–13803 RSC.
- M. D. Elola and J. Rodriguez, J. Phys. Chem. C, 2019, 123, 3622–3633 CrossRef CAS.
- M. N. Garaga, M. Persson, N. Yaghini and A. Martinelli, Soft Matter, 2016, 12, 2583–2592 RSC.
- Y. Uchida, T. Matsumoto, T. Akita and N. Nishiyama, J. Mater. Chem. C, 2015, 3, 6144–6147 RSC.
- M. N. Garaga, L. Aguilera, N. Yaghini, A. Matic, M. Persson and A. Martinelli, Phys. Chem. Chem. Phys., 2017, 19, 5727–5736 RSC.
- I. Bou-Malham and L. Bureau, Soft Matter, 2010, 6, 4062–4065 RSC.
- M. Nayeri, M. T. Aronson, D. Bernin, B. F. Chmelka and A. Martinelli, Soft Matter, 2014, 10, 5618–5627 RSC.
- G. Ori, F. Villemot, L. Viau, A. Vioux and B. Coasne, Mol. Phys., 2014, 112, 1350–1361 CrossRef CAS.
- M. N. Garaga, V. Dracopoulos, U. Werner-Zwanziger, J. W. Zwanziger, M. Maréchal, M. Persson, L. Nordstierna and A. Martinelli, Nanoscale, 2018, 10, 12337–12348 RSC.
- S. Vavra, K. Elamin, L. Evenäs and A. Martinelli, J. Phys. Chem. C, 2021, 125, 2607–2618 CrossRef CAS.
- P. Wu, J. Huang, V. Meunier, B. G. Sumpter and R. Qiao, ACS Nano, 2011, 5, 9044–9051 CrossRef CAS PubMed.
- Z. Lian, H. Chao and Z. G. Wang, ACS Nano, 2021, 15, 11724–11733 CrossRef CAS.
- D. E. Jiang, Z. Jin and J. Wu, Nano Lett., 2011, 11, 5373–5377 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp01634f |
| ‡ Indeed, thinning proton exchange membranes (PEMs) is a ubiquitous challenge for material scientists in fuel cells research. |
| § The small difference in the values found for Rbulk for the cases of bare ITO and ITO + Film is most likely due to a small change in the cell setup, i.e. a possibly different distance established between the working and counter electrodes during the EIS measurements. |
| ¶ Determining the static dielectric constant of ionic liquids experimentally is not an easy task due to strong polarization effects in the low-frequency domain of the dielectric spectrum, which has been a subject of debate.22,30,31 The BDS instrumentation used by us in this work was not judged appropriate to estimate such a value (since the static dielectric constant of ionic liquids should be evaluated at frequencies between 100 MHz and 5 GHz),30 hence we have used a predicted value instead.32 |
| || The capacitance of a silica gel was measured to be in the range 125–155 pF, only slightly depending on the concentration of –OH groups.34 |
| ** The electrical resistivity values of silica and ITO are 1012 Ω cm35 and 10−4 Ω cm respectively, reflecting the insulating (silica) and conductive (ITO) property of these two materials. Moreover, the resistivity of a silica gel increases slightly with the concentration of –OH groups.35 |
| †† Surface effects become less important and over-screened by the bulk-like behavior of the molecules not directly interacting with the pore walls in the case of very large pores. At the same time, functionalization of the pore walls may have effects on the local molecular structuration, as was for instance demonstrated for the ionic liquid [C16mim][PF6] confined in cylindrical pores functionalized with CTAB. For this system, and for temperatures at which the smectic phase is adopted, the anisotropic character of ionic conductivity was enhanced compared to the case of bulk liquid.39 |
| ‡‡ And 29 μF cm−2 if Rbulk is replaced by Rpore in the expression of eqn (1). In any case, given the Qdl and α values retrieved from the modelling equivalent circuit, the specific (areal) capacitance in the case of the deposited film is always larger than for the bare ITO, as revealed by the simulated functions for variable values of the term within parenthesis in eqn (1), Fig. S11 in Section IV of the ESI.† |
| This journal is © the Owner Societies 2022 |