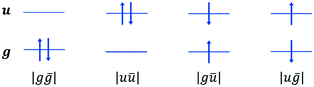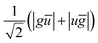Environmental effects on the singlet fission phenomenon: a model Hamiltonian-based study

Abstract

In the screening of compounds for singlet fission, the relative energies of the constitutive units are decisive to fulfil the thermodynamic rules. From a model Hamiltonian constructed on the local spin states of an active chromophore and its environment, it is suggested that embedding greatly influences the energy differences of the active monomer spin states. Even in the absence of charge transfer, the field generated by a singlet environment produces an increase of the [E(S₁) − E(S₀)]/[E(T₁) − E(S₀)] critical ratio by up to 6% as compared to the one of a free chromophore. Besides, variations are observed when the intimate electronic structure of the singlet environment is modified. This propensity towards singlet fission is even more pronounced (10%) when the environment is switched to the triplet state. Finally, the embedding is likely to reverse the spin state ordering in the limit of vanishing atomic orbital overlaps. Despite its simplicity, the model stresses the importance of the environment spin nature in the quest for singlet fission candidates, and more generally in spectroscopy analysis.

---

Introduction

In the field of photophysics, singlet fission continues to attract much interest from many fundamental and applied research groups.^1–4 Back to its origin in organic compounds, the conversion of excited singlets into pairs of correlated triplets was revived from its utility in the design of efficient solar cells.⁵ This phenomenon differs from competing inter-system crossing or multiple excitation generation in inorganic semiconductors where conversion into vibrational energy occurs. Alternant acene-like hydrocarbons are natural target systems; for the excited singlet–triplet, splitting is sizable and connected to a large exchange integral (ca. 1 eV) involving the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO), so-called frontier orbitals^6–8 (see Scheme 1). Following the three-class classification of organic chromophores, many theoretical efforts have been dedicated to the positioning of the relevant energy levels (first excited singlet S₁ and triplet T₁ states) to foresee the chemical conditions to stabilize the first excited singlet state S₁. Since the T₁–S₁ energy difference is almost insensitive to the acene size, the so-called energy level matching condition of the singlet fission E(S₁) − E(S₀) > 2[E(T₁) − E(S₀)] is attainable by a reduction of the S₁–S₀ energy gap. This is the thermodynamic condition.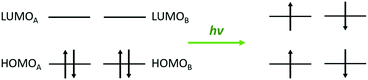

Scheme 1 Schematic description of the singlet fission phenomenon from the frontier orbital diagram of a class I compound built on A and B chromophores.

In the meantime, the kinetics of the spin-allowed transition was depicted based on electron transfer or energy transfer theories.^9–11 A critical parameter that governs singlet fission is the coupling between neighbouring units.^12,13 Following this concern, computational studies have also much contributed to the definition of a well-balanced coupling strength and to the identification of the best chromophores.^14–18 While too strong an interaction is not favourable for the triplets to separate and move apart, too weak a coupling reduces the rate of singlet fission.^19,20 The role of excimer formation in singlet fission still deserves particular attention.^21,22 Its formation is a critical step for the generation of pairs of triplets and the energy positioning is traditionally approximated from the monomer values.^23–29 Irrespective of the level of theory, wave function-based theory or density functional theory (WFT and DFT, respectively) calculations, such an approximation is considered to be satisfactory for molecular crystals and more questionable in covalent dimers.^30–34

However, one may wonder how much the immediate environment of a given monomer may modulate its spectroscopy. In the design of singlet fission compounds, we felt that attention should be paid to the molecular description, and to go beyond the free monomer description. Practically, one would like to stress, if sizable, the influence of the electronic structure of a monomer spin state (so-called environment) on the relative energies of a given neighbouring unit (so-called active chromophore). The importance of the environment is known and was reported in complex systems for which local and collective effects are likely to compete.^35,36 Prime examples are spin-crossover compounds where the magnetic response can be modulated under crystallization conditions.³⁷ Evidently, the appropriate definition of the spin nature of the environment in ab initio calculations calls for particular care, not to mention the system size which might make it not tractable from quantum chemistry methods. Our intention is to set the environment characteristics to foresee its impact on the energies of the active chromophore. For a neighbouring closed-shell chromophore, a single configuration might be an acceptable approximation and one strategy would be to freeze the molecular orbitals (MOs) to mimic such a closed-shell environment. However, the presence of a neighbouring open-shell chromophore (e.g. triplet) is more problematic since the electronic structures and spin values of the sub-parts cannot be decided in standard quantum chemistry calculations. Indeed, in a non-relativistic description, the total spin is a good quantum number and any calculation produces spin eigen-states of the full system.

Therefore, a model Hamiltonian built on the local spin states of the two H₂ sub-systems was considered to complement the current views on molecules with potential applications for singlet fission. A much more sophisticated environment may enrich the description at a cost of a less comprehensive analysis. The model aims at capturing the environment effects using this minimal picture consisting of a single H₂ molecule. The relevance of traditional approaches based on isolated chromophores can be examined from this simple H₄ model. Following the standard crystal-field theory that relies on a closed-shell structure of the coordination sphere, we wanted to trace the importance of the spin value of the environment and the resulting modifications of the Coulomb and exchange contributions.

Description of the model

Theoretical inspections greatly concentrate on the HOMO and LUMO frontier orbitals.^38–41 The S₀–S₁ transition in popular class I singlet fission chromophores is reasonably described by a HOMO–LUMO electronic transition.⁴² Thus, the model Hamiltonian is constructed on local spin states of a pair of interacting H₂-like molecules (i.e. two electrons in two MOs). Indeed, the most promising candidates are slip-stacked chromophores where the direct mechanism can be optimized.^36,43–45 Therefore, charge transfer states which might become competitive were not included in our description by simply constraining the number of electrons on the active chromophore and the environment, a realistic picture when L ≫ l (see Fig. 1). The possibility of mediation by the charge-transfer mechanism was explored elsewhere in covalent dimers.^11,31,32 For preliminary inspections, singlet fission is limited to the direct coupling mechanism. In summary, the construction is nothing but a projection of the configuration interaction space into a selection of configurations that preserve the electron numbers and spin states on the subunits.

Fig. 1 Model system built on the active (A) and environment (E) chromophores with relevant geometrical parameters l = 0.74 Å (fixed intra-chromophore distance) and L (inter-chromophore distance).

The bonding (g_A and g_E) and anti-bonding (u_A and u_E) local MOs of the active (A) and environment (E) subunits (see Fig. 1) are easily constructed from a minimal 1s atomic orbital (AO) basis set i_A, j_A, i_E and j_E. Then, the configurations are combined into configuration state functions Γ_A and Γ_E to span the tensorial product space Γ_A⊗Γ_E. All matrix elements were first analytically calculated as functions of mono-electronic and bi-electronic integrals expressed in the minimal AOs basis set. Evidently, the model Hamiltonian parametrization could be used. However, we preferred to introduce the chemical details of the structure, as any ab initio approach would do, to possibly extend to any realistic singlet fission chromophore. All integrals are distance-dependent and numerically available from the PSI4 suite of programs⁴⁶ (see Fig. 1).

By construction, the MOs of the active subunit are not orthogonal to the MOs of the environment. In fused-benzene compounds, orthogonality between the carbon-2p AOs becomes numerically acceptable in the π–π interaction regime characterized by ∼2.5 times the carbon–carbon π-bond distance (1.43 Å). Indeed, the 2p carbon AOs σ-overlap is calculated as 0.01 for L = 3.6 Å. At shorter separation distances, the AO overlaps can no longer be neglected, similarly is the hydrogen–1s AO overlap in the H₄-model system for distances smaller than L ∼ 2.5l ∼ 1.9 Å. Following the procedure described by Slater,⁴⁷ the matrix elements were corrected to account for non-orthogonality. Four overlaps must be a priori evaluated between the MOs localized on the A and E subunits. However, S_gAuE = S_uAgE = 0 for symmetry reasons.

All determinants are built in the M_S = 0 manifold and the energies are compared to the ones obtained in the absence of the environment subunit. Within our approach restricted to the direct coupling mechanism (i.e. no charge transfer), the singlet state environment S_E is constructed as a contraction on the three configuration state functions (see Scheme 2):

Such a contraction allows one to (i) generate a given electronic structure that is not affected by the presence of the active chromophore (frozen embedding picture) and (ii) extend our model to non-symmetric active-environment pairs. By varying the coefficients in the contraction, the nature of the environment can be selectively modified to account for the aggregate formation and to reproduce different regimes. In contrast, the electronic structures of active chromophore singlets S_A,0, S_A,1 and S_A,2 are fully relaxed as linear combinations of |g_Aḡ_A|, |u_Aū_A| and configurations:

Scheme 2 Schematic representation of the closed-shell |gḡ|, |uū|, and the open-shell |gū|, |uḡ|, M_s = 0 configurations on a dimer. The singlet and triplet configuration state functions are and , respectively.

Let us mention that a S_E environment is readily achieved by freezing the occupied and virtual localized MOs of the environment in an ab initio procedure. Evidently, the triplet state consists of a single configuration , the energy of which is immediately calculated in the S_E field.

A similar inspection was then performed when the environment is switched into a triplet state T_E. However, some particular care must be taken since a global triplet state emerges from the local triplet states T_A and T_E. Such a triplet can mix in with the triplet state built from the 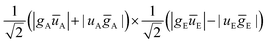configuration (i.e. S_A⊗T_E). The eigenvector analysis evidences the contributions of the singlet and triplet in the active chromophore.

In this study, we are primarily concerned with the impact of the environment spin structure on the energy level matching conditions. Thus, the objective is to examine the sensitivity of the low-energy state ordering of an active chromophore A in the field generated by a L-distant environment E. Therefore, the condition for singlet fission reads ρ = [E(S_A,1) − E(S_A,0)]/[E(T_A,1) − E(S_A,0)] > 2.

Results and discussion

Let us first concentrate on the active chromophore energy levels in the field of a singlet state environment S_E. In the M_s = 0 manifold, the S_A⊗S_E space is spanned by three determinants. A single determinant built as T_A⊗S_E defines the local triplet state energy on the active chromophore. Overall, three singlet states S_A,i and one single triplet T_A,1 energy are evaluated in the presence of a frozen singlet environment. All energies depend on the inter-dimer distance L as well as on the contraction coefficients e₁, e₂, and e₃ (see eqn (1)).

In the long-distance regime (L > 3.5 Å), the H₂ monomers do not interact, all integrals becoming vanishingly small. The asymptotic limit of the critical ratio ρ = [E(S_A,1) − E(S_A,0)]/[E(T_A,1) − E(S_A,0)] (ca. 1.60) corresponds to the value that is usually reported from calculations performed on a single chromophore. However, ρ is very sensitive to the presence of a surrounding partner (see Fig. 2(a)), even in this simplified picture. The nature and amplitude of the dipole–dipole interactions are responsible for this differentiating effect. For interacting π-systems, the ratio between the intramolecular carbon–carbon distance and the packing separation is ca. 2.5. In analogy, one expects that, below L ∼ 2.5l ∼ 1.9 Å, charge transfer contributions should be included between 1s hydrogen AOs and our simplified view would be invalidated. However, even at this low-distance limit, ρ is increased up to 1.70 (Fig. 2(a)).

Fig. 2 (a) Critical ratio ρ = [E(S_A,1) − E(S_A,0)]/[E(T_A,1) − E(S_A,0)] in the fields of the singlet environment as a function of the inter-dimer distance L. The singlet environment S_E consists of a contraction e₁ = 0.85, e₂ = 0.45, and e₃ = 0.27. (b) Upper panel: Variations of the low-lying triplet state energies (eV) for a triplet environment. The ground state consists of a pure singlet on A, and its energy is used as a reference. The excited triplet states are labelled with the dominant contributions on A. The intra-chromophore distance l is set to the equilibrium H₂ distance to 0.74 Å. The ρ value variations are given in the lower panel.

As soon as the environment spin state is switched to the triplet, the picture is somewhat modified. Irrespective of the inter-dimer distance, the ground state singlet (reference energy in Fig. 2(b)) is a pure singlet on A dominated by the |g_Aḡ_A| configuration. As mentioned before, the excited triplet states result from the mixing between different spin-coupling schemes (S_A⊗T_E and T_A⊗T_E). From our numerical inspections, these states labelled as T_A,1 and S_A,1 in Fig. 2(b) are largely dominated (ca. 98% at L = 2 Å) by the triplet and singlet on A, respectively. Thus, these energies can be compared to the ones obtained from an isolated chromophore picture for which ρ = 1.60. Not only does the S_A,1–T_A,1 energy difference increases with the decreasing inter-chromophore distance, but also the singlet fission thermodynamic condition ρ > 2 is fulfilled for L values close to 1.9 Å (see Fig. 2(b), lower panel). For comparison, the triplet–singlet energy difference and the ρ value for L = 2.5 Å were calculated as 14.8 eV and 1.61 at the CAS[4,4]SCF level in a minimal 1s AOs basis set, respectively.⁴⁸ In this regime, the contracted view of the model (see Fig. 2(b) upper panel) reproduces not only the CASSCF energy splitting but also the asymptotic value ρ = 1.60.

Despite its simplicity, our model stresses that the presence of the environment significantly modifies the spin state ordering. As expected, the field generated by the environment depends on its spin state, giving rise to an enhanced singlet fission inclination in the presence of a triplet environment T_E.

The observed critical regime of 1.9–2.6 Å in the H₄ model agrees with the traditional range of the manifestation of π–stacking interactions in conjugated organic molecules up to a scaling factor based on the intra- and inter-molecular distances. In conclusion, the ρ variations for such hydrogen-based model compounds are in accordance with what is found for carbon-based compounds.

It is known that realistic synthetic systems for singlet fission are acene-like and our model may look at first over-simplistic. First, the hydrogen 1s AO σ-overlap is 0.66 for l = 0.74 Å, whereas the π-overlap between the 2p carbon AOs is reduced down to 0.19 for a typical carbon–carbon distance. Then, the density of states increases with the number of carbon atoms in polyacene. Together, these elements favour a reduction of the HOMO–LUMO gap within the chromophore. In the π-stacking acene arrangements, the inter-chromophore interactions are governed by negligible 2p carbon AO σ-overlap (0.01 for L = 3.6 Å). For all these reasons, we felt that setting all overlap values to zero (intra- and inter-chromophores) in our model would allow in making the contact with synthetic compounds and in analysing the leading mechanisms at work in the hierarchization of the spin states. Importantly, all the one-electron and two-electron energy integrals were maintained as numerically evaluated from PSI4. Different singlet environment structures were generated by varying the amplitudes e₁, e₂ and e₃ (see Fig. 3).

Fig. 3 Singlet and triplet state energies (eV) as a function of the inter-dimer distance L in the vicinity of a contracted singlet environment S_E with the increasing weight on the |u_Eū_E| configuration. (a) e₁ = 1 and e₂ = e₃ = 0, (b) e₁ = 0.91 and e₂ = e₃ = 0.29, and (c) e₁ = 0.85, e₂ = 0.45, and e₃ = 0.27. All AO overlaps are set to zero. Following the Tanabé–Sugano representation, the ground state energy E_GS is taken as a reference. Its nature changes for a characteristic L distance which is marked by a vertical dashed line. Horizontal dashed lines represent the spectroscopy of an isolated chromophore.

In the asymptotic limit, the spectroscopy evidently does not depend on the environment singlet structure and exhibits a singlet ground state S_A,0. Nevertheless, the absolute energy of the latter is sensitive to the structure of the environment and the ρ value is modulated. By inspecting the different contributions, the leading one arises from the two-electron integral (i_Aj_A, i_Ej_E)†. This a slowly decaying 1/L integral that destabilizes |g_Aḡ_Ag_Eḡ_E| and |u_Aū_Au_Eū_E| configurations, whereas it stabilises |u_Aū_Ag_Eḡ_E| and |g_Aḡ_Au_Eū_E| configurations. As a consequence, the energy of the S_A,0 state increases in the presence of a mono-determinantal environment |g_Eḡ_E| (e₁ = 1, e₂ = e₃ = 0). Conversely, it is lowered for the |u_Eū_E| environment (e₁ = 0, e₂ = 1, e₃ = 0). For symmetry reasons, the energy of S_A,0 is not sensitive to the open-shell environment (e₁ = e₂ = 0, e₃ = 1). This state of affairs changes for the excited triplet T_A,1 and singlet S_A,1 states. Indeed, the dominant integral (i_Aj_A, i_Ej_E) has no impact on their energies and the S_A,1–T_A,1 splitting remains constant and equal to 2K_gAuA (exchange integral). As a result of the long-range 1/L potential, the critical ratio ρ is still sensitive to the environment even for L = 20 Å where ρ_|gEḡE| = 1.70, ρ_|uEūE| = 1.53 and .

For L ca. 5 Å, the ρ > 2 regime is reached, in sharp contrast with what was observed previously. When L is further reduced, the energy of the S_A,0 state continuously increases, and eventually the nature of the ground state switches to high-spin T_A,1. Such an observation somewhat reconsiders the traditional picture “strong field-low spin’’ in metal ion coordination compounds. Interestingly, the switching L distance is shifted to lower values (see Fig. 3 where all AO overlaps are set to zero) as the weight of the |u_Eū_E| configuration increases. This is a reflection of the competing effects of the |g_Eḡ_E| and |u_Eū_E| configurations on the stabilization of the S_A,0 state.

The examined electronic structure is evidently reminiscent of the one in cyclobutadiene. As seen in Fig. 3, the ground state of the four-electron four-orbital system is the singlet whatever the structure of the singlet environment. This observation is in agreement with the pseudo Jahn–Teller effect manifestation: the triplet square structure is unstable and a distortion to the rectangular geometry leads to a singlet ground state. In contrast, our constrained wave function description favours a triplet ground state (T_A,1⊗S_E) even for strong deviations from the square geometry. The contracted structure of the E part and the resulting absence of charge transfers are responsible for this behaviour. However, our model highlights the significant impact of the electronic structure of the environment.

Conclusions

The importance of the spin structure of the environment on the energy states of a two-electron active chromophore was examined by building up a model Hamiltonian that affords the splitting into local spin states. The active chromophore state ordering is much affected in the presence of a triplet or a singlet environment. As a consequence, the critical ratio ρ = [E(S₁) − E(S₀)]/[E(T₁) − E(S₀)] defined on the excitation energies of the first singlet and triplet excited states may reach the lower bound ρ = 2 value for the singlet fission condition to occur. A simplified description that neglects overlaps leads to an even deeper modification. The ground state is switched from the low-spin singlet to the high-spin triplet when the distance between the active chromophore and the environment is ca. 2.5 Å. This critical distance is governed by the structure of the singlet state environment acting as a field that controls the spin state hierarchisation. Even in the absence of charge transfers between the subunits, our model suggests that spin-dependent environment effects should be taken into account. The simplicity of the H₄-based model brings some insights and means of interpretation that should be transferable in the theoretical quest of singlet fission candidates.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

P. R. would like to thank the French minister for the financial support of his PhD grant. We would like to dedicate this scientific work to Professor Bernard Bigot, an enlightening mentor, who passed away in the course of revision of this contribution.

Notes and references

1. D. Casanova, Chem. Rev., 2018, 118, 7164–7207.
2. M. B. Smith and J. Michl, Chem. Rev., 2010, 110, 6891–6936.
3. M. B. Smith and J. Michl, Annu. Rev. Phys. Chem., 2013, 64, 361–386.
4. O. Ostroverkhova, Chem. Rev., 2016, 116, 13279–13412.
5. M. C. Hanna and A. J. Nozik, J. Appl. Phys., 2006, 100, 074510.
6. K. Aryanpour, A. Shukla and S. Mazumdar, J. Phys. Chem. C, 2015, 119, 6966–6979.
7. R. E. Merrifield, J. Chem. Phys., 1961, 34, 1835–1839.
8. C. J. Bardeen, Annu. Rev. Phys. Chem., 2014, 65, 127–148.
9. T. C. Berkelbach, M. S. Hybertsen and D. R. Reichman, J. Chem. Phys., 2013, 138, 114103.
10. D. Beljonne, H. Yamagata, J. L. Brédas, F. C. Spano and Y. Olivier, Phys. Rev. Lett., 2013, 110, 226402.
11. B. Alam, A. F. Morrison and J. M. Herbert, J. Phys. Chem. C, 2020, 124, 24653–24666.
12. A. F. Morrison and J. M. Herbert, J. Phys. Chem. Lett., 2017, 8, 1442–1448.
13. N. V. Korovina, S. Das, Z. Nett, X. Feng, J. Joy, R. Haiges, A. I. Krylov, S. E. Bradforth and M. E. Thompson, J. Am. Chem. Soc., 2016, 138, 617–627.
14. J. C. Johnson and J. Michl, Top. Curr. Chem., 2017, 375, 80.
15. E. Pradhan, J. N. Bentley, C. B. Caputo and T. Zeng, ChemPhotoChem, 2020, 4, 5279–5287.
16. S. Sardar, J. Mol. Graphics Modell., 2020, 98, 107608.
17. L. Shen, Y. Chen, X. Li and C. Li, J. Mol. Graphics Modell., 2016, 66, 187–195.
18. M. Zhang, Z. Hua, W. Liu, H. Liu, S. He, C. Zhu and Y. Zhu, J. Mol. Model., 2020, 26, 32.
19. H. L. Stern, A. Cheminal, S. R. Yost, K. Broch, S. L. Bayliss, K. Chen, M. Tabachnyk, K. Thorley, N. Greenham, J. M. Hodgkiss, J. Anthony, M. Head-Gordon, A. J. Musser, A. Rao and R. H. Friend, Nat. Chem., 2017, 9, 1205–1212.
20. N. V. Korovina, J. Joy, X. Feng, C. Feltenberger, A. I. Krylov, S. E. Bradforth and M. E. Thompson, J. Am. Chem. Soc., 2018, 140, 10179–10190.
21. X. Feng and A. I. Krylov, Phys. Chem. Chem. Phys., 2016, 18, 7751–7761.
22. C. B. Dover, J. K. Gallaher, L. Frazer, P. C. Tapping, A. J. Petty, M. J. Crossley, J. E. Anthony, T. W. Kee and T. W. Schmidt, Nat. Chem., 2018, 10, 305–310.
23. D. Padula, Ö. H. Omar, T. Nematiaram and A. Troisi, Energy Environ. Sci., 2019, 12, 2412–2416.
24. O. El Bakouri, J. R. Smith and H. Ottosson, J. Am. Chem. Soc., 2020, 142, 5602–5617.
25. D. S. Patil, K. C. Avhad and N. Sekar, Comput. Theor. Chem., 2018, 1138, 75–83.
26. Y. Gawale and N. Sekar, J. Photochem. Photobiol., B, 2018, 178, 472–480.
27. K. J. Fallon, P. Budden, E. Salvadori, A. M. Ganose, C. N. Savory, L. Eyre, S. Dowland, Q. Ai, S. Goodlett, C. Risko, D. O. Scanlon, C. W. M. Kay, A. Rao, R. H. Friend, A. J. Musser and H. Bronstein, J. Am. Chem. Soc., 2019, 141, 13867–13876.
28. M. Baranac-Stojanović, J. Org. Chem., 2019, 84, 13582–13594.
29. Z. Liu, L. Lin, Q. Jia, Z. Cheng, Y. Jiang, Y. Guo and J. Ma, J. Chem. Inf. Model., 2021, 61, 1066–1082.
30. J. C. Johnson, A. J. Nozik and J. Michl, Acc. Chem. Res., 2013, 46, 1290–1299.
31. C. M. Mauck, Y. J. Bae, M. Chen, N. Powers-Riggs, Y.-L. Wu and M. R. Wasielewski, ChemPhotoChem, 2018, 2, 223–233.
32. E. A. Margulies, C. E. Miller, Y. Wu, L. Ma, G. C. Schatz, R. M. Young and M. R. Wasielewski, Nat. Chem., 2016, 8, 1120–1125.
33. T. Zeng, J. Phys. Chem. Lett., 2016, 7, 4405–4412.
34. V. I. Minkin, A. G. Starikov and A. A. Starikova, J. Phys. Chem. A, 2021, 125, 6562–6570.
35. L. Wang, Y. Olivier, O. V. Prezhdo and D. Beljonne, J. Phys. Chem. Lett., 2014, 5, 3345–3353.
36. N. Renaud, P. A. Sherratt and M. A. Ratner, J. Phys. Chem. Lett., 2013, 4, 1065–1069.
37. J. Olguín and S. Brooker, Coord. Chem. Rev., 2011, 255, 203–240.
38. M. E. Sandoval-Salinas and D. Casanova, ChemPhotoChem, 2021, 5, 282–293.
39. A. Thomas, C. Ji, B. Siddlingeshwar, P. U. Manohar, F. Ying and W. Wu, Phys. Chem. Chem. Phys., 2021, 23, 1050–1061.
40. K. Tanaka, D. Sakamaki and H. Fujiwara, Chem. – Eur. J., 2021, 27, 4430–4438.
41. X. Feng, A. V. Luzanov and A. I. Krylov, J. Phys. Chem. Lett., 2013, 4, 3845–3852.
42. E. A. Buchanan, Z. Havlas and J. Michl, in Advances in Quantum Chemistry, ed. J. R. Sabin and E. J. Brändas, Academic Press, 2017, vol. 75, pp. 175–227.
43. K. Kolata, T. Breuer, G. Witte and S. Chatterjee, ACS Nano, 2014, 8, 7377–7383.
44. K. M. Felter and F. C. Grozema, J. Phys. Chem. Lett., 2019, 10, 7208–7214.
45. A. Zaykov, P. Felkel, E. A. Buchanan, M. Jovanovic, R. W. A. Havenith, R. K. Kathir, R. Broer, Z. Havlas and J. Michl, J. Am. Chem. Soc., 2019, 141, 17729–17743.
46. D. G. A. Smith, L. A. Burns, A. C. Simmonett, R. M. Parrish, M. C. Schieber, R. Galvelis, P. Kraus, H. Kruse, R. D. Remigio, A. Alenaizan, A. M. James, S. Lehtola, J. P. Misiewicz, M. Scheurer, R. A. Shaw, J. B. Schriber, Y. Xie, Z. L. Glick, D. A. Sirianni, J. S. O’Brien, J. M. Waldrop, A. Kumar, E. G. Hohenstein, B. P. Pritchard, B. R. Brooks, H. F. SchaeferIII, A. Y. Sokolov, K. Patkowski, A. E. DePrinceIII, U. Bozkaya, R. A. King, F. A. Evangelista, J. M. Turney, T. D. Crawford and C. D. Sherrill, J. Chem. Phys., 2020, 152, 184108.
47. J. C. Slater, Quantum theory of molecules and solids: Volume 1: Electronic structure of molecules, McGraw-Hill, 1963.
48. F. Aquilante, J. Autschbach, R. K. Carlson, L. F. Chibotaru, M. G. Delcey, L. De Vico, I. F. Galván, N. Ferré, L. M. Frutos, L. Gagliardi, M. Garavelli, A. Giussani, C. E. Hoyer, G. Li Manni, H. Lischka, D. Ma, P. Å. Malmqvist, T. Müller, A. Nenov, M. Olivucci, T. B. Pedersen, D. Peng, F. Plasser, B. Pritchard, M. Reiher, I. Rivalta, I. Schapiro, J. Segarra-Martí, M. Stenrup, D. G. Truhlar, L. Ungur, A. Valentini, S. Vancoillie, V. Veryazov, V. P. Vysotskiy, O. Weingart, F. Zapata and R. Lindh, J. Comput. Chem., 2016, 37, 506–541.

---

Footnote

†

---