Double proton transfer in hydrated formic acid dimer: Interplay of spatial symmetry and solvent-generated force on reactivity

Abstract

The double proton transfer (DPT) reaction in the hydrated formic acid dimer (FAD) is investigated at molecular-level detail. For this, a global and reactive machine learned (ML) potential energy surface (PES) is developed to run extensive (more than 100 ns) mixed ML/MM molecular dynamics (MD) simulations in explicit molecular mechanics (MM) solvent at MP2-quality for the solute. Simulations with fixed – as in a conventional empirical force field – and conformationally fluctuating – as available from the ML-based PES – charge models for FAD show a significant impact on the competition between DPT and dissociation of FAD into two formic acid monomers. With increasing temperature the barrier height for DPT in solution changes by about 10% (∼1 kcal mol⁻¹) between 300 K and 600 K. The rate for DPT is largest, ∼1 ns⁻¹, at 350 K and decreases for higher temperatures due to destabilisation and increased probability for dissociation of FAD. The water solvent is found to promote the first proton transfer by exerting a favourable solvent-induced Coulomb force along the O–H⋯O hydrogen bond whereas the second proton transfer is significantly controlled by the O–O separation and other conformational degrees of freedom. Double proton transfer in hydrated FAD is found to involve a subtle interplay and balance between structural and electrostatic factors.

---

1 Introduction

Understanding the molecular details of chemical reactions in solution is one of the challenges in physical and general chemistry at large.^1–10 These processes are at the center of interest of organic, inorganic and biological chemistry as the environment in which they take place can determine reaction products, their rates and propensities. However, the direct and atomistically resolved experimental characterization by which the solvent influences reactions is challenging because simultaneous control over temporal (i.e. “rates”) and spatial (“collocation” and local solvation) aspects of the process along the progression coordinate is rarely possible. On the other hand, computer simulations have matured to a degree that allows the study of realistic processes at a sufficiently high level of theory including the environment.^11,12

More specifically, polar solvents such as water, can stabilize the transition state (TS) of the reactant.^4,13,14 For the Claisen rearrangement the origin of the catalytic effect of the water solvent is the differentially stronger hydrogen bonding to the TS structure (allyl phenyl ether) compared with that to the reactant structure because the TS is more polar which lowers the reaction barrier.^15,16 Further stabilization of the TS and lowering of the reaction barrier by the water solvent can be affected by solvent polarizability and dipole–dipole interaction between solute in its TS structure and the solvent.¹⁶ The explicit description of solvent effects by full ab initio MD simulations for reactive systems in solution is computationally very demanding and can be typically only followed on the picosecond time scale.^17,18 To avoid this, the (reactive) solute can be treated quantum mechanically (QM – ranging from tight-binding to post-Hartree–Fock methods) whereas the remaining degrees of freedom are described by an empirical force field.^19–21 Alternatively, reactive force fields have been developed which allow to follow chemical reactions in solution on extended time scales.^1,22,23 More recently, another possibility has emerged by developing a machine learned (ML) representation for the solute that can be used together with an implicit^24,25 or explicit description of the environment at an empirical level. The present work develops such a scheme and applies it to the formic acid dimer in solution.

The formic acid dimer (FAD) has been the subject of several computational^26–41 and experimental studies.^36,42–48 In the gas phase, formic acid exists as hydrogen bonded dimers⁴⁹ making it a prototype for complexes with hydrogen bonds such as enzymes or DNA base pairs.⁵⁰ Such conformations allow double proton transfer (DPT) to occur which leads to broadening of the line shape for the O–H frequency in IR-spectra.³⁶ The dissociation energy of FAD into two formic acid monomers (FAMs) has been determined from spectroscopy and statistical thermodynamics to be D₀ = −59.5(5) kJ mol⁻¹ (∼−14.22 kcal mol⁻¹)⁴⁷ which compares with −14.23 ± 0.08 kcal mol⁻¹ from recent computations.⁴¹

Another quantity that has been accurately measured experimentally is the tunneling splitting for which a recent value of 331.2 MHz is available from microwave spectroscopy.⁵¹ From this, a barrier for DPT of 2559 cm⁻¹ (30.6 kJ mol⁻¹ or 7.3 kcal mol⁻¹) from analysis of a 3D model was determined.⁵¹. The tunneling splitting from the microwave data compares with values of 0.011 cm⁻¹ (340.8 MHz)⁵² and 0.016 cm⁻¹ (473.7 MHz)^53,54 from infrared spectroscopy. Computationally, a high-quality (CCSD(T)-F12a/haTZ), full-dimensional PES for FAD has been determined and represented as permutationally invariant polynomials which features a DPT barrier of 2853 cm⁻¹ (8.16 kcal mol⁻¹).³⁵ The computed splitting on this PES from using a ring-polymer instanton approach was 0.014 cm⁻¹ (420 MHz).³⁷

Given its thorough characterization in the gas phase, FAD is also an interesting system to study reactions in solution. In particular the balance between DPT and the dissociation of FAD into two monomers provides an attractive aspect of the system to be explored also as a proxy for DNA base-pair dimers.^55,56 The homologous series of carboxylic acids (formic, acetic, propionic, butyric) in water have also served as model systems for studying the balance and role of hydrogen bonding, hydrophobicity and entropy changes which is of particular relevance in the context of protein folding and stability.⁵⁷

For FAD in pure water detailed experimental results are scarce. Early work reported that dimerization is most relevant for the low-concentration range for all carboxylic acids investigated, including formic acid.⁵⁸ This was subsequently challenged and measurements in 3 m NaCl by potentiometric titrations were interpreted as leading to singly H-bonded, extended formic acid oligomers.⁵⁹ The hydration of formic acid in pure water was also investigated with neutron diffraction experiments for higher formic acid concentrations.⁶⁰ At all conditions studied, a pronounced peak for the O⋯O separation with a maximum at 2.7 Å was reported which, together with a peak for the OH⋯O angle at 180°, supports formation of singly H-bonded or cyclic FAD. It is of interest to note that the extended structures proposed by Scheraga are incompatible with the neutron scattering results.⁶⁰ Surface scattering experiments found that FAD colliding with the liquid water surface almost completely inserts in its cyclic form into bulk water even at low collision energies.⁶¹ This indicates that H-bond breaking in FAD is not essential for uptake. Whether or not and for how long FAD remains in its cyclic form inside water was, however, not determined in these studies.⁶¹ Accompanying ab initio MD simulations reported that the cyclic dimer has fewer FAD–water hydrogen bonds (i.e. is “more hydrophobic”) than the branched, singly H-bonded FAD isomer.⁶² Finally, a study considering clathrate formation involving formic acid and water interpreted the measured infrared spectra as partially originating from water-mediated cyclic formic acid dimers in which the two formic acid monomers are H-bonded by a bridging water molecule.⁶³ An independent MD simulation for FAD in water reported⁵⁷ a negligible stabilization free energy for cyclic FAD of 0.6 kcal mol⁻¹ which is surprising given the substantial gas phase stability of FAD of −16.8 kcal mol⁻¹.^33,41 Very recent Raman spectroscopy measurements reported formation of both, singly and cyclic H-bonded FADs.⁶⁴ Taken together, the available studies suggest that FAD on and in pure water can exist as an equilibrium between cyclic and singly H-bonded dimers. Therefore, the present work will focus on the dynamics of cyclic FAD in pure water.

The aim of the present work is to characterize DPT dynamics in FAD in aqueous solution. First, the methods and the ML/MM embedding are described. Next, the quality of the PES is reported and the structural dynamics, free energies, and rates together with conformational coordinates relevant for DPT of FAD in solution are discussed. This is followed by an analysis of the solvent distributions for reactant and transition state structures, and the effect of the solvent-generated electrical field. Finally, the results are discussed in a broader context.

2 Methods

This section describes the generation of the potential energy surface for the simulation of FAD in water and the molecular dynamics (MD) simulations performed within the Atomic Simulation Environment (ASE).⁶⁵ In the following the potential energy of FAD is represented as a Neural Network (NN),⁶⁶ referred to as “ML” or “PhysNet” whereas solvent water is described with the TIP3P model (MM).⁶⁷ First, the reference data generation, the training of the NN-based PES and the embedding of the ML (FAD) part in the MM environment (water) is described. This is followed by a description of the MD simulations and their analysis.

2.1 Potential energy surface

All electronic structure calculations were carried out at the MP2/aug-cc-pVTZ level of theory using the MOLPRO software package.⁶⁸ The reference data included structures, energies, forces, and dipole moments for FAM (5000 structures), FAD (47 069), and a number (6000) of related fragments (“amons”)⁶⁹ including H₂, CO, H₂O, CH₄, CH₂O and CH₃OH. Structures were generated from MD simulations, carried out at the PM7 level of theory using ASE. The “amons” were only used for training the NN and help in generalizing the ML model. Additional FAD structures were generated from simulations in solution (akin to adaptive sampling) by using PhysNet trained only on gas-phase structures.^41,70 The energies of the FAD structures cover a range up to ∼100 kcal mol⁻¹ above the global minimum compared with the TS for DPT which is ∼8 kcal mol⁻¹ above the global minimum. For the final training the 58 069 reference structures were split into training (49 300), validation (5800) and testing (2969) sets. The parameters of PhysNet were fitted to reproduce ab initio energies, forces and dipole moments of the training set.⁶⁶ Including FAD conformations exhibiting two, one or no H-bond in the training set has been shown essential to ensure the correct propensity towards the global minimum conformation of FAD with two formed H-bonds.

PhysNet computes the total potential energy E for given coordinates x⃑ and nuclear charges Z of N atoms from atomic energies E_i and pairwise electrostatic and dispersion interactions according to

The prediction of the atomic energies E_i and charges q_i is based on feature vectors that encode the local chemical environment of each atom i ∈ N to all atoms j within a cutoff radius that was r_cut = 10 Å in the present work.⁷¹ For charge conservation, the partial charges q_i are scaled to the correct total charge of the system and used for the calculation of the electrostatic interaction energy where k_e is the Coulomb constant and r_ij is the distance between atoms i and j. For small distances the electrostatic energy is damped to avoid instabilities due to the singularity at r_ij = 0.⁶⁶ The initial parameters for the dispersion correction E_D3 are the standard values recommended for the revPBE level of theory.⁷² Since the atomic features, electrostatic and dispersion interaction depend only on pairwise distances and are combined by summation, the PES is invariant to translation, rotation and permutation of equivalent atoms. The forces F⃑ with respect to the atomic coordinates x⃑ are computed by reverse mode automatic differentiation provided by Tensorflow.^73,74 For further details, the reader is referred to ref. 66.

For the water solvent the TIP3P model⁶⁷ as implemented in the GPAW program package⁷⁵ is used with a cutoff range of 10 Å due to its improved performance compared to that of ASE. The interaction between formic acid and the water solvent includes van der Waals and electrostatic terms which were treated with a cutoff at 14 Å or half the simulation box edge length at most. The van der Waals interactions are calculated using the Lennard-Jones-potential and the parameters from CGenFF⁷⁶ for formic acid.

The electrostatic interactions between the TIP3P atomic charges of water and the NN-predicted atomic charges of FAD are computed within PhysNet. This allows exploitation of reverse mode automatic differentiation to calculate the necessary derivatives of the fluctuating atomic charges from the atomic coordinates and ensures energy conservation. For the van der Waals and electrostatic interactions between the “high level” treatment (here PhysNet) and MM atoms a switch function s(r)

was used to set the interactions zero in the range from r₁ = 13 Å to r₂ = 14 Å, where r is the separation between ML and MM atoms, respectively. Additionally, the electrostatic Coulomb potential V_C is shifted to zero at the cutoff distance of r_cut = 14 Å following the shifted force method to prevent the inconsistent gradient at the cutoff point.⁷⁷ While the van der Waals interaction between both species become negligible at that cutoff distances, this is not the case for the Coulomb forces between two charges q_i and q_j of atoms i from the ML part and j from the MM part separated by r_ij.An ASE calculator class for the PhysNet model was written as interface to the ASE program package. Further extensions are implemented to enable constant atomic charges in formic acid only for the calculation of the electrostatic potential between the ML and MM part of the simulation setup. In addition, custom energy functions were added to the potential energy to perform biased simulations.⁷⁸

2.2 Molecular dynamics simulations

All MD simulations were performed using Python packages of a modified version of ASE (3.20.1).⁶⁵ Simulations are initialized with FAD in its minimum conformation in a cubic simulation box with edge length 28.036 Å containing 729 water molecules which corresponds to a density of 0.997 g cm⁻³. The density is not adjusted for simulations at different temperatures. All simulations were run with periodic boundary conditions. To maintain the solute near the center of the simulation box a center-of-mass harmonic constraint with a force constant of 0.23 kcal mol⁻¹ Å⁻² was applied on formic acid molecules when moving further than 10 Å from the center of the simulation box. RATTLE-type holonomic constraints⁷⁹ as implemented in the GPAW program package⁸⁰ were applied to the oxygen–hydrogen and hydrogen–hydrogen distances of the water molecules. The simulations are carried out in the NVT ensemble using the Langevin propagator with a time step of Δt = 0.2 fs and a friction coefficient of 10 ps⁻¹.

First, the structure of the system was minimized to release strain. A heating run is performed for 10 ps to reach the respective target temperatures of 300 K, 350 K, 400 K, 450 K, 500 K and 600 K. As no rigorous implementation of a barostat is available in ASE, simulations at constant volume but increased temperature were carried out to qualitatively assess the influence of increased pressure on the DPT dynamics. The system equilibrates within 5 ps during the heating runs. Equilibration is followed by production simulations of 100 ps each, accumulating to a total of 16 ns simulation time at each temperature. Positions and momenta are stored (1) every 10 fs for the complete trajectory and (2) every 1 fs in a time window of Δt = [−20, +50] fs around every attempt of a reaction registered during the simulation (see Analysis).

The implementation is validated by examining energy conservation for a 100 ps NVE MD simulation at 600 K. The total energies at each time step are within a standard deviation of 6.1 × 10⁻³ kcal mol⁻¹ from the average total energy with a maximum deviation of ±25.2 × 10⁻³ kcal mol⁻¹ and no drift is found. This confirms that the forces are correctly implemented.

To determine the impact of the fluctuating atomic charges available from PhysNet on the dynamics and energetics, MD simulations were also performed by fixing the atomic charges to those of the TS structure of FAD to retain the symmetry of the system before and after PT. These fixed atomic charges were used for the solute–solvent interaction only. For the internal interaction of the ML part (FAD) fluctuating charges were retained in order to correctly represent the PES for the isolated solute. Finally, as FAD was found to be largely hydrophobic from earlier simulations^57,62 and to probe the effect of the electrostatic interactions between solute and solvent on DPT, simulations were also carried out with zeroed charges on all atoms of the solute.

2.3 Analysis

Proton transfer (PT) is a transient process. To characterize a PT event it is often useful to use a geometric criterion.⁸¹ Here, the criterion was the distance between the hydrogen and the oxygen atoms O_A and O_B of the respective H-bond. A PT in one H-bond was identified by a sign change of the progression (or reaction) coordinate ξ = d(H–O_A) − d(H–O_B). Further, the oxygen atom bonded to the hydrogen atom is the donor oxygen (O_don) and the second oxygen atom in the H-bond is the acceptor oxygen (O_acc), see Fig. 1. Successful and attempted DPT always involve two consecutive PTs, see Fig. S1 (ESI†). For “successful” DPT the two PTs include a “first” and a “second” hydrogen atom H_A and H_B in both H-bonds, respectively, whereas for an “attempted” DPT both PTs involve only hydrogen atom H_A. DPT is considered to be successful when a sign change in both progression coordinates ξ₁ and ξ₂ occurs. Attempted – as opposed to successful – DPT events are those for which only one forth and back PT occurs along the first H-bond without PT along the second H-bond.

Fig. 1 Correlation between the MP2/aug-cc-pVTZ reference and the NN-predicted energies from PhysNet for the test set. The 2969 randomly chosen structures which were not used during training contain samples of FAM, FAD, and their “amons”. The RMSE between reference and NN-predicted energies is 0.336 kcal mol⁻¹ with a Pearson coefficient of R² = 1–2 × 10⁻⁶. The red cross indicates the energy for the TS. A sketch of FAD with atom labels is shown in the upper left corner. The vector pointing from O_don towards O_acc, R⃑, is also reported.

In addition to unbiased simulations, biased simulations were carried out at different temperatures for FAD in the gas phase and in solution. For this, an artificial harmonic potential involving both progression coordinates ξ₁ and ξ₂ was added to the total potential energy. For FAD in solution the force constant was k_bias = 16.1 kcal mol⁻¹ Å⁻² and 5 × 10⁶ snapshots were recorded from 1 ns trajectories at each temperature. Both constraining harmonic potentials are centered at the TS coordinate, ξ_1,TS = ξ_2,TS = 0, and the magnitude of the force constant was chosen to lift the potential of the equilibrium conformation (ξ_eq = ±0.66 Å) of FAD roughly to the level of the TS conformation. Additional tests were run with lower values of k_bias. The resulting potentials of mean force (PMFs) were found to be insensitive of this choice, see Fig. S2 (ESI†).

3 Results

3.1 Quality of the potential energy surface

Fig. 1 shows the quality of the ML PES by comparing reference MP2 energies with those predicted from the trained PhysNet model for formic acid dimer for 2969 test structures. The energies of the smaller fragments (“amons”) are outside the energy range of the graph but are included in the root mean squared error (RMSE) of 0.336 kcal mol⁻¹ and the Pearson coefficient is R² = 1–2 × 10⁻⁶. The energy deviation between the MP2 energy and the PhysNet model prediction is smaller than 3 × 10⁻³ kcal mol⁻¹ for the minimum conformation of FAD and the TS for DPT.

The MP2 method is a good compromise between speed and accuracy. For example, the barrier for DPT of 6.7 kcal mol⁻¹ compares with a value of 7.2 kcal mol⁻¹ from a morphed MMPT-MP2 force field that is consistent with infrared spectroscopy³⁶ and a barrier height of 7.3 kcal mol⁻¹ from analysis of microwave spectroscopy data.⁵¹ Calculations at the CCSD(T) level of theory report somewhat higher barriers of 7.9 kcal mol⁻¹ and 8.2 kcal mol⁻¹, depending on the basis set and additional F12 corrections used.^35,36 Furthermore, the dissociation of the dimer into two monomers is of interest. In the gas phase the PhysNet model yields D_e = −16.8 kcal mol⁻¹ which is also the value from the reference MP2/aug-cc-pVTZ calculations. Ab initio calculations at the higher CCSD(T)/aug-cc-pVTZ level of theory find D_e = −16.8 kcal mol^−1 33,41 and −16.0 kcal mol⁻¹ at the basis set limit.³³

Next, the energetics of increasingly hydrated FAD is determined from the present ML/MM energy function, from the CGenFF⁷⁶ parametrization of FAD together with the TIP3P water model, and from electronic structure calculations. For this, 50 snapshots from a 2 ns ML/MD simulation with FAD in its dimeric structure were extracted. The 15 water molecules closest to the center of mass of FAD were retained for each snapshot. Electronic structure calculations for this analysis were carried out at the B3LYP+D3/aug-cc-pVDZ level of theory^82–84 because MP2/aug-cc-pVTZ calculations for FAD surrounded by up to 15 water molecules are computationally too demanding. The total interaction energies for FAD–(H₂O)_n (n = 1,…,15) complexes were determined. Water molecules were retained in increasing order of their distance from FAD. The results are reported in Fig. S3 and S4 (ESI†) and the analysis shows that the interaction energies with 15 water molecules from the MM/ML energy function differ on average by less than 1 kcal mol⁻¹ from the reference B3LYP+D3 calculations whereas CGenFF underestimates the reference results by about 4 kcal mol⁻¹.

The 50 snapshots were also analyzed from retaining the 4, 8, and 12 closest water molecules and correlating the MM/ML and CGenFF interaction energies with those from the reference B3LYP+D3 calculations (Fig. S5–S7, ESI†). Mean absolute errors between MM/ML and DFT reference calculations are 1.13, 2.06 and 2.85 kcal mol⁻¹ compared with 2.42, 3.36 and 3.62 kcal mol⁻¹ for CGenFF. It is also worth to point out that CGenFF finds a dimer stabilization energy of only 9 kcal mol⁻¹ in the gas phase compared with high-level electronic structure calculations that yield −16.8 kcal mol^−1 33,41 and −17.4 kcal mol⁻¹ at the B3LYP+D3/aug-cc-pVDZ level which is −0.6 kcal mol⁻¹ lower than for the MP2 and CCSD(T) levels of theory with the aug-cc-pVTZ basis set. Overall, the comparison with the B3LYP+D3 results validates the quality of the ML/MM energy function whereas the CGenFF parametrization is found to considerably underestimate the stability of FAD.

3.2 Structural dynamics in solution

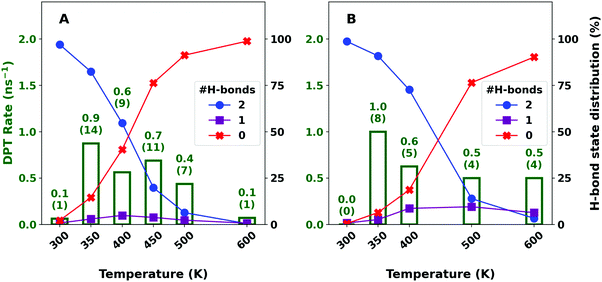
Fig. 2 reports the propensity of FAD to exist as a doubly (blue circle) or singly (violet square) H-bonded dimer or as two separate monomers (red cross) in water. This is consistent with what has been inferred from experiments.^60,61 For the equilibrium conformation the O_don–O_acc distance is ∼2.66 Å. An H-bond in FAD is considered “broken” if the O_don–O_acc distance exceeds 4 Å. MD simulations with fluctuating atomic charges on FAD show (Fig. 2A) that the propensity for a doubly H-bonded FAD decreases from 97.0% at 300 K to 0.4% at 600 K. The probability for the singly H-bonded dimer increases from 0.8% at 300 K to a maximum of 4.9% at 400 K and decreases again to 0.7% at 600 K. At the temperature with the highest DPT rate (350 K) both H-bonds are formed for 82.4% of the propagation time.

Fig. 2 DPT rates and distribution of the number of formed H-bonds in the simulation of FAD in water at different temperatures using fluctuating atomic charges (panel A) and fixed atomic charges (panel B). The green numbers atop the bars show the respective rate and absolute number of observed DPT events. The markers show the propensity of FAD to have two formed H-bonds (blue circle), to be partially dissociated (purple square) or completely separated into two formic acid monomers (red cross). The lines are to guide the eye.

In conventional force fields the partial charges are fixed⁷⁶ and do not change with conformation. PhysNet provides geometry-dependent charges, see Fig. S8 (ESI†), which fluctuate by ±0.05 e to ±0.1 e around their mean. The average charges for the C, H_C and one of the oxygen atoms from PhysNet are similar to those in CGenFF whereas for the H_O and the second oxygen they differ by about 0.1 e. It is also found that the charge distributions from PhysNet differ for cyclic and branched FAD. Given these differences it is of interest to determine the differences between the simulations analyzed with conformationally fluctuating charges and those with fixed partial charges on the FAD. The charges assigned to the atoms are those of the TS structure to ensure a symmetric atomic charge distribution before and after successful DPT. The distribution of formed H-bonds for FAD in water with fluctuating and fixed charges in Fig. 2 shows that the propensity for H-bond formation significantly depends on fixing the charges. With the fixed charge model the probability for the doubly H-bonded dimer to exist is larger at all temperatures from 300 K (98.7%) to 600 K (3.3%) compared with the fluctuating charge model (97.0% and 0.4% at 300 K and 600 K, respectively). In addition, the probability for singly H-bonded FAD and two separate monomers at 600 K differs with the fixed charge model with 6.4% and 90.3%, respectively, from the fluctuating charge model with 0.7% and 98.8%. Thus, a fixed charge model with charges from the TS structure predicts a higher propensity for FAD to exist in solution compared to the fluctuating charge model.

The higher propensity for dimer dissociation in solution using fluctuating rather than fixed charges correlates with the differences in the magnitudes of the atomic charges between the two charge models. From the equilibrium conformation of FAD towards separated FAMs the polarization along the atoms in the H-bond increases. The fluctuating charges along the O_don–H⋯O_acc bond change from [−0.39, +0.32, −0.43] e in the equilibrium dimer conformation to [−0.42, +0.36, −0.45] e for separated monomers, respectively, which compares with [−0.40, +0.30, −0.40] e in the fixed charge models with charges taken from the TS structure. Comparable amplitudes for charge transfer (δq = 0.025 e) have been found for the HO_don–H⋯O_accH₂ hydrogen bond in bulk water when the energy function was fit to match experimental frequencies and intensities of the infrared and Raman bands.⁸⁵ The larger absolute values of the atomic charges in the fluctuating charge model (differences of up to 20% and 13% for the hydrogen and oxygen atoms of the H-bonds relative to the charges in the TS structure, respectively) lead to stronger electrostatic interactions with the surrounding solvent. This also impacts on the conformational sampling and the reaction barrier height.

To evaluate the effect of the water solvent on dissociation, NVT simulations for FAD in the gas phase were performed using the same setup as for the simulations in solution. The presence of both H-bonds is a prerequisite for DPT to occur as the top of the barrier becomes inaccessible if even one H-bond is broken. Thus, dissociation of the FAD competes with DPT and therefore governs the DPT rate. In the gas phase it is found that – similar to the situation in solution – the propensity towards broken H-bonds increases for higher temperatures. At 300 K both H-bonds are formed for 99.4% of the propagation time. This fraction decreases at higher temperatures: 27.3% and 2.1% at 500 K and 600 K, respectively.

3.3 Free energies of activation and rates for DPT

Biased simulations were performed to investigate the free energy barrier for DPT. Fig. 3 shows the 1-dimensional cuts along the constrained progression coordinate ξ. The 2-dimensional free energy surfaces G(ξ₁, ξ₂) are given in Fig. S9 (ESI†). The energies around the equilibrium ξ_eq = ±0.66 Å are set to zero. Biased simulations are carried out for fluctuating and fixed charges. Between 300 K and 600 K the free energy barrier increases from 7.45 kcal mol⁻¹ to 8.13 kcal mol⁻¹ for simulations using the fluctuating charge model. With fixed charges the barriers change from 7.53 kcal mol⁻¹ to 8.39 kcal mol⁻¹. Thus, as a function of temperature, the barrier increases by 0.68 kcal mol⁻¹ with fluctuating charges, compared with 0.85 kcal mol⁻¹ with fixed charges. In other words, the change of the barrier height as a function of temperature differs by 25% from fluctuating to fixed charges on solution.

Fig. 3 Free energy profile for DPT in FAD with fluctuating (panel A) and fixed charges (panel B) for different temperatures in solution. The free energy curve follows the minimum energy path of the 2-dimensional free energy surface of antiparallel reactive coordinates ξ₁ = −ξ₂. The average temperature of FAD in solution in the NVT simulations are given in the legend and the standard deviation ranges from ±6 K at 300 K to ±13 K at 600 K. The PMF is symmetrized around ξ₁ = ξ₂ = 0 to increase data sampling as the artifacts at large absolute values of ξ result from insufficient sampling especially for biased simulations at low temperatures.

Simulations were also carried out in the NVE ensemble for FAD in the gas phase and yield a free energy barrier for DPT of 8.25 kcal mol⁻¹ at a temperature of 310 K which was determined from the kinetic energy of all atoms in this biased simulation. Earlier classical ab initio metadynamics simulations with the same reaction coordinates as those used in the present work at the BLYP level with a plane wave basis for FAD in the gas phase reported a free energy barrier height of 4.7 kcal mol⁻¹ at 300 K compared with the potential barrier height of 5.0 kcal mol⁻¹.³² This differs qualitatively from the present results for which the free energy barrier in the gas phase increases from the potential barrier of 6.7 kcal mol⁻¹.

To quantify the electrostatic contribution of the solute/solvent interactions to the free energy barrier, biased simulations of FAD in solution were performed with the atomic charges of FAD set to zero. At 300 K the free energy of activation is 7.46 kcal mol⁻¹ and increases by +0.87 kcal mol⁻¹ to 8.33 kcal mol⁻¹ at 600 K. This compares with 7.45 and 7.53 kcal mol⁻¹ with fluctuating and fixed charges at 300 K, respectively, which increase to 8.13 and 8.39 kcal mol⁻¹ at 600 K. At 300 K the contribution of fluctuating electrostatics is thus −0.01 kcal mol⁻¹ as opposed to + 0.07 kcal mol⁻¹ if the charges are fixed and a reduction by −0.20 kcal mol⁻¹ and an increase of +0.06 kcal mol⁻¹ at 600 K for fluctuating and fixed charges, respectively. This finding suggests that FAD behaves largely as a hydrophobic solute for which direct electrostatic interactions with the solvent are less relevant.

The T-dependence to the free energy (−TΔS) suggests that the change ΔS between the reactant and the TS state is negative for all charge models used but the magnitude of ΔS differs. This difference is accommodated in the solvent ordering around the solute. Linear interpolation of the free energy barriers at the different temperatures yields an activation enthalpy and activation entropy of [ΔU, ΔS] = [6.87 kcal mol⁻¹, −2.1 cal mol⁻¹ K⁻¹] for fluctuating charges, [6.62 kcal mol⁻¹, −2.9 cal mol⁻¹ K⁻¹] for fixed charges, and [6.70 kcal mol⁻¹, −2.7 cal mol⁻¹ K⁻¹] for zero charges.

Because the constraints in the biased simulations favour FAD over two separated monomers (and the dimer has been found to dissociate at higher temperatures for free dynamics) it is mandatory to also run and analyze unbiased simulations that allow DPT to occur in solution. For this, an aggregate of 16 ns simulations was run and analyzed at each temperature. As the barrier for DPT is relatively high, DPT is a rare event. DPT rates in unbiased simulations are highest at 350 K for both fluctuating and fixed charge models, see Fig. 2A and B. With the fluctuating charge model (Fig. 2A) the rate is 0.9 ns⁻¹ at 350 K and decreases to 0.4 ns⁻¹ at 500 K, while the dimer is only present for 82.4% and 6.4% of the propagation time, respectively. Hence, the true rates are ∼6.5 times higher at 500 K compared with those at 350 K. Within transition state theory energy barriers of ∼8 kcal mol⁻¹ from the biased simulations correspond to rates of ∼0.1 ns⁻¹ which is consistent with results from unbiased simulations shown in Fig. 2.

With the fixed charge model a similar increase of the DPT rates is observed. At 300 K, no DPT was observed during 8 ns of propagation time whereas for T = 350 K and 500 K they are 1.0 ns⁻¹ and 0.5 ns⁻¹, respectively. As the simulation time with fixed charges is 8 ns – shorter than simulations with the fluctuating charge model – the rates for DPT are based on fewer events with larger uncertainties which are not quantified in this work.

3.4 Conformational coordinates involved in DPT

Conformationally relevant degrees of freedom to consider are the O_don–O_acc and the CO bond distances. The involvement of the O_don–O_acc separation becomes apparent from noting that it contracts from d_eq(OO) = 2.66 Å in the global minimum to d_TS(OO) = 2.41 Å in the TS. In other words, compressing the O–O separation towards the TS structure facilitates (D)PT. The CO bond in the COH moiety has bond order 1 (BO = 1) whereas the second CO bond is formally a double bond (BO = 2). This bonding pattern reverses after DPT and for the TS structure all bond orders are 1.5.

The first PT leads to a short-lived, metastable ion-pair with one protonated formic acid monomer and the corresponding anion, see Fig. S1 (ESI†). Subsequently, the transferred hydrogen atom returns either to where it came from (attempted DPT) within an average delay time of 4.8 ± 2.9 fs at 350 K or the hydrogen atom along the second H-bond transfers (successful DPT) with an average delay time of 5.9 ± 2.6 fs. At 450 K the analysis of unbiased simulations find delay times of 5.1 ± 3.9 fs and 8.2 ± 7.1 fs for attempted and successful DPT, respectively. This is consistent with results from earlier work that reported an average delay time of ∼8 fs for successful DPT.³⁰

Fig. 4A and D compare the instantaneous O_don–O_acc separations at the time of the second PT. The probability distribution functions P(d_OO,A, d_OO,B) for the O–O separations in unbiased simulations at 350 K and 400 K peak at (2.75 ± 0.18) Å and (2.78 ± 0.22) Å, respectively. These distances shorten significantly to (2.40 ± 0.05) Å and (2.42 ± 0.06) Å for successful DPT; see Fig. 4. For successful DPT both O–O separations are between 2.4 Å and 2.6 Å whereas for attempted DPT the first O–O separation ranges from 2.3 Å to 2.5 Å but the second oxygen donor-acceptor distance covers a range between 2.4 and 2.9 Å. This suggests that a more symmetrical geometry at the time of the first PT increases the probability for successful DPT during the second step, i.e. if the distances between both oxygen atoms in the H-bonds are simultaneously contracted.

Fig. 4 Bond distance distributions in FAD from simulations at 350 K (A–C) and 400 K (D–F). The blue colormap (panels A and D) shows the probability distribution of the O_don–O_acc distances P(d_OO,A, d_OO,B) in both H-bonds. Oxygen–oxygen separations d_OO for successful (green diamonds) and attempted DPT events (red circles) at the time of the second PT are shown for both hydrogen bonds. The blue and red distributions (panels B, C, E, and F) show the distribution P(d_CO,acc) and P(d_CO,don) for the complete simulations. Distributions P(d_CO,A) (blue cross) and P(d_CO,B) (red plus) at the time of the second PT are reported for successful (B and E) or attempted DPT (C and F). For successful DPT they peak at the same CO separation (symmetric) whereas for attempted DPT they overlap less.

Next, the CO bond lengths are analysed. Fig. 4B, C, E, and F shows the distribution of the CO_acc double and CO_don single bond distances from all MD simulations at 350 K and 400 K. The maximum peak positions are clearly distinguishable and demonstrate the single and double bond character of the CO bonds with BO = 1 and BO = 2, respectively. In addition, the histograms for the CO distances at the second PT of a successful (panels B and E) and attempted (panels C and F) DPTs are reported. For successful DPT the distributions overlap for both temperatures and BO = 1.5 whereas for attempted DPT they are clearly non-overlapping and closer to BO = 1 and BO = 2, respectively.

The correlation between narrowly overlapping distance distributions of the CO single and double bond and the higher probability for successful DPT can be explained by the respective OH bond potential in the protonated formic acid monomer. Fig. 5 shows the PhysNet potential along the progression coordinate ξ₁ of a hydrogen atom in the TS of FAD. With all other bond lengths frozen in the TS conformation, a scan along ξ₁ is performed for three different distances of the CO bond involved in the first H-bond as in A) the TS conformation, B) a CO single bond and C) CO double bond (see illustration in Fig. 5). The remaining CO bonds are kept frozen at the TS bond length of 1.26 Å. For d_TS(CO) = 1.26 Å (TS conformation with BO = 1.5) the potential minimum along the reactive coordinate is at ξ₁ = 0 Å, which changes if the CO bond contracts (B) or extends (C). The OH-stretch potential is energetically more attractive in the covalent bonding range if the CO bond has BO = 1 rather than BO = 2. Vice versa, the OH-stretch potential becomes repulsive at shorter CO distances as in CO double bonds. Thus, hydrogen abstraction from an oxygen donor atom involved in a CO double bond is energetically more favourable compared to that involved in a CO single bond.

Fig. 5 Scan of the potential curve along the reactive coordinate ξ₁ of the hydrogen atom in the H-bond of FAD in the TS conformation. The three cases are for different elongations of the CO bond involving the first H-bond. CO distances are for the (A) TS conformation d_TS(CO) (solid line, blue), (B) average CO single bond separation d₁(CO) (dotted line, orange) and (C) average CO double bond length d₂(CO) (dashed line, green). The minimum of the potential for the TS conformation is shifted to 0 for reference.

3.5 Solvent distribution

MD simulations also provide information about the solvent distribution along the reaction path. Fig. 6 reports the radial and distribution of the water oxygen atoms in the vicinity of the hydrogen atoms in the H-bonds of FAD from simulations at 300 K and 400 K. The solvent distributions are obtained either from unbiased MD simulations with FAD primarily in its reactant state and from biased simulations with FAD constrained close to its TS conformation by applying harmonic constraints along ξ₁ and ξ₂ with a force constant of k = 115 kcal mol⁻¹ Å⁻². Analysis of the solvent distribution in the TS compared with the reactant structure is of interest to assess the amount of solvent reorganization that is required to reach the TS.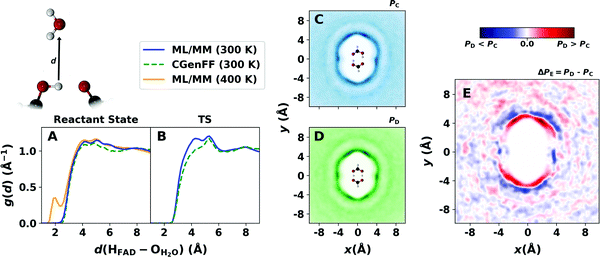

Fig. 6 The radial distribution function g(d) for the water–oxygen atoms around hydrogen atoms H_A and H_B of FAD in the reactant (A) and TS (B) structure from the from ML/MM (blue line) and CGenFF (dashed green line) simulations at 300 K. Panel (A) also shows g(d) from one entire ML/MM simulation at 400 K (orange line) including formic acid dominantly as cyclic dimer and separated monomers (see Fig. 2A). Panels (C and D) report the solvent distribution functions P(x, y) around FAD from ML/MM MD simulations in its reactant (C) and TS (D) structures, respectively, and panel (E) reports the difference ΔP(x, y) = P_D − P_C between the two.

The solvent radial distribution functions around the hydrogen atoms of the H-bonds in Fig. 6A and B exhibit a weak double peak between 4 and 6 Å. The maxima indicate the first solvation shell around FAD and the double peak structure is more pronounced for simulations with FAD in its TS structure. In the biased simulations FAD is more rigid which leads to a more structured solvent distribution. The radial distribution also shows a broad maximum around 8 Å that can be associated with a second solvation shell. The solvent radial distribution from simulation at 400 K (orange line in Fig. 6A) features an additional peak around 2 Å that represents H-bond formation between branched, i.e. non-cyclic FAD, separated formic acid monomers and water molecules. Such H-bonds become available in simulation at temperatures higher than 300 K as the probability for almost exclusively cyclic FAD decreases significantly (see Fig. 2A).

For a more comprehensive characterization of the changes in the hydration of FAD between product/reactant geometries and the TS structure, 2-dimensional solvent distributions were determined. Fig. 6C and D show the actual distributions projected onto the xy-plane which is the average plane containing the solute. Fig. 6E reports the solvent density difference around FAD in its reactant and TS conformation, i.e. the difference density from panels C and D in Fig. 6. In the 2d-histograms the first and second solvation shells are clearly visible as was also found from the radial distribution functions (Fig. 6A and B). There is also a dent for the first solvation shell at (−4, 0) Å and (4, 0) Å along the horizontal axis joining the hydrogen atoms along the H-bonds of FAD.

The solvent distribution difference in Fig. 6E indicates a shift of the first solvation shell closer to the side of the CH group of FAD for the biased simulations due to the short monomer–monomer distance in the TS structure compared with the reactant state. Hence, the solvent probability in this region is higher for FAD in its TS than in its reactant state. This is consistent with the shorter monomer–monomer distance of FAD in the TS conformation. The monomer–monomer contraction in the TS also flattens the dent towards the hydrogen atoms in the H-bond as shown by the blue area that indicates a lower solvent distribution density around FAD in the TS than the reactant state conformation. Finally, the solvent distribution difference exhibits the symmetry of FAD which indicates the convergence of the simulations.

3.6 Influence of the solvent-generated electrical field

Finally, DPT events are analyzed from the perspective of the alignment of the H-transfer motif relative to the solvent-generated electric field. Although cyclic FAD was found to be rather hydrophobic, the long ranged nature of the solvent-generated electric field can still significantly impact H-transfer along the progression coordinate for DPT. The effect of external fields on chemical reactions has been demonstrated from both, experiments⁸⁶ and computations.⁸⁷

In the following the electric field at the position of the transferring hydrogen atoms along the hydrogen bond was analyzed. For this, the force on the transferring hydrogen atom at the time of PT was determined as the linear interpolation of the forces for the 1 fs-frame before and after PT. The “time of PT” was determined by the sign change of the linearly interpolated reactive coordinate of the respective H-bond along which PT occurs. In Fig. 7 and Fig. S10 (ESI†) the first PT – to which hydrogen atom H_A is attributed – is associated with the horizontal x-axis. In a successful DPT, the second PT is performed by hydrogen atom H_B (vertical y-axis) whereas in an attempted DPT the second PT is also performed by H_A (back-transfer).

Fig. 7 Correlation between the magnitude and direction of the electrostatic component of the solvent-generated Coulomb force F⃑^MM_C at the position of the transferring hydrogen atom during the first PT that leads to successful (green) or attempted (red) DPT; for definitions see Analysis. Results from unbiased (A and B) and biased simulations (C and D) are shown separately. The panels show the results from simulation at (A and C) 350 K and (B and D) 400 K. The forces on the hydrogen atom H_A that has completed the first PT are given along the horizontal axis. On the vertical axis the forces on the hydrogen atom H_B are shown for either supporting or inhibiting the second PT (for successful DPT or attempted DPT, respectively). By definition, the force vector always points towards O_acc in the H-bond. Effective electrostatic force on the hydrogen atom for a PT towards O_acc in the respective H-bond is “supportive”, and “inhibiting” otherwise. For the same analysis involving the second PT, see Fig. S10 (ESI†).

Fig. 7 and Fig. S10 (ESI†) report the projection of the solvent-generated (MM) Coulomb (C) force F^MM_C,A along the O_don–H_A⋯O_acc and O_don–H_B⋯O_acc hydrogen bonds for successful and attempted DPTs during the first and second PT, respectively. As per definition, a positive force always supports PT of a hydrogen atom whereas a negative force has an inhibitory effect. The analysis was carried out for the second PT independent of whether transfer of H_B did (successful DPT) or did not (attempted DPT with H_A transferring back) occur.

In the unbiased simulations, the first PT is typically accompanied by a supportive Coulomb force. This effect is more pronounced at higher temperatures (T = 400 K, see Fig. 7B) than at lower ones (see Fig. 7A). Biased simulations increase the probability for DPT and provide improved statistics which also allows to fit 2-dimensional Gauss distributions to the data (Fig. 7C and D). These results demonstrate that for the first PT the field along the H_A-bond is typically supportive. Interestingly, for an attempted DPT the field along the first H_A-bond at the time of PT is supportive but F^MM_C,B along the second H_B-bond is more inhibiting. This applies to both, unbiased and biased simulations, see red distributions in Fig. 7. Regarding Fig. 7 the gravity center of the average solvent-generated Coulomb force is [F̄^MM_C,A, F̄^MM_C,B] = [0.24, −0.23] and [0.86, −1.50] kcal mol⁻¹ Å⁻¹ for successful and attempted DPT at 350 K, respectively, and shifts to [0.51, −0.56] and [−0.93, −1.65] kcal mol⁻¹ Å⁻¹ at 400 K. In biased simulations the gravity centers are at [0.45, −0.43] and [0.56, −0.78] kcal mol⁻¹ Å⁻¹, [0.56, −0.55] and [−0.51, −0.81] kcal mol⁻¹ Å⁻¹ accordingly. Hence, for successful DPT the opposing electrostatic field along the second H-bond is considerably smaller in magnitude than for attempted DPT in all cases.

For the second PT the solvent-generated Coulomb force along both H-bonds is in general inhibiting (red distributions in Fig. S10, ESI†). In unbiased simulations at 350 K the center of gravity of the average solvent-generated Coulomb force is at [F̄^MM_C,A, F̄^MM_C,B] = [−0.21, −0.22] and [−0.84, −1.52] kcal mol⁻¹ Å⁻¹ for successful and attempted DPT, respectively. This shifts to [−0.52, −0.58] and [−0.92, −1.64] kcal mol⁻¹ Å⁻¹ at 400 K. In biased simulations the gravity centers are at [−0.45, − 0.42] and [−0.56, −0.78] kcal mol⁻¹ Å⁻¹ at 350 K and [−0.56, −0.54] and [−0.51, −0.81] kcal mol⁻¹ Å⁻¹ at 400 K. Except for the sign change in the projection of the Coulomb force on the hydrogen atoms of the H_A-bond the center of gravity does not change significantly between the first and second PT in successful and attempted DPT.

Comparison of the solvent-generated Coulomb force for successful and attempted DPT further establishes that the field of the water molecules at the position of the transferring hydrogen atom does not change appreciably within ∼14 fs, which is the maximum time between first and second PT observed in the simulations at 350 K. This is expected as the rotational reorientation time of water in solution is on the order of several picoseconds.⁸⁸ The time evolution of the Coulomb force along the H-bonds is shown in Fig. S11 and S12 (ESI†) for an example of a successful and attempted DPT, respectively.

In summary, successful DPT for FAD in water is often accompanied by a mildly supporting solvent-generated Coulomb force along the first PT in the H_A-bond whereas for the second PT in the H_B-bond the force is inhibiting but smaller in magnitude than for the back transfer along the first H_A-bond. As the inhibiting force along the H_B-bond increases, back-transfer along the first H_A-bond becomes favoured and results in attempted DPT with FAD returning to its initial reactant conformation, see Fig. S1 (ESI†). The findings complete the picture that the probability for successful DPT primarily depends on the conformation of FAD itself at the first PT event. At conformation of high symmetry and low reaction barriers for PT events in both H-bonds, the solvent-generated Coulomb field impacts the probability of performing one PT in both H-bonds each (successful DPT) or a forth and back PT along one H-bond (attempted DPT).

4 Discussion and conclusions

In this work double proton transfer in cyclic FAD in solution was characterized from extensive ML/MM MD simulations (total of ∼100 ns for all temperatures and all charge models considered) using an energy function at MP2/aug-cc-pVTZ level quality for the solute akin to a QM/MM treatment at this level of quantum chemical theory. To put the present simulations in context it is worthwhile to note that 100 ps of a ML/MM MD simulation (with ML trained at the MP2/aug-cc-pVTZ level) on 1 CPU takes ∼5 days for the 5 × 10⁵ energy and force evaluations. At the MP2/aug-cc-pVTZ level of theory the 5 × 10⁵ energy evaluations alone, i.e. without calculating forces, on 1 CPU would take at least 4200 days. Clearly, QM/MM simulation at such a level of theory are not feasible at present and in the foreseeable future. It is further worth to mention that the PhysNet representation captures bond polarization through geometry-dependent, fluctuating charges. On the other hand, intramolecular polarization of FAD by the water solvent is not included but is expected to be small due to the hydrophobicity of cyclic FAD.

Spontaneous DPT is observed on the nanosecond time scale at 300 K to 350 K with a maximum rate of 0.9 ns⁻¹ at 350 K. The total ML/MM energy function used was validated vis-à-vis B3LYP+D3 calculations and agrees to within ∼1 kcal mol⁻¹ for hydrated FAD with up to 15 surrounding water molecules. One particularly interesting aspect of the dynamics of FAD in solution is the fact that dissociation into a branched, singly H-bonded structure or into two separate formic acid monomers competes with DPT. The present results (see Fig. 2) suggest that on the ∼14 ns time scale the probability to form branched, singly H-bonded structures is considerably smaller than for cyclic FAD to exist (which decreases as T increases) or that of forming two separated monomers (which increases as T increases). Simulations at higher temperature allow to qualitatively assess conditions at higher pressure which has been used to induce proton transfer in other systems.^89,90

Results from previous simulation studies are somewhat ambiguous. Recent ab initio MD simulations using the BLYP functional including dispersion correction point towards pronounced hydrophobicity of cyclic FAD⁶² as was also found from earlier simulations using a fully empirical force field.⁵⁷ Both are consistent with the present work. On the other hand, simulations with this non-reactive, fully empirical force field report facile transitions from FAD to branched structures.⁵⁷ Such branched structures were also implied from experiments which were, however, carried out in 3 molal NaCl.⁵⁹ Analysis of the T-dependent free energies for DPT yields a change in solvation entropy of ΔS = −2.1 cal mol⁻¹ K⁻¹. It is of interest to juxtapose this value with earlier work that rather focused on dissociation of FAD into two separated monomers for which ΔS_D = −3 cal mol⁻¹ K⁻¹ was reported also using the TIP3P water model.⁵⁷ However, it is quite likely that the two entropy values which differ by about 30% are not directly comparable as dimerization is driven by the different arrangements of solvent molecules around FAD and the FAMs whereas for DPT the reorganization is less pronounced; see Fig. 6E.

As the calculated pK_D underestimates the experimentally measured one by 1 to 2 units (0.25 vs. 1.2 to 2.1),⁵⁷ it is expected that the energy function used in these earlier free energy simulations for cyclic FAD⁵⁷ underestimate the enthalpic contribution by about one order of magnitude. The reported stabilization from umbrella sampling simulations using the CHARMM22 force field was ΔG ∼ −0.5 kcal mol⁻¹. Hence, to be consistent with the experimentally determined pK_D, the enthalpic contribution to the stabilization of FAD in solution should rather be −5 kcal mol⁻¹ or larger. Adding this to the stabilization energy for FAD in the gas phase using the CGenFF energy function (−9 kcal mol⁻¹) yields an estimated stabilization of −14 kcal mol⁻¹ or larger which is more consistent with results from recent high-level electronic structure calculations which find a gas-phase stability for cyclic FAD of −16 kcal mol⁻¹.^33,41 In other words, the unreactive, empirical CGenFF energy function considerably underestimates the stabilization of cyclic FAD in the gas phase and in solution which is also confirmed by the results in Fig. S3–S7 (ESI†) and leads to ready dissociation of FAD into two FAMs from such simulations.⁵⁷

Successful DPT is found to chiefly depend on the conformation of the cyclic FAD. In particular, increased symmetry with simultaneously contracted O–O distances in both H-bonds and CO bonds with BO ≈ 1.5 lowers the reaction barrier for PT along both H-bonds. Successful DPT requires the solvent induced electrostatic force to be only mildly inhibiting ∼−0.5 kcal mol⁻¹ Å⁻¹ along the second H-bond. If the inhibiting force originating from the solvent is too strong along the second H-bond, attempted DPT dominates. For DPT, the MD simulations show an average delay between two PT events of ∼5 and ∼6 fs for attempted and successful DPT at 350 K, respectively, and the solvent-generated Coulomb field assists the first PT. A time difference of ∼6 fs between the successive PT events for successful DPT compares with a time scale of ∼155 fs for the O_don–O_acc vibration. This suggests that DPT in hydrated FAD is essentially concerted and not stepwise; both PTs occur within one O_don–O_acc vibration period. For a stepwise DPT the intermediate state (both protons on one FAM) would need to stabilize, i.e. have a lifetime, which is, however, not what is found here.

From a chemical perspective, one point of particular note is the successful and correct description of the change between bond orders 1 and 2 for the CO bond in PhysNet. Conventional empirical force fields encode the bond order in the equilibrium separation of the bonded term which does not allow easily for changes in the bond order depending on changes in the chemical environment. Although there are examples for capturing such effects⁹¹ making provisions for it in the context of empirical force fields is cumbersome. As Fig. 4B, C, E, and F demonstrate, a NN-trained energy function based on reference electronic structure calculations successfully captures such chemical effects.

In summary, a ML/MM MD scheme was implemented and applied to DPT for FAD in solution. The results from ∼100 ns of ML/MM MD simulations show that DPT and dissociation into two FAMs compete depending on temperature. FAD is predominantly hydrophobic which agrees with earlier findings, and the rate for DPT of ∼0.1 ns⁻¹ is consistent between biased and unbiased simulations. Extending the present work to other reaction types and protein–ligand binding will provide deeper chemical understanding and improved models suitable for statistically significant sampling to give molecular level insight into processes in the condensed phase. Contrary to straight AIMD simulations at the correlated level, an ML/MM MD ansatz is feasible even for nanosecond time scale simulations.

Data availability

The data needed for the PhysNet representation of the MP2 PES is available at https://github.com/MMunibas/fad.git.

Conflicts of interest

​There are no conflicts to declare.

Acknowledgements

This work was supported by the Swiss National Science Foundation grants 200021-117810, 200020-188724, NCCR MUST, and the University of Basel which is gratefully acknowledged. This project received funding from the European Union's Horizon 2020 research and innovation program under the Marie Skłodowska-Curie grant agreement no. 801459 – FP-RESOMUS.

References

1. A. Warshel and R. M. Weiss, An empirical valence bond approach for comparing reactions in solutions and in enzymes, J. Am. Chem. Soc., 1980, 102, 6218–6226.
2. J. Åqvist and A. Warshel, Simulation of enzyme reactions using valence bond force fields and other hybrid quantum/classical approaches, Chem. Rev., 1993, 93, 2523–2544.
3. J. Gajewski and N. Brichford, Secondary deuterium kinetic isotope effects in the aqueous Claisen rearrangement: Evidence against an ionic transition state, J. Am. Chem. Soc., 1994, 117, 3165–3166.
4. S. Brickel and M. Meuwly, Molecular determinants for rate acceleration in the Claisen rearrangement reaction, J. Phys. Chem. B, 2019, 123, 448–456.
5. M. Meuwly, Machine learning for chemical reactions, Chem. Rev., 2021, 121, 10218–10239.
6. S. C. Kamerlin, M. Haranczyk and A. Warshel, Are mixed explicit/implicit solvation models reliable for studying phosphate hydrolysis? A comparative study of continuum, explicit and mixed solvation models, Chem. Phys. Chem., 2009, 10, 1125–1134.
7. A. Plech, M. Wulff, S. Bratos, F. Mirloup, R. Vuilleumier, F. Schotte and P. A. Anfinrud, Visualizing chemical reactions in solution by picosecond X-ray diffraction, Phys. Rev. Lett., 2004, 92, 125505.
8. H. Hu and W. Yang, Free energies of chemical reactions in solution and in enzymes with ab initio quantum mechanics/molecular mechanics methods, Ann. Rev. Phys. Chem., 2008, 59, 573–601.
9. K. H. Kim, J. G. Kim, S. Nozawa, T. Sato, K. Y. Oang, T. Kim, H. Ki, J. Jo, S. Park and C. Song, et al., Direct observation of bond formation in solution with femtosecond X-ray scattering, Nature, 2015, 518, 385–389.
10. M. Meuwly, Reactive molecular dynamics: From small molecules to proteins, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2019, 9, e1386.
11. P. S. Nerenberg and T. Head-Gordon, New developments in force fields for biomolecular simulations, Curr. Opin. Struct. Biol., 2018, 49, 129–138.
12. D. Koner, S. M. Salehi, P. Mondal and M. Meuwly, Non-conventional force fields for applications in spectroscopy and chemical reaction dynamics, J. Chem. Phys., 2020, 153, 010901.
13. J. M. Guest, J. S. Craw, M. A. Vincent and I. H. Hillier, The effect of water on the Claisen rearrangement of allyl vinyl ether: Theoretical methods including explicit solvent and electron correlation, J. Chem. Soc., Perkin Trans. 2, 1997, 71.
14. Y. Jung and R. A. Marcus, On the theory of organic catalysis “on water”, J. Am. Chem. Soc., 2007, 129, 5492–5502 , PMID: 17388592.
15. W. N. White and E. F. Wolfarth, The O-Claisen rearrangement. VIII. Solvent effects, J. Org. Chem., 1970, 35, 2196.
16. O. Acevedo and K. Armacost, Claisen rearrangements: Insight into solvent effects and “on water” reactivity from QM/MM simulations, J. Am. Chem. Soc., 2010, 132, 1966.
17. S. C. van Keulen, A. Solano and U. Rothlisberger, How Rhodopsin tunes the equilibrium between protonated and deprotonated forms of the retinal chromophore, J. Chem. Theory Comput., 2017, 13, 4524–4534 , PMID: 28731695.
18. K. El Hage, S. Brickel, S. Hermelin, G. Gaulier, C. Schmidt, L. Bonacina, S. C. van Keulen, S. Bhattacharyya, M. Chergui and P. Hamm, et al., Implications of short time scale dynamics on long time processes, Struct. Dyn., 2017, 4, 061507.
19. A. J. Mulholland, P. D. Lyne and M. Karplus, Ab initio QM/MM study of the citrate synthase mechanism. A low-barrier hydrogen bond is not involved, J. Am. Chem. Soc., 2000, 122, 534–535.
20. H. M. Senn and W. Thiel, QM/MM methods for biomolecular systems, Angew. Chem., Int. Ed., 2009, 48, 1198–1229.
21. G. Groenhof, in Biomolecular Simulations: Methods and Protocols, ed. L. Monticelli and E. Salonen, Humana Press, Totowa, NJ, 2013, pp. 43–66.
22. A. C.-T. van Duin, S. Dasgupta, F. Lorant and W. A. Goddard III, ReaxFF: A reactive force field for hydrocarbons, J. Phys. Chem. A, 2001, 105, 9396–9409.
23. T. Nagy, J. Yosa Reyes and M. Meuwly, Multisurface adiabatic reactive molecular dynamics, J. Chem. Theory Comput., 2014, 10, 1366–1375.
24. S. J. Ang, W. Wang, D. Schwalbe-Koda, S. Axelrod and R. Gómez-Bombarelli, Active learning accelerates ab initio molecular dynamics on reactive energy surfaces, Chem, 2021, 7, 738–751.
25. L. Böselt, M. Thürlemann and S. Riniker, Machine learning in QM/MM Molecular dynamics simulations of condensed-phase systems, J. Chem. Theory Comput., 2021, 17, 2641–2658.
26. Y. Pan and M. A. McAllister, Characterization of low-barrier hydrogen bonds. 1. Microsolvation effects. An ab initio and DFT investigation, J. Am. Chem. Soc., 1997, 119, 7561–7566.
27. J.-H. Lim, E. K. Lee and Y. Kim, Theoretical study for solvent effect on the potential energy surface for the double proton transfer in formic acid dimer and formamidine dimer, J. Phys. Chem. A, 1997, 101, 2233–2239.
28. S. Miura, M. E. Tuckerman and M. L. Klein, An ab initio path integral molecular dynamics study of double proton transfer in the formic acid dimer, J. Chem. Phys., 1998, 109, 5290–5299.
29. J. Kohanoff, S. Koval, D. A. Estrin, D. Laria and Y. Abashkin, Concertedness and solvent effects in multiple proton transfer reactions: The formic acid dimer in solution, J. Chem. Phys., 2000, 112, 9498–9508.
30. H. Ushiyama and K. Takatsuka, Successive mechanism of double-proton transfer in formic acid dimer: A classical study, J. Chem. Phys., 2001, 115, 5903–5912.
31. R. Kalescky, E. Kraka and D. Cremer, Local vibrational modes of the formic acid dimer-the strength of the double hydrogen bond, Mol. Phys., 2013, 111, 1497–1510.
32. S. D. Ivanov, I. M. Grant and D. Marx, Quantum free energy landscapes from ab initio path integral metadynamics: Double proton transfer in the formic acid dimer is concerted but not correlated, J. Chem. Phys., 2015, 143, 124304.
33. E. Miliordos and S. S. Xantheas, On the validity of the basis set superposition error and complete basis set limit extrapolations for the binding energy of the formic acid dimer, J. Chem. Phys., 2015, 142, 094311.
34. D. P. Tew and W. Mizukami, Ab initio vibrational spectroscopy of cis- and trans-formic acid from a global potential energy surface, J. Phys. Chem. A, 2016, 120, 9815–9828.
35. C. Qu and J. M. Bowman, An ab initio potential energy surface for the formic acid dimer: Zero-point energy, selected anharmonic fundamental energies, and ground-state tunneling splitting calculated in relaxed 1-4-mode subspaces, Phys. Chem. Chem. Phys., 2016, 18, 24835–24840.
36. K. Mackeprang, Z.-H. Xu, Z. Maroun, M. Meuwly and H. G. Kjaergaard, Spectroscopy and dynamics of double proton transfer in formic acid dimer, Phys. Chem. Chem. Phys., 2016, 18, 24654–24662.
37. J. O. Richardson, Full- and reduced-dimensionality instanton calculations of the tunnelling splitting in the formic acid dimer, Phys. Chem. Chem. Phys., 2017, 19, 966–970.
38. C. Qu and J. M. Bowman, High-dimensional fitting of sparse datasets of CCSD(T) electronic energies and MP2 dipole moments, illustrated for the formic acid dimer and its complex IR spectrum, J. Chem. Phys., 2018, 148, 241713.
39. C. Qu and J. M. Bowman, Quantum and classical Ir spectra of (HCOOH)₂, (DCOOH)₂ and (DCOOD)₂ using ab initio potential energy and dipole moment surfaces, Faraday Discuss., 2018, 212, 33–49.
40. C. Qu and J. M. Bowman, Ir spectra of (HCOOH) ₂ and (DCOOH) ₂: Experiment, VSCF/VCI, and ab initio molecular dynamics calculations using full-dimensional potential and dipole moment surfaces, J. Phys. Chem. Lett., 2018, 9, 2604–2610.
41. S. Käser and M. Meuwly, Transfer learned potential energy surfaces: Accurate anharmonic vibrational dynamics and dissociation energies for the formic acid monomer and dimer, Phys. Chem. Chem. Phys., 2022.
42. F. Ito and T. Nakanaga, A jet-cooled infrared spectrum of the formic acid dimer by cavity ring-down spectroscopy, Chem. Phys. Lett., 2000, 318, 571–577.
43. M. Freytes, D. Hurtmans, S. Kassi, J. Liévin, J. Vander Auwera, A. Campargue and M. Herman, Overtone spectroscopy of formic acid, Chem. Phys., 2002, 283, 47–61.
44. R. Georges, M. Freytes, D. Hurtmans, I. Kleiner, J. Vander Auwera and M. Herman, Jet-cooled and room temperature FTIR spectra of the dimer of formic acid in the gas phase, Chem. Phys., 2004, 305, 187–196.
45. P. Zielke and M. Suhm, Raman jet spectroscopy of formic acid dimers: Low frequency vibrational dynamics and beyond, Phys. Chem. Chem. Phys., 2007, 9, 4528–4534.
46. Z. Xue and M. A. Suhm, Probing the stiffness of the simplest double hydrogen bond: The symmetric hydrogen bond modes of jet-cooled formic acid dimer, J. Chem. Phys., 2009, 131, 054301.
47. F. Kollipost, R. W. Larsen, A. Domanskaya, M. Nörenberg and M. Suhm, Communication: The highest frequency hydrogen bond vibration and an experimental value for the dissociation energy of formic acid dimer, J. Chem. Phys., 2012, 136, 151101.
48. A. Nejad and M. A. Suhm, Concerted pair motion due to double hydrogen bonding: The formic acid dimer case, J. Ind. Inst. Sci., 2020, 100, 5–19.
49. W. Reutemann and H. Kieczka, Ullmann's Encyclopedia of Industrial Chemistry, American Cancer Society, 2011.
50. R. M. Balabin, Polar (acyclic) isomer of formic acid dimer: Gas-phase Raman spectroscopy study and thermodynamic parameters, J. Phys. Chem. A, 2009, 113, 4910–4918.
51. W. Li, L. Evangelisti, Q. Gou, W. Caminati and R. Meyer, The barrier to proton transfer in the dimer of formic acid: A pure rotational study, Angew. Chem., Int. Ed., 2019, 58, 859–865.
52. Y. Zhang, W. Li, W. Luo, Y. Zhu and C. Duan, High resolution jet-cooled infrared absorption spectra of (HCOOH)₂, (HCOOD)₂, and HCOOH-HCOOD complexes in 7.2 μm region, J. Chem. Phys., 2017, 146, 244306.
53. M. Ortlieb and M. Havenith, Proton transfer in (HCOOH) ₂: An IR high-resolution spectroscopic study of the antisymmetric C-O stretch, J. Phys. Chem. A, 2007, 111, 7355–7363.
54. K. G. Goroya, Y. Zhu, P. Sun and C. Duan, High resolution jet-cooled infrared absorption spectra of the formic acid dimer: A reinvestigation of the C-O stretch region, J. Chem. Phys., 2014, 140, 164311.
55. V. Zoete and M. Meuwly, Double proton transfer in the isolated and DNA-embedded guanine-cytosine base pair, J. Chem. Phys., 2004, 121, 4377–4388.
56. A. A. Arabi and C. F. Matta, Effects of intense electric fields on the double proton transfer in the Watson–Crick guanine-cytosine base pair, J. Phys. Chem. B, 2018, 122, 8631–8641.
57. J. Chen, C. L. Brooks and H. A. Scheraga, Revisiting the carboxylic acid dimers in aqueous solution: Interplay of hydrogen bonding, hydrophobic interactions, and entropy, J. Phys. Chem. B, 2008, 112, 242–249.
58. A. Katchalsky, H. Eisenberg and S. Lifson, Hydrogen bonding and ionization of carboxylic acids in aqueous solutions, J. Am. Chem. Soc., 1951, 73, 5889–5890.
59. E. E. Schrier, M. Pottle and H. A. Scheraga, The influence of hydrogen and hydrophobic bonds on the stability of the carboxylic acid dimers in aqueous solution, J. Am. Chem. Soc., 1964, 86, 3444–3449.
60. S. Soffientini, L. Bernasconi and S. Imberti, The hydration of formic acid and acetic acid, J. Mol. Liq., 2015, 205, 85–92.
61. T. B. Sobyra, M. P. Melvin and G. M. Nathanson, Liquid microjet measurements of the entry of organic acids and bases into salty water, J. Phys. Chem. C, 2017, 121, 20911–20924.
62. V. Hänninen, G. Murdachaew, G. M. Nathanson, R. B. Gerber and L. Halonen, Ab initio molecular dynamics studies of formic acid dimer colliding with liquid water, Phys. Chem. Chem. Phys., 2018, 20, 23717–23725.
63. E. Tarakanova, G. Voloshenko, I. Kislina, V. Mayorov, G. Yukhnevich and A. Lyashchenko, Composition and structure of hydrates formed in aqueous solutions of formic acid, J. Struct. Chem., 2019, 60, 255–267.
64. Z. Dou, L. Wang, J. Hu, W. Fang, C. Sun and Z. Men, Hydrogen bonding effect on Raman modes of formic acid-water binary solutions, J. Mol. Liq., 2020, 313, 113595.
65. A. H. Larsen, J. J. Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer and C. Hargus, et al., The atomic simulation environment – A Python library for working with atoms, J. Phys.: Condens. Matter, 2017, 29, 273002.
66. O. T. Unke and M. Meuwly, Physnet: A neural network for predicting energies, forces, dipole moments, and partial charges, J. Chem. Theory Comput., 2019, 15, 3678–3693.
67. W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, Comparison of simple potential functions for simulating liquid water, J. Chem. Phys., 1983, 79, 926–935.
68. H.-J. Werner, P. J. Knowles, F. R. Manby, J. A. Black, K. Doll, A. Helmann, D. Kats, A. Köhn, T. Korona and D. A. Kreplin, et al., The Molpro quantum chemistry package, J. Chem. Phys., 2020, 152, 144107.
69. B. Huang and O. A. von Lilienfeld, Quantum machine learning using atom-in-molecule-based fragments selected on the fly, Nat. Chem., 2020, 12, 945–951.
70. J. Behler, Constructing high-dimensional neural network potentials: A tutorial review, Int. J. Quantum Chem., 2015, 115, 1032–1050.
71. O. T. Unke and M. Meuwly, A reactive, scalable, and transferable model for molecular energies from a neural network approach based on local information, J. Chem. Phys., 2018, 148, 241708.
72. S. Grimme, S. Ehrlich and L. Goerigk, Effect of the damping function in dispersion corrected density functional theory, J. Comput. Phys., 2011, 32, 1456–1465.
73. M. Abadi, A. Agarwal, P. Barham, E. Brevdo, Z. Chen, C. Citro, G. S. Corrado, A. Davis, J. Dean, M. Devin, et al., TensorFlow: Large-scale Machine Learning on Heterogeneous Systems, 2015, https://tensorflow.org/, Software available from http://tensorflow.org.
74. A. G. Baydin, B. A. Pearlmutter, A. A. Radul and J. M. Siskind, Automatic differentiation in machine learning: A survey, J. Mach. Learn. Res., 2018, 18, 1–43.
75. J. J. Mortensen, L. B. Hansen and K. W. Jacobsen, Real-space grid implementation of the projector augmented wave method, Phys. Rev. B, 2005, 71, 035109.
76. K. Vanommeslaeghe, E. Hatcher, C. Acharya, S. Kundu, S. Zhong, J. Shim, E. Darian, O. Guvench, P. Lopes and I. Vorobyov, et al., CHARMM general force field: A force field for drug-like molecules compatible with the CHARMM all-atom additive biological force fields, J. Comput. Phys., 2010, 31, 671–690.
77. E. Spohr, Effect of electrostatic boundary conditions and system size on the interfacial properties of water and aqueous solutions, J. Chem. Phys., 1997, 107, 6342–6348.
78. G. M. Torrie and J. P. Valleau, Nonphysical sampling distributions in Monte Carlo free-energy estimation: Umbrella sampling, J. Chem. Phys., 1977, 23, 187–199.
79. H. C. Andersen, Rattle: A “velocity” version of the shake algorithm for molecular dynamics calculations, J. Comput. Phys., 1983, 52, 24–34.
80. J. Enkovaara, C. Rostgaard, J. J. Mortensen, J. Chen, M. Dułak, L. Ferrighi, J. Gavnholt, C. Glinsvad, V. Haikola and H. A. Hansen, et al., Electronic structure calculations with GPAW: A real-space implementation of the projector augmented-wave method, J. Phys.: Condens. Matter, 2010, 22, 253202.
81. M. Meuwly and M. Karplus, Simulation of proton transfer along ammonia wires: An “ab initio” and semiempirical density functional comparison of potentials and classical molecular dynamics, J. Chem. Phys., 2002, 116, 2572–2585.
82. A. D. Becke, Density-functional thermochemistry. III. The role of exact exchange, J. Chem. Phys., 1993, 98, 5648–5652.
83. C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B, 1988, 37, 785–789.
84. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104.
85. D. Sidler, M. Meuwly and P. Hamm, An efficient water force field calibrated against intermolecular THz and Raman spectra, J. Chem. Phys., 2018, 148, 244504.
86. X. Huang, C. Tang, J. Li, L.-C. Chen, J. Zheng, P. Zhang, J. Le, R. Li, X. Li and J. Liu, et al., Electric field-induced selective catalysis of single-molecule reaction, Sci. Adv., 2019, 5, eaaw3072.
87. S. Shaik, S. P. De Visser and D. Kumar, External electric field will control the selectivity of enzymatic-like bond activations, J. Am. Chem. Soc., 2004, 126, 11746–11749.
88. J. Ropp, C. Lawrence, T. Farrar and J. Skinner, Rotational motion in liquid water is anisotropic: A nuclear magnetic resonance and molecular dynamics simulation study, J. Am. Chem. Soc., 2001, 123, 8047–8052.
89. D. M.-S. Martins, D. S. Middlemiss, C. R. Pulham, C. C. Wilson, M. T. Weller, P. F. Henry, N. Shankland, K. Shankland, W. G. Marshall and R. M. Ibberson, et al., Temperature- and pressure-induced proton transfer in the 1:1 adduct formed between squaric acid and 4,4'-bipyridine, J. Am. Chem. Soc., 2009, 131, 3884–3893.
90. Z. Ma, J. Li, C. Sun and M. Zhou, High pressure spectroscopic investigation on proton transfer in squaric acid and 4,4′-bipyridine co-crystal, Sci. Rep., 2017, 7, 4677.
91. Z.-H. Xu and M. Meuwly, Vibrational spectroscopy and proton transfer dynamics in protonated oxalate, J. Phys. Chem. A, 2017, 121, 5389–5398.

---

Footnote

† Electronic supplementary information (ESI) available: It reports additional graphics S1–S14. See DOI: https://doi.org/10.1039/d2cp01583h

---