Donors, acceptors, and a bit of aromatics: electronic interactions of molecular adsorbates on hBN and MoS₂ monolayers

Abstract

The design of low-dimensional organic–inorganic interfaces for the next generation of opto-electronic applications requires in-depth understanding of the microscopic mechanisms ruling electronic interactions in these systems. In this work, we present a first-principles study based on density-functional theory inspecting the structural, energetic, and electronic properties of five molecular donors and acceptors adsorbed on freestanding hexagonal boron nitride (hBN) and molybdenum disulfide (MoS₂) monolayers. All considered interfaces are stable, due to the crucial contribution of dispersion interactions, which are maximized by the overall flat arrangement of the physisorbed molecules on both substrates. The level alignment of the hybrid systems depends on the characteristics of the constituents. On hBN, both type-I and type-II interfaces may form, depending on the relative energies of the frontier orbitals with respect to the vacuum level. On the other hand, all MoS₂-based hybrid systems exhibit a type-II level alignment, with the molecular frontier orbitals positioned across the energy gap of the semiconductor. The electronic structure of the hybrid materials is further determined by the formation of interfacial dipole moments and by the wave-function hybridization between the organic and inorganic constituents. These results provide important indications for the design of novel low-dimensional hybrid materials with suitable characteristics for opto-electronics.

---

1 Introduction

Hybrid materials formed by carbon-conjugated molecules adsorbed on low-dimensional semiconductors and insulators have been attracting attention due to the their structural versatility and electronic tunability.^1–9 Depending on their density on the substrate and on their physico-chemical characteristics, physisorbed moieties can introduce localized electronic states,^10–12 dispersive bands,⁷ or a combination thereof.^13–15 The electronic structure of the interface results from the level alignment between the organic and inorganic components^16–20 and the hybridization between their electronic wave-functions.^15,21–24 As both these effects depend on the intrinsic nature of the building blocks, the need for systematic analyses on the electronic structure of hybrid systems are in high demand.

Electronic structure calculations based on density-functional theory (DFT) are particularly suited for this purpose^25,26 and for exploring various material combinations without requiring empirical parameters. With the electron density being its central quantity, DFT grants immediate access to the charge redistribution induced by adsorption.^13,14,21,27 This way, it is possible to assess the type of ground-state doping and to gain insight into the spatial extension of the electron cloud at the interface. Furthermore, DFT calculations are able to deliver work functions, level alignments, band structures, and (projected) density of states, among other important properties.^2,13–15,27 While state-of-the-art first-principles methods to obtain the electronic structure of solid-state materials are currently based on many-body perturbation theory,^18,28,29 the choice of range-separated hybrid functionals to approximate the exchange–correlation potential in DFT offers the optimal trade-off between accuracy and computational costs.^15,27 Proper inclusion of van der Waals interactions improves the prediction of structural arrangements and hence the description of electronic properties.³⁰ The level of accuracy currently achieved by such ab initio calculations ensures reliable results complementary to experiments.^2,27,31

In this work, we present a DFT study on the structural, energetic, and electronic properties of five representative organic molecules, including donor and acceptor compounds as well as a purely aromatic moiety, adsorbed on freestanding hexagonal boron nitride (hBN) and molybdenum disulfide (MoS₂) monolayers. The former is a known insulator, widely used as a substrate and/or as an encapsulating material in low-dimensional interfaces,¹⁷ which has been receiving increasing attention in surface and interface science,^32–38 for instance to sustain the growth of well-defined organic thin films.^9,39,40 MoS₂ belongs to the family of transition-metal dichalcogenides, the most promising emerging class of low-dimensional semiconductors. By performing geometry optimizations using the generalized-gradient approximation (GGA) and refining the analysis of the electronic structure using a range-separated hybrid functional, we rationalize how the nature of the constituents of the hybrid interface determines the level alignment and the projected density of states. Our findings offer useful indications to interpret and predict the electronic properties of similar low-dimensional hybrid interfaces from the character of substrates and adsorbates.

2 Methods and systems

2.1 Computational details

All results presented in this work are obtained from DFT⁴¹ electronic structure calculations through the solution of the Kohn-Sham equations.⁴² The structures are optimized at the GGA level of theory, using the Perdew–Burke–Ernzerhof (PBE) functional.⁴³ To compute electronic properties on each optimized structure, including densities of states, energy levels alignment and molecular orbitals, the Heyd–Scuseria–Ernzerhof (HSE06)⁴⁴ range-separated hybrid functional is adopted.

Based on the assessed reproducibility of DFT calculations,⁴⁵ we adopted two different software packages to produce the two sets of results presented in this work. For all complexes with hBN as a substrate, we employ the Gaussian and plane-wave formalism, as implemented in the CP2K package.⁴⁶ We choose the short-range-double-ζ MOLOPT basis sets⁴⁷ for the expansion of the valence electron density, while the interaction with the atomic cores is represented by Godecker–Teter–Hutter (GTH) pseudopotentials.^48–50 The expansion of the density in an auxiliary plane waves basis is truncated at the kinetic-energy cutoff of 600 Ry. The van der Waals (vdW) contributions are included either according to the Grimme-D3 scheme⁵¹ or by augmenting the exchange–correlation functional with the self-consistent rVV10 functional,⁵² which in combination with PBE is known to provide reliable structural properties for similar hybrid interfaces.⁵³ We apply the quasi-Newtonian Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm to minimize interatomic forces with a convergence criterion of 5 × 10⁻⁴ Ha bohr⁻¹ in the energy gradients. This approach does not ensure access to global energy minima, in contrast with other methods such as, for example, those presented in ref. 54–57. However, given the weak and dispersive nature of the interaction forces between the organic and inorganic components (see Section 3.1 below), we have checked that this choice does not impact our results nor our conclusions. The Brillouin zone is sampled at the Γ-point only given the insulating character of monolayer hBN⁵⁸ and the relatively large supercell employed in these calculations. For the MoS₂-based interfaces, we use the plane-wave expansion of the wave-functions and the electron density as implemented in the Quantum Espresso code,⁵⁹ with a cutoff of 30 and 300 Ry respectively, and the projector augmented-wave method.⁶⁰ BFGS optimization is carried out with a threshold for the interatomic forces of 5 × 10⁻⁴ Ha bohr⁻¹. A uniform 6 × 6 × 1 k-point mesh is adopted to sample the Brillouin zone in light of the dispersive character of the conduction bands of MoS₂ and vdW corrections are included according to the Grimme-D3 scheme.⁵¹ The combination of results obtained on the same theoretical footing with Quantum Espresso and CP2K has been already proposed in the literature (for a recent example, see ref. 61).

2.2 Model systems

We consider two-dimensional (2D) hybrid interfaces formed by five carbon-conjugated moieties physisorbed on monolayer hBN and MoS₂. The organic molecules considered in this study exhibit different electronic characteristics: tetrathiafulvalene (TTF) and 2,2′-bithiophene (2T) are known to act as donors, while 7,7,8,8-tetracyanoquinodimethane (TCNQ) and its tetrafluorinated derivative (F₄−TCNQ) are strong acceptors;⁶² for comparison, we additionally consider pyrene,^63,64 a polycyclic aromatic hydrocarbon⁶⁵ of similar size as the aforementioned molecules. The hybrid model interfaces are constructed by placing in the simulation cell one molecule on top of the two dimensional material with parallel backbone with respect to the substrate and running a geometry optimization (see Fig. 1 and 2).

Fig. 1 (a) A 6 × 6 supercell of hBN monolayer; top and side views of the hybrid interfaces formed by (b) tetrathiafulvalene (TTF), (c) bithiophene (2T), (d) pyrene, (e) tetracyanoquinodimethane (TCNQ), and (f) fluorinated TCNQ (F₄−TCNQ) adsorbates.

Fig. 2 (a) A 4 × 4 supercell of MoS₂ monolayer; top and side views of hybrid interfaces formed by (b) tetrathiafulvalene (TTF), (c) bithiophene (2T), (d) pyrene, (e) tetracyanoquinodimethane (TCNQ) and (f) fluorinated TCNQ (F₄–TCNQ) adsorbates.

In all cases, the lattice parameter of the two-dimensional substrate is optimized in its unit cell by performing volume optimization in conjunction with a minimization of the interatomic forces. From this procedure, we obtain a_hBN = 2.50 Å and a_MoS2 = 3.19 Å. Both values are in excellent agreement with available theoretical and experimental references for hBN^66–68 and MoS₂.^69–71 In order to host the considered molecules in a flat arrangement, hBN is modelled in a 6 × 6 supercell, while for MoS₂ we use a 4 × 4 supercell. A sufficiently large amount of vacuum (20 Å with MoS₂ and 40 Å with hBN) above the interfaces prevents spurious interactions between the replicas under the applied periodic boundary conditions.

3 Results and discussion

3.1 Structural properties

All molecules adsorb approximately flat on top of hBN, thus maximising dispersion interactions. The distance of the molecular species from the substrate plane ranges from 3.3 to 3.4 Å. Upon adsorption, the molecular structures do not change appreciably compared to the gas-phase configurations. Exceptions concern a concave bending of TTF of about 11° towards the substrate (see Fig. 1b), in contrast with previous results on metallic surfaces,^72,73 where the molecule bends in a convex fashion due to the strong interactions with the metal electronic charge density. Furthermore, 2T undergoes a backbone “twist” with a dihedral angle of 7° (Fig. 1c). Finally, hBN is subject to a slight rippling as a result of the attractive π–π interactions with the physisorbed molecules. Specifically, B and N atoms in closest vicinity with the physisorbed moiety tend to be attracted by it and hence to be up-shifted with respect to the basal plane of the monolayer. Corresponding values estimated as the vertical displacement of the aforementioned atoms with respect to those unaffected by interactions with the molecule are equal to 0.21 Å, 0.23 Å, 0.27 Å, and 0.29 Å in the interfaces with TTF and 2T, with TCNQ, with F₄–TCNQ, and with pyrene, respectively, see Fig. 1.

In the hybrid interface including the MoS₂ substrate (Fig. 2a), the donor molecules TTF and 2T exhibit the same concave bending and backbone twisting as in the hBN-based ones discussed above (see Fig. 2b and c). As a result, in these molecules, the hydrogen atoms are closer to the substrate than the carbon atoms, at a distance of 3.39 Å. When physisorbed on MoS₂, the acceptors TCNQ and F₄–TCNQ are slightly bent, too, with the nitrogen atoms pointing towards the substrate and being displaced 0.2 Å downwards with respect to the backbone plane lying at 3.39 Å above the monolayer (see Fig. 2e and f). This behavior is analogous to the one exhibited by these molecules on ZnO,⁷⁴ on graphene,⁷⁵ and on the hydrogenated Si(111) surface.^76,77 Finally, pyrene, which is planar in the gas phase,⁶⁵ remains such also upon adsorption, and lays at a distance of 3.32 Å from MoS₂.

3.2 Energetics

In order to quantify the energetic stability of the considered hybrid interfaces, we introduce the adsorption energy defined as:

E_ads = E^opt_mol@surf − E^opt_surf − E^opt_mol, (1)

where the superscript “opt” refers to the optimized geometries and the subscripts “mol” and “surf” stand for the molecular and surface, respectively. In the hBN-based interfaces, the adsorption strength increases from donor-like systems to the acceptors (see Table 1) with F₄–TCNQ, the most electron-withdrawing molecule among the considered ones, leading to the most stable interface precisely on account of this characteristic.^38,78 To better characterize the nature of the molecule-substrate interactions in the hybrid systems, it is convenient to single out the dispersion contribution from the interaction strength, by introducing the interaction energy

E_int = E^opt_mol@surf − E_surf − E_mol, (2)

where E_surf and E_mol are the single-point energies computed for the individual subsystems taken with the same coordinates as in the optimized complex. The dispersion contribution to each term is defined as the energy difference at fixed coordinates between a calculation with the vdW correction and one without it. The final contribution to the adsorption is given by the dispersion energy, defined as:

E_disp = E^disp_mol@surf − E^disp_surf − E^disp_mol. (3)

As expected, in the case of the hBN-based interfaces, the dispersion contribution turns out to be predominant (see Table 1), confirming that no chemical bond is formed between the molecules and the monolayer. The small, yet noticeable, differences between adsorption and interaction energies (20–40 meV) indicate that the charge distribution and also the original geometries of both molecules and substrate are slightly perturbed upon physisorption. When comparing the interaction energy with the dispersion contribution, one observes that the latter is slightly more negative. This result points to a minor destabilization effect due to distortions upon molecular adsorption. Indeed, the interaction term must include some repulsive (Pauli) contributions owing to the overlap of the electronic distributions of molecule and substrate, whereas the dispersion part is purely attractive.

Table 1 Adsorption energy (E_ads) calculated for the hBN-based interface at the PBE-vdW level, using both the D3 and rVV10 scheme for the vdW contributions; interaction energy (E_int) and dispersion energy (E_disp) computed at the PBE-rVV10 level of theory. All values are in eV

System	E ads (D3)	E ads (rVV10)	E int (rVV10)	E disp (rVV10)
TTF@hBN	−0.96	−1.06	−1.08	−1.09
2T@hBN	−0.85	−0.96	−0.98	−1.02
Pyrene@hBN	−1.13	−1.30	−1.33	−1.44
TCNQ@hBN	−1.04	−1.21	−1.24	−1.31
F4–TCNQ@hBN	−1.14	−1.41	−1.45	−1.49

---

Depending on the choice of vdW functional, the relative magnitude of dispersion vs. interaction may somewhat vary, but our comparison between two approaches demonstrates the same qualitative picture (see Table 1). In both cases, all adsorption energies lie between −0.9 and −1.4 eV and the relative trends in stability are the same. The following electronic-structure calculations involving the hBN substrate are then restricted to the rVV10 approach only, which proved to yield reliable adsorption and structural properties.⁵³ The adsorption of TCNQ and TTF on hBN was investigated in a previous work by Tang and coworkers⁷⁹ who applied DFT with the PBE functional and no additional vdW correction. The resulting adsorption energies are −0.112 eV and −0.041 eV, respectively, i.e., significantly weaker due to the missing dispersion contribution.

Moving now to the MoS₂-based interfaces, we find a qualitatively similar trend in the adsorption energies as the one discussed above for the interfaces with hBN (see Table 2). Among the considered systems, the least stable one is 2T@MoS₂, due to the twisted backbone of the molecule that reduces the attractive π–π interactions with the substrate. Unsurprisingly, the most negative value of E_ads is found for pyrene, which adsorbs flat on MoS₂ (see Fig. 2d). On the other hand, in all MoS₂-based interfaces, adsorption and interaction energies exhibit differences on the order of 10⁻³ eV, as a sign of negligible energy relaxation of the molecules and of the MoS₂ monolayer when the hybrid interfaces are formed. These variations are one order of magnitude smaller than those computed for the hBN-based interfaces (see Table 1). A reason for these contrasting behaviors can be ascribed to the chemical nature of the two substrates: While hBN is characterized by a N-rich surface, MoS₂ has instead a S-rich one. Such bare distinction in the composition of the two inorganic materials affects the affinity of the adsorbates towards them. Indeed, N-containing molecules such as TCNQ and its fluorinated sibling adsorb more favorably on hBN than TTF and 2T which are S-rich, likely as a consequence of orbital overlap between atoms of same kind. The values of dispersion energies shown in Table 2 exhibit a qualitative difference with respect to their counterparts in Table 1, namely, the dispersion contribution for pyrene on MoS₂ is larger than the one for F₄–TCNQ. This behavior which can be explained again based on the chemical affinity argument presented above.

Table 2 Adsorption energy (E_ads), interaction energy (E_int) and dispersion energy (E_disp) for the MoS₂-based heterostrustructures computed at the PBE-Grimme-D3 level of theory. All values are in eV

System	E ads (D3)	E int (D3)	E disp (D3)
TTF@MoS2	−0.91	−0.91	−0.94
2T@MoS2	−0.77	−0.77	−0.82
Pyrene@MoS2	−1.02	−1.02	−1.17
TCNQ@MoS2	−0.88	−0.88	−0.97
F4–TCNQ@MoS2	−0.97	−0.97	−1.01

---

3.3 Electronic properties

In the last part of our analysis, we inspect the electronic properties of the considered hybrid interfaces analyzing in particular the energy level alignment and the projected density of states. Again, we start from the hybrid systems including hBN. Like its bulk counterpart^66,80–82 monolayer hBN is an insulator⁵⁸ with a computed value of the quasi-particle band-gap above 7 eV.^83,84 Our result obtained from DFT with the HSE06 hybrid functional (6.08 eV, see Fig. 3) underestimates that value but it significantly improves it with respect to the one obtained from local DFT.⁸⁴ The agreement with experimental references is also very good.^38,66,85 The large electronic gap of hBN and the absolute energies of its band edges determine the alignment with respect to the molecular frontier levels (Fig. 3). Both frontier states of TTF, 2T, and pyrene fall within the energy gap of hBN, leading to a type-I lineup. In these three interfaces, the band edges lie within the band-gap of hBN, however, they are systematically downshifted by a few hundreds of meV with respect to the frontier states of the molecules. In the interfaces including TCNQ and F₄–TCNQ, instead, the highest-occupied molecular orbital (HOMO) of the gas-phase molecules lies below the valence-band maximum (VBM) of free-standing hBN, giving rise to a type-II level alignment. In these cases, the highest occupied (lowest-unoccupied) level of the hybrid interface is downshifted (upshisfted) by a few tens of meV with respect to the respective counterpart in the isolated monolayer (molecule), see Fig. 3.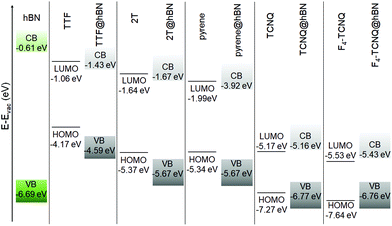

Fig. 3 Energy level alignment computed for the hBN-based hybrid interfaces using the HSE06 + rVV10 hybrid functional.

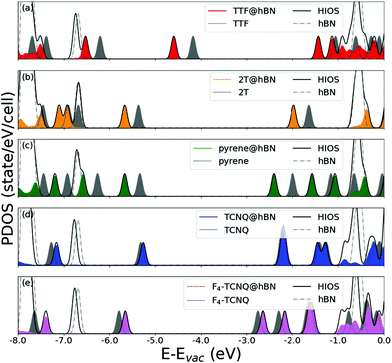
The plots of the projected density of states (PDOS) reported in Fig. 4 confirm the picture rendered by Fig. 3. Furthermore, they visually show that the localization of the frontier states reflects the energetic lineup of the electronic levels. For a more detailed analysis, we include in Fig. 4 the density of states of the isolated constituents. For further comparison, the contributions of the molecules within the electronic structure of the hybrid interfaces are shown, too. By inspecting these results, we identify two concomitant effects in the PDOS of the interfaces. First, the energy levels of the physisorbed molecules undergo a shift with respect to their counterparts in gas-phase. As the direction of this shift depends on the electron-donating (downwards) or -accepting (upwards) character of the molecule, we can rationalize this effect in terms of charge transfer. With the moiety releasing or withdrawing electrons to or from the substrate, an interfacial dipole is formed. For the chosen molecules, the electron-donating character of the donor is stronger in magnitude than the withdrawing ability of the acceptors. As a result, the frontier levels of TTF, 2T, and pyrene are subject to a downshift of a few hundreds of meV, up to 0.5 eV; those of TCNQ and its tetrafluorinated counterpart undergo instead an upshift of the order of 100 meV. The second effect disclosed by Fig. 4 is the electronic hybridization between the molecular orbitals and the hBN bands, which is particularly evident in the valence region of TTF@hBN, 2T@hBN, and, to a lesser extent, of pyrene@hBN (Fig. 4a–c), as well as in the conduction region of the interfaces hosting the molecular acceptors (Fig. 4d and e). With the partial exception of the lowest-unoccupied molecular orbital (LUMO) of TTF and the HOMO of F₄–TCNQ, the frontier states of the hybrid systems do not hybridize with hBN bands.

Fig. 4 Projected density of states for the hBN-based hybrid inorganic–organic systems (HIOS, black solid lines), including (a and b) the donors, TTF and 2T, (c) the aromatic molecule pyrene, and (d and e) the acceptors, TCNQ and F₄–TCNQ, calculated at the HSE06 + rVV10 level of theory and compared against the results obtained for the isolated constituents shown by dashed lines (hBN) and gray areas (molecules).The contributions of the molecules within the hybrid interfaces are depicted by colored areas. A broadening of 50 meV is applied in all plots. The energy scale is offset to the vacuum level (E_vac).

Moving now to the electronic properties of the MoS₂-based hybrid interfaces, we notice that all these systems exhibit a type-II level alignment, with the band edges of the interfaces being determined by the electron-donating ability of the absorbed molecule (see Fig. 5). Upon adsorption of TTF, 2T, and pyrene, the highest-occupied state of the interface corresponds to the HOMO of the adsorbate, whereas the lowest-unoccupied one is given by the conduction-band minimum (CBM) of free-standing MoS₂. On the contrary, the LUMO of the molecular acceptors, TCNQ and F₄–TCNQ, falls within the energy gap of MoS₂, whereas the HOMO of these molecules is lower than the VBM of the 2D material, in agreement with the known behavior of electron accepting molecules on this type of substrates.¹⁴

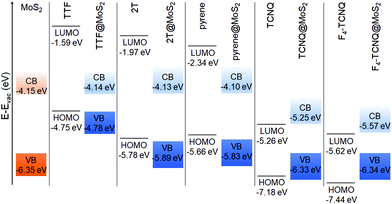Fig. 5 Energy level alignment computed for MoS₂-based hybrid interfaces using the HSE06 + D3 functional.

The PDOS calculated for the MoS₂-based interfaces and reported in Fig. 6 illustrate well the distribution of the molecular states of the adsorbates with respect to the electronic bands of the substrate. In the occupied region, hybridization between MoS₂ states and molecular orbitals can be seen especially for the interfaces including the donor molecules and pyrene (Fig. 6a–c). This effect manifests itself as a broadening of the peaks associated with molecular states, which are no longer δ-like maxima as in the isolated counterpart. On the other hand, acceptor molecules do not exhibit any signs of hybridization with the MoS₂ bands, at least in the energy window displayed in Fig. 6d and e.

Fig. 6 Projected density of states of all MoS₂-based hybrid inorganic–organic systems (HIOS, black solid lines), including (a and b) the donor molecules TTF and bithiophene, (c) the aromatic molecule pyrene, and (d and e) the molecular acceptors, TCNQ and F₄–TCNQ, calculated at the HSE06 + D3 level of theory and compared against the results obtained for the isolated constituents shown by dashed lines (MoS₂) and gray areas (molecules). The contributions of the molecules within the hybrid interfaces are depicted by colored areas. A broadening of 50 meV is applied in all plots. The energy scale is offset to the vacuum level (E_vac).

Additionally, in Fig. 6, consequences of charge transfer between the molecule and the substrate can be seen, as already discussed for the hBN-based interfaces. When the donor molecules TTF and 2T are adsorbed on MoS₂, their energy levels are downshifted with respect to their counterparts in the isolated moieties. The size of such shifts is not rigid. In TTF@MoS₂, the highest-occupied state coinciding with the HOMO of the molecule is only 51 meV below the highest-occupied orbital of the gas-phase donor. On the other hand, the HOMO−1 and the HOMO−2 are downshifted by 130 meV and 200 meV, respectively. In the PDOS of the 2T@MoS₂ interface, the HOMO is downshifted by 110 meV with respect to the gas-phase counterpart. For the HOMO−1, HOMO−2, and HOMO−3, the shift of the molecular levels due to charge transfer is entangled with the hybridization with MoS₂ bands, which induces a remarkable smearing in the corresponding peaks. As a result, a quantitative assessment of the former effect is not straightforward. A similar behavior is shown also by the PDOS of the pyrene@MoS₂ interface, whereby, interestingly, the downshift of the HOMO is the largest among those seen in Fig. 6. In this system, the three occupied states of pyrene that are visible in Fig. 6c are also subject to the joint action of charge-transfer-induced downshift and hybridization with MoS₂ bands. The energy levels of the molecular acceptors adsorbed on MoS₂ are upshifted by the creation of an interfacial dipole with the monolayer. Similar to the scenario offered by the hBN-based interfaces, the magnitude of this effect is much less pronounced than for the donors and signs of hybridization with the substrate bands are hardly visible. In the TCNQ@MoS₂ interface (Fig. 6d), the molecular levels are essentially aligned with their counterparts in the isolated molecule. The PDOS of F₄–TCNQ@MoS₂ exhibits a similar behavior (Fig. 6d) but, in this case, the upshift of the HOMO and LUMO levels of F₄–TCNQ is almost rigid and as large as 60 meV.

4 Summary and conclusions

In summary, we presented a DFT study of hybrid interfaces formed by hBN and MoS₂ monolyers acting as substrates for five physisorbed molecules: two electron-donor species, TTF and 2T, two acceptors, TCNQ and F₄–TCNQ, and the purely aromatic hydrocarbon, pyrene. All molecules adsorb substantially flat on both substrates, although structural modifications can be seen depending on the chemical nature of adsorbates and substrates: Donor and acceptor compounds undergo minor distortions due to the presence of S and N atoms therein, respectively; hBN ripples slightly when interacting with the physisorbed molecules while, owing to its larger rigidity, the structure of MoS₂ in the hybrid interfaces is unchanged compared to the isolated configuration. From an energetic point of view, all material combinations form stable interfaces thanks to the contribution of dispersive interactions, which are quantitatively accounted for in our calculations. As a general trend, pyrene and the acceptors adsorb more favorably on both substrates than the considered donors.

From the analysis of the electronic structure, we noticed weak coupling between molecules and hBN, as expected from the chemically inert and insulating character of this 2D material. In the considered hBN-based interfaces, both type-I and type-II level alignments are formed. Straddling lineups appear for the donor molecules, TTF and 2T, and for pyrene; staggered ones are driven by the acceptors TCNQ and F₄–TCNQ and their relatively low frontier levels with respect to the vacuum. In contrast, all MoS₂-based hybrid systems exhibit a type-II level alignment, with the highest-occupied (lowest-unoccupied) level of the interface coinciding with the HOMO (LUMO) of the electron-donating (-withdrawing) molecule. The projected density of states of all considered interfaces show two concomitant effects: (i) hybridization between the electronic states of the inorganic and organic components, involving only marginally the frontier orbitals of the physisorbed molecules and (ii) charge transfer between the molecules and the monolayer substrates shifting the molecular energy levels up- or downwards, depending on the electron-donating or electron-withdrawing nature of the organic compounds. Interestingly, both effects are qualitatively and, to a large extent, also quantitatively similar regardless of the substrate.

The results of this work provide important indications to rationalize the design of low-dimensional hybrid interfaces for opto-electronic applications. Our findings suggest that the characteristics of the physisorbed molecules play a bigger role in determining the details of the electronic structure of the interface than those of the inorganic substrate. However, the band-gap of the latter and the relative energies of their band edges rules to the largest extend the level alignment of the hybrid system. Future work on the characterization of the electronic excitations is expected to supplement this analysis for a deeper understanding of the opto-electronic activity of these novel materials.

Author contributions

Giacomo Melani: investigation, data curation, visualization, writing – original draft; Juan Pablo Guerrero Felipe: investigation, data curation, visualization, writing – original draft; Ana M. Valencia: data curation, visualization, supervision, writing – original draft; Jannis Krumland: supervision, writing – review editing; Caterina Cocchi: conceptualization, supervision, project administration, funding acquisition, writing – review editing; Marcella Iannuzzi: conceptualization, supervision, project administration, funding acquisition, writing – review editing.

Data availability statement

All data produced in this work are available free of charge at 10.5281/zenodo.6388531.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was carried out in the framework of the strategic partnership between the University of Zürich and the Humboldt Universität zu Berlin. G. M. and M. I. gratefully acknowledge computational support from the Swiss National Supercomputing Centre (CSCS) under project s965 “Molecules at interfaces from density functional theory”. G. M. acknowledges funding from the University of Zürich Forschungskredit Postdoctoral Fellowship. J. P. G, A. M. V., J. K., and C. C. appreciate funding from the German Research Foundation (DFG), project number 182087777 – CRC 951, and computational resources from the North-German Supercomputing Alliance (HLRN), project bep00104. Additional support is acknowledged by A. M. V. and C. C. to the German Federal Ministry of Education and Research (Professorinnenprogramm III), and by the State of Lower Saxony (Professorinnen für Niedersachsen).

Notes and references

1. G.-H. Lee, C.-H. Lee, A. M. van der Zande, M. Han, X. Cui, G. Arefe, C. Nuckolls, T. F. Heinz, J. Hone and P. Kim, APL Mater., 2014, 2, 092511.
2. Y. J. Zheng, Y. L. Huang, Y. Chen, W. Zhao, G. Eda, C. D. Spataru, W. Zhang, Y.-H. Chang, L.-J. Li, D. Chi, S. Y. Quek and A. T. S. Wee, ACS Nano, 2016, 10, 2476–2484.
3. T. Breuer, T. Maßmeyer, A. Mänz, S. Zoerb, B. Harbrecht and G. Witte, Phys. Status Solidi RRL, 2016, 10, 905–910.
4. M. Gobbi, E. Orgiu and P. Samorì, Adv. Mater., 2018, 30, 1706103.
5. L. Daukiya, J. Seibel and S. De Feyter, Adv. Phys: X, 2019, 4, 1625723.
6. N. Mrkyvkova, M. Hodas, J. Hagara, P. Nadazdy, Y. Halahovets, M. Bodik, K. Tokar, J. W. Chai, S. J. Wang, D. Z. Chi, A. Chumakov, O. Konovalov, A. Hinderhofer, M. Jergel, E. Majkova, P. Siffalovic and F. Schreiber, Appl. Phys. Lett., 2019, 114, 251906.
7. K. Rijal, F. Rudayni, T. R. Kafle and W.-L. Chan, J. Phys. Chem. Lett., 2020, 11, 7495–7501.
8. J.-W. Qiao, M.-S. Niu, Z.-C. Wen, X.-K. Yang, Z.-H. Chen, Y.-X. Wang, L. Feng, W. Qin and X.-T. Hao, 2D Mater., 2021, 8, 025026.
9. S. H. Amsterdam, T. J. Marks and M. C. Hersam, J. Phys. Chem. Lett., 2021, 12, 4543–4557.
10. P. Choudhury, L. Ravavarapu, R. Dekle and S. Chowdhury, J. Phys. Chem. C, 2017, 121, 2959–2967.
11. C. Zhong, V. K. Sangwan, C. Wang, H. Bergeron, M. C. Hersam and E. A. Weiss, J. Phys. Chem. Lett., 2018, 9, 2484–2491.
12. K. Wang and B. Paulus, Phys. Chem. Chem. Phys., 2020, 22, 11936–11942.
13. Y. Cai, H. Zhou, G. Zhang and Y.-W. Zhang, Chem. Mater., 2016, 28, 8611–8621.
14. Y. Jing, X. Tan, Z. Zhou and P. Shen, J. Mater. Chem. A, 2014, 2, 16892–16897.
15. J. Krumland and C. Cocchi, Electron. Struct., 2021, 3, 044003.
16. T. Zhu, L. Yuan, Y. Zhao, M. Zhou, Y. Wan, J. Mei and L. Huang, Sci. Adv., 2018, 4, eaao3104.
17. L. Zhang, A. Sharma, Y. Zhu, Y. Zhang, B. Wang, M. Dong, H. T. Nguyen, Z. Wang, B. Wen, Y. Cao, B. Liu, X. Sun, J. Yang, Z. Li, A. Kar, Y. Shi, D. Macdonald, Z. Yu, X. Wang and Y. Lu, Adv. Mater., 2018, 30, 1803986.
18. O. Adeniran and Z.-F. Liu, J. Chem. Phys., 2021, 155, 214702.
19. S. Park, N. Mutz, S. A. Kovalenko, T. Schultz, D. Shin, A. Aljarb, L.-J. Li, V. Tung, P. Amsalem, E. J. W. List-Kratochvil, J. Stähler, X. Xu, S. Blumstengel and N. Koch, Adv. Sci., 2021, 8, 2100215.
20. L. Ye, Y. Liu, Q. Zhou, W. Tao, Y. Li, Z. Wang and H. Zhu, J. Phys. Chem. Lett., 2021, 12, 8440–8446.
21. Z. Song, T. Schultz, Z. Ding, B. Lei, C. Han, P. Amsalem, T. Lin, D. Chi, S. L. Wong, Y. J. Zheng, M.-Y. Li, L.-J. Li, W. Chen, N. Koch, Y. L. Huang and A. T. S. Wee, ACS Nano, 2017, 11, 9128–9135.
22. N. Shen and G. Tao, Interfaces, 2017, 4, 1601083.
23. X.-Y. Xie, X.-Y. Liu, Q. Fang, W.-H. Fang and G. Cui, J. Phys. Chem. A, 2019, 123, 7693–7703.
24. Y. Guo, L. Wu, J. Deng, L. Zhou, W. Jiang, S. Lu, D. Huo, J. Ji, Y. Bai, X. Lin, S. Zhang, H. Xu, W. Ji and C. Zhang, Nano Res., 2022, 15, 1276–1281.
25. S. Y. Quek and K. H. Khoo, Acc. Chem. Res., 2014, 47, 3250–3257.
26. O. T. Hofmann, E. Zojer, L. Hörmann, A. Jeindl and R. J. Maurer, Phys. Chem. Chem. Phys., 2021, 23, 8132–8180.
27. S. Park, H. Wang, T. Schultz, D. Shin, R. Ovsyannikov, M. Zacharias, D. Maksimov, M. Meissner, Y. Hasegawa, T. Yamaguchi, S. Kera, A. Aljarb, M. Hakami, L.-J. Li, V. Tung, P. Amsalem, M. Rossi and N. Koch, Adv. Mater., 2021, 33, 2008677.
28. C. Draxl, D. Nabok and K. Hannewald, Acc. Chem. Res., 2014, 47, 3225–3232.
29. I. Gonzalez Oliva, F. Caruso, P. Pavone and C. Draxl, Phys. Rev. Mater., 2022, 6, 054004.
30. A. Tkatchenko, L. Romaner, O. T. Hofmann, E. Zojer, C. Ambrosch-Draxl and M. Scheffler, MRS Bull., 2010, 35, 435–442.
31. X. Liu, J. Gu, K. Ding, D. Fan, X. Hu, Y.-W. Tseng, Y.-H. Lee, V. Menon and S. R. Forrest, Nano Lett., 2017, 17, 3176–3181.
32. S. Joshi, D. Ecija, R. Koitz, M. Iannuzzi, A. P. Seitsonen, J. Hutter, H. Sachdev, S. Vijayaraghavan, F. Bischoff, K. Seufert, J. V. Barth and W. Auwärter, Nano Lett., 2012, 12, 5821–5828.
33. Y. Lin and J. W. Connell, Nanoscale, 2012, 4, 6908–6939.
34. J. Gomez Diaz, Y. Ding, R. Koitz, A. P. Seitsonen, M. Iannuzzi and J. Hutter, Theor. Chem. Acta, 2013, 132, 1350.
35. Q. Weng, X. Wang, X. Wang, Y. Bando and D. Golberg, Chem. Soc. Rev., 2016, 45, 3989–4012.
36. K. Zhang, Y. Feng, F. Wang, Z. Yang and J. Wang, J. Mater. Chem. C, 2017, 5, 11992–12022.
37. K. K. Kim, H. S. Lee and Y. H. Lee, Chem. Soc. Rev., 2018, 47, 6342–6369.
38. W. Auwärter, Surf. Sci. Rep., 2019, 74, 1–95.
39. M. Kratzer, A. Matkovic and C. Teichert, J. Phys. D, 2019, 52, 383001.
40. A. Matković, J. Genser, M. Kratzer, D. Lüftner, Z. Chen, O. Siri, P. Puschnig, C. Becker and C. Teichert, Adv. Funct. Mater., 2019, 29, 1903816.
41. P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871.
42. W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138.
43. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
44. J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2006, 124, 219906.
45. K. Lejaeghere, G. Bihlmayer, T. Björkman, P. Blaha, S. Blügel, V. Blum, D. Caliste, I. E. Castelli, S. J. Clark, A. D. Corso, S. de Gironcoli, T. Deutsch, J. K. Dewhurst, I. D. Marco, C. Draxl, M. Dułak, O. Eriksson, J. A. Flores-Livas, K. F. Garrity, L. Genovese, P. Giannozzi, M. Giantomassi, S. Goedecker, X. Gonze, O. GrÅnäs, E. K. U. Gross, A. Gulans, F. Gygi, D. R. Hamann, P. J. Hasnip, N. A. W. Holzwarth, D. IuÅŸan, D. B. Jochym, F. Jollet, D. Jones, G. Kresse, K. Koepernik, E. Küçükbenli, Y. O. Kvashnin, I. L. M. Locht, S. Lubeck, M. Marsman, N. Marzari, U. Nitzsche, L. Nordström, T. Ozaki, L. Paulatto, C. J. Pickard, W. Poelmans, M. I. J. Probert, K. Refson, M. Richter, G.-M. Rignanese, S. Saha, M. Scheffler, M. Schlipf, K. Schwarz, S. Sharma, F. Tavazza, P. Thunström, A. Tkatchenko, M. Torrent, D. Vanderbilt, M. J. van Setten, V. V. Speybroeck, J. M. Wills, J. R. Yates, G.-X. Zhang and S. Cottenier, Science, 2016, 351, aad3000.
46. T. D. Kühne, M. Iannuzzi, M. Del Ben, V. V. Rybkin, P. Seewald, F. Stein, T. Laino, R. Z. Khaliullin, O. Schütt, F. Schiffmann, D. Golze, J. Wilhelm, S. Chulkov, M. H. Bani-Hashemian, V. Weber, U. Borštnik, M. Taillefumier, A. S. Jakobovits, A. Lazzaro, H. Pabst, T. Müller, R. Schade, M. Guidon, S. Andermatt, N. Holmberg, G. K. Schenter, A. Hehn, A. Bussy, F. Belleflamme, G. Tabacchi, A. Glöβ, M. Lass, I. Bethune, C. J. Mundy, C. Plessl, M. Watkins, J. VandeVondele, M. Krack and J. Hutter, J. Chem. Phys., 2020, 152, 194103.
47. J. VandeVondele and J. Hutter, J. Chem. Phys., 2007, 127, 114105.
48. S. Goedecker, M. Teter and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703–1710.
49. C. Hartwigsen, S. Goedecker and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 3641–3662.
50. M. Krack, Theor. Chem. Acc., 2005, 114, 145–152.
51. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
52. R. Sabatini, T. Gorni and S. de Gironcoli, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 041108.
53. M. Iannuzzi, F. Tran, R. Widmer, T. Dienel, K. Radican, Y. Ding, J. Hutter and O. Gröning, Phys. Chem. Chem. Phys., 2014, 16, 12374–12384.
54. S. Goedecker, W. Hellmann and T. Lenosky, Phys. Rev. Lett., 2005, 95, 055501.
55. J. B. Davis, A. Shayeghi, S. L. Horswell and R. L. Johnston, Nanoscale, 2015, 7, 14032–14038.
56. H. Pan, H. Zhang, Y. Sun, Y. Ding, J. Chen, Y. Du and N. Tang, Phys. Chem. Chem. Phys., 2017, 19, 14801–14810.
57. S. Kaappa, E. G. Del Ro and K. W. Jacobsen, Phys. Rev. B, 2021, 103, 174114.
58. C. Elias, P. Valvin, T. Pelini, A. Summerfield, C. Mellor, T. Cheng, L. Eaves, C. Foxon, P. Beton, S. Novikov, B. Gil and G. Cassabois, Nat. Commun., 2019, 10, 1–7.
59. P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. B. Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. D. Corso, S. de Gironcoli, P. Delugas, R. A. DiStasio, A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H.-Y. Ko, A. Kokalj, E. Küçükbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H.-V. Nguyen, A. O. de-la Roza, L. Paulatto, S. Poncé, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, J. Phys.: Condens. Matter, 2017, 29, 465901.
60. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
61. X. Bidault and S. Chaudhuri, J. Chem. Phys., 2021, 154, 164105.
62. L. Sun, Y. Wang, F. Yang, X. Zhang and W. Hu, Adv. Mater., 2019, 31, 1902328.
63. A. Picchiotti, A. Nenov, A. Giussani, V. I. Prokhorenko, R. D. Miller, S. Mukamel and M. Garavelli, J. Phys. Chem. Lett., 2019, 10, 3481–3487.
64. K. R. Herperger, J. Krumland and C. Cocchi, J. Phys. Chem. A, 2021, 125, 9619–9631.
65. J. R. Dias, Acc. Chem. Res., 1985, 18, 241–248.
66. K. Watanabe, T. Taniguchi and H. Kanda, Nat. Mat., 2004, 3, 404–409.
67. T. T. Tran, K. Bray, M. J. Ford, M. Toth and I. Aharonovich, Nat. Nanotechnol., 2016, 11, 37–41.
68. R. J. Hunt, B. Monserrat, V. Zólyomi and N. Drummond, Phys. Rev. B, 2020, 101, 205115.
69. T. Böker, R. Severin, A. Müller, C. Janowitz, R. Manzke, D. Voß, P. Krüger, A. Mazur and J. Pollmann, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 235305.
70. M. Kan, J. Wang, X. Li, S. Zhang, Y. Li, Y. Kawazoe, Q. Sun and P. Jena, J. Phys. Chem. C, 2014, 118, 1515–1522.
71. H.-M. Dong, S.-D. Guo, Y.-F. Duan, F. Huang, W. Xu and J. Zhang, Front. Phys., 2018, 13, 1–6.
72. Y. Wang, C. Urban, J. Rodríguez-Fernández, J. M. Gallego, R. Otero, N. Martín, R. Miranda, M. Alcamí and F. Martín, J. Phys. Chem. A, 2011, 115, 13080–13087.
73. P. Kretz, K. Waltar, Y. Geng, C. Metzger, M. Graus, A. Schöll, F. Reinert, S. X. Liu, S. Decurtins, M. J. Osterwalder and L. Castiglioni, New J. Phys., 2021, 23, 013002.
74. Y. Xu, O. T. Hofmann, R. Schlesinger, S. Winkler, J. Frisch, J. Niederhausen, A. Vollmer, S. Blumstengel, F. Henneberger, N. Koch, P. Rinke and M. Scheffler, Phys. Rev. Lett., 2013, 111, 226802.
75. A. Kumar, K. Banerjee, M. Dvorak, F. Schulz, A. Harju, P. Rinke and P. Liljeroth, ACS Nano, 2017, 11, 4960–4968.
76. H. Wang, S. V. Levchenko, T. Schultz, N. Koch, M. Scheffler and M. Rossi, Adv. Energy Mater., 2019, 5, 1800891.
77. M. Jacobs, J. Krumland, A. M. Valencia, H. Wang, M. Rossi and C. Cocchi, Adv. Phys: X, 2020, 5, 1749883.
78. H. Cun, A. P. Seitsonen, S. Roth, S. Decurtins, S.-X. Liu, J. Osterwalder and T. Greber, Surf. Sci., 2018, 678, 183–188.
79. Q. Tang, Z. Zhou and Z. Chen, J. Phys. Chem. C, 2011, 115, 18531–18537.
80. X. Blase, A. Rubio, S. G. Louie and M. L. Cohen, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 6868.
81. B. Arnaud, S. Lebègue, P. Rabiller and M. Alouani, Phys. Rev. Lett., 2006, 96, 026402.
82. W. Aggoune, C. Cocchi, D. Nabok, K. Rezouali, M. A. Belkhir and C. Draxl, Phys. Rev. B, 2018, 97, 241114.
83. T. Galvani, F. Paleari, H. P. C. Miranda, A. Molina-Sánchez, L. Wirtz, S. Latil, H. Amara and F. M. C. Ducastelle, Phys. Rev. B, 2016, 94, 125303.
84. F. Paleari, T. Galvani, H. Amara, F. Ducastelle, A. Molina-Sánchez and L. Wirtz, 2D Mater., 2018, 5, 045017.
85. G. Cassabois, P. Valvin and B. Gil, Nat. Photonics, 2016, 10, 262–266.

---

Footnotes

† Electronic Supplementary Information (ESI) available: Additional details are provided on the structural and electronic properties of the considered interfaces. See DOI: https://doi.org/10.1039/d2cp01502a

‡ Equal contribution.

---