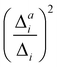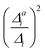Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Tailored anharmonic–harmonic vibrational profiles for fluorescent biomarkers†
Nghia
Nguyen Thi Minh
and
Carolin
König
 *
*
Institut für Physikalische Chemie und Elektrochemie, Leibniz Universität Hannover, Callinstr. 3A, 30167 Hannover, Germany. E-mail: carolin.koenig@pci.uni-hannover.de
First published on 13th June 2022
Abstract
We propose a hybrid anharmonic–harmonic scheme for vibrational broadenings, which embeds a reduced-space vibrational configuration interaction (VCI) anharmonic wave function treatment in the independent-mode displaced harmonic oscillator (IMDHO) model. The resulting systematically-improvable VCI-in-IMDHO model allows including the vibronic effects of all vibrational degrees of freedom, while focusing the effort on the important degrees of freedom with minimal extra computational effort compared to a reduced-space VCI treatment. We show for oligothiophene examples that the VCI-in-IMDHO approach can yield accurate vibrational profiles employing smaller vibrational spaces in the VCI part than the reduced-space VCI approach. By this, the VCI-in-IMDHO model enables accurate calculation of vibrational profiles of common fluorescent dyes with more than 100 vibrational degrees of freedom. We illustrate this for three examples of fluorescent biomarkers of current interest. These are the oligothiophene-based fluorescent dye called HS84, 1,4-diphenylbutadiene, and an anthracene diimide. For all examples, we assess the impact of the anharmonic treatment on the vibrational broadening, which we find to be more pronounced for the intensities than for the peak positions.
1 Introduction
The calculation of accurate vibrational line shapes in optical spectra is of interest in various ways: they are needed for direct comparison of theoretical to experimental spectra1–4 as well as for elucidating the colour of a dye.5,6 Optical line shapes are therefore also essential for the rational design of dyes.7 Moreover, the line shape of emission peaks can significantly be altered within different environments. This is for example the case for the oligothiophene-based fluorescent dye denoted HS84: in solution, a broad fluorescent signal is obtained, while a structured fluorescent signal occurs for HS84 mixed with recombinant Aβ 1–42 amyloid-like fibrils.8 Deposition of amyloid fibrils is a hallmark for neurodegenerative diseases such as Alzheimer's and Parkinson's disease.9 The aggregation of the HS84 dye to the amyloid fibril is associated with a change of the fluorescence colour. This colour change is of particular relevance as it is a promising route for improved detection of amyloid fibrils also in vivo.10 Such luminescent conjugated oligothiophenes (LCOs) have, hence, been developed as candidates for improved diagnosis of these wide-spread diseases by fluorescence imaging. LCOs have been shown to detect a wider range of disease-associated protein aggregates10–12 than more conventional ligands such as thioflavin S or congo red.Given that the line shape of fluorescent spectra of the oligothiophenes13 can well be recovered from theoretical models for vibrational broadenings,14–16 the observed structure in the fluorescence spectrum can be assigned to vibronic couplings. Still, supporting computational studies to understand the mechanism behind the colour change rely fully on conformational averaging of vertical transition and cannot recover the line shape in the emission spectrum.17
The main reason, why vibrational line shapes are typically not considered in such studies is their large computational cost, particularly when anharmonic effects need to be accounted for. In ref. 16, a reduced-space anharmonic model is proposed, in which a selected vibrational subspace is treated by means of vibrational configuration interaction (VCI) wave functions18–21 using anharmonic potential energy surfaces accounting for mode–mode couplings and correlations. It was found that the vibrational progression of oligothiophenes is dominated by only a small number of modes.15,16 Notably, the number of important modes does not increase significantly with an increasing number of thiophene rings.16
For estimating the impact of individual modes on the vibronic profile, we previously applied the harmonic displacement between the minima of the two involved electronic states within the independent mode displaced harmonic oscillator (IMDHO) model.22,23 The IMDHO model is a rather crude approximation, that allows the calculation of vibrational line shapes from harmonic frequencies of the initial state and the atomic gradients of the final state at the equilibrium structure of the initial state alone.
In this work, we suggest using the information on the IMDHO-type vibrational line shape not only for the assessment of the impact of a mode on the vibrational spectrum, but also for treating all modes that are considered less important or to a high degree harmonic. By this, we obtain a hybrid scheme for vibrational broadenings, which we denote VCI-in-IMDHO model. This means, we treat a selected set of vibrational modes by VCI methods and all others within the IMDHO model. In contrast to other hybrid schemes for vibrational line shapes,14,24–29 the VCI-in-IMDHO is not a mixed quantum–classical approach, but rather a mixed quantum–quantum scheme. So far, this model is restricted to Frank–Condon factors, which can be assumed to be a good approximation for the bright transitions considered in this study.
After validation of the VCI-in-IMDHO method for oligothiophenes with two to five thiophene rings, we apply it to the fluorescent dyes depicted in Fig. 1. Among those is the HS84 fluorescent marker for amyloid fibrils already mentioned above. It is a pentameric oligothiophene derivative that belongs to the LCO dyes.30 Additionally, we study 1,4-diphenylbutadiene (DPB) and an anthracene diimide (ADI) derivate. DPB is a fluorescent derivative of linear polyenes, which have been extensively investigated as a model for the photochemical and photobiological systems.31,32 ADIs and related compounds are functional organic dyes with outstanding chemical, thermal, and photochemical properties.33–35 During the past decade, this class of dyes has attracted increasing interest as promising scaffolds for several exciting applications such as photovoltaic cells,34,36 chemosensors,37,38 fluorescence dyes in biological media.39
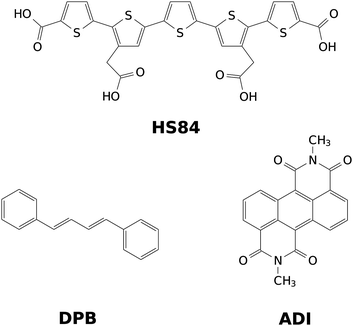 | ||
| Fig. 1 Representation of the investigated dyes: pentameric oligothiophene derivative (HS84), 1,4-diphenylbutadiene (DPB) and anthracene diimide (ADI). | ||
This work is organized as follows. First, we present the VCI-in-IMDHO model and the measures for the division of the vibrational spaces (Section 2). Second, the computational details are presented in Section 3. The results are discussed and compared to the experiment in Section 4 and followed by the conclusion (Section 5).
2 Methodology
In the VCI-in-IMDHO model, we treat all important anharmonic modes with an accurate VCI wave function, which accounts for the one-mode anharmonicity as well as for mode–mode couplings and correlations, usually restricted to low orders. For all other modes, we employ the IMDHO model, which is purely harmonic and neglects frequency differences in the involved electronic states as well as Duschinsky rotations.40 It, however, has the advantage that it offers closed formulas for the Franck–Condon factors:22,23,41–43 the Franck–Condon factors from the vibrational ground state (0) of the initial electronic state to the nth vibrational state of the final electronic state can in the IMDHO model be expressed in atomic units as23,41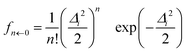 | (1) |
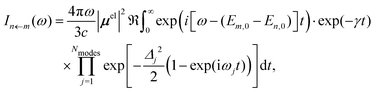 | (2) |
In our hybrid scheme, we chose a small subset of modes for the VCI calculations leading to a set of Franck–Condon factors. The resulting stick spectra are then broadened with a line shape obtained from the IMDHO autocorrelation function [eqn (2)] for the remaining subset of modes,
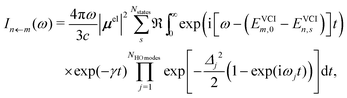 | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) modes modes not accounted for in the VCI treatment. Note that in case all modes are accounted for anharmonically, the Lorentzian line shape for all peaks is recovered within this methodology.
modes modes not accounted for in the VCI treatment. Note that in case all modes are accounted for anharmonically, the Lorentzian line shape for all peaks is recovered within this methodology.
For the above-described hybrid scheme, the modes must be divided into two sets. This division is done based on three criteria:
(1) Importance of the mode for vibrational progression: Harmonic displacement (Δi) based on the IMDHO model.
This first measure estimates the impact of the mode under consideration on the vibrational progression, i.e., whether more than the 0–0 transition are significant. Similar as in ref. 16 and 47, we use the harmonic displacements Δi to rank the modes with decreasing importance and assess the threshold by the convergence of the theoretical spectra.
(2) Resolution of the vibrational progression with a given HWHM (γ): crossing point between the Lorentzian broadening the 0–0 and 1–0 transition (σ).
Besides the ratio of the Franck–Condon factors, it is also important that their effect is also resolved when assuming a line broadening, i.e., that the additional peaks are not hidden below the broadened lines. In ref. 16, this was accounted for by discarding all vibrational modes with frequencies smaller than half the chosen HWHM. This approach, however, does not account for the relation between the height of the satellite peaks (in the IMDHO model determined by the displacement Δi) and the resolution. We therefore replace this pure frequency criterion by a more nuanced criterion, which is the HWHM at which the maximum of the 1 ← 0 peak broadened with a Lorentzian line shape lies on the Lorentzian band of the 0 ← 0 peak. Within the IMDHO approximation, this value is given by
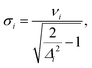 | (4) |
(3) Impact of one-mode anharmonicity on the vibrational profile: with this third measure for anharmonicity, we aim at an estimate, whether individual modes need to be treated anharmonically or whether a harmonic treatment within the IMDHO model is sufficient. We assess this by comparing the one-mode vibrational profiles within the IMDHO model and anharmonic treatment. Additionally, we also consider the ratio 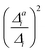 between the squared anharmonic (Δai) and harmonic displacements (Δi). For this, we project the difference between the optimized structures in the initial and final electronic states on the normal modes employed in the IMDHO model. By this procedure, we obtain the anharmonic displacements Δai for all modes i. As analysed below, these two measures do not correlate clearly and we focus by default on the comparison of the one-mode profiles.
between the squared anharmonic (Δai) and harmonic displacements (Δi). For this, we project the difference between the optimized structures in the initial and final electronic states on the normal modes employed in the IMDHO model. By this procedure, we obtain the anharmonic displacements Δai for all modes i. As analysed below, these two measures do not correlate clearly and we focus by default on the comparison of the one-mode profiles.
By a combination of these measures, we identify those modes that are important to be treated accurately. We stress that one criterion alone cannot achieve this. For example, the vibrational progression caused by a mode with a high displacement, may not be seen due to a poor resolution, or it might already be well described in the harmonic picture. In these cases, a computationally expensive VCI treatment is not in proportion to the minor improvements to be expected. Similarly, some very anharmonic modes, such as certain torsion motions,14,27 do not necessarily contribute significantly to the vibrational progression. Also here, a VCI treatment may not be beneficial due to the accuracy–cost considerations.
Within this study, no attempts were made to include finite-temperature effects.
3 Computational details
All electronic-structure calculations have been performed with the Gaussian16 program package48 using (time-dependent) density-functional theory [(TD)DFT] with the CAM-B3LYP49 density functional and a def2-TZVP basis set.50,51 The calculations are performed for the dyes in vacuum, if not specified otherwise. To get a rough estimate of the impact of the solvent environment on the vibrational progression, we performed the pure IMDHO computations additionally for each dye using the integral equation formalism of the polarizable-continuum model (IEF-PCM)52,53 with the default dielectric constants in Gaussian16. We choose for each dye the solvent of the respective experimental spectrum compared to, that is, water for HS84 (note that the experiment was done in a phosphate buffered saline), hexane for 1,4-diphenylbutadiene and dichloromethane for the anthracene diimide.For oligothiophenes, we have used the potential energy surfaces (PESs) from ref. 16. For new combinations of coordinates treated anharmonically, not present in ref. 16, we have deleted the respective regions from potential energy surfaces generated in ref. 16.
For the PES generation and anharmonic vibrational wave function calculations, we employed a locally modified version of the Molecular Interactions Dynamics And Simulation C++ package (MidasCpp)54 version 2019.04.0. For all vibrational profile calculations, we employed the normal modes and vibrational frequencies of the first excited state. The vibrational coordinates of the excited state were also employed for the reduced-space anharmonic PESs for both the ground and excited state. The ground- and excited-state PESs for the fluorescent dyes were obtained with the multi-state extension55,56 to the adaptive density guided approach (ADGA)57 obtaining reliable PESs for at least the lowest six vibrational states in both electronic states. Additionally, mode–mode coupling up to second order in n-mode expansion is considered in the PES generation within a selected set of modes. The relative ADGA convergence criterion threshold was set to 1.0 × 10−2 while the absolute ADGA convergence criterion threshold was set to 1.0 × 10−6. Both was increased by a factor of 10 for the two-mode coupling part of the PES. The PES cuts were fitted to polynomials with the maximal polynomial order of eight. All vibrational self-consistent field (VSCF) calculations were performed with B-spline basis sets58 with a basis set density of 0.8.
The anharmonic Franck–Condon factors were obtained from vibrational configuration interaction (VCI) calculations. For all cases with four or more modes in the VCI treatment up to quadruply substituted configurations are included in the VCI treatment (VCI[4]). For smaller vibrational subspaces, full vibrational configuration interaction (FVCI) calculations have been conducted. The VCI Franck–Condon factors59–62 were obtained as overlaps of the anharmonic VCI wave functions of the different vibrational states within the final electronic state with the vibrational ground state of the initial electronic state. The sum of FCs was required to be more than 0.98 to ensure that most of the intensity was captured in the calculated spectra. To reach this, different numbers modals were included in the configurational space for different molecules. The calculations of the Franck–Condon factors were performed using the respective implementation16,56 in MidasCpp.54
The different measures as well as the IMDHO line shapes according to eqn (2) have been implemented in a python framework. Therefore, scipy.integrate.quad with techniques from the Fortran library QUADPACK63 is used for the integration parts.
For a consistent theory–experiment comparison, the experimental spectra measured in wavelength scale are transformed in line shapes by applying an intensity correction proportional to ω2.64,65 We further normalized the area under the peak to 1 in all spectral comparisons and shifted the maxima of the experiment to the same position as the maxima of the respective most advanced calculation.
4 Results and discussion
4.1 Oligothiophenes, revisited
The above-mentioned reduced-space approach for anharmonic vibrational broadenings was assessed for oligothiophenes of different lengths.16 In this previous work, all chosen vibrations (i.e. all with Δi ≤ 0.6 and νi > 161 cm−1) were included anharmonically and all others were neglected. We have chosen these examples as first testbed for our hybrid approach and the refined criteria described above. In view of the similar spectra obtained with different conformers of the oligothiophenes,16 we restrict the discussion here to the all-trans conformers. The experimental spectra we compare to ref. 13 are taken in ethanol at 77 K, that is, below the melting point of ethanol. Hence, thermal broadening is likely suppressed in these spectra.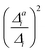 as well as the resolution measure σi and the qualitative impact of one-mode anharmonicity in the respective anharmonic calculation for this mode only. The latter is obtained by visual inspection of the respective spectra, which can be found in Fig. S1 in the ESI.†
as well as the resolution measure σi and the qualitative impact of one-mode anharmonicity in the respective anharmonic calculation for this mode only. The latter is obtained by visual inspection of the respective spectra, which can be found in Fig. S1 in the ESI.†
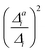 , the resolution measure σi in cm−1, and the effect of one-mode anharmonicity on the vibronic profile (1-mode AH)
, the resolution measure σi in cm−1, and the effect of one-mode anharmonicity on the vibronic profile (1-mode AH)
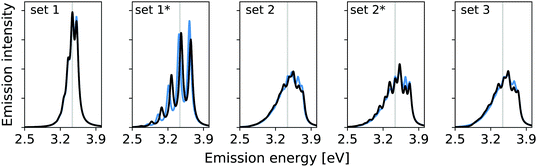
In the previous work, modes 14, 36, and 7 were deemed important. Additionally, modes 5 and 29 were assessed. The resolution measure σi for the modes 5 and 7 lies below the chosen γ value of 322.6 cm−1 (0.04 eV). This suggests that mode 5 and 7 are likely not well resolved and may therefore be neglected. Fig. 2 shows the vibrational broadening of the emission spectrum obtained with the IMDHO model and by VCI for the following reduced spaces, containing
set 1: only the mode with the largest IMDHO displacement, i.e., mode 14,
set 1*: only the mode with most pronounced one-mode anharmonicity among the five modes with the largest IMDHO displacement, i.e., mode 36,
set 2: three modes with the largest IMDHO displacements according to the procedure in ref. 16, i.e., modes 14, 36, 7,
set 2*: three modes with the largest IMDHO displacements and a resolution measure larger than the chosen half width at half maximum, i.e., modes 14, 36, and 29, and
set 3: all five previously investigated modes, i.e., modes 14, 36, 7, 5, and 29.
For mode 14, which has the largest harmonic displacement, the one-mode harmonic and anharmonic spectra are very similar (set 1), while the respective spectra for only mode 36 (set 1*) differ significantly. The same also holds for all other sets, that are set 2, set 2*, and set 3, which all include the anharmonic mode 36. We further observe significant differences between set 2 and set 2*, which both contain three modes.
Fig. 3 shows the vibrational profiles, for which the above-mentioned sets of modes were treated by VCI and all other modes by the IMDHO model. Additionally, set 0 is depicted, which is a pure IMDHO treatment of all vibrational modes. The respective vibrational profile is hardly altered, when treating mode 14 anharmonically (set 1), but slight differences are obtained for treating only mode 36 (set 1*) anharmonically. Similar slight modifications of the vibrational profiles are observed for set 2 and set 2*. The vibrational profile for the hybrid scheme with set 3 is almost perfectly resembled by that for set 2*. For a more quantitative comparison of the convergence of the vibrational profiles to that obtained for the hybrid scheme with the different sets of modes, we quantify the difference between the two spectra by
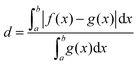 | (5) |
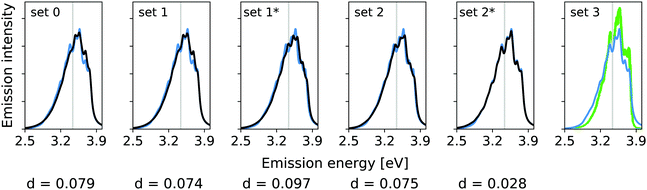 | ||
| Fig. 3 Hybrid VCI-in-IMDHO vibrational profiles for the S0 ← S1 emission for trans bithiophene for the different sets of vibrational coordinates treated by VCI (black) and that for the largest set of modes set 3 (blue) with a HWHM of 0.04 eV compared to a corrected experimental spectrum of bithiophene at 77 K in ethanol13 (green). For the definition of the reduced spaces, see the main text. The vertical transition energy is given as a vertical grey line. The experiment al spectrum is shifted by 0.105 eV to get the same position of maximum as calculated spectrum. Additionally, the deviation between the shown spectra according to eqn (5) is quantified below the respective graphs. | ||
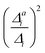 , the resolution measure σi in cm−1 and the effect of one-mode anharmonicity on the vibronic profile (1-mode AH)
, the resolution measure σi in cm−1 and the effect of one-mode anharmonicity on the vibronic profile (1-mode AH)
The calculated hybrid spectra treating above-described sets of modes anharmonically are depicted in Fig. 4. Again, we see a convergence of the spectrum towards the set 3 results already for set 2. This convergence is illustrated by the decreasing d measures, also shown in Fig. 4. In this case, however, the consideration of the remaining modes within the IMDHO model has only little influence on the result compared to the reduced-space VCI result already presented in ref. 16. The agreement with experiment (most right graph in Fig. 4), is, however, only moderate. We note that the experimental data is obtained in ethanol solution, so that many factors may play a role, that are not accounted for in our present computational setup. Note also that better agreement with the experiment is obtained with a reduced HWHM value of γ = 0.02 eV (see Fig. 5).
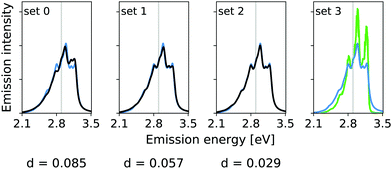 | ||
| Fig. 4 Hybrid VCI-in-IMDHO vibrational profiles for the S0 ← S1 emission for all-trans terthiophene for the different sets of vibrational coordinates treated by VCI (black) and that for the largest set of modes set 3 (blue) with a HWHM of 0.04 eV compared to a corrected experimental spectrum of terthiophene at 77 K in ethanol13 (green). For the definition of the reduced spaces, see the main text. The vertical transition energy is given as a vertical grey line. The experiment al spectrum is shifted by 0.093 eV to get the same position of maximum as calculated spectrum. Additionally, the deviation between the shown spectra according to eqn (5) is quantified below the respective graphs. | ||
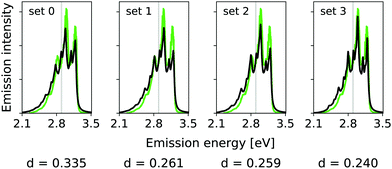 | ||
| Fig. 5 Hybrid VCI-in-IMDHO vibrational profiles for the S0 ← S1 emission for all-trans terthiophene for the different sets of vibrational coordinates treated by VCI (black) with a HWHM of 0.02 eV compared to a corrected experimental spectrum of terthiophene at 77 K in ethanol13 (green). For the definition of the reduced spaces, see the main text. The vertical transition energy is given as a vertical grey line. The experiment al spectrum is shifted by 0.000 eV to get the same position of maximum as calculated spectrum. Additionally, the deviation between the shown spectra according to eqn (5) is quantified below the respective graphs. | ||
In this case, however, already the pure IMDHO model (set 0) results in good agreement with experiment. Still, the VCI-in-IMDHO treatment leads to a systematic further improvement of this agreement as illustrated by the d values.
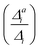 . If the squared ratio for a mode is equal to 1, we expect the IMDHO treatment to be a good approximation and for large deviations, the respective mode is more likely to exhibit anharmonic contributions. For the thiophene test cases, all modes with significant (moderate) effect of one-mode anharmonicity on the one-mode vibrational profiles have an anharmonicity measure of
. If the squared ratio for a mode is equal to 1, we expect the IMDHO treatment to be a good approximation and for large deviations, the respective mode is more likely to exhibit anharmonic contributions. For the thiophene test cases, all modes with significant (moderate) effect of one-mode anharmonicity on the one-mode vibrational profiles have an anharmonicity measure of 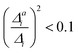 . For pentathiophene, we observe, however, two modes with very small anharmonicity measures below that value that do not show significant one-mode anharmonicities (see Table SII and Fig. S8 in the ESI†). Similar observations are also made for the organic dyes below (see Tables SIII, SIV, and SV as well as Fig. S9, S11, and S13 in the ESI†).
. For pentathiophene, we observe, however, two modes with very small anharmonicity measures below that value that do not show significant one-mode anharmonicities (see Table SII and Fig. S8 in the ESI†). Similar observations are also made for the organic dyes below (see Tables SIII, SIV, and SV as well as Fig. S9, S11, and S13 in the ESI†).
In summary, the correlation of 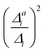 to the observed anharmonicities is less clear than hoped for. This observation might be related to that the Franck–Condon region has a larger influence on the vibrational profile than the region around the equilibrium of the final state, as has been reported earlier.66 We, hence, speculate that the proposed anharmonicity measure focuses too much on the adiabatic region to give a clear guideline for the effect of the anharmonicity on the vibrational profile. For this reason, we further apply the computationally more expensive comparison of the effect of the one-mode anharmonicity on the one-mode vibronic spectra directly.
to the observed anharmonicities is less clear than hoped for. This observation might be related to that the Franck–Condon region has a larger influence on the vibrational profile than the region around the equilibrium of the final state, as has been reported earlier.66 We, hence, speculate that the proposed anharmonicity measure focuses too much on the adiabatic region to give a clear guideline for the effect of the anharmonicity on the vibrational profile. For this reason, we further apply the computationally more expensive comparison of the effect of the one-mode anharmonicity on the one-mode vibronic spectra directly.
We note that among the modes investigated for anharmonicity, those with high harmonic displacements also exhibit the largest anharmonicity effects on the vibrational profiles. An exception is, however, obtained for bithiophene, for which the mode with the second largest displacement exhibits the largest one-mode anharmonicity of the tested modes. We should, however, keep in mind that we have a very limited set of modes here. Furthermore, known highly anharmonic modes like the torsion in oligothiophenes14 only contribute little to the vibrational profile. The observed correlation between high one-mode anharmonicity and large harmonic displacements can, hence, not be considered robust to predict the impact of anharmonicity of a given mode.
4.2 Organic biomarkers
In the previous section, we have seen that reduced-space VCI vibrational profiles can be combined with IMDHO-type line shapes to the VCI-in-IMDHO model. This combination can lead to a faster convergence of the vibrational profile. This accompanying reduction in computational cost allows us to apply this methodology also to the somewhat larger organic fluorescent dyes introduced in Fig. 1. In interest of computational cost, we only included two-mode couplings in the PESs for modes, for which |Δi| > 0.6 for these larger examples. For all organic biomarkers, we compare also to experimental spectra. In contrast to the experimental spectra for oligothiophenes above, the broadening in the experimental spectra for the organic biomarkers can be assumed to be dominated by thermal broadening. Fewer details are resolved in these spectra.| Mode | ν i /cm−1 | |Δi| | σ i /cm−1 | 1-Mode AH |
|---|---|---|---|---|
| 133 | 1576 | 1.120 | 2044 | Weak |
| 131 | 1547 | 0.699 | 879 | Weak |
| 68 | 735 | 0.697 | 416 | Weak |
| 107 | 1264 | 0.420 | 393 | Weak |
| 126 | 1488 | 0.313 | 338 | Weak |
The corresponding calculated vibrational line shapes of the emission spectra for HS84 obtained for reduced-space VCI, IMDHO and VCI-in-IMDHO models are shown in Fig. 6 for a HWHM of 0.04 eV.
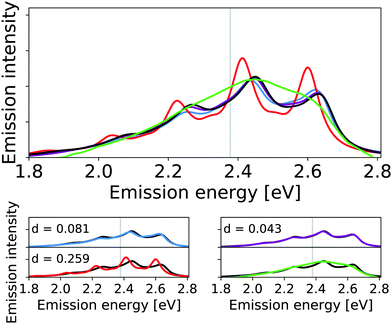 | ||
| Fig. 6 Calculated harmonic (blue), reduced-space VCI (red), VCI-in-IMDHO without mode–mode couplings in the PES (magenta) and VCI-in-IMDHO (black) broadened emission spectra of HS84 molecule with a HWHM of 0.04 eV compared to a corrected experimental spectrum in PBS8 (green). Vertical electronic emission energy with grey lines. The VCI spectrum is obtained by conventional Lorentzian broadening. In the bottom part, the calculated spectra are directly compared to the best approximation (VCI-in-IMDHO) and the experimental spectrum, respectively. Additionally, the deviation between the calculated spectra according to eqn (5) is quantified in the respective graphs. The modes treated by VCI in the reduced-space VCI are 131, 133, 68, 107, 126, out of which only the modes 133, 131, and 68 were coupled in the underlying PESs. The experimental spectra are shifted by 0.144 eV to get the same position of maximum as VCI-in-IMDHO spectra. | ||
The energy differences between the main peaks are similar in all approaches (between 0.180 eV and 0.187 eV). With the reduced-space VCI model, small additional side peaks are obtained. The reduced-space VCI results differ more from the VCI-in-IMDHO spectrum than the IMDHO spectrum. This somewhat better “resolution” of the reduced-space VCI spectrum compared to the VCI-in-IMDHO spectrum, as well as the largest deviation for the reduced-space VCI model, can most likely be attributed to the neglect of the broadening effect of the remaining vibrational degrees of freedom in the reduced-space model.
The differences between the VCI-in-IMDHO and pure IMDHO spectra mainly concern the intensity rather than the position of the peaks. For none of the selected modes, we observe a strong effect of one-mode anharmonicity (see Fig. S9 in the ESI†). Further, we obtain a slight deviation for the VCI-in-IMDHO spectrum with all the modes from Table 3 accounted for anharmonically including two-mode couplings for selected modes in the PES compared to that with only one-mode anharmonicities in the reduced-space PES (see Fig. 6). This suggests that mode–mode coupling effects, similar to one-mode anharmonicities, play a small role here.
Fig. 6 additionally shows an experimental reference for the emission spectra in solution. This experimental spectrum is however very broad so that the vibrational progression is not resolved. For the HS84, we further observe a pronounced sensitivity of the pure IMDHO spectrum on the inclusion of solvent effects by a continuum solvation model (see Fig. S10 in the ESI†). Hence, solvent effects are expected to be not negligible in this case.
| Mode | ν i /cm−1 | |Δi| | σ i /cm−1 | 1-Mode AH |
|---|---|---|---|---|
| 70 | 1691 | 1.270 | 3452 | Moderate |
| 53 | 1285 | 0.849 | 964 | Weak |
| 69 | 1653 | 0.527 | 663 | Weak |
| 41 | 1016 | 0.372 | 277 | Weak |
| 60 | 1435 | 0.303 | 314 | Weak |
| 57 | 1363 | 0.290 | 286 | Weak |
| 64 | 1544 | 0.202 | 223 | Weak |
In total, we identify seven modes with a harmonic displacement larger than 0.2 and a σi larger than 200 cm−1 (0.025 eV), out of which two modes have harmonic displacements larger than 0.6 and are therefore coupled in the PES. Again, the mode with the largest harmonic displacement (mode 70) also has the largest σi and strongest one-mode anharmonicity among the ranked modes. All other ranked modes show only weak one-mode anharmonicity.
The vibrational line shapes of the emission spectra of 1,4-diphenylbutadiene for harmonic, reduced-space VCI, and VCI-in-IMDHO treatment of different reduced spaces are shown in Fig. 7 along with an experimental spectrum.65,67 Again, the treatment of reduced-space anharmonicity has a significant impact. This holds in particular for the intensities, but also the energy differences are shifted. This shift in intensities mostly concerns an increase of the peak around 3.1 eV and a decreased intensity, of the peak around 3.5 eV when considering reduced-space anharmonicity. This shift leads to a better qualitative agreement with the experimental spectrum, similar to the conclusions drawn on the effect of full-space ground-state anharmonicity in ref. 65. We also note that accounting only for the anharmonicity of mode 70, leads already to a rather similar result as the VCI-in-IMDHO result with the seven highest ranked modes in this case (see Fig. 7). This means that the impact of one-mode anharmonicity of mode 70 on the vibrational profile is larger than the mode–mode coupling contributions in this case. Further, we find this effect to be more significant than the impact of the dichloromethane solution treated by continuum solvation model on the IMDHO spectrum (see Fig. S12 in the ESI†).
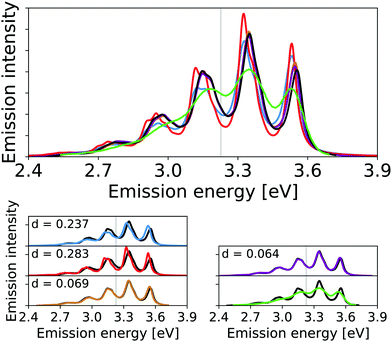 | ||
| Fig. 7 Calculated harmonic (blue), reduced-space VCI (red), one-mode VCI-in-IMDHO (orange), VCI-in-IMDHO without mode–mode couplings (magenta) and VCI-in-IMDHO (black) broadened emission spectra of 1,4-diphenylbutadiene with a HWHM of 0.025 eV compared to a corrected experimental spectrum in hexane65,67 (green). Vertical electronic emission energy with grey lines. The VCI spectrum is obtained by conventional Lorentzian broadening. In the bottom part, the calculated spectra are directly compared to the best approximation (VCI-in-IMDHO) and the experimental spectrum, respectively. Additionally, the deviation between the calculated spectra according to eqn (5) is quantified in the respective graphs. The modes treated by VCI in the reduced-space VCI are 70, 53, 69, 41, 60, 57, and 64, out of which only the modes 70 and 53 where coupled in the underlying PESs. Only mode 70 is VCI treated in the one-mode VCI-in-IMDHO treatment. The experimental spectra are shifted by 1.549 eV to get the same position of maximum as VCI-in-IMDHO spectra. | ||
The vibrational profile of this molecule has previously been assessed by means of harmonic calculations accounting for Duschinsky rotations and the different harmonic frequencies in the two involved electronic states as well as including ground-state anharmonicity effects.7 The authors of this study found significant deviations from the experimental reference with all applied approaches as well a strong dependence on ground state anharmonicity, which, however, was highly dependent on the applied density functional.
The mode ranking (see Table 5) leads to nine modes with a harmonic displacement larger than 0.2 and a resolution measure larger than 200 cm−1 out of which three have a harmonic displacement larger than 0.6. All of these modes exhibit only weak one-mode anharmonicity.
| Mode | ν i /cm−1 | |Δi| | σ i /cm−1 | 1-Mode AH |
|---|---|---|---|---|
| 79 | 1447 | 0.706 | 833 | Weak |
| 75 | 1398 | 0.642 | 712 | Weak |
| 92 | 1652 | 0.607 | 785 | Weak |
| 29 | 512 | 0.566 | 223 | Weak |
| 65 | 1215 | 0.352 | 312 | Weak |
| 81 | 1473 | 0.332 | 356 | Weak |
| 88 | 1546 | 0.318 | 367 | Weak |
| 89 | 1574 | 0.252 | 285 | Weak |
| 82 | 1502 | 0.227 | 244 | Weak |
We find a moderate effect of the anharmonicity on the emission spectrum of the ADI (see Fig. 8). Again, this effect is more pronounced for the intensities than for the energy differences. For the two highest-energy peaks (at about 2.5 eV and about 2.7 eV, respectively) we find for the IMDHO model and pure anharmonic model that the peak at 2.7 eV has the highest intensity. This difference is reduced in the VCI-in-IMDHO treatment. In this case, we obtain a negligible effect of the one-mode anharmonicities (cf. d values for the pure IMDHO model and the VCI-in-IMDHO model without mode–mode couplings in the PES from the VCI-in-IMDHO result with mode–mode couplings), but a larger effect of the mode–mode couplings compared to the above examples. Overall, the effect of anharmonicities on the vibrational line shape is similar to that of the continuum solvent (see Fig. S14 in the ESI†). Still, all simulated spectra exhibit large deviations from the experimental reference.
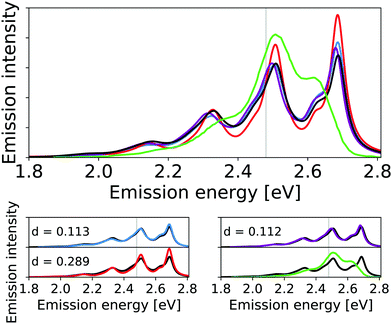 | ||
| Fig. 8 Calculated harmonic (blue), reduced-space VCI (red), VCI-in-IMDHO without mode–mode couplings in the PES (magenta) and VCI-in-IMDHO (black) broadened emission spectra of the anthracene diimide with a HWHM of 0.025 eV compared to a corrected experimental spectrum in dichloromethane7,68 (green). Vertical electronic emission energy with grey lines. The VCI spectrum is obtained by conventional Lorentzian broadening. In the bottom part, the calculated spectra are directly compared to the best approximation (VCI-in-IMDHO) and the experimental spectrum, respectively. Additionally, the deviation between the calculated spectra according to eqn (5) is quantified in the respective graphs. The modes treated by VCI in the reduced-space VCI are 79, 75, 92, 29, 65, 81, 88, 89, 82 out of which only the modes 79, 75, and 92 were coupled in the underlying PESs. The experimental spectra are shifted by 1.124 eV to get the same position of maximum as VCI-in-IMDHO spectra. | ||
The here calculated vibrational line shapes for the ADI applying CAM-B3LYP/def2-TZVP remind of those obtained both harmonically and with ground-state anharmonicity with M06-2X in ref. 7. In view of the pronounced functional dependence on the vibrational line shapes for the anthracene diimide, it can be speculated that the deviations obtained from experiments may be more likely dominated by a challenging electronic structure of the involved electronic states rather than the applied vibrational treatment.
5 Summary and conclusions
With the VCI-in-IMDHO model, we introduce a hybrid treatment for vibrational line shapes of optical spectra. This model allows us to treat selected modes by highly accurate and anharmonic vibrational wave function methods (VCI) and the remaining modes by the very approximate IMDHO model. No mode–mode coupling is considered within the modes treated by the IMDHO model and in between the two sets of modes. The Franck–Condon factors for the reduced vibrational space obtained by VCI are broadened by a system-specific line shape obtained from the IMDHO autocorrelation function for a given half-width at half maximum considering all modes but the ones treated by VCI.For the separation of the modes into these two sets, we refined and extended the criteria introduced in ref. 16. One criterion is the impact on the vibrational progression estimated by the displacement of the minima in the two involved electronic states within the IMDHO model (|Δi|), which has also been applied in earlier work.16,47 We refined the resolution criterion σi, which excludes modes due to the expected poor resolution of the vibrational modes rather than a simple frequency criterion.16,47 We show for oligothiophene examples that the harmonic treatment of the modes with a large Δi but a σi below the chosen half-width at half maximum leads to negligible deviations in the resulting VCI-in-IMDHO spectra compared to the case, where these modes are included in the VCI treatment. We also attempted to assess the impact of the anharmonicity a priori by comparing the displacement within the IMDHO model |Δi| to the displacement between the optimized minima of the two electronic states projected on the respective mode |Δai|. We, however, could not find a clear correlation of 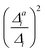 with the impact of anharmonicity on the one-mode vibrational profiles and therefore resorted to the comparison of calculated harmonic and anharmonic one-mode vibrational profiles: if the one-mode vibrational spectra are affected by anharmonicity, the multi-mode anharmonic spectrum will also be. Unfortunately, this cannot be turned around. That means, weak one-mode anharmonicity is no guarantee for negligible overall anharmoncity, as we saw, for the anthracene diimide.
with the impact of anharmonicity on the one-mode vibrational profiles and therefore resorted to the comparison of calculated harmonic and anharmonic one-mode vibrational profiles: if the one-mode vibrational spectra are affected by anharmonicity, the multi-mode anharmonic spectrum will also be. Unfortunately, this cannot be turned around. That means, weak one-mode anharmonicity is no guarantee for negligible overall anharmoncity, as we saw, for the anthracene diimide.
For the three investigated dyes, i.e., the oligothiophene-based dye HS84, 1,4-diphenylbutadiene, and an anthracene diimide, we found between five and nine modes above the thresholds to be included in the VCI treatment. For two to three modes of these, we also accounted for mode–mode couplings in the underlying potential energy surfaces. For all examples, we find some impact on anharmonicity, which is larger for the intensity of the peaks than on the peak positions. This means Franck–Condon factors are more sensitive toward anharmonicity than the vibrational energies. The cases, however, differ in the impact of one-mode anharmonicity and/or mode–mode coupling: for HS84 both anharmonic effects are small but visible. The anharmonic effect in the vibrational line shape of 1,4-diphenylbutadiene is dominated by one-mode anharmonicity, with small contribution from the mode–mode coupling. And for the anthracene diimide, we find negligible effect of one-mode anharmonicity, but a somewhat larger effect of the mode–mode couplings. In case of 1,4-diphenylbutadiene, the VCI-in-IMDHO model leads to an improved agreement with experiment compared to the pure IMDHO results. For HS84, the agreement is unclear due to a not very well resolved experimental reference, which is furthermore affected by the solvent. For the anthracene diimide, the experimental spectrum could not be recovered with any of the models. The strong functional dependence of the harmonic vibrational line shape7 suggests that this failure might be due to deficiencies in the applied electronic-energy methods for this molecule.
With the presented VCI-in-IMDHO model, we hence reduce the computational cost compared to the reduced-space VCI approach.16 It allows computations of emission line shapes of organic dyes accounting for anharmonicity in both involved electronic states, where required. We systematically converge the vibrational profile with increasing vibrational space described by accurate VCI methods. For this, we assess both the overall impact of the mode on the vibrational progression as well as the resolution of the resulting vibronic peaks in a spectrum with a given line width. What remains a challenge is to estimate the anharmonic effect and particularly the impact of mode–mode couplings a priori. Still, the hybrid nature of the VCI-in-IMDHO model combined with possibility to systematically increase the vibrational space treated by VCI provides reliable, yet affordable computational setup for vibrational profiles for typical fluorescent dyes. For the organic dyes, we additionally calculated the IMDHO vibrational profiles in continuum solvation models. In particular for the HS84, this effect was significant and larger than that of the anharmonicity. For the other molecules, the impact of anharmonicity and solvation effects are more similar. This suggests that both effects have to be included for accurate computations. Furthermore, for the calculation of vibronic profiles in heterogeneous environments, such as HS84 at an amyloid fibril, more multi-level aspects, e.g., on the electronic-structure calculations and dynamics of the environment are required. The combination of accurate vibrational profiles with different environmental description will be considered in future work.
Author contributions
NNTM: data curation, software, formal analysis, validation, visualization, writing. CK: conceptualization, methodology, writing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been supported by the Deutsche Forschungsgemeinschaft (DFG) through the Emmy Noether Young Group Leader Programme (project KO 5423/1-1). We are further grateful to Diana Madsen for the potential energy surfaces for the oligothiophenes.Notes and references
- J. Neugebauer, E. Jan Baerends, M. Nooijen and J. Autschbach, J. Chem. Phys., 2005, 122, 234305 CrossRef PubMed.
- Y. Nakai, T. Mori and Y. Inoue, J. Phys. Chem. A, 2013, 117, 83–93 CrossRef CAS PubMed.
- D. Padula, J. Cerezo, G. Pescitelli and F. Santoro, Phys. Chem. Chem. Phys., 2017, 19, 32349–32360 RSC.
- S. Höfener, B. A. Günther, M. E. Harding and L. H. Gade, J. Phys. Chem. A, 2019, 123, 3160–3169 CrossRef PubMed.
- D. Jacquemin, E. Brémond, I. Ciofini and C. Adamo, J. Phys. Chem. Lett., 2012, 3, 468–471 CrossRef CAS PubMed.
- S. Di Tommaso, D. Bousquet, D. Moulin, F. Baltenneck, P. Riva, H. David, A. Fadli, J. Gomar, I. Ciofini and C. Adamo, J. Comput. Chem., 2017, 38, 998–1004 CrossRef CAS PubMed.
- Y. Houari, A. D. Laurent and D. Jacquemin, J. Phys. Chem. C, 2013, 117, 21682–21691 CrossRef CAS.
- H. Shirani, M. Linares, C. J. Sigurdson, M. Lindgren, P. Norman and K. P. R. Nilsson, Chem. – Eur. J., 2015, 21, 15133–15137 CrossRef CAS PubMed.
- J. L. Price and J. C. Morris, Ann. Neurol., 1999, 45, 358–368 CrossRef CAS PubMed.
- A. Åslund, C. J. Sigurdson, T. Klingstedt, S. Grathwohl, T. Bolmont, D. L. Dickstein, E. Glimsdal, S. Prokop, M. Lindgren and P. Konradsson, et al. , ACS Chem. Biol., 2009, 4, 673–684 CrossRef PubMed.
- I. Berg, K. P. R. Nilsson, S. Thor and P. Hammarström, Nat. Protoc., 2010, 5, 935–944 CrossRef CAS PubMed.
- V. Mahajan, T. Klingstedt, R. Simon, K. P. R. Nilsson, A. Thueringer, K. Kashofer, J. Haybaeck, H. Denk, P. M. Abuja and K. Zatloukal, Gastroenterology, 2011, 141, 1080–1090 CrossRef CAS PubMed.
- R. S. Becker, J. Seixas De Melo, A. L. Maçanita and F. Elisei, J. Phys. Chem., 1996, 100, 18683–18695 CrossRef CAS.
- R. Improta, F. J. Ferrer, E. Stendardo and F. Santoro, ChemPhysChem, 2014, 15, 3320–3333 CrossRef CAS PubMed.
- M. Wehrle, M. Šulc and J. Vanícek, J. Chem. Phys., 2014, 140, 244114 CrossRef PubMed.
- D. Madsen, O. Christiansen, P. Norman and C. König, Phys. Chem. Chem. Phys., 2019, 21, 17410–17422 RSC.
- C. Gustafsson, M. Linares and P. Norman, J. Phys. Chem. A, 2020, 124, 875–888 CrossRef CAS PubMed.
- J. M. Bowman, K. Christoffel and F. Tobin, J. Phys. Chem., 1979, 83, 905–912 CrossRef CAS.
- O. Christiansen, J. Chem. Phys., 2004, 120, 2149–2159 CrossRef CAS PubMed.
- O. Christiansen, Phys. Chem. Chem. Phys., 2007, 9, 2942–2953 RSC.
- O. Christiansen, Phys. Chem. Chem. Phys., 2012, 14, 6672–6687 RSC.
- P. M. Champion and A. C. Albrecht, J. Chem. Phys., 1980, 72, 6498–6506 CrossRef CAS.
- A. B. Myers, R. A. Mathies, D. J. Tannor and E. J. Heller, J. Chem. Phys., 1982, 77, 3857–3866 CrossRef CAS.
- J. Cerezo, F. J. Avila Ferrer, G. Prampolini and F. Santoro, J. Chem. Theory Comput., 2015, 11, 5810–5825 CrossRef CAS PubMed.
- R. Zalesny, N. A. Murugan, F. Gel'mukhanov, Z. Rinkevicius, B. Osmiałowski, W. Bartkowiak and H. Ågren, J. Phys. Chem. A, 2015, 119, 5145–5152 CrossRef CAS PubMed.
- J. Cerezo, D. Aranda, F. J. Avila Ferrer, G. Prampolini and F. Santoro, J. Chem. Theory Comput., 2020, 16, 1215–1231 CrossRef CAS PubMed.
- A. Segalina, J. Cerezo, G. Prampolini, F. Santoro and M. Pastore, J. Chem. Theory Comput., 2020, 16, 7061–7077 CrossRef CAS PubMed.
- T. J. Zuehlsdorff, S. V. Shedge, S. Y. Lu, H. Hong, V. P. Aguirre, L. Shi and C. M. Isborn, Annu. Rev. Phys. Chem., 2021, 72, 165–188 CrossRef CAS PubMed.
- P. P. Fehér, Á. Madarász and A. Stirling, J. Chem. Theory Comput., 2021, 17, 6340–6352 CrossRef PubMed.
- R. A. Simon, H. Shirani, K. O. A. Åslund, M. Bäck, V. Haroutunian, S. Gandy and K. P. R. Nilsson, Chem. – Eur. J., 2014, 20, 12537–12543 CrossRef CAS PubMed.
- S. E. Wallace-Williams, S. Moeller, R. A. Goldbeck, K. M. Hanson, J. W. Lewis, W. A. Lee and D. S. Kliger, J. Phys. Chem., 1993, 97, 9587–9592 CrossRef CAS.
- Y.-P. Sun, C. E. Bunker, P. L. Wickremesinghe, H. W. Rollins and G. E. Lawson, J. Phys. Chem., 1995, 99, 3423–3429 CrossRef CAS.
- H. Langhals, Heterocycles, 1995, 40, 477–500 CrossRef CAS.
- X. Zhan, A. Facchetti, S. Barlow, T. J. Marks, M. A. Ratner, M. R. Wasielewski and S. R. Marder, Adv. Mater., 2011, 23, 268–284 CrossRef CAS PubMed.
- C. Li and H. Wonneberger, Adv. Mater., 2012, 24, 613–636 CrossRef CAS PubMed.
- J. Li, F. Dierschke, J. Wu, A. C. Grimsdale and K. Müllen, J. Mater. Chem., 2006, 16, 96–100 RSC.
- H. Cao, D. I. Diaz, N. DiCesare, J. R. Lakowicz and M. D. Heagy, Org. Lett., 2002, 4, 1503–1505 CrossRef CAS PubMed.
- Y. Che, X. Yang, S. Loser and L. Zang, Nano Lett., 2008, 8, 2219–2223 CrossRef CAS PubMed.
- L. Zhu, W. Wu, M.-Q. Zhu, J. J. Han, J. K. Hurst and A. D. Li, J. Am. Chem. Soc., 2007, 129, 3524–3526 CrossRef CAS PubMed.
- F. Duschinsky, Acta Physicochim. U.R.S.S., 1937, 7, 551–566 Search PubMed.
- A. B. Myers and R. A. Mathies, Biol. Appl. Raman Spectrosc., 1987, 2, 1–58 Search PubMed.
- E. U. Condon, Phys. Rev., 1928, 32, 858–872 CrossRef CAS.
- T. Sharp and H. Rosenstock, J. Chem. Phys., 1964, 41, 3453–3463 CrossRef CAS.
- D. J. Tannor and E. J. Heller, J. Chem. Phys., 1982, 77, 202–218 CrossRef CAS.
- F. Neese, T. Petrenko, D. Ganyushin and G. Olbrich, Coord. Chem. Rev., 2007, 251, 288–327 CrossRef CAS.
- T. Petrenko and F. Neese, J. Chem. Phys., 2012, 137, 234107 CrossRef PubMed.
- D. Barton, C. König and J. Neugebauer, J. Chem. Phys., 2014, 141, 164115 CrossRef PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision C.01, Gaussian Inc., Wallingford CT, 2016 Search PubMed.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- E. Cancès, B. Mennucci and J. Tomasi, J. Chem. Phys., 1997, 107, 3032–3041 CrossRef.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094 CrossRef CAS PubMed.
- O. Christiansen, I. H. Godtliebsen, E. M. Gras, W. Györffy, M. B. Hansen, M. B. Hansen, E. L. Klinting, J. Kongsted, C. König, S. A. Losilla, D. Madsen, N. K. Madsen, P. Seidler, K. Sneskov, M. Sparta, B. Thomsen, D. Toffoli and A. Zoccante, Molecular Interactions Dynamics And Simulation C++ (MidasCPP) package Search PubMed.
- D. Madsen, PhD thesis, Aarhus University, 2019.
- T. Moitra, D. Madsen, O. Christiansen and S. Coriani, J. Chem. Phys., 2020, 153, 234111 CrossRef CAS PubMed.
- M. Sparta, D. Toffoli and O. Christiansen, Theor. Chem. Acc., 2009, 123, 413–429 Search PubMed.
- D. Toffoli, M. Sparta and O. Christiansen, Mol. Phys., 2011, 109, 673–685 CrossRef CAS.
- J. M. Bowman, X. Huang, L. B. Harding and S. Carter, Mol. Phys., 2007, 104, 33–45 CrossRef.
- J. M. Luis, B. Kirtman and O. Christiansen, J. Chem. Phys., 2006, 125, 154114 CrossRef PubMed.
- V. Rodriguez-Garcia, K. Yagi, K. Hirao, S. Iwata and S. Hirata, J. Chem. Phys., 2006, 125, 014109 CrossRef PubMed.
- G. Rauhut, J. Phys. Chem. A, 2015, 119, 10264–10271 CrossRef CAS PubMed.
- R. Piessens, E. de Doncker-Kapenga, C. W. Überhuber and D. K. Kahaner, Quadpack: A subroutine package for automatic integration, Springer-Verlag, Berlin Heidelberg, 1983 Search PubMed.
- F. J. Avila Ferrer, J. Cerezo, E. Stendardo, R. Improta and F. Santoro, J. Chem. Theory Comput., 2013, 9, 2072–2082 CrossRef CAS PubMed.
- A. Charaf-Eddin, A. Planchat, B. Mennucci, C. Adamo and D. Jacquemin, J. Chem. Theory Comput., 2013, 9, 2749–2760 CrossRef CAS PubMed.
- W. Domcke, L. Cederbaum, H. Köppel and W. von Niessen, Mol. Phys., 1977, 34, 1759–1770 CrossRef CAS.
- H. Du, R.-C. A. Fuh, J. Li, L. A. Corkan and J. S. Lindsey, Photochem. Photobiol., 1998, 68, 141–142 CAS.
- A. R. Mohebbi, C. Munoz and F. Wudl, Org. Lett., 2011, 13, 2560–2563 CrossRef CAS PubMed.
- L. Chen, C. Li and K. Müllen, J. Mater. Chem. C, 2014, 2, 1938–1956 RSC.
- B. Zhang, H. Soleimaninejad, D. J. Jones, J. M. White, K. P. Ghiggino, T. A. Smith and W. W. Wong, Chem. Mater., 2017, 29, 8395–8403 CrossRef CAS.
- R. Matthews, J. Swisher, K. M. Hutchins and E. B. Pentzer, Chem. Mater., 2018, 30, 3571–3577 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Analysis of one-mode anharmonicity on the vibrational profile for all tested molecules; mode ranking of all-trans quaterthiophene, all-trans pentathiophene, and the organic dyes; details of vibrational profiles of all-trans quaterthiophene, all-trans pentathiophene; pure IMDHO vibronic spectrum of all investigated organic dyes in a respective solvent. See DOI: https://doi.org/10.1039/d2cp01486f |
| This journal is © the Owner Societies 2022 |