Isotope effects on the dynamics of amorphous ices and aqueous phosphoric acid solutions

Abstract

The glass transitions of amorphous ices as well as of aqueous phosphoric acid solutions were reported to display very large ¹H/²H isotope effects. Using dielectric spectroscopy, in both types of glassformers for equimolar protonated/deuterated mixtures an almost ideal isotope-mixing behavior rather than a bimodal relaxation is found. For the amorphous ices this finding is interpreted in terms of a glass-to-liquid rather than an orientational glass transition scenario. Based on calorimetric results revealing that major ¹⁶O/¹⁸O isotope effects are missing, the latter scenario was previously favored for the amorphous ices. Considering the dielectric results on ¹⁸O substituted amorphous ices and by comparison with corresponding results for the aqueous phosphoric acid solutions, it is argued that the present findings are compatible with the glass-to-liquid scenario. To provide additional information regarding the deeply supercooled state of ¹H/²H isotopically mixed and ¹⁸O substituted glassformers, the aqueous phosphoric acid solutions are studied using shear mechanical spectroscopy as well, a technique which so far could not successfully be applied to characterize the glass transitions of the amorphous ices.

---

1. Introduction

Ninety years ago, and slightly preceded by the insight into how the discovery of the ¹⁸O isotope¹ affected the then measurable abundance of the deuteron,² the study of isotope effects in H₂O began with first electrolytic isolations of heavy water.^3,4 Soon thereafter the scientific exploration of the structural⁵ and kinetic⁶ differences of H₂O and D₂O waters and of light and heavy ices⁷ commenced, topics that remain fascinating and relevant to study in various contexts⁸ to the present day.

The major attraction this topic enjoys is obviously due to the profound practical and scientific importance arising from an understanding of the properties of water and aqueous solutions in all its liquid and even solid forms.^9–11 Therefore, it comes as no surprise that numerous theoretical approaches have been devised and various experimental techniques applied to explore the behaviors of the different isotopologues of H₂O. Several informative recent overviews regarding water's liquid phases exist.^12–15

A survey focusing on dielectric spectroscopy investigations of water and aqueous solutions conveys the impression that the effects of a ¹H/²H replacement^16–19 are much more frequently addressed than those induced by an ¹⁶O/¹⁸O substitution.^14,20 The same applies also for the amorphous ices: here, in recent years, the ¹H and ²H labeled low-density amorphous (LDA) and high-density amorphous (HDA) forms have been under intense scrutiny,^21–27 while dielectric studies of oxygen-18 enriched amorphous ices are still missing. Yet, some information on these (as well as on oxygen-17) labeled ices is available from calorimetry,²⁸ thermal desorption spectroscopy,²⁹ and nuclear magnetic resonance (NMR).³⁰

In crystalline solids, e.g., in perovskite materials, the replacement of ¹⁶O by ¹⁸O sometimes causes dramatic effects: it can, for instance, induce phase transitions which are absent in natural abundance samples.³¹ Interestingly such phenomena have been observed also in H/D substituted crystals, where the temperature at which the transition to an ordered low-temperature phase occurs, is not at all a linear function of the deuteron concentration.^32,33

Similar nonlinear compositional effects were identified for hydrated salts, e.g., for SnCl·(H₂O)_x(D₂O)_1−x solid solutions in which, depending on the isotopic composition x, the crystal-water molecules can form an orientational glass state.³⁴ Also for the bulk and the shear elastic moduli of amorphous (H₂O)_x(D₂O)_1−x, prepared as unannealed HDA, strong deviations from an ideal mixing behavior were reported to show up as a function of x.³⁵ Deviations from a linear x dependence were also noted from a study of the electrical conductivity.³⁶ By contrast, the dielectric main relaxation in liquid H₂O/D₂O mixtures as well as their shear viscosity were found to change linearly as the composition is varied.³⁷

The behavior of the amorphous ices is often compared to those of supercooled and glassforming aqueous solutions featurung various kinds of solutes.^38,39 To provide a useful basis for comparison with the isotope effects in the amorphous ices, and to keep the present work focused, we concentrate on a single mixing partner. To this end, we have chosen phosphorous pentoxide (P₂O₅) as a solute, because in the deeply supercooled state its aqueous solutions are known to exhibit very strong H/D isotope effects.^40,41 This contrasts with the minute isotope effects of many other supercooled liquids that are rarely larger than 1–2 K.^22,42,43

For numerous aqueous solutions it was reported that in the limit of infinite dilution their glass transition temperatures approach that of glassy water.^44,45 However, the aqueous P₂O₅ system seems to be one of the few examples where the composition dependence of the isotope effect was systematically explored and for decreasing P₂O₅ fractions found to approach 10 K.⁴⁰ This tremendously large isotope effect is compatible with that of glassy water.^22,23,25,26

The calorimetric glass transition temperatures T_g of the aqueous pentoxide solutions, here written as P₂O₅·RH₂O, have already been studied for a wide range of molar ratios R.⁴⁶ These T_gs can be compared with that of (protonated) supercooled water (corresponding to R → ∞), T_g,LDA = 136 K,⁴⁷ or other forms of amorphous ice such as amorphous solid water and hyperquenched glassy water.^48–50 For finite R, higher T_gs result, e.g., when R decreases from 6 to 5, then T_g increases by 6 K.⁴⁶ Moreover, the composition with the molar ratio R = 5 can equivalently be viewed as H₃PO₄·H₂O, i.e., the monohydrate of orthophosphoric acid (PA).

For hydrated PA, H/D isotope effects were studied previously implicitly or explicitly, e.g., by means of dielectric⁴⁰ and mechanical^40,51 spectroscopies as well as with the aid of NMR.⁵² For this method also oxygen-17 labeling was used,^53,54 but we are not aware of investigations of PA dealing with solutions that employ ¹⁸O labeling.

One of the central issues regarding the amorphous ices is whether their glass transition involves an unfreezing of only reorientational or also of translational degrees of freedom. Based on a differential scanning calorimetry study of H₂¹⁸O the former scenario was favored.²⁸ This idea was contested based on a calorimetric H/D isotope study.²⁶ However, we feel that the importance of this question warrants further studies using another technique and comparison with ¹⁶O/¹⁸O substitution effects in aqueous PA solutions, where it is beyond doubt that the glass transition involves reorientational and translational degrees of freedom.

Furthermore, as stated above, H₂O/D₂O mixtures were already variously studied, but to our knowledge so far not examined near the glass transition temperatures of the amorphous ices. For a thorough comparison and as a basis for discussion of the emergence of conceivable effects, the consequences of H/D mixing are also addressed for the aqueous PA solutions.

Thus, the present study will focus on the dynamic properties of the amorphous ices, and since the aqueous PA (or P₂O₅) solutions are used for comparison, some additional information regarding them is warranted: the aqueous PA solutions are excellent electrical conductors and hence their dielectric response is strongly overlaid by conductivity effects. Proton and oxygen NMR studies revealed that in pure PA a structural diffusion (or Grotthus) mechanism prevails and thus PA can be viewed as a good proton conductor.⁵³ When adding water, a vehicular process involving the diffusion of H₃O⁺, acting as a proton transporter that diffuses faster than the phosphate species, quickly gains importance.⁵³ While the specific conduction mechanism in the PA hydrates is not relevant for the present work, the conductivity timescale is of importance, albeit it is known to decouple from that of the structural relaxation.⁴⁰ To probe the latter directly, in the present work, in addition to dielectric spectroscopy also shear mechanical measurements are performed on the aqueous solutions. Unlike the amorphous ices which have been studied rheologically only under conditions of nanoscopic confinement⁵⁵ but not in the bulk, the solutions can be loaded into a rheometer at room temperature in a straightforward manner.

The present detection of the charge or structural relaxation processes relies on the acquisition of well-resolved dielectric loss or shear mechanical loss spectra. The prime information drawn from these spectra are the loss peak frequencies, and from the inverse frequencies, characteristic time scales can directly be inferred. Although we first focus on dielectric spectroscopy, the following general considerations can be applied analogously to shear rheology.

Unfortunately, the HDA and LDA ices are stable only within a rather limited temperature window: upon heating, both of them transform to other states when the characteristic time scales reach about 1 s.²¹ Thus, dielectric loss peaks are resolved only in a relatively narrow range of frequencies ν. For both amorphous ices the shape of their dielectric loss peaks has been found invariant.⁵⁶ So, by means of frequency-temperature-superposition, which can be considered valid if the data overlap after vertical shifting the spectra along the logarithmic frequency axis, one can achieve a significant extension of the range in which characteristic time scales can be extracted. Additionally, the examination of the spectral shape of the loss peak itself is instructive: in the absence of a distribution of correlation times, a Lorentzian, Debye-type shape is found as, e.g., for hexagonal ice. Such a single-exponential behavior (in the time domain), in the frequency domain is typically recognized from a ∝ν^−α high-frequency flank of the loss peak where the exponent α is 1.²⁷ The observation of smaller exponents 0 < α < 1 indicates the presence of a distribution of time constants, with smaller α signaling larger degrees of dynamic heterogeneity. Indeed, the existence of nonexponential relaxation is a typical hallmark of the dynamics in supercooled liquids and further disordered systems,⁵⁷ be it in their dielectric, their mechanical, or other responses.

2. Experimental details

We used 200 μl MilliQ-¹H₂O and 200 μl deuterium oxide (99.96 atom% D) to prepare the 50 : 50 (by volume) mixture. This corresponds to (¹H₂¹⁶O)_0.5(²H₂¹⁶O)_0.5 and will be called ^1,2H₂¹⁶O-HDA and likewise for the LDA variant. Oxygen-18 labeled water with an enrichment of 97 atom% was purchased from Eurisotop and the ices produced thereof are called ¹H₂¹⁸O-HDA and ¹H₂¹⁸O-LDA.

The amorphous ices were prepared in Innsbruck as described elsewhere.^11,25 In brief, HDA was made by pressure-amorphization of hexagonal ice at 77 K, annealing at 160 K and 1.1 GPa, followed by decompression at 140 K to 0.10 GPa. Such samples are called expanded HDA (eHDA^0.1) to distinguish them from the less stable unannealed HDA (uHDA). For deuterated samples, because of the isotope effect in the phase behavior, a slightly higher temperature is necessary:⁵⁸ so we decompressed at 141.5 K for the (¹H₂¹⁶O)_0.5(²H₂¹⁶O)_0.5 sample. Ultimately, the samples were quenched at 0.1 GPa to 77 K and recovered and stored at ambient pressure. After transporting them under liquid nitrogen conditions to Dortmund, they were crushed until a fine powder was obtained which then was cold-loaded into a parallel-plate capacitor. Like in previous work, this kind of preparation does not allow one to obtain the dielectric loss on an absolute scale and therefore, also in this work, they are given in arbitrary units. The aqueous solutions were mostly used as received and at room temperature filled as liquids into the capacitor, so that here the determination of absolute values is relatively straightforward.

The molar ratio R of the phosphorous pentoxide⁴⁶ or PA solutions can be calculated from the weight (or mass) fraction w of H₃PO₄ as typically given by the supplier, the molecular mass M_PA of the relevant PA isotopologue, and that of water M_water as follows

The PA solutions, that will be referred to as P₂¹⁶O₅·5¹H₂¹⁶O, P₂¹⁶O₅·5²H₂¹⁶O, and P₂¹⁸O₅·6¹H₂¹⁸O were obtained from Sigma Aldrich. Detailed information regarding the specific mixing ratios is given in Table 1. The isotopic enrichment of the deuterated solution is 98 atom% and that of the ¹⁸O-labelled solution 95 atom%. The P₂¹⁶O₅·5^1,2H₂¹⁶O sample was obtained by mixing equal masses of P₂¹⁶O₅·5¹H₂¹⁶O and P₂¹⁶O₅·5²H₂¹⁶O. The remaining solutions mentioned in Table 1 were produced by diluting with protonated MilliQ-water or with deuterated water (99.9 atom% D) from Sigma.

Table 1 Molar ratios used for the PA solutions from our previous⁵¹ and in the present work (marked with the letter a). Note that throughout this paper, the solutions with R ≈ 5 will be denoted as R = 5 and likewise for R ≈ 6

	R	R
P2^16O5·R^1H2^16O	4.9^51	5.8^a
P2^16O5·R^2H2^16O	4.8^51	5.7^a
P2^18O5·R^1H2^18O	—	6.1^a
P2^16O5·R^1,2H2^16O	4.8^a	—

---

All dielectric investigations were performed using an Alpha-A analyzer in combination with a Quatro temperature controller from Novocontrol. During each frequency sweep the temperature was stabilized within 0.1 K.

The measurements of the shear loos modulus G′′ were carried out using a stress-controlled rheometer MCR 502 from Anton-Paar. A parallel-plate configuration with a gap of 1 mm between the oscillating 4 mm plates was employed. All spectra were recorded in the small-deformation limit after the temperature was stabilized within 0.2 K.

3. Experimental results

A. Amorphous ices

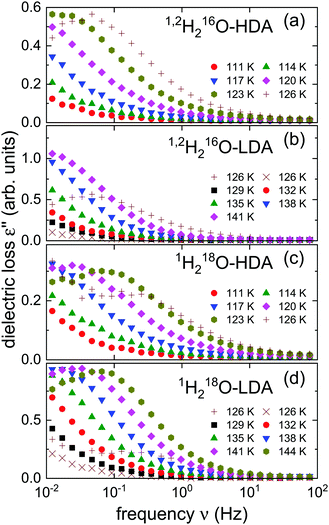
After the HDA was loaded into the capacitor at 77 K, in a first cycle the temperature was successively increased to 129 K in steps of 3 K and stabilized so that isothermal frequency scans could be recorded. At 129 K the samples were kept for more than an hour in order to obtain equilibrated LDA. Then the temperature was lowered by at least 9 K and in a second cycle further measurements were taken in steps of 3 K upon heating.

In Fig. 1 we present the dielectric loss spectra obtained for the isotopically enriched ices. One recognizes that for the isotopically mixed ^1,2H-HDA a dielectric loss peak is barely visible in our frequency window, while for ¹⁸O-HDA the spectra, recorded at the same temperatures, are shifted to somewhat higher frequencies. The same observation can be made when comparing ^1,2H-LDA and ¹⁸O-LDA.

Fig. 1 Dielectric loss spectra of (a) and (b) half deuterated and (c) and (d) ¹⁸O enriched amorphous ices. The spectra shown in frames (a) and (b) as well as those in frames (c) and (d) were each obtained from the same samples. All spectra were recorded during heating. The plusses (+) mark spectra featuring some irregularities, signaling that during data acquisition (in the first cycle) the transition from HDA to LDA takes place. The plusses in frames (a) and (b) on the one hand, and those in frames (c) and (d) on the other, represent the same data. The crosses (×) refer to measurements from the second cycle recorded at the same temperature.

The measurements recorded at 126 K during the first cycle (see the plusses shown in Fig. 1) show some “scatter” which, as we have documented in previous work,²¹ can arise as the sample transitions from HDA to LDA. This suggests that for the present measurements the transformation takes place at the same temperature. Also in harmony with previous observations, from Fig. 1 one recognizes that for dielectric loss peak frequencies >0.1 Hz, i.e., when the corresponding time constants are in the range of seconds,²¹ HDA transforms to LDA and later LDA transforms to ice I. Towards lower temperatures, the loss moves out of the accessible frequency window and thus, peaks can only be resolved in a relatively narrow range. Therefore, after checking its applicability in Section 4, below, we will use frequency-temperature-superposition to extract, e.g., timescale information from these spectra.

B. Aqueous phosphoric acid solutions

As mentioned in Section 1, in contrast to the amorphous ices, the aqueous P₂O₅ solutions exhibit a dielectric response which is typical of electrically conducting materials. Considering that for this system (i) the motion of the phosphate species is much slower than that of the H⁺ or D⁺ charge carriers,⁴⁰ (ii) its dielectric strength displays an anti-Curie temperature dependence⁵¹ previously identified as a hallmark of a conductivity relaxation,⁵¹ and (iii) its dielectric spectra, including the sigmoidal shape of the real part of the complex permittivity can be described well by conductivity models.⁵¹ Taken together it becomes clear that the dielectric response of the aqueous P₂O₅ solutions is governed by the translational dynamics of free charges. In this situation, a permittivity loss peak is not discernible in the spectra, and it is more convenient to present the electrical impedance data in the format of the electric loss modulus, M′′ = ε′′/(ε′² + ε′′²), where ε′ and ε′′ designate the dielectric constant and dielectric loss, respectively. In Fig. 2 we show the M′′ spectra obtained for P₂¹⁶O₅·5^1,2H₂¹⁶O and P₂¹⁸O₅·6¹H₂¹⁸O. The frequency-dependent loss moduli display well-defined peaks from which so-called conductivity relaxation times are typically extracted, see Section 4, below.

Fig. 2 Frequency dependence of the electric loss modulus M′′ (a) for P₂¹⁶O₅·5^1,2H₂¹⁶O and (b) for P₂¹⁸O₅·6¹H₂¹⁸O. For the lowest temperatures the solid lines indicate the presence of an approximate power-law behavior.

Here, it may suffice to note that without further analysis it can be seen in Fig. 2 that, like for the amorphous ices, also in the phosphoric acid solutions the dynamics of the ¹⁸O labeled species appears to be somewhat faster than that of the partially deuteron substituted sample. Overall, the evolution of the loss spectra for P₂¹⁶O₅·5^1,2H₂¹⁶O looks rather similar to those for P₂¹⁸O₅·6¹H₂¹⁸O. Fig. 2 also includes data recorded below the glass transition temperatures of these samples. In this range, M′′ displays power laws involving very small exponents which thus signal a nearly-constant-loss behavior⁵¹ that is considered to be a universal feature of glassy conductors.⁵⁹

The two phosphorous pentoxide solutions were also studied rheologically, and the results are presented in Fig. 3 in terms of the loss part of the shear mechanical modulus, G′′. This quantity can be considered as shear mechanical equivalent of the electric loss modulus M′′ that is presented in Fig. 2. In Fig. 3 one recognizes well-defined peaks in G′′ and that the overall shear responses of the two isotopologues display some differences regarding their shape, and also that the temperature scales are different.

Fig. 3 Frequency dependence of the shear loss modulus G′′ recorded (a) for P₂¹⁶O₅·5^1,2H₂¹⁶O and (b) for P₂¹⁸O₅·6¹H₂¹⁸O.

It is obvious that for P₂¹⁸O₅·6¹H₂¹⁸O the peak shape is relatively invariant as the temperature is varied. By contrast, some width variation is noted for the shear loss peaks of P₂¹⁶O₅·5^1,2H₂¹⁶O, which furthermore are generally somewhat broader than those for the oxygen-18 labeled sample. Despite the significant amount of hydrogen bonding in the presently studied glassformers, their rheological responses are qualitatively similar to those displayed by any nonassociating (and nonpolymeric) liquid. Not the least, this indicates the good miscibility of the components from which P₂¹⁸O₅·6¹H₂¹⁸O is formed. The same applies also for P₂¹⁶O₅·5^1,2H₂¹⁶O: despite the fact that its mechanical response is somewhat broader, clearly, a two-peak structure (no matter whether it would originate from resolvable component responses or separated H-and-D responses) can be ruled out on the basis of these data.

4. Discussion

When comparing the data for the amorphous ices with those for the aqueous P₂O₅ solutions, it becomes clear that the experimentally accessible frequency range is much larger for the latter substances. When attempting to extend this range nevertheless, and with the goal to access the timescale also of slower molecular motions, one may check whether or not the shape of the loss peaks is temperature invariant. If so, frequency-temperature-superposition can be applied to obtain relaxation times in an extended temperature range.

A. Spectral shapes

In Fig. 4, for the amorphous ices, we show their dielectric mastercurves, obtained by vertically shifting the loss spectra along the logarithmic frequency axis. In harmony with previous findings for other isotopologues of HDA and LDA,^27,56 in each case a well-defined mastercurve is seen to emerge. This finding confirms that within experimental uncertainty the shape of the ^1,2H-LDA and of the ¹⁸O-LDA spectra remains unchanged in the accessible temperature range. Obviously, this statement refers more to the high-, rather than to the low-frequency part of the loss spectra.

Fig. 4 Dielectric loss master curves of the partially deuterated (frames (a) and (b)) as well as the ¹⁸O enriched amorphous ices (frames (c) and (d)). All spectra were recorded during heating and are normalized with respect to their peak frequency ν_peak. The black solid lines indicate a power law ε′′ ∝ ν^–α.

From Fig. 4 one recognizes that the high-frequency flanks of the mastercurves are characterized by approximate power laws, ε′′ ∝ ν^–α. For the presently studied isotope substituted HDA and LDA samples, we find exponents α of 0.5 and 0.8, respectively. These exponents agree with those previously reported for the fully protonated amorphous ices.²⁷ Thus, it appears that for HDA the shape of their loss spectra is not affected by isotope substitution and the same is true for LDA. The present experiments thus underscore that, as reflected by its smaller high-frequency exponent α, the dynamic heterogeneity in HDA is larger than that in LDA, a finding which recently was borne out using an analysis of spin-lattice relaxation times as well.³⁰

To put the exponents into a larger context, it is instructive to observe that for the crystalline ices (I, IV, V, VI, and XII) for which this information has been compiled,²⁷ it was found that 0.8 ≤ α ≤ 1. Thus, the exponent for LDA is within this range. This is also true for GeO₂, another tetrahedrally bonded inorganic glassformer.⁵⁷ For HDA the much smaller α in fact agrees with the exponent found for numerous organic glassforming liquids that often lack a relatively well-defined local bonding pattern.⁶⁰

It is interesting to examine whether or not the spectral-shape similarity among the various isotopologues of the amorphous ices is analogously displayed by the aqueous pentoxide reference system. This issue is readily addressed by means of Fig. 5 which summarizes the amplitude-normalized spectral shapes of the electrical and mechanical loss moduli for various hydrated PAs. In Fig. 5(a) and (b) one recognizes that the M′′ peaks all exhibit very similar shapes, in harmony with the observations made from Fig. 2 and from previous work for R = 5.⁵¹ In particular, the shape similarity observed for ^1,2H₂¹⁶O-HDA and ^1,2H₂¹⁶O-LDA with respect to the isotopically pure systems applies analogously for P₂¹⁶O₅·5^1,2H₂¹⁶O.

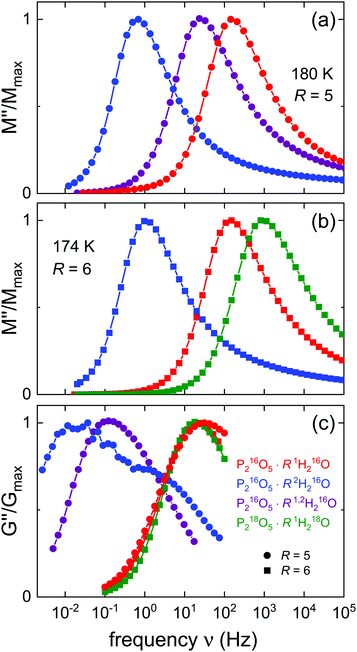Fig. 5 Amplitude-normalized responses of the presently investigated aqueous acids: (a) isothermal comparison of the electric loss modulus M′′ for R = 5 including the H/D isotope mixture. (b) Isothermal M′′ comparison for R = 6 including the ¹⁸O enriched sample. (c) Quasi-isothermal comparison of the shear loss modulus G′′ for R = 5 at T = 180 K and R = 6 at T = 174 K. The data for P₂¹⁶O₅·5¹H₂¹⁶O and for P₂¹⁶O₅·5²H₂¹⁶O are from ref. 51, all others are from the present work.

To facilitate the comparison with the data for R = 6, for Fig. 5(b), we have chosen a slightly lower temperature so that the modulus peaks for P₂¹⁶O₅·R¹H₂¹⁶O, and likewise for P₂¹⁶O₅·R²H₂¹⁶O, appear at the same frequency as for R = 5. Furthermore, this representation conveys a good impression of the isotope related shifts.

At first glance, it may appear surprising that the heavier, ¹⁸O substituted material displays a somewhat faster conductivity response than the ¹⁶O analog. However, as inferred from Table 1, the ¹⁸O sample has a significantly larger water content (R differs by 0.3…0.4 units) than the others shown in Fig. 5(b). With ΔT_g/ΔR about −6 K,⁴⁶ which implies faster isothermal response, it is clear that most of the apparent shift to larger frequencies seen in Fig. 5(b) is simply a consequence of the slight difference in water content.

This argument applies of course also to the G′′ data shown in Fig. 5(c). Here, the spectra of the protonated samples (R = 5 at 180 K and R = 6 at 174 K) as well as those of the ¹⁸O labeled ones are seen to be peaked at about the same frequency. For P₂¹⁶O₅·6²H₂¹⁶O one observes a double-peak structure analogous to that already documented in ref. 51 for R = 5: this double-peak structure signals that not only the low-frequency structural relaxation, but also the faster, decoupled charge transport leaves its mark on the mechanical loss spectra. For the isotopically mixed sample, a significant broadening is observed, but a resolved double-peak structure is not present, indicating that here the degree of decoupling between charge transport and structural relaxation is smaller than for the fully deuterated sample.

When comparing the rheological with the electric modulus spectra shown in Fig. 5 one recognizes that the G′′ spectra (for P₂¹⁶O₅·6²H₂¹⁶O see the main peak) are shifted to lower frequencies with respect to the M′′ spectra. This indicates that in most cases the mobility of the charge carriers is at least partially decoupled from the structural dynamics. As will become evident in Section 4.B, below, in the aqueous solutions this decoupling becomes most pronounced for temperatures below T_g.

B. Temperature dependent relaxation times

In Fig. 6 we show the dielectric relaxation times for the amorphous high- and low-density ices. The lower right part of that figure summarizes the time scales obtained for the various isotopologues of HDA and the upper left part compiles those for LDA. For both amorphous ices the same pattern emerges: (i) the resulting energy barrier against dipolar relaxation is essentially left unaltered by the isotope substitution. (ii) An ¹⁶O/¹⁸O isotope effect on the relaxation is largely absent, in harmony with a previous calorimetric study.²⁸ (iii) The mixed-isotope sample reveals time constants intermediate between those of H₂O and D₂O.

Fig. 6 Structural relaxation times of amorphous ices recorded for various isotopic substitutions using dielectric spectroscopy. Filled symbols indicate time scales that were directly determined from the dielectric loss peaks, open symbols mark time scales calculated on the basis of frequency-temperature-superposition. Triangles pointing down and up refer to cooling and heating runs, respectively. The relaxation times for (fully) deuterated HDA and LDA are taken from ref. 25 and references cited therein, all other time constants are from the present work.

Owing to the relatively narrow frequency range which is typically accessible in dielectric studies of amorphous ices, it is clear that, in general, the description in terms of an Arrhenius law, which seems to characterize all relaxation time traces seen in Fig. 6, may be considered to be approximately sufficient. In fact, it was argued that the behavior of HDA deviates slightly from the strong-liquid limit,²¹ while that of LDA was termed⁶¹ ‘superstrong’, thus indeed following an Arrhenian dependence.²¹

The experimental facts that mixed-isotope samples do not display spectral complexities and that the time constants are intermediate between those of H₂O and D₂O, indicate a dynamic averaging specific to well-mixed (at a microscopic level) binary systems. In this regard, it is worth noting that in both amorphous ices the origin of the strong H/D isotope effects was previously assigned to the difference between the zero-point librational frequencies specific to the protonated as compared to those of the deuterated constituents.²² This difference was quantitatively argued to be at the origin of the large contrast between the effective local activation energies for the proton or the deuteron motions.²² We emphasize that the frequency of the librational motions does not depend on the masses of the oxygen isotope but only on those of the protons or deuterons.^22,23 Based upon this insight of localized, site-specific dynamics, one may expect that the responses of the presently considered mixtures should be bimodal (or trimodal if the HDO species are taken into account), reflecting the differences between the individual hopping/reorientation rates corresponding to the protonated and deuterated species. According to the present results, such a bimodal behavior is obviously not observed for the amorphous ices. Before briefly discussing possible consequences of this finding, we will first summarize the relaxation pattern of the aqueous P₂O₅ solutions.

Fig. 7 shows that, as compared to the amorphous ices, the dynamics of the aqueous solutions could be traced over a much larger range. At least for the conductivity relaxation times that were determined from the M′′ spectra, a rather complex pattern is observed: at high temperatures a super-Arrhenius type of dependence prevails, while near T_g for all isotopologues the relaxation times bend over to an Arrhenius behavior. In order not to overload Fig. 7, we show the data for R = 5 in frame (a) and those for R = 6 in frame (b). Both panels also include the relaxation times assessed from the peaks of the shear modulus spectra from which the evolution of the structural relaxation times can be inferred. As expected for well mixed liquids the resulting time constants are intermediate between those of the two mixing partners.⁴⁶ Furthermore, for all samples one recognizes that near T_g, at which the structural relaxation time is about 100 s, the conductivity relaxation is roughly 2 decades faster than the structural relaxation. A decoupling of charge and mass transport is in fact characteristic for many ion conductors.^38,62

Fig. 7 Time constants characterizing the presently studied PA solutions: (a) R = 5 and (b) R = 6. Filled symbols represent time scales determined directly from the peaks of the electric loss moduli M′′. Relaxation times obtained by means of frequency-temperature-superposition from M′′ are shown as open symbols. Partially filled symbols indicate structural relaxation times from the peaks of the shear loss modulus G′′. The star refers to the structural relaxation time of a fully protonated sample determined using a dielectric physical aging experiment. The other data for P₂¹⁶O₅·5¹H₂¹⁶O and those for P₂¹⁶O₅·5²H₂¹⁶O are taken from ref. 51. All other data are from the present work.

Like for the amorphous ices, from Fig. 5 one notes that, in contrast to P₂¹⁶O₅·5²H₂¹⁶O, for the mixed-isotope sample a resolved two-peak electrical relaxation is not observed. Yet, in the representation of the shear mechanical spectra of P₂¹⁶O₅·5^1,2H₂¹⁶O shown in Fig. 5, about one decade above the peak frequency, one recognizes a shoulder in G′′ which hints at a bimodal response. However, this has nothing to do with an H/D substitution related effect, since this bimodality is even more pronounced in isotopically “pure” P₂¹⁶O₅·5²H₂¹⁶O. As detailed elsewhere,⁵¹ the occurrence of the two peaks in the G′′ spectra of P₂¹⁶O₅·5²H₂¹⁶O indicates that not only the structural relaxation but also the (decoupled) ion transport impacts on the mechanical response of the PA solutions. Obviously, for P₂¹⁶O₅·5^1,2H₂¹⁶O the same phenomenon is observed, albeit with a reduced decoupling.

The absence of a bimodality in the H/D-mixed amorphous ices is relevant for our understanding of their glass transition: if only strictly local processes like on-site reorientations governed their dynamics, a bimodality would be expected. The presence of distinct proton- and deuteron-related zero-point energy changes would cause different effective energy barriers for protons and deuterons, i.e., two distinct relaxation time scales would be expected.

However, an exchange-induced averaging of time scales and thus a single-peak structure becomes possible if also nonlocal, i.e., translational processes are involved. This is clear for PA, where the electrical conductivity is governed by effects of a so-called structural diffusion.⁵¹ In the same vein, the analogous argument applied to the mixed-isotope amorphous ices suggests that in the vicinity of T_g not only local dynamic processes are operative. In other words, the current results suggest that translational motions contribute to the observed dynamics of the amorphous ices as well.

Thus, our findings vindicate the statement expressed in view of ref. 14 that “Recently, the central role of translational diffusion for dielectric relaxation was explicitly demonstrated by studying isotope effects on the dielectric relaxation spectra.”⁶³

C. Comparison of isotope effects

To compare the isotope effects of the amorphous ices with those for the phosphorous pentoxide solutions, rather than on the basis of the time constants, one may also resort to the associated glass transition temperatures T_g, here defined via the mentioned 100 s-criterion.

In Fig. 8(a) we show the T_gs thus inferred for the various isotopologues of LDA and HDA. This compilation illustrates nicely, again, that an ¹⁶O/¹⁸O isotope shift is practically absent, and that the T_g of the mixed-isotope sample is roughly halfway between those of the H₂O and the D₂O species. The form of representation chosen for Fig. 8 has the advantage that results from calorimetric measurements, in Fig. 8(a) those from ref. 28, can directly be included: here, one recognizes that the H/D isotope effect appears smaller than inferred from dielectric spectroscopy. This phenomenon was elsewhere²² discussed at length in relation to the higher scanning rates typically used in calorimetry than for the experiments reported here.

Fig. 8 Panel (a) summarizes the glass transition temperatures of the amorphous ices for different isotopic species as a function of the average molecular weight. The filled symbols represent the temperature at which the dielectric relaxation time equals 100 s. The open symbols mark the onset temperatures of the glass transition from calorimetric measurements performed with a heating rate of 10 K min⁻¹ (from ref. 28). Panel (b) shows the glass transition temperatures of the aqueous PA solutions. The designation ‘from G′′’ refers to the temperature at which the shear mechanical time constant reaches or is extrapolated to 100 s. The designation ‘from M′′’ refers to the crossover of the electrical modulus time constants from a super-Arrhenius to an Arrhenius temperature dependence, cf.Fig. 7. Panel (c) compiles the melting temperatures for various isotopologues of pure water.⁶⁴ The dashed lines are meant to guide the eye.

To compare the data for the aqueous solutions on the same footing, one can determine T_g either by applying the 100 s-criterion to the shear data or by inferring T_g from the point at which the electric modulus times cross over from the super-Arrhenius to the Arrhenius behavior. In Fig. 8(b) we include the results for both kinds of analysis. Except for P₂¹⁶O₅·6¹H₂¹⁶O, the two determinations agree well within experimental uncertainty. For P₂¹⁸O₅·6H₂¹⁸O the water content (i.e., R) is somewhat larger than for the corresponding samples devoid of oxygen-18 to which it is compared directly. As already noted above a slightly larger R systematically leads to a slightly lower T_g.

In ref. 28, based on a comparison with results from crystalline ice VI where similar ¹H/²H and essentially missing ¹⁶O/¹⁸O isotope effects appear, it was argued that these observations favor an interpretation of the glass transitions in HDA and LDA in terms of an orientational glass transition, rather than in terms of a glass-to-liquid transition. In other words, in this scenario only the reorientational but not the translational degrees would unfreeze as the amorphous ices are heated across T_g. However, transformations involving both types of motions, e.g., those from the crystal to the liquid, can lead to the same isotope effect pattern. This is seen from Fig. 8(c) where we include the melting temperatures for the different isotopologues of H₂O.⁶⁴

An H/D isotope effect is absent in the transformation kinetics that leads from HDA to LDA²⁵ and among other amorphous ices.⁶⁵ This observation is in harmony with the fact that this transformation is governed by a restructuring of the amorphous oxygen network. From Fig. 1, a major ¹⁶O/¹⁸O shift of the HDA → LDA transition could, however, also not be resolved.

For comparison with the present results (that are based on measurements of dynamic rather than thermodynamic quantities) it is reassuring that also kinetic observables such as the (zero-frequency) viscosity,⁶⁶ the dielectric microwave absorption,¹⁴ and even responses in the terahertz and infrared regimes of liquid water and aqueous solutions show the same trends regarding the isotope shifts.^67,68

5. Conclusions

In the present work, we studied the impact of ¹H/²H and of ¹⁶O/¹⁸O isotope substitution on the dynamics of the amorphous ices as well as on aqueous solutions of phosphoric pentoxide (that can equivalently be viewed as PA hydrates). Previously, both glassforming systems were reported to show enormously large H/D isotope effects amounting to 10–12 K for HDA and LDA and to 8 K for PA monohydrate (corresponding to a molar water-to-P₂O₅ ratio of R = 5). For the fully deuterated with respect to the fully protonated sample the magnitude of their isotope effects was previously termed ‘anomalous’ since they are very much larger than compatible with the familiar factor.^22–24,40

We performed dielectric and rheological measurements not only for samples with R = 5, but also for several samples with R = 6. While for the aqueous solutions the electrical measurements are sensitive to the proton conductivity which essentially traces the structural diffusion above T_g and exhibits a thermally activated behavior at lower temperatures, the rheological experiments monitor the structural relaxation dynamics directly.

In particular, we studied ¹H/²H mixed-isotope (R = 5) and oxygen-18 enriched (R = 6) aqueous solutions for comparison with and in view of the implications regarding the analogously isotope substituted HDA and LDA ices. For the ^1,2H₂¹⁶O ices as well as for the P₂¹⁶O₅·5^1,2H₂¹⁶O solutions the dielectric or electric modulus spectra display loss peak frequencies that are compatible with an ideal mixing behavior. Furthermore, the spectra are devoid of indications hinting at a bimodal structure. Such a structure would have been expected in a straightforward quantum mechanical interpretation of the isotope effect which invokes a localized isotope-specific H/D-replacement-induced change of the zero-point energy and the consequent alteration of the effective local energy barriers. The observation of single-peak relaxations in the mixed-isotope samples thus highlights the importance of non-local relaxation processes. While this conclusion appears trivial for the proton conducting PA solutions, for the amorphous ices it suggests that not only on-site (reorientational) but also off-site (translational) motions of the water molecules are relevant in the glass transition ranges of HDA and LDA.

Experiments on ¹⁸O substituted ices were already previously exploited to address the nature of the glass transition in the amorphous ices.²⁸ To further scrutinize this issue, we performed dielectric (and for the PA hydrates also rheological) measurements on correspondingly labeled samples and confirm the absence of significant ¹⁶O/¹⁸O isotope effects. Not the least with reference to the dynamics in the PA hydrates and to the melting behavior of variously isotope substituted ices, in the present work we argue that this experimental finding is compatible with the appearance of glass-to-liquid transitions in HDA as well as in LDA.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

This work was financially supported by the Deutsche Forschungsgemeinschaft under Project No. 413265854. C. M. T. is a recipient of a DOC fellowship of the Austrian Academy of Sciences ÖAW and is supported by the Early Stage Funding 2021 of the University of Innsbruck and by the Center for Molecular Water Sciences CMWS-Early Science Project (DESY).

References

1. W. F. Giauque and H. L. Johnston, An isotope of oxygen, mass 18. Interpretation of the atmospheric absorption bands, J. Am. Chem. Soc., 1929, 51, 1436,  DOI:10.1021/ja01380a018.
2. H. C. Urey, F. G. Brickwedde and G. M. Murphy, A hydrogen isotope of mass 2 and its concentration, Phys. Rev., 1932, 40, 1.
3. E. W. Washburn and H. C. Urey, Concentration of the H Isotope of hydrogen by the fractional electrolysis of water, Proc. Natl. Acad. Sci. U. S. A., 1932, 18, 496.
4. G. N. Lewis and R. T. Macdonald, Concentration of H² Isotope, J. Chem. Phys., 1933, 1, 341,  DOI:10.1063/1.1749300.
5. G. W. Stewart, Comparison of x-ray diffraction curves of water and deuterium oxide at 25 °C, J. Chem. Phys., 1934, 2, 558.
6. W. N. Baker, A new comparison of the viscosity of D₂O with that of H₂O, J. Chem. Phys., 1936, 4, 294.
7. P. W. Bridgman, The Pressure-volume-temperature relations of the liquid, and the phase diagram of heavy water, J. Chem. Phys., 1935, 3, 597,  DOI:10.1063/1.1749561.
8. J. R. Gat, Oxygen and hydrogen isotopes in the hydrologic cycle, Annu. Rev. Earth Planet. Sci., 1996, 24, 225.
9. P. Gallo, K. Amann-Winkel, C. A. Angell, M. A. Anisimov, F. Caupin, C. Chakravarty, E. Lascaris, T. Loerting, A. Z. Panagiotopoulos, J. Russo, J. A. Sellberg, H. E. Stanley, H. Tanaka, C. Vega, L. Xu and L. G. M. Pettersson, Water: A tale of two liquids, Chem. Rev., 2016, 116, 7463.
10. S. Cerveny, F. Mallamace, J. Swenson, M. Vogel and L. Xu, Confined water as model of supercooled water, Chem. Rev., 2016, 116, 7608.
11. K. Amann-Winkel, R. Böhmer, C. Gainaru, F. Fujara, B. Geil and T. Loerting, Water's controversial glass transitions, Rev. Mod. Phys., 2016, 88, 011002.
12. S. Capaccioli and K. L. Ngai, Resolving the controversy on the glass transition temperature of water?, J. Chem. Phys., 2011, 135, 104504.
13. M. Ceriotti, W. Fang, P. G. Kusalik, R. H. McKenzie, A. Michaelides, M. A. Morales and T. E. Markland, Nuclear quantum effects in water and aqueous systems: Experiment, theory and current challenges, Chem. Rev., 2016, 116, 7529.
14. B. Kutus, A. Shalit, P. Hamm and J. Hunger, Dielectric response of light, heavy and heavy oxygen water: Isotope effects on the hydrogen bonding network's collective relaxation dynamics, Phys. Chem. Chem. Phys., 2021, 23, 5467.
15. T. E. Markland and M. Ceriotti, Nuclear quantum effects enter the mainstream, Nat. Rev. Chem., 2018, 2, 0109.
16. O. A. Nabokov and Y. A. Lubimov, The dielectric relaxation and the percolation model of water, Mol. Phys., 1988, 65, 1473.
17. K. Okada, M. Yao, Y. Hiejima, H. Kohno and Y. Kajihara, Dielectric relaxation of water and heavy water in the whole fluid phase, J. Chem. Phys., 1999, 110, 3026.
18. H. Vada, M. Nagai and K. Tanaka, The intermolecular stretching vibration mode in water isotopes investigated with broadband terahertz time-domain spectroscopy, Chem. Phys. Lett., 2009, 473, 279.
19. C. Rønne, P.-O. Åstrand and S. R. Keiding, THz Spectroscopy of Liquid H₂O and D₂O, Phys. Rev. Lett., 1999, 82, 2888.
20. J. H. Melillo and S. Cerveny, Isotope Effect on the Dynamics of Hydrophilic Solutions at Supercooled Temperatures, in Broadband Dielectric Spectroscopy: A Modern Analytical Technique, ed. W. H. H. Woodward, American Chemical Society, Washington, DC, 2021, ch. 12, pp. 263–281 DOI:10.1021/bk-2021-1375.ch012.
21. K. Amann-Winkel, C. Gainaru, H. Nelson, P. H. Handle, M. Seidl, R. Böhmer and T. Loerting, Water's second glass transition, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 17720.
22. C. Gainaru, A. L. Agapov, V. Fuentes-Landete, K. Amann-Winkel, H. Nelson, K. W. Köster, A. I. Kolesnikov, V. N. Novikov, R. Richert, R. Böhmer, T. Loerting and A. P. Sokolov, Anomalously large isotope effect in the glass transition of water, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 17402.
23. A. L. Agapov, A. I. Kolesnikov, V. N. Novikov, R. Richert and A. P. Sokolov, Quantum effects in the dynamics of deeply supercooled water, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 022312.
24. V. N. Novikov and A. P. Sokolov, Quantum effects in dynamics of water and other liquids of light molecules, Eur. Phys. J. E: Soft Matter Biol. Phys., 2017, 40, 57.
25. S. Lemke, P. H. Handle, L. J. Plaga, J. N. Stern, M. Seidl, V. Fuentes-Landete, K. Amann-Winkel, K. W. Köster, C. Gainaru, T. Loerting and R. Böhmer, Relaxation dynamics and transformation kinetics of deeply supercooled water: Temperature, pressure, doping, and proton/deuteron isotope effects, J. Chem. Phys., 2017, 147, 034506.
26. V. Fuentes Landete, L. J. Plaga, M. Keppler, R. Böhmer and T. Loerting, Nature of water's second glass transition elucidated by doping and isotope substitution experiments, Phys. Rev. X, 2019, 9, 011015.
27. L. J. Plaga, A. Raidt, V. Fuentes Landete, K. Amann-Winkel, B. Massani, T. Gasser, B. Massani, C. Gainaru, T. Loerting and R. Böhmer, Amorphous and crystalline ices studied by dielectric spectroscopy, J. Chem. Phys., 2019, 150, 244501.
28. J. J. Shephard and C. G. Salzmann, Molecular reorientation dynamics govern the glass transitions of the amorphous ices, J. Phys. Chem. Lett., 2016, 7, 2281.
29. S. M. McClure, E. T. Barlow, M. C. Akin, D. J. Safarik, T. M. Truskett and C. B. Mullins, Transport in amorphous solid water films:  Implications for self-diffusivity, J. Phys. Chem. B, 2006, 110, 17987.
30. L. Hoffmann, J. Beerwerth, M. Adjei-Körner, V. Fuentes-Landete, C. M. Tonauer, T. Loerting and R. Böhmer, Oxygen NMR studies of high-density and low-density amorphous ice, J. Chem. Phys., 2022, 156, 084503.
31. M. Itoh, R. Wang, Y. Inaguma, T. Yamaguchi, Y.-J. Shan and T. Nakamura, Ferroelectricity induced by oxygen isotope exchange in strontium titanate perovskite, Phys. Rev. Lett., 1999, 82, 3540.
32. Y. Moritomo, Y. Tokura, N. Nagaosa, T. Suzuki and K. Kumagai, Quantum phase transition in K₃D_1−xH_x(SO₄)₂, Phys. Rev. Lett., 1993, 71, 2833.
33. A. Titze, J. Kusz, H. Böhm, H.-J. Weber and R. Böhmer, X-ray diffraction, optical birefringence and ⁸⁷Rb-NMR spectroscopy of the paraelectric and antiferroelectric phases of Rb₃D_xH_1−x(SO₄)₂, J. Phys.: Condens. Matter, 2002, 14, 895.
34. H. Suga and S. Seki, Frozen-in states of orientational and positional disorder in molecular solids, Faraday Discuss. Chem. Soc., 1980, 69, 221,  10.1039/DC9806900221.
35. E. L. Gromnitskaya, I. V. Danilov, A. G. Lyapin and V. V. Brazhkin, Influence of isotopic disorder on solid state amorphization and polyamorphism in solid H₂O–D₂O solutions, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 134104.
36. H. Weingärtner and C. A. Chatzidimitriou-Dreismann, Anomalous H⁺ and D⁺ conductance in H²O–D²O mixtures, Nature, 1990, 246, 548.
37. U. Kaatze, Dielectric relaxation of H₂O/D₂O mixtures, Chem. Phys. Lett., 1993, 203, 1.
38. C. A. Angell, Dynamic processes in ionic glasses, Chem. Rev., 1990, 90, 523.
39. S. Schneider and M. Vogel, NMR studies on the coupling of ion and water dynamics on various time and length scales in glass-forming LiCl aqueous solutions, J. Chem. Phys., 2018, 149, 104501.
40. M. Heres, Y. Wang, P. J. Griffin, C. Gainaru and A. P. Sokolov, Proton conductivity in phosphoric acid: The role of quantum effects, Phys. Rev. Lett., 2016, 117, 156001.
41. Y. Wang, N. A. Lane, C.-N. Sun, F. Fan, T. A. Zawodzinski and A. P. Sokolov, Ionic conductivity and glass transition of phosphoric acids, J. Phys. Chem. B, 2013, 117, 8003.
42. T. Jörg, R. Böhmer, H. Sillescu and H. Zimmermann, Isotope effects on the dynamics of a supercooled van der Waals liquid, Europhys. Lett., 2000, 49, 746.
43. M. A. Ramos, C. Talón, R. J. Jiménez-Riobóo and S. Vieira, Low-temperature specific heat of structural and orientational glasses of simple alcohol, J. Phys.: Condens. Matter, 2003, 15, S1007.
44. D. R. MacFarlane and C. A. Angell, Glass transition for amorphous solid water, J. Phys. Chem., 1984, 88, 759.
45. C. A. Angell, Liquid fragility and the glass transition in water and aqueous solutions, Chem. Rev., 2002, 102, 2627.
46. H. R. Corti, F. J. Nores-Pondal and C. A. Angell, Heat capacity and glass transition in P₂O₅–H₂O solutions: Support for Mishima's conjecture on solvent water at low temperature, Phys. Chem. Chem. Phys., 2011, 13, 19741.
47. M. S. Elsaesser, K. Winkel, E. Mayer and T. Loerting, Reversibility and isotope effect of the calorimetric glass → liquid transition of low-density amorphous ice, Phys. Chem. Chem. Phys., 2010, 12, 708.
48. G. P. Johari, A. Hallbrucker and E. Mayer, The glass–liquid transition of hyperquenched water, Nature, 1987, 330, 552.
49. A. Hallbrucker, E. Mayer and G. P. Johari, The heat capacity and glass transition of hyperquenched glassy water, Philos. Mag. B, 1989, 60, 179.
50. A. Hallbrucker, E. Mayer and G. P. Johari, Glass-liquid transition and the enthalpy of devitrification of annealed vapor-deposited amorphous solid water: A comparison with hyperquenched glassy water, J. Phys. Chem., 1989, 93, 4986.
51. S. Ahlmann, P. Münzner, K. Moch, A. P. Sokolov, R. Böhmer and C. Gainaru, The relationship between charge and molecular dynamics in viscous acid hydrates, J. Chem. Phys., 2021, 155, 014505.
52. Y. Aihara, A. Sonai, M. Hattori and K. Hayamizu, Ion conduction mechanisms and thermal properties of hydrated and anhydrous phosphoric acids studied with ¹H, ²H, and ³¹P NMR, J. Phys. Chem. B, 2006, 110, 24999.
53. J. P. Melchior, K. D. Kreuer and J. Maier, Proton conduction mechanisms in the phosphoric acid–water system (H₄P₂O₇–H₃PO₄·2H₂O): A ¹H, ³¹P and ¹⁷O PFG-NMR and conductivity study, Phys. Chem. Chem. Phys., 2017, 19, 587.
54. J. P. Melchior and B. Frick, On the nanosecond proton dynamics in phosphoric acid–benzimidazole and phosphoric acid–water mixtures, Phys. Chem. Chem. Phys., 2017, 19, 28540.
55. V. Soprunyuk and W. Schranz, DMA study of water's glass transition in nanoscale confinement, Soft Matter, 2018, 14, 7246.
56. J. Stern, M. Seidl, C. Gainaru, V. Fuentes-Landete, K. Amann-Winkel, P. H. Handle, K. W. Köster, H. Nelson, R. Böhmer and T. Loerting, Experimental evidence for two distinct deeply supercooled liquid states of water—Response to “Comment on ‘Water's second glass transition’ by G. P. Johari, Thermochim. Acta (2015), Thermochim. Acta, 2015, 617, 200.
57. R. Böhmer, K. L. Ngai, C. A. Angell and D. J. Plazek, Non-exponential relaxations in strong and fragile glass-formers, J. Chem. Phys., 1993, 99, 4201.
58. K. Winkel, M. Bauer, E. Mayer, M. Seidl, M. S. Elsaesser and T. Loerting, Structural transitions in amorphous H₂O, and D₂O: The effect of temperature, J. Phys.: Condens. Matter, 2008, 20, 494212.
59. K. L. Ngai, Relaxation and Diffusion in Complex Systems, Springer, New York, 2011.
60. A. I. Nielsen, T. Christensen, B. Jakobsen, K. Niss, N. B. Olsen, R. Richert and J. C. Dyre, Prevalence of approximate √t relaxation for the dielectric α process in viscous organic liquids, J. Chem. Phys., 2009, 130, 154508.
61. C. A. Angell, C. T. Moynihan and M. Hemmati, “Strong” and “superstrong” liquids, and an approach to the perfect glass state via phase transition, J. Non-Cryst. Solids, 2000, 274, 319.
62. J. Habasaki, C. León and K. L. Ngai, Dynamics of Glassy, Crystalline and Liquid Ionic Conductors: Experiments, Theories, Simulations, Springer, Switzerland, 2017.
63. C. Hölzl, H. Forbert and D. Marx, Dielectric relaxation of water: Assessing the impact of localized modes, translational diffusion,and collective dynamics, Phys. Chem. Chem. Phys., 2021, 23, 20875.
64. F. Steckel and S. Szapiro, Physical properties of heavy oxygen water. Part 1. Density and thermal expansion, Trans. Faraday Soc., 1963, 59, 331.
65. L. Kringle, W. A. Thornley, B. D. Kay and G. A. Kimmel, Isotope effects on the structural transformation and relaxation of deeply supercooled water, J. Chem. Phys., 2022, 156, 084501.
66. A. I. Kudish, D. Wolf and F. Steckel, Physical properties of heavy-oxygen water. Absolute viscosity of H₂¹⁸O between 15 and 35 °C, J. Chem. Soc., Faraday Trans., 1972, 68, 2041.
67. A. Berger, G. Ciardi, D. Sidler, P. Hamm and A. Shalit, Impact of nuclear quantum effects on the structural inhomogeneity of liquid water, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 2458 and references cited therein.
68. M. R. Bittermann, C. López-Bueno, M. Hilbers, F. Rivadulla, F. Caporaletti, G. Wegdam, D. Bonn and S. Woutersen, Austen in Amsterdam: Isotope effect in a liquid–liquid transition in supercooled aqueous solution, J. Non-Cryst. Solids: X, 2022, 13, 100077.

---

Footnote

† These authors contributed equally to this work.

---