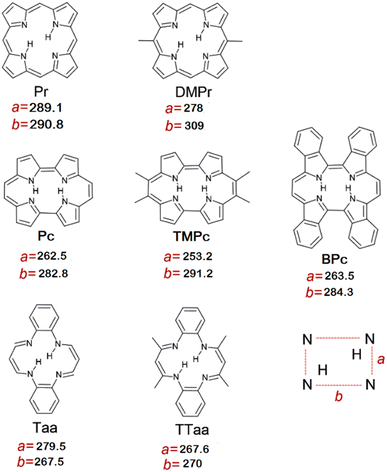
Open Access Article
Open Access ArticleSearching for correlations between geometric and spectroscopic parameters of intramolecular hydrogen bonds in porphyrin-like macrocycles†
Sylwester
Gawinkowski
 * and
Om
Prakash
* and
Om
Prakash
Institute of Physical Chemistry, Polish Academy of Sciences, Kasprzaka 44/52, 01-224 Warsaw, Poland. E-mail: sgawinkowski@gmail.com; oprakash@ichf.edu.pl
First published on 7th September 2022
Abstract
Chemical bond lengths and angles are characteristic structural parameters of a molecule. Similarly, the frequencies of the vibrational modes and the NMR chemical shifts are unique “chemical fingerprints” specific to a compound. These are the basic parameters describing newly obtained compounds and enabling their identification. Intramolecular hydrogen bonding significantly influences the physicochemical properties of macrocyclic compounds with a porphyrin-like structure. This work presents the verification for correlations between geometric and spectroscopic parameters related to hydrogen bonds in this type of macrocyclic compounds. In particular, such relationships were investigated for a large group of porphyrin, porphycene, and dibenzotetraaza[14]annulene derivatives and a group of other macrocycles with similar structure. A very strong linear correlation was found only between the vibrational frequencies of the NH groups involved in a hydrogen bond and the length of this bond, which applied to all macrocyclic compounds of this type. Several other relationships were found between spectroscopic (IR, Raman, NMR) and geometric (X-ray) parameters, highlighting differences and similarities between different families of macrocycles. Apart from providing a better understanding of the nature of hydrogen bonds and their characteristics in porphyrin-like macrocyclic compounds, these relationships will facilitate the identification of new macrocycles and the extrapolation of their spectroscopic properties.
Introduction
Porphyrins are a unique class of chemicals. Decades of intensive research on porphyrin-like substances have been motivated by the biological importance of these compounds and have identified new potential applications in various fields, such as medicine,1,2 molecular electronics,3,4 optics,5,6 energy harvesting,7–10 and analytical chemistry.11,12 Porphyrin and its analogues have also been the target of fundamental research.13–18 The great applicability of porphyrins is due to their physical and chemical properties, which originate from the unique geometric and electronic structure of the molecule.19–21 The combination of four pyrrole rings with methylene bridges leads to an aromatic system, ensuring the high stability and flat geometry of the macrocycle.22,23 Four nitrogen atoms create a square-shaped cavity, and two hydrogen atoms located in the cavity form two intramolecular NH⋯N hydrogen bonds. This represents an effective model for studying systems involving two hydrogen bonds as well as hydrogen atom transfer processes.24–27By replacing methylene bridges with shorter and longer links, it is possible to maintain the aromaticity of the macrocycle and obtain several structural isomers of porphyrin. Porphycene is the most symmetrical isomer of porphyrin; similar to porphyrin, it has excellent application potential in different branches of technology and can also serve as a model molecule.2,28–34 Two different but symmetrically distributed bridges connect pyrrole rings, causing the intramolecular cavity of porphycene to adopt a rectangular shape. Consequently, hydrogen bonds are significantly shorter and stronger, and hydrogen atoms can be transferred at a much faster rate than in porphyrin.31
Appropriate substituents allow tuning the physical and chemical properties of the macrocycle. The substituent often influences the shape and size of the intramolecular cavity and the strength of the hydrogen bonds. This may lead to dramatic changes in the double hydrogen atom transfer dynamics and mechanism.35,36 Moreover, it is possible to enlarge the cavity of porphycene to bring its size closer to that of the porphyrin cavity and vice versa. The question then arises as to what extent the size and shape of the intramolecular cavity are responsible for the properties of the two molecules. Previous reports suggest that the dimensions of the cavity can significantly affect intramolecular hydrogen bonds.35,36
Previous studies have investigated the relationships of the distance between the hydrogen bond donor and acceptor atoms with the spectroscopic parameters of a group of different molecules forming intermolecular and intramolecular hydrogen bonds.37–47 Significant correlations between these parameters were demonstrated, especially for groups of similar molecules. Porphyrins and porphycenes form intermolecular hydrogen bonds. Moreover, in these two molecules, the acceptor atoms of the hydrogen bonds are also part of the aromatic system of the whole macrocycle. As a result, the electron density on the acceptor atom of the hydrogen bond and on the hydrogen bond itself can be modified by introducing electron-donating or electron-withdrawing substituents in the macrocycle. Larger substituents may also affect the geometry of the macrocycle, owing to steric effects.
Irrespective of the mechanism behind the changes induced by the substitution, modifying the geometry of the molecule usually alters its physicochemical properties. Therefore, it is reasonable to hypothesise that the geometric parameters of the cavity may be correlated with other characteristic signatures of the compound. In particular, one can expect that the strength and spectroscopic signatures of intramolecular hydrogen bonds correlate with the geometry of the cavity. For example, previous studies have revealed correlations between electronic properties such as fluorescence quantum yield or tautomerisation rate and the hydrogen bond parameters of porphycenes, e.g., the N⋯N distance.48–52 It has also been shown that properly selected substituents can alter the geometry of the porphyrin cavity, bringing its dimensions closer to those of porphycene. As a result of a change in cavity geometry, the hydrogen transfer rate was observed to increase by several orders of magnitude.35,52 Extrapolation of this finding suggests that porphyrin and porphycene may exhibit even more similar properties if their cavities are forced to adopt similar geometries. The rich literature covering the physicochemical characteristics of numerous derivatives of both compounds allows verifying this hypothesis. The main geometrical parameters reflecting the strength of the NH⋯N hydrogen bond are the NH bond length, the N⋯N distance, and the NHN angle. The 1H chemical shift in the NMR spectra can be used to determine the hydrogen bond strength, and the frequency of the NH stretching band in the IR or Raman spectra can also be used for this purpose.
The objective of the present work is to identify possible relationships between structural parameters of intramolecular hydrogen bonds in porphyrins and porphycenes and their spectroscopic characteristics, such as vibrational frequencies of NH stretching, lengths of NH⋯N hydrogen bonds, and the respective 1H chemical shifts in NMR spectra. We used quantum chemical simulations to examine the relationship between these parameters. We studied a large set of porphyrin and porphycene derivatives. The analysis also included dibenzotetraaza[14]annulenes, another group of macrocyclic compounds structurally similar to porphyrins and porphycenes. Unlike porphyrins and porphycenes, dibenzotetraaza[14]annulenes are anti-aromatic. The inclusion of these compounds in the study enabled determining the degree of influence of the aromaticity of the macrocycle ring on the observed relationships, and establishing whether these correlations could be used in other families of macrocycles having similar cavities (e.g., porphyrazines and phthalocyanines).
Our correlation search was based on two methods. The first involved the collection of literature data, including spectroscopic and crystallographic parameters. The other approach consisted in quantum chemical simulations of the same type of data by forcing the appropriate cavity geometry in unsubstituted macrocycles and checking the effect of such forced geometry on spectroscopic and geometric parameters. The results obtained with the two approaches were then compared. The analysis revealed which physicochemical parameters exhibited strong or weak correlations. These relationships may contribute to improve our understanding of intramolecular hydrogen bonds, as well as help to predict some physicochemical properties of such macrocycles and design their chemical synthesis and functionalisation.
Methods
The search for correlations connecting the structural and spectroscopic parameters of macrocycles was based on the comparison of three types of data describing the structural and spectroscopic parameters of macrocycles: experimental data collected from the literature, data calculated using the quantum-chemical method for fully optimized molecular structures, and data calculated by the forced cavity deformation method. In the forced cavity deformation method the structural and spectroscopic parameters of the macrocycles were calculated as a function of their intramolecular cavity size. All quantum-chemical simulations were performed using the B3LYP/6-31G(d,p) functional/basis set combination, as implemented in the Gaussian 09 and Gaussian 16 software packages.53,54 Seven macrocyclic molecules with double intramolecular NH⋯N hydrogen bonds were selected for the study, based on the significant differences between their cavity sizes: porphycene (Pc), 9,10,19,20-tetramethylporphycene (TMPc), tetrabenzoporphycene (BPc), porphyrin (Pr), 5,15-dimethylporphyrin (DMPr), dibenzotetraaza[14]annulene (Taa), 1,2,10,12-tetramethyldibenzotetraaza[14]annulene (TTaa) (Scheme 1).In the first step, we optimised the equilibrium geometries of all molecules in the electronic ground state, and then calculated the harmonic frequencies and chemical shifts. In the second step, two parallel N⋯N distances along hydrogen bonds were distorted (stretched or shortened) by 50 pm and fixed at this value; all other geometrical parameters were optimised again (forced cavity deformation). This step was repeated for N⋯N distances systematically changed in the 200–400 pm range. Vibrational analysis and NMR shift calculations were performed on all forced geometries obtained in this way. Selected geometric and spectroscopic parameters were then extracted, and their mutual relationships were plotted.
In the following step, the obtained relationships were compared with the experimental datasets reported in previous studies. We only considered compounds for which both X-ray structure and 1H chemical shifts were available. If available, we also considered IR and Raman data reported in the literature. The experimental dataset was supplemented with a similarly sized dataset obtained from the simulation of a large group of macrocycles (including those for which experimental data were found, plus another group of compounds for which such data were not available), whose molecular geometries were fully optimised. The various geometric and spectroscopic parameters obtained for this group originated solely from the substitution of the parent macrocycles. The experimental and simulated datasets were fitted with linear or second-order polynomial functions, to highlight mutual relationships between geometric and spectroscopic properties. Resulting parameters of fittings are collected in the Table 1.
| X | Y | Porphycenes | Porphyrins | Dibenzotetraaza[14]annulenes | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | B | C | R 2 | A | B | C | R 2 | A | B | C | R 2 | |||
| N⋯N | N⋯N | E | — | −0.71 ± 0.031 | 510 ± 15 | 0.911 | — | −1.41 ± 0.06 | 698 ± 17 | 0.96 | — | −0.040 ± 0.040 | 280 ± 11 | 0.000 |
| S | — | −0.84 ± 0.056 | 471 ± 8 | 0.885 | — | −1.29 ± 0.12 | 669 ± 35 | 0.871 | — | −0.040 ± 0.040 | 270 ± 23 | 0.077 | ||
| N⋯N | 1H NMR | E | 0.0089 ± 0.0018 | −4.99 ± 0.98 | 702 ± 129 | 0.876 | 0.0029 ± 0.0032 | 1.63 ± 1.76 | 229 ± 245 | 0.038 | — | — | — | — |
| S | 0.011 ± 0.002 | −6.25 ± 1.39 | 882 ± 186 | 0.893 | −0.0052 ± 0.0039 | 2.83 ± 2.19 | 390 ± 307 | 0.343 | — | — | — | — | ||
| N⋯N | NH freq. | S | −0.55 ± 0.05 | 320 ± 28 | −43488 ± 3761 | 0.992 | −0.36 ± 0.03 | 211 ± 19 | −27096 ± 2602 | 0.983 | −0.68± 0.71 | 384 ± 391 | −41788 ± 13967 | 0.911 |
| N⋯N | NH bond | S | 0.0031 ± 0.0003 | −1.80 ± 0.17 | 365 ± 23 | 0.989 | 0.0018 ± 0.0002 | −1.06 ± 0.09 | 255 ± 13 | 0.984 | 0.0031 ± 0.001 | −1.77 ± 0.45 | 354 ± 61 | 0.936 |
| NH bond | 1H NMR | S | — | 2.34 ± 0.16 | −244 ± 17 | 0.881 | — | 1.43 ± 0.84 | −150 ± 85 | 0.107 | — | 0.105 ± 0.357 | −2.809 ± 36.6 | 0.075 |
| NH bond | NH freq. | S | — | 22465 ± 116 | 186 ± 1 | 0.999 | — | 22701 ± 1195 | −189 ± 12 | 0.95 | — | 22077 ± 420 | −183 ± 4 | 0.993 |
| NH bond | 1H NMR | S | — | −0.0126 ± 0.0008 | 37.9 ± 2.5 | 0.886 | — | −0.0074 ± 0.0047 | 21.2 ± 16.6 | 0.087 | — | — | — | — |
The last step was to verify the validity of the established relationships. As a proof of concept, a group of 25 porphyrin-like macrocycles were chosen as model molecules to interpolate and predict their spectroscopic and structural features. The selection of these molecules aimed to ensure the largest possible variations in their cavity size and NMR parameters. All selected molecules were fully optimised, and their vibrational (IR and Raman) frequencies and NMR spectra were calculated with the same DFT method. All literature data are listed in Tables S1–S4 (ESI†).
Finally, all three data types were plotted in diagrams showing the relationships between pairs of parameters (Fig. 1–7). For clarity, different types of data are presented in different ways: asterisks represent experimental data, while circles denote data calculated for fully optimised molecular structures. The data obtained by the forced cavity deformation method are displayed as solid lines. In addition, in all graphs, data corresponding to the same family of compounds are presented in similar colours, e.g., shades of green for porphyrins and shades of blue for dibenzotetraaza[14]annulenes. Additional black stars and circles represent data corresponding to macrocycles that could not be included in one of the three analysed families, such as extended porphyrins, extended porphycenes, porphyrazines, and phthalocyanines (Table S4, ESI†). The correlations between pairs of parameters in data obtained from simulations of fully optimised structures and experimental data from the literature were analysed numerically using Origin 2020b.55
Results and discussion
The analysis of the results of the simulations focused on the relationships between parameters that could be verified experimentally (mainly by IR, Raman, NMR, and crystallography methods) and that might improve our understanding of the hydrogen bonds in the present systems. Only the trans configuration of hydrogen atoms in the cavity was considered in the analysis. This restriction is justified by the predominance of this configuration in porphyrins and porphycenes.31 The cis form is much less common and was reported only for molecules in particular conditions, such as adsorption on metal surfaces at ultralow temperatures or specific asymmetric substitution of the parent macrocycle.56–59 The predominant existence of the trans tautomer in porphyrins, porphycenes, and dibenzotetraaza[14]annulenes is also supported by the calculated relative energies of different tautomers.60–62 The cis form has higher energy and could not be detected experimentally in standard conditions. Setting the molecule in a specific environment may be required to detect different tautomers; for example, the cis form of porphycene was detected upon adsorption on copper and gold surfaces.58,59,63The reproducibility of the experimental results by the simulations was tested by comparing the geometric and spectroscopic parameters obtained for a set of test compounds for which experimental data were available. This analysis shows that using a relatively small basis set 6-31G(d,p) and the B3LYP functional allowed the accurate reproduction of the experimental data. The errors in reproducing the experimental parameters were estimated to be several percent (ESI†).
Relationships between two N⋯N distances
Fig. 1 shows the influence of change of N⋯N distances along the hydrogen bond on the N⋯N distances perpendicular to the hydrogen bond (N1⋯N2 vs. N2⋯N3). The plotted lines were obtained by the forced cavity deformation approach discussed above. The obtained curves for different porphyrins and porphycenes were separated, but they were almost identical for dibenzotetraaza[14]annulenes.Fig. 1 also shows the datapoints extracted from crystallographic results and those obtained from fully optimised structures at the density functional theory (DFT) level. In addition, the figure shows crystallographic and DFT simulation data for macrocycles that did not belong to the selected groups or were asymmetrically substituted (black stars and circles). For all three families of macrocycles, both the experimental and DFT-simulated datapoints were located close to the lines. Steeper slopes were observed for porphyrins and porphycenes; however, even at the boundaries of the considered range of N⋯N distances, the datapoints did not diverge dramatically from the forced geometry lines. Even smaller differences were observed in the case of dibenzotetraaza[14]annulenes. The small slope of the forced geometry curves in the case of the dibenzotetraaza[14]annulenes shows that the change in the N⋯N distance along the hydrogen bond had a very small or almost negligible effect on the other N⋯N distance. Moreover, the curves obtained for Taa and TTaa were much closer to each other than those obtained for different porphycenes and porphyrins.
The deviations from the curves of the experimental and calculated datapoints were small. The most significant deviation was observed for one porphyrin derivative. However, the point corresponding to the experimental result showed a much smaller deviation. All datapoints collected for porphyrins and porphycenes (experimental and obtained from simulations) could be fitted with linear functions (Fig. S4 and S5 in the ESI†). The obtained R2 parameter for experimental data was 0.96 and 0.911 for porphyrins and porphycenes, respectively. The corresponding values for the simulation data were 0.871 and 0.885. In the case of dibenzotetraaza[14]annulenes, the situation was completely different. Although the linear dependence is shown by the data obtained from the forced cavity deformation method (Fig. 1), the significant dispersion of the datapoints from the experiments and for fully optimized geometries showing no correlation with the R2 parameter close to 0 (Fig. S6 in the ESI†). Even though the correlations are high for porphycenes and porphyrins considered separately, the linear functions obtained for each group of molecules were significantly different from each other, showing that all datapoints could not be described by a single relationship. The linear functions obtained for the experimental datapoints and simulations have similar slopes but are slightly offset from each other. This offset indicates that the dimensions of the intramolecular cavity obtained from the DFT simulation in relation to the data from the crystallography are overestimated by a few percent. Based on the slopes of all lines, the strongest mutual dependence of the two N⋯N distances was observed for porphyrins, whereas almost no dependences were observed for dibenzotetraaza[14]annulenes. This difference originates from the non-aromaticity of dibenzotetraaza[14]annulenes, as opposed to the aromaticity of porphyrins and porphycenes. In aromatic macrocycles, changes in the N⋯N distance along hydrogen bonds have a much stronger impact on the other N⋯N distances.
Relationships between N⋯N distances and 1H NMR chemical shifts
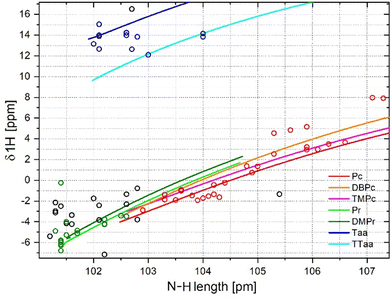
Fig. 2 shows the dependences of the 1H NMR chemical shift of the hydrogen atom participating in the hydrogen bond on the N⋯N distance between the donor and acceptor atoms of the same bond. The magnitude of this shift can be used to determine the strength of the hydrogen bond, and is also an indicator of the aromaticity of the macrocycle ring.64–66 In particular, a decrease in this shift reflects an increasing aromaticity of the macrocycle; such a change also indicates a weakening of the hydrogen bond. The forced cavity deformation method showed that the relationship is slightly nonlinear (Fig. 2). The curves for each family of molecules are clearly separated. Again, an upward shift is observed between the trend of the simulated datapoints with respect to the trend of the experimental datapoints for porphycenes and porphyrins. Due to the large scattering of points around the trend (Fig. 2), the fitting of datapoints did not show strong correlation between the distance N⋯N and the chemical shift (Fig. S7–S9 in the ESI†). The relatively good relationship was determined with quadratic function only for porphycenes, with R2 equal to 0.876 and 0.893 for experimental and simulated data. The fitting of the other two families of macrocycles, either with quadratic or linear functions, gave R2 below 0.5 or even close to 0 (Table 1). The scatter of points corresponding to the Taa derivatives seems to be completely random. Thus, the size of the cavity only to some extent influences the chemical shift value in aromatic macrocycles and is negligible in the case of dibenzotetraaza[14]annulenes.It is worth noting that the lines obtained by the forced cavity deformation method for porphycenes and porphyrins did not intersect in the studied N⋯N distance range. The close structural similarity of the two macrocycles suggests the possibility to obtain similar physicochemical properties for the two compounds by appropriate modification of the dimensions of their cavities. For example, the symmetric substitution of the two opposite methyl bridges of porphyrin can distort its square-like cavity and bring its dimensions closer to those of the rectangular cavity of porphycene.35 As a result, a dramatic increase of the hydrogen atom transfer rate was observed. One would expect the properties of porphyrin to become identical to those of porphycene if their cavities matched. The lack of intersection between the porphyrin and porphycene curves in Fig. 2 does not support this expectation. A similar conclusion can be drawn by analysing the clustering of experimental and calculated points corresponding to the optimised geometries. The slopes of the curves obtained for porphyrins and porphycenes were significantly different. The same difference is also present in the distribution of experimental and simulated datapoints. The chemical shifts measured for the porphycenes varied in the 0 to 11 ppm range (Table S1 in the ESI†). In general, the larger values of 1H chemical shifts for porphycenes than porphyrins indicate that the former had lower aromaticity and stronger hydrogen bonds. The substitution of methylene bridges in porphyrin led to a more significant distortion of its cavity, but this resulted in relatively small changes in the 1H chemical shifts. The wider range of 1H chemical shifts observed for substituted porphycenes than porphyrins indicates that the properties of porphycenes can be tuned to a much greater extent simply by an appropriate selection of substituents. A significant number of other macrocycles with the same experimental values of 1H chemical shift and N⋯N distances are visible in the Fig. 2 (black starts), possibly indicating that their properties are similar to those of porphycenes and porphyrins. The chemical shifts of the dibenzotetraaza[14]annulenes seemed insensitive to N⋯N distance changes; 1H chemical shifts ranging between 12.5 and 14 ppm were observed in the corresponding distribution (Table S3 in the ESI†). Moreover, the spread of this distribution was greater than that derived from the forced cavity deformation method.
Despite the lack of a close correlation between the N⋯N distance and the chemical shift of the cavity hydrogens, the observed trends may still be useful. For example, to correctly assign the NMR bands corresponding to the cavity hydrogen atoms based on the crystallographic data in case of difficulties in their unambiguous assignment. 1H NMR bands corresponding to cavity hydrogens usually exhibit a low intensity. The band assignments would be even more difficult for poorly soluble porphycene derivatives and for most phthalocyanines. In these cases, the above relationships may prove helpful by revealing the possible spectral regions corresponding to the cavity hydrogens.
Relationships between N⋯N distances and NH stretching frequencies
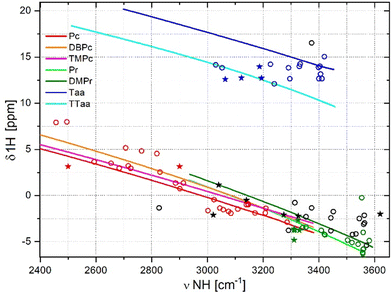
The influence of the N⋯N distance on the NH stretching frequencies is shown in Fig. 3. The macrocycle molecules have two NH stretching modes: in-phase and out-of-phase. Due to its low sensitivity, the standard Raman technique is rarely used in organic chemistry, and scarce data have been reported on the NH stretching frequency in the Raman spectra of porphyrins, porphycenes, and dibenzotetraaza[14]annulenes. However, the IR technique is commonly used for identifying new chemical compounds; nevertheless, the relatively low NH stretching band intensities in the IR spectra makes the corresponding assignments problematic. The OH stretching band for water embedded in KBr pellets or deposited on the cooled detector window is often incorrectly assigned as the NH stretching band. Additionally, in the case of strong hydrogen bonds, the NH band may be downshifted to the 3000 cm−1 region, where strong bands corresponding to CH stretching modes usually exist; as a result, a straightforward assignment is difficult. For example, the NH stretching band was not identified in the experimental spectra of porphycene for a very long time. DFT calculations suggested that this band should be located around 2800 cm−1 and exhibit a very high intensity, but no such band appeared in IR or Raman spectra. Eventually, it was shown that this band lies in the expected spectral region, but extends over a very broad region (several hundreds of cm−1); hence, its local intensity is low.67Because of the scarcity of data, Fig. 3 includes only a few datapoints corresponding to macrocycles whose NH frequencies were experimentally determined and reported in the literature. The frequency of the NH stretching mode reflects the strength of the hydrogen bond and, to a certain extent, determines the potential for intramolecular hydrogen transfer. The rate of this process depends on the hydrogen donor–acceptor distance that, for the macrocycles analysed here, corresponds to the N⋯N distance. It should be noted that the curves obtained by the forced cavity deformation approach overlap with the datapoints corresponding to the fully optimised geometries of substituted porphyrins and porphycenes. However, the experimental datapoints are located below the curves; this is mainly because scaling factors were not used in this analysis. Moreover, the Taa and TTaa curves, as well as the datapoints representing fully optimised derivatives of Taa, show relatively broad distributions. This indicates that the frequency of the NH vibration in porphyrins and porphycenes depends strongly on the N⋯N distance, and only to a much lower extent on other factors such as the electronic properties of the substituents. Based on the comparison of Fig. 2 and 3, one can conclude that the frequency of the NH stretching is more strongly correlated with the length of the hydrogen bond than with the electron density on the hydrogen atom (and on the whole hydrogen bond), as represented by the 1H chemical shift. The dependence of the NH stretching frequency on the interatomic N⋯N distances corresponding to the optimised macrocycle geometries is described by second-order polynomial functions (Fig. S10–S12 in the ESI†). The strong correlation of simulation datapoints is indicated by R2 = 0.992 for porphycenes and R2 = 0.983 for porphyrins (Table 1). Data for Taa derivatives are less correlated (R2 = 0.911 for simulations and R2 = 0.783 for experimental data).
A similar distribution of datapoints for the OH hydrogen bonds in minerals was fitted by exponential function.68 However, Hansen et al.69 showed linear correlation between such parameters. This difference in using diverse functions results from the considered range of hydrogen bond lengths. For small changes in the distance between the heavy atoms forming the hydrogen bond, the frequency changes can be approximated by a linear function. For large ranges of these changes, a curvilinear fit is necessary.
Fig. 3 shows that the frequency of the NH stretching modes for porphycenes with the largest cavity is similar to that of porphyrins with the smallest cavity. This suggests that derivatives of porphyrins and porphycenes having similar cavities exhibit similar properties. Such conclusion should be corroborated with experimental data when they become available. The much greater slope of the curves obtained for the porphycenes reflects their higher potential in controlling the hydrogen transfer rate through substitution and modification of the intramolecular cavity. This may be useful, for example, for the design of light-activated single-molecule electronic switches based on the control of the position (transfer) of hydrogen atoms. Increased intramolecular cavity sizes and hydrogen bond lengths have been reported for the electronically excited states of porphyrin and porphycene.70 Thus, a relatively small change in the N⋯N distance of porphycenes as a result of electronic excitation can significantly slow down the hydrogen transfer process, and even completely stop it under adequately selected conditions.71
Relationships between N⋯N distances and NH bond lengths
Fig. 4 shows the dependence of the N⋯N distance on the NH bond length. Similarly to the previously considered dependencies, good agreement is observed between the datapoints obtained for fully optimised geometries of porphyrins with the curves representing the relationships obtained from forced cavity deformation. Also, apparent discrepancies are present between the Taa and TTaa curves and the points representing the optimised Taa derivatives. The curves representing porphycenes show a much stronger dependence of the NH bond length on the N⋯N distance compared to the other macrocycles. Due to the deficiency of data in the literature, the plot lacks experimental datapoints. Because of their low electron density, hydrogen atoms scatter X-rays weakly, making it difficult to precisely determine their location from crystallographic data. Therefore, it is necessary to use hardly available, intense X-ray sources or neutron scattering sources to resolve this issue. The electron density on the hydrogen atom of the hydrogen bond is largely shifted towards the nitrogen atom, which may lead to a significant underestimation of the bond lengths; in addition, the hydrogen bonds may shift and blur the electron density along the hydrogen bond. The low values of the 1H NMR chemical shifts show that the hydrogen atoms of porphyrins are indeed significantly deshielded. The relationship between the NH bond length and the N⋯N distance would therefore be valuable in determining the exact position of the hydrogen atoms in the cavity.As in the case of the NH vibration, the dependence of the NH bond length on the N⋯N distance can be fitted by second-order polynomial functions (Fig. S13–S15, ESI†). The fit shows a strong correlation between the N⋯N distance and the NH bond length for porphycenes, with the parameter R2 = 0.989 (Table 1). Only a slightly lower value of R2 = 0.984 shows the fit obtained for porphyrins. For Taa derivatives, R2 takes the value of 0.936, which still indicates a significant correlation of values. The strict linear correlation between the N⋯N distances obtained from the crystallographic data and from the simulations (Fig. S2, ESI†) highlights the relatively good accuracy of the present calculation method. Therefore, the curves representing the NH dependence on the N⋯N distance should also provide a reliable estimation of the NH bond length, assuming that the scaling factor between the simulated and experimental values is determined.
Relationships between NH bond lengths and 1H chemical shifts
Fig. 5 displays the relationship between NH bond lengths and 1H chemical shifts. Very similar and partially overlapping curves obtained by the forced cavity deformation approach are observed for porphycenes and porphyrins. This indicates that these two molecules have similar structural and spectroscopic characteristics. Furthermore, the datapoints obtained for the fully optimised geometries follow these curves. However, the curves for Taa and other derivatives show a very different trend, with highly dispersed datapoints compared to porphycenes and porphyrins. As in the previous case, the relatively high accuracy of the N⋯N distances predicted by the DFT calculations (Fig. S2, ESI†) suggests that these calculations can predict the NH bond lengths with similar accuracy. The datapoints could be fitted with linear function (Fig. S16–S18 in the ESI†), but in this case the dispersion of datapoints is relatively large. The R2 parameter for porphyrins is relatively high, with a value of 0.881, but its values for fittings obtained for porphyrins and dibenzotetraaza[14]annulenes are close to zero (Table 1) That indicates that the NH bond lengths can be predicted on the basis of these relationships only for porphycenes and may be subject to a significant error.In the case of the macrocycles considered here, the predicted length of the NH bond varies between 101 and 108 pm. In addition, an NH bond length shorter than 95 pm was measured by X-ray crystallography.72 Woińska et al.73 showed that it is possible to accurately determine the position of the hydrogen atom even without using neutron scattering, and reported the NH bond length in aromatic systems to be approximately 105 μm. This average value is in the range predicted by our DFT simulations. However, the applicability of the correlations of NH bond length with other parameters presented here requires experimental determination of this length for at least a few molecules in each macrocycle family.
Relationships between NH stretching frequencies and 1H chemical shifts
The relationships between the NH stretching frequency and the 1H chemical shift presented in Fig. 6 also require additional experimental data. The distribution of datapoints and curves is analogous to that observed in Fig. 5. The data corresponding to porphyrins and porphycenes show a similar distribution, while those obtained for dibenzotetraaza[14]annulenes are separated and much more scattered. In Fig. 6, the datapoints obtained for the fully optimised macrocycles are distributed around the curves obtained from the forced cavity deformation of the reference macrocycles. Porphycene data points can be fitted with a linear function, with the relatively large R2 parameter of 0.886 (Table 1). An analogous linear fit of the data points for porphyrins gives R2 of only 0.087, and for Taa derivatives, the scattering of the datapoints is too large for linear fitting. Relatively many experimental points exist for Taa derivatives, but the large dispersion of these points also indicates the lack of correlation of the NH frequency with the chemical shift for this family of macrocycles. Reliable NMR data are also available for a few porphyrins. These datapoints follow the trend predicted by simulation but all of them are grouped in narrow range of NH stretching frequencies. For the same NH vibrational frequency range, the dibenzotetraaza[14]annulenes showed higher values of 1H chemical shifts than porphycenes and porphyrins. This is because the dibenzotetraaza[14]annulene derivatives are non-aromatic and non-planar, while porphycenes, porphyrins, and derivatives exhibit aromatic and planar structures. The aromaticity and planarity of the macrocycles affect the charge density or electron distribution near the cavity, therefore influencing the 1H chemical shift in the NMR spectra.65,66Relationships between NH bond lengths and NH stretching frequencies
Fig. 7 shows linear and very strong correlations between NH bond lengths and NH stretching frequencies. The curves obtained by the forced cavity deformation of the reference macrocycles are in excellent agreement with the datapoints representing fully optimised geometries, with minimal deviations. At variance with all parameter correlations considered above, in this case all curves and datapoints (including those of dibenzotetraaza[14]annulenes) exhibit the same linear trend (Fig. 7 and Fig. S19–S21 in ESI†). All datapoints corresponding to the fully optimised geometries could be fitted by one linear function Y = 22386 − 186·X, R2 = 0.996. This linear correlation, independent of the type and degree of aromaticity of the macrocycle, reflects the dominant effect of the NH⋯N hydrogen bond length on the NH stretching frequency. Also, the set of datapoints representing the group of testing molecules (black circles) is distributed along the same line. This consistency suggests the commonality of the correlations for other macrocyclic compounds, and is not limited to just the three families considered here. Nevertheless, significantly different relationships have been reported for non-macrocyclic molecules. Hansen et al.69 showed that the OH bond length vs. OH stretching frequency relationship for strong intramolecular hydrogen bonds follows a second-order polynomial function. Nakamoto et al.42 also reported a nonlinear relationship. However, Pimentel et al.74 and Bertolasi et al.75 reported that relative frequencies are linearly dependent on bond length distances. Different relationships determined for different compounds indicate differences in the behaviour of hydrogen bonds. In the case of the macrocycles studied here, the determined linearity is very strong with small deviations.The frequency of the NH stretching mode reflects the potential controlling the hydrogen atom motion in the stretching direction. The shape of this potential influences the vibrational frequency and the possible hydrogen transfer process along the hydrogen bond. Although such transfer takes place on a multidimensional potential energy surface, and the frequency of the NH stretching vibration corresponds to only one dimension, this mode is one of only few vibrations that closely control the potential for such reaction.
Apart from the NH stretching, the vibrations bringing the two nitrogen atoms participating in the hydrogen bond closer to each other and the NH bending vibrations that modify the hydrogen bond angle (NH⋯N) also significantly influence the hydrogen transfer. Therefore, the determination of the NH stretching frequency is essential for understanding the hydrogen atom transfer mechanism, and has been the subject of previous research on model porphyrin and porphycene molecules. However, despite the large intensities of the IR bands corresponding to the NH stretching vibrations predicted by the DFT calculations, these bands are difficult to identify in the experimental spectra. In the case of porphyrins and dibenzotetraaza[14]annulenes, the intensities of these bands are very low, and usually smaller than those of the bands corresponding to the CH stretching vibrations.62,63 Moreover, for molecules with shorter N⋯N distances, the NH stretching band lies in the same spectral region as the CH vibrations, making it difficult to identify it unequivocally. In this case, comparative measurements on deuterated samples in which the respective ND stretching vibrations are significantly shifted towards lower frequencies can be helpful. However, the situation is even more difficult in the case of porphycenes. For these systems, the simulations predict the NH stretching band to be located much below the frequency of CH vibrations; however, this band is difficult to detect in the experimental spectra: to date, it has only been identified for the porphycene molecule.67 For these reasons, and also because of the problems with the experimental determination of the length of NH bonds mentioned above, the experimental datapoints were not included in Fig. 7. However, very strong correlation of data obtained by DFT simulations indicates a high probability of observing a similar relationship for experimental data when they become available.
Conclusions
Based on theoretical and experimental results, it can be concluded that the geometry of the internal cavity in macrocycles with two intramolecular hydrogen bonds largely determines the properties of these bonds. Artificially adjusting the cavity size shows that the latter influences the spectroscopic and geometric parameters associated with hydrogen bonds, and thus some physicochemical properties of macrocycles containing double hydrogen bonds. The analysis of these relationships for a group of selected macrocycles with significantly different cavity sizes showed that, in most cases, the cavity size is not the main factor affecting the values of other hydrogen bond parameters. The curves resulting from the forced cavity deformation are often shifted relative to each other, even within the same macrocycle family. This differences between different macrocycle families were confirmed by comparing the distribution of datapoints obtained from fully optimised geometries and experiments.The relationship between the NH stretching frequency and the NH bond length shows a behaviour different from that of other pairs of hydrogen bond parameters. The curves corresponding to geometries obtained by the forced cavity deformation method and the points associated with the fully optimised geometries were closely aligned along a single straight line. This is the only strong correlation that is common to all the macrocycles under consideration. Moreover, all datapoints representing other macrocycles than porphyrins, porphycenes, and dibenzotetraaza[14]annulenes are also follow the estimated correlation indicating that the determined dependence of the frequency of NH vibrations on the length of the NH bond can be universal for macrocycles with a double intramolecular hydrogen bond of this type. However, due to the challenging experimental determination of these two parameters, no experimental data are available to confirm the presence of such close correlation and its effectiveness in practical predicting the properties of macrocycles upon changing the substituent. Nevertheless, based on the comparison of the simulation results for other parameters with the experimental data, it can be expected that the curve fitted to the experimental data will retain the shape obtained in this study, but with a different slope.
For most of the investigated relationships between pairs of hydrogen bonding parameters, the corresponding datapoints show a relatively large dispersion. Only in a few cases, a clear relationship was found between the pairs of parameters, but these relationships were usually limited to only one family of macrocycles. In the remaining cases, the large spread of the data points showed only a general trend, consistent with the curves obtained from the forced cavity deformation. Consequently it is impossible to make even moderately accurate predictions of hydrogen bonding parameters based solely on the change in cavity size due to substituent change. This conclusion is different from those of most published studies of various groups of compounds with intermolecular and intramolecular hydrogen bonds, where this type of correlation was reported to be relatively strong. In the case of the macrocyclic compounds with a double intramolecular hydrogen bond studied here, the electronic properties of the substituent influence the hydrogen bond parameters also through effects other than the change in the cavity geometry itself.
A weak correlation with the N⋯N distance was found for the NH bond length and NH stretching frequency when each family of macrocycles was considered separately. This shows that the differences between distinct families of macrocycles are much larger than expected. Some parameters of porphyrins and porphycene molecules exhibit similar relationships, showing that these two families of macrocyclic compounds are not completely different. Nevertheless, the similarities are not very strong, and it is impossible to mimic the properties of porphycenes by changing only the porphyrin cavity and vice versa. Some of the relationships found for the dibenzotetraaza[14]annulenes are rather similar to those found for porphycenes and porphyrins, even though they are anti-aromatic and usually far from flat, unlike aromatic porphyrins and porphycenes. However, these differences are much more significant than those between porphyrins and porphycenes.
Author contributions
SG conceptualized, performed simulations and data analysis, wrote original draft, funding acquisition. OP and SG discussed the result and wrote final manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Polish National Science Center, Grant No. 2017/27/B/ST4/02822. The research was supported in part by PLGrid Infrastructure.References
- M. Ethirajan, Y. Chen, P. Joshi and R. K. Pandey, Chem. Soc. Rev., 2011, 40, 340–362 RSC.
- C. J. Stockert, M. Canete, A. Juarranz, A. Villanueva, W. R. Horobin, I. J. Borrell, J. Teixido and S. Nonell, Curr. Med. Chem., 2007, 14, 997–1026 CrossRef.
- M. Jurow, A. E. Schuckman, J. D. Batteas and C. M. Drain, Coord. Chem. Rev., 2010, 254, 2297–2310 CrossRef CAS PubMed.
- Z.-F. Liu, S. Wei, H. Yoon, O. Adak, I. Ponce, Y. Jiang, W.-D. Jang, L. M. Campos, L. Venkataraman and J. B. Neaton, Nano Lett., 2014, 14, 5365–5370 CrossRef CAS PubMed.
- A. D. Phan, D. T. Nga, T.-L. Phan, L. T. M. Thanh, C. T. Anh, S. Bernad and N. A. Viet, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 062707 CrossRef CAS.
- M. O. Senge, M. Fazekas, E. G. A. Notaras, W. J. Blau, M. Zawadzka, O. B. Locos and E. M. N. Mhuircheartaigh, Adv. Mater., 2007, 19, 2737–2774 CrossRef CAS.
- S. S. Rajasree, X. Li and P. Deria, Commun. Chem., 2021, 4, 47 CrossRef CAS.
- J. Lin and D. Shi, Appl. Phys. Rev., 2021, 8, 011302 CAS.
- L.-L. Li and E. W.-G. Diau, Chem. Soc. Rev., 2013, 42, 291–304 RSC.
- M. C. So, G. P. Wiederrecht, J. E. Mondloch, J. T. Hupp and O. K. Farha, Chem. Commun., 2015, 51, 3501–3510 RSC.
- G. Lisak, T. Tamaki and T. Ogawa, Anal. Chem., 2017, 89, 3943–3951 CrossRef CAS PubMed.
- R. Paolesse, S. Nardis, D. Monti, M. Stefanelli and C. Di Natale, Chem. Rev., 2017, 117, 2517–2583 CrossRef CAS PubMed.
- D. Dolphin, The Porphyrins, Academic Press, New York, 1978 Search PubMed.
- W. Auwärter, D. Écija, F. Klappenberger and J. V. Barth, Nat. Chem., 2015, 7, 105–120 CrossRef.
- K. M. Kadish, K. M. Smith and R. Guilard, Handbook of Porphyrin Science (Volume 7: Physicochemical Characterization), World Scientific, 2010 Search PubMed.
- L. T. Bergendahl and M. J. Paterson, RSC Adv., 2013, 3, 9247–9257 RSC.
- S. Saito and A. Osuka, Angew. Chem., Int. Ed., 2011, 50, 4342–4373 CrossRef CAS PubMed.
- V. I. Gael, J. Appl. Spectr., 2001, 68, 267–279 CrossRef CAS.
- S. S. Rajasree, X. Li and P. Deria, Commun. Chem., 2021, 4, 47 CrossRef CAS.
- D. Lamoen and M. Parrinello, Chem. Phys. Lett., 1996, 248, 309–315 CrossRef CAS.
- J. I. Wu, I. Fernández and P. V. R. Schleyer, J. Am. Chem. Soc., 2013, 135, 315–321 CrossRef CAS PubMed.
- T. D. Lash, J. Porph. Phtal., 2011, 15, 1093–1115 CrossRef CAS.
- J. Baker, P. M. Kozlowski, A. A. Jarzecki and P. Pulay, Theor. Chem. Acc., 1997, 97, 59–66 Search PubMed.
- Z. Smedarchina, W. Siebrand, A. Fernández-Ramos and R. Meana-Pañeda, Z. Phys. Chem., 2008, 222, 1291–1309 CrossRef CAS.
- D. K. Maity, R. L. Bell and T. N. Truong, J. Am. Chem. Soc., 2000, 122, 897–906 CrossRef CAS.
- Z. Smedarchina, W. Siebrand and T. A. Wildman, Chem. Phys. Lett., 1988, 143, 395–399 CrossRef CAS.
- H. H. Limbach, J. M. Lopez and A. Kohen, Philos. Trans. R. Soc., B, 2006, 361, 1399–1415 CrossRef CAS PubMed.
- K. Oohora, Y. Kihira, E. Mizohata, T. Inoue and T. Hayashi, J. Am. Chem. Soc., 2013, 135, 17282–17285 CrossRef CAS.
- T. Hayashi, H. Dejima, T. Matsuo, H. Sato, D. Murata and Y. Hisaeda, J. Am. Chem. Soc., 2002, 124, 11226–11227 CrossRef CAS.
- H. Saeki, M. Misaki, D. Kuzuhara, H. Yamada and Y. Ueda, Jpn. J. Appl. Phys., 2013, 52, 111601 CrossRef.
- J. Waluk, Chem. Rev., 2017, 117, 2447–2480 CrossRef CAS PubMed.
- J. Dobkowski, Y. Lobko, S. Gawinkowski and J. Waluk, Chem. Phys. Lett., 2005, 416, 128–132 CrossRef CAS.
- M. Pietrzak, M. F. Shibl, M. Bröring, O. Kühn and H.-H. Limbach, J. Am. Chem. Soc., 2007, 129, 296–304 CrossRef CAS PubMed.
- J. N. Ladenthin, T. Frederiksen, M. Persson, J. C. Sharp, S. Gawinkowski, J. Waluk and T. Kumagai, Nat. Chem., 2016, 8, 935–940 CrossRef CAS PubMed.
- S. Gawinkowski, G. Orzanowska, K. Izdebska, M. O. Senge and J. Waluk, Chem. – Eur. J., 2011, 17, 10039–10049 CrossRef CAS PubMed.
- P. Fita, N. Urbańska, C. Radzewicz and J. Waluk, Chem. – Eur. J., 2009, 15, 4851–4856 CrossRef CAS PubMed.
- R. E. Rundle and M. Parasol, J. Chem. Phys., 1952, 20, 1487–1488 CrossRef CAS.
- R. M. Badger, J. Chem. Phys., 1940, 8, 288–289 CrossRef CAS.
- G. C. Pimentel and C. H. Sederholm, J. Chem. Phys., 1956, 24, 639–641 CrossRef CAS.
- R. S. Krishnan and K. Krishnan, Proc. Indiana Acad. Sci., 1964, 60, 11 CrossRef CAS.
- L. J. Bellamy and A. J. Owen, Spectrochim. Acta, Part A, 1969, 25, 329–333 CrossRef CAS.
- K. Nakamoto, M. Margoshes and R. E. Rundle, J. Am. Chem. Soc., 1955, 77, 6480–6486 CrossRef CAS.
- R. C. Lord and R. E. Merrifield, J. Chem. Phys., 1953, 21, 166–167 CrossRef CAS.
- L. J. Bellamy and A. J. Owen, Spectrochim. Acta, Part A, 1969, 25, 329–333 CrossRef CAS.
- A. Novak, Large Molecules, Springer Berlin Heidelberg, 1974, 18, 177–216 Search PubMed.
- E. Libowitzky, in Hydrogen Bond Research, ed. P. Schuster and W. Mikenda, Springer Vienna, Viena, 1999, 103–115 Search PubMed.
- Y. Kameda, M. Kowaguchi, K. Tsutsui, Y. Amo, T. Usuki, K. Ikeda and T. Otomo, J. Phys. Chem. B, 2021, 125, 11285–11291 CrossRef CAS.
- A. Listkowski, N. Masiera, M. Kijak, R. Luboradzki, B. Leśniewska and J. Waluk, Chem. – Eur. J., 2021, 27, 6324–6333 CrossRef CAS PubMed.
- A. Gorski, B. Leśniewska, G. Orzanowska and J. Waluk, J. Porphyrins Phthalocyanines, 2016, 20, 367–377 CrossRef CAS.
- T. Ono, D. Koga, K. Yozad and Y. Hisaeda, Chem. Commun., 2017, 53, 12258–12261 RSC.
- D. Koga, T. Ono, H. Shinjo and Y. Hisaeda, J. Phys. Chem. Lett., 2021, 12, 10429–10436 CrossRef CAS PubMed.
- P. Fita, N. Urbańska, C. Radzewicz and J. Waluk, Chem. – Eur. J., 2009, 15, 4851–4856 CrossRef CAS.
- W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2261 CrossRef CAS.
- V. A. Rassolov, J. A. Pople, M. A. Ratner and T. L. Windus, J. Chem. Phys., 1998, 109, 1223–1229 CrossRef CAS.
- OriginPro, Version 2020b, OriginLab Corporation, Northampton, MA, USA Search PubMed.
- K. E. Thomas, L. J. McCormick, H. Vazquez-Lima and A. Ghosh, Angew. Chem., Int. Ed., 2017, 56, 10088–10092 CrossRef CAS PubMed.
- K. Oohora, A. Ogawa, T. Fukuda, A. Onoda, J. Hasegawa and T. Hayashi, Angew. Chem., Int. Ed., 2015, 54, 6227–6230 CrossRef CAS PubMed.
- T. Kumagai, F. Hanke, S. Gawinkowski, J. Sharp, K. Kotsis, J. Waluk, M. Persson and L. Grill, Nat. Chem., 2014, 6, 41–46 CrossRef CAS PubMed.
- S. Gawinkowski, M. Pszona, A. Gorski, J. Niedziółka-Jönsson, I. Kamińska, W. Nogala and J. Waluk, Nanoscale, 2016, 8, 3337–3349 RSC.
- A. Ghosh and K. Jynge, J. Phys. Chem. B, 1997, 101, 5459–5462 CrossRef CAS.
- P. M. Kozlowski, M. Z. Zgierski and J. Baker, J. Chem. Phys., 1998, 109, 5905–5913 CrossRef CAS.
- S. Gawinkowski, J. Eilmes and J. Waluk, J. Mol. Str., 2010, 976, 215–225 CrossRef CAS.
- H. Böckmann, S. Gawinkowski, J. Waluk, M. B. Raschke, M. Wolf and T. Kumagai, Nano Lett., 2018, 18, 152–157 CrossRef PubMed.
- E. D. Becker and R. B. Bradley, J. Chem. Phys., 1959, 31, 1413–1414 CrossRef CAS.
- W. S. Caughey and W. S. Koski, Biochemistry, 1962, 1, 923–931 CrossRef CAS PubMed.
- K. M. Smith, D. A. Goff, R. J. Abraham and J. E. Plant, Org. Magn. Reson., 1983, 21, 505–511 CrossRef CAS.
- S. Gawinkowski, Ł. Walewski, A. Vdovin, A. Slenczka, S. Rols, M. R. Johnson, B. Lesyng and J. Waluk, Phys. Chem. Chem. Phys., 2012, 14, 5489–5503 RSC.
- E. Libowitzky, Monatshefte für Chemie/Chemical Monthly, 1999, 130, 1047–1059 CrossRef CAS.
- P. E. Hansen and J. Spanget-Larsen, Molecules, 2017, 22, 552 CrossRef PubMed.
- J. Waluk, Acc. Chem. Res., 2006, 39, 945–952 CrossRef CAS.
- P. Fita, L. Grill, A. Listkowski, H. Piwoński, S. Gawinkowski, M. Pszona, J. Sepioł, E. Mengesha, T. Kumagai and J. Waluk, Phys. Chem. Chem. Phys., 2017, 19, 4921–4937 RSC.
- F. H. Allen and I. J. Bruno, Acta Cryst., 2010, 66, 380–386 CAS.
- M. Woińska, S. Grabowsky, P. M. Dominiak, K. Woźniak and D. Jayatilaka, Sci. Adv., 2016, 2, e1600192 CrossRef.
- G. C. Pimentel and C. H. Sederholm, J. Chem. Phys., 1956, 24, 639–641 CrossRef CAS.
- V. Bertolasi, P. Gilli, V. Ferretti and G. Gilli, Chem. – Eur. J., 1996, 2, 925–934 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp01195f |
| This journal is © the Owner Societies 2022 |