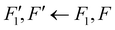Open Access Article
Open Access ArticleDipolar spin–spin coupling as an auxiliary tool for the structure determination of small isolated molecules
Luca
Bizzocchi
 *a,
Silvia
Alessandrini
*a,
Silvia
Alessandrini
 *ab,
Mattia
Melosso
*ab,
Mattia
Melosso
 *ac and
Cristina
Puzzarini
*ac and
Cristina
Puzzarini
 *a
*a
aDipartimento di Chimica “Giacomo Ciamician”, Università di Bologna, via F. Selmi 2, 40126 Bologna, Italy. E-mail: luca.bizzocchi@unibo.it; cristina.puzzarini@unibo.it
bScuola Normale Superiore, Piazza dei Cavalieri 7, 56126 Pisa, Italy. E-mail: silvia.alessandrini@sns.it
cScuola Superiore Meridionale, Università di Napoli Federico II, Largo San Marcellino 10, 80138 Naples, Italy. E-mail: mattia.melosso@unina.it
First published on 16th May 2022
Abstract
The “gold standard” for obtaining accurate equilibrium structures is the so-called semi-experimental (SE) approach, which exploits the structural information contained in rotational constants. Within the SE approach, ground-state rotational constants—accurately obtained from high-resolution spectroscopic studies—are computationally corrected in order to remove vibrational effects. The resulting SE equilibrium rotational constants for a significant set of isotopic species allow for retrieving a unique set of equilibrium bond lengths and angles for the molecule under consideration. However, in some cases, the lack of isotopic substitution hampers or even prevents a rigorous and complete structure determination. In this perspective, we introduce the use of dipolar spin–spin coupling constants as an additional source of structural information in support of the standard SE approach. As a proof-of-concept, we tested this new strategy on some prototypical species, such as water, ammonia, phosphine, and their fluorinated counterparts. Our results indicate that—even when the molecular structure can be obtained from a large set of isotopic rotational constants—the use of dipolar spin–spin coupling constants guarantees a better accuracy and reduces the correlations among the geometrical parameters. Moreover, we point out that our approach offers the possibility to fully derive the molecular structure of PF3, a species for which any isotopic substitution is not possible.
1 Introduction
The knowledge of the structural properties and dynamic behavior of molecules is at the heart of a deep understanding of their stability, spectroscopy, and reactivity. The accurate determination of molecular structures is thus one of the principal aims in many areas of physical chemistry and chemical physics, which—in the last few decades—has involved the efforts of experimentalists and theoreticians.1,2 In particular, for all spectroscopies, there is a strong relationship between the experimental outcome and the underlying electronic structure of the system under consideration (see, for example, ref. 3–7). In this respect, a great advantage of molecular spectroscopy is the capability of probing molecular properties in a non-invasive manner. In the gas phase, rotational spectroscopy is the technique of choice to derive accurate structural information because of the strong dependence of the rotational constants on the molecular geometry.5,8–12 Unfortunately, it is seldom straightforward to retrieve the molecular structure from the experimental information. Indeed, for a given molecule, there are at most three rotational constants, with the structural parameters being up to 3N − 6 (where N is the number of atoms). The way-out is to resort to different isotopic species of the same molecule in order to increase the number of data. Different isotopologues of a given molecule share the same equilibrium structure (re), i.e. the minimum geometry on the Born–Oppenheimer potential energy surface but not the vibrationally averaged structure which depends on the atomic masses. This is the limitation hampering the vibrationally averaged r08 structure that is obtained from the direct analysis of the vibrational ground-state rotational constants for different isotopologues, without any explicit consideration of vibrational effects.1,2 As a consequence, vibrationally averaged structures depend on the set of isotopic species considered.1,2 To avoid these limitations, one has to resort to re.From a pure experimental point of view, for small molecules, it might be feasible to derive experimental vibrational contributions that can be used to correct the ground-state rotational constants. The equilibrium rotational constants then obtained for different isotopic species can be used for the determination of the equilibrium structure. However, such a procedure becomes unpractical already for medium-sized molecular systems. This difficulty can be efficiently tackled using the so-called semi-experimental (SE) approach.2,9–11 Within this framework, quantum-chemical calculations are employed to recover vibrational effects. For different isotopologues, computed vibrational corrections are combined with the corresponding experimental ground-state rotational constants to obtain the so-called SE equilibrium rotational constants and, from them, the SE equilibrium structure. This method proved to be powerful and allowed the derivation of the accurate equilibrium structures of small- to medium-sized molecules and non-covalent molecular complexes,2,5,10–17 thus superseding the previously used Kraitchman's substitution method (the rs structure).18 Since rs structures do not explicitly and rigorously treat the vibrational contributions, they might lead to inaccurate and biased results.5
However, the SE approach has some limitations, since a balanced fit is obtained only with a large set of experimental data including several isotopic substitutions. Ideally, one should have at least one isotopic substitution for each nucleus of the system under consideration.2 This might be unpractical from an experimental point of view, but, in some cases, it can be simply impossible because of the lack of different stable isotopes for a given atom. This is the case, for example, for fluorine and phosphorous.
Interestingly, there are other spectroscopic parameters than the rotational constants that directly depend on the molecular geometry. This is the case of the dipolar spin–spin coupling constants, which describe the interaction of two nuclear magnetic moments in a molecule. In nuclear magnetic resonance (NMR), in the spectroscopic investigation of non-isotropic media, dipolar coupling interactions are responsible for the signal splitting and represent the dominant coupling mechanism.19 In rotational spectroscopy, dipolar couplings are, in addition to spin-rotation interactions and nuclear quadrupole couplings, responsible for the hyperfine structure of the spectra.5,8 The experimentally determined dipolar spin–spin coupling constants can be used to obtain the structural information even in those cases where isotopic substitutions are not feasible.5 More generally, they can enrich the set of experimental data to be used in the SE approach.
This perspective inspects the use of dipolar spin–spin coupling constants in support of the SE structure determination. In particular, we explore their role when the isotopic substitution is limited or not feasible. For this purpose, we have selected three light hydrides and their fully fluorinated counterparts: (i) H2O and OF2, (ii) NH3 and NF3 and, (iii) PH3 and PF3. These have been chosen because they range from systems for which a large number of data are available with great precision, such as NH3 and H2O, to systems for which isotopic substitution is limited (OF2 and NF3) or not possible at all (such as PF3). In the following, all relevant theoretical details of the form of the dipolar spin–spin coupling tensor are provided. Then, computational details and the methodology for the derivation of structural parameters are given. Subsequently, the results are collected and discussed.
2 Theoretical details
The dipolar interaction between the IL and IM nuclear magnetic moments is described by the following Hamiltonian| HLMdip = IL·DLM·IM, | (1) |
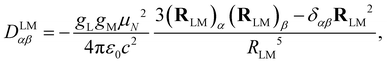 | (2) |
The tensor D is symmetric and traceless by definition and it is customary to express its diagonal elements (for a prolate-type rotor) as Dzz and Dxx–Dyy. For linear molecules, these reduce to one independent component due to the cylindrical symmetry around the z-axis:
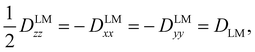 | (3) |
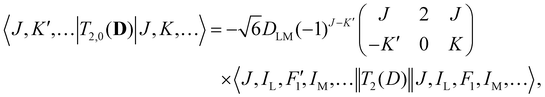 | (4) |
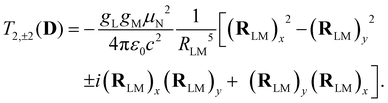 | (5) |
Analogous to eqn (4), for the matrix elements of T2,±2(D), one has
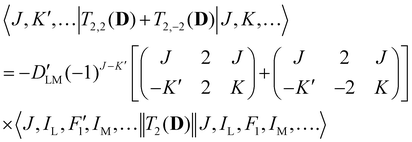 | (6) |
From an experimental point of view, the geometry that determines dipolar spin–spin coupling effects is that of the molecule at the moment of the measurements, which is usually that the molecule assumes in the vibrational ground state. Hence, in analogy to what is performed for rotational constants within the SE approach, dipolar spin–spin coupling constants should be corrected for zero-point vibrational (ZPV) effects:
| DLMe = DLM0 − ΔDLMZPV, | (7) |
3 Methodology
As briefly mentioned in the Introduction, to demonstrate the use of the dipolar spin–spin coupling constants in structural determination, we have chosen three model systems: NH3, PH3, and H2O. The hyperfine structures of these species have been extensively studied in the past and various experimental determinations of dipolar spin–spin coupling constants are present in the literature. Furthermore, their molecular geometry is completely determined by two parameters (one bond length and one angle) and, in the parent species, only two independent rotational constants are available for the structure determination. All these species possess a fluorinated counterpart, namely NF3, PF3, and OF2, for which access to isotopologue data is limited, if not impossible (i.e. PF3). These molecules thus provide an ideal benchmark to assess how the additional information provided by the dipolar spin–spin coupling can assist the structure determination by breaking the correlations among determinable parameters and by estimating more statistically sound uncertainties for the retrieved geometry parameters.As a starting point of our analysis, we determined a SE equilibrium structure for each of the model molecules using a set of isotopologues: 8 for NH3, 4 for PH3 and 6 for H2O. Following the standard procedure, ground state rotational constants X0 (where X = A, B, and C) taken from experimental studies were computationally corrected for ZPV contributions (see Section 3.1) to obtain SE equilibrium rotational constants:
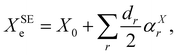 | (8) |
Based on a series of previous case studies (see e.g. ref. 5), we assume an error of about 1% for the ZPV contributions. The corresponding relative error on the SE equilibrium rotational constants is then summed in quadrature with the fractional uncertainty due to the neglected ΔXel
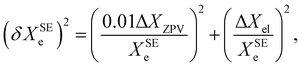 | (9) |
The second step is to insert the equilibrium values of the dipolar spin–spin D tensor elements into the structural least-squares fit. The experimental values are available for 4 isotopic species of NH3, 6 isotopic species of H2O and for the parent species of PH3, NF3, and OF2 (see Tables 1–3). The experimental dipolar spin–spin coupling constants are corrected for the corresponding ZPV contributions using eqn (7) and then incorporated in the analysis with a weight derived from their corresponding 1σ experimental error. Given the small effect produced in the hyperfine structures by these constants, they are usually determined with a moderate precision, even when obtained by very high-resolution molecular beam measurements (i.e. 1% at best). Such an uncertainty is clearly dominant over the inherent inaccuracy of the ab initio ZPV contributions ΔDZPV.
| Parameter | Experiment | ab initio equilibriuma | ab initio vib. averageda |
|---|---|---|---|
| a Computed at the ae-CCSD(T)/cc-pwCVQZ level of theory. b From our analysis of the molecular beam data of ref. 23, 29 and 30. c From ref. 31 d From ref. 32. | |||
| NH3 | |||
| D NH | 4.807(35)b | 4.738 | 4.594 |
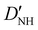
|
−20.88(39)b | −21.538 | −20.622 |
| D HH | 27.524(97)b | 28.304 | 27.763 |
| 15NH3 | |||
| D NH | −6.02(25)b | −6.646 | −6.447 |
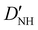
|
31.1(19)b | 30.214 | 28.934 |
| D HH | 28.09(19)b | 28.305 | 27.761 |
| ND3 | |||
| D ND | 0.67(16)c | 0.728 | 0.710 |
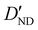
|
−3.28(74)d | −3.306 | −3.200 |
| D DD | 0.56(36)c | 0.667 | 0.658 |
| 15ND3 | |||
| D ND | — | −1.020 | −0.996 |
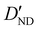
|
6.2(20)d | 4.637 | 4.491 |
| D DD | — | 0.667 | 0.658 |
| NH2D | |||
| D ND yy | — | −2.378 | −2.315 |
| D ND xx−zz | — | 0.201 | 0.190 |
| ND2H | |||
| D ND yy | — | −1.190 | −1.159 |
| D ND xx–zz | — | −0.808 | −0.791 |
Lastly, we computed a set of SE equilibrium structures using a mixed rotational/spin–spin data set from a single isotopologue for each species considered. The goodness of this last approach is evaluated in comparison with the corresponding reference structure.
3.1 Quantum chemical calculations
To have highly accurate reference values for the equilibrium dipolar spin–spin coupling constants, the equilibrium structures of the selected molecules have been obtained at the CCSD(T)/cc-pwCVQZ level of theory, with all electrons (ae) correlated but the 1s for third-row atoms. In the acronym above, CCSD(T) stands for coupled-cluster (CC) singles and doubles with perturbative treatment of triples,42 and cc-pwCVQZ43 is a weighted core-valence quadruple-zeta set, purposely set up for accurately describing core–core and core–valence correlation effects. For small molecules containing first- to third-row atoms, this level of theory provides equilibrium bond lengths and angles accurate to 0.001 Å and 0.2 degrees, respectively.34ZPV corrections have been computed for both rotational and dipolar spin–spin coupling constants. For the three hydrides used as model systems, the same level of the geometry optimization, i.e. ae-CCSD(T)/cc-pwCVQZ, has been employed. For fluorine-bearing species, to reduce the computational cost, calculations were carried out using second-order Møller–Plesset Perturbation theory (MP2),44 within the frozen core (fc-) approximation, in conjunction with a partially augmented basis set of triple-zeta quality, i.e. jun-cc-pVTZ.45,46 For phosphorous, the corresponding d-augmented basis set, jun-cc-pV(T+d)Z, has been employed.46,47 Regardless of this, the basis is denoted as jun-cc-pVTZ for all the molecules considered in this work.
The computed values of the equilibrium and vibrationally averaged dipolar spin–spin coupling constants for ammonia isotopologues are reported in Table 1, and those for the other symmetric-top species NF3, PH3 and PF3 are listed in Table 2. The values obtained for H2O and OF2 are presented in Table 3. All computations have been performed using the CFOUR package.24,48
| Parameter | Experimental | ab initio equilibriuma | ab initio vib. averagedb |
|---|---|---|---|
| a Computed at the ae-CCSD(T)/cc-pwCVQZ level of theory. b Zero-point vibrational contributions computed at the fc-MP2/jun-cc-pVTZ level of theory. c From ref. 35. d From ref. 36. | |||
| NF3 | |||
| D NF | — | 1.327 | 1.306 |
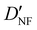
|
— | 3.870 | 3.815 |
| D FF | 11.3(67)c | 11.133 | 11.014 |
| PH3 | |||
| D PH | 2.04(42)d | 2.107 | 1.972 |
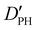
|
— | 18.372 | 17.730 |
| D HH | 12.65(95)d | 13.831 | 13.690 |
| PF3 | |||
| D PF | — | 3.198 | 3.204 |
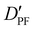
|
— | 13.635 | 13.525 |
| D FF | — | 8.199 | 7.891 |
| Parameter | Experimental | ab initio equilibriuma | ab initio vib. averageda |
|---|---|---|---|
| a Computed at the (CCSD(T)/cc-pwCVQZ level of theory for H2O). For F2O, the equilibrium values are computed at CCSD(T)/cc-pwCVQZ and zero-point vibrational contributions computed at the fc-MP2/jun-cc-VTZ level of theory. b From ref. 37. c From ref. 26. d From ref. 38. e From ref. 39. f From ref. 40. g Derived from the 〈r−3〉 value reported in ref. 41. | |||
| H2O | |||
| D HH zz | −67.5(15)b | −69.668 | −68.658 |
| HDO | |||
| D HD zz | −8.33(87)c | −8.574 | −8.416 |
| D2O | |||
| D DD zz | −1.57(41)d | −1.641 | −1.625 |
| H217O | |||
| D OH zz | 15.67(22)e | 16.142 | 15.656 |
| D OH xx –DOHyy | 20.53(35)e | 21.019 | 20.578 |
| D HH zz | −67.1(16)e | −69.668 | −68.658 |
| HD17O | |||
| D OD zz | 5.47(62)f | 5.030 | 4.919 |
| D OH zz | −5.2(11)f | −4.188 | −3.844 |
| D HD zz | −8.5(19)f | −8.525 | −8.368 |
| D217O | |||
| D OD zz | 1.64(87)f | 2.478 | 2.421 |
| D DD zz | — | −1.641 | −1.625 |
| OF2 | |||
| D FF zz | −20.0(11)g | −20.042 | −19.828 |
4 Results and discussion
4.1 Ammonia (NH3)
Six isotopic species have been considered for NH3 structural determination. For each SE parameter, an average fractional uncertainty of 3 × 10−4 has been considered, which has been obtained through eqn (9) by considering average values of 3 GHz for the ZPV contribution and 75 MHz for the electronic effects.33 This average fractional uncertainty has been used to determine the weights adopted in the fitting procedure. The structural parameters derived from 20 SE equilibrium rotational constants are listed in the first row of Table 4 and are labeled as “reference”. Within the quoted error ranges (3σ for the present calculation), they are consistent with the most recent SE results from the literature11 (also reported in Table 4), with discrepancies of 0.0003 Å for re(NH) and 0.11 deg. for θe(HNH).| Data set | Isoa (data) | r e(NH)/Å | θ e(HNH)/deg. | σ w,ROT | σ w,SS |
|---|---|---|---|---|---|
| Note: numbers in parentheses indicate 3σ uncertainties in units of the last quoted digit.a Number of isotopologues and, in parentheses, number of data.b Weighted rms deviation of the rotational constants.c Weighted rms deviation of the dipolar spin–spin coupling constants.d Ref. 11. | |||||
| Reference | 8(20) | 1.0107(4) | 106.83(9) | 4.1 | — |
| Mixed | 8(30) | 1.0106(4) | 106.8338(16) | 4.1 | 1.5 |
| NH3 | 1(5) | 1.0104(4) | 106.88(6) | 0.3 | 1.1 |
| 15NH3 | 1(5) | 1.0104(8) | 106.87(13) | 0.2 | 2.3 |
| ND3 | 1(4) | 1.0110(4) | 106.98(2) | 0.0 | 0.3 |
| 15ND3 | 1(4) | 1.0110(4) | 106.98(4) | 0.0 | 0.8 |
| Literatured | 1.0110(2) | 106.94(2) | |||
For the four top-symmetric ammonia isotopologues (NH3, 15NH3, ND3 and 15ND3), the dipolar spin–spin interaction constants were experimentally determined. In this work, values for NH3 and 15NH3 have been newly derived by re-analyzing the molecular beam hyperfine data for several rotation–inversion transitions available in the literature.23,29,30 For ND3 and 15ND3, the spin–spin coupling parameters have been directly taken from the corresponding literature studies.31,32 In total, 10 DLM constants have been corrected for the ZPV contribution through eqn (7) and fitted together with the 20 SE equilibrium rotational constants. This new geometry is labelled as “mixed” and the corresponding parameters are reported in the second row of Table 4. It can be noticed that the inclusion of the dipolar spin–spin information has a beneficial effect in alleviating the correlation between the two geometry parameters of ammonia without producing any significant structural distortion. Indeed, the quality of the two fits is essentially the same, but the statistical uncertainty of the θe(HNH) is reduced by a factor of ∼60.
Single-isotopologue data sets, containing both rotational and SE dipolar spin–spin constants, have then been analyzed separately for each top-symmetric variant of ammonia; the derived structural parameters are presented in Table 4. The values of the structural parameters are mainly determined by the rotational constants, which are almost exactly reproduced in all cases. Still, the independent and uncorrelated information provided by the dipolar spin–spin constants (3 for NH3 and 15NH3 and 2 for ND3 and 15ND3) prevents a major distortion of the retrieved geometry and provides a meaningful estimate of the uncertainty interval. Indeed, all obtained re(NH) and θe(HNH) agree well within the statistical uncertainties.
4.2 Phosphine (PH3)
Four isotopic variants of phosphine have been considered in the “reference”: PH3, PD3, PH2D, and PHD2. An average fractional uncertainty of 1 × 10−4 has been used to estimate the weights of their SE equilibrium rotational constants. This corresponds essentially to 1% of the theoretical ZPV contributions, as the ΔXel is very small (∼1 × 10−5).49 Studies of the hyperfine spectra of PH3 are scarcer than those of NH3 and only two experimental determinations of dipolar spin–spin coupling constants actually exist, namely DPH and DHH for the parent isotopologue.36 These two values were corrected for the ZPV contribution and used in the “mixed” structural fit. Inspection of Table 5 points out that the “reference” and “mixed” structures are essentially identical and very close to the best SE structure presently available in the literature,49 with minor discrepancies of 7 × 10−5 Å and 0.003 deg. for re(PH) and θe(HPH), respectively. Use of the parent species only (which implies two rotational constants and two spin–spin constants as input data) does not change significantly the picture, as the derived structural parameters remain consistent within the uncertainties. Only a minor increase of the statistical error is produced, in spite of the much less parameters employed, i.e. 4 vs. 14 employed in the “mixed” structure.| Data set | Isoa (data) | r e(PH)/Å | θ e(HPH)/deg. | σ w,ROT | σ w,SS |
|---|---|---|---|---|---|
| Note: numbers in parentheses indicate 3σ uncertainties in units of the last quoted digit.a Number of isotopologues and, in parentheses, number of data.b Weighted rms deviation of the rotational constants.c Weighted rms deviation of the dipolar spin–spin coupling constants.d Ref. 49. | |||||
| Reference | 4(10) | 1.41188(4) | 93.380(4) | 0.5 | — |
| All mixed | 4(14) | 1.41188(5) | 93.380(4) | 0.5 | 0.8 |
| PH3 | 1(4) | 1.41193(13) | 93.379(11) | 0.0 | 0.8 |
| Literatured | 1.41195(8) | 93.383(10) | |||
4.3 Water (H2O)
The data set for the “reference” structure of the water molecule comprises seven isotopic species: H217O, H217O and their singly and doubly deuterated variants plus H218O. Given the planarity of the molecule, only two out of three equilibrium rotational constants are actually independent and can be used simultaneously in a structural least-squares fit.8 In the present case, the B0, C0 pair has been adopted. Their SE equilibrium values have been obtained, as already described for NH3 and PH3, by subtracting the ZPV (ae-CCSD(T)/cc-pwCVQZ) contributions from the experimental B0, C0. The SE equilibrium parameter weights have been estimated assuming the fractional uncertainty of 33 × 10−4, which is obtained from eqn (9) when using average values of 5 GHz for the ZPV contribution and 150 MHz for the electronic effects.33 The derived “reference” structural parameters are reported in the first row of Table 6.| Data set | Isoa (data) | r e(OH)/Å | θ e(HOH)/deg. | σ w,ROT | σ w,SS |
|---|---|---|---|---|---|
| Note: numbers in parentheses indicate 3σ uncertainties in units of the last quoted digit.a Number of isotopologues and, in parentheses, number of data.b Weighted rms deviation of the rotational constants.c Weighted rms deviation of the dipolar spin–spin coupling constants.d Ref. 11. | |||||
| Reference | 7(14) | 0.95798(19) | 104.39(5) | 1.1 | — |
| Mixed | 7(24) | 0.95798(17) | 104.39(5) | 1.1 | 0.7 |
| H2O | 1(3) | 0.9581(3) | 104.36(6) | 0.0 | 0.5 |
| HDO | 1(3) | 0.95832(5) | 104.238(17) | 0.0 | 0.1 |
| D2O | 1(3) | 0.95795(5) | 104.422(12) | 0.0 | 0.1 |
| H217O | 1(5) | 0.9581(2) | 104.36(5) | 0.0 | 0.4 |
| HD17O | 1(5) | 0.9578(6) | 104.42(18) | 0.1 | 1.0 |
| D217O | 1(3) | 0.9577(5) | 104.48(11) | 0.0 | 1.0 |
| Literatured | 0.9573(1) | 104.53(1) | |||
A number of detailed studies devoted to the hyperfine structure of water rotational transitions are present in the literature. As a consequence, dipolar spin–spin coupling constants are available for six isotopologues. They are presented in Table 3 along with the corresponding literature references. The correction for the ZPV contribution through eqn (7) allowed us to obtain the set of SE equilibrium dipolar spin–spin tensor elements to be employed in the “mixed” structural calculation. For water, the “reference” and “mixed” equilibrium structures are identical, thus indicating that the structural information brought by the dipolar spin–spin coupling constants perfectly matches that established by the rotational parameters. The comparison with the most up to date SE equilibrium structure available in the literature11 reveals small, but significant discrepancies, with re(OH) longer by 0.0007 Å and θe(HOH) smaller by 0.14 deg., both slightly exceeding the overlap range of the corresponding quoted uncertainties. This is likely due to the different treatment of the electronic contribution to the rotational constants, which may have a magnified effect on the estimate of geometrical parameters due to the planarity relationship.
Six single-isotopologue “mixed” structure calculations have been finally performed to evaluate the spread of the geometry parameters determined using the supporting contribution of the dipolar spin–spin coupling constants. Although determined with different precision, the six pairs of structural parameters make up a consistent (within 3σ) data set symmetrically spread around the “reference” geometry. This proves that the additional geometric information carried by the SE D tensor elements is capable of providing a reliable estimate of the distortion effects typically produced by the H–D isotopic substitution.
4.4 Fluorinated species (NF3, OF2, and PF3)
Minimal data sets are available for the fluorinated analogues of the chosen model molecules. For NF3, the experimental values of the B0 and C0 constants were determined, while only B0 is available for 15NF3.53,54 The experimental value of the dipolar spin–spin DFF constant for the main isotopic species has been reported by Novick et al.35 The B0 and C0 constants of PF3 have been determined in several infrared investigations; here, we use the value provided by Najib (2014).51 Instead, no experimental information on its hyperfine structure is presently available in the literature. To the best of our knowledge, only the rotational spectrum of the parent species of OF2 has been investigated and its ground state rotational constants still come from a microwave study performed in the 60's.55 An estimate of the F–F dipolar spin–spin coupling constants was obtained by molecular beam electric resonance measurements more than twenty years later.41The SE equilibrium values for the rotational and spin–spin coupling constants of these three species have been obtained using the ZPV contributions computed in this work (fc-MP2/jun-cc-pVTZ) and then employed to derive the “mixed” equilibrium structures. As performed for the model molecules in previous sections, the weights of the rotational constants have been set to 1 × 10−4 of the corresponding values, mostly on the basis of the ZPV contribution accuracy. The impact of the electronic contributions has been estimated from the g constants56,57 and was found to be essentially negligible. The derived structural parameters are reported in Table 7 together with the best available equilibrium geometries from the literature.50–52
| Data set | Isoa (data) | r e(XF)/Å | θ e(FXF)/deg. | σ w,ROT | σ w,SS |
|---|---|---|---|---|---|
| Note: Numbers in parentheses indicate 3σ uncertainties in units of the last quoted digit.a Number of isotopologues and, in parentheses, number of data.b Weighted rms deviation of the rotational constants.c Weighted rms deviation of the dipolar spin–spin constants.d Average values from ref. 50.e At the ae-CCSD(T)/cc-pwCVQZ level of theory.f No degrees of freedom, thus errors cannot estimated.g Experimental value from ref. 51. Uncertainties obtained by error propagation.h Experimental value from ref. 52. | |||||
| NF3 | 2(4) | 1.36797(3) | 101.878(3) | 0.0 | 0.1 |
| Literatured | 1.3675(10) | 101.86(10) | |||
| Theorye | 1.366 | 101.9 | |||
| PF3f | 1(2) | 1.56111 | 97.561 | ||
| Literatureg | 1.560986(43) | 97.566657(64) | |||
| Theorye | 1.561 | 97.6 | |||
| OF2 | 1(3) | 1.40625(18) | 103.08(2) | 0.0 | 0.3 |
| Literatureh | 1.4053(4) | 103.07(5) | |||
| Theorye | 1.403 | 103.1 | |||
For NF3 and OF2, our “mixed” SE approach yields equilibrium geometrical parameters more precise than those available in the literature, with the set two sets of values agreeing within the quoted error ranges. The only exception is the O–F bond length in OF2 for which our determination provides a value 0.001 Å longer than the corresponding literature value. However, it should be noted that the values of re(XF) and θe(FXF) from ref. 50–52 were obtained using a minimal set of constants and, being purely experimental, they may also be affected by residual perturbations on the retrieved equilibrium rotational constants. This aspect is particularly critical for PF3, for which the two structural parameters were derived from only two rotational constants and the uncertainty range, estimated by error propagation, is clearly underestimated (Table 7). Unfortunately, the lack of any experimental information on the dipolar spin–spin coupling prevents us from computing a “mixed” equilibrium structure for PF3 and providing a reliable uncertainty range on its geometry parameters. In Table 7, the structural parameters optimized at the ae-CCSD(T)/cc-pwCVQZ level of theory are also reported. Their comparison with the literature and SE results points out a good agreement. In view of the accuracy of ae-CCSD(T)/cc-pwCVQZ geometries discussed above,34 the observed agreement supports the reliability of the SE/experimental structural determinations even when carried out with a very limited number of data.
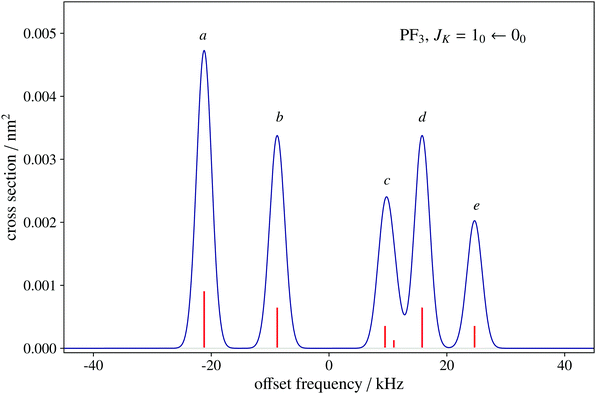
To date, there are no studies devoted to the hyperfine structure of the rotational transitions of PF3, despite the fact that the J = 1 ← 0 line is located at 15.6 GHz, a frequency region easily achievable using a Ball–Flygare-type high-resolution Fourier-transform microwave (FT-MW) spectrometer (see e.g. ref. 58). Our theoretical calculations provide a full characterization of the hyperfine structure of this transition and provide a valuable guide for future laboratory measurements. Besides the P–F and F–F dipolar spin–spin coupling constants listed in Table 2, we have also computed the nuclear spin-rotation coupling tensor C for the P and F nuclei at the ae-CCSD(T)/cc-pwCVQZ level of theory. The values of the isotropic constant (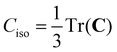 ) are Ciso(F) = −12.77 kHz and Ciso(P) = −9.23 kHz. The hyperfine pattern of the J = 1 ← 0 rotational transition of PF3 has then been evaluated using the SPCAT program59 and is plotted in Fig. 1 assuming a typical pulsed-jet FT-MW line full width at half maximum of 3 kHz. Under these experimental conditions, the hyperfine structure of the J = 1 ← 0 transition is predicted to be well resolved. This indicates that its spectral analysis would lead to an accurate determination of dipolar spin–spin coupling constants, thus opening the route towards a complete structural determination of PF3.
) are Ciso(F) = −12.77 kHz and Ciso(P) = −9.23 kHz. The hyperfine pattern of the J = 1 ← 0 rotational transition of PF3 has then been evaluated using the SPCAT program59 and is plotted in Fig. 1 assuming a typical pulsed-jet FT-MW line full width at half maximum of 3 kHz. Under these experimental conditions, the hyperfine structure of the J = 1 ← 0 transition is predicted to be well resolved. This indicates that its spectral analysis would lead to an accurate determination of dipolar spin–spin coupling constants, thus opening the route towards a complete structural determination of PF3.
5 Conclusions
In this perspective, we have investigated the use of dipolar spin–spin coupling constants in the structure determination of isolated molecules. The SE approach is powerful and allows the determination of equilibrium geometries with minimum experimental efforts. However, it is effective only if the number of available isotopic substitutions is greater than the number of internal coordinates describing the molecular system. Furthermore, an unbalanced set of data due to impossible isotopic substitution (as in the case of F and P) can lead to biased results. In those cases for which obtaining a sufficiently large set of data is unpractical due to the lack of isotopic data or totally unfeasible (as for PF3), dipolar spin–spin coupling constants can be considered as an additional source of information for the SE least-squares fitting procedure. Spin–spin coupling in rotational spectra only produces small effects, usually detected as perturbations of more important interactions, such as nuclear quadrupole coupling and/or nuclear spin-rotation interactions. In the past, the determination of dipolar spin–spin constants was a prerogative of molecular beam maser techniques, which are characterized by an extremely high resolving power. Nowadays, adequate resolution to reveal spin–spin coupling effects is achievable routinely using a Fourier-transform spectrometer coupled with supersonic expansions of the gas sample. Although experimentally determined with moderate precision (typically 1–10%), the dipolar spin–spin coupling constants can effectively support the determination of the molecule structural parameters within the SE approach. Their incorporation in an isotopically balanced fit does not generally alter the value of the structural parameters, but can lead to a significant reduction of their statistical error, as they provide independent and statistically uncorrelated information for the least-squares fit procedure. In critical cases, when there is a shortage of isotopic rotational data, their inclusion in the computation provides additional degrees of freedom (thus leading to a significant improvement of the fit and geometrical parameters).Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the MIUR (PRIN Grant Number 202082CE3T) and the University of Bologna (RFO funds). The SMART@SNS Laboratory (http://smart.sns.it) is acknowledged for providing high-performance computing facilities.Notes and references
- Accurate molecular structures: their determination and importance, ed. A. Domenicano and I. Hargittai, Oxford University Press, Oxford, UK, 1992 Search PubMed.
- Equilibrium Molecular Structures: From Spectroscopy to Quantum Chemistry, ed. J. Demaison, J. E. Boggs and A. G. Császár, CRC Press, Taylor & Francis Group, Boca Raton, FL, US, 2011 Search PubMed.
- A. Mazzanti and D. Casarini, WIREs Comput. Mol. Sci., 2012, 2, 613–641 CrossRef CAS.
- Computational Strategies for Spectroscopy, from Small Molecules to Nano Systems, ed. V. Barone, John Wiley & Sons, Inc., Hoboken, New Jersey, 2011 Search PubMed.
- C. Puzzarini, J. F. Stanton and J. Gauss, Int. Rev. Phys. Chem., 2010, 29, 273–367 Search PubMed.
- C. Puzzarini, J. Bloino, N. Tasinato and V. Barone, Chem. Rev., 2019, 119, 8131–8191 CrossRef CAS PubMed.
- V. Barone, S. Alessandrini, M. Biczysko, J. R. Cheeseman, D. C. Clary, A. B. McCoy, R. J. DiRisio, F. Neese, M. Melosso and C. Puzzarini, Nat. Rev. Methods Primers, 2021, 1, 1–27 CrossRef.
- W. Gordy and R. L. Cook, Microwave molecular spectra, Wiley, New York, 1984 Search PubMed.
- P. Pulay, W. Meyer and J. E. Boggs, J. Chem. Phys., 1978, 68, 5077–5085 CrossRef CAS.
- F. Pawłowski, P. Jørgensen, J. Olsen, F. Hegelund, T. Helgaker, J. Gauss, K. L. Bak and J. F. Stanton, J. Chem. Phys., 2002, 116, 6482–6496 CrossRef.
- M. Piccardo, E. Penocchio, C. Puzzarini, M. Biczysko and V. Barone, J. Phys. Chem. A, 2015, 119, 2058–2082 CrossRef CAS PubMed.
- C. Puzzarini and V. Barone, Acc. Chem. Res., 2018, 51, 548–556 CrossRef CAS PubMed.
- C. Degli Esposti, M. Melosso, L. Bizzocchi, F. Tamassia and L. Dore, J. Mol. Struct., 2019, 1203, 127429 CrossRef.
- H. Ye, M. Mendolicchio, H. Kruse, C. Puzzarini, M. Biczysko and V. Barone, J. Mol. Struct., 2020, 1211, 127933 CrossRef CAS.
- J. Lei, S. Alessandrini, J. Chen, Y. Zheng, L. Spada, Q. Gou, C. Puzzarini and V. Barone, Molecules, 2020, 25, 4899 CrossRef CAS PubMed.
- D. A. Obenchain, L. Spada, S. Alessandrini, S. Rampino, S. Herbers, N. Tasinato, M. Mendolicchio, P. Kraus, J. Gauss and C. Puzzarini, et al. , Angew. Chem., Int. Ed., 2018, 57, 15822–15826 CrossRef CAS PubMed.
- X. Li, L. Spada, S. Alessandrini, Y. Zheng, K. G. Lengsfeld, J.-U. Grabow, G. Feng, C. Puzzarini and V. Barone, Angew. Chem., Int. Ed., 2022, 61, e202113737 CAS.
- J. Kraitchman, Am. J. Phys., 1953, 21, 17–24 CrossRef CAS.
- A. Abragam, The principles of nuclear magnetism, Clarendon Press, Oxford, 1989 Search PubMed.
- J. M. Brown and A. Carrington, Rotational Spectroscopy of Diatomic Molecules, Cambridge University Press, 2003 Search PubMed.
- G. R. Gunther-Mohr, C. H. Townes and J. H. van Vleck, Phys. Rev., 1954, 94, 1191–1203 CrossRef CAS.
- J. P. Gordon, Phys. Rev., 1955, 99, 1253–1263 CrossRef CAS.
- S. G. Kukolich, Phys. Rev., 1967, 156, 83–92 CrossRef CAS.
- J. F. Stanton, J. Gauss, L. Cheng, M. E. Harding, D. A. Matthews and P. G. Szalay, CFOUR, Coupled-Cluster techniques for Computational Chemistry, a quantum-chemical program package, with contributions from A. A. Auer, R. J. Bartlett, U. Benedikt, C. Berger, D. E. Bernholdt, Y. J. Bomble, O. Christiansen, F. Engel, R. Faber, M. Heckert, O. Heun, M. Hilgenberg, C. Huber, T.-C. Jagau, D. Jonsson, J. Jusélius, T. Kirsch, K. Klein, W. J. Lauderdale, F. Lipparini, T. Metzroth, L. A. Mück, D. P. O'Neill, D. R. Price, E. Prochnow, C. Puzzarini, K. Ruud, F. Schiffmann, W. Schwalbach, C. Simmons, S. Stopkowicz, A. Tajti, J. Vázquez, F. Wang, J. D. Watts and the integral packages MOLECULE (J. Almlöf and P. R. Taylor), PROPS (P. R. Taylor), ABACUS (T. Helgaker, H. J. Aa. Jensen, P. Jørgensen, and J. Olsen), and ECP routines by A. V. Mitin and C. van Wüllen. For the current version, see http://www.cfour.de.
- C. Puzzarini, G. Cazzoli, M. E. Harding, J. Vázquez and J. Gauss, J. Chem. Phys., 2009, 131, 234304 CrossRef PubMed.
- G. Cazzoli, V. Lattanzi, J. L. Alonso, J. Gauss and C. Puzzarini, Astroph. J., 2015, 806, 100 CrossRef.
- M. Melosso, L. Dore, J. Gauss and C. Puzzarini, J. Mol. Spectrosc., 2020, 370, 111291 CrossRef CAS.
- M. Melosso, M. L. Diouf, L. Bizzocchi, M. E. Harding, F. M. Cozijn, C. Puzzarini and W. Ubachs, J. Phys. Chem. A, 2021, 125, 7884–7890 CrossRef CAS PubMed.
- S. G. Kukolich, Phys. Rev., 1968, 172, 59–63 CrossRef CAS.
- S. G. Kukolich and S. C. Wofsy, J. Chem. Phys., 1970, 52, 5477–5481 CrossRef CAS.
- R. Garvey, F. De Lucia and J. Cederberg, Mol. Phys., 1976, 31, 265–287 CrossRef CAS.
- J. van Veldhoven, R. T. Jongma, B. Sartakov, W. A. Bongers and G. Meijer, Phys. Rev. A: At., Mol., Opt. Phys., 2002, 66, 032501 CrossRef.
- C. Puzzarini, M. Heckert and J. Gauss, J. Chem. Phys., 2008, 128, 194108 CrossRef PubMed.
- S. Coriani, D. Marchesan, J. Gauss, C. Hättig, T. Helgaker and P. Jørgensen, J. Chem. Phys., 2005, 123, 184107 CrossRef PubMed.
- S. E. Novick, W. Chen, M. R. Munrow and K. J. Grant, J. Mol. Spectrosc., 1996, 179, 219–222 CrossRef CAS.
- G. Cazzoli and C. Puzzarini, J. Mol. Spectrosc., 2006, 239, 64–70 CrossRef CAS.
- G. Cazzoli, C. Puzzarini, M. E. Harding and J. Gauss, Chem. Phys. Lett., 2009, 473, 21–25 CrossRef CAS.
- G. Cazzoli, L. Dore, C. Puzzarini and J. Gauss, Mol. Phys., 2010, 108, 2335–2342 CrossRef CAS.
- C. Puzzarini, G. Cazzoli, M. E. Harding, J. Vázquez and J. Gauss, J. Chem. Phys., 2009, 131, 234304 CrossRef PubMed.
- C. Puzzarini, G. Cazzoli, M. E. Harding, J. Vázquez and J. Gauss, J. Chem. Phys., 2015, 142, 124308 CrossRef PubMed.
- R. L. DeLeon, D. Prichard and J. S. Muenter, J. Chem. Phys., 1985, 83, 4962–4966 CrossRef CAS.
- K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479–483 CrossRef CAS.
- K. A. Peterson and T. H. Dunning Jr., J. Chem. Phys., 2002, 117, 10548–10560 CrossRef CAS.
- C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618 CrossRef.
- T. H. Dunning Jr., J. Chem. Phys., 1989, 90, 1007 CrossRef.
- E. Papajak and D. G. Truhlar, J. Chem. Theory Comput., 2011, 7, 10–18 CrossRef CAS PubMed.
- D. E. Woon and T. H. Dunning, J. Chem. Phys., 1993, 98, 1358–1371 CrossRef CAS.
- D. A. Matthews, L. Cheng, M. E. Harding, F. Lipparini, S. Stopkowicz, T.-C. Jagau, P. G. Szalay, J. Gauss and J. F. Stanton, J. Chem. Phys., 2020, 152, 214108 CrossRef CAS PubMed.
- J. Breidung and W. Thiel, J. Phys. Chem. A, 2019, 123, 5600–5612 CrossRef CAS PubMed.
- J. Breidung, L. Constantin, J. Demaison, L. Margulès and W. Thiel, Mol. Phys., 2003, 101, 1113–1122 CrossRef CAS.
- H. Najib, J. Mol. Spectrosc., 2014, 305, 17–21 CrossRef CAS.
- Y. Morino and S. Saito, J. Mol. Spectrosc., 1966, 19, 435–453 CrossRef CAS.
- G. Cazzoli and C. Puzzarini, J. Mol. Spectrosc., 2006, 239, 59–63 CrossRef CAS.
- H. Najib, N. Ben Sari-Zizi, J. Demaison, B. Bakri, J. M. Colmont and E. B. MKadmi, J. Mol. Spectrosc., 2003, 220, 214–222 CrossRef CAS.
- L. Pierce, R. Jackson and N. DiCianni, J. Chem. Phys., 1961, 35, 2240–2241 CrossRef CAS.
- W. Flygare and R. Benson, Mol. Phys., 1971, 20, 225–250 CrossRef CAS.
- D. J. Wilson, C. E. Mohn and T. Helgaker, J. Chem. Theory Comput., 2005, 1, 877–888 CrossRef CAS PubMed.
- L. Bizzocchi, B. M. Giuliano and J.-U. Grabow, J. Mol. Struct., 2007, 833, 175–183 CrossRef CAS.
- H. M. Pickett, J. Mol. Spectrosc., 1991, 148, 371–377 CrossRef CAS.
| This journal is © the Owner Societies 2022 |