 Open Access Article
Open Access ArticleAlignment and impact angular dependence to O2 sticking and dissociation on Pt(111) and close-packed steps†
Maatje J. E.
de Willigen
a,
Mitsunori
Kurahashi
 b and
Ludo B. F.
Juurlink
b and
Ludo B. F.
Juurlink
 *a
*a
aLeiden Institute of Chemistry, Leiden University, Einsteinweg 55, 2333 CC, Leiden, The Netherlands. E-mail: l.juurlink@chem.leidenuniv.nl; Tel: +31 71 527 4221
bSurface Characterization Group, National Institute for Materials Science, 1-2-1 Sengen, Tsukuba, Ibaraki 305-0047, Japan
First published on 25th July 2022
Abstract
Oxygen's interaction with Pt surfaces serves as a model system in the development of an accurate theoretical description of reaction mechanisms that involve multiple precursor states. To benchmark the influence of surface structure on the dynamics of this interaction, we report absolute values of the initial sticking probability of O2 onto Pt(111) and two vicinal surfaces for state-selected and rotationally-aligned O2 molecules. Sticking probabilities vary significantly for helicoptering and cartwheeling molecules. Our data can be understood if normal energy scaling holds for all molecular orientations relative to the surface. Vicinal surfaces are much more reactive than Pt(111) with little to no dependence on the molecule's alignment and a more complex angular dependence. At low incident energies, sticking probabilities are highest for incidence into step facets. The weak alignment dependence points toward predominant scattering into a physisorbed state preceding chemisorbed states over a wide angular range.
1 Introduction
Molecular oxygen plays an important role in many heterogeneously catalysed oxidation reactions. Amongst transition metal catalysts, Pt has relevant applications in the oxygen reduction reaction (ORR) in fuel-cells1–3 and the automotive exhaust gas treatment, where O2 oxidises CO and residual hydrocarbons.4,5 Such applications draw interest from scientific and technical communities, while the cost of this precious metal stimulates efforts to develop cheaper catalysts. A rational approach in this effort requires a detailed understanding of the interactions of O2 with the catalyst's surface. Model studies combining ultrahigh vacuum (UHV), surfaces of single crystals, and supersonic molecular beam techniques allow for unravelling the principles that govern the adsorption dynamics.6Molecular oxygen's interaction with catalytic platinum surfaces is known to be complex. To understand the dynamics of adsorption and dissociation, it was originally studied extensively on a Pt(111) model catalyst surface.7 The quantified dependences of the initial sticking probability (S0) on incident kinetic energy (Ei), surface temperature (Ts), and angle of incidence (θi) were first interpreted to indicate both indirect and direct dissociative adsorption. This idea was corrected later by the determination of the species adsorbed using vibrational spectroscopy, and it was shown that O2 molecular dissociation always proceeds via molecular chemisorption and subsequent thermal dissociation.8,9 In these studies, two molecular chemisorbed states were identified, a superoxo (O2−) and a peroxo species (O22−). A physisorbed state is only populated extensively at lower surface temperatures.10 Infrared spectroscopy showed that it serves as a precursor to the superoxo species.11
The corrugation on the Pt(111) surface, e.g. introduced by regular monoatomic steps, drastically increases the sticking probability.12–14 A lack of identification of the species resulting from sticking made it impossible to conclude whether steps open up a channel to direct dissociative adsorption, as speculated from a study on Pt(533).12 At the same time, independence of step type for sticking at low incident energy was speculated to result from the increased importance of the physisorbed state in the dynamics of trapping and dissociation.13 Desorption and scanning tunnelling microscopy (STM) studies point to differences in the influence of step-type on adsorption and dissociation,15–18 but could not make claims regarding the adsorption dynamics.
While most of these studies of O2 impacting onto Pt used randomly oriented O2 beams, Kurahashi and Yamauchi developed a technique to study alignment effects with a high level of control over the impacting orientation of the O2 molecule.19 Since O2 is a paramagnetic linear molecule, a hexapole magnet may be used to select a single spin state in a molecular beam. The (2,2) state is generally selected and, subsequently, oriented by a magnetic field surrounding the crystal to impact onto a surface with either a helicoptering (H) or cartwheeling (C) motion relative to the normal of the crystal surface. The technique and some applications have been reviewed previously.20 Even more recently, an alignment effect in the chemisorption of oxygen on Pt(111) was examined.21 This study showed that for lower collision energies, impact with the O2's internuclear axis continuously aligned with the (111) surface plane, i.e. helicopters, strongly increases S0 relative to the cartwheeling alignments. It was interpreted to reflect the molecular chemisorbed peroxo and superoxo states with their O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond lying parallel to the (111) plane, and the activation energy required to reach them from the gas phase. With increasing incident energy, S0 for the different alignments changed relatively, explaining the asymptotic dependence of S0 with kinetic energy and levelling well below S0 = 1, as found previously for Pt(111).
O bond lying parallel to the (111) plane, and the activation energy required to reach them from the gas phase. With increasing incident energy, S0 for the different alignments changed relatively, explaining the asymptotic dependence of S0 with kinetic energy and levelling well below S0 = 1, as found previously for Pt(111).
A subsequent study employing stepped Pt(111) crystals showed that the increased sticking at low incident energies previously observed without state-selection and alignment showed no alignment dependence near Ei = 0.1 eV.22 This result was interpreted to indicate that, at low impact energies, steps aid in trapping the O2 molecule by initially scattering it into the physisorbed state, as such a state is rotationally (nearly) isotropic. The results also showed that the step influence on Pt is twofold; sticking probabilities are strongly enhanced by scattering into a physisorbed state at low incident energy, but with increasing incident energy, direct adsorption into chemisorbed states at the step edges starts contributing to the overall sticking.
Despite this detailed understanding of the mechanisms by which O2 traps and sticks to Pt surfaces, there are still aspects to be addressed. First, as Cao et al.22 only published relative values of S0 for H and C aligned molecules, a comparison of absolute values for such alignments for Pt(111) and stepped surfaces is lacking. Such absolute values are required to address the accuracy of theoretical calculations and the quality of potential energy surfaces developed for gas-surface interactions.23 Second, to predict catalytic rates, unravelling parallel mechanisms leading to sticking and dissociation must be done in an absolute sense. This requires not only the energy dependence for normal incidence but also the impact's angular dependence. For Pt(111), incidence at higher Ei was previously shown to reflect normal energy scaling, i.e. showing a cos2(θi) dependence, but was found to be more complex at lower energies.7 The angular dependences for the various alignments on Pt(111) directly sticking into a chemisorbed molecular state have not been investigated, nor how the impact angle affects scattering from monoatomic steps into the physisorbed state. As for H2 direct dissociation on stepped Pt surfaces an increase in sticking was observed for molecules impacting into the step facet,24,25 and we hypothesize that a similar effect is observed for O2 impacting on such surfaces. At low incident energy, we also expect this effect to be mostly independent of alignment as scattering seems to occur predominantly in a physisorbed state.
Herein, we investigate how changes in the alignment of the rotational axis of the O2 molecule upon collision with steps and (111) terraces affect sticking on the Pt surface. We report absolute values for the sticking of various alignments for both Pt(111) and two-stepped Pt(111) surfaces and investigate the angle dependences. We quantify sticking at steps vs. terraces by separating the measured sticking probability into local sticking probabilities, S1110 and Sstep0. These are weighted by an estimate of their relative surface areas as previously done for H2 dissociation on stepped Pt surfaces.26–28
2 Methods
Stereodynamically sensitive experiments were executed in Tsukuba, Japan. The apparatus has been described before.20,29 Briefly, supersonically expanded mixtures of O2 in He pass through a magnetic hexapole. The hexapole contains a variable number of hexapole elements. The number matches the variable kinetic energy of state-selected O2. Stern–Gerlach (SG) and TOF analyses of O2 [(J,M) = (2,2)] indicate that the purity of the (J,M) = (2,2) state is nearly 100%. The estimated velocity spread (Δv/v) is at most 10–15%.29 The supersonic molecular beam passes through multiple differentially pumped chambers that are separated by aligned skimmers and small orifices. A UHV chamber at the end of this sequence of chambers houses the Pt(553), Pt(533), or Pt(111) crystal upon which the state-selected O2 molecules impinge. The crystals are suspended from a X, Y, Z, Θ manipulator. The crystals are attached to transfer plates that allow for moving the crystal into a second UHV chamber used for cleaning the crystals' surfaces, verification of long-range order by low-energy electron diffraction (LEED), and verification of cleanliness by Auger Electron Spectroscopy (AES). As reported previously, after the standard cleaning procedures of multiple sputtering-annealing cycles, the crystals show no measurable levels of impurities. The obtained LEED patterns are as expected for these crystals.22 The direction of the rotation of the hexagonal split-spot pattern for the stepped surfaces allows us to determine the direction of the steps.Currents through three sets of the Helmholtz coils surrounding three different axial directions outside of the UHV chamber are alternated every 2 seconds. This alternation switches the impact geometry for state-selected O2. The sticking of O2 is measured using the King and Wells technique with the molecular beam striking the surface for at least one minute. Here, the pressure in the chamber as measured by a magnetically shielded ion gauge is used for the King & Wells measurement. It is corrected for the contribution of He to the total pressure, as determined by separate measurements of the ratio of He and O2 using a quadrupole mass spectrometer (QMS). Experiments using two alternating impact geometries are generally, but not always, performed twice using both possibilities for the starting order of impact geometries. Initial sticking probabilities are obtained by a fit to the data as discussed in detail below. The time dependence may, in principle, be used to determine the coverage dependence of the sticking probability. Here, it cannot be determined for reasons described in detail in the ESI.†
3 Results and discussion
Fig. 1 shows the reference frame for the experimental setup with laboratory frame axes defining translational motion and the three directions of rotational motion relative to the step directions within the surface of Pt crystals for O2. The beam containing O2 molecules enters along the x-axis. Alignment of rotation within the xy plane yields molecules acting as cartwheels with a rotational momentum vector aligned along z (Cz). Similar rotation within the xz plane yields cartwheels with a rotational momentum along the y-axis (Cy). Rotation in the yz plane yields helicoptering molecules (H). Note that the magnetic fields do not align molecules uniquely. Molecules impinge with a distribution of rotational angles centred along x, y, or z.20 | ||
| Fig. 1 Schematic illustrating the x, y and z laboratory frame axes, the sample, and the alignment of O2 molecules as H, Cz, and Cy. | ||
Fig. 2 shows in blue and red two typical sets of data prior to any analysis or treatment, collected with identical experimental settings. The kinetic energy of O2 molecules, Ei, is 0.33 eV and the incident angle is 0° relative to the Pt(111) surface normal. The data were taken on the same day with several similar measurements performed in between. The figure shows the ion gauge current collected by a magnetically shielded nude ion gauge in the UHV chamber over time when a mixed O2/He beam is sequentially allowed to enter the UHV chamber and impinge onto a Pt(111) surface. Initially, the mixed O2/He beam does not enter the UHV chamber. The ion gauge current is low. After approximately 10 s, at timestamp T1, a beam valve is opened and the beam enters the chamber but scatters off an inert flag. The nearly instantaneous pressure rise reflects the flux of O2 molecules diluted in He, Φ, entering the UHV chamber. After a fixed amount of time, at timestamp T2 (see the inset of the expanded signal), the inert flag is removed and the beam impinges directly onto the clean Pt(111) surface. A sharp electronic spike in the data accurately defines the starting point for the incident flux of O2 molecules to hit and partially stick to the surface. Sticking of O2 and its subsequent dissociation leads to a pressure drop. It may also be considered a lower reflectivity due to the sticking of O2 to the Pt(111) sample compared to the inert flag. From this point onward, the magnetic field at the crystal is also continuously switched for both experiments. The switching causes the O2 to impinge alternatingly as cartwheels with rotational momentum along the z axis and helicopters. The sequence starts with H. Clearly, switching between H and Cz modulates the reflectivity of (or the sticking to) the surface. With time, the reflectivity smoothly increases as the surface fills up with atomic oxygen from dissociated O2, although modulated by the magnetic field altering the incident rotational alignment. The ion gauge current ultimately approaches the value obtained for the reflectivity of the inert flag, i.e. in between T1 and T2. The beam is allowed to impinge onto the surface for approximately 40 s, after which the inert flag is placed back at timestamp T3. This is again characterized by an electronic spike. The small step function in the data at this point suggests that sticking, even after 40 s, had not yet fully saturated the surface. If the surface is fully passivated toward sticking, its reflectivity should equal that of the inert flag. The effect is most clearly observed in the blue trace.
The surface temperature during our measurements is somewhere between 300 and 400 K, but varies by at most 30 K. The variation results from differences in the required time to move the crystal between the preparation chamber and the UHV scattering chamber, hence the time that the crystal cools after annealing. The exact temperature is unknown due to lack of temperature measurement in the latter chamber. The estimated range of 30 K is based on more recent measurements of temperature for similar experiments. For this range, surface temperature effects on sticking coefficients can be neglected.13
Prior to analyzing the data to obtain sticking coefficients, we study the traces in greater detail. First, we note that the absolute base current, i.e. the current detected prior to T1, for the two traces is not the same for experiments with identical settings. As the ion gauge detects residual gas indiscriminately (although with varying sensitivity), this may reflect a minor difference in the base pressure of the UHV chamber. This difference in base pressure is not unexpected as repetitively allowing intense beams into the chamber may increase the base pressure during the day. However, the fluxes Φ1 and Φ2 also differ between these identical experiments. The starting pressure at T1 may for the latter experiment (red) be higher, but the immediate increase is slightly smaller than for the former experiment (blue). This could be a result of a lowered detection efficiency of the ion gauge. It may also reflect a change in the beam. The absolute beam flux may have dropped a little or the relative composition of O2 and He may have shifted toward the less easily ionized species, i.e. He. Also, we observe in the blue trace that the ion gauge signal within a single experiment changes as a function of time. When the beam scatters of the inert flag between T1 and T2, the ion gauge current is slightly lower than after T3. The detector's sensitivity improved, the beam flux increased or the composition changed toward the more easily ionizable species (O2). As the experiment represented by the blue data was performed prior to the experiment represented by the red data, and the red data show no difference between the ion gauge sensitivity measured prior to T2 and after T3, we expect that the beam flux or composition changed slightly over time and only stabilized well after the initial (blue) experiment. Although the effects are small, in the ESI,† we show that this and other seemingly small effects ultimately render us incapable of accurately quantifying the sticking probability's dependence on the atomic oxygen coverage, i.e. S(ΘO).
Regardless of the variations in the obtained signal for identical experiments, the data allows us to obtain accurate initial sticking probabilities for variations in kinetic energy and incident angle, i.e. S0(Ei,θi), for the individual alignments (Cz, Cy, and H). To do so, the data presented in Fig. 2 were converted by performing the following steps. First, the background signal (base level) was deducted from the data. We use the average of the ion current up to T1. Subsequently, the average between T1 and T2 is determined. The entire signal is normalized to this value and subsequently spans a relative current or flux between 0 and 1. The signal is then inverted and shifted to span the range of 0 to 1. This remaining signal, starting at T1, represents S(t) with Θ0 = 0 at t = T1.
Fig. 3 shows the resulting time-dependent sticking probability of O2 on a Pt(111) surface. It was created from the raw data presented in blue in Fig. 2. Against the top and on the right axis, we show the block function that illustrates the alternating rotational alignment. It modulates between 0 and 1 for H. The inverse function would characterize the impact of Cz-aligned O2. The decaying sticking probability follows the switching between the alignments. However, the signal also reflects the vacuum time constant for O2 of the vacuum system. After the nearly instantaneous switch of the magnetic field, it takes some time for the system to adapt to the new decaying equilibrium and follow the sticking probability trend. This equilibration time was found to be between 270 and 310 ms with an average of 300 ms. The block function indicating the switching of rotational alignment was then altered to omit the first 300 ms after each switch. The adjusted block function used as a data mask in the subsequent fitting procedure (see below) is depicted as a dotted line in Fig. 3 for H. It is 0 for the times that the magnetic field selects the other alignment and for the times that the vacuum time constant affects the data. For Cz, the inverted block function is used and adapted analogously to create a data mask when fitting Cz data.
As a single exponential decay does not capture the trend accurately, a functional form containing two exponential decays is fitted to the data for each of the rotational alignments.
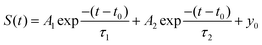 | (1) |
The offset, y0, was set to zero as the baseline was already established. The remaining fitting parameters A1 and τ1 capture the fast decay at the start of the experiment, while A2 and τ2 capture a second, slower decay. The start time, t0, is defined as the exact average between the removal of the inert flag (marked by the electronic spike at T2) and the start of the adsorption signal. We have checked the sensitivity of S0 to minor changes in the definition of t0 by varying the latter in between the removal of the inert flag (T2 in Fig. 2) and the start of the adsorption signal (the first peak in the blue line in Fig. 3). Changing t0 within this range yields a variation in the ultimately determined value of S0 between 0.5–3%. The uncertainty in t0 is, therefore, insignificant.
The data masks ensure that only relevant data is selected in the fitting procedure. The fits to the time-dependent sticking of both alignments are shown as red dotted lines passing through the data. The upper fit represents the H and the lower fit represents the Cz alignment. The fits deviate most from the data at the start of the experiment, although the overall fits seem to capture the absolute values very well. With the fitting parameters determined, we calculate S0 using t = t0. In this particular example, we find that the S0(H) is considerably higher than S0(Cz), 0.173 for S0(H) and 0.114 for S0(Cz).
Fig. 4 shows the initial sticking probability as a function of incident angle, θi, for Pt(111) at an incident energy of 0.33 eV. The three different rotational alignments are colour-coded with H in blue, Cy in black and Cz in red. This colour-coding is maintained in the presentation of data. The data shows that helicoptering molecules are considerably more reactive than cartwheeling molecules at normal incidence. This difference becomes smaller when the angle from the surface normal increases. The two types of cartwheeling molecules show identical sticking probabilities at normal incidence. With the increasing incident angle, a minor discrepancy develops with S0(Cy) being consistently slightly larger than S0(Cz). Values for S0(H) also approach S0(Cy) at 45 incidence.
Normal energy scaling (NES) has been established for O2 sticking on Pt(111),7 Ag(001),30 Cu(111), Cu(110), and Cu(100).31 It is often interpreted to signal activated adsorption with a barrier positioned in the entrance channel. To judge whether NES also applies to sticking on Pt(111) for all individual alignments, traces of the form
| S0(θi) = (S0(0°) × cos(θi))2 | (2) |
As noted, at the incident angles of −45 and 45°, S0(H) has dropped to almost the same value as S0(Cy) while S0(Cz) is distinctly lower than S0(Cy). This behaviour is as expected. In the experiment, we rotate the crystal along the z-axis. This alters both the angle between the macroscopic surface normal and velocity vector of the O2 molecule, and the angle between the molecular rotational plane and the surface plane. The H alignment at θi = 0° turns into Cy and vice versa with increasing θi. On the other hand, Cz remains unique and only contains a cartwheel character irrespective of θi. Considering that the H character results in higher S0 values, it is not surprising that Cz is the least reactive at the most extreme angles. At the same time, the data for both H and Cy are exactly in between their original helicopter and cartwheel character at ±45°. Although the angle between the (111) surface plane and their rotational plane is the same, the data suggest that S0(H) is slightly larger than S0(Cy) at this incident angle. This may be an artefact caused by the order in which the sticking for different rotational alignments is determined. For this particular set of data, we mostly started experiments with the H impinging first. This may cause a slight advantage as the second alignment never truly experiences an entirely clean surface. Its S0 may, therefore, be slightly underestimated. However, the difference may also be a consequence of an actual difference for H and Cy at the incident angle of 45°. Even though H and Cy are identical with respect to their rotational plane relative to the surface plane at ±45° incidence, they are different in the alignments of their velocity vectors and rotational momenta. For the alignment indicated as H for normal incidence, these momenta are aligned, while for the original Cy they are orthogonal. This difference may affect the ratio of scattering vs. sticking by coupling rotational and kinetic energy in the collision. Here, however, rotational energy is small compared to the kinetic energy. Hence, we feel that more detailed experiments are required to draw any conclusion beyond that normal energy scaling seems to hold for the rotational alignments indicated as H, Cy, and Cz.
To illustrate the influence of monoatomic steps in the Pt surface on sticking, Fig. 5a displays the dependence of S0 for the three alignments as a function of θi for the stepped Pt(533) surface with Ei = 0.1 eV. The data are qualitatively representative of both Pt(533) and Pt(553) and show a clear maximum for molecules impinging into steps. In Fig. 5b the same type of data is shown for Pt(553) for a higher incident energy, i.e. Ei = 0.33 eV, i.e. the same as for Pt(111) in Fig. 4. The incident angles in both panels are relative to the macroscopic normal of the crystal. Incidence along [111], hence normal to the 4 atom-wide (111) terraces, occurs at +12.3° +14.4° from the Pt(553) and Pt(533) surfaces, respectively. While the data for low incident energy shows a broad maximum at negative impact angles, at higher Ei the maximum shifts toward [111]. This reflects the increasing contribution of direct adsorption into chemisorbed states on the (111) facets.22
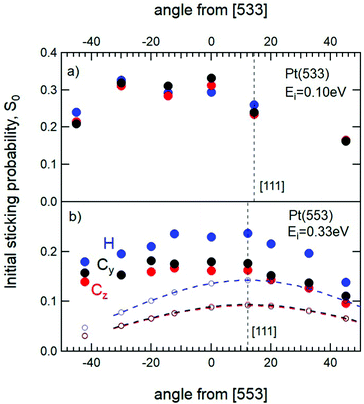 | ||
| Fig. 5 Initial sticking probability of O2 as a function of θi on (a) Pt(533) for Ei = 0.1 eV and (b) Pt(553) at Ei = 0.33 eV. The vertical straight dashed lines indicate the [111] normal. The coloured dashed curves in (b) are identical to those shown in Fig. 4 for Pt(111) and centered at [111], but multiplied by 0.8. The open circles indicate the contribution of (111) facets to the measured S0 values for Pt(553). | ||
When compared to Fig. 4, three clear distinctions arise from Fig. 5. First, sticking is considerably higher on stepped surfaces than on Pt(111) for both incident energies, at all angles, and for all rotational alignments. Second, the significant difference between H and C for Pt(111) occurring over a wide angular range disappears at the lowest incident energy for stepped surfaces. Finally, the angular dependence is not symmetric along the macroscopic normal, nor does it reflect normal energy scaling along the [111] or any other normal. A fourth point that we note is more subtle. Sticking probabilities at negative impact angles are consistently higher for Cy as compared to Cz.
To discuss our interpretation of these results, we depict the reference frame separately in Fig. 6. Positive and negative angles are denoted by + and − and correspond to the angular axis in Fig. 5. The left panel of Fig. 6 depicts incidence relative to the Pt(111) facets. Fig. 4 shows that any contribution to sticking resulting from incidence onto a (111) terrace should reflect normal energy scaling. It will therefore show a symmetrical dependence with respect to [111] reflecting eqn (2). In the right panel, the incident beam impinging at or very near the steps of the (533) surface is illustrated. Positive impact angles lead to incidence more along [111]. At negative angles, the beam directs molecules more into the step facet.
If we consider the sticking probability to be predominantly determined by the point of impact, the observed initial sticking probability, S0(θi), is simply the average of local sticking probabilities weighted by the relative surface areas of steps and terraces.12,24,26,33
 | (3) |
Considering that Pt(553) is nominally equal to Pt[4(111) × (110)],33 the surface area with a potential energy surface (PES) resembling extended (111) terraces is expected to be at most on the order of 80% of the total surface area.34 Taking A111 at 80%, we calculate from the data in Fig. 5b and eqn (3) the local sticking probability for steps. In Fig. 7, our rough estimates for Sstep0 for all three alignments are shown. Two observations stick out. First, sticking by scattering from or reacting at steps is far less sensitive to the rotational alignment of the molecule prior to impact compared to Pt(111) at the same incident energy. Whereas H was up to 1.8 times more reactive than C on Pt(111),21 we find that the various alignments are much more similar. The remaining difference may also be artificially enhanced by the somewhat arbitrary differentiation between step and terrace surface areas. In any case, the lack of a strong alignment dependence at this incident energy indicates that the predominant mechanism leading to O2 sticking proceeds via a state that is rotationally isotropic.22 Hence, the data indicate that the high absolute sticking probability in comparison to Pt(111) is a consequence of molecular scattering from the step edges into a physisorbed state. Second, scattering into the step, i.e. at negative angles, yields high sticking probabilities. The actual values obviously depend on the same division of surface areas for step and terrace. We conclude that the steps are very effective in converting a large enough fraction of the incident 0.33 eV into another form an energy – at least large enough that the molecule does not escape the physisorbed state. This conversion of kinetic energy may occur into phonons, e-h pairs, rotational motion, or into kinetic energy with a momentum vector oriented parallel to the surface. Our experiments cannot distinguish between these origins of trapping.
 | ||
| Fig. 7 The estimated local sticking probability at steps (Sstep0) as a function of the angle for Pt(553) at Ei = 0.33 eV. Data result from the deconvolution of S0 into two components as described by eqn (3). | ||
The dominance of a mechanism that relies on scattering into a physisorbed state should decline with incident energy. A larger collision energy is more difficult to convert to an extent that the molecule becomes trapped. One may, therefore, expect that with increasing kinetic energy, alignment dependencies similar to those observed for Pt(111) return. Fig. 8 shows that this is the case. The data represent the absolute initial sticking probability of O2 as a function of the incident kinetic energy for the Pt(553) crystal surface at three incident angles. The step and terrace directions are identical to those illustrated in Fig. 6 for Pt(533), but with the [111] normal occurring at +12.3°. The top panel shows S0 at an incident angle of 0°, hence normal to the macroscopic surface. The middle panel displays the data for 12.3°, hence normal for the short (111) planes. The bottom panel shows the data for 45° incidence, hence beyond the [111] normal and further away from the influence of the step facets. Data are separated for the three directions of rotational motion. They illustrate that, with increasing kinetic energy, helicopters again attain a unique status and show a higher initial sticking probability than cartwheels. Even for increasing incident energy with the associated drop and levelling of S0, the H alignment is clearly more reactive than the C alignments. For all incident angles and energies the relative sticking probabilities do not vary as strongly as for normal incidence onto Pt(111), but the ratio of SH0 to SC0 increases to approximately 1.3 at 45 incidence. In line with our previous interpretation,22 we conclude that with increasing collision energy, the relative importance of parallel mechanisms leading to sticking and dissociation shifts from scattering into a physisorbed state toward direct activated adsorption into chemisorbed states. The alignment of such states with the internuclear axis parallel to the surface is reflected in the higher sticking coefficient for H vs. C.
We finally address the fourth, more subtle, observation from Fig. 5 mentioned previously. The consistency of higher sticking probability values determined for Cy in comparison to Cz at 0.1 and 0.33 eV impact energy and negative impact angles also holds true for the Pt(553) surface. In line with our previous suggestion,22 where the argument was based solely on impingement normal to the (111) facets but for a range of impact energies, we attributed this effect to direct access to an alignment chemisorbed molecular state at the step. In DFT-based calculations, the energy difference for chemically-bound molecular states of O2 at these step types was found to strongly favor the interatomic O–O axis aligned with the step and binding to the upper edge.35,36 Molecular impingement with the Cy geometry partially probes this orientation, while Cz does not. We believe that direct scattering into this edge-bound molecular state causes the difference in the observed sticking probabilities for the two cartwheeling motions. Its effect is seen over a range of impact angles near the [111] normal.
4 Summary
The dependence of initial sticking probabilities on incident angle and kinetic energy was determined and analysed for three orthogonal alignments of the O2 molecule onto platinum single crystal surfaces. We show sets of representative data for the (111), (533), and (553) planes. At 0.33 eV incident energy, sticking to the (111) plane shows a strong alignment dependence with H being more reactive than C, but normal energy scaling seems to hold for all alignments. It reflects an activation barrier to molecular chemisorption in the entrance channel of the reaction and alignment of chemisorbed molecular states parallel to the (111) surface plane.The sticking probabilities' angular dependence for stepped Pt surfaces shows an additional contribution to sticking at low incident energy. Incidence into the step facet increases sticking most drastically. A simple model suggests that a local sticking probability at the step reaches values near 0.5 for 0.33 eV incidence energy with a velocity vector aiming into the step. The lack of a clear rotational alignment dependence to this second sticking mechanism confirms that it does not result in direct binding into an aligned surface-bound state. Instead, sticking proceeds primarily via initial scattering into a more weakly bound, free rotor state at low collision energies. We expect it to predominantly result from geometric corrugation introduced by the step. With increasing collision energy, the dominance of this mechanism is reduced and alignment effects reappear. At the same time, we find a minor discrepancy for cartwheeling molecules. When the rotational plane is parallel to the step direction, molecules stick slightly better as a molecular bound state existing at the step edge is more easily accessed than when molecules approach with their rotational plane normal to the step direction.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
L. J. and M. K. acknowledge funding by the National Institute for Materials Science, Japan. M. K. also acknowledges the support of JSPS KAKENHI, Nos 16H03874, 20H02623, and 20K21148.Notes and references
- N. Marković, T. Schmidt, V. Stamenković and P. Ross, Fuel Cells, 2001, 1, 105–116 CrossRef.
- J. A. Keith, G. Jerkiewicz and T. Jacob, ChemPhysChem, 2010, 11, 2779–2794 CrossRef CAS PubMed.
- N. Hoshi, M. Nakamura and A. Hitotsuyanagi, Electrochim. Acta, 2013, 112, 899–904 CrossRef CAS.
- M. AL-Harbi, R. Hayes, M. Votsmeier and W. S. Epling, Can. J. Chem. Eng., 2012, 90, 1527–1538 CrossRef CAS.
- M. V. Twigg, Catal. Today, 2011, 163, 33–41 CrossRef CAS.
- A. Kleyn, Chem. Soc. Rev., 2003, 32, 87–95 RSC.
- A. Luntz, M. Williams and D. Bethune, J. Chem. Phys., 1988, 89, 4381–4395 CrossRef CAS.
- P. Nolan, B. Lutz, P. Tanaka, J. Davis and C. Mullins, Phys. Rev. Lett., 1998, 81, 3179 CrossRef CAS.
- P. Nolan, B. Lutz, P. Tanaka, J. Davis and C. Mullins, J. Chem. Phys., 1999, 111, 3696–3704 CrossRef CAS.
- J. Grimblot, A. Luntz and D. Fowler, J. Electron Spectrosc. Relat. Phenom., 1990, 52, 161–174 CrossRef CAS.
- K. Gustafsson and S. Andersson, J. Chem. Phys., 2004, 120, 7750–7754 CrossRef CAS PubMed.
- A. T. Gee and B. E. Hayden, J. Chem. Phys., 2000, 113, 10333–10343 CrossRef CAS.
- L. Jacobse, A. den Dunnen and L. B. Juurlink, J. Chem. Phys., 2015, 143, 014703 CrossRef PubMed.
- A. Walker, B. Klötzer and D. King, J. Chem. Phys., 1998, 109, 6879–6888 CrossRef CAS.
- C. Badan, R. G. Farber, Y. Heyrich, M. T. Koper, D. R. Killelea and L. B. Juurlink, J. Phys. Chem. C, 2016, 120, 22927–22935 CrossRef CAS.
- M. J. van der Niet, A. den Dunnen, L. B. Juurlink and M. T. Koper, J. Chem. Phys., 2010, 132, 174705 CrossRef PubMed.
- C. Badan, M. T. Koper and L. Juurlink, J. Phys. Chem. C, 2015, 119, 13551–13560 CrossRef CAS.
- R. G. Farber, M. E. Turano, E. C. Oskorep, N. T. Wands, L. B. Juurlink and D. R. Killelea, J. Phys.: Condens. Matter, 2017, 29, 164002 CrossRef PubMed.
- M. Kurahashi, T. Suzuki, X. Ju and Y. Yamauchi, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 024407 CrossRef.
- M. Kurahashi, Prog. Surf. Sci., 2016, 91, 29–55 CrossRef CAS.
- H. Ueta and M. Kurahashi, Angew. Chem., Int. Ed., 2017, 56, 4174–4177 CrossRef CAS PubMed.
- K. Cao, R. van Lent, A. W. Kleyn, M. Kurahashi and L. B. Juurlink, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 13862–13866 CrossRef CAS PubMed.
- G.-J. Kroes, J. Phys. Chem. Lett., 2015, 6, 4106–4114 CrossRef CAS PubMed.
- I. Groot, K. Schouten, A. Kleyn and L. Juurlink, J. Chem. Phys., 2008, 129, 224707 CrossRef CAS PubMed.
- A. Gee, B. Hayden, C. Mormiche and T. Nunney, J. Chem. Phys., 2000, 112, 7660–7668 CrossRef CAS.
- D. A. McCormack, R. A. Olsen and E. J. Baerends, J. Chem. Phys., 2005, 122, 194708 CrossRef PubMed.
- I. M. Groot, A. W. Kleyn and L. B. Juurlink, Angew. Chem., Int. Ed., 2011, 50, 5174–5177 CrossRef CAS PubMed.
- I. Groot, A. Kleyn and L. Juurlink, J. Phys. Chem. C, 2013, 117, 9266–9274 CrossRef CAS.
- M. Kurahashi and Y. Yamauchi, Rev. Sci. Instrum., 2009, 80, 083103 CrossRef PubMed.
- F. B. De Mongeot, M. Rocca and U. Valbusa, Surf. Sci., 1996, 363, 68–72 CrossRef CAS.
- G. Anger, A. Winkler and K. Rendulic, Surf. Sci., 1989, 220, 1–17 CrossRef CAS.
- C. Rettner and C. Mullins, J. Chem. Phys., 1991, 94, 1626–1635 CrossRef CAS.
- M. Van Hove and G. Somorjai, Surf. Sci., 1980, 92, 489–518 CrossRef CAS.
- E. N. Ghassemi, E. W. Smeets, M. F. Somers, G.-J. Kroes, I. M. Groot, L. B. Juurlink and G. Füchsel, J. Phys. Chem. C, 2019, 123, 2973–2986 CrossRef CAS PubMed.
- Ž. Šljivančanin and B. Hammer, Surf. Sci., 2002, 515, 235–244 CrossRef.
- P. Gambardella, Ž. Šljivančanin, B. Hammer, M. Blanc, K. Kuhnke and K. Kern, Phys. Rev. Lett., 2001, 87, 056103 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp00934j |
| This journal is © the Owner Societies 2022 |





