Comparative electron irradiations of amorphous and crystalline astrophysical ice analogues

Abstract

Laboratory studies of the radiation chemistry occurring in astrophysical ices have demonstrated the dependence of this chemistry on a number of experimental parameters. One experimental parameter which has received significantly less attention is that of the phase of the solid ice under investigation. In this present study, we have performed systematic 2 keV electron irradiations of the amorphous and crystalline phases of pure CH₃OH and N₂O astrophysical ice analogues. Radiation-induced decay of these ices and the concomitant formation of products were monitored in situ using FT-IR spectroscopy. A direct comparison between the irradiated amorphous and crystalline CH₃OH ices revealed a more rapid decay of the former compared to the latter. Interestingly, a significantly lesser difference was observed when comparing the decay rates of the amorphous and crystalline N₂O ices. These observations have been rationalised in terms of the strength and extent of the intermolecular forces present in each ice. The strong and extensive hydrogen-bonding network that exists in crystalline CH₃OH (but not in the amorphous phase) is suggested to significantly stabilise this phase against radiation-induced decay. Conversely, although alignment of the dipole moment of N₂O is anticipated to be more extensive in the crystalline structure, its weak attractive potential does not significantly stabilise the crystalline phase against radiation-induced decay, hence explaining the smaller difference in decay rates between the amorphous and crystalline phases of N₂O compared to those of CH₃OH. Our results are relevant to the astrochemistry of interstellar ices and icy Solar System objects, which may experience phase changes due to thermally-induced crystallisation or space radiation-induced amorphisation.

---

1 Introduction

Laboratory irradiations of low-temperature astrophysical ice analogues using charged particles (i.e., ions and electrons) and ultraviolet photons have demonstrated the formation of complex organic molecules relevant to biology, such as amino acids and nucleobases.^1–4 Such results have highlighted the importance of fully characterising the radiation chemistry occurring within the ice mantles adsorbed on interstellar dust grains, as well as that occurring on the surfaces of outer Solar System bodies such as comets, moons, and Kuiper Belt Objects. To this end, several studies have demonstrated the dependence of this radiation (astro)chemistry on a number of different experimental parameters. Of these, the best studied is perhaps ice temperature, with previous studies documenting the variation in the abundance of molecular products yielded after irradiation at different ice temperatures.^5,6

One experimental parameter which has received considerably less attention is that of the phase of the molecular ice being irradiated. Indeed, to the best of the authors’ knowledge, only a handful of studies have directly compared the radiation chemistry between different phases of an astrophysical ice analogue.^7–9 These studies have all considered the electron irradiation of amorphous and cubic crystalline D₂O, and have shown that the formation of D₂, O₂, and D₂O₂ was significantly more rapid in the amorphous case. This observation was attributed to the increased ability of radiolytically generated radicals to diffuse through the solid structure in amorphous ices due to their increased structural defects and porosities.

Further understanding the role that the phase of an ice may play in influencing the outcome or productivity of an astrochemical reaction requires that systematic and comparative experiments be performed on a range of molecular ices. Two species which are interesting candidates for such experimental work are CH₃OH and N₂O, due to the different intermolecular attractions which characterise their solid phases. CH₃OH is a polar molecule (μ = 1.69 D) which is expected to form strong hydrogen-bonds. Conversely, N₂O is only anticipated to exhibit weak dipole interactions and van der Waals forces as its main intermolecular interactions in the solid phase, due to its very weakly polar (μ = 0.17 D) nature. The phase adopted by each molecular ice may have a determining influence on the extent of these intermolecular forces of attraction in the solid ice, which may manifest as differences in the observed radiation chemistry.

CH₃OH and N₂O are also good candidates for such a study since both species are relevant to astrochemistry. CH₃OH ices are ubiquitous in various astrophysical settings, including on Solar System objects such as comets and centaurs^10–12 and around young stellar objects in interstellar space.^13–15 Their presence in such settings is thought to arise from chemical processes within icy grain mantles embedded in dense interstellar molecular clouds, such as the sequential hydrogenation of CO or H₂CO^16–19 or the radiolysis of interstellar or Solar System carbon-bearing water-rich ices.^20,21 N₂O has also been detected in interstellar settings such as stellar nurseries and towards low-mass protostars.^22,23 The presence of N₂O ice, although yet to be confirmed, is expected on the surfaces of outer Solar System moons and dwarf planets, where N₂ and O₂ ices are known to co-exist in radiation environments driven by giant planetary magnetospheres or the solar wind.^24–26

Although the literature contains a great number of publications concerned with the radiation chemistry of pure CH₃OH and N₂O astrophysical ice analogues,^27–38 few make explicit reference to the phase of the ice their experiments are concerned with. This is perhaps unexpected, as prior work has well-documented the phase chemistry of these ices.^39–48 As a solid ice, CH₃OH may exist as an amorphous structure up to a temperature of 128 K,³⁹ after which it undergoes crystallisation. Two crystalline phases are known: a low-temperature α-phase which persists to about 160 K^43,44 and a high-temperature β-phase which persists to liquification at the triple point temperature (175.61 K).⁴⁹ X-ray and neutron diffraction studies have shown that both the α- and β-crystalline phases exhibit orthorhombic symmetry with four molecules per unit cell.^41,42,50 The main distinctions between the phases are the orientation of the hydrogen-bond chains linking adjacent molecules, and the space group to which they belong: the α-phase belongs to the D₄²-P2₁2₁2₁ space group while the β-phase belongs to the D_2h¹⁷-Cmcn space group.⁴³

Solid N₂O may exist as one of two phases under high-vacuum conditions: an amorphous phase which dominates at temperatures below 30 K and a crystalline phase which exists at higher temperatures and adopts a Pa3 structure.^47,48 Interestingly, the phase adopted by a pure N₂O ice is not only determined by the temperature at which it was prepared, but also by its rate of condensation from the gas phase. Hudson et al.⁴⁷ demonstrated that faster deposition rates are conducive to the formation of a partially or wholly crystalline N₂O ice. The crystalline phase has been described as a ‘disordered crystal’ due to the fact that the lack of inversion symmetry in the N₂O molecule allows for more than one possible orientation of the weak molecular dipole parallel to the body diagonals of the unit cell. Such a description should not be construed to imply a lack of structure, however, as the crystalline phase is still characterised by an ordering of the constituent N₂O molecules.

To further investigate the possible influence of the phase of a solid ice in determining the outcome of its radiation chemistry, we have performed systematic and comparative irradiations of the amorphous and crystalline phases of pure CH₃OH and N₂O ices using 2 keV electrons. We note that we have not included the β-crystalline phase of CH₃OH in this study due to the high sublimation rates of solid CH₃OH at the temperatures required to synthesise this phase under high-vacuum conditions.⁴⁴ We believe that our results constitute the most in-depth analysis of this topic to date.

2 Experimental methodology

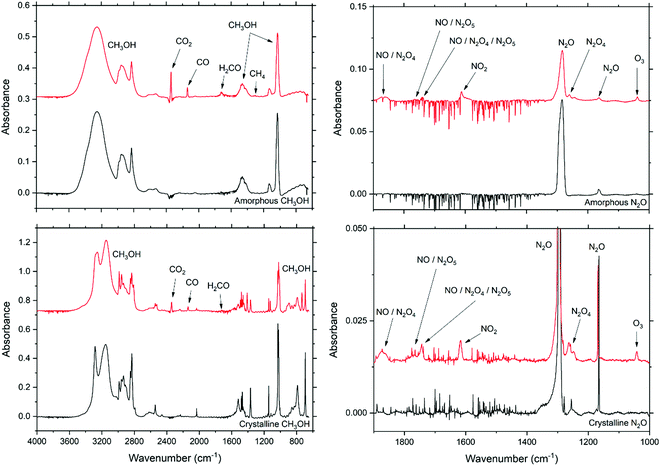
Experimental work was performed using the Ice Chamber for Astrophysics–Astrochemistry (ICA) located at the Institute for Nuclear Research (Atomki) in Debrecen, Hungary. The set-up and protocols used have been described in detail in previous publications,^51,52 and so only a brief overview is provided here. The ICA is a high-vacuum chamber in the centre of which is a vertically mounted copper sample holder containing a series of ZnSe substrate discs. The sample holder may be cooled to 20 K by a closed-cycle helium cryostat, although the actual temperature may be regulated in the range 20–300 K using a sophisticated temperature control system. The pressure in the chamber is nominally maintained at a few 10⁻⁹ mbar by the combined use of a dry rough vacuum pump and a turbomolecular pump.

The preparation of astrophysical ice analogues on the ZnSe substrates was achieved via background deposition by allowing the relevant gas or vapour into a pre-mixing line before dosing it into the main chamber at a nominal pressure of a few 10⁻⁶ mbar through an all-metal needle valve. This deposition pressure was reduced to a few 10⁻⁷ mbar during preparation of the amorphous N₂O samples, due to the known dependence on deposition rate of the phase adopted by this molecular ice.⁴⁷ In the case of CH₃OH (VWR, VLSI grade), the liquid was first de-gassed in a glass vial using the standard liquid nitrogen freeze–thaw technique prior to directing the vapour into the pre-mixing line. For N₂O, the gas (Linde, 99.5%) was introduced directly into the pre-mixing line without any additional preparation.

Amorphous CH₃OH and N₂O ices were prepared by deposition at 20 K, while their crystalline phases were prepared at 140 and 60 K, respectively. The deposition of these ices could be followed in situ using Fourier-transform mid-infrared (FT-IR) transmission absorption spectroscopy. Quantitative measurements made with FT-IR spectroscopy (spectral range = 4000–650 cm⁻¹; spectral resolution = 1 cm⁻¹) were used to determine the amount of a particular molecular species present within the ice by using eqn (1) to calculate its molecular column density, N (molecules cm⁻²):

where P is the peak area of an absorption band characteristic to a particular molecule (cm⁻¹) and A_ν is the integrated band strength constant for that band (cm molecule⁻¹). A list of the characteristic absorption bands and their associated band strength constants used in this study is given in Table 1. From the column density of the initially deposited ice, it is possible to determine the overall ice thickness, d (μm), through eqn (2):where Z is the molar mass of the deposited ice (CH₃OH = 32 g mol⁻¹; N₂O = 44 g mol⁻¹), N_A is the Avogadro constant (6.02 × 10²³ molecules mol⁻¹), and ρ is the mass density of the ice, which we have taken to be 0.636 and 0.838 g cm⁻³ for amorphous and crystalline CH₃OH, and 1.263 and 1.591 g cm⁻³ for amorphous and crystalline N₂O.^47,53 The constant value 10⁴ is included in this equation as a conversion factor so as to express d in μm. More information on the initial column densities and thicknesses of the ices investigated in this study may be found in Table 2.

Table 1 List of characteristic FT-IR absorption bands and their associated band strength constants for the species considered quantitatively in this study. Data collected from various ref. 34,51,52,54

Species	FT-IR absorption band (cm^−1)	A ν (10^−17 cm molecule^−1)
CH3OH (amorphous)	1027 (ν8)	1.61
CH3OH (crystalline)	1027 (ν8)	1.28
CO	2138 (ν1)	1.10
CO2	2343 (ν3)	11.80
H2CO	1725 (ν4)	0.96
CH4	1300 (ν4)	0.80
N2O (amorphous)	1283 (ν1)	1.20
N2O (crystalline)	1283 (ν1)	0.98
NO2	1614 (ν3)	0.62
N2O4	1261 (ν12)	0.51
O3	1039 (ν3)	1.40

---

Table 2 List of initial column densities and ice thicknesses of the CH₃OH and N₂O ices investigated in this study

Ice	Species	Phase	N (10^18 molecule cm^−2)	d (μm)
1	CH3OH	Amorphous	1.29	1.08
2	CH3OH	Amorphous	1.13	0.95
3	CH3OH	Amorphous	1.17	0.98
Average			1.20	1.00
4	CH3OH	Crystalline	1.50	1.20
5	CH3OH	Crystalline	1.10	0.88
6	CH3OH	Crystalline	1.09	0.87
Average			1.23	0.98
7	N2O	Amorphous	0.29	0.17
8	N2O	Amorphous	0.28	0.16
Average			0.29	0.17
9	N2O	Crystalline	0.58	0.27
10	N2O	Crystalline	0.61	0.28
Average			0.60	0.28

---

Once deposited, ices were irradiated using 2 keV electrons with projectile electrons impacting the target ices at angles of 36° to the normal over an area of 0.9 cm². The beam current and profile homogeneity were determined prior to commencing irradiation using the method described by Mifsud et al.,⁵² and an average flux of 4.5 × 10¹³ electrons cm⁻² s⁻¹ was used. Since the FT-IR spectroscopic beam covered an area of 1.1 cm², most (>80%) of the observed ice surface was directly irradiated. Electron irradiations were carried out at 20 K irrespective of the ice phase (i.e., both amorphous and crystalline ices were irradiated at 20 K) so as to exclude any increased mobility of radiolytically derived radicals due to higher temperatures, with FT-IR spectra collected at several intervals throughout the irradiations. As detailed in Table 2, multiple irradiations were performed for each solid ice phase so as to ensure good repeatability of the experiment.

CASINO simulations⁵⁵ revealed that impinging 2 keV electrons penetrate to a maximum depth of 0.22 and 0.13 μm within the CH₃OH and N₂O ices, respectively (Fig. 1). Given that the thicknesses of the deposited ices were significantly larger than this value, electrons were effectively implanted into the ice. This means that it is true to state that there exists an ‘active’ zone towards the surface of the ice in which the physico-chemical effects of electron irradiation are manifested. As such, it is often preferable to correct for the ‘inactive’ zone which is observed spectroscopically but does not play host to any radiation chemistry or physics so as to better illustrate the physico-chemical changes occurring within the ‘active’ zone of the ice.

Fig. 1 Results of CASINO simulations showing the integrated 2 keV electron count as a function of penetration depth into amorphous (solid traces) and crystalline (dashed traces) CH₃OH (blue traces) and N₂O (red traces) ices. Electrons were simulated to impact the ices at 36° to the normal.

In this study, we have made use of a correction factor when analysing CH₃OH and N₂O column densities so as to exclude as much as possible the diluting effect of the ‘inactive’ zones within these ices. To do this, measured column densities were first normalised to the column density measured prior to commencing irradiation. The normalised column density, N_n, was then converted to a corrected normalised column density, N_c, by means of applying eqn (3):

where N_p refers to the plateau or asymptotic value that the column density of the parent ice reaches after prolonged irradiation as a result of its rates of radiation-induced production and destruction being equal (i.e., the so-called ‘steady state’). To calculate N_p, we plotted N_n as a function of fluence for each irradiated ice and fitted an exponential decay function to the data. From the equation of this exponential decay function, we calculated the N_n value which would be reached after supplying a theoretical fluence of 1.0 × 10²⁰ electrons cm⁻² (four orders of magnitude higher than what was actually supplied in this study), and assumed this to be equal to N_p. This assumption is justified by the fact that the value for N_n calculated for a fluence of 1.0 × 10²⁰ electrons cm⁻² (which we have taken to be N_p) is equal to that calculated for a fluence of 1.0 × 10¹⁹ electrons cm⁻² for all ices considered, indicating that the steady state would have indeed been reached by this fluence. We wish to draw attention to the fact that this correction factor has only been applied to the CH₃OH and N₂O parent ices, and not to any radiolytically derived product molecules.

3 Results and discussion

3.1 Radiation-induced decay of amorphous and crystalline ices

In this study, the amorphous and crystalline phases of pure CH₃OH and N₂O astrophysical ice analogues were irradiated using 2 keV electrons at 20 K. As shown in Fig. 2, the radiolytic decay rate of CH₃OH was found to be more rapid in the case of the amorphous ice compared to the crystalline one. Conversely, the radiolytic decay trend of the amorphous and crystalline N₂O ices were observed to be more similar to each other, although that of the amorphous phase was still more rapid than that of the crystalline one. In an effort to quantify the difference in or similarity between the radiolytic decay functions of the irradiated amorphous and crystalline ice phases, the weighted Jaccard coefficient J_w (also referred to as the Tanimoto coefficient) was computed.^56,57 For two real, non-zero measurable functions f and g measured over a given parameter space (in this instance, electron fluence φ), J_w is given as:

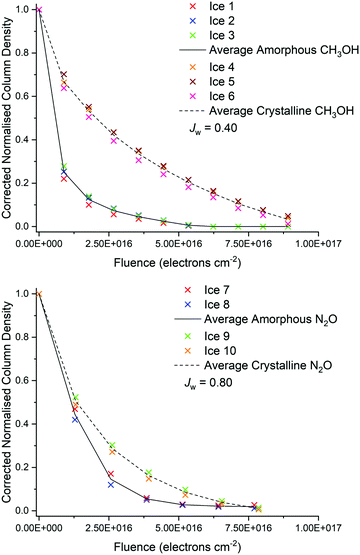Fig. 2 Electron-induced decay of CH₃OH (above) and N₂O (below) ice phases with increasing electron fluence.

As such, J_w varies between 0 and 1, with the latter indicating identical functions and the former indicating no statistical similarity whatsoever. For the interpolated electron-induced decay rate data presented in Fig. 2, J_w was calculated to be 0.40 in the case of CH₃OH, and 0.80 in the case of N₂O. These results suggest that, although statistical differences do exist between the decay rates of the amorphous and crystalline phases of both molecular species, they are significantly more pronounced in the case of CH₃OH than they are in the case of N₂O.

To quantify further, upon supplying an electron fluence of 8.9 × 10¹⁵ electrons cm⁻², the CH₃OH column density in the ‘active’ zone of the amorphous ice dropped to an average 25% of its original value, while for the crystalline ice this value, on average, only dropped to 67%. This phase-dependent decay of CH₃OH was apparent throughout the irradiation of the ices, with the amorphous ice requiring a fluence of 2.7 × 10¹⁶ electrons cm⁻² for the ‘active’ zone column density to drop below 10% of its initial value, while triple this fluence was needed to observe this effect in the crystalline phase. Conversely, the average decay trends for amorphous and crystalline N₂O were more similar (Fig. 2), with 44% and 52% of the N₂O in the ‘active’ zone remaining after a fluence of 1.3 × 10¹⁶ electrons cm⁻² had been respectively delivered to the amorphous and crystalline phases.

These observations may be rationalised in terms of the difference in the nature and extent of the intermolecular bonding present within the different ice phases of CH₃OH and N₂O and, by extension, the stability against radiolytic decay such bonding is able to offer. In the case of CH₃OH, the regularity of the crystalline lattice permits an extensive array of hydrogen-bonds which confers an additional degree of stability to the ice. This network of hydrogen-bonds then requires an increased supply of energy (i.e., dose) to be overcome, with some of the incident electrons’ kinetic energy being required for this purpose. The amorphous phase is not characterised by this extensive hydrogen-bonding network, and so there is more available energy which may be used for driving electron-induced radiolytic dissociation of this phase, leading to a more rapid initial depletion of CH₃OH parent molecules. It should be noted that, although some hydrogen-bonding between small molecular clusters is expected in the amorphous phase, this would not have the stabilising effect of the extensive lattice found in the crystalline phase, particularly in light of the fact that hydrogen-bonding in CH₃OH is known to be a co-operative phenomenon in which the presence of a hydrogen-bond in the array strengthens subsequent hydrogen-bonds via electrostatic effects.^58,59

The need to overcome the hydrogen-bonding network implies that the electron irradiation of the crystalline CH₃OH ice should result in a degree of localised amorphisation of the ice in the ‘active’ zone into which the projectile electrons penetrate.⁶⁰ This is observed in our acquired FT-IR spectra, particularly in the broad absorption band centred at around 3200 cm⁻¹ (Fig. 3). In the unirradiated crystalline ice, this band presents as a double peaked structure consisting of a defined, narrow higher wavenumber peak and a broader lower wavenumber peak. On the other hand, this band appears as a very broad single peaked structure in the pure amorphous phase. Upon the onset of electron irradiation of the crystalline CH₃OH ice (and particularly so after fluences of 4.5 × 10¹⁶ electrons cm⁻² have been delivered), however, this band is observed to broaden. The effect of this broadening is most visible in the narrower, higher wavenumber constituent peak (Fig. 3) and represents a localised transition to a less ordered ice structure. Once the hydrogen-bonding network has been disrupted, radiolytic dissociation of the CH₃OH molecules may take place more efficiently.

Fig. 3 The broadening of the double peaked FT-IR absorption band at about 3200 cm⁻¹ in crystalline CH₃OH ice as a result of electron irradiation is an indication of localised amorphisation. This broadening is most evident in the higher wavenumber constituent peak. Note that spectra are vertically shifted for clarity.

Given such results, the next point to consider is perhaps the possibility of a charged projectile not having sufficient energy to disrupt the hydrogen-bonding network and thus not induce any significant radiolytic dissociation of the CH₃OH crystalline phase that would otherwise occur in the amorphous phase. A similar scenario was considered by Bag et al.,⁶¹ who demonstrated that CH₂⁺ molecular ions with kinetic energies of <8 eV fired towards a D₂O target ice exhibited hydrogen-deuterium exchange reactions when the ice was amorphous, but not when it was crystalline. In terms of electrons as projectiles, although previous studies using lower energies (2.5–20 eV) have been performed, to the best of our knowledge all of these irradiations have been performed on an amorphous target CH₃OH ice.^{31–33,62,63} It would therefore be interesting to study the differences between the radiolysis of amorphous and crystalline CH₃OH ices when using a series of lower energy (<20 eV) electrons with the aim of reproducing the results of Bag et al.⁶¹ and of this present study.

The average radiolytic decay trend of amorphous and crystalline N₂O ices were observed to be significantly more similar than were the decay trends of amorphous and crystalline CH₃OH, as evidenced by their higher J_w value. Unlike in CH₃OH, no hydrogen-bonding network is present in solid N₂O. Instead, the dominant intermolecular interactions between adjacent N₂O molecules are weak dipole interactions and van der Waals forces. The large-scale orientation of molecular dipoles in the regular crystalline lattice confers an additional degree of stability against radiolytic decay. However, since dipole interactions are weaker than hydrogen-bonds, this increase in the resistance to radiolytic decay of crystalline N₂O ice compared to its amorphous phase is not as large as that of the crystalline CH₃OH ice compared to its amorphous phase. Once again, we note that some limited clustering due to orientation of dipoles is anticipated in the amorphous phase, particularly due to the known existence of gas-phase N₂O dimers, trimers, and tetramers.^64–66 Such molecular clusters are preserved during condensation and, indeed, the structure of the slipped parallel dimer (or an extension thereof) is thought to be key to the so-called ‘spontelectric’ (i.e., spontaneously electric) properties of condensed N₂O.^67–69

Our results therefore provide quantitative indications of the increased resistance to radiation-induced decay of crystalline ices compared to their amorphous phases. This resistance is the result of more extensive intermolecular forces of attraction in the regular crystalline lattice which must be overcome before molecular dissociation may take place. Stronger and more long-ranging intermolecular interactions, such as the hydrogen-bonding network in crystalline CH₃OH, are able to provide greater resistance than weaker ones, such as the molecular dipole interactions in N₂O. As such, we conjecture that the difference in the radiolytic decay trends of amorphous and crystalline ice phases should become negligible for those molecular species which are non-polar and should be more pronounced for those which exhibit very strong and extensive hydrogen-bonding networks in the crystalline phase.

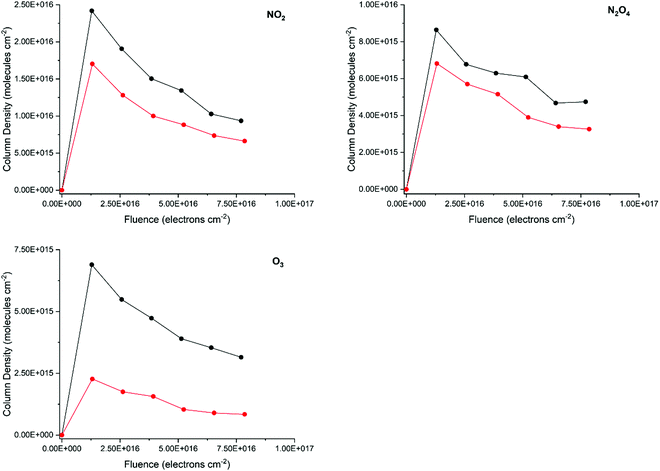
3.2 Radiation-induced chemistry

Previous studies have conclusively demonstrated that the chemistry occurring in ices as a result of their irradiation by ions or electrons is in fact driven by a cascade of tens of thousands of low-energy (<20 eV), non-thermal secondary electrons that are released along the track of the incident charged projectile.^62,63,70 In this study, we have also performed an analysis of the formation of radiation products after the irradiation of amorphous and crystalline pure CH₃OH and N₂O ices. Although we have documented the formation of many new molecular species as a result of the electron irradiation of these ices, we shall limit our discussion to the formation of those species that present well-defined and unambiguous absorption bands in the acquired FT-IR spectra (Fig. 4) and for which the integrated band strength constants are known. In the case of the electron-irradiated CH₃OH ices, these are CO, CO₂, H₂CO, and CH₄, while for the electron-irradiated N₂O ices these are NO₂, N₂O₄, and O₃.

Fig. 4 FT-IR absorption spectra of the unirradiated (black traces) and 2 keV electron-irradiated (red traces) amorphous and crystalline phases of CH₃OH and N₂O ice. In these spectra, the delivered fluences to the irradiated ices were 8.9 × 10¹⁶ and 1.3 × 10¹⁶ electrons cm⁻² for the CH₃OH and N₂O ices, respectively. Note also that spectra displayed in the same panel are vertically offset for clarity.

For both molecular species, the formation of products as a result of electron irradiation was greater after irradiation of the amorphous phase compared to the crystalline phase by a factor of between 1.25–3.00 at peak production, depending on the product considered (Fig. 5 and 6). Although it is perhaps intuitive to consider this to be the result of a more rapid dissociation of the parent molecular species in the amorphous phase, an additional contributing cause for this observation are the differences in the porosities and structural defects between amorphous and crystalline ices.

Fig. 5 Mean spectroscopically measured molecular column densities for the products of amorphous (black traces) and crystalline (red traces) CH₃OH irradiation by 2 keV electrons. Although CH₄ was detected in our post-irradiative crystalline CH₃OH FT-IR spectra, the quantities observed were below the limit of quantitation of our spectroscopic instruments. Note that lines joining the data points are not fits and are plotted only to guide the eye.

Fig. 6 Mean spectroscopically measured molecular column densities for the products of amorphous (black traces) and crystalline (red traces) N₂O irradiation by 2 keV electrons. Note that lines joining the data points are not fits and are plotted only to guide the eye.

At 20 K, radicals formed as a result of the radiolytic dissociation of the parent species are mobile within the ice matrix,^71,72 and may therefore diffuse and react with other radicals and molecules to form new species. In amorphous ices, the increase in porosity and structural defects compared to the corresponding crystalline phases allows for these radicals to diffuse more easily throughout the solid matrix.^7,73,74 As such, any recycling reactions leading back to the formation of the parent species are disfavoured due to the necessary radicals having migrated away from each other at the site of their radiolytic formation. With competition from such recycling reactions being lessened, reactions leading to the formation of new product molecules are favoured leading to a greater abundance of these species in the irradiated amorphous phases.

3.3 Astrochemical implications

Our experiments simulate the processing that interstellar icy grain mantles undergo as a result of their interaction with galactic cosmic rays, or of Solar System ices as a result of their interaction with the solar wind or giant planetary magnetospheric plasmas. Such astrophysical environments are known to allow for the cycling of molecular material through different solid phases via thermally-induced crystallisation and space radiation-induced amorphisation. For instance, although ices in dense, quiescent interstellar clouds are believed to be principally amorphous, those in stellar accretion discs are more likely to be crystalline.⁷⁵

Our results imply that those ices which are able to form strong and long-ranging intermolecular interactions (such as the hydrogen-bonds in CH₃OH) will exhibit a greater resistance to radiation-induced decay in their crystalline phase. Conversely, ices which only exhibit weak intermolecular interactions (such as the dipole interactions in N₂O) should exhibit a lesser resistance to radiation-induced decay on transitioning from the amorphous to the ordered, crystalline phase. This interpretation carries implications for assessing the survivability and residence times of different molecular species in various astrophysical radiation environments, and thus highlights the need for both experimental and modelling work in this area of research to take into account the phase of the molecular ice under consideration.

Our results have also demonstrated that, irrespective of the nature, strength, or extent of the intermolecular bonds present within a molecular ice, the amorphous phase is typically more chemically productive than the crystalline one. This has been attributed largely to the increased porosity and structural defects present within the amorphous phase which allow radiolytically generated radicals to diffuse away from the point of their formation more efficiently, thus promoting the formation of new molecules at the expense of the recombination of the parent molecule.^7,73,74 However, our results also suggest that the increased availability of radicals from the faster radiolytic decay rates of the amorphous ices is also likely to contribute to the more rapid accumulation of products in this phase.

The formation of complex organic molecules as a result of the irradiation of an interstellar ice which is rich in species capable of hydrogen-bonding is thus likely to be less productive once the ice has been crystallised as a result of thermal processing (for example, during stellar birth and evolution). As such, the formation of such complex organic molecules may occur to a greater extent in the earliest stages of dense interstellar cloud evolution (i.e., before stellar birth and evolution begin) or in those areas of the dense cloud which are not influenced by the thermal emission of young stellar objects. This idea is not unreasonable, particularly in light of the recent spate of discoveries of complex organic molecules in the pre-stellar cloud TMC-1.^76–79 It is expected that the recently launched NASA James Webb Space Telescope will allow researchers to map out the degree of crystallinity of interstellar and outer Solar System ices in unprecedented detail, thus permitting the influence of solid phase on the outcome of various astrochemical reactions to be further explored.⁸⁰

Lastly, we comment briefly on the experimental approach used in this study. This work is a typical example of a one-factor-at-a-time (OFAT) study, in which one experimental parameter (in this case, the phase of the ice under consideration) is varied and the results of such variation on the resultant physico-chemical evolution of the ice is analysed.⁸¹ It has been suggested that such OFAT studies may not be ideal in revealing the true chemical complexity of an astrochemical reaction or process, and that statistically designed experiments and systems science approaches may be more appropriate.⁸²

Nevertheless, we consider our use of an OFAT approach to be justified, as a great deal of chemical complexity related to the radiolysis of CH₃OH and N₂O ices has already been revealed by previous studies. Moreover, our primary aim in this present study was to determine whether any changes in the physico-chemical evolution of an astrophysical ice undergoing electron irradiation could be induced solely via a change in the phase of the ice, thus necessitating the adoption of an OFAT approach. The results of this study confirm the importance of considering the effect of ice phase in determining the outcome of a radiation astrochemistry experiment, and so highlight the need to build this parameter into more exhaustive systems astrochemistry experiments.⁸²

4 Conclusions

We have performed systematic and comparative 2 keV electron irradiations of the amorphous and crystalline phases of pure CH₃OH and N₂O astrophysical ice analogues under high-vacuum conditions at 20 K. Our results have revealed that the rate of electron-induced decay of amorphous CH₃OH is significantly more rapid than that of the crystalline phase, whereas smaller differences could be seen between the electron-irradiated amorphous and crystalline N₂O phases. We have attributed this observation to the fact that the crystalline CH₃OH phase is characterised by an extensive network of strong intermolecular hydrogen-bonds throughout the lattice, which does not exist to the same extent in the amorphous phase. As such, some of the incident electrons’ energy must be expended upon first disrupting this network of hydrogen-bonds before driving radiolytic chemistry. In contrast, the weak dipole interactions in N₂O are able to stabilise the crystalline phase to a much lesser degree compared to the amorphous phase, thus leading to a slightly faster radiation-induced decay rate in the latter.

Such results are of direct relevance to astrochemistry, and allow researchers in the experimental and modelling communities to make predictions as to the survivability of various molecules and the rapidity of astrochemical reactions in different astrophysical environments characterised by the competing processes of thermally-induced crystallisation of the ices and their space radiation-induced amorphisation. For example, we hypothesise that other molecular ices capable of forming strong and extensive hydrogen-bonding networks (such as H₂O, HF, or NH₃) should also exhibit slower radiation-induced decay rates in the crystalline phase when compared to the amorphous phase, while non-polar molecules (such as CH₄) will show negligible differences in the radiation-induced decay rates of their crystalline and amorphous phases. We believe that the results presented in this study constitute the most in-depth experimental analysis of the role played by the solid phase of an astrophysical ice in defining its radiation physics and chemistry to date, and anticipate that they may act as a good starting point for other studies seeking to further comprehend this topic.

Author contributions

The experiment was designed by Duncan V. Mifsud and Perry A. Hailey, and performed by Duncan V. Mifsud, Péter Herczku, Béla Sulik, Zoltán Juhász, Sándor T. S. Kovács, and Béla Paripás. Data analysis was carried out by Duncan V. Mifsud and Zuzana Kaňuchová. All authors contributed to the interpretation of the results, as well as to the preparation of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We acknowledge funding from the Europlanet 2024 RI which has been funded by the European Union Horizon 2020 Research Innovation Programme under grant agreement No. 871149. The main components of the experimental apparatus were purchased using funding obtained from the Royal Society through grants UF130409, RGF/EA/180306, and URF/R/191018.

Duncan V. Mifsud is the grateful recipient of a University of Kent Vice-Chancellor's Research Scholarship. The research of Zuzana Kaňuchová is supported by VEGA – the Slovak Grant Agency for Science (grant No. 2/0059/22) and the Slovak Research and Development Agency (contract No. APVV-19-0072). Sergio Ioppolo acknowledges the Royal Society for financial support. The research of Béla Paripás is supported by the European Union and the State of Hungary and is co-financed by the European Regional Development Fund (grant GINOP-2.3.4-15-2016-00004).

We would also like to thank Andrew M. Cassidy (University of Aarhus, Denmark) for the fruitful and stimulating discussions which allowed us to improve our manuscript.

References

1. G. M. Muñoz-Caro, U. J. Meierhenrich, W. A. Schutte, B. Barbier, A. Arcones Segovia, H. Rosenbauer, W. H. P. Thiemann, A. Brack and J. M. Greenberg, Nature, 2002, 416, 403.
2. M. Nuevo, Y.-J. Chen, T.-S. Yih, W.-H. Ip, H.-S. Fung, C.-Y. Cheng, H.-R. Tsai and C.-Y. R. Wu, Adv. Space Res., 2007, 40, 1628.
3. R. L. Hudson, M. H. Moore, J. P. Dworkin, M. P. Martin and Z. D. Pozun, Astrobiology, 2008, 8, 771.
4. M. Nuevo, S. N. Milam and S. A. Sandford, Astrobiology, 2012, 12, 295.
5. B. Sivaraman, B. N. Rajasekhar, D. Fulvio, A. Hunniford, R. W. McCullough, M. E. Palumbo and N. J. Mason, J. Chem. Phys., 2013, 139, 074706.
6. D. V. Mifsud, Z. Kaňuchová, S. Ioppolo, P. Herczku, A. Traspas Muiña, T. A. Field, P. A. Hailey, Z. Juhász, S. T. S. Kovács, N. J. Mason, R. W. McCullough, S. Pavithraa, K. K. Rahul, B. Paripás, B. Sulik, S.-L. Chou, J.-I. Lo, A. Das, B.-M. Cheng, B. N. Rajasekhar, A. Bhardwaj and B. Sivaraman, J. Mol. Spectrosc., 2022, 385, 111599.
7. G. A. Grieves and T. M. Orlando, Surf. Sci., 2005, 593, 180.
8. W. Zheng, D. Jewitt and R. I. Kaiser, Chem. Phys. Lett., 2007, 435, 289.
9. T. M. Orlando and M. T. Sieger, Surf. Sci., 2003, 528, 1.
10. D. Bockelée-Morvan, P. Colom, J. Crovisier, D. Despois and G. Paubert, Nature, 1991, 350, 318.
11. P. Eberhardt, R. Meier, D. Krankowsky and R. R. Hodges, Astron. Astrophys., 1994, 288, 315.
12. D. P. Cruikshank, T. L. Roush, M. J. Bartholomew, T. R. Geballe, Y. J. Pendleton, S. M. White, J. F. Bell III, J. K. Davies, T. C. Owen, C. de Bergh, D. J. Tholen, M. P. Bernstein, R. H. Brown, K. A. Tryka and C. M. Dalle Ore, Icarus, 1998, 135, 389.
13. K. M. Pontopiddan, E. Dartois, E. F. van Dishoeck, W.-F. Thi and L. d’Hendecourt, Astron. Astrophys., 2003, 404, L17.
14. E. M. Penteado, A. C. A. Boogert, K. M. Pontopiddan, S. Ioppolo and H. M. Cuppen, Mon. Not. R. Astron. Soc., 2015, 454, 531.
15. D. An, K. Sellgren, A. C. A. Boogert, S. V. Ramírez and T.-S. Pyo, Astrophys. J., Lett., 2017, 843, L36.
16. N. Watanabe and A. Kouchi, Astrophys. J., 2002, 571, L173.
17. K.-J. Chuang, G. Fedoseev, S. Ioppolo, E. F. van Dishoeck and H. Linnartz, Mon. Not. R. Astron. Soc., 2016, 455, 1702.
18. R. L. Hudson and M. H. Moore, Icarus, 1999, 140, 451.
19. A. Wada, N. Mochizuki and K. Hiraoka, Astrophys. J., 2006, 644, 300.
20. G. W. Fuchs, H. M. Cuppen, S. Ioppolo, C. Romanzin, S. E. Bisschop, S. Andersson, E. F. van Dishoeck and H. Linnartz, Astron. Astrophys., 2009, 505, 629.
21. D. Qasim, K.-J. Chuang, G. Fedoseev, S. Ioppolo, A. C. A. Boogert and H. Linnartz, Astron. Astrophys., 2018, 612, A83.
22. L. M. Ziurys, A. J. Apponi, J. M. Hollis and L. E. Snyder, Astrophys. J., 1994, 436, L181.
23. N. F. W. Ligterink, H. Calcutt, A. Coutens, L. E. Kristensen, T. L. Bourke, M. N. Drozdovskaya, H. S. P. Müller, S. F. Wampfler, M. H. D. van der Wiel, E. F. van Dishoeck and J. K. Jørgensen, Astron. Astrophys., 2018, 619, A28.
24. S. Ioppolo, Z. Kaňuchová, R. L. James, A. Dawes, N. C. Jones, S. V. Hoffmann, N. J. Mason and G. Strazzulla, Astron. Astrophys., 2020, 641, A154.
25. C. R. Ponciano, R. Martinez, L. S. Farenzena, P. Iza, M. G. P. Homem, A. Naves de Brito, K. Wien and E. F. da Silveira, J. Mass Spectrom., 2008, 43, 1521.
26. P. Boduch, A. Domaracka, D. Fulvio, T. Langlinay, X. Y. Lv, M. E. Palumbo, H. Rothard and G. Strazzulla, Astron. Astrophys., 2012, 544, A30.
27. M. E. Palumbo, A. C. Castorina and G. Strazzulla, Astron. Astrophys., 1999, 342, 551.
28. P. Modica, M. E. Palumbo and G. Strazzulla, Planet. Space Sci., 2012, 73, 425.
29. Y.-J. Chen, A. Ciaravella, G. M. Muñoz-Caro, C. Cecchi-Pestellini, A. Jiménez-Escobar, K.-J. Chuang and T.-S. Yih, Astrophys. J., 2013, 778, 162.
30. C. J. Bennett, S.-H. Chen, B.-J. Sun, A. H. H. Chang and R. I. Kaiser, Astrophys. J., 2007, 660, 1588.
31. M. D. Boamah, K. K. Sullivan, K. E. Shulenberger, C. M. Soe, L. M. Jacob, F. C. Yhee, K. E. Atkinson, M. C. Boyer, D. R. Haines and C. R. Arumainayagam, Faraday Discuss., 2014, 168, 249.
32. F. Schmidt, P. Swiderek and J. H. Bredehöft, ACS Earth Space Chem., 2021, 5, 391.
33. C. R. Arumainayagam, R. T. Garrod, M. C. Boyer, A. K. Hay, S.-T. Bao, J. S. Campbell, J. Wang, C. M. Nowak, M. R. Arumainayagam and P. J. Hodge, Chem. Soc. Rev., 2019, 48, 2293.
34. B. Sivaraman, S. Ptasinska, S. Jheeta and N. J. Mason, Chem. Phys. Lett., 2008, 460, 108.
35. G. C. Almeida, S. Pilling, A. L. F. de Barros, C. A. P. da Costa, R. C. Pereira and E. F. da Silveira, Mon. Not. R. Astron. Soc., 2017, 471, 1330.
36. D. Fulvio, G. A. Baratta, B. Sivaraman, N. J. Mason, E. F. da Silveira, A. L. F. de Barros, O. Pandoli, G. Strazzulla and M. E. Palumbo, Mon. Not. R. Astron. Soc., 2019, 483, 381.
37. P. R. B. Oliveira, R. Martinez, D. Fulvio and E. F. da Silveira, Mon. Not. R. Astron. Soc., 2021, 502, 1423.
38. A. L. F. de Barros, E. F. da Silveira, D. Fulvio, P. Boduch and H. Rothard, Mon. Not. R. Astron. Soc., 2017, 465, 3281.
39. G. S. Parks, J. Am. Chem. Soc., 1925, 47, 338.
40. A. B. Dempster and G. Zerbi, J. Chem. Phys., 1971, 54, 3600.
41. B. H. Torrie, S.-X. Weng and B. M. Powell, Mol. Phys., 1989, 67, 575.
42. B. H. Torrie, O. S. Binbrek, M. Strauss and I. P. Swainson, J. Solid State Chem., 2002, 166, 415.
43. S. Lucas, D. Ferry, B. Demirdjian and J. Suzanne, J. Phys. Chem. B, 2005, 109, 18103.
44. Ó. Gálvez, B. Maté, B. Martín-Llorente, V. J. Herrero and R. Escribano, J. Phys. Chem. A, 2009, 113, 3321.
45. S. Ioppolo, B. A. McGuire, M. A. Allodi and G. A. Blake, Faraday Discuss., 2014, 168, 461.
46. B. A. McGuire, S. Ioppolo, M. A. Allodi and G. A. Blake, Phys. Chem. Chem. Phys., 2016, 18, 20199.
47. R. L. Hudson, M. J. Loeffler and P. A. Gerakines, J. Chem. Phys., 2017, 146, 024304.
48. B. Kuchta, R. D. Etters and R. LeSar, J. Chem. Phys., 1992, 97, 5662.
49. H. G. Carlson and E. F. Westrum Jr., J. Chem. Phys., 1971, 54, 1464.
50. K. J. Tauer and W. N. Lipscomb, Acta Crystallogr., 1952, 5, 606.
51. P. Herczku, D. V. Mifsud, S. Ioppolo, Z. Juhász, Z. Kaňuchová, S. T. S. Kovács, A. Traspas Muiña, P. A. Hailey, I. Rajta, I. Vajda, N. J. Mason, R. W. McCullough, B. Paripás and B. Sulik, Rev. Sci. Instrum., 2021, 92, 084501.
52. D. V. Mifsud, Z. Juhász, P. Herczku, S. T. S. Kovács, S. Ioppolo, Z. Kaňuchová, M. Czentye, P. A. Hailey, A. Traspas Muiña, N. J. Mason, R. W. McCullough, B. Paripás and B. Sulik, Eur. Phys. J. D, 2021, 75, 182.
53. R. Luna, G. Molpeceres, J. Ortigoso, M. A. Satorre, M. Domingo and B. Maté, Astron. Astrophys., 2018, 617, A116.
54. C. S. Jamieson, C. J. Bennett, A. M. Mebel and R. I. Kaiser, Astrophys. J., 2005, 624, 436.
55. D. Drouin, A. R. Couture, D. Joly, X. Tastet, V. Aimez and R. Gauvin, Scanning, 2007, 29, 92.
56. P. Jaccard, Bull. Soc. Vaudoise Sci. Nat., 1908, 44, 223.
57. R. Real and J. M. Vargas, Syst. Biol., 1996, 45, 380.
58. H. Kleeberg and W. A. P. Luck, Z. Phys. Chem., 1989, 270, 613.
59. A. K. Sum and S. I. Sandler, J. Phys. Chem. A, 2000, 104, 1121.
60. R. L. Hudson and M. H. Moore, Radiat. Phys. Chem., 1995, 45, 779.
61. S. Bag, R. G. Bhuin and T. Pradeep, J. Phys. Chem. C, 2013, 117, 12146.
62. M. C. Boyer, N. Rivas, A. A. Tran, C. A. Verish and C. R. Arumainayagam, Surf. Sci., 2016, 652, 26.
63. K. K. Sullivan, M. D. Boamah, K. E. Shulenberger, S. Chapman, K. E. Atkinson, M. C. Boyer and C. R. Arumainayagam, Mon. Not. R. Astron. Soc., 2016, 460, 664.
64. M. Dehghani, M. Afshari, Z. Abusara, N. Moazzen-Ahmadi and A. R. W. McKellar, J. Chem. Phys., 2007, 126, 164310.
65. R. E. Miller and L. Pederson, Chem. Phys. Lett., 1997, 275, 307.
66. R. E. Miller and L. Pederson, J. Chem. Phys., 1998, 108, 436.
67. O. Plekan, A. Cassidy, R. Balog, N. C. Jones and D. Field, Phys. Chem. Chem. Phys., 2011, 13, 21035.
68. D. Field, O. Plekan, A. Cassidy, R. Balog, N. C. Jones and J. Dunger, Int. Rev. Phys. Chem., 2013, 32, 345.
69. O. Plekan, A. Rosu-Finsen, A. M. Cassidy, J. Lasne, M. R. S. McCoustra and D. Field, Eur. Phys. J. D, 2017, 71, 162.
70. N. J. Mason, B. Nair, S. Jheeta and E. Szymańska, Faraday Discuss., 2014, 168, 235.
71. W. Zheng, D. Jewitt and R. I. Kaiser, Astrophys. J., 2006, 639, 534.
72. W. Zheng, D. Jewitt and R. I. Kaiser, Astrophys. J., 2006, 648, 753.
73. K. Isokoski, J.-B. Bossa, T. Triemstra and H. Linnartz, Phys. Chem. Chem. Phys., 2014, 16, 3456.
74. G. Stechauner and E. Kozeschnik, J. Mater. Eng. Perform., 2014, 23, 1576.
75. C. A. Poteet, S. T. Megeath, D. M. Watson, N. Calvet, I. S. Remming, M. K. McClure, B. A. Sargent, W. J. Fischer, E. Furlan, L. E. Allen, J. E. Bjorkman, L. Hartmann, J. Muzerolle, J. J. Tobin and B. Ali, Astrophys. J., Lett., 2011, 733, L32.
76. A. M. Burkhardt, K. L. K. Lee, P. B. Changala, C. N. Shingledecker, I. R. Cooke, R. A. Loomis, H. Wei, S. B. Charnley, E. Herbst, M. C. McCarthy and B. A. McGuire, Astrophys. J., Lett., 2021, 913, L18.
77. K. L. K. Lee, R. A. Loomis, A. M. Burkhardt, I. R. Cooke, C. Xue, M. A. Siebert, C. N. Shingledecker, A. Remijan, S. B. Charnley, M. C. McCarthy and B. A. McGuire, Astrophys. J., Lett., 2021, 908, L11.
78. K. L. K. Lee, P. B. Changala, R. A. Loomis, A. M. Burkhardt, C. Xue, M. A. Cordiner, S. B. Charnley, M. C. McCarthy and B. A. McGuire, Astrophys. J., Lett., 2021, 910, L2.
79. J. Cernicharo, C. Cabezas, M. Agúndez, B. Tercero, J. R. Pardo, N. Marcelino, J. D. Gallego, F. Tercero, J. A. López-Pérez and P. de Vicente, Astron. Astrophys., 2021, 648, L3.
80. J. Kalirai, Contemp. Phys., 2018, 59, 251.
81. V. Czitrom, Am. Stat., 1999, 53, 126.
82. N. J. Mason, P. A. Hailey, D. V. Mifsud and J. S. Urquhart, Front. Astron. Space Sci., 2021, 8, 739046.

---