Electrochemical evaluation of the de-/re-activation of oxygen evolving Ir oxide

Abstract

Understanding the influence of dynamic and stationary polarization on the deactivation of state-of-the-art IrO_x catalysts is imperative for the design and operation of robust and efficient proton exchange membrane water electrolyzers. In this work, the deactivation and activity regeneration of a commercial IrO_x catalyst were investigated under potentiodynamic and potentiostatic conditions in acidic media using rotating disk electrode and electrogravimetry methods. Systematic electrochemical protocols were designed to decouple reversible from irreversible activity losses. Cyclic voltammetry provided a metric of the active surface area and traced the charge growth under different oxygen evolution reaction conditions. A direct log t dependent charge growth is observed, accompanied by the same fractional kinetic activity decay under potentiodynamic conditions. The loss is essentially recoverable after electrochemical reductive treatment, however at the expense of mild material dissolution. In contrast, an extended potentiostatic operation induced irreversible intrinsic degradation after a critical time (0.5–1 h), accompanied by stability enhancement. This irreversible deactivation is attributed to a gradual transformation of the hydrated IrO_x to a dehydrated condensed oxide. Our results suggest that Ir dissolution during the regenerative treatment is not prohibitive, as long as the low potential modulations are not frequent.

---

Introduction

Hydrogen is indispensable for a sustainable, carbon-neutral, energy supply. Thus, hydrogen production via a PEMWE is preferable among the different water electrolysis technologies, for direct coupling with the intermittent and fluctuating renewable energy sources, due to its flexible operating characteristics.^1,2 However, the highly acidic environment necessitates the usage of corrosion resistant noble metal-based catalysts. Although Pt loading in the cathode can be minimized,³ the anode environment is much more demanding. So far, only Ir based catalysts can offer acceptable OER kinetics, in conjunction with a sufficient corrosion resistance.^4,5 As highly conductive and corrosion resistant anode supports are yet to be found,⁶ unsupported Ir and its oxides are employed in PEMWE anodes,^7,8 which accommodate high loadings to achieve high performance and acceptable degradation.^3,9,10 Therefore, the scarcity and high cost of Ir challenge the deployment of PEMWEs on a large scale.³

Enhancing the activity and durability can partly compensate for the investment cost of PEMWEs and help in the direction of reducing Ir loading. Among Ir surfaces, the activity decreases and the resistance to dissolution increases from metals to hydrous oxides to crystalline oxides.¹¹ However, the active surface dynamically responds to the OER conditions. It reconstructs in response to the oxidative electrochemical potential,¹² as well as to the operating protocol, when stationary or dynamic potential excursions to low potentials are involved, which can be frequently encountered during the PEMWE operation.^7–10 Depending on the starting material, different surface transformations may occur. Metallic Ir surfaces are oxidized under stationary OER conditions to eventually form a rutile IrO₂ surface at long polarization times,^13,14 whereas fast potential cycling between oxidative and reductive potentials results in the formation of thick, highly hydrated IrO_x over-layers.^15,16 However, the thick over-layers are prone to dissolution at a high anodic polarization (>1.65 V).¹⁷ In addition, the OER activity declines with time, ascribed to the formation of crystalline IrO₂,¹³ which displays one order of magnitude lower intrinsic activity,¹⁸ but higher stability than that of hydrous surfaces.¹⁹

Due to the four electrons transferred in the OER, several mechanisms can be operative.^20,21 Lately, with the help of DFT calculations,^22,23 there is a general consent that the OER on Ir oxides proceeds via a peroxo-mechanism.^22–24 However, the role of the active surface and the speciation of the active site are under discussion. The superior OER activity of hydrated over-layers is attributed to their disordered hydrous (OH/H₂O) structure with a mixed Ir valence, +3/+4.^17,25 Because of the flexibility of Ir in accommodating different oxidation states (+3 to +5) and promoting the OER electro-catalytic cycle,²⁶ Ir is considered as the active site, while even higher Ir oxidation states have been suggested.^27,28 On the other hand, an oxygen absorption pre-edge feature on electrochemically oxidized Ir nanoparticles was assigned to electron-deficient oxygen, proposed as the active site.²⁵ Because of the covalent Ir–O bond character and the sharing of electrons and holes, it is likely that both centers are oxidized and participate in the O–O bond formation.^24,25,29

The intensive transient dissolution of Ir based surfaces in aqueous electrolytes, in comparison to that under stationary OER conditions,^5,16 is not translated to intensive degradation in PEMWEs with the currently employed high Ir loadings (≥1 mg cm⁻²).^7–9 In fact, the performance losses are less severe under dynamic operation, rather than under stationary operation,^7,8 being essentially reversible. This type of deactivation is attributed to mass transport issues in PEMWEs,⁷ and the influence of micro-bubbles in liquid electrolyte half-cells.³⁰ The reversible deactivation in state-of-the-art nanocrystalline IrO_x anodes in a dynamically operated PEMWE single cell is significantly lower in comparison to the stationary operation.⁸ This was attributed to the influence of transient negative currents upon fast cathodic potential sweeping to the apparent OER onset, whereas lower potential values were required to achieve the full recovery. It was long ago recognized that a part of the OER activity decay of hydrous IrO_x overlayers can be recovered by low potential excursions.¹⁷ Recently, the reversible OER deactivation was traced with Ir foils,³¹ and Ir and hydrous IrO_x nanoparticles,¹⁴ partly recoverable by cathodic reduction. The irreversible decay was hypothesized to arise by a loss of active sites capable of forming the Ir=O species via progressive cross-linking of Ir sites by bridging μ-oxides.³¹

Despite the gap in the stability between aqueous electrolyte half-cells and PEMWEs,^32,33 measurements in half-cells are a fast and easy way to assess the mechanistic information at short times.²⁴ The 1–2 orders of magnitude lower catalyst loadings employed in half-cell studies, with respect to those commonly used in PEMWEs, result in comparable operating voltages, despite the 1–2 orders of magnitude higher geometric current densities in PEMWEs.³⁰ Meanwhile, using an eQCM is a useful electro-analytical technique, because of its high mass sensitivity, suitable for monitoring electrochemical reactions involving mass changes at or very near the electrode surface. Valuable information can be extracted from the combination of electrochemistry and eQCM regarding the nature and mechanism of electrochemical processes.³⁴ The eQCM has been widely used to study the deposition of metals,³⁵ dissolution,³⁶ and the injection and expulsion of anions onto and from the catalyst surface during an electrochemical reaction.³⁷ Juodkazyte et al. investigated the electrogravimetric profiles of the thermally formed Ir layer and assigned the main pair of voltammetric peaks above 0.8 V in acidic media to the transition Ir(0) to Ir(IV),³⁸ showcasing the formation of gel-like hydrous oxide layers on the metal surface.³⁹ This behavior agrees with the observations of Birss et al.,^40,41 who also showed the participation of solution anions in the injection/expulsion of protons during the reduction/oxidation of the hydrous IrO_x/Ir films. The involvement of H⁺/H₂O species during the charging/discharging capacitive process of a SnO₂–IrO₂ catalyst highlighted the importance of catalyst hydration and dehydration,⁴² which is in agreement with the recent evidence of H₂O uptake during the potential cycling of commercial IrO₂ powders.⁴³

In this work, the OER deactivation under potentiodynamic and potentiostatic conditions and the activity restoration upon the electrochemical reductive treatment of a, well-characterized,⁴⁴ state-of-the-art commercial IrO_x catalyst are investigated in half-cells using RDE and eQCM techniques. The structure of the manuscript is as follows. First, the OER de-/re-activation under potentiodynamic conditions is presented, along with its association with the charge growth. Then, the influence of the regenerative cathodic potential is provided, followed by the influence of time under potentiodynamic and potentiostatic OER conditions on the activity decay. Finally, the stability trends regarding the different operating modes are discussed. The well-defined deactivation profiles, in conjunction with the information from the in situ mass changes, and the quantification of the amount of Ir dissolved provide valuable insights into the understanding of deactivation phenomena and the development of suitable operating strategies of PEMWEs.

Experimental

Unsupported Ir oxide (Alfa Aesar, Premion, 84.5% Ir, product number 43396) was used in all electrochemical measurements, hereafter denoted as IrO_x, due to the high percentage of surface Ir in the +3 oxidation state.^8,44 The supporting electrolyte was 0.1 M H₂SO₄, prepared from 96% H₂SO₄, Suprapur®, Supelco. RDE studies were performed in a PTFE based three-electrode cell (180 ml electrolyte volume) at room temperature. The RHE (Hydroflex®, Gaskatel) was connected via a home-made PEEK based Luggin capillary, placed 1 mm below the edge of the active area (0.196 cm²) of the PEEK based RDE tip (Origalys). The RHE was frequently calibrated against a Pt mesh dipped in the same electrolyte under H₂ purging. The Pt mesh counter electrode was separated from the working electrode by a NAFION 115 membrane and sealed with a Viton O-ring, to suppress cross-contamination by metal dissolved species. Aliquots of 2 ml were sampled and replaced by 2 ml of the fresh electrolyte for post-test analysis via ICP-MS (PlasmaQuant MS Elite, AnalytikJena). A five-point (3, 1, 0.1, 0.05, and 0 ppb) calibration was performed at the beginning of each series of ICP-MS measurements. An additional Ir standard solution was prepared and measured after every 3–5 sample measurements to detect and correct the possible drifts of the device signal. Electrochemical measurements were performed using two potentiostats (Autolab PGSTAT302, AUT72731, staircase voltammetry and Solartron 1287, linear ramp voltammetry), always with a rotation (≥3600 rpm). Staircase voltammograms were acquired with two different sampling parameter values (α = 1 and 0.3). The electrolyte was purged with N₂ (O₂ purging also inspected). The catalyst was dispersed in a water/isopropanol mixture (≈80 : 20 vol), sonicated for 20 min, followed by horn-sonication for 30 s. 10 μl was immediately drop-casted on the RDE substrate, prior polished with 0.3 μm alumina, to provide 10–50 μg cm⁻² nominal IrO_x loading per geometric area. The solvent was dried under environmental conditions by rotation (200 rpm). The Nafion ionomer suspension (LIQUION, 1100 EW, 5 wt%, Ion Power) was diluted with a 1 : 1 water/isopropanol mixture, sonicated for 15 min, drop-casted (10 μl) atop the catalyst film, and dried as above, to provide 5–10 wt% dry ionomer loading. The ionomer served as a H⁺ conducting binder, in order to adhere and stabilize the catalyst film on the substrate. The absence of the ionomer resulted in severe detachment under OER conditions. The ionomer was drop-casted atop the catalyst film to avoid the blockage of the electron percolation pathways to/from the substrate, a situation that might be encountered in mixed catalyst/ionomer inks at high ionomer loadings.³²

Two different flow cells were coupled using an eQCM (10M, Gamry) and an ICP-OES (Spectroblue, Ametek), the former to record mass changes during electrochemical measurements and the latter to follow on-line catalyst dissolution. The eQCM flow cell was equipped with a Pt hollow rod as the counter electrode and Ag/AgCl as the reference electrode. The catalyst inks were prepared by mixing 5 mg of catalyst in 1 ml of H₂O. After 30 min sonication, 4 μl containing 20 μg of catalyst was drop-casted onto a 100 nm thick Au layer deposited on the 5 MHz eQCM discs with an electroactive area of 0.2 cm². Upon oven drying at 50 °C for 10 min, a drop of the Nafion ionomer was casted on the top of the catalyst to obtain a Nafion-to-catalyst mass ratio of 0.17, followed by oven drying at 50 °C for another 30 min. Thereafter, the eQCM discs were inserted into the eQCM flow cell. A similar procedure was followed to apply the catalyst film on the 0.196 cm² Au pellet, previously polished with fine 1 and 0.05 μm alumina powder. After ultra-sonication for 15 min in MilliQ water, the pellet was mounted on a special sample holder and inserted into the ICP-OES flow cell. The details of the ICP-OES flow cell and the ICP-OES measuring system and the calibration procedure were given elsewhere.^45,46 All electrochemical measurements in both flow cells were performed using a Gamry 1010E interface at room temperature.

Similar electrochemical protocols were applied in all types of half-cells. They comprised initial CVs (0.4–1.4 V, 50 mV s⁻¹) that served as the reference for comparing with the CV measurements subsequent to OER studies. CVs with different LPLs (0.04, 0.4, 0.6, 0.8, and 1 V) were added, when the respective CVs were pursued after the OER. The CV charge (0.4–1.4 V, 50 mV s⁻¹) was a metric of the ECSA. After the pre-testing phase and prior to OER studies, EIS at 1.3 V (5 mV rms) was performed for the electrolyte resistance, which was utilized for on-line iR compensation or post-test iR correction. In the flow through cells, the OER activity was evaluated by three CV cycles (5 mV s⁻¹, 1.3–1.6 V, RHE), followed by base CVs without the current interruption. In the RDE setup, the OER cycles were performed at 2 mV s⁻¹, in a measured potential window of 1.3–1.8 V (an upper iR free potential of 1.63–1.69 V, RHE, post-test corrected). During the third cathodic sweep, the current was interrupted at 1.45 V, followed by three base CV cycles (5 or 50 mV s⁻¹) with the chosen LPL, before resettling the aforementioned measuring sequence (EIS-OER-CV). A representative potential profile of the potentiodynamic protocol is shown in Fig. 1(a). An experiment with an increased number of OER cycles was also performed to inspect the influence of time under potentiodynamic conditions on the OER activity.

Fig. 1 Representative potential profiles vs. the time of the experimental protocols applied to study IrO_x de-/re-activation during (a) potentiodynamic OER cycles (2 mV s⁻¹, 1.3–1.8 V as measured, post-test iR correction shown in the figure) and (b) interim potentiostatic operation at 1.575 V, RHE (iR compensated).

The protocol adopted to study the de-/re-activation under stationary operating conditions was similar to the potentiodynamic protocol, but the OER cycles replaced by potential ramps to iR compensated 1.55 or 1.575 V, RHE, with 5 or 10 mV s⁻¹, respectively, and holds for different times (5 s–3 h). After every stationary interim, CV was applied without the current interruption down to 0.4 V (Fig. 1(b)), followed by a base voltammogram to detect ECSA losses. The OER sweeps, as in the potentiodynamic protocol, were measured before and after the potentiostatic interims to discriminate reversible and irreversible degradation modes induced by the interim stationary operations.

Results and discussion

Electrochemical de-/re-activation under potentiodynamic conditions

The OER activity decays with the number of OER cycles, i.e. with time under potentiodynamic OER conditions, as shown in Fig. 2(a). The most significant activity loss occurs during (after) the first anodic sweep, being essentially recoverable after sweeping down to 0.4 V (Fig. 2(b) and Fig. S1 in the ESI†) and subsequently to 0.04 V (Fig. S2, ESI†). The deactivation is accompanied by cathodic charge growth (Fig. 2(b), defined as Δq = q_c,i − q_c,f, i.e. the charge difference of the first few from the final cathodic sweeps), the majority of which is located below ca. 1.35 V and over a well-defined cathodic peak at ca. 0.75–0.8 V. The cathodic peak at ca. 1.1 V is due to the reduction of the Au surface oxide, which is formed mostly during the first anodic OER sweep (Fig. S3, ESI†). Its contribution to the cathodic charge can be subtracted, as it is superpositioned on the pseudo-capacitive contributions of IrO_x (comparison with a glassy carbon substrate in Fig. S4, ESI†). The influence of the reduction of the gas phase O₂ and/or of O₂ micro-bubbles entrapped in the catalyst film,³⁰ on the cathodic charge is negligible, if any, down to 0.4 V (Fig. S5 and S6 in the ESI†). Control experiments with O₂ purging (Fig. S5, ESI†) showed that the ORR is not favored on the IrO_x surface; instead, it comes from the exposed to the electrolyte Au surface and becomes significant below 0.4 V (see Fig. 3(b) below).

Fig. 2 (a) Current density in the logarithmic scale vs. post-test corrected iR free potential, RHE, during ten (black) and three (red) potentiodynamic OER cycles (2 mV s⁻¹, 1.3–1.8 V as measured). Dashed arrows show the sweeping direction, and solid arrows show the activity decay. (b) The first three CV cycles (50 mV s⁻¹, 1.45–0.4 V, α = 1) after interrupting the OER at 1.45 V, RHE, cathodic, and t_OCP ≈ 15 s (after 10 OER cycles, black, and after 3 OER cycles, red). The current is normalized to the charge of the third CV cycle (as measured current densities in Fig. S1 in the ESI†). RDE, N₂ purging, 50 μg cm⁻² IrO_x nominal, 5% wt ionomer, Au tip.

Fig. 3 (a) Mass variation (left y-axis, black line) and current response in the logarithmic scale (right y-axis, red line) against the potential during OER sweeping (1.3–1.6 V, RHE, 5 mV s⁻¹, first full cycle). (b) Subsequent two CV cycles (1.4–0.04 V, RHE, 5 mV s⁻¹, right y-axis, red solid and orange dashed lines), measured after three OER cycles without the current interruption, and respective mass variations (left y-axis, black and grey) against the potential. (c) Mass variations over the CV charge (absolute integration) corresponding to the CVs in (b). 20 μg of IrO_x and the eQCM flow cell.

The associated mass changes during a full OER cycle (Fig. 3(a)) and the subsequent first two CV cycles down to 0.04 V (Fig. 3(b)) were investigated by electrogravimetry. A faster sweeping (5 mV s⁻¹) and a lower upper potential (1.6 V, RHE) were chosen in the potentiodynamic OER cycles compared to the RDE (Fig. 2(a)) to minimize the influence of bubbles formation on the eQCM frequency response.³⁴ Interpreting the eQCM response of a porous layer deposited from an ink can be challenging.⁴³ The frequency variation during potential cycling could arise from changes in the viscoelastic properties of the film, detachment of particles, local density changes, or chemical changes to the film.^34,43 However, only small (in the order of ng), but measurable dissolution could be detected during CV and OER measurements by on line ICP-OES and batch mode ICP-MS (see Table 1 further below). Therefore, the frequency response of the eQCM (in the order of 100–600 Hz, equivalent to 0.4–2.2 μg, Fig. 3(b)) can be mostly associated with potential dependent surface reactions at the potential windows investigated (see Fig. S7 and S8 and respective discussion in the ESI†).

Table 1 Dissolved Ir mass and percentage with regard to the nominal Ir loading, the average intrinsic dissolution rate and stability number for different operating schemes. The values in parentheses represent the lower and upper bounds of different measurements (10–50 μg IrO_x cm⁻²)

Operating mode	Δm (ng)	Δm/min(%)	m Ir dissolved/Qcv/tOER (g C^−1 s^−1) × 10^−9	Stability number (mole O2/mole Ir) × 10^4
a Measurements with a flow cell with a high active area (5 cm^2, 100 μg IrOx cm^−2). b Total amount; number of CV cycles (≥3) are not accounted.
OER sweeps	25.8 (6.5–57.2^a)	0.37 (0.007^a–0.68)	6.36 (3.96–9.76)	5.45 (4.13–7.5)
Short CA/CVs (≤ 500 s)	13.3 (9–17.3)	0.17 (0.13–0.2)	3.55 (3.51–3.58)	3.59 (3.22–3.95)
Long CA/CVs (> 500 s)	17.2 (6.9–27.6)	0.22 (0.1–0.32)	0.96 (0.38–1.53)	9.82 (5.43–14.2)
CVs to 1.575 V	2.3 (1.2–3.3)	0.026 (0.014–0.04)	26.2 (14.5–37.9)	0.235 (0.13–0.34)
CV after OER sweeps	27.1^a	0.0054^a	—	—
Base CVs^b	6.6 (0.4–16.1^a)	0.041 (0.003^a–0.13)	—	—

---

Upon sweeping the potential above 1.3 V, a mild mass increase (up to 1.4 V) is followed by a mass decrease concomitant with the apparent OER onset at ca. 1.45 V (Fig. 3(a)), in qualitative agreement with the Ir dissolution detected by ICP-OES with an identical catalyst film (Fig. S9, ESI†). Upon sweep reversal, the mass increases again, steeper below ca. 1.53 V. Hysteresis is observed in both profiles of mass and current against the potential (Fig. 3(a)). The mass loss in a full OER cycle (113 ng) is 4 times the Ir mass loss detected by ICP-OES (27.3 ng, Fig. S9, ESI†), indicating additional means of mass loss, which we attribute to deprotonation/dehydration of the catalyst during the OER, in accordance with ex situ spectroscopic observations on hydrated anodic Ir oxide films after OER polarization;²⁷ca. 30 H⁺/H₂O molecules are removed per Ir atom dissolved, without accounting for the possible influence of anions. Meanwhile, the integral mass variation within a full anodic or cathodic sweep is 5–6 times higher than the irreversible mass loss, showing that the major part is reversible down to 1.3 V under the present experimental conditions.

Fig. 3(b) shows the electrogravimetric profile during two consecutive CV cycles between 1.4 and 0.04 V, RHE, subsequent to the potentiodynamic OER (Fig. 3(a)). The mass in the first cathodic sweep increases steeper than that in the subsequent sweep, in response to the different current profiles, whereas both mass and current profiles are similar in the anodic sweeps. A mass plateau is formed below 0.4 V, coinciding with the ORR onset that commences on the bare Au surface (Fig. S5, ESI†); the electrolyte was not purged with inert gas and contained dissolved O₂. Despite the charge difference between the first and the second cathodic sweeps, the integral mass variations are quite similar in Fig. 3(b).

The relationship between the mass variations over the absolute integrated CV charge is displayed in Fig. 3(c). The high mass-to-charge ratios (14–142 H⁺/e) indicate that H⁺/H₂O and solution anions are injected into and expulsed from the catalyst layer during the cathodic and anodic sweeps, respectively.^40,47 In the first cathodic sweep after the OER and in the potential region of 1.4–0.8 V, the mass-to-charge ratio approximates the injection of a hydronium per electron, while (bi-)sulfates start inserting only below 0.8 V to counterbalance the accumulated positive charge. The kink at high potentials is due to the charge associated with the reduction of Au oxide, the influence of which is negligible on the measured mass changes.⁴³ The slight mass decrease below ca. 0.2 V in both sweeping directions in the Au/ORR active region may be attributed to the dissolution of both Ir and Au.^16,48 The mass-to-charge ratio is exaggerated upon sweep reversal (142 H⁺/e in both anodic sweeps), due to the expulsion of H⁺/H₂O/anions, while it is significantly lower in the first cathodic sweep subsequent to the OER than that in the consecutive sweeps below 0.8 V (Fig. 3(c)). The same trend is observed in HClO₄ (Fig. S10, ESI†), but with lower mass-to-charge ratios, indicating the higher affinity of Ir surfaces for the adsorption of (bi-)sulfates.^49,50

The low potential cathodic peak is commonly associated with the reduction of Ir sites from 4+ to 3+, also involving the bulk Ir centers.^15,17,51 X-ray absorption spectroscopy (XAS) at the O K-edge, in combination with molecular dynamics simulations at the DFT level, speciated oxidized under coordinated surface O-species that appear as the pre-edge feature at potentials lower than the OER onset and under OER conditions.⁵² Potentiodynamic measurements highlighted that the protonation of the surface μ2–O moieties (O-species coordinated with two Ir atoms, Ir–O–Ir, simplified scheme in the inset of Fig. 4(a)) extends to low potentials,⁵² a process that is apparently accompanied by hydration and anion adsorption (Fig. 3(c)). Ion mobility mass spectrometry (IMMS) on small Ir–O clusters indicated that the bridging μ2–O motif is favored by increasing the cluster size and the number of O atoms bound on Ir atoms.⁵³ On this ground, we tentatively assign the excessive cathodic charge appearing after the OER to the protonation of the surface bridging O species, oxidized during the preceding OER, occurring simultaneously with the injection of a higher number of species with low mass, e.g. H⁺/H₂O, than in the subsequent sweeps. Assuming the injection of one hydronium per electron, half the amount of bisulfates adsorbs per electron in the first cathodic sweep, indicating the reduction of subsurface Ir centers.^24,44 The intercalation by solution anions is not expected to extend into the bulk of IrO_x, considering that the ionic radius of solvated sulfates is greater than the Ir–O interatomic distance in rutile IrO₂.^54,55 The influence of cathodic Ir dissolution, which has been shown to set in below ca. 0.5 V with hydrous IrO_x overlayers on metallic Ir,¹⁶ is 3 orders of magnitude lower (see Table 1 further below) than the integral mass variations in the 0.8–0.4 V potential region (Fig. 3(b) and (c)) and hence negligible.

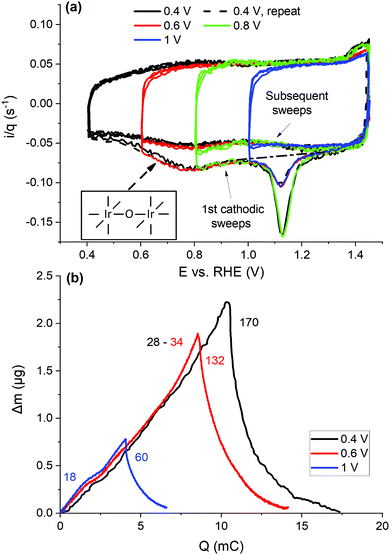Fig. 4 (a) Linear ramp CVs (50 mV s⁻¹, 3 cycles) with different LPLs (see the figure legend) measured after three potentiodynamic OER cycles, with the charge normalized current density. The dashed line is the baseline for subtracting Au oxide contributions; N₂ purging, RDE. The inset displays a simplified view of surface bridging O species, μ2–O, with Ir centers represented with a coordination number of six, typical for bulk rutile structures. (b) Mass changes vs. CV charge (absolute integration) during the first CV cycles (5 mV s⁻¹, eQCM flow cell), after the potentiodynamic OER (respective profiles of the consecutive cycles in Fig. S11, ESI†).

The effect of the reactivation potential

In this section, the influence of the cathodic potential and the respective charge passed during the regenerative CVs on the restoration of the OER activity is investigated. Therefore, CVs with different LPLs were acquired (0.4–1 V, Fig. 4(a)), after interrupting three potentiodynamic OER cycles at 1.45 V cathodically and resuming sweeping cathodically from OCP. Each of these measurements was accompanied by subsequent potentiodynamic OER measurements (Fig. 1(a)) to assess the recovery of the intrinsic OER activity.

Representative CVs are displayed in Fig. 4(a), with the current density normalized to the charge of the third CV cycle, when LPL = 0.4 V, as the measurements were performed with two different catalyst loadings (10 and 20 μg IrO_x cm⁻², as measured current densities along with that of the bare Au in Fig. S12a, ESI†), but also to account for occasional charge losses during the potentiodynamic OER (Fig. S13, ESI†). When the LPL is greater than 0.4 V, the charge is interpolated between the respective values before and after each OER/CV testing sequence (e.g. see in Fig. S13, ESI†). Despite the different loadings, the first cathodic sweeps highly overlap in their common portion, with the only exception of the magnitude of the Au oxide reduction peak, which is higher the lower the IrO_x loading, and correspondingly the larger is the bare Au surface exposed to the electrolyte. Upon reversing the sweep, the charge normalized current density is slightly lower than that of the subsequent anodic sweeps when the LPL is higher than 0.4 V (Fig. 4(a)), suggesting that reduction currents are superimposed to the anodic current. This charge difference is accounted for as a cathodic contribution in the charge integrations. The consecutive cathodic sweeps overlap down to ca. 1.1 V, RHE (Fig. 4(a)), while the lower potential is required to protonate the μ2–O species, not reduced in the preceding CV cycle, when the LPL is greater than 0.4 V. The additional reductive currents, with respect to the base CV, are clearer in the staircase CVs with the sparse current sampling (α = 1), in which the double-layer non-faradaic contributions are suppressed (see Fig. S12 and S14 and discussion in the ESI†). This charge is also accounted as cathodic contributions appearing after the OER.

The mass profiles vs. the integrated charge of the first CV cycles after the potentiodynamic OER are depicted in Fig. 4(b), measured in the eQCM flow cell without the current interruption. The cathodic sweeps overlap fairly well, in accordance with the charge normalized CVs in Fig. 4(a). With the increasing LPL, not only the mass-to-charge ratio decreases in the subsequent anodic sweep, but also a mass gain is observed at the end of a full CV cycle that increases with the LPL. A part of the mass loss during the preceding OER sweeps is reversible by the protonation/hydration of the oxide network and the injection of anions at lower potentials. The influence of Ir dissolution becomes apparent at potentials lower than 0.6 V, indicating that the electrochemical reductive regeneration comes at a cost of Ir loss.

The cumulative additional cathodic charge of all CV cycles, measured after three potentiodynamic OER cycles, over the base CV charge (Δq/q) is displayed in Fig. 5(a) against the applied LPL. The fractional charge profiles of the first cathodic sweeps with the LPL of 0.4 V are also displayed for two catalyst loadings (data assessed by staircase CVs with the sampling parameter α = 1 are jointly presented in Fig. S15, ESI†). The excessive fractional charge passing in multiple (up to 9) CV cycles exceeds that of the first cathodic sweep (black lines in Fig. 5(a)) by a fraction of 0.05–0.1. Fig. 5(a) is complemented with the fractional activity loss (= [(i/q)_k,1 − (i/q)_k,3]/(i/q)_k,1), always observed between the first, (i/q)_k,1, and the third anodic OER sweep, (i/q)_k,3, where k is the potentiodynamic OER sequence, with the numbered subscript referring to the anodic sweep. Ca. 50% of the activity is lost within three OER cycles (shaded rectangle in Fig. 5(a)). The fractional activity regeneration (= [(i/q)_k+1,1 − (i/q)_k,3]/(i/q)_k,1) in the subsequent to the regenerative CVs first anodic OER sweep, (k + 1),1, is also added (red circles in Fig. 5(a)), defined as the difference between the regenerated activity, (i/q)_k+1,1, and that of the third anodic sweep of the preceding OER sequence, (i/q)_k,3, over the initial activity of the preceding OER sequence, (i/q)_k,1. With these definitions, the full activity recovery is achieved when both fractions of the activity loss and regeneration are equal. The charge normalized activity () is used as an activity metric, in order to account for occasional charge losses (Fig. S13, ESI†) and variations in the IrO_x loading. The activity is evaluated at 1.5 V, RHE (dashed vertical line in Fig. 2(a)), as it lies well within the Tafel slope region, hence essentially free of mass transport contributions. A graphical representation of the fractional activity loss and regeneration is shown in Fig. S18 (ESI†).

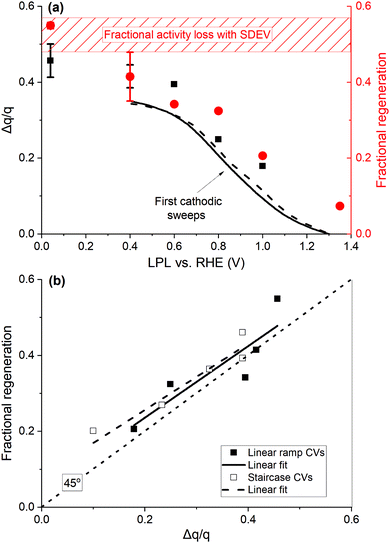Fig. 5 (a) Cumulative excessive fractional cathodic charge (black squares, left y-axis), passed during multiple linear ramp CV cycles after the potentiodynamic OER, vs. the LPL. Lines display the excessive charge fraction of the first cathodic sweeps down to 0.4 V for two catalyst loadings (10, dashed, and 20 μg IrO_x cm⁻², solid line). Regeneration fraction in the OER sweeps subsequent to regenerative CVs (red circles, right y-axis). The dashed rectangle denotes the fractional activity decay with the standard deviation in three potentiodynamic OER cycles. (b) Regeneration fraction against the excessive fractional charge. The dotted line has a 45° slope, passing through the origin. Data from (a), ramp CVs, filled symbols, and Fig. S15 (ESI†), staircase CVs, hollow symbols, and respective linear regressions (solid and dashed lines).

The profile of the regeneration fraction follows the Δq/q profile vs. the LPL in Fig. 5(a), with the full recovery achieved when LPL is ≤ 0.4 V. This is further elaborated in Fig. 5(b), where the fractional regeneration is plotted against Δq/q for both types of CVs, showing an almost 1 : 1 correlation. The following major conclusions are deduced. First, the base CV charge is a reliable representation of the number of sites involved in H⁺/e transfers and the ECSA, and double-layer and pseudo-capacitive types of charges are not distinguishable.²⁴ Second, the μ2-O surface terminations, associated with the excessive charge at low potentials, are initially OER active, when in hydroxylated/hydrated form μ2-OH(H₂O)_x. These sites account for a fraction of ca. 0.4–0.5 (Fig. 5(a)) after three OER cycles with respect to the number of charge generating sites in base CVs. Their oxidation (deprotonation/dehydration) during the OER induces a proportional intrinsic kinetic activity decay. Such a behavior resembles poisoning/blocking phenomena and can be represented by a (1 − θ) pre-exponential term (i = i_o(1 − θ)10^η/b, where b is the Tafel slope), where θ = Δq/q, in the context of Tafel-like kinetics. The increasing population of μ2-O species during the OER indicates that their deprotonation extends within the bulk OER potential region, in accordance with potentiodynamic XAS,⁵² also involving the transport of subsurface H⁺/H₂O, as suggested by electrogravimetry (Fig. 3(c), 4(b) and Fig. S11, ESI†). The μ2-O species are computed to possess a radical characteristic,²² hence favoring an electrophilic attack by H₂O molecules and the O–O bond formation.^24,29,52 These species appear to be OER active until they are fully oxidized, resulting in the recoverable, upon their protonation, activity decay. An alternative plausible mechanistic scenario, based on DFT calculations that predict that the μ1-O surface species (O-species single coordinated with Ir atoms, Ir–O, simplified scheme in the inset of Fig. 7 further below) are more active,^22,24,52,55 may be considered. The hydrated μ2-OH(H₂O)_x species act as H₂O reservoirs for the OER to proceed by the active sites, so that the degree of hydration tunes the OER activity, while the OER itself regulates the degree of hydration/dehydration of the Ir oxide.

Deactivation under potentiodynamic OER conditions over time

In order to understand the link between the activity decay and the charge growth with time under potentiodynamic OER conditions, the fractional activity loss at 1.5 V, RHE, observed during three and ten OER cycles (ca. 1.5 h, Fig. 2(a)), is plotted in Fig. 6 against the number of OER cycles, along with the respective charge fractions, measured subsequently to the OER.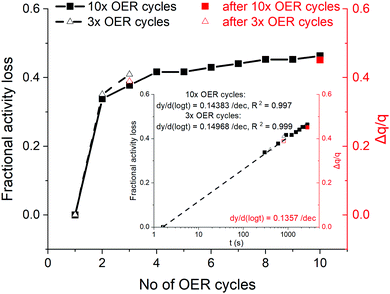

Fig. 6 Fractional activity loss (black symbols, left-y axis), assessed on the anodic portion of potentiodynamic OER against the number of cycles (data from Fig. 2(a) and Fig. S18, ESI†). The fractional charge grown during the OER sweeps (Fig. 2(b) and Fig. S2, ESI†) is embedded (red symbols, right-y axis). (Inset) Same plotted against time in the logarithmic scale and respective linear fits.

Despite the limited number of data points of the fractional charge, they accord with the fractional activity loss. When both quantities are plotted vs. time in the logarithmic scale with an initial time, the current sampling time after reaching 1.5 V, RHE (1.6 s, see Fig. S19 and respective discussion in the ESI†), the apparently linear fractional activity decay on log t includes the first OER anodic sweep, suggesting log t dependent fractional deactivation (inset in Fig. 6), which is accompanied by an almost 1 : 1 fractional charge growth. The excellent match implies that the latter quantity also grows linearly with log t, at least in the timespan of the present potentiodynamic OER measurements (1.5 h max.), resembling a direct log t dependent charge growth rate. Direct log t dependencies have been long observed in chemisorption^56,57 and the formation and extension of oxide films on metals.^58,59 The presented results are in favor of a restructuring process, which involves the progressive oxidation and growth of the μ2-O population, concomitant to the dehydration of the close to the surface oxide network, under potentiodynamic OER conditions.

De-/re-activation under potentiostatic operation

To further understand the growth of the cathodic charge with time under OER conditions, potentiostatic interims at iR compensated 1.575 V, RHE, were adopted at different durations from 10 s to 3 h, each one followed by CV without the current interruption down to 0.4 V (Fig. 1(b)), and consecutively to 0.04 V. Representative CVs after 30 and 8000 s are shown in Fig. 7, along with a CV acquired after three potentiodynamic OER cycles, interrupted at 1.45 V cathodic and 3 s at OCP, measured concomitant to the stationary/regenerative interims. The full set of CVs is presented in Fig. S20 (ESI†).

Fig. 7 Exemplary staircase CVs (sampling parameter α = 0.3) after 30 (black) and 8000 s (red) at 1.575 V iR compensated without the current interruption, complemented with a CV after the potentiodynamic OER and the current interruption at 1.45 V cathodic (blue). RDE, 50 mV s⁻¹, 50 μg IrO_x cm⁻² nominal loading. The inset displays a simplified view of surface atop O species, μ1-O, with the Ir center represented with a coordination number of six. It is noted that edge Ir sites will be likely under-coordinated, thus accommodating lower valence than bulk Ir sites.

When the potential is swept cathodic to low potentials without the current interruption, regardless of the time spent at 1.575 V, a high potential peak emerges (>1.3 V, RHE), which is not appearing after interrupting the OER (Fig. 2(b), 4(a) and 7; the influence of time at OCP is displayed in Fig. S6, ESI†). This is an indication that the associated species are discharged fast in the absence of applied bias. Similar spectroscopic evidence has been provided for the μ1-O species (the inset in Fig. 7).⁵² Hence, the high potential peak is tentatively attributed to the reduction/protonation of the μ1-O^I− oxyl species, which are formed during the OER,^{24,25,29,51,52} and the reduction of the associated Ir centers. It is noted that edge Ir sites, expected to be abundantly present in the semi-crystalline IrO_x studied herein,^8,44,60 are able to accommodate lower oxidation states than bulk Ir centers, due to their under-coordination. Both cathodic peaks, i.e. the population of μ1-O and μ2-O species, grow with time under OER conditions (Fig. 7). The low potential cathodic peak displays a positive potential shift with time, whereas the high potential peak progressively shifts negatively by up to 100 mV. The protonation of the μ2-O species is not hindered with their population growth, whereas an increasing irreversibility in the reduction of the μ1-O moieties is exerted under stationary OER conditions at long times.

The respective chronoamperograms, preceding CVs in Fig. 7, are presented in Fig. 8(a), vs. time in the logarithmic scale, with the current density normalized over the base CV charge, assessed prior to each current transient (Fig. 1(b)). The curves are complemented by similar measurements performed with the eQCM flow cell, but at a slightly lower potential of 1.55 V, RHE. Both potential values are located at the bent part of the polarization curves (Fig. 2(a)), hence representing conditions of appreciable coverage by reaction intermediates.^61,62 Again, the log t dependent OER activity decay is discerned, with a change in the slope at ca. 5–10 min, marked with a vertical dashed line in Fig. 8(a). Meanwhile, all curves fairly overlap in their common dwells, with the only exception of the lower intrinsic activity displayed in the last current transient (curve 5), performed after a preceding 1.1 h hold, which accords with the increasing irreversibility in the reduction of the μ1-O species with time (Fig. 7 and Fig. S20, ESI†).

Fig. 8 (a) Charge normalized activity at two iR compensated potentials (legend in the figure) with the eQCM flow cell (black) and the RDE (grey) vs. time in the logarithmic scale (left y-axis). Examples with as measured current in Fig. S21 (ESI†). The numbers refer to the duration of the current transients (1: 90 s, 2: 500 s, 3: 1500 s, 4: 4000 s, 5: 8000 s). The charge ratio of the first cathodic sweep after each chronoamperogram over that of the third cathodic sweep (right y-axis); the eQCM flow cell (red squares), the RDE from Fig. S20, ESI† (orange solid circles) and a repeat experiment with a LPL of 0.4 V (orange hollow circles). (b) μ1-O (filled) and μ2-O (hollow symbols) charge fractions normalized to the base CV charge (0.4–1.45 V), measured after each CA/CV sequence (left y-axis), and their ratio (right y-axis) vs. the time of the preceding CA in the logarithmic scale. The two repeats with the RDE differ in the LPL of the regenerative CVs (0.04 V, squares, and 0.4 V, triangles).

The charge ratios of the first cathodic sweep following potentiostatic operations over that of the third cathodic sweep (e.g.Fig. 7 and Fig. S20, ESI†) are also plotted in Fig. 8(a). This normalization neglects the charge growth due to the upper potential limit (1.55 or 1.575 V, Fig. 1(b)), as we are interested in the influence of time in the charge growth, but also excludes charge losses. Almost the same slope is observed in the charge growth against log t in all measurements, irrespective of the cell and the applied potential. A similar behavior is observed in the growth and extension of oxide layers over broad potential ranges.⁵⁹ In an effort to decipher the possible reasons for the intensive activity decay under stationary OER conditions (Fig. 8(a)), the distinct reducibility behavior of the μ-O species with regard to potential and upon current interruption (Fig. 4 and 7) is considered in the de-convolution of the μ1-O reductive charge contributions from the remaining charge portion. The first cathodic sweeps, after interrupting the potentiodynamic OER at 1.45 V, are used as descriptors of the charge contributions related to the protonation of the μ2-O species (Fig. 2(b), 4(a) and 7). An example of the de-convolution procedure is shown in Fig. S22 (ESI†).

The μ1-O and μ2-O redox active fractions normalized to the base CV charge (0.4–1.45 V, RHE) are displayed in Fig. 8(b), against the time of the preceding stationary interim in the logarithmic scale, along with their ratio for the two repeats with the RDE. Both grow linearly with log t, giving a relatively constant μ1-O/μ2-O species ratio (≈0.15), albeit up to a critical time (0.5–1 h), marked with vertical dashed lines for the two repeats in Fig. 8(b). At longer times, the population of the μ2-O species increases more steeply, at the expense of the μ1-O population, without distorting the overall charge linearity on log t (Fig. 8(a)). The conversion of the μ1-O to μ2-O species at long times, with a simultaneous negative potential shift of the reduction of the μ1-O species, is accompanied by an irreversible deactivation (curve 5 in Fig. 8(a)), which persists in potentiodynamic OER measurements performed subsequently to stationary interims and regenerative CVs down to 0.04 V (Fig. S23, ESI†).

Accounting for the 1 : 1 correlation between the growth of the μ2-O species and the recoverable intrinsic deactivation under potentiodynamic OER conditions, a breakdown of the deactivation in stationary operation is attempted (Fig. S24, ESI†). From an overall 85% charge normalized activity decay (Fig. 8(a)), 32% recoverable deactivation is attributed to the growth of the μ2-O population, while an additional 13% is irreversible (Fig. S23 and S24, ESI†). The latter value almost coincides with the fractional difference between the linearly projected against log t μ1-O population before their decay from that measured after the longest stationary interim (10.9%). A remaining portion of 40%, roughly half of the overall activity decay, is also recoverable and may be attributed to the influence of micro-bubbles grown under stationary conditions.³⁰ It is noteworthy that the population of the μ1-O species is doubled up to the critical time with respect to that in the shortest stationary interim (Fig. 8(b)). Although a similar to the μ2-O induced recoverable deactivation might be also envisaged with the increasing with time μ1-O population, detailed potential and time dependent measurements are required in order to assess the influence of the growth of the μ1-O species on the OER activity, which is matter of subsequent work.

The log t dependent increase of the μ1-O and μ2-O populations with time (Fig. 6 and 8) indicates a decelerating deprotonation/dehydration process under OER conditions (Fig. 3(a)). The depleted H⁺/H₂O are partially replenished during cathodic sweeping down to 1.3 V during the potentiodynamic OER that results in the reprotonation of the μ1-O species, whereas significantly lower potentials are required for the protonation of the μ2-O species and the hydration of the subsurface oxide matrix (Fig. 4 and 5). In contrast, under stationary OER conditions, the IrO_x structure is continuously depleted of H⁺/H₂O, resulting in an intensive activity decay (Fig. 8(a)). The direct log t dependence in the growth of μ1-O and μ2-O populations suggests a close link between the OER and IrO_x oxidation, in a similar manner to that in the oxidation of metals,^58,59 involving both Ir and O centers and the transport and consumption of subsurface H⁺/H₂O.⁴⁴ This process can be reverted upon excursing the potential to low values (≤0.4 V) that fully restores the intrinsic activity. However, uninterrupted OER polarization for long times results in the conversion of the μ1-O to μ2-O species (Fig. 8(b)), a sign of irreversible condensation of the hydrous IrO_x structure towards a denser H₂O-free form that displays lower intrinsic activity. Ab initio thermodynamic calculations indicated that faceting to the less active (111) IrO₂ surface is favorable at high potentials,⁶³ a surface that is richer in μ2-O species than the more active (110) terminations.²⁹ Such surface reconstructions will even more involve the abundantly present under-coordinated Ir sites, which gradually will transform into surface terminations with lower surface energy. It is noteworthy that the formation of surface crystalline domains has been observed in a dynamically operated PEMWE.⁸ The critical time for the prevalence of condensation is longer the lower the potential in the regenerative CVs (0.04 vs. 0.4 V, Fig. 8(b)), i.e. the more intensive the IrO_x reduction, suggesting a dynamic IrO_x reconstruction in response to potential modulations.⁶³

Stability trends under potentiodynamic and potentiostatic conditions

It is important to decipher the penalty of applying the restructuring regenerative procedure, in view of the mass loss observed during the regenerative CVs (Fig. 3 and 4) and the transient dissolution reported for Ir surfaces.¹⁶ The accumulated dissolved Ir mass in a potentiodynamic regeneration experiment with the RDE half-cell is presented in Fig. 9(a), along with the potential profile, vs. the experimental time. After 1 h base CVs, the amount of dissolved Ir detected by ICP-MS is only 1.23 ng, corresponding to 0.064% mass loss, equivalent to ca. 0.5% of a ML (calculations in the ESI†). This mass loss is accompanied by a slight charge increase (Fig. S25, ESI†). A slight roughening of the IrO_x particles and/or an effect on the surface chemistry, e.g. via amorphization, induced by the repetitive potential cycling, may be suggested. As soon as the potential is driven into the OER region (2 mV s⁻¹, 1.69 V, RHE maximum potential), Ir dissolution enhances (Fig. 9(a) and Fig. S9, ESI†). Ca. 0.05 ML of IrO_x dissolved, one order of magnitude higher than that dissolved after 1 h base CVs.

Fig. 9 (a) Potential profile (left y-axis) vs. time of a representative potentiodynamic experiment (Fig. 1(a)). Accumulated dissolved Ir mass in the electrolyte (red right y-axis) and average intrinsic Ir dissolution rate (blue right y-axis), vs. the experimental time. (b) Average intrinsic Ir dissolution rate vs. the time of the potentiostatic OER/regeneration experiment in Fig. 8 (left y-axis). Differential of the dissolved Ir mass over the integral charge passed during the OER (right y-axis). The different operating interims are mentioned in the figure. The respective potential and current profiles are shown in Fig. S26 (ESI†).

The amount of Ir dissolved during the first three potentiodynamic OER cycles in three different experiments is proportional to the respective initial CV charges (Fig. S27, ESI†) and hence to the catalyst loading. Furthermore, as the charge profile over time follows closely that of the dissolved Ir (Fig. S25, ESI†), the latter is normalized against the CV charge (dissolved Ir mass/Q_CV, in g C⁻¹), assessed at the specific or the closest time of electrolyte sampling. Proportionality between the charge and the active surface area is assumed, a condition likely fulfilled at least under potentiodynamic OER conditions.⁸ The differential of the dissolved Ir mass normalized to the base CV charge over the time under OER conditions (dissolved Ir mass/Q_CV/t_OER, in g C⁻¹ s⁻¹) represents the average intrinsic Ir dissolution rate, neglecting the influence of cathodic Ir dissolution at low potentials (one order of magnitude lower mass losses, Table 1). The charge and time under the OER accounted for potentials greater than the apparent OER onset (1.45 V, RHE, Fig. 2(b), 3(b) and Fig. S9, ESI†). The average of the values deduced by different OER sweeps is reported in Table 1, along with their span (ca. 4–10 × 10⁻⁹ g C⁻¹ s⁻¹). The intrinsic dissolution rate increases with the number of the potentiodynamic OER/regeneration sequences (blue triangles in Fig. 9(a)). Furthermore, the re-protonation/hydration of the IrO_x structure (Fig. 3) is accompanied by mild Ir dissolution, evaluated by collecting the electrolyte outlet of a flow cell with a large active area in a batch mode (Table 1). A structural amorphization imposed by cycling to low potentials is suggested that weakens the IrO_x structure, making it more vulnerable to dissolution.

Meanwhile, as shown in Fig. 9(b), the average intrinsic dissolution rate during the potentiostatic operation is of the same order (3.51 × 10⁻⁹ g C⁻¹ s⁻¹) in the first few interims with short dwell times (up to 500 s) and progressively decreases with the increasing dwell time down to one order of magnitude lower values (3.81 × 10⁻¹⁰ g C⁻¹ s⁻¹ for 3 h dwell, Table 1 and Fig. S28, ESI†). The stabilization of the IrO_x structure is accompanied by almost one order of magnitude activity decay (Fig. 8(a)). The log t dependent OER induced deprotonation/dehydration process (Fig. 3 and 4) propagates towards the bulk and gradually transforms the hydrated structure to a more condensed crystalline oxide,^13,64,65via an electro-crystallization process,⁶⁶ resulting in a less active, but more resistant to the dissolution oxide rigid structure. The reductive regeneration reconstructs the μ2-O sites, formed during the extended stationary OER, back into μ1-OH or μ1-H₂O at low potentials, inevitably involving bond breaking that is accompanied by mild dissolution.

As a stability metric that accounts for both Ir dissolution and O₂ generation, the ratio between the dissolved Ir mass over the charge passed under OER conditions (e.g. see Fig. S26b in the ESI†) is depicted in Fig. 9(b) for the potentiostatic experiment with a LPL of 0.04 V (Fig. 8). The respective data from the repeat experiment are shown in Fig. S28 (ESI†). This parameter is proportional to the reciprocal of the stability number (mole O₂ produced/mole Ir dissolved).¹⁹ The stability numbers for different operating schemes are reported in Table 1, being in line with the literature.^19,33 The following are deduced from Fig. 9(b), Fig. S28, ESI† and Table 1. (i) The reciprocal of the stability number during the stationary operation with short dwells exceeds that assessed in the potentiodynamic OER, but not significantly. Low potential excursions may be beneficial for restoring the activity, but at the expense of Ir dissolution, which intensifies upon re-entering to OER potentials.¹⁶ This is confirmed by the one order of magnitude higher values, when the electrolyte sampling evaluates only the regenerative CVs (1.575 to 0.4 and 1.4 to 0.04 V, Fig. 9(b) and Table 1). (ii) The reciprocal of the stability number in the potentiodynamic OER is 2–2.5 times higher than that during the extended stationary dwells (Fig. 9(b)), with the latter increasing by a factor of 1.5 (± 0.1) when low potential excursions are involved (Fig. S28, ESI†). These values are not prohibitive for applying the regenerative low potential excursions, as long as the frequency of the potential modulations is maintained relatively low.

Conclusions

The OER induced deactivation and the regeneration of activity upon the electrochemical reductive treatment of a current state-of-the-art commercial IrO_x catalyst were investigated using RDE and eQCM in half-cell configurations and acidic media. A direct log t dependent charge growth that is traced at potentials below ca. 1.1 V, RHE, is observed under potentiodynamic OER conditions, accompanied by a 1 : 1 fractional deactivation, which is ascribed to the deprotonation/dehydration of μ2-OH(H₂O)_x and subsurface species during the OER. Their re-protonation/hydration upon electrochemical reduction (≤0.4 V, RHE) fully restores the activity, but at the expense of the mild material loss via dissolution. Meanwhile, the inherent instability towards OER induced Ir dissolution, associated with the reductive regeneration, suggests a restructuring (amorphization) imposed by the regenerative treatment.

On the other hand, the extended stationary operation induces irreversible intrinsic deactivation, which becomes apparent after a critical time in the order of 0.5–1 h, after which an accelerated log t dependent growth of the μ2-O species sets in, at the expense of μ1-O species, but in a manner that the overall charge linearity on log t is preserved. This irreversible process comes along with an enhancement in stability, roughly proportional to the activity decay. The hydrated IrO_x structure gradually transforms to a more condensed crystalline oxide that results in a less active, but more resistant to dissolution, rigid network. These results not only demonstrate the dynamic nature of the IrO_x chemistry and structure in response to the electrochemical potential modulations, but also indicate the fact that the OER regulates the hydration degree of Ir oxides depending on the starting phase, e.g. by dehydrating hydrous structures and hydrating thermally prepared anhydrous oxides.⁶⁶ It is imperative to validate this view by thoroughly investigating the interplay between OER, catalyst oxidation and dissolution, since all three phenomena are interrelated, but are expected to display distinct kinetics and dependence on the potential and current density, a matter of subsequent work.

The beneficial role of the dynamic operation in restraining the kinetic deactivation of PEMWE IrO_x based anodes is highlighted. However, stability concerns arise for the next-generation nanostructured IrO_x catalysts. This work aids in the development of a deactivation metric suitable for digital data analysis and serves as a descriptor for the interplay between the electrocatalyst and operating mode.

Author contributions

Georgios Papakonstantinou: conceptualization, methodology, formal analysis, investigation, writing – original draft, writing – review and editing, and visualization. Ioannis Spanos: conceptualization, methodology, formal analysis, investigation, writing – review and editing, and visualization. An Phuc Dam: investigation and writing – review and editing. Robert Schlögl: conceptualization, writing – review and editing, supervision, funding acquisition, and project administration. Kai Sundmacher: conceptualization, writing – review and editing, supervision, funding acquisition, and project administration.

Nomenclature

CA	Chronoamperometry
CV	Cyclic voltammetry
ECSA	Electrochemical surface area
EIS	Electrochemical impedance spectroscopy
eQCM	Electrochemical quartz crystal microbalance
ICP-MS	Inductively coupled plasma mass spectrometry
ICP-OES	Inductively coupled plasma optical emission spectroscopy
LPL	Low potential limit
OCP	Open circuit potential
OER	Oxygen evolution reaction
ORR	Oxygen reduction reaction
PEMWE	Proton exchange membrane water electrolyzer
RDE	Rotating disc electrode
RHE	Reversible hydrogen electrode
b	Tafel slope, V dec^−1 of current
E	Potential, V
i	Current density, A cm^−2 geometric area
i o	Exchange current density, A cm^−2 geometric area
i/q	Charge normalized current density, s^−1
m	Mass, g or μg or ng
Q	Charge, C
q	Charge per geometric area, C cm^−2
t	Time, s
u	Sweep rate, V s^−1
Δm	Mass change, g
ΔmIr	Differential mass of dissolved Ir, g
Δq/q	Fractional excessive charge passed during CVs after OER
ΔQOER	Total charge during the OER, C
α	Sampling parameter in staircase CVs
η	Overpotential, V
θ	Coverage

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge the MAXNET Energy Consortium of the Max Planck Society, and the EU-program ERDF (European Regional Development Fund) of the German Federal State Saxony-Anhalt within the Research Center of Dynamic Systems (CDS), for financial support. Mr Muhammad Aleem is thanked for his in-part assistance in the electrochemical measurements with the RDE. Open Access funding provided by the Max Planck Society.

References

1. M. Carmo, D. L. Fritz, J. Mergel and D. Stolten, Int. J. Hydrogen Energy, 2013, 38, 4901–4934.
2. A. Buttler and H. Spliethoff, Renewable Sustainable Energy Rev., 2018, 82, 2440–2454.
3. M. Bernt, A. Siebel and H. A. Gasteiger, J. Electrochem. Soc., 2018, 165, F305–F314.
4. N. Danilovic, R. Subbaraman, K.-C. Chang, S. H. Chang, Y. J. Kang, J. Snyder, A. P. Paulikas, D. Strmcnik, Y.-T. Kim, D. Myers, V. R. Stamenkovic and N. M. Markovic, J. Phys. Chem. Lett., 2014, 5, 2474–2478.
5. S. Cherevko, A. R. Zeradjanin, A. A. Topalov, N. Kulyk, I. Katsounaros and K. J.-J. Mayrhofer, ChemCatChem, 2014, 6, 2219–2223.
6. F. Claudel, L. Dubau, G. Berthome, L. Sola-Hernandez, C. Beauger, L. Piccolo and F. Maillard, ACS Catal., 2019, 9, 4688–4698.
7. C. Rakousky, U. Reimer, K. Wippermann, S. Kuhri, M. Carmo, W. Lueke and D. Stolten, J. Power Sources, 2017, 342, 38–47.
8. G. Papakonstantinou, G. Algara-Siller, D. Teschner, T. Vidakovic-Koch, R. Schlögl and K. Sundmacher, Appl. Energy, 2020, 280, 115911.
9. A. Weiss, A. Siebel, M. Bernt, T. H. Shen, V. Tileli and H. A. Gasteiger, J. Electrochem. Soc., 2019, 166, F487–F497.
10. S. M. Alia, S. Stariha and R. L. Borup, J. Electrochem. Soc., 2019, 166, F1164–F1172.
11. S. Cherevko, S. Geiger, O. Kasian, N. Kudyk, J. P. Grote, A. Savan, B. R. Shrestha, S. Merzlikin, B. Breitbach, A. Ludwig and K. J.-J. Mayrhofer, Catal. Today, 2016, 262, 170–180.
12. T. Binninger, R. Mohamed, K. Waltar, E. Fabbri, P. Levecque, R. Kötz and T. J. Schmidt, Sci. Rep., 2015, 5, 12167.
13. T. Li, O. Kasian, S. Cherevko, S. Zhang, S. Geiger, C. Scheu, P. Felfer, D. Raabe, B. Gault and K. J.-J. Mayrhofer, Nat. Catal., 2018, 1, 300–305.
14. X. Tan, J. Shen, N. Semagina and M. Secanell, J. Catal., 2019, 371, 57–70.
15. B. E. Conway and J. Mozota, Electrochim. Acta, 1983, 28, 9–16.
16. S. Cherevko, S. Geiger, O. Kasian, A. Mingers and K. J.-J. Mayrhofer, J. Electroanal. Chem., 2016, 773, 69–78.
17. S. Gottesfeld and S. Srinivasan, J. Electroanal. Chem., 1978, 86, 89–104.
18. T. Reier, D. Teschner, T. Lunkenbein, A. Bergmann, S. Selve, R. Kraehnert, R. Schlögl and P. Strasser, J. Electrochem. Soc., 2014, 161, F876–F882.
19. S. Geiger, O. Kasian, M. Ledendecker, E. Pizzutilo, A. M. Mingers, W. T. Fu, O. Diaz-Morales, Z. Li, T. Oellers, L. Fruchter, A. Ludwig, K. J.-J. Mayrhofer, M. T.-M. Koper and S. Cherevko, Nat. Catal., 2018, 1, 508–515.
20. J. O. Bockris, J. Chem. Phys., 1956, 24, 817–827.
21. T. Reier, H. N. Nong, D. Teschner, R. Schlögl and P. Strasser, Adv. Energy Mater., 2017, 7, 1601275.
22. Y. Ping, R. J. Nielsen and W. A. Goddard, J. Am. Chem. Soc., 2017, 139, 149–155.
23. J. Rossmeisl, Z.-W. Qu, H. Zhu, G.-J. Kroes and J. K. Norskov, J. Electroanal. Chem., 2007, 607, 83–89.
24. H. N. Nong, L. J. Falling, A. Bergmann, M. Klingenhof, H. P. Tran, C. Spöri, R. Mom, J. Timoshenko, G. Zichittella, A. Knop-Gericke, S. Piccinin, J. Pérez-Ramírez, B. R. Cuenya, R. Schlögl, P. Strasser, D. Teschner and T. E. Jones, Nature, 2020, 587, 408–413.
25. V. Pfeifer, T. E. Jones, J. J. Velasco Vélez, R. Arrigo, S. Piccinin, M. Hävecker, A. Knop-Gericke and R. Schlögl, Chem. Sci., 2017, 8, 2143–2149.
26. A. Minguzzi, C. Locatelli, O. Lugaresi, E. Achilli, G. Cappelletti, M. Scavini, M. Coduri, P. Masala, B. Sacchi, A. Vertova, P. Chigna and S. Rondinini, ACS Catal., 2015, 5, 5104–5115.
27. R. Kötz, H. Neff and S. Stucki, J. Electrochem. Soc., 1984, 131, 72–77.
28. O. Kasian, J. P. Grote, S. Geiger, S. Cherevko and K. J.-J. Mayrhofer, Angew. Chem., Int. Ed., 2018, 57, 2488–2491.
29. J.-J. Velasco-Vélez, E. A. Carbonio, C.-H. Chuang, C.-J. Hsu, J.-F. Lee, R. Arrigo, M. Hävecker, R. Wang, M. Plodinec, F. R. Wang, A. Centeno, A. Zurutuza, L. J. Falling, R. V. Mom, S. Hofmann, R. Schlögl, A. Knop-Gericke and T. E. Jones, J. Am. Chem. Soc., 2021, 143, 12524–12534.
30. M. F. Tovini, A. Hartig-Weiß, H. A. Gasteiger and H. A. El-Sayed, J. Electrochem. Soc., 2021, 168, 014512.
31. R. Tang-Kong, C. E.-D. Chidsey and P. C. McIntyre, J. Electrochem. Soc., 2019, 166, H712–H717.
32. S. M. Alia and G. C. Anderson, J. Electrochem. Soc., 2019, 166, F282–F294.
33. J. Knöppel, M. Möckl, D. Escalera-López, K. Stojanovski, M. Bierling, T. Böhm, S. Thiele, M. Rzepka and S. Cherevko, Nat. Commun., 2021, 12, 2231.
34. D. A. Buttry and M. D. Ward, Chem. Rev., 1992, 92, 1355–1379.
35. E. Gileadi and V. Tsionsky, J. Electrochem. Soc., 2000, 147, 567–574.
36. R. Frydendal, E. A. Paoli, B. P. Knudsen, B. Wickman, P. Malacrida, I. E.-L. Stephens and I. Chorkendorff, ChemElectroChem, 2014, 1, 2075–2081.
37. M. Tian, W. G. Pell and B. E. Conway, Electrochim. Acta, 2003, 48, 2675–2689.
38. J. Juodkazytė, B. Šebeka, G. Stalnionis and K. Juodkazis, Electroanalysis, 2005, 17, 1734–1739.
39. L. D. Burke and R. A. Scannell, Platinum Met. Rev., 1984, 28, 56–61.
40. V. I. Birss, H. Elzanowska and S. Gottesfeld, J. Electroanal. Chem., 1991, 318, 327–333.
41. C. Bock and V. I. Birss, J. Electroanal. Chem., 1999, 475, 20–27.
42. A. Vertova, L. Borgese, G. Cappelletti, C. Locatelli, A. Minguzzi, C. Pezzoni and S. Rondinini, J. Appl. Electrochem., 2008, 38, 973–978.
43. C. E. Moore, F. Afsahi, A. P. Young and E. L. Gyenge, J. Phys. Chem. C, 2019, 123, 23361–23373.
44. V. Pfeifer, T. E. Jones, J. J. Velasco Velez, C. Massue, R. Arrigo, D. Teschner, F. Girgsdies, M. Scherzer, M. T. Greiner, J. Allan, M. Hashagen, G. Weinberg, S. Piccinin, M. Hävecker, A. Knop-Gericke and R. Schlögl, Surf. Interface Anal., 2016, 48, 261–273.
45. I. Spanos, A. A. Auer, S. Neugebauer, X. Deng, H. Tüysüz and R. Schlögl, ACS Catal., 2017, 7, 3768–3778.
46. J. R. Esquius, D. J. Morgan, I. Spanos, D. G. Hewes, S. J. Freakley and G. J. Hutchings, ACS Appl. Energy Mater., 2020, 3, 800–809.
47. V. I. Birss, C. Bock and H. Elzanowska, Can. J. Chem., 1997, 75, 1687–1693.
48. S. Cherevko, A. R. Zeradjanin, G. P. Keeley and K. J.-J. Mayrhofer, J. Electrochem. Soc., 2014, 161, H822–H830.
49. I. T.-E. Fonseca, M. I. Lopes and M. T.-C. Portela, J. Electroanal. Chem., 1996, 415, 89–96.
50. J. A. Arminio-Ravelo, A. W. Jensen, K. D. Jensen, J. Quinson and M. Escudero-Escribano, ChemPhysChem, 2019, 20, 2956–2963.
51. V. A. Saveleva, L. Wang, D. Teschner, T. Jones, A. S. Gago, K. A. Friedrich, S. Zafeiratos, R. Schlögl and E. R. Savinova, J. Phys. Chem. Lett., 2018, 9, 3154–3160.
52. L. J. Frevel, R. Mom, J.-J. Velasco-Vélez, M. Plodinec, A. Knop-Gericke, R. Schlögl and T. E. Jones, J. Phys. Chem. C, 2019, 123, 9146–9152.
53. R. Tomihara, K. Koyasu, T. Nagata, J. W.-J. Wu, M. Nakano, K. Ohshimo, F. Misaizu and T. Tsukuda, J. Phys. Chem. C, 2019, 123, 15301–15306.
54. Y. Marcus, Chem. Rev., 1988, 88, 1475–1498.
55. H. N. Nong, T. Reier, H.-S. Oh, M. Gliech, P. Paciok, T. H.-T. Vu, D. Teschner, M. Heggen, V. Petkov, R. Schlögl, T. Jones and P. Strasser, Nat. Catal., 2018, 1, 841–851.
56. P. T. Landsberg, J. Chem. Phys., 1955, 23, 1079–1087.
57. M. J.-D. Low, Chem. Rev., 1960, 60, 267–312.
58. B. E. Conway, Prog. Surf. Sci., 1995, 49, 331–452.
59. B. E. Conway, B. Barnett, H. Angerstein-Kozlowska and B. V. Tilak, J. Chem. Phys., 1990, 93, 8361–8373.
60. E. Willinger, C. Massué, R. Schlögl and M. G. Willinger, J. Am. Chem. Soc., 2017, 139, 12093–12101.
61. E. Gileadi, Adsorption in Electrochemistry (Ch. 1) in Electrosorption, Plenum Press, New York, 1967, pp. 1–18.
62. A. P. Dam, G. Papakonstantinou and K. Sundmacher, Sci. Rep., 2020, 10, 14140.
63. D. Opalka, C. Scheurer and K. Reuter, ACS Catal., 2019, 9, 4944–4950.
64. O. Kasian, S. Geiger, T. Li, J.-P. Grote, K. Schweinar, S. Zhang, C. Scheu, D. Raabe, S. Cherevko, B. Gault and K. J.-J. Mayrhofer, Energy Environ. Sci., 2019, 12, 3548–3555.
65. Z. Pavlovic, C. Ranjan, Q. Gao, M. van Gastel and R. Schlögl, ACS Catal., 2016, 6, 8098–8105.
66. S. Ardizzone, C. L. Bianchi, G. Cappelletti, M. Ionita, A. Minguzzi, S. Rondinini and A. Vertova, J. Electroanal. Chem., 2006, 589, 160–166.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp00828a

---