The reaction between HgBr and O3: kinetic study and atmospheric implications†
Received
14th February 2022
, Accepted 10th May 2022
First published on 10th May 2022
Abstract
The rate constants of many reactions currently considered to be important in the atmospheric chemistry of mercury remain to be measured in the laboratory. Here we report the first experimental determination of the rate constant of the gas-phase reaction between the HgBr radical and ozone, for which a value at room temperature of k(HgBr + O3) = (7.5 ± 0.6) × 10−11 cm3 molecule s−1 (1σ) has been obtained. The rate constants of two reduction side reactions were concurrently determined: k(HgBr + O) = (5.3 ± 0.4) × 10−11 cm3 molecule s−1 and k(HgBrO + O) = (9.1 ± 0.6) × 10−11 cm3 molecule s−1. The value of k(HgBr + O3) is slightly lower than the collision number, confirming the absence of a significant energy barrier. Considering the abundance of ozone in the troposphere, our experimental rate constant supports recent modelling results suggesting that the main atmospheric fate of HgBr is reaction with ozone to form BrHgO.
1. Introduction
The atmospheric chemistry of mercury has attracted a lot of attention in the last decade, with the publication of several reviews1–3 and state-of-the-art chemical modelling studies presenting revised chemical mechanisms and discussing major uncertainties.4–6 Mercury is a neurotoxic pollutant of global concern which is released to the atmosphere from contemporary anthropogenic (∼39%) and natural (∼6%) sources, and from legacy mercury deposits of both natural and anthropogenic origin (∼55%).7 The atmosphere is a minor reservoir of mercury, but plays a fundamental role in the chemical processing, dispersion and deposition of mercury compounds. The oxidation of Hg0 starts with the formation of HgI intermediates, that undergo further reactions to form HgII. The latter are soluble and are thought to partition into aerosol and deposit readily both by dry and wet mechanisms. In the condensed phase, HgII is reprocessed forming inorganic compounds that can partition back to the gas phase, or become bioavailable by forming organic compounds.7 Hg0 is also believed to be directly bioaccumulated.7 This gas- and condensed-phase chemical cycle is complicated by the reversibility of many of the mercury transformations.8,9 Global atmospheric modelling is crucial for understanding the mercury cycle and for predicting future Hg exposure. Despite significant progress in our understanding of the oxidation mechanism of mercury, major knowledge gaps remain. Crucially, large uncertainties exist in reaction rate constants, and many reactions and photochemical processes have not been validated experimentally.10
Experimental studies of the atmospheric chemistry of mercury in the gas phase are scarce and most of them deal with the oxidation of gaseous elemental mercury Hg0.1,2,10,11 Reactions between Hg0 and important atmospheric trace gases (O3, OH, HO2, H2O2 and NO3) have been investigated and found to be slow. Currently, the main oxidation path is thought to be initiated by atomic bromine.12 The third-body reaction between Hg(0) and bromine Br generates oxidized mercury HgI in the form of the unstable HgBr radical,13 which is predicted to redissociate and photolyze at the same rate.9,14 However, theoretical calculations suggest that HgBr can also be competitively oxidized by major radical oxidant species (OH, NO2, HO2 and the halogen atoms and monoxides) to form oxidized mercury HgII.14–17 It has been shown18,19 that the strong laser induced fluorescence (LIF) of HgBr in the visible20 can be used to monitor its reaction kinetic, but to date only the HgBr + NO2 atmospherically relevant reaction has been studied experimentally.21 Regarding HgII compounds, only HgX2 (X = Cl, Br, I) have been detected in the gas phase in laboratory studies.22 Chemical and photochemical reactions of HgII are thought to compete with partitioning to cloud droplets and aerosol, but the only information available on these processes to date is provided by ab initio electronic structure calculations and rate theory.4,23–29 Atmospheric mercury modelling depends almost entirely on calculated rate constants.4–6,8 State-of-the-art theoretical methods generally produce sound predictions of rate constants and, in addition, provide their temperature and pressure-dependences, which is useful for conditions that cannot be achieved in experimental settings. However important differences between theory and experiment are sometimes found.17,21 Hence, there is a clear need for experimental data on mercury reactions to anchor these calculations. Laboratory studies of mercury chemistry are challenging due to a number of factors, including the toxicity of mercury compounds, complications from side reactions and surface chemistry and the small number of relevant species amenable to spectroscopic detection (Hg, HgBr and HgCl). Research on mass spectrometric detection of HgII compounds that could be used in field and laboratory experiments has only just begun.30–32
The title reaction has been proposed by Saiz-Lopez et al.4 as a key step in the atmospheric cycle of mercury:
| | HgBr + O3 → BrHgO + O2 ΔHr (298 K) = −140 kJ mol−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 26 26 | (R1) |
This reaction had not been documented in the previous literature, although according to
ab initio thermochemical data it is exothermic and barrierless. An upper limit of
k1 < 10
−10 cm
3 molecule
−1 s
−1 has been predicted, corresponding to a hard sphere collision radius of 2.9 Å at a temperature of 285 K.
4 A more recent estimate of
k1 = 3 × 10
−11 cm
3 molecule
−1 s
−1 has been proposed to account for steric constraints for successful reactive collisions.
5 In either case,
(R1) should be the primary oxidation process of Hg
I to Hg
II, since O
3 is far more abundant than NO
2 and HO
2, whose reactions with HgBr at 298 K and 1 bar have rate constants of ∼3 × 10
−11 cm
3 molecule
−1 s
−1.
17,21
Considering the relevance given to (R1) in the recent literature and the lack of experimental data, we have conducted a kinetic study using the Pulsed Laser Photolysis-Laser Induced Fluorescence (PLP-LIF) technique to validate the theoretical estimates. Our study confirms the atmospheric importance of this reaction, showing that its rate constant is indeed lower than the estimated upper limit,4 although 2.5 times faster than the lower value estimated by Shah and co-workers.5
2. Experimental section
This work has been carried out at the University of Leeds with a classic PLP-LIF system. A schematic of this experimental set-up is shown in Fig. 1. The reactor consists of a cylindrical stainless-steel chamber with five orthogonal arms, four in the same horizontal plane and one vertical arm along the longitudinal axis. Pre-mixed precursor, reagent and buffer gases flow into the reactor via quarter inch ports placed at the vertical arm and two of the horizontal arms, while the fourth horizontal arm is fitted with a needle valve and connected to a pump (Edwards E2M28). Gas flow rates are controlled using calibrated mass flow controllers (MKS instruments). The pressure inside the reactor is measured by calibrated capacitance manometers (MKS Baratron) and controlled by the valve at the exit line. The reactor is enclosed in a thermally insulated container, which can be operated as a furnace or filled with dry ice. Temperatures inside the reactor are monitored by a shielded K-type thermocouple inserted directly into the centre of the chamber. Two of the horizontal arms are fitted with viewports with Brewster angle quartz windows, in order to pass the photolytic and the probe laser beams through the reaction volume, while the vertical arm interfaces to a photomultiplier detector, enabling collection of LIF orthogonally to the laser beams. The system is operated as a slow flow reactor, i.e. the residence time in the reactor (hundreds of milliseconds to seconds) is much longer than the chemical reaction times under study (sub-microsecond to millisecond scale). Synchronized pulsed lasers enable accurate time definition of the chemical events, which are initiated by the photolysis laser shot (t = 0) and can be probed at any delay time with respect to t = 0 using a delay generator (BNC 535). Concentration vs. time traces are constructed by scanning the delay between the photolysis and the probe lasers and can be arbitrarily accumulated for improved statistics. The repetition rate is adjusted to ensure that the reaction volume contains a fresh gas mixture before each photolysis laser shot. The concentrations of stable reagent gases are determined from known storage pressures, chamber pressure and mass flow controller readings. The concentration of unstable reagents produced online (e.g. O3, OH), are determined by ancillary spectroscopic methods. We have extensively employed this versatile set up to study the atmospheric chemistry of meteoric metal (Na, K, Mg, Ca, Fe, Ni, Al), semi-metal (Si) and non-metal (P) atoms and cations, and diatomic and triatomic molecules and cations bearing such atoms.33–38
 |
| | Fig. 1 Schematic of the PLP-LIF experimental set-up (MFC = Mass Flow Controller, IF = Interference Filter, PMT = Photomultiplier, S = Spectrometer, CM = Capacitance Manometer, DS = Doubling Stage, PC = Personal Computer). The thick black arrows indicate the direction of the gas flow. The delay generator (synchronization) and the oscilloscope (signal recording) are controlled by a LabView custom program run in a PC. | |
In the present work, the mercury (I) bromide radical (HgBr) was generated from single photon dissociation at 248 nm of mercury (II) bromide (HgBr2) using a KrF excimer laser (Lambda Physik, COMPEX 102). The excimer laser beam cross section was given a circular shape with an area of 0.72 cm2 by using an iris. The laser fluence at the centre of the reactor (7–80 mJ cm−2 pulse−1) was determined by measuring the laser power at the entrance and exit windows with a powermeter (Gentec-EO UNO). HgBr(X2Σ) fluorescence was induced by the frequency-doubled output of a Nd-YAG-pumped dye laser (a Continuum Surelite 10-II pumping a Sirah Cobra-stretch CBST-G-18 with a BBO doubling crystal). The dye and excimer laser beams counterpropagated through opposing arms of the reactor and were aligned collinearly. Since the dye laser beam cross section is much smaller than the excimer cross section, this ensured that HgBr was probed at the core of the photolyzed volume, which reduced the effect of diffusion on the observed LIF traces. The Coumarin 510 laser dye was used to span the wavelength range between 252 nm and 259 nm. This spectral region contains a number of vibrational bands of the D2Π3/2 ← X2Σ electronic transition that can be used for spectral identification and for probing ground state HgBr.18,21,39,40 In particular, time-resolved LIF was followed by probing the X2Σ, v′′ = 0 state at 255.97 nm, i.e. the (2,0) vibrational transition. Non-resonant fluorescence from the B2Σ → X2Σ electronic transition was collected at 500 nm as indicated in ref. 18 through a narrow band (10 nm FWHM) interference filter (Thorlabs FB500-10) using a photomultiplier tube (Electron Tubes, model 9816QB). The signal was digitized and integrated using an oscilloscope (LeCroy Waverunner, LT 342). The scope and the delay generator were controlled via GPIB by a customized LabView data acquisition program. The experiments were run at a laser pulse repetition frequency of 10 Hz. Each HgBr decay was obtained by averaging three consecutive decay traces, where each point is the average of 5 measurements. The decays consist typically of 300 points plus 10 pre-trigger points (signal baseline), and the time step was adapted in accord to the time constant of each particular decay, which depends on the concentration of the reagent (O3).
The experiments were carried out using N2 as carrier gas (total flow 800–1300 sccm). The total pressure in the system ranged between 5 and 60 torr and the experiments were performed at room temperature (295 K). O3 was made by flowing O2 through a commercial ozonizer (EASELEC, ELO-3G) to produce a mixture of 4% O3 in O2. The O3 concentration in the reactor was varied by setting different flow rates in the mass flow controller downstream of the ozonizer, or by changing the power of the discharge. HgBr2 powder (mass = 3 g) was stored in a sealed temperature-stabilized stainless-steel container with Swagelok taps at the same pressure as the reactor. The HgBr2 vapour at 338 K (equilibrium vapour pressure 7 mtorr41) was entrained in a flow of 100 sccm of N2. This flow was delivered by heated pipes to a mixing manifold, where it was mixed with the N2 carrier gas and O2/O3. The gas mixture was introduced into the reactor at the arms with optical ports to create gas curtains preventing deposition of reaction products on the inner sides of the windows (one of the horizontal arms was not used in these experiments and was blocked off). Under these conditions, the concentration of HgBr2 in the reactor was estimated to be ∼1013 molecule cm−3 from its equilibrium vapour pressure.21,42 O3 concentrations were monitored downstream of the reactor by UV absorption spectroscopy (see Fig. 1). The light from a Hg Pen-ray lamp was passed through a 1 m absorption cell and focussed into the entrance slit of a monochromator set at 257.3 nm (Optometrics, Mini-Chrom MC1-02, 300 μm slits) coupled to a photomultiplier (Hamamatsu, H9306-13). The signal was read from the screen of a digital oscilloscope. The minimum detectable O3 concentration was 1013 molecule cm−3, while the maximum O3 concentration safely within the Beer–Lambert law regime was around 5.5 × 1014 molecule cm−3. The O3 concentration was varied in this range to determine the rate constant of the title reaction.
UV light absorption of HgBr2 leads to photodissociation into HgBr + Br in various ground and excited states.43 Hence, photolysis of HgBr2 at 193 nm (ArF), 266 nm (4th Nd:YAG harmonic) or 248 nm (KrF) are convenient sources of HgBr.18,21,42,44 The absorption cross section of HgBr2 at 248 nm is σ = 2 × 10−18 cm2.43 For a laser fluence of 60 mJ cm−2 pulse−1, and [HgBr2] ∼ 1013 molecule cm−3, this results in [HgBr] ∼ 1012 molecule cm−3, assuming a unit quantum yield for HgBr formation. Similar HgBr concentrations have been estimated in previous experiments where this radical has been observed by LIF.21 A 248 nm photon does not have enough energy to generate HgBr in the B state, so the single photon KrF photolysis products of HgBr2 are ground state HgBr(X2Σ+) and Br.40 ArF photolysis, by contrast, produces 60% of HgBr in the B state,44 which would cause an initial fluorescence burst. The disadvantage of using KrF photolysis is that O3 photolyzes readily at this wavelength, producing O(1D). For a fluence of 60 mJ cm−2 pulse−1, 50% of O3 photolyzes. O(1D) is rapidly quenched to O(3P) by N2 and O2. O(3P) (hereafter O) is likely to react both with HgBr (R2) and BrHgO (R3)
| | HgBr + O → Hg + BrO ΔHr (298 K) = −168 kJ mol−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 26 26 | (R2) |
| | BrHgO + O → HgBr + O2 ΔHr (298 K) = −252 kJ mol−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 26 26 | (R3) |
It is however possible to disentangle the effect of
reactions (R1)–(R3) on the LIF decays of HgBr by performing experiments at different photolysis laser energies, provided that the post-photolysis concentrations of O and O
3 are well known. Hence, the use of KrF enables the determination of rate constants for three
reactions (R1)–(R3) that have not been previously studied experimentally.
Materials
N2 (99.9995%, BOC Gases), O2 (99.999%, BOC Gases) and HgBr2 (Merck, ACS grade) were used without further purification.
3. Results
The spectral proof of HgBr is shown in Fig. 2. The dye laser was scanned within the range allowed by Coumarin 510 in auto-tracked synchrony with the doubling crystal to obtain the excitation spectrum of HgBr between 252 nm and 259 nm. The wavelength positions of the observed bands are in agreement with the literature.39,40 The dye laser wavelength was then set to 512 nm (frequency-doubled to 256 nm) to carry out the kinetic study. Nine series of kinetic experiments were conducted where the initial O3 concentration ([O3]0) was varied for each LIF decay measured, while keeping the photolysis laser energy constant (see example in Fig. 3a). Two additional series were obtained by changing the laser energy while keeping [O3]0 constant (example shown in Fig. 3c). Each series comprises between eight and fifteen different decays, including two decays at [O3]0 = 0 to determine the background decay rate, which encompasses diffusional and chemical losses. The experimental conditions are listed in Table 1. The HgBr LIF decays are biexponential, with a fast and a slow component as shown in Fig. 3b and d. The fast component becomes faster with increasing [O3] (Fig. 3b, varying [O3] with photolysis laser energy constant). The second component results in a stronger recycling of HgBr for increasing [O] (Fig. 3d, varying photolysis laser energy with constant [O3]). In the absence of O3 the background loss of HgBr is slower by 1–2 orders of magnitude. This behaviour is explained by reactions (R1)–(R3), with the addition of diffusional and background chemical losses:The time dependence of HgBr and BrHgO can be obtained by integrating the system of two linear homogeneous first-order constant-coefficient ordinary differential equations (ODE) corresponding to reactions (E1)–(E5):| |  | (E1) |
| |  | (E2) |
The diffusional and background reactive losses of HgBr and HrBrO are assumed to proceed at the same rate 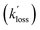 .
.
 |
| | Fig. 2 HgBr spectral proof: LIF excitation spectrum of HgBr in the wavelength range of 252.5–259.2 nm with a resolution of 0.0012 nm. The spectrum agrees well with previously reported spectra.18,21,39 | |
 |
| | Fig. 3 HgBr fluorescence signal as a function of photolysis-probe delay time (in microseconds) at 295 K and 17 torr. Panel (a) Raw LIF decays for different O3 concentrations at a fixed photolysis laser power (45 mJ pulse−1, 50% O3 photolysis): no O3 (squares), 1.7 × 1013 molecules cm−3 (triangles), 4.1 × 1013 molecules cm−3 (diamonds), 1.1 × 1014 molecules cm−3 (pentagons), 2.2 × 1014 molecules cm−3 (stars) and 4.5 × 1014 molecules cm−3 (circles). Panel (b) Decay of the LIF signal in panel a using a logarithmic scale, with biexponential decay fits (solid lines). Panel (c) Raw LIF decays for different photolysis laser energies at fixed initial ozone concentration ([O3]0 = 4.6 × 1014 molecule cm−3, except the squares, which correspond to no O3): 36 mJ pulse−1 (triangles), 21 mJ pulse−1 (diamonds), 14 mJ pulse−1 (pentagons), 7 mJ pulse−1 (stars) and 5 mJ pulse−1 (circles). Panel (d) Decay of the LIF signal in panel (c) using a logarithmic scale, with biexponential decay fits (solid lines). | |
Table 1 Experimental conditions and rate constants obtained for each series of experiments
|
P/torr |
E/mJ pulse−1 |
ϕ
|
[O3]0/1014![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
n
|
k
1/10−11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c c |
k
2/10−11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c c |
k
3/10−11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c c |
|
In molecule cm−3.
Number of decays with [O3]0 > 0.
In cm3 molecule−1 s−1. Errors are 1σ.
|
| 5 |
45 |
0.50 |
0.5–5.5 |
13 |
7.3 ± 1.6 |
5.3 ± 1.3 |
9.0 ± 1.8 |
| 30 |
41.5 |
0.49 |
0.5–5.5 |
8 |
7.3 ± 1.1 |
5.3 ± 0.8 |
8.4 ± 1.8 |
| 60 |
38 |
0.46 |
0.2–5.5 |
7 |
7.4 ± 1.1 |
6.0 ± 0.6 |
9.2 ± 1.0 |
| 17 |
6 |
0.10 |
0.4–5 |
6 |
8.8 ± 0.8 |
6.0 ± 0.8 |
9.8 ± 1.2 |
| 30 |
6–50 |
0.10–0.54 |
4.6 |
9 |
7.5 ± 1.5 |
5.0 ± 0.5 |
9.2 ± 1.0 |
| 17 |
6 |
0.09 |
0.2–4.5 |
6 |
8.7 ± 1.3 |
5.1 ± 1.0 |
7.1 ± 1.5 |
| 17 |
14 |
0.21 |
0.2–4.5 |
7 |
7.9 ± 1.0 |
5.4 ± 0.7 |
9.0 ± 0.9 |
| 17 |
43 |
0.51 |
0.2–4.5 |
6 |
7.7 ± 1.6 |
5.2 ± 0.7 |
8.8 ± 1.6 |
| 17 |
33 |
0.41 |
0.2–4.4 |
10 |
7.0 ± 1.6 |
4.6 ± 0.9 |
9.5 ± 1.7 |
| 17 |
23 |
0.30 |
0.2–4.6 |
8 |
6.4 ± 1.7 |
5.6 ± 0.9 |
10.2 ± 0.18 |
| 17 |
6–36 |
0.10–0.44 |
4.6 |
9 |
6.8 ± 0.7 |
4.9 ± 0.6 |
9.95 ± 0.18 |
The time dependence of HgBr is given by:45
| |  | (E3) |
where
C1 and
C2 are constants, and
| |  | (E4) |
By fitting the analytical expression
(E3) to the experimental decays the values of

and
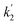
can be obtained. Effective rate constants
k1eff and
k2eff can be calculated by plotting

and

against [O
3]
0 and performing linear regressions (
Fig. 4a and b).
 |
| | Fig. 4 Examples of bimolecular-style plots of the bi-exponential decay rates  (panels a and c) and (panels a and c) and  (panels b and d) vs. the initial ozone concentration (panels a and b) and vs. the photolysis energy (panels c and d). The slopes of the plots in panels (a) and (b) are k1eff and k2eff, and are equal to the expressions given by (E4). Straight lines are linear regressions with error in both coordinates. The shaded area indicates the 95% confidence bands. The E = 6 mJ pulse−1 data (triangles) in panel a is an exception and corresponds to decay rates obtained by fitting straight lines to the logarithm of the fast part of the decays at that photolysis energy. In this case the slope of the (panels b and d) vs. the initial ozone concentration (panels a and b) and vs. the photolysis energy (panels c and d). The slopes of the plots in panels (a) and (b) are k1eff and k2eff, and are equal to the expressions given by (E4). Straight lines are linear regressions with error in both coordinates. The shaded area indicates the 95% confidence bands. The E = 6 mJ pulse−1 data (triangles) in panel a is an exception and corresponds to decay rates obtained by fitting straight lines to the logarithm of the fast part of the decays at that photolysis energy. In this case the slope of the  vs. [O3]0 plot is an approximation to k1 = k1eff (E = 0 mJ pulse−1). vs. [O3]0 plot is an approximation to k1 = k1eff (E = 0 mJ pulse−1). | |
3.1. Analytical estimation of rate constants
Fig. 4c and d show the dependence of  and
and 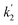 on photolysis laser energy for an experiment where the initial [O3] was kept constant. For [O] = 0, i.e. zero photolysis laser energy, the decay rates are given by
on photolysis laser energy for an experiment where the initial [O3] was kept constant. For [O] = 0, i.e. zero photolysis laser energy, the decay rates are given by  and
and 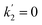 . Experiments at zero laser energy cannot be performed, because HgBr2 photolysis at 248 nm is the source of HgBr, but the rate constant of reaction (R1) can be estimated by linear extrapolation of the
. Experiments at zero laser energy cannot be performed, because HgBr2 photolysis at 248 nm is the source of HgBr, but the rate constant of reaction (R1) can be estimated by linear extrapolation of the  scatter plot (Fig. 4c) towards zero energy and dividing by the pre-photolysis ozone concentration ([O3]0). Similarly, k1 can be estimated by plotting k1eff from the series of experiments at constant laser energy and variable [O3] against laser energy (since most of these experiments series were acquired at different laser energies, see Table 1) and extrapolating towards zero energy (Fig. 5a). From these two calculations, an estimated value of k1 = (8.7 ± 1.0) × 10−11 cm3 molecule s−1 can be determined. Note that there is a hint of curvature in the
scatter plot (Fig. 4c) towards zero energy and dividing by the pre-photolysis ozone concentration ([O3]0). Similarly, k1 can be estimated by plotting k1eff from the series of experiments at constant laser energy and variable [O3] against laser energy (since most of these experiments series were acquired at different laser energies, see Table 1) and extrapolating towards zero energy (Fig. 5a). From these two calculations, an estimated value of k1 = (8.7 ± 1.0) × 10−11 cm3 molecule s−1 can be determined. Note that there is a hint of curvature in the 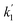 and k1effvs. energy plots, and therefore this value likely overestimates the true value of k1. As an alternative, the measurements with the lowest photolysis energy (6 mJ pulse−1) can be analysed as single exponential decays by masking the second section of the decay (equivalent to fit a straight line to the logarithm of the fast part of the decays, see e.g. the curve for the lowest photolysis energy in Fig. 3d). This relies on the fact that at zero energy
and k1effvs. energy plots, and therefore this value likely overestimates the true value of k1. As an alternative, the measurements with the lowest photolysis energy (6 mJ pulse−1) can be analysed as single exponential decays by masking the second section of the decay (equivalent to fit a straight line to the logarithm of the fast part of the decays, see e.g. the curve for the lowest photolysis energy in Fig. 3d). This relies on the fact that at zero energy  and
and 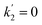 and (E3) becomes a single exponential with offset. Using this technique, linear fitting of the bimolecular plot of
and (E3) becomes a single exponential with offset. Using this technique, linear fitting of the bimolecular plot of  vs. [O3] (triangles in Fig. 4a) yields an estimate of k1 = (7.2 ± 0.3) × 10−11 cm3.
vs. [O3] (triangles in Fig. 4a) yields an estimate of k1 = (7.2 ± 0.3) × 10−11 cm3.
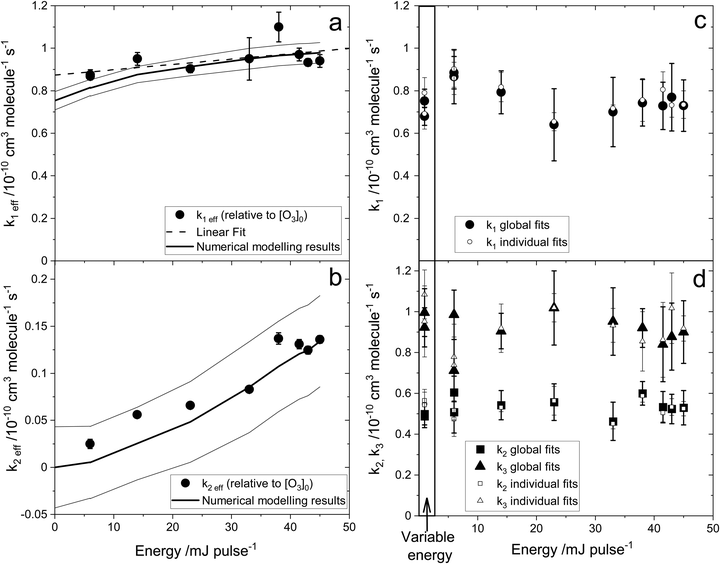 |
| | Fig. 5 Effective rate constants from analytical fitting of the observations (left panels) and true rate constants of (R1)–(R3) determined by fitting simulations to observations (right panels). Panel (a) Effective rate constants determined from  bimolecular plots like those in Fig. 4a (y0 = constant intercept) for 9 series of experiments where the energy is constant and [O3]0 is varied. The dashed line is a linear fit used to extrapolate to zero energy to estimate k1. The solid line is the reconstruction of k1eff using the average rate constants k1, k2 and k3 obtained by numerical modelling (the thin lines indicate the uncertainties of the reconstructed k1eff). Panel (b): As panel (a) for k2eff. Panel (c): k1 obtained by fitting simulated traces to observed decays for eleven datasets. The different determinations are plotted vs. photolysis energy, except for the symbols inside the rectangular box, which correspond to experiments with variable energy and constant [O3]0. Large full symbols and thick error bars refer to global series fits, with the corresponding error bar including the uncertainty in the [O3] and photolyzed fraction. Small empty symbols refer to the averages of the individual fits within each series, with the error bar indicating only the spread of the determinations within each series. Panel (d): As panel (c) for k2 and k3. bimolecular plots like those in Fig. 4a (y0 = constant intercept) for 9 series of experiments where the energy is constant and [O3]0 is varied. The dashed line is a linear fit used to extrapolate to zero energy to estimate k1. The solid line is the reconstruction of k1eff using the average rate constants k1, k2 and k3 obtained by numerical modelling (the thin lines indicate the uncertainties of the reconstructed k1eff). Panel (b): As panel (a) for k2eff. Panel (c): k1 obtained by fitting simulated traces to observed decays for eleven datasets. The different determinations are plotted vs. photolysis energy, except for the symbols inside the rectangular box, which correspond to experiments with variable energy and constant [O3]0. Large full symbols and thick error bars refer to global series fits, with the corresponding error bar including the uncertainty in the [O3] and photolyzed fraction. Small empty symbols refer to the averages of the individual fits within each series, with the error bar indicating only the spread of the determinations within each series. Panel (d): As panel (c) for k2 and k3. | |
For the determination of the rate constants of reactions (R2) and (R3), the two equations in (E4) may be rearranged as follows:
| |  | (E5) |
| |  | (E6) |
where
C = 1/
ϕ − 1 and
ϕ = Δ[O
3]/[O
3]
0 = [O]/[O
3]
0 is the ozone photolyzed fraction, which depends on the photolysis laser energy. As an alternative to
(E6):
| |  | (E7) |
The slopes of the bimolecular plots
 vs.
vs. [O] and
 vs.
vs. [O]
2 can be determined by linear regression. If the slopes of
(E5) and
(E6) (or
(E5) and
(E7)) are equated to the regression values, a system of two equations with three unknowns results. Since
k1 has been determined by extrapolation to zero laser energy as explained above, these two equations may be used in principle to determine the remaining unknows (
k2 and
k3). However,
(E6) and
(E7) involve quadratic terms that magnify relatively small errors in the experimentally determined slopes. The first estimate of
k1 (8.6 × 10
−11 cm
3 molecule s
−1) is likely too high, because it produces negative numbers under square roots. By using the second estimate of
k1 (7.2 × 10
−11 cm
3 molecule
−1 s
−1) reasonable values are obtained, with
k2 = 5 × 10
−11 cm
3 molecule
−1 s
−1 and
k3 = 10
−10 cm
3 molecule
−1 s
−1. However, the propagated uncertainties are large, especially for
k2 (50% errors are obtained). In summary, this method is unsuitable for the determination of
k2 and
k3, although it provides useful information for fitting a numerical model to the observations.
3.2. Determination of k1, k2 and k3 by numerical modelling
A simple kinetic numerical model including reactions (R1)–(R5) was therefore constructed to simulate the time-dependent behaviour of HgBr. Quenching of O(1D) by N2 and O3 occurs on sub-μs time scales, and hence does not interfere in the chemistry under study. The experiments were performed at a range of pressures (Table 1) for which the recombination of O and O2 occurs in hundreds of ms and therefore can also be neglected compared to the μs to ms time scale of the observed decays. Reactions of HgBr2 with O, O2(1Δ) and O3 are endothermic. The reaction HgBr2 + O(1D) → HgBr + BrO is exothermic, but O(1D) is quenched very rapidly and does not have a chance to react with any other species in this system. Interferences by second-order chemistry are expected to be negligible considering the low concentration of radicals generated by HgBr2 photolysis (of the order of 1012 cm−3). Thermochemically possible reactions generating or removing HgBr are:| | Hg + Br → HgBr ΔHr (298 K) = −69 kJ mol−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 26 26 | (R6) |
| | HgBr + HgBr → HgBr2 + Hg ΔHr (298 K) = −234 kJ mol−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 26 26 | (R7) |
| | HgBr + Br → HgBr2 ΔHr (298 K) = −301 kJ mol−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 26 26 | (R8a) |
| | → Hg + Br2 ΔHr (298 K) = −123 kJ mol−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 26 26 | (R8b) |
Reaction (R6) has a rate constant of k6 = 9.5 × 10−14 cm3 molecule−1 s−1 at 200 torr and 298 K,13 and therefore it is too slow to significantly regenerate HgBr on sub-second time scales. An upper limit of 5 × 10−16 cm3 molecule−1 s−1 has been determined for the rate constant of reaction (R7),46 which is also too slow. Reaction (R8a) is close to its high-pressure limit at 1 bar, with a theoretical estimate of k8a = 2.5 × 10−10 cm3 molecule−1 s−1 at 298 K.14 There are no estimates of this rate constant at pressures relevant for this study. Reaction (R8b) is barrierless47 and theoretical predictions of its rate constant are around 5 × 10−11 cm3 molecule−1 s−1 at 298 K.48 However, even if the overall process R8 proceeds at ∼2 × 10−10 cm3 molecule−1 s−1, the first order removal rate of HgBr would be k′8 ∼ 200 s−1, which is of the order of the HgBr background loss rates observed in the present study in the absence of O3. Hence, we consider this potential chemical loss of HgBr to be encompassed in the measured  .
.
The differential equations corresponding to the chemical mechanism (R1)–(R5) were integrated using an ODE integrator available within the Matlab ODE toolbox. The simulated time traces were then fitted to the observed data using a constrained nonlinear least-squares routine with the rate constants k1, k2 and k3 as floating parameters. The background loss rates of HgBr and HgBrO (R4) and (R5) were set to the loss rates measured experimentally for HgBr (100–300 s−1). The rate coefficients of interest were then obtained by fitting the [HgBr] vs. time curves measured for different [O3]0 or laser energies. The first point of the decay was taken as [HgBr]0 and the estimates of k1, k2 and k3 obtained from the biexponential analysis (see above) were used as initial guesses of the rate constants in the non-linear optimization of χ2. Individual fits of each HgBr time trace can be performed, but global fits of complete series of experiments are preferred since they provide a more robust determination of the free parameters. In a similar manner to a bimolecular plot for a single reaction under first order conditions, a global fit yields parameter optimized across a range of conditions (regression of k′ vs. the concentration of the reactant in excess). Typical results are shown in Fig. 6 (constant laser energy) and Fig. 7 (constant [O3]0). Contour plots of χ2 for the global fit of the data in Fig. 7 are shown in Fig. 8. Here, we map the values of χ2 by varying two rate constants while keeping one fixed. It can be seen that a global of χ2 minimum for the three parameters is well defined. The results of the global fits of the eleven series of experiments are listed in Table 1. The global fit optimized parameters and the averages of the individual fits are compared in Fig. 5c and d, showing good agreement.
 |
| | Fig. 6 Global fit of nine HgBr decays (concentration in arbitrary units, a.u.) with varying [O3]0 at constant laser energy. The solid red lines along the decays (circles) are the simulated curves fitted to the data and the squares are the fit residuals. | |
 |
| | Fig. 7 As Fig. 6 for nine HgBr decays with varying laser energy at constant [O3]0. The green, blue and cyan lines correspond to fit results for k9 = 5 × 10−11 cm3 molecule−1 s−1, k9 = 10−11 cm3 molecule−1 s−1 and k9 = 2 × 10−11 cm3 molecule−1 s−1, respectively. Green, blue and cyan simulated traces are only shown in those panels where they do not overlap with the red traces. Note that for the bottom right panel the residual is shifted by an arbitrary constant for clarity. | |
 |
| | Fig. 8 Colour contour plots of χ2 for global fitting of the data in Fig. 7 using the numerical model with reactions (R1)–(R5). Panel (a): χ2 dependence on k2 and k3 (k1 fixed at the optimal value). Panel (b): χ2 dependence on k3 and k1 (k2 fixed at the optimal value). Panel (c): χ2 dependence on k1 and k2 (k3 fixed at the optimal value). The symbols indicate the optimal values of k1, k2 and k3 obtained from the global fit. The solid white contours indicate the region enclosing 68% of the data generated in 1000 Monte Carlo runs where the [O3] and [O] concentrations are varied randomly within their uncertainties. The dashed line indicates the boundary of the data generated in these Monte Carlo simulations. | |
In order to propagate the uncertainties of the ozone concentration, the photolyzed fraction and the background removal rates, Monte Carlo selection of these model parameters within their uncertainties was performed. The kinetic model and the non-linear fitting were run for each random variation of the parameters to obtain new optimized fits. For each series of experiments, the standard deviation of the three rate constants obtained from 1000 global fits provides the estimated uncertainty propagated from the model parameters. The white line contours in Fig. 8 show the χ2 region containing 68% of the fit results generated in the Monte Carlo runs corresponding to the data series shown in Fig. 7. The uncertainties in Table 1 combine the propagated uncertainties and the formal parameter fit errors.
The average rate constants for (R1)–(R3) at 298 K are k1 = (7.5 ± 0.6) × 10−11 cm3 molecule s−1, k2 = (5.3 ± 0.4) × 10−11 cm3 molecule s−1 and k3 = (9.1 ± 0.6) × 10−11 cm3 molecule s−1. The errors at 1σ level encompass the formal error of the fits and the uncertainties in [O3] and [O]. With these values, it is possible to reconstruct the energy dependence of the effective rate constants obtained from biexponential fitting of the decays (Fig. 5a and b).
3.3. Other secondary chemistry
Regarding interferences from other reactions that may have been overlooked, the main candidates are:| | BrHgO + O3 → BrHg + O2 + O2 ΔHr (298 K) = −143 kJ mol−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15 15 | (R9) |
| | BrHgO + O3 → BrHgO2 + O2 ΔHr (298 K) = −171 kJ mol−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15,26 15,26 | (R10) |
BrHgO2 is bound by only −27 kJ mol−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15 with respect to BrHg + O2, so given the exothermicity of (R10) it is likely that the only pathway at room temperature is (R9). A number of model runs were therefore conducted replacing (R3) by (R9) to test if the recycling of HgBr is driven by O3 rather than O. For those series of experiments where the photolysis energy was fixed and [O3]0 varied, global fits of similar quality to those with (R3) were obtained. However, the values of k9 obtained for series at different energies are significantly different. For example, k9 is one order of magnitude larger at 45 mJ pulse−1 compared with 6 mJ pulse−1. The global fits of the two series of experiments where the energy was varied and [O3]0 was constant are poor. The fits of individual traces within these two series are good, yet again the k9 values extracted from every trace depend on [O3], showing a linear dependence with negative slope and an order of magnitude difference between the lowest and highest energy. Obviously, the extracted rate constants must be independent of the concentration of the excess reactant, which is the case of the original model (see Table 1) including (R3) instead of (R9). Hence, we conclude that the main HgBr recycling pathway is (R3).
15 with respect to BrHg + O2, so given the exothermicity of (R10) it is likely that the only pathway at room temperature is (R9). A number of model runs were therefore conducted replacing (R3) by (R9) to test if the recycling of HgBr is driven by O3 rather than O. For those series of experiments where the photolysis energy was fixed and [O3]0 varied, global fits of similar quality to those with (R3) were obtained. However, the values of k9 obtained for series at different energies are significantly different. For example, k9 is one order of magnitude larger at 45 mJ pulse−1 compared with 6 mJ pulse−1. The global fits of the two series of experiments where the energy was varied and [O3]0 was constant are poor. The fits of individual traces within these two series are good, yet again the k9 values extracted from every trace depend on [O3], showing a linear dependence with negative slope and an order of magnitude difference between the lowest and highest energy. Obviously, the extracted rate constants must be independent of the concentration of the excess reactant, which is the case of the original model (see Table 1) including (R3) instead of (R9). Hence, we conclude that the main HgBr recycling pathway is (R3).
Nevertheless, (R9) could coexist with (R3) and regenerate a minor fraction of HgBr. To determine an upper limit for this reaction, we performed a second set of sensitivity tests with the two datasets obtained at varying laser energies including (R9) in the model alongside (R3). When k9 is floated with the rest of the parameters, similar χ2 values to the original model are obtained for k9 ∼ 10−13 cm3 molecule−1 s−1. When k9 is set at different values between 10−13 cm3 molecule−1 s−1 and 2 × 10−11 cm3 molecule−1 s−1 and the other rate constants are floated, the fits become increasingly poor with increasing k9, and the optimal values of k1 and k3 also change (e.g. k1 is 20% higher and k3 25% lower for k9 = 2 × 10−11 cm3 molecule−1 s−1). Fig. 7 shows that the increasingly poor quality of the fits results mainly from the low photolysis energy (high [O3]) traces, and in particular from the plateau that follows the initial decay. The green trace (k9 = 5 × 10−12 cm3 molecule−1 s−1) in the lowest energy trace ([O3] = 4.6 × 1014 molecule cm−3, bottom right panel) is outside of the 2σ band of the data between 0.2 and 0.8 ms. Hence, we take k9 < 5 × 10−12 cm3 molecule−1 s−1. For this upper limit the rate constants of reactions (R1)–(R3) are essentially the same within error as those listed in Table 1.
4. Discussion
4.1. HgBr + O3
Saiz-Lopez et al.4 found no energy constrains on the title reaction at the B3LYP/aug-cc-pVQZ level of theory and estimated an upper limit of k1 ≤ 10−10 cm3 molecule−1 s−1, which corresponds to a hard sphere collision radius of 2.9 Å at a temperature of 285 K. This is an upper limit because it does not account for steric constraints. Subsequent work by Shah et al.5 confirmed the absence of barriers in the potential energy surface (PES) at different levels of theory. Preliminary kinetic data cited in that work indicates a rate coefficient of the order of k1 ∼ 10−11 cm3 molecule−1 s−1, although Shah et al. recommend a value of k1 = 3 × 10−11 cm3 molecule−1 s−1. Our experimental result of k1 = 7.5 × 10−11 cm−3 molecule−1 s−1 indicates that steric constraints may in fact play a role, although the lower experimental estimate by Shah et al. suggests that the recycling of HgBr via(R3) has not been considered in their preliminary analysis.
4.2. HgBr + O
No experimental rate constants or product studies have been published, although there have been some previous studies of chemical systems where this reaction may have played a role. Photolysis of HgBr2 followed by (R1)–(R3), and in particular reduction of HgI to Hg0via(R2), may explain the large photoreduction of HgBr2 observed in recently published steady state experiments in the presence of O3 and UV light.49 Direct reaction between atomic O and HgBr2 is proposed in that study as the first reduction step but note that reactions between O and HgX2 (X = Br, Cl) are endothermic.
This is an interesting reaction that belongs to the Hg–Br–O PES. HgBr + O is one of the endothermic product channels of the Hg + BrO reaction, which has been examined in the past as a potential atmospheric Hg0 oxidation pathway. The rate constant of Hg + BrO has not been determined but its products have been studied experimentally, and mass spectrometric evidence of BrHgO (which cannot be distinguished from its geometric isomers, HgBrO and HgOBr) was found in the condensed phase.50 The PES of this system has been partially studied using ab initio methods.28,48,51,52 The isomers HgBrO and HgOBr have been found to be weakly bound against dissociation to Hg + BrO,52 and a barrier of ∼167 kJ mol−1 has been reported for the insertion of Hg48 into BrO. A HgBrO–BrHgO isomerization barrier can also be expected. On these grounds, the Hg + BrO reaction is not believed to be an important Hg0 oxidation pathway. Coming back to the forward reaction HgBr + O, it is worth noting that BrHgO is stable against dissociation (D(BrHg–O) = −250 kJ mol−1). We estimate the energy of the BrHgO–HgBrO isomerization barrier to be −18 kJ mol−1 below HgBr + O (see computational details below), which indicates that (R2) proceeds to Hg + BrO in all HgBr–O collision geometries.
4.3. BrHgO + O
The formation of an adduct is very exothermic (−273 kJ mol−1) but as mentioned above BrHgO2 is bound by only −27 kJ mol−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15 with respect to BrHg + O2. The HgO + BrO product channel is endothermic by 67 kJ mol−1. Therefore, it is likely that the only channel of (R3) at room temperature is HgBr + O2.
15 with respect to BrHg + O2. The HgO + BrO product channel is endothermic by 67 kJ mol−1. Therefore, it is likely that the only channel of (R3) at room temperature is HgBr + O2.
4.4. BrHgO + O3
Recent calculations suggest that the main fate of BrHgO in the troposphere is reaction with methane:| | BrHgO + CH4 → BrHgOH + CH3 (ΔHr (298 K) = −45 kJ mol−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25) 25) | (R11) |
The calculated rate constant for (R11) is k11 = 2.3 × 10−13 cm−3 molecule−1 s−1,25 resulting in a tropospheric removal rate of 0.1 s−1 (1.5 ppmv of CH4). The PES of (R11) has a barrier of 11 kJ mol−1 at CCSD(T)/M06-2X/AVTZ level of theory.25 If the rate constant of (R9) was close to the upper limit determined above, k9 < 5 × 10−12 cm−3 molecule−1 s−1, this would imply a loss rate of 0.1 s−1 for 80 ppbv of O3. Therefore, at the upper limit determined in this work, (R9) would be a competitive loss of BrHgO in the troposphere.
In order to assess the importance of (R9) compared to (R11), we have carried out ab initio calculations on its PES. The Gaussian 16 package53 has been used to perform hybrid density functional calculations (B3LYP) together with Dunning's quadruple-ζ aug-cc-pVQZ correlation consistent basis, augmented with diffuse functions.54 For Hg, the aug-cc-pVQZ basis set of was used. Molecular geometries were first optimized and checked for wave function stability. We have obtain a barrier at the B3LYP/aug-cc-pVQZ level of theory for reaction (R11) of 10 kJ mol−1, in agreement with the published value.25 Regarding (R9), our results indicate that O3 does not attack the O end of BrHgO. Instead, it forms a very weak complex with the Hg atom. There is then a barrier of 84 kJ mol−1 to forming BrOHgO + O2 (formation of BrOHgO + O2 is exothermic by 95 kJ mol−1). Therefore, our conclusion is that O3 does not react with BrHgO.
4.5. Atmospheric implications
Our results confirm that the title reaction is the main global oxidation process of HgI to HgII, as proposed by Saiz-Lopez et al.4 Previous work assumed that oxidation of HgBr by HO2 and NO2 were the main routes towards HgII. These reactions have similar rate constants under surface conditions to that of HgBr + O3, but O3 is far more abundant. Hence, we recommend that (R1) should now be considered part of the established atmospheric cycle of mercury. Note that (R1) would still dominate over (R8a) even during extreme polar ozone depletion events (e.g. for 1 ppbv of O3 and 20 pptv of Br, (R1) would be ∼15 times faster than (R8a)).
The reaction product, BrHgO, has not been detected in the gas phase. Ab initio calculations of the excited states of this radical have been published recently,29 indicating a strong absorption band in the UV-visible, peaking at 400 nm (σ ∼ 3 × 10−18 cm2 molecule−1) and two weaker bands in the visible range. This results in a global tropospheric photolysis rate of 3 × 10−2 s−1 and a lifetime of 33 s. However, the estimated removal rate by methane in the troposphere is 0.1 s−1, which is somewhat faster than the estimated photolysis rate. BrHgOH is processed by aerosol to particulate HgII, which can undergo photoreduction or be reemitted to the gas phase as HgIIX (X = Br, Cl).5 Calculations also indicate that BrHgOH has a short photolytic lifetime of approximately 1 day, leading to regeneration of Hg0 and increasing the atmospheric lifetime of mercury.29
5. Conclusions
We have carried out the first kinetic study of the reaction between HgBr and ozone using the PLP-LIF technique. As usual in the context of mercury chemistry, the oxidation process is partially reversible, in this case due to the presence of atomic oxygen generated by the photolysis of ozone. This therefore requires careful consideration of secondary chemistry in the analysis of the LIF decays, in order to obtain an accurate rate constant. Hence, we have also determined the rate constants for the reduction of HgBr and BrHgO by atomic oxygen, which have not been reported previously. Our results show that the recent theoretical predictions for the title reaction are essentially correct and confirm that reaction with O3 is globally the main atmospheric fate of the HgBr radical. Many other reactions of the mercury cycle remain to be examined experimentally in order to validate the theoretical estimates of their rate constants. Additional efforts are needed to develop techniques for detecting HgII compounds that enable their reaction kinetics and photochemistry to be studied.
Data availability
The datasets supporting this article have been uploaded as part of the ESI.†
Author contributions
Conceptualization: J. C. G. M., J. M. C. P., A. S.-L.; formal analysis: J. C. G. M.; funding acquisition: A. S.-L.; investigation: J. C. G. M., T. R. L.; methodology: J. C. G. M., M. A. B., K. M. D.; writing – original draft: J. C. G. M.; writing – review & editing: M. A. B., K. M. D., J. M. C. P., A. S.-L.
Conflicts of interest
There are no conflicts of interest to declare.
Acknowledgements
J. C. G. M. acknowledges financial support from the State Agency for Research of the Spanish MCINN through the “Center of Excellence Severo Ochoa” award to the Instituto de Astrofísica de Andalucía (SEV-2017-0709) and the Ramon y Cajal Program (RYC-2016-19570). This study has received funding from the European Research Council Executive Agency under the European Union's Horizon 2020 Research and Innovation programme (Project ‘ERC-2016-COG 726349 CLIMAHAL’).
References
- P. A. Ariya, M. Amyot, A. Dastoor, D. Deeds, A. Feinberg, G. Kos, A. Poulain, A. Ryjkov, K. Semeniuk, M. Subir and K. Toyota, Mercury Physicochemical and Biogeochemical Transformation in the Atmosphere and at Atmospheric Interfaces: A Review and Future Directions, Chem. Rev., 2015, 115, 3760–3802 CrossRef CAS PubMed.
- L. Si and P. A. Ariya, Recent Advances in Atmospheric Chemistry of Mercury, Atmosphere, 2018, 9, 76 CrossRef.
- S. N. Lyman, I. Cheng, L. E. Gratz, P. Weiss-Penzias and L. Zhang, An updated review of atmospheric mercury, Sci. Total Environ., 2020, 707, 135575 CrossRef CAS PubMed.
- A. Saiz-Lopez, O. Travnikov, J. E. Sonke, C. P. Thackray, D. J. Jacob, J. Carmona-García, A. Francés-Monerris, D. Roca-Sanjuán, A. Ulises Acuña, J. Z. Dávalos, C. A. Cuevas, M. Jiskra, F. Wang, J. Bieser, J. M.-C. Plane and J. S. Francisco, Photochemistry of oxidized Hg(I) and Hg(II) species suggests missing mercury oxidation in the troposphere, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 30949–30956 CrossRef CAS PubMed.
- V. Shah, D. J. Jacob, C. P. Thackray, X. Wang, E. M. Sunderland, T. S. Dibble, A. Saiz-Lopez, I. Cernusák, V. Kellö, P. J. Castro, R. Wu and C. Wang, Improved mechanistic model of the atmospheric redox chemistry of mercury, Environ. Sci. Technol., 2021, 55, 14445–14456 CrossRef CAS PubMed.
- H. M. Horowitz, D. J. Jacob, Y. Zhang, T. S. DIbble, F. Slemr, H. M. Amos, J. A. Schmidt, E. S. Corbitt, E. A. Marais and E. M. Sunderland, A new mechanism for atmospheric mercury redox chemistry: Implications for the global mercury budget, Atmos. Chem. Phys., 2017, 17, 6353–6371 CrossRef CAS.
-
AMAP/UN, Technical Background Report for the Global Mercury Assessment, 2018. Arctic monitoring assessment programme Oslo, Norway/UN environment programme chemical health branch, Geneva, Switzerland, 2019.
- A. Saiz-Lopez, S. P. Sitkiewicz and D. Roca-Sanjuán,
et al., Photoreduction of gaseous oxidized mercury changes global atmospheric mercury speciation, transport and deposition, Nat. Commun., 2018, 9, 4796, DOI:10.1038/s41467-018-07075-3.
- A. Saiz-Lopez, A. U. Acuña, T. Trabelsi, J. Carmona-García, J. Z. Dávalos, D. Rivero, C. A. Cuevas, D. E. Kinnison, S. P. Sitkiewicz, D. Roca-Sanjuán and J. S. Francisco, Gas-Phase Photolysis of Hg(I) Radical Species: A New Atmospheric Mercury Reduction Process, J. Am. Chem. Soc., 2019, 141, 8698–8702 CrossRef CAS PubMed.
- M. Subir, P.-a Ariya and A. P. Dastoor, A review of uncertainties in atmospheric modeling of mercury chemistry I. Uncertainties in existing kinetic parameters - Fundamental limitations and the importance of heterogeneous chemistry, Atmos. Environ., 2011, 45, 5664–5676 CrossRef CAS.
- P. A. Ariya, H. Skov, M. M.-L. Grage and M. E. Goodsite, Gaseous Elemental Mercury in the Ambient Atmosphere: Review of the Application of Theoretical Calculations and Experimental Studies for Determination of Reaction Coefficients and Mechanisms with Halogens and Other Reactants, Adv. Quantum Chem., 2008, 55, 43–55 CrossRef CAS.
- C. D. Holmes, D. J. Jacob, E. S. Corbitt, J. Mao, X. Yang, R. Talbot and F. Slemr, Global atmospheric model for mercury including oxidation by bromine atoms, Atmos. Chem. Phys., 2010, 10, 12037–12057 CrossRef CAS.
- D. L. Donohoue, D. Bauer, B. Cossairt and A. J. Hynes, Temperature and pressure dependent rate coefficients for the reaction of Hg with Br and the reaction of Br with Br: A pulsed laser photolysis-pulsed laser induced fluorescence study, J. Phys. Chem. A, 2006, 110, 6623–6632 CrossRef CAS PubMed.
- M. E. Goodsite, J. M.-C. Plane and H. Skov, A Theoretical Study of the Oxidation of Hg0 to HgBr2 in the Troposphere, Environ. Sci. Technol., 2004, 38, 1772–1776 CrossRef CAS PubMed.
- T. S. Dibble, M. J. Zelie and H. Mao, Thermodynamics of reactions of ClHg and BrHg radicals with atmospherically abundant free radicals, Atmos. Chem. Phys., 2012, 12, 10271–10279 CrossRef CAS.
- Y. Jiao and T. S. Dibble, Quality Structures, Vibrational Frequencies, and Thermochemistry of the Products of Reaction of BrHg. with NO2, HO2, ClO, BrO, and IO, J. Phys. Chem. A, 2015, 119, 10502–10510 CrossRef CAS PubMed.
- Y. Jiao and T. S. Dibble, First kinetic study of the atmospherically important reactions BrHg˙ + NO2 and BrHg˙ + HOO, Phys. Chem. Chem. Phys., 2017, 19, 1826–1838 RSC.
-
D. L. Donohoue, PhD thesis, University of Miami, 2008.
- A. C. Erlandson and T. A. Cool, On the regeneration mechanism of HgBr/2 in HgBr/HgBr2 dissociation lasers, Chem. Phys. Lett., 1983, 96, 685–689 CrossRef CAS.
- J. H. Parks, Laser action on the B2Σ + 1/2 → X2Σ + 1/2 band of HgBr at 5018 Å, Appl. Phys. Lett., 1977, 31, 297 CrossRef CAS.
- R. Wu, C. Wang and T. S. Dibble, First experimental kinetic study of the atmospherically important reaction of BrHg + NO2, Chem. Phys. Lett., 2020, 759, 137928 CrossRef CAS.
- C. Roxlo and A. Mandl, Vacuum ultraviolet absorption cross sections for halogen containing molecules, J. Appl. Phys., 1980, 51, 2969 CrossRef CAS.
- Y. Jiao and T. S. Dibble, Structures, Vibrational Frequencies, and Bond Energies of the BrHgOX and BrHgXO Species Formed in Atmospheric Mercury Depletion Events, J. Phys. Chem. A, 2017, 121, 7976–7985 CrossRef CAS PubMed.
- K. T. Lam, C. J. Wilhelmsen and T. S. Dibble, BrHgO + C2H4 and BrHgO + HCHO in Atmospheric Oxidation of Mercury: Determining Rate Constants of Reactions with Prereactive Complexes and Bifurcation, J. Phys. Chem. A, 2019, 123, 6045–6055 CrossRef CAS PubMed.
- K. T. Lam, C. J. Wilhelmsen, A. C. Schwid, Y. Jiao and T. S. Dibble, Computational Study on the Photolysis of BrHgONO and the Reactions of BrHgO ¢ with CH4, C2H6, NO, and NO2: Implications for Formation of Hg(II) Compounds in the Atmosphere, J. Phys. Chem. A, 2019, 123, 1637–1647 CrossRef CAS PubMed.
- F. J. Guzman and J. Bozzelli, Thermodynamics of OHgX, XHgOH, XHgOCl, XHgOBr, and HOHgY Gaseous Oxidized Mercury Molecules from Isodesmic, Isogyric, and Atomization Work Reactions (X = Halogen, y = OH, OCl, OBr), J. Phys. Chem. A, 2019, 123, 4452–4464 CrossRef CAS PubMed.
- D. Khiri, F. Louis, I. Černušák and T. S. Dibble, BrHgO˙ + CO: Analogue of OH + CO and Reduction Path for Hg(II) in the Atmosphere, ACS Earth Sp. Chem., 2020, 4, 1777–1784 CrossRef CAS.
- N. B. Balabanov and K.-a Peterson, Mercury and Reactive Halogens: The Thermochemistry of Hg + {Cl2, Br2, BrCl, ClO, and BrO}, J. Phys. Chem. A, 2003, 107, 7465–7470 CrossRef CAS.
- A. Francés-Monerris, J. Carmona-García, A. U. Acuña, J. Z. Dávalos, C. A. Cuevas, D. E. Kinnison, J. S. Francisco, A. Saiz-Lopez and D. Roca-Sanjuán, Photodissociation Mechanisms of Major Mercury(II) Species in the Atmospheric Chemical Cycle of Mercury, Angew. Chem., 2020, 132, 7675–7680 CrossRef.
- C. P. Jones, S. N. Lyman, D. A. Jaffe, T. Allen and T. L. O’Neil, Detection and quantification of gas-phase oxidized mercury compounds by GC/MS, Atmos. Meas. Tech., 2016, 9, 2195–2205 CrossRef CAS.
- A. F. Khalizov, F. J. Guzman, M. Cooper, N. Mao, J. Antley and J. Bozzelli, Direct detection of gas-phase mercuric chloride by ion drift - Chemical ionization mass spectrometry, Atmos. Environ., 2020, 238, 117687 CrossRef CAS.
- T. S. Dibble, M. J. Zelie and Y. Jiao, Quantum chemistry guide to PTRMS studies of as-yet undetected products of the bromine-atom initiated oxidation of gaseous elemental mercury, J. Phys. Chem. A, 2014, 118, 7847–7854 CrossRef CAS PubMed.
- J. M.-C. Plane, Atmospheric Chemistry of Meteoric Metals, Chem. Rev., 2003, 103, 4963–4984 CrossRef CAS PubMed.
- J. M.-C. Plane, W. Feng and E. C.-M. Dawkins, The Mesosphere and Metals: Chemistry and Changes, Chem. Rev., 2015, 115, 4497–4541 CrossRef CAS PubMed.
- T. P. Mangan, K. M. Douglas, R. E. Lade, D. Gobrecht, L. Decin and J. M.-C. Plane, Kinetic Study of the Reactions of AlO with H2O and H2; Precursors to Stellar Dust Formation, ACS Earth Space Chem., 2021, 5, 3395 Search PubMed.
- T. P. Mangan, N. McAdam, S. M. Daly and J. M.-C. Plane, Kinetic Study of Ni and NiO Reactions Pertinent to the Earth's Upper Atmosphere, J. Phys. Chem. A, 2019, 123, 601–610 CrossRef CAS PubMed.
- J. C. Gómez Martín, M.-a Blitz and J. M.-C. Plane, Kinetic studies of atmospherically relevant silicon chemistry. Part II: silicon monoxide reactions, Phys. Chem. Chem. Phys., 2009, 11, 10945–10954 RSC.
- J. C. Gómez Martín, M. A. Blitz and J. M.-C. Plane, Kinetic studies of atmospherically relevant silicon chemistry: Part I: Silicon atom reactions, Phys. Chem. Chem. Phys., 2009, 11, 671–678 RSC.
- G. Greig, H. E. Gunning and O. P. Strausz, Reactions of Metal Atoms. II. The Combination of Mercury and Bromine Atoms and the Dimerization of HgBr, J. Chem. Phys., 1970, 52, 3684 CrossRef CAS.
- D. Zevgolis and P. Papagiannakopoulos, Krypton monofluoride laser multiphoton dissociation of mercuric bromide, J. Phys. Chem., 1988, 92, 4654–4658 CrossRef CAS.
-
J. R. Rumble, T. J. Bruno and M. J. Doa, CRC handbook of chemistry and physics: a ready-reference book of chemical and physical data, 2021 Search PubMed.
- X. Tong, R. B. Barat and A. T. Poulos, Detection of Mercuric Bromide in a Gas Phase Flow Cell by Laser Photofragment Fluorescence Spectroscopy, Environ. Sci. Technol., 1999, 33, 3260–3263 CrossRef CAS.
- J. Maya, Ultraviolet absorption cross sections of HgI2, HgBr2, and tin(II) halide vapors, J. Chem. Phys., 1977, 67, 4976 CrossRef CAS.
- N. H. Cheung, J. A. McGarvey, A. C. Erlandson and T. A. Cool, The vibrational distribution of HgBr (X2Σ) molecules formed by photodissociation of HgBr2 at (193 nma), J. Chem. Phys., 1998, 77, 5467 CrossRef.
-
A. D. Polyanin and V. F. Zaitsev, Handbook of ordinary differential equations: Exact solutions, methods, and problems, CRC Press, 2017 Search PubMed.
- A. M. Schilowitz and J. R. Wiesenfeld, Time-resolved study of mercury atom production and removal following the photolysis of HgBr2 at 193 nm, Chem. Phys. Lett., 1982, 89, 438–442 CrossRef CAS.
- G. Q. Ren, A. P. Fu, S. P. Yuan and T. S. Chu, The dynamics of the Br + HgBr (v = 0, j = 0) → Br2 + Hg reaction based on quasi-classical trajectory calculations, Can. J. Phys., 2018, 96, 926–932 CrossRef CAS.
- N. B. Balabanov, B. C. Shepler and K. A. Peterson, Accurate Global Potential Energy Surface and Reaction Dynamics for the Ground State of HgBr2, J. Phys. Chem. A, 2005, 109, 8765–8773 CrossRef CAS PubMed.
- Y. Tong, H. Zhang, H. Lin, B. de Foy, L. Chen, W. Zhang, X. Wang and C. Guan, A potential route for photolytic reduction of HgCl2 and HgBr2 in dry air and analysis about the impacts from Ozone, Atmos. Res., 2021, 249, 105310 CrossRef CAS.
- F. Raofie, G. Snider and P. A. Ariya, Reaction of gaseous mercury with molecular iodine, atomic iodine, and iodine oxide radicals—Kinetics, product studies, and atmospheric implications, Can. J. Chem., 2008, 86, 811–820 CrossRef CAS.
- N. B. Balabanov and K. A. Peterson, Accurate theoretical near-equilibrium potential energy and dipole moment surfaces of HgClO and HgBrO, J. Chem. Phys., 2004, 120, 6585 CrossRef CAS PubMed.
-
B. C. Shepler, PhD thesis, Whashington State University, 2006.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci and D. J. Hratch, Gaussian 16 Rev. C.01, Wallingford CT, 2016 Search PubMed.
- D. E. Woon and T. H. Dunning, Gaussian basis sets for use in correlated molecular calculations. III. The atoms aluminum through argon, J. Chem. Phys., 1993, 98, 1358–1371 CrossRef CAS.
|
| This journal is © the Owner Societies 2022 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
Thomas R.
Lewis
bc,
Kevin M.
Douglas
c,
Mark A.
Blitz
*a,
Thomas R.
Lewis
bc,
Kevin M.
Douglas
c,
Mark A.
Blitz
 c,
Alfonso
Saiz-Lopez
c,
Alfonso
Saiz-Lopez
 *b and
John M. C.
Plane
*b and
John M. C.
Plane
 c
c
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 26
26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 26
26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 26
26

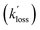 .
.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a
a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c
c![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c
c![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c
c

 and
and 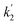 can be obtained. Effective rate constants k1eff and k2eff can be calculated by plotting
can be obtained. Effective rate constants k1eff and k2eff can be calculated by plotting  and
and  against [O3]0 and performing linear regressions (Fig. 4a and b).
against [O3]0 and performing linear regressions (Fig. 4a and b).

 (panels a and c) and
(panels a and c) and  (panels b and d) vs. the initial ozone concentration (panels a and b) and vs. the photolysis energy (panels c and d). The slopes of the plots in panels (a) and (b) are k1eff and k2eff, and are equal to the expressions given by (E4). Straight lines are linear regressions with error in both coordinates. The shaded area indicates the 95% confidence bands. The E = 6 mJ pulse−1 data (triangles) in panel a is an exception and corresponds to decay rates obtained by fitting straight lines to the logarithm of the fast part of the decays at that photolysis energy. In this case the slope of the
(panels b and d) vs. the initial ozone concentration (panels a and b) and vs. the photolysis energy (panels c and d). The slopes of the plots in panels (a) and (b) are k1eff and k2eff, and are equal to the expressions given by (E4). Straight lines are linear regressions with error in both coordinates. The shaded area indicates the 95% confidence bands. The E = 6 mJ pulse−1 data (triangles) in panel a is an exception and corresponds to decay rates obtained by fitting straight lines to the logarithm of the fast part of the decays at that photolysis energy. In this case the slope of the  vs. [O3]0 plot is an approximation to k1 = k1eff (E = 0 mJ pulse−1).
vs. [O3]0 plot is an approximation to k1 = k1eff (E = 0 mJ pulse−1). and
and 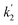 on photolysis laser energy for an experiment where the initial [O3] was kept constant. For [O] = 0, i.e. zero photolysis laser energy, the decay rates are given by
on photolysis laser energy for an experiment where the initial [O3] was kept constant. For [O] = 0, i.e. zero photolysis laser energy, the decay rates are given by  and
and 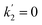 . Experiments at zero laser energy cannot be performed, because HgBr2 photolysis at 248 nm is the source of HgBr, but the rate constant of reaction (R1) can be estimated by linear extrapolation of the
. Experiments at zero laser energy cannot be performed, because HgBr2 photolysis at 248 nm is the source of HgBr, but the rate constant of reaction (R1) can be estimated by linear extrapolation of the  scatter plot (Fig. 4c) towards zero energy and dividing by the pre-photolysis ozone concentration ([O3]0). Similarly, k1 can be estimated by plotting k1eff from the series of experiments at constant laser energy and variable [O3] against laser energy (since most of these experiments series were acquired at different laser energies, see Table 1) and extrapolating towards zero energy (Fig. 5a). From these two calculations, an estimated value of k1 = (8.7 ± 1.0) × 10−11 cm3 molecule s−1 can be determined. Note that there is a hint of curvature in the
scatter plot (Fig. 4c) towards zero energy and dividing by the pre-photolysis ozone concentration ([O3]0). Similarly, k1 can be estimated by plotting k1eff from the series of experiments at constant laser energy and variable [O3] against laser energy (since most of these experiments series were acquired at different laser energies, see Table 1) and extrapolating towards zero energy (Fig. 5a). From these two calculations, an estimated value of k1 = (8.7 ± 1.0) × 10−11 cm3 molecule s−1 can be determined. Note that there is a hint of curvature in the 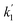 and k1effvs. energy plots, and therefore this value likely overestimates the true value of k1. As an alternative, the measurements with the lowest photolysis energy (6 mJ pulse−1) can be analysed as single exponential decays by masking the second section of the decay (equivalent to fit a straight line to the logarithm of the fast part of the decays, see e.g. the curve for the lowest photolysis energy in Fig. 3d). This relies on the fact that at zero energy
and k1effvs. energy plots, and therefore this value likely overestimates the true value of k1. As an alternative, the measurements with the lowest photolysis energy (6 mJ pulse−1) can be analysed as single exponential decays by masking the second section of the decay (equivalent to fit a straight line to the logarithm of the fast part of the decays, see e.g. the curve for the lowest photolysis energy in Fig. 3d). This relies on the fact that at zero energy  and
and 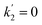 and (E3) becomes a single exponential with offset. Using this technique, linear fitting of the bimolecular plot of
and (E3) becomes a single exponential with offset. Using this technique, linear fitting of the bimolecular plot of  vs. [O3] (triangles in Fig. 4a) yields an estimate of k1 = (7.2 ± 0.3) × 10−11 cm3.
vs. [O3] (triangles in Fig. 4a) yields an estimate of k1 = (7.2 ± 0.3) × 10−11 cm3.

 bimolecular plots like those in Fig. 4a (y0 = constant intercept) for 9 series of experiments where the energy is constant and [O3]0 is varied. The dashed line is a linear fit used to extrapolate to zero energy to estimate k1. The solid line is the reconstruction of k1eff using the average rate constants k1, k2 and k3 obtained by numerical modelling (the thin lines indicate the uncertainties of the reconstructed k1eff). Panel (b): As panel (a) for k2eff. Panel (c): k1 obtained by fitting simulated traces to observed decays for eleven datasets. The different determinations are plotted vs. photolysis energy, except for the symbols inside the rectangular box, which correspond to experiments with variable energy and constant [O3]0. Large full symbols and thick error bars refer to global series fits, with the corresponding error bar including the uncertainty in the [O3] and photolyzed fraction. Small empty symbols refer to the averages of the individual fits within each series, with the error bar indicating only the spread of the determinations within each series. Panel (d): As panel (c) for k2 and k3.
bimolecular plots like those in Fig. 4a (y0 = constant intercept) for 9 series of experiments where the energy is constant and [O3]0 is varied. The dashed line is a linear fit used to extrapolate to zero energy to estimate k1. The solid line is the reconstruction of k1eff using the average rate constants k1, k2 and k3 obtained by numerical modelling (the thin lines indicate the uncertainties of the reconstructed k1eff). Panel (b): As panel (a) for k2eff. Panel (c): k1 obtained by fitting simulated traces to observed decays for eleven datasets. The different determinations are plotted vs. photolysis energy, except for the symbols inside the rectangular box, which correspond to experiments with variable energy and constant [O3]0. Large full symbols and thick error bars refer to global series fits, with the corresponding error bar including the uncertainty in the [O3] and photolyzed fraction. Small empty symbols refer to the averages of the individual fits within each series, with the error bar indicating only the spread of the determinations within each series. Panel (d): As panel (c) for k2 and k3.


 vs. [O] and
vs. [O] and  vs. [O]2 can be determined by linear regression. If the slopes of (E5) and (E6) (or (E5) and (E7)) are equated to the regression values, a system of two equations with three unknowns results. Since k1 has been determined by extrapolation to zero laser energy as explained above, these two equations may be used in principle to determine the remaining unknows (k2 and k3). However, (E6) and (E7) involve quadratic terms that magnify relatively small errors in the experimentally determined slopes. The first estimate of k1 (8.6 × 10−11 cm3 molecule s−1) is likely too high, because it produces negative numbers under square roots. By using the second estimate of k1 (7.2 × 10−11 cm3 molecule−1 s−1) reasonable values are obtained, with k2 = 5 × 10−11 cm3 molecule−1 s−1 and k3 = 10−10 cm3 molecule−1 s−1. However, the propagated uncertainties are large, especially for k2 (50% errors are obtained). In summary, this method is unsuitable for the determination of k2 and k3, although it provides useful information for fitting a numerical model to the observations.
vs. [O]2 can be determined by linear regression. If the slopes of (E5) and (E6) (or (E5) and (E7)) are equated to the regression values, a system of two equations with three unknowns results. Since k1 has been determined by extrapolation to zero laser energy as explained above, these two equations may be used in principle to determine the remaining unknows (k2 and k3). However, (E6) and (E7) involve quadratic terms that magnify relatively small errors in the experimentally determined slopes. The first estimate of k1 (8.6 × 10−11 cm3 molecule s−1) is likely too high, because it produces negative numbers under square roots. By using the second estimate of k1 (7.2 × 10−11 cm3 molecule−1 s−1) reasonable values are obtained, with k2 = 5 × 10−11 cm3 molecule−1 s−1 and k3 = 10−10 cm3 molecule−1 s−1. However, the propagated uncertainties are large, especially for k2 (50% errors are obtained). In summary, this method is unsuitable for the determination of k2 and k3, although it provides useful information for fitting a numerical model to the observations.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 26
26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 26
26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 26
26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 26
26 .
.


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15
15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15,26
15,26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15 with respect to BrHg + O2, so given the exothermicity of (R10) it is likely that the only pathway at room temperature is (R9). A number of model runs were therefore conducted replacing (R3) by (R9) to test if the recycling of HgBr is driven by O3 rather than O. For those series of experiments where the photolysis energy was fixed and [O3]0 varied, global fits of similar quality to those with (R3) were obtained. However, the values of k9 obtained for series at different energies are significantly different. For example, k9 is one order of magnitude larger at 45 mJ pulse−1 compared with 6 mJ pulse−1. The global fits of the two series of experiments where the energy was varied and [O3]0 was constant are poor. The fits of individual traces within these two series are good, yet again the k9 values extracted from every trace depend on [O3], showing a linear dependence with negative slope and an order of magnitude difference between the lowest and highest energy. Obviously, the extracted rate constants must be independent of the concentration of the excess reactant, which is the case of the original model (see Table 1) including (R3) instead of (R9). Hence, we conclude that the main HgBr recycling pathway is (R3).
15 with respect to BrHg + O2, so given the exothermicity of (R10) it is likely that the only pathway at room temperature is (R9). A number of model runs were therefore conducted replacing (R3) by (R9) to test if the recycling of HgBr is driven by O3 rather than O. For those series of experiments where the photolysis energy was fixed and [O3]0 varied, global fits of similar quality to those with (R3) were obtained. However, the values of k9 obtained for series at different energies are significantly different. For example, k9 is one order of magnitude larger at 45 mJ pulse−1 compared with 6 mJ pulse−1. The global fits of the two series of experiments where the energy was varied and [O3]0 was constant are poor. The fits of individual traces within these two series are good, yet again the k9 values extracted from every trace depend on [O3], showing a linear dependence with negative slope and an order of magnitude difference between the lowest and highest energy. Obviously, the extracted rate constants must be independent of the concentration of the excess reactant, which is the case of the original model (see Table 1) including (R3) instead of (R9). Hence, we conclude that the main HgBr recycling pathway is (R3).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15 with respect to BrHg + O2. The HgO + BrO product channel is endothermic by 67 kJ mol−1. Therefore, it is likely that the only channel of (R3) at room temperature is HgBr + O2.
15 with respect to BrHg + O2. The HgO + BrO product channel is endothermic by 67 kJ mol−1. Therefore, it is likely that the only channel of (R3) at room temperature is HgBr + O2.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25)
25)


