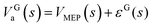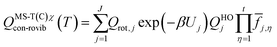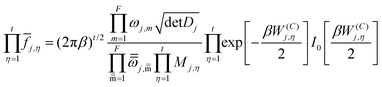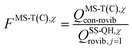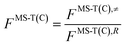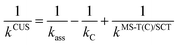The effect of hydrogen bonding on the reactivity of OH radicals with prenol and isoprenol: a shock tube and multi-structural torsional variational transition state theory study

Abstract

The presence of two functional groups (OH and double bond) in C₅ methyl-substituted enols (i.e., isopentenols), such as 3-methyl-2-buten-1-ol (prenol) and 3-methyl-3-buten-1-ol (isoprenol), makes them excellent biofuel candidates as fuel additives. As OH radicals are abundant in both combustion and atmospheric environments, OH-initiated oxidation of these isopentenols over wide ranges of temperatures and pressures needs to be investigated. In alkenes, OH addition to the double bond is prominent at low temperatures (i.e., below ∼700 K), and H-atom abstraction dominates at higher temperatures. However, we find that the OH-initiated oxidation of prenol and isoprenol displays a larger role for OH addition at higher temperatures. In this work, the reaction kinetics of prenol and isoprenol with OH radicals was investigated over the temperature range of 900–1290 K and pressure of 1–5 atm by utilizing a shock tube and OH laser diagnostic. To rationalize these chemical systems, variational transition state theory calculations with multi-structural torsional anharmonicity and small curvature tunneling corrections were run using a potential energy surface characterized at the UCCSD(T)/jun-cc-pVQZ//M06-2X/6-311++G(2df,2pd) level of theory. A good agreement was observed between the experiment and theory, with both predicting a non-Arrhenius behavior and negligible pressure effects. OH additions to the double bond of prenol and isoprenol were found to be important, with at least 50% contribution to the total rate constants even at temperatures as high as 700 and 2000 K, respectively. This behavior was attributed to the stabilizing effect induced by hydrogen bonding between the reacting OH radical and the OH functional group of isopentenols at the saddle points. These stabilizing intermolecular interactions help mitigate the entropic effects that hinder association reactions as temperature increases, thus extending the prominent role of addition pathways to high temperatures. The site-specific rate constants were also found to be slower than their analogous reactions of OH + n-alkenes.

---

1 Introduction

Alcohols with more than three carbons (C4–C6) are better than ethanol as substitutes for conventional fuels, as pure fuels, or in blends, due to their superior physical and chemical properties.^1–3 Higher alcohols have higher energy density¹ and are more compatible with combustion engines because of their lower volatility, which results in fewer volatile organic compound (VOC) emissions.⁴ Extensive experimental studies have shown that higher alcohol blends with diesel improve engine performance and result in reduced emissions.^2,5–9 The higher octane number of alcohols compared to their analogous alkanes can also improve the performance of SI engines, either as a pure fuel or in fuel blends.^3,10 Additionally, the presence of double bond(s) along with the OH functional group can further increase the octane number.¹¹ Moreover, methyl substitution (i.e., branching) and cyclization in alcohols have been found to increase the octane number.^12–16 Consequently, isopentenols such as 3-methyl-2-buten-1-ol (prenol) and 3-methyl-3-buten-1-ol (isoprenol) are unique unsaturated alcohols because of the presence of both hydroxyl and double bond functional groups. On one hand, the double bond decreases the reactivity of alkenes as a result of the formation of resonantly stabilized allylic radicals as intermediates.¹⁷ On the other hand, the presence of the OH functional group lowers the bond dissociation energies of the α-C–H bond adjacent to the hydroxyl group. As a result, hydrogen abstraction reaction occurs predominantly at the α-C–H site producing α-radical, which can undergo chain propagation and termination reactions at low temperatures and compete with chain branching reactions.³ The former reaction pathways produce less reactive intermediates (e.g., aldehydes) at low temperatures, thereby decreasing ignition propensity (i.e., increased octane number).⁹

Prenol and isoprenol can, therefore, be excellent candidates for future second-generation biofuels. There have been extensive studies exploring the high-specificity synthetic routes for the production of these alcohols.^11,18–22 One of the routes involves biosynthetic production via microbial fermentation. However, very few studies explored the oxidation of prenol and isoprenol under combustion conditions. Recently, Ninnemann et al.²³ investigated the combustion behavior of these fuels by conducting ignition delay times, laminar burning velocities, and CO₂ time-history measurements. The effect of a double bond at low temperatures was studied by Welz et al.²⁴ Particularly, the authors investigated an O₂ addition to prenol and isoprenol radicals theoretically and experimentally at 500 K and 8 torr. Allylic radicals were found to be the major products produced via hydrogen abstraction reactions initiated by Cl atoms, which underwent O₂ addition forming α/γ-RO₂ radicals. These peroxy radicals of unsaturated alcohols favored the formation of unsaturated aldehydes + HO₂ which suppresses the low-temperature reactivity. Kinetically, Bruycker et al.²⁵ studied prenol and isoprenol oxidation and pyrolysis in a JSR experiment at φ = 0.5, 1 and ∞, in the temperature range of 500–1100 K and a pressure of 0.107 MPa. A comprehensive high and low temperature chemical kinetic model for prenol and isoprenol was also developed. They observed low-temperature reactivity for prenol in contrary to its analogous alkene, 2-methyl-2-butene, wherein the hydroxyl group in the former stabilizes the peroxy radicals and allows for aldehyde formation. They showed that the presence of O₂ can initiate low-temperature chemistry. Furthermore, Bruycker et al.²⁵ performed CBS-QB3, transition state theory calculations to deduce bimolecular reactions of these fuels with H and CH₃ radicals along with unimolecular reactions involving beta-scission and aldehyde decomposition. They observed that isoprenol undergoes a retro-ene type of decomposition reaction via a six-member transition state to yield formaldehyde and isobutene and that the observed unimolecular decomposition of isoprenol was found to be ∼300 times faster than the retro-ene reaction of 1-pentene to produce propene and ethylene. This surprising reactivity behavior of isoprenol was attributed to the OH functional group which resulted in a substantially lower barrier height (the energy of activation for isoprenol is ∼18 kcal mol⁻¹ lower as compared to 1-pentene for the similar retro-ene reaction). Therefore, one can expect that OH initiated oxidation of isoprenol and prenol exhibits a large reactivity difference as compared to alkenes + OH reactions, and hence, the strategy of estimating the rate coefficients by using reaction analogy can introduce large uncertainty. Lokachari et al.²⁶ also investigated the oxidation of prenol by developing a chemical kinetic model that was validated against JSR and flame speed data from literature, as well as HPST and RCM ignition delay time data measured in their study at φ = 1 and 2, in the temperature range of 600–1400 K and at pressures of 15 and 30 bar. Their model showed a suppressed auto-ignition behavior which they attributed to the unique structure of prenol which contains a branch, a double bond and an alcohol functional group. Additionally, the OH addition to the double bond of prenol and the subsequent O₂ addition highly affected the prenol auto-ignition characteristics as the subsequently formed RO₂ and QOOH radicals terminated via either Waddington pathway or the formation of aldehyde + HO₂ instead of undergoing a complete low temperature chemistry (chain branching). Lokachari et al.²⁶ model was further utilized by Fioroni et al.²⁷ to study the RON predictions of prenol blend with four components surrogates (iso-octane, toluene, n-heptane and 1-hexene); nevertheless, the model failed to capture the synergetic effect observed experimentally and further model refinements were recommended.

The chemistry of isopentenols is also important from the atmospheric standpoint as they are emitted to the atmosphere via biogenic and anthropogenic sources.^28–30 Their oxidation mechanisms at atmospheric conditions are well investigated. Rodriguez et al.³¹ studied the products of different Cl atom initiated reactions of unsaturated alcohols in a reaction chamber under atmospheric conditions. They found that acetone is the major product of the prenol + Cl reaction, which suggests that the addition pathway is more important than abstraction. The Cl addition occurs at the less substituted carbon in the double bond of prenol, and with the presence of oxygen, the produced alkoxy radical decomposes to produces acetone. The rate constant of prenol + Cl was measured by Rodriguez et al.³² at atmospheric conditions. Generally, OH radicals are the dominant oxidant for the removal of volatile organic compounds (VOCs) in the atmosphere. Therefore, the reaction of unsaturated alcohols with OH has also been extensively studied. For instance, Du et al.³³ explored the potential energy surfaces of isoprenol + OH, where the OH addition channel was found to be the most energetically favored pathway under atmospheric conditions. Du et al.³³ also studied the effect of the presence of O₂ and NO on the reaction rate. Cometto et al.³⁴ measured the rate coefficients of OH radical reactions with different unsaturated alcohols, e.g., 3-methyl-3-buten-1-ol, 2-buten-1-ol, 2-methyl-2-propen-1-ol, and 3-buten-1-ol using the relative rate method and pulsed laser photolysis laser-induced fluorescence technique over the temperature range of 263–371 K. Imamura et al.³⁵ studied the reaction of OH with methylbutenols at 298 K using the relative rate method. To the best of our knowledge, there are no earlier reports of the reactions of OH radicals with prenol and isoprenol under combustion-relevant conditions. Particularly, the site-specific rate coefficients that are valuable for detailed kinetic modeling.

The reactions of OH radicals with isopentenols are expected to exhibit complex Arrhenius behavior due to many possible chemical pathways that are accessible under combustion and atmospheric environments. The reaction of prenol or isoprenol with OH radicals may proceed via two pathways: hydrogen abstraction by OH from the different C–H and OH sites, and the addition of the OH radical to the double bond, as detailed in the reaction Scheme 1. Here, abstraction pathways are denoted as absXn, where X is the type of the abstracted site (C for carbon and O for OH functional group), and n is the location of the carbon atom from the OH moiety. The addition of OH radicals to the double bond will be described as addXn, where X and n have the same previous meanings.

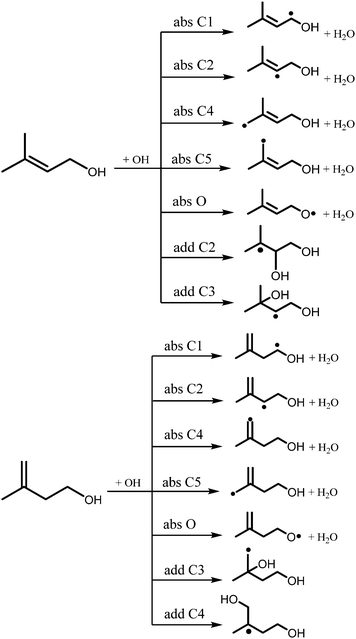Scheme 1 Reaction pathways of prenol (left panel) and isoprenol (right panel) with OH. See text for absXn or addXn reaction nomenclature.

A detailed study of these chemical systems, characterizing the complex temperature and pressure dependence of the title reactions, is not yet available. The existing kinetic model for the oxidation of prenol and isoprenol does not consider the various important pathways with OH radicals. Therefore, we aim to fully characterize these reactions by employing both experimental and theoretical methods to discern the role of addition and abstraction reactions over a wide range of conditions. We performed the experiments in a shock tube by employing a UV laser diagnostic for OH detection over the temperature range of 900–1290 K and the pressure range of 1–5 atm. Additionally, we computed the rate coefficients by employing high-level electronic structure and variational transition state theory calculations with multi-structural torsional anharmonicity and small curvature tunneling corrections. Pressure and temperature dependence of the rate constants, branching ratios, and site-specific rate constants are reported and discussed.

2 Methodology

2.1 Experimental methods

The reaction kinetics of OH radicals with prenol and isoprenol was investigated with a low-pressure shock tube (LPST) and UV laser diagnostic over a wide range of experimental conditions (T = 900–1290 K and P ∼ 1.0–5.0 atm).

2.1.1 Low-pressure shock tube (LPST) facility. A detailed description of the LPST facility is provided elsewhere,^36,37 and only a brief description is given here. It is a stainless-steel shock tube comprising of a 9 m driven section and a variable-length driver section with an inner diameter of 14.2 cm. In this study, a 3 m long driver section was used to achieve a steady test time of ∼1.5 ms behind the reflected shock waves. Shock waves were generated by pressure bursting of the polycarbonate diaphragms of variable thicknesses. Helium was used as the driver gas. A series of five piezoelectric transducers (PCB 113B26) was linearly placed along the last 1.5 m section of the driven section for measuring the shock speed. The incident shock speed was then linearly extrapolated to the end-wall location to account for shock attenuation. The reaction conditions behind the reflected shock waves, T₅ and P₅, were calculated by employing the Rankine–Hugoniot shock relationship³⁸ using the measured incident shock speed and thermodynamic data of the test gas mixture. The uncertainties in T₅ and P₅ were ∼±1% which mainly stem from the uncertainty of the measured incident shock velocity (∼0.2%).

2.1.2 Hydroxyl UV laser diagnostic. tert-Butyl hydroperoxide (TBHP) was used for rapid thermal generation of OH radicals (half-life ≤ 1 μs for T ≥ 1000 K).³⁹ The reaction progress was followed by monitoring OH radicals near 307 nm probing the center (306.6868 nm) of the well-characterized R1(5) absorption line in the (0, 0) vibrational band of the A²Σ⁺ ← X²Π electronic transition of OH radical. This strong and isolated transition of OH radical was probed by employing a narrow linewidth CW laser system comprising of an Nd:YAG 532 nm pump laser, a ring-dye visible laser, and a frequency doubler. The ring dye laser employs a rhodamine 6G dye inside the laser cavity to generate visible laser light near 613.4 nm after excitation by the 532 nm pump laser. An external frequency doubler ultimately produces UV light near 306.69 nm. For optical detection of OH radicals, the laser beam was guided through the cross-section of the shock tube via two quartz windows which are installed 2 cm away from the shock tube end-wall. Two modified Thorlab PDA36-EC photodetectors (spectral range 305–1100 nm) were used to measure the laser intensity before and after the shock tube. A common-mode-rejection (CMR) scheme was employed to account for fluctuations in laser beam intensity. After CMR, the noise of the laser beam was less than 0.1% of the signal. The transmitted laser intensity time-profile was quantitatively converted into OH mole fraction (X_OH) time-profile by using Beer–Lambert law: I/I₀ = exp(−K_OHX_OHPL), where I and I₀ are transmitted and incident laser intensities, K_OH is the OH absorption coefficient,⁴⁰P is the total pressure (atm), and L is the path length.

2.1.3 Mixture preparation. A 70% TBHP solution in water, prenol (99.0%), and isoprenol (≥98%) were obtained from Sigma-Aldrich, whereas helium (99.9%) and argon (99.999%) were purchased from Abdullah Hashim Gases. The mixtures were prepared manometrically in a 24 l Teflon-coated stainless-steel vessel which is equipped with a magnetically driven stirrer. Two MKS Baratron pressure gauges with full-scale ranges of 20–1000 torr were employed to accurately measure the partial pressure of the gases. Before mixture preparation, the mixing vessel was turbo-pumped down to 10⁻⁵ mbar. The mixtures were left for at least two hours to ensure homogeneity.

2.2 Computational methods

An extensive conformational analysis was performed to optimize and characterize all the conformers of the reactant, saddle point, and product species using Gaussian09.⁴¹ All dihedrals (except terminal methyl groups) were simultaneously rotated by 120°, and rotations of 60° were used for the rotors involved in hydrogen bonding formation (e.g., C–C–O–H, C–H⋯O–H, and often C–C–C–OH) for a more comprehensive exploration of the conformational space. Those conformers were optimized at the M06-2X/6-31+G(d,p)^42–45 level of theory. The M06-2X method was used because it has been proven to describe accurately the kinetics and thermochemistry of reactive systems involving C, H, O, and N atoms,⁴² as well intermolecular interactions such as hydrogen-bonds,⁴⁶ which are important in our reactive systems. Distinguishable geometries were re-optimized at the higher level M06-2X/6-311++G(2df,2pd)^42–45 to a further and more accurately confirmation of the global minimum of each species, to calculate their vibrational frequencies and zero-point energy (ZPE), and to conduct our kinetic study. UltraFine grid (99 590 grid) was used to optimize and characterize the minimum energy conformer of each species, and no changes were observed when the larger 99 974 grid is used.

Single point energy coupled-cluster calculations with single and double excitations including the quasiperturbative treatment of connected triple excitations, and also using Dunning's correlation-consistent polarized valence quadruple zeta basis set (UCCSD(T)/jun-cc-pVQZ^47–49), were performed in Gaussian16⁵⁰ software for a better energetic description of the optimized minimum conformers of reactants and saddle points. The basis set jun-cc-pVQZ accurately approximates the complete basis set (CBS) limit of the UCCSD(T) method,⁵¹ and therefore the UCCSD(T)/jun-cc-pVQZ values are used as a benchmark. Cartesian coordinates, vibrational frequencies, and single-point energies of all optimized stationary points are compiled in the ESI.†

GaussRate17⁵² was used to calculate the minimum energy path (MEP) within the reaction coordinate range of −1.9 and 1.9 bohr, with a step size of 0.1 Bohr in mass-scaled coordinates and a scaling mass of 1 amu. The region near the saddle point is very important for an accurate description of the variational and tunneling effects; therefore, a step size of 0.0472 Bohr was used between −1.038 and 1.038 Bohr. Hessians were calculated at every three points along the MEP.

The high-pressure limit rate constants for hydrogen abstraction and addition reactions of OH with prenol and isoprenol were calculated with Polyrate 2016-2A⁵³ using the canonical variational transition state theory^54,55 with small curvature tunneling^56,57 corrections (CVT/SCT). The low-lying electronically excited state ²Π_1/2 of the OH species (140 cm⁻¹) was included in the reactant electronic partition function to account for the spin–orbit coupling, which is assumed to be fully quenched in the transition state region. The normal modes transverse to the MEP (reaction valley) were described by using a well-defined set of curvilinear internal coordinates with bonds, angles, and dihedral angles, which do not yield imaginary frequencies along the MEP. This allowed us to calculate the ground-state vibrational adiabatic potential energy curve, V^G_a(s), which was used to estimate the SCT tunneling coefficients,

where s is the reaction coordinate, V_MEP(s) is the ZPE exclusive potential energy, defined with respect to that of the reactants, and ε^G(s) is the local ZPE.

The effect of the multiple conformers, i.e. multi-structural anharmonicity, as well as torsional anharmonicity, were included using the MSTor 2017 software,^58,59 which was employed to calculate multi-structural partition functions with a coupled torsional potential as follows,

where χ denotes reactant (R) or saddle point (≠), J is the total number of distinguishable conformers of species χ, labeled as 1, 2, …, J, being j = 1 the conformer with the lowest potential energy (global minimum), Q_rot,j is the classical rotational partition function of conformer j, β is 1/k_BT, k_B is the Boltzmann constant, U_j is the ZPE exclusive potential energy of conformer j relative to that of the global minimum, Q^HO_j is the quasiharmonic vibrational partition function of the conformer j, t is the number of coupled torsions, and f̄_j,η is a factor that introduces torsional anharmonicity for the η coupled torsion of the conformer j. The product of f̄_j,η can be calculated as follows,
where ω_j,m represents the normal mode vibrational frequency of mode m of conformer j and 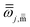is the corresponding torsional-projected normal mode frequency, D_j is the Kilpatrick and Pitzer torsional moment of inertia matrices, M_j,η is the local periodicity parameter, W^(C)_j,η is the effective coupled barrier height, and I₀ is a modified Bessel function. The parameters M_j,η are necessary to calculate the partition functions, and they were estimated with the Voronoi method implemented in MSTor. The adopted scheme (NS:SC) for the different stationary points is detailed in the ESI,† where NS and SC refer to nearly separable and strongly coupled torsions.

The multi-structural torsional factors of the reactants and saddle points were calculated as follows,

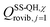where is the single-structural quasiharmonic rovibrational partition function of the global minimum conformer for species χ. The multi-structural torsional factors of the reactant and saddle points were used to calculate those for the corresponding reactions as follows,
where ≠ and R are the saddle point and reactant species involved in that specific reaction, respectively. To account for multi-structural torsional anharmonicity effects, the factor F^MS-T(C) was introduced as a multiplicative factor in the CVT/SCT rate constants derived from Polyrate to obtain our final rate constants, hereafter labeled as k^MS-T(C)/SCT.

The effect of the pre-reaction complexes (PRCs) in the high-pressure limit rate constants was estimated with the canonical unified statistical theory (CUS).⁶⁰ This effect, which is usually found to be important only at low temperatures when the outer saddle point controls reactivity, was only investigated for the addition pathways since these have the lowest potential energy barriers along the MEP. For the stepwise mechanism via a PRC, the CUS model defines the rate constant as

where k_ass is the association reaction to form PRC, and k_C is a rate constant calculated for a dividing surface located at the free energy minimum corresponding to PRC. The association rate constant k_ass was estimated using the hard-sphere collision rate constant model:
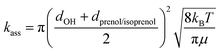
where d is the van der Waals diameter and μ is the reduced mass of the reactive system. A van der Waals radius of 0.97 Å for OH radical and 5 Å for both alcohols were assumed. A more sophisticated approach to estimate the effect of the complex is the two transition state model developed by Greenwald et al.⁶¹ together with the variable reaction coordinate (VRC) method^62,63 for the calculation of k_ass. However, the VRC method is computationally very expensive for systems with several heavy atoms, especially for the investigated reactions whose barrier heights were observed to be very sensitive to the size of the basis set. The hard-sphere collision model represents a less accurate but cost-effective approach whose performance can be verified by comparing to the experimental rate constant.

To account for pressure effects, which may affect the OH addition reaction to the double bond of prenol and isoprenol, we did not only conduct our shock tube experiments at different pressures, but also used our recent implementation^64,65 of the system-specific quantum Rice–Ramsperger–Kassel (SS-QRRK) utility code which improves the original formulation^66–68 by adopting an alternative definition for the collision efficiency parameter β_c. Details of the original and improved versions of the SS-QRRK method can be found elsewhere.^64–68 For these calculations, we used the Lennard-Jones parameters of n-propanol, i.e. σ = 4.549 Å and ε/k_b = 576.7 K, for prenol and isoprenol species; these parameters have been successfully used for other species containing double bonds and OH groups.^69,70 We used argon as bath gas in the calculations to be consistent with our experiments, whose Lennard-Jones parameters are σ = 3.542 Å and ε/k_b = 93.3 K. In our calculations, the average energy transfer per down collision was estimated by the expression 〈ΔE〉_down = Θ(T/300)ⁿ, where Θ = 300 cm⁻¹ and n = 0.85,⁷¹ and pressures as low as 1.0 atm were considered.

3 Results and discussion

3.1 Experimental rate constants

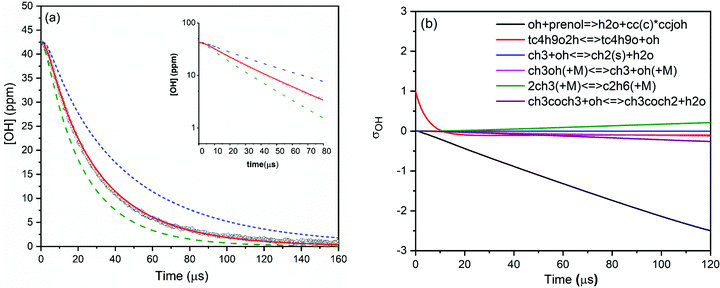
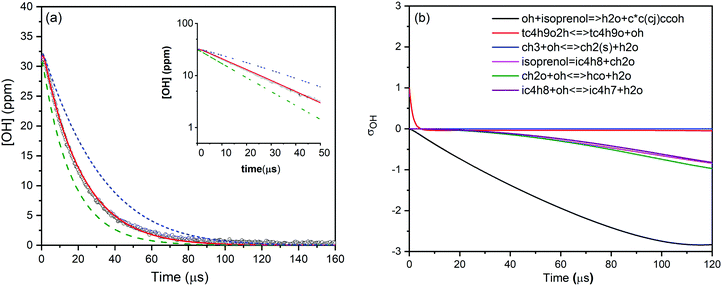
Various mixtures of prenol or isoprenol and TBHP diluted in argon were shock heated to a range of post-shock temperatures (900–1290 K) and pressures (0.96–5.0 atm) to measure the overall reaction rate constants. The mixture compositions were tailored in such a way that OH radical decay obeyed pseudo-first-order kinetics. A representative OH time-history trace recorded for prenol + OH reaction at 984 K and 0.94 atm is shown in Fig. 1. As expected, OH time-history decayed exponentially illustrating that the pseudo-first-order kinetics analysis can be applied to extract the rate constants (see the inset of Fig. 1). However, upward curvature of ln[OH] vs. time plot was noticed at the early reaction time as a consequence of the competition between OH build-up kinetics from TBHP decomposition and OH consumption by the title reaction. Additionally, such simple kinetic analysis may not yield reliable rate constants as it neglects the secondary chemistry which may affect the OH profile. Therefore, the measured OH-time traces were fitted iteratively using Aramco 2.0^72–75 kinetic model as the base model supplemented by the TBHP sub-mechanism from Pang et al.³⁹ An illustrative example of the best fit of the kinetic model with the experimentally measured OH profile is displayed in Fig. 1. The best fit of the kinetic simulation yielded a rate constant of 1.75 × 10⁻¹¹ cm³ molecule⁻¹ s⁻¹ at the specified conditions. Fig. 1 also shows perturbations of ±50% from the best-fit value to demonstrate the sensitivity of OH profiles to the target reaction. A brute force sensitivity analysis was carried out at 984 K and 0.94 atm for prenol (200 ppm) and TBHP (20 ppm) mixture in 0.94 atm argon to gain deeper insights into the role of various reactions influencing the OH radical loss. Fig. 1b provides the results of the sensitivity analysis. As seen, prenol + OH is the most sensitive reaction for OH loss. The secondary reactions, including CH₃OH(+M) ↔ CH₃ + OH(+M), 2CH₃(+M) ↔ C₂H₆(+M), and CH₃ + OH ↔ CH₂(S) + H₂O, have minor importance in the measured OH-time history over a few tens of microseconds. Note that the sensitivity coefficients are defined as σ_OH = ln(OH_i⁺/OH_i⁻)/ln(2.0/0.5) with OH_i⁺ and OH_i⁻ being the OH radical concentration computed after multiplying the rate coefficient of the ith reaction by a factor of 2 and 0.5, respectively.

Fig. 1 (a) OH concentration time-profile measured at 984 K and 0.94 atm for prenol and TBHP mixture in argon (black circles). The solid red line represents the best fit (k = 1.75 × 10⁻¹¹ cm³ molecule⁻¹ s⁻¹) to the experimental profile and the dashed lines show perturbations of the rate constants from the best fit by ±50%. The inset plot displays ln[OH] vs. time to show that OH decay follows the first-order kinetics. (b) Hydroxyl sensitivity analysis for prenol + OH reaction using the kinetic mechanism of Aramco2.0 at the same conditions.

For isoprenol + OH reaction, similar method was employed to determine the rate constants. We note here that the reaction of OH with isoprenol was investigated below 1180 K because isoprenol efficiently undergoes a retro-ene type of decomposition reaction at high temperatures to yield formaldehyde and isobutene (half-life τ_1/2 ∼ 340 μs at 1000 K),²⁵ and hence it will interfere with the pseudo-first-order decay of OH radicals. An example of OH decay profile, the best fit of the kinetic simulation and sensitivity analysis of isoprenol + OH at a representative condition of 1055 K and 0.96 atm is illustrated in Fig. 2. The best fit yielded a value of 1.83 × 10⁻¹¹ cm³ molecule⁻¹ s⁻¹ for the rate constant of isoprenol + OH reaction. The measured rate constants for the reaction of OH with prenol and isoprenol at the specified conditions are detailed in the ESI† and also shown in Fig. 3.

Fig. 2 (a) OH concentration time-profile measured at 1055 K and 0.96 atm for isoprenol and TBHP mixture in argon (black circles). The solid red line represents the best fit (k = 1.83 × 10⁻¹¹ cm³ molecule⁻¹ s⁻¹) to the experimental profile and the dashed lines show perturbations of the rate constants from the best fit by ±50%. The inset plot displays ln[OH] vs. time to show that OH decay follows the first-order kinetics. (b) Hydroxyl sensitivity analysis for the isoprenol + OH reaction using the kinetic mechanism of Aramco2.0 at the same conditions.

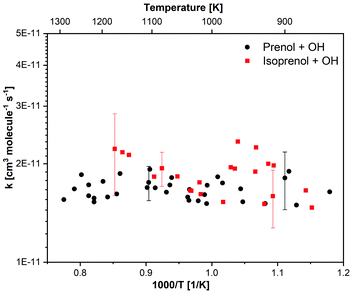Fig. 3 Measured rate constants for the reactions of OH radicals with prenol and isoprenol as a function of temperature.

The estimated uncertainty in the measured rate constants is ∼±20% and ∼±12% at low (<900 K) and high (>1100 K) temperatures, respectively. For isoprenol + OH reaction, the uncertainty starts increasing when the temperature exceeds 1100 K, e.g., the uncertainty reaches ∼±28% at 1173 K. Therefore, our reported data are limited to 1173 K for isoprenol + OH. Although the detailed uncertainty analysis can be found in our previous works,⁷⁶ we briefly describe it here. First, we identified and quantified various sources of errors e.g., temperature behind the reflected shock wave ±2%, chemical impurity ±2%, fuel concentration ±5%, fitting procedure ±5%, OH signal noise 3%, secondary chemical reactions (TBHP + OH ⇒ TBUTOXY + OH, ±30%; CH₃ + OH = CH₂ + H₂O a factor of 2). Second, each source of error was perturbed within its uncertainty bound while performing the kinetic modeling to acquire the best fit to the experimentally measured OH profiles by adjusting the rate coefficient of the target reaction. This way, the uncertainty in the rate coefficient from each source of error was determined for a given temperature and pressure. Finally, the uncertainties were lumped together using the root-mean-square method to obtain the overall uncertainty in the reported experimental data.

For both chemical systems, the measured rate constants (Fig. 3) did not exhibit discernible pressure dependence over the range of pressures investigated (1–5 atm). This observation is in agreement with our theoretical calculations, as discussed later. Interestingly, both molecules showed similar high-temperature reactivity with OH radicals under our experimental conditions. Moreover, both reactions virtually exhibited no temperature dependence within our experimental uncertainty. These observations may have two possible implications: (i) hydrogen abstraction reactions, which are expected to be more relevant at high temperatures, do not have sizable barrier heights (almost barrierless), (ii) OH addition to the double bond contributes significantly to the total rate constants even at high temperatures, and its negative temperature dependence is nullified by the opposite temperature effect of hydrogen abstraction reactions. The experimental observations for the trends of the rate constants will be analyzed in detailed by means of a theoretical study in the next sections.

3.2 Theoretical results

3.2.1 Topology of the potential energy surface (PES).
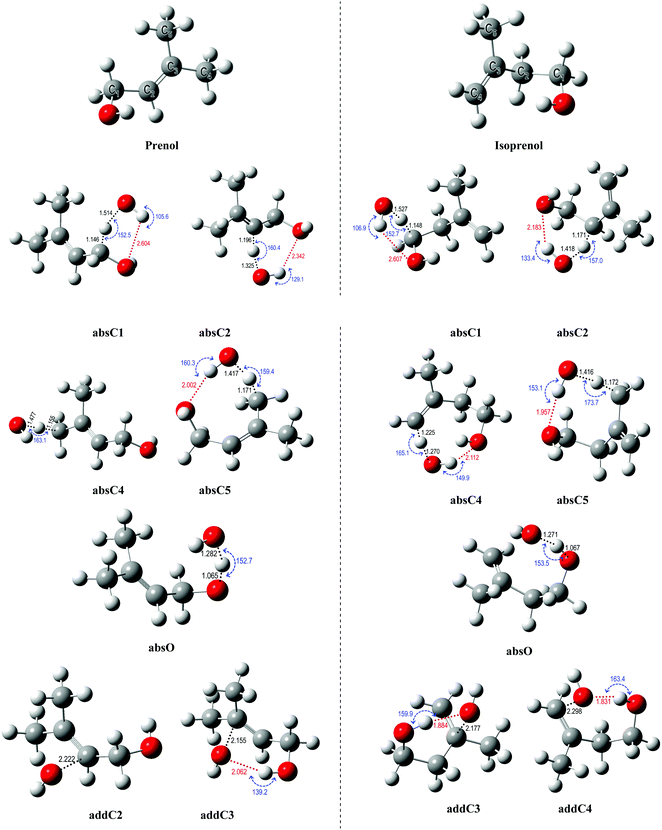
Hydrogen abstraction and addition pathways. For deeper insights into the branching ratios and the competition between different abstraction and addition channels over a wide temperature and pressure range, potential energy surfaces (PES) of the title reactions were mapped out using various levels of theory as the first step in our kinetic study. The different conformers of the reactants, saddle points, and products were optimized and characterized by following the procedure described in Section 2.2. The optimized geometries of all species are provided in the ESI.†Fig. 4 shows the optimized geometries of the global minimum conformer of each species on the PES for both reactions calculated at the M06-2X/6-311++G(2df,2pd) level of theory. All the sites available for H abstraction by OH and OH addition to the double bond are depicted.

Fig. 4 Global minimum conformers of the reactant and saddle point species on the PES of the investigated reactions for the prenol + OH and isoprenol + OH reactive systems at the M06-2X/6-311++G(2df,2pd) level. Angles, bond distances, and hydrogen bonds are shown. Saddle points for all possible H abstraction and OH addition to double bond pathways are depicted. See text for the absXn and addXn nomenclature.

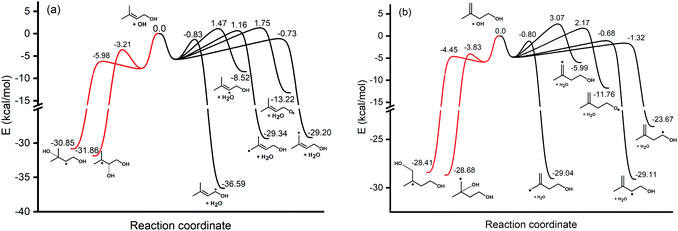
The hydrogen bonds formed between the alcohol functional group in prenol (or isoprenol) and the reacting OH radical are expected to stabilize most of the saddle points, thereby lowering the corresponding reaction barriers. Adiabatic (ZPE corrected) barrier heights calculated at both, M06-2X/6-311++G(2df,2pd) and UCCSD(T)/jun-cc-pVQZ//M06-2X/6-311++G(2df,2pd) levels of theory, are shown in Table 1. Free energy barriers calculated at 298 K are also tabulated in Table 1. The adiabatic potential energy profiles computed at the UCCSD(T)/jun-cc-pVQZ//M06-2X/6-311++G(2df,2pd) level of theory for all reaction pathways of prenol + OH and isoprenol + OH are shown in Fig. 5. The discussion below will be based on the UCCSD(T)/jun-cc-pVQZ//M06-2X/6-311++G(2df,2pd) adiabatic potential and free energy barrier heights. The free energy barriers for the different reaction pathways at different temperatures (298, 500, 1000, and 2000 K) are plotted in Fig. S1 of the ESI.†

Table 1 Adiabatic and free energy (298 K) barrier heights (kcal mol⁻¹) calculated at the M06-2X/6-311++G(2df,2pd) and UCCSD(T)/jun-cc-pVQZ//M06-2X/6-311++G(2df,2pd) levels of theory

Reaction pathway	Prenol + OH			Isoprenol + OH
	Adiabatic barrier heights		Free energy barrier heights (298 K)^b	Adiabatic barrier heights		Free energy barrier heights (298 K)^b
	M06-2X/6-311++G(2df,2pd)	UCCSD(T)/jun-cc-pVQZ^a		M06-2X/6-311++G(2df,2pd)	UCCSD(T)/jun-cc-pVQZ^a
a Energies calculated at the UCCSD(T)/jun-cc-pVQZ//M06-2X/6-311++G(2df,2pd) level of theory. b Free energies calculated at 298 K using UCCSD(T)/jun-cc-pVQZ//M06-2X/6-311++G(2df,2pd) single-point energies and M06-2X/6-311++G(2df,2pd) thermal corrections to Gibbs free energy.
absC1	−1.84	−0.83	5.95	−2.16	−1.32	6.05
absC2	0.07	1.47	8.58	−1.81	−0.68	6.86
absC4	0.37	1.16	7.96	1.21	3.07	10.16
absC5	−1.61	−0.73	7.23	−2.07	−0.80	6.71
absO	−0.99	1.75	7.46	−0.73	2.17	8.03
addC2	−4.03	−3.21	4.23	NA	NA	NA
addC3	−6.85	−5.98	2.65	−4.94	−3.83	4.35
addC4	NA	NA	NA	−6.00	−4.45	2.52

---

Fig. 5 Vibrationally adiabatic ground-state potential energy profile of (a) prenol + OH and (b) isoprenol + OH, calculated at the UCCSD(T)/jun-cc-pVQZ//M06-2X/6-311++G(2df,2pd) level of theory. For the sake of clarity, intermediate complexes for the different pathways are not shown, and only arbitrary wells are displayed.

The multi-reference character of the stationary points was assessed by calculating the T₁ diagnostic parameter (tabulated in Table S1 of the ESI†). The T₁ values are found to be less than 0.02 and 0.04 for closed-shell and open-shell systems, respectively, which indicates that the UCCSD(T) single-reference method is suitable for the current chemical systems.⁷⁷ Spin contamination was checked by analyzing the 〈S²〉 expectation value, confirming negligible contribution from the higher spin states.

As expected, hydrogen abstraction from α-carbon (absC1) is the most kinetically favored channel for prenol + OH reaction in terms of adiabatic potential energy (−0.83 kcal mol⁻¹) as this secondary allylic hydrogen atom is adjacent to the OH group. However, absC5 pathway, which corresponds to the H abstraction from one of the primary allylic hydrogen atoms, also proceeds via a comparable adiabatic potential energy barrier of −0.73 kcal mol⁻¹. This can be explained by the existence of a hydrogen bond in the saddle point of absC5 pathway between the OH radical and the O atom of the OH-moiety of prenol, as these three atoms adopt a nearly collinear orientation (160.3°) favoring a highly stabilizing interaction. That hydrogen bond makes the corresponding absC5 saddle point tight enough to make the free energy barrier (at 298 K) of this pathway 1.28 kcal mol⁻¹ larger than that of absC1 pathway, with even larger differences as temperature increases (10.46 kcal mol⁻¹ at 2000 K (Fig. S1, ESI†)). Such a highly stabilizing hydrogen bond does not exist in the saddle point of pathway absC4 and, therefore, even though C4 and C5 carbon atoms are of the same chemical nature (primary allylic), absC4 pathway needs to surmount a potential energy barrier of 1.16 kcal mol⁻¹. Nevertheless, the strained hydrogen bond ring-like structure lowers the entropy for absC5 process, making its free energy barrier at 298 K almost equal to that of absC4. Despite its potential energy barrier being 1.89 kcal mol⁻¹ lower than that of absC4, the free energy barrier of absC5 is larger by 10.08 kcal mol⁻¹ at 2000 K (Fig. S1, ESI†). This may result in lower rate constants of absC5, as discussed later, which highlights the role played by hydrogen bonds. Though absC2 occurs via a hydrogen bonding saddle point, this pathway has a relatively larger barrier height of 1.47 kcal mol⁻¹ indicating that vinylic hydrogen abstraction is not energetically favored. As for the addition pathways, the OH addition to the C3 site proceeds through an energy barrier that is 2.77 kcal mol⁻¹ lower than that of the addition to the C2 site, even though the latter yields a tertiary carbon radical. Both saddle points of the addition reactions, addC3 and addC2, are stabilized by the OH⋯π bond interaction; however, addC3 saddle point is further stabilized by an O⋯H–O hydrogen bond that is absent in addC2 saddle point (Fig. 4). This again highlights the importance of the hydrogen bonds in the investigated reaction systems. The additional hydrogen bond makes the free energy barrier of addC3 larger than that of addC2 at temperatures beyond 500 K (Fig. S1, ESI†).

As seen in Fig. 4, all abstraction and addition saddle points of isoprenol + OH reaction exhibit a strong stabilizing hydrogen bond. This is attributed to the difference in structures between prenol and isoprenol, where the possibility of C2–C3 bond rotations in the latter results in more flexible structures to form hydrogen bonds. Abstraction from α-C1 (absC1) has the lowest barrier of −1.32 kcal mol⁻¹, followed by the abstraction from the allylic sites, absC2 and absC5, with barriers of −0.68 and −0.80 kcal mol⁻¹, respectively. Hydrogen abstraction from the terminal vinylic C–H (absC4) has the highest barrier of 3.07 kcal mol⁻¹. Both addition channels of isoprenol + OH reaction proceed via the formation of hydrogen bonds at the saddle point structure, contributing to lower corresponding barrier heights. The addC3 saddle point is found to be 0.62 kcal mol⁻¹ less stable than that of addC4, which might be due to the eclipsed structure (C1 and C4 atoms) and to the formation of a primary radical in the former.

Compared to Du et al.³³ calculations of isoprenol + OH at the UCCSD(T)/6-31++G(d,p)//MP2(full)/6-31G(d,p) level of theory, the barrier heights obtained are 3.26 and 4.17 kcal mol⁻¹ higher than our values for addC3 and addC4, respectively. These discrepancies may be attributed to the different levels of theory used in these two studies, and also to the fact that Du et al.³³ saddle points were optimized to non-hydrogen bonded structures. Moreover, the pre-reactive complex (PRC) optimized by Du et al.³³ for the addition of OH to the double bond of isoprenol is 2.6 kcal mol⁻¹ below the entrance channel compared to the 5.0–6.0 kcal mol⁻¹ found in this work. Their reported value is in the range of PRC stabilization energies of n-alkenes + OH reactions.^78–80 The optimized structures and single-point energies of PRCs for the addition channels are provided in the ESI.†

It is worth noting that in both reactive systems, the free energy barriers of the addition reaction pathways remain below those of the corresponding hydrogen abstraction pathways even at temperatures as high as 1000 K (Fig. S1, ESI†). Therefore, besides the reduction of the entropy in the addition reaction pathways as both reacting fragments become covalently bonded, those pathways remain kinetically competitive. This might be attributed to the much lower potential energy barriers of the addition reactions due to the numerous stabilizing OH⋯π and O⋯H–O hydrogen bonds which may outbalance the effect of entropy. However, the effect of the multiple conformers is also expected to influence the rate constants and branching ratios in the investigated reactive systems; this effect is analyzed in the next section.

Addition adducts pathways. The adducts formed by the addition pathways can undergo unimolecular processes either by C–C and C–O bond scission or intramolecular hydrogen transfer reactions leading eventually to bimolecular products. Therefore, it is pertinent to map out the most kinetically favored unimolecular reaction pathways that can deplete the adducts to eventually form bimolecular products. To do so, we optimized several saddle points for the C–C and C–O bond scissions as well as some plausible intramolecular hydrogen transfer reactions that may rule the fate of prenol addition adducts (addC2 and addC3). Details of the calculations and the corresponding vibrationally adiabatic ground-state potential energy profiles are provided in the ESI† (see Fig. S2). We confirmed that among those unimolecular processes originating from the adducts, even those with the lowest adiabatic barrier heights, which are the intramolecular hydrogen transfer reaction via a 5-member ring and the C–O bond scission reaction for addC2 and addC3 adducts, respectively, are not kinetically relevant. Our calculations revealed that the barrier height for the most plausible unimolecular reaction of the adducts (addC2 and addC3) is ∼26 kcal mol⁻¹, which is not competitive with the barrierless O₂ addition reaction that is expected to consume those adducts in practical combustion/oxidation environments (see Fig. S2, ESI† and the corresponding discussion for additional details). This barrier height is very comparable to the lowest lying channel for the decomposition of the similar adduct formed by the allyl alcohol + OH reaction system (see Zhang et al.⁸¹). Taking the reaction analogy with allyl alcohol + OH, under our experimental conditions, we can safely rule out the isomerization and decomposition reactions of the prenol/isoprenol + OH adduct leading to bimolecular products. Hence, our current theoretical treatment is adequate to reasonably predict the rate coefficients for the current chemical system without worrying about the multiwell-multichannel character of the PES.

3.2.2 Multi-structural torsional anharmonicity. The variation of the multi-structural torsional anharmonicity factors with temperature for the reactants and saddle points, F^MS-T(C),χ, and for the reactions, F^MS-T(C), are shown in Fig. 6 for both reactive systems. A bar chart is also provided in Fig. S1 of the ESI† for the multi-structural torsional anharmonicity factors for the different reaction pathways at different temperatures (298, 500, 1000, and 2000 K) for convenient comparison. As can be seen, F^MS-T(C) factors increase with the increase of temperature in most of the cases, thus affecting the overall rates significantly. In the prenol + OH case, except for addC2 and absC5, multi-structural torsional parameters for all the saddle points are larger than those for prenol at T ≥ 450 K (Fig. 6a). This results in an enhancement of the system reactivity (Fig. 6b) that would be missed in a single-structural treatment. Interestingly, F^MS-T(C) of addC3 in the prenol + OH case is an order of magnitude higher than that of addC2 at T ≥ 650 K, which will significantly affect the site-specific rate constants and the trend at these temperatures. For isoprenol + OH, multi-structural torsional anharmonicity also plays an important role (see Fig. 6c and d) as the reactivity of all pathways is enhanced at high temperatures (T ≥ 750 K). Similarly, F^MS-T(C) of addC3 in the isoprenol + OH case is an order of magnitude higher than that of addC4 in the entire temperature range, resulting in a considerable effect on the site-specific rate constants.

Fig. 6 Temperature dependence of multi-structural torsional anharmonicity factors: (a) and (c) are for the reactant and saddle points (F^MS-T(C),χ) of prenol + OH and isoprenol + OH reactions, respectively. (b) and (d) are the parameters (F^MS-T(C)) for the different pathways of prenol + OH and isoprenol + OH reactions, respectively.

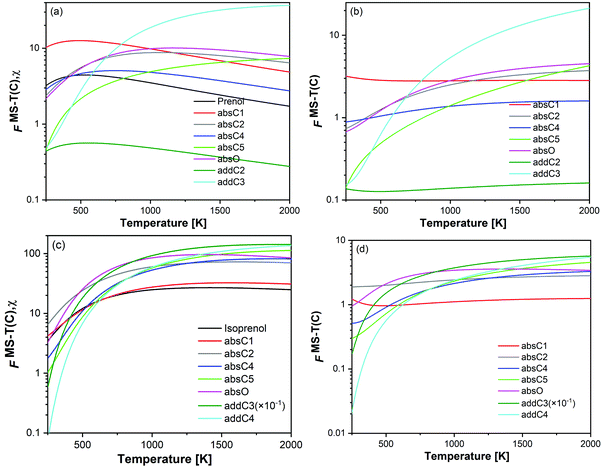
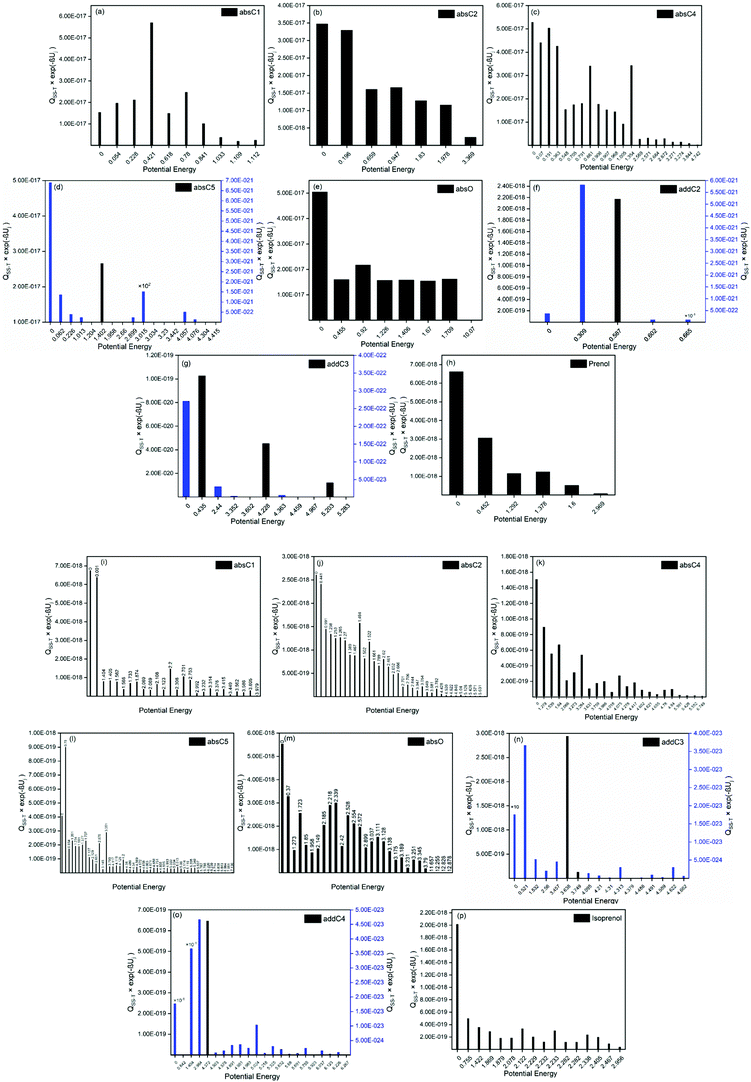
For a better assessment of the extent of the hydrogen bonds in the reactants and saddle points species of the investigated reactions, we also looked into the ro-vibrational partition functions of each of their multiple conformers. In Fig. 7 the values of those ro-vibrational partition functions at 700 K and weighted by the Boltzmann factor exp(−βU_j) are represented as a function of the potential energy of the conformers for the different species (panels (a)–(h) and panels (i)–(p) for prenol + OH and isoprenol + OH related species, respectively). There are two interesting features in those distributions. First, the values of those ro-vibrational weighted single-structural partition functions, which are proportional to the contribution of that conformer to the total multi-structural ro-vibrational partition function and thus to reactivity, indicate that the global minimum conformer (U_j = 0 kcal mol⁻¹) is not always the one with the largest contribution to reactivity. This might be an indication that entropy effects make the free energy of those highly stabilized global minimum conformers higher than that of conformers with higher potential energy, lowering their role in reactivity. Second, it can be seen that for the isoprenol + OH case, not only a significantly larger number of conformers is found for each of the stationary points compared to the prenol + OH case, but also that those conformers are distributed over a wider energy range. This may be attributed to the higher flexibility of the isoprenol saddle points to establish hydrogen bonds by the rotation of the C2–C3 bond, which is hindered by the non-terminal double bond in prenol, as discussed in Section 3.2.1.

Fig. 7 Ro-vibrational partition functions at 700 K weighted by the Boltzmann exponential factor exp(−βU_j) as a function of the potential energy of the different conformers for (a)–(h) prenol + OH and (i)–(p) isoprenol + OH.

In fact, the intermolecular interactions between the prenol/isoprenol and OH fragments, and thus the entropy effects, are, in some cases, strong enough to cause significant differences between the ro-vibrational partition functions of the conformers of a given species. This is the case of the saddle point of the addC2 pathway of prenol, whose three lowest energy conformers, with similar relative potential energy values, i.e. 0.000 (j = 0), 0.309 (j = 1), and 0.587 (j = 2) kcal mol⁻¹, have ro-vibrational partition functions with values that differ by three orders of magnitude (Fig. 7(f)). We performed a natural bond orbital (NBO) analysis on the optimized geometries of those three conformers with the Gaussian 16⁵⁰ package, and analyzed the large interaction that takes place between one of the lone pair orbitals of the O atom of the OH radical (donor) and the π anti-bonding orbital associated with the double bond (acceptor). The stabilization energy of this intermolecular interaction in the j = 0, j = 1, and j = 2 conformers is 5.08, 3.89, and 1.27 kcal mol⁻¹, respectively, indicating a larger stabilization in the conformer j = 0 but with the cost of a lower entropy and a significantly lower value for the ro-vibrational partition function compared to the other two conformers. The observed intermolecular interaction is expected to weaken the double bond of the prenol fragment in that saddle point, which in fact adopts bond distance values of 1.352, 1.348, and 1.339 Å in the conformers j = 0, j = 1, and j = 2, respectively, in line with the trend of the stabilization energy in the three conformers. Furthermore, the interatomic distance between the O and C atoms that are becoming covalently bonded in the conformers j = 0, j = 1, and j = 2 is also in line with the observed trends, with values of 2.223, 2.281, and 2.554 Å, respectively, indicating a stronger C⋯O interaction in the conformer j = 0. This analysis is also an indication that different reactivity trends can be expected in species with different functional groups, i.e. double bonds, OH groups, etc., as it is the case of the alkenes and alkenols species, and this should be taken into account when the rate constants are estimated by analogies.

3.2.3 Site-specific rate constants. Fig. 8 compares the calculated values of the high-pressure limit rate constants k^MS-T(C)/SCT with the experimental data. The site-specific rate constants are also plotted in Fig. 8 and compiled in the ESI†, together with the SCT transmission coefficient values. Fitted parameters of the modified Arrhenius equation over the temperature range of 650–2000 K are provided in Table 2. Fig. 8 shows the experimental data compared to the overall calculated rate constant. For addition pathways, canonical unified statistical theory (CUS)⁶⁰ was employed to include the effect of the pre-reaction complexes (PRC) in the reaction scheme; we observed that PRC only plays a minor role in the temperature range of 250–400 K.

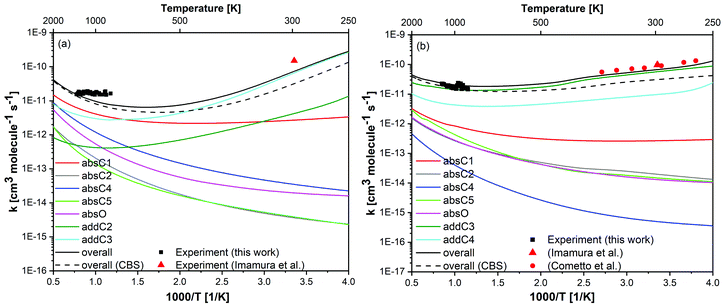Fig. 8 Calculated rate constants (lines) for (a) prenol + OH and (b) isoprenol + OH at the UCCSD(T)/jun-cc-pVQZ//M06-2X/6-311++G(2df,2pd) level of theory, compared to the measured rate constants in this work (black symbols) and those from literature^34,35 (red symbols). Black dashed lines is the overall rate constant calculated at UCCSD(T)/CBS//M06-2X/6-311++G(2df,2pd).

Table 2 High-pressure-limit fitting parameters of the modified Arrhenius equation for prenol + OH and isoprenol + OH reactive systems derived from our calculations at the UCCSD(T)/jun-cc-pVQZ//M06-2X/6-311++G(2df,2pd) level of theory. Fitting parameters are given for the temperature range of 650–2000 K (reported on a per carbon atom basis for abstraction reactions)

	Prenol + OH = products			Isoprenol + OH = products
	A (cm^3 molecule^−1 s^−1)	n	E a (cal mol^−1)	A (cm^3 molecule^−1 s^−1)	n	E a (cal mol^−1)
absC1	5.19 × 10^−21	2.78	−2529.349	1.99 × 10^−21	2.72	−2004.899
absC2	8.64 × 10^−21	2.56	1335.283	7.42 × 10^−21	2.52	21.311
absC4	9.82 × 10^−20	2.45	1195.688	1.68 × 10^−21	2.64	2395.160
absC5	7.95 × 10^−27	4.28	−1802.965	2.64 × 10^−20	2.46	766.881
absO	1.90 × 10^−21	2.91	1177.066	9.07 × 10^−20	2.23	936.192
addC2	4.04 × 10^−22	2.67	−4630.333
addC3	9.85 × 10^−23	3.15	−4828.697	9.80 × 10^−17	1.56	−2221.120
addC4	—	—	—	3.05 × 10^−21	2.75	−4088.810

---

Despite the prominence of the addition pathways relative to the abstraction ones even at intermediate and high temperatures, as will be discussed later, our total rate constants revealed no pressure dependence at a pressure as low as 1 atm, which is in line with our experimental data. This indicates that our measured rate constants are already close to the high-pressure limit, which is not surprising considering the complexity of the molecular system (prenol/isoprenol + OH reactions). Overall calculated rate constants reasonably agree with the experimental data, showing a positive and negative temperature dependence at high and low temperatures, respectively. The competition between abstraction and addition reaction pathways resulted in a non-Arrhenius behavior with a minimum at intermediate temperatures. For such a convoluted chemical system, the non-Arrhenius behavior is encountered due to channel switching. The theoretical results predict a slightly stronger temperature dependence than the experimental data for the prenol + OH system, in which reactivity is controlled by hydrogen abstraction reactions at temperatures higher than 700 K and by OH addition at lower temperatures, the maximum deviations from the experiments are observed at 298 and 850 K, where the overall calculated rate constants are slower by a factor of ∼2.0. For the isoprenol + OH system, in which reactivity is controlled by OH addition within the entire temperature range, the maximum deviations from the experiment occur at 263 and 926 K, where the overall calculated rate constants deviate from the experiment by a factor of 1.4 and 1.3, respectively, indicating a very good agreement between our calculations and experiments. The observed discrepancies for the prenol + OH case may lie in the uncertainties of the experiments (as detailed in Section 3.1) and the calculations, especially in the determination of the barrier heights. In order to assess the effect of the barrier height in the calculated rate constants we also estimated rate constants using barrier heights calculated at the complete basis set (CBS) extrapolation scheme⁸² (UCCSD(T)/CBS//M06-2X/6-311++G(2df,2pd) level of theory). The overall rate constant at the CBS is plotted in Fig. 8 (overall (CBS)), while the values for the site-specific rate constants are provided in the ESI† (Tables S8, S9 and Fig. S3). It can be seen that rate constants calculated at UCCSD(T)/jun-cc-pVQZ//M06-2X/6-311++G(2df,2pd) level of theory shows a relatively better agreement with the experimental values at intermediate and low temperatures, while both levels of theory yield very similar results at high temperatures. Therefore, results obtained at UCCSD(T)/jun-cc-pVQZ//M06-2X/6-311++G(2df,2pd) level of theory will be used and discussed throughout the manuscript.

The small deviations observed between the calculated and experimental rate constants at low temperatures may also be due to the tunneling effect, which is expected to be especially pronounced when a light particle, i.e. a hydrogen atom, is transferred between two heavy particles, i.e., carbon and oxygen atoms. Although the SCT method used in this work is relatively robust, it is a semiclassical method and not a purely quantum method. Thus, our tunneling coefficients at very low temperatures may show some uncertainties, contributing to the subtle discrepancies between the theory and experiments in that temperature regime (see Fig. 8). Tunneling through the barrier separating the PRCs and the saddle points can be also expected to contribute to the tunneling mechanism at very low temperatures (assuming that those PRCs are collisionally stabilized at those very low temperatures). However, based on the calculations that we performed in our former study⁷⁰ for a reactive system with a much larger barrier height separating the PRC and saddle point, and thus more prone to a tunneling mechanism than the current ones, we can safely rule out any effect of the PRCs of the investigated reactions in the tunneling mechanism since even in that former work, with a more stabilized PRC, similar transmission coefficients were obtained at temperatures as low as 298 K when tunneling was calculated with either the barrier separating the reactants and saddle point or with the one that separates the PRC and the saddle point. Nevertheless, at extremely low temperatures (below 200 K), we cannot rule out a tunneling mechanism through the inner barrier.

Variational effects are significant for most pathways of both reactive systems except for the addition and absO pathways of prenol + OH, and absO for isoprenol + OH. The re-crossing transmission coefficient Γ (defined as the ratio of the variational to the non-variational rate constants) is plotted as a function of temperature for all the investigated pathways in Fig. S4 of the ESI.† As seen, for certain reaction pathways of both reaction systems, these re-crossing transmission coefficients can lower the rate constants by a factor of two or more.

Hydrogen abstraction pathways. The site-specific rate constants and their contribution to the total rate constant can be better addressed by considering the free energy barriers (which include the enthalpic and entropic terms), and multi-structural torsional anharmonicity. For prenol + OH reaction, absC1 shows relatively larger rate constants compared to other abstraction pathways over the entire temperature range investigated here, which is consistent with its relatively lower potential and free energy barrier heights. Although both, absC1 and absC5 pathways, have very similar potential energy barrier heights, absC5 pathway shows a lower rate constant. This is due to the tight hydrogen-bonded saddle point structure of absC5 pathway which results in a higher free energy barrier (Fig. S1, ESI†), and also to the fact that the absC1 pathway is more favored by multi-structural torsional anharmonicity over almost the entire temperature range. This hindering effect of the hydrogen bond in the saddle point of the absC5 pathway is also evident when compared to absC4 pathway. The latter, with no hydrogen bond in its saddle point and a potential energy barrier height that is 1.89 kcal mol⁻¹ higher than that of the former, shows higher rate constants than absC5 due to higher entropic effects (Fig. S1, ESI†) and even though both show similar trends in their multi-structural torsional anharmonicity factors. We conclude that the strong and highly stabilizing hydrogen bond present in absC5 saddle point, which forms an eight-membered ring, lowers the entropic term for this pathway and outbalances its low potential energy barrier height. As for isoprenol + OH, all abstraction saddle points seem to be stabilized by hydrogen bonds and therefore, their effect is not so evident and the site-specific rate constants followed the trend of the potential and free energy barrier heights for all the cases but one (Fig. S1, ESI†); the exception is the addC3 pathway, which despite its relatively higher free energy compared to other pathways, it is the dominant one due to its favorable multi-structural torsional anharmonicity factors.
OH addition pathways. The OH addition to the double bond is usually considered to be less important at high temperatures as compared to hydrogen abstraction by OH. For instance, different alkene^76,78–80 and allyl alcohol⁸¹ studies showed that OH addition is dominant over abstraction at temperatures below 500–700 K. Addition reactions bring two reactants together which form an adduct. During this process, entropy is significantly lowered, yielding positive free energy barriers that are significantly higher than their negative potential energy barriers. As a result, entropy effects, which control reactivity at high temperatures, make addition pathways not competitive in that temperature regime. These two energy components, i.e., potential and free energy barriers, will determine the relative role of addition and abstraction pathways.

Our calculations, in contrast with former studies^76,78–80 on different alkene + OH reactive systems, predict that the addition of OH to the double bond of isoprenol is prominent even at temperatures as high as 2000 K, with a contribution of ∼78%. Calculations also predict an important role of OH addition to the double bond in the prenol + OH reactive system (contribution of ∼50% at 700 K), although in this case the reactivity trend is more alike to that observed for alkene + OH reactive systems. This peculiar reactivity of OH radicals with prenol and isoprenol might be due to the more stabilizing interaction between OH radicals and alcohol functional group in the entrance and exit channels of the PES which kinetically favors the addition reaction. This intermolecular interaction between the two reacting fragments, which is absent in OH addition to alkene reactions, may help to cancel out the hindering effect of entropy within a broader temperature range. This is also reflected in the stabilization energies of the PRCs of the investigated reactions. Energies for the PRCs on the PES of the reactions of alkenes with OH are usually within 2.0–2.6 kcal mol⁻¹ below the reactants,^78–80 while the PRCs for the isopentanol + OH reactions are stabilized by 4.0–6.0 kcal mol⁻¹ with respect to the reactants. Despite the presence of the alcohol functional group in the allyl alcohol + OH system studied by Zhang et al.,⁸¹ their non-hydrogen bonded PRC was only stabilized by 2.22 kcal mol⁻¹ with respect to the reactants, similarly to the alkene + OH chemistry case and therefore, their system exhibited a similar reactivity trend in which abstraction by OH took over reactivity at temperatures beyond 600 K and OH addition was prominent at lower temperatures.

On the other hand, the competition between various addition channels seems to be influenced by multi-structural torsional anharmonicity as well. For prenol + OH reaction, even though the addC3 pathway has a significantly larger free energy barrier than the addC2 pathway at high temperatures (Fig. S1, ESI†), the former is more competitive due to a significant enhancement by multi-structural torsional anharmonicity compared to the latter which is hindered (Fig. S1, ESI†). In terms of free energy and multi-structural torsional anharmonicity, the same situation applies to isoprenol + OH (Fig. S1, ESI†), for which the addition pathway with the highest free energy barrier, i.e. addC3, is the prominent one because of the multi-structural anharmonicity effect.

3.2.4 Branching ratios. Fig. 9 depicts the calculated branching ratios for the different pathways using the overall rate constant. For prenol, the addition channel is dominant at low temperatures up to 700 K, beyond which the abstraction channel becomes more important. absC1 and absC4 pathways of prenol are the dominant abstraction pathways, contributing for more than 66% of the total abstraction over the entire temperature range. For isoprenol, the addition of OH to the double bond rules reactivity at low temperatures and is more important than abstraction at temperatures as high as 2000 K. absC1 and absC5 pathways control abstraction in isoprenol, representing more than 63% of the total abstraction pathway over the entire range of temperatures. The prominence of the addC3 pathway in isoprenol + OH reaction is particularly noteworthy, which dominates reactivity at temperatures as high as 1500 K due to the multi-structural anharmonicity effect.

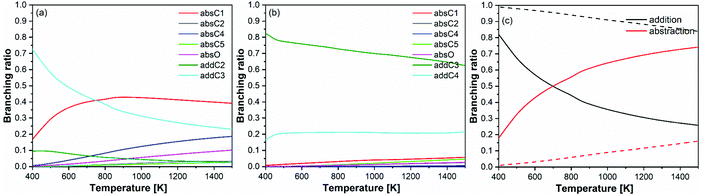Fig. 9 Branching ratios of (a) prenol + OH, (b) isoprenol + OH, and (c) overall abstraction versus addition pathways for prenol (solid lines) and isoprenol (dashed lines).

The observed branching ratios are the result of the calculated rate constants. The rate constants trends have been explained in previous sections in terms of hydrogen bonds, potential and free energy barriers, and multi-structural torsional anharmonicity. It is also important to discuss at this point two features of the prenol + OH and isoprenol + OH reactive systems that result in the different branching ratios for their abstraction/addition channels, and thus explain why isoprenol + OH system deviates more than the former from the chemistry observed in alkene + OH systems. First, the more flexible structure of isoprenol allows for more stabilizing hydrogen bonds, which efficiently cancel out the entropy impediment of the association reaction. This is supported by the significantly larger number of conformers found for isoprenol and the corresponding saddle points compared to the prenol + OH system, as shown in Fig. 7. Secondly, it seems that not only the addition channels are more kinetically favored in isoprenol + OH than in prenol + OH, but also that the abstraction ones are less kinetically favored in the former than in the latter, which explains why isoprenol primarily undergoes OH addition within the 250–2000 K temperature range. This not only highlights the importance of the presence of the OH functional group in determining different reactivity trends between alkenols and alkenes, but also the location of the double bond in the alkenol.

3.3 Reactivity comparison with n-alkene and alcohol

In this work, we have highlighted the importance of the presence and location of the two functional groups (double bond and OH) to explain the reactivity behavior of prenol and isoprenol with OH radicals. Therefore, it is interesting to compare the reactivity of the investigated isopentenols in this study to their analogous alkenes and alcohols.

Fig. 10 shows the high pressure limit site-specific rate constants of the reaction of OH with prenol or isoprenol, grouped per chemical nature of the reaction sites, and compared to site-specific high-pressure limit rate constants of propene + OH from Zador et al.,⁷⁸ 1-butene + OH from Vasu et al.,⁸³ and isobutanol + OH from Zheng et al.⁸⁴ The chemical sites in prenol and isoprenol are very unique and thus contribute to quite a different Arrhenius behavior. Of course, some differences may have originated from the different levels of theory and kinetic methods used in the earlier studies and the current work, as well as from other features that characterize each chemical system (i.e. torsional anharmonicity), so only qualitative comparisons will be discussed. Zador et al.⁷⁸ calculated the rate constants using RQCISD(T)/cc-pV∞Z//B3LYP/6-311++G(d,p) level and RRKM-based multiwell master equation method.⁸⁵ Vasu et al.⁸³ used canonical transition state theory with Eckart tunneling at CCSD(T)/6-311++G(d,p)//QCISD/6-31G(d)) level and Zheng et al.⁸⁴ used CCSD(T)-F12a/jun-cc-pVTZ//M08-HX/6-311+G(2df,2p) electronic structure calculations with multi-path canonical variational transition-state theory and SCT method for tunneling.

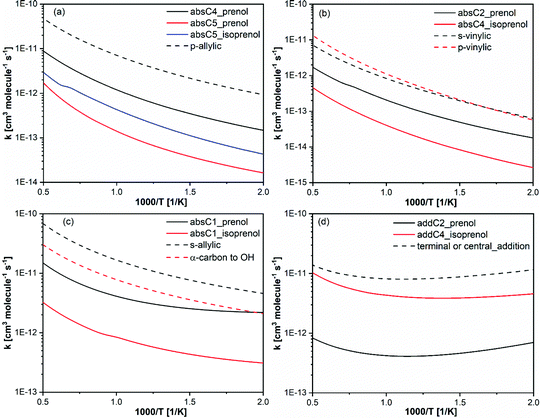Fig. 10 Calculated rate constants (solid lines) in this work compared with analogous rate constants per H-atom basis, from propene + OH,⁷⁸ 1-butene + OH⁸³ and isobutanol + OH.⁸⁴

In Fig. 10a, the rate constants of the formation of primary allylic radicals via absC4 and absC5 in prenol + OH, along with absC5 in isoprenol + OH, are compared to the p-allylic H-abstraction by OH from propene.⁷⁸ The primary allylic hydrogen in propene displays the highest reactivity. This can be attributed to the tight saddle point of absC5 pathway in prenol and isoprenol, which makes the reaction go over a high free energy barrier (Fig. 4). Note that the rate constant of the non-hydrogen bonding structure of absC4 pathway in prenol is closer to that of the allylic hydrogen abstraction in propene + OH reaction. For similar reasons, absC2 and absC4 pathways in prenol and isoprenol, respectively, show decreased reactivity as compared to the abstraction of primary and secondary vinylic hydrogen atoms from n-alkenes⁷⁸ (Fig. 10b).

absC1 pathway in prenol is the abstraction from α-carbon to the OH moiety which results in the formation of a secondary allylic radical. Therefore, this reaction pathway is compared with hydrogen abstraction reaction of α-carbon in iso-alcohol⁸⁴ and secondary allylic in n-alkene⁸³ in Fig. 10c. As expected, hydrogen bonding in absC1 from prenol resulted in lower rate constants compared to secondary allylic hydrogen abstraction in n-alkene. However, hydrogen bonding is present in the saddle points of α-carbon hydrogen abstraction from n-alcohol and of absC1 pathways of both prenol and isoprenol. In this case, the double bond present in prenol and isoprenol may be one of the reasons for the differences, although there might be others. Moreover, absC1 pathway in prenol is kinetically and thermodynamically more favorable than that of isoprenol. The secondary allylic radical in prenol is 13 kcal mol⁻¹ more stable than the radical formed by absC1 of isoprenol.

Finally, the rate constants of OH addition to propene,⁷⁸ terminal or center carbon, are compared to addC2 and addC4 in prenol and isoprenol, respectively, in Fig. 10d. The calculated rate constants from this study are slower than the analogous rate constants of n-alkene + OH. Again, hydrogen bonding, causing the entropic loss, may be responsible for lowering the reactivity of addC2 and addC4 in prenol and isoprenol, respectively. Another reason for the low reactivity observed for addC2 pathway for prenol compared to OH addition to propene is the very low values (<1) of the multi-structural torsional anharmonicity factors (Fig. 6); such treatment was missing in the work of propene + OH.

The above discussion shows that having two functional groups significantly alters the rate constants, and analogies should be cautiously used when developing chemical kinetic models for similar compounds. In Fig. 11, our calculated rate constants compared with those used by Bruycker et al.²⁵ in their prenol and isoprenol chemical kinetic models. Our calculated rate constants are generally slower than those used in the kinetic model, which were obtained from reaction analogy. It is worth noting that the automatic mechanism generator (Genesys) used by Bruycker et al.²⁵ assumed that the hydrogen in C4 and C5 of prenol are identical and that absC4 and absC5 exhibit similar reactivity. This would lead to an overestimation of the branching ratio for this channel as our calculations show that the rate constants for absC4 and absC5 pathways differ by a factor of ∼6.

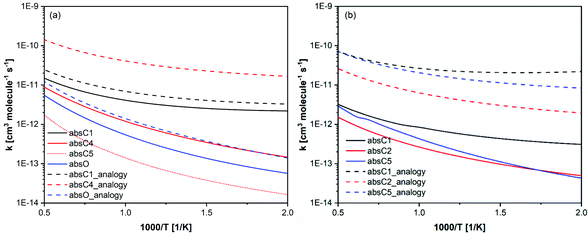Fig. 11 Calculated rate constants per H-atom basis (solid and dotted lines) for (a) prenol + OH and (b) isoprenol + OH, compared with analogous rate constants used in Bruycker et al.²⁵ kinetic model (dashed lines).

4 Conclusions

For the first time, the reactions of OH radicals with prenol and isoprenol were investigated experimentally and theoretically over a wide range of conditions. A shock tube and UV laser diagnostic were employed to carry out experiments over the temperature and pressure ranges of 900–1290 K and 1–5 atm, respectively. A high level of theory (UCCSD(T)/jun-cc-pVQZ//M06-2X/6-311++G(2df,2pd)) was used to map out the various reaction pathways in the potential energy surfaces of the title reactions. The energetic descriptions along with the molecular parameters from our electronic structure calculations were utilized to calculate site-specific rate constants, which are very difficult to determine experimentally though very much needed for kinetic modeling. The rate constants were calculated using the canonical variational transition state theory (CVT) with small curvature tunneling (SCT) and multi-structural torsional anharmonicity (MS-T) corrections. Pressure-dependent rate constants for the addition pathways were estimated using the system-specific quantum Rice–Ramsperger–Kassel (SS-QRRK) theory, which showed that pressure effects are not important under both atmospheric and combustion relevant conditions. Our calculated and measured rate constants show a relatively good agreement especially for the isoprenol + OH reactive system.

Prenol and isoprenol were found to display an interesting reactivity with OH radicals. In stark contrast to n-alkenes + OH, these isopentenols showed a more prominent role of the addition pathways over abstraction even at moderately high temperatures. Our calculations showed that OH addition remains dominant up to 700 K in prenol + OH, becoming even more important in isoprenol + OH in which those reactions take over reactivity within the 250–2000 K temperature range. Another peculiarity about the title reactions is the existence of a negative barrier for the allylic hydrogen abstraction pathway. Such negative barriers are not encountered in n-alkene + OH reactions. We infer that this behavior is the result of a more stabilizing interaction between the OH functional group of isopentenols and the abstracting OH radical. Such interaction, not present in n-alkene + OH reactions, leads to the formation of more stabilized saddle points and pre-reactive intermediate complexes, helping to cancel out the hindering entropy effect that governs high-temperature reactivity of addition reactions. This conclusion may apply to other unsaturated enols as well. Our calculated values of the site-specific rate constants are highly useful for kinetic models of combustion and atmospheric applications.

We also conclude that not only the presence of the OH functional group in alkenols makes a difference in their reactivity towards OH radicals compared to that of alkenes, but also the location of that functional group. This is demonstrated by the calculated addition/abstraction branching ratios for the isoprenol + OH and prenol + OH reactive systems, which indicate a more unique reactivity trend of the former.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Research reported in this publication was funded by the Office of Sponsored Research (OSR) at King Abdullah University of Science and Technology (KAUST) (Grant OSR-2016-CRG5-3022). We also acknowledge the resources of the Supercomputer Laboratory at KAUST.

References

1. S. Atsumi, T. Hanai and J. C. Liao, Non-fermentative pathways for synthesis of branched-chain higher alcohols as biofuels, Nature, 2008, 451, 86–90.
2. D. Rakopoulos, C. Rakopoulos, E. Giakoumis, A. Dimaratos and D. Kyritsis, Effects of butanol–diesel fuel blends on the performance and emissions of a high-speed DI diesel engine, Energy Convers. Manage., 2010, 51, 1989–1997.
3. S. M. Sarathy, P. Oßwald, N. Hansen and K. Kohse-Höinghaus, Alcohol combustion chemistry, Prog. Energy Combust. Sci., 2014, 44, 40–102.
4. P. S. Nigam and A. Singh, Production of liquid biofuels from renewable resources, Prog. Energy Combust. Sci., 2011, 37, 52–68.
5. L. Siwale, L. Kristóf, T. Adam, A. Bereczky, M. Mbarawa, A. Penninger and A. Kolesnikov, Combustion and emission characteristics of n-butanol/diesel fuel blend in a turbo-charged compression ignition engine, Fuel, 2013, 107, 409–418.
6. G. Valentino, F. E. Corcione, S. E. Iannuzzi and S. Serra, Experimental study on performance and emissions of a high speed diesel engine fuelled with n-butanol diesel blends under premixed low temperature combustion, Fuel, 2012, 92, 295–307.
7. J. Campos-Fernandez, J. M. Arnal, J. Gomez, N. Lacalle and M. P. Dorado, Performance tests of a diesel engine fueled with pentanol/diesel fuel blends, Fuel, 2013, 107, 866–872.
8. L. Wei, C. Cheung and Z. Huang, Effect of n-pentanol addition on the combustion, performance and emission characteristics of a direct-injection diesel engine, Energy, 2014, 70, 172–180.
9. L. Li, J. Wang, Z. Wang and J. Xiao, Combustion and emission characteristics of diesel engine fueled with diesel/biodiesel/pentanol fuel blends, Fuel, 2015, 156, 211–218.
10. S. M. Sarathy, S. Vranckx, K. Yasunaga, M. Mehl, P. Oßwald, W. K. Metcalfe, C. K. Westbrook, W. J. Pitz, K. Kohse-Höinghaus, R. X. Fernandes and H. J. Curran, A comprehensive chemical kinetic combustion model for the four butanol isomers, Combust. Flame, 2012, 159, 2028–2055.
11. Y. Zheng, Q. Liu, L. Li, W. Qin, J. Yang, H. Zhang, X. Jiang, T. Cheng, W. Liu, X. Xu and M. Xian, Metabolic engineering of Escherichia coli for high-specificity production of isoprenol and prenol as next generation of biofuels, Biotechnol. Biofuels, 2013, 6, 57.
12. S. M. Sarathy, Fuel class higher alcohols, Biofuels from lig-nocellulosic biomass, Wiley-VCH, Germany, 2016, pp. 29–57.
13. S. M. Sarathy, S. Park, B. W. Weber, W. Wang, P. S. Veloo, A. C. Davis, C. Togbe, C. K. Westbrook, O. Park and G. Dayma, A comprehensive experimental and modeling study of iso-pentanol combustion, Combust. Flame, 2013, 160, 2712–2728.
14. S. Park, O. Mannaa, F. Khaled, R. Bougacha, M. S. Mansour, A. Farooq, S. H. Chung and S. M. Sarathy, A comprehensive experimental and modeling study of 2-methylbutanol combustion, Combust. Flame, 2015, 162, 2166–2176.
15. L. Cai, L. Kröger, M. Döntgen, K. Leonhard, K. Narayanaswamy, S. M. Sarathy, K. A. Heufer and H. Pitsch, Exploring the combustion chemistry of a novel lignocellulose-derived biofuel: cyclopentanol. Part I: quantum chemistry calculation and kinetic modeling, Combust. Flame, 2019, 210, 490–501.
16. A. S. AlRamadan, J. Badra, T. Javed, M. Al-Abbad, N. Bokhumseen, P. Gaillard, H. Babiker, A. Farooq and S. M. Sarathy, Mixed butanols addition to gasoline surrogates: Shock tube ignition delay time measurements and chemical kinetic modeling, Combust. Flame, 2015, 162, 3971–3979.
17. M. Mehl, W. J. Pitz, C. K. Westbrook and H. J. Curran, Kinetic modeling of gasoline surrogate components and mixtures under engine conditions, Proc. Combust. Inst., 2011, 33, 193–200.
18. S. T. Withers, S. S. Gottlieb, B. Lieu, J. D. Newman and J. D. Keasling, Identification of isopentenol biosynthetic genes from Bacillus subtilis by a screening method based on isoprenoid precursor toxicity, Appl. Environ. Microbiol., 2007, 73, 6277–6283.
19. H. H. Chou and J. D. Keasling, Synthetic Pathway for Production of Five-Carbon Alcohols from Isopentenyl Diphosphate, Appl. Environ. Microbiol., 2012, 78, 7849–7855.
20. K. W. George, A. Chen, A. Jain, T. S. Batth, E. E.-K. Baidoo, G. Wang, P. D. Adams, C. J. Petzold, J. D. Keasling and T. S. Lee, Correlation analysis of targeted proteins and metabolites to assess and engineer microbial isopentenol production, Biotechnol. Bioeng., 2014, 111, 1648–1658.
21. H. Liu, Y. Wang, Q. Tang, W. Kong, W.-J. Chung and T. Lu, MEP pathway-mediated isopentenol production in metabolically engineered Escherichia coli, Microb. Cell Fact., 2014, 13, 135.
22. K. W. George, M. G. Thompson, A. Kang, E. Baidoo, G. Wang, L. J.-G. Chan, P. D. Adams, C. J. Petzold, J. D. Keasling and T. Soon Lee, Metabolic engineering for the high-yield production of isoprenoid-based C(5) alcohols in E. coli, Sci. Rep., 2015, 5, 11128.
23. E. Ninnemann, G. Kim, A. Laich, B. Almansour, A. C. Terracciano, S. Park, K. Thurmond, S. Neupane, S. Wagnon and W. J. Pitz, Co-optima fuels combustion: A comprehensive experimental investigation of prenol isomers, Fuel, 2019, 254, 115630.
24. O. Welz, J. D. Savee, D. L. Osborn and C. A. Taatjes, Chlorine atom-initiated low-temperature oxidation of prenol and isoprenol: The effect of CC double bonds on the peroxy radical chemistry in alcohol oxidation, Proc. Combust. Inst., 2015, 35, 401–408.
25. R. De Bruycker, O. Herbinet, H.-H. Carstensen, F. Battin-Leclerc and K. M. Van Geem, Understanding the reactivity of unsaturated alcohols: Experimental and kinetic modeling study of the pyrolysis and oxidation of 3-methyl-2-butenol and 3-methyl-3-butenol, Combust. Flame, 2016, 171, 237–251.
26. N. Lokachari, S. W. Wagnon, G. Kukkadapu, W. J. Pitz and H. J. Curran, Experimental and Kinetic Modeling Study of 3-Methyl-2-butenol (Prenol) Oxidation, Energy Fuels, 2021, 35, 13999–14009.
27. G. M. Fioroni, M. J. Rahimi, C. K. Westbrook, S. W. Wagnon, W. J. Pitz, S. Kim and R. L. McCormick, Chemical kinetic basis of synergistic blending for research octane number, Fuel, 2022, 307, 121865.
28. P. Harley, V. Fridd-Stroud, J. Greenberg, A. Guenther and P. Vasconcellos, Emission of 2-methyl-3-buten-2-ol by pines: A potentially large natural source of reactive carbon to the atmosphere, J. Geophys. Res.: Atmos., 1998, 103, 25479–25486.
29. J. Kesselmeier and M. Staudt, Biogenic Volatile Organic Compounds (VOC): An Overview on Emission, Physiology and Ecology, J. Atmos. Chem., 1999, 33, 23–88.
30. G. W. Schade and A. H. Goldstein, Plant physiological influences on the fluxes of oxygenated volatile organic compounds from ponderosa pine trees, J. Geophys. Res. Atmos., 2002, 107, ACH 2-1–ACH 2-8.
31. A. Rodríguez, D. Rodríguez, A. Soto, I. Bravo, Y. Diaz-de-Mera, A. Notario and A. Aranda, Products and mechanism of the reaction of Cl atoms with unsaturated alcohols, Atmos. Environ., 2012, 50, 214–224.
32. D. Rodriguez, A. Rodriguez, A. Soto, A. Aranda, Y. Diaz-de-Mera and A. Notario, Kinetics of the reactions of Cl atoms with 2-buten-1-ol, 2-methyl-2-propen-1-ol, and 3-methyl-2-buten-1-ol as a function of temperature, J. Atmos. Chem., 2008, 59, 187–197.
33. B. Du and W. Zhang, Theoretical study on the reaction mechanism of the OH-initiated oxidation of CH2 = C(CH3)CH2CH2OH, Struct. Chem., 2011, 22, 589–604.
34. P. M. Cometto, P. R. Dalmasso, R. A. Taccone, S. I. Lane, F. Oussar, V. Daële, A. Mellouki and G. L. Bras, Rate Coefficients for the Reaction of OH with a Series of Unsaturated Alcohols between 263 and 371 K, J. Phys. Chem. A, 2008, 112, 4444–4450.
35. T. Imamura, Y. Iida, K. Obi, I. Nagatani, K. Nakagawa, I. Patroescu-Klotz and S. Hatakeyama, Rate coefficients for the gas-phase reactions of OH radicals with methylbutenols at 298 K, Int. J. Chem. Kinet., 2004, 36, 379–385.
36. J. Badra, A. E. Elwardany, F. Khaled, S. S. Vasu and A. Farooq, A shock tube and laser absorption study of ignition delay times and OH reaction rates of ketones: 2-Butanone and 3-buten-2-one, Combust. Flame, 2014, 161, 725–734.
37. J. Badra, F. Khaled, B. R. Giri and A. Farooq, A shock tube study of the branching ratios of propene + OH reaction, Phys. Chem. Chem. Phys., 2015, 17, 2421–2431.
38. J. N. Bradley, Shock waves in chemistry and physics, Methuen, 1962.
39. G. A. Pang, R. K. Hanson, D. M. Golden and C. T. Bowman, High-temperature measurements of the rate constants for reactions of oh with a series of large normal alkanes: N-pentane, n-heptane, and n-nonane, Z. Phys. Chem., 2011, 225, 1157–1178.
40. J. T. Herbon, Shock tube measurements of CH₃+ O₂ kinetics and the heat of formation of the OH radical, Stanford University, Stanford, CA, 2004.
41. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Gaussian, Inc., Wallingford, CT, USA, 2009.
42. Y. Zhao and D. G. Truhlar, The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class functionals and 12 other functionals, Theor. Chem. Acc., 2008, 120, 215–241.
43. Y. Zhao and D. G. Truhlar, Density Functionals with Broad Applicability in Chemistry, Acc. Chem. Res., 2008, 41, 157–167.
44. W. J. Hehre, R. Ditchfield and J. A. Pople, Self-Consistent Molecular Orbital Methods. XII. Further Extensions of Gaussian—Type Basis Sets for Use in Molecular Orbital Studies of Organic Molecules, J. Chem. Phys., 1972, 56, 2257–2261.
45. M. J. Frisch, J. A. Pople and J. S. Binkley, Self-consistent molecular orbital methods 25. Supplementary functions for Gaussian basis sets, J. Chem. Phys., 1984, 80, 3265–3269.
46. K. S. Thanthiriwatte, E. G. Hohenstein, L. A. Burns and C. D. Sherrill, Assessment of the Performance of DFT and DFT-D Methods for Describing Distance Dependence of Hydrogen-Bonded Interactions, J. Chem. Theory Comput., 2011, 7, 88–96.
47. E. Papajak, J. Zheng, X. Xu, H. R. Leverentz and D. G. Truhlar, Perspectives on Basis Sets Beautiful: Seasonal Plantings of Diffuse Basis Functions, J. Chem. Theory Comput., 2011, 7, 3027–3034.
48. K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, A fifth-order perturbation comparison of electron correlation theories, Chem. Phys. Lett., 1989, 157, 479–483.
49. R. J. Bartlett, Coupled-cluster approach to molecular structure and spectra: a step toward predictive quantum chemistry, J. Phys. Chem., 1989, 93, 1697–1708.
50. M. Frisch, G. Trucks, H. Schlegel, G. Scuseria, M. Robb, J. Cheeseman, G. Scalmani, V. Barone, G. Petersson and H. Nakatsuji, Gaussian 16, Gaussian, Inc., Wallingford, CT, 2016.
51. E. Papajak and D. G. Truhlar, Convergent Partially Augmented Basis Sets for Post-Hartree−Fock Calculations of Molecular Properties and Reaction Barrier Heights, J. Chem. Theory Comput., 2011, 7, 10–18.
52. J. Zheng, S. Zhang, J. Corchado, Y. Chuang, E. Coitino, B. Ellingson and D. Truhlar, Gaussrate 2016, University of Minnesota, Minneapolis, MN, 2016.
53. J. Zheng, J. Bao, R. Meana-Pañeda, S. Zhang, B. Lynch, J. Corchado, Y. Chuang, P. Fast, W. Hu, Y. Liuet al., POLYRATE, version 2016-2A, University of Minnesota, Minneapolis, 2016.
54. B. Garrett and D. Truhlar, Additions and Corrections - Generalized Transition State Theory. Classical Mechanical Theory and Applications to Collinear Reactions of Hydrogen Molecules, J. Phys. Chem., 1983, 87, 4553.
55. B. C. Garrett and D. G. Truhlar, Criterion of minimum state density in the transition state theory of bimolecular reactions, J. Chem. Phys., 1979, 70, 1593–1598.
56. Y. P. Liu, G. C. Lynch, T. N. Truong, D. H. Lu, D. G. Truhlar and B. C. Garrett, Molecular modeling of the kinetic isotope effect for the [1,5]-sigmatropic rearrangement of cis-1,3-pentadiene, J. Am. Chem. Soc., 1993, 115, 2408–2415.
57. R. T. Skodje, D. G. Truhlar and B. C. Garrett, Vibrationally adiabatic models for reactive tunneling, J. Chem. Phys., 1982, 77, 5955–5976.
58. J. Zheng, R. Meana-Pañeda and D. G. Truhlar, MSTor version 2013: A new version of the computer code for the multi-structural torsional anharmonicity, now with a coupled torsional potential, Comput. Phys. Commun., 2013, 184, 2032–2033.
59. J. Zheng, S. L. Mielke, J. L. Bao, R. Meana-Pañeda, K. L. Clarkson and D. G. Truhlar, MSTor computer program, version 2017, University of Minnesota, Minneapolis, MN, 2017, vol. 2017.
60. B. C. Garrett and D. G. Truhlar, Canonical unified statistical model. Classical mechanical theory and applications to collinear reactions, J. Chem. Phys., 1982, 76, 1853–1858.
61. E. E. Greenwald, S. W. North, Y. Georgievskii and S. J. Klippenstein, A two transition state model for radical− molecule reactions: A case study of the addition of OH to C2H4, J. Phys. Chem. A, 2005, 109, 6031–6044.
62. Y. Georgievskii and S. J. Klippenstein, Variable reaction coordinate transition state theory: Analytic results and application to the C 2 H 3+ H→ C 2 H 4 reaction, J. Chem. Phys., 2003, 118, 5442–5455.
63. Y. Georgievskii and S. J. Klippenstein, Transition state theory for multichannel addition reactions: Multifaceted dividing surfaces, J. Phys. Chem. A, 2003, 107, 9776–9781.
64. E. Grajales-González, M. Monge-Palacios and S. M. Sarathy, Collision efficiency parameter influence on pressure-dependent rate constant calculations using the SS-QRRK theory, J. Phys. Chem. A, 2020, 124, 6277–6286.
65. E. Grajales-González, M. Monge-Palacios and S. M. Sarathy, A theoretical study of the Ḣ-and HOȮ-assisted propen-2-ol tautomerizations: Reactive systems to evaluate collision efficiency definitions on chemically activated reactions using SS-QRRK theory, Combust. Flame, 2021, 225, 485–498.
66. J. L. Bao, J. Zheng and D. G. Truhlar, Kinetics of hydrogen radical reactions with toluene including chemical activation theory employing system-specific quantum RRK theory calibrated by variational transition state theory, J. Am. Chem. Soc., 2016, 138, 2690–2704.
67. J. L. Bao, X. Zhang and D. G. Truhlar, Barrierless association of CF2 and dissociation of C2F4 by variational transition-state theory and system-specific quantum Rice–Ramsperger–Kassel theory, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 13606–13611.
68. J. L. Bao, X. Zhang and D. G. Truhlar, Predicting pressure-dependent unimolecular rate constants using variational transition state theory with multidimensional tunneling combined with system-specific quantum RRK theory: A definitive test for fluoroform dissociation, Phys. Chem. Chem. Phys., 2016, 18, 16659–16670.
69. E. Grajales-González, M. Monge-Palacios and S. M. Sarathy, Theoretical Kinetic Study of the Unimolecular Keto–Enol Tautomerism Propen-2-ol↔ Acetone. Pressure Effects and Implications in the Pyrolysis of tert-and 2-Butanol, J. Phys. Chem. A, 2018, 122, 3547–3555.
70. M. Monge-Palacios, E. Grajales-González and S. M. Sarathy, Ab Initio, Transition State Theory, and Kinetic Modeling Study of the HO2-Assisted Keto–Enol Tautomerism Propen-2-ol+ HO2 ⇔ Acetone+ HO2 under Combustion, Atmospheric, and Interstellar Conditions, J. Phys. Chem. A, 2018, 122, 9792–9805.
71. J. P. Senosiain, S. J. Klippenstein and J. A. Miller, Reaction of ethylene with hydroxyl radicals: a theoretical study, J. Phys. Chem. A, 2006, 110, 6960–6970.
72. Y. Li, C.-W. Zhou, K. P. Somers, K. Zhang and H. J. Curran, The oxidation of 2-butene: A high pressure ignition delay, kinetic modeling study and reactivity comparison with isobutene and 1-butene, Proc. Combust. Inst., 2017, 36, 403–411.
73. C.-W. Zhou, Y. Li, E. O'Connor, K. P. Somers, S. Thion, C. Keesee, O. Mathieu, E. L. Petersen, T. A. DeVerter and M. A. Oehlschlaeger, A comprehensive experimental and modeling study of isobutene oxidation, Combust. Flame, 2016, 167, 353–379.
74. S. M. Burke, U. Burke, R. Mc Donagh, O. Mathieu, I. Osorio, C. Keesee, A. Morones, E. L. Petersen, W. Wang and T. A. DeVerter, An experimental and modeling study of propene oxidation. Part 2: Ignition delay time and flame speed measurements, Combust. Flame, 2015, 162, 296–314.
75. S. M. Burke, W. Metcalfe, O. Herbinet, F. Battin-Leclerc, F. M. Haas, J. Santner, F. L. Dryer and H. J. Curran, An experimental and modeling study of propene oxidation. Part 1: Speciation measurements in jet-stirred and flow reactors, Combust. Flame, 2014, 161, 2765–2784.
76. F. Khaled, B. R. Giri and A. Farooq, A high-temperature shock tube kinetic study for the branching ratios of isobutene+ OH reaction, Proc. Combust. Inst., 2017, 36, 265–272.
77. J. C. Rienstra-Kiracofe, W. D. Allen and H. F. Schaefer, The C2H5 + O2 Reaction Mechanism:  High-Level ab Initio Characterizations, J. Phys. Chem. A, 2000, 104, 9823–9840.
78. J. Zador, A. W. Jasper and J. A. Miller, The reaction between propene and hydroxyl, Phys. Chem. Chem. Phys., 2009, 11, 11040–11053.
79. L. K. Huynh, H. R. Zhang, S. Zhang, E. Eddings, A. Sarofim, M. E. Law, P. R. Westmoreland and T. N. Truong, Kinetics of enol formation from reaction of OH with propene, J. Phys. Chem. A, 2009, 113, 3177–3185.
80. C.-W. Zhou, Z.-R. Li and X.-Y. Li, Kinetics and mechanism for formation of enols in reaction of hydroxide radical with propene, J. Phys. Chem. A, 2009, 113, 2372–2382.
81. Y. Zhang, K. Chao, J. Sun, Z. Su, X. Pan, J. Zhang and R. Wang, Theoretical Study on the Gas Phase Reaction of Allyl Alcohol with Hydroxyl Radical, J. Phys. Chem. A, 2013, 117, 6629–6640.
82. J. M. Martin, Ab initio total atomization energies of small molecules—towards the basis set limit, Chem. Phys. Lett., 1996, 259, 669–678.
83. S. S. Vasu, L. K. Huynh, D. F. Davidson, R. K. Hanson and D. M. Golden, Reactions of OH with butene isomers: measurements of the overall rates and a theoretical study, J. Phys. Chem. A, 2011, 115, 2549–2556.
84. J. Zheng, R. Meana-Pañeda and D. G. Truhlar, Prediction of Experimentally Unavailable Product Branching Ratios for Biofuel Combustion: The Role of Anharmonicity in the Reaction of Isobutanol with OH, J. Am. Chem. Soc., 2014, 136, 5150–5160.
85. J. A. Miller and S. J. Klippenstein, Master Equation Methods in Gas Phase Chemical Kinetics, J. Phys. Chem. A, 2006, 110, 10528–10544.

---

Footnotes

† Electronic supplementary information (ESI) available: Tabulation of the: (1) calculated energies at M06-2X/6-311++G(2df,2pd), UCCSD(T)/jun-cc-pVQZ levels of theory and T1 diagnostic, (2) frequencies and rotational constants data, (3) Cartesian coordinates for all stationary points in PES, (4) NS:SC scheme for the different pathways, (5) high-pressure limit rate constants for the different reaction pathways and SCT coefficient, (6) experimentally measured rate constants. Plots for the temperature dependence of Gibbs free energy, multi-structural torsional anharmonicity factors, and the re-crossing transmission coefficient Γ. See DOI: https://doi.org/10.1039/d2cp00737a

‡ These authors contributed equally.

§ Current address: National Renewable Energy Laboratory, Golden, CO 80401, USA.

¶ Current address: Transport Technologies Division, R&DC, Saudi Aramco, Dhahran, Saudi Arabia.

---