Vibrational mode-specific dynamics of the F⁻ + CH₃CH₂Cl multi-channel reaction

Abstract

We investigate the mode-specific dynamics of the ground-state, C–Cl stretching (v₁₀), CH₂ wagging (v₇), sym-CH₂ stretching (v₁), and sym-CH₃ stretching (v₃) excited F⁻ + CH₃CH₂Cl(v_k = 0, 1) [k = 10, 7, 1, 3] → Cl⁻ + CH₃CH₂F (S_N2), HF + CH₃CHCl⁻, FH⋯Cl⁻ + C₂H₄, and Cl⁻ + HF + C₂H₄ (E2) reactions using a full-dimensional high-level analytical global potential energy surface and the quasi-classical trajectory method. Excitation of the C–Cl stretching, CH₂ stretching, and CH₂/CH₃ stretching modes enhances the S_N2, proton abstraction, and FH⋯Cl⁻ and E2 channels, respectively. Anti-E2 dominates over syn-E2 (kinetic anti-E2 preference) and the thermodynamically-favored S_N2 (wider reactive anti-E2 attack angle range). The direct (a) S_N2, (b) proton abstraction, (c) FH⋯Cl⁻ + C₂H₄, (d) syn-E2, and (e) anti-E2 channels proceed with (a) back-side/backward, (b) isotropic/forward, (c) side-on/forward, (d) front-side/forward, and (e) back-side/forward attack/scattering, respectively. The HF products are vibrationally cold, especially for proton abstraction, and their rotational excitation increases for proton abstraction, anti-E2, and syn-E2, in order. Product internal-energy and mode-specific vibrational distributions show that CH₃CH₂F is internally hot with significant C–F stretching and CH₂ wagging excitations, whereas C₂H₄ is colder. One-dimensional Gaussian binning technique is proved to solve the normal mode analysis failure caused by methyl internal rotation.

---

I. Introduction

Mode specificity has been widely studied for atom + molecule reactions,^1–23 however, the effect of vibrational excitations is less known for ion–molecule reactions,^24–37 such as the bimolecular nucleophilic substitution (S_N2). A typical S_N2 reaction in the gas phase has a submerged transition state as well as deep pre- and post-reaction minima supporting long-lived complex formations, which may undermine the mode-specific behavior. Nevertheless, a few early studies revealed non-statistical and mode-specific dynamics for S_N2 reactions,^{24–29,38,39} however, these investigations only considered the Cl⁻ + CH₃Y [Y = Cl and Br] systems using quasi-classical trajectory (QCT)²⁴ or 4-dimensional time-independent quantum methods^26–29 as well as kinetics³⁸ and spectroscopy^25,39 experiments. In the past decade the mode-specific dynamics of the X⁻ + CH₃Y [X = F, Cl; Y = Cl, I] non-identity reactions were studied using high-level analytical potential energy surface (PES)-based QCT simulations^32,34,35 and time-dependent quantum computations.^30,31,33 Moreover, in 2018 Wester and co-workers reported the first direct measurement of the mode-specific dynamics of the F⁻ + CH₃I S_N2 and proton-transfer reactions.³⁴ On one hand, these recent experimental and theoretical studies showed that CH stretching excitation has little effect on the S_N2 reactivity, whereas significantly enhances the proton-transfer channel.^34,35 On the other hand, CY stretching and umbrella-bending excitations promote the S_N2 reaction, showing that barrier-less complex-forming processes may also have mode-specific characters.³⁵

All the previous mode-specific S_N2 studies focused on reactions of methyl–halides. Moving to more complex reactions of X⁻ + CH₃CH₂Y introduces a new reaction channel via base-induced elimination (E2) leading to Y⁻ + HX + C₂H₄, besides the S_N2 pathways resulting in Y⁻ + CH₃CH₂X. Following a couple of pioneering electronic structure,^40–43 density functional theory-based direct dynamics,⁴⁴ and Car–Parrinello molecular dynamics^45,46 studies focusing on the F⁻ + CH₃CH₂Y [Y = F, Cl, Br, I] reactions, in 2017 we reported a high-level ab initio characterization of the PES of the F⁻ + CH₃CH₂Cl system considering S_N2 via Walden inversion, front-side attack, and double inversion as well as E2 and various high-energy product channels such as HF + CH₃CHCl⁻, FH⋯Cl⁻ + C₂H₄, H⁻ + CH₃CHClF/CH₂FCH₂Cl, and FCl⁻ + CH₃CH₂.⁴⁷ Utilizing the stationary-point information, we recently developed a full-dimensional coupled-cluster-based analytical PES for the multi-channel F⁻ + CH₃CH₂Cl reaction, allowing efficient QCT simulations and direct comparison with crossed-beam experiments.⁴⁸ Simulations played an essential role in distinguishing between the S_N2 and E2 channels, because the current experiments detected the ionic products, which is the same (Cl⁻) for the two competing channels. We found that the E2 channel usually dominates over the thermodynamically favored S_N2 reaction, due to the wider range of the reactive attack angles for the former.⁴⁸

In the present work, we investigate the mode-specific dynamics of the F⁻ + CH₃CH₂Cl multi-channel reaction utilizing our recently-developed analytical PES⁴⁸ and the QCT method. The computations reveal the effect of initial mode-specific vibrational excitations on the reactivity and dynamics of the different reaction pathways and product channels. Besides the usual results of a standard QCT analysis, we report mode-specific polyatomic product-state distributions and utilize the energy-based Gaussian binning (1GB) technique,^49–51 for the first time, for an 8-atomic molecule (CH₃CH₂F). The computational details and methods are described in Section II, the results are presented and discussed in Section III, and the paper ends with summary and conclusion in Section IV.

II. Computational details

We perform QCT simulations for the F⁻ + CH₃CH₂Cl reaction for the vibrational ground-state (v = 0), symmetric CH₂ (v₁ = 1) and CH₃ (v₃ = 1) as well as the C–Cl (v₁₀ = 1) stretching-excited states, and the CH₂ wagging-excited (v₇ = 1) state of the polyatomic reactant (see Fig. 1) on a high-level ab initio full-dimensional analytical PES recently developed by the present authors⁴⁸ using the Robosurfer program system.⁵² The initial vibrational states of CH₃CH₂Cl are prepared by standard normal mode sampling.⁵³ The rotational angular momentum of CH₃CH₂Cl is set to zero by modifying the initial velocities, and the relative orientation of the reactants is randomly sampled. We run QCTs at five different collision energies (8.1, 19.1, 26.5, 36.9, and 45.7 kcal mol⁻¹) and for five different vibrational states of CH₃CH₂Cl. The initial distance between the reactants is , where x = 25 bohr, and the value of the b impact parameter (the distance between the velocity vectors of the reactants) is varied between zero and b_max, (where the reaction probability vanishes) with 0.5 bohr step size. Each trajectory is propagated until the longest atom-atom distance becomes larger by 1 bohr than the longest initial one. We run 1000 trajectories at each impact parameter – reactant excitation – collision energy combination; thus, this study is based on a total number of 595 000 trajectories.

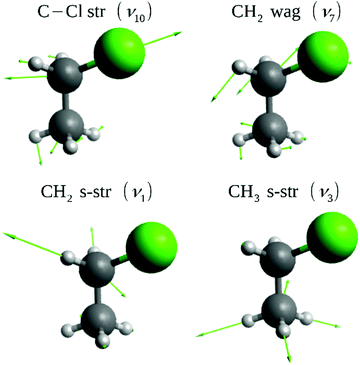Fig. 1 Normal modes of CH₃CH₂Cl excited in the present dynamics simulations. The harmonic frequencies on the PES are ω₁₀ = 697, ω₇ = 1330, ω₁ = 3104, and ω₃ = 3048 cm⁻¹.

Integral cross sections (ICSs) are calculated using a b-weighted numerical integration of the P(b) opacity functions (the P reaction probabilities as a function of b). Differential cross sections are obtained using standard histogram binning (HB). We apply different zero-point energy (ZPE) restrictions for the ICSs: (1) soft: the sum of the classical vibrational energies of the products must be larger than the sum of the harmonic ZPEs of the polyatomic products and, in the case of the proton-transfer channel and the two E2 channels, the sum of the classical internal energy of HF and the vibrational energy of the polyatomic product must be larger than sum of the anharmonic ZPE of the diatomic HF molecule corresponding to its given rotational state and the harmonic ZPE of the polyatomic product. The variationally-determined anharmonic rovibrational levels of the HF molecule are taken from ref. 54. (2) hard: the previous constraints are set separately for each product and we exclude trajectories from the reactive ones if any condition does not hold. We apply no ZPE-constraints to differential cross sections.

We distinguish between the retained or inverted configuration of the polyatomic product for the S_N2 channel by using a vector-projection scheme, which was introduced in ref. 55. First we define a Cartesian coordinate system with the alpha-carbon (CH₂–carbon) atom at the origin and calculate the cross product of the position vectors of the beta-carbon (CH₃–carbon) atom and the halogen atom. Then, we evaluate the dot product of the obtained normal vector and the difference of the position vectors of the two hydrogen atoms bound to alpha carbon. Dot-product values are determined in the case of the initial (CH₃CH₂Cl) and final (CH₃CH₂F) geometries of the reactive S_N2 trajectories, and we compare the signs of the dot products: the same and opposite signs refer to retention and inversion, respectively.

To distinguish between the front-side-attack (FS S_N2) and double-inversion⁵⁶ (DI S_N2) pathways, we scan the trajectories in a backward direction until we reach a transition state (TS) defined by the C–Cl distance becoming less than 4.0 bohr (2.1 Å) as the C–Cl distances at the front-side attack and Walden-inversion TSs are 2.362 and 2.197 Å on the PES, respectively. At this TS geometry, we separate the front-side attack TS from the Walden-inversion TS (second TS of the DI S_N2 pathway) by applying a limit of 111° (based on ref. 55 and 57) to the F–C–Cl attack angle (γ). Thus, γ less than 111° is a sign of front-side attack, whereas γ greater than 111° refers to the double-inversion mechanism.

In case of the two types of E2 trajectories, syn and anti, we find the TS region at 3.8 bohr C–Cl distance following the E2 trajectories backwards similarly to the above-described retention case. At the TS geometry we calculate the cosine of the Cl–C_α–C_β–F dihedral angle and if its value is positive (negative), then the trajectory is assigned to the syn- (anti-) pathway. We note that the present reaction channel and pathway assignment is not exactly the same as the one used in ref. 48, which results in somewhat different numerical results, especially for the minor FH⋯Cl⁻ complex forming and syn-E2 channels, but this does not affect any conclusions.

We determine the mode-specific vibrational energies of the polyatomic products based on the procedure described in detail in ref. 51. First, we perform normal-mode analysis for the optimized products to obtain their harmonic vibrational frequencies (ω_k) and normal-mode eigenvectors. Then, we remove the angular momentum of the products by modifying velocities. In the next step, we use an Eckart-transformation,^51,58 also taking H-atom permutations into account, to find the best overlap⁵⁹ between the optimized/reference and the actual/final structure. Then, we transform the mass-scaled Cartesian displacement coordinates and velocities by using the eigenvectors obtained in the first step to determine the normal coordinates (Q_k) and momenta (P_k). Finally, we determine the mode-specific harmonic vibrational energies (E_k) and the integer vibrational quantum numbers (n_k), in atomic units, as

where the floor sign ⌊ ⌋ refers to rounding down to an integer value and k = 1, …, 3N − 6, where N is 8 and 6 for CH₃CH₂F and C₂H₄, respectively. For the diatomic HF product, rotational and vibrational quantum numbers are assigned as detailed in ref. 54.

Vibrational distributions are obtained by histogram binning and in the case of the CH₃CH₂F products one-dimensional Gaussian binning (1GB)^49–51 is also employed. For 1GB we use the GB(harm-exact) approach, as proposed in ref. 51, which defines a Gaussian weight for each product as

where n = (n₁, n₂,…,n_3N−6), , δ is the full-width at half-maximum, is the exact classical vibrational energy of the pth product obtained by using the final Cartesian coordinates and velocities, E(n) is the harmonic vibrational energy obtained by the quantum mechanical energy expression of a harmonic oscillator, and E(0) is the harmonic ZPE. In the present 1GB analysis for the mode-specific vibrational distributions of the CH₃CH₂F products, δ is set to 0.2, after testing different values between 0.1 and 1.0.

III. Results and discussion

A. Reaction pathways

The different reaction pathways and their energetics of the F⁻ + CH₃CH₂Cl S_N2 and E2 reactions are shown in Fig. 2. The S_N2 channel is highly exothermic and its energetically favored Walden-inversion (or back-side attack, bs) pathway proceeds via a pre-reaction complex (Premin C_s), a submerged Walden-inversion transition state (W TS), and a post-reaction minimum (S_N2 postmin) leading to the Cl⁻ + CH₃CH₂F products. Furthermore, the S_N2 reaction has two retention pathways: double inversion⁵⁶ begins with a proton abstraction induced inversion via DI TS, followed by a second inversion via W TS, whereas front-side attack goes over a high-energy FS TS as Fig. 2 shows. In the case of the inversion via DI TS, it is also possible that this first inversion is not followed by a reactive substitution event and an inverted reactant molecule is formed. We call this process as induced inversion.⁵⁶ Beside the S_N2 channel, the title reaction can produce Cl⁻ + HF + C₂H₄ products via elimination, which is also exothermic, but thermodynamically less favored. The E2 reaction can proceed with anti- and syn-E2 mechanisms via the submerged Anti-E2 and Syn-E2 TSs (see Fig. 2), where the simultaneously leaving FH and Cl⁻ groups are in anti and syn arrangements, respectively. Energetically the anti-E2 pathway is preferred, as the Anti-E2 TS is below Syn-E2 TS by about 10 kcal mol⁻¹, whereas Anti-E2 and W TSs have the same energy within 1 kcal mol⁻¹; thus, one may expect high competition between the anti-E2 and S_N2 channels. It is also important to note that the syn-E2 pathway goes through FH⋯Cl⁻ + C₂H₄, which is the most exothermic product channel of the title reaction below the S_N2 and E2 products by about 11 and 23 kcal mol⁻¹, respectively. Of course, upon dissociation of the FH⋯Cl⁻ complex, this channel may also lead to E2 products. Besides the exothermic pathways, proton abstraction from the alpha carbon atom may produce HF + CH₃CHCl⁻ products via an endothermic process. Note that proton abstraction from the beta carbon leads to E2 breakup, thus HF + CH₂CH₂Cl⁻ products are not expected (CH₂CH₂Cl⁻ does not exist in a stable form). Fig. 2 also shows the comparison of relative energies of the stationary points along the different reaction pathways obtained on the analytical PES⁴⁸ with all-electron CCSD(T)/complete-basis-set-quality benchmark data.^47,60 As seen, the PES values usually agree with the benchmark data within 0.5 kcal mol⁻¹ confirming the high-accuracy of the full-dimensional analytical PES.

Fig. 2 Schematic potential energy surface of the F⁻ + CH₃CH₂Cl reaction showing the classical relative energies (in kcal mol⁻¹) of the stationary points along the different reactions pathways corresponding to the fitted PES⁴⁸ and (benchmark CCSD(T)-F12b/aug-cc-pVQZ + Δ_core[CCSD(T)-F12b/cc-pCVTZ-F12] level of theory).^47,60

B. Intramolecular vibrational-energy redistribution

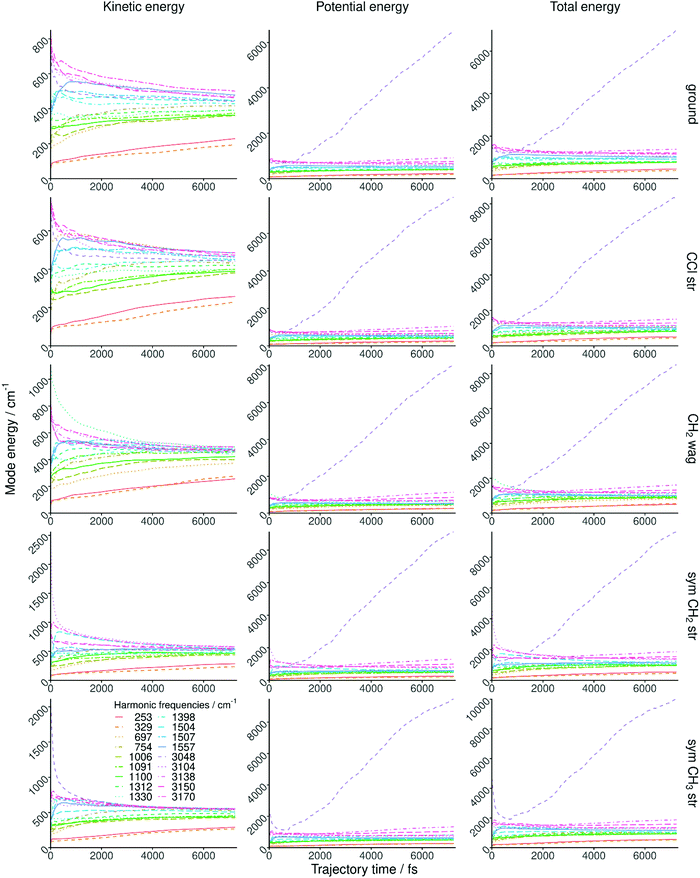
One of the main concerns about mode specificity in polyatomic reaction dynamics is the intramolecular vibrational-energy redistribution (IVR) prior to collision. In order to investigate IVR in CH₃CH₂Cl, we follow the ground-state and vibrationally-excited reactant in time without interaction with F⁻ and compute the mode-specific vibrational energies as shown in Fig. 3. As seen, IVR does occur even in the first picosecond, the low frequency modes gain energy on the expense of the high-energy ones; nevertheless, some mode specificity is maintained even after 6 ps. In the case of the CH stretching excited modes the energy loss is fast and these mode energies approach the energies of the non-excited CH stretching modes in the first few hundred femtoseconds. Thus, IVR may partially undermine mode specificity in the title reaction, nevertheless, some effects may be expected as the mode energies remain non-statistical during the timeframe of collision in the present simulations. Regarding the mode-specific normal mode analysis, we must highlight a technical issue related to the fast unphysical increase of the symmetric CH₃ stretching mode energy after 1 ps. This is due to the failure of the rectilinear normal coordinates and the harmonic approximation at highly distorted geometries; occurring, in the present case, at eclipsed conformations resulting in large displacement coordinates for the beta H atoms relative to the staggered reference structure. This issue does not cause problem in the kinetic energy part, but unphysically increases the harmonic potential part and thus the total vibrational symmetric CH₃ stretching mode energy as seen in Fig. 3. Nevertheless, it is important to note that this technical issue of the normal mode analysis does not affect the QCT computations, because the trajectories are propagated in the Cartesian space using the fully-anharmonic PES.

Fig. 3 Mode specific vibrational energies and their kinetic and potential energy parts of the CH₃CH₂Cl(v_k = 0, 1) [k = 10, 7, 1, 3] molecules as a function of time (t) averaged over 100 trajectories and time from 0 to t. The potential and total energies for the symmetric CH₃ stretching mode (ω₃ = 3048 cm⁻¹) are unphysical (see text for details).

C. Separation of the different reaction pathways

Before we present the QCT results, let us discuss the separation of the different reaction pathways leading to the same products. In the case of the double-inversion and front-side attack S_N2 retention pathways the transition-state-attack-angle-based approach was discussed in detail in ref. 55 and 57; thus, in the present article we focus on the E2 mechanisms. Fig. 4 shows the Cl–C_α–C_β–F transition-state dihedral angle distributions for the E2 trajectories. At the lowest collision energy, the distribution peaks at 180°, decreases with decreasing angle, and virtually vanishes around 90°, showing the dominance of the anti-E2 pathway. As the collision energy increases a second peak emerges around 30° as a signature of the syn-E2 mechanism. At higher collision energies the syn-E2 probability becomes significant, but anti-E2 remains the dominant E2 pathway. As Fig. 4 shows at all collision energies the two peaks around small and large angles are clearly distinct and the probabilities around 90° are close to zero; thus, the syn- and anti-E2 pathways can be almost unambiguously separated using a dividing limit of 90° for the Cl–C_α–C_β–F transition-state dihedral angle. This is comforting, because visual analysis of tenths of thousands of E2 trajectories considered in the present study would be highly exhaustive and undesired.

Fig. 4 Distributions of the Cl–C_α–C_β–F dihedral angles at the E2 transition states for the F⁻ + CH₃CH₂Cl(v_k = 0, 1) → Cl⁻ + HF + C₂H₄ [k = 10, 7, 1, 3] reactions at different collision energies.

D. Mode-specific reactivity

Mode-specific cross sections as a function of collision energy for the S_N2 inversion, proton-abstraction, FH⋯Cl⁻ complex formation, and syn/anti-E2 channels are given in Fig. 5. The S_N2 cross sections are large and decrease with increasing collision energy as expected for a barrier-less (W TS is below the reactants) exothermic reaction. C–Cl stretching excitation clearly enhances the S_N2 reactivity by 20, 36, 48, 54, and 47% at collision energies of 8.1, 19.1, 26.5, 36.9, and 45.7 kcal mol⁻¹, respectively, whereas the effects of the other modes are less significant. The ZPE-constrained cross sections are virtually the same as the non-constrained ones, due to the fact that the CH₃CH₂F products are usually internally hot. Note that in the case of the S_N2 channel the soft and hard constraints are exactly the same, because there is only one multi-atomic product.

Fig. 5 Cross sections for the different product channels or pathways of the F⁻ + CH₃CH₂Cl(v_k = 0, 1) [k = 10, 7, 1, 3] reactions as a function of collision energy obtained without and with soft and hard ZPE constraints.

The reactivity of proton abstraction increases with increasing collision energy and for this channel significant mode specificity is seen. Reactant vibrational excitation enhances the reactivity, and the most substantial effect is found for the CH₂ stretching, as expected, because the proton is abstracted from the CH₂ group. ZPE constraints significantly reduce the abstraction reactivity and shifts the threshold energy toward larger values, in agreement with the endothermicity. These results clearly show that most of the proton-abstraction products violate ZPE, and with hard constraint only the CH₂ stretching excited reaction provides considerable reactivity at high collision energy.

The cross sections for the FH⋯Cl⁻ + C₂H₄ and syn-E2 channels show similar dependence on collision energy and initial vibrational excitation as expected, because both pathways go through the same Syn-E2 TS. In both cases the reactivity decreases with increasing collision energy and CH₂ and CH₃ stretching excitations enhance the reaction the most efficiently. On one hand, this effect of the CH₃ stretching mode is expected, because in both cases a proton is abstracted from the beta carbon atom. On the other hand, the enhancement upon CH₂ stretching excitation is due to IVR between these modes. Considering the magnitude of the CH₂/CH₃ vibrational enhancement factors, we find more substantial enhancement by a factor of 2–4, especially with ZPE constraints, for the syn-E2 channel, than in the case of the FH⋯Cl⁻ channel. This may be explained by the fact that vibrational excitation facilitates the dissociation of the FH⋯Cl⁻ complex, thereby enhancing the syn-E2 channel. ZPE constraints reduce the reactivity for the syn-E2 channel, nevertheless, the shapes of the excitations functions are not significantly affected. For the highly-exothermic FH⋯Cl⁻ channel, ZPE violation is negligible.

The anti-E2 channel dominates the title reaction, this pathway is strongly favored over syn-E2, as expected since the Anti-E2 TS is well below the Syn-E2 TS and the Anti-E2 postmin is less deep than the Syn-E2 postmin (see Fig. 2). Furthermore, the anti-E2 reactivity is even larger than that of the S_N2 channel, especially at low collision energies and usually expect in the hard constrained case. This finding is somewhat unexpected, because the S_N2 reaction is thermodynamically preferred and kinetic control also does not explain this substantial reactivity difference, because the Anti-E2 and W TSs are nearly isoenergetic. The reason must be in the different dynamics of the two channels,⁴⁸ which will be revealed and discussed later. Similar to the syn-E2 channel, CH₂/CH₃ stretching excitations enhance the anti-E2 channel the most efficiently, especially when ZPE constraints are applied and ZPE constraints decrease the reactivity. The constraints, especially the hard one, have more substantial effects on the less exothermic E2 channel than in the case of the S_N2 reaction where ZPE violation is negligible, this is why the E2/S_N2 reactivity ratio changes when hard constraint is applied. Furthermore, we note that ZPE constraints may artificially enhance the mode-specific effects on the E2 channel as less product ZPE violation is expected if the reactant is vibrationally excited.

Cross sections (Fig. S1, ESI†) and reaction probabilities (Fig. S2, ESI†) for the front-side attack, double-inversion, and induced-inversion pathways are shown in the ESI.† Retention and induced-inversion reactivity is small, around 0.1% as Fig. S2 (ESI†) shows, and we only find retention trajectories for the initially excited reactions. Front-side attack opens above 30 kcal mol⁻¹ as expected based on its barrier height (29.4 kcal mol⁻¹). Double inversion dominates at lower collision energies (20–40 kcal mol⁻¹) and it is the most efficiently enhanced by CH₂ stretching excitation, because the first inversion begins with a proton abstraction from the alpha carbon atom. We also find induced-inversion trajectories in similar collision energy range and with similar reactivity as double inversion, though for induced inversion one reactant ground-state trajectory is also found at collision energy of 19.1 kcal mol⁻¹. In the case of the retention and induced-inversion pathways the CH₃CH₂F and the inverted-CH₃CH₂Cl molecules are formed internally hot; thus, the soft and hard constraints do not affect the cross sections as seen in Fig. S1 (ESI†), in accord with our previous findings for the F⁻ + CH₃Br reaction.⁵⁷ Furthermore, we note that for the F⁻ + methyl–halide systems the retention and induced-inversion reactivity is significantly larger than in the present case,^55,57 indicating that the CH₃ ligand hinders these channels.

E. Opacity functions and angular distributions

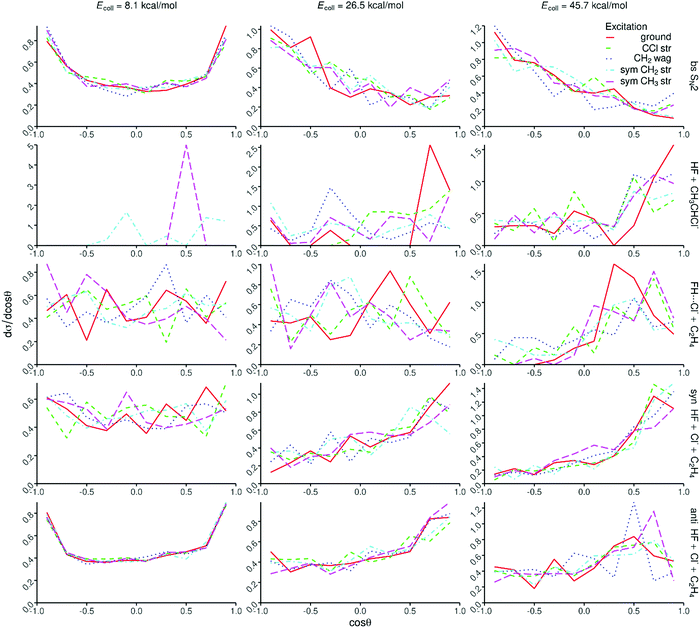
Opacity functions, scattering angle distributions, and initial attack angle distributions at different collision energies are shown in Fig. 6, 7, and 8, respectively. For the S_N2 channel the reaction probabilities decrease with increasing impact parameter and collision energy, and the b_max values also decrease with increasing collision energy from about 15 bohr at 8.1 kcal mol⁻¹ and reaching a nearly constant value of ∼6 bohr at 26.5 kcal mol⁻¹. The corresponding scattering angle distributions are backward–forward symmetric at the lowest collision energy and become backward dominant at higher collision energies, in accord with the smaller b_max values favoring backward scattering. The attack angle distributions are almost isotropic at the lowest collision energy with only slight back-side attack preference, whereas as the collision energy increases the back-side attack dominance becomes more and more significant. At the highest collision energy of 45.7 kcal mol⁻¹ basically no reactivity is seen from the front-side (Cl-side) attack hemisphere (0–90°). These findings indicate that the S_N2 reaction is indirect at low collision energies and becomes direct rebound dominated favoring back-side attack and backward scattering as the collision energy increases, in accord with the textbook picture of Walden inversion. The increase of the S_N2 reactivity upon C–Cl stretching excitation is clearly seen in Fig. 6, but the shapes of the opacity functions and the different angle distributions do not change within statistical accuracy.

Fig. 6 Reaction probabilities for the different product channels or pathways of the F⁻ + CH₃CH₂Cl(v_k = 0, 1) [k = 10, 7, 1, 3] reactions as a function of impact parameter at different collision energies obtained without ZPE constraint.

Fig. 7 Scattering angle distributions for the different product channels or pathways of the F⁻ + CH₃CH₂Cl(v_k = 0, 1) [k = 10, 7, 1, 3] reactions at different collision energies. The scattering angle is defined as the supplement of the angle between the velocity vector of F⁻ and the (center of mass) velocity vector of Cl⁻ or (CH₃CHCl⁻ or FH⋯Cl⁻).

The proton-abstraction channel of the ground-state reaction has small reactivity, usually below 1% even at the highest collision energy considered in the present study. Upon vibrational excitation of the reactant, especially for the CH₂ stretching, the reaction probabilities as well as the b_max values significantly increase as seen in Fig. 6. The scattering angle distributions show forward scattered dominance indicating significant stripping mechanism. The attack angle distributions are somewhat isotropic with large statistical uncertainty due to the small reactivity, which hinders any conclusion about the mode-specific effects on the abstraction mechanism.

On one hand, the decaying opacity functions and the nearly isotropic angle distributions of the FH⋯Cl⁻ + C₂H₄ and syn-E2 channels are similar at the lowest collision energy, indicating indirect pathways in both cases. On the other hand, as the collision energy increases and the reactions become more direct, interesting differences emerge between the two channels, which are the most pronounced at the highest collision energy. While both channels are mainly forward scattered, the b_max values become much smaller for the FH⋯Cl⁻ formation. Considering the attack angle distributions, the side-on collisions (relative to the C–Cl bond) favor the FH⋯Cl⁻ formation, whereas clear front-side attack preference is seen for the syn-E2 channel. These findings show the different direct pathways of the two channels. In the case of syn-E2, F⁻ comes parallel with the C–Cl bond from the Cl-side, abstracts the proton, and Cl⁻ leaves forward while HF moves into somewhat opposite direction, without the possibility of FH⋯Cl⁻ complex formation. FH⋯Cl⁻ formation can occur when F⁻ approaches from the CH₃ group perpendicular to the C-Cl bond, abstracts the proton, and the HF fragment moves toward the leaving Cl⁻ and the forming FH⋯Cl⁻ complex scatters forward considering the path of the Cl ligand.

In the case of the anti-E2 channel the b_max values are larger than those of syn-E2 and S_N2, especially at higher collision energies in the latter case. At high collision energies the opacity functions show a small peak at large impact parameters as a signature of direct striping mechanism. At the lowest collision energy, the anti-E2 scattering angle distributions are backward–forward symmetric indicating indirect dynamics, and as the collision energy increases and the reaction becomes more direct, the forward scattering dominates. This finding indicates that F⁻ usually strips the proton from the CH₃ group while the leaving Cl⁻ moves forward without significantly changing its direction. The anti-E2 attack angle distributions nearly mirror the corresponding syn-E2 ones, i.e., back-side attack favors the anti-E2 pathway, especially at higher collision energies, as expected looking at the structure of the Anti-E2 TS. At this point we can explain the larger reactivity of the E2 pathway compared to S_N2. As seen in Fig. 6, the opacity functions of the anti-E2 pathway show higher preference of large impact parameters than the S_N2 channel, and at higher collision energies, the reactive attack angle range is much wider for the E2 pathways than in the case of S_N2 as seen in Fig. 8. For the FH⋯Cl⁻ and E2 channels one can see the initial vibrational excitation effects on the reaction probabilities; however, the changes in the shapes of the opacity functions and angle distributions are not significant at the given level of statistics.

Fig. 8 Initial attack angle distributions for the different product channels or pathways of the F⁻ + CH₃CH₂Cl(v_k = 0, 1) [k = 10, 7, 1, 3] reactions at different collision energies. The attack angle is defined as the angle between the velocity vector of the center of mass of CH₃CH₂Cl and the vector from C_α to Cl at time zero.

F. Internal energy distributions

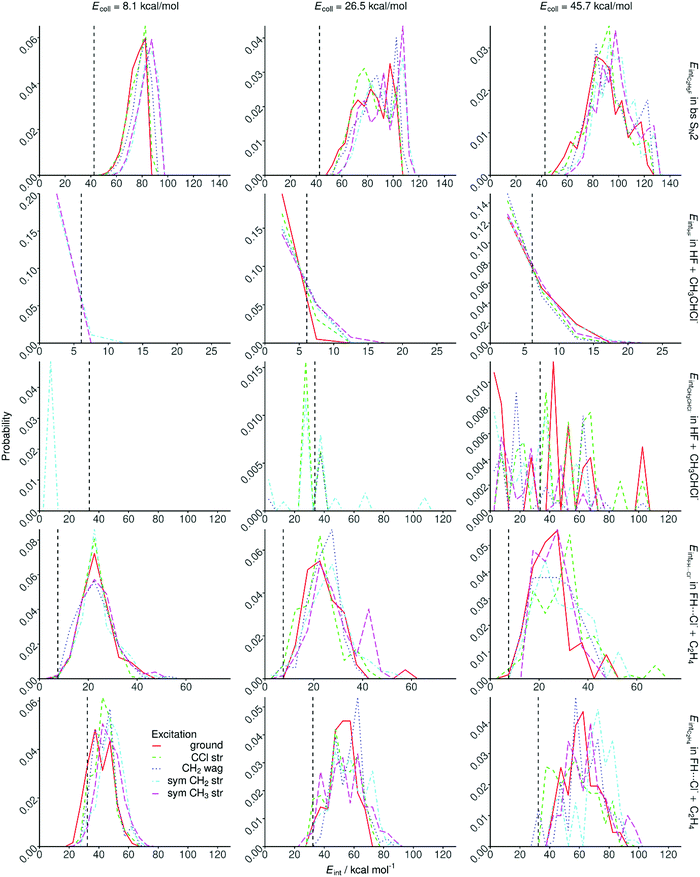
Internal energy distributions of the products of the different reaction channels or pathways are shown in Fig. 9 and 10. Fig. 9 shows that the CH₃CH₂F product of the S_N2 channel is formed internally highly excited. The CH₃CH₂F distributions become blue-shifted, broader, and their peaks shift toward lower energies indicating the dominance of direct dynamics as collision energy increases. Initial CH₂/CH₃ stretching excitations blue-shift the product internal energies, showing that these high-frequency “spectator” modes usually remain excited in the S_N2 product as well. For the C–Cl stretching mode the effects on the product internal energies are less significant due to the stronger coupling of this mode with the reaction coordinate.

Fig. 9 Normalized product internal energy distributions for the F⁻ + CH₃CH₂Cl(v_k = 0, 1) [k = 10, 7, 1, 3] → Cl⁻ + CH₃CH₂F, HF + CH₃CHCl⁻, and FH⋯Cl⁻ + C₂H₄ reactions at different collision energies. Vertical dashed lines indicate the ZPE of the products.

Fig. 10 Normalized product internal energy distributions for the F⁻ + CH₃CH₂Cl(v_k = 0, 1) [k = 10, 7, 1, 3] syn- and anti-E2 reactions at different collision energies. Vertical dashed lines indicate the ZPE of the products.

As Fig. 9 also shows, the proton-abstraction channel forms cold HF molecules; their internal energy distributions peak at the lowest energies showing significant ZPE violation, especially at low collision energies. The CH₃CHCl⁻ co-product is more excited, but significant ZPE violation is also seen. Here mode-specific effects cannot be assessed due to the low statistical accuracy of this minor channel.

The FH⋯Cl⁻ complex and the C₂H₄ co-product have Gaussian-like, rather hot internal energy distributions with negligible ZPE violation. The FH⋯Cl⁻ distributions peak around the D_e value (23.1 kcal mol⁻¹) of the complex, thus, significant fraction of the products has larger internal energy than the dissociation energy; thus, this complex exists in a Feshbach-type resonance⁶¹ state. The initial vibrational energy transfers rather into the C₂H₄ fragment as the blue-shifted distributions show in Fig. 9. We may also assume that in the case of significant vibrational energy transfer into the FH⋯Cl⁻ fragment, the complex dissociates and E2 products are formed.

The internal energy distributions for the syn- and anti-E2 products are shown in Fig. 10. Significant differences between the product distributions obtained for the two pathways are not found. In both cases the HF molecules are internally cold, their internal energy distributions peak at zero energy showing substantial ZPE violation, in accord with the ZPE-constrained cross sections shown in Fig. 5. Note that the HF molecules formed by the proton-abstraction channel are even more colder, as expected, because proton abstraction is an endothermic, whereas E2 is an exothermic process. The C₂H₄ E2 co-products are internally hot with only little ZPE violation, except for the ground-state reaction at low collision energies. As collision energy increases a tail emerges in the C₂H₄ distributions at higher internal energies, which is the best seen for the anti-E2 channel. Initial vibrational energy mainly transfers into the C₂H₄ product, though some shifts toward higher energies are also seen for HF as well.

G. HF vibrational and rotational distributions

Quantum-state-resolved vibrational distributions for the HF products of the proton-abstraction, syn-E2, and anti-E2 channels are shown in Fig. 11. In the case of the proton-abstraction channel, the HF product molecules are almost always in vibrational ground state, only a few % v = 1 population is seen at the highest collision energy. For the E2 pathways the HF products are slightly more excited, but the ground-state HF is still the dominant (80–90%). The population of the v = 1 state is 10–20%, and a few % probability is found for v = 2. The excitation of HF often increases by only 1–2% upon initial vibrational excitation and/or the increase of the collision energy. The HF vibrational populations do not show any significant dependence on the syn- and anti-mechanism of the E2 channel. These findings are in agreement with the HF internal energy distributions shown in Fig. 9 and 10.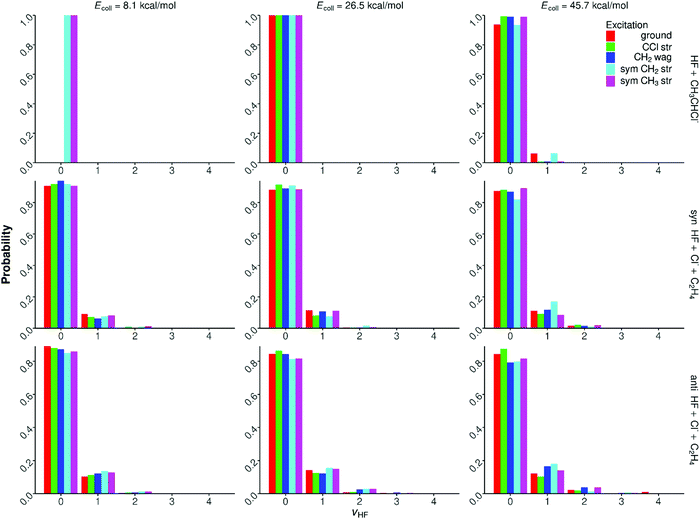

Fig. 11 Normalized HF vibrational distributions for the F⁻ + CH₃CH₂Cl(v_k = 0, 1) [k = 10, 7, 1, 3] → HF + CH₃CHCl⁻, syn-E2, and anti-E2 reactions at different collision energies.

The HF rotational distributions for the above-discussed channels are shown in Fig. 12. The HF molecules formed by proton abstraction are rotationally cold; the rotational distributions usually peak at J = 1–2. Some initial translational and vibrational energy transfer into HF rotation are seen, but this finding is not significant at the given level of statistics. The HF products of the E2 channel are rotationally hotter, and unlike for the vibrational distributions, here significant syn/anti mechanism dependence is found, i.e., the syn-E2 HF products are rotationally more excited than the anti-E2 ones. Collision energy transfer into HF product rotation is seen, whereas the vibrational energy transfer is not significant.

Fig. 12 Normalized HF rotational distributions for the F⁻ + CH₃CH₂Cl(v_k = 0, 1) [k = 10, 7, 1, 3] → HF + CH₃CHCl⁻, syn-E2, and anti-E2 reactions at different collision energies.

H. Mode-specific vibrational distributions for polyatomic products

We have also computed mode-specific vibrational distributions for the polyatomic product (CH₃CH₂F) of the S_N2 channel as shown for selected modes in Fig. 13 and 14. However, for the symmetric CH₃ stretching mode the standard HB provides unphysically high vibrational excitations up to 20 quanta as shown in Fig. 13. This is due to the failure of the normal mode analysis caused by internal rotation of the CH₃ group as already discussed for the IVR analysis of the CH₃CH₂Cl reactant. The 1GB approach solves this issue by assigning nearly zero weights for the unphysical states, thereby providing realistic vibrational populations for the symmetric CH₃ stretching mode as also shown in Fig. 13. We note that we have tested different Gaussian widths (δ values) as shown in Fig. S3 (ESI†). As δ decreases the unphysical populations tend to vanish while the statistical uncertainty increases. Since the results with δ = 0.2 and 0.1 become very similar, we use the statistically more robust δ = 0.2 in this study.

Fig. 13 Normalized symmetric CH₃ stretching mode specific vibrational distributions for the CH₃CH₂F product of the F⁻ + CH₃CH₂Cl(v_k = 0, 1) [k = 10, 7, 1, 3] S_N2 reactions at different collision energies obtained with histogram binning (HB) and Gaussian binning (GB).

Fig. 14 Normalized CF stretching, CH₂ wagging, and symmetric CH₂ stretching mode specific vibrational distributions for the CH₃CH₂F product of the F⁻ + CH₃CH₂Cl(v_k = 0, 1) [k = 10, 7, 1, 3] S_N2 reactions at different collision energies obtained with Gaussian binning.

According to the 1GB results shown in Fig. 13 and 14, the CH₂ and CH₃ stretching modes are mainly in vibrational ground state (80–90%) and 10–20% one-quantum excitations are seen. Upon CH₂/CH₃ initial stretching excitations the corresponding product modes are not found significantly more excited, as a signature of strong IVR. For the CF stretching and CH₂ wagging modes significantly more excitations are obtained up to about 4 quanta (Fig. 14), as expected, because these modes couple with the reaction coordinate the most efficiently. We also see some translational and vibrational energy transfer into these modes, in accord with the internal energy distributions. Unlike for the symmetric CH₃ stretching, for the CF and CH₂ stretching as well as CH₂ wagging modes HB provides similar vibrational distributions with only slightly higher excitations and better statistics as 1GB, as shown in Fig. S4 (ESI†).

For the C₂H₄ products, where internal rotation is not a concern, we apply HB and give the mode-specific vibrational distributions in Fig. S5–S7 (see ESI†) for the FH⋯Cl⁻ + C₂H₄, syn-E2, and anti-E2 channels, respectively. Here we consider different CH₂ wagging and stretching modes and the results and conclusions are similar to the above-discussed findings for the CH₃CH₂F product of the S_N2 channel.

IV. Summary and conclusions

Following our recent join theoretical–experimental study⁴⁸ on the dynamics of the F⁻ + CH₃CH₂Cl(v = 0) S_N2 and E2 processes, we have carried out mode-specific QCT computations for the C–Cl stretching, CH₂ wagging, CH₂ stretching, and CH₃ stretching excited F⁻ + CH₃CH₂Cl(v_k = 1) [k = 10, 7, 1, 3] reactions using our full-dimensional analytical high-level PES.⁴⁸ The most important results and conclusions of the present study can be summarized as follows:

(a) The analytical PES usually reproduces the all-electron CCSD(T)/complete-basis-set-quality benchmark^47,60 stationary-point relative energies within a few tenths of a kcal mol⁻¹.

(b) IVR prior to collision is significant, nevertheless, some mode specificity is maintained.

(c) Normal mode analysis for the symmetric CH₃ stretching mode of the CH₃CH₂Cl and CH₃CH₂F molecules fails due to the internal rotation of the methyl group, which issue can be treated by using the 1GB method^49–51 for mode-specific polyatomic product vibrational analysis.

(d) The syn- and anti-E2 pathways can be almost unambiguously separated numerically based on the Cl–C_α–C_β–F dihedral angles at the E2 transition states.

(e) C-Cl stretching excitation enhances the S_N2 channel, proton abstraction occurs from the alpha carbon and enhanced by CH₂ stretching excitation, and the FH⋯Cl⁻ + C₂H₄ and E2 channels proceed with beta proton transfer and are enhanced by both CH₂ and CH₃ stretching excitations due to IVR.

(f) Anti-E2 is kinetically preferred and thus dominates over syn-E2. Furthermore, anti-E2 has even higher reactivity than the thermodynamically favored S_N2, due to the wider reactive attack angle range for the former as also proposed in ref. 48.

(g) Double-inversion and front-side attack S_N2 pathways and induced inversion of the reactant are minor with only about 0.1% probability for the title reaction.

(h) As collision energy increases and the reactions become direct, scattering angle distributions show backward dominance for S_N2 and forward preference for FH⋯Cl⁻ complex formation and E2. For the proton-abstraction channel forward scattering is found indicating significant direct stripping mechanism.

(i) Attack angle distributions show that the direct S_N2, FH⋯Cl⁻ complex-forming, syn-E2, and anti-E2 channels favor initial back-side, side-on, front-side, and back-side attack, respectively.

(j) The S_N2 channel produce internally hot CH₃CH₂F molecules, where mainly the CF stretching and CH₂ wagging modes are excited. Initial CH₂/CH₃ stretching excitation energy transfers into the internal energy of the CH₃CH₂F S_N2 and C₂H₄ E2 products.

(k) A significant fraction of the FH⋯Cl⁻ complexes are in a Feshbach-type resonance state with higher internal energies than the dissociation energy of the complex.

(l) HF products are vibrationally and rotationally cold, especially for the proton abstraction channel. The HF products have significantly higher rotational excitations via the syn-E2 channel than anti-E2.

(m) Standard histogram binning provides significant populations for energetically forbidden CH₃ stretching vibrational states of CH₃CH₂F, whereas the 1GB method assigns nearly zero weights for these unphysical states and gives realistic cold distributions. Histogram binning performs well for mode-specific vibrational analysis of C₂H₄, which is not affected by internal rotations.

The present study and the above results show the current state-of-the-art of polyatomic reaction dynamics for a 9-atomic system. We hope that the techniques used in this study may be utilized in future similar theoretical investigations. The timescale of IVR may hinder mode-specific experimental studies for the title reaction; nevertheless, we hope that the present findings may motivate future measurements of vibrational effects on the dynamics of ion–molecule reactions.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

We thank the financial support of the National Research, Development and Innovation Office − NKFIH (K-125317); the Ministry of Human Capacities, Hungary (20391-3/2018/FEKUSTRAT); Project no. TKP2021-NVA-19, provided by the Ministry of Innovation and Technology of Hungary from the National Research, Development and Innovation Fund, financed under the TKP2021-NVA funding scheme; and the Momentum (Lendület) Program of the Hungarian Academy of Sciences. Furthermore, we acknowledge KIFÜ for awarding us access to computational resource based in Hungary at Debrecen.

References

1. G. C. Schatz, M. C. Colton and J. L. Grant, J. Phys. Chem., 1984, 88, 2971.
2. A. Sinha, M. C. Hsiao and F. F. Crim, J. Chem. Phys., 1990, 92, 6333.
3. M. J. Bronikowski, W. R. Simpson, B. Girard and R. N. Zare, J. Chem. Phys., 1991, 95, 8647.
4. D. H. Zhang and J. C. Light, J. Chem. Soc., Faraday Trans., 1997, 93, 691.
5. S. Yoon, S. Henton, A. N. Zivkovic and F. F. Crim, J. Chem. Phys., 2002, 116, 10744.
6. C. Murray and A. J. Orr-Ewing, Int. Rev. Phys. Chem., 2004, 23, 435.
7. S. Yan, Y. Wu, B. Zhang, X.-F. Yue and K. Liu, Science, 2007, 316, 1723.
8. W. Zhang, H. Kawamata and K. Liu, Science, 2009, 325, 303.
9. J. Li, B. Jiang and H. Guo, J. Am. Chem. Soc., 2013, 135, 982.
10. B. Jiang and H. Guo, J. Am. Chem. Soc., 2013, 135, 15251.
11. W. Yan, F. Meng and D. Y. Wang, J. Phys. Chem. A, 2013, 117, 12236.
12. J. Espinosa-Garcia, J. Phys. Chem. A, 2014, 118, 3572.
13. R. Welsch and U. Manthe, J. Chem. Phys., 2014, 141, 051102.
14. G. Czakó and J. M. Bowman, J. Phys. Chem. A, 2014, 118, 2839.
15. J. Qi, H. Song, M. Yang, J. Palma, U. Manthe and H. Guo, J. Chem. Phys., 2016, 144, 171101.
16. B. Fu, X. Shan, D. H. Zhang and D. C. Clary, Chem. Soc. Rev., 2017, 46, 7625.
17. D. Zhang, J. Yang, Z. Chen, R. Chen, B. Jiang, D. Dai, G. Wu, D. Zhang and X. Yang, Phys. Chem. Chem. Phys., 2017, 19, 13070.
18. D. Lu and J. Li, Theor. Chem. Acc., 2020, 139, 157.
19. D. Lu, J. Li and H. Guo, CCS Chem., 2020, 2, 882.
20. D. Papp, J. Li, H. Guo and G. Czakó, J. Chem. Phys., 2021, 155, 114303.
21. D. Gao and D. Wang, Phys. Chem. Chem. Phys., 2021, 23, 26911.
22. A. Marjollet, L. Inhester and R. Welsch, J. Chem. Phys., 2022, 156, 044101.
23. H. Song, W. Xie, C. Zhang and M. Yang, J. Phys. Chem. A, 2022, 126, 663.
24. S. R. Vande Linde and W. L. Hase, J. Am. Chem. Soc., 1989, 111, 2349.
25. P. Ayotte, J. Kim, J. A. Kelley, S. B. Nielsen and M. A. Johnson, J. Am. Chem. Soc., 1999, 121, 6950.
26. S. Schmatz, ChemPhysChem, 2004, 5, 600.
27. C. Hennig and S. Schmatz, J. Chem. Phys., 2004, 121, 220.
28. C. Hennig and S. Schmatz, J. Chem. Phys., 2005, 122, 234307.
29. C. Hennig and S. Schmatz, Chem. Phys. Lett., 2007, 446, 250.
30. M. Kowalewski, J. Mikosch, R. Wester and R. de Vivie-Riedle, J. Phys. Chem. A, 2014, 118, 4661.
31. Y. Wang, H. Song, I. Szabó, G. Czakó, H. Guo and M. Yang, J. Phys. Chem. Lett., 2016, 7, 3322.
32. I. Szabó and G. Czakó, J. Chem. Phys., 2016, 145, 134303.
33. Y. Li, Y. Wang and D. Wang, J. Phys. Chem. A, 2017, 121, 2773.
34. M. Stei, E. Carrascosa, A. Dörfler, J. Meyer, B. Olasz, G. Czakó, A. Li, H. Guo and R. Wester, Sci. Adv., 2018, 4, eaas9544.
35. B. Olasz and G. Czakó, J. Phys. Chem. A, 2018, 122, 8143.
36. T. Michaelsen, B. Bastian, P. Strübin, J. Meyer and R. Wester, Phys. Chem. Chem. Phys., 2020, 22, 12382.
37. M. Pan, H. Xiang, Y. Li and H. Song, Phys. Chem. Chem. Phys., 2021, 23, 17848.
38. A. A. Viggiano, R. A. Morris, J. S. Paschkewitz and J. F. Paulson, J. Am. Chem. Soc., 1992, 114, 10477.
39. D. S. Tonner and T. B. McMahon, J. Am. Chem. Soc., 2000, 122, 8783.
40. F. M. Bickelhaupt, E. J. Baerends, N. M. M. Nibbering and T. Ziegler, J. Am. Chem. Soc., 1993, 115, 9160.
41. A. P. Bento, M. Solà and F. M. Bickelhaupt, J. Chem. Theory Comput., 2008, 4, 929.
42. X.-P. Wu, X.-M. Sun, X.-G. Wei, Y. Ren, N.-B. Wong and W.-K. Li, J. Chem. Theory Comput., 2009, 5, 1597.
43. L. Yang, J. Zhang, J. Xie, X. Ma, L. Zhang, C. Zhao and W. L. Hase, J. Phys. Chem. A, 2017, 121, 1078.
44. E. Carrascosa, J. Meyer, J. Zhang, M. Stei, T. Michaelsen, W. L. Hase, L. Yang and R. Wester, Nat. Commun., 2017, 8, 25.
45. M. Mugnai, G. Cardini and V. Schettino, J. Phys. Chem. A, 2003, 107, 2540.
46. B. Ensing and M. L. Klein, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 6755.
47. V. Tajti and G. Czakó, J. Phys. Chem. A, 2017, 121, 2847.
48. J. Meyer, V. Tajti, E. Carrascosa, T. Győri, M. Stei, T. Michaelsen, B. Bastian, G. Czakó and R. Wester, Nat. Chem., 2021, 13, 977.
49. G. Czakó and J. M. Bowman, J. Chem. Phys., 2009, 131, 244302.
50. L. Bonnet and J. Espinosa-García, J. Chem. Phys., 2010, 133, 164108.
51. G. Czakó, J. Phys. Chem. A, 2012, 116, 7467.
52. T. Győri and G. Czakó, J. Chem. Theory Comput., 2020, 16, 51.
53. W. L. Hase, Encyclopedia of Computational Chemistry, Wiley, New York, 1998, pp. 399–407.
54. G. Czakó, B. C. Shepler, B. J. Braams and J. M. Bowman, J. Chem. Phys., 2009, 130, 084301.
55. P. Papp, V. Tajti and G. Czakó, Chem. Phys. Lett., 2020, 755, 137780.
56. I. Szabó and G. Czakó, Nat. Commun., 2015, 6, 5972.
57. V. Tajti, T. Győri and G. Czakó, J. Chem. Phys., 2021, 155, 124301.
58. A. Y. Dymarsky and K. N. Kudin, J. Chem. Phys., 2005, 122, 124103.
59. K. N. Kudin and A. Y. Dymarsky, J. Chem. Phys., 2005, 122, 224105.
60. G. Czakó, T. Győri, B. Olasz, D. Papp, I. Szabó, V. Tajti and D. A. Tasi, Phys. Chem. Chem. Phys., 2020, 22, 4298.
61. M. L. Weichman, J. A. DeVine, M. C. Babin, J. Li, L. Guo, J. Ma, H. Guo and D. M. Neumark, Nat. Chem., 2017, 9, 950.

---

Footnote

† Electronic supplementary information (ESI) available: Cross sections and reaction probabilities for double inversion, front-side attack, and induced inversion; Gaussian width test for 1GB; and mode-specific vibrational distributions for the CH₃CH₂F and C₂H₄ products obtained with histogram binning. See DOI: 10.1039/d2cp00685e

---