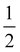Water on porous, nitrogen-containing layered carbon materials: the performance of computational model chemistries
Christopher
Penschke
 a,
Robert Edler
von Zander
a,
Alkit
Beqiraj
a,
Anna
Zehle
a,
Nicolas
Jahn
a,
Rainer
Neumann
a and
Peter
Saalfrank
a,
Robert Edler
von Zander
a,
Alkit
Beqiraj
a,
Anna
Zehle
a,
Nicolas
Jahn
a,
Rainer
Neumann
a and
Peter
Saalfrank
 *ab
*ab
aUniversität Potsdam, Institut für Chemie, Karl-Liebknecht-Str. 24-25, D-14476 Potsdam-Golm, Germany. E-mail: peter.saalfrank@uni-potsdam.de
bUniversität Potsdam, Institut für Physik und Astronomie, Karl-Liebknecht-Str. 24-25, D-14476 Potsdam-Golm, Germany
First published on 29th April 2022
Abstract
Porous, layered materials containing sp2-hybridized carbon and nitrogen atoms, offer through their tunable properties, a versatile route towards tailormade catalysts for electrochemistry and photochemistry. A key molecule interacting with these quasi two-dimensional materials (2DM) is water, and a photo(electro)chemical key reaction catalyzed by them, is water splitting into H2 and O2, with the hydrogen evolution reaction (HER) and the oxygen evolution reaction (OER) as half reactions. The complexity of some C/N-based 2DM in contact with water raises special needs for their theoretical modelling, which in turn is needed for rational design of C/N-based catalysts. In this work, three classes of C/N-containing porous 2DM with varying pore sizes and C/N ratios, namely graphitic carbon nitride (g-C3N4), C2N, and poly(heptazine imides) (PHI), are studied with various computational methods. We elucidate the performance of different models and model chemistries (the combination of electronic structure method and basis set) for water and water fragment adsorption in the low-coverage regime. Further, properties related to the photo(electro)chemical activity like electrochemical overpotentials, band gaps, and optical excitation energies are in our focus. Specifically, periodic models will be tested vs. cluster models, and density functional theory (DFT) vs. wavefunction theory (WFT). This work serves as a basis for a systematic study of trends for the photo(electro)chemical activity of C/N-containing layered materials as a function of water content, pore size and density.
I. Introduction
Porous two-dimensional materials (2DM) with sp2-hybridized carbon and nitrogen have gained, among other applications, tremendous interest in recent years as catalysts for the photochemical, electrochemical or photo(electro)chemical transformation of molecules.1,2A particularly successful material in this respect is graphitic carbon nitride, g-C3N4, with an (ideal) C/N ratio of 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4.3 g-C3N4 is an electron-rich organic semiconductor with connected tri-s-triazine (also called heptazine, C6N7H3) building blocks (see below). The material was originally suggested for photocatalytic water splitting, but proved to be highly successful also for many other photochemical, electrochemical or photo(electro)chemical (redox) reactions.4–6 Since then, further C/N-containing 2DM have been synthesized and characterized. Several of them surpass the performance of g-C3N4 either in quantitative terms, for example by showing higher turnover frequencies, or in qualitative terms, e.g., by catalyzing other reactions. The success of C/N-containing 2DM in general is rooted in their tunable pore size, pore density and controllable C/N ratio, resulting in tunable properties such as band gaps and band edges optimally adapted for photo(electro)chemical reactions. (Other control parameters are loading with metal ions or other co-catalysts, adding sacrificial electron donors or acceptors, doping with heteroatoms such as fluorine, sulphur or oxygen, or co-polymerization with other species. In this work, however, we shall only consider metal-free, undoped and “pure” 2DM.) For instance, quite recently N-richer 2DM of formal composition C2N and smaller pore sizes than those of g-C3N4 have been synthesized,7,8 showing promising performance for molecular sieving and electrochemical N2 reduction, for example.9,10 A third class of materials we will consider below, are poly(heptazine imides) (PHI), which also derive from tri-s-triazine building blocks as g-C3N4 but featuring larger pore sizes.11,12 PHIs can be loaded with metals (M-PHI, M = metal) but come also in a protonated, metal-free form (H-PHI). M-PHIs and H-PHI have shown excellent performance towards several photo(electro)chemical reactions of adsorbed molecules.13,14
4.3 g-C3N4 is an electron-rich organic semiconductor with connected tri-s-triazine (also called heptazine, C6N7H3) building blocks (see below). The material was originally suggested for photocatalytic water splitting, but proved to be highly successful also for many other photochemical, electrochemical or photo(electro)chemical (redox) reactions.4–6 Since then, further C/N-containing 2DM have been synthesized and characterized. Several of them surpass the performance of g-C3N4 either in quantitative terms, for example by showing higher turnover frequencies, or in qualitative terms, e.g., by catalyzing other reactions. The success of C/N-containing 2DM in general is rooted in their tunable pore size, pore density and controllable C/N ratio, resulting in tunable properties such as band gaps and band edges optimally adapted for photo(electro)chemical reactions. (Other control parameters are loading with metal ions or other co-catalysts, adding sacrificial electron donors or acceptors, doping with heteroatoms such as fluorine, sulphur or oxygen, or co-polymerization with other species. In this work, however, we shall only consider metal-free, undoped and “pure” 2DM.) For instance, quite recently N-richer 2DM of formal composition C2N and smaller pore sizes than those of g-C3N4 have been synthesized,7,8 showing promising performance for molecular sieving and electrochemical N2 reduction, for example.9,10 A third class of materials we will consider below, are poly(heptazine imides) (PHI), which also derive from tri-s-triazine building blocks as g-C3N4 but featuring larger pore sizes.11,12 PHIs can be loaded with metals (M-PHI, M = metal) but come also in a protonated, metal-free form (H-PHI). M-PHIs and H-PHI have shown excellent performance towards several photo(electro)chemical reactions of adsorbed molecules.13,14
Despite the many different (redox) reactions which can be catalyzed by C/N-based 2DM, still the most popular key molecule, often used as a “drosophila” to study photo(electro) catalytic performance of new materials, is water. And here the key reaction to be studied is water splitting, with the hydrogen evolution reaction (HER) and the oxygen evolution reaction (OER) being the relevant half reactions. The variability/tunability of C/N-based 2DM in contact with water offers not only a route towards tailor-made and efficient catalysts, it also comes with considerable structural complexity. This, in turn, is a challenge for theoretical modelling of these materials, the latter needed to acquire a basic understanding of trends and mechanisms for guiding the rational design of new catalysts.
The goals of our study of water on C/N-containing 2DM are twofold. First, we wish to investigate for the three classes of materials mentioned, graphitic carbon nitride (g-C3N4), C2N, and poly(heptazine imides) (PHI), the performance of computational models and methods, i.e., periodic vs. cluster models, and density functional theory (DFT) vs. highly correlated wavefunction theory (WFT). This is important because, all of these models and model chemistries (the combination of electronic structure method and basis set) are characterized by different computational effort, strengths and weaknesses which need to be evaluated. Second, we wish to study trends of water-covered C/N-based 2DM, namely, for water adsorption energies, electrochemical overpotentials, vibrational spectra, and optoelectronic properties including the band gap as a function of water content, pore size and C/N ratio. Some of these properties are central for the performance of these materials as photo(electro)catalysts, while others are needed for their physico-chemical characterization. The first goal is the subject of the present paper, while the second one will be attacked in a forthcoming report.15
The rest of the paper is organized as follows. In Section 2 we describe the three classes of C/N-based 2DM studied in this work (Section 2.1) and summarize the different model chemistries based on periodic and non-periodic DFT and WFT, respectively (Section 2.2). In Section 3, we then test the various model chemistries and methods using specific examples, with the goal to identify approaches with a price-performance ratio as optimal as possible and to unravel critical cases and issues. We shall concentrate on the properties mentioned above, which are directly or indirectly related to the performance of photo(electro)catalysts. A final Section 4 summarizes and concludes our work.
II. Computational methods and models
A. Materials and models
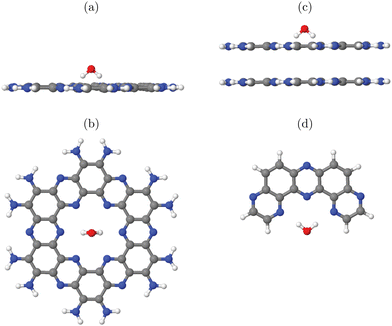
In this work, three classes of C/N-containing, porous 2DM will be considered:1. Graphitic carbon nitride (g-C3N4), for which a single layer and a corresponding 2D elementary (3 × 3) cell is shown in Fig. 1(a). The figure results from an optimized structure on the PBE+D3 level of theory (see below for details). The chosen cell allows for a stabilizing, non-planar reconstruction of the 2D material with wave-like structural pattern as shown in Fig. 1(a) (sideview), which was also found in ref. 16. The structure consists of tri-s-triazine (C6N7) triangles, nine per (3 × 3) cell, connected by shared triangular N-bridges. This results in a C/N ratio of 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4, i.e. C3N4. With PBE+D3 optimized hexagonal lattice constants a = b = 20.37 Å, γ = 120° for the 2D (3 × 3) cell, the resulting structure has a density of close to 4.6 amu Å−2 (with amu = atomic mass unit). Idealizing the pores as isosceles triangles (with two sides of 6.68 Å, one with 7.05 Å), the pore size is 20.8 Å2. g-C3N4 is a semiconductor as mentioned earlier, with an experimental, optical band gap of 2.7 eV.3
4, i.e. C3N4. With PBE+D3 optimized hexagonal lattice constants a = b = 20.37 Å, γ = 120° for the 2D (3 × 3) cell, the resulting structure has a density of close to 4.6 amu Å−2 (with amu = atomic mass unit). Idealizing the pores as isosceles triangles (with two sides of 6.68 Å, one with 7.05 Å), the pore size is 20.8 Å2. g-C3N4 is a semiconductor as mentioned earlier, with an experimental, optical band gap of 2.7 eV.3
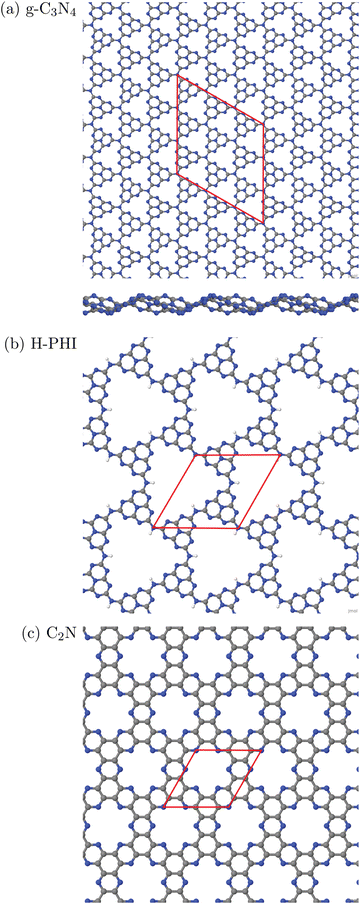 | ||
| Fig. 1 Periodic single-layer models used for (a) g-C3N4, (3 × 3) cell, top and sideview; (b) H-PHI; (c) C2N. Elementary cells in red, C in grey, N in blue, H in white. | ||
2. Protonated Poly(heptazine imide) (H-PHI), consisting also of tri-s-triazine units as g-C3N4. A periodic model with two tri-s-triazine units and chemical formula C12N17H3 is shown in Fig. 1(b). The C/N ratio for this material is slightly lower than for g-C3N4 (C/N = 12/17 = 0.706) and it contains hydrogen (or metal ions, M, in case of M-PHI). The main difference is the larger pore size, about four times larger than those of g-C3N4, and the density is smaller than the one of g-C3N4. Using optimized lattice parameters (on the PBE+D3 level of theory, see below), gives lattice constants a = b = 12.92 Å and γ = 120°. (Experimental parameters are very similar,12 see below.) For the structure shown in Fig. 1(b), we have ρ ∼ 2.7 amu Å−2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12 and a pore size (idealized as equilateral triangular) of 81.3 Å2, cf.Table 1. Unlike M-PHIs, H-PHI forms ideally flat single layers at least according to theoretical periodic and cluster models (see below and ref. 12). Both M-PHI and H-PHI are semiconductors with respective experimental, optical band gaps of 2.90 eV for H-PHI and 2.68 eV for K-PHI, for example.17
12 and a pore size (idealized as equilateral triangular) of 81.3 Å2, cf.Table 1. Unlike M-PHIs, H-PHI forms ideally flat single layers at least according to theoretical periodic and cluster models (see below and ref. 12). Both M-PHI and H-PHI are semiconductors with respective experimental, optical band gaps of 2.90 eV for H-PHI and 2.68 eV for K-PHI, for example.17
| Material | g-C3N4 | H-PHI | C2N |
|---|---|---|---|
| a From a periodic single-layer PBE+D3 calculation, (3 × 3) cell in Fig. 1(a). b From a periodic bulk PBE+D3 calculation, (1 × 1) cell in Fig. 1(b), see also Table 5 below. c From computational models in ref. 9, (1 × 1) cell in Fig. 1(c). d Idealizing the pores as isosceles triangles. e Idealizing the pores as equilateral triangles. f Idealizing the pores as 18-gons as shown in Fig. 1(c). g Experimental optical gap according to ref. 3. h Experimental optical gap according to ref. 17. i Experimental optical gap according to ref. 7. | |||
C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N ratio N ratio |
0.75 | 12/17 = 0.706 | 2.0 |
| Lattice parameters a = b (Å) | 20.37a | 12.92b | 8.4c |
| Layer mass density ρ (amu Å−2) | 4.6 | 2.7 | 3.7 |
| Pore size Apore (Å2) | 20.8d | 81.3e | 36.1f |
| Band gap (eV) | 2.7g | 2.9h | 1.96i |
3. Finally, we consider a C/N-based 2DM of composition C2N, derived from hexaazatriphenyle-hexacarbonitrile (HAT-CN).8 C2N has a C/N ratio (C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N = 2
N = 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) larger than and a pore size in between, the two former ones. As shown in Fig. 1(c), the ideal single-layer structure can be seen as condensed pyrazine-like rings, whereby each pyrazinic unit (C4N2) lies also between two pores. With lattice parameters a = b = 8.4 Å (calculated in ref. 9), the pore size, now idealized as the area of the 18-gon, is 36.1 Å2. Also C2N is a semiconductor, with a reported band gap of 1.96 eV.7
1) larger than and a pore size in between, the two former ones. As shown in Fig. 1(c), the ideal single-layer structure can be seen as condensed pyrazine-like rings, whereby each pyrazinic unit (C4N2) lies also between two pores. With lattice parameters a = b = 8.4 Å (calculated in ref. 9), the pore size, now idealized as the area of the 18-gon, is 36.1 Å2. Also C2N is a semiconductor, with a reported band gap of 1.96 eV.7
In what follows, both periodic and cluster models will be adopted for these materials. All three classes of C/N compounds mentioned, form stacked layer structures with sheets held together mainly by van der Waals forces, and interlayer distances around 3.2–3.3 Å. We use ideal, fully polymerized structural models here but note that the materials studied in this work are sometimes only partially polymerized or contain other imperfections (see ref. 18 for the example of g-C3N4). Various stacking sequences are possible. For C2N we use A–A–A–⋯ stacked structures following earlier computational models in ref. 9. g-C3N4 shows A–B–A–B⋯stacking,16 while H-PHI has a triclinic unit cell12 with laterally shifted neighbouring layers (see below). Both cluster and periodic models will also be used to study the adsorption of water and water fragments, and properties related to photo(electro)catalysis.
B. Computational methods and model chemistries
In this section we outline methods and model chemistries used in this work, both for periodic and cluster models. The periodic approaches have a number of advantages, e.g., high efficiency, absence of artificial boundary conditions and direct access to the (electronic) band gap. Disadvantages are the much larger effort if large unit cells are needed (e.g., when modelling low-density defects), or highly accurate calculations beyond DFT-GGA (DFT in the Generalized Gradient Approximation). Also, the calculation of localized electronic excitations and resulting optical spectra, possibly with vibronic resolution, is difficult in periodic approaches. Here the cluster approaches offer clear advantages. For them, a large variety of powerful electronic structure methods exist, both from DFT and wavefunction theory (WFT). A brief summary of specific methods and models used here is as follows.a. Periodic DFT and GW calculations. The structures shown in Fig. 1 arise from periodic models, for which several variants of density functional theory with periodic boundary conditions have been used. In particular, we adopted first principles DFT-GGA functionals, typically PBE.19 If not stated otherwise, dispersion corrections were included using Grimme's D3 correction20 with Becke–Johnson damping.21 Most periodic DFT calculations were done using the projection augmented wave (PAW) approach22,23 with the Vienna ab inito simulation package (VASP).24,25 Further, plane-wave bases with a certain cutoff, Vc, and Monkhorst–Pack k-point sampling26 as specified below were adopted. To test basis set dependencies and shortcomings of pseudopotentials in periodic calculations, also the all-electron FHI-aims program27 was used which employs numeric atom-centered basis functions (NAOs, numeric atomic orbitals)28 instead of plane waves (PW). Like PW bases, NAOs are essentially free of basis set superposition error, in contrast to Gaussian orbital basis sets (see below). GGA is known to underestimate band gaps,29 for example, which is why also hybrid functionals were used in selected cases, namely PBE0,30 B3LYP31–33 and HSE06.34,35
In some cases we went beyond Kohn-Sham density functional theory by introducing many-body corrections on the non-self consistent G0W0 level of theory,36–38 typically on a GGA reference, e.g., G0W0@PBE. The resulting quasiparticle band structure usually improves band gaps. Most G0W0 calculations below were done with the exciting code, which is based on all-electron DFT using the linearized augmented plane wave (LAPW) method.39
In the periodic DFT calculations, for quasi-2D (single- or few-layer) materials supercell geometries with large vacuum gaps were adopted, while bulk materials were treated by 3D unit cells. Structures were either optimized (atom coordinates and sometimes also cell parameters) or adapted from other sources (experiment or previous theory).
b. Periodic DFTB calculations. For selected examples, also the semiempirical DFT based tight-binding (DFTB) method was used, as implemented in the DFTB+ package.40 Specifically, a self-consistent charge approach (SCC-DFTB) was chosen, adopting the 3ob-3-1 parametrization of ref. 41 and dispersion corrections taken from the UFF forcefield42 – see also ref. 16. The DFTB approach is extremely efficient and therefore applicable when larger unit cells or multi-layer systems are to be considered.
c. Normal mode analysis and thermochemical properties. Within the periodic approaches, Normal Mode Analyses (NMA) to obtain frequencies were done by diagonalizing the dynamical matrix at the Γ-point, mostly for calculating thermochemical quantities. In particular, reaction (free) energies were calculated as ΔE = E(product) − E(reactant) and ΔG = G(product) − G(reactant), respectively, with E denoting the sum of electronic energy and nuclear repulsion. Enthalpic, H(T) and entropic, S(T), finite-temperature contributions to the free energies, G(T) = E + H(T) − TS(T), were calculated using standard procedures as outlined, e.g., in ref. 43. For surface structures, only vibrational contributions (in harmonic approximation) were considered since translation and rotation of adsorbate species become frustrated in this case. For free species rotations and translations were included, the former in rigid-rotor approximation, the latter at standard pressure if not stated otherwise.
d. Excited-state calculations: Bethe–Salpeter equation. Again for a few cases, optical (excited-state) properties of C/N-containing materials were calculated using the Bethe-Salpeter Equation (BSE).44 The BSE can be done directly on a Kohn-Sham reference, e.g., BSE@PBE, or on a quasiparticle reference obtained from a GW calculation, e.g., BSE@G0W0@PBE. The method gives the optical band gap and accounts for excitonic effects. The BSE calculations reported below were also done with the exciting code.39
a. Ground-state DFT calculations. After having selected a suitable cluster model (see below), DFT can also be applied in this case. Below, we used either the ORCA code, version 4.0.0.2,45 Gaussian 16,46 or Turbomole.47 Apart from PBE,19 also hybrid density functionals such as B3LYP31–33 and long-range corrected CAM-B3LYP(+D3)48 were adopted. For clusters, in all cases atom-centered Gaussian atomic orbital bases were used as specified below. The latter cause a basis set superposition error (BSSE) as mentioned above which will be quantified in this work and, where necessary, corrected by the counterpoise (CP) method.49,50 As for the periodic models, ground state DFT calculations will be used for geometry optimization, normal mode analysis and thermochemical properties, in the harmonic approximation for vibrations. Again, rotations and translations were left out for adsorbed species but included for the free species.
b. Excited-state TD-DFT calculations. For several clusters, time-dependent density functional theory (TD-DFT) in Casida's linear-response formalism51 was applied to compute excitation energies Ei and oscillator strengths fi, out of the ground state.
c. Ground-state correlated wavefunction theory. We also used highly correlated wavefunction methods for selected cluster models, as a reference for DFT results. In particular, we used the “gold standard” CCSD(T)52 for sufficiently small clusters, and Domain Based Local Pair-Natural Orbitals CCSD(T), DLPNO-CCSD(T), for larger ones.53,54
d. Excited-state correlated wavefunction theory. Besides for ground states, also for excited states WFT was used in this work, mostly for comparison to TD-DFT. The two methods employed here are the Coupled Cluster CC2 response method,55,56 and the Algebraic Diagrammatic Construction scheme in second order, ADC(2).57 Also, for larger clusters the semiempirical ZINDO/S (Zerner's Intermediate Neglect of Differential Overlap method for Spectroscopy)58 was used, which is a CI (Configuration Interaction) calculation with orbitals derived from the ZINDO Hamiltonian.
III. Results and discussion
A. Adsorption and reaction energies
| Eads = E*H2O− (E* + EH2O). | (1) |
In (1), E* and EH2O are the energy of bare cluster or isolated periodic surface and isolated water, respectively, and E*H2O is the energy of the bound water-cluster complex or the water-covered periodic surface. When choosing a cluster as a representative for a periodic solid with atoms held together by covalent bonds, two main questions arise:
• Which cluster to choose by cutting which bonds?
• How to saturate resulting dangling bonds?
We try to answer these questions by specific examples. For this, let us consider water adsorption on C2N (Fig. 1(c)) first, starting with cluster models. In case of quasi-2D layered materials with layers held weakly together mostly by van der Waals forces, considering a single layer seems to be a good choice both for cluster and periodic models, in particular when adsorption on the upper layer is considered as decisive for the catalytic activity. Another reasonable assumption for selecting clusters is that one should use full pores if possible. Let us briefly address the validity of one-layer models for the example of adsorption of a single water molecule on 1-pore cluster models of C2N, for one up to four layers. Selected cluster structures are shown in Fig. 2(a) and (b) for the one-layer system and Fig. 2(c) for the double-layer model, respectively. In constructing the clusters, the following procedure was followed: (i) We adopted vertical (c = 3.3 Å) and lateral lattice constants (a = b = 8.4 Å, see Table 1) and C and N positions from earlier periodic models of C2N.9 (ii) We then cut out a single pore and saturated dangling bonds with NH2 groups. (iii) Next we added a single water molecule on-top. First N-H bondlengths and then the position of water were optimized on the chosen level of theory, which is PBE+D3/6-311G** in Fig. 3. Note that the stacking sequence is A–A for the double-layer (and A–A–⋯ –A for poly-layer systems) as in ref. 9. (In this context we note that periodic PBE+D3 calculations of the type described below indicate that A–B–A–B⋯ is in fact slightly (by ∼20 meV per atom) more stable than A–A stacking, and ab initio molecular dynamics calculations show that both forms are interconvertible at 300 K. The A–B–A–B⋯ stacked system turns out to have very similar water adsorption energies, though.) The NH2 -saturated cluster model with one pore and one water molecule is denoted as 1-p/NH2 +1H2O in the table (entry 1).
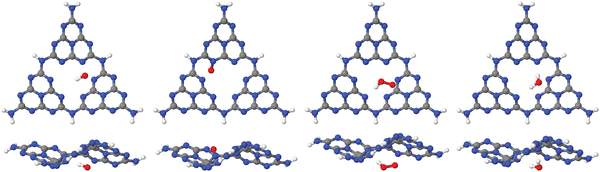 | ||
| Fig. 3 Adsorption of OH, O and OOH (the products of reactions A, B and C in the OER), and of H2O, on a single-pore cluster model of g-C3N4, NH2-saturated. Shown are the topviews (upper panels) and sideviews (lower panels) of the single-layer models. All structures calculated based on periodic PBE+D3 starting structures of ref. 16, then a constrained reoptimization on the PBE+D3/6-311G** level of theory was performed as described in the text. | ||
In that entry 1, we list the adsorption energies as a function of layers for this model, and, for one and four layers, representative bondlengths, distances and bond angles. We shall discuss the found adsorption geometries and also alternative structures in more detail elsewhere15 (also considering interlayer adsorption), and merely mention for now that the most stable configuration we found is a water molecule with hydrogens pointing down to the pore, forming this way favourable hydrogen bonds with two N atoms as shown in Fig. 2(a)–(c). From the table it is seen that, both the structures and the adsorption energies depend somewhat on the number of considered layers. In particular, adding a second layer increases the adsorption energy by about 10% on this level of theory, while adding further layers has much less an effect. Still, in many of the examples below single-layer models will be used, while keeping the ∼10% error in mind.
About the same multi-layer effect is found in periodic PBE+D3/plane wave calculations, which are shown for one-and four-layer models as entry 8 in the table. Again, adding further layers increases the binding energy of water somewhat. The adsorption geometries are analogous to those of the cluster models in Fig. 2(a),(b) (not shown). In the periodic calculations, we adopted a (2 × 2 × 1) supercell geometry with one (entry 8) or four water molecules (entry 9), corresponding to coverages of 0.25 and 1.0 H2O molecules per pore, respectively. The water geometry was optimized on the PBE+D3 level, using a plane wave basis with a cutoff of 600 eV, Γ -centered Monkhorst–Pack k-point meshes (2 × 2 × 1) for the one-layer and (2 × 2 × 3) for the four-layer system. A vacuum gap 15 Å wide, and experimental lateral lattice constants given in Table 1 were adopted. (Reoptimization had only a very small effect on adsorption energies and structures).
In Table 2, entries 2 and 3, we consider NH2-saturated single-layer 2-pore models with either one (2-p/CN + 1H2O) or two water molecules (one on each pore, 2-p/CN + 2H2O). The adsorption energies per water molecule do not depend significantly on the presence of a second pore (loaded or empty). Thus single-pore models should be sufficient at low coverages, and water-water interactions are small in this case.
| C2N | Layers | ||||||
|---|---|---|---|---|---|---|---|
| Entry | Model | Coverage | Quantity | 1 | 2 | 3 | 4 |
| 1 | 1-p/NH2+1H2O | 1.0 | E ads (w/o CP) | −0.625 | −0.690 | −0.701 | −0.715 |
| (−0.866) | (−0.939) | (−0.949) | (−0.964) | ||||
| r O–H (Å) | 0.976 | 0.977 | |||||
| θ H–O–H (°) | 100.5 | 100.1 | |||||
| Z O–p (Å) | 1.642 | 1.584 | |||||
| 1b | PBE+D3/def2-SVP | 1.0 | E ads | −0.602 | |||
| 1c | B3LYP+D3/6-311G** | 1.0 | E ads | −0.626 | |||
| 2 | 2-p/NH2+2H2O | 1.0 | E ads | −0.607 | |||
| 3 | 2-p/NH2+1H2O | 0.5 | E ads | −0.610 | |||
| 4 | 1-p/CN+1H2O | 1.0 | E ads | −0.481 | −0.512 | −0.510 | |
| 5 | 2-p/CN+2H2O | 1.0 | E ads | −0.493 | |||
| 6 | 2-p/CN+1H2O | 0.5 | E ads | −0.491 | |||
| 7 | 1-p/H+1H2O | 1.0 | E ads | −0.563 | |||
| 8 | Periodic+1H2O | 0.25 | E ads | −0.527 | −0.573 | ||
| r O–H (Å) | 0.977 | 0.978 | |||||
| θ H–O–H (°) | 101.6 | 101.7 | |||||
| Z O–p (Å) | 1.760 | 1.617 | |||||
| 9 | Periodic+4H2O | 1.0 | E ads | −0.515 | −0.555 | ||
When comparing the adsorption energies obtained with the NH2 -saturated clusters (entries 1–3) with those of the periodic calculations (entries 8 and 9), it is obvious that the former are by around 100 meV larger than the latter. This cannot be due to the BSSE, which is indeed large in the present examples (>0.2 eV) but which has been corrected for by the counterpoise method. (See the uncorrected values “w/o CP” in entry 1 of the table for comparison.) It can also not be due to lateral water–water interactions and/or the different coverages, because the former are weak at low coverages as just demonstrated. It can also be seen from the periodic models in entries 8 (coverage 0.25) and 9 (coverage 1.0), respectively, featuring almost identical adsorption energies. Also, basis set errors for the Gaussian basis sets applied for the clusters are expected to be not decisive in this case: A PBE+D3 calculation with the smaller def2-SVP basis for 1-p/CN + 1H2O, gives Eads = −0.602 eV instead of −0.625 eV, see entry 1b. The main reason for the discrepancy between the cluster and periodic calculations is due to the saturation of the dangling bonds by NH2 groups. In fact, replacing the amino by cyano (CN) groups which more realistically mimic the C2N solid, gives adsorption energies to within 30–40 meV (3–4 kJ mol−1) of the values obtained with the periodic model, as can be seen from the 1-p/CN and 2-p/CN models of Table 2, entries 4–6. (Remaining small differences can be attributed to remaining basis set and saturation errors and differences in coverages.) Note that also a simple saturation of dangling bonds by hydrogen gives absolute adsorption energies already comparable to those obtained by CN-saturation (model 1-p/H, entry 7).
| A: * + H2O→*OH + H+ + e− |
| B: *OH → *O + H+ + e− |
| C: *O + H2O → *OOH + H+ + e− |
| D: *OOH → * + O2 + H+ + e− |
In Table 3, upper half, we list adsorption energies analogous to eqn (1), for water and various fragments, using DFT and DLPNO-CCSD(T), for clusters at PBE+D3/6-311G** geometries. In the lower half of the table, reaction energies A-D are shown, for PBE+D3 and DLPNO-CCSD(T) with various basis sets. The reaction energies do not account for any vibrational or temperature effects – Gibbs free energies G will be considered below.
| Model chemistry | E ads (O)a | E ads (OH) | E ads (OOH) | E ads (H2O) (w/o CP) |
|---|---|---|---|---|
| a Calculated as Eads(O) = E(3O) + E (1*) − E(1*O), BSSE-corrected for clusters by CP method (w/o CP for selected examples in brackets). b Reaction energies ΔE for X → Y + H+ + e− calculated as ΔE = E(Y) − E (X), BSSE-corrected. | ||||
| Adsorption energies | ||||
| PBE+D3/6-311G** | −2.36 | −0.58 | −0.86 | −0.57 (−0.84) |
| periodic PBE+D3/PW (ref. 16) | −2.73 | −0.61 | −0.66 | −0.55 |
| DLPNO-CCSD(T)/cc-pVTZ | −1.10 | −0.30 | −0.55 | −0.48 (−0.65) |
| Model chemistry | A | B | C | D |
|---|---|---|---|---|
| Reaction energy ΔE for OER stepb | ||||
| PBE+D3/6-311G** | 2.43 | 0.56 | 0.99 | 0.53 |
| DLPNO-CCSD(T)/6-311G** | 2.57 | 1.52 | 0.49 | 0.26 |
| DLPNO-CCSD(T)/cc-pVDZ | 2.52 | 1.55 | 0.33 | 0.22 |
| DLPNO-CCSD(T)/aug-cc-pVDZ | 2.57 | 1.40 | 0.81 | 0.50 |
| DLPNO-CCSD(T)/cc-pVTZ | 2.65 | 1.32 | 0.75 | 0.48 |
Considering the upper half of Table 3 with adsorption energies first, we see almost no deviation for water adsorption between cluster and periodic calculations when both are performed with PBE+D3 (0.57 vs. 0.55 eV). For the cluster model, DLPNO-CCSD(T)/cc-pVTZ predicts a by ∼0.1 eV lower adsorption energy compared to PBE-6311G**. In this context, we also refer to a very recent publication in which water adsorption on g-C3N4 was studied with periodic DFT and correlated wavefunction methods.59 There, the adsorption energy of a single H2O was found to be −0.53 eV at the PBE+D3 level (−0.35 eV with PBE without D3), and −0.51 eV at the CCSD(T):RPA (RPA = Random Phase Approximation) level. That is, also there a slightly lower adsorption energy is found for the correlated WFT method, but differences to PBE+D3 method are small. We shall see shortly that the difference can be much larger for other adsorbates.
Secondly, we note from Table 3, upper half, that the BSSE is larger for the 6-311G** than for the larger cc-pVTZ basis set (0.27 eV for PBE+D3/6-311G** and 0.17 eV for DLPNO/CCSD(T)/cc-pVTZ). This finding will be supported below for the other two materials studied in this work, C2N and H-PHI.
Third, for adsorption of open-shell species O, OH and OOH, we note some larger deviation (by up to 0.37 eV for O) between cluster and periodic PBE+D3 calculations. We also find large differences there for the WFT method, DLPNO-CCSD(T), compared to PBE+D3, particularly for Eads (O). In this case, a covalent bond is formed in contrast to OH, OOH and H2O which are only H-bonded to the catalyst.
Considering the OER reaction energies A–D in the lower half of the table, we recognize for DLPNO-CCSD(T), a quite substantial difference to PBE+D3 for reaction B (dissociation of *OH). Reaction energies A, C and D are more similar for both methods. Further, for DLPNO-CCSD(T) the well-known large dependence of highly correlated WFT methods on basis set size is seen. In contrast, DFT shows a much less severe basis-set dependence (cf.Table 2 for H2O:C2N, entries 1 and 1b). The need of large basis sets makes highly correlated WFT methods costly. In this context we state that the domain-based DLPNO-CCSD(T) reported in the table, which contains additional approximations to a full CCSD(T) calculation but is much “cheaper”, introduces only small errors beyond CCSD(T): for a “half-pore” cluster model of C2N, as shown in Fig. 1(d), for example, BSSE-corrected DLPNO-CCSD(T)/cc-pVDZ and CCSD(T)/cc-pVDZ adsorption energies on PBE+D3/6-311G** optimized geometries, deviated only by 5 meV from each other.
The partially substantial deviation in adsorption and reaction energies between DFT and WFT is hard to explain quantitatively, and here we only can give qualitative statements because a systematic study goes beyond the scope of this paper. We first recall that the DLPNO-CCSD(T) calculations are single-point, i.e., no geometry reoptimization has been made in contrast to DFT. Secondly, it was recently demonstrated that typical DFT functionals (including PBE) for reactions involving molecular O2 come with errors of 0.3 eV and larger.60 This does not necessarily explain why in particular the oxygen adsorption energy (where we start from the 3 O atom and not the molecule) in the upper half of Table 3 shows such a large method dependence, nor why reaction D in the lower half (which involves molecular oxygen) does not. Still ref. 60 demonstrates that care has to be taken when using PBE for OER or similar reactions. While DFT correction schemes have been suggested to reduce these inaccuracies,61 we shall still use PBE below, also for Gibbs free energies, because the method is fast and reliable enough to quantify trends in comparable situations, e.g. for screening of different materials or checking cluster vs. periodic models. Note finally that step A of the OER, the rate-limiting step, shows only moderate method dependence according to Table 3.
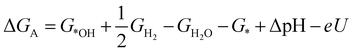 | (2) |
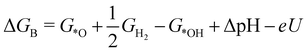 | (3) |
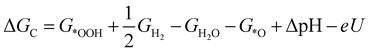 | (4) |
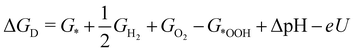 | (5) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(10)·pH. The method makes use of Nørskov's model of the normal hydrogen electrode (NHE), accounts for finite pH (through the term ΔpH) and voltage, U, in an electrochemical setup. It can be used to calculate the overpotential for electrochemical, anodic OER16,17,62,63 but is also applied to estimate the energetics of photoinduced OER. There a photogenerated exciton takes the role of “providing the voltage”, U.64,65 Note that already in ref. 65, cluster models were used to compute overpotentials.
ln(10)·pH. The method makes use of Nørskov's model of the normal hydrogen electrode (NHE), accounts for finite pH (through the term ΔpH) and voltage, U, in an electrochemical setup. It can be used to calculate the overpotential for electrochemical, anodic OER16,17,62,63 but is also applied to estimate the energetics of photoinduced OER. There a photogenerated exciton takes the role of “providing the voltage”, U.64,65 Note that already in ref. 65, cluster models were used to compute overpotentials.
The Gibbs free energies GX for adsorbed species X were calculated by neglecting rotational and translational contributions (also in the cluster models), but the latter were included for the free species as described above. Vibrations, needed for zero-point energy and thermal contributions to vibrational enthalpy and the entropy are treated in harmonic approximation. The free energies of H+ and e− are computed as 1/2G (H2) in the Nørskov model. The method does not account for additional reaction barriers and will thus only give lower boundaries to overpotentials. In Fig. 4, we show the free-energy profiles obtained from the cluster model of Fig. 3 and of the periodic calculation done in ref. 16, respectively, for various voltages U, always at T = 300 K and pH = 7.
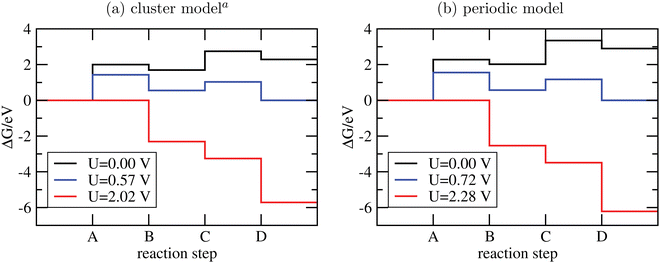 | ||
| Fig. 4 Free-energy plots for the OER steps A-D on g-C3N4 using cluster models and PBE+D3/6-311G** (a) or periodic models and PBE+D3/PW ((b), data taken from ref. 16). In both cases, T = 300 K and pH = 7; for not-adsorbed species a pressure of 1 bar was assumed, except for water, where p = 0.035 bar to mimick liquid water. Different voltages are indicated. aSince the clusters of Fig. 3 are not fully optimized to preserve the tilted structure found in periodic DFT, a few frequencies were imaginary and were not considered for thermodynamics. | ||
From the figure, we realize first of all that the reaction energetics at U = 0 is quite similar for cluster and periodic models (black curves). In particular, step A of the OER is by far the energetically most demanding step. Closer inspection reveals some quantitative differences. The largest deviation is for steps A and C, where the periodic model finds a by ∼0.25 eV larger reaction free energy than the cluster model. Both steps involve the adsorption of water. Possible sources of error are the constrained geometry optimization of the clusters (footnote a) in Fig. 4), and their saturation with NH2 groups.
There are also moderate differences in the estimated equilibrium voltage (at which the reaction sequence becomes thermoneutral, blue lines in Fig. 4), and in the overpotential for the reaction, η. The latter is calculated as the difference between the voltage for the thermoneutral and the all-downhill case, where no “barrier” is found anymore in the ΔG scheme16,62 (red curves). We find thermoneutral behaviour at U = 0.57 V and 0.72 V for the cluster and periodic models, respectively. For the overpotentials, we get η = 2.02 − 0.57 V = 1.45 V for the cluster and η = 2.28 − 0.72 V = 1.56 V for the periodic model.
Apart from quantitative differences in the energetics for steps A and C, periodic and cluster models agree well, which proves the validity of the cluster approach also for thermodynamics. An advantage of using clusters is that charged intermediate species can easily be handled, as suggested in ref. 65, which is less straightforward in a periodic model.
From the figure, we note that water lying flat in the pore is most stable. Then a stable 6-ring involving one O–H bond of water, and two N, one C and one inner H atom of the pore can be formed. This is a consequence of the larger pore size compared to C2N, for example, where water adsorbing “perpendicular” was more stable (see Fig. 1(a) and (b) above). For water on g-C3N4, the situation is intermediate between the two, showing a tilted water with hydrogen bonds to two N atoms in the (buckled) pore (see Fig. 3, right, and ref. 16 and 59).
Further, in Table 4, we show adsorption energies for water at the “full”, “1/2” and the two “2/3” clusters, with and without BSSE, for B3LYP+D3/TZVP and PBE+D3/6-311G**. Also shown in the table are adsorption energies for fragments related to OER (i.e., O, OH and OOH), and computed overpotentials η for OER (in this case for T = 298.15 K). Adsorption energies were calculated as before for g-C3N4, from spin-polarized (UB3LYP or UPBE) calculations if necessary for open-shell systems in their lowest-energy spin state.
| B3LYP+D3/TZVP | PBE+D3/6-311G** | |||||||
|---|---|---|---|---|---|---|---|---|
| Cluster | Large | Large | ||||||
| E ads (H2O) (eV) (with CP correction) | −0.49 (−0.46) | −0.49 (−0.46) | −0.48 (−0.44) | −0.50 (−0.46) | −0.59 (−0.45) | −0.60 (−0.46) | −0.58 (−0.44) | −0.61 (−0.46) |
| E ads (O) (eV) | −2.07 | −2.07 | 2.07 | −2.05 | −2.03 | −2.05 | −2.03 | −2.01 |
| E ads (OH) (eV) | −0.47 | −0.46 | −0.47 | −0.45 | −0.65 | −0.64 | −0.70 | −0.62 |
| E ads (OOH) (eV) (with CP correction) | −0.79 (−0.75) | −0.77 (−0.73) | −0.78 (−0.74) | −0.75 (−0.71) | −0.97 (−0.81) | −0.95 (−0.79) | −0.95 (−0.79) | −0.93 (−0.77) |
| η (V) | 1.07 | 1.05 | 1.06 | 1.05 | 0.95 | 0.94 | 0.95 | 0.94 |
Considering (U)B3LYP+D3/TZVP first (left half of the table), we note that the water adsorption energies for all clusters are similar to each other, scattering around −0.49 eV without CP correction. The same is true for geometry parameters (not shown), and for adsorption energies of O, OH and OOH (center part of the table). The corresponding most stable structures found on the B3LYP+D3/TZVP level are shown, for the 1/2 cluster, in the lower row of Fig. 5. (PBE+D3/6-311G** geometries are similar.)
In the right half of Table 4, the corresponding values are given for (U)PBE+D3/6-311G**. Also there, differences between various cluster models are small, in the order 0.02 eV typically, sometimes (for OOH) slightly larger. The most striking difference between (U)B3LYP+D3/TZVP and (U)PBE+D3/6-311G** is that the latter leads often to larger adsorption energies, from ∼ 0.1 eV (for water adsorption) to about ∼0.2 eV (for O and OOH adsorption). (For O adsorption, however, the PBE energies are quite similar to those of B3LYP.) Note that this tendency of overbinding of PBE w.r.t. more accurate methods (like B3LYP), is consistent with our findings above for other systems (cf.Table 3 for g-C3N4).
We also find a small difference (∼0.1 eV) in the overpotentials for OER, calculated with either B3LYP or PBE. Note that within a given model chemistry, the overpotentials are remarkably independent of cluster size. The overpotentials of about 1 eV are smaller than those reported for g-C3N4 above (∼ 1.5 eV with PBE+D3); a more detailed comparison of various layered materials will be given elsewhere.15
Two further remarks are as follows. First, most energies in Table 4 are without counterpoise correction to remove the BSSE. For water and also for OOH adsorption, we also did a BSSE correction resulting in smaller adsorption energies as shown. Interestingly, the BSSE is much smaller for B3LYP/TZVP (ca. −0.04 eV for both species) than for PBE/6-311G** (ca. −0.15 eV). Also in Table 2 for C2N comparatively large BSSE corrections were found for water adsorption (∼0.25 eV). This is due to the fact that the smaller 6-311G** basis comes with a larger BSSE compared to TZVP. As a consequence, for water adsorption on H-PHI at least, the overbinding of PBE is almost nullified compared to B3LYP. For other cases, such as the OOH adsorption, some, albeit small, overbinding of PBE remains.
Second, in a recent paper the same adsorbates H2O, O, OH and OOH on H-PHI were studied by periodic PBE+D3/PW.17 There, other adsorption geometries were reported for H2O and OOH, both with only one hydrogen bond to the substrate17 rather than two as in Fig. 4. For OH adsorption, formation of a covalent N–O–H unit rather than a H-bond with N as in Fig. 4 was found in ref. 17. Our geometries do not depend much on cluster size. The differences between ref. 17 and here may in part be due to different H-PHI cell parameters (see below). Still, when using different starting structures we found alternative structures for some of the adsorbates, suggesting a multi-valley structure of the potential energy landscape. Interestingly though, the free-energy profiles for the OER reaction steps A-D of ref. 17 are semi-quantitatively very similar to those from our cluster models.
B Band gaps, band edges and excited states
For photochemistry and electrochemistry electronic band gaps are important, for the former also optical band gaps and optical properties in general. Further, the energetic position of valence and conduction bands counts, for reduction or oxidation half reactions. For electronic band gaps periodic calculations are the method of choice, since they don't suffer from artifical boundary effects. Nowadays, periodic GGA-DFT calculations with plane waves are routinely done which are fast but underestimate band gaps as stated above. Here we test several methods to calculate band gaps by GGA, hybrid functionals and methods including many-body corrections (G0W0 and BSE). BSE gives also optical spectra, including excitonic effects. In the cluster world, on the other hand, “band gaps” are often estimated from HOMO–LUMO gaps, or from excitation energies from TD-DFT or more costly WFT methods such as CC255,56 and ADC(2).57 Here we study the performance of some of these methods for C/N-containing materials, for band gaps and optical excitations.a. DFT calculations. Starting with the example of H-PHI, we study band gaps calculated with various DFT methods and periodic models in Table 5. Both the bulk material and single-layer surface models are considered, the latter without or with additional water molecules, respectively. Besides the smallest indirect and direct band gaps, also the position of valence band maxima and conduction band minima are listed for most cases. A systematic comparison for different C/N-containing catalysts will be given in ref. 15.
| Model | Method | VBM | CBM | ΔEg (min.) | ΔEg (dir.) |
|---|---|---|---|---|---|
| a (1 × 1 × 1) triclinic cell from ref. 12 (cell parameters a = b = 12.922 Å, c = 4.326 Å, α = β = 109.6°, γ = 120.4°), then fully reoptimized after removing water with PBE+D3/PW, Vc = 600 eV, k-mesh (3 × 3 × 5); resulting new cell parameters: a = b = 12.917 Å, c = 4.519 Å, α = β = 111.1°, γ = 120.0°. b Same cell parameters as in a, but with atom positions reoptimized on that level. c Same cell parameters as in a, atom positions reoptimized on DFTB/UFF/3ob-3-1 level. d Same cell parameters and (PBE+D3/PW-optimized) atom positions as in a, FHI-aims calculation with tier 2 basis. e Same cell parameters and atom positions as for HSE06/PW above, FHI-aims calculation with tier 2 basis. f In ref. 17 a hexagonal (1 × 1 × 1) cell with a = b = 12.5 Å, c = 3.2 Å, α = β = 90.0°, γ = 120° was used. g Taken from ref. 17; VBM and CBM taken from their Fig. 3. h same lateral cell parameters a, b, γ and in-layer atom positions as in a, supercell model with c = 20 Å (and α = β = 90°). i Same cell parameters as in h, then seven water molecules were added and all atom positions optimized at the PBE+D3/PW level. | |||||
| Bulk | PBE+D3/PWa | −6.25 | −3.96 | 2.28 | 2.34 |
| HSE06/PWb | −6.89 | −3.58 | 3.31 | 3.39 | |
| PBE0/PWb | −7.27 | −3.24 | 4.03 | 4.08 | |
| B3LYP/PWb | −7.01 | −3.38 | 3.63 | 3.69 | |
| Bulk | DFTBc | −5.65 | −2.74 | 2.91 | 2.93 |
| Bulk | PBE/NAO (tier 2)d | −6.24 | −3.96 | 2.28 | 2.33 |
| HSE06/NAO (tier 2)e | −6.89 | −3.60 | 3.29 | 3.37 | |
| Bulk | PBE+D3/PW, ref. 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) f f |
1.65 | |||
HSE06/PW, ref. 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) fg fg |
−6.1 | −3.6 | 2.54 | ||
| Bulk | Optical, experiment,g![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ref. 17 ref. 17 |
−6.3 | −3.4 | 2.90 | |
| One layer | PBE+D3/PWh | −6.28 | −3.93 | 2.34 | 2.34 |
| One layer, 7 H2O | PBE+D3/PWi | −6.45 | −4.23 | 2.22 | 2.23 |
If not stated otherwise, for bulk H-PHI we started with triclinic lattice parameters of ref. 12 (obtained for structures which also contained water), and re-optimized them by periodic PBE+D3/PW using VASP, with a cutoff Vc = 600 eV and a (3 × 3 × 5) k-point mesh. The resulting lattice parameters, given in footnote a) of Table 5, were then used throughout, but atom positions were reoptimized with every respective method used here, namely PBE0/PW, HSE06/PW and B3LYP/PW, always with Vc = 600 eV. In addition, for the bulk, a DFTB/UFF/3ob-3-1 optimization of atom positions was performed (entry “DFTB”), using the DFTB+ code. Next, band structures were calculated using the same k-point mesh and minimal direct and indirect band gaps were determined with each method. PBE and HSE06 band structure calculations were also done, at the PBE+D3/PW and HSE06/PW geometries, using FHI-aims and employing the tier 2 localized basis set (entries PBE/NAO (tier 2) and HSE06/NAO (tier 2)). Finally for the bulk, a comparison to literature values obtained from experiment or theory from ref. 17 is given.
Further, for one-layer models, a single layer obtained from our bulk PBE+D3/PW calculation was used, and a supercell with a vacuum gap of 20 Å constructed. In case of water adsorption, seven water molecules were added (see also ref. 12) and all atom positions reoptimized by PBE+D3/PW. Again, band structures were calculated, all done with VASP.
All valence band maxima (VBM) and conduction band minima (CBM) shown in the table are referenced to the vacuum level. The latter was obtained from the calculated electrostatic potential far from the surface for the one-layer supercell model with 20 Å vacuum, or from ref. 17 when comparing to that source.
When considering the experimental optical band gap for bulk H-PHI of 2.90 eV (last row of the “bulk” part of table),17 we note that the lowest (indirect, “fundamental”) band gap from a periodic PBE+D3/PW calculation is underestimated, by 0.62 eV, in this case mostly because the minimum of the conduction band (CBM) is too low compared to experiment. The red-shift of the gap w.r.t. experiment reduces to about 0.56 eV if the lowest direct gap is taken as a measure for the optical gap instead, which is more realistic.
DFT functionals containing exact exchange, PBE0, HSE06, and B3LYP, on the other hand give indirect and direct gaps by up to more than one eV larger (for the PBE0 direct gap) than the measured optical gap.
In Table 5 we also report the PBE and HSE06 gaps obtained with our structures, when applying the FHI-aims code and an all-electron NAO (tier 2) atomic orbital basis. One obtains essentially the same gap values and band edges as for the VASP/PW calculations.
The SCC-DFTB calculation for the bulk gives gaps close to the measured, optical one, however, band positions (VBM and CBM) are quite inaccurate in this case.
From Table 5 we see that in ref. 17, lowest fundamental band gaps ΔEg (min) have been reported for H-PHI by PBE+D3/PW and HSE06/PW which are much lower, by 0.63 eV for PBE and 0.77 eV for HSE06, than ours. In that reference, however, a different unit cell was chosen, namely a hexagonal one (with A–A–A–⋯ layer stacking) rather than a triclinic cell with shifted neighbouring layers and also smaller lateral lattice constants a, b were adopted than we did. (For details, see the footnotes to Table 5.) When using the lattice parameters of ref. 17 instead and reoptimizing atom positions, we got a less stable, buckled-layer crystal but PBE and HSE06 gaps close to those found in ref. 17. This shows that the calculated band gap can be quite sensitive to details of the 3D structure of the material.
According to Table 5 a periodic single-layer model of H-PHI gives a by ∼0.06 eV larger, smallest indirect gap ΔEg (min.) than the bulk, on the PBE+D3 level, and the effect on the smallest direct gap is negligible. A corresponding HSE06/PW single-layer calculation gave similarly small changes w.r.t. the bulk (not shown). We note, though, that larger effects when going from 3D to 2D structures can be observed for other C/N-containing materials, in particular for A–A–A–⋯ stacked systems such as C2N (see below). In fact, as just argued, in general the 3D structure of a layered material can have a non-negligible effect on band gaps (while adsorption properties seem to depend less on the presence of neighbouring layers). Adding water on single H-PHI layers has some influence on (PBE+D3) gaps and band edges according to Table 5, however, effects are in the order of 0.1–0.2 eV only.
In the context of water splitting half reactions OER and HER, band gaps but also the positions of the valence band maximum and of the conduction band minimum are decisive. To split water photochemically, for example, the catalyst should have a band gap larger than 1.23 eV.16,17 To trigger OER and HER half reactions, the VBM should be below the OER potential (−5.67 eV at pH = 0 on the vacuum scale according to ref. 17), and the CBM should be above the HER potential (-4.44 eV at pH = 017), respectively. H-PHI fulfills these conditions according to experiment17 but also according to theory (Table 5 and ref. 17). Among the DFT methods studied here, compared to experiment HSE06/PW performs best for the band gap (slightly overestimating it) and for the CBM, while PBE strongly underestimates the gap (but performs well for the VBM). The trends of gaps for GGA and hybrid DFT methods are well known from literature as stated earlier.
b. GW and BSE calculations. Still, and also before comparing to cluster calculations, we make a little detour regarding the calculation of direct and optical gaps with periodic Kohn-Sham models and beyond. The optical gap can both be lower or larger than the electronic gap. The latter can happen when the lowest-energy transitions are indirect and/or unlikely/forbidden. Thus, oscillator strengths need to be determined. Further, excitonic binding energies (for allowed transitions) should be considered, as well as (other) many-body corrections which shift Kohn-Sham bands by quasiparticle formation. Here we study many-body and excitonic effects in some detail for the C2N bulk material.
Technically, in this case we first optimized the structure (lattice parameters and atom positions) using a (1× 1 × 1) cell and PBE+D3/PW (Vc = 600 eV), with VASP. The adopted stacking sequence was A–A–A⋯ as in ref. 9. By reoptimization, we found for the A–A stacking model a = b = 8.32 Å, c = 3.60 Å, α = β = 90°, γ = 120°. In ref. 9 (and above where we studied water adsorption) the angles were the same but a = b = 8.4 Å, c = 3.3 Å. Note that in particular the interlayer distance is somewhat larger in (our) theory, compared to ref. 9, and also compared to an experimental interlayer distance of 3.27 Å according to ref. 7. [Doubling the unit cell along c ((1× 1 × 2) cell) and considering an A–B–A–B⋯ stacked system instead, gives a slightly more stable structure (see above) with an interlayer distance of ∼3.3 Å on the PBE+D3 level of theory.] Since for C2N, in contrast to the H2O adsorption energies of above, the gap properties depend considerably on the interlayer distance (see below), we will report calculations in which we fixed the latter (i.e., the c lattice constant of a (1× 1 × 1) cell) to 3.27 Å instead.
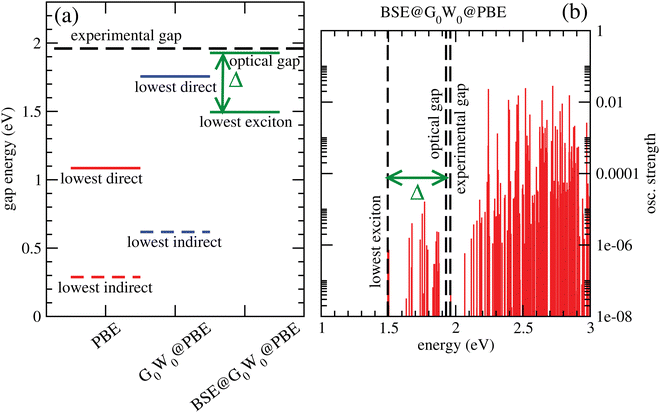
Fig. 6(a) shows lowest direct band gaps as solid bars and lowest indirect gaps as dashed bars, obtained from PBE (red) and G0W0 @PBE (blue), respectively. PBE and G0W0 @PBE calculations were done with a converged LAPW basis using the exciting code. Again the lowest direct gaps, representative for optical gaps, are too low with PBE (by ∼0.9 eV) compared to the experimental optical gap (1.96 eV).7 (HSE06, not shown, gave too large gaps as expected.) G0W0 @PBE corrects the PBE lowest direct gap to ∼1.8 eV.
From a BSE calculation on top of G0W0 @PBE, i.e., BSE@G0W0 @PBE, we get oscillator strengths and optical spectra for transitions from occupied (valence) bands into the conduction band. The onset of the continuum states with non-zero oscillator strengths above the last bound exciton state defines the “optical gap” in the figure. The bound exciton states at energies below the optical gap are due to electron-hole pair stabilization and quantization. The optical gap (1.93 eV), the lowest bound exciton state (1.50 eV) and the largest exciton binding energy, Δ = 0.43 eV are indicated in Fig. 6(a). The lowest-exciton state carries a small oscillator strength. In Fig. 6(b), we depict the situation for BSE@G0W0 @PBE in more detail, showing computed oscillator strengths along with lowest-exciton and optical gap energies. In the energy range shown (up to 3 eV), the largest oscillator strength is into states above the “optical gap”. The computed optical gap is in excellent agreement with the experimental value of 1.96 eV, the latter obtained from a Tauc plot in ref. 7. The agreement should be considered fortituous, given experimental uncertainties and also because theory could be improved substantially: One could go beyond non-self consistent G0W0, use better references than PBE, or account for broadening. Still, our analysis shows that the BSE optical gap is closer to experiment than any other measure so far, for C2N.
Two further points to mention: First, the calculated PBE-derived band gaps depend quite sensitively on the interlayer distance for A–A–A⋯ stacked C2N. For example, with c = 3.6 Å, one obtains an optical gap of about 2.8 eV with BSE@G0W0 @PBE. Second, the lowest direct band gap for C2N is not at the Γ-point according to our calculations.
a. HOMO–LUMO gaps and TD-DFT excitation energies. We now return to H-PHI, for which in Table 6 various gap measures obtained from cluster calculations are reported. By comparison with Table 5 it is first of all seen that the B3LYP/TZVP HOMO–LUMO gaps of clusters (“H–L gap”) grossly overestimate the measured optical gap for H-PHI, of 2.9 eV, and even the fundamental gap obtained from periodic calculations with functionals containing exact exchange. The HOMO–LUMO gap becomes even larger for smaller clusters (“1/2” vs. “large”, for example), which is to be expected.
| Model | Quantity | “Gap” (eV) | Comment |
|---|---|---|---|
| Large cluster, no H2O | H–L gap | 3.94 | (2.60 with PBE+D3/6-311G**) |
| Large cluster, 1H2O | H–L gap | 3.83 | (2.45 with PBE+D3/6-311G**) |
| 1/2 cluster, no H2O | H–L gap | 4.11 | (2.74 with PBE+D3/6-311G**) |
| Lowest transition | 3.35 | (TD-DFT, f = 0.01) | |
| Brightest transition | 4.28 | (TD-DFT, f = 1.70) | |
| 1/2 cluster, 1H2O | H–L gap | 4.08 | (2.60 with PBE+D3/6-311G**) |
| Lowest transition | 3.44 | (TD-DFT, f = 0.002) | |
| Brightest transition | 4.23 | (TD-DFT, f = 1.30) |
A better measure for electronic or optical band gaps are excitation energies beyond simple orbital energy differences, calculated at the TD-B3LYP/TZVP level of theory in the table and indicated there by “TD-DFT”. Shown are the lowest transitions for the 1/2 cluster only, with and without a water molecule (cf.Fig. 5). The lowest-energy transitions have only small oscillator strengths, f, followed by transitions with higher oscillator strengths. The former are essentially n → π* transitions, slightly allowed since the “1/2” cluster is not ideally flat (see above). The higher-energy, allowed transitions are π → π * excitations.
Attaching a water molecule to the cluster has only small effects (in the order of ∼ 0.1 eV or less) on HOMO–LUMO gaps and on TD-DFT excitation energies, in agreement with the periodic band gap calculations above. Further, all HOMO–LUMO gaps are significantly lower with PBE+D3/6-311G** compared to B3LYP+D3/TZVP, again as expected.
We also note that the lowest-energy transition for the “1/2” cluster, for example, is about 0.28 eV lower in energy than the B3LYP gap found in the periodic calculation (3.35 eV vs. 3.63 eV). Despite the same functional, a comparison of both values should be done with care, because models and methods are not the same. Still, a lowering of the gap in TD-DFT compared to simple band energy (or orbital energy) differences can be anticipated.
A final word about HOMO and LUMO energies, which are sometimes taken also as simple measures for valence band maxima and conduction band minima, respectively. For the water-free large cluster they are at −6.66 eV (HOMO) and −2.72 eV (LUMO) at B3LYP+D3/TZVP level, respectively, compared to the periodic B3LYP+D3/PW values giving VBM = −7.01 eV and CBM = −3.38 eV (cf.Table 5). Like the HOMO–LUMO gaps, they should therefore be taken with some care but may still be useful for predicting trends.
b. Convergence of excitation properties with cluster size. To address another aspect of calculating optical properties of C/N materials with cluster models, we consider g-C3N4. In Fig. 7, upper part, we show different representative cluster models for g-C3N4 of increasing size. What we call the “[2 × 2]” cluster there, is the same cluster model as shown in Fig. 3. Attaching more heptazine units while preserving the triangular shape gives clusters “[n × n]” with n = 3 to 6. For these, TD-DFT/6-311G** calculations with different functionals were performed, for n up to 4. For n up to 6 the semiempirical ZINDO58 method was used in addition for excited states. Due to the slightly distorted, non-planar nature of the clusters, even the very lowest transitions carry some oscillator strength. In the figure (lower panel), we show the wavelengths of the lowest-energy excitations for increasing n, in comparison to the experimental optical gap (horizontal dashed line).
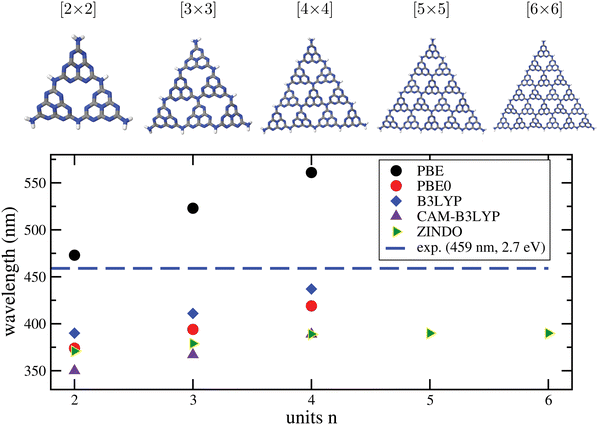 | ||
| Fig. 7 Upper part: Different [n × n] cluster models used in this work to characterize the optical properties of g-C3N4. As in Fig. 3, cluster structures were taken from the periodic calculations of ref. 16, and only the N–H distances were reoptimized, with PBE+D3/6-311G**. Lower panel: Wavelengths for the lowest-energy TD-DFT excitations obtained by TD-DFT/6-311G** (DFT = PBE, PBE0, B3LYP, CAM-B3LYP) and by the semiempirical ZINDO method, for various cluster sizes. The experimental gap (2.7 eV, 459 nm) is shown for comparison as a horizontal line. | ||
From there, we note the following. First, all methods show the onset of absorption being shifted to the red with increasing cluster size, as expected. A clearly convergent behaviour could only be observed for ZINDO at n ≥ 4, while for the “more expensive” TD-DFT methods up to n = 4 the redshift still continues.
Second, taking the n = 4 case as a reference, PBE is found to underestimate the optical gap, with a wavelength ∼100 nm too large compared to experiment. The hybrid functionals PBE0 and B3LYP perform better according to this criterion, in particular B3LYP, which is only 22 nm blue-shifted compared to experiment, for n = 4. On the other hand, the range-separated CAM-B3LYP functional predicts a blue-shift by 70 nm. We also mention that a comparison between theory and experiment is not always straightforward because some of the materials, like g-C3N4, are typically not fully polymerized as stated earlier.18 Not fully polymerized fragments are expected to give rise to larger excitation energies (lower wavelengths) according to Fig. 7.
c. WFT calculations for excited states and vibronic fine structures. We close our survey by testing correlated WFT methods for excited states and optical properties of C/N catalysts. For this purpose, we consider as a minimal cluster model for g-C3N4 a single heptazine molecule, with and without a water molecule attached. Note that heptazine is not only a model for a polymeric material, it works itself as a molecular photocatalyst, e.g., for water splitting.66,67 In Fig. 8(a), an optimized structure (on the B3LYP+D3/TZVP level) of the heptazine-water complex is shown. Further, in Table 7 we list singlet excitation energies (out of the S0 ground state) and corresponding oscillator strengths, obtained with various TD-DFT methods in comparison to WFT methods, ADC(2) and CC2. In upper and lower halves of the table heptazine without and with water is listed, respectively.
| Method | ADC(2) | CC2 | TD-CAM-B3LYP | TD-B3LYP | ||||
|---|---|---|---|---|---|---|---|---|
| E/eV | f | E/eV | f | E/eV | f | E/eV | f | |
| State | Heptazine, no water | |||||||
| S1 (ππ*) | 2.51 | 0.00 | 2.66 | 0.00 | 3.02 | 0.00 | 2.83 | 0.00 |
| S2 (nπ*) | 3.64 | 0.00 | 3.73 | 0.00 | 4.11 | 0.00 | 3.61 | 0.00 |
| S3 (nπ*) | 3.75 | 0.00 | 3.86 | 0.00 | 4.15 | 0.00 | 3.69 | 0.00 |
| S4 (nπ*) | 3.75 | 0.00 | 3.86 | 0.00 | 4.15 | 0.00 | 3.69 | 0.00 |
| S5 (π π*) | 4.41 | 0.29 | 4.73 | 0.28 | 4.96 | 0.25 | 4.59 | 0.15 |
| S6 (π π*) | 4.41 | 0.29 | 4.73 | 0.28 | 4.96 | 0.25 | 4.59 | 0.15 |
| S7 (nπ*) | 4.85 | 0.00 | 4.97 | 0.00 | 5.11 | 0.00 | 4.68 | 0.00 |
| State | Heptazine, with water | |||||||
| S1(ππ*) | 2.54 | 0.00 | 2.66 | 0.00 | 3.05 | 0.00 | 2.86 | 0.00 |
| S2 (nπ*) | 3.67 | 0.00 | 3.77 | 0.00 | 4.10 | 0.00 | 3.19 (CT) | 0.00 |
| S3 (nπ*) | 3.75 | 0.00 | 3.86 | 0.00 | 4.18 | 0.00 | 3.63 | 0.00 |
| S4 (nπ*) | 3.81 | 0.00 | 3.93 | 0.00 | 4.21 | 0.00 | 3.68 | 0.00 |
| S5 (ππ*) | 4.40 | 0.29 | 4.58 | 0.29 | 4.91 (CT) | 0.00 | 3.69 | 0.00 |
| S6 (ππ*) | 4.41 | 0.30 | 4.59 | 0.28 | 4.96 | 0.25 | 4.21 (CT) | 0.00 |
| S7 (nπ*) | 4.82 | 0.00 | 4.93 | 0.00 | 4.97 (ππ*) | 0.27 | 4.23 (CT) | 0.00 |
| S8 (nπ*) | 4.90 | 0.00 | 5.00 | 0.00 | 5.09 | 0.00 | 4.60 (ππ*) | 0.15 |
From there we see that up to relatively large energies (≥4 eV) singlet states are dark, with oscillator strengths zero or smaller than 0.01. This is due to the heptazine molecule being flat (making n → π* transitions forbidden) and small (causing large energy gaps), compared to polymeric g-C3N4, the latter buckled and with an optical gap of 2.7 eV (Table 1).
Second, we note bright states which are exactly or nearly degenerate between 4 and 5 eV for all methods. One also gets artifical water to heptazine charge transfer (CT) states in the heptazine-water complex, in particular for TD-B3LYP. One may expect such behaviour since this method is known to suffer from this problem.68 “True” excited CT states are found at higher energies according to the higher-level WFT methods, at ∼5.4 eV with ADC(2) and ∼5.6 eV for CC2 (not shown).
Third, we see that ADC(2) and CC2 give similar excitation energies and oscillator strengths, however, with ADC(2) lying typically 0.1–0.3 eV below the CC2 excitations, which we assume to be the most reliable. Due to artificial low-energy CT excitations for heptazine/water, the order of TD-DFT states differs from those obtained with WFT. TD-B3LYP excitation energies are quite similar to those of ADC(2), except for the lowest-energy excitations to S1, where TD-B3LYP predicts a higher excitation energy, by ∼ 0.3 eV. TD-CAM-B3LYP gives always clearly higher excitation energies than all other methods.
Fourth, from Table 7 we also realize that adding one molecule has only a small effect on the spectra in the energy range shown (apart from the occurrence of artificial CT states for some methods). As mentioned, at higher energies true CT states come into play.
We finally note that our CC2 excitation energies are in reasonable agreement with those presented in ref. 66. There, the water-heptazine complex was also studied by CC2, with a different geometry (based on MP2 optimization) and basis set, however.
As emphasized earlier, an advantage of cluster models for excited states is that a powerful machinery of accurate, molecular quantum chemistry methods is available, including the possibility to compute vibronically resolved spectra. We demonstrate this in Fig. 8(b) and (c) for heptazine with and without water, where vibrationally resolved absorption and emission spectra are shown for the lowest-energy bright transitions obtained with TD-CAM-B3LYP, i.e., S0 ↔ S5 for heptazine and S0 ↔ S6 for heptazine/water. Specifically, the so-called IMDHO (Independent Mode Displaced Harmonic Oscillator) method in a time-dependent correlation function framework was used,69,70 with a Lorentzian broadening scheme.
From the figures we first of all note that being of ππ*-type, the spectra are hardly affected by the presence of water, in the regime shown. More importantly, we realize that the vibrational broadening is – independent from the Lorentzian damping – large (in the order of ∼0.5 eV), and that maxima (other than at the 0–0 transition) are shifted by several tenths of an eV w.r.t. vertical excitation energies. This indicates that apart from excitonic effects, optical band gaps in C/N-based materials can also be affected by vibronic effects.
IV. Summary and conclusions
In this work, for three different layered materials based on unsaturated C/N networks, C2N, g-C3N4, and H-PHI, energetic, thermodynamic and optoelectronic properties have been computed, all related to the photo(electro)catalytic transformation of water. The focus was on studying the performance of various model chemistries (a combination of electronic structure method and basis set), and on the use of structural models (periodic vs. cluster). The most important findings are as follows.• Both periodic and cluster approaches have their specific advantages and disadvantages, regarding efficiency, range of applicability and accessible information.
• For predicting adsorption and reaction energies involving water and water fragments plus the corresponding thermodynamic properties, cluster models perform remarkably similar to periodic models, provided dangling bonds of the cluster are properly saturated. (Hydrogen saturation works well in most cases.) For these properties, also smaller (less than one pore) cluster models can be used for large-pore systems at least.
• For optoelectronic properties such as band gaps, optical excitation energies and spectra, the situation is less straightforward. For clusters, excitation energies depend strongly on their size, at least if delocalized over the substrate. The situation can be different for local excitations, of the adsorbate for example. Also, excitation energies and approximate methods to characterize them (e.g., HOMO–LUMO gaps), of clusters and extended periodic materials can be quite different from periodic calculations, admittedly because they are often based also on different model chemistries.
• Some of the more frequently applied standard model chemistries, notably gradient-corrected DFT with dispersion corrections, perform in general reasonably well when compared to experiments, however, they are not accurate enough for certain properties. In the context of water (fragment) adsorption, PBE+D3 for example overbinds somewhat compared to more accurate methods, such as correlated WFT like CCSD(T). It usually (but not always) overbinds also w.r.t. hybrid DFT like B3LYP (cf.Table 4).
• Decisive quantities for photo(electro)catalysis involving C/N materials, are electronic and optical band gaps and band positions, where GGA-DFT often fails (by predicting too small gaps, for example), and also hybrid-DFT does (by predicting tentatively too large gaps). To get accurate information, one has to go beyond Kohn-Sham theory. Further, the big scatter of results in Tables 5 and 6 shows that, great care has to be taken and also a clear distinction has to be made between electronic and optical gaps when comparing to experiment. (Other quantities related to catalysis can be reaction barriers in ground states, which are typically much too low with DFT-GGA and which were not separately considered here, see ref. 71 for a criticial study of this point.)
• On a more technical side, for cluster models with Gaussian basis sets the BSSE should be accounted for if the basis is not very large. Boundary effects should be minimized by proper saturation (see above). Sometimes also the (non-)planarity of the material found in experiment must be enforced when (too) small clusters are chosen. Further, both for the cluster and periodic approaches, single-layer models of layered C/N-based materials in contact with water are a reasonable starting point.
These findings serve as a critical basis for a systematic, comparative study of different C/N-based layered materials, which will be provided in a forthcoming paper.15
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank M. Oschatz (Jena) and A. Thomas (Berlin) for fruitful discussions. This work was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany's Excellence Strategy – EXC 2008/1-390540038. C. P. is grateful to the Alexander von Humboldt foundation for financial support.References
- W. Shen and W. Fan, J. Mat. Chem. A, 2013, 1, 999–1013 RSC.
- H.-W. Liang, X. Zhuang, S. Bruller, X. Feng and K. Müllen, Nat. Commun., 2014, 5, 4973 CrossRef CAS PubMed.
- X. Wang, K. Maeda, A. Thomas, K. Takanabe, G. Xin, J. Carlsson, K. Domen and M. Antonietti, Nat. Mater., 2009, 8, 76 CrossRef CAS PubMed.
- X. Wang, S. Blechert and M. Antonietti, ACS Catal., 2012, 2, 1596–1606 CrossRef CAS.
- Y. Gong, M. Li, H. Li and Y. Wang, Green Chem., 2015, 17, 715–736 RSC.
- J. Lin, Z. Pan and X. Wang, ACS Sustainable Chem. Eng., 2014, 2, 353–358 CrossRef CAS.
- J. Mahmood, E. K. Lee, M. Jung, D. Shin, I. Y. Jeon, S. M. Jung, H. J. Choi, J. M. Seo, S. Y. Bae, S. D. Sohn, N. Park, J. H. Oh, H. J. Shin and J. B. Baek, Nat. Commun., 2015, 6, 6486 CrossRef CAS PubMed.
- R. Walczak, B. Kurpil, A. Savateev, T. Heil, J. Schmidt, Q. Qin, M. Antonietti and M. Oschatz, Angew. Chem., Int. Ed., 2018, 57, 10765–10770 CrossRef CAS PubMed.
- R. Walczak, A. Savateev, J. Heske, N. Tarakina, S. Sahoo, J. Epping, T. Kühne, B. Kurpil, M. Antonietti and M. Oschatz, Sustainable Energy Fuels, 2019, 3, 2819–2878 RSC.
- S. Sahoo, J. Heske, M. Antonietti, Q. Qin, M. Oschatz and T. Kühne, ACS Appl. Energy Mater., 2020, 3, 10061–10069 CrossRef CAS PubMed.
- A. Savateev, D. Dontsova, B. Kurpil and M. Antonietti, J. Catal., 2017, 350, 203–211 CrossRef CAS.
- H. Schlomberg, J. Kröger, G. Savasci, M. W. Terban, S. Bette, I. Moudrakovski, V. Duppel, F. Podjaski, R. Siegel, J. Senker, R. Dinnebier, C. Ochsenfeld and B. Lotsch, ACS Chem. Mater., 2019, 31, 7478–7486 CrossRef CAS PubMed.
- B. Kurpil, Y. Markushyna and A. Savateev, ACS Catal., 2019, 9, 1531–1538 CrossRef CAS.
- M.-Y. Ye, S. Li, X. Zhao, N. Tarakina, C. Teutloff, W. Chow, R. Bittl and A. Thomas, Adv. Mater., 2020, 32, 1903942 CrossRef CAS PubMed.
- C. Penschke, A. Zehle, N. Jahn, R. E. von Zander, R. Neumann, D. Ojha, A. Beqiraj and P. Saalfrank, to be published.
- J. Wirth, R. Neumann, M. Antonietti and P. Saalfrank, Phys. Chem. Chem. Phys., 2014, 16, 15917–15926 RSC.
- S. Sahoo, I. Teixera, A. Naik, J. Heske, D. Cruz, M. Antonietti, A. Savateev and T. Kühne, J. Phys. Chem. C, 2021, 125, 13749–13758 CrossRef CAS PubMed.
- F. Fina, S. Callear, G. Carins and J. Irvine, Chem. Mater., 2015, 27, 2612 CrossRef CAS.
- J. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- P. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- H. Monkhorst and J. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- V. Blum, R. Gehrke, F. Hanke, P. Havu, V. Havu, X. Ren, K. Reuter and M. Scheffler, Comput. Phys. Commun., 2009, 180, 2175–2196 CrossRef CAS.
- B. Delley, J. Chem. Phys., 2000, 113, 7756 CrossRef CAS.
- J. Paier, M. Marsman, K. Hummer, G. Kresse, I. C. Gerber and J. G. Ángyán, J. Chem. Phys., 2006, 124, 154709 CrossRef CAS PubMed.
- J. Perdew, M. Ernzerhof and K. Burke, J. Chem. Phys., 1996, 105, 9982–9985 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS PubMed.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Chem. Phys., 1994, 98, 11623 CrossRef CAS.
- J. Heyd, G. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207 CrossRef CAS.
- J. Heyd, G. Scuseria and M. Ernzerhof, J. Chem. Phys., 2006, 124, 219906 CrossRef.
- W. Ku and A. G. Eguiluz, Phys. Rev. Lett., 2002, 89, 126401 CrossRef PubMed.
- T. Kotani and M. van Schilfgaarde, Solid State Commun., 2002, 121, 461–465 CrossRef CAS.
- F. Fuchs, J. Furthmüller, F. Bechstedt, M. Shishkin and G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 115109 CrossRef.
- A. Gulans, S. Kontur, C. Meisenbichler, D. Nabok, P. Pavone, S. Rigamonti, S. Sagmeister, U. Werner and C. Draxl, J. Phys.: Condens. Matter, 2014, 26, 363202 CrossRef PubMed.
- B. Aradi, B. Hourahine and T. Frauenheim, J. Phys. Chem. A, 2007, 111, 5678–5684 CrossRef CAS PubMed.
- M. Gaus, A. Goez and M. Elstner, J. Chem. Theory Comput., 2013, 9, 338–354 CrossRef CAS PubMed.
- A. Rappe, C. Casewit, K. Colwell, W. Goddard and W. Skiff, J. Am. Chem. Soc., 1992, 114, 10024–10035 CrossRef CAS.
- F. Jensen, Introduction to Computational Chemistry, Wiley, 2007 Search PubMed.
- G. Onida, L. Reining and A. Rubio, Rev. Mod. Phys., 2002, 74, 601–659 CrossRef CAS.
- F. Neese, J. Chem. Phys., 1994, 152, 224108 CrossRef PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian16 Revision C.01, Gaussian Inc., Wallingford CT, 2016 Search PubMed.
- TURBOMOLE V6.5 2013, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989-2007, TURBOMOLE GmbH, since 2007, available from https://www.turbomole.com.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- H. Jansen and P. Ros, Chem. Phys. Lett., 1969, 3, 140–143 CrossRef CAS.
- S. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566 CrossRef CAS.
- M. E. Casida, Time-Dependent Density Functional Response Theory for Molecules, in Recent Advances in Density Functional Methods, Chapter, 1995, pp. 155–192 Search PubMed.
- K. Raghavachari, G. Trucks, J. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 154, 479 CrossRef.
- C. Riplinger and F. Neese, J. Chem. Phys., 2013, 138, 034106 CrossRef PubMed.
- C. Riplinger, P. Sandhoefer, A. Hansen and F. Neese, J. Chem. Phys., 2013, 139, 134101 CrossRef PubMed.
- O. Christiansen, H. Koch and P. Jørgensen, Chem. Phys. Lett., 1995, 243, 409–418 CrossRef CAS.
- C. Hättig and F. Weigend, J. Chem. Phys., 2000, 113, 5154–5161 CrossRef.
- A. Dreuw and M. Wormit, WIREs Comput. Mol. Sci., 2015, 5, 82–95 CrossRef CAS.
- J. Ridley and M. Zerner, Theor. Chim. Acta, 1973, 32, 111–134 CrossRef CAS.
- T. Schäfer, A. Gallo, A. Irmler, F. Hummel and A. Grüneis, J. Chem. Phys., 2021, 155, 244103 CrossRef PubMed.
- E. Sargeant, F. Illas, P. Rodríguez and F. Calle-Valejo, J. Electroanal. Chem., 2021, 896, 115178 CrossRef CAS.
- A. Wang, R. Kingsbury, M. McDermott, M. Horton, A. Jain, S. Ong, S. Dwaraknath and K. Persson, Sci. Repts., 2021, 11, 15496 CrossRef CAS PubMed.
- J. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindquist, J. Kitchin, T. Bligaars and H. Jónsson, J. Phys. Chem. B, 2004, 108, 17886 CrossRef.
- R. E.-v Zander and P. Saalfrank, J. Phys. Chem. C, 2020, 124, 10239–10245 CrossRef PubMed.
- Á. Valdés, Z.-W. Qu, G.-J. Kroes, J. Rossmeisl and J. Nørskov, J. Phys. Chem. C, 2008, 112, 9872 CrossRef.
- Á. Valdés and G.-J. Kroes, J. Phys. Chem. C, 2010, 114, 1701 CrossRef.
- J. Ehrmaier, T. Karsili, A. Sobolewski and W. Domcke, J. Phys. Chem. A, 2017, 121, 4754–4764 CrossRef CAS PubMed.
- W. Domcke, A. Sobolewski and C. Schlenker, J. Chem. Phys., 2020, 153, 100902 CrossRef CAS PubMed.
- A. Dreuw and M. Head-Gordon, J. Am. Chem. Soc., 2004, 126, 4007–4016 CrossRef CAS PubMed.
- T. Petrenko and F. Neese, J. Chem. Phys., 2007, 127, 164319 CrossRef PubMed.
- S. Banerjee, T. Stüker and P. Saalfrank, Phys. Chem. Chem. Phys., 2015, 17, 19656–19669 RSC.
- S. Heiden, D. Usvyat and P. Saalfrank, J. Phys. Chem. C, 2019, 123, 6675–6684 CrossRef CAS.
| This journal is © the Owner Societies 2022 |