Non-intersecting ring currents in [12]infinitene

Abstract

The aromaticity of the newly synthesized [12]infinitene is addressed via analysis of the magnetically induced current density and the induced magnetic field. Our calculations reveal that [12]infinitene responds to an external magnetic field by creating two current-density pathways that flow diatropically along the edges of the molecule. The current-density pathways do not intersect. The entire structure is completely shielded suggesting that the infinitene molecule is aromatic, contrary to what the Möbius rule for twisted annulene structures predicts. We also studied the dication of [12]infinitene, which sustains two paratropic ring currents flowing along the edges. The space between the stacked rings at the crossing point is shorter for the dication as compared to the neutral molecule. Hence, a strong through-space current density appears at the crossing point of π–π stacked rings.

---

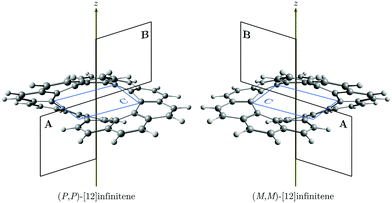
Recently, Krzeszewski et al. reported the synthesis of an infinity-shaped polyarylene with twelve six-membered rings (6-MRs) belonging to the D₂ point group.¹ The molecular structure can formally be obtained by fusing a [6]helicene with its chiral counterpart at their terminal rings. Consequently, [12]infinitene has two chiral isomers, i.e., (P,P)-infinitene and (M,M)-infinitene (see Fig. 1). They also noted that [12]infinitene can be considered as a twisted helical isomer of [12]circulene.¹

Fig. 1 The two enantiomers of [12]infinitene. Integration planes for calculation of current-density strengths are also shown. The A and B planes intersect a C–C bond at the edge of the molecule, while plane C is perpendicular to the z axis.

Among the family of novel non-planar aromatic systems, [12]infinitene represents an unexplored challenge to understand the three-dimensional electron delocalization. The 6-MRs experience π–π stacking due to the molecular topology, which has been shown to strongly affect the interpretation of the aromaticity because in general π–π stacked rings show strong magnetic shieldings.^2–4

It has been shown that twisted structures obey the Möbius rule for aromaticity, which is related to the topological number of twists in a closed structure through the so-called linking number (L_k), which can be further divided into the sum of the local twist (T_w) and non-local writhing (W_r) numbers.^5–7 The L_k number can be zero, a positive or a negative integer. L_k = 0 usually corresponds to a non-twisted structure, while L_k ≠ 0 leads to chiral structures with several twists and deformations of the ring. The L_k number determines the aromatic character, whereas the degree of aromaticity is determined by T_w.^5–7 The twist, writhing, and linking numbers are multiplied by π to get their corresponding angles in radians.⁸ Molecules with even L_k have the π-electron counting classification of Hückel's aromaticity rule. For odd L_k values, molecules with 4n π electrons are expected to be aromatic, while those with 4n + 2 electrons will favor open-shell configurations or antiaromaticity.^9–11 The (P,P) and (M,M) structures of infinitene are mirror images corresponding to the case where L_k = ±2 (T_w = ±0.57 and W_r = ±1.43). They are double twisted molecules with two faces and 48 π electrons delocalized around the ring. Hence, according to the above rules they are expected to be antiaromatic. The Hückel 4n + 2 and Möbius 4n aromaticity rules are derived from the Hückel energy spectrum of annulenes. Hückel's aromaticity rule also holds for planar, approximately circular molecules because the aufbau principle involves σ, π, δ, orbitals leading to magic electronic numbers of 4n + 2 electrons for closed-shell molecules. However, infinitene does not belong to these classes of molecules.

Diagonalization of the Hückel Hamiltonian of infinitene shows that it is a closed-shell molecule with a large energy gap between the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) suggesting that its aromatic character cannot be estimated based on the Hückel and Möbius aromaticity rules. Planar circulenes exhibit concentric counter-rotating currents,^12,13 making simple classifications of the aromaticity of infinitene even harder. In the study by Krzeszewski et al.,¹ nucleus-independent chemical shift (NICS) calculations¹⁴ on [12]infinitene suggest that the aromatic character varies from one ring to another. However, NICS(0) calculations on non-planar molecules, especially in helical structures, are not reliable for elucidating the π delocalization, since they only give a very local picture of the magnetic behavior.^4,15

In this work, we study the magnetic response of [12]infinitene in the presence of an external magnetic field by analyzing the magnetically induced current density and the induced magnetic field. Our calculations reveal that (P,P)- and (M,M)-infinitene respond to the external magnetic field by creating two current-density pathways that flow diatropically along the edges of the molecule. The current-density pathways do not intersect. They create a shielding cone over the entire structure suggesting that [12]infinitene is aromatic. The picture of the electron delocalization and aromatic character is clearer when considering only the π electron component of the magnetic response. The calculations suggest that all rings have approximately the same degree of electron delocalization since there are only global ring currents along the edges of the molecule rather than local π circulations in each of the 6-MRs. The current density is reminiscent of the one of helicenes.^16,17 We also consider the dication of [12]infinitene to study how oxidation affects the magnetic response.

Since hybrid long-range corrected functionals in conjunction with the D3(BJ) dispersion correction yield energies of stacked π–π structures in good agreement with CCSD(T) calculations,¹⁸ all molecular structures were fully optimized at the CAM-B3LYP-D3(BJ) level using the def2-TZVP basis set.^19–21 The calculated and experimental molecular structure agree well. The structural parameters differ by less than 0.02 Å.¹ The Cartesian coordinates of the optimized structures are given in the ESI.† Magnetic properties computed with hybrid functionals have been found to be in close agreement with those calculated at the CCSD(T) level.^5,22–24 The nuclear magnetic resonance (NMR) computations were carried out at the CAM-B3LYP level using the def2-SVP and the def2-TZVP basis sets²¹ in conjunction with gauge-including atomic orbitals (GIAOs).^25,26 Calculated shielding constants are given in the ESI.† All these calculations were performed with the Turbomole program.^27,28

The magnetically induced current density (J^ind),^29–32 and the induced magnetic field^33–35 (B^ind) were computed using the gauge-including magnetically induced currents (GIMIC) method^29–31 and the Aromagnetic³⁶ program, respectively. The Aromagnetic program calculates the induced magnetic field in each point of a three-dimensional grid with the molecule at the center. Thus, with the Aromagnetic program one is able to calculate one-dimensional profiles, two-dimensional isolines or isosurfaces of the magnetic shielding function.^4,16,37 The GIMIC program can be used for calculating ring-current strengths, which are obtained by integrating the current-density flowing through a plane intersecting one or several chemical bonds.^29–31,38 The integration planes used in this study are shown in Fig. 1. We have also used the inexpensive pseudo-π model to approximate the π electron contribution to J^ind and B^ind (^pπJ^ind and ^pπB^ind, respectively).^16,39,40 The pseudo-π modeled response was obtained by calculating the magnetic response using the optimized molecular structure where the hydrogens were erased and the carbon atoms were replaced by hydrogen atoms in the same positions. A unit external field (|B^ext| = 1T) was applied parallel to the symmetry axis of the molecule, which coincides with the z axis, to induce ring currents and magnetic shielding.⁴¹ For this direction of the external magnetic field, the z component is the most important Cartesian contribution to B^ind (B_z^ind). Hence, the B^ind analysis can be reduced to B_z^ind. The unit for the ring-current (susceptibility) strength is nA/T, while B_z^ind is given in ppm. For visualization purposes, the skeleton shown in the figures of the pseudo-π magnetic response correspond to the original carbon structure instead of the all-hydrogen system.

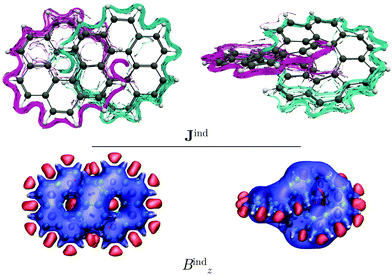
Coronene has a paratropic ring current flowing along the inner contour in the non-classical direction and a diatropic ring current flowing along the outer edge in the classical direction.¹³ Circulenes such as corannulene or kekulene also exhibit this kind of magnetic behavior.^16,42 However, for the latter small local circulations appear in some of the 6-MRs. Helicenes can be understood as three-dimensional broken circulenes. [7]Helicene responds to an external magnetic field by producing a diatropic helical ring current which changes its relative direction near the helical axis giving rise to an inner deshielding cone.^4,16 The question is whether there will be similar current-density pathways in infinitene since it formally consists of two fused helicenes. When the external magnetic field is parallel to the z axis, i.e., parallel to the symmetry axis shown in Fig. 1, [12]infinitene responds by sustaining two diatropically non-intersecting ring currents flowing along the peripheral carbons as shown in Fig. 2.

Fig. 2 The magnetic response of (P,P)-infinitene computed at the CAM-B3LYP/def2-SVP level. In the top panel: Streamlines and vector representation of the total J^ind, showing the two non-intersecting current-density pathways in pink and green, respectively. In the bottom panel: Isosurfaces of the total B_z^ind. The shielding (−10 ppm) and deshielding (+10 ppm) cones are shown in blue and red, respectively. The external field is parallel to the z axis, which is perpendicular to the molecule in the left picture.

The aromatic character of [12]infinitene can be understood when considering that it sustains two almost independent ring currents along the outer edges of the molecule. The two conjugation pathways fulfil the rule of cylindrical aromaticity.^31,43,44 The linear combination of the π orbitals along the two pathways can be positive or negative similar to even and odd parity. The aufbau principle then leads to a closed-shell system and aromaticity with 4n π electrons.³¹ Since [12]infinitene is doubly twisted with L_k = ±2, the twisted structure has the same aromaticity rules as a non-twisted one with L_k = 0.

[12]Infinitene is aromatic rather than non-aromatic because the size of the ring-current loop is smaller in one half of the molecule, where the ring current takes the inner curve. The ring current flows there in the non-classical direction even though it is diatropic. Since the loop with the classical direction of the ring current is larger, the global ring current becomes diatropic leading to aromaticity. In case the two loops are of equal size, the contradicting directions of the ring current in the two loops would lead to non-aromaticity. The driving force of the ring current originates from the different size of the ring-current loops.

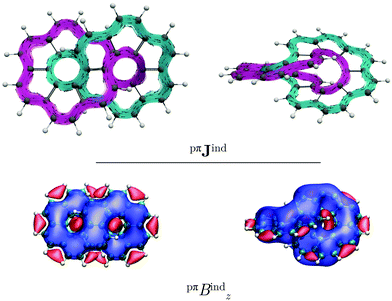
Similar to helicenes, local deshielding cones (in red) appear in the middle of the two loops of the eight-shaped structure due to different relative directions of the ring current, whereas the magnetic shielding appears along the whole molecular structure (see Fig. 2). This can be seen more clearly when studying the magnetic response using the pseudo-π model because it does not consider the local σ currents in the middle of the 6-MRs and along the C–C bonds (see Fig. 3). The pseudo-π current density reveals the flux of delocalized π electrons in planar and three-dimensional organic molecules.^16,39,45,46 An interactive visualization of the non-intersecting current-density flux in [12]infinitene is shown by animations in the ESI.† Since infinitene has a three-dimensional molecular structure, we also study its magnetic response when the external field is parallel to the y axis. Infinitene consists of a single molecular ring when it is viewed in that direction. However, since the direction of the p orbitals is perpendicular to the magnetic field, J^ind consists mainly of local diatropic circulations at the individual 6-MRs and a diatropic flux along that single molecular ring (see Fig. S1 in the ESI†). Qualitatively the same current densities are obtained in the current-density calculation as well as when employing the pseudo-π model (see Fig. S1 and S2, ESI†). The y component to B^ind (B_y^ind) has local shielding over the whole carbon skeleton.

Fig. 3 The magnetic response in (P,P)-infinitene obtained with the pseudo-π model computed at the CAM-B3LYP/def2-SVP level. In the top panel: Streamlines and vector representation of the ^pπJ^ind, showing the two non-intersecting current-density pathways in pink and green, respectively. In the bottom panel: Isosurfaces of ^pπB_z^ind. The shielding (−10 ppm) and deshielding (+10 ppm) cones are shown in blue and red, respectively. The external field is parallel to the z axis, which is perpendicular to the molecule in the left picture.

Integrating the current density yields a ring-current strength of 12.74 nA T⁻¹, while with the pseudo-π model, a ring-current strength of 12.82 nA T⁻¹ is obtained (see Table 1). These values agree well with those obtained for benzene,^16,29 suggesting that the degree of aromaticity is about the same as for benzene. (M,M)-[12]infinitene and (P,P)-[12]infinitene have identical magnetic response (see Fig. S3 and S4, ESI†). Since the separation between the crossing polyarylene moieties is only 2.96 Å at CAM-B3LYP-D3(BJ)/def2-TZVP level, the ring current may take a shortcut across the narrow gap between them. The integrated current density passing through space between the crossing polyarylene moieties is 6.09 nA T⁻¹. The strength of the through-space current density of the chiral (M,M) enantiomer is equal but it seems to flow in the opposite direction but with the same global tropicity as the (P,P) enantiomer. The pseudo-π calculations on the neutral isomers result in a small through-space flux of 2.09 nA T⁻¹. The global ring current vanishes when the external magnetic field is parallel to the y axis.

Table 1 Ring-current strengths (in nA/T) of (P,P)-infinitene (neutral and dication) divided into their diatropic and paratropic components calculated at the CAM-B3LYP/def2-TZVP level when the external field points parallel to z axis. The ring-current strengths of the (M,M) and (P,P) enantiomers of [12]infinitene are identical. The ring-current strength passing plane A and B are equal. The position of the integration planes are shown in Fig. 1. The ring-current strengths obtained for dication with the pseudo-π model are not reported because they are not reasonable

Molecule	Plane	Total				Pseudo-π
		Diatropic	Paratropic	Net	Diatropic	Paratropic	Net
(P,P)	A	16.99	−4.24	12.74	12.82	0.0	12.82
	C	6.52	−0.42	6.09	2.33	−0.24	2.09
(P,P)^2+	A	4.01	−50.51	−46.50	—	—	—
	C	7.18	−52.98	−45.80	—	—	—

---

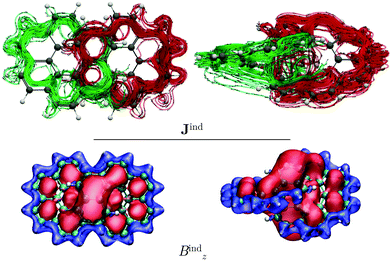
We also studied the magnetic response of the [12]infinitene dication because the structure optimization at the CAM-B3LYP-D3(BJ)/def2-TZVP level yielded a slightly shorter separation of 2.91 Å between the polyarylene moieties at the crossing point. Current-density calculations show that the dication sustains two paratropic ring currents around the edge of the projected coronene-like structures. The paratropic ring current takes a shortcut route via a strong through-space ring current of −46 nA T⁻¹ between the stacked π–π rings at the crossing point (see Fig. 4). This is also reflected in the B_z^ind calculations, which show a strong deshielding cone above 6-MRs indicating an antiaromatic behavior. Consequently, drastic changes rise on the shieldings of the nuclei as compared to those of the neutral infinitene (see ESI†). The resulting NMR chemical shifts for the neutral and charged infinitene are in good agreement with the experimental chemical shifts reported by Krzeszewski et al.¹

Fig. 4 The magnetic response of the (P,P)-infinitene dication computed at the CAM-B3LYP/def2-SVP level. In the top panel: Streamlines and vector representation of the total J^ind, showing the two non-intersecting current-density pathways in red and green, respectively. Isosurfaces of the total B_z^ind are shown in the bottom panel. The shielding (−25 ppm) and deshielding (+25 ppm) cones are shown in blue and red, respectively. The external field is parallel to the z axis, perpendicularly to the left view.

The integration of the current-density on the dication yielded a ring-current strength of −46.5 nA T⁻¹. When the external magnetic field is applied parallel to y axis, largely the same topology of the current density is obtained for the dication as for the neutral molecule. However, the local ring currents at the 6-MRs and the single molecular ring are paratropic (see Fig. S5, ESI†).

Calculations on the charged [12]infinitene using the pseudo-π model display an aromatic-like magnetic behavior, which does not agree with the current density obtained in the all-electron magnetic response calculations (see Fig. S6, ESI†). The pseudo-π calculations on the dication of [12]infinitene yield a very strong ring current of 312 nA T⁻¹ and exaggerated magnetic shielding suggesting that pseudo-π calculations on the charged molecule are not reliable. The reason may be that the two missing electrons of the dication can be compensated by the rest of the electrons in the all-electron calculation, whereas at the pseudo-π level, the screening effect is weaker or even absent because the model has only one electron per carbon site.

Conclusions

We analyzed the magnetic response of [12]infinitene and its dication by calculating the magnetically induced current density and the induced magnetic field for both of (P,P) and (M,M) enantiomers. The neutral [12]infinitene sustains two ring currents along the edges of the entire molecule. The two current-density pathways never cross, which is even clearer seen when visualizing the current density sustained by the π orbitals at the pseudo-π level. The neutral [12]infinitene molecule is aromatic since it can be considered as a doubly twisted molecule fulfilling the rule of cylindrical aromaticity. Analysis of the calculated induced magnetic field reveals that [12]infinitene is shielded along the polyarylene skeleton, whereas a small deshielding cone appears in the center of the two loops of the eight-shaped structure, similar to helicenes. The magnetic response of both enantiomers is identical.

We also studied the magnetic response of the [12]infinitene dication. The calculations showed that the dication sustains two strong paratropic ring currents along the outer edges of the two projected coronene-like structures via a through-space current-density pathway. The two paratropic ring currents are about four times stronger than the two diatropic ring currents along the edges around the entire neutral molecule. The strong through-space current-density pathway makes shortcuts between the stacked benzene rings at the crossing point in the middle of the molecule. The neutral molecule has a through-space current-density pathway, which is diatropic and much weaker than in the dication.

These calculations indicate that the neutral and dication infinitene are globally aromatic and antiaromatic, respectively, contrary to what is expected based on the Möbius aromaticity rule for annulenes. [12]Infinitene does not obey the Möbius and Hückel aromaticity rules, since it is not an annulene but a polyarylene with two nearly independent ring-current pathways suggesting that 4n π electrons lead to aromaticity. The aromaticity of new twisted structures^47–49 must be addressed carefully, taking into consideration the magnetic response properties, since counting the number of π electrons in the delocalization pathway may lead to incorrect conclusions concerning their aromatic character.

Author contributions

M. O.-I. and R. R. V. suggested current-density studies of infinitene. M. O.-I. and D. S. performed the calculations. All authors discussed the results and contributed to the final manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work has been supported by the Academy of Finland through project numbers 314821 and 340583, by the Magnus Ehrnrooth Foundation, Waldemar von Frenckell's foundation, and the Swedish Cultural Foundation in Finland. We acknowledge computational resources from the Finnish Grid and Cloud Infrastructure (persistent identifier urn:nbn:fi:research-infras-2016072533) and the CSC – IT Center for Science, Finland. R. R. V. thanks the Ministry of Education and Science of the Russian Federation Program No. 075-03-2021-287/6 and Academy of Finland through project number 340582.

Notes and references

1. M. Krzeszewski, H. Ito and K. Itami, J. Am. Chem. Soc., 2022, 144, 862–871.
2. G. Portella, J. Poater, J. M. Bofill, P. Alemany and M. Solà, J. Org. Chem., 2005, 70, 2509–2521.
3. D. Sundholm, M. Rauhalahti, N. Özcan, R. Mera-Adasme, J. Kussmann, A. Luenser and C. Ochsenfeld, J. Chem. Theory Comput., 2017, 13, 1952–1962.
4. M. Orozco-Ic, J. Barroso, N. D. Charistos, A. Muñoz-Castro and G. Merino, Chem. – Eur. J., 2019, 26, 326–330.
5. L. N. Wirz, M. Dimitrova, H. Fliegl and D. Sundholm, J. Phys. Chem. Lett., 2018, 9, 1627–1632.
6. F. B. Fuller, Proc. Natl. Acad. Sci. U. S. A., 1978, 75, 3557–3561.
7. F. B. Fuller, Proc. Natl. Acad. Sci. U. S. A., 1971, 68, 815–819.
8. S. M. Rappaport and H. S. Rzepa, J. Am. Chem. Soc., 2008, 130, 7613–7619.
9. H. S. Rzepa, Chem. Rev., 2005, 105, 3697–3715.
10. P. W. Fowler and H. S. Rzepa, Phys. Chem. Chem. Phys., 2006, 8, 1775–1777.
11. S. Martín-Santamaría and H. S. Rzepa, Chem. Commun., 2000, 1503–1504.
12. A. Acocella, R. W. A. Havenith, E. Steiner, P. W. Fowler and L. W. Jenneskens, Chem. Phys. Lett., 2002, 363, 64–72.
13. E. Steiner, P. W. Fowler and L. W. Jenneskens, Angew. Chem., Int. Ed., 2001, 40, 362–366.
14. Z. Chen, C. S. Wannere, C. Corminboeuf, R. Puchta and P. V. R. Schleyer, Chem. Rev., 2005, 105, 3842–3888.
15. G. Monaco and R. Zanasi, J. Phys. Chem. Lett., 2017, 8, 4673–4678.
16. M. Orozco-Ic, M. Dimitrova, J. Barroso, D. Sundholm and G. Merino, J. Phys. Chem. A, 2021, 125, 5753–5764.
17. S. A. E. Cherni, B. Champagne and V. Liégeois, Phys. Chem. Chem. Phys., 2019, 21, 14678–14691.
18. S. Tsuzuki and T. Uchimaru, Phys. Chem. Chem. Phys., 2020, 22, 22508–22519.
19. T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57.
20. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
21. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
22. R. R. Valiev, H. Fliegl and D. Sundholm, Chem. Commun., 2017, 53, 9866–9869.
23. R. R. Valiev, I. Benkyi, Y. V. Konyshev, H. Fliegl and D. Sundholm, J. Phys. Chem. A, 2018, 122, 4756–4767.
24. S. Lehtola, M. Dimitrova, H. Fliegl and D. Sundholm, J. Chem. Theory Comput., 2021, 17, 1457–1468.
25. R. Ditchfield, Mol. Phys., 1974, 27, 789–807.
26. K. Wolinski, J. F. Hinton and P. Pulay, J. Am. Chem. Soc., 1990, 119, 8251–8260.
27. R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165–169.
28. F. Furche, R. Ahlrichs, C. Hättig, W. Klopper, M. Sierka and F. Weigend, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 91–100.
29. J. Jusélius, D. Sundholm and J. Gauss, J. Chem. Phys., 2004, 121, 3952–3963.
30. H. Fliegl, S. Taubert, O. Lehtonen and D. Sundholm, Phys. Chem. Chem. Phys., 2011, 13, 20500–20518.
31. D. Sundholm, H. Fliegl and R. J. F. Berger, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2016, 6, 639–678.
32. D. Sundholm, M. Dimitrova and R. J. F. Berger, Chem. Commun., 2021, 57, 12362–12378.
33. G. Merino, T. Heine and G. Seifert, Chem. – Eur. J., 2004, 10, 4367–4371.
34. T. Heine, R. Islas and G. Merino, J. Comput. Chem., 2007, 28, 302–309.
35. R. Islas, T. Heine and G. Merino, Acc. Chem. Res., 2012, 45, 215–228.
36. M. Orozco-Ic, J. L. Cabellos and G. Merino, Aromagnetic, CINVESTAV-Mexico, 2016.
37. M. Orozco-Ic, C. A. Celaya and D. Sundholm, RSC Adv., 2020, 10, 18124–18130.
38. J. Jusélius and D. Sundholm and co-workers, GIMIC, Gauge-Including Magnetically Induced Currents, a stand-alone program for the calculation of magnetically induced current density., https://github.com/qmcurrents/gimic.
39. P. W. Fowler and E. Steiner, Chem. Phys. Lett., 2002, 364, 259–266.
40. N. D. Charistos, A. Muñoz-Castro and M. P. Sigalas, Phys. Chem. Chem. Phys., 2019, 21, 6150–6159.
41. F. A. L. Anet and D. J. OLeary, Concepts Magn. Reson., Part A, 1991, 3, 193–214.
42. E. Steiner, P. W. Fowler, A. Acocella and L. W. Jenneskens, Chem. Commun., 2001, 659–660.
43. M. P. Johansson, J. Phys. Chem. C, 2009, 113, 524–530.
44. S. Taubert, D. Sundholm and F. Pichierri, J. Org. Chem., 2010, 75, 5867–5874.
45. M. Orozco-Ic and G. Merino, Chemistry, 2021, 3, 1381–1391.
46. M. Antić, S. Đorđević, B. Furtula and S. Radenković, J. Phys. Chem. A, 2020, 124, 371–378.
47. R. G. Clevenger, B. Kumar, E. M. Menuey and K. V. Kilway, Chem. – Eur. J., 2018, 24, 3113–3116.
48. W. Fan, T. Matsuno, Y. Han, X. Wang, Q. Zhou, H. Isobe and J. Wu, J. Am. Chem. Soc., 2021, 143, 15924–15929.
49. K. Itami, Y. Segawa, T. Watanabe, K. Yamanoue, M. Kuwayama, K. Watanabe, J. Pirillo and Y. Hijikata, ChemRxiv, 2021 DOI:10.26434/chemrxiv-2021-w09lc.

---

Footnote

† Electronic supplementary information (ESI) available: Cartesian coordinates of the optimized molecular structures, isotropic magnetic shielding constants, chemical shifts, and pictures of magnetically induced current densities and magnetic shielding functions are reported. Animations of the current-density plots are also provided. See DOI: 10.1039/d2cp00637e

---