Providing theoretical insight into the role of symmetry in the photoisomerization mechanism of a non-symmetric dithienylethene photoswitch

Abstract

Dithienylethene (DTE) molecular photoswitches have shown to be excellent candidates in the design of efficient optoelectronic devices, due to their high photoisomerization quantum yield (QY), for which symmetry is suggested to play a crucial role. Here, we present a theoretical study on the photochemistry of a non-symmetric dithienylethene photoswitch, with a special emphasis on the effect of asymmetric substitution on the photocyclization and photoreversion mechanisms. We used the Spin-Flip Time Dependent Density Functional Theory (SF-TDDFT) method to locate and characterize the main structures (conical intersections and minima) of the ground state and the first two excited states, S₁ and S₂, along the ring-opening/closure reaction coordinate of the photocyclization and photoreversion processes, and to identify the important coordinates governing the radiationless decay pathways. Our results suggest that while the main features that characterize the photoisomerization of symmetric DTEs are also present for the photoisomerization of the non-symmetric DTE, the lower energy barrier on S₁ along the cycloreversion reaction speaks in favor of a more efficient and therefore a higher cycloreversion QY for the non-symmetric DTEs, making them a better candidate for molecular optoelectronic devices than their symmetric counterparts.

---

1 Introduction

Dithienylethenes (DTEs) are a type of photochromic molecules which can switch between two stable isomers using light. This photoswitching behavior takes place through a cyclization (open-ring (O) to closed-ring (C) isomer) induced by the light absorption in the range of UV and a cycloreversion reaction (closed-ring to open-ring isomer) in the visible range^1,2 (see Fig. 1). Each isomeric form has different electronic properties, for example, in the open-ring, the discontinuity between the π-systems of the thiophene-rings causes a poor electronic interaction between the thiophene-rings and consequently to the functional groups attached (see Fig. 1). Instead, in the closed-ring, the π-systems of the thiophene-rings are continuous; this creates a delocalization of the π-electrons over the whole molecule^2–5 making the conductivity between the thiophene-rings easier. Additionally, DTEs show high fatigue resistance,^2,6 thermal irreversibility,^2,6 and large quantum yield (QY) of photoisomerization.² These features make them excellent candidates for developing modern technologies, for example, application of molecular photoswitches^1,2 and photomolecular motors^2,7 in nanomachines⁸ and molecular electronic devices.^7,9–11

Fig. 1 Chemical structure of the DTE studied in this work. Left side represents the open-ring and right side represents the closed-ring. The numbers in the isomers describe the chromophores CHD and cZc-HT, respectively. The torsion angles (in red) ϕ₁ and ϕ₂ are determined by the dihedral angles ∠C₁–C₆–C₅–C₄ and ∠C₂–C₃–C₄–C₅, respectively.

Several authors have studied numerous DTE derivatives from both experimental^{1–4,11–18} and theoretical^{1,2,5,16–25} perspectives for more than three decades. Although many aspects of DTEs have been clarified, the control of the QY of the photocyclization and photoreversion is still a puzzle. In this respect, it has been observed experimentally that the photoisomerization QY is highly dependent on the substituent groups that are attached to the thiophene-rings.²⁶ Furthermore, photocyclization and photoreversion processes of DTEs take place in a small volume space as well as in the range of the picoseconds.^11,27 Additionally, most DTEs do not show emission,²³ suggesting the internal conversion process, mediated by conical intersections (CIs), as an active excited-state non-radiative decay channel.^2,17,21

CIs play an essential role in the excited-state deactivation process of the central backbone of DTEs, the cyclohexadiene (CHD) chromophore.²¹ In fact, the photoisomerization of the CHD triggers the photochromic switching behavior in the DTEs.²⁸ It is known that the photochemical interconversion of CHD (isolated) occurs at least through two CIs,^29–34 and recently we have proposed an alternative deactivation path through a third CI 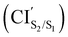.³⁴ Nowadays, it is generally accepted that in DTEs (specifically, symmetric DTEs, i.e. DTEs where the attached substituent groups to thiopheny groups are the same), the photocyclization reaction takes place as follow² (see Fig. 2): upon photoexcitation of the open-ring to the bright state S₁ (this state belongs to the irreducible representation 1¹B under C₂ symmetry in a symmetric DTE), a rapid decay undergoes on the excited state 1¹B followed by an internal conversion to the excited state 2¹A via a CI. Afterwards, the DTE moves along 2¹A, until it reaches the CI_{S1(2¹A)/S0(1¹A)}. Once this crossing is reached, a decay occurs to either the ground state of the closed-ring or the open-ring. Likewise, the photoreversion process starts after the photoexcitation on the closed-ring has reached the Franck-Condon (FC) region in state S₁ (this state belongs to the irreducible representation 1¹B under C₂ symmetry in a symmetric DTE). It is subjected a rapid decay until the DTE undergoes an internal conversion to the excited state 2¹A via a CI. After this CI, the reaction encounters an energy barrier (up to 4.2 kcal mol^{−1 2,35–37} from a local minimum on 2¹A) in 2¹A before the DTE reaches the same CI_{S1(2¹A)/S0(1¹A)} of the photocyclization reaction. From there, a decay occurs to either the ground state of the open-ring or the closed-ring.

Fig. 2 Schematic representation of the photocyclization and the photoreversion reactions of a symmetric DTE. The dashed lines represent the crossing between excited states S₂(2¹A) and S₁(1¹B), and S₁(2¹A) and the ground state S₀(1¹A). FC, C and O refer to the Franck-Condon region, closed-ring and open-ring, respectively. Adopted from Fig. 5 of ref. 2.

In order to locate and characterise these CIs, theoretical works have been performed on various DTEs, using multireference wavefunction methods,^17,23,38,39 semi-empirical methods^12,40 and time dependent density functional theory (TDDFT).^1,41–43 The complete active space self-consistent field method (CASSCF) is one the most used multireference methods to study photoisomerisation processes of DTEs.^2,28 Calculations based on these method by Boggio-Pasqua et al.²¹ and Asano et al.²³ show the importance of the CIs in the photoisomerization reaction of DTEs during the photoreversion process. Although the results obtained using CASSCF method are consistent with experimental findings (in the region after the local minimum on S₁(2¹A)) explaining the correlation between the QY of photoreversion with the substituent groups that are attached to the thiophene-rings,^2,17,23 it fails to reproduce the correct order of the states S₁(1¹B) and S₂(2¹A) in the FC region.^17,21,23 This fact has restricted the use of the CASSCF method to study this mechanism to the states S₁(2¹A) and S₀(2¹A). This behavior has been reported in previous works focused on the photochemistry of the CHD chromophore.^44–47 The second-order perturbation theory for the CASSCF method (CASPT2) is also a multireference method widely used to study photoisomerisation processes of DTEs.^2,23,28 The lack of dynamical correlation in CASSCF that is incorporated in CASPT2 shows a correct order of the S₁(1¹B) and S₂(2¹A) in the FC region.²³ It is known that in the photochemical processes, the adequate balance of both dynamical and non-dynamical correlation plays a fundamental role, for example, in the correct description of the energies and CIs.^21,33,40,48 Recently, Jankowska et al.⁴⁰ used a semi-empirical method called orthogonalization- and dispersion-corrected multireference configuration interaction approach (ODM2/MRCI)^49–52 which allowed to fully include both non-dynamic and dynamic correlation effects. Their results provide for the first time a detailed description of the role of both correlations in the photochemistry of DTEs.

Single reference character methods, such as DFT and TDDFT, have the capability to describe the dynamic correlation energy. Additionally, it has been shown that, for DTEs,^19,24 TDDFT is able to describe the right ordering for the S₁(1¹B) and S₂(2¹A) states in the FC region. However, these methods have some important limitations, for example, they can not recover the non-dynamic correlation as well as serious problems to describe CIs^53,54 (at least CIs between the ground and the excited states), where multi-reference description is a necessary component. An extension to TDDFT proposed by Shao et al.,⁵⁵ called spin-flip time-dependent density functional theory (SF-TDDFT), developed to describe diradicals with strong nondynamical correlation, has shown a great performance for describing CIs in ethylene,⁵⁶ uracil,⁵⁷cis-stilbene,⁵⁸ CHD³⁴ and recently light-driven rotary molecular motors.⁵⁹ Within this approach, a high-spin triplet state is chosen as the initial reference state allowing that the S₀ and the singlet excited states to be treated at the same footing. SF-TDDFT recovers both nondynamical and dynamical correlation from SF and DFT, respectively.^55,60 These features have made SF-TDDFT a great alternative to address photochemical processes.

Our recent theoretical study³⁴ on the photochemical interconversion between cyclohexadiene and hexatriene has shown that SF-TDDFT can successfully describe and characterize the most important geometries on the potential energy surfaces along the ring-opening/closure reaction coordinate, in an agreement with those obtained by multireference wavefunction methods. Our benchmark calculations on the two fisrt excited states of the CHD revelas that SF-TDDFT, in particular in combination with the BHHLYP functional (see ref. 34 and the Table 1 in the ESI†) shows a reasonable performance compared with wavefunction-based method (XMS-CASPT2⁶¹ and ADC(2)⁶²) and experimental results, suggesting that SF-TDDFT could be a good low-cost method to study complex molecules that contain the CHD chromophore as their central backbone, such as the DTE molecules considered here (Fig. 1).

Table 1 Energies (in eV), C₁–C₂ bond distances (in Å) and torsion angles (in degrees) for the important geometries of the S₀, S₁ and S₂ PESs obtained with ωB97X-D/cc-pVDZ for the ground state and with SF-BHHLYP/cc-pVDZ for the excited states, in gas phase. The energies are relative to S_0min energy of the open-ring. C and O in parenthesis stand for closed-ring and open-ring, respectively and EB stands for the highest energy barrier between the minimum S₁(C) and CI_S1/S0

Structures	Energy (eV)	C1–C2 (Å)	ϕ 1	ϕ 2
S0 (C)	0.26	1.54	5.78	6.90
S1FC (C)	3.16	1.54	5.78	6.90
CIS2/S1	2.79	1.57	14.91	13.06
S1min (C)	2.58	1.59	8.59	19.95
S1EB(C)	2.69	1.75	10.19	23.88
TS0	2.16	1.97	23.51	26.53
CIS1/S0	2.60	2.08	8.21	24.19
	3.70	3.07	29.97	18.78
S1min (O)	3.41	3.22	29.76	40.54
S2FC (O)	4.69	3.50	45.71	48.10
S0 (O)	0.00	3.50	45.71	48.10

---

Controlling the QY of photoisomerization of DTEs has important implications for the design of efficient optoelectronic devices since the efficiency of these devices depend on a large QY (close to 100%) in photocyclization as well as photoreversion.^2,23,38,41 Although many aspects of the photoisomerization mechanism of the symmetric DTEs have been clarified both experimentally^{1,2,13,14,16,17} and theoretically,^{1,2,17,21–23} to the best of our knowledge, the non-symmetric DTEs remained largely unexplored. It has been shown that non-symmetric DTEs (i.e. DTEs with asymmetrically substituted compounds attached to the thiophene-rings) exhibit a similar or in some cases a superior QY of photoisomerization compared to the symmetric counterparts.^2,63,64 For example, in the extensive review by Irie et al.,² the photocyclization and photoreversion QYs of typical DTEs in n-hexane are reported. There, the non-symmetric DTE bearing phenyl/methyl substituent groups shows a similar photocyclization QY with respect to the symmetric counterpart bearing phenyl/phenyl substituent groups. While, it shows a similar photoreversion QY with respect to the symmetric counterpart bearing methyl/methyl substituent groups. Another interesting example is reported in the work by Pariani et al.,⁶⁴ where the non-symmetric DTE bearing phenyl/methylthienyl substituent groups shows higher photocyclization and photoreversion QYs with respect to both symmetric counterparts. Furthermore, in the work by Browne et al.¹⁵ on the ring-closure process on a set of asymmetrically substituted DTEs, it is reported that the non-symmetric DTE bearing phenyl/chlorine substituent groups (see Fig. 1) shows a higher percentage (99%) of photostationary states (PSS) for closed-ring with respect to both symmetric counterparts. A high percentage of PSS formed indicates that the QY for photoreversion is considerably lower than the QY for photocyclization. Thus, the primary question of interest that motivates this work is how asymmetry affects the QY of the photoisomerization. Here we provide theoretical insight into the photocyclization as well as photoreversion of the non-symmetric DTE (Fig. 1) and subsequently shed light on its photoizomerization QY, crucial factor for its application as an efficient molecular switch in molecular electronic devices.

This paper is organised as follow: Section 2 describes the computational details. Our results and discussions are presented in Section 3 and finally our concluding remarks are given in Section 4.

2 Computational details

Ground state geometry optimization of the open and closed form were performed at the ωB97X-D/cc-pVDZ level of theory,^65,66 including Grimme's dispersion correction.⁶⁷ Subsequent frequency calculations were undertaken to confirm the nature of the minima. The vertical excitation energies (VEEs) of the first (S₁) and the second (S₂) excited state of both isomers and their optimized geometries were obtained using SF-TDDFT(BHHLYP)/cc-pVDZ. Additionally, these excited states were analyzed in terms of natural transition orbitals (NTOs).^68,69 Furthermore, to take into account the effect of the solvent, the VEEs of S₁ and S₂ were computed at SF-TDDFT(BHHLYP)/cc-pVDZ in acetonitrile as solvent, according to the Conductor-like Polarizable Continuum Model (C-PCM) scheme.^70,71 The dielectric constant (ε) and the optical dielectric constant (ε_∞) used to describe acetonitrile were 37.50 and 1.81, respectively. (Un)relaxed potential energy surface (PES) scans of S₀, S₁ and S₂ were carried out, along C₁–C₂ bond distance at the SF-TDDFT(BHHLYP)/cc-pVDZ level of theory in gas phase. A state-tracking algorithm, based on the overlap of attachment/detachment densities was used to follow the excited-state character during optimization of the S₁ and S₂ excited states. The minimum energy crossing points (MECP) optimisation between S₂/S₁ and S₁/S₀ were located at the SF-TDDFT(BHHLYP)/cc-pVDZ level of theory by using the penalty function method.^56,58 All the calculations were performed using Q-Chem 5.3 package.⁷² Cartesian coordinates of all the relevant structures are given in the ESI.†

3 Results and discussions

3.1 Stationary geometries

Fig. 3(a) and (b) illustrate the optimised ground state geometries for the open and closed isomers, respectively. Notice that the C₁–C₂ bond/breaking distance is defined as the reaction coordinate. The C₁–C₂ distance for the closed-ring is 1.54 Å and 3.44 Å for the open-ring. These distances are very close to those reported in our previous work³⁴ carried out on the central backbone of this DTE, the cyclohexadiene (CHD) for the closed-ring and all-cis-hexatriene (cZc-HT) for the open-ring. Furthermore, from the geometry point of view, the corresponding central unit in these molecular units have approximately the C₂ symmetry on the S_0min (see Fig. 3(a) and (b) and Table 1). In other words, even when CHD and cZC-HT are part of a non-symmetric DTE, these central units trend to conserve their C₂ symmetry in the ground state. In the case of the S₁ geometry optimisations, the open-ring and closed-ring converged to different minima (see Fig. 3(c) and (d)) with an energy of 2.58 eV, and the C₁–C₂ distance of being 1.59 Å for the open-ring, and an energy of 3.41 eV, and the C₁–C₂ distance of being 3.22 Å for the closed-ring. Notice that the distance between the reactive carbons C₁–C₂ from the S_0min does not change (difference 0.05 Å longer) for the closed-ring, but it shortened by 0.28 Å from the S_0min for the open-ring. In our previous work, the CHD and cZc-HT molecular units converge to the same minimum which C₁–C₂ distance is quite different to the C₁–C₂ distance (difference 0.57 Å shorter and 1.06 Å longer for the closed-ring and open-ring, respectively) of the minima found here. However, other works in similar DTEs^2,21,23,38 show a minimum on the S₁ state close to the C₁–C₂ distance reported here for the S_1min (C). A second minimum was located in a C₁–C₂ distance similar to the S_0min of the open-ring. To the best of our knowledge, a second minimum has not been previously reported in other DTEs. Similarly, the S₂ state optimisations of the open-ring (see Fig. 3(e)) and closed-ring converged to different minima, with the S_2min (C) converging to the S_1min (C) (here, we only show the S_1min (C); see Fig. 3(d)). The S_2min (O) shows an energy of 3.70 eV and the C₁–C₂ distance of being 3.07 Å. It must be noted that the distance between the reactive carbons C₁–C₂ is shortened by 0.43 Å from the S_0min for the open-ring. Interestingly, this structure coincides in geometry and energy with the CI between the S₂ and S₁ states. Unlike the S_0min for the closed-ring and open-ring, the CHD unit in the S_1min (C), and the cZc-HT unit in S_1min (O) and S_2min (O), do not tend to conserve the C₂ symmetry. It must be noticed that unconstrained geometry optimisation of the S₁ state from the S_0min closed-ring leads directly to a crossing region between the S₂ and S₁ states with a difference of 0.03 Å longer than the C₁–C₂ distance of the S_0min closed-ring. On the other hand, unconstrained geometry optimisation of the S₂ state from the S_0min open-ring leads directly to a crossing region between the S₂ and S₁ state with a difference of 0.43 Å longer than the C₁–C₂ distance of the S_0min open-ring. These crossings will be discussed in more detail later (see Section 3.3). Moreover, our results show an internal conversion between the closed-ring and the open-ring via a transition state (see Fig. 3(i)) on the S₀ state with a C₁–C₂ distance of 1.97 Å and an energy barrier of 2.16 eV (49.81 kcal mol⁻¹). This energy value indicates that an interconversion between the closed-ring and the open-ring for this DTE can be excluded via thermal electrocyclic reaction.

Fig. 3 Optimized geometries with DFT(ωB97X-D)/cc-pVDZ: (a) ground state closed DTE, (b) ground state open DTE. Optimized geometries with SF-TDDFT(BHHLYP)/cc-pVDZ: (c) S_1min (from Open form), (d) S_1min and S_2min (from Closed form), (e) S_2min (from Open form), (f) CI_S2/S1 (from Closed form), (g) (from Open form), (h) CI_S1/S0 (from the highest energy barrier of PES-S₁) and (i) S₀ transition state. Distances are in Å.

3.2 Vertical excitation energies and excited-state characterization

Table 3 summarises the vertical excitation energies (VEEs) for the two lowest singlet excited states of the closed-ring and the open-ring calculated with SF-TDDFT(BHHLYP)/cc-pVDZ in gas phase and acetonitrile as a solvent within the C-PCM scheme, as well as experimental results.¹⁵ Notice that we have rescrited our study to the singlet excited states since a photocyclization reaction via triplet states is present in DTEs bearing chromophores such as transition-metal complexes, perylenebisimide, or triplet sensitizers,² we observe that, both in gas phase and in the acetonitrile solvent, the states with the highest oscillator strength agree with the experimental results; for the closed-ring, the VEE of the brightest state (S₁) agrees within 0.65 eV and for the open-ring, the VEE of the brightest state (S₂) agrees within 0.20 eV. In order to characterize these excitations, we used natural transition orbitals NTOs.^68,69 The hole/electron NTOs provide a compact interpretation of any excited state.⁷³ Because we do not observe any significant difference between gas phase and solvent, we restrict our further descriptions just to the brightest states in gas phase (see Fig. S3 in the ESI†).

Fig. 4 depicts the NTOs for the lowest bright state, i.e. the S₁ state for the closed-ring and the S₂ state for the open-ring, in the gas phase. One can observe that the hole/electron excitations have a π–π* character, and they are distributed mostly over the thiophene-rings and the π-conjugated system of the CHD chromophore for both isomers. In the case of the closed-ring, the hole NTO is localized over the π-conjugated system of the CHD chromophore and the thiophene-rings. Instead, the electron NTO is more localized on the π-conjugated system of the CHD chromophore than the thiophene-rings. Moreover, a close look at the NTOs shape reveals that the interaction between the reactive carbons C₁ and C₂ is bonding for the hole NTO and anti-bonding for the electron NTO. This spatial distribution of the hole/electron NTOs and the character of the reactive carbons distance (i.e. bonding and anti-bonding) have been observed previously in the frontier orbitals in similar DTEs.^1,24 In the case of the open-ring, the hole/electron NTOs are localized mostly on the thiophene-ring bearing the phenyl-ring. Here, it is observed a strong contribution of the sulfur atom, for the hole NTO, and the C₂ atom, for the electron NTO. Unlike the closed-ring, in the open-ring, we can not clearly identify (looking at the shape of the hole/electron NTOs) if the interaction between the reactive carbons C₁ and C₂ has a bonding or anti-bonding character. It must be noticed that the shape of the hole/electron NTOs has been observed as well in the frontier orbitals in previous work by Fihey et al.²⁴ with non-symmetric DTEs. Our previous study on the central unit of this non-symmetric DTE (the CHD and cZc-HT molecular units³⁴) has shown that their NTOs are symmetric around these units, for both the closed-ring and the open-ring. The Fig. 4 clearly reveals that the asymmetric substitution leads to an asymmetric distribution of the hole/electron NTOs around the central unit, with the effect being more pronounced for the open-ring. Additionaly, we performed a wavefunction analysis to provide information on the character of the S₀ → S₁ and S₀ → S₂ transitions. The analysis is based on the squared norm (Ω) of the one-particle transition density matrix (1TDM)⁷⁴ between the ground state and the S₁ and S₂ excited states, the NTO participation ratio (PR_NTO) and the number of entangled states (Z_HE).⁷⁵ It must be mentioned that Ω is a universal measure of single-excitation character and PR_NTO and Z_HE provide inherent information on the multiconfigurational character of the transition. The value of Ω goes typically from 0 to 1, where 1 indicates a pure single excited state. However, values significantly lower than 1 indicate that higher excitations are involved. The PR_NTO and Z_HE descriptors take values close to 1 for states described by a single orbital transition and take higher values when several configurations are involved.⁷⁵Table 2 summarizes the results of the 1TDM and entanglement descriptors. Notice that for the SF-TDDFT method, the wavefunction analysis is performed for each spin (α and β) of the state. Thus, the descriptor Ω is defined as the sum of Ω_α and Ω_β and for the PR_NTO and Z_HE descriptors the values for each spin α and β have to be analyzed individually. We observe that the total Ω of S₁ for the closed-ring and S₂ for the open-ring is higher than 0.96 which speaks in favor a single-excitation character. Analyzing the entanglement descriptors, we can see that PR_NTO has values close to 1 and Z_HE has values not higher than 1.5 for all the spins. As expected the values of Z_HE are somewhat larger than PR_NTO, this is explained due to the fact that the NTO amplitudes are in general not equal (see ref. 75). Therefore, these values suggest a lower multiconfiguration character for the S₀ → S₁ and S₀ → S₂ transitions for both closed- and open-ring.

Fig. 4 NTOs calculated with SF-TDDFT(BHHLYP)/cc-pVDZ (cutoff value of 0.04) in gas phase for the lowest bright state with significant oscillator strength. (a) DTE closed-ring S₁, (b) DTE open-ring S₂.

Table 2 Wavefunction analysis based on the squared norm (Ω) of the one-particle transition density matrix (1TDM), the NTO participation ratio (PR_NTO) and the number of entangled states (Z_HE)

Descriptors	Closed-ring				Open-ring
	S1		S2		S1		S2
	α	β	α	β	α	β	α	β
Ω	0.411	0.555	0.589	0.227	0.161	0.788	0.769	0.202
PRNTO	1.041	1.017	1.010	1.036	1.009	1.002	1.001	1.022
Z HE	1.500	1.430	1.400	1.430	1.350	1.210	1.230	1.400

---

Table 3 Vertical excitation energies in eV for the two lowest singlet excited states of the open and closed form computed using SF-TDDFT(BHHLYP)/cc-pVDZ in gas phase and acetonitrile solvent. The oscillator strengths are given in parentheses

Environment	Closed-ring/states		Open-ring/states
	S1	S2	S1	S2
Gas phase	2.90(0.574)	3.24(0.017)	4.09(0.037)	4.69(0.161)
Acetonitrile	2.88(0.571)	3.23(0.016)	3.99(0.037)	4.67(0.159)
Experiment^15 (Acetonitrile)	2.26	—	—	4.86

---

3.3 Minimum energy crossing points

The photoisomerization mechanism of DTEs is essentially controlled by the MECPs between the states²: S₂–S₁, and S₁–S₀. In this DTE, three different MECPs were found, CI_S2/S1,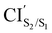 and CI_S1/S0. Their relatives energies to S_0min of the open-ring are listed in Table 1 and the optimised structures of these geometries are shown in Fig. 3. The calculation of these MECPs along the optimization steps are described in Fig. S1 and S2 (ESI†).

CI_S2/S1 was obtained starting from closed-ring S_0min geometry, with an energy of 2.79 eV and the C₁–C₂ distance of being 1.57 Å (see Table 1 and Fig. 3(f)). We can notice that the nature of this structure is rather similar to the closed-ring S_1min with respect to the geometry of their CHD molecular units (all the bond distances of their CHD molecular units agree within 0.03 Å), but is energetically 0.21 eV higher. Moreover, the energy of CI_S2/S1 is 0.37 eV lower than the energy of the closed-ring S_1FC. Hence, it is natural to assume that the closed-ring S_0min will undergo vibrational relaxation downhill from the FC region, towards the CI_S2/S1, and from there towards the S_1min. It must be noticed that, this vibrational relaxation is inducing a remarkable twisting motion (around ϕ₁) of the thiophene-ring bearing the chloride group (see Table 1 and Fig. 5(b)-(iii)). Interestingly, a similar twisting motion around ϕ₁ was reported by Asano et al.²³ in a theoretical study on the photochromic cycloreversion reactions of symmetric DTEs.

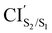was obtained starting from the open-ring S_0min geometry, with an energy of 3.70 eV and a C₁–C₂ distance of being 3.07 Å (see Table 1 and Fig. 3(g)). We can notice that the nature of this structure is rather similar to the open-ring S_2min. In fact, we do not observe any significant difference between their geometries, symmetries with respect to their cZc-HT chromophores (C₂ symmetry is almost retained in both cZc-HT chromophores) and energies. The latter speaks in favour of the fact that both structures are located extremely close to each other. Notice that the energy of the is 0.99 eV lower than the energy of the open-ring S_2FC. Thus, it is natural to assume that the open-ring S_0min will undergo vibrational relaxation downhill from the FC region and reach the 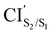and from there towards the S_2min.

CI_S1/S0 was computed starting from a geometry related to highest energy point on a relaxed PES scan on S₁ state. All attempts to optimize this crossing did not converge within 500 steps using the penalty function method. The reason is that after the first 40th optimization steps, the states show a high spin contamination, i.e. 〈Ŝ²〉≈ 1.5. It must be noted that states with 〈Ŝ²〉< 1.2 are assigned as singlet states. This high spin contamination causes an oscillation of the energies of the excited states S₁ and S₀ along the optimization steps^76,77 (see Fig. S2(i) in the ESI†). One way to avoid such an issue is to take a look at the structures along the S₁/S₀ MECP optimization steps with high non-adiabatic coupling norm values (see Fig. S2(ii) in the ESI†) and analyze the orbitals involved at these structures in order to select the closest one to the CI_S1/S0. Another way to tackle this issue is using the spin-adapted spin-flip DFT method (SA-SF-DFT).^76,77 This method is free of spin contamination, thus one can get proper singlet excited states. Because this method lacks analytical gradients, it can be used as a spot-check along the optimization steps in the region of high spin contamination. Using the former protocol from a set of structures with high nonadiabatic coupling (NAC) norm values, we chose the CI_S1/S0 structure (see Table 1 and Fig. 3(h)) with the lowest difference of energy between S₀ and S₁ computed with the SF-TDDFT method (<0.00014 eV) and SA-SF-DFT method (<0.2 eV) and the highest NAC norm value (745). Interestingly, the geometry of the CHD molecular unit of this CI shows close similarities (0.03 Å lower for C₁–C₂, 0.02 Å lower for C₆–C₁, 0.01 Å lower for C₄–C₅ and C₅–C₆, and 0.00 Å for C₂–C₃ and C₃–C₄) with the corresponding geometry of the CHD molecular unit of the CI_S1/S0 point obtained by Boggio-Pasqua et al.²¹ in an ab initio molecular orbital study of three different diarylethene derivatives using the CASSCF method. The energy of the CI_S1/S0 is 0.19 eV and 1.10 eV lower than the energies of the CI_S2/S1 and , respectively. Therefore, it is natural to assume that, both the open-ring and the closed-ring will go downhill from the CI_S2/S1 and , in the corresponding relaxation processes, towards the CI_S1/S0, and from there, towards either the open-ring S_0min or the closed-ring S_0min. In fact, comparing the energies (difference of 0.44 eV) and the geometries (difference of 0.11 Å for the bond distance C₁–C₂) between the CI_S1/S0 and the TS₀, both structures are quite similar.

3.4 Potential energy surface

In order to shed light on the photocyclization and photoreversion processes of the non-symmetric DTE considered in this work, we analyzed the main features of the lowest three singlet states (S₀, S₁ and S₂) computed by (un)relaxed PES scans along C₁–C₂ coordinate with SF-BHHLYP/cc-pVDZ. Here, we only show the relaxed PES scan on S₁ in Fig. 5. The analogous PES scans are represented in the ESI.† An outline of this analysis is depicted in Fig. 6. As it is shown in Fig. 6, the S₀ PES has two minima corresponding to the closed-ring with C₁–C₂ distance of 1.54 Å and the open-ring with C₁–C₂ distance of 3.50 Å. Connecting these minima, we found a transition state structure at 1.97 Å along C₁–C₂ coordinate with an energy barrier of 2.16 eV (49.81 kcal mol⁻¹). This large energy barrier shows that an operative reaction path for an interconversion between the closed-ring and the open-ring for this DTE can be via photoexcitation and excludes a thermal electrocyclic reaction as a likely mechanism.

Fig. 5 (a) Relaxed S₁-PES scan: potential energies curves (i) and ϕ torsion angles (ii) along the C₁–C₂ bond distance obtained with SF-BHHLYP/cc-pVDZ. The energies are relatives to the S_0min energy of the open-ring. Notice how the torsion angles change dramatically along the distance of the reactive carbons. (b) Schematic description of the torsion angles ϕ₁ (iii) and ϕ₂ (iv) of the important geometries along the C₁–C₂ bond distance of the photocyclization (O → C) and the photoreversion (C → O) processes.

Fig. 6 Schematic representation of the PESs of DTE Open form/Closed form photochemical interconversion. The reaction coordinate is the C₁–C₂ bond distance. The ground state is in blue, the state S₁ is in green and the state S₂ is in red. The curves are a pictorial description that connects the important geometries computed with SF-BHHLYP/cc-pVDZ. The ground state curve is a PES scan trough the C₁–C₂ bond distance computed with SF-BHHLYP/cc-pVDZ. The cones in purple represent the MEPCs. The arrows depict how the photochemical interconversion process follow after an absorption of a photon generates the population of the second excited state (S₂) of open form and the first excited state (S₁) of closed form. The energies are relatives to the S_0min energy of the open-ring.

Ring-closing reaction. Upon light absorption, the ground state of the open-ring isomer is vertically excited to the bright state S₂ with an energy of 4.69 eV. From the FC region, the open-ring undergoes a vibrational relaxation which induces a C₁–C₂ bond shortening (0.43 Å shorter) as well as smaller torsion angles (ϕ₁ and ϕ₂ being 15.74 and 29.32 degrees smaller, respectively), and subsequently hits the where occurs an internal conversion. This behavior is typical of processes when the CI is accessible from the FC region without significant energy barriers, as is the case here. From this point, the reaction pathway may bifurcate in two branches, depending on which adiabatic state the wavefunction takes after the system leaves the crossing region. Hence, we can define two scenarios; (1) if the adiabatic S₂ state changes to S₁, then the system will evolve directly towards the CI_S1/S0 (at 2.08 Å with an energy of 2.60 eV) that triggers an ultra-fast internal conversion process and provides a funnel of fast access to the ground state, on which the system can evolve either to the S_0min of closed-ring or the S_0min of open-ring. Notice that this relaxation path is rather similar to the path of the symmetric DTEs described by Irie et al.² in their review about photochromism of diarylethene molecules. (2) if the adiabatic S₂ state does not change, then the system evolves towards the CI_S2/S1, and from there, towards the S_1min (C) (at 1.59 Å and energy of 2.58 eV). There, the excess of vibrational energy after photoexcitation should enable the system to overcome the energy barrier (0.11 eV higher) and to hit again the CI_S1/S0, that acts as a doorway for an ultra-fast internal conversion to the ground state, either to the open-ring S_0min or the closed-ring S_0min.

Ring-opening reaction. Upon light absorption, the ground state of the closed-ring isomer is vertically excited to the bright state S₁ with an energy of 3.16 eV. From the FC region, the closed-ring undergoes a vibrational relaxation which induces a C₁–C₂ bond elongation (0.03 Å larger) as well as larger torsion angles (ϕ₁ and ϕ₂ being 9.13 and 6.16 degrees larger, respectively), and subsequently hits the CI_S2/S1 where occurs an internal conversion. From there, the system evolves towards the S_1min(C), where the excess of vibrational energy after photoexcitation should enable the system to overcome the energy barrier (2.5 kcal mol⁻¹ higher) and to hit the CI_S1/S0. Notice that the nature of this energy barrier as TS on S₁ has been confirmed using the intrinsic reaction coordinate (IRC) algorithm, which is essentially a series of steepest descent steps going downhill from the TS to the adjacent minimum which is S_1min(C). At the CI, an ultra-fast internal conversion takes place to the ground state, either to the open-ring S_0min or the closed-ring S_0min. It must be noted that this relaxation path is rather similar to the path of the symmetric DTEs described by Irie et al.² in their review about photochromism of diarylethene molecules.

In general, we observe that upon photoexcitation and the subsequent vibration relaxation, the torsion angles ϕ₁ and ϕ₂ as well as the C₁–C₂ bond distance undergo significant changes for both ring-opening and closing reactions, making them crucial coordinates in the radiationless pathways. For example, in the case of the photoreversion process, the twisting motion around ϕ₁ governs the pathways connecting the FC region at S₁ with the S_1min(C) through the CI_S2/S1 (see Fig. 5(b)-(iii)). A similar twisting motion around ϕ₁ was also reported by Asano et al.,²³ in their work focused on the photoreversion reaction of symmetric DTEs. In summary, we observe that the principal features that characterize the photoreversion and photocyclization processes in symmetric DTEs^16,17 are also present for the photoisomerization of this non-symmetric DTE, for example, the energy barrier (S_1EB(C)) on S₁ in the cycloreversion process and no energy barrier in the cyclization process, as well as the presence of the CI_S1/S0 for both electrocyclic reactions. However, it must be noted that the energy barrier (S_1EB(C)) on S₁ along the cycloreversion process for the non-symmetric DTE considered in this work is around 2.5 kcal mol⁻¹ that is almost half of the enery barrier predicted experimentally^2,35–37 (around 4.2 kcal mol⁻¹) for the symmetric DTEs, which can potentially lead to a higher cycloreversion QY for the non-symmetric DETs compared to the symmetric counterparts. The latter should be further investigated since in a recent study,³⁶ on the dynamics of the cycloreversion reaction of a photochromic DTE derivative, it is shown that the QY of the photoreversion process depends on the branching ratio around the CI_S1/S0 rather than the energy barrier on S₁.

Furthermore, in previous theoretical works,^17,38 it has been shown that the energy difference between the CI_S1/S0 and S_1min(C) is correlated with the experimental QYs of the photoreversion process. Although these works were performed using the CASSCF method, which lacks the dynamic correlation, the energy difference between the CI_S1/S0 and S_1min (C) may be used as an index of the cycloreversion QY.³⁸ Thus, when the energy difference between the CI_S1/S0 and S_1min(C) is positive, the efficiency to reach the CI decreases². For the non-symetric DTE considered here, the computed energy difference between the CI_S1/S0 and S_1min (C) is 0.46 kcal mol⁻¹ (0.02 eV, see Table 1). To the best of our knowledge, the QYs of the photoreversion and photocyclization processes are not reported for the non-symmetric DTE considered in this work. However, in the work by Browne et al.,¹⁵ it has been concluded that the QY of the ring-opening is considerably lower than the QY of the ring-closing for this non-symmetric DTE which is in agreement with our analysis and results presented here.

In summary, comparing the calculated PESs along ring-opening and closing reactions and the corresponding structures for this non-symmetric DTE with the experimental and theoretical results^17,38 for the symmetric DTEs, we observe that while there exists a close resemblance between the photoreversion of this non-symmetric DTE with the symmetric counterparts,^78,79 the lower energy barrier (S_1EB(C)) on S₁ along the cycloreversion reaction speaks in favor of a more efficient and higher QY of the cycloreversion process for the non-symmetric DTEs. Additionally, the computed energy difference between the CI_S1/S0 and S_1min(C) suggests that the QY photoreversion for this non-symmetric DTE resemble more the symmetric counterpart with Chlorine atom which shows a higher photoreversion QY than the symmetric counterpart with the phenyl substituents.^78,79

4 Conclusions

In the present study, we have used the SF-TDDFT(BHHLYP)/cc-pVDZ level of theory to describe and characterize the photochemistry of a non-symmetric DTE. Our results show how the geometric changes induced by the vibration relaxation after the initial photoexcitation play an important role in the deactivation processes, mainly, the torsion angle ϕ₁ for the photoreversion reaction. Moreover, while the main features that characterize the photoisomerization of a symmetric DTE are also present for the photoisomerization of this non-symmetric DTE, the lower energy barrier (S_1EB(C)) on S₁ along the cycloreversion reaction speaks in favor of a more efficient and higher QY of the cycloreversion process for the non-symmetric DTEs. Additionally, the computed energy difference between the CI_S1/S0 and S_1min (C) suggests that the QY photoreversion for this non-symmetric DTE resemble more the symmetric counterpart with Chlorine atom which shows a higher photoreversion QY than the symmetric counterpart with the phenyl substituents. Finally, the SF-TDDFT method shows excellent performance in reproducing important geometries as well as features reported in previous works on DTEs where multireference methods were used. This suggests that SF-TDDFT could be a cheaper alternative to the multireference methods to study complex systems with the same degree of complexity and size as the non-symmetric DTE considered in this work, that are relevant for molecular electronic devices.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors would like to thank Prof. Ryan Chiechi and Dr. Sumit Kumar for fruitful discussions on this non-symmetric DTE molecule. This work is part of Innovational Research Incentives Scheme Vidi 2017 with project number 016.Vidi.189.044, which is financed by the Dutch Research Council (NWO).

References

1. A. Staykov, J. Areephong, W. R. Browne, B. L. Feringa and K. Yoshizawa, ACS Nano, 2011, 5, 1165–1178.
2. M. Irie, T. Fukaminato, K. Matsuda and S. Kobatake, Chem. Rev., 2014, 114, 12174–12277.
3. S. M. Mendoza, M. Lubomska, M. Walko, B. L. Feringa and P. Rudolf, J. Phys. Chem. C, 2007, 111, 16533–16537.
4. V. Balzani, A. Credi and M. Venturi, Switching Electron- and Energy-Transfer Processes, Wiley-Blackwell, 2008, ch. 5, pp. 107–133.
5. J. Li, G. Speyer and O. F. Sankey, Phys. Rev. Lett., 2004, 93, 248302.
6. M. Irie, Chem. Rev., 2000, 100, 1685–1716.
7. D. Roke, C. Stuckhardt, W. Danowski, S. J. Wezenberg and B. L. Feringa, Angew. Chem., Int. Ed., 2018, 57, 10515–10519.
8. J. T. Foy, Q. Li, A. Goujon, J.-R. Colard-Itté, G. Fuks, E. Moulin, O. Schiffmann, D. Dattler, D. P. Funeriu and N. Giuseppone, Nat. Nanotechnol., 2017, 12, 540–545.
9. S. E. Lyshevski, Nano and molecular electronics handbook, CRC Press, 2016.
10. M. Baroncini, M. Canton, L. Casimiro, S. Corra, J. Groppi, M. La Rosa, S. Silvi and A. Credi, Eur. J. Inorg. Chem., 2018, 4589–4603.
11. W. Danowski, T. van Leeuwen, W. R. Browne and B. L. Feringa, Nanoscale Adv., 2021, 3, 24–40.
12. S. Nakamura and M. Irie, J. Org. Chem., 1988, 53, 6136–6138.
13. M. Irie, Chem. Rev., 2000, 100, 1685–1716.
14. S. Nakatsuji, Chem. Soc. Rev., 2004, 33, 348–353.
15. W. R. Browne, J. J.-D. de Jong, T. Kudernac, M. Walko, L. N. Lucas, K. Uchida, J. H. van Esch and B. L. Feringa, Chem. – Eur. J., 2005, 11, 6430–6441.
16. J. Ern, A. Bens, H.-D. Martin, S. Mukamel, D. Schmid, S. Tretiak, E. Tsiper and C. Kryschi, Chem. Phys., 1999, 246, 115–125.
17. D. Guillaumont, T. Kobayashi, K. Kanda, H. Miyasaka, K. Uchida, S. Kobatake, K. Shibata, S. Nakamura and M. Irie, J. Phys. Chem. A, 2002, 106, 7222–7227.
18. A. G. Lvov, M. Herder, L. Grubert, S. Hecht and V. Z. Shirinian, J. Phys. Chem. A, 2021, 125, 3681–3688.
19. D. Majumdar, H. M. Lee, J. Kim, K. S. Kim and B. J. Mhin, J. Chem. Phys., 1999, 111, 5866–5872.
20. K. Uchida, D. Guillaumont, E. Tsuchida, G. Mochizuki, M. Irie, A. Murakami and S. Nakamura, J. Mol. Struct.: THEOCHEM, 2002, 579, 115–120.
21. M. Boggio-Pasqua, M. Ravaglia, M. J. Bearpark, M. Garavelli and M. A. Robb, J. Phys. Chem. A, 2003, 107, 11139–11152.
22. P. Sauer and R. E. Allen, Chem. Phys. Lett., 2007, 434, 260–264.
23. Y. Asano, A. Murakami, T. Kobayashi, A. Goldberg, D. Guillaumont, S. Yabushita, M. Irie and S. Nakamura, J. Am. Chem. Soc., 2004, 126, 12112–12120.
24. A. Fihey, A. Perrier and F. Maurel, J. Photochem. Photobiol., A, 2012, 247, 30–41.
25. C. Van Dyck, V. Geskin, A. J. Kronemeijer, D. M. de Leeuw and J. Cornil, Phys. Chem. Chem. Phys., 2013, 15, 4392–4404.
26. M. Irie, K. Sakemura, M. Okinaka and K. Uchida, J. Org. Chem., 1995, 60, 8305–8309.
27. N. Tamai and H. Miyasaka, Chem. Rev., 2000, 100, 1875–1890.
28. B. C. Arruda and R. J. Sension, Phys. Chem. Chem. Phys., 2014, 16, 4439–4455.
29. H. Tamura, S. Nanbu, H. Nakamura and T. Ishida, Chem. Phys. Lett., 2005, 401, 487–491.
30. T. Mori and S. Kato, Chem. Phys. Lett., 2009, 476, 97–100.
31. O. Schalk, T. Geng, T. Thompson, N. Baluyot, R. D. Thomas, E. Tapavicza and T. Hansson, J. Phys. Chem. A, 2016, 120, 2320–2329.
32. M. Filatov, S. K. Min and K. S. Kim, Mol. Phys., 2019, 117, 1128–1141.
33. I. Polyak, L. Hutton, R. Crespo-Otero, M. Barbatti and P. J. Knowles, J. Chem. Theory Comput., 2019, 15, 3929–3940.
34. E. Salazar and S. Faraji, Mol. Phys., 2020, 118, e1764120.
35. Y. Ishibashi, T. Umesato, S. Kobatake, M. Irie and H. Miyasaka, J. Phys. Chem. C, 2012, 116, 4862–4869.
36. H. Sotome, K. Une, T. Nagasaka, S. Kobatake, M. Irie and H. Miyasaka, J. Chem. Phys., 2020, 152, 034301.
37. C. R. Honick, G. M. Peters, J. D. Young, J. D. Tovar and A. E. Bragg, Phys. Chem. Chem. Phys., 2020, 22, 3314–3328.
38. S. Nakamura, T. Kobayashi, A. Takata, K. Uchida, Y. Asano, A. Murakami, A. Goldberg, D. Guillaumont, S. Yokojima, S. Kobatake and M. Irie, J. Phys. Org. Chem., 2007, 20, 821–829.
39. I. N. Ioffe and A. A. Granovsky, J. Chem. Theory Comput., 2013, 9, 4973–4990.
40. J. Jankowska, M. Martyka and M. Michalski, J. Chem. Phys., 2021, 154, 204305.
41. Y. Asano, A. Murakami, T. Kobayashi, S. Kobatake, M. Irie, S. Yabushita and S. Nakamura, J. Mol. Struct.: THEOCHEM, 2003, 625, 227–234.
42. M. G. Chiariello, U. Raucci, F. Coppola and N. Rega, Phys. Chem. Chem. Phys., 2019, 21, 3606–3614.
43. A. Jarota, E. Pastorczak and H. Abramczyk, Phys. Chem. Chem. Phys., 2020, 22, 5408–5412.
44. M. Merchán, L. Serrano-Andrés, L. S. Slater, B. O. Roos, R. McDiarmid and X. Xing, J. Phys. Chem. A, 1999, 103, 5468–5476.
45. M. Garavelli, C. S. Page, P. Celani, M. Olivucci, W. E. Schmid, S. A. Trushin and W. Fuss, J. Phys. Chem. A, 2001, 105, 4458–4469.
46. M. Boggio-Pasqua, M. J. Bearpark, M. Klene and M. A. Robb, J. Chem. Phys., 2004, 120, 7849–7860.
47. A. Nenov, P. Kölle, M. A. Robb and R. de Vivie-Riedle, J. Org. Chem., 2010, 75, 123–129.
48. S. Karashima, A. Humeniuk, R. Uenishi, T. Horio, M. Kanno, T. Ohta, J. Nishitani, R. Mitrić and T. Suzuki, J. Am. Chem. Soc., 2021, 143, 8034–8045.
49. W. Weber and W. Thiel, Theor. Chem. Acc., 2000, 103, 495–506.
50. A. Koslowski, M. E. Beck and W. Thiel, J. Comput. Chem., 2003, 24, 714–726.
51. P. O. Dral, X. Wu, L. Spörkel, A. Koslowski, W. Weber, R. Steiger, M. Scholten and W. Thiel, J. Chem. Theory Comput., 2016, 12, 1082–1096.
52. P. O. Dral, X. Wu and W. Thiel, J. Chem. Theory Comput., 2019, 15, 1743–1760.
53. S. L. Li, A. V. Marenich, X. Xu and D. G. Truhlar, J. Phys. Chem. Lett., 2014, 5, 322–328.
54. S. Matsika, Chem. Rev., 2021, 121, 9407–9449.
55. Y. Shao, M. Head-Gordon and A. I. Krylov, J. Chem. Phys., 2003, 118, 4807–4818.
56. N. Minezawa and M. S. Gordon, J. Phys. Chem. A, 2009, 113, 12749–12753.
57. X. Zhang and J. M. Herbert, J. Phys. Chem. B, 2014, 118, 7806–7817.
58. Y. Harabuchi, K. Keipert, F. Zahariev, T. Taketsugu and M. S. Gordon, J. Phys. Chem. A, 2014, 118, 11987–11998.
59. F. Romeo-Gella, I. Corral and S. Faraji, J. Chem. Phys., 2021, 154, 064111.
60. D. Casanova and A. I. Krylov, Phys. Chem. Chem. Phys., 2020, 22, 4326–4342.
61. T. Shiozaki, W. Györffy, P. Celani and H.-J. Werner, J. Chem. Phys., 2011, 135, 081106.
62. J. Schirmer and A. B. Trofimov, J. Chem. Phys., 2004, 120, 11449–11464.
63. S. Pu, L. Yan, Z. Wen, G. Liu and L. Shen, J. Photochem. Photobiol., A, 2008, 196, 84–93.
64. G. Pariani, M. Quintavalla, L. Colella, L. Oggioni, R. Castagna, F. Ortica, C. Bertarelli and A. Bianco, J. Phys. Chem. C, 2017, 121, 23592–23598.
65. J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620.
66. T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023.
67. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
68. R. L. Martin, J. Chem. Phys., 2003, 118, 4775–4777.
69. I. Mayer, Chem. Phys. Lett., 2007, 437, 284–286.
70. V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995–2001.
71. M. Cossi, N. Rega, G. Scalmani and V. Barone, J. Comput. Chem., 2003, 24, 669–681.
72. E. Epifanovsky, et al. , J. Chem. Phys., 2021, 155, 084801.
73. F. Plasser, M. Wormit and A. Dreuw, J. Chem. Phys., 2014, 141, 024106.
74. F. Plasser, A. I. Krylov and A. Dreuw, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, n/a, e1595.
75. F. Plasser, J. Chem. Phys., 2016, 144, 194107.
76. X. Zhang and J. M. Herbert, J. Chem. Phys., 2015, 143, 234107.
77. J. M. Herbert, X. Zhang, A. F. Morrison and J. Liu, Acc. Chem. Res., 2016, 49, 931–941.
78. M. Irie, T. Lifka, S. Kobatake and N. Kato, J. Am. Chem. Soc., 2000, 122, 4871–4876.
79. K. Higashiguchi, K. Matsuda, Y. Asano, A. Murakami, S. Nakamura and M. Irie, Eur. J. Org. Chem., 2005, 91–97.

---

Footnote

† Electronic supplementary information (ESI) available: Cartesian coordinates of all the relevant structures, figures of the minimum energy crossing points optimisation between S₂/S₁ and S₁/S₀ along the optimization steps, natural transition orbitals for open-ring and closed-ring in solvent, benchmarking between SF-TDDFT and multireference methods, and the absorption maximum wavelengths (λ_max) and quantum yields of the non-symmetric DTE and its symmetric counterparts. See DOI: https://doi.org/10.1039/d2cp00550f

---