 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Terahertz spectroscopy of the helium endofullerene He@C60
Tanzeeha
Jafari
 a,
George
Razvan Bacanu
b,
Anna
Shugai
a,
George
Razvan Bacanu
b,
Anna
Shugai
 a,
Urmas
Nagel
a,
Urmas
Nagel
 a,
Mark
Walkey
a,
Mark
Walkey
 b,
Gabriela
Hoffman
b,
Malcolm H.
Levitt
b,
Gabriela
Hoffman
b,
Malcolm H.
Levitt
 b,
Richard J.
Whitby
b,
Richard J.
Whitby
 b and
Toomas
Rõõm
b and
Toomas
Rõõm
 *a
*a
aNational Institute of Chemical Physics and Biophysics, Akadeemia tee 23, Tallinn 12618, Estonia. E-mail: toomas.room@kbfi.ee
bSchool of Chemistry, University of Southampton, SO17 1BJ Southampton, UK
First published on 21st April 2022
Abstract
We studied the quantized translational motion of single He atoms encapsulated in molecular cages by terahertz absorption. The temperature dependence of the THz absorption spectra of 3He@C60 and 4He@C60 crystal powder samples was measured between 5 and 220 K. At 5 K there is an absorption line at 96.8 cm−1 (2.90 THz) in 3He@C60 and at 81.4 cm (2.44 THz) in 4He@C60, while additional absorption lines appear at higher temperature. An anharmonic spherical oscillator model with a displacement-induced dipole moment was used to model the absorption spectra. Potential energy terms with powers of two, four and six and induced dipole moment terms with powers one and three in the helium atom displacement from the fullerene cage center were sufficient to describe the experimental results. Excellent agreement is found between potential energy functions derived from measurements on the 3He and 4He isotopes. One absorption line corresponds to a three-quantum transition in 4He@C60, allowed by the anharmonicity of the potential function and by the non-linearity of the dipole moment in He atom displacement. The potential energy function of icosahedral symmetry does not explain the fine structure observed in the low temperature spectra.
1 Introduction
The highly symmetric fullerene, C60, has attracted considerable attention since its discovery in 1985.1 One of the fascinating features is its ability to hold an atom or small molecule within a hollow molecular cavity, forming a complex known as an endofullerene. The discovery of the first endofullerene, La@C60, occurred soon after by the same group of researchers, when they were able to capture lanthanum by a laser ablation technique.2 Endofullerenes provide a rare opportunity to examine the behavior of guest species under conditions that have never been studied before such as the confinement of guest species inside a nano-scale cage which is non-polar, homogeneous and in the case of C60, highly symmetric.3,4Different methods have been used to synthesize endofullerenes. Endofullerenes may be synthesized by the arc discharge method in which carbon is evaporated at high temperature in the presence of a metal5 or an inert gas.6,7 Insertion of atoms into the fulllerene cage is possible by exposing the fullerene to high temperatures and high pressures of inert gas8 or by ion bombardment.9–11 However, these methods are not suited to capture small molecules and the production yield is small. In a major development, the group of Komatsu12 synthesized H2@C60 endofullerenes by a process known as molecular surgery.13 Following in the footsteps of Komatsu, the group of Murata successfully encapsulated a water molecule inside C60.14 Molecular surgery has been the most successful process to produce high-yield endofullerenes until today. A large number of endofullerenes are now available in macroscopic quantities, such as12 and its isotopologues,15 H2O@C60,14 HF@C6016 and CH4,17 and atoms like Ar,18 He19,20 and Ne.20
Endofullerenes are of great interest due to quantum effects which are more evident at cryogenic temperatures. The encapsulation isolates atoms and molecules from each other preventing them from forming liquid or solid condensates even at the lowest temperatures. This provides a unique opportunity to study their internal degrees of freedom at the lowest temperatures. The translational motion becomes quantized due to the confining potential. The confinement also prompts the coupling of translational and rotational motions of the encapsulated molecule. The combination of small molecular mass and tight confinement inside the nano cage gives rise to a discrete and well separated translation-rotational energy level structure. The most studied endohedral complex is H2@C60, which laid the basis for understanding the quantum dynamics of the isolated systems.4,21 Different spectroscopic techniques have been used to demonstrate the effect of the highly symmetric trapping potential on the quantum dynamics of the hydrogen molecule, including infrared spectroscopy (IR)22–24 and inelastic neutron scattering (INS).25–28
There is a growing interest in extending spectroscopic studies to noble gas endofullerenes. The research interest in noble gas endofullerenes is evident from the theoretical studies that have been done so far.29–36 The incarceration of large noble gas atoms results in the structural and electronic distortion of which has been examined by IR and Raman,34 NMR,37 X-ray38 and electronic spectroscopy.39
The first experimental evidence of a noble gas endofullerene was He@C60. It was spotted by mass spectrometry when the 4 atom was incorporated in C60 as the highly accelerated C60+ ions struck with helium gas9 and later found in fullerenes produced by arc discharge in the He gas.6 Despite that, and the 2010 synthesis of He@C60 by molecular surgery,19 the He endofullerene potential energy function study was restricted to theoretical explanations31,33,40 and the experimental data were inadequate for supporting the available information. Recently, the translational energies of He@C60 were determined by inelastic neutron scattering and THz spectroscopy studies and the experimentally derived potential was compared to estimates from quantum chemistry calculations and from sums of empirical two-body potentials.41
Here, as compared to ref. 41, we present a more detailed temperature-dependence study of THz absorption by endohedral 3 and 4 isotopes between 5 and 220 K. Also, we obtained a better fit of line intensities by including an r3 term in the expansion of the dipole moment in the helium atom displacement r. The temperature dependence and the new fit of line intensities confirms the assignment of the He atom translational energy levels and the accuracy of the derived potential energy surface reported in our previous paper.41
2 Theory
The potential energy surface of the He atom stems from its interaction with the interior of the C60 molecule. Although the molecule has icosahedral symmetry we approximate it by spherical symmetry. Within this approximation we may ignore the coupling of the C60 rotations and librations to the He motion. Since the masses of and C60 He are different by two orders of magnitude, MC60 ≫ MHe, we assume that the C60 center of the mass position is not affected by the motion of C60 the He atom. Also, we ignore the effect of translational motion of in the crystal lattice and its molecular vibrations. Thus, in this model the He atom moves in a spherically symmetric rigid potential well. This motion can be described by the harmonic spherical oscillator model42–44 where the coordinate r is the displacement of He center of mass from the C60 center of mass. To obtain agreement with the observed THz spectra, we add anharmonic corrections to the harmonic potential function. This makes the separation of energy levels non-equidistant.In general, a free He atom does not absorb electromagnetic radiation at THz frequencies due to the lack of an electric dipole moment. However, similar to the encapsulated hydrogen molecule,15,22,23 He atoms acquire a dipole moment from the interaction with the inner surface of C60. This interaction is modulated by the translational motion of the He atom causing the translational modes to become THz-active.
2.1 Anharmonic spherical oscillator
The Hamiltonian Ĥ for one helium trapped in a spherical potential well is given asĤ = Ĥ0 + ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) ′, ′, | (1) |
![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) ′ = V4r4 + V6r6 ′ = V4r4 + V6r6 | (2) |
 | (3) |
The harmonic Hamiltonian has eigenstates
|n,![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ,m〉 = Rn ,m〉 = Rn![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) (r)Y (r)Y![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) m(θ,ϕ), m(θ,ϕ), | (4) |
 | (5) |
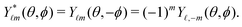 | (6) |
The radial wavefunction is42
 | (7) |
 | (8) |
The eigenenergies of the harmonic Hamiltonian (3) are
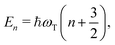 | (9) |
 | (10) |
The problem can be solved by diagonalizing the Hamiltonian (1) using the basis set of functions (4) where n ∈ {0, 1,…, nmax}. The angular momentum quantum number ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) is given by
is given by ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ∈ {0, 2… n} for even n and
∈ {0, 2… n} for even n and ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ∈ {1, 3… n} for odd n.
∈ {1, 3… n} for odd n.
It is practical to use the reduced matrix elements, 〈![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) f‖Tk‖
f‖Tk‖![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i〉, of the spherical tensor operator Tkq of rank k, q ∈ {−k, −k + 1,…, k}, which are independent of m and q.46 The matrix element of Tkq is
i〉, of the spherical tensor operator Tkq of rank k, q ∈ {−k, −k + 1,…, k}, which are independent of m and q.46 The matrix element of Tkq is
 | (11) |
 | (12) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) f −
f − ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i| ≤ k ≤
i| ≤ k ≤ ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) f +
f + ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i and mf + q + mi = 0 are not satisfied; if mf = q = mi = 0, then the 3j-symbol is not zero if the sum
i and mf + q + mi = 0 are not satisfied; if mf = q = mi = 0, then the 3j-symbol is not zero if the sum ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) f + k +
f + k + ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i is an even number.46
i is an even number.46
For the isotropic spherical potential, eqn (2), the rank of potential spherical operator is k = 0. Therefore, the states with different ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) and m are not mixed. Perturbation VNrN mixes states with different n and the eigenstate of Hamiltonian (1), |τ,
and m are not mixed. Perturbation VNrN mixes states with different n and the eigenstate of Hamiltonian (1), |τ,![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ,m〉, is a linear superposition of states |n,
,m〉, is a linear superposition of states |n,![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ,m〉, eqn (4). Evaluation of matrix elements of the radial part of harmonic oscillator wavefunction, 〈Rnf
,m〉, eqn (4). Evaluation of matrix elements of the radial part of harmonic oscillator wavefunction, 〈Rnf![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) f|rN|Rni
f|rN|Rni![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i〉 with
i〉 with ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) f =
f = ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i, shows that non-zero elements are |nf − ni| ≤ N where ni and nf must have the same parity. Because each energy level of the anharmonic Hamiltonian (1) is (2
i, shows that non-zero elements are |nf − ni| ≤ N where ni and nf must have the same parity. Because each energy level of the anharmonic Hamiltonian (1) is (2![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) + 1)-fold degenerate in m, it is sufficient to include only the |n,
+ 1)-fold degenerate in m, it is sufficient to include only the |n,![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ,0〉 functions in the basis set. This reduces the number of states by a factor 2
,0〉 functions in the basis set. This reduces the number of states by a factor 2![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) + 1 for each
+ 1 for each ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) .
.
2.2 THz absorption line strengths of the spherical oscillator
We write the dipole moment in spherical harmonics Y1q(θ,ϕ) as a function of He displacement keeping the first two terms, linear and cubic in r, | (13) |
 as follows from the normalization of spherical harmonics,
as follows from the normalization of spherical harmonics,  .
.
Using the Fermi golden rule we write the THz absorption line area for the radiation polarized linearly in the z direction, which couples to the dipole moment z component, dz = d10. Since the energy E of Hamiltonian (1) is degenerate in initial and final state quantum numbers m we perform the summation over mi and mf for a given transition frequency, ωfi = (Ef − Ei)/hc0. The absorption line area Sfi is
 | (14) |
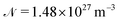 is the number density of molecules in the solid and
is the number density of molecules in the solid and  is the filling factor;
is the filling factor;  where
where  is the number density of filled and
is the number density of filled and  is the number density of empty cages. All units are SI and the transition frequency, ωfi, is measured in wavenumbers, number of waves in one meter, [ωfi] = m−1. pi and pf are the thermal Boltzmann populations of the initial and final states:
is the number density of empty cages. All units are SI and the transition frequency, ωfi, is measured in wavenumbers, number of waves in one meter, [ωfi] = m−1. pi and pf are the thermal Boltzmann populations of the initial and final states: | (15) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) j + 1 is the degeneracy of state |τj,
j + 1 is the degeneracy of state |τj,![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) j,mj〉 in quantum number mj.
j,mj〉 in quantum number mj.
The sum over mi and mf in eqn (14) is
 | (16) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i〉 is the reduced matrix element of d1q with the angular part given by eqn (12). Since for the dipole moment k = 1, a selection rule of THz absorption by a spherical oscillator,
i〉 is the reduced matrix element of d1q with the angular part given by eqn (12). Since for the dipole moment k = 1, a selection rule of THz absorption by a spherical oscillator, ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) f =
f = ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i ± 1, follows from the properties of the 3j-symbol. The selection rule for n comes from the matrix element of the radial part of harmonic oscillator wavefunction,〈Rnf
i ± 1, follows from the properties of the 3j-symbol. The selection rule for n comes from the matrix element of the radial part of harmonic oscillator wavefunction,〈Rnf![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i±1|rN|Rni
i±1|rN|Rni![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i〉. For the linear term in eqn (13) it is nf = ni ± 1 and for the cubic term it is |nf − ni| ≤ 3, where ni and nf must have different parities.
i〉. For the linear term in eqn (13) it is nf = ni ± 1 and for the cubic term it is |nf − ni| ≤ 3, where ni and nf must have different parities.
3 Experimental
3He@C60 and 4He@C60 were synthesised using a solid-state process for the critical step, as described in ref. 20. The initial filling factors were 30% to 50%. The samples were further purified by recirculating HPLC on Cosmosil Buckyprep columns to remove trace impurities of H2O@C60 and empty C60. Finally, the 4He@C60 sample had a filling factor of f0 = (88.2 ± 0.5)% while the 3He@C60 had a filling factor of f0 = (97.2 ± 0.5)%, as determined by 13C NMR. Samples were sublimed under vacuum.The sublimed powdered sample was put inside the 3 mm diameter hole of cylindrical brass frame and pressed under the vacuum into a pellet. The mass and thickness of the 3He@C60 pellet were 28 mg and 2.16 mm and of the 4He@C60 pellet were 21 mg and 1.72 mm. The brass frame with the pellet was inserted into a sample chamber with two thin-film polypropylene windows and with a vacuum line for pumping and filling with helium heat exchange gas. The sample chamber was in a thermal contact with the cold finger of the cryostat. The cryostat was placed inside the interferometer Vertex 80v sample compartment. The cold finger with the sample chamber was moved up and down by letting the beam through the sample chamber or through a reference hole with 3 mm diameter. The transmission spectra were recorded up to 300 cm−1 using a Hg lamp, a 6 μm Mylar beam splitter, and a 4 K bolometer. The spectral resolution was 0.2 cm−1 which was found to be smaller than the width of the He absorption lines or their sub-components.
The absorption spectra were calculated from  where α(ω) is the absorption coefficient,
where α(ω) is the absorption coefficient,  is the transmission, and
is the transmission, and  is the amount of light lost in reflections from the pellet surfaces and the sample chamber windows. The measured transmission is
is the amount of light lost in reflections from the pellet surfaces and the sample chamber windows. The measured transmission is  , where Is(ω) is the beam intensity at the bolometer with the sample chamber in the beam and Ir(ω) is the beam intensity at the bolometer with the reference hole in the beam. The reflection losses and the absorption in the sample chamber windows affect the background absorption but do not affect the absorption line areas of helium.
, where Is(ω) is the beam intensity at the bolometer with the sample chamber in the beam and Ir(ω) is the beam intensity at the bolometer with the reference hole in the beam. The reflection losses and the absorption in the sample chamber windows affect the background absorption but do not affect the absorption line areas of helium.
4 Results
The THz absorption spectra of 3He@C60 and 4He@C60 at different temperatures in a spectral range between 75 and 150 cm−1 are shown in Fig. 1. The baseline of the 5 K spectrum was fitted and then subtracted. The same procedure but covering only the spectral range around the line no. 1 was applied to the spectra of higher temperatures. For the rest of the spectra above the line no. 1 the average of 5 and 15 K spectra was used for the baseline subtraction. The broad line at about 140 cm−1 in the 5 K spectrum is the absorption feature of the mylar windows on the sample cell.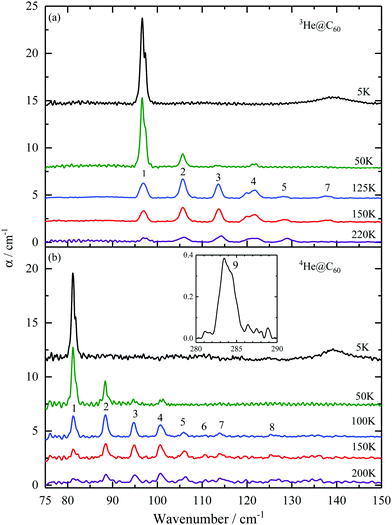 | ||
| Fig. 1 Temperature dependence of THz absorption spectra of 3He@C60 (a) and 4He@C60 (b). Absorption lines are numbered according to the transitions between the energy levels as shown in Fig. 3. Inset to (b) shows the 4He@C60 line no. 9 at 5 K. The line intensities are not corrected for the filling factor f0, see eqn (14). | ||
The spectra from the two isotopes share the same pattern of absorption spectra but with the 4He lines shifted to higher energy relative to the 4He lines. The line intensities of the two isotopes are similar. For 3He, a line at 97 cm−1 is the only line present at 5 K and its intensity decreases with increasing temperature. This indicates that it corresponds to a transition from the ground state. With the rise in temperature, energy levels above the ground state become thermally populated and we observe six more absorption lines: 106, 114, 120, 122, 128 and 138 cm−1.
In the case of 4He@C60, we observed two transitions from the ground state, at 81 cm−1 and at 284 cm−1. By increasing the temperature additional absorption lines become visible at 88, 95, 101, 106, 111, 114 and 126 cm−1. The line no. 9 starts from the ground state as is confirmed by its T dependence, Fig. 7 in the Appendix. This line cannot be detected in 3He@C60 THz spectra because of the strong absorption by the fullerene at its resonance frequency, 340.6 cm−1 in Table 4, but was observed in the inelastic neutron scattering spectrum, line no. e in ref. 41.
The lowest energy peak has a two-component structure which is visible at low temperatures. The separation of components is approximately 0.8 cm−1 for 3He@C60 and 0.7 cm−1 for 4He@C60, Tables 4 and 5 in the Appendix. We did not see any additional structure at the best resolution we used, 0.2 cm−1. The possible origin of line no. 1 and no. 9 splitting is discussed in Section 5.
The synthetic spectra were fitted with a spherical oscillator model, as described in the Appendix, and the result is shown in Fig. 2. The best spherical oscillator model fit parameters are listed in Table 2. As compared to our previous fit41 the extra term, A3r3, was added to the dipole moment expansion, eqn (13). This gives a better fit of the line intensities. The spherical oscillator fit revealed that line number 4 consists of three closely spaced transitions, and lines 5 and 6 of two transitions. The energy diagram together with the numbered transitions is shown in Fig. 3 and the energies of corresponding levels in Table 2. The list of line frequencies and intensities calculated with the spherical oscillator model best fit parameters for 3He (125 K) and 4He (100 K) is given in the Appendix, Tables 4 and 5.
 | ||
| Fig. 2 Synthetic experimental THz spectrum (solid black line) and the best fit result (blue dashed line) of 3He@C60 at 125K (a) and 4He@C60 at 100 K (b). | ||
 | ||
Fig. 3 Energy level diagram and THz transitions of He@C60. The principal translational quantum number is n and the angular momentum quantum number is ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) . The energy levels of a spherical harmonic oscillator are degenerate in . The energy levels of a spherical harmonic oscillator are degenerate in ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , shown on left. The anharmonic terms in the potential, and V6, split the energy levels with different , shown on left. The anharmonic terms in the potential, and V6, split the energy levels with different ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) and each energy level has the unique and each energy level has the unique ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) value within the spherical symmetry, on the right. The mixing of states with different n by V4 - and V6 -term is not shown on the diagram. The THz transitions between the translational energy levels observed in the experiment are labeled with numbers, see Fig. 1 and Tables 4 and 5, and the translational energies are in Table 2. value within the spherical symmetry, on the right. The mixing of states with different n by V4 - and V6 -term is not shown on the diagram. The THz transitions between the translational energy levels observed in the experiment are labeled with numbers, see Fig. 1 and Tables 4 and 5, and the translational energies are in Table 2. | ||
In Fig. 4 the areas of the first five THz absorption lines of 3He@C60 and 4He@C60 are compared with the temperature dependence of line areas derived from the spherical oscillator model fit. The line areas at each temperature are calculated using the parameters {V2,V4,V6,A1,A3} obtained from the anharmonic oscillator model fit of 125 K and 100 K spectra of 3He and 4He, respectively. For each line the line areas are normalized to the maximum of the theoretical intensity versus temperature curve. Same normalization factors are applied to each experimental line respectively.
 | ||
| Fig. 4 Temperature dependence of normalized THz absorption lines areas Sn of 3He@C60, panels (a) and (b) and of 4He@C60, panels (c) and (d). Symbols are experimental line areas with errors from the fit with Gaussian lines and solid lines are theoretical areas calculated with the parameters from Table 1. Line areas have been normalized to the maximum value in the T dependence of theoretical area for each line. The lines are numbered according to the transitions shown in Fig. 3 and listed in Tables 4 and 5. | ||
5 Discussion
The overlap of potential energy curves of two He isotopes proves the reliability of our fit as the difference of potential curves is only about ±0.5 cm−1 over the energy scale probed by THz spectroscopy, Fig. 5(b). The potential is strongly anharmonic. It can be seen that for the displacement r > 75 pm the anharmonic contribution to the potential energy, V4r4 + V6r6, starts to dominate over the harmonic part, V2r2. The significance of anharmonic correction is also evidenced by the composition of the oscillator wave function: as the energy increases the single n-component of a wavefunction becomes less dominant meaning that the components with other n values are mixed in Table 2. States with different![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) values are not mixed by the isotropic potential and each level is 2
values are not mixed by the isotropic potential and each level is 2![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) + 1 degenerate in the quantum number m.
+ 1 degenerate in the quantum number m.
 | ||
| Fig. 5 (a) Potential energy curves of 3He and 4He, V (r) = V2r2 + V4r4 + V6r6, calculated with parameters from Table 1. The harmonic part of 3He potential curve, V2r2, is plotted as blue solid line. The potential curves of two isotopes, green solid line of 3He and red dashed line of 3He, are indistinguishable in this plot. (b) The difference between the potential curves of 3He and 4He, ΔV = V3 − V4, is less than ±0.5 cm−1. | ||
| κ i | 3He@C60 | 4He@C60 | Unit |
|---|---|---|---|
| V 2 | (2.500 ± 0.015) × 10−3 | (2.46 ± 0.04) × 10−3 | meV pm−2 |
| V 4 | (3.64 ± 0.03) × 10−7 | (3.77 ± 0.08) × 10−7 | meV pm−4 |
| V 6 | (2.560 ± 0.017) × 10−11 | (2.46 ± 0.06) × 10−11 | meV pm−6 |
| A 1 | (3.83 ± 0.10) × 10−4 | (3.73 ± 0.22) × 10−4 | D pm−1 |
| A 3 | (1.7 ± 0.3) × 10−8 | (2.3 ± 0.6) × 10−8 | D pm−3 |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) (single-valued for each energy level), and the amplitude squared of the main component of eigenstate with the principal quantum number n. The zero point energy 125.7 cm−1 (106.5 cm−1) of 3He (4He) has been subtracted
(single-valued for each energy level), and the amplitude squared of the main component of eigenstate with the principal quantum number n. The zero point energy 125.7 cm−1 (106.5 cm−1) of 3He (4He) has been subtracted
| 3He@C60 | 4He@C60 | ||||||
|---|---|---|---|---|---|---|---|
| E/cm−1 | ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) |
n | |ξn|2 | E/cm−1 | ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) |
n | |ξn|2 |
| 0 | 0 | 0 | 0.95 | 0 | 0 | 0 | 0.95 |
| 96.8 | 1 | 1 | 0.87 | 81.4 | 1 | 1 | 0.88 |
| 202.6 | 2 | 2 | 0.77 | 169.8 | 2 | 2 | 0.79 |
| 218.3 | 0 | 2 | 0.64 | 182.1 | 0 | 2 | 0.68 |
| 316.3 | 3 | 3 | 0.65 | 264.5 | 3 | 3 | 0.69 |
| 340.6 | 1 | 3 | 0.43 | 283.7 | 1 | 3 | 0.48 |
| 437.3 | 4 | 4 | 0.54 | 365.1 | 4 | 4 | 0.58 |
| 469.4 | 2 | 6 | 0.39 | 390.6 | 2 | 6 | 0.39 |
| 483.0 | 0 | 6 | 0.40 | 401.1 | 0 | 6 | 0.40 |
| 565.1 | 5 | 5 | 0.43 | 471.1 | 5 | 5 | 0.47 |
| 604.3 | 3 | 7 | 0.36 | 502.0 | 3 | 7 | 0.38 |
| 625.8 | 1 | 7 | 0.31 | 519.0 | 1 | 7 | 0.35 |
| 699.3 | 6 | 8 | 0.37 | 582.2 | 6 | 6 | 0.38 |
| 745.1 | 4 | 10 | 0.29 | 618.2 | 4 | 8 | 0.31 |
| 774.0 | 2 | 10 | 0.30 | 640.8 | 2 | 10 | 0.30 |
| 787.4 | 0 | 10 | 0.30 | 650.5 | 0 | 10 | 0.31 |
Experimentally determined translational energies of A@C60 endohedral complexes are summarized in Table 3. Although the anharmonic contributions to the potential have been determined experimentally,15,22,23 a more detailed comparison with is not meaningful as firstly, has translation–rotation coupling terms in the potential and secondly, it misses the V6 term in the potential fit. The shape of the potential curve is not known for other A species. We approximate the translational energy, ωT, as the difference of energies between the ground state and the first excited translational state,. Assuming harmonic approximation, VA2 ≈ MAω012/2, we scaled the potential of other species, VA2, relative to hydrogen, V2H2. The last column demonstrates that  scaling of translational frequency of different A species has no predictive power. In general, the interaction of neutral A with can be separated into repulsive interaction and electrostatic interaction expanded in induction and dispersion terms.33 Since has no electric dipole nor quadrupole moment the induction terms are zero. The absence of induction terms may only partially explain the “softness” of potential because the dominant interactions are repulsion and dipole–dipole dispersion for endohedral atoms and molecules.33 In general, modern quantum chemistry calculations of He@C60 give a good description of V(r).41
scaling of translational frequency of different A species has no predictive power. In general, the interaction of neutral A with can be separated into repulsive interaction and electrostatic interaction expanded in induction and dispersion terms.33 Since has no electric dipole nor quadrupole moment the induction terms are zero. The absence of induction terms may only partially explain the “softness” of potential because the dominant interactions are repulsion and dipole–dipole dispersion for endohedral atoms and molecules.33 In general, modern quantum chemistry calculations of He@C60 give a good description of V(r).41
To further validate the potential parameters of obtained from the fit of single high temperature spectra we compare the temperature dependence of line intensities of measured and calculated spectra, Fig. 4. The parameters determined from the 3He (4He) fit at 125 K (100 K) describe the temperature dependence from 5 to 200 K rather well except for the line no. 5. Other lines, no. 6, no. 7, no. 8 and no. 9, are weak and their intensities could not be determined reliably from the experimental spectra and therefore their T dependence was not analyzed. The intensity of the lowest frequency line no. 1, transition from the ground state, is overestimated by the fit at the lowest temperatures. The discrepancy of calculated and measured T dependence could be due the thermal motion of C60 not taken into account in our model.
The dipole moment of is induced by the displacement from the C60 cage center. The estimate for the displacement of the first transition can be made from the potential energy which is half of the total energy, V(r) = E1/2. Using the data from Table 2, E1 = 222.5 cm−1 (3He) and E1 = 187.9 cm−1 (4He), we obtain the displacement to be about 60 pm. The dipole moment induced by 60 pm displacement is d = A1r + A3r3 = 2.7 × 10−2 D, small compared to permanent dipole moments of molecules. For example, the permanent screened dipole moment of C60 endohedral water is about 0.5 D.49,50
Transition no. 9 starts from the ground state with ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 0 and predominantly with n = 0 radial content. The final state is the
= 0 and predominantly with n = 0 radial content. The final state is the ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1 state, see Fig. 3 and Table 2, but with predominantly n = 3 radial part. It is an allowed electric dipole transition with the selection rule Δ
= 1 state, see Fig. 3 and Table 2, but with predominantly n = 3 radial part. It is an allowed electric dipole transition with the selection rule Δ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = +1 but three translation quanta are created, Δn = +3. All other lines, no. 1 to no. 8, are ordinary one quantum transitions, Δn = +1. The r3 term in the dipole moment expansion allows the Δn = + 3 excitation by radiation. However, because of the mixing of states by anharmonic potential, n = 0 state is mixed with n = 2 and n = 3 state is the mixed n = 1 state, the linear term in r of the dipole moment expansion with the selection rule Δn = +1 can induce the three-quantum transition. Thus, in there are two factors what activate the three-quantum transition, the anharmonicity of the potential and the r3 term in the dipole moment expansion.
= +1 but three translation quanta are created, Δn = +3. All other lines, no. 1 to no. 8, are ordinary one quantum transitions, Δn = +1. The r3 term in the dipole moment expansion allows the Δn = + 3 excitation by radiation. However, because of the mixing of states by anharmonic potential, n = 0 state is mixed with n = 2 and n = 3 state is the mixed n = 1 state, the linear term in r of the dipole moment expansion with the selection rule Δn = +1 can induce the three-quantum transition. Thus, in there are two factors what activate the three-quantum transition, the anharmonicity of the potential and the r3 term in the dipole moment expansion.
Two absorption lines, no. 1 and no. 9, show partially resolved fine structure at 5 K, Fig. 1. These lines are the transitions from the ground state with ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 0 to the state
= 0 to the state ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1, see Fig. 3 and Table 2. In the icosahedral potential the first Ag symmetry representation after fully spherical potential, rank k = 0, is a combination of spherical harmonics of rank k = 6.51 Rank 6 term in the potential splits states with
= 1, see Fig. 3 and Table 2. In the icosahedral potential the first Ag symmetry representation after fully spherical potential, rank k = 0, is a combination of spherical harmonics of rank k = 6.51 Rank 6 term in the potential splits states with ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ≥ 3, which cannot explain the fine structure of helium line no. 1 and no. 9. To explain the spectral line splitting, a potential with symmetry lower than the icosahedral or two different exohedral environments must be invoked.
≥ 3, which cannot explain the fine structure of helium line no. 1 and no. 9. To explain the spectral line splitting, a potential with symmetry lower than the icosahedral or two different exohedral environments must be invoked.
Fullerene molecules stop rotating below 90 K.52 This leads to two sites distinguished by the relative orientation of the central cage and its 12 nearest-neighbor C60.53 In the pentagonal orientation the electron-rich double bonds are facing pentagonal rings and in the hexagonal orientation the electron-rich double bonds are facing hexagonal rings of nearest-neighbor cages. It was proposed by Felker et al.54 that the orientational order creates electrostatic field that interacts with the quadrupole moment of endohedral molecule. Their model explains the splitting of J = 1 rotational state observed in H2@C60,22,23,28 HF@C6016 and H2O@C60.49,55,56 This mechanism is not applicable to the helium atom because it does not have rotational degrees of freedom nor quadrupole moment. The icosahedral symmetry of V(r) could still be disturbed by the nearest-neighbor C60 molecules. A splitting similar to the splitting of line no. 1 was observed in H2@C60 for the ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 0 →
= 0 → ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1 transition of para-H2@C60 in the J = 0 rotational state.22,23 Application of pressure changes the relative population of pentagon- and hexagon-oriented molecules.57 The analysis of the inelastic neutron scattering spectra of pressure-treated H2@C60 shows that the potential and the energy levels of are sensitive to the orientation of neighboring cages.28 Similar THz and infrared spectroscopy experiments are planned to verify the effect of orientational order on the potential energy function of endohedral molecules and atoms in C60.
= 1 transition of para-H2@C60 in the J = 0 rotational state.22,23 Application of pressure changes the relative population of pentagon- and hexagon-oriented molecules.57 The analysis of the inelastic neutron scattering spectra of pressure-treated H2@C60 shows that the potential and the energy levels of are sensitive to the orientation of neighboring cages.28 Similar THz and infrared spectroscopy experiments are planned to verify the effect of orientational order on the potential energy function of endohedral molecules and atoms in C60.
In summary, with the THz absorption spectroscopy we have determined the energy level structure of quantized translational motion of single 3He and 4He atoms trapped in the C60 molecular cages. The fitted potential energy curves and the induced dipole moments of two isotopes overlap with high precision. However, there are deviations between the modeled and measured spectra. Firstly, the fine structure of spectral lines observed in the low temperature spectra cannot be explained by icosahedral symmetry of C60 molecule. Secondly, there are some discrepancies between the measured and modeled spectra in the line intensities and their temperature dependence. Both deviations could be due to the orientational order and the thermal motion of C60 molecules in the solid.
Conflicts of interest
There are no conflicts to declare.Appendix
Fit of anharmonic spherical oscillator and dipole moment parameters
The experimental THz absorption spectrum was fitted using Gaussian line shapes to find the line areas, line widths and frequencies, see Fig. 6. A synthetic experimental spectrum y(ωn), the distance between the points in the spectrum ωn − ωn−1 = Δω/4, was then generated consisting of lines with equal full width at half maximum, Δω = 1.5 cm−1, while keeping the line areas and frequencies of the original experimental lines. The synthetic spectrum approach was needed as the model did not include any line broadening mechanism. | ||
| Fig. 6 THz absorption spectrum of 3He at 125 K (a) and 4He at 100 K (b), black solid line, and the fit with Gaussian lineshapes, blue solid lines. Red dashed line is the sum of Gaussians. The line intensities are not corrected for the filling factor f0, see eqn (14). | ||
The synthetic spectra were fitted using the anharmonic spherical oscillator model. The reduced basis was limited to nmax = 18 providing 100 states in the reduced basis |n,![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 〉. For a given model and basis, matrix elements of the Hamiltonian, eqn (1), and the dipole operator, eqn (13), were evaluated analytically in a symbolic form using the Mathematica software. At each step of minimizing chi squared,
〉. For a given model and basis, matrix elements of the Hamiltonian, eqn (1), and the dipole operator, eqn (13), were evaluated analytically in a symbolic form using the Mathematica software. At each step of minimizing chi squared, 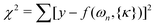 , the Hamiltonian was diagonalized numerically. Here f(ωn,{κ}) is the theoretical spectrum with the same linewidth and lineshape as the synthetic experimental spectrum; {κ} = {V2,V4,V6,A1,A3} is the set of Hamiltonian and dipole operator fit parameters. Errors were calculated using the method described in ref. 49. Adding the V6 term to V4 in the potential reduced χ2 of 3He and 4He fit by three and two times, respectively. The frequencies and intensities of experimental spectra and spectra calculated using the best fit parameters are given in Tables 4 and 5.
, the Hamiltonian was diagonalized numerically. Here f(ωn,{κ}) is the theoretical spectrum with the same linewidth and lineshape as the synthetic experimental spectrum; {κ} = {V2,V4,V6,A1,A3} is the set of Hamiltonian and dipole operator fit parameters. Errors were calculated using the method described in ref. 49. Adding the V6 term to V4 in the potential reduced χ2 of 3He and 4He fit by three and two times, respectively. The frequencies and intensities of experimental spectra and spectra calculated using the best fit parameters are given in Tables 4 and 5.
| Line no. | Experiment | Model fit | ||
|---|---|---|---|---|
| f/cm−1 | S/cm−2 | f/cm−1 | S/cm−2 | |
| 5 K | ||||
| 1 | 96.6 | 8.5 | 96.8 | 11.7 |
| 97.4 | 2.2 | — | — | |
| 9 | — | — | 340.6 | 0.4 |
| 125 K | ||||
|---|---|---|---|---|
| 1 | 96.9 | 2.7 | 96.8 | 2.7 |
| 2 | 105.7 | 3.3 | 105.7 | 3.3 |
| 3 | 113.6 | 2.3 | 113.7 | 2.2 |
| 4 | 119.8 | 0.6 | 121.0 | 1.1 |
| 121.6 | 1.8 | 121.4 | 0.8 | |
| — | — | 122.4 | 0.5 | |
| 5 | 128.1 | 0.3 | 127.8 | 0.5 |
| — | — | 128.8 | 0.4 | |
| 7 | 137.7 | 0.5 | 138.0 | 0.6 |
| Line no. | Experiment | Model fit | ||
|---|---|---|---|---|
| f/cm−1 | S/cm−2 | f/cm−1 | S/cm−2 | |
| 5 K | ||||
| 1 | 81.2 | 6.1 | 81.4 | 8.0 |
| 81.9 | 1.2 | — | — | |
| 9 | 283.3 | 0.3 | 283.7 | 0.3 |
| 284.3 | 0.4 | — | — | |
| 100 K | ||||
|---|---|---|---|---|
| 1 | 81.3 | 2.1 | 81.4 | 2.0 |
| 2 | 88.4 | 2.3 | 88.4 | 2.4 |
| 3 | 94.8 | 1.5 | 94.8 | 1.5 |
| 4 | 100.4 | 0.4 | 100.6 | 0.7 |
| 101.0 | 1.3 | 100.8 | 0.6 | |
| — | — | 101.6 | 0.3 | |
| 5 | 105.9 | 0.5 | 106.0 | 0.3 |
| — | — | 106.7 | 0.2 | |
| 6 | 110.6 | 0.1 | 111.0 | 0.09 |
| — | — | 111.7 | 0.10 | |
| 7 | 113.9 | 0.4 | 113.9 | 0.4 |
| 8 | 125.7 | 0.2 | 125.9 | 0.2 |
Acknowledgements
This research was supported by the Estonian Ministry of Education and Research institutional research funding IUT23-3, Estonian Research Council grant PRG736, the European Regional Development Fund project TK134 and by EPSRC-UK, grant numbers EP/P009980/1 and EP/T004320/1.References
- H. Kroto, J. Heath, S. O'Brian, R. F. Curl and R. E. Smalley, Nature, 1985, 318, 162–163 CrossRef CAS.
- J. R. Heath, S. C. O'Brien, Q. Zhang, Y. Liu, R. F. Curl, F. K. Tittel and R. E. Smalley, J. Am. Chem. Soc., 1985, 107, 7779–7780 CrossRef CAS.
- M. H. Levitt, Philos. Trans. R. Soc., A, 2013, 371, 20120429 CrossRef PubMed.
- Z. Bačić, J. Chem. Phys., 2018, 149, 100901 CrossRef PubMed.
- L. Dunsch and S. Yang, Small, 2007, 3, 1298–1320 CrossRef CAS PubMed.
- M. Saunders, H. A. Jiménez-Vázquez, R. J. Cross and R. J. Poreda, Science, 1993, 259, 1428–1430 CrossRef CAS PubMed.
- M. Saunders, H. A. Jiménez-Vázquez, R. J. Cross, S. Mroczkowski, M. L. Gross, D. E. Giblin and R. J. Poreda, J. Am. Chem. Soc., 1994, 116, 2193–2194 CrossRef CAS.
- M. Saunders, R. J. Cross, H. A. Jiménez-Vázquez, R. Shimshi and A. Khong, Science, 1996, 271, 1693–1697 CrossRef CAS.
- T. Weiske, T. Wong, W. Krätschmer, J. K. Terlouw and H. Schwarz, Angew. Chem., Int. Ed. Engl., 1992, 31, 183–185 CrossRef.
- T. A. Murphy, T. Pawlik, A. Weidinger, M. Höhne, R. Alcala and J.-M. Spaeth, Phys. Rev. Lett., 1996, 77, 1075–1078 CrossRef CAS PubMed.
- C. Knapp, N. Weiden, H. Kass, K.-P. Dinse, B. Pietzak, M. Waiblinger and A. Weidinger, Mol. Phys., 1998, 95, 999–1004 CrossRef CAS.
- K. Komatsu, M. Murata and Y. Murata, Science, 2005, 307, 238–240 CrossRef CAS PubMed.
- Y. Rubin, T. Jarrosson, G.-W. Wang, M. D. Bartberger, K. N. Houk, G. Schick, M. Saunders and R. J. Cross, Angew. Chem., Int. Ed., 2001, 40, 1543 CrossRef CAS PubMed.
- K. Kurotobi and Y. Murata, Science, 2011, 333, 613–616 CrossRef CAS PubMed.
- M. Ge, U. Nagel, D. Hüvonen, T. Rõõm, S. Mamone, M. H. Levitt, M. Carravetta, Y. Murata, K. Komatsu, X. Lei and N. J. Turro, J. Chem. Phys., 2011, 135, 114511 CrossRef PubMed.
- A. Krachmalnicoff, R. Bounds, S. Mamone, S. Alom, M. Concistrè, B. Meier, K. Kouřil, M. E. Light, M. R. Johnson, S. Rols, A. J. Horsewill, A. Shugai, U. Nagel, T. Rõõm, M. Carravetta, M. H. Levitt and R. J. Whitby, Nat. Chem., 2016, 8, 953–957 CrossRef CAS PubMed.
- S. Bloodworth, G. Sitinova, S. Alom, S. Vidal, G. R. Bacanu, S. J. Elliott, M. E. Light, J. M. Herniman, G. J. Langley, M. H. Levitt and R. J. Whitby, Angew. Chem., Int. Ed., 2019, 58, 1–7 CrossRef PubMed.
- S. Bloodworth, G. Hoffman, M. C. Walkey, G. R. Bacanu, J. M. Herniman, M. H. Levitt and R. J. Whitby, Chem. Commun., 2020, 56, 10521–10524 RSC.
- Y. Morinaka, F. Tanabe, M. Murata, Y. Murata and K. Komatsu, Chem. Commun., 2010, 46, 4532–4534 RSC.
- G. Hoffman, M. C. Walkey, J. Gräsvik, G. R. Bacanu, S. Alom, S. Bloodworth, M. E. Light, M. H. Levitt and R. J. Whitby, Angew. Chem., Int. Ed., 2021, 60, 8960–8966 CrossRef CAS PubMed.
- M. Xu, F. Sebastianelli, Z. Bačić, R. Lawler and N. J. Turro, J. Chem. Phys., 2008, 128, 011101 CrossRef PubMed.
- S. Mamone, M. Ge, D. Hüvonen, U. Nagel, A. Danquigny, F. Cuda, M. C. Grossel, Y. Murata, K. Komatsu, M. H. Levitt, T. Rõõm and M. Carravetta, J. Chem. Phys., 2009, 130, 081103 CrossRef CAS PubMed.
- M. Ge, U. Nagel, D. Hüvonen, T. Rõõm, S. Mamone, M. H. Levitt, M. Carravetta, Y. Murata, K. Komatsu, J. Y.-C. Chen and N. J. Turro, J. Chem. Phys., 2011, 134, 054507 CrossRef PubMed.
- T. Rõõm, L. Peedu, M. Ge, D. Hüvonen, U. Nagel, S. Ye, M. Xu, Z. Bačić, S. Mamone, M. H. Levitt, M. Carravetta, J. Chen, X. Lei, N. J. Turro, Y. Murata and K. Komatsu, Philos. Trans. R. Soc., A, 2013, 371, 20110631 CrossRef PubMed.
- A. J. Horsewill, K. S. Panesar, S. Rols, M. R. Johnson, Y. Murata, K. Komatsu, S. Mamone, A. Danquigny, F. Cuda, S. Maltsev, M. C. Grossel, M. Carravetta and M. H. Levitt, Phys. Rev. Lett., 2009, 102, 013001 CrossRef CAS PubMed.
- A. J. Horsewill, S. Rols, M. R. Johnson, Y. Murata, M. Murata, K. Komatsu, M. Carravetta, S. Mamone, M. H. Levitt, J. Y.-C. Chen, J. A. Johnson, X. Lei and N. J. Turro, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 081410 CrossRef.
- A. J. Horsewill, K. S. Panesar, S. Rols, J. Ollivier, M. R. Johnson, M. Carravetta, S. Mamone, M. H. Levitt, Y. Murata, K. Komatsu, J. Y.-C. Chen, J. A. Johnson, X. Lei and N. J. Turro, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 205440 CrossRef.
- S. Mamone, M. R. Johnson, J. Ollivier, S. Rols, M. H. Levitt and A. J. Horsewill, Phys. Chem. Chem. Phys., 2016, 18, 1998–2005 RSC.
- A. L. R. Bug, A. Wilson and G. A. Voth, J. Phys. Chem., 1992, 96, 7864–7869 CrossRef CAS.
- C. Williams, M. Whitehead and L. Pang, J. Phys. Chem., 1993, 97, 11652–11656 CrossRef CAS.
- L. Pang and F. Brisse, J. Phys. Chem., 1993, 97, 8562–8563 CrossRef CAS.
- P. Pyykkö, C. Wang, M. Straka and J. Vaara, Phys. Chem. Chem. Phys., 2007, 9, 2954–2958 RSC.
- C. Wang, M. Straka and P. Pyykkö, Phys. Chem. Chem. Phys., 2010, 12, 6187–6203 RSC.
- F. Cimpoesu, S. Ito, H. Shimotani, H. Takagi and N. Dragoe, Phys. Chem., 2011, 13, 9609–9615 RSC.
- B. Frecus, C. M. Buta, C. I. Oprea, A. Stroppa, M. V. Putz and F. Cimpoesu, Theor. Chem. Acc., 2016, 135, 133 Search PubMed.
- S. Jalife, J. Arcudia, S. Pan and G. Merino, Chem. Sci., 2020, 11, 6642–6652 RSC.
- M. S. Syamala, R. J. Cross and M. Saunders, J. Am. Chem. Soc., 2002, 124, 6216–6219 CrossRef CAS PubMed.
- N. Dragoe, A. M. Flank, P. Lagarde, S. Ito, H. Shimotani and H. Takagi, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 155448 CrossRef.
- E. K. Campbell, E. S. Reedy, J. Rademacher, R. J. Whitby and G. Hoffman, Astrophys. J., 2020, 897, 88 CrossRef CAS.
- S. Patchkovskii and W. Thiel, J. Chem. Phys., 1997, 106, 1796–1799 CrossRef CAS.
- G. R. Bacanu, T. Jafari, M. Aouane, J. Rantaharju, M. Walkey, G. Hoffman, A. Shugai, U. Nagel, M. Jiménez-Ruiz, A. J. Horsewill, S. Rols, T. Rõõm, R. J. Whitby and M. H. Levitt, J. Chem. Phys., 2021, 155, 144302 CrossRef CAS PubMed.
- W. H. Shaffer, Rev. Mod. Phys., 1944, 16, 245–259 CrossRef CAS.
- S. Flügge, Practical Quantum Mechanics, Springer-Verlag, Berlin, 1971, vol. 1 Search PubMed.
- C. Cohen-Tannoudji, B. Diu and F. Laloë, Quantum Mechanics, John Wiley & Sons, 2005 Search PubMed.
- D. A. Varshalovich, A. N. Moskalev and V. K. Khersonskii, Quantum Theory of Angular Momentum, World Scientific, 1988 Search PubMed.
- R. N. Zare, Angular Momentum, John Wiley & Sons, Inc., 1988 Search PubMed.
- D. L. Dexter, Phys. Rev., 1956, 101, 48–55 CrossRef CAS.
- C. C. Homes, P. J. Horoyski, M. L. W. Thewalt and B. P. Clayman, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 7052–7055 CrossRef CAS PubMed.
- A. Shugai, U. Nagel, Y. Murata, Y. Li, S. Mamone, A. Krachmalnicoff, S. Alom, R. J. Whitby, M. H. Levitt and T. Rõõm, J. Chem. Phys., 2021, 154, 124311 CrossRef CAS PubMed.
- B. Meier, S. Mamone, M. Concistrè, J. Alonso-Valdesueiro, A. Krachmalnicoff, R. J. Whitby and M. H. Levitt, Nat. Commun., 2015, 6, 8112 CrossRef CAS PubMed.
- S. L. Altmann and P. Herzig, Point-Group Theory Tables, University of Vienna, Vienna, 2nd edn, 2011 Search PubMed.
- W. I. F. David, R. M. Ibberson, T. J. S. Dennis, J. P. Hare and K. Prassides, Europhys. Lett., 1992, 18, 219–225 CrossRef CAS.
- P. A. Heiney, J. Phys. Chem. Solids, 1992, 53, 1333–1352 CrossRef CAS.
- P. M. Felker, V. Vlček, I. Hietanen, S. FitzGerald, D. Neuhauser and Z. Bačić, Phys. Chem. Chem. Phys., 2017, 19, 31274–31283 RSC.
- C. Beduz, M. Carravetta, J. Y.-C. Chen, M. Concistré, M. Denning, M. Frunzi, A. J. Horsewill, O. G. Johannessen, R. Lawler, X. Lei, M. H. Levitt, Y. Li, S. Mamone, Y. Murata, U. Nagel, T. Nishida, J. Ollivier, S. Rols, T. Rõõm, R. Sarkar, N. J. Turro and Y. Yang, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 12894–12898 CrossRef CAS PubMed.
- K. S. K. Goh, M. Jimenez-Ruiz, M. R. Johnson, S. Rols, J. Ollivier, M. S. Denning, S. Mamone, M. H. Levitt, X. Lei, Y. Li, N. J. Turro, Y. Murata and A. J. Horsewill, Phys. Chem. Chem. Phys., 2014, 16, 21330–21339 RSC.
- B. Sundqvist, Adv. Phys., 1999, 48, 1–134 CrossRef CAS.
| This journal is © the Owner Societies 2022 |

