 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Statistical vibrational autodetachment and radiative cooling rates of para-benzoquinone
Mark H
Stockett
 *a,
James N
Bull
*a,
James N
Bull
 b,
Henning T
Schmidt
b,
Henning T
Schmidt
 a and
Henning
Zettergren
a and
Henning
Zettergren
 a
a
aDepartment of Physics, Stockholm University, Stockholm, Sweden. E-mail: Mark.Stockett@fysik.su.se
bSchool of Chemistry, University of East Anglia, Norwich, UK
First published on 2nd May 2022
Abstract
We report measurements of the statistical vibrational autodetachment (VAD, also called thermionic emission) and radiative cooling rates of isolated para-benzoquinone (pBQ, C6H4O2) radical anions using the cryogenic electrostatic ion storage ring facility DESIREE. The results are interpreted using master equation simulations with rate coefficients calculated using statistical detailed balance theory. The VAD rate is determined by measuring the time-dependent yield of neutral pBQ due to spontaneous electron emission from a highly-excited ensemble of anions formed in an electron-attachment ion source. Competition with radiative cooling quenches the VAD rate after a critical time of τc = 11.00(5) ms. Master equation simulations which reproduce the VAD yield provide an estimate of the initial effective vibrational temperature of the ions of 1100(20) K, and provide insight into the anion formation scenario. A second measurement of the radiative cooling rate of pBQ− stored for up to 0.5 s was achieved using time-dependent photodetachment action spectroscopy across the 2Au ← 2B2g and 2B2u ← 2B2g transitions. The rate at which hot-band contributions fade from the action spectrum is quantified by non-negative matrix factorisation. This is found to be commensurate with the average vibrational energy extracted from the simulations, with 1/e lifetimes of 0.16(3) s and 0.1602(7) s, respectively. Implications for astrochemistry are discussed.
1 Introduction
Quinones are ubiquitous links in biochemical electron transport chains, including the classic Z-scheme of photosynthesis.1para-Benzoquinone (pBQ, C6H4O2, Fig. 1) is considered the archtypical “electrophore” of the quinone family. Previous studies have found that isolated pBQ has the ability to capture and retain electrons,2–4 and that its electronic structure is only weakly perturbed by environmental interactions such as nano-solvation.5,6Quinones may also play a role in the chemistry of interstellar clouds.7,8 For example, irradiation of Polycyclic Aromatic Hydrocarbons (PAHs) in cosmic ice analogs is known to efficiently produce quinone-functionalised species in laboratory experiments.9–14 In dark interstellar clouds, where functionalised aromatic molecules have been recently observed,15,16 molecular anions are thought to be the dominant carriers of negative charge.17 Given their efficient electron capture dynamics and high electron affinities, quinone functionalised PAHs, dubbed QPAHs, could contribute significantly to this role even if they are present in low concentrations relative to non-functionalised PAHs.
The aim of the present study is to provide benchmark data for astrochemical models considering the role of QPAH anions in space. pBQ− is chosen as the target molecule due to the wealth of knowledge about its formation process and spectroscopy in vacuo. We focus on the destruction side of the anion lifecycle, measuring the absolute neutralisation rate of pBQ− by statistical Vibrational Autodetachment (VAD, also called thermionic emission). Radiative cooling by emission of infrared photons corresponding to vibrational transitions of pBQ− competes with VAD at energies close to the electron affinity. We determine the rates for VAD and radiative cooling by measuring the time-dependent yield of neutral pBQ due to spontaneous electron emission from a highly-excited ensemble of anions formed in an electron-attachment ion source. The results of master equation simulations, with rate coefficients calculated from detailed balance expressions, are in agreement with the experimental result, given reasonable assumptions about the initial vibrational energy distribution of the ensemble.
To further validate our statistical model, we perform two-dimensional (i.e. storage-time dependent) action spectroscopy on the stored anions up to 0.5 s after formation. The rates at which partially-resolved spectral features vary in relative intensity with storage time are extracted from the 2D action spectra using non-negative matrix factorisation, and agree with the results of our simulations. On longer timescales of up to 5 s, the anion spectrum asymptotically approaches one resembling room temperature.
2 Materials and methods
2.1 Experiments
Experiments were conducted using the Symmetric Ring of the DESIREE (Double ElectroStatic Ion Ring ExpEriment) infrastructure at Stockholm University.18 Cryogenic cooling of the storage ring, which is schematically shown in Fig. 1, to a temperature of approximately 13 K results in a residual gas density on the order of ∼104 cm−3, consisting mosly of H2.19 These conditions enable isolation of reactive ions in a collision free environment for hours.20,21 Cryogenic electrostatic ion storage devices like DESIREE feature sampling times exceeding 1 s, which is suitable for observing delayed processes such as statistical VAD that are relevent for astrochemistry.22,23pBQ (Sigma-Aldrich >98%) was sublimed from powder in a resistively heated (310 K) ampule connected to a home-built electron-attachment ion source based on the design of Yamada et al.24 Anions extracted from the source were accelerated to 10 keV. Mass-selected beams of pBQ− (m/z = 108) were stored in the DESIREE ion storage ring illustrated in Fig. 1.
After ion injection into the DESIREE storage ring, neutral products are formed from ions that still possess significant internal energy from their formation in the ion source. Neutrals formed in the observation arm (upper straight section in Fig. 1) of the storage ring continue to travel with high velocity towards the detector system. Neutrals striking this detector impact a glass plate with a graphene coating which emits secondary electrons that in turn are detected by the micro-channel plate (MCP). This arrangement allows for colinear overlap of the laser light with the ion beam in this straight section. The detector utilises custom ultra-high dynamic range MCPs (Photonis) that are suitable for high count rates at cryogenic temperatures.25
The measured neutral yield R (t), in counts per revolution, is related to the absolute decay rate Γ (t) by:
 | (1) |
An OPO laser system (EKSPLA NT242, 1 kHz frequency, 5 μJ per pulse unfocused) provided light at wavelengths resonant with the electronic transitions of pBQ− (405–560 nm). Only prompt photo-action was observed, yielding a single peak of laser-induced signal over background following each laser shot, delayed by the flight time to the detector. Each signal peak is integrated and the counts in a background window are subtracted to give a net laser-induced signal. The laser wavelength was incremented between ion injections to record two-dimensional (2D, i.e. storage-time dependent) action spectra.
The 2D action spectra were analysed by non-negative matrix factorisation (NMF). NMF is a variational method where the data matrix X, which is composed of action spectra recorded at n different storage times and m laser wavelengths, is approximated as X = WH. H is an l × m array of l < n, m latent component spectra with time-dependent weights given by W. We choose l = 2 components, with an initial guess for H being two spectra of random numbers. We employ a multiplicative update solver to minimise the Kullback–Leibler divergence ||X–WH||KL, as implemented in the NMF routine in the scikit-learn package written in Python.27 Our best estimates of W and H are taken as the mean values of the results of 128 runs of the algorithm with different initial random seeds, with uncertainties given by their standard deviations. Compared to other dimensionality-reduction procedures such as principal component analysis, NMF includes the constraint that W and H are strictly non-negative, corresponding to the physical constraint that the neutral yield must be non-negative. This leads to the straightforward interpretation of the component spectra, but with the caveat that we must choose the number l of components to model a priori. For the datasets presented here, attempts to fit models with l > 2 components resulted in components representing only spurious statistical fluctuations.
2.2 Simulations
Our master equation simulation approach has previously been sucessfully applied to carbon cluster anions29,30 and PAH cations.26,31,32 The rate coefficient for statistical VAD is obtained from the detailed balance expression:33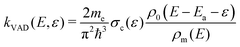 | (2) |
The electron capture cross section of the neutral is approximated by the Langevin cross section:33
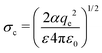 | (3) |
It is worth noting that the term VAD is also used by the photoelectron spectroscopy and femtosecond/picosecond time-resolved dynamics community to explain non-statistical autodetachment processes facilitated by certain vibrational modes. In those cases, autodetachment occurs from excited electronic states or dipole-bound states before statistical intramolecular energy redistribution occurs. The statistical VAD mechanism in this work (called thermionic emission in photo–electron literature) is due to electron loss from the ground electronic state of the anion after intramolecular energy redistribution.
The infrared (vibrational) radiative cooling rate coefficient kIR is calculated within the Simple Harmonic Cascade approximation:37
 | (4) |
There are no known electronic excited states of pBQ− situated below the detachment threshold, and thus recurrent fluorescence38 – radiative cooling by optical emission from thermally populated excited states – is not expected to be relevant in the present experiments. Starting from an initial vibrational energy distribution g(E, t = 0) normalised such that  , radiative cooling propagates the distribution according to the Master equation:
, radiative cooling propagates the distribution according to the Master equation:
 | (5) |
The first term in brackets represents ν + 1→ ν emission from levels above E while the second is ν → ν − 1 emission to levels below E. Dissociation depletes the population by dg (E, t)/dt = − kd(E)g(E, t) = − Γ(t). The time step dt is chosen to match the experimental data, with 32 extra points prior to the first experimental time bin to allow for the ion transit time from the source to the storage ring.
The inset of Fig. 2 shows the survival probability of pBQ− derived from a series of simulations initialised with mono-energetic vibrational energy distributions. Radiative cooling competes with VAD for vibrational energies up to about 0.2 eV above Ea. This range corresponds roughly to the energy of the dominant IR-active transition, the asymmetric stretch at 1545 cm−1.
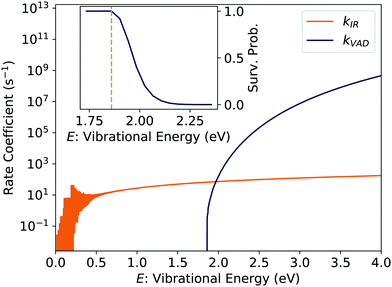 | ||
| Fig. 2 Calculated rate coefficients for infrared radiative cooling (kIR) statistical vibrational autodetachment (kVAD) of pBQ−. The inset shows the survival probability near the electron affinity Ea = 1.860 eV.28 | ||
3 Results
3.1 Neutralisation rate
The neutral yield from source-heated pBQ− is shown in Fig. 3. The right vertical axis gives the experimental counts per revolution accumulated over 6400 storage cycles. The left vertical axis is the neutralization rate given by eqn (1). At early times, the rate follows a power law Γ(t) ∝ 1/t, which is typical for ensembles of molecules with broad energy distributions.39 After a critical time τc, an exponential cutoff is observed and interpreted as “quenching” of the neutralization process by competition with radiative cooling,40 giving the decay rate: | (6) |
 | ||
| Fig. 3 Neutral yield from pBQ− formed in an electron attachment ion source. The uncertainty in the experimental count (“Expt.”) is given by the shaded area. The curve labelled ”Fit” is a fit to eqn (6). The collision-limited beam storage lifetime is τstore = 250(90) s. Two simulation results are shown for the best fit parameters from the two formation scenarios (see text). | ||
The dotted curve labeled ‘Fit’ in Fig. 3 is a fit to this equation. The constant count rate at times >100 ms is due to collisions with residual gas in the storage ring which limit the beam storage lifetime τstore = 250(90) s; the detector dark count rate has been subtracted. As has been noted in previous studies,30 the fitted value of τc = 11.00(5) ms is close to the inverse of the calculated infrared radiative cooling rate coefficient (Fig. 2) at the electron binding energy i.e.1/kIR (Ea) = 15 ms.
We have simulated the neutralisation rate using the master equation approach described in Section 2.2. To model the initial vibrational energy distribution g (E, t = 0), we considered two scenarios for the formation of pBQ−: (I) electron attachment to isolated pBQ, and (II) stabilisation of nascent hot anions through collisions with background gas in the ion source and/or attachment to pBQ clusters. Formation of pBQ− is known to occur by electron attachment to the 2Au shape resonance lying ∼1 eV above the neutral ground state followed by rapid internal conversion to the anionic 2B2g ground state.2,41 However, both time-resolved and frequency-resolved photo–electron experiments on pBQ− have shown that the 2Au state has a sub-picosecond lifetime, decaying mainly through autodetachment, with internal conversion being a minor channel.3,28 Thus, we do not expect electron attachment to isolated pBQ (scenario I) to be particularly efficient. However, experiments have shown that for larger molecular derivatives,42 or anionic gas–phase clusters of pBQ,4 internal conversion is significantly more efficient. Clusters of pBQ have been shown to readily form in evaporation-based ion sources, with excitation of resonance states (here by electron attachment) leading to dissociation of the complexes.4 Dissociation of the complexes dilutes the vibrational excitation, helping to stabilise the resulting free anion.
Including the vertical electron attachment energy, but ignoring the small contribution to the internal energy from the 310 K oven from which the molecules are sublimated, electron attachment via the 2Au resonance gives about 2.5 eV of vibrational energy after internal conversion.3 For scenario I, we assume a Gaussian initial energy distribution centered at this energy, with the width taken as a free parameter. In scenario II, we assume a Boltzmann distribution of vibrational energy with the vibrational temperature taken as a free parameter. In either scenario, the decay rate within the time window of the experiment is determined by the population density in a small interval above the adiabatic electron affinity Ea; ions with more than ∼0.5 eV vibrational energy above Ea decay before reaching the storage ring.
The results of our simulations are plotted in Fig. 3. For each formation scenario, we find the parameter (Gaussian width or Boltzmannian temperature T) that minimises the χ2 between the experimental and simulated decay rates. Scenario II with an initial temperature of T = 1100(20) K reproduces the experimental result satisfactorily. For scenario I, a Gaussian width of 0.2 eV (FWHM 0.47 eV) comes closest to reproducing the experimental result, and is consistent with the width of the shape resonance from photo-detachment spectroscopy measurements3, but overall the agreement is poor. Thus the data support scenario II and we adopt the initial temperature of T = 1100 K in our remaining analysis.
The Langevin cross section assumed in calculating the kVAD (eqn 2) is usually considered as an upper limit. As has been noted previously,30 simulated neutralisation rates based on eqn 2 are rather insensitive to the absolute scaling of kVAD. In the present case, reducing kVAD by a factor of 10−3 requires only a slight change in the initial temperature (to T = 1180(20) K) to achieve agreement with the absolute rate measured in the experiment, although this agreement is notably poorer than for the simulation shown in Fig. 3.
3.2 Action spectroscopy
Time slices through the 2D action spectrum spanning the 2Au ← 2B2g and 2B2u ← 2B2g transitions of pBQ− are presented in Fig. 4. The neutral yield at the peak of the 2B2u ← 2B2g transition (≈440 nm) increases with storage time, while hot-band contributions at wavelengths longer than 500 nm fade with time. These spectral changes can be quantified using Non-negative Matrix Factorisation (NMF, see Section 2.1).The NMF-factorised action spectra Hi (i = 0,1) are plotted in the middle panel of Fig. 4, along with the total time-integrated action spectrum, all normalised so that the wavelength-integrated area is unity. The uncertainty in the factorised data includes both the experimental counting statistics and the variation in the result of the NMF algorithm initialised with different random seeds. The NMF reconstruction explains about 52% of the variation in the experimental data. We interpret H0 and H1 as ‘cold’ and ‘hot’ components, respectively. Relative to the total action spectrum, H0 is more intense at 440 nm while H1 is more intense at wavelengths longer than 500 nm. The weights of these components Wi are plotted in the lower panel of Fig. 4 and are highly symmetric, implying that the spectrum transforms from hot to cold as vibrationally excited states relax. The timescale for this transformation, from a combined single exponential fit to W0 and W1, is 0.19(2) s. Note that this is an average rate across the whole spectrum, which includes multiple transitions with hot-band contributions that decay at different rates.
Our master equation simulations readily provide an interpretation of the data in Fig. 4. The initial and final vibrational energy distributions g(E, t), t = 0 s and t = 0.5 s, are shown in Fig. 5. The distributions have little overlap and are roughly equal at an energy Ex = 0.57 eV, indicated by the vertical dashed line. The cumulative sum along the time dimension of the simulated g(Ex, t) gives the fractions of the population above/below Ex, which is plotted in the inset. These sums, which are symmetric by construction, transform with an exponential time constant of 0.206(7) s, which closely matches the experimental lifetimes determined from W0 and W1, 0.19(2) s. This supports our identification of the NMF-factorised component spectra with those of hot/cold ions with vibrational energies above/below Ex. The difference in the relative amplitudes between experiment and simulation may be attributable to differing absorption probabilities for the hot and cold ions.
For a more quantitative comparison to calculated vibrational relaxation rates, we present the time-sliced 2D spectrum in Fig. 6, which includes only wavelength region longer than 500 nm where hot-bands contribute most exclusively. According to the NMF analysis, nearly all the time variation in this wavelength region is due to the diminution of the hot component H1 with a time constant of 0.16(3) s, while the cold component H0 rapidly increases to a plateau with a time constant of 0.03(7) s. For comparison, single exponential fits of the time series at each wavelength give lifetimes increasing monotonically from 0.066(11) s at 555 nm to 0.5(2) s at 505 nm, with a variance-weighted average lifetime of 0.130(7) s. Here, the NMF reconstruction accounts for about 73% of the experimental variation, but the uncertainty in the components is larger than the previous spectrum (Fig. 4) as a wider range of solutions reproduce the relatively soft features in Fig. 6.
Previous studies of carbon cluster anions have identified the decay rate of hot-band contributions to their photodetachment spectra with that of the average vibrational energy of the ensemble Eavg.29 This holds also for pBQ−. The decay lifetime for Eavg from our master equation simulations (plotted in Fig. 6) is 0.1602(7) s, in good agreement with the experimental lifetime of W1 of 0.16(3) s.
The increase at short times of the cold component may be interpreted as a recovery of low-lying vibrationally excited states by radiative relaxation. The recovery rate is nearly equal to the exponential lifetime of the cumulative sum of the fraction of the population distribution below a vibrational energy of about 1.5 eV. At this energy, the infrared rate coefficient is nearly equal to the inverse lifetime of the cumulative sum. Such highly-excited ions, evidently, are outside the region of favourable Franck–Condon overlap with the low-energy edge of the 2Au ← 2B2g transition. This cutoff energy may be a measure of the change in geometry between the neutral and anionic ground states, which is large for pBQ.3 Similar effects have been observed previously for carbon cluster anions.29,30
Finally, in Fig. 7, we give a higher resolution action spectrum across the low-energy bands of pBQ−. This spectrum is a simple time-integration of the photoneutral yield from 0.5 to 5.0 seconds storage time. As the time-evolution of the action spectrum appears nearly complete after 0.5 s, this represents the ‘cold’ action spectrum. Vibronic features of both the 2Au ← 2B2g and 2B2u ← 2B2g transitions are observed. The spectral features generally agree with a simulated T = 300 K Franck–Condon profile given by the sticks in Fig. 7, where the intensities of the main contributing transtions were taken from Kunitsa and Bravaya,44 but with the adiabatic (0–0) transition energies from Horke et al.2 and the present anharmonic vibrational frequencies. The previously reported5 anion depletion action spectrum is also given in Fig. 7. This spectrum was recorded for pBQ− formed by electrospray ionisation and thermalised to room temperature in a linear ion trap prior to laser excitation. Finally, the absorption spectrum of pBQ− isolated in an Ar matrix at 13 K is included for comparison.43 The matrix spectrum has been blue-shifted by 0.05 eV to align with the gas–phase spectrum.
 | ||
| Fig. 7 ‘Expt.’: Action spectrum of pBQ− integrated over 0.5–5 s storage time. ‘Depl.’: ion depletion action spectrum for room temperature pBQ−.5 ‘Matrix’: absorption spectrum of pBQ− in a 13 K Ar matrix.43 The sticks are calculated positions of vibronic transitions and their intensities at T = 300 K. | ||
The above comparisons of earlier data to the present results suggest that after 0.5 s, the stored ion ensemble has reached an internal energy distribution at which its action spectrum more closely resembles that of room temperature ions than that of ions in a cryogenic matrix. Indeed, the asymptotic value of the average vibrational energy (Fig. 6) corresponds to roughly T = 470 K, according the caloric curve calculated from the vibrational frequencies. This value is nominal as the energy distribution is not Boltzmannian, but qualitatively confirms the above observation. The vibrational energy distribution for T = 472 K is included in Fig. 5 for comparison to the simulated distribution after 0.5 s. That the ions do not continue to cool to the 13 K ambient temperature of the storage ring is due to the very low cooling rate at such low vibrational temperatures. Due to the high symmetry of pBQ, more than half of the vibrational modes are infrared inactive, which leads to trapping of the population in dark states, at least in the simulation. Further cooling on longer timescales may occur through anharmonic couplings with nearby bright levels.
The DESIREE cold spectrum shows vibrational structure over the 2Au band consistent with that observed in the matrix isolation studies.43,45 Here we can observe that the first few vibronic transitions of the 2Au ← 2B2g transition are suppressed in the matrix spectrum relative to the present gas–phase data. This is unsurprising given the significant difference in equilibrium geometry between the two states. This suppression is relieved at the elevated vibrational temperature of the present experiment. In both spectra the width of vibronic peaks is consistent with the lifetime-broadened lineshape of the 2Au transition observed by Schiedt and Weinkauf in their cryogenic photodetachment spectrum.28
4 Summary and conclusions
We have measured the neutralisation rate of hot pBQ radical anions isolated in a cryogenically cooled electrostatic storage ring. Master equation simulations using rate coefficients from detailed balance reproduce the absolute decay rates across three orders of magnitude in time, and enable us to discriminate between different possible anion formation scenarios. An improved method based on Non-negative Matrix Factorisation is presented for extracting cooling rates from two-dimensional action spectra. The results confirm that vibrational energy of the ions decreases to that of room temperature ions within 0.5 s from ion formation, and that further cooling through IR emission is inefficient on our experimental timescale. Hot band contributions to the action spectrum decrease at a rate commensurate with the average internal energy from the simulations.The Boltzmannian initial distribution of vibrational energy consistent with our experimental results indicates that long-lived pBQ− may be formed by attachment to pBQ clusters or through collisional stabilisation of hot pBQ− by background gas in the ion source. The latter mechanism is unlikely in interstellar clouds. Electron capture by QPAHs clustered in very small grains or adsorbed on ice mantles in such clouds could lead to thermal desorption and be a source of molecular anions.8 Furthermore, because the electron affinity increases with clusterisation, we expect that some of the unbound electronic excited states will become bound with clusterisation, providing an alternative and longer-lifetime route for internal conversion. In the interstellar medium, such clusterisation perturbation may be provided by adsorption onto a dust grain or through coordination with species like PAHs or water molecules.
Compared to pBQ, larger and/or substituted QPAHs with either valence- or dipole-bound electronic states close to the detachment threshold may be more likely to form stable anions upon electron capture by free molecules,46 due both to the lower excess vibrational energy and the possibility for efficient radiaitve stabilisation by recurrent fluorescence. The present experiments show rate coefficients approximated by statistical theories provide a reliable guide to computational searches for QPAHs with these favourable qualities.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Swedish Research Council (Grant numbers 2016-03675, 2016-04181, 2018-04092 and 2020-03437), the Olle Engkvist Foundation (Grant number 200–575), and the Swedish Foundation for International Collaboration in Research and Higher Education (STINT, grant number PT2017-7328 awarded to JNB and MHS). We acknowledge the DESIREE infrastructure for provisioning of facilities and experimental support, and thank the operators and technical staff for their invaluable assistance, especially Mikael Björkhage who developed the ion source used in this experiment. The DESIREE infrastructure receives funding from the Swedish Research Council under the Grant numbers 2017-00621 and 2021-00155. This article is based upon work from COST Action CA18212 - Molecular Dynamics in the GAS phase (MD-GAS), supported by COST (European Cooperation in Science and Technology).References
- F. L. Crane and M. D. Henninger, Function of Quinones in Photosynthesis, Vitamins & Hormones, Academic Press, 1967, vol. 24, pp. 489–517 Search PubMed.
- D. A. Horke, Q. Li, L. Blancafort and J. R.-R. Verlet, Nat. Chem., 2013, 5, 711–717 CrossRef CAS PubMed.
- C. W. West, J. N. Bull, E. Antonkov and J. R.-R. Verlet, J. Phys. Chem. A, 2014, 118, 11346–11354 CrossRef CAS PubMed.
- C. S. Anstöter, J. N. Bull and J. R. Verlet, Int. Rev. Phys. Chem., 2016, 35, 509–538 Search PubMed.
- M. H. Stockett and S. Brøndsted Nielsen, Phys. Chem. Chem. Phys., 2016, 18, 6996–7000 RSC.
- G. Mensa-Bonsu, A. Lietard and J. R.-R. Verlet, Phys. Chem. Chem. Phys., 2019, 21, 21689–21692 RSC.
- F. D.-S. Simonsen, P. A. Jensen, A. W. Skov, R. Jaganathan, J. D. Thrower and L. Hornekær, Proc. Int. Astron. Union, 2019, 15, 264–266 CrossRef CAS PubMed.
- A. Lietard, G. Mensa-Bonsu and J. R.-R. Verlet, Nat. Chem., 2021, 13, 737–742 CrossRef CAS PubMed.
- M. P. Bernstein, S. A. Sandford, L. J. Allamandola, J. S. Gillette, S. J. Clemett and R. N. Zare, Science, 1999, 283, 1135–1138 CrossRef CAS PubMed.
- M. P. Bernstein, M. H. Moore, J. E. Elsila, S. A. Sandford, L. J. Allamandola and R. N. Zare, Astrophys. J., Lett., 2002, 582, L25 CrossRef.
- M. P. Bernstein, J. E. Elsila, J. P. Dworkin, S. A. Sandford, L. J. Allamandola and R. N. Zare, Astrophys. J., 2002, 576, 1115 CrossRef CAS.
- A. M. Cook, A. Ricca, A. L. Mattioda, J. Bouwman, J. Roser, H. Linnartz, J. Bregman and L. J. Allamandola, Astrophys. J., 2015, 799, 14 CrossRef.
- J. A. Noble, C. Jouvet, C. Aupetit, A. Moudens and J. Mascetti, Astron. Astrophys., 2017, 599, A124 CrossRef.
- J. A. Noble, E. Michoulier, C. Aupetit and J. Mascetti, Astron. Astrophys., 2020, 644, A22 CrossRef CAS.
- B. A. McGuire, A. M. Burkhardt, S. Kalenskii, C. N. Shingledecker, A. J. Remijan, E. Herbst and M. C. McCarthy, Science, 2018, 359, 202–205 CrossRef CAS PubMed.
- B. A. McGuire, R. A. Loomis, A. M. Burkhardt, K. L.-K. Lee, C. N. Shingledecker, S. B. Charnley, I. R. Cooke, M. A. Cordiner, E. Herbst, S. Kalenskii, M. A. Siebert, E. R. Willis, C. Xue, A. J. Remijan and M. C. McCarthy, Science, 2021, 371, 1265–1269 CrossRef CAS PubMed.
- T. J. Millar, C. Walsh and T. A. Field, Chem. Rev., 2017, 117, 1765–1795 CrossRef CAS PubMed.
- R. D. Thomas, H. T. Schmidt, G. Andler, M. Björkhage, M. Blom, L. Brännholm, E. Bäckström, H. Danared, S. Das, N. Haag, P. Halldén, F. Hellberg, A. I.-S. Holm, H. A.-B. Johansson, A. Källberg, G. Källersjö, M. Larsson, S. Leontein, L. Liljeby, P. Löfgren, B. Malm, S. Mannervik, M. Masuda, D. Misra, A. Orbán, A. Paál, P. Reinhed, K.-G. Rensfelt, S. Rosén, K. Schmidt, F. Seitz, A. Simonsson, J. Weimer, H. Zettergren and H. Cederquist, Rev. Sci. Instrum., 2011, 82, 065112 CrossRef CAS PubMed.
- H. T. Schmidt, R. D. Thomas, M. Gatchell, S. Rosén, P. Reinhed, P. Löfgren, L. Brännholm, M. Blom, M. Björkhage, E. Bäckström, J. D. Alexander, S. Leontein, D. Hanstorp, H. Zettergren, L. Liljeby, A. Källberg, A. Simonsson, F. Hellberg, S. Mannervik, M. Larsson, W. D. Geppert, K. G. Rensfelt, H. Danared, A. Paál, M. Masuda, P. Halldén, G. Andler, M. H. Stockett, T. Chen, G. Källersjö, J. Weimer, K. Hansen, H. Hartman and H. Cederquist, Rev. Sci. Instrum., 2013, 84, 055115 CrossRef CAS PubMed.
- E. Bäckström, D. Hanstorp, O. M. Hole, M. Kaminska, R. F. Nascimento, M. Blom, M. Björkhage, A. Källberg, P. Löfgren, P. Reinhed, S. Rosén, A. Simonsson, R. D. Thomas, S. Mannervik, H. T. Schmidt and H. Cederquist, Phys. Rev. Lett., 2015, 114, 143003 CrossRef PubMed.
- M. Gatchell, J. Ameixa, M. Ji, M. H. Stockett, A. Simonsson, S. Denifl, H. Cederquist, H. T. Schmidt and H. Zettergren, Nat. Commun., 2021, 12, 6646 CrossRef CAS PubMed.
- M. Wolf, H. V. Kiefer, J. Langeland, L. H. Andersen, H. Zettergren, H. T. Schmidt, H. Cederquist and M. H. Stockett, Astrophys. J., 2016, 832, 24 CrossRef.
- S. Iida, S. Kuma, M. Kuriyama, T. Furukawa, M. Kusunoki, H. Tanuma, K. Hansen, H. Shiromaru and T. Azuma, Phys. Rev. A, 2021, 104, 043114 CrossRef CAS.
- K. Yamada, A. Chiba, Y. Hirano and Y. Saitoh, AIP Conf. Proc., 2018, 2011, 050020 CrossRef.
- E. K. Anderson, PhD thesis, Stockholm University, Department of Physics, 2019.
- M. H. Stockett, J. N. Bull, J. T. Buntine, E. Carrascosa, M. Ji, N. Kono, H. T. Schmidt and H. Zettergren, J. Chem. Phys., 2020, 153, 154303 CrossRef CAS PubMed.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and E. Duchesnay, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- J. Schiedt and R. Weinkauf, J. Chem. Phys., 1999, 110, 304–314 CrossRef CAS.
- J. N. Bull, M. S. Scholz, E. Carrascosa, M. K. Kristiansson, G. Eklund, N. Punnakayathil, N. de Ruette, H. Zettergren, H. T. Schmidt, H. Cederquist and M. H. Stockett, J. Chem. Phys., 2019, 151, 114304 CrossRef PubMed.
- M. H. Stockett, J. N. Bull, J. T. Buntine, E. Carrascosa, E. K. Anderson, M. Gatchell, M. Kaminska, R. F. Nascimento, H. Cederquist, H. T. Schmidt and H. Zettergren, Eur. Phys. J. D, 2020, 74, 150 CrossRef CAS.
- M. H. Stockett, M. Björkhage, H. Cederquist, H. Schmidt and H. Zettergren, Faraday Discuss., 2019, 217, 126–137 RSC.
- M. H. Stockett, M. Björkhage, H. Cederquist, H. T. Schmidt and H. Zettergren, Proc. Int. Astron. Union, 2019, 15, 127–131 CrossRef CAS.
- J. U. Andersen, E. Bonderup and K. Hansen, J. Phys. B, 2002, 35, R1–R30 CAS.
- T. Beyer and D. F. Swinehart, Commun. ACM, 1973, 16, 379 CrossRef.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ã. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 16 Revision B.01, Gaussian Inc., Wallingford CT, 2016 Search PubMed.
- M. Gussoni, M. Rui and G. Zerbi, J. Mol. Struct., 1998, 447, 163–215 CrossRef CAS.
- V. Chandrasekaran, B. Kafle, A. Prabhakaran, O. Heber, M. Rappaport, H. Rubinstein, D. Schwalm, Y. Toker and D. Zajfman, J. Phys. Chem. Lett., 2014, 5, 4078–4082 CrossRef CAS PubMed.
- Y. Ebara, T. Furukawa, J. Matsumoto, H. Tanuma, T. Azuma, H. Shiromaru and K. Hansen, Phys. Rev. Lett., 2016, 117, 133004 CrossRef PubMed.
- K. Hansen, J. U. Andersen, P. Hvelplund, S. P. Møller, U. V. Pedersen and V. V. Petrunin, Phys. Rev. Lett., 2001, 87, 123401 CrossRef CAS PubMed.
- J. Andersen, E. Bonderup and K. Hansen, J. Chem. Phys., 2001, 114, 6518–6525 CrossRef CAS.
- A. A. Kunitsa and K. B. Bravaya, J. Phys. Chem. Lett., 2015, 6, 1053–1058 CrossRef CAS PubMed.
- J. N. Bull and J. R.-R. Verlet, Phys. Chem. Chem. Phys., 2017, 19, 26589–26595 RSC.
- J. Gebicki and J. Michl, J. Phys. Chem., 1988, 92, 6452–6454 CrossRef CAS.
- A. A. Kunitsa and K. B. Bravaya, Phys. Chem. Chem. Phys., 2016, 18, 3454–3462 RSC.
- K. Piech, T. Bally, T. Ichino and J. Stanton, Phys. Chem. Chem. Phys., 2014, 16, 2011–2019 RSC.
- J. N. Bull, C. W. West and J. R.-R. Verlet, Chem. Sci., 2015, 6, 1578–1589 RSC.
| This journal is © the Owner Societies 2022 |




