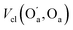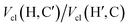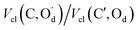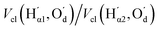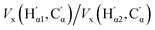Towards an atomistic understanding of polymorphism in molecular solids

Abstract

Understanding and controlling polymorphism in molecular solids is a major unsolved problem in crystal engineering. While the ability to calculate accurate lattice energies with atomistic modelling provides valuable insight into the associated energy scales, existing methods cannot connect energy differences to the delicate balances of intra- and intermolecular forces that ultimately determine polymorph stability ordering. We report herein a protocol for applying Quantum Chemical Topology (QCT) to study the key intra- and intermolecular interactions in molecular solids, which we use to compare the three known polymorphs of succinic acid including the recently-discovered γ form. QCT provides a rigorous partitioning of the total energy into contributions associated with topological atoms, and a quantitative and chemically intuitive description of the intra- and intermolecular interactions. The newly-proposed Relative Energy Gradient (REG) method ranks atomistic energy terms (steric, electrostatic and exchange) by their importance in constructing the total energy profile for a chemical process. We find that the conformation of the succinic acid molecule is governed by a balance of large and opposing electrostatic interactions, while the H-bond dimerisation is governed by a combination of electrostatics and sterics. In the solids, an atomistic energy balance emerges that governs the contraction, towards the equilibrium geometry, of a molecular cluster representing the bulk crystal. The protocol we put forward is as general as the capabilities of the underlying quantum-mechanical model and it can provide novel perspectives on polymorphism in a wide range of chemical systems.

---

Introduction

Antibiotic resistance is fast becoming a major public health concern.¹ The development of new drugs has been drastically held back by the time and costs involved in research, with no new classes of antibiotic having been discovered since 1987.² Among the most difficult steps in taking a new drug molecule to a marketable formulation is identifying and controlling the resulting solid form. This solid form dictates key physical properties including the compressibility and the dissolution rate, which in turn determine processability and bioavailability, respectively.^3,4 The conformational flexibility and broad spectrum of intermolecular interactions often enables molecules to crystallise into multiple polymorphs and/or solvates under different crystallisation conditions. These polymorphs may subsequently transform into different forms under processing and storage conditions.⁵ Polymorphs and solvates often display significant differences in physicochemical properties, introducing an extra level of complexity to drug design and manufacturing.⁶

A number of well-documented cases highlighting the impact of polymorphism on the pharmaceutical industry have made this an important contemporary research area.^7,8 In 1998, the capsule form of the HIV drug Ritonavir had to be temporarily removed from the market because the original Form I converted to a more stable and less soluble form, Form II, in the final formulation.⁹ Although Form II was not discovered in the four years from initial development to marketing, once production lines became contaminated, the supply of the drug was drastically reduced while a new formulation was developed. Another example is the 1991 patent dispute over the anti-ulcer drug ranitidine hydrochloride. Ranitidine hydrochloride has two polymorphic forms, Form I and Form II, with very similar solubility and bioavailability but Form II is easier to prepare than Form I. After discovering Form II, GSK obtained a new patent and, given the difficulty of preparing phase-pure Form I, the company was able to limit competition from generic manufacturers once the original patent on Form I expired.¹⁰

A recent statistical analysis of molecular crystals in the Cambridge Structural Database found that as many as 50% of known molecules display polymorphism, and that differences in lattice energy very often lie within the chemical accuracy threshold of 1 kcal mol⁻¹ (4 kJ mol⁻¹).⁸ Despite the inherent challenge these circumstances pose to theoretical methods, crystal-structure prediction (CSP)¹¹ is a highly active research field. The field has even invoked methods that are perhaps quite unexpected in this context, such as the Fukui function from Conceptual density-functional theory (DFT), which inspired the concept of “crystallisation forces”¹² (where crystallisation looks like effective electron transfer from an atomic point of view) that revealed the intermolecular interactions in the 7 polymorphs of 5-methyl-2-[(2-nitrophenyl)amino]-3-thiophenecarbonitrile (ROY). In a typical CSP study, 10³–10⁴ candidate crystal structures are generated and their lattice energies evaluated using a parameterised force field model, a first-principles electronic-structure method such as DFT, or a combination of the two. Depending on the system, CSP may find a single (global) energy minimum or a set of energetically similar metastable polymorphs.¹¹ CSP will always find many structures but the differences in energy can vary. Sometimes the global minimum is well separated from all other structures and sometimes not. CSP has evolved with computing capability to become a useful counterpart to experiment, for example, to screen for unidentified polymorphs of new drugs.¹³ Nevertheless, even moderately complex systems can challenge current state-of-the-art methods.¹⁴

A key disadvantage common to most contemporary CSP methods is the difficulty of ascribing the subtle energy differences between competing structures to specific chemical interactions. The implications of this situation are twofold. Firstly, it limits the insight available from CSP studies, which may otherwise point to predictive rules or “smarter” screening approaches. Secondly, in the cases where CSP fails to predict experimental outcomes, it is difficult to identify the classes of interactions that the underlying total-energy methods cannot describe appropriately. Still, and presumably exactly because of these challenges, CSP is a very active field as for example made clear by the last (i.e. sixth) blind test¹⁴ hosted by the Cambridge Crystallographic Data Centre (and the seventh blind test coming out in the summer of 2022). This paper, which contains a wealth of references, lists a variety of generation methods (e.g. random search, genetic algorithm) as well as final ranking methods (e.g. SAPT(DFT), atomic multipoles). The choice of the latter is amongst long-standing issues for CSP methods, where the majority of methods base their final rankings on differences in static, 0 K lattice energies. The sixth blind test saw 10 more participating research teams than in the fifth blind test of 2010, and some of the former's very successful predictions led to some mitigated exuberance.¹⁵ In spite of such local success, at least eight open questions¹⁶ in organic crystal polymorphism remain, even in 2020, such as whether we are even able to detect and determine all polymorphs. However, in 2019, a reliable and practical computational description of molecular crystal polymorphs was proposed¹⁷ based on a combination of the most successful crystal structure sampling strategy with the most successful first-principles energy ranking strategy of the sixth blind test. However, even more recently, in 2020, a fragment-based dispersion-corrected second-order Møller–Plesset perturbation theory was called for¹⁸ to fix residual inadequacy of current-generation DFT functionals to make CSP truly reliable.

The current state-of-the-art for analysing total energies is to use quantum-chemical topology (QCT) methods^19,20 such as the Interacting Quantum Atoms (IQA) energy decomposition scheme.²¹ IQA examines the molecular quantum-mechanical wavefunction (or the corresponding electron density function in DFT) to rigorously partition the total energies obtained from electronic-structure calculations into a sum of intra- and interatomic terms with intuitive chemical interpretations. We and others have successfully applied IQA, in conjunction with tools such as the Relative Energy Gradients (REG) method,²² to examine many different phenomena. A few examples include hydrogen²² and halogen²³ bonding, the fluorine gauche effect,²⁴ the biphenyl torsional angle energy barrier,²⁵ and the reaction mechanism of the peptide hydrolysis of HIV-1 protease.²⁶ In this work, we apply these methods to elucidate the chemical origin of the polymorphism in succinic acid (SA). By combining complementary periodic electronic-structure calculations with IQA analyses of SA monomers, dimers and clusters, we explore the delicate energetic balances that ultimately determine the structure and stability of the three known SA polymorphs. This method is general and provides a foundation for future studies to improve our fundamental understanding of polymorphism and to devise and improve novel CSP methods.

Computational methods

a. Periodic calculations

Periodic plane-wave DFT calculations were performed on the crystal structures of the α, β and γ polymorphs of SA using the Vienna Ab initio Simulation Package (VASP) code.²⁷ A plane wave basis with a kinetic-energy cut off of 850 eV was used with Projector Augmented-Wave (PAW) pseudopotentials^28,29 including the H 1s and C and O 2s/2p electrons in the valence shell. Calculations were performed with six different exchange–correlation functionals: (i) the PBE generalised-gradient approximation (GGA) functional,³⁰ (ii) the PBE0³¹ and (iii) B3LYP³² hybrid functionals, (iv) PBE with the DFT-D2 correction,³³ (v) PBE with the DFT-D3 correction,³⁴ and (vi) PBE with the Tkatchenko-Scheffler (TS) dispersion correction.³⁵Γ-Centered Monkhorst–Pack k-point meshes³⁶ with 2 × 2 × 3 (α-SA), 2 × 1 × 3 (β-SA) and 2 × 1 × 1 subdivisions (γ-SA) were used for the Brillouin-zone integrations. This choice of mesh guarantees convergence of the total energy to <1 meV (or <0.1 kJ mol⁻¹) per atom.

Only dispersion-corrected functionals provide a feasible route to account for dispersion via electronic structure theory in these types of systems. Perturbation theory substantially overestimates dispersion effects while coupled cluster approximations are simply not feasible. Furthermore, we explicitly show that all the functionals we tested give very similar monomer and dimer geometries such that only acceptable errors occur in the reproduction of these structures. The use of D2-corrected pure functionals yields structures of extended systems that are similar³⁷ to those determined both by functionals designed for solids and by experiment.

A series of gas-phase calculations were also performed as follows. SA molecules and H-bonded dimers were extracted from the experimental structures and placed at the centre of a large periodic box with a size such that there is 15 Å between the closest atoms in periodic images. Note that this does not mean that the box size was 15 Å. These geometries were then optimised with the same technical parameters as used for the crystal structures but with Γ-point Brillouin zone sampling. In all calculations, the PAW projection was performed in reciprocal space and non-spherical contributions to the gradient corrections inside the PAW spheres were accounted for. A tolerance of 10⁻⁸ eV on the total energy was applied when optimising the Kohn–Sham orbitals. Geometry relaxations were performed with the atomic positions, and the lattice parameters and cell volumes in the periodic structures, allowed to vary until the magnitude of the forces on the ions fell below 10⁻² eV Å⁻¹.

b. Molecular calculations

Gas-phase electronic-structure optimisations and single-point calculations were performed on SA monomer, dimer and multi-molecule cluster models using B3LYP³² and the 6-31+G(d,p) split-valence basis set³⁸ with the GAUSSIAN09³⁹ software. The Kohn–Sham orbitals were optimised with tolerances of 10⁻⁶ and 10⁻⁸ a.u. on the maximum and root-mean-square (RMS) changes in the density matrix, respectively. Geometry optimisations were performed to tolerances of 4.5 × 10⁻⁴ and 3 × 10⁻⁴ a.u. on the maximum and RMS force, and 1.8 × 10⁻³ and 1.2 × 10⁻³ a.u. on the maximum and RMS displacements, respectively. For the larger cluster calculations, we used the recommended SuperFineGrid setting for computing integrals.

c. Quantum-chemical topology calculations

The Kohn–Sham electron densities obtained from the molecular calculations were analysed using the IQA partitioning scheme as implemented in the AIMAll package.⁴⁰ The largest value of L(Ω) was 1.5 × 10⁻³ a.u for the carboxylic carbon atoms in the γ conformation, where L(Ω) is essentially the difference between two types of (atomic) kinetic energy, which should ideally be the same and hence L(Ω) should ideally vanish. The integration strategy was carefully and successfully optimised to reduce the absolute recovery error, defined as the difference between the calculated total energy and the sum of the IQA energy terms, to below 1 kJ mol⁻¹ for all SA monomers and dimers. As outlined in the Results and Discussion section, series of IQA calculations for configurations along carefully-selected “control coordinates” were analysed using the Relative Energy Gradient (REG) method implemented in our in-house ANANKE software.²²

Results and discussion

a. Solid-state calculations

Succinic acid has three reported polymorphs: a triclinic P1̄ (α) phase and the two monoclinic P2₁/c (β) and C2/c (γ) phases (Fig. 1). All three structures are built from chains of SA molecules formed by strong directional H-bonded carboxylic acid dimers, which pack parallel with weaker intermolecular interactions between adjacent chains. β-SA crystallises from solution and is stable under ambient conditions,^41,42 while α-SA is obtained by rapid quenching of a melt above ∼135 °C⁴³ and can also be prepared by sublimation.⁴²

Fig. 1 Solid-state polymorphism in the succinic acid molecule. The SA molecule can adopt planar (a) and twisted (b) conformations. There are three known polymorphs of SA, viz. α (c) and β (d), which are based on the planar SA geometry, and γ (e), which is based on the twisted geometry. These images were generated using the VESTA software.⁴⁵

The α → β phase transition is slow, and once prepared, α-SA remains stable for long periods of time. γ-SA was isolated⁴⁴ serendipitously in 2018 and differs markedly from α- and β-SA in that the SA molecules adopt a “folded” or “twisted” rather than planar geometry. SA adopts the planar geometry in ∼89% of its crystals, most of which are cocrystals,⁴⁴ making the twisted configuration comparatively rare.

PBE predicts an energetic ordering of α < γ < β, with energy differences of 1.2 and 1.7 kJ mol⁻¹ per SA molecule between the α and γ polymorphs, and the γ and β polymorphs, respectively, which we denote ΔE(α − γ) and ΔE(γ − β). These energy differences are both well within the 4 kJ mol⁻¹ chemical accuracy threshold. The two hybrid functionals, PBE0 and B3LYP, predict an ordering of γ < β < α, and these XC-functionals notably predict the γ polymorph to be 7.2 and 5.9 kJ mol⁻¹ lower in energy than the α and β phases, respectively (Table S1 of the ESI†). When one of the three dispersion corrections is applied to PBE, the energy differences between polymorphs are reduced to within 1–2 kJ mol⁻¹ per SA molecule. Our PBE-D2 and PBE-TS results for α and β are in line with the calculations carried out by Lucaioli et al.,⁴⁴ and a full set of energy differences calculated with the six functionals is given in Table S1 (ESI†). Overall, there are six possible energy orderings, of which four are recovered by the six levels of theory tested, and none of the orderings is predicted by more than two of the functionals.

By comparing the optimised and experimental structures, we find that PBE and B3LYP overpredict the unit cell volumes by 13–19%, PBE0 overpredicts by 8–11%, and the three dispersion-corrected functionals predict smaller volume changes ranging from a 1% expansion to a 6% contraction (Tables S2–S4, ESI†). All six functionals predict similar molecular conformations, with RMSD values from 8.1 × 10⁻³ Å to 2.8 × 10⁻² Å compared to the PBE structure (overlay plots in Fig. S1–S3 and Table S5, ESI†). The six functionals also predict similar SA dimer H-bond distances with a maximum difference of ∼0.1 Å across the three polymorphs (Table S6, ESI†).

Gas-phase calculations on the planar and twisted SA conformation of the single molecule consistently predict the twisted form to be lower in energy than the planar conformer, with energy differences ranging from 0.7 kJ mol⁻¹ with PBE to 1.9 kJ mol⁻¹ with PBE-D2 (Table S7, ESI†). Calculations on gas-phase dimers in both conformations indicate formation energies (E_F) from 65 to 84 kJ mol⁻¹, and all six functionals predict the twisted dimer to be more stable than the planar dimer by 0.8–1.4 kJ mol⁻¹ (Tables S7 and S8, ESI†).

The gas-phase calculations consistently show the twisted monomer and dimer to be the lowest in energy, and the solid-state calculations predict similar molecular geometries and H-bond distances. We therefore infer that the large differences in the cell volumes, and the variability in the energetic ordering predicted by the six functionals, is due to differences in how these functionals describe the weaker intermolecular forces between the SA chains.

b. The IQA energy decomposition scheme

Having established a baseline for our calculations, we next applied the IQA method to determine the origin of the predicted energetic differences between the SA conformations and the three solid-state polymorphs. The IQA scheme emerges from the Quantum Theory of Atom in Molecules (QTAIM) approach as a rigorous decomposition of the total energy into a sum of intra- and interatomic energy terms,^21,46 and provides detailed and quantitative descriptions of the underlying chemical interactions.

The total energy is decomposed into a sum of the IQA energies E_IQA of the N topological atoms in the molecular system (single molecule or molecular aggregate) according to:

The E_IQA(i) energy of the i-th topological atom can be expanded as a sum of intra- and inter-atomic contributions:The energetic contribution E_Intra comprises a sum of the atomic kinetic energy T(i) and the electron–electron and electron-nucleus potential energy V_e–e(i) and V_e–n(i). These energies are obtained from volume integrals of appropriate quantum-mechanical densities over the topological atoms. The intra-atomic energy E_Intra is a measure of the intrinsic stability of an atom in its chemical environment, which defines many stereo-electronic phenomena including steric hindrance in rotational barriers.²⁵V_Inter(i, j) are the interatomic contributions to the potential energy due to the interactions between atoms i and j, which are calculated as:

V_Inter(i, j) = V_n–n(i, j) + V_e–n(i, j) + V_n–e(i, j) + V_e–e(i, j), (3)

where V_e–n(i, j) and V_n–e(i, j) are, respectively, the potential energy contributions due to interaction of the electrons associated with atom i and the nucleus of atom j, and vice versa, i.e. the order of the subscripts is significant. The electron–electron potential energy V_e–e incorporates the classical Coulomb (V_Coul) and quantum-mechanical exchange–correlation (V_xc) interactions:

V_e–e(i, j) = V_Coul(i, j) + V_xc(i, j). (4)

V_Coul(i, j) is the Coulombic interaction between the electrons in atoms i and j while V_xc(i, j) primarily reflects the degree of covalent bonding between the two atoms.⁴⁷ Finally, it is often convenient to group the “classical” (“cl”) terms in eqn (3) and (4), viz. V_n–n, V_e–n, V_n–e and the purely electrostatic part of V_e–e, i.e. V_Coul, into a single term V_cl(i, j).This new term allows eqn (3) to be rewritten:

V_Inter(i, j) = V_cl(i, j) + V_xc(i, j) (5)

The interatomic terms arising from electron–electron interactions are calculated from a six-dimensional integration of the appropriate densities over the volumes of the two topological atoms involved. The classical electrostatic terms capture the electrostatic energies along with charge transfer effects, while the exchange–correlation interactions capture, at DFT level, only covalency and (hyper)conjugation.

A limitation of all current IQA implementations is that they only work with molecular (and thus aperiodic) systems. We therefore identified and analysed the three main interactions involved in the SA crystal packing using appropriate molecular models. These models are the planar and twisted conformers of the SA molecule, dimers of SA molecules in the two conformations, and H-bonded chains packed to form larger clusters representative of the extended crystal structure. We chose to perform our calculations with the B3LYP hybrid functional, as this is a typical choice for molecular quantum chemistry, but we note that IQA can in principle be applied to the wavefunctions (or electronic densities in the case of DFT) obtained from any electronic-structure method.

c. The relative energy gradient method

The number of individual energy terms in an IQA decomposition rapidly becomes large as the size of the system increases, making manual analysis of the data impractical. As a result, it becomes hard to answer a crucial chemical question: which individual energy terms are most responsible for the energetic behaviour of the total system? This question is at the heart of any chemical phenomenon, such as hydrogen bonding, the gauche effect, the anomeric effect, and rotational energy barriers, to name a few. In the current study, we aim to identify which atoms play a pivotal role in the crystallisation of SA into its three polymorphs, and which type of energy (i.e. steric, electrostatic or exchange) controls the relevant interactions. The Relative Energy Gradient (REG) method is designed to answer this question, and to do so by unbiased computation. REG operates on a dynamic change, i.e. it requires a sequence of molecular geometries and the corresponding energies that represent the chemical phenomenon being studied. For example, a REG analysis of a rotational energy barrier requires a series of geometries generated by varying the relevant torsion angle, termed the “control coordinate”. In the case of a REG analysis of a hydrogen bond, the control coordinate is typically the H-acceptor distance. In the current study we perform three different REG analyses, each with its own control coordinate: (i) the central C–C torsional angle within one SA molecule, or both molecules in a SA dimer; (ii) the hydrogen bond distance between two SA molecules; and (iii) the unit cell volume in the crystal structures.

As the name suggests, the REG compares two energy gradients by calculating their (dimensionless) ratio, which is termed the REG coefficient. The gradient of each energy contribution is compared to the gradient of the total energy, both of which vary along the control coordinate. These ratios are then ranked to identify the most significant energy components in terms of their impact on the overall change in total energy. The key idea is to identify the largest positive REG coefficients, corresponding to the atomic energy contributions that most support the total energy change, and the most negative REG coefficients, which identify the energy terms that most oppose the total energy change.

The control coordinate is divided into segments whose extremes are at critical points of the potential energy surface (PES) as a function of the control coordinate (i.e. minima, maxima and/or saddle points). The behaviour over each segment is analysed separately, and both IQA and total energies are calculated over a number of geometries determined by the control coordinate. The REG coefficient (R_k) for the k-th IQA term is calculated as follows:

ε_k = R_k × E_IQA + c_k (6)

where R_k denotes the coefficient of the linear regression used to fit (over all geometries of a given segment) the IQA energy term ε_k and the IQA energy of the total system E_IQA, and c_k are constants without physical meaning. The REG coefficient R_k measure how large the change in ε_k are, compared to the change in the total energy within each segment. Note that the sign of R_k and its interpretation (i.e. whether a term supports or opposes the change in total energy) is independent of the direction in which the analysis is performed (i.e. from minimum to maximum or vice versa).

d. Conformation of the succinic acid monomer

To explore the energetic differences between the planar α/β and twisted γ conformations of SA, we performed a scan of the PES associated with the C–C torsion angle (Fig. 2). The PES has two unique minima at dihedral angles of 70 and 180° corresponding to the twisted (γ) and planar (α/β) conformations, respectively. These calculations predict the twisted conformation to be lower in energy than its planar counterpart by 0.3 kJ mol⁻¹ with a rotation barrier of 5 kJ mol⁻¹. The 0.3 kJ mol⁻¹ energy difference between the twisted and planar forms is of the same order of magnitude as the 0.7 kJ mol⁻¹ computed with B3LYP plane-wave calculations. Fig. 2 also compares the total electronic energies obtained from the molecular calculations (E_DFT) to those obtained by summing the terms in the IQA partitions (E_IQA). There is an excellent agreement between the two data sets, indicating minimal IQA recovery errors.

Fig. 2 Conformational analysis of the succinic acid monomer. (a and b) Optimised geometries of the twisted (γ; a) and planar (α/β; b) conformers showing the atom labelling scheme employed in the text and the C–C torsion angle ϕ varied during the PES scan. (c) Change in energy as a function of ϕ. The two curves compare the total energies from the B3LYP calculations (E_DFT, red squares) to the sum of IQA energy terms (E_IQA, blue circles). The black box marks the region of the profile from 70° to 180° representing the rotational energy barrier between the two conformers. (d and e) REG analysis of this section of the profile in two segments indicated by the dotted vertical line at the local maximum energy at 120°. The analysis highlights the main energetic contributions to the barrier as (d) the attractive interaction between the C atom and acceptor O atom at opposite ends of the molecule, and (e) the repulsive interaction between the pair of acceptor O atoms and pair of C atoms.

In order to gain insight into the factors underlying the energy difference between the twisted and planar conformations, we performed a REG analysis of the section of the profile in Fig. 2(c) between 70 and 180°. These segments correspond to the paths (i) from the twisted γ conformation to the energetic maximum, and (ii) from the maximum to the planar α/β conformer. Table 1 identifies the largest REG coefficients (in absolute value), which are the most important to understand the chemical origin of the rotational barrier.

Table 1 REG analysis of the IQA energies along the paths linking (i) the twisted (γ) SA conformer with the energy maximum (Segment 1), and (ii) the maximum and the planar (α/β) conformation (Segment 2). These segments are marked on the PES as a function of the C–C torsion angle in SA shown in Fig. 2(a and b), which also shows the atom labelling scheme. The notation V_cl(i, j) denotes a classical electrostatic interaction between the pair of atoms in parentheses. For each segment, the terms with the largest absolute REG coefficient R_k are shown along with the (Pearson) correlation (R) to the total energy

Segment 1			Segment 2
IQA term	R k	R	IQA term	R k	R
	27.4/27.2	0.98	V cl(C,C′)	12.1	0.99
	12.6	0.98		12.0	0.99
	6.5/6.4	0.98		4.6/4.5	0.89
	−6.5	−0.98		4.5	0.89
	−12.7/−12.9	−0.98		4.4	0.95
	−23.2	−0.98		−3.8	−0.89
V cl(C,C′)	−30.0	−0.98		−4.0	−0.96
				−12.3	−0.99

---

The most significant terms in both segments are the classical electrostatic interactions V_cl among atoms in the carboxylic acid groups at opposite ends of the SA molecule. In Segment 1, the attractive interactions (i) between opposing carbonyl C and acceptor O atoms, (ii) between opposing carbonyl C and donor O atoms, and (iii) between opposing acidic H and acceptor O atoms all feature with the highest positive REG coefficients. Hence these 3 electrostatic interactions work to support the total energy barrier. In other words, the attraction between the carboxyl groups becomes less and less stabilising along the path from the energy minimum to the maximum. The terms with negative R_k counteract the energy barrier. Since C and C’ have the same atomic charge, as do and O_a, the corresponding interactions are repulsive in nature. Because they counteract the barrier, they must decrease in strength along the path from the minimum to the maximum in the PES.

In Segment 2, which corresponds to torsion from the local maximum to the minimum at the planar conformation, these same repulsive interactions support the decrease in total energy, i.e. the repulsion energy decreases and thereby stabilises the planar minimum. However, new electrostatic interactions become significant, viz. those between the carbonyl atoms and the methylenic hydrogens in both 1,3 and 1,4 relationships. Finally, the attractive interaction between the two opposing carboxyl groups now emerge as the most dominant negative R_k values, indicating that these interactions continue to strengthen on approach to the planar minimum.

In conclusion, the above analysis shows that the rotational barrier is governed by classical electrostatic interactions, in particular those of the two carboxylic acid groups. Indeed, a comparison of the two REG analyses (one for each Segment) identifies the most important terms with the largest absolute R_k to be (i) the attractive interactions between opposing carbonyl C and acceptor O atoms, , (ii) the repulsive contacts between carbonyl C atoms, V_cl(C,C′), and (iii) the repulsive interactions between acceptor O atoms, . As shown in Fig. 2(d and e), the rotation from the twisted to the planar conformer, via the PES maximum, leads to a continuous weakening of all three interactions. The twisted conformer therefore maximises the attractive interaction relative to the two repulsive terms, making it slightly more stable. We note that the changes in energy associated with these electrostatic terms are some two orders of magnitude larger than the barrier height itself. The energy difference between the two conformers, and thus the PES, arises from a balance of energetically large, but opposing, chemical interactions.

e. H-bond dimerisation

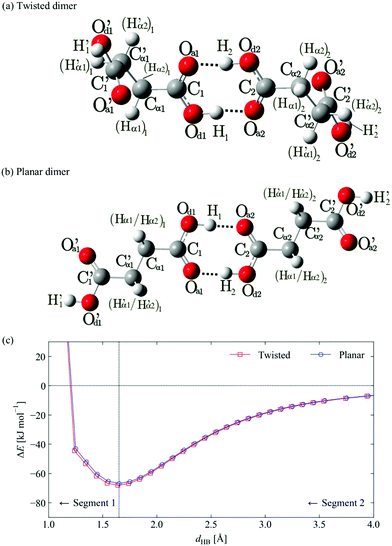
We next examined the formation of H-bonded dimers of both SA conformers, as the H-bond between carboxylic acid groups likely represents the strongest single intermolecular interaction in all three SA polymorphs. Here the H-bond distance was taken as the control coordinate in REG analyses of the twisted and planar dimers. The coordinate was adjusted from the calculated equilibrium distance of ∼1.65 Å to values between 1.15 Å (compression), and 4.55 Å (extension) in steps of 0.1 Å (Fig. 3). The resulting potential energy curves predict dimer formation energies of −66.8 and −68.0 kJ mol⁻¹ for the planar and the twisted dimers, respectively, which are once again very similar to those computed from the plane-wave calculations (−65.1 and −65.5 kJ mol⁻¹). The twisted dimer is predicted to be 1.4 kJ mol⁻¹ per SA molecule more stable than the planar dimer, which is a fivefold increase on the energy difference between the monomers, although the plane-wave calculations predict a much smaller stabilisation of 0.2 kJ mol⁻¹ per molecule.

Fig. 3 Analysis of the H-bond dimerisation between two molecules of succinic acid (marked “1” and “2”) in planar and twisted conformations. (a and b) Optimised twisted (a) and planar (b) SA dimers showing the atom labelling used in the text. The H-bond distances d_HB used as control coordinates are marked by dashed black lines. (c) Total energy of the twisted and planar dimers as a function of the H-bond distance. The energy is expressed relative to a separation of 4.6 Å, which effectively corresponds to two isolated SA dimers. The vertical black line marks the equilibrium H-bond distances at which the two PES curves were split into compression and extension segments marked Segment 1 and Segment 2, respectively.

In order to gain further insight into the selective stabilisation of the dimer, the curves in Fig. 3 were divided into two segments corresponding to the repulsive and attractive parts of the potential energy curves, respectively at small and large monomer separations. The IQA decomposition of the total energies of the configurations in each segment was analysed using REG, in order to identify the most important terms summarised in Table 2.

Table 2 REG analysis of the partitioned IQA energies along the H-bond compression (Segment 1) and lengthening (Segment 2) regions of the H-bond potential energy curves for the planar and twisted succinic acid dimers shown in Fig. 3. The two monomers in the dimer are indicated by the subscripts “1” and “2”. The parameters R_k and R have the same meaning as in Table 1. The E_Intra refer to the intra-atomic energies of the atoms in parentheses, and the V_cl refer to the classical electrostatic interactions between the pairs of atoms in parentheses. The atom labelling is shown in Fig. 3(a) and (b)

IQA term	Planar		Twisted
	R k	R	R k	R
Segment 1
E Intra(Od1)/EIntra(Od2)	1.4	0.98	1.4	0.98
V cl(C1,H2)/Vcl(C2,H1)	1.4	0.90	1.3	0.90
V cl(C1,C2)	1.1	0.90	1.2	0.91
V cl(Od1,Oa2)/Vcl(Od2,Oa1)	1.0	0.96	1.0	0.96
V cl(C1,Od2)/Vcl(C2,Od1)	−1.0	−0.93	−1.0	−0.93
V cl(C1,Od1)/Vcl(C2,Od2)	−1.5	−0.77	−1.6	−0.87
V cl(H1,Oa2)/Vcl(H2,Oa1)	−1.6	−0.87	−1.6	−0.79
Segment 2
V cl(C1,Od2)/Vcl(C2,Od1)	5.9	0.99	5.9	0.99
V cl(C1,Oa2)/Vcl(C2,Oa1)	5.5	0.98	5.6	0.98
V cl(Oa1,H2)/Vcl(Oa2,H1)	5.2	0.99	5.2	0.99
V cl(Oa1,Oa2)	−3.8	−0.96	−3.9	−0.96
V cl(Od1,Od2)	−4.1	−0.99	−4.0	−0.99
V cl(H1,C2)/Vcl(H2,C1)	−5.0	−0.99	−5.0	−0.99
V cl(Od1,Oa2)/Vcl(Od2,Oa1)	−5.5	−0.99	−5.5	−0.99
V cl(C1,C2)	−6.9	−0.98	−7.1	−0.98

---

We discuss the complete energy profile from long to short H-bond distances, beginning with Segment 2. While it is possible to perform this analysis in the reverse direction, it is more intuitive to start with widely-separated SA monomers and identify the chemical interactions that drive them to form the H-bonded dimers. Continuing to analyse Segment 1, where the dimer is compressed to shorter H-bond distances, allows us to further elucidate the nature of the corresponding energy barrier.

We find that electrostatic interactions between atoms in the two carboxyl groups involved in the H bond play the largest role in the formation of the dimer (Segment 2). Attractions between the carbonyl carbon and donor/acceptor oxygen atoms on the opposing group make a substantial supporting contribution, as does the attraction between the acceptor oxygen and donor acidic proton. The latter phenomenon is expected and has been seen in REG analyses of other H-bonded systems, and confirms the H-bond in the SA dimer to be predominantly electrostatic in nature. We emphasise that while the two OH hydrogen bonds feature much in stabilising the SA dimer, they do so alongside non-bonded C⋯O contacts between the two adjacent carboxyl groups.

Energy terms with negative REG coefficients identify destabilising interactions that oppose the H-bond formation. In principle, the positive REG coefficients suffice to explain the nature of the attraction between the monomers when forming the dimer. However, the negative REG coefficients provide an alternative narrative, which is again identical for both the planar and twisted dimers. The dominant negative REG coefficients again involve atoms from opposing carboxyls. This time all electrostatic interactions are repulsive in nature, starting with the most dominant one, which is the repulsion between the carbonyl carbons. As expected, all possible O⋯O interactions across the carboxyls play a dominant role. More surprising, however, is the strong repulsion between the acidic protons and the carbonyl carbons.

We now explain the nature of Segment 1, starting with the most positive REG coefficients. As for Segment 2, the analysis is qualitatively the same for the planar and the twisted dimer. As the dimer is compressed beyond its equilibrium geometry, the intra-atomic energy E_Intra of the donor O atoms increases most, compared to other types of local energy. This indicates a steric effect where the atom's kinetic energy is combined with the potential energy of the deforming electron cloud to strengthen the energy barrier to compression. The next three most dominant energy contributions are all electrostatic, and by deduction repulsive, because they help in constructing the compression energy barrier. Perhaps unexpectedly, the interaction between the carbonyl C and the acidic proton of the opposite COOH plays a leading role. The interaction between the two carbonyl carbon atoms follows closely, as does that between the donor and acceptor oxygen atoms. Finally, the alternative narrative associated with the negative REG coefficients shows that increased electrostatic attraction between the carboxyl groups play the most important role in counteracting the energy barrier. This assertion reinforces the role of the electrostatic interaction between the carboxyl groups over the whole energy profile, throughout the two segments.

The REG coefficients for the twisted and planar dimers are similar, and thus do not highlight any clear differences in H-bond strength that might explain the higher stability of the twisted dimer. We therefore investigated the hypothesis that this higher stability is instead due to differences in the intramolecular interactions within the SA monomers. A set of calculations analogous to those performed on the SA monomer in Fig. 2, but where both molecules in the dimer are rotated from the twisted to the planar form, were therefore run, as shown in Fig. 4(a). This procedure yields a rotational barrier of 11.1 kJ mol⁻¹ (5.5 kJ mol⁻¹ per SA molecule), which is ∼10% higher than in the monomer. A REG analysis taking as the control coordinate the C–C torsion angle – again in both monomers – confirms that the same terms govern the rotational barrier in the monomer and dimer (Table 3).

Fig. 4 Conformational analysis of the C–C torsion angle in the succinic acid dimer. The atom labelling is the same as used in Fig. 3 but without the molecular subscript index, for brevity. Note that the two monomers in the dimers are equivalent. (a) Structure of the planar SA dimer showing the atom labelling used in the text and the two C–C torsion angles, ϕ, varied together during the PES scan. (b) Change in the total energy ΔE_DFT as a function of ϕ from 75–180°. As in the monomer PES scan in Fig. 2, the PES is divided into the two segments marked by the vertical dotted line, and each is characterised using a REG analysis of the IQA decomposition of the total energies of each configuration. (c) Contribution to the total energy of the attractive interaction between the carbonyl C and opposing acceptor O atoms within the SA monomers. (d) Contributions to the total energy from the repulsive interactions between pairs of acceptor O and carboxyl C atoms within the SA monomers.

Table 3 Comparison of the REG coefficients R_k for the three major electrostatic interactions determining the variation in energy along the rotational PES between the twisted (γ) conformations of the succinic acid monomer and dimer and the local energy maximum (Segment 1), and the maximum and the planar (α/β) monomer and dimer (Segment 2). These segments are marked on the twist potential energy surfaces in Fig. 2 and 4. The atom labelling scheme follows that used in Fig. 2 and 4. Note that the two monomers in the dimers are equivalent. The notation V_cl(A,B) denotes the classical electrostatic interaction between the pairs of atoms in parentheses

IQA term	Monomer				Dimer
	Segment 1		Segment 2		Segment 1		Segment 2
	R k	R	R k	R	R k	R	R k	R
	27.4	0.98	−12.3	−0.99	9.7	0.99	−6.0	−0.99
	−23.2	−0.99	12.0	0.99	−8.5	−0.99	6.2	0.99
V cl(C,C′)	−30.0	−0.98	12.1	0.99	−10.4	−0.99	5.7	0.99

---

Further insight can be obtained by comparing the QTAIM atomic charges in the SA molecules in the monomers and dimers in the planar and twisted conformations (Table 4). Importantly, these charges are obtained directly from the same type of volume integral as the IQA energies, a uniformity not found in other common partitioning schemes. There is little difference between the charges in the twisted and planar conformations, whether in the monomer or the dimer. However, the dimerisation leads to a clear redistribution of charge, on the order of tens of milli-electrons. In both the planar and twisted dimers, there is a quantitatively similar charge transfer within the carboxyl group involved in the H-bonding. Upon dimerisation the H and acceptor O both become more positive, while the carboxyl C atom becomes more negative, which can be interpreted as an internal charge transfer. The increase in positive charge of the hydrogen-bonded H atoms is well known and can be observed through enhanced infrared activity in H-bonded systems.^48–50

Table 4 Atomic net charges q (a.u.) on each atom in the planar and twisted conformations of the succinic acid monomers and dimers found in α-/β-SA and γ-SA, respectively (note that the two monomers in the dimers are equivalent). The charge difference (Δ) for atom A is defined as q_A(dimer) − q_A(monomer). The atom labels are shown in Fig. 2 and 4

Atom	Monomer		Dimer		Δ
	Planar	Twisted	Planar	Twisted	Planar	Twisted
H	0.61	0.61	0.64	0.64	0.03	0.03
H′	0.61	0.61	0.58	0.58	−0.03	−0.03
Od	−1.15	−1.15	−1.15	−1.15	0	0
	−1.15	−1.15	−1.09	−1.09	0.06	0.06
C	1.59	1.60	1.53	1.54	−0.06	−0.06
C′	1.59	1.60	1.51	1.52	−0.08	−0.08
Oa	−1.22	−1.22	−1.18	−1.17	0.04	0.05
	−1.22	−1.22	−1.15	−1.15	0.07	0.07
Cα	0.09	0.09	0.04	0.04	−0.05	−0.05
	0.09	0.09	0.04	0.04	−0.05	−0.05
Hα1	0.04	0.04	0.06	0.06	0.02	0.02
	0.04	0.02	0.06	0.06	0.02	0.04
Hα2	0.04	0.02	0.05	0.04	0.01	0.02
	0.04	0.04	0.04	0.04	0	0

---

f. Crystal packing and polymorphism

Finally, to probe the additional intermolecular interactions in the bulk SA crystals, we developed a model comprising clusters of molecules from each of the periodic structures with a central SA molecule surrounded by the full set of nearest-neighbours present in the bulk environment. This leads to molecular models with 15 and 17 SA molecules for the α/β and γ polymorphs, respectively (210 and 238 atoms). The sizes of these systems are at the limit of what it is currently feasible to analyse using IQA.

In these analyses, the volume of the unit cell in the periodic calculation provides a natural control coordinate for REG analyses because the expansion and contraction of the volume about the computed equilibrium (i.e. the energy/volume equation of state (EoS) curve) probes the full range of energetic interactions that determine the equilibrium structure. We therefore performed a set of periodic calculations in which each of the three SA structures was re-optimised with the cell volume fixed to ±5% of the calculated equilibrium value in steps of 1%. Due to the significant computational overhead of hybrid functionals in the periodic electronic-structure calculations, it was not possible to compute the EoS curves using B3LYP. We therefore used PBE instead, as this functional predicts the most similar equilibrium volume to B3LYP, and we performed a series of B3LYP single-point energy calculations on the PBE-optimised structures. This procedure is equivalent to the rapid volume optimisation method outlined by Jackson et al..⁵¹ The resulting energy/volume curves are shown in Fig. 5. A fit of the Birch–Murnaghan equation of state⁵² to the PBE E/V curve yields equilibrium energies, E₀, within 0.5 kJ mol⁻¹ per molecule and equilibrium volumes, V₀, within 4–6% of the values obtained by variable-cell optimisation. Fitting the E/V curve obtained with the B3LYP single-point energies computed with PBE structures yields a similar error in the predicted V₀ but a rather larger ∼3.5 kJ mol⁻¹ error in the E₀. Nevertheless, the computed energies predict the same stability ordering of γ-SA < β-SA < α-SA.

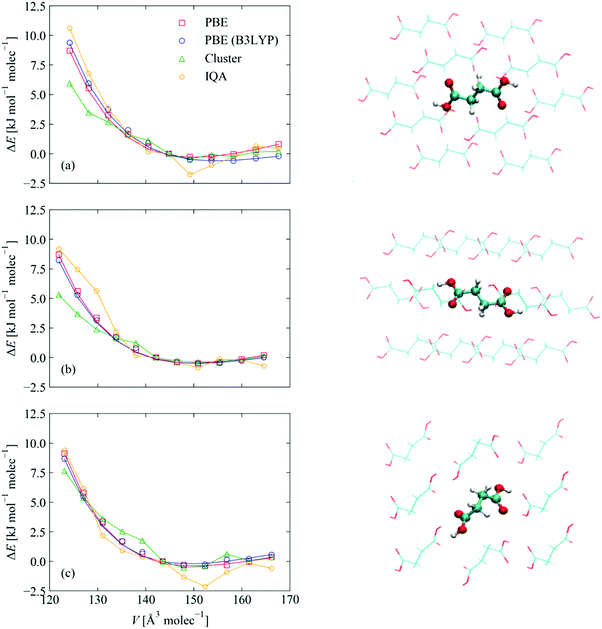Fig. 5 Calculated energy/volume curves for (a) α-SA, (b) β-SA and (c) γ-SA as a function of volume. The red curves show the energies obtained from a series of structures optimised at constant volume with PBE. The blue curves show the energies obtained from single-point B3LYP calculations on the PBE structures. The green curves show the energies from single-point B3LYP calculations on clusters of molecules extracted from the periodic structures. Some examples of these structures, viewed along one of the crystallographic axes, are shown to the right part of the figure. Note that the viewpoint may hide some of the molecules. Finally, the orange curves indicate the energies of the “bulk-like” reference molecules (extracted with the IQA energy partitioning) in the centre of the clusters, represented in the images using balls and sticks rather than lines. The images were produced with the VMD software.⁵³

To examine how well the cluster models reproduce the solid-state E/V curves, we compared single-point energy calculations on the clusters, using B3LYP, with single-point B3LYP calculations on the periodic structures. The gas-phase computations show a reasonable overlap with the solid-state calculations at expanded volumes but the calculations on α-SA and β-SA deviate significantly at compressed volumes. This is likely because the outer shell of molecules in the clusters are in a very different chemical environment to those inside the periodic structure. Partitioning the total energies using the IQA and extracting the energy of the reference “bulk like” molecule largely corrects this discrepancy, which suggests that the central molecules in these clusters are representative of the monomers within the corresponding crystal structures. However, we note that the cluster and IQA calculations both predict a different energetic ordering to the periodic calculations, viz. α < β < γ (Fig. S4(b), ESI†) and α < γ < β (Fig. S4(d), ESI†), respectively. The comparison of the full energy/volume curves (Fig. S4, ESI†) shows that this effect is not due to the noise in the energies. Instead, we attribute the discrepancy between the periodic and molecular B3LYP calculations to implementation differences in the periodic and aperiodic codes used for the solid-state and molecular cluster models. Given the small energy differences between the polymorphs predicted by the initial periodic calculations, the differences in qualitative stability ordering are perhaps inevitable.

Nonetheless, we proceed to analyse the energy differences based on the partitioned energies of the different types of atoms in the reference molecules (Table 5). Comparison of the IQA contributions in α-SA and β-SA, for which the reference SA molecule is in the planar conformation, shows that the higher energy of the β-SA phase is almost entirely by virtue of the destabilisation of the donor O atoms. The same is true when comparing the α-SA and γ-SA reference molecules, for which the higher electronic energy of the latter occurs through a balance of (i) stabilisation of the acidic H and both C atoms, and (ii) destabilisation of the two O atoms and the methylene (α) H atoms. The respective stabilisation and destabilisation of the C and donor O atoms in the carboxylic acid groups are particularly significant.

Table 5 Differences in atomic energies ΔE of the central reference molecules in β-SA and γ-SA with respect to α-SA. A negative/positive value of ΔE implies that the atom is more/less stable relative to the equivalent atom in α-SA. The atomic energies are calculated for the cluster molecules for those volumes closest to the equilibrium predicted based on single-point B3LYP calculations on PBE-optimised structures. The energies are summed over atoms of the same type (e.g. H/H′, , all four H_α, etc.). The atom labelling is shown in Fig. 2

Atom	ΔE [kJ mol^−1]
	Δ(β − α)	Δ(γ − α)
H	−0.5	−11.8
C	0.2	−25.8
Oa	1.7	9.3
Od	5.7	34.0
Cα	1.0	−6.6
Hα	−2.7	4.4
Total	5.4	3.4

---

To better understand these effects, each E/V curve in Fig. 5 was separated into two segments bounded by the volume with the lowest energy, resulting in two segments corresponding to volume compression and expansion. We found that these changes in volume have a minimal effect on the conformations of the SA monomers and the H-bond distances. We observed a maximum RMSD of 2.5 × 10⁻² Å in the atomic positions of the SA monomers and a maximum change in the H-bond distance of 5.7 × 10⁻² Å across the full set of expansions and compression for all three structures (Tables S9–S11, ESI†). Thus, the differences in cell volume are almost entirely due to changes in the distances between the SA chains. Therefore, the region of the EoS curve from the most expanded volume to equilibrium mimics the process of the SA chains coming together to form the crystals, and the analysis of this section of the EoS curve gives insight relevant to crystal growth. Likewise, examination of the compression region would be relevant to explain changes to the crystal structure under pressure, which is in itself an interesting topic but which we do not pursue here. We therefore analysed the IQA energy curves only over the expansion region using the REG method. It is natural to analyse this energy segment from the expanded configuration to the equilibrium, i.e. in the direction corresponding to forming the equilibrium crystal. Thus energy terms with positive (negative) efficients correspond to terms that stabilise (destabilise) the crystal formation.

Due to the size of the clusters, we restricted the number of energy terms calculated in the IQA decompositions by using two complementary analysis modes, viz. AB and AA′. The AB analysis considers for each atom in the reference molecule an intra-atomic (A) energy and a series of pairwise interactions with the other atoms in the reference molecule (AB). This procedure yields a total of 14(14 − 1)/2 + 14 = 105 energy terms and describes how the atoms in a single SA molecule interact with each other in the bulk environment of the crystal. This AB analysis does not take into account explicit interactions with the other molecules in the crystal but it does consider the influence of the environment on the intra- and inter-atomic energies with respect to the gas-phase monomer in the gas-phase dimer. On the other hand, the AA′ analysis returns only a single energy term for each of the 14 atoms in the reference molecule, but these energies include both the intra-atomic energy and the interaction energies with all the other atoms in the cluster. In other words, the AA′ analysis adds a description of how the energies of the atoms in the reference molecule are influenced by explicit interactions with the other neighbouring molecules in the crystal. The comparison of these two analyses allows the separation of the energetic contributions due to (i) the conformation of the molecule, and (ii) the intermolecular interactions associated with the crystal packing.

REG analyses show that the dominant energetic terms governing the packing in the SA crystal structure are again predominantly electrostatic in nature (Table 6), except for the weak steric stabilisation (E_intra) of the carbonyl C atoms in the β-SA and γ-SA polymorphs. The majority of the energy contributions are attractive electrostatic interactions between the acidic H, methylene (α) H and carbonyl C on one hand, and the donor and acceptor O atoms on the other hand. Furthermore, the positive R_k values indicate that the conformations of the monomers adapt to the crystal environment in order to optimise these attractive contacts. In the planar α and β polymorphs, the equilibrium conformation also reduces the repulsion between the acidic H and carbonyl C atoms, whereas in γ-SA the repulsion between the two carbonyl C atoms is reduced. However, these reduced repulsions are counteracted by V_x terms between the methylene C and H atoms, as reflected by their negative R_k values, indicating that they oppose the change in total energy. The adapted conformation thus weakens the covalent bonding between these atoms. Finally, the electrostatic stabilisation is strongly counteracted by the steric destabilisation of the methylenic H and acceptor O atoms in all three polymorphs, and by the steric destabilisation of the donor O in the α and β-SA polymorphs. Thus, the crystal packing also leads to destabilising deformation of the electron densities of the atoms in the monomers.

Table 6 REG analysis of the partitioned IQA energies of the central reference molecules in cluster models of the α-SA, β-SA and γ-SA crystal structures, computed with the AB analysis, as the unit-cell volume is adjusted from the expanded to the equilibrium volume. E_Intra denote intra-atomic energies modified by deformation of the atomic densities, while V_cl(A, B) and V_x(A, B) denote, respectively, classical electrostatic and exchange interactions between the pairs of atoms in parentheses. The R_k are only shown for polymorphs where the corresponding energetic terms are significant. Positive (negative) R_k values correspond to energy terms that stabilise (destabilise) the crystal as unit-cell volume is adjusted from an expanded volume to the equilibrium. The atom labelling is shown in Fig. 3

IQA term	α-SA		β-SA		γ-SA
	R k	R	R k	R	R k	R
E Intra(C)/EIntra(C′)	—	—	—/0.2	—/0.75	0.1/0.2	0.78/0.89
V cl(C,C′)	—	—	—	—	0.2	0.94
	0.6	0.72/0.75	—/0.3	—/0.76	—	—
	0.2	0.93/0.96	0.3/—	0.93/—	0.1	0.86/0.83
V cl(H,C)	0.2	0.89	0.1	0.86	—	—
	0.2	0.84/0.85	0.1	0.84/0.87	—	—
	0.2	0.91/0.89	0.3/—	0.93/—	0.1/—	0.75/—
V cl(Hα1,Od)/Vcl(Hα2,Od)	0.2/—	0.89/—	—/0.3	—/0.93	—/0.1	—/0.75
	0.2	0.92	0.3	0.93	0.1	0.76
	0.2	0.81	0.1	0.82	—	—
	0.1	0.91/0.90	0.3	0.93	0.1	0.74
V cl(Hα2,Oa)	0.1	0.91	0.3	0.93	0.1	0.76
	−0.2/−0.1	−0.91/−0.89	−0.2	−0.92/−0.95	−0.1	−0.74/−0.73
E Intra(Hα1)/EIntra(Hα2)	−0.3	−0.90	−0.2/−0.3	−0.95/−0.92	−0.1	−0.76
	−0.4/−0.3	−0.91/−0.90	−0.3/−0.2	−0.92/−0.93	−0.1	−0.76
	−0.6	−0.91	−0.7	−0.91	−0.2	−0.75
	−1.1	−0.87	−1.0/−1.1	−0.90/−0.91	—	—

---

The complementary AA′ analysis shows that the interactions with neighbouring molecules include a variety of classical electrostatic, exchange interactions and steric influences (Table 7). All three polymorphs show stabilising exchange interactions at the donor O atoms. The α-SA and β-SA forms both show strong electrostatic stabilisation of the donor O atoms, together with weaker exchange stabilisation of the acceptor O atoms. All three polymorphs also show weak exchange stabilisation of the α H. In α-SA and β-SA the strongest destabilisation is in the intra-atomic energy of the donor O atoms, while a similar steric destabilisation of the acceptor O and α H atoms is present in all three polymorphs. We note that the overall steric destabilisation on adjusting the volume to the equilibrium is consistent with the AB analysis.

Table 7 REG analysis of the partitioned IQA energies of the central reference molecules in cluster models of the α-, β- and γ-SA crystal structures, computed with the AA′ analysis, as the unit cell-volume is adjusted from the expanded to the equilibrium volume. E_Intra denote intra-atomic energies modified by deformation of the atomic densities, while V_cl(A) and V_x(A) denote respectively classical electrostatic and exchange interactions associated with the atom in parentheses. The R_k are only shown for polymorphs where the corresponding energetic terms are significant. Positive (negative) R_k values correspond to energy terms that stabilise (destabilise) the crystal as unit-cell volume is adjusted from an expanded volume to the equilibrium. The atom labelling is shown in Fig. 3

IQA term	α-SA		β-SA		γ-SA
	R k	R	R k	R	R k	R
	0.8	0.86/0.87	0.6/0.5	0.89/0.88	—	—
	0.5	0.91	0.5	0.92	—	0.76
	0.4	0.87	0.4	0.9	—	—
E Intra(C′)	—	—	0.2	0.75	0.2	0.89
	0.3	0.93	0.4	0.91	0.1	0.81
V x(Hα1)/Vx(Hα2)	0.2	0.91	0.1	0.87/0.93	0.1/0.03	0.76/0.73
	0.2	0.90/0.91	0.1	0.93/0.90	0.03/0.1	0.74/0.76
	0.1	0.86/0.87	—/0.1	—/0.87	—	—
	0.1	0.75	0.1	0.78	0.1	0.92
V cl(C)/Vcl(C′)	−0.1/—	−0.83/—	−0.2	−0.82/−0.79	−0.1	−0.79/−0.92
E Intra(Hα1)/EIntra(Hα2)	−0.3	−0.90	−0.2/−0.3	−0.95/−0.92	−0.1	−0.76
	−0.4/−0.3	−0.91	−0.3/−0.2	−0.92/−0.93	−0.1	−0.76
	−0.6	−0.91	−0.7	−0.91	−0.2	−0.75
	−1.1	−0.87	−1.1/−1.0	−0.91/−0.90	—	—

---

By taking these analyses together, we can extract the following general trends. In the bulk crystal environments, the monomers optimise the intra-molecular electrostatic interactions between atoms at the expense of steric destabilisation of some atoms. The interaction with neighbouring molecules produces additional stabilisation through a mix of electrostatic and covalent interactions associated mainly with the O atoms and the methylene groups. Within the IQA analysis, the V_x and V_cl terms reflect covalent and polar interactions respectively, and their importance in the AA′ analysis can be attributed to the formation of strong H-bonds with neighbouring molecules. This observation indicates that the dominant interaction in the SA crystals is the formation of hydrogen bonds with neighbouring chains in the cluster.

The REG analyses also provide additional insight into the origin of the (predicted) energy differences between the polymorphs. The AB analysis shows that the intra-molecular electrostatic interaction between the donor O and C atoms in the carboxylic acid group has a larger R_k value for the α-SA than for β-SA. On the other hand, the AA′ analysis shows that electrostatic stabilisation of the donor O atoms is more important in lowering the energy of the α phase as the crystal is formed. This suggests that the difference between the two planar SA polymorphs is primarily due to differences in the electrostatics. On the other hand, the AB analysis shows that some of the intra-molecular electrostatic interactions that stabilise the α and β polymorphs are not important in γ-SA, while the AA′ analysis shows a reduced significance of V_x terms, in particular interactions with the acceptor O atoms, in γ-SA. However, both analyses notably show that the increased E_Intra of the donor O atoms, which constitutes a significant destabilising effect in the α and β polymorphs, is not important in the formation of the γ-SA crystal. This observation is consistent with the comparison of the atomic energies in Table 5, but provides greater insight into the chemical interactions responsible for the differences. Thus, as for the SA monomer, the differences in energy between the twisted and planar polymorphs may be a balance of energetically large, but opposing effects, which partially explains the differences in qualitative stability ordering obtained with different functionals.

Before moving on to the general conclusions, two remarks on future developments are useful. Firstly, the small energy differences, on the order of kJ mol⁻¹, between the three succinic acid polymorphs is fairly typical of molecular solids and challenges the accuracy of theoretical methods. In particular, it is possible that an accurate description of dispersion forces may be important to account for the correct energetic ordering between polymorphs. The IQA can be used with more accurate electronic-structure methods such as MP2. This approximation should provide an improved description of electron correlation and it would more accurately model dispersion. However, calculations on the large cluster models used here to represent the bulk crystal structure are likely to be prohibitively expensive. Nonetheless, analyses of the type outlined here may provide useful quantitative information on why different DFT functionals predict different energetic ordering, which may inform future development of new electronic-structure methods.

Secondly, current implementations of IQA are restricted to non-periodic systems. While our cluster model obtained from a solid-state energy–volume curve appears to work reasonably well in this case, adapting IQA for periodic systems would likely be both more accurate and more efficient. On the other hand, many molecular solids have unit cells containing hundreds of atoms, and periodic plane-wave DFT calculations on such systems with hybrid functionals or post-DFT methods are likely to be prohibitively expensive. This problem may be partially mitigated by periodic DFT implementations with local orbitals. On the other hand, the development of improved functionals is an active development area, and advances in software efficiency and computing power are steadily enabling more accurate calculations to be performed on larger systems. We would therefore expect that the protocol we put forward here will be applicable to a wide variety of interesting and topical polymorphism problems in the near future.

Next we comment on the possibility to also analyse differences in lattice dynamics between polymorphs in terms of the atomic contributions. The small energy differences between polymorphs mean that vibrational entropic energy contributions,⁵⁴ and even zero-point energy contributions⁵⁵ are important in understanding polymorph relative stabilities. At some level, our method could offer some capability to add to the understanding of these energy differences. The vibrational frequencies are derived from the change in energy with respect to displacement along the normal-mode coordinates, and one could use this as a control coordinate. It would be somewhat tedious or impractical to carry out 3N IQA/REG analyses but it might be possible to analyse key vibrational modes whose frequencies differ substantially between polymorphs and therefore contribute most to the differences in the vibrational free energy.

Finally, we note that our calculations do not include temperature effects but our developing force field FFLUX,^56,57 which is IQA-compatible, will be able to do so in the future, and even in conjunction with REG. Thus, at present, the differences in the motions of the molecules within the crystal structure (the temperature-dependent energy terms) are not incorporated in our analysis. However, Fig. S22 of the ESI of ref. 44 demonstrates that β is stabilised relative to γ by larger vibrational entropy using periodic PBE-TS harmonic phonon frequencies.

Conclusions

The present case study of succinic acid demonstrates that detailed information from quantum-chemical topology calculations can provide atomistic chemical insight into polymorphism in molecular solids. The REG method, when combined with intra-atomic and interatomic energies from Quantum Chemical Topology, identifies the energy terms that best represent and thereby govern the energetic behaviour of the total system. We studied all three known polymorphs of succinic acid (α, β and γ), for which the twisted conformer, corresponding to γ, is consistently the lowest in energy in the gas phase, at any level of theory used. Three REG analyses were performed on the monomer, the dimer and clusters of succinic acid molecules, representing the different interactions in the solid-state.

Firstly, the relative energies and rotational barrier between the twisted and planar forms of succinic acid result from a balance of large and opposing electrostatic interactions that are 2 to 3 orders of magnitude larger than the corresponding energy differences. The rotation barrier between the twisted (γ) and planar (α, β) conformers is electrostatic in nature, and governed by atoms from the two COOH groups at opposite ends of succinic acid. More precisely, we find that repulsive C⋯C interactions and attractive C⋯O(=C) interactions dominate the rotation barrier.

Secondly, the assembly of a H-bonded dimer of either planar or twisted succinic acid molecules is again determined predominantly by electrostatic interactions between the two COOH groups involved in the hydrogen bond. Remarkably, the four non-bonded C⋯O contacts between the two adjacent COOH groups are slightly more important in determining the equilibrium H-bond distance than the O⋯H interactions themselves. As the dimer is compressed beyond its equilibrium geometry, the intra-atomic energy of the donor O atoms explains the increase in total energy and thus the barrier to compression, followed closely in importance by repulsive interactions between the carbons, and between the carbon and acidic proton. The same terms govern the rotational barrier in the monomer and dimer. Upon dimerisation, the acidic H and acceptor O both become more positive, while the carboxyl C becomes less positive.

Thirdly, analysis of molecular clusters representative of the bulk crystal shows that the predicted higher energy of the β- and γ-polymorphs compared to the α-polymorph is almost entirely by virtue of the destabilisation of the donor O atom. The attractive segment of the energy/volume equation of state curve (expanded to equilibrium volume) mimics the process of the succinic acid chains coming together. Furthermore, the dominant energetic terms governing the packing in the crystal structure are again predominantly electrostatic in nature, except for the weak steric stabilisation of the carbonyl C atoms in the β and γ polymorphs. A further analysis was also performed focusing on a single energy term for each of the 14 atoms in a reference succinic acid molecule in a bulk-like chemical environment, which includes both the intra-atomic energy and the interaction energies with all the other atoms α in the cluster. This revealed that all three polymorphs show stabilising exchange interactions of the donor O atoms. However, only the α and β forms show strong electrostatic stabilisation of the donor O atoms.

Conflicts of interest

The authors declare no competing financial interests.

Acknowledgements

The calculations in this study made use of HPC resources provided by The University of Manchester through the Computational Shared Facility (CSF) and by the National Autonomous University of Mexico through the DGTIC/UNAM project LANCAD-UNAM-250. We also made use of the UK Archer HPC facility via membership of the UK Materials Chemistry Consortium (MCC), which is funded by the UK Engineering and Physical Sciences Research Council (Grant No. EP/L000202, EP/R029431). ASDLV gratefully acknowledges the financial support from CONACyT/Mexico (Grant No. 702090 and MSc Scholarship No. 787272). JMS is supported by a UKRI Future Leaders Fellowship (MR/T043121/1) and is grateful to the University of Manchester for the award of a Presidential Fellowship. LJD thanks the São Paulo FAPESP programme for a PhD fellowship (2017/22741-3, 2018/24844-7). AFS thanks the Brazilian government FAPESP and CAPES programmes for postdoctoral funding (2014/21241-9, 2015/22247-3). PLAP thanks the EPSRC for the award of an Established Career Fellowship (grant no. EP/K005472).

References

1. E. Tacconelli, E. Carrara, A. Savoldi, S. Harbarth, M. Mendelson, D. L. Monnet, C. Pulcini, G. Kahlmeter, J. Kluytmans, Y. Carmeli, M. Ouellette, K. Outterson, J. Patel, M. Cavaleri, E. M. Cox, C. R. Houchens, M. L. Grayson, P. Hansen, N. Singh, U. Theuretzbacher, N. Magrini, A. O. Aboderin, S. S. Al-Abri, N. Awang Jalil, N. Benzonana, S. Bhattacharya, A. J. Brink, F. R. Burkert, O. Cars, G. Cornaglia, O. J. Dyar, A. W. Friedrich, A. C. Gales, S. Gandra, C. G. Giske, D. A. Goff, H. Goossens, T. Gottlieb, M. Guzman Blanco, W. Hryniewicz, D. Kattula, T. Jinks, S. S. Kanj, L. Kerr, M.-P. Kieny, Y. S. Kim, R. S. Kozlov, J. Labarca, R. Laxminarayan, K. Leder, L. Leibovici, G. Levy-Hara, J. Littman, S. Malhotra-Kumar, V. Manchanda, L. Moja, B. Ndoye, A. Pan, D. L. Paterson, M. Paul, H. Qiu, P. Ramon-Pardo, J. Rodríguez-Baño, M. Sanguinetti, S. Sengupta, M. Sharland, M. Si-Mehand, L. L. Silver, W. Song, M. Steinbakk, J. Thomsen, G. E. Thwaites, J. W. van der Meer, N. Van Kinh, S. Vega, M. V. Villegas, A. Wechsler-Fördös, H. F. L. Wertheim, E. Wesangula, N. Woodford, F. O. Yilmaz and A. Zorzet, Discovery, research, and development of new antibiotics: the who priority list of antibiotic-resistant bacteria and tuberculosis, Lancet Infect. Dis., 2018, 18(3), 318–327,  DOI:10.1016/s1473-3099(17)30753-3.
2. World Health Organization, Global Action Plan on Antimicrobial Resistence, 2017.
3. T. Beyer, G. M. Day and S. L. Price, The prediction, morphology, and mechanical properties of the polymorphs of paracetamol, J. Am. Chem. Soc., 2001, 123(21), 5086–5094,  DOI:10.1021/ja0102787.
4. R. Censi and P. Di Martino, Polymorph impact on the bioavailability and stability of poorly soluble drugs, Molecules, 2015, 20(10), 18759–18776,  DOI:10.3390/molecules201018759.
5. J. Sood, B. Sapra, S. Bhandari, M. Jindal and A. K. Tiwary, Understanding pharmaceutical polymorphic transformations I: Influence of process variables and storage conditions, Ther. Delivery, 2014, 5(10), 1123–1142,  DOI:10.4155/tde.14.68.
6. J.-P. Brog, C.-L. Chanez, A. Crochet and K. M. Fromm, Polymorphism, what it is and how to identify It: A systematic review, RSC Adv., 2013, 3(38), 16905,  10.1039/c3ra41559g.
7. J. Haleblian and W. McCrone, Pharmaceutical applications of polymorphism, J. Pharm. Sci., 1969, 58(8), 911–929,  DOI:10.1002/jps.2600580802.
8. A. J. Cruz-Cabeza, S. M. Reutzel-Edens and J. Bernstein, Facts and fictions about polymorphism, Chem. Soc. Rev., 2015, 44(23), 8619–8635,  10.1039/c5cs00227c.
9. J. Bauer, S. Spanton, R. Henry, J. Quick, W. Dziki, W. Porter and J. Morris, Ritonavir: An extraordinary example of conformational polymorphism, Pharm. Res., 2001, 18(6), 859–866,  DOI:10.1023/a:1011052932607.
10. S. Aldridge, The shape shifters https://www.chemistryworld.com/features/the-shape-shifters/3004850.article (accessed 2020–07–27).
11. S. L. Price, Predicting crystal structures of organic compounds, Chem. Soc. Rev., 2014, 43(7), 2098–2111,  10.1039/c3cs60279f.
12. T. Li, P. W. Ayers, S. Liu, M. J. Swadley and C. Aubrey-Medendorp, Crystallization force – A density functional theory concept for revealing intermolecular interactions and molecular packing in organic crystals, Chem. – Eur. J., 2009, 15(2), 361–371,  DOI:10.1002/chem.200801056.
13. S. Z. Ismail, C. L. Anderton, R. C. B. Copley, L. S. Price and S. L. Price, Evaluating a crystal energy landscape in the context of industrial polymorph screening, Cryst. Growth Des., 2013, 13(6), 2396–2406,  DOI:10.1021/cg400090r.
14. A. M. Reilly, R. I. Cooper, C. S. Adjiman, S. Bhattacharya, A. D. Boese, J. G. Brandenburg, P. J. Bygrave, R. Bylsma, J. E. Campbell, R. Car, D. H. Case, R. Chadha, J. C. Cole, K. Cosburn, H. M. Cuppen, F. Curtis, G. M. Day, R. A. DiStasio Jr, A. Dzyabchenko, B. P. van Eijck, D. M. Elking, J. A. van den Ende, J. C. Facelli, M. B. Ferraro, L. Fusti-Molnar, C.-A. Gatsiou, T. S. Gee, R. de Gelder, L. M. Ghiringhelli, H. Goto, S. Grimme, R. Guo, D. W. M. Hofmann, J. Hoja, R. K. Hylton, L. Iuzzolino, W. Jankiewicz, D. T. de Jong, J. Kendrick, N. J. J. de Klerk, H.-Y. Ko, L. N. Kuleshova, X. Li, S. Lohani, F. J. J. Leusen, A. M. Lund, J. Lv, Y. Ma, N. Marom, A. E. Masunov, P. McCabe, D. P. McMahon, H. Meekes, M. P. Metz, A. J. Misquitta, S. Mohamed, B. Monserrat, R. J. Needs, M. A. Neumann, J. Nyman, S. Obata, H. Oberhofer, A. R. Oganov, A. M. Orendt, G. I. Pagola, C. C. Pantelides, C. J. Pickard, R. Podeszwa, L. S. Price, S. L. Price, A. Pulido, M. G. Read, K. Reuter, E. Schneider, C. Schober, G. P. Shields, P. Singh, I. J. Sugden, K. Szalewicz, C. R. Taylor, A. Tkatchenko, M. E. Tuckerman, F. Vacarro, M. Vasileiadis, A. Vazquez-Mayagoitia, L. Vogt, Y. Wang, R. E. Watson, G. A. de Wijs, J. Yang, Q. Zhu and C. R. Groom, Report on the sixth blind test of organic crystal structure prediction methods, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72(4), 439–459,  DOI:10.1107/S2052520616007447.
15. E. Gibney, Software predicts slew of fiendish crystal structures, Nature, 2015, 527(7576), 20–21,  DOI:10.1038/527020a.
16. A. J. Cruz-Cabeza, N. Feeder and R. J. Davey, Open questions in organic crystal polymorphism, Commun. Chem., 2020, 3(1), 142,  DOI:10.1038/s42004-020-00388-9.
17. J. Hoja, H.-Y. Ko, M. A. Neumann, R. Car, R. A. DiStasio and A. Tkatchenko, Reliable and practical computational description of molecular crystal polymorphs, Sci. Adv., 2019, 5(1), eaau3338,  DOI:10.1126/sciadv.aau3338.
18. C. Greenwell, J. L. McKinley, P. Zhang, Q. Zeng, G. Sun, B. Li, S. Wen and G. J. O. Beran, Overcoming the difficulties of predicting conformational polymorph energetics in molecular crystals via correlated wavefunction methods, Chem. Sci., 2020, 11(8), 2200–2214,  10.1039/C9SC05689K.
19. R. F. W. Bader, Atoms in Molecules.: A Quantum Theory, Oxford Univesity Press, 1990.
20. P. L. A. Popelier, Quantum Chemical Topology, in The Chemical Bond II: 100 Years Old and Getting Stronger, ed. Mingos, D. M. P., Springer International Publishing, Cham, 2016, pp. 71–117 DOI:10.1007/430_2015_197.
21. M. A. Blanco, A. Martín Pendás and E. Francisco, Interacting quantum atoms: A correlated energy decomposition scheme based on the quantum theory of atoms in molecules, J. Chem. Theory Comput., 2005, 1(6), 1096–1109,  DOI:10.1021/ct0501093.
22. J. C. R. Thacker and P. L. A. Popelier, The ANANKE relative energy gradient (reg) method to automate IQA analysis over configurational change, Theor. Chem. Acc., 2017, 136(7), 86,  DOI:10.1007/s00214-017-2113-z.
23. N. Orangi, K. Eskandari, J. C. R. Thacker and P. L. A. Popelier, Directionality of halogen bonds: An interacting quantum atoms (IQA) and relative energy gradient (REG) study, ChemPhysChem, 2019, 20(15), 1922–1930,  DOI:10.1002/cphc.201900250.
24. J. C. R. Thacker and P. L. A. Popelier, Fluorine gauche effect explained by electrostatic polarization instead of hyperconjugation: An interacting quantum atoms (IQA) and relative energy gradient (REG) study, J. Phys. Chem. A, 2018, 122(5), 1439–1450,  DOI:10.1021/acs.jpca.7b11881.
25. P. L. A. Popelier, P. I. Maxwell, J. C. R. Thacker and I. Alkorta, A relative energy gradient (REG) study of the planar and perpendicular torsional energy barriers in biphenyl, Theor. Chem. Acc., 2019, 138(1), 12,  DOI:10.1007/s00214-018-2383-0.
26. J. C. R. Thacker, M. A. Vincent and P. L. A. Popelier, Using the relative energy gradient method with interacting quantum atoms to determine the reaction mechanism and catalytic effects in the peptide hydrolysis in HIV-1 protease, Chem. – Eur. J., 2018, 24(43), 11200–11210,  DOI:10.1002/chem.201802035.
27. G. Kresse and J. Hafner, Ab initio molecular dynamics for liquid metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47(1), 558–561,  DOI:10.1103/physrevb.47.558.
28. P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50(24), 17953–17979,  DOI:10.1103/physrevb.50.17953.
29. G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59(3), 1758–1775,  DOI:10.1103/physrevb.59.1758.
30. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77(18), 3865–3868,  DOI:10.1103/physrevlett.77.3865.
31. C. Adamo and V. Barone, Toward reliable density functional methods without adjustable parameters: The PBE0 model, J. Chem. Phys., 1999, 110(13), 6158–6170,  DOI:10.1063/1.478522.
32. A. D. Becke, A new mixing of Hartree–Fock and local density-functional theories, J. Chem. Phys., 1993, 98(2), 1372–1377,  DOI:10.1063/1.464304.
33. S. Grimme, Semiempirical GGA-type density functional constructed with a long-range dispersion correction, J. Comput. Chem., 2006, 27(15), 1787–1799,  DOI:10.1002/jcc.20495.
34. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132(15), 154104,  DOI:10.1063/1.3382344.
35. A. Tkatchenko and M. Scheffler, Accurate molecular van der Waals interactions from ground-state electron density and free-atom reference data, Phys. Rev. Lett., 2009, 102(7), 073005,  DOI:10.1103/PhysRevLett.102.073005.
36. H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B: Solid State, 1976, 13(12), 5188–5192,  DOI:10.1103/physrevb.13.5188.
37. D. Tunega, T. Bučko and A. Zaoui, Assessment of ten DFT methods in predicting structures of sheet silicates: Importance of dispersion corrections, J. Chem. Phys., 2012, 137(11), 114105,  DOI:10.1063/1.4752196.
38. R. Ditchfield, D. P. Miller and J. A. Pople, Self-consistent molecular orbital methods. XI. Molecular orbital theory of NMR chemical shifts, J. Chem. Phys., 1971, 54(10), 4186–4193,  DOI:10.1063/1.1674657.
39. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 09, Gaussian, Inc., Wallingford, CT, 2006.
40. A. K. Todd, AIMALL, TK Gristmill Software, Overland Park KS, USA, 2019.
41. J. L. Leviel, G. Auvert and J. M. Savariault, Hydrogen bond studies. A neutron diffraction study of the structures of succinic acid at 300 and 77 K, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1981, 37(12), 2185–2189,  DOI:10.1107/s0567740881008352.
42. Q. Yu, L. Dang, S. Black and H. Wei, Crystallization of the polymorphs of succinic acid via sublimation at different temperatures in the presence or absence of water and isopropanol vapor, J. Cryst. Growth, 2012, 340(1), 209–215,  DOI:10.1016/j.jcrysgro.2011.12.050.
43. G. D. Rieck, The crystal structure of α-succinic acid, Recl. Trav. Chim. Pays-Bas, 2010, 63(9), 170–180,  DOI:10.1002/recl.19440630902.
44. P. Lucaioli, E. Nauha, I. Gimondi, L. S. Price, R. Guo, L. Iuzzolino, I. Singh, M. Salvalaglio, S. L. Price and N. Blagden, Serendipitous isolation of a disappearing conformational polymorph of succinic acid challenges computational polymorph prediction, CrystEngComm, 2018, 20(28), 3971–3977,  10.1039/c8ce00625c.
45. K. Momma and F. Izumi, VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data, J. Appl. Crystallogr., 2011, 44(6), 1272–1276,  DOI:10.1107/S0021889811038970.
46. I. Alkorta, J. C. R. Thacker and P. L. A. Popelier, An interacting quantum atom study of model S_N2 reactions (X⁻⋯CH₃X, X = F, Cl, Br, and I), J. Comput. Chem., 2018, 39(10), 546–556,  DOI:10.1002/jcc.25098.
47. J. L. McDonagh, A. F. Silva, M. A. Vincent and P. L. A. Popelier, Quantifying electron correlation of the chemical bond, J. Phys. Chem. Lett., 2017, 8(9), 1937–1942,  DOI:10.1021/acs.jpclett.7b00535.
48. A. Martín Pendás, M. A. Blanco and E. Francisco, The nature of the hydrogen bond: A synthesis from the interacting quantum atoms picture, J. Chem. Phys., 2006, 125(18), 184112,  DOI:10.1063/1.2378807.
49. L. J. Duarte, A. F. Silva, W. E. Richter and R. E. Bruns, Infrared intensification and hydrogen bond stabilization: Beyond point charges, J. Phys. Chem. A, 2019, 123(30), 6482–6490,  DOI:10.1021/acs.jpca.9b03105.
50. J. M. Guevara-Vela, R. Chávez-Calvillo, M. García-Revilla, J. Hernández-Trujillo, O. Christiansen, E. Francisco, Á. Martín Pendás and T. Rocha-Rinza, Hydrogen-bond cooperative effects in small cyclic water clusters as revealed by the interacting quantum atoms approach, Chem. – Eur. J., 2013, 19(42), 14304–14315,  DOI:10.1002/chem.201300656.
51. A. J. Jackson, J. M. Skelton, C. H. Hendon, K. T. Butler and A. Walsh, Crystal structure optimisation using an auxiliary equation of state, J. Chem. Phys., 2015, 143(18), 184101,  DOI:10.1063/1.4934716.
52. F. Birch, Finite elastic strain of cubic crystals, Phys. Rev., 1947, 71(11), 809–824,  DOI:10.1103/PhysRev.71.809.
53. W. Humphrey, A. Dalke and K. Schulten, VMD: Visual molecular dynamics, J. Mol. Graph., 1996, 14(1), 33–38,  DOI:10.1016/0263-7855(96)00018-5.
54. J. Nyman and G. M. Day, Static and lattice vibrational energy differences between polymorphs, CrystEngComm, 2015, 17(28), 5154–5165,  10.1039/C5CE00045A.
55. C. Červinka and G. J. O. Beran, Ab initio thermodynamic properties and their uncertainties for crystalline α-methanol, Phys. Chem. Chem. Phys., 2017, 19(44), 29940–29953,  10.1039/C7CP06605H.
56. P. L. A. Popelier, QCTFF: On the construction of a novel protein force field, Int. J. Quantum Chem., 2015, 115, 1005–1011.
57. M. J. Burn and P. L. A. Popelier, Creating Gaussian process regression models for molecular simulations using adaptive sampling, J. Chem. Phys., 2020, 153, 054111.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d2cp00457g

---