Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Determining nanorod dimensions in dispersion with size anisotropy nanoparticle tracking analysis†
William H.
Hoffmann
 abc,
Bo
Gao
a,
Niall M. C.
Mulkerns
abc,
Bo
Gao
a,
Niall M. C.
Mulkerns
 ab,
Alexander G.
Hinton
ac,
Simon
Hanna
a,
Simon R.
Hall
ab,
Alexander G.
Hinton
ac,
Simon
Hanna
a,
Simon R.
Hall
 bc and
Henkjan
Gersen
bc and
Henkjan
Gersen
 *ab
*ab
aH.H. Wills Physics Laboratory, University of Bristol, Tyndall Avenue, Bristol BS8 1TL, UK. E-mail: h.gersen@bristol.ac.uk
bBristol Centre for Functional Nanomaterials, University of Bristol, Tyndall Avenue, Bristol BS8 1TL, UK
cSchool of Chemistry, University of Bristol, Cantock's Close, Bristol BS8 1TS, UK
First published on 18th May 2022
Abstract
Control over nanorod dimensions is critical to their application, requiring fast, robust characterisation of their volume and aspect ratio whilst in their working medium. Here, we present an extension of Nanoparticle Tracking Analysis which determines the aspect ratio of nanoparticles from the polarisation state of scattered light in addition to a hydrodynamic diameter from Brownian motion. These data, in principle, permit the determination of nanorod dimensions of any composition using Nanoparticle Tracking Analysis. The results are compared with transmission electron microscopy and show that this technique can additionally determine the aggregation state of the nanorod dispersion if single nanorod dimensions are determined with a complementary technique. We also show it is possible to differentiate nanoparticles of similar hydrodynamic diameter by their depolarised scattering. Finally, we assess the ability of the technique to output nanorod dimensions and suggest ways to further improve the approach. This technique will enable rapid characterisation of nanorods in suspension, which are important tools for nanotechnology.
1 Introduction
Nanoparticle shape plays a key role in the control of their behaviour in a diversity of disciplines, including nanomedicine,1 nanocatalysis,2 and nanocomposites.3 Nanorods, in particular, are utilised for a variety of applications including labelling for biological imaging,4 plasmonic sensing,5 and display technology.6 The ability to use nanorod dimensions to tune their optical properties and diffusion is integral to their use in these applications. As such, control over the dimensions for this class of nanomaterial is critical. Simple, robust characterisation of nanorods is key to realising consistent syntheses.A multitude of techniques have been employed to characterise nanorods. Gold nanorod characterisation, for example, is usually performed with transmission electron microscopy (TEM) and UV-visible spectroscopy (UV-vis), which are complementary techniques.7 Whilst TEM can determine dimensions directly on the single nanoparticle level, it is inefficient for characterising large populations, potentially resulting in a size distribution which misrepresents the sample. TEM also requires high vacuum and therefore a dry sample, which prevents characterisation of nanorods in dispersion. UV-vis characterises gold nanorods in dispersion, developing a population representation of the optical behaviour, but this method loses single nanoparticle resolution and typically requires a plasmon resonance peak.
Specialised techniques have been used to extract size parameters from nanorods in dispersion. Optical extinction spectroscopy, similar to UV-vis, has been shown to extract the aspect ratio distribution and mean width of a nanorod sample.8 Dynamic light scattering (DLS), which measures the translational and rotational diffusion coefficients of nanoparticles via relaxation time constants, has been used to relate nanorod dimensions to their diffusive behaviour.9–13 Flow dichroism, which measures the linear dichroism of nanoparticles oriented in flow, can determine the aspect ratio of nanorod samples.14 These techniques, like UV-vis, all report sample-averaged properties, which is potentially problematic where the knowledge of single nanoparticle dimensions is important, like in the case of nanoprobing studies.15–17
Single nanoparticle sizing techniques collect data from individual nanoparticles to develop an understanding of the whole sample. Wide-field optical imaging of nanorods has been performed which can characterise asphericity,18 and monitor gold nanorod growth,19,20 but these techniques required confinement of the nanorods to a glass surface. Electrochemical sizing has been performed which determines the dimensions of individual nanoparticles, but it is destructive.21In situ optical characterisation using a polarimetric analysis permitted the extraction of aspect ratio22 and shape23 on the single nanoparticle level, but these devices analyse nanoparticles one-by-one and are therefore slower than an imaging configuration. A technique which is in situ, non-destructive, and able to rapidly characterise the dimensions of a statistically significant number of nanoparticles on the single nanoparticle level is still required.
Nanoparticle Tracking Analysis (NTA) is an established technique for the size characterisation of nanoparticles which satisfies these requirements.24 However, NTA outputs a hydrodynamic diameter distribution, which contains no information on nanoparticle aspect ratio. Brownian motion from rods is indistinguishable from that of spheres on long time scales,25 making an assessment of nanoparticle shape with NTA difficult if not impossible. NTA has been employed previously to characterise nanorods,26–28 but only hydrodynamic diameters were reported and compared with expected values.
In this work, we have developed an NTA technique with the ability to resolve the polarisation state of scattering from single nanoparticles, allowing for the interrogation of aspect ratio whilst simultaneously determining hydrodynamic diameter from Brownian motion. These two parameters in principle uniquely describe nanoparticle dimensions in the case of a nanorod. We term this technique Size Anisotropy Nanoparticle Tracking Analysis (SANTA). Here we show that SANTA is able to distinguish nanoparticle samples based on both size and aspect ratio, allowing nanorods to be distinguished from nanospheres and other nanorods using an NTA technique. In principle, this technique can be applied to nanorods of any composition, provided sufficient depolarisation signal is collected.
2 Theory
2.1 Nanoparticle tracking analysis
NTA is an optical technique which outputs individual nanoparticle hydrodynamic diameter by tracking nanoparticle diffusion in a video.24 Using a tracking algorithm, scattering centres are localised and then linked between video frames to determine nanoparticle displacements. The nanoparticle displacements are related to the translational diffusion coefficient of the nanoparticle by| 〈Δr2〉 = 4Dtt, | (1) |
 | (2) |
In the case of non-spherical nanoparticles e.g. nanorods, the hydrodynamic diameter output is a nominal nanoparticle size with no information on the nanoparticle anisotropy. The hydrodynamic diameter is the equivalent sphere which diffuses with the same translational diffusion coefficient. The translational diffusion coefficient of a nanorod can be calculated with16
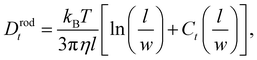 | (3) |
The rotational diffusion coefficient of a nanorod about its short axis is16
 | (4) |
2.2 Aspect ratio from scattering polarisation
Whilst NTA determines nanoparticle hydrodynamic diameter from diffusion behaviour, it also records intensity information from the scattering centre in the video. The polarisation of the scattering can be interrogated by comparing scattering intensity along orthogonal axes to extract information on the nanoparticle anisotropy.29,30 This is the additional data point that is collected with SANTA. For each individual nanoparticle, both diffusion and intensity information are recorded in videos. Fig. 1A shows this pictorially. In SANTA, incident light is linearly polarised along the y-axis, and depolarisation signal on the x-axis indicates non-sphericity. The depolarisation ratio, ρ, compares the polarisation components on orthogonal axes:31–33 | (5) |
Gold nanorod polarisability can be calculated analytically using the prolate ellipsoid approximation in Rayleigh–Gans theory,29,34 with additional analytical and numerical modelling possible to account for the magnetic dipole and electric quadrupole contributions to scattering30 as well as phase retardation.34–36 We note that most of the nanoparticles used in this study are not strictly in the regime where Raleigh–Gans theory is a completely accurate representation of the scattering behaviour; however, for the sake of simplicity and noting that more robust modelling can be performed if required, we interpret our results with respect to the Raleigh–Gans theory. Detailed equations are shown in the ESI.† This theory shows that the depolarisation ratio is dependent solely on material and medium relative permittivities and aspect ratio. From these calculations, polarisability along the long axis, α‖, and along the short axis, αp, can be determined. The depolarisation ratio is related to the polarisability components by31,32
 | (6) |
 . Because the polarisability components depend on nanorod aspect ratio, the depolarisation ratio determined via scattering intensity can be used to determine nanoparticle anisotropy. Fig. 1B shows the relationship between depolarisation ratio and aspect ratio. A given depolarisation ratio is uniquely matched with an aspect ratio and is not dependent on nanorod size as long as the nanorod optical properties are well-described by the Rayleigh–Gans theory.
. Because the polarisability components depend on nanorod aspect ratio, the depolarisation ratio determined via scattering intensity can be used to determine nanoparticle anisotropy. Fig. 1B shows the relationship between depolarisation ratio and aspect ratio. A given depolarisation ratio is uniquely matched with an aspect ratio and is not dependent on nanorod size as long as the nanorod optical properties are well-described by the Rayleigh–Gans theory.
It is important to note that eqn (6) only applies in the case where a nanoparticle has rotated many times during the collection time as is typically the case for nanoparticles characterised with NTA. In fact, a strength of this technique as compared to DLS tools is the reduced temporal resolution requirement; because averaged depolarisation ratios are used, only sufficient temporal resolution to resolve the lateral motion of the rods (10 s of ms) is required.
The one-to-one correspondence between depolarisation ratio and aspect ratio contrasts with hydrodynamic diameter, where nanorods of many aspect ratios can diffuse with the same behaviour as a sphere with the same hydrodynamic diameter; however, the collection of depolarisation ratio permits the determination of that aspect ratio. SANTA combines the independent outputs of hydrodynamic diameter from diffusion and aspect ratio from depolarisation to, in principle, uniquely determine nanorod length and width. Fig. 1C shows a map with axes corresponding to the two data points collected from each nanoparticle, hydrodynamic diameter and depolarisation ratio, along with contour lines of nanorod lengths. This map shows that with these two data points, the nanorod length and width can be determined.
3 Experimental
The SANTA apparatus is shown in Fig. 2A. A 633 nm Helium–Neon laser (JDSU 1137P) was coupled into a single-mode fibre (Thorlabs S405-XP) and collimated (Thorlabs A110TM-A). The output was linearly polarised (Qioptiq G335718000) along the y-axis and then shaped with a cylindrical lens (Thorlabs LJ1567RM-A) and another lens (Thorlabs AC080-016-A-ML) into a light sheet with a thickness of approximately 40 μm, similar to our previous work.37 The light sheet propagated through the sample in a stoppered glass cuvette (International Crystal Laboratories 0023T-2382) to irradiate nanoparticles. Glass was used to avoid modification of the incident and detected polarisation state. A detection lens (Thorlabs AC064-013-A-ML) mounted orthogonally to the incident light collected the scattered light. The light was then passed through polarising beam splitters (Qioptiq G335718000) to decompose the scattered light into x- and y-polarised light. Three polarising beam splitters were used to enhance the extinction of the undesired polarisation in each polarisation channel. The light in each path was passed through another lens (Thorlabs AC254-500-A-ML) and focused onto a camera (Ximea MQ013MG-E2). Fig. 2B shows example inverted image stills collected with SANTA, highlighting the differences in the relative depolarised scattering signal between nanospheres and nanorods. The image pixel size was calibrated with dispersion of 0.99(2) μm silica microparticles (ThermoFisher Scientific 8100) and determined to be 138.4(6) nm per pixel. The cameras were synced with an external trigger to record videos. Videos were collected in 10 second increments with 1 second spacing at either 25 or 30 frames per second. Camera exposure, gain, and frame rate were kept the same on both paths for each sample.Nanoparticle tracking was performed using the Python package Trackpy (version 0.4.2), which is based on the Crocker–Grier tracking algorithm.38 Individual nanoparticle hydrodynamic diameters were calculated from a linear regression of mean squared displacement and lag time (eqn (1)) utilising the first five lag times39 to calculate the diffusion coefficient, which was converted to a hydrodynamic diameter with eqn (2). Ensemble nanoparticle hydrodynamic diameters were calculated using the ensemble mean squared displacement and the first 30 lag times. Sizing is performed with the y-polarised channel due to higher signal levels.
Scattering centre pairs were determined using an affine transformation as described previously.40 Three scattering centres on each polarisation channel were matched manually to calculate the affine transformation matrix. Scattering centres on the y-polarised channel were mapped to those on the x-polarised channel using the matrix. The intensity of each scattering centre was determined by integrating the pixel intensity with a diameter of five pixels around the centre of the nanoparticle. Background noise was removed from each pixel by subtracting the video modal value of the pixel from its intensity. The intensities were summed for each polarisation along the whole nanoparticle track before determining the depolarisation ratio. Unless otherwise stated, only nanoparticles present in the field of view for more than 30 frames were accepted into the data sets.
Nanorods (Nanopartz A12-40-1064-CTAB-DIH-1-1, A12-40-980-CTAB-DIH-1-1, A12-50-800-CTAB-DIH-1-1 and Nanocomposix GRCN660, labelled in this work as 167 nm × 36 nm, 195 nm × 50 nm, 145 nm × 66 nm, and 42 nm × 18 nm, respectively) and nanospheres (BBI Solutions EM.GC100, labelled in this work as 105 nm) were purchased and diluted in Milli-Q water for analysis.
4 Results and discussion
For each nanoparticle sample, TEM was performed to compare with the values of hydrodynamic diameter and depolarisation ratio determined by SANTA. Table 1 summarises the results. Additional data including representative TEM images, TEM dimension distributions, expected hydrodynamic diameter distributions (from TEM), and expected depolarisation ratio distributions (from TEM) are available in the ESI.† At least 100 nanoparticles were characterised for each nanoparticle type. Nanoparticle dimensions as determined by TEM are used to label them in this work. The expected hydrodynamic diameters of the 145 nm × 66 nm, 195 nm × 50 nm, and 167 nm × 36 nm nanorods are calculated from theory considering the addition of a bilayer of cetyltrimethylammonium bromide (CTAB),9 which is not visible in TEM. A bilayer of CTAB adds approximately 8 nm to both the length and width of the nanorod, and is added to the measurements taken from TEM results. The capping agent for the nanosphere and 42 nm × 18 nm nanorod was citrate, which is much smaller than CTAB and was not added to the dimensions in the calculation of expected hydrodynamic diameters. With the exception of the 42 nm × 18 nm nanorod, the expected hydrodynamic diameters of the nanoparticles are similar, indicating issues with differentiating the nanoparticle samples by this parameter.| Nanoparticle type | Rod | Sphere | Rod | Rod | Rod |
|---|---|---|---|---|---|
| Length (nm) | 42(7) | 105(8) | 145(28) | 195(28) | 167(38) |
| Width (nm) | 18(2) | — | 66(12) | 50(5) | 36(5) |
| Aspect ratio | 2.4(5) | — | 2.3(6) | 3.9(5) | 4.7 1.1 |
| Expected hydrodynamic diameter (nm) | 28(2) | 105(8) | 106(13) | 111(10) | 90(13) |
| Experimental hydrodynamic diameter (nm) | 36(1) | 109(3) | 139(4) | 113(3) | 145(4) |
| Expected depolarisation ratio | 0.21(7) | 0 | 0.19(9) | 0.34(2) | 0.36(2) |
| Experimental depolarisation ratio | 0.26(4) | 0.03(4) | 0.28(12) | 0.36(5) | 0.39(6) |
| Experimental dimensions (nm × nm) | 58 × 22 | 126 × 93 | 226 × 78 | 220 × 49 | 334 × 48 |
Expected depolarisation ratios are also shown in Table 1. They were calculated using the dimensions as determined from TEM assuming the contribution of the CTAB bilayer to the polarisability of the nanoparticles is negligible. There is overlap in some of the distributions, but the peaks should be sufficiently resolved to be able to tell the difference between some nanoparticle samples based on depolarisation ratio.
Fig. 3 shows hydrodynamic diameter distributions for each nanoparticle sample determined experimentally with SANTA. The distribution contains individual contributions from all nanoparticles accepted into the distribution. There is strong overlap between distributions of all the nanoparticle samples with the exception of the 42 nm × 18 nm nanorods as expected. This finding confirmed the relative hydrodynamic diameters predicted by TEM; these samples have similar hydrodynamic diameters and thus cannot be easily distinguished based on these distributions. Clearly, any information about nanoparticle anisotropy is lost. The distributions are broader than those calculated from TEM (see the ESI† for calculated hydrodynamic diameters from TEM measurements), but size distribution broadening is a known artefact of NTA; limited sampling of displacements increases the uncertainty in individual nanoparticle size.24
For comparison with the TEM results, the ensemble hydrodynamic diameter is used, as it incorporates displacement contributions from all the nanoparticles into a hydrodynamic diameter representative of the whole sample. Table 1 shows the ensemble hydrodynamic diameters of each nanoparticle type. There is excellent agreement between the expected hydrodynamic diameters calculated from TEM data and ensemble hydrodynamic diameters output by SANTA for the 105 nm and 195 nm × 50 nm nanoparticles. For the 42 nm × 18 nm, 145 nm × 66 nm, and 167 nm × 36 nm nanoparticles, SANTA outputs an ensemble hydrodynamic diameter larger than that expected by the TEM data. Aggregated nanorods in the solution could increase the ensemble average hydrodynamic diameter. In principle, dispersing in a solution of CTAB could prevent aggregation, but scatterers in CTAB solution of about 100 nm hydrodynamic diameter seen previously27 would complicate the imaging. In TEM, information about nanoparticle behaviour in dispersion is lost due to drying. If aggregation is the cause of the increased hydrodynamic diameter, this points to SANTA's utility to characterise the dispersion state of nanorods; a nominal size can be determined via TEM, then the hydrodynamic diameter from SANTA can be compared with that of TEM to determine the aggregation state of the nanorods. Assessment of aggregation state is important to acquiring a relevant representation of a nanoparticle dispersion, as size and shape influence nanoparticle properties.1 However, SANTA cannot determine aggregation state without additional information about the nanoparticles.
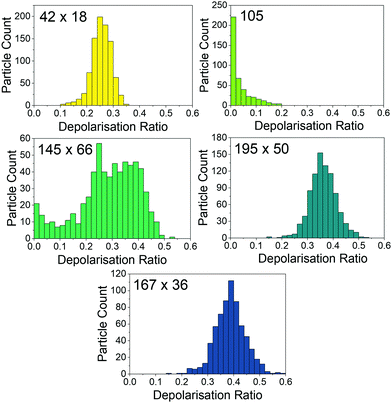
Fig. 4 shows the distribution of nanoparticle depolarisation ratios determined by SANTA, with averages shown in Table 1. The distributions all look different with the exception of the 195 nm × 50 nm and 167 nm × 36 nm nanoparticles. There is good agreement between the nanorod depolarisation ratios determined by SANTA and expected values from the TEM sizing, confirming the ability of SANTA to output expected depolarisation ratios. The nanospheres have comparatively low depolarisation ratios as well. For the nanospheres, the presence of depolarisation implies asphericity, which the TEM data validates by showing aspherical nanoparticles (see the ESI†). Even so, the nanospheres are able to be clearly differentiated from the nanorod samples.
The 42 nm × 18 nm sample shows depolarisation ratios lower than those of the 195 nm × 50 nm and 167 nm × 36 nm samples, which means these samples can be differentiated based on both size and depolarisation ratio. The 195 nm × 50 nm and 167 nm × 36 nm samples have comparable depolarisation ratios as expected from the TEM. Interestingly, whilst the hydrodynamic diameter for the 167 nm × 36 nm sample implies aggregation, the depolarisation distribution is not different from the 195 nm × 50 nm sample. Aggregation may not be detectable in this range of aspect ratios due to the low relative depolarisation ratio change as a function of aspect ratio at an aspect ratio of about 5 (Fig. 1B).
This lack of change in the depolarisation ratio contrasts with the observation of the 145 nm × 66 nm sample depolarisation ratio distribution. There is a significant spread of depolarisation ratio values, which matches well with the expected range based on the TEM. The reason for this spread in comparison to the 167 nm × 36 nm sample could be that the average aspect ratio of 2.3 as determined with TEM is on the region of the curve where there is significant change in the depolarisation ratio as a function of aspect ratio as shown in Fig. 1B. SANTA is more sensitive to aspect ratio differences at low aspect ratios. To determine whether the depolarisation ratio distribution is affected by aggregation, the data for the 167 nm × 36 nm sample can be filtered by nanoparticle hydrodynamic diameter to eliminate contribution from larger nanoparticles. This is a major advantage of SANTA in that different sub-populations can be probed based on hydrodynamic diameter or aspect ratio. Performing this filter, no noticeable change in the depolarisation ratio distribution is observed, indicating that the observed depolarisation ratio is not significantly affected by aggregation (distributions are shown in the ESI†). Interestingly, the spread of depolarisation ratios is not as pronounced for the 42 nm × 18 nm sample despite having a similar expected depolarisation ratio. However, there is a smaller spread on expected depolarisation ratios based on the TEM, which may contribute to the observed smaller spread from SANTA.
To highlight the ability of SANTA to resolve nanoparticle populations based on both hydrodynamic diameter and depolarisation ratio, Fig. 5A shows a scatter plot of individual nanoparticle contributions from each of the 42 nm × 18 nm, 105 nm, and 195 nm × 50 nm samples with reference lines showing the expected mean values based on TEM. This plot has the same axes as those of Fig. 1C. The reference lines have good agreement with the data. We note that the 42 nm × 18 nm sample has a population of depolarisation ratios higher than expected from the TEM data, possibly due to the inability to detect very low depolarisation signals of this comparatively weakly scattering nanoparticle population. A scatter plot of expected depolarisation ratio vs. expected hydrodynamic diameter from TEM data is plotted in the ESI† to show these lower depolarisation ratios as well as good agreement between the TEM data and the SANTA data considering the limited sample size from TEM.
Importantly, the three samples are clearly localised in different regions of the graph in Fig. 5A. The 42 nm × 18 nm and 105 nm samples can be differentiated based on both hydrodynamic diameter and depolarisation ratio. The 105 nm and 195 nm × 50 nm samples overlap significantly in hydrodynamic diameter but are distinguishable by depolarisation ratio. Finally, the 42 nm × 18 nm and the 195 nm × 50 nm samples are able to be distinguished by both size and depolarisation ratio. In Fig. 5B, Gaussian mixture modelling to computationally determine whether the clusters can be resolved is shown. The Python package scikit-learn (0.24.2)41 is used to perform the modelling. The only input into the model was the number of clusters. The model is able to clearly differentiate between the samples in the data set, with 98.3% of the nanoparticles being grouped in the correct cluster.
The sample dimensions as determined by the average hydrodynamic diameter and average depolarisation ratio are shown in Table 1. In general, the calculated dimensions are larger than those output by TEM analysis, which is in part due to nanoparticle aggregation. The uncertainties in hydrodynamic diameter (Fig. 3) for a single nanoparticle make it difficult to assign dimensions to individual nanoparticles. Furthermore, most of the depolarisation ratio distributions are larger than expected from the TEM (Fig. 4); the presence of depolarisation ratios greater than 0.4 make it difficult to assign aspect ratios to individual nanoparticles. The width of the depolarisation ratio histograms is currently being investigated, but we hypothesise that the distribution is due to out-of-plane motion changing the relative polarisation signals on each channel, in combination with the use of optics not optimised for polarisation-resolved imaging. Improvements to the microscope could be made by optimising the light sheet dimensions and the depth of view so that out-of-focus scattering centres are less prominent, whilst ensuring that particles are tracked for a long time. This work also places a low threshold on nanoparticle residence time; imaging for longer periods of time could increase the number of nanoparticles present for a long period of time in the field of view, improving the sampling error on particle displacements.37,42 Furthermore, the sensitivity can be further improved taking inspiration from Interferometric Cross-Polarisation Microscopy.43,44 Despite these drawbacks, the Gaussian mixture modelling shows that most single nanoparticles from these samples can be easily categorised into a sample type if the identities of the nanoparticles were unknown. The ability of SANTA to resolve different populations indicates the possibility of using this technique to monitor changes in nanorod dimensions due to assembly or aggregation.
We have demonstrated measurement of hydrodynamic diameter and depolarisation ratio of nanorods in the tens to low hundreds of nm in dimension. In principle, this technique could measure nanorods of other sizes within the range of conventional NTA: 10–1000 nm.24 A couple of additional considerations need to be made to extend the measurement capability across this range. The most simple is the requirement that a sufficient depolarisation signal is collected so the aspect ratio can be determined. For gold, relatively large depolarisation signal is generated, but dielectric materials would produce a much smaller depolarisation ratio. Additional laser power may be required to increase the signal, and a neutral density filter may be needed on the detection arm along the polarisation channel corresponding to the polarisation of the input beam to collect the videos at the same collection parameters on both cameras due to finite well depth. However, care should be taken to ensure the additional laser power does not induce convection currents and affect the measurement.37 The second consideration is the speed of rotational Brownian motion; for large and high-aspect-ratio nanorods, the rotation slows, taking longer for the nanorod to sample all orientations. Eqn (3) and (6) assume rotational averaging of the nanorod motion. In principle, as long as the optical properties can be modelled and the rotation is sufficiently quick, nanorods of a diverse selection of materials could be characterised using this method.
5 Conclusion
In summary, a new development of NTA to interrogate the hydrodynamic diameter and aspect ratio of nanorod samples from depolarised scattering has been demonstrated. This is, to the best of our knowledge, the first demonstration of using the combination of diffusion and scattering polarisation to characterise nanorods from single nanoparticle contributions in NTA. We observe larger nanoparticles in some of the samples via the ensemble hydrodynamic diameter, but this is not obvious from the depolarisation ratios collected. SANTA requires only polarisation components in addition to the conventional NTA apparatus design, making it simple to incorporate into existing systems. We can see this technique being useful in the characterisation of nonspherical nanoparticles in their working medium, where controlled size and shape is paramount for their application or in cases where size and shape change due to degradation or assembly.Data access statement
The underlying data are provided within this paper and within the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
W. H. H. thanks Adrian Crimp and his team at the University of Bristol Mechanical Workshop for machining components of the device as well as Michael O'Donnell for discussions about light scattering theory. W. H. H., S. R. H., and H. G. acknowledge the Engineering and Physical Sciences Research Council (EPSRC) for funding under grant number EP/L016648/1. W. H. H. and S. R. H. acknowledge support by MagnaPharm, a European Union Horizon 2020 Research and Innovation programme under grant agreement number 736899. B. G. acknowledges the China Scholarship Council and the University of Bristol for funding and providing the High Performance Computing platform. N. M. and H. G. acknowledge support from an NPIF grant cofunded by Carbometrics under grant number EP/R51245/X. Electron microscopy studies were carried out in the Chemical Imaging Facility, University of Bristol with equipment funded by EPSRC under Grant “Atoms to Applications” EP/K035746/1.Notes and references
- C. Kinnear, T. L. Moore, L. Rodriguez-Lorenzo, B. Rothen-Rutishauser and A. Petri-Fink, Chem. Rev., 2017, 117, 11476–11521 CrossRef CAS PubMed.
- R. Narayanan and M. A. El-Sayed, J. Phys. Chem. B, 2005, 109, 12663–12676 CrossRef CAS PubMed.
- S. T. Knauert, J. F. Douglas and F. W. Starr, J. Polym. Sci., Part B: Polym. Phys., 2007, 45, 1882–1897 CrossRef CAS.
- L. Tong, Q. Wei, A. Wei and J. X. Cheng, Photochem. Photobiol., 2009, 85, 21–32 CrossRef CAS PubMed.
- J. Becker, A. Trügler, A. Jakab, U. Hohenester and C. Sönnichsen, Plasmonics, 2010, 5, 161–167 CrossRef CAS.
- A. K. Srivastava, W. Zhang, J. Schneider, A. L. Rogach, V. G. Chigrinov and H. S. Kwok, Adv. Mater., 2017, 29, 1701091 CrossRef PubMed.
- L. Scarabelli, A. Sánchez-Iglesias, J. Pérez-Juste and L. M. Liz-Marzán, J. Phys. Chem. Lett., 2015, 6, 4270–4279 CrossRef CAS PubMed.
- N. Xu, B. Bai, Q. Tan and G. Jin, Opt. Express, 2013, 21, 2987 CrossRef CAS PubMed.
- J. Rodríguez-Fernández, J. Pérez-Juste, L. M. Liz-Marzán and P. R. Lang, J. Phys. Chem. C, 2007, 111, 5020–5025 CrossRef.
- M. Glidden and M. Muschol, J. Phys. Chem. C, 2012, 116, 8128–8137 CrossRef CAS.
- M. Haghighi, M. N. Tahir, W. Tremel, H. J. Butt and W. Steffen, J. Chem. Phys., 2013, 139, 064710 CrossRef PubMed.
- S. Alam and A. Mukhopadhyay, J. Phys. Chem. C, 2014, 118, 27459–27464 CrossRef CAS.
- S. Balog, L. Rodriguez-Lorenzo, C. A. Monnier, B. Michen, M. Obiols-Rabasa, L. Casal-Dujat, B. Rothen-Rutishauser, A. Petri-Fink and P. Schurtenberger, J. Phys. Chem. C, 2014, 118, 17968–17974 CrossRef CAS.
- N. K. Reddy, J. Pérez-Juste, I. Pastoriza-Santos, P. R. Lang, J. K. Dhont, L. M. Liz-Marzán and J. Vermant, ACS Nano, 2011, 5, 4935–4944 CrossRef CAS PubMed.
- Y. Peng, B. Xiong, L. Peng, H. Li, Y. He and E. S. Yeung, Anal. Chem., 2015, 87, 200–215 CrossRef CAS PubMed.
- M. Molaei, E. Atefi and J. C. Crocker, Phys. Rev. Lett., 2018, 120, 118002 CrossRef CAS PubMed.
- C. Sönnichsen and A. P. Alivisatos, Nano Lett., 2005, 5, 301–304 CrossRef PubMed.
- L. M. Payne, W. Langbein and P. Borri, Appl. Phys. Lett., 2013, 102, 131107 CrossRef.
- J. Becker, O. Schubert and C. Sönnichsen, Nano Lett., 2007, 7, 1664–1669 CrossRef CAS PubMed.
- K. A. Sablon, Nanoscale Res. Lett., 2008, 3, 348–349 CrossRef CAS.
- B. J. Plowman, N. P. Young, C. Batchelor-McAuley and R. G. Compton, Angew. Chem., 2016, 128, 7116–7119 CrossRef.
- B. Al-Qadi and T. Saiki, Jpn. J. Appl. Phys., 2010, 49, 125001 CrossRef.
- L. F. Guerra, T. W. Muir and H. Yang, Nano Lett., 2019, 19, 5530–5536 CrossRef CAS PubMed.
- P. Hole, in Characterization of Nanoparticles: Measurement Processes for Nanoparticles, ed. V.-D. Hodoroaba, W. E. Unger and A. G. Shard, Elsevier, 2020, ch. 3.1.2, pp. 79–96 Search PubMed.
- Y. Han, A. M. Alsayed, M. Nobili, J. Zhang, T. C. Lubensky and A. G. Yodh, Science, 2006, 314, 626–630 CrossRef CAS PubMed.
- R. A.-D. Arancon, S. H. Lin, G. Chen, C. S.-K. Lin, J. Lai, G. Xu and R. Luque, RSC Adv., 2014, 4, 17114–17119 RSC.
- B. M. Hoover and R. M. Murphy, J. Pharm. Sci., 2020, 109, 452–463 CrossRef CAS PubMed.
- J. G. Mehtala and A. Wei, Langmuir, 2014, 30, 13737–13743 CrossRef CAS PubMed.
- C. F. Bohren and D. R. Huffman, Absorption and Scattering of Light by Small Particles, Wiley-VCH, Weinheim, Germany, 2004 Search PubMed.
- W. Heller and M. Nakagaki, J. Chem. Phys., 1974, 61, 3619–3625 CrossRef CAS.
- D. Long, Raman Spectroscopy, McGraw-Hill International Book Company, London, UK, 1977 Search PubMed.
- B. Santra, M. N. Shneider and R. Car, Sci. Rep., 2017, 7, 40230 CrossRef CAS PubMed.
- B. N. Khlebtsov, V. A. Khanadeev and N. G. Khlebtsov, J. Phys. Chem. C, 2008, 112, 12760–12768 CrossRef CAS.
- H. Chen, L. Shao, Q. Li and J. Wang, Chem. Soc. Rev., 2013, 42, 2679–2724 RSC.
- R. Yu, L. M. Liz-Marzán and F. J. García De Abajo, Chem. Soc. Rev., 2017, 46, 6710–6724 RSC.
- E. Stefan Kooij and B. Poelsema, Phys. Chem. Chem. Phys., 2006, 8, 3349–3357 RSC.
- W. H. Hoffmann, N. M. Mulkerns, S. R. Hall and H. Gersen, Nanoscale Adv., 2021, 3, 5694–5702 RSC.
- J. C. Crocker and D. G. Grier, J. Colloid Interface Sci., 1996, 179, 298–310 CrossRef CAS.
- M. Warzecha, M. S. Safari, A. J. Florence and P. G. Vekilov, Cryst. Growth Des., 2017, 17, 6668–6676 CrossRef CAS.
- I. B. Lee, H. M. Moon, J. H. Joo, K. H. Kim, S. C. Hong and M. Cho, ACS Photonics, 2018, 5, 797–804 CrossRef CAS.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and E. Duchesnay, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- M. A. Catipovic, P. M. Tyler, J. G. Trapani and A. R. Carter, Am. J. Phys., 2013, 81, 485–491 CrossRef CAS.
- B. T. Miles, E. C. Robinson, E. M. Van Dijk, I. D. Lindsay, N. F. Van Hulst and H. Gersen, ACS Photonics, 2015, 2, 1705–1711 CrossRef CAS.
- B. T. Miles, A. B. Greenwood, D. Benito-Alifonso, H. Tanner, M. C. Galan, P. Verkade and H. Gersen, Sci. Rep., 2017, 7, 1–7 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp00432a |
| This journal is © the Owner Societies 2022 |