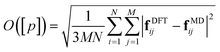Computational development of a phase-sensitive membrane raft probe

Abstract

Derivatives of the widely used 1,6-diphenyl-1,3,5-hexatriene molecular probe have been considered using a multiscale approach involving spin-flip time-dependent density functional theory, classical molecular dynamics and hybrid quantum mechanics/molecular mechanics. We identify a potential probe of membrane phase (i.e. to preferentially detect liquid-ordered regions of lipid bilayers), which exhibits restricted access to a conical intersection in the liquid-ordered phase but is freely accessible in less ordered molecular environments. The characteristics of this probe also mark it as a candidate for an aggregation induced emission fluorophore.

---

1. Introduction

Lipid membranes are heterogeneous structures that not only define the boundaries of cells, but are also responsible for regulating many key processes in living cells. In regions of membranes with high concentrations of sphingolipids and cholesterol, liquid-ordered (L_o) phases can occur, often known as lipid rafts. These can be characterised by thickening of the bilayer and relatively small tilt angles for cholesterol,^1,2 and having sizes between 10 and 200 nm.³ These ordered regions are critical to many of the processes regulated by the cell membrane, including signalling, exo- and endocytosis and protein trafficking.^4,5 Small molecules can be directly trafficked through a membrane without a specific protein. In a recent study by Ghysels et al.,⁶ trafficking of oxygen and water molecules through membranes is made possible by transiting along the boundary regions of the different membrane phases. Direct observation of rafts in vivo is still elusive, leading to results that can seem at odds with each other.⁷ Initially, extraction of raft regions was performed with detergent assays, although differing temperatures and detergent concentrations have led to very different molecular compositions of the raft domains, even from similar initial conditions.^8–10 While fluorescent probes which are sensitive to membrane environments have generally been very successful on reporting within general lipid bilayers, there has been less success in fluorescent labelling of specific membrane phases.¹¹ A simple probe of L_o phase existence would therefore prove invaluable to understanding the existence and effects of raft nanodomains in a cell.

During the last decade, a new class of membrane probes that report on lateral forces present in lipid membranes have been developed by the Matile group.^12–22 These probes, based on a dithienothiophene molecular structure, exhibit large shifts in their excitation spectra upon partitioning into regions of highly-ordered lipid domains. A computational approach identified the planarization of the structure as the key element in the large spectral shifts observed between the probe in L_o and liquid-disordered (L_d) regions of lipid membranes.¹⁴ A single dihedral angle linking the two thienothiophene moieties exhibits mechano-sensitivity and rotates in response to forces exerted by the molecular environment, leading to a red-shift of the absorption spectrum and increased intensity of the emission spectrum upon ordering of the surrounding membrane environment.¹⁴

We have previously studied contemporary and novel fluorescent probes of membrane structure and function, including di-8-ANEPPS and BODIPY derivatives commonly encountered in membrane characterisation.^23–27 In the current work, we explore a series of molecules inspired by the design principles of molecules which exhibit aggregation-induced emission (AIE) effect in their fluorescent behaviour. In AIE, aggregation of specially designed fluorophores leads to enhanced emission, often due to restriction of rotation at key points within molecules, leading to restriction of access to non-radiative decay pathways (e.g. conical intersections). We investigate, from first principles calculations, simple derivatives of the widely used 1,6-diphenyl-1,3,5-hexatriene (DPH) probe.^28,29 DPH itself doesn’t show much sensitivity with respect to fluorescence wavelength and intensity between different phases of a lipid bilayer, although it does demonstrate fluorescence anisotropy differences between different phases.^28,29 Inspired by the simple substitutions made to 1,4-distyrylbenzene which significantly enhance the AIE effect,³⁰ we demonstrate that inclusion of methyl groups along the polyene chain of DPH disrupts the planar nature of the molecule in gas-phase and solvated environments, while the forces involved within a raft-like membrane planarise the DPH derivatives resulting in emission being “switched on” within the raft domains due to a restricted availability to access the conical intersection.³¹

2. Computational details

Our overall approach to identifying and confirming a fluorescent probe sensitive to phase changes in a membrane are summarised in Scheme 1. In essence, we start with gas phase calculations to identify probes that have a conical intersection in which the minimum energy conical intersection (MECI) geometry has a twist in a polyene backbone. We then look to see if the conical intersection is thermally accessible in the S₁ electronic state. Once we have identified any such probe(s), we then perform classical molecular dynamics (MD) simulations to equilibrate the lipid bilayer and probe molecule, followed by hybrid quantum mechanics/molecular mechanics (QM/MM) simulations to ensure that the conical intersection becomes less accessible as the ordering of the lipid bilayer increases.

Scheme 1 Multi-layer approach to identifying potential candidates for phase-sensitive lipid membrane probes under standard temperature and pressure (STP) conditions.

2.1 Gas phase

We investigated the DPH derivatives shown in Fig. 1, along with unsubstituted DPH. The structures for the S₀ electronic states of each molecule were optimised using density functional theory (DFT) with the BHHLYP functional^32,33 and 6-31G(d,p) basis set. The S₁ geometries were optimised using time-dependent DFT (TD-DFT) using the same functional and basis set. MECI geometries were optimised using spin-flip TDDFT (SF-TDDFT) and analytical non-adiabatic coupling derivatives,^34,35 as we have previously found this approach (along with BHHLYP) to be in good agreement with XMS-CASPT2 results.³⁶ The starting guess for the MECI search was generated from the S₁ optimised geometry, where the planarity of the polyene backbone was disrupted by moving the carbon atom at which methyl substitution(s) occurs 0.1 Å out of the plane of the conjugated polyene.

Fig. 1 Molecular structures of the 1,6-diphenyl-1,3,5-hexatriene derivatives considered in this work, along with the abbreviated names used throughout this study.

Ab initio molecular dynamics (AIMD) simulations were performed for each of the molecules, using the same method and basis set combinations above, and were propagated on the S₁ potential energy surface for 5000 steps with a timestep of 0.484 fs. Initial velocities were taken from a random sampling of a Maxwell–Boltzmann distribution. A Fock matrix extrapolation scheme was employed, in which the previous 12 Fock matrices are saved and extrapolated using a sixth-order polynomial to give a guess for the Fock matrix at the current iteration.^37,38

2.2 Classical molecular dynamics

Force-field parameters for the DPH-derivatives in their S₀ electronic state were generated using the CHARMM General Force-Field (CGenFF).^39,40 In this approach, a penalty is given to each parameter as a measure of the confidence of the quality of the parameter. Scores below 10 indicate good analogy of the CGenFF assigned parameter, while scores above 10 require further parameterisation.⁴⁰ The majority of the new parameters with penalty scores above 10 were dihedral terms. We re-optimised each of the dihedral terms with penalty scores greater than 10 using a force-matching algorithm,⁴¹ which we briefly outline here.

The force-field is optimised by considering the set of parameters, [p], with CGenFF scores greater than 10 and minimising an objective function, O([p]):

where N is the number of atoms in the molecule, M is the number of reference structures (in this case, 15 reference structures sampled at equal timesteps from the AIMD simulations were used), and f_ij are the forces of atom i from reference structure j from DFT or MD. A simple gradient descent approach is then used to calculate the descent direction of the parameter set. The gradient of the objective function, G_i, for each parameter, p_i, is obtained numerically:
and each parameter is changed using the negative of the gradient:

P^new_i = p_i − αG

where α is a scaling parameter to determine the step-size of the descent. A total of 500 reference structures taken from the AIMD simulations were used in the parameterisation scheme given above.

The optimised force-fields were used to equilibrate the molecular probe and surrounding lipid membrane system using molecular dynamics as follows: the CHARMM-GUI web service⁴² was used, along with the optimised CGenFF force-field, to create a membrane system comprising a single probe molecule and 200 lipids per leaflet (total of 400 sphingomyelin (d18:1/18 : 0) lipids for the “non-raft” system; 30 molar% of cholesterol was used for the “raft” system, as liquid-ordered phases are known to form at this concentration,⁴³ giving 280 sphingomyelin (d18:1/18 : 0) and 120 cholesterol molecules, distributed equally between the leaflets. We abbreviate sphingomyelin as SSM from herein). Water molecules were added to a minimum thickness of 22.5 Å above each leaflet of the bilayer, giving a total of 12 500–12 900 water molecules for the different systems considered. Potassium and chloride ions were added at a concentration of 0.15 M. The system was minimised for 10 000 steps and equilibrated for 1875 ps over six steps using the CHARMM-GUI Membrane Builder,^44–47 which slowly removes restraints (see the ESI† for full details of the applied restraints at each step of equilibration). Production dynamics proceeded for 100 ns with a 2 fs timestep to give a fully equilibrated system. Simulations were performed at three different temperatures: 310 K, 320 K and 330 K, all using the NPT ensemble. Constant pressure was maintained using the Nosé–Hoover Langevin-piston algorithm^48,49 and constant temperature was achieved through Langevin dynamics. Long-range electrostatics were described using the Particle Mesh Ewald method,⁵⁰ using 6th-order interpolation. Lennard-Jones interactions were used to describe van der Waals’ interactions, with a force-switching function acting in the range of 10–12 Å.⁵¹ The CHARMM36 lipid force-field^52–54 and TIP3P water model^55,56 were used.

Electron density profiles were constructed by calculating electron densities with a slab thickness of 0.8 Å after recentering the bilayer to place the leaflet interface at Z = 0 Å. Deuterium order parameters were calculated using the equation

where θ is the angle between a given C–H vector and the membrane normal.

2.3 QM/MM simulations

Hybrid QM/MM simulations were started from the final frame of the classical MD simulation(s), with the probe molecule treated at the QM level and the rest of the system using MM. For each of the S₀ and S₁ states, five repeats consisting of 16 000 QM/MM dynamics steps (with a 2 fs timestep) were generated, using the same conditions as above. The BHHLYP functional and 6-31G(d,p) basis set were employed to be consistent with the gas phase calculations.

The NAMD software suite⁵⁷ was used for all MD simulations (including QM/MM⁵⁸), while Q-Chem⁵⁹ was employed for all quantum chemical calculations, including QM/MM. Analysis of the electron density profiles and order parameters were performed with CHARMM.⁶⁰

3. Results and discussion

3.1 Gas phase

The optimised geometries for the S₀ and S₁ states, along with the S₁/S₀ MECIs, are given in the ESI,† while the MECI geometries are also shown in Fig. 2. The MECI geometries all share a common motif: a significant distortion from planarity close to one of the methyl groups. This is to be expected, given that the initial guess geometries were distorted at this position. In all cases, the conical intersection exhibits a peaked topology.

Fig. 2 MECI geometries calculated using SF-TDDFT and full analytical non-adiabatic couplings using the BHHLYP functional and 6-31G(d,p) basis set.

For an isolated molecule to exhibit phase-dependent quenching behaviour, and thus potentially membrane phase-dependent emission, fast non-radiative decay pathways must be easily accessible to prevent fluorescence in the gas-phase and in solution. Critical dihedral angles for the MECI geometries from the AIMD simulations are given in Tables S1–S10 in the ESI.† With the exception of 2Me, none of the molecules has an average dihedral angle close to those required to access the conical intersection from the AIMD simulations, and we posit that these molecules are unlikely to exhibit environment-sensitive behaviour based on this. However, 2Me has average angles (and large standard deviations) that indicate rotation around the bonds is not energetically costly and thus the molecule is able to freely rotate towards the MECI in the S₁ state (Table 1). In contrast, DPH would be unlikely to access the conical intersection in the gas phase, and would be expected to remain fluorescent, consistent with experimental findings.^28,29 Given this, 2Me shows promise as a candidate for environment-sensitive emission behaviour.

Table 1 Selected calculated geometrical parameters for DPH and 2Me

	Dihedral angles (DPH)/°	Dihedral angle (2Me)/°
	C8–C9–C10–C11	C1–C6–C7–C8	C6–C7–C8–C9
S0	0.0	38.2	2.1
S1	0.0	14.5	6.5
MECI	34.3	47.4	36.9
AIMD (S1)	4.7 ± 3.1	30.0 ± 19.5	48.3 ± 27.0

---

Potential energy scans of 2Me in the S₀ and S₁ electronic states are given in Fig. S2 and S3 (ESI†), respectively. In the ground state, the energy minimum is found with the C1–C6–C7–C8 dihedral angle at ∼35°, while in the S₁ excited state, the minimum is close to zero, indicating that emission occurs preferentially from a planar geometry (see Fig. S1 for atom numbering for dihedral angles, ESI†). In Fig. S4 (ESI†) is the emission energy as a function of the C1–C6–C7–C8 dihedral angle taken from the S₁ potential energy scan. The emission energy is at a maximum at ∼90° and at a minimum (∼3.4 eV) at ∼0°, demonstrating a 0.5 eV shift between the two extremes. In Fig. S5 (ESI†), we consider the oscillator strengths for the S₁ ← S₀ transition along the S₁ potential energy scan (i.e. as an approximation to emission intensity). Where emission is the only process occurring for de-excitation, this would be a good indication of the emission intensity. In our case, we know that at a dihedral angle of ∼47°, the MECI is a highly competitive process to emission, which would reduce emission intensity further still. Given this, we would expect emission to shift to higher energies and lower intensities as the C1–C6–C7–C8 dihedral angle increases. From our AIMD results in the gas phase, we would expect non-radiative decay via the MECI and hence little to no emission. The properties shown here suggest that, if 2Me is responsive to the phase change from non-raft to raft regions, then we would expect either emission energy to significantly shift (and intensity change) upon detecting a phase change (see Fig. S6, ESI†), or emission to switch on only when the raft-like environment causes the C1–C6–C7–C8 dihedral angle to remain near planar.

A scan of the C1–C6–C7–C8 potential energy surface for both the lowest two singlet states is shown in Fig. 3. While only an approximation to the exact g and h vectors of the conical intersection seam, this dihedral is very important in accessing the MECI and has a very wide range of angles at which the S₀ and S₁ states are near-degenerate. This suggests that, at angles greater than ∼20°, the MECI becomes accessible for 2Me.

Fig. 3 Scan of the S₀ (filled circles) and S₁ (open circles) reaction coordinate of the S₁ electronic state through the MECI of 2Me using values of the C1–C6–C7–C8 dihedral angle, using BHHLYP/6-31G(d,p). S₁ energies were calculated within the SF-TDDFT formalism. Geometries for each point were taken from a reaction pathway calculation calculated along the S₁ potential energy surface.

3.2 Classical molecular dynamics

We next turn our attention to the behaviour of 2Me within a cholesterol-containing lipid membrane, representative of the composition of a membrane raft, in comparison to a bilayer without the presence of cholesterol. The primary aim of the classical MD simulations is to equilibrate the probe within the lipid bilayers, as well as equilibrate the lipids (including cholesterol) and water, prior to QM/MM simulations. Upon visual inspection of the simulations at a temperature of 310 K (using VMD⁶¹), a gel-phase was observed in both the pure SSM and mixed SSM/cholesterol simulations. This is not surprising, since the melting temperature of SSM is around ∼314 K. As such, we only consider the results from the 320 K and 330 K simulations from here on, unless specifically stated. The modified CGenFF force-fields for each of the DPH derivatives are given in the ESI.† Shown in Fig. S7–S10 are the electron density profiles for the membranes and the DPH derivative, 2Me, in each of the simulations (ESI†). The bilayer thickness in each simulation is given in Table 2. As expected, the bilayers containing cholesterol are thicker than the SSM-only bilayers. 2Me remains in the hydrophobic tail region throughout the simulation (in all conditions; see Fig. S9 and S10, ESI†). 2Me remains in the upper leaflet in all simulations, with the exception of the raft simulation at 330 K, where the probe crosses leaflets early in the simulation and remains in the lower leaflet afterwards.

Table 2 Calculated bilayer thicknesses for each of the simulations. Bilayer thickness calculated as the distance between electron density peaks (Fig. S7 and S8, ESI)

Temperature (K)	Bilayer thickness (non-raft) (Å)	Bilayer thickness (raft) (Å)
310	41.6	44.8
320	41.6	46.4
330	41.6	45.6

---

The calculated deuterium order parameters for the C–H bonds of SSM in the raft-like simulation are shown in Fig. 4. These are typical of those seen in mixtures of SSM and cholesterol from experimental^62,63 and theoretical studies,⁶⁴ with a substantial increase in acyl chain order for SSM when cholesterol is present. The order parameters averaged over all carbons in both chains is 0.30 for the raft-like simulation and 0.22 for the non-raft simulation (both at 330 K), in good agreement with previous MD studies of the formation of liquid-ordered domains in SSM/cholesterol systems⁶⁴ and more general lipid liquid-ordered systems.⁶⁵ Given these values, we can determine that the cholesterol-containing bilayer is in a liquid-ordered state prior to the start of the QM/MM partitioning.

Fig. 4 Calculated deuterium order parameters for SSM for the sphingosine chain (top) and stearoyl chain (bottom) at 310 K (left), 320 K (middle) and 330 K (right). Filled circles are from the SSM/cholesterol simulation; open circles taken from the SSM-only simulation.

3.3 QM/MM simulations

Given in Table 3 are the tilt angles for the lipids and 2Me in the raft-like membrane (containing both SSM and cholesterol). The cholesterol tilt angle is representative of membrane raft structure, in which relatively low tilt angles and small standard deviations are observed.^1,2 This confirms that the lipid bilayer is representative of the L_o phase that we were targeting. The tilt angle for 2Me is lower than both the lipids and cholesterol. The equivalent value in the non-raft region at the same temperature is 13.1° (±5.1). Given that the transition dipole moment for the electronic transition of interest lies along the same axis, then we expect that 2Me would exhibit fluorescence anisotropy properties similar to the parent DPH probe; in more fluid regions, the fluorescence anisotropy will increase.²⁸

Table 3 Tilt angles of lipids and 2Me (in degrees) taken from the S₁ QM/MM simulations in the raft-like lipid bilayer at the highest temperature considered (330 K). Standard deviations given in parentheses. The tilt angle was estimated from the projection of the C1–C6 vector (2Me), C3–C17 vector (cholesterol) or C5–C13 vectors (SSM) on to the membrane normal

Tilt angle (2Me)	9.1 (±3.3)
Tilt angle (SSM)	17.5 (±0.3) d18:1
	19.4 (±0.3) d18:0
Tilt angle (cholesterol)	17.2 (±0.4)

---

The average values of the C1–C6–C7–C8 dihedral angle taken from the QM/MM simulations are given in Table 4. In the S₀ simulations, there is relatively free rotation around this dihedral angle, as demonstrated by the large average values and standard deviations. However, upon excitation to the S₁ state, the average dihedral angles are reduced in both the non-raft and raft-like environment. The value from the raft environment (16.3° at 330 K) is below that at which the conical intersection is accessible. The average value in the non-raft environment is 25.6° at the same temperature, in the region in which the conical intersection becomes accessible (see Fig. 3). If the conical intersection is accessed, this would then result in non-radiative decay and hence the fluorescence switches off. In the event that fluorescence still occurs, the emission shift (and change in intensity) with respect to changes in the C1–C6–C7–C8 dihedral are large (see Fig. S6, ESI†) resulting in substantial reduction in intensity with increasing dihedral angle, thus, the probe will consistently report on the membrane environment.

Table 4 C1–C6–C7–C8 average dihedral angles for 2Me taken from the QM/MM simulations. Standard deviations are given in parentheses

	Dihedral angle/°
	T = 310 K	T = 320 K	T = 330 K
Non-raft (S0)	44.0 (±14.2)	40.0 (±13.2)	44.4 (±14.6)
Non-raft (S1)	24.3 (±9.7)	20.3 (±11.9)	25.6 (±10.6)
Raft (S0)	34.3 (±16.3)	49.5 (±13.8)	46.7 (±15.8)
Raft (S1)	18.4 (±10.2)	16.9 (±10.5)	16.3 (±10.3)

---

In contrast, the QM/MM simulations of unsubstituted DPH (Table 5) reveal the critical dihedral angle (C8–C9–C10–C11) remains below 10°, and therefore below the MECI dihedral angle of 34.3° at all temperatures in both raft and non-raft environments, hence fluorescence would be expected in all cases. This non-dependence of emission on membrane phase is consistent with that seen experimentally.^28,29

Table 5 C8–C9–C10–C11 average dihedral angles for DPH taken from the QM/MM simulations. Standard deviations are given in parentheses

	Dihedral angle/°
	T = 310 K	T = 320 K	T = 330 K
Non-raft (S0)	5.8 (±4.4)	5.8 (±4.5)	5.8 (±4.4)
Non-raft (S1)	7.3 (±5.6)	7.1 (±5.3)	7.1 (±5.4)
Raft (S0)	5.4 (±4.1)	6.3 (±4.7)	6.9 (±5.0)
Raft (S1)	6.2 (±4.7)	7.3 (±5.5)	7.7 (±5.7)

---

4. Conclusions

We have considered several modifications to the widely used membrane probe, DPH, using a computational protocol. From the gas phase calculations, we determined that the 2-methyl derivative (2Me) possessed the correct characteristics to act in an AIE-like fashion, in which access to the conical intersection between the S₀ and S₁ states is easily accessible as the molecule is able to freely rotate, but which shows restricted access to the conical intersection in the L_o phase of the SSM and cholesterol lipid bilayer considered. This is due to the forces imposed by the ordered molecular environment of the raft-like membrane, similar to the operation of the dithienothiophene probes.^12–22 Access to the conical intersection is possible in the L_d lipid bilayer (containing only SSM), and as such we conclude that 2Me is capable of detecting a phase change in a lipid membrane. We predict that emission will be strong in a raft environment, and either cease within a non-raft region, or substantially shift to longer wavelengths (and have a reduction in intensity), while exhibiting similar fluorescence anisotropy properties to DPH. These properties demonstrate the potential benefits of a simple modification to the widely used membrane probe, DPH, in detecting raft regions of lipid membranes. We highly anticipate experimental confirmation of our findings.

Conflicts of interest

The are no conflicts of interest to declare.

Acknowledgements

We acknowledge the use of Athena at HPC Midlands+, which was funded by the EPSRC on grant EP/P020232/1, in this research. We also thank NTU for provision of the Hamilton HPC service. M. W. thanks NTU for a studentship, during which this work was performed.

References

1. J. De Joannis, P. S. Coppock, F. Yin, M. Mori, A. Zamorano and J. T. Kindt, Atomistic simulation of cholesterol effects on miscibility of saturated and unsaturated phospholipids: Implications for liquid-ordered/liquid-disordered phase coexistence, J. Am. Chem. Soc., 2011, 133, 3625–3634.
2. D. Hakobyan and A. Heuer, Key molecular requirements for raft formation in lipid/cholesterol membranes, PLoS One, 2014, 9, e87369.
3. L. J. Pike, Rafts defined: A report on the Keystone symposium on lipid rafts and cell function, J. Lipid Res., 2006, 47, 1597–1598.
4. K. Simons and E. Ikonen, Functional rafts in cell membranes, Nature, 1997, 387, 569–572.
5. E. Sezgin, I. Levental, S. Mayor and C. Eggeling, The mystery of membrane organization: Composition, regulation and roles of lipid rafts, Nat. Rev. Mol. Cell Biol., 2017, 18, 361–374.
6. A. Ghysels, A. Krämer, R. M. Venable, W. E. Teague, E. Lyman, K. Gawrisch and R. W. Pastor, Permeability of membranes in the liquid ordered and liquid disordered phases, Nat. Commun., 2019, 10, 5616.
7. E. Klotzsch and G. J. Schütz, A critical survey of methods to detect plasma membrane rafts, Philos. Trans. R. Soc., B, 2013, 368, 20120033.
8. S. Schuck, M. Honsho, K. Ekroos, A. Shevchenko and K. Simons, Resistance of cell membranes to different detergents, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 5795–5800.
9. S. Mayor and F. R. Maxfield, Insolubility and redistribution of GPI-anchored proteins at the cell surface after detergent treatment, Mol. Biol. Cell, 1995, 6, 929–944.
10. D. Lichtenberg, F. M. Goñi and H. Heerklotz, Detergent-resistant membranes should not be identified with membrane rafts, Trends Biochem. Sci., 2005, 30, 430–436.
11. A. S. Klymchenko and R. Kreder, Fluorescent probes for lipid rafts: From model membranes to living cells, Chem. Biol., 2014, 21, 97–113.
12. A. Fin, A. Vargas Jentzsch, N. Sakai and S. Matile, Oligothiophene amphiphiles as planarizable and polarizable fluorescent membrane probes, Angew. Chem., Int. Ed., 2012, 51, 12736–12739.
13. M. Dal Molin, Q. Verolet, A. Colom, R. Letrun, E. Derivery, M. Gonzalez-Gaitan, E. Vauthey, A. Roux, N. Sakai and S. Matile, Fluorescent flippers for mechanosensitive membrane probes, J. Am. Chem. Soc., 2015, 137, 568–571.
14. G. Licari, K. Strakova, S. Matile and E. Tajkhorshid, Twisting and tilting of a mechanosensitive molecular probe detects order in membranes, Chem. Sci., 2020, 11, 5637–5649.
15. Q. Verolet, A. Rosspeintner, S. Soleimanpour, N. Sakai, E. Vauthey and S. Matile, Turn-On Sulfide π Donors: An Ultrafast Push for Twisted Mechanophores, J. Am. Chem. Soc., 2015, 137, 15644–15647.
16. S. Soleimanpour, A. Colom, E. Derivery, M. Gonzalez-Gaitan, A. Roux, N. Sakai and S. Matile, Headgroup engineering in mechanosensitive membrane probes, Chem. Commun., 2016, 52, 14450–14453.
17. G. Licari, J. S. Beckwith, S. Soleimanpour, S. Matile and E. Vauthey, Detecting order and lateral pressure at biomimetic interfaces using a mechanosensitive second-harmonic-generation probe, Phys. Chem. Chem. Phys., 2018, 20, 9328–9336.
18. K. Strakova, S. Soleimanpour, M. Diez-Castellnou, N. Sakai and S. Matile, Ganglioside-Selective Mechanosensitive Fluorescent Membrane Probes, Helv. Chim. Acta, 2018, 101, e1800019.
19. M. Riggi, K. Niewola-Staszkowska, N. Chiaruttini, A. Colom, B. Kusmider, V. Mercier, S. Soleimanpour, M. Stahl, S. Matile, A. Roux and R. Loewith, Decrease in plasma membrane tension triggers PtdIns(4,5)P₂ phase separation to inactivate TORC2, Nat. Cell Biol., 2018, 20, 1043–1051.
20. A. Goujon, A. Colom, K. Straková, V. Mercier, D. Mahecic, S. Manley, N. Sakai, A. Roux and S. Matile, Mechanosensitive Fluorescent Probes to Image Membrane Tension in Mitochondria, Endoplasmic Reticulum, and Lysosomes, J. Am. Chem. Soc., 2019, 141, 3380–3384.
21. A. Goujon, K. Straková, N. Sakai and S. Matile, Streptavidin interfacing as a general strategy to localize fluorescent membrane tension probes in cells, Chem. Sci., 2019, 10, 310–319.
22. A. S. Klymchenko, Solvatochromic and Fluorogenic Dyes as Environment-Sensitive Probes: Design and Biological Applications, Acc. Chem. Res., 2017, 50, 366–375.
23. D. Robinson, N. A. Besley, P. Obshea and J. D. Hirst, Di-8-ANEPPS emission spectra in phospholipid/cholesterol membranes: a theoretical study, J. Phys. Chem. B, 2011, 115, 4160–4167.
24. H. L. Blake and D. Robinson, QM/MM studies of contemporary and novel membrane raft fluorescent probes, Molecules, 2014, 19, 10230–10241.
25. L. Jiao, C. Yu, J. Wang, E. A. Briggs, N. A. Besley, D. Robinson, M. J. Ruedas-Rama, A. Orte, L. Crovetto, E. M. Talavera, J. M. Alvarez-Pez, M. Van Der Auweraer and N. Boens, Unusual spectroscopic and photophysical properties of meso-tert-butylBODIPY in comparison to related alkylated BODIPY dyes, RSC Adv., 2015, 5, 89375–89388.
26. A. Orte, E. Debroye, M. J. Ruedas-Rama, E. Garcia-Fernandez, D. Robinson, L. Crovetto, E. M. Talavera, J. M. Alvarez-Pez, V. Leen, B. Verbelen, L. Cunha Dias De Rezende, W. Dehaen, J. Hofkens, M. Van Der Auweraer and N. Boens, Effect of the substitution position (2, 3 or 8) on the spectroscopic and photophysical properties of BODIPY dyes with a phenyl, styryl or phenylethynyl group, RSC Adv., 2016, 6, 102899–102913.
27. C. Ripoll, C. Cheng, E. Garcia-Fernandez, J. Li, A. Orte, H. Do, L. Jiao, D. Robinson, L. Crovetto, J. A. González-Vera, E. M. Talavera, J. M. Alvarez-Pez, N. Boens and M. J. Ruedas-Rama, Synthesis and Spectroscopy of Benzylamine-Substituted BODIPYs for Bioimaging, Eur. J. Org. Chem., 2018, 2561–2571.
28. B. R. Lentz, Membrane ‘fluidity’ as detected by diphenylhexatriene probes, Chem. Phys. Lipids, 1989, 50, 171–190.
29. B. R. Lentz, Use of fluorescent probes to monitor molecular order and motions within liposome bilayers, Chem. Phys. Lipids, 1993, 64, 99–116.
30. C. J. Bhongale, C. W. Chang, C. S. Lee, E. W. G. Diau and C. S. Hsu, Relaxation dynamics and structural characterization of organic nanoparticles with enhanced emission, J. Phys. Chem. B, 2005, 109, 13472–13482.
31. X. L. Peng, S. Ruiz-Barragan, Z. S. Li, Q. S. Li and L. Blancafort, Restricted access to a conical intersection to explain aggregation induced emission in dimethyl tetraphenylsilole, J. Mater. Chem. C, 2016, 4, 2802–2810.
32. A. D. Becke, A new mixing of Hartree–Fock and local density-functional theories, J. Chem. Phys., 1993, 98, 1372–1377.
33. C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
34. X. Zhang and J. M. Herbert, Analytic derivative couplings for spin-flip configuration interaction singles and spin-flip time-dependent density functional theory, J. Chem. Phys., 2014, 141, 064104.
35. M. J. Bearpark, M. A. Robb and H. Bernhard Schlegel, A direct method for the location of the lowest energy point on a potential surface crossing, Chem. Phys. Lett., 1994, 223, 269–274.
36. M. Winslow, W. B. Cross and D. Robinson, Comparison of Spin-Flip TDDFT-Based Conical Intersection Approaches with XMS-CASPT2, J. Chem. Theory Comput., 2020, 16, 3253–3263.
37. J. M. Herbert and M. Head-Gordon, Accelerated, energy-conserving Born-Oppenheimer molecular dynamics via Fock matrix extrapolation, Phys. Chem. Chem. Phys., 2005, 7, 3269–3275.
38. P. Pulay and G. Fogarasi, Fock matrix dynamics, Chem. Phys. Lett., 2004, 386, 272–278.
39. K. Vanommeslaeghe and A. D. MacKerell, Automation of the CHARMM general force field (CGenFF) I: Bond perception and atom typing, J. Chem. Inf. Model., 2012, 52, 3144–3154.
40. K. Vanommeslaeghe, E. P. Raman and A. D. MacKerell, Automation of the CHARMM General Force Field (CGenFF) II: Assignment of Bonded Parameters and Partial Atomic Charges, J. Chem. Inf. Model., 2012, 52, 3155–3168.
41. K. Claridge and A. Troisi, Developing Consistent Molecular Dynamics Force Fields for Biological Chromophores via Force Matching, J. Phys. Chem. B, 2019, 123, 428–438.
42. J. Lee, X. Cheng, J. M. Swails, M. S. Yeom, P. K. Eastman, J. A. Lemkul, S. Wei, J. Buckner, J. C. Jeong, Y. Qi, S. Jo, V. S. Pande, D. A. Case, C. L. Brooks III, A. D. MacKerell Jr., J. B. Klauda and W. Im, CHARMM-GUI Input Generator for NAMD, GROMACS, AMBER, OpenMM, and CHARMM/OpenMM Simulations Using the CHARMM36 Additive Force Field, J. Chem. Theory Comput., 2016, 12, 405–413.
43. J. Zidar, F. Merzel, M. Hodošček, K. Rebolj, K. Sepčić, P. Maček and D. Janežič, Liquid-ordered phase formation in cholesterol/sphingomyelin bilayers: All-atom molecular dynamics simulations, J. Phys. Chem. B, 2009, 113, 15795–15802.
44. S. Jo, T. Kim, V. G. Iyer and W. Im, CHARMM-GUI: A web-based graphical user interface for CHARMM, J. Comput. Chem., 2008, 29, 1859–1865.
45. S. Jo, T. Kim and W. Im, Automated builder and database of protein/membrane complexes for molecular dynamics simulations, PLoS One, 2007, 2, e880.
46. E. L. Wu, X. Cheng, S. Jo, H. Rui, K. C. Song, E. M. Dávila-Contreras, Y. Qi, J. Lee, V. Monje-Galvan, R. M. Venable, J. B. Klauda and W. Im, CHARMM-GUI membrane builder toward realistic biological membrane simulations, J. Comput. Chem., 2014, 35, 1997–2004.
47. S. Jo, J. B. Lim, J. B. Klauda and W. Im, CHARMM-GUI Membrane Builder for Mixed Bilayers and Its Application to Yeast Membranes, Biophys. J., 2009, 97, 50–58.
48. G. J. Martyna, D. J. Tobias and M. L. Klein, Constant pressure molecular dynamics algorithms, J. Chem. Phys., 1994, 101, 4177–4189.
49. S. E. Feller, Y. Zhang, R. W. Pastor and B. R. Brooks, Constant pressure molecular dynamics simulation: The Langevin piston method, J. Chem. Phys., 1995, 103, 4613–4621.
50. T. Darden, D. York and L. Pedersen, Particle mesh Ewald: An N·log(N) method for Ewald sums in large systems, J. Chem. Phys., 1993, 98, 10089–10092.
51. P. J. Steinbach and B. R. Brooks, New spherical-cutoff methods for long-range forces in macromolecular simulation, J. Comput. Chem., 1994, 15, 667–683.
52. J. B. Klauda, R. M. Venable, J. A. Freites, J. W. O’Connor, D. J. Tobias, C. Mondragon-Ramirez, I. Vorobyov, A. D. MacKerell and R. W. Pastor, Update of the CHARMM All-Atom Additive Force Field for Lipids: Validation on Six Lipid Types, J. Phys. Chem. B, 2010, 114, 7830–7843.
53. J. B. Lim, B. Rogaski and J. B. Klauda, Update of the cholesterol force field parameters in CHARMM, J. Phys. Chem. B, 2012, 116, 203–210.
54. R. M. Venable, A. J. Sodt, B. Rogaski, H. Rui, E. Hatcher, A. D. MacKerell, R. W. Pastor and J. B. Klauda, CHARMM all-atom additive force field for sphingomyelin: Elucidation of hydrogen bonding and of positive curvature, Biophys. J., 2014, 107, 134–145.
55. W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, Comparison of simple potential functions for simulating liquid water, J. Chem. Phys., 1983, 79, 926–935.
56. S. R. Durell, B. R. Brooks and A. Ben-Naim, Solvent-induced forces between two hydrophilic groups, J. Phys. Chem., 1994, 98, 2198–2202.
57. J. C. Phillips, D. J. Hardy, J. D. C. Maia, J. E. Stone, J. V. Ribeiro, R. C. Bernardi, R. Buch, G. Fiorin, J. Hénin, W. Jiang, R. McGreevy, M. C. R. Melo, B. K. Radak, R. D. Skeel, A. Singharoy, Y. Wang, B. Roux, A. Aksimentiev, Z. Luthey-Schulten, L. V. Kalé, K. Schulten, C. Chipot and E. Tajkhorshid, Scalable molecular dynamics on CPU and GPU architectures with NAMD, J. Chem. Phys., 2020, 153, 044130.
58. M. C. R. Melo, R. C. Bernardi, T. Rudack, M. Scheurer, C. Riplinger, J. C. Phillips, J. D. C. Maia, G. B. Rocha, J. V. Ribeiro, J. E. Stone, F. Neese, K. Schulten and Z. Luthey-Schulten, NAMD goes quantum: an integrative suite for hybrid simulations, Nat. Methods, 2018, 15, 351–354.
59. Y. Shao, Z. Gan, E. Epifanovsky, A. T. B. Gilbert, M. Wormit, J. Kussmann, A. W. Lange, A. Behn, J. Deng, X. Feng, D. Ghosh, M. Goldey, P. R. Horn, L. D. Jacobson, I. Kaliman, R. Z. Khaliullin, T. Kuś, A. Landau, J. Liu, E. I. Proynov, Y. M. Rhee, R. M. Richard, M. A. Rohrdanz, R. P. Steele, E. J. Sundstrom, H. L. Woodcock, P. M. Zimmerman, D. Zuev, B. Albrecht, E. Alguire, B. Austin, G. J. O. Beran, Y. A. Bernard, E. Berquist, K. Brandhorst, K. B. Bravaya, S. T. Brown, D. Casanova, C.-M. Chang, Y. Chen, S. H. Chien, K. D. Closser, D. L. Crittenden, M. Diedenhofen, R. A. DiStasio, H. Do, A. D. Dutoi, R. G. Edgar, S. Fatehi, L. Fusti-Molnar, A. Ghysels, A. Golubeva-Zadorozhnaya, J. Gomes, M. W. D. Hanson-Heine, P. H. P. Harbach, A. W. Hauser, E. G. Hohenstein, Z. C. Holden, T.-C. Jagau, H. Ji, B. Kaduk, K. Khistyaev, J. Kim, J. Kim, R. A. King, P. Klunzinger, D. Kosenkov, T. Kowalczyk, C. M. Krauter, K. U. Lao, A. D. Laurent, K. V. Lawler, S. V. Levchenko, C. Y. Lin, F. Liu, E. Livshits, R. C. Lochan, A. Luenser, P. Manohar, S. F. Manzer, S.-P. Mao, N. Mardirossian, A. V. Marenich, S. A. Maurer, N. J. Mayhall, E. Neuscamman, C. M. Oana, R. Olivares-Amaya, D. P. O’Neill, J. A. Parkhill, T. M. Perrine, R. Peverati, A. Prociuk, D. R. Rehn, E. Rosta, N. J. Russ, S. M. Sharada, S. Sharma, D. W. Small, A. Sodt, T. Stein, D. Stück, Y.-C. Su, A. J. W. Thom, T. Tsuchimochi, V. Vanovschi, L. Vogt, O. Vydrov, T. Wang, M. A. Watson, J. Wenzel, A. White, C. F. Williams, J. Yang, S. Yeganeh, S. R. Yost, Z.-Q. You, I. Y. Zhang, X. Zhang, Y. Zhao, B. R. Brooks, G. K. L. Chan, D. M. Chipman, C. J. Cramer, W. A. Goddard, M. S. Gordon, W. J. Hehre, A. Klamt, H. F. Schaefer, M. W. Schmidt, C. D. Sherrill, D. G. Truhlar, A. Warshel, X. Xu, A. Aspuru-Guzik, R. Baer, A. T. Bell, N. A. Besley, J.-D. Chai, A. Dreuw, B. D. Dunietz, T. R. Furlani, S. R. Gwaltney, C.-P. Hsu, Y. Jung, J. Kong, D. S. Lambrecht, W. Liang, C. Ochsenfeld, V. A. Rassolov, L. V. Slipchenko, J. E. Subotnik, T. Van Voorhis, J. M. Herbert, A. I. Krylov, P. M. W. Gill and M. Head-Gordon, Advances in molecular quantum chemistry contained in the Q-Chem 4 program package, Mol. Phys., 2015, 113, 184–215.
60. B. R. Brooks, C. L. Brooks, A. D. Mackerell, L. Nilsson, R. J. Petrella, B. Roux, Y. Won, G. Archontis, C. Bartels, S. Boresch, A. Caflisch, L. Caves, Q. Cui, A. R. Dinner, M. Feig, S. Fischer, J. Gao, M. Hodoscek, W. Im, K. Kuczera, T. Lazaridis, J. Ma, V. Ovchinnikov, E. Paci, R. W. Pastor, C. B. Post, J. Z. Pu, M. Schaefer, B. Tidor, R. M. Venable, H. L. Woodcock, X. Wu, W. Yang, D. M. York and M. Karplus, CHARMM: The biomolecular simulation program, J. Comput. Chem., 2009, 30, 1545–1614.
61. W. Humphrey, A. Dalke and K. Schulten, VMD: Visual molecular dynamics, J. Mol. Graph., 1996, 14, 33–38.
62. T. Yasuda, M. Kinoshita, M. Murata and N. Matsumori, Detailed comparison of deuterium quadrupole profiles between sphingomyelin and phosphatidylcholine bilayers, Biophys. J., 2014, 106, 631–638.
63. N. Matsumori, T. Yasuda, H. Okazaki, T. Suzuki, T. Yamaguchi, H. Tsuchikawa, M. Doi, T. Oishi and M. Murata, Comprehensive molecular motion capture for sphingomyelin by site-specific deuterium labeling, Biochemistry, 2012, 51, 8363–8370.
64. E. Wang and J. B. Klauda, Examination of Mixtures Containing Sphingomyelin and Cholesterol by Molecular Dynamics Simulations, J. Phys. Chem. B, 2017, 121, 4833–4844.
65. A. J. Sodt, M. L. Sandar, K. Gawrisch, R. W. Pastor and E. Lyman, The molecular structure of the liquid-ordered phase of lipid bilayers, J. Am. Chem. Soc., 2014, 136, 725–732.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d2cp00431c

---