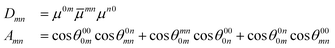First-order hyperpolarizabilities of propellanes: elucidating structure–property relationships†
Received
24th January 2022
, Accepted 5th May 2022
First published on 10th May 2022
Abstract
Following recent experimental work demonstrating strong nonlinear optical properties, namely second harmonic generation of light, in crystals composed of 16,20-dinitro-(3,4,8,9)-dibenzo-2,7-dioxa-5,10-diaza[4.4.4]propellane molecules [A. Miniewicz, S. Bartkiewicz, E. Wojaczyńska, T. Galica, R. Zaleśny and R. Jakubas, J. Mater. Chem. C, 2019, 7, 1255–1262] in this paper we aim to investigate “structure–property” relationships for a series of 16 propellanes presenting a wide palette of substituents with varying electron-accepting/donating capabilities. To that end, we use electronic- and vibrational-structure theories and a recently developed generalized few-state model combined with a range-separated CAM-B3LYP functional to analyze electronic and vibrational contributions to the first hyperpolarizability for the whole series of molecules. The variations in computed properties are large among the studied set of substituents and can reach an order of magnitude. It has been demonstrated that the maximum values of frequency-independent first hyperpolarizability are expected for strong electron-accepting NO2 substituents, but only at the preferred position with respect to the electronegative oxygen atom in the 1,4-oxazine moiety. This holds for electronic as well as vibrational counterparts.
1 Introduction
Propellanes are molecular systems owing their name to the propeller-like structure. In the case of smaller members of the family, the three rings connected through a common covalent bond cause very strained and unstable geometries. Owing to this, propellanes undergo polymerization to produce interesting structures such as staffanes. Snatzke and Zanati were the first to synthesize propellane in 1965.1 Propellanes, however, have been presumably obtained in some earlier preparations.2,3 The name “propellane” was first used by Ginsberg in 1966.4 Since then, several research groups have synthesized and studied the properties of different propellanes including heteropropellanes – where the ring structures are not necessarily hydrocarbons.5–11
Apart from their strained geometry, propellanes are popular due to their diverse applications in synthetic chemistry ranging from materials to natural products.5 It is important to note that although the research on propellanes started about 80 years ago, these systems are very common in natural products. Propellanes containing larger rings are stable enough to provide a platform for designing desired molecular structures such as for highly efficient organic light-emitting diodes.12 The common covalent bond in propellanes can easily be broken and the resultant valency can be satisfied by different groups. In this way, the unstrained propellane moiety can be attached to different types of molecular entities (e.g. during polymerization). This provides a number of possibilities in synthetic chemistry.13,14 The preparation of staffanes and various dendrimers essentially involves the breaking of the said common covalent bond.5,15 These experimental advances were supported, in parallel, by the theoretical studies5,16–19 on propellanes. However, these studies were limited to strain energy, the mechanism of the polymerization reaction of propellane, and singlet–triplet transition, to name a few.
In spite of numerous applications of various propellanes in organic synthesis, there are very few studies focusing on non-linear optical properties of such compounds. Very recently, some of the present authors have synthesized a heteropropellane-based molecule, 16,20-dinitro-(3,4,8,9)-dibenzo-2,7-dioxa-5,10-diaza[4.4.4]propellane (DDDDP) and studied its second-order nonlinear optical (NLO) properties.11 It was found, using 1064 nm nanosecond laser pulses, that the crystalline powder of DDDDP displays a very high second harmonic generation (SHG) efficiency.11 This was the first SHG study for a propellane-based system. These promising experimental results for a single propellane and the on-going quest for second-order NLO materials20 motivated the present theoretical work, in which we wish to study the molecular first hyperpolarizability for larger sets of propellane derivatives. In particular, we aim to establish “structure–property” relationships using a palette of substituents at different positions. To that end, we employed several state-of-the-art theoretical approaches combined with electronic- and vibrational-structure calculations. In fact, computer simulations provide an invaluable tool in the analysis of second-order nonlinear optical properties of molecules and their assemblies.21–29
2 Theory and computational methods
In the presence of an electric field (F), the Cartesian component of the total dipole moment μi may be expressed as a Taylor series:30| | 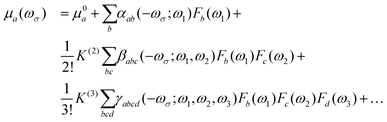 | (1) |
where μ0a is the a-th component of the permanent dipole moment; αab, βabc and γabcd are the components of the molecular polarizability, and first and second hyperpolarizability tensors, respectively. ωσ is the sum of the interacting fields with frequencies ωi; and K(2) and K(3) are factors ensuring that all hyperpolarizabilities of the same order have the same static limit. Using perturbation theory, the (hyper)polarizabilities can be expressed as a sum-over all the states of the system (in general rovibronic). In this work, we are interested in the first hyperpolarizability, whose general sum-over-states expression is given as31| |  | (2) |
where  represents the summation over all the permutations of the pairs (a, −ωσ), (b, ω1), and (c, ω2) and Ei = ħωi (i = 1, 2, σ). The prime over the double summation in eqn (2) represents a restricted summation where none of the indices could label the ground state. Emn and μmna stand for the excitation energy and ath component of the transition dipole moment for m → n transition, respectively. Note that
represents the summation over all the permutations of the pairs (a, −ωσ), (b, ω1), and (c, ω2) and Ei = ħωi (i = 1, 2, σ). The prime over the double summation in eqn (2) represents a restricted summation where none of the indices could label the ground state. Emn and μmna stand for the excitation energy and ath component of the transition dipole moment for m → n transition, respectively. Note that ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) mn =
mn = ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) mn − μ00. The static limit of the tensor components can be obtained by setting all three angular frequencies to zero. The commonly used first hyperpolarizability, β‖, can be calculated from the βabc components using the following relation:32
mn − μ00. The static limit of the tensor components can be obtained by setting all three angular frequencies to zero. The commonly used first hyperpolarizability, β‖, can be calculated from the βabc components using the following relation:32| | 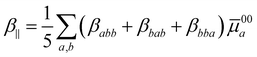 | (3) |
In the above equations ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) 00a stands for the ground-state dipole unit in the direction of the ground-state dipole moment (μ00a/|μ00|).
00a stands for the ground-state dipole unit in the direction of the ground-state dipole moment (μ00a/|μ00|).
Within the Born–Oppenheimer (BO) approximation, the molecular (hyper)polarizabilities defined by eqn (1) may be separated into pure electronic (Pe) and pure vibrational (Pv) contributions, as well as the zero-point vibrational averaging (ZPVA) correction:32
where
P =
α,
β,
γ. Alternatively, one can divide the property
P into electronic, nuclear relaxation (
Pnr) and curvature (
Pcurv) contributions:
32| | | P = Pcurv + Pnr + Pcurv | (5) |
The latter separation is employed in this study and we only focus on the nuclear relaxation contribution to first hyperpolarizability. The Pnr terms are usually larger than Pcurv terms. In order to treat the effect of molecular vibrations on electric properties, Bishop and Kirtman proposed a double (electrical and mechanical) perturbation theory (BKPT) treatment.33 The Pnr contributions are given by the leading terms of each type of “square bracket” term of BKPT pure vibrational contributions. Within this approach, the nuclear relaxation first and second hyperpolarizability may be expressed in the “square bracket” notation as:
| | | βnr = [μα](0,0) + [μ3](1,0) + [μ3](0,1) | (6) |
Each square bracket involves products of the normal coordinate derivatives of the electronic electrical properties indicated, as well as harmonic vibrational frequencies and anharmonic force constants. Each term is labeled by a pair of superscripts (p, q) denoting the order in electrical and mechanical anharmonicities, respectively. There is an efficient finite-field nuclear relaxation method (FF-NR)34,35 for computing nuclear relaxation hyperpolarizabilities. However, in this study the field-induced coordinates (FICs) approach is used36,37 to determine the anharmonicity contributions to nuclear relaxation first hyperpolarizability. FICs are linear combinations of field-free normal coordinates associated with the change in equilibrium geometry induced by a static electric field. The displacement of the i-th field-free normal coordinate at the field-relaxed geometry is given by:36
| |  | (7) |
where,
| |  | (8) |
and
| |  | (9) |
The indices i, j and k stand for normal coordinates whereas a and b label the Cartesian directions. aij…ab…nm involves the n-th and m-th derivatives of the potential energy V (Q, F) with respect to normal coordinates and field components, respectively. The first-order FICs:
| |  | (10) |
are sufficient to compute the static nuclear relaxation contribution to first hyperpolarizability:
36| |  | (11) |

indicates the sum over all permutations of the indices
a,
b,…
Electronic and vibrational structure calculations, assuming C2 symmetry point group for all compounds but one, were performed with the Gaussian suite of programmes.38 To that end we used the range-separated CAM-B3LYP functional39 and the aug-cc-pVDZ basis set.40 The choice of this functional is dictated by its satisfactory performance in predicting electronic and vibrational contributions to the electric properties of various orders.41–44 The results of these calculations were used for computing vibrational hyperpolarizabilities using custom computer routines. Additionally, the components of static electronic β and different transition dipole moments were calculated using the LSDALTON programme package using the CAM-B3LYP/6-31+G level of theory to study the convergence of β with the number of electronic states based on the generalized few-state model (GFSM).45 The GFSM calculations were performed using in-house code.
3 Results and discussion
The structures of all the sixteen compounds studied in this work are given in Fig. 1. All these molecules are propellane derivatives with three wings: one consisting of unsubstituted cyclohexane, and the other two are identical benzo-oxazine moieties. The two benzo-oxazine wings are substituted with various groups such as –NH2, –CF3 (mono- and di-), –SCH3, –SO2CH3, –SCF3, –OCF3, dioxolane, –CH2OCH3, and –NO2 yielding a set composed of 16 compounds (Fig. 1). The methodology of preparation of this type of compound, based on the reaction of cyclic 1,2-diketones and ortho-aminophenols has been already developed and it can be adapted for the synthesis of most promising derivatives. The whole series of compounds, except 5, can be divided into three major categories covering a wide range of Hammett substituent constants:46 (a) Singly-substituted compounds (at each wing) in the para position in relation to the ether oxygen; their order in the series can be established according to the electron-accepting capabilities of the substituent: 13 (–NO2, substituent constant is 0.78) 4 (–SO2CH3, 0.72), 3 (–CF3, 0.54), 7 (–SCF3, 0.50), 8 (–OCF3, 0.35), 10 (–CH2OCH3, 0.01), 2 (–SCH3, 0.00). (b) Singly-substituted compounds (at each wing) in positions other than para: 11 (m-NO2, 0.71), 12, and 14; 15 (m-NH2, −0.16 and m-NO2, 0.71) and 16 (m-NH2, −0.16). (c) Doubly-substituted compounds (on each wing): 1 (p-CH3, −0.17 and m-CF3, 0.43), 6 (p-SCH3, 0.00 and m-CH3, −0.07), 9 (two m-CF3 groups, 0.43). It is worth pointing out that the oxygen atom was chosen as a “standard” because its electronegativity is higher than that of nitrogen (NH group). Note that the experimentally studied DDDDP molecule11 is also included in the set shown in Fig. 1 (as compound 11).
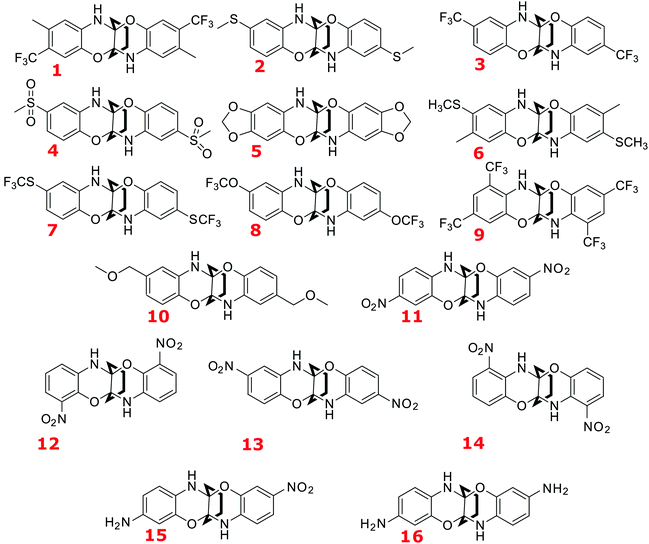 |
| | Fig. 1 Compounds studied in this work and their labelling. | |
The values of electronic first hyperpolarizability (β‖e) for all the compounds calculated using the aug-cc-pVDZ basis set and CAM-B3LYP functional are presented in Table 1. We will start the discussion with the purely electronic counterpart as it contributes significantly to second-order processes involving both static and dynamic fields. Compound 11 has the maximum value for β‖e and compound 16 has the least value (in magnitude). The ratio between the maximum and minimum values of β‖e is 54![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The compound with the second largest β‖e is 15, which is the only compound asymmetrically substituted (–NO2 and –NH2) at para positions. We note that the replacement of one electron-accepting group with an electron-donating one, while preserving the positions of the substituents, does not lead to deterioration of the electronic first hyperpolarizability. It is interesting to note that compounds 1, 3 and 9 have almost the same values for β‖e indicating that there is almost no effect of adding an extra –CF3 group or changing the position of the –CF3 group in the benzo-oxazine wings. Similarly, compounds 2 and 6 have similar values for β‖e indicating that there is no effect of adding an extra methyl group in the benzo-oxazine ring. On replacing –SCH3 by –CF3, i.e., on moving from compound 2 to 3, there is an increase in β‖e value. Replacing –CF3 by –OCF3 (compound 3 to compound 8) leaves the β‖e values practically unchanged and replacing –CF3 by –SCF3, i.e., on moving from compound 3 to 7, the β‖e values are almost doubled. This is probably because of the available vacant d-orbital on the S-atom. On replacing –SCH3 (compound 2) by –SO2CH3 (compound 4) there is about a three-fold increase in the β‖e values and replacing –SCH3 (compound 2) by –SCF3 (compound 7) there is a corresponding 2.5-fold increase. Compounds 12 and 14 show a variation in β‖e which emphasizes the importance of substituent placement. Finally, let us recall that compound 16 has two electron-donating substituents at the meta position and exhibits the smallest β‖e value. Such substituent placement maximizes β‖e but only for strong electron-donating groups.
1. The compound with the second largest β‖e is 15, which is the only compound asymmetrically substituted (–NO2 and –NH2) at para positions. We note that the replacement of one electron-accepting group with an electron-donating one, while preserving the positions of the substituents, does not lead to deterioration of the electronic first hyperpolarizability. It is interesting to note that compounds 1, 3 and 9 have almost the same values for β‖e indicating that there is almost no effect of adding an extra –CF3 group or changing the position of the –CF3 group in the benzo-oxazine wings. Similarly, compounds 2 and 6 have similar values for β‖e indicating that there is no effect of adding an extra methyl group in the benzo-oxazine ring. On replacing –SCH3 by –CF3, i.e., on moving from compound 2 to 3, there is an increase in β‖e value. Replacing –CF3 by –OCF3 (compound 3 to compound 8) leaves the β‖e values practically unchanged and replacing –CF3 by –SCF3, i.e., on moving from compound 3 to 7, the β‖e values are almost doubled. This is probably because of the available vacant d-orbital on the S-atom. On replacing –SCH3 (compound 2) by –SO2CH3 (compound 4) there is about a three-fold increase in the β‖e values and replacing –SCH3 (compound 2) by –SCF3 (compound 7) there is a corresponding 2.5-fold increase. Compounds 12 and 14 show a variation in β‖e which emphasizes the importance of substituent placement. Finally, let us recall that compound 16 has two electron-donating substituents at the meta position and exhibits the smallest β‖e value. Such substituent placement maximizes β‖e but only for strong electron-donating groups.
Table 1 Vectorial electronic and harmonic vibrational contributions to the first hyperpolarizability (in au) computed at the CAM-B3LYP/aug-cc-pVDZ level
| Compound |
β
‖
e
|
[μα]‖(0,0) |
Sum |
|
1
|
196 |
3053 |
3249 |
|
2
|
218 |
1814 |
2032 |
|
3
|
246 |
3291 |
3537 |
|
4
|
−521 |
−5997 |
−6518 |
|
5
|
112 |
538 |
650 |
|
6
|
247 |
1442 |
1689 |
|
7
|
534 |
3307 |
3841 |
|
8
|
212 |
2839 |
3051 |
|
9
|
251 |
3358 |
3609 |
|
10
|
449 |
−1481 |
−1032 |
|
11
|
1198 |
7330 |
8528 |
|
12
|
368 |
3060 |
3428 |
|
13
|
710 |
5862 |
6572 |
|
14
|
214 |
−226 |
−12 |
|
15
|
1087 |
6896 |
7983 |
|
16
|
22 |
−2117 |
−2095 |
In order to shed light on large values of β‖e found for 11, we employed the corresponding generalized few-state model (GFSM) developed by some of the current authors.45 Within GFSM, the expression for β‖e is given as45
| |  | (12) |
where
| | 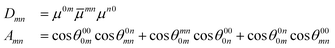 | (13) |
and for the static case,
| |  | (14) |
and
θcdab is the angle between transition dipole moments
μab and
μcd. The prime in
eqn (12) indicates a restricted summation, where the ground state is not included. Other terms have their usual meanings. Each
βGFSMmn can either be positive or negative depending on the values of
Amn,
i.e., the relative orientation of the involved transition dipole moment vectors. We have included up to 50 excited states in GFSM calculations. The convergence of
β‖e with the number of states involved in GFSM for
11 is shown in
Fig. 2. The corresponding data for some other studied propellanes are presented in Fig. S1 in the ESI
† file and allow for drawing a conclusion that
β‖e is slowly convergent with respect to the number of electronic excited states, thus indicating that there are no key electronic states determining the first hyperpolarizability. In contrast, the results shown in
Fig. 2 for
11 indicate that GFSM is quite successful in the quantitative prediction of
β‖e values, including its sign.
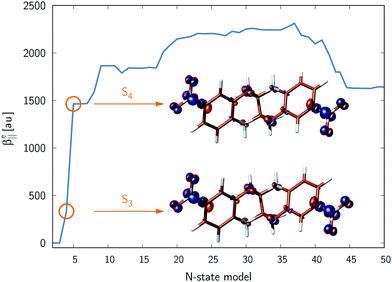 |
| | Fig. 2 Convergence of the electronic first hyperpolarizability for 11 with the number of electronic states (N-state model accounts also for electronic ground state). The inset shows the electronic density difference (Δρ (r)) between electronic singlet state ρ (r, Si) and the ground electronic state ρ (r, S0). The contour value of density was set at 0.005 au and positive (negative) values of Δρ (r) are represented by blue (red) color. Calculations were performed at the CAM-B3LYP/6-31+G level. | |
We have noticed that involving all the 50 excited states gives β‖GFSM = 1642 au, 75% of which is contributed by the top five positive and the top five negative terms. βmn as well as the corresponding dipole (Dmn), angle (Amn), and energy (Emn) terms are given in Table 2.
Table 2 Largest βGFSMmn terms for compound 11 computed at the CAM-B3LYP/6-31 + G level
|
m, n |
β
mn
= βnm |
D
mn
|
A
mn
|
5.0 × Emn |
| 3, 3 |
333 |
6.3544 |
1.0 |
0.0191 |
| 3, 4 |
327 |
6.4129 |
0.98 |
0.0192 |
| 4, 4 |
477 |
3.0659 |
3.0 |
0.0193 |
| 3, 11 |
−40 |
1.4270 |
−0.7 |
0.0251 |
| 4, 11 |
−70 |
1.8760 |
−0.94 |
0.0252 |
| 4, 12 |
−51 |
0.4353 |
−3.0 |
0.0255 |
| 8, 8 |
81 |
0.6591 |
3.0 |
0.0245 |
It is interesting to note that the large positive terms, i.e., β33, β34, and β44 have the largest dipole contributions. The first two have an angle term ∼1, whereas the last one has an angle term equal to 3 (which is maximum). The dipole contribution in β44 is less than half of those in either β33 or β34, but the corresponding maximum angle contribution makes it the largest contributing βmn. The character of two key electronic states (S3 and S4) is shown in the inset in Fig. 2 – there is a symmetric density shift from 1,4-oxazine moieties towards nitro groups. The angles between each pair of contributing transition dipole moments are presented in Table 3, which clearly indicates that in β44 and β88 all the transition dipole moments are aligned parallel to each other making the angular contribution the maximum. In the group of negative βmn contributors, one of the pairs of transition dipole moments makes an angle larger than 90 leading to an overall negative term. Among all the major negative contributors, the dipole contributions are very small and the corresponding energy contributions are slightly higher than the positive βmn and hence for compound 11β‖e is the largest. Let us close this section highlighting that although the GFSM analysis was performed using 6-31+G basis, the data in Table S1 in the ESI† file indicate that there is a satisfactory agreement with property values obtained with the larger aug-cc-pVDZ basis set.
Table 3 Angle between transition dipole moments involved in major βmn terms
|
β
mn
|
a
|
b
|
c
|
d
|
θ
cd
ab
|
β
mn
|
a
|
b
|
c
|
d
|
θ
cd
ab
|
|
β
33
|
0 |
0 |
0 |
3 |
90 |
β
311
|
0 |
11 |
3 |
11 |
90 |
| 0 |
0 |
3 |
3 |
0 |
0 |
3 |
3 |
11 |
90 |
| 0 |
3 |
3 |
3 |
90 |
0 |
11 |
0 |
0 |
90 |
|
β
34
|
0 |
4 |
3 |
4 |
90 |
0 |
3 |
0 |
11 |
45 |
| 0 |
3 |
3 |
4 |
12 |
0 |
0 |
3 |
11 |
180 |
| 0 |
0 |
0 |
4 |
0 |
β
411
|
0 |
11 |
4 |
11 |
160 |
| 0 |
3 |
0 |
4 |
90 |
0 |
4 |
4 |
11 |
90 |
| 0 |
0 |
3 |
4 |
90 |
0 |
4 |
0 |
11 |
90 |
|
β
44
|
0 |
0 |
4 |
4 |
0 |
0 |
0 |
4 |
11 |
90 |
| 0 |
4 |
4 |
4 |
0 |
β
412
|
0 |
12 |
4 |
12 |
180 |
|
β
88
|
0 |
0 |
0 |
8 |
0 |
0 |
4 |
4 |
12 |
180 |
| 0 |
0 |
8 |
8 |
0 |
0 |
12 |
0 |
0 |
0 |
| 0 |
8 |
8 |
8 |
0 |
0 |
4 |
0 |
12 |
0 |
|
|
|
|
|
|
0 |
0 |
4 |
12 |
180 |
We will now turn to the analysis of vibrational contributions to the first hyperpolarizability. In order to gain an insight into their importance to the static property, we have computed the purely harmonic term, as defined by eqn (6), for 1–16. The results are assembled in Table 1 and demonstrate that the [μα]‖(0,0) term prevails over the electronic counterpart and in many cases the ratio reaches up to the factor of 10. Similarly to what has been demonstrated for the purely electronic β‖e term, the largest harmonic vibrational counterpart is found for 11. On passing from electronic contributions to the sum of electronic and vibrational terms, the property-based ordering of compounds changes, albeit the largest value is found in both cases for 11. It should be highlighted that we consider here frequency-independent first hyperpolarizability and the vibrational contributions become less significant for dynamic fields. However, if at least one static field is involved, they might add a substantial contribution to the overall second-order nonlinear optical response.47 In what follows we will analyze in more detail compounds 11 as well 12–14 with the NO2 group placed at various positions. Table 4 and Fig. 3 show lowest-order anharmonic terms contributing to β‖. Three major conclusions can be drawn from these data, namely: (i) both electrical and mechanical anharmonicities make a substantial contribution to the vibrational counterpart (e.g., for compound 11 the absolute value of the (1,0) term is 40% of (0,0)), (ii) anharmonic corrections may significantly reduce the purely harmonic term, as they are of opposite signs (see e.g.11), and (iii) there is no clear pattern of the electrical and mechanical anharmonicities for compounds 11–14. It should be thus concluded that for static hyperpolarizability these terms should be evaluated explicitly as they might have a significant effect on overall trends in β‖.
Table 4 Breakdown of vibrational first hyperpolarizability (in au) into anharmonic terms
| Compound |
[μ3]‖(1,0) |
[μ3]‖(0,1) |
[μ3]‖(1,0) + [μ3]‖(0,1) |
|
11
|
−2959 |
−1258 |
−4217 |
|
12
|
−655 |
1148 |
493 |
|
13
|
808 |
−2078 |
−1270 |
|
14
|
1052 |
−622 |
430 |
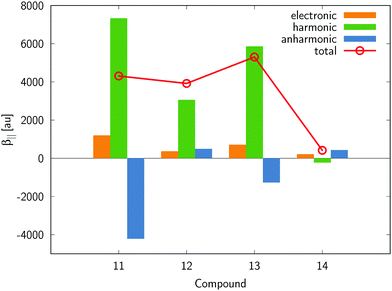 |
| | Fig. 3 Breakdown of β‖ for 11–14 into electronic and vibrational contributions. | |
In what follows we will analyze in more detail the origins of large harmonic vibrational hyperpolarizability for compound 11. Fig. 4 shows the orientation of compound 11 in the cartesian coordinate system (note that the two-fold symmetry axis is parallel to the cartesian z direction). The breakdown of [μα]‖(0,0) into symmetry-unique non-vanishing cartesian components is presented in Fig. 5. As seen, the cartesian zzz component parallel to the symmetry axis is by far the largest. In order to link this component with the vibrational structure of 11 we performed the sum-over-normal modes calculations and the results are shown in Fig. 6. It is clear that the first normal mode with wavenumber 17 cm−1 makes the dominant contribution (91% of [μα]zzz(0,0)). Atomic displacements for the normal mode in question show the symmetric vibrations of the propellane wings (see Fig. 4). For propellane molecule 11, in a noncentrosymmetric crystal structure with the z-axis parallel to the crystal polar axis,11 the existence of such “butterfly motion” polar mode could be beneficial for the crystal electrooptic properties, especially in the THz frequency range.48 Strong second-order nonlinear optical properties of organic crystals, e.g., such as found for DAST crystals,49,50 can be exploited for both generation and detection of THz radiation. Organic crystals possessing high THz-generation efficiencies are highly desired for THz spectroscopy, imaging and analysis due to unique penetration properties of THz radiation.51,52
 |
| | Fig. 4 The orientation of compound 11 in the cartesian coordinate system. Atomic displacements corresponding to the lowest-frequency normal mode are indicated by arrows. | |
 |
| | Fig. 5 Cartesian components of harmonic vibrational hyperpolarizability (in au) for compound 11. | |
 |
| | Fig. 6 Convergence of the zzz component of harmonic vibrational hyperpolarizability (in au) for compound 11. | |
4 Conclusions
Aiming to establish “structure–property” relations, in this work we have employed computational quantum chemistry methods to study first order hyperpolarizabilities of 16 propellanes. In particular, we considered a wide palette of symmetrically-placed substituents (–CF3, –SCH3, –SO2CH3, –SCF3, –OCF3, –CH2OCH3, dioxolane and –NO2) which cover a wide range of values of Hammett substituent constants. It has been demonstrated that the maximum values of frequency-independent first hyperpolarizability can be obtained for strong electron-accepting NO2 substituents but only at the preferred positions with respect to the electronegative oxygen atom in the 1,4-oxazine moiety. This holds for electronic as well as vibrational counterparts. However, asymmetric substitution with NO2 and NH2 groups at these preferred positions (compound 15) leads to equally high electronic and vibrational hyperpolarizability values. The variations in computed properties are large among the studied set of substituents and can reach an order of magnitude. In order to shed light on these findings, we employed a generalized few state model to study the electronic counterpart. It turned out that the overall convergence of the first hyperpolarizability with respect to the number of electronic states is slow, indicating a complicated origin of this property. Some of the studied herein propellanes (7, 10, 13), due to similar molecular structure with compound 11 and large values of their first hyperpolarizabilities can be considered as promising candidates for synthesis, crystal growth and the evaluation of their second order NLO properties, providing that they will crystallize in noncentrosymmetric point groups.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
The authors cordially thank Miss Elizaveta F. Petrusevich for the preparation of the graphical abstract. The authors acknowledge the Wroclaw Center for Networking and Supercomputing for granting computational resources. MMA acknowledges the research initiation grant from IIT Bhilai.
References
- G. Snatzke and G. Zanati, Justus Liebigs Ann. Chem., 1965, 684, 62–78 CrossRef CAS.
- O. Diels and W. Friedrichsen, Justus Liebigs Ann. Chem., 1934, 513, 145–155 CrossRef CAS.
- G. Wittig and U. Mayer, Chem. Ber., 1963, 96, 342–348 CrossRef CAS.
- J. Altman, E. Babad, J. Itzchaki and D. Ginsburg, Tetrahedron, 1966, 22, 279–304 CrossRef.
- A. M. Dilmaç, E. Spuling, A. de Meijere and S. Bräse, Angew. Chem., Int. Ed., 2017, 56, 5684–5718 CrossRef PubMed.
- A. M. Dilmaç, T. Wezeman, R. M. Bär and S. Bräse, Nat. Prod. Rep., 2020, 37, 224–245 RSC.
- J. Kanazawa and M. Uchiyama, Synlett, 2019, 1–11 CrossRef CAS.
- F. Reuß and P. Heretsch, Angew. Chem., Int. Ed., 2020, 59, 10232–10234 CrossRef PubMed.
- F.-S. He, S. Xie, Y. Yao and J. Wu, Chin. Chem. Lett., 2020, 31, 3065–3072 CrossRef CAS.
- M. M.-D. Pramanik, H. Qian, W.-J. Xiao and J.-R. Chen, Org. Chem. Front., 2020, 7, 2531–2537 RSC.
- A. Miniewicz, S. Bartkiewicz, E. Wojaczyńska, T. Galica, R. Zaleśny and R. Jakubas, J. Mater. Chem. C, 2019, 7, 1255–1262 RSC.
- X.-Y. Liu, X. Tang, Y. Zhao, D. Zhao, J. Fan and L.-S. Liao, ACS Appl. Mater. Interfaces, 2018, 10, 1925–1932 CrossRef CAS PubMed.
- K. B. Wiberg and S. T. Waddell, J. Am. Chem. Soc., 1990, 112, 2194–2216 CrossRef CAS.
- K. C. Nicolaou, J. Yin, D. Mandal, R. D. Erande, P. Klahn, M. Jin, M. Aujay, J. Sandoval, J. Gavrilyuk and D. Vourloumis, J. Am. Chem. Soc., 2016, 138, 1698–1708 CrossRef CAS PubMed.
- J. Kaleta, Z. Janoušek, M. Nečas and C. Mazal, Organometallics, 2015, 34, 967–972 CrossRef CAS.
- P. R. Khoury, J. D. Goddard and W. Tam, Tetrahedron, 2004, 60, 8103–8112 CrossRef CAS.
- K. Jug and A. Poredda, J. Am. Chem. Soc., 1991, 113, 761–764 CrossRef CAS.
- D. Nied, W. Klopper and F. Breher, Angew. Chem., Int. Ed., 2009, 48, 1411–1416 CrossRef CAS PubMed.
- F. Zerbetto, Chem. Phys. Lett., 1995, 241, 445–449 CrossRef CAS.
- F. Castet, V. Rodriguez, J.-L. Pozzo, L. Ducasse, A. Plaquet and B. Champagne, Acc. Chem. Res., 2013, 46, 2656–2665 CrossRef CAS PubMed.
- C. Bouquiaux, C. Tonnelé, F. Castet and B. Champagne, J. Phys. Chem. B, 2020, 124, 2101–2109 CrossRef CAS PubMed.
- J. Seibert, B. Champagne, S. Grimme and M. de Wergifosse, J. Phys. Chem. B, 2020, 124, 2568–2578 CrossRef CAS PubMed.
- C. Bouquiaux, F. Castet and B. Champagne, J. Phys. Chem. B, 2021, 125, 10195–10212 CrossRef CAS PubMed.
- J. Quertinmont, L. Maschio, A. Datta and B. Champagne, J. Phys. Chem. C, 2020, 124, 24451–24459 CrossRef CAS.
- E. Rtibi and B. Champagne, Symmetry, 2021, 13, 1636 CrossRef CAS.
- K. Pielak, F. Bondu, L. Sanguinet, V. Rodriguez, F. Castet and B. Champagne, Dyes Pigm., 2019, 160, 641–646 CrossRef CAS.
- F. Castet, A. Gillet, F. Bureš, A. Plaquet, V. Rodriguez and B. Champagne, Dyes Pigm., 2021, 184, 108850 CrossRef CAS.
- T. N. Ramos, S. Canuto and B. Champagne, J. Chem. Inf. Model., 2020, 60, 4817–4826 CrossRef CAS PubMed.
- P. Beaujean, B. Champagne, S. Grimme and M. de Wergifosse, J. Phys. Chem. Lett., 2021, 12, 9684–9690 CrossRef CAS PubMed.
- D. P. Shelton and J. E. Rice, Chem. Rev., 1994, 94, 3–29 CrossRef CAS.
- B. J. Orr and J. F. Ward, Mol. Phys., 1971, 20, 513–526 CrossRef CAS.
- D. M. Bishop, Adv. Chem. Phys., 1998, 104, 1–40 CAS.
- D. M. Bishop and B. Kirtman, J. Chem. Phys., 1991, 95, 2646 CrossRef CAS.
- D. M. Bishop, M. Hasan and B. Kirtman, J. Chem. Phys., 1995, 103, 4157–4159 CrossRef CAS.
- J. M. Luis, M. Duran, J. L. Andrés, B. Champagne and B. Kirtman, J. Chem. Phys., 1999, 111, 875–884 CrossRef CAS.
- J. M. Luis, M. Duran, B. Champagne and B. Kirtman, J. Chem. Phys., 2000, 113, 5203–5213 CrossRef CAS.
- J. M. Luis, M. Duran and B. Kirtman, J. Chem. Phys., 2001, 115, 4473–4483 CrossRef CAS.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 Revision D.01, Gaussian Inc.; Wallingford CT, 2009 Search PubMed.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- R. Zaleśny, I. W. Bulik, W. Bartkowiak, J. M. Luis, A. Avramopoulos, M. G. Papadopoulos and P. Krawczyk, J. Chem. Phys., 2010, 133, 244308 CrossRef PubMed.
- I. W. Bulik, R. Zaleśny, W. Bartkowiak, J. M. Luis, B. Kirtman, G. E. Scuseria, A. Avramopoulos, H. Reis and M. G. Papadopoulos, J. Comput. Chem., 2013, 34, 1775–1784 CrossRef CAS PubMed.
- A. Baranowska-Łaczkowska, W. Bartkowiak, R. W. Góra, F. Pawłowski and R. Zaleśny, J. Comput. Chem., 2013, 34, 819–826 CrossRef PubMed.
- R. Zaleśny, M. Medved’, S. Sitkiewicz, E. Matito and J. M. Luis, J. Chem. Theory Comput., 2019, 15, 3570–3579 CrossRef PubMed.
- M. M. Alam, M. T.-P. Beerepoot and K. Ruud, J. Chem. Phys., 2020, 152, 244106 CrossRef CAS PubMed.
- C. Hansch, A. Leo and R. W. Taft, Chem. Rev., 1991, 91, 165–195 CrossRef CAS.
- D. M. Bishop, B. Kirtman, H. A. Kurtz and J. E. Rice, J. Chem. Phys., 1993, 98, 8024–8030 CrossRef CAS.
- M. Jazbinsek, U. Puc, A. Abina and A. Zidansek, Appl. Sci., 2019, 9, 882 CrossRef CAS.
- C. Bosshard, R. Spreiter, L. Degiorgi and P. Günter, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 205107 CrossRef.
- Z. Yang, L. Mutter, M. Stillhart, B. Ruiz, S. Aravazhi, M. Jazbinsek, A. Schneider, V. Gramlich and P. Günter, Adv. Funct. Mater., 2007, 17, 2018–2023 CrossRef CAS.
- Q. Sun, Y. He, K. Liu, S. Fan, E. P.-J. Parrott and E. Pickwell-MacPherson, Quant. Imaging Med. Surg., 2017, 7, 345–355 CrossRef PubMed.
- B. Graber, C. Kim and D. H. Wu, Appl. Phys. Lett., 2017, 111, 221107 CrossRef.
|
| This journal is © the Owner Societies 2022 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
Swati Singh
Rajput
b,
Marta
Chołuj
c,
Elżbieta
Wojaczyńska
a,
Swati Singh
Rajput
b,
Marta
Chołuj
c,
Elżbieta
Wojaczyńska
 c,
Andrzej
Miniewicz
c,
Andrzej
Miniewicz
 c,
Md. Mehboob
Alam
c,
Md. Mehboob
Alam
 *b and
Robert
Zaleśny
*b and
Robert
Zaleśny
 *c
*c
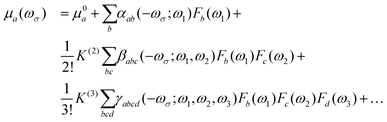

 represents the summation over all the permutations of the pairs (a, −ωσ), (b, ω1), and (c, ω2) and Ei = ħωi (i = 1, 2, σ). The prime over the double summation in eqn (2) represents a restricted summation where none of the indices could label the ground state. Emn and μmna stand for the excitation energy and ath component of the transition dipole moment for m → n transition, respectively. Note that
represents the summation over all the permutations of the pairs (a, −ωσ), (b, ω1), and (c, ω2) and Ei = ħωi (i = 1, 2, σ). The prime over the double summation in eqn (2) represents a restricted summation where none of the indices could label the ground state. Emn and μmna stand for the excitation energy and ath component of the transition dipole moment for m → n transition, respectively. Note that ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) mn =
mn = ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) mn − μ00. The static limit of the tensor components can be obtained by setting all three angular frequencies to zero. The commonly used first hyperpolarizability, β‖, can be calculated from the βabc components using the following relation:32
mn − μ00. The static limit of the tensor components can be obtained by setting all three angular frequencies to zero. The commonly used first hyperpolarizability, β‖, can be calculated from the βabc components using the following relation:32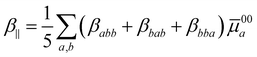
![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) 00a stands for the ground-state dipole unit in the direction of the ground-state dipole moment (μ00a/|μ00|).
00a stands for the ground-state dipole unit in the direction of the ground-state dipole moment (μ00a/|μ00|).




 indicates the sum over all permutations of the indices a, b,…
indicates the sum over all permutations of the indices a, b,…
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The compound with the second largest β‖e is 15, which is the only compound asymmetrically substituted (–NO2 and –NH2) at para positions. We note that the replacement of one electron-accepting group with an electron-donating one, while preserving the positions of the substituents, does not lead to deterioration of the electronic first hyperpolarizability. It is interesting to note that compounds 1, 3 and 9 have almost the same values for β‖e indicating that there is almost no effect of adding an extra –CF3 group or changing the position of the –CF3 group in the benzo-oxazine wings. Similarly, compounds 2 and 6 have similar values for β‖e indicating that there is no effect of adding an extra methyl group in the benzo-oxazine ring. On replacing –SCH3 by –CF3, i.e., on moving from compound 2 to 3, there is an increase in β‖e value. Replacing –CF3 by –OCF3 (compound 3 to compound 8) leaves the β‖e values practically unchanged and replacing –CF3 by –SCF3, i.e., on moving from compound 3 to 7, the β‖e values are almost doubled. This is probably because of the available vacant d-orbital on the S-atom. On replacing –SCH3 (compound 2) by –SO2CH3 (compound 4) there is about a three-fold increase in the β‖e values and replacing –SCH3 (compound 2) by –SCF3 (compound 7) there is a corresponding 2.5-fold increase. Compounds 12 and 14 show a variation in β‖e which emphasizes the importance of substituent placement. Finally, let us recall that compound 16 has two electron-donating substituents at the meta position and exhibits the smallest β‖e value. Such substituent placement maximizes β‖e but only for strong electron-donating groups.
1. The compound with the second largest β‖e is 15, which is the only compound asymmetrically substituted (–NO2 and –NH2) at para positions. We note that the replacement of one electron-accepting group with an electron-donating one, while preserving the positions of the substituents, does not lead to deterioration of the electronic first hyperpolarizability. It is interesting to note that compounds 1, 3 and 9 have almost the same values for β‖e indicating that there is almost no effect of adding an extra –CF3 group or changing the position of the –CF3 group in the benzo-oxazine wings. Similarly, compounds 2 and 6 have similar values for β‖e indicating that there is no effect of adding an extra methyl group in the benzo-oxazine ring. On replacing –SCH3 by –CF3, i.e., on moving from compound 2 to 3, there is an increase in β‖e value. Replacing –CF3 by –OCF3 (compound 3 to compound 8) leaves the β‖e values practically unchanged and replacing –CF3 by –SCF3, i.e., on moving from compound 3 to 7, the β‖e values are almost doubled. This is probably because of the available vacant d-orbital on the S-atom. On replacing –SCH3 (compound 2) by –SO2CH3 (compound 4) there is about a three-fold increase in the β‖e values and replacing –SCH3 (compound 2) by –SCF3 (compound 7) there is a corresponding 2.5-fold increase. Compounds 12 and 14 show a variation in β‖e which emphasizes the importance of substituent placement. Finally, let us recall that compound 16 has two electron-donating substituents at the meta position and exhibits the smallest β‖e value. Such substituent placement maximizes β‖e but only for strong electron-donating groups.