Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Catalytic formation of oxalic acid on the partially oxidised greigite Fe3S4(001) surface†
David
Santos-Carballal
 *a and
Nora H
de Leeuw
*a and
Nora H
de Leeuw
 ab
ab
aSchool of Chemistry, University of Leeds, Leeds LS2 9JT, UK. E-mail: D.Santos-Carballal@leeds.ac.uk; N.H.deLeeuw@leeds.ac.uk; Tel: +44 (0) 11 3343 9008
bDepartment of Earth Sciences, Utrecht University, Princetonplein 8A, 3584 CD Utrecht, The Netherlands. E-mail: N.H.deLeeuw@uu.nl
First published on 5th August 2022
Abstract
Greigite (Fe3S4), with its ferredoxin-like 4Fe–4S redox centres, is a naturally occurring mineral capable of acting as a catalyst in the conversion of carbon dioxide (CO2) into low molecular-weight organic acids (LMWOAs), which are of paramount significance in several soil and plant processes as well as in the chemical industry. In this paper, we report the reaction between CO2 and water (H2O) to form oxalic acid (H2C2O4) on the partially oxidised greigite Fe3S4(001) surface by means of spin-polarised density functional theory calculations with on-site Coulomb corrections and long-range dispersion interactions (DFT+U−D2). We have calculated the bulk phase of Fe3S4 and the two reconstructed Tasker type 3 terminations of its (001) surface, whose properties are in good agreement with available experimental data. We have obtained the relevant phase diagram, showing that the Fe3S4(001) surface becomes 62.5% partially oxidised, by replacing S by O atoms, in the presence of water at the typical conditions of calcination [Mitchell et al. Faraday Discuss. 2021, 230, 30–51]. The adsorption and co-adsorption of the reactants on the partially oxidised Fe3S4(001) surface are exothermic processes. We have considered three mechanistic pathways to explain the formation of H2C2O4, showing that the coupling of the C–C bond and second protonation are the elementary steps with the largest energy penalty. Our calculations suggest that the partially oxidised Fe3S4(001) surface is a mineral phase that can catalyse the formation of H2C2O4 under favourable conditions, which has important implications for natural ecosystems and is a process that can be harnessed for the industrial manufacture of this organic acid.
1. Introduction
Oxalic acid (H2C2O4), which is the smallest dicarboxylic low molecular weight organic acid (LMWOA),1 has traditionally been regarded as a major player in the chemical industry2,3 and natural systems.4 Oxalic acid is widely used for the treatment of metallic surfaces5–8 and textiles,9–11 as a bleaching agent,12–15 for the preparation of esters,16–18 as a reagent in chemical synthesis19–21 and for separation of rare-earth elements.22–25 The most sophisticated methods currently used in the industrial production of oxalic acid involve the oxidation of carbohydrates,26–29 ethylene glycol30,31 and carbon monoxide.32 Moreover, oxalic acid is the metabolic product of plants,33–35 soil fungi36–38 and bacteria,39–41 and to a lesser extent of animals,42–44 playing a key role in modulating the interactions between these organisms.4,45,46 Three main pathways have been suggested for the biosynthesis of oxalic acid, including the cytoplasmatic pathway,47 the tricarboxylic acid pathway48 and the glyoxylate pathway.36,49,50From a catalytic point of view, ferredoxins have gained renewed significance owing to their biological role in electron transfers in several metabolic reactions.51,52 Ferredoxins are iron–sulfur proteins, with one of the most notable families containing cubane Fe4–S4 catalytic centres.53 The catalytic centre of ferredoxins can be either exposed or hidden to solvent, leading to low reduction potentials with a minimum of −600 mV or high potentials with a maximum of +350 mV, respectively.53,54 Structurally, ferredoxins contain Fe ions in the oxidation states +2 and +3, which are forming tetrahedrally coordinated FeS4 units, whereas each S atom is bonded to three Fe ions.54 Ferredoxin oxidoreductases are responsible for the coupling of the C–C from CO2 at cellular level in the reductive tricarboxylic acid cycle.55 Attempts to synthesise biomimetic Fe4–S4 clusters have been successful in controlling the binding of substrate through remote steric effects, but their preparation requires carefully controlled conditions, toxic chemicals and complex steps.56
Greigite (Fe3S4) is a naturally occurring mineral that contains Fe4–S4 clusters with the cubane structure,57 very similar to the catalytic centre in ferredoxins. Unsurprisingly, this mineral phase has been found to be catalytically active towards the activation and conversion of CO2 into small organic molecules, including formic acid, acetic acid, pyruvic acid and methanol.58–60 Recent studies have suggested that the surfaces of Fe3S4 become partially oxidised easily in air or wet conditions, forming core–shell iron sulfide–iron oxide nanoparticles,61,62 which enhances the catalytic activity.
The important biocatalytic role of ferredoxins and the structural similarities with Fe3S4 have led us to study the catalytic conversion of CO2 and H2O into H2C2O4 over the partially oxidised Fe3S4(001) surface by means of spin polarised density functional theory (DFT) calculations. We have modelled the bulk phase of Fe3S4, as well as the two reconstructed Tasker type 3 terminations of its (001) surface, and discuss the changes in several structural, electronic and magnetic properties. We have also calculated the effect of the ratio of the partial pressures of H2O, i.e. the reactant, and H2S, i.e. the product of the oxidation, and temperature on the oxygen coverage of the Fe3S4(001) surface. Next, we have considered the adsorption of the single CO2 and H2O molecules at different sites on the partially oxidised Fe3S4(001) surface and assessed a number of descriptors of the chemical activation. We have calculated the structures and energies of possible surface-bound intermediates and saddle points and constructed the reaction profiles for three mechanisms, i.e. via (i) oxalate, (ii) carboxylate and (iii) bicarbonate pathways.
2. Computational methods
2.1. Calculation details
The bulk phase, pristine and partially oxidised (001) surfaces of Fe3S4, as well as the reaction mechanisms were calculated using unrestricted DFT calculations as implemented in the Vienna ab initio simulation package (VASP).63–66 The strongly constrained and appropriately normed (SCAN) functional, which meets all 17 known exact constraints within the meta-generalised gradient approximation (meta-GGA), was used for the exchange-correlation energy functional.67 Meta-GGA functionals, which comprise up to the second order derivative of the electron density, i.e. the non-interacting kinetic energy density term, provide energies and structures that are in excellent agreement with experiments.68–72 The projector augmented wave (PAW) formalism was used to treat the core states of Fe: [Ar], O: [He], C: [He] and S: [Ne], their kinetic energies and the interactions with the valence orbitals.73,74 The aspherical components of the density gradient were also considered within the PAW one-centre terms, which is required by meta-GGA functionals to describe properly the strongly directional Fe 3d states. The D2 semiempirical method of Grimme was included in our calculations to correct the long-range dispersion interactions,75 which is particularly important for an appropriate description of materials and interface properties.59,68,76–85 A periodic plane-wave basis set with an upper kinetic energy threshold fixed at 400 eV was employed to expand the Kohn-Sham valence states. The electronic ground state was determined using a preconditioned conjugate gradients minimisation algorithm, which optimises completely and self-consistently the total (free) energy, which is the variational quantity within this methodology.86–88 This stable and robust electronic minimisation technique is preferred for modelling surface slabs with vacuum gaps when using meta-GGA functionals, as it applies an all band simultaneous update of orbitals. The time step needed to carry out the line optimisation of the energy along the preconditioned conjugate gradient was scaled automatically. The optimisation of the electronic density was terminated when the energy difference between two consecutive self-consistent loop steps was smaller than 10−5 eV. The internal coordinates were relaxed to their equilibrium positions using a Newton line optimiser, an efficient conjugate gradients technique,89,90 which was stopped when the Hellmann–Feynman forces were below 0.01 eV Å−1.We have also used a mean-field Hubbard model, i.e. the so-called DFT+U method, to enhance the calculation of the delocalised Fe 3d states.91–93 We have applied a simplified rotationally invariant strong intra-atomic Coulomb interaction94 and developed the value for the effective parameter Ueff = 5.26 eV following the linear response approach of Cococcioni et al.,95 which has been used successfully for the simulation of (Ni,Fe) oxyhydroxides (Ni1−xFexOOH)96 and defective ceria CeO2.97 We have carried out a series of static calculations to determine the Ueff value, where we used the conventional cubic unit cell of Fe3S4 with ferrimagnetic ordering with the experimental lattice parameter and internal positions.57 We broke the symmetry of the tetrahedral (FeA) and octahedral Fe (FeB) sublattices one at a time, by treating one of these atoms differently to the rest. We calculated the number of d electrons (Nd) for (i) a standard DFT, (ii) a non-self-consistent response function (NSCRF) and (iii) a self-consistent response function (SCRF) to various spherical potentials (V) acting on both channels of the spin of that cation site. The NSCRF and SCRF were found by fitting linearly Ndvs. V, see Fig. SI1 (ESI†). The optimal Ueff value was obtained by calculating the weighted arithmetic mean of the difference between the reciprocals of the gradients of the linear fittings.
2.2 Surface and molecular models
The (001) surface was investigated using the periodic p(1 × 1) supercell, which was created from the bulk Fe3S4 using the METADISE code.98 A vacuum of 18 Å was added in the direction perpendicular to the surface to prevent interaction with the periodically repeated images and to ensure that the surface can accommodate, in any conformation, the H2C2O4 molecule, which has a length of 4.7 Å. We considered four formula unit (f.u.) layers for the simulation of the (001) surface slab, with an area of 102.517 Å2. The atoms in the two topmost layers were allowed to relax during geometry optimisations, to mimic the surface, while those atoms in the remaining two bottom layers were kept at their optimised bulk positions. The Brillouin zone of the surface was sampled using a Γ-centred Monkhorst-Pack (MP) mesh of 5 × 5 × 1 k-points.99 For the geometry optimisations, the partial occupancies were determined using the finite temperature Gaussian smearing method87 with 0.01 eV for the width of the smearing, which was tested to ensure that the electronic entropy (TS) vanished. The free energy (F), which is the variational quantity in the finite temperature Gaussian smearing approach differs from E(σ) by TS.87,100 However, we employed the tetrahedron method with Blöchl corrections101 for the calculation of accurate energies as well as the electronic and magnetic properties in static simulations of the optimised structures. Convergence of energy differences within 1 meV per atom was further tested for the simulation supercell using different vacuum thicknesses, cut off energy values as well as various numbers of total and relaxed atomic layers. Dipole corrections were also included perpendicular to the surface plane to compensate for any dipole created by the chemical species added onto the relaxed side of the slab and to enhance the electronic convergence.102,103The isolated CO2 and H2O molecules were modelled in a periodic box of 14 × 15 × 16 Å3 to ensure negligible interaction with their images in the neighbouring cells. The Gaussian scheme was used to determine the electronic partial occupancies during geometry optimisations and energy calculations, sampling only the Γ point of the Brillouin zone.
The effective Bader atomic charges were obtained using an improved grid of charge density values without lattice bias,104–106 whereas the magnetic moments were integrated within the same atomic basins. The work function (Φ), which is the minimum thermodynamic work required for an electron to leave the Fe3S4(001) surface, was calculated as Φ = Evac − EF, where Evac is the potential at the vacuum level and EF is the Fermi level of the slab. The STM images were calculated using the Tersoff-Hamann method107 in the implementation of Vanpoucke and Brocks.108 The wavenumbers of the fundamental harmonic vibrational modes were determined using the central finite differences approach, by allowing each atom to move by a small displacement in the three Cartesian directions. The atomic displacements are used to calculate the elements of the Hessian matrix, which are computed by numerical differentiation of the analytical gradients of the energy with respect to the energy. The saddle points and minimum energy pathways (MEP) between initial and final states were calculated using the climbing image nudged elastic band (cNEB) method.109,110 The cNEB algorithm used for modelling the MEPs has been employed successfully before to obtain the saddle point structures and energies of several processes in heterogeneous catalysis.59,61,68,78,111 We have used five images to model the MEP, which were optimised globally by means of the limited-memory Broyden–Fletcher–Goldfarb–Shannon (LBFGS) method.89,112 The saddle points were characterised by a single imaginary frequency along the reaction coordinate, which were determined using the central finite differences method.
2.3 Surface energy diagrams
The surface energies for the slab before (γu) and after relaxation (γr) were evaluated as, | (1) |
 | (2) |
The temperature-corrected energy [EM(T,p°)] for the adsorbate molecule (M) was calculated according to,
| EM(T,p°) = EM − TS(T,p°) | (3) |
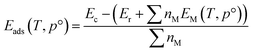 | (4) |
The process of partial oxidation of the Fe3S4(001) surface can be represented by the following chemical reaction,
| Fe24S32(001) + nH2O(g) = Fe24S32−nOn(001) + nH2S(g) | (5) |
For the partially oxidised surfaces, the effect of temperature on the surface free energy [σ(T,p)] was introduced as follows,85,114–116
 | (6) |
The activation free energy (Fai) was calculated as the difference between the free energy of the saddle point and the free energy of the reactants, where the index i refers to each of the three elemental steps that we calculated. The free energy of the elemental step (ΔFi) was obtained as the difference of the free energy of the products and the free energy of the reactants. The energy diagrams were prepared using the most stable binding modes of the reactants, intermediates and final products, which were connected by saddle points and MEPs. The Helmholtz free energy (ΔF) was calculated as ΔF = ΔE − TΔSvib where Svib is the vibrational entropy, which was obtained as follows for the adsorbed species,
 | (7) |
3. Results and discussion
3.1. Bulk phase of greigite (Fe3S4)
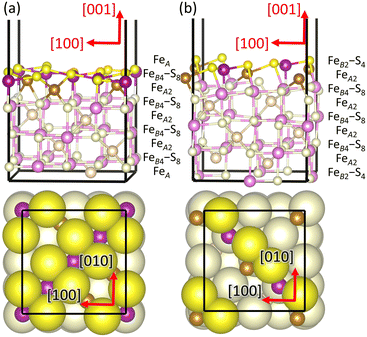
We first investigated the optimised bulk structure of Fe3S4, which is later used to create the (001) surface for the calculation of the phase diagrams, molecular adsorptions and reaction mechanisms. Our starting point for Fe3S4 is the bulk structure characterised by Li and collaborators using room temperature powder X-ray diffraction (XRD).57 Fe3S4 has the typical face-centred cubic (fcc) lattice of the spinel structure and crystallises in the space group Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (no. 227). Fig. 1 depicts the conventional cubic unit cell of Fe3S4 containing 8 f.u. and the periodically repeated images of those ions located at the edges and corners of the cell. The sulfide anions are formally in the 2− oxidation state and exhibit a nearly regular cubic close-packed (ccp) distribution along the [111] direction. The S atoms occupy the tetrahedrally distorted Wyckoff 32e positions with coordinates (u, u, u) and are surrounded by 12 other equidistant nearest-neighbour anions. The difference of the sulfur parameter u from ¼, in direct coordinates, represents the shift of the anions in the [111] direction to accommodate cations of different coordination number and radii in the interstitial sites. Fe3S4 is an inverse 2–3 type spinel, as it contains two 3+ and one 2+ cations per formula unit. The tetrahedral FeA atoms are in the highest 3+ oxidation state and occupy the 8a crystallographic positions at (1/8, 1/8, 1/8). The octahedral FeB cations, which have two equal populations in the 2+ and 3+ valence states each, fill the 16d octahedral holes with coordinates (1/2, 1/2, 1/2). However, only 1/8 of the total number of tetrahedral positions and half of the total number of octahedral holes are filled by the cations. The cations form two different types of alternate layers in the [111] direction, one composed only by FeB ions and the other by both FeA and FeB.
m (no. 227). Fig. 1 depicts the conventional cubic unit cell of Fe3S4 containing 8 f.u. and the periodically repeated images of those ions located at the edges and corners of the cell. The sulfide anions are formally in the 2− oxidation state and exhibit a nearly regular cubic close-packed (ccp) distribution along the [111] direction. The S atoms occupy the tetrahedrally distorted Wyckoff 32e positions with coordinates (u, u, u) and are surrounded by 12 other equidistant nearest-neighbour anions. The difference of the sulfur parameter u from ¼, in direct coordinates, represents the shift of the anions in the [111] direction to accommodate cations of different coordination number and radii in the interstitial sites. Fe3S4 is an inverse 2–3 type spinel, as it contains two 3+ and one 2+ cations per formula unit. The tetrahedral FeA atoms are in the highest 3+ oxidation state and occupy the 8a crystallographic positions at (1/8, 1/8, 1/8). The octahedral FeB cations, which have two equal populations in the 2+ and 3+ valence states each, fill the 16d octahedral holes with coordinates (1/2, 1/2, 1/2). However, only 1/8 of the total number of tetrahedral positions and half of the total number of octahedral holes are filled by the cations. The cations form two different types of alternate layers in the [111] direction, one composed only by FeB ions and the other by both FeA and FeB.
Table 1 summarises the calculated and previously reported structural, electronic and magnetic properties for the Fe3S4 bulk material. Our calculations reveal that the lattice parameter for the cubic unit cell of Fe3S4 was overestimated by 0.25 Å with respect to experiment,57 but is in excellent agreement with the value reported by Devey et al. when using PW91+U where Ueff = 5 eV.118 The atomic positions were allowed to relax fully, but the cations remained in their ideal crystallographic sites. However, the value obtained for the sulfur u parameter is just slightly larger than in experiment, indicating that the anions suffer a relatively larger displacement in the simulation cell. The anion–cation bond distances, which are mathematically related to the sulfur parameter by 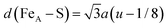 and d(FeB–S) = a(1/2 − u), were overestimated by 0.08 and 0.05 Å, respectively, compared to a previous study119 but in agreement with a larger lattice parameter. Our computational setup provides better atomic Bader charges (q) and magnetic moments (ms) than calculations using small values of Ueff,118,120 and our results are in better agreement for comparable Hubbard parameters to the one used in this study.118 Although the atomic charges of 1.371e− for FeA, 1.189e− for FeB and −0.937e− for S are still underestimated with regards to their oxidation states, this is a common finding with Bader charges, and they do provide evidence that our Fe3S4 is indeed an inverse spinel as q(FeA) > q(FeB), which has been observed before.57,121 The larger magnetic moment of −4.177μB atom−1 for FeA refers to the high-spin electronic distribution
and d(FeB–S) = a(1/2 − u), were overestimated by 0.08 and 0.05 Å, respectively, compared to a previous study119 but in agreement with a larger lattice parameter. Our computational setup provides better atomic Bader charges (q) and magnetic moments (ms) than calculations using small values of Ueff,118,120 and our results are in better agreement for comparable Hubbard parameters to the one used in this study.118 Although the atomic charges of 1.371e− for FeA, 1.189e− for FeB and −0.937e− for S are still underestimated with regards to their oxidation states, this is a common finding with Bader charges, and they do provide evidence that our Fe3S4 is indeed an inverse spinel as q(FeA) > q(FeB), which has been observed before.57,121 The larger magnetic moment of −4.177μB atom−1 for FeA refers to the high-spin electronic distribution 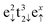 , whereas we can assign the configuration
, whereas we can assign the configuration 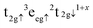 to the antiparallel aligned FeB, implying that the conduction mechanism involves both cation sublattices. Our total spin magnetisation of saturation (MS) of 2.00μB f.u.−1 is in excellent agreement with the early works of Morrish and collaborators using Mössbauer spectroscopy.121,122 Note that a wide range of different values have been reported for Fe3S4, corresponding to other electronic and magnetic properties.119,123–127Fig. 2 displays the electronic density of states (DOS) for the bulk phase of Fe3S4. The occupied e and t2 states of the FeA ions appear strongly hybridised as a narrow single peak in the minority channel of spins at around −8.5 eV. The FeA cations also have a small e band crossing the Fermi level in the α channel, illustrative of the itinerant electron provided by the t2g valence band of the FeB sublattice in the minority channel of the spins. The t2g and eg valence bands of the FeB cations are located between −7.0 and −3.0 eV in the majority channel of the spins. The virtual e and t2 states of FeA and the t2g and eg conduction bands of FeB appear above 1.5 eV. Importantly, the hybridisation of the S p levels with the t2g states of the FeB cations observed in the minority spin channel of the DOS of the bulk of Fe3S4 explains the small magnetic moment of −0.263μB calculated for the anion.
to the antiparallel aligned FeB, implying that the conduction mechanism involves both cation sublattices. Our total spin magnetisation of saturation (MS) of 2.00μB f.u.−1 is in excellent agreement with the early works of Morrish and collaborators using Mössbauer spectroscopy.121,122 Note that a wide range of different values have been reported for Fe3S4, corresponding to other electronic and magnetic properties.119,123–127Fig. 2 displays the electronic density of states (DOS) for the bulk phase of Fe3S4. The occupied e and t2 states of the FeA ions appear strongly hybridised as a narrow single peak in the minority channel of spins at around −8.5 eV. The FeA cations also have a small e band crossing the Fermi level in the α channel, illustrative of the itinerant electron provided by the t2g valence band of the FeB sublattice in the minority channel of the spins. The t2g and eg valence bands of the FeB cations are located between −7.0 and −3.0 eV in the majority channel of the spins. The virtual e and t2 states of FeA and the t2g and eg conduction bands of FeB appear above 1.5 eV. Importantly, the hybridisation of the S p levels with the t2g states of the FeB cations observed in the minority spin channel of the DOS of the bulk of Fe3S4 explains the small magnetic moment of −0.263μB calculated for the anion.
| Property | This work | Previous reports | Ref. |
|---|---|---|---|
| a (Å) | 10.1251 | 9.8719 | 57 |
| u | 0.2586 | 0.2546 | 57 |
| d(FeA–S) (Å) | 2.29 | 2.21 | 119 |
| d(FeB–S) (Å) | 2.47 | 2.42 | 119 |
| q(FeA) (e− atom−1) | 1.371 | 1.1 | 120 |
| q(FeB) (e− atom−1) | 1.189 | 1.0 | 120 |
| q(S) (e− atom−1) | −0.937 | −0.8 | 120 |
| m s(FeA) (μB atom−1) | −4.177 | −2.8 | 120 |
| m s(FeB) (μB atom−1) | 3.614 | 3.0 | 120 |
| m s(S) (μB atom−1) | −0.263 | 0.1 | 120 |
| M S(Fe3S4) (μB f.u.−1) | 2.000 | 2.00 | 121 |
3.2. Pristine Fe3S4(001) surface
We have also simulated the two non-polar stoichiometric and symmetric terminations of the pristine Fe3S4(001) surface, where we have kept the cell borders fixed at the parameters calculated for the bulk, represented in Fig. 3. The stacking of the atomic planes is (FeA)–(FeB4–S8)–(FeA) and (FeB2–S4)–(FeA2)–(FeB2–S4) for the terminations FeA and FeB–S, respectively, where the atoms within parenthesis are located approximately within the same layers. We have employed single surface unit cells to simulate terminations FeA and FeB–S of the pristine Fe3S4(001) surface, which are the smallest periodically repeating surface unit cells that we can use to model the stacking sequences of these systems. Both terminations FeA and FeB–S are reconstructed Tasker type 3 surfaces,128 where the dipole moment was removed before geometry optimisation by displacing half of the ions from the exposed stoichiometric stacking sequence at the top of the slab to the bottom of the slab. Termination FeA has a bulk-like structure comprising a full monolayer (ML) of S atoms, where 25% are 4-fold and the remaining 75% have one dangling bond. The topmost plane of termination FeA also contains 0.5 ML of 5-fold FeB cations, which form alternating rows in the [110] direction, on top of which are 0.125 ML of 2-fold FeA ions with the symmetry, according to the vectorial notation of Wood.129 Termination FeB–S presents 0.5 ML of 2-fold S atoms, unsurprisingly also forming alternating rows in the [110] direction, alongside 0.25 ML of FeB with 3 dangling bonds, whereas the layer beneath contains 0.25 ML of 2-fold FeA ions.
symmetry, according to the vectorial notation of Wood.129 Termination FeB–S presents 0.5 ML of 2-fold S atoms, unsurprisingly also forming alternating rows in the [110] direction, alongside 0.25 ML of FeB with 3 dangling bonds, whereas the layer beneath contains 0.25 ML of 2-fold FeA ions.
Fig. 4 shows the relaxation of the interplanar distances, which was calculated as 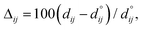 where dij is the separation between the relaxed i and j = i + 1 layers and
where dij is the separation between the relaxed i and j = i + 1 layers and 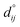 is the separation for the equivalent planes in the bulk.130 Following the geometry optimisation of both terminations, we found a relaxation behaviour that was increasingly attenuated towards the bulk. Each pair of layers FeA-i and FeB–S-j that were allowed to relax showed a preference to move together in alternating directions. For termination FeA, the protruding twofold FeA-1 ions suffered a strong inward relaxation of 141%, recovering their bulk tetrahedral coordination, when they merged with the subsurface layer FeA-3 where 0.25 ML of fourfold FeA are located, see Fig. 3(a) and 4. The negatively charged subsurface plane FeB–S-2 experienced only a moderate 13% shift towards the bulk, as it was pulled electrostatically by the merged layer beneath containing a larger number of FeA ions and therefore more positive charge carriers than in the bulk. The outward displacement of 16% of the subsurface layer FeA-3 can also be rationalised in terms of the Coulomb attraction exerted by the plane FeB–S-2 above, which lies closer as a result of its inward relaxation. The subsurface layer FeB–S-4 shifted by 9% towards the surface, to compensate for the expansion of the plane FeA-3 above, whereas FeA-5 preferred to reduce its interplanar distance to the closer FeB–S-6 layer that was not allowed to relax. The relaxation pattern of termination FeA for the Fe3S4(001) surface is in excellent agreement with the relaxation reported for the same termination of the magnetite Fe3O4(001) surface.116 Moreover, the contractions and expansions of the interplanar distances FeB–S-2 and FeA-3 are considerably larger for termination FeB–S that than for termination FeA, see Fig. 4. However, the inward shift of the topmost layer FeB–S-2 of termination FeB–S is only half of the contraction of the exposed layer FeA-1 of termination FeA.
is the separation for the equivalent planes in the bulk.130 Following the geometry optimisation of both terminations, we found a relaxation behaviour that was increasingly attenuated towards the bulk. Each pair of layers FeA-i and FeB–S-j that were allowed to relax showed a preference to move together in alternating directions. For termination FeA, the protruding twofold FeA-1 ions suffered a strong inward relaxation of 141%, recovering their bulk tetrahedral coordination, when they merged with the subsurface layer FeA-3 where 0.25 ML of fourfold FeA are located, see Fig. 3(a) and 4. The negatively charged subsurface plane FeB–S-2 experienced only a moderate 13% shift towards the bulk, as it was pulled electrostatically by the merged layer beneath containing a larger number of FeA ions and therefore more positive charge carriers than in the bulk. The outward displacement of 16% of the subsurface layer FeA-3 can also be rationalised in terms of the Coulomb attraction exerted by the plane FeB–S-2 above, which lies closer as a result of its inward relaxation. The subsurface layer FeB–S-4 shifted by 9% towards the surface, to compensate for the expansion of the plane FeA-3 above, whereas FeA-5 preferred to reduce its interplanar distance to the closer FeB–S-6 layer that was not allowed to relax. The relaxation pattern of termination FeA for the Fe3S4(001) surface is in excellent agreement with the relaxation reported for the same termination of the magnetite Fe3O4(001) surface.116 Moreover, the contractions and expansions of the interplanar distances FeB–S-2 and FeA-3 are considerably larger for termination FeB–S that than for termination FeA, see Fig. 4. However, the inward shift of the topmost layer FeB–S-2 of termination FeB–S is only half of the contraction of the exposed layer FeA-1 of termination FeA.
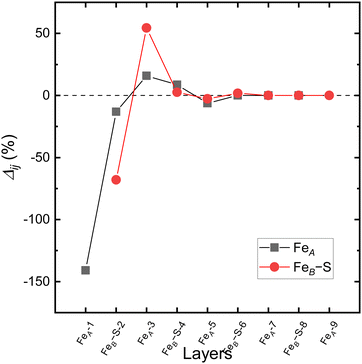 | ||
| Fig. 4 Relaxation (Δij) of the interplanar distance for the terminations (a) FeA and (b) FeB–S of the Fe3S4(001) surface in black and red, respectively. | ||
From our calculations of the surface energies before and after geometry optimisation, we have found that termination FeA is the most stable of the Fe3S4(001) planes, see Table 2. The largest relaxation of R = 50.68% obtained for termination FeA is a testament of the strong inward displacement of the protruding FeA ion to the subsurface layer. We have calculated the atomic Bader charges, which are lower for the exposed FeA and S ions than for their bulk counterparts. The (001) surface cations, FeA and FeB, are more ionic at termination FeA than at termination FeB–S, whereas we observed the opposite trend for the S anion. We also found an increment by 0.068e− atom−1 in the positive charge of the FeB ions in termination FeA compared to their bulk values. The magnetic moments calculated for all the under-coordinated atoms are larger in termination FeA than in termination FeB–S. Our calculations only predict larger magnetic moments than in the bulk for the FeB ions with dangling bonds in both terminations, FeA and FeB–S, and for the exposed S atoms in the termination FeA. In contrast to the bulk, we found that the charges and magnetic moments are larger for the exposed FeB cations than for the FeA ions for the two terminations considered in this study. We also noted that the small magnetic moments of the S atoms, which are aligned parallel to the FeA ions in the bulk, prefer to align parallel to the FeB cations in both terminations of the Fe3S4(001) surface. The work function indicates that termination FeA is marginally less reactive, by 0.055 eV, than termination FeB–S, which can provide more easily the loosest held electron required for the catalytic formation of H2C2O4. From here, we do not consider the FeB–S termination for further analysis due to its large relaxed surface energy, which makes it unlikely to be expressed in the crystal morphology of Fe3S4.
| Termination | FeA | FeB–S |
|---|---|---|
| γ u (meV Å−2) | 66.3 | 118.7 |
| γ r (meV Å−2) | 32.7 | 75.2 |
| R (%) | 50.68 | 36.69 |
| q(FeA) (e− atom−1) | 1.187 | 1.004 |
| q(FeB) (e− atom−1) | 1.257 | 1.022 |
| q(S) (e− atom−1) | −0.845 | −0.919 |
| m s(FeA) (μB atom−1) | −3.858 | −3.679 |
| m s(FeB) (μB atom−1) | 4.040 | 3.713 |
| m s(S) (μB atom−1) | 0.318 | 0.139 |
| Φ (eV) | 5.613 | 5.558 |
3.3. Partially oxidised Fe3S4(001) surface
We next analysed the relative stabilities of termination FeA of the Fe3S4(001) surface containing different coverages of oxygen as a function of the ratio of the partial pressures of H2O and H2S and temperature. We have successfully used these ab initio thermodynamic techniques previously to model the oxidation115 and hydrogenation78 of cobalt, the hydration of platinum85 and the redox behaviour of Fe3O4.116 We have calculated several coverages, by replacing in turn each of the S atoms with dangling bonds by O atoms. There is strong experimental evidence, backed up by calculations, that different iron and nickel sulfide phases, including Fe3S4,61,62 troilite (hexagonal FeS),131 pyrrhotite (hexagonal Fe1−xS),68,132 polydymite (Ni3S4)68 and violarite (FeNi2S4)68 oxidise partially and easily when they are in contact with water, forming catalytically active core–shell sulfide–oxide nanoparticles. The dimension of our computational slab allows the substitution of up to eight S atoms from termination FeA of the Fe3S4(001) surface. We have considered several distributions of the S and O atoms for each O coverage and used eqn (6) to calculate their surface free energies. The atomic configurations with the lowest surface free energies for each ratio of the two anions were selected to build the surface phase diagram. The surface free energies for each O coverage are represented by non-planar potential energy surfaces that intersect each other at specific temperatures and ratios of partial pressures of H2O and H2S, as shown in a bird's eye view in Fig. SI2 (ESI†). The curves formed where two potential energy surfaces cross correspond to the conditions required to modify the extent of the partial oxidation of the Fe3S4(001) surface. However, the most convenient way to depict and analyse this type of diagram is by making a bi-dimensional projection along the surface free energy axis onto the plane formed by the temperature and ratio of partial pressures of H2O and H2S, see Fig. 5(a). The surface phase diagram shows that termination FeA of the Fe3S4(001) surface requires temperatures above 230 K and a ratio of partial pressures of H2O and H2S below 100 to remain pristine. The lowest possible oxygen coverage of C = 0.98 O nm−2 is achieved for a maximum temperature of 300 K and a minimum ratio of partial pressures of H2O and H2S of 102.2. The coverages 2.93 and 3.90 O nm−2, with very limited ranges of stabilities and equivalent to three and four O atoms, respectively, appear at higher temperatures and higher ratio of partial pressures of H2O and H2S than the 0.98 O nm−2 coverage. The surface is capable of accommodating five O atoms, i.e. a coverage of 4.88 O nm−2 if the temperature is increased up to 530 K for a ratio of partial pressures of H2O and H2S smaller than 105.5. Fig. 5(b) displays this coverage of O atoms, which is consistent with a 62.5% partial oxidation, and is in good agreement with our previous work on FeNi2S4, where we found that 75% of the surface S could be replaced by O.68 Our results for the Fe3S4(001) surface suggest that a coverage of C = 4.88 O nm−2 has a relatively wide range of stabilities between 300 and 530 K when H2O is the predominant gas. For comparison, FeNi2S4 suffers spontaneous surface oxidation when it is calcined at 473 K in air or moisture.68 The coverage is expanded to 6.83 O nm−2, or seven O atoms, if the ratio of partial pressures of H2O and H2S is increased by a further 100.5 with respect to C = 4.88 O nm−2 and the temperature does not exceed 600 K. The full coverage of C = 7.80 O nm−2 only becomes thermodynamically favourable for a temperature and ratio of partial pressures of H2O and H2S larger than the values required for the incorporation of seven O atoms in our surface. Coverages C = 1.95 and 5.85 O nm−2, corresponding to two and six O atoms, respectively, are not accessible, as they are the least energetically stable partially oxidised Fe3S4(001) surface slab models within the conditions of pressure and temperature of our phase diagram.The STM images of both the pristine termination FeA of the Fe3S4(001) surface and with an oxygen coverage of C = 4.88 O nm−2 are represented in Fig. 6. The negative sample bias of −2.5 eV used to generate these STM images indicates that the electrons hop from the valence band to the probe tip, as expected for the half-metal properties predicted in the DOS for the bulk of Fe3S4. The S atoms appear as the brightest spots in the pristine and oxidised surfaces, whereas the cations are not well resolved. The O atoms can be identified in the oxidised surface, but they are less bright and smaller than the S anions, in agreement with their smaller ionic radius. The pristine surface displays a pattern of well-ordered arrays of S atoms along the [1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] direction, which is lost after oxidation.
0] direction, which is lost after oxidation.
To provide additional insight into the Fe3S4(001) surface, we have also analysed its thermodynamic stability, electronic and magnetic properties, as well as the surface reactivity as a function of the oxygen coverage. The surface free energy (σ) at 0 K, which quantifies the work needed to create the surface of a material and indicates its stability, increases gradually with the oxygen coverage, indicating that partially oxidising the Fe3S4(001) facet is an energetically unfavourable process, see Fig. 7(a). Our calculations suggest that the surface free energy increases relatively rapidly for coverages from 0.00 O nm−2 < C < 1.95 O nm−2 and especially for 4.88 O nm−2 < C < 5.85 O nm−2 and 6.83 O nm−2 < C < 7.80 O nm−2. The surface free energy barely changes for the coverages 2.93 and 3.90 O nm−2, explaining the narrow range of conditions which need to be controlled precisely to develop these particular partial degrees of oxidation. Interestingly, the partially oxidised surface with a coverage of 6.83 O nm−2 is approximately 13 meV Å−2 more stable than the facet with C = 5.85 O nm−2. The atomic charges and magnetic moments do not change noticeably and remain fairly constant for any oxygen coverage, with the exception of the smaller negative charge of the S atom for C = 6.83 O nm−2 as shown in Fig. 7(b) and (c). The work function shows two minima at the coverages C = 1.95 and 5.85 O nm−2, suggesting that these partial degrees of oxidation make the Fe3S4(001) surface considerably more reactive, see Fig. 7(d).
3.4. Molecular adsorptions on the partially oxidised Fe3S4(001) surface
We have investigated the interaction of the single molecules CO2 and H2O on the Fe3S4(001) surface with a coverage 4.88 O nm−2, which from hereon is the surface model of our catalyst. In order to simplify the notation used in this paper, we will refer to the Fe3S4(001) surface with a 62.5% degree of partial oxidation as “62.5O–Fe3S4(001).” We have assessed the effect of these molecular adsorptions on the surface free energy, charge transfer, atomic magnetic moment and work function of the 62.5O–Fe3S4(001) surface. We also discuss the geometries of the most favourable adsorption modes and the shifts of the fundamental scaled vibrational modes of the adsorbates. Fig. 5(b) shows the four adsorption sites investigated in this study, including atop the (i) FeA, (ii) FeB, (iii) S and (iv) O atoms.
Table 3 lists the calculated bond distances (d), bond angles (∠) as well as the harmonic (unscaled) and scaled asymmetric stretching (νasym), symmetric stretching (νsym) and bending (δ) fundamental vibrational modes for the CO2 and H2O adsorbates, which we have used to benchmark our computational SCAN-D2 setup. Our calculations indicate that we have obtained, up to the second decimal, the correct equilibrium bond distances for the CO2 and H2O molecules compared to the experimental values.133,134 The bond angle of 180° predicted for the CO2 molecule is in perfect agreement with the value inferred from electronic spectroscopy,133 whereas the bond angle calculated for the H2O molecule is only slightly overestimated with respect to experiment.134 Despite their different point groups, i.e. C2v for H2O and D∞h for CO2, both molecules are characterised by only three fundamental vibrational modes. Compared to previous reports, our calculated asymmetric stretching, symmetric stretching and bending harmonic vibrational modes are red-shifted for CO2133 and H2O,135,136 although the computational description is better for the former adsorbate than for the latter. The smallest deviation from the experimental value was calculated for the bending mode of CO2 and the largest difference was calculated for the asymmetric stretching mode of H2O, which were overestimated by 2 and 167 cm−1, respectively. The discrepancies with experiment are larger for H2O than for CO2 due to the larger anharmonicity of the vibrations for the hydrogen-containing bonds with respect to the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonds. Our harmonic vibrational frequencies are calculated as the second derivative of the potential energy with respect to the atomic positions in the vicinity of the minimum of the well. This section of the potential energy surface shows quadratic behaviour, leading to harmonic vibrational energy levels that are equally separated. However, experimental fundamental modes represent the transition between the ground state and the first state vibrational energy levels of an anharmonic potential energy surface. We have also determined the empirical scaling factors needed to convert our harmonic frequencies calculated for the isolated molecules into anharmonic vibrational modes, which can be compared directly with experiment.137–141 The scaling factor (c) was estimated as
O bonds. Our harmonic vibrational frequencies are calculated as the second derivative of the potential energy with respect to the atomic positions in the vicinity of the minimum of the well. This section of the potential energy surface shows quadratic behaviour, leading to harmonic vibrational energy levels that are equally separated. However, experimental fundamental modes represent the transition between the ground state and the first state vibrational energy levels of an anharmonic potential energy surface. We have also determined the empirical scaling factors needed to convert our harmonic frequencies calculated for the isolated molecules into anharmonic vibrational modes, which can be compared directly with experiment.137–141 The scaling factor (c) was estimated as
 | (8) |
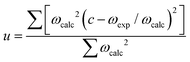 | (9) |
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) and d(H–O)], bond angles [∠(O
O) and d(H–O)], bond angles [∠(O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) and ∠(H–O–H)] and wavenumbers for the fundamental vibrational modes for the isolated CO2 and H2O molecules, respectively. The presented harmonic vibrational modes, both unscaled and scaled, are the asymmetric stretching (νasym), symmetric stretching (νsym) and bending (δ) modes for the O
O) and ∠(H–O–H)] and wavenumbers for the fundamental vibrational modes for the isolated CO2 and H2O molecules, respectively. The presented harmonic vibrational modes, both unscaled and scaled, are the asymmetric stretching (νasym), symmetric stretching (νsym) and bending (δ) modes for the O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O and H–O–H groups in the CO2 and H2O molecules, respectively
O and H–O–H groups in the CO2 and H2O molecules, respectively
| CO2 | H2O | ||
|---|---|---|---|
| d (Å) | Calculated | 1.165 | 0.964 |
| Experimental | 1.162 (ref. 133) | 0.958 (ref. 134) | |
| ∠ (°) | Calculated | 180.00 | 105.09 |
| Experimental | 180.00 (ref. 133) | 104.48 (ref. 134) | |
| ν asym (cm−1) | Unscaled | 2447 | 3923 |
| Scaled | 2363 | 3770 | |
| Experimental | 2349 (ref. 133) | 3756 (ref. 135) | |
| ν sym (cm−1) | Unscaled | 1366 | 3807 |
| Scaled | 1319 | 3658 | |
| Experimental | 1333 (ref. 133) | 3657 (ref. 136) | |
| δ (cm−1) | Unscaled | 669 | 1623 |
| Scaled | 646 | 1560 | |
| Experimental | 667 (ref. 133) | 1595 (ref. 136) |
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) = 130°.58,59,76,111,142–146 To characterise the adsorption configurations of our CO2 molecule, we have borrowed the notation widely used in organometallics to describe the bonding and structural types of metal–CO2 complexes, which is based on the hapticity of the ligand (μn) and the number of surface atoms (m) it can bridge (ηm).147–149 We approached the bent CO2 molecule in the μ3–η3 configuration, with both the C2 rotational axis and the vertical mirror plane σv perpendicular to the surface, i.e. with the C atom coordinating the exposed O or S atoms of the catalyst and the molecular O atoms bonding the Fe cations with dangling bonds. We have also considered the initial η1-O adsorption modes, where the symmetry elements C2 and σv of the adsorbate lie parallel and perpendicular, respectively, to the surface and the molecular O atom is interacting with the under-coordinated FeA or FeB ions. We placed the CO2 molecule at 1.8 Å from the partially oxidised surface of the thiospinel before allowing the atomic positions of the interface to relax.
O) = 130°.58,59,76,111,142–146 To characterise the adsorption configurations of our CO2 molecule, we have borrowed the notation widely used in organometallics to describe the bonding and structural types of metal–CO2 complexes, which is based on the hapticity of the ligand (μn) and the number of surface atoms (m) it can bridge (ηm).147–149 We approached the bent CO2 molecule in the μ3–η3 configuration, with both the C2 rotational axis and the vertical mirror plane σv perpendicular to the surface, i.e. with the C atom coordinating the exposed O or S atoms of the catalyst and the molecular O atoms bonding the Fe cations with dangling bonds. We have also considered the initial η1-O adsorption modes, where the symmetry elements C2 and σv of the adsorbate lie parallel and perpendicular, respectively, to the surface and the molecular O atom is interacting with the under-coordinated FeA or FeB ions. We placed the CO2 molecule at 1.8 Å from the partially oxidised surface of the thiospinel before allowing the atomic positions of the interface to relax.
Our calculations indicate that the CO2 molecule energetically prefers to interact molecularly with the O ion of the 62.5O–Fe3S4(001) surface in the μ3–η3 configuration, where it releases 0.746 eV, see Table 4 and Fig. 8(a). We also found evidence that the CO2 molecule binds exothermically to the FeA ion in the end-on η1–O configuration, with an adsorption energy Eads = −0.188 eV, which is less favourable than at the O site. Despite starting in the μ3–η3 configuration, the optimised structure of the adsorption of CO2 on the S site is the side-on μ2–η2–(C,O) mode, which is a slightly endothermic process requiring 0.016 eV. The η1–O interaction configuration with the exposed FeB atoms of the 62.5O–Fe3S4(001) surface displays the largest positive energy at Eads = 0.589 eV. The trend of binding energies on the anion sites can be rationalised in terms of the number of interactions that the CO2 molecule forms with the surface, i.e. three in the μ3–η3 configuration on the most exothermic O position, and two in the μ2–η2–(C,O) mode on the S atom. However, the trend of the adsorption strength on the cation sites depends on their total number of dangling bonds, i.e. two and one for the FeA and FeB atoms, respectively. Quesne and collaborators reported that chemisorption of the activated CO2 molecule on the surfaces of transition metal carbides occurs either directly, spontaneously and barrierless, or via a linearly physisorbed intermediate with a small energy barrier.150 Both the chemisorption and physisorption processes of CO2 on the surfaces of transition metal carbides are exothermic, with the former releasing more energy than the latter.150 Thus, regardless of the adsorption mechanism of CO2 on the partially oxidised 62.5O–Fe3S4(001) surface, we expect this process to take place on the O site, given its relatively large exothermic adsorption energy of −0.746 eV.
| Adsorption site | O | S | FeA | FeB |
|---|---|---|---|---|
| Structural type | μ 3–η3 | μ 2–η2–(C,O) | η 1–O | η 1–O |
| E ads (eV) | −0.746 | 0.016 | −0.188 | 0.589 |
| d(Omol–Fe) (Å) | 2.047 | 1.997 | 2.308 | 2.157 |
| d(C–Osurf) (Å) | 1.353 | — | — | — |
| d(C–Ssurf) (Å) | — | 1.899 | — | — |
d(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Omol) (Å) Omol) (Å) |
1.277 | 1.255 | 1.171 | 1.177 |
∠(O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) (°) O) (°) |
127.98 | 130.47 | 177.46 | 172.67 |
ν
asym(O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C = O) (cm−1) C = O) (cm−1) |
1520 | 1690 | 2329 | 2272 |
ν
sym(O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) (cm−1) O) (cm−1) |
1225 | 1088 | 1297 | 1278 |
δ(O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) (cm−1) O) (cm−1) |
795 | 671 | 581 | 594 |
| Δq (e−) | −0.209 | −0.537 | 0.003 | 0.003 |
| Φ (eV) | 5.172 | 5.687 | 4.662 | 4.221 |
| σ (meV Å−2) | 65.1 | 72.5 | 70.5 | 78.1 |
The interactions have a noticeable impact on the geometry of the interface, the vibrational properties of the CO2 molecule, as well as on the electronic properties and thermodynamic stability of the partially oxidised surface of our catalyst. The largest interfacial O–Fe distances, with the values d = 2.308 and 2.157 Å were calculated for the η1–O structures on the FeA and FeB sites, respectively, indicating that the only coordination bond for these adsorption modes is weak. The CO2 molecule is more strongly attached to the anion sites, and particularly to the surface O atom, since the distances for both the interfacial secondary O–Fe and main C–S (C–O) coordination bonds are the smallest overall. The intramolecular C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond distances, which experience minor elongations for the η1–O interactions with the two types of Fe cation sites, are stretched by 0.090 and 0.112 Å for the μ3–η3 adsorption on the O and μ2–η2–(C,O) configuration on the S positions, respectively. Despite introducing a pre-activated bent CO2 molecule, which remained in this geometry on the anion sites during geometry optimisation, we observed that the adsorbed molecule became approximately linear on the cation positions, similar to the molecule in its isolated state. This has also been found in other iron sulfide and oxide catalytic materials, where a pre-activated molecule is introduced but allowed to relax unconstrainedly during geometry optimisation.58,60,111,146
O bond distances, which experience minor elongations for the η1–O interactions with the two types of Fe cation sites, are stretched by 0.090 and 0.112 Å for the μ3–η3 adsorption on the O and μ2–η2–(C,O) configuration on the S positions, respectively. Despite introducing a pre-activated bent CO2 molecule, which remained in this geometry on the anion sites during geometry optimisation, we observed that the adsorbed molecule became approximately linear on the cation positions, similar to the molecule in its isolated state. This has also been found in other iron sulfide and oxide catalytic materials, where a pre-activated molecule is introduced but allowed to relax unconstrainedly during geometry optimisation.58,60,111,146
The changes observed in the intramolecular C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond distances are directly proportional to the red-shift of the asymmetric stretching vibrational modes compared to the isolated adsorbate, with the smallest value of 1520 cm−1 obtained for the ground state μ3–η3 binding configuration on the surface O site. Our results suggest that the variations in the symmetric stretching and average bending vibrational modes cannot be rationalised in terms of the reduction of the intramolecular C
O bond distances are directly proportional to the red-shift of the asymmetric stretching vibrational modes compared to the isolated adsorbate, with the smallest value of 1520 cm−1 obtained for the ground state μ3–η3 binding configuration on the surface O site. Our results suggest that the variations in the symmetric stretching and average bending vibrational modes cannot be rationalised in terms of the reduction of the intramolecular C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond length. As expected, the symmetric stretching vibrational modes for the CO2 molecule adsorbed on the anion sites are smaller than on the cation positions, but the largest wavenumbers at each type of site were calculated for the most stable adsorption modes on the O and FeA positions. The interaction of CO2 with the surface O and S atoms leads to a blue-shift of the average bending vibrational mode with regard to the isolated adsorbate, whereas the η1–O coordination to the Fe sites causes a red-shift. Table SI1 (ESI†) summarises both the unscaled and scaled vibrational frequencies calculated for the adsorbed CO2 molecule.
O bond length. As expected, the symmetric stretching vibrational modes for the CO2 molecule adsorbed on the anion sites are smaller than on the cation positions, but the largest wavenumbers at each type of site were calculated for the most stable adsorption modes on the O and FeA positions. The interaction of CO2 with the surface O and S atoms leads to a blue-shift of the average bending vibrational mode with regard to the isolated adsorbate, whereas the η1–O coordination to the Fe sites causes a red-shift. Table SI1 (ESI†) summarises both the unscaled and scaled vibrational frequencies calculated for the adsorbed CO2 molecule.
The charge transfers denote that the cation sites, which are deficient in electrons, receive a minor charge Δq = 0.03e− from the adsorbate. However, the electron-rich O and S positions donate −0.209 and −0.537e−, respectively, to the σ* antibonding molecular orbital of the CO2 molecule, which weakens the intramolecular C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond, forcing a bent configuration. The adsorption of the CO2 molecule reduces the work function, which makes the 62.5O–Fe3S4(001) surface of our catalyst more reactive, except for the μ2–η2–(C,O) interaction with the S site. The lowest work function values Φ = 4.662 and 4.221 eV required to remove the loosest held electron were predicted when the adsorbate binds the FeA and FeB sites, respectively, as the surfaces have increased marginally their electron density after adsorption of CO2. The exothermic interactions of a single CO2 molecule enhance the thermodynamic stability of our 62.5O–Fe3S4(001) surface, with the lowest value of the surface free energy σ = 65.087 meV Å−2 computed for the μ3–η3 adsorption on the O site.
O bond, forcing a bent configuration. The adsorption of the CO2 molecule reduces the work function, which makes the 62.5O–Fe3S4(001) surface of our catalyst more reactive, except for the μ2–η2–(C,O) interaction with the S site. The lowest work function values Φ = 4.662 and 4.221 eV required to remove the loosest held electron were predicted when the adsorbate binds the FeA and FeB sites, respectively, as the surfaces have increased marginally their electron density after adsorption of CO2. The exothermic interactions of a single CO2 molecule enhance the thermodynamic stability of our 62.5O–Fe3S4(001) surface, with the lowest value of the surface free energy σ = 65.087 meV Å−2 computed for the μ3–η3 adsorption on the O site.
Previous studies have shown that the (001) and (111) surfaces of the thiospinels Fe3S458,111 and FeNi2S476 are unable to activate the CO2 molecule, which only remains physisorbed. Among the pure sulfides, the (111) surface of mackinawite (tetragonal FeS) is the only catalyst able to dissociate a chemically activated CO2 molecule into stable fragments.111,146 The Fe3O4(001) and (111) surfaces are also capable of strongly chemisorbing the adsorbate, but the dissociation reaction has large activation energies, while the CO and O fragments are at least 1.5 eV less stable than the CO2 molecule.111 To date, the catalytic activity towards the reduction of bicarbonate has been reported for the major surfaces of the partially oxidised sulfides Fe3S4,58,62 hexagonal Fe1−xS,68,132 Ni3S468 and FeNi2S4,68 with the latter described as the most efficacious system due to the synergism between Fe and Ni and the O content. Our DFT calculations show that the activation of the adsorbed CO2 molecule can be enhanced via partial oxidation of the least reactive Fe3S4(001) surface.
Table 5 lists the exothermic adsorption energies calculated for H2O, which are clearly more favourable than for the interaction of the CO2 molecule with the 62.5O–Fe3S4(001) surface. The dissociative adsorption modes release 0.507 and 0.219 eV less than the molecular binding configurations at the (FeA, FeA) and FeB sites, respectively, suggesting that H2O prefers to remain undissociated at the surface of our catalyst. The order of decreasing stabilities are Eads (FeA, FeA) < Eads (FeA) ≪ Eads (FeB) and Eads (FeA, FeA) ≪ Eads (FeB) for the molecular and dissociative binding modes, respectively, showing that the adsorption energies have a strong dependence on the type of Fe site. The trend of adsorption energies can be explained in terms of the total number of dangling bonds of the cation sites. The most stable FeA, FeA binding site with the μ4–η4 configuration has a total of three dangling bonds, see Fig. 8(b), whereas the FeA and FeB sites with the μ3–η3 structure have two and one dangling bonds, respectively.
| Adsorption site | FeA | FeA, FeA | FeB | ||
|---|---|---|---|---|---|
| Type | Molecular | Molecular | Dissociative | Molecular | Dissociative |
| Structural type | μ 3–η3 | μ 4–η4 | μ 3–η3 | μ 3–η3 | μ 3–η3 |
| E ads (eV) | −1.094 | −1.318 | −0.811 | −0.510 | −0.291 |
| d(Omol–Fe) (Å) | 2.151 | 2.301 | 2.060 | 2.089 | 1.909 |
| d(H1–Osurf) (Å) | 2.436 | 2.800 | 2.704 | — | — |
| d(H2–Osurf) (Å) | — | — | 0.980 | 1.466 | 1.023 |
| d(H1–S) (Å) | — | — | — | 2.599 | 2.753 |
| d(H2–S) (Å) | 2.242 | 1.963 | 2.650 | — | — |
| d(H1–Omol) (Å) | 0.981 | 0.977 | 0.973 | 0.979 | 0.974 |
| d(H2–Omol) (Å) | 1.001 | 1.044 | 2.728 | 1.069 | 1.639 |
| ∠(H–O–H) (°) | 107.73 | 106.65 | 175.77 | 106.77 | 110.15 |
| ν asym(H–O–H) (cm−1) | 3461 | 3549 | 3602 | 3511 | 3578 |
| ν sym(H–O–H) (cm−1) | 3053 | 2339 | 3356 | 2003 | 2585 |
| δ(H–O–H) (cm−1) | 1514 | 1468 | 807 | 1514 | 904 |
| Δq (e−) | −0.005 | −0.032 | 0.020 | 0.010 | 0.041 |
| Φ (eV) | 5.660 | 4.996 | 5.504 | 5.623 | 5.405 |
| σ (meV Å−2) | 61.7 | 59.5 | 64.5 | 67.4 | 69.5 |
The average interfacial O–Fe binding distances for H2O, which are marginally smaller than in the interaction of CO2, are inversely proportional to the adsorption energies. The smallest distances d(Omol–Fe) = 1.909 and 2.060 Å were calculated for the thermodynamically least stable dissociative adsorptions on the FeB and (FeA, FeA) sites, respectively, as the OH group is a better ligand than H2O. Our calculations indicate that the molecular and dissociated H2O molecules are able to form hydrogen-bonds with the surface O and S atoms. The interfacial hydrogen-bonds with S are stronger than with O for the interactions with the FeA and (FeA, FeA) sites, as evidenced by the H–S distances, which are smaller than the H–Osurf lengths. We also found that the hydrogen-bond lengths with the surface O atoms are directly proportional to the adsorption energies for the molecularly adsorbed H2O molecule, with the largest value d(H–O) = 2.800 Å calculated for the ground state μ4–η4 adsorption mode. However, the opposite effect of the binding energies was observed for the hydrogen-bond lengths with the S atoms, with the smallest value d(H–S) = 1.963 Å obtained for the most stable μ4–η4 binding configuration. The H–Osurf distance of 2.704 Å suggests that the OH group adsorbed on the (FeA, FeA) site in the μ3–η3 structure is able to form a hydrogen-bond with the surface, which is not observed for the dissociative adsorption mode on the FeB site. Furthermore, the dissociated H atom prefers to sit slightly closer at 0.043 Å to the surface O atom for the interaction with the (FeA, FeA) site than for the FeB site, in agreement with their relative adsorption energies. The adsorption of H2O induces minor changes on the intramolecular H–O distances, which are between 0.009 and 0.105 Å larger for the two types of adsorption modes than in the isolated adsorbate. Our calculations show that the dissociated H atom diffuses 1.089 Å further away from the O of the OH group for the interaction with the most stable (FeA, FeA) site than with the least favourable FeB position. Note that we did not find evidence of a dissociated H atom binding to a nearby surface S atom. The intramolecular bond angle is less sensitive to adsorption of H2O than CO2, with the largest value ∠ = 107.73° calculated for the molecular μ3–η3 adsorption on the FeA site. However, this geometrical descriptor can be used to discriminate the dissociative from the molecular adsorption modes of H2O, as the intramolecular bond angle values are typically larger for the former than for the latter.
The three fundamental vibrational modes become smaller as a result of the molecular and dissociative adsorption of H2O. The asymmetric stretching vibrational mode is below 3549 cm−1 for the molecular adsorption configurations, whereas it lies above 3578 cm−1 for the dissociated OH groups. The symmetric stretching vibrational modes, which appear in a wide range of values between 3356 and 2003 cm−1, show no clear correlation with any of the properties discussed. The bending vibrational modes were estimated between 1514 and 1468 cm−1 for the molecular adsorption modes and the calculated values were smaller than 904 cm−1 for the dissociative binding configurations. Table SI2 (ESI†) displays both the harmonic and scaled vibrational modes observed for the adsorbed H2O molecule. We calculated only minor charge transfers, with the H2O molecule receiving no more than 0.032e− for the most stable molecular adsorptions on the FeA and (FeA, FeA) sites. Our results indicate that, unlike the linear CO2 molecule, the activation and adsorption of the angular H2O species does not require charge density from the surface. The work functions are Φ ∼ 5.5 eV for all the adsorption modes, except for the molecular μ4–η4 binding configuration on the (FeA, FeA) site, which is around 0.5 eV smaller than the value for the 62.5O–Fe3S4(001) surface. The large reduction of the surface free energy after adsorption of the H2O molecule demonstrates that the 62.5O–Fe3S4(001) surface becomes more stable, even compared to the catalyst interacting with CO2. In line with our results, previous calculations have also shown that the molecular adsorption of water is energetically preferred over the dissociative mode for CaO,156 CaF2156,165 and the Fe3S4(001) surface.161 Moreover, the partially oxidised 62.5O–Fe3S4(001) surface also displays an improved activity towards the adsorption of H2O than the (001) facet of pure Fe3S4.
3.5 H2C2O4 formation on the partially oxidised Fe3S4(001) surface
We have examined three pathways for the catalytic conversion of CO2 and H2O into H2C2O4 on the 62.5O–Fe3S4(001) surface, see Fig. 9. Our selection of mechanisms, which describe the combination of the reactants into key intermediates that are transformed into the desired H2C2O4 and by-product O2, are discussed in terms of their structural, local electronic and vibrational properties. The Helmholtz free energies (ΔF), which are plotted at the representative temperature of 300 K, are referenced in our energy diagrams compared to the isolated reactants and the heterogeneous catalyst, i.e. two CO2 molecules, one H2O molecule and the 62.5O–Fe3S4(001) surface slab. Note that the vibrational frequencies of the adsorbed species were scaled by 0.9632, which is the average of the scaling factors calculated for the isolated CO2 and H2O molecules, before estimating the vibrational entropy of the adsorbed species, see Tables SI3 and SI4 (ESI†). For the purpose of comparison, the Helmholtz free energy profiles at 0 and 600 K are provided in Fig. SI3 and SI4 (ESI†). The first step, which is common to the three pathways, is the co-adsorption of the reactants to the surface of the catalyst. Note that the adsorbed species are indicated with the symbol *.![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) ∼ 1.28 Å, in agreement with the single molecule adsorption. The H2O species sits on the (FeA, FeA) site at approximately the same distance calculated for the most stable single molecule μ4–η4 adsorption, with the intramolecular distances and bond angle remaining relatively undisturbed. However, the surface S and O atoms forming the hydrogen-bonds are 0.120 Å further away and 0.262 Å closer to the H2O molecule, respectively, than in the ground state single molecule adsorption configuration. The charge analysis of the co-adsorption state indicates that the perpendicularly adsorbed CO2 molecule received 0.027e− less charge than in the case of the single molecule adsorption, which was compensated for by the identical electron density gained by the tilted species. On the other hand, the H2O adsorbate received only a negligible charge of Δq = 0.002e−, which is considerably less than in the case of the single molecule μ4–η4 adsorption. We attribute the smaller charges received by the H2O and perpendicular CO2 molecules to the fact that they share the same surface FeA ion.
O) ∼ 1.28 Å, in agreement with the single molecule adsorption. The H2O species sits on the (FeA, FeA) site at approximately the same distance calculated for the most stable single molecule μ4–η4 adsorption, with the intramolecular distances and bond angle remaining relatively undisturbed. However, the surface S and O atoms forming the hydrogen-bonds are 0.120 Å further away and 0.262 Å closer to the H2O molecule, respectively, than in the ground state single molecule adsorption configuration. The charge analysis of the co-adsorption state indicates that the perpendicularly adsorbed CO2 molecule received 0.027e− less charge than in the case of the single molecule adsorption, which was compensated for by the identical electron density gained by the tilted species. On the other hand, the H2O adsorbate received only a negligible charge of Δq = 0.002e−, which is considerably less than in the case of the single molecule μ4–η4 adsorption. We attribute the smaller charges received by the H2O and perpendicular CO2 molecules to the fact that they share the same surface FeA ion.
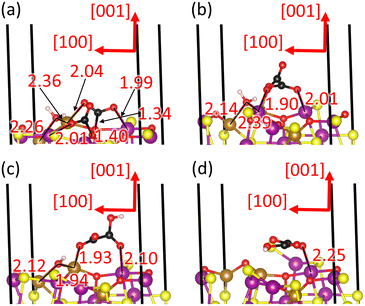
The oxalate pathway leads to the combination of the two CO2* molecules into the C2O4* intermediate, which is an endothermic process with a reaction free energy of 2.100 eV and a saddle point A at 3.296 eV, as shown in Fig. 9. The large free energy barrier of this process is required to break the strong covalent bonds within the adsorbed carbonate-like groups, leading to the C atoms moving to at least 3.0 Å away from the nearest surface O atoms, see Fig. 10(b). The product of this elementary step, which is the least stable intermediate, is a staggered C2O4* group with the dihedral angle ∠(O–C–C–O) = 66° and the point group of reduced symmetry D2d. The C2O4* species is anchored to the exposed Fe cations of the surface through three O atoms, with d(O–Fe) ∼ 2.0 Å, which is slightly smaller than for the co-adsorption state. The C–C bond distance is 1.539 Å for the C2O4* intermediate, whereas the intramolecular C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O distances and O
O distances and O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O angles do not change noticeably with respect to the previous state. The calculated Bader charges show that the C2O4* species draws −1.367e− from the surface, which is considerably larger than for two co-adsorbed CO2 molecules, explaining the low stability of this intermediate.
O angles do not change noticeably with respect to the previous state. The calculated Bader charges show that the C2O4* species draws −1.367e− from the surface, which is considerably larger than for two co-adsorbed CO2 molecules, explaining the low stability of this intermediate.
The C2O4* species accepts one H atom from the H2O molecule to form HC2O4* in state 4 of our energy diagram, see Fig. 9. The free energy released during this elementary step is 0.846 eV, but it requires 1.679 eV to cross the saddle point B. The protonated O atom, with the typical distance of 0.98 Å for the O–H bond, is the closest to the donor H2O molecule, belonging to the bidentate CO2 moiety in the previous state, as shown in Fig. 10(c). The dihedral angle becomes more orthogonal with ∠(O–C–C–O) = 81.82° after protonation, whereas the largest intramolecular distances of d(C–O) ∼1.31 Å were calculated in each molecular moiety for the protonated O and the O coordinating the surface Fe ion. The OH* fragment moves 0.442 Å closer to the FeA ion that is shared with the HC2O4*, as the basicity of the former increases and the latter decreases, compared to H2O* and C2O4* respectively. However, the shift of the OH* species happens at the cost of an increase in the H⋯S hydrogen bond-distance by 0.383 Å. The protonation reduces almost by half the charge of the HC2O4* intermediate to q = −0.704e− with respect to C2O4*, whereas the OH* is able to retain −0.650e− from the proton that it ceded.
Fig. 9 illustrates that the HC2O4* intermediate is capable of admitting a second proton from the OH* group, which is also an endothermic process with a reaction free energy of 2.202 eV and an activation free energy C of 4.027 eV. The protonation increases the symmetry of H2C2O4* to point group C2v, implying that the molecule becomes essentially flat with the dihedral angle ∠(O–C–C–O) = 164°, see Fig. 10(d). The intramolecular bond distances d(C–C) = 1.548 Å, d(C = O) ∼1.22 Å, d(H–O) ∼1.00 Å and d(C–OH) ∼ 1.341 Å and angle ∠(O–C–O) = 125.8° of H2C2O4* are very similar to the values calculated for the C2O4*. Our calculations suggest that H2C2O4* is still coordinating one FeA and two FeB, with the smallest Fe–O distance of 2.248 Å for the unprotonated O and the largest distances of 2.92 Å for the protonated O atoms. The O* species moves approximately 0.2 Å towards the bulk after losing its H atom. The transfer of the second proton quenches the negative charge of H2C2O4* to −0.037e−, whereas O* has −1.108e−, almost duplicating the electron density of OH* in the previous state.
In the final step, the surface releases one H2C2O4 and 0.5 O2 molecules, leaving the system ready for the next catalytic cycle. These desorptions are endothermic processes that require 0.477 eV. The final state is the overall highest in free energy in our energy diagram, lying 3.518 eV above the reactants. To calculate these energies, we modelled the isolated O2 molecule in the triplet state and the isolated H2C2O4 in the point group C2h, which are the electronic and structural ground states, respectively, of these species.
Fig. 9 depicts the protonation of the second CO2* species, which is an endothermic process with a reaction free energy of 1.547 eV and a saddle point E at 3.066 eV. We found that the structural properties of the two CO2H* species, such as the H–O and C–O bond distances and the O–C–O angle are very similar to the protonated group of the previous state, as shown in Fig. 11(b). However, our calculations show that each CO2H* group can only coordinate a single FeB cation via the unprotonated O atom at the slightly different distances of 2.058 and 2.245 Å. The two CO2H* species have a positive charge of ∼0.5e−, whereas the O* gains approximately half of one electron.
The combination of the two carboxylate groups to form the adsorbed H2C2O4* molecule is an endothermic process with a reaction free energy of 2.650 eV, which is 0.448 eV larger than the free energy required to transfer the second proton to the HC2O4* in the oxalate pathway, see Fig. 9. The free energy of the saddle point F is 3.998 eV for the formation of the C–C bond in the carboxylate pathway, whereas it is ∼0.7 eV smaller for the saddle point A in the oxalate pathway.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond distance is 1.28 Å for the CO3H* species and 1.300 and 1.233 Å for the O end coordinating the surface FeB and the free O end, respectively, of the CO2* molecule. The dissociated H* atom, which stays coordinated to the S atom that was part of the hydrogen-bond, diffuses to the subsurface layer to increase its stability. The incorporation of the OH group into the CO3H* species increases its negative charge to −0.672e− with respect to the value of −0.213e− for the CO2* molecule, whereas the subsurface H* atom becomes almost neutral with 0.053e−.
O bond distance is 1.28 Å for the CO3H* species and 1.300 and 1.233 Å for the O end coordinating the surface FeB and the free O end, respectively, of the CO2* molecule. The dissociated H* atom, which stays coordinated to the S atom that was part of the hydrogen-bond, diffuses to the subsurface layer to increase its stability. The incorporation of the OH group into the CO3H* species increases its negative charge to −0.672e− with respect to the value of −0.213e− for the CO2* molecule, whereas the subsurface H* atom becomes almost neutral with 0.053e−.
Fig. 9 depicts the protonation of the second CO2* molecule in our free energy profile. This elementary step releases −0.384 eV, which is the smallest exothermic free energy value reported in this study, and has a saddle point of 2.120 eV. The newly formed CO2H* species remains bound to a surface O anion at 1.295 Å and to a FeB ion at 1.755 Å through the molecular C and OH group, respectively, as shown in Fig. 11(d). Our calculations suggest that the intramolecular OH distance is 0.976 Å. However, we found that the proton diffusion only leads to negligible changes in the structure of the CO3H* species, including the length of the Fe–O and hydrogen-bonds with the surface and CO2H* intermediate, respectively. The protonation provides the CO2*H intermediate with a positive charge of 0.382e−, whereas CO3H* increases its negative charge by 0.038e−.
Finally, the coupling of the CO3H* and CO2H* species is an endothermic elementary step with a reaction free energy ΔF = 3.143 eV and the largest activation energy value of 5.177 eV calculated in this work, see Fig. 9.
4. Conclusions
We have used DFT methods to model the catalytic conversion of CO2 and H2O into H2C2O4 on the partially oxidised Fe3S4(001) surface. First, we have modelled the bulk phase of Fe3S4 and found that the structural, electronic and magnetic properties are in good agreement with previous reports. We have elucidated the relaxation patterns of the interplanar distances, as well as the values for the surface energies, atomic charges, atomic magnetic moments and work functions for the two reconstructed Tasker type 3 terminations of the Fe3S4(001) surface. The thermodynamically most stable facet, which terminates in two-fold FeA ions with symmetry, has the largest relaxation, work function, ionic character and magnetisation. We have predicted the phase diagram as a function of the ratio of partial pressures of H2O and H2S and temperature and found that the processes of replacing sequentially each S atom with dangling bonds by an O atom are endothermic. Only selected coverages of O are allowed in the Fe3S4(001) surface, with 62.5% of partial oxidation becoming prominent at the typical experimental conditions in which samples of the catalyst are calcined.
symmetry, has the largest relaxation, work function, ionic character and magnetisation. We have predicted the phase diagram as a function of the ratio of partial pressures of H2O and H2S and temperature and found that the processes of replacing sequentially each S atom with dangling bonds by an O atom are endothermic. Only selected coverages of O are allowed in the Fe3S4(001) surface, with 62.5% of partial oxidation becoming prominent at the typical experimental conditions in which samples of the catalyst are calcined.
We have also reported the interaction between single molecules of CO2 and H2O and the Fe3S4(001) surface with 62.5% of partial oxidation. Adsorption at the O site, which is energetically preferred, bends and activates the CO2 molecule and the σ* antibonding molecular orbital receives electronic density from the partially oxidised Fe3S4(001) surface. The H2O molecule releases the largest adsorption energy when it coordinates two surface FeA cations and forms hydrogen-bonds with the exposed S and O anions, but no charge transfers were identified. The co-adsorption of two CO2 and one H2O molecule at nearby surface sites is also an exothermic process, although 2390 meV less favourable than the interaction of the single species.
We have calculated three minimum energy pathways for the formation of H2C2O4, where we have considered the formation of an oxalate, carboxylate or bicarbonate intermediate in the first elementary step. The energy profiles show that C2O4* and HC2O4* are particularly unstable intermediates, whose formation requires crossing saddle points of large energy barriers. However, the carboxylate CO2H* intermediate is the most stable species when it is co-adsorbed with CO2*, and to a lesser extent, with the bicarbonate CO3H*. The saddle points with the largest energies were observed for the coupling of the C–C bond, whereas the transfer of protons are the elementary steps with the smallest activation barriers. Our reaction mechanisms suggest that the energy released during the co-adsorption of the reactants is not enough to cross all the saddle points or to reach the final state. We would therefore argue that the feasibility of the conversion of CO2 into H2C2O4 depends strongly on the source of hydrogen and the reactivity of the surface. The high energy saddle points and intermediate species would become accessible if the catalytic process over the partially oxidised Fe3S4(001) surface is carried out within a continuous electrochemical cell with an appropriate voltage.
Future work will be focused on calculating the catalytic formation of pyruvic acid, which is an important intermediate in several metabolic pathways, on the partially oxidised surfaces of Fe3S4, including not only the stable (001) surface, but also more reactive surfaces such as the (111) plane. The reaction profiles for the conversion of CO2 into pyruvic acid will allow us to compare this process and interconnect it into the catalytic formation of acetic acid, formic acid and oxalic acid.
Conflicts of interest
The authors have no conflicts of interest to declare.Acknowledgements
Via our membership of the UK's HEC Materials Chemistry Consortium, which is funded by EPSRC (EP/L000202/1 and EP/R029431/1), this work made use of the ARCHER2 UK National Supercomputing Service (https://www.archer2.ac.uk). This research was undertaken using the supercomputing facilities at Cardiff University operated by Advanced Research Computing at Cardiff (ARCCA) on behalf of the Cardiff Supercomputing Facility and the HPC Wales and Supercomputing Wales (SCW) projects. We acknowledge the support of the latter, which is part-funded by the European Regional Development Fund (ERDF) via the Welsh Government. Further work was undertaken on ARC4, part of the High-Performance Computing facilities at the University of Leeds, UK. All data are provided in full in the Results and Discussion section of this paper.References
- B. W. Strobel, Influence of vegetation on low-molecular-weight carboxylic acids in soil solution—a review, Geoderma, 2001, 99, 169–198 CrossRef CAS.
- W. Riemenschneider and M. Tanifuji, Ullmann's Encyclopedia of Industrial Chemistry, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany, 2011 Search PubMed.
- H. Sawada and T. Murakami, Kirk-Othmer Encyclopedia of Chemical Technology, Wiley, 2000 Search PubMed.
- F. Palmieri, A. Estoppey, G. L. House, A. Lohberger, S. Bindschedler, P. S. G. Chain and P. Junier, Advances in Applied Microbiology, Elsevier Inc., 1st edn, 2019, vol. 106, pp. 49–77 Search PubMed.
- D. Panias, M. Taxiarchou, I. Paspaliaris and A. Kontopoulos, Mechanisms of dissolution of iron oxides in aqueous oxalic acid solutions, Hydrometallurgy, 1996, 42, 257–265 CrossRef CAS.
- W. W. Frenier and F. B. Growcock, Mechanism of Iron Oxide Dissolution—A Review of Recent Literature, Corrosion, 1984, 40, 663–668 CrossRef CAS.
- E. Baumgartner, M. A. Blesa, H. Marinovich and A. J. G. Maroto, Heterogeneous electron transfer as a pathway in the dissolution of magnetite in oxalic acid solutions, Inorg. Chem., 1983, 22, 2224–2226 CrossRef CAS.
- S. O. Lee, T. Tran, B. H. Jung, S. J. Kim and M. J. Kim, Dissolution of iron oxide using oxalic acid, Hydrometallurgy, 2007, 87, 91–99 CrossRef CAS.
- B. Hong, G. Xue, X. Guo and L. Weng, Kinetic study of oxalic acid pretreatment of moso bamboo for textile fiber, Cellulose, 2013, 20, 645–653 CrossRef CAS.
- B. Hong, L. Chen, G. Xue, Q. Xie and F. Chen, Optimization of oxalic acid pretreatment of moso bamboo for textile fiber using response surface methodology, Cellulose, 2014, 21, 2157–2166 CrossRef CAS.
- D. Marković, J. Ašanin, T. Nunney, Ž. Radovanović, M. Radoičić, M. Mitrić, D. Mišić and M. Radetić, Broad Spectrum of Antimicrobial Activity of Cotton Fabric Modified with Oxalic Acid and CuO/Cu2O Nanoparticles, Fibers Polym., 2019, 20, 2317–2325 CrossRef.
- J. A. Krasowski and J. Marton, The Formation of Oxalic Acid During Bleaching of Kraft Pulp, J. Wood Chem. Technol., 1983, 3, 445–458 CrossRef CAS.
- A. Brolin, J. Gierer and Y. Zhang, On the selectivity of ozone delignification of softwood kraft pulps, Wood Sci. Technol., 1993, 27, 115–129 CAS.
- M. B. Roncero, J. F. Colom and T. Vidal, Why oxalic acid protects cellulose during ozone treatments?, Carbohydr. Polym., 2003, 52, 411–422 CrossRef.
- M. B. Roncero, J. F. Colom, T. Vidal and M. A. Queral, The Role of Oxalic Acid in the Ozone Bleaching Kinetics of an Xo-Kraft Pulp, J. Wood Chem. Technol., 2000, 20, 147–167 CrossRef CAS.
- G. Gardea-Hernández, R. Ibarra-Gómez, S. G. Flores-Gallardo, C. A. Hernández-Escobar, P. Pérez-Romo and E. A. Zaragoza-Contreras, Fast wood fiber esterification. I. Reaction with oxalic acid and cetyl alcohol, Carbohydr. Polym., 2008, 71, 1–8 CrossRef.
- L. Chen, J. Y. Zhu, C. Baez, P. Kitin and T. Elder, Highly thermal-stable and functional cellulose nanocrystals and nanofibrils produced using fully recyclable organic acids, Green Chem., 2016, 18, 3835–3843 RSC.
- D. Li, J. Henschen and M. Ek, Esterification and hydrolysis of cellulose using oxalic acid dihydrate in a solvent-free reaction suitable for preparation of surface-functionalised cellulose nanocrystals with high yield, Green Chem., 2017, 19, 5564–5567 RSC.
- R. Bharti, C. B. Reddy and P. Das, Oxalic Acid as Sustainable CO Source for Pyrrolone-Fused Benzosuberenes Synthesis through Palladium Catalyzed Carbonylative Cyclization, ChemistrySelect, 2017, 2, 4626–4629 CrossRef CAS.
- N. R. Guha, V. Thakur, D. Bhattacherjee, R. Bharti and P. Das, Supported Rhodium Nanoparticle-Catalyzed Intermolecular Regioselective Carbonylative Cyclization of Terminal Alkynes using Oxalic Acid as Sustainable C1 Source, Adv. Synth. Catal., 2016, 358, 3743–3747 CrossRef CAS.
- P. Langer, J. Wuckelt, M. Döring and R. Beckert, Reaction of Ambident Dianions with Oxalic Acid Dielectrophiles – Effect of the Heteroatoms of the Dinucleophile on the Regiochemistry of Cyclization, Eur. J. Org. Chem., 1998, 1467–1470 CrossRef CAS.
- E. Jorjani and M. Shahbazi, The production of rare earth elements group via tributyl phosphate extraction and precipitation stripping using oxalic acid, Arab. J. Chem., 2016, 9, S1532–S1539 CrossRef CAS.
- W. Zhang, A. Noble, B. Ji and Q. Li, Effects of contaminant metal ions on precipitation recovery of rare earth elements using oxalic acid, J. Rare Earths, 2022, 40, 482–490 CrossRef CAS.
- T. V. Hoogerstraete, B. Blanpain, T. Van Gerven and K. Binnemans, From NdFeB magnets towards the rare-earth oxides: a recycling process consuming only oxalic acid, RSC Adv., 2014, 4, 64099–64111 RSC.
- R. Chi and Z. Xu, A solution chemistry approach to the study of rare earth element precipitation by oxalic acid, Metall. Mater. Trans. B, 1999, 30, 189–195 CrossRef.
- M. Gürü, A. Y. Bilgesü and V. Pamuk, Production of oxalic acid from sugar beet molasses by formed nitrogen oxides, Bioresour. Technol., 2001, 77, 81–86 CrossRef.
- S. D. Deshpande and S. N. Vyas, Oxidation of Sugar to Oxalic Acid and Absorption of Oxides of Nitrogen to Sodium Nitrite, Ind. Eng. Chem. Prod. Res. Dev., 1979, 18, 69–71 CrossRef CAS.
- K. E. Richardson and N. E. Tolbert, Oxidation of Glyoxylic Acid to Oxalic Acid by Glycolic Acid Oxidase, J. Biol. Chem., 1961, 236, 1280–1284 CrossRef CAS PubMed.
- S. K. Dube, P. Vasudevan and B. L. Khandelwal, Oxalic acid manufacture, J. Chem. Technol. Biotechnol., 2007, 32, 909–919 CrossRef.
- T. Matsumoto, M. Sadakiyo, M. L. Ooi, S. Kitano, T. Yamamoto, S. Matsumura, K. Kato, T. Takeguchi and M. Yamauchi, CO2-Free Power Generation on an Iron Group Nanoalloy Catalyst via Selective Oxidation of Ethylene Glycol to Oxalic Acid in Alkaline Media, Sci. Rep., 2015, 4, 5620 CrossRef PubMed.
- T. Matsumoto, M. Sadakiyo, M. L. Ooi, T. Yamamoto, S. Matsumura, K. Kato, T. Takeguchi, N. Ozawa, M. Kubo and M. Yamauchi, Atomically mixed Fe-group nanoalloys: catalyst design for the selective electrooxidation of ethylene glycol to oxalic acid, Phys. Chem. Chem. Phys., 2015, 17, 11359–11366 RSC.
- F. Goodridge and G. Presland, The electrolytic reduction of carbon dioxide and monoxide for the production of carboxylic acids, J. Appl. Electrochem., 1984, 14, 791–796 CrossRef CAS.
- P. A. Nakata, Advances in our understanding of calcium oxalate crystal formation and function in plants, Plant Sci., 2003, 164, 901–909 CrossRef CAS.
- M. A. Webb, Cell-Mediated Crystallization of Calcium Oxalate in Plants, Plant Cell, 1999, 11, 751–761 CrossRef CAS PubMed.
- J. C. Yang and F. A. Loewus, Metabolic Conversion of l-Ascorbic Acid to Oxalic Acid in Oxalate-accumulating Plants, Plant Physiol., 1975, 56, 283–285 CrossRef CAS PubMed.
- M. V. Dutton and C. S. Evans, Oxalate production by fungi: its role in pathogenicity and ecology in the soil environment, Can. J. Microbiol., 1996, 42, 881–895 CrossRef CAS.
- J. A. L. Kan, M. W. Shaw and R. T. Grant-Downton, Botrytis species: relentless necrotrophic thugs or endophytes gone rogue?, Mol. Plant Pathol., 2014, 15, 957–961 CrossRef PubMed.
- J.-C. Arvieu, F. Leprince and C. Plassard, Release of oxalate and protons by ectomycorrhizal fungi in response to P-deficiency and calcium carbonate in nutrient solution, Ann. For. Sci., 2003, 60, 815–821 CrossRef CAS.
- R. Hamel, R. Levasseur and V. D. Appanna, Oxalic acid production and aluminum tolerance in Pseudomonas fluorescens, J. Inorg. Biochem., 1999, 76, 99–104 CrossRef CAS PubMed.
- P. A. Nakata, The oxalic acid biosynthetic activity of Burkholderia mallei is encoded by a single locus, Microbiol. Res., 2011, 166, 531–538 CrossRef CAS PubMed.
- P. A. Nakata and C. He, Oxalic acid biosynthesis is encoded by an operon in Burkholderia glumae, FEMS Microbiol. Lett., 2010, 304, 177–182 CrossRef CAS PubMed.
- D. Markovich and P. S. Aronson, Specificity and Regulation of Renal Sulfate Transporters, Annu. Rev. Physiol., 2007, 69, 361–375 CrossRef CAS PubMed.
- T. Wang, A. L. Egbert, T. Abbiati, P. S. Aronson and G. Giebisch, Mechanisms of stimulation of proximal tubule chloride transport by formate and oxalate, Am. J. Physiol. Physiol., 1996, 271, F446–F450 CrossRef CAS PubMed.
- S. Albrecht, H. Brandl and C. Schönfels, Human Oxalate—Really Just an End-Product of Metabolism?, Angew. Chem., Int. Ed. Engl., 1994, 33, 1780–1781 CrossRef.
- M. B. Rudnick, J. A. van Veen and W. de Boer, Oxalic acid: a signal molecule for fungus-feeding bacteria of the genus C ollimonas?, Environ. Microbiol. Rep., 2015, 7, 709–714 CrossRef CAS PubMed.
- L.-M. Zeng, J. Zhang, Y.-C. Han, L. Yang, M. Wu, D.-H. Jiang, W. Chen and G.-Q. Li, Degradation of oxalic acid by the mycoparasite Coniothyrium minitans plays an important role in interacting with Sclerotinia sclerotiorum, Environ. Microbiol., 2014, 16, 2591–2610 CrossRef CAS PubMed.
- Y. Han, H.-J. Joosten, W. Niu, Z. Zhao, P. S. Mariano, M. McCalman, J. van Kan, P. J. Schaap and D. Dunaway-Mariano, Oxaloacetate Hydrolase, the C–C Bond Lyase of Oxalate Secreting Fungi, J. Biol. Chem., 2007, 282, 9581–9590 CrossRef CAS PubMed.
- A. Mattevi, G. Obmolova, E. Schulze, K. Kalk, A. Westphal, A. de Kok and W. Hol, Atomic structure of the cubic core of the pyruvate dehydrogenase multienzyme complex, Science, 1992, 255, 1544–1550 CrossRef CAS PubMed.
- M. R. Mäkelä, K. Hildén and T. K. Lundell, Oxalate decarboxylase: Biotechnological update and prevalence of the enzyme in filamentous fungi, Appl. Microbiol. Biotechnol., 2010, 87, 801–814 CrossRef PubMed.
- C. Plassard and P. Fransson, Regulation of low-molecular weight organic acid production in fungi, Fungal Biol. Rev., 2009, 23, 30–39 CrossRef.
- J. M. Schuller, J. A. Birrell, H. Tanaka, T. Konuma, H. Wulfhorst, N. Cox, S. K. Schuller, J. Thiemann, W. Lubitz, P. Sétif, T. Ikegami, B. D. Engel, G. Kurisu and M. M. Nowaczyk, Structural adaptations of photosynthetic complex I enable ferredoxin-dependent electron transfer, Science, 2019, 363, 257–260 CrossRef CAS PubMed.
- G. Kurisu, M. Kusunoki, E. Katoh, T. Yamazaki, K. Teshima, Y. Onda, Y. Kimata-Ariga and T. Hase, Structure of the electron transfer complex between ferredoxin and ferredoxin-NAPD+ reductase, Nat. Struct. Biol., 2001, 8, 117–121 CrossRef CAS PubMed.
- A. Dey, T. Glaser, M. M. J. Couture, L. D. Eltis, R. H. Holm, B. Hedman, K. O. Hodgson and E. I. Solomon, Ligand K-Edge X-ray Absorption Spectroscopy of [Fe4S4] 1+, 2+, 3+ Clusters: Changes in Bonding and Electronic Relaxation upon Redox, J. Am. Chem. Soc., 2004, 126, 8320–8328 CrossRef CAS PubMed.
- R. H. Holm, P. Kennepohl and E. I. Solomon, Structural and Functional Aspects of Metal Sites in Biology, Chem. Rev., 1996, 96, 2239–2314 CrossRef CAS PubMed.
- P. Y.-T. Chen, B. Li, C. L. Drennan and S. J. Elliott, A Reverse TCA Cycle 2-Oxoacid:Ferredoxin Oxidoreductase that Makes C–C Bonds from CO2, Joule, 2019, 3, 595–611 CrossRef CAS PubMed.
- A. C. Brown and D. L. M. Suess, Controlling Substrate Binding to Fe4S4 Clusters through Remote Steric Effects, Inorg. Chem., 2019, 58, 5273–5280 CrossRef CAS PubMed.
- G. Li, B. Zhang, F. Yu, A. A. Novakova, M. S. Krivenkov, T. Y. Kiseleva, L. Chang, J. Rao, A. O. Polyakov, G. R. Blake, R. A. de Groot and T. T. M. Palstra, High-Purity Fe3S4 Greigite Microcrystals for Magnetic and Electrochemical Performance, Chem. Mater., 2014, 26, 5821–5829 CrossRef CAS.
- A. Roldan, N. Hollingsworth, A. Roffey, H.-U. Islam, J. B. M. Goodall, C. R. A. Catlow, J. A. Darr, W. Bras, G. Sankar, K. B. Holt, G. Hogarth and N. H. De Leeuw, Bio-inspired CO2 conversion by iron sulfide catalysts under sustainable conditions, Chem. Commun., 2015, 51, 7501–7504 RSC.
- D. Santos-Carballal, A. Roldan and N. H. de Leeuw, CO2 reduction to acetic acid on the greigite Fe3S4{111} surface, Faraday Discuss., 2021, 229, 35–49 RSC.
- A. Roldan and N. H. de Leeuw, Methanol formation from CO2 catalyzed by Fe3S4{111}: formate versus hydrocarboxyl pathways, Faraday Discuss., 2016, 188, 161–180 RSC.
- D. Santos-Carballal, A. Roldan and N. H. de Leeuw, Early Oxidation Processes on the Greigite Fe3S4(001) Surface by Water: A Density Functional Theory Study, J. Phys. Chem. C, 2016, 120, 8616–8629 CrossRef CAS.
- S. N. A. Zakaria, N. Hollingsworth, H. U. Islam, A. Roffey, D. Santos-Carballal, A. Roldan, W. Bras, G. Sankar, G. Hogarth, K. B. Holt and N. H. de Leeuw, Insight into the Nature of Iron Sulfide Surfaces During the Electrochemical Hydrogen Evolution and CO2 Reduction Reactions, ACS Appl. Mater. Interfaces, 2018, 10, 32078–32085 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Ab initio molecular dynamics for liquid metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Ab initio molecular-dynamics simulation of the liquid-metal–amorphous-semiconductor transition in germanium, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- J. Sun, A. Ruzsinszky and J. Perdew, Strongly Constrained and Appropriately Normed Semilocal Density Functional, Phys. Rev. Lett., 2015, 115, 1–6 Search PubMed.
- C. E. Mitchell, D. Santos-Carballal, A. M. Beale, W. Jones, D. J. Morgan, M. Sankar and N. H. de Leeuw, The role of surface oxidation and Fe–Ni synergy in Fe–Ni–S catalysts for CO2 hydrogenation, Faraday Discuss., 2021, 230, 30–51 RSC.
- D. Mejía-Rodríguez and S. B. Trickey, Meta-GGA performance in solids at almost GGA cost, Phys. Rev. B, 2020, 102, 1–4 CrossRef.
- J. H. Yang, D. A. Kitchaev and G. Ceder, Rationalizing accurate structure prediction in the meta-GGA SCAN functional, Phys. Rev. B, 2019, 100, 1–10 Search PubMed.
- Y. Zhang, J. Sun, J. P. Perdew and X. Wu, Comparative first-principles studies of prototypical ferroelectric materials by LDA, GGA, and SCAN meta-GGA, Phys. Rev. B, 2017, 96, 035143 CrossRef.
- J. Sun, R. C. Remsing, Y. Zhang, Z. Sun, A. Ruzsinszky, H. Peng, Z. Yang, A. Paul, U. Waghmare, X. Wu, M. L. Klein and J. P. Perdew, Accurate first-principles structures and energies of diversely bonded systems from an efficient density functional, Nat. Chem., 2016, 8, 831–836 CrossRef CAS PubMed.
- P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- S. Grimme, Semiempirical GGA-type density functional constructed with a long-range dispersion correction, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- S. Posada-Pérez, D. Santos-Carballal, U. Terranova, A. Roldan, F. Illas and N. H. de Leeuw, CO2 Interaction with Violarite (FeNi2S4) Surfaces: A Dispersion-Corrected DFT Study, Phys. Chem. Chem. Phys., 2018, 20, 20439–20446 RSC.
- O. Lupan, D. Santos-Carballal, N. Ababii, N. Magariu, S. Hansen, A. Vahl, L. Zimoch, M. Hoppe, T. Pauporté, V. Galstyan, V. Sontea, L. Chow, F. Faupel, R. Adelung, N. H. de Leeuw and E. Comini, TiO2/Cu2O/CuO Multi-Nanolayers as Sensors for H2 and Volatile Organic Compounds: An Experimental and Theoretical Investigation, ACS Appl. Mater. Interfaces, 2021, 13, 32363–32380 CrossRef CAS PubMed.
- D. Santos-Carballal, A. Cadi-Essadek and N. H. de Leeuw, Catalytic Conversion of CO and H2 into Hydrocarbons on the Cobalt Co(111) Surface: Implications for the Fischer–Tropsch Process, J. Phys. Chem. C, 2021, 125, 11891–11903 CrossRef CAS.
- O. Lupan, N. Ababii, D. Santos-Carballal, M. I. Terasa, N. Magariu, D. Zappa, E. Comini, T. Pauporté, L. Siebert, F. Faupel, A. Vahl, S. Hansen, N. H. de Leeuw and R. Adelung, Tailoring the selectivity of ultralow-power heterojunction gas sensors by noble metal nanoparticle functionalization, Nano Energy, 2021, 88, 106241 CrossRef CAS.
- X. Liang, X. Lin, G. Wei, L. Ma, H. He, D. Santos-Carballal, J. Zhu, R. Zhu and N. H. De, Leeuw, Competitive adsorption geometries for the arsenate As(V) and phosphate P(V) oxyanions on magnetite surfaces: Experiments and theory, Am. Mineral., 2021, 106, 374–388 CrossRef.
- L. M. Botha, D. Santos-Carballal, U. Terranova, M. G. Quesne, M. J. Ungerer, C. G. C. E. van Sittert and N. H. de Leeuw, Mixing thermodynamics and electronic structure of the Pt1−xNix (0 ≤ x ≤ 1) bimetallic alloy, RSC Adv., 2019, 9, 16948–16954 RSC.
- B. Ramogayana, D. Santos-Carballal, P. A. Aparicio, M. G. Quesne, K. P. Maenetja, P. E. Ngoepe and N. H. de Leeuw, Ethylene carbonate adsorption on the major surfaces of lithium manganese oxide Li1−xMn2O4 spinel (0.000 < x < 0.375): a DFT+U-D3 study, Phys. Chem. Chem. Phys., 2020, 22, 6763–6771 RSC.
- L. Reguera, N. L. López, J. Rodríguez-Hernández, M. González, C. E. Hernandez-Tamargo, D. Santos-Carballal, N. H. de Leeuw and E. Reguera, Synthesis, Crystal Structures, and Properties of Zeolite-Like [T3(H3O)2M(CN)6]2·uH2O (T = Co, Zn; M = Ru, Os), Eur. J. Inorg. Chem., 2017, 2980–2989 CrossRef CAS.
- A. Vahl, O. Lupan, D. Santos-Carballal, V. Postica, S. Hansen, H. Cavers, N. Wolff, M.-I. Terasa, M. Hoppe, A. Cadi-Essadek, T. Dankwort, L. Kienle, N. H. de Leeuw, R. Adelung and F. Faupel, Surface functionalization of ZnO:Ag columnar thin films with AgAu and AgPt bimetallic alloy nanoparticles as an efficient pathway for highly sensitive gas discrimination and early hazard detection in batteries, J. Mater. Chem. A, 2020, 8, 16246–16264 RSC.
- M. J. Ungerer, D. Santos-Carballal, A. Cadi-Essadek, C. G. C. E. van Sittert and N. H. de Leeuw, Interaction of H2O with the Platinum Pt(001), (011), and (111) Surfaces: A Density Functional Theory Study with Long-Range Dispersion Corrections, J. Phys. Chem. C, 2019, 123, 27465–27476 CrossRef CAS PubMed.
- T. A. Arias, M. C. Payne and J. D. Joannopoulos, Ab initio molecular dynamics: Analytically continued energy functionals and insights into iterative solutions, Phys. Rev. Lett., 1992, 69, 1077–1080 CrossRef CAS PubMed.
- M. J. Gillan, Calculation of the vacancy formation energy in aluminium, J. Phys.: Condens. Matter, 1989, 1, 689–711 CrossRef CAS.
- I. Štich, R. Car, M. Parrinello and S. Baroni, Conjugate gradient minimization of the energy functional: a new method for electronic structure calculation, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 39, 4997–5004 CrossRef PubMed.
- D. Sheppard, R. Terrell and G. Henkelman, Optimization methods for finding minimum energy paths, J. Chem. Phys., 2008, 128, 134106 CrossRef PubMed.
- M. R. Hestenes and E. Stiefel, Methods of conjugate gradients for solving linear systems, J. Res. Natl. Bur. Stand., 1952, 49, 409–436 CrossRef.
- V. I. Anisimov, J. Zaanen and O. K. Andersen, Band theory and Mott insulators: Hubbard U instead of Stoner I, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 943–954 CrossRef CAS PubMed.
- A. Rohrbach, J. Hafner and G. Kresse, Electronic correlation effects in transition-metal sulfides, J. Phys.: Condens. Matter, 2003, 15, 979–996 CrossRef CAS.
- O. Bengone, M. Alouani, P. Blöchl and J. Hugel, Implementation of the projector augmented-wave LDA+U method: application to the electronic structure of NiO, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 16392–16401 CrossRef CAS.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Electron-energy-loss spectra and the structural stability of nickel oxide: an LSDA+U study, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509 CrossRef CAS.
- M. Cococcioni and S. de Gironcoli, Linear response approach to the calculation of the effective interaction parameters in the LDA+U method, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 035105 CrossRef.
- D. Friebel, M. W. Louie, M. Bajdich, K. E. Sanwald, Y. Cai, A. M. Wise, M.-J. Cheng, D. Sokaras, T.-C. Weng, R. Alonso-Mori, R. C. Davis, J. R. Bargar, J. K. Nørskov, A. Nilsson and A. T. Bell, Identification of Highly Active Fe Sites in (Ni,Fe)OOH for Electrocatalytic Water Splitting, J. Am. Chem. Soc., 2015, 137, 1305–1313 CrossRef CAS PubMed.
- S. Fabris, S. de Gironcoli, S. Baroni, G. Vicario and G. Balducci, Taming multiple valency with density functionals: A case study of defective ceria, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 041102 CrossRef.
- G. W. Watson, E. T. Kelsey, N. H. de Leeuw, D. J. Harris and S. C. Parker, Atomistic simulation of dislocations, surfaces and interfaces in MgO, J. Chem. Soc., Faraday Trans., 1996, 92, 433–438 RSC.
- H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192 CrossRef.
- N. D. Mermin, Thermal Properties of the Inhomogeneous Electron Gas, Phys. Rev., 1965, 137, A1441–A1443 CrossRef.
- P. E. Blöchl, O. Jepsen and O. K. Andersen, Improved tetrahedron method for Brillouin-zone integrations, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 16223–16233 CrossRef PubMed.
- G. Makov and M. C. Payne, Periodic boundary conditions in ab initio calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 4014–4022 CrossRef CAS PubMed.
- J. Neugebauer and M. Scheffler, Adsorbate-substrate and adsorbate-adsorbate interactions of Na and K adlayers on Al(111), Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 16067–16080 CrossRef CAS PubMed.
- G. Henkelman, A. Arnaldsson and H. Jónsson, A fast and robust algorithm for Bader decomposition of charge density, Comput. Mater. Sci., 2006, 36, 354–360 CrossRef.
- E. Sanville, S. D. Kenny, R. Smith and G. Henkelman, Improved grid-based algorithm for Bader charge allocation, J. Comput. Chem., 2007, 28, 899–908 CrossRef CAS PubMed.
- W. Tang, E. Sanville and G. Henkelman, A grid-based Bader analysis algorithm without lattice bias, J. Phys.: Condens. Matter, 2009, 21, 084204 CrossRef CAS PubMed.
- J. Tersoff and D. R. Hamann, Theory of the scanning tunneling microscope, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 31, 805–813 CrossRef CAS PubMed.
- D. E. P. Vanpoucke and G. Brocks, Formation of Pt-induced Ge atomic nanowires on Pt/Ge(001): a density functional theory study, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 241308 CrossRef.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, A climbing image nudged elastic band method for finding saddle points and minimum energy paths, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- G. Henkelman and H. Jónsson, Improved tangent estimate in the nudged elastic band method for finding minimum energy paths and saddle points, J. Chem. Phys., 2000, 113, 9978–9985 CrossRef CAS.
- D. Santos-Carballal, A. Roldan, N. Y. Dzade and N. H. de Leeuw, Reactivity of CO2 on the surfaces of magnetite (Fe3O4), greigite (Fe3S4) and mackinawite (FeS), Philos. Trans. R. Soc., A, 2018, 376, 20170065 CrossRef PubMed.
- J. Nocedal, Updating Quasi-Newton Matrices with Limited Storage, Math. Comput., 1980, 35, 773 CrossRef.
- M. W. J. Chase, NIST JANAF Thermochemical Tables, American Chemical Society and American Institute of Physics for the National Institute of Standards and Technology, Washington DC, 1998 Search PubMed.
- X.-G. Wang, W. Weiss, S. K. Shaikhutdinov, M. Ritter, M. Petersen, F. Wagner, R. Schlögl and M. Scheffler, The Hematite (α-Fe2O3) (0001) Surface: Evidence for Domains of Distinct Chemistry, Phys. Rev. Lett., 1998, 81, 1038–1041 CrossRef CAS.
- B. Farkaš, D. Santos-Carballal, A. Cadi-Essadek and N. H. de Leeuw, A DFT+U study of the oxidation of cobalt nanoparticles: implications for biomedical applications, Materialia, 2019, 7, 100381 CrossRef.
- D. Santos-Carballal, A. Roldan, R. Grau-Crespo and N. H. de Leeuw, A DFT study of the structures, stabilities and redox behaviour of the major surfaces of magnetite Fe3O4, Phys. Chem. Chem. Phys., 2014, 16, 21082–21097 RSC.
- R. D. Johnson III, NIST Computational Chemistry Comparison and Benchmark Database, https://cccbdb.nist.gov/.
- A. J. Devey, R. Grau-Crespo and N. H. de Leeuw, Electronic and magnetic structure of Fe3S4: GGA+U investigation, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 195126 CrossRef.
- L. Chang, B. D. Rainford, J. R. Stewart, C. Ritter, A. P. Roberts, Y. Tang and Q. Chen, Magnetic structure of greigite (Fe3S4) probed by neutron powder diffraction and polarized neutron diffraction, J. Geophys. Res., 2009, 114, B07101 Search PubMed.
- A. Roldan, D. Santos-Carballal and N. H. de Leeuw, A comparative DFT study of the mechanical and electronic properties of greigite Fe3S4 and magnetite Fe3O4, J. Chem. Phys., 2013, 138, 204712 CrossRef CAS PubMed.
- J. M. D. Coey, M. R. Spender and A. H. Morrish, The magnetic structure of the spinel Fe3S4, Solid State Commun., 1970, 8, 1605–1608 CrossRef CAS.
- M. R. Spender, J. M. D. Coey and A. H. Morrish, The Magnetic Properties and Mössbauer Spectra of Synthetic Samples of Fe3S4, Can. J. Phys., 1972, 50, 2313–2326 CrossRef CAS.
- V. Hoffmann, Greigite (Fe3S4): magnetic properties and first domain observations, Phys. Earth Planet. Inter., 1992, 70, 288–301 CrossRef CAS.
- L. Chang, A. P. Roberts, A. R. Muxworthy, Y. Tang, Q. Chen, C. J. Rowan, Q. Liu and P. Pruner, Magnetic characteristics of synthetic pseudo-single-domain and multi-domain greigite (Fe3S4), Geophys. Res. Lett., 2007, 34, L24304 CrossRef.
- M. Uda, On the Synthesis of Greigite, Am. Mineral., 1965, 50, 1487–1489 Search PubMed.
- M. J. Dekkers and M. A. A. Schoonen, Magnetic properties of hydrothermally synthesized greigite (Fe3S4)-I. Rock magnetic parameters at room temperature, Geophys. J. Int., 1996, 126, 360–368 CrossRef.
- Z. He, S.-H. Yu, X. Zhou, X. Li and J. Qu, Magnetic-Field-Induced Phase-Selective Synthesis of Ferrosulfide Microrods by a Hydrothermal Process: Microstructure Control and Magnetic Properties, Adv. Funct. Mater., 2006, 16, 1105–1111 CrossRef CAS.
- P. W. Tasker, The stability of ionic crystal surfaces, J. Phys. C: Solid State Phys., 1979, 12, 4977–4984 CrossRef CAS.
- E. A. Wood, Vocabulary of Surface Crystallography, J. Appl. Phys., 1964, 35, 1306–1312 CrossRef CAS.
- A. Kiejna, T. Ossowski and T. Pabisiak, Surface properties of the clean and Au/Pd covered Fe3O4(111): DFT and DFT+U study, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 125414 CrossRef.
- U. Terranova, C. Mitchell, M. Sankar, D. Morgan and N. H. de Leeuw, Initial Oxygen Incorporation in the Prismatic Surfaces of Troilite FeS, J. Phys. Chem. C, 2018, 122, 12810–12818 CrossRef CAS.
- C. E. Mitchell, U. Terranova, A. M. Beale, W. Jones, D. J. Morgan, M. Sankar and N. H. de Leeuw, A surface oxidised Fe–S catalyst for the liquid phase hydrogenation of CO2, Catal. Sci. Technol., 2021, 11, 779–784 RSC.
- G. Herzberg, Electronic spectra and electronic structure of polyatomic molecules, Van Nostrand, New York, 1966 Search PubMed.
- A. R. Hoy and P. R. Bunker, A precise solution of the rotation bending Schrödinger equation for a triatomic molecule with application to the water molecule, J. Mol. Spectrosc., 1979, 74, 1–8 CrossRef CAS.
- K. P. Huber and G. Herzberg, Molecular Spectra and Molecular Structure, Springer US, Boston, MA, 1979, pp. 8–689 Search PubMed.
- T. Shimanouchi, Tables of molecular vibrational frequencies, consolidated volume I, 1972, vol. 39 Search PubMed.
- K. K. Irikura, R. D. Johnson and R. N. Kacker, Uncertainties in Scaling Factors for ab Initio Vibrational Frequencies, J. Phys. Chem. A, 2005, 109, 8430–8437 CrossRef CAS PubMed.
- J. A. Pople, A. P. Scott, M. W. Wong and L. Radom, Scaling Factors for Obtaining Fundamental Vibrational Frequencies and Zero-Point Energies from HF/6-31G* and MP2/6-31G* Harmonic Frequencies, Isr. J. Chem., 1993, 33, 345–350 CrossRef CAS.
- M. W. Wong, Vibrational frequency prediction using density functional theory, Chem. Phys. Lett., 1996, 256, 391–399 CrossRef CAS.
- A. P. Scott and L. Radom, Harmonic Vibrational Frequencies:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) An Evaluation of Hartree–Fock, Møller−Plesset, Quadratic Configuration Interaction, Density Functional Theory, and Semiempirical Scale Factors, J. Phys. Chem., 1996, 100, 16502–16513 CrossRef CAS.
An Evaluation of Hartree–Fock, Møller−Plesset, Quadratic Configuration Interaction, Density Functional Theory, and Semiempirical Scale Factors, J. Phys. Chem., 1996, 100, 16502–16513 CrossRef CAS. - M. D. Halls, J. Velkovski and H. B. Schlegel, Harmonic frequency scaling factors for Hartree-Fock, S-VWN, B-LYP, B3-LYP, B3-PW91 and MP2 with the Sadlej pVTZ electric property basis set, Theor. Chem. Acc., 2001, 105, 413–421 Search PubMed.
- A. K. Mishra, A. Roldan and N. H. de Leeuw, CuO Surfaces and CO2 Activation: A Dispersion-Corrected DFT+U Study, J. Phys. Chem. C, 2016, 120, 2198–2214 CrossRef CAS.
- A. Cadi-Essadek, A. Roldan and N. H. de Leeuw, Density functional theory study of the interaction of H2O, CO2 and CO with the ZrO2 (111), Ni/ZrO2 (111), YSZ (111) and Ni/YSZ (111) surfaces, Surf. Sci., 2016, 653, 153–162 CrossRef CAS.
- A. K. Mishra, A. Roldan and N. H. de Leeuw, A density functional theory study of the adsorption behaviour of CO2 on Cu2O surfaces, J. Chem. Phys., 2016, 145, 044709 CrossRef PubMed.
- M. G. Quesne, A. Roldan, N. H. de Leeuw and C. R. A. Catlow, Carbon dioxide and water co-adsorption on the low-index surfaces of TiC, VC, ZrC and NbC: a DFT study, Phys. Chem. Chem. Phys., 2019, 21, 10750–10760 RSC.
- N. Y. Dzade, A. Roldan and N. H. de Leeuw, Activation and dissociation of CO2 on the (001), (011), and (111) surfaces of mackinawite (FeS): a dispersion-corrected DFT study, J. Chem. Phys., 2015, 143, 094703 CrossRef CAS PubMed.
- D. H. Gibson, Carbon dioxide coordination chemistry: metal complexes and surface-bound species. What relationships?, Coord. Chem. Rev., 1999, 185–186, 335–355 CrossRef CAS.
- D. H. Gibson, The Organometallic Chemistry of Carbon Dioxide, Chem. Rev., 1996, 96, 2063–2096 CrossRef CAS PubMed.
- M. Aresta, A. Dibenedetto and E. Quaranta, Reaction Mechanisms in Carbon Dioxide Conversion, Springer Berlin Heidelberg, Berlin, Heidelberg, 2016, pp. 35–69 Search PubMed.
- M. G. Quesne, A. Roldan, N. H. de Leeuw and C. R. A. Catlow, Carbon dioxide and water co-adsorption on the low-index surfaces of TiC, VC, ZrC and NbC: a DFT study, Phys. Chem. Chem. Phys., 2019, 21, 10750–10760 RSC.
- S. C. Parker, N. H. de Leeuw and S. E. Redfern, Atomistic simulation of oxide surfaces and their reactivity with water, Faraday Discuss., 1999, 114, 381–393 RSC.
- N. H. de Leeuw and T. G. Cooper, Surface simulation studies of the hydration of white rust Fe(OH)2, goethite α-FeO(OH) and hematite α-Fe2O3, Geochim. Cosmochim. Acta, 2007, 71, 1655–1673 CrossRef CAS.
- N. H. de Leeuw and S. C. Parker, Computer simulation of dissociative adsorption of water on CaO and MgO surfaces and the relation to dissolution, Res. Chem. Intermed., 1999, 25, 195–211 CrossRef CAS.
- N. H. de Leeuw, G. W. Watson and S. C. Parker, Atomistic Simulation of the Effect of Dissociative Adsorption of Water on the Surface Structure and Stability of Calcium and Magnesium Oxide, J. Phys. Chem., 1995, 99, 17219–17225 CrossRef CAS.
- S. C. Parker, P. M. Oliver, N. H. De Leeuw, J. O. Titiloye and G. W. Watson, Atomistic simulation of mineral surfaces: Studies of surface stability and growth, Phase Transitions, 1997, 61, 83–107 CrossRef CAS.
- N. H. de Leeuw, J. A. Purton, S. C. Parker, G. W. Watson and G. Kresse, Density functional theory calculations of adsorption of water at calcium oxide and calcium fluoride surfaces, Surf. Sci., 2000, 452, 9–19 CrossRef CAS.
- Z. Du and N. H. de Leeuw, Molecular dynamics simulations of hydration, dissolution and nucleation processes at the α-quartz (0001) surface in liquid water, Dalton Trans., 2006, 2623–2634 RSC.
- N. H. de Leeuw, F. M. Higgins and S. C. Parker, Modeling the surface structure and stability of α-quartz, J. Phys. Chem. B, 1999, 103, 1270–1277 CrossRef CAS.
- N. H. de Leeuw, Z. Du, J. Li, S. Yip and T. Zhu, Computer Modeling Study of the Effect of Hydration on the Stability of a Silica Nanotube, Nano Lett., 2003, 3, 1347–1352 CrossRef CAS.
- N. Y. Dzade, A. Roldan and N. H. de Leeuw, DFT-D2 Study of the Adsorption and Dissociation of Water on Clean and Oxygen-Covered {001} and {011} Surfaces of Mackinawite (FeS), J. Phys. Chem. C, 2016, 120, 21441–21450 CrossRef CAS.
- A. Roldan and N. H. de Leeuw, Catalytic water dissociation by greigite Fe3S4 surfaces: density functional theory study, Philos. Trans. R. Soc., A, 2016, 472, 20160080 CAS.
- N. Y. Dzade, A. Roldan and N. H. de Leeuw, DFT-D2 simulations of water adsorption and dissociation on the low-index surfaces of mackinawite (FeS), J. Chem. Phys., 2016, 144, 174704 CrossRef CAS PubMed.
- S. Haider, A. Roldan and N. H. De Leeuw, Catalytic dissociation of water on the (001), (011), and (111) surfaces of violarite, FeNi2S4: A DFT-D2 study, J. Phys. Chem. C, 2014, 118, 1958–1967 CrossRef CAS.
- A. Roldan and N. H. de Leeuw, A kinetic model of water adsorption, clustering and dissociation on the Fe3S4 {001} surface, Phys. Chem. Chem. Phys., 2017, 19, 12045–12055 RSC.
- N. H. de Leeuw and T. G. Cooper, A computational study of the surface structure and reactivity of calcium fluoride, J. Mater. Chem., 2003, 13, 93–101 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp00333c |
| This journal is © the Owner Societies 2022 |