 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A study of the dynamics and structure of the dielectric anomaly within the molecular solid TEA(TCNQ)2†
Adam
Berlie
 *a,
Ian
Terry
b,
Marek
Szablewski
*a,
Ian
Terry
b,
Marek
Szablewski
 b,
Mark
Telling
a,
David
Apperley
c,
Paul
Hodgkinson
b,
Mark
Telling
a,
David
Apperley
c,
Paul
Hodgkinson
 c and
Dominik
Zeller
d
c and
Dominik
Zeller
d
aISIS Neutron and Muon Source, STFC Rutherford Appleton Laboratory, Chilton, Oxfordshire, OX11 0QX, UK. E-mail: adam.berlie@stfc.ac.uk
bDepartment of Physics, Durham University, South Road, Durham, DH1 3LE, UK
cDepartment of Chemistry, Durham University, South Road, Durham, DH1 3LE, UK
dInstitut Laue Langevin, BP 156, 38042 Grenoble Cedex 9, France
First published on 1st March 2022
Abstract
With rising interest in organic-based functional materials, it is important to understand the nature of magnetic and electrical transitions within these types of systems. One intriguing material is triethylammonium bis-7,7,8,8-tetracyanoquinodimethane (TEA(TCNQ)2) where there is an order–disorder transition at ∼220 K. This work focuses on novel neutron scattering techniques to understand the motion of the TEA cations at this transition and explain why we see the dielectric behaviour and possible ferroelectricity within this type of system. We show that the motion of the methyl groups of the TEA cation is spatially restricted below 220 K, whereas above the dielectric anomaly at 220 K, they are free to re-orientate, which ultimately leads to some rich behaviour that could be further exploited. Lastly, we also study the dynamics at this transition using a variety of additional techniques, helping to provide a consistent picture of the motions of the cations.
1 Introduction
With the increasing demand of technology to provide more interesting and intricate uses, scientists are having to look away from oxide or metal materials in an attempt to produce novel devices and systems. In this context, purely organic materials are of significant interest and potential. For example, in recent years, organic materials have shown increasing promise and attractiveness as photovoltaics, in part due to their ability to form thin films with high dielectric constants.1 One thing that separates inorganic and organic materials for these dielectric applications is the origin of the ferroelectricity or high polarisability. Generally, within inorganic or ceramic materials, the polarisation is due to ionic displacement, however in organic materials, the polarisation is a result of the distribution of electron density or the freezing of molecular motion2,3 which requires a different approach to material design and, consequently, provides many challenges.4 There has also been much interest in organic systems where one can couple both the magnetic and electronic polarisation, similar to that seen within multiferroics.5–7 Ultimately, organic systems present researchers with an interesting fundamental playground of electrical and magnetic materials that can be developed into some fascinating devices.7,7,8,8-Tetracyanoqunidimethane (TCNQ) is a system that was able to not only stabilise a radical anion but also displayed quasi-1D electrical conductivity.8–11 The fact that the reduced TCNQ molecule stabilised a radical, allowed this S = 1/2 system to be used to synthesise many interesting magnetic systems.12–18 Even interfaces and defects have been shown to be extremely important within these types of materials and have their own unique electrical conducting behaviour19,20 that emphasises the low dimensional nature of the molecule and interactions, along with the possible existence of correlated magnetism.21
One such derived system is TEA(TCNQ)2, where TEA = triethylammonium, which was one of the salts listed by Melby et al. within their original work.10 Within the crystal structure of TEA(TCNQ)2,22 a single electron (or electronic charge) is delocalised across two TCNQ molecules, which form a strongly correlated dimer through π-orbital overlap. These TCNQ dimers are stacked in a quasi-1D structure, with the TCNQ molecules in tetramers at low temperature (i.e. two dimers together), with an inversion centre in the middle of the 4 stacked TCNQ molecules and in between these stacks are the TEA cations as can be seen from Fig. 1.
 | ||
| Fig. 1 A view of the structure of the high temperature phase of TEA(TCNQ)2, at T = 298 K, shown along the a-axis, where the C = grey, N = green and H = light blue. Note that the hydrogen positions are an approximation deduced from a Fourier map to give an idea of their different environments, and the ammonium hydrogens (N–H) are not shown as their positions could not be determined. The structure was taken from work within ref. 27. | ||
The sample, TEA(TCNQ)2, undergoes two transitions; one at 220 K and another at 120 K. In the low temperature phase (<120 K), the system enters a bulk magnetic state where the strongly interacting tetramers form a 3D coupled singlet state.23 This is, in part, due to the fact that there are strong interactions between TCNQ tetramers and as the temperature increases, the lattice expands and the interactions between TCNQ dimers decreases. At 120 K, the magnetic moments on each TCNQ dimer are separated to the point that they become isolated and behave paramagnetically. The higher temperature transition, at 220 K, is ambiguous, however single crystal diffraction experiments suggest that this is an order–disorder transition where below 220 K the TEA cation freezes into one of two orientations22 and the occupancy of these orientations is purely random, with no additional evidence of any ordering of the TEA cations being present in the diffraction pattern, such as through diffuse scattering. Through the N–H bond on the TEA cation, the molecule also is able to interact with the N atoms on the TCNQ, although there has been limited work on how the H-bonding affects the order–disorder transition. There may be a few possibilities; one is that the H-bond is broken and it is this barrier that must be overcome for the TEA to flip between orientations, or the H-bond is not vital in the TEA flipping and the interaction persists above the 220 K transition, which would mean that the orientational motion of the TEA is dominated by the motion of the ethyl side arms. Interestingly, on warming through this transition, the conductivity of TEA(TCNQ)2 has also been shown to dramatically increase,24 illustrating that this order–disorder transition may have a wider effect on the TCNQ–TCNQ interactions. A study on the molecular motion of the TEA cation was conducted by Travers et al.25 where they used 1H NMR to look at the second moment as a function of temperature. Based on their results, they were able to show that different molecular motions were turned on as the temperature was increased up to 220 K. However, their data were limited; there was little information on how the TEA cation actually moves between positions and with no energy scale associated with the transition. Detailed magnetic susceptibility measurements made by Takagi26 showed that there was a clear, step-like anomaly at approximately 215 K, which was thought to be due to a change in spin dynamics related to the TCNQ dimers. The low temperature susceptibility data taken below 125 K were also fit using a spin-pair model where 2J/kB = 440 K.
Recently we have shown that at both the low and high temperature transitions, there are anomalies in the dielectric data.27 At low temperatures, we were able to observe changes in the capacitance and loss that coupled with the magnetisation, presenting strong evidence for magneto-electric coupling. At the higher temperature transition, which hereafter will be referred to as the dielectric transition, we found that the capacitive response was glassy and akin to a relaxor-ferroelectric.28 Two processes were seen which had activation energies of 1430(50) K and 750(30) K when modeled using the Vogel–Fulcher analysis and were within different frequency regimes, 27–300 kHz and 0.6–22 kHz for the high and low activation energies respectively.27 Using a simple activated behaviour to analyse the dielectric data resulted in significantly increased values for the activation energy and attempt frequencies. Given this intriguing dielectric behaviour, it is important to revisit this dielectric transition and explore both the underlying dynamics and molecular motions to fully understand it. Such an investigation will aid future application of TEA(TCNQ)2 as a potential dielectric material. This work utilises a variety of different experimental techniques to look at the dielectric transition across a wide range of frequencies. Using neutron scattering methods that can probe both space (Q-space) and time, we have probed the molecular motions of the TEA cation motion, and have found some intriguing results that suggest the TEA cation may not rotate with the nitrogen atom at the centre. Instead, the methyl groups are confined below the transition and it is only above the dielectric transition, where they can freely rotate. Additionally, the ethyl-carbons also begin to move upon warming, where the arms of the triethylammonium cation flip between orientations rather the whole molecule rocking about a sphere. Furthermore, muon spin spectroscopy provides evidence that the dielectric transition is also accompanied by a change in spin dynamics on the TCNQ anions that results in changes of the electron density across the dimer.
2 Experimental
The TEA(TCNQ)2 was synthesised using a route outlined by Melby et al.10 where triethylammonium was refluxed with half the molarity of TCNQ in stoichiometric quantities in acetonitrile. Crystals were formed on slow cooling of the solution. Deuterated TCNQ was also synthesised using a method by Dolphin et al.,29 where the deuterated analogue of TEA(TCNQ)2 could be easily synthesised as above. Within all of our experiments, deuterated TEA(TCNQ)2 was used to minimise any coupling between the probe and the protons, or in this case deuterons, on the TCNQ molecules.Fixed window energy scans, where here the energy transfered between the scattered neutron and sample, ΔE, equals 0, were taken on the IN13 spectrometer at the Institute Laue-Langevin using a technique known as Elastic Incoherent Neutron Scattering (EINS); a method which reaches values of Q out to approximately 4 to 5 Å−1. Quasi-Elastic Neutron Spectroscopy (QENS) measurements were taken on the IRIS spectrometer at the ISIS Neutron and Muon Source.30 The IRIS instrument is capable of reaching Q values of approximately 1.8 Å−1. In both cases helium closed-cycle refrigerators were used to control the temperature. The raw data were reduced using Mantid and LAMP for the IRIS and IN13 data respectively.
Proton experimental NMR data were collected using a Bruker Avance III HD spectrometer operating at 400 MHz and a 5 mm diameter horizontal coil probe. Spin–lattice relaxation times (T1) were recorded using a saturation-recovery method. Spin–lattice relaxation in the rotating frame times (T1ρ) were obtained from a 90° pulse followed by a variable duration spin-lock pulse applied at a field equivalent to 50 kHz. Both types of measurement incorporated a solid echo. A solid echo pulse sequence was also used to record a proton spectrum.
Muon spin spectroscopy (μSR) experiments were conducted on the CHRONUS spectrometer on the RIKEN-RAL muon facility at the ISIS Neutron and Muon Source using a helium flow cryostat to vary the temperature.31 More on the technique and data analysis can be found within the ESI.†
3 Results
3.1 Structural changes – elastic incoherent neutron scattering
Neutron spectroscopy is an ideal tool for studying organic based system32 as the large incoherent scattering cross-section of the proton allows one to probe the motion and spatial distribution of the hydrogen atoms. EINS, in particular, is an underused technique to explore these types of systems where one can probe the intensity of the incoherent scattering on the elastic line, i.e. where ΔE = 0, providing information on the how the molecules move within the crystal structure.Using the IN13 instrument, one is able to access a Q range of up to 4.36 Å−1, or ∼1.4 Å in real space. The data were collected by scanning the intensity of the scattered neutrons at different Q values and at the elastic line (where ΔE = 0). Here, we are looking at all the elastic or, ω ≈ 0 Hz, incoherent scattering from the protons on the TEA. From a simple chemical point of view, the TEA cation has three different proton environments; methyl groups, ethyl groups and the ammonium proton that is bonded directly to the nitrogen. The percentage of the protons that accounts for the ammonium proton, is small and so it is plausible that this doesn't contribute to the overall scattering from the protons; the largest fraction of protons are within the methyl groups.
Detected neutron intensity as a function of Q was collected at various temperatures and this was plotted as a 2D rainbow graph, (Fig. 2). All data were normalised and so the highest possible intensity value is one. The change in intensity provides information on the probability of finding a particle at a given value of Q. Therefore when Q ≈ 0 Å−1, the intensity is always one due to the proton or particle always being present with respect to the long range order of the crystal structure. The data taken at 20 K were used to represent the spectrometer's resolution function. Here all motion is expected to be frozen out which, after data reduction, produces a Q-independent response. Above 50 K, there is a small decrease in the intensity across most of Q, which is due to the onset of proton mobility. This intensity gradually decreases as more protons start moving and the probability of finding the proton at a specific value of Q decreases; the motion becoming more diffuse. Above 120 K, a new region is entered and the tail at high Q begins to drop further as an additional process causes the intensity on the elastic line to be pushed out into the quasi-elastic region (i.e. a region where ΔE ≠ 0). Since at 150 K, the intensity at lower values of Q remains fairly high, the process associated with this response is likely to indicate more local motion, such as the onset of methyl group rotation. The plateau denoted within the green region in Fig. 2 persists until 200 K, afterwhich the intensity drops across the whole Q range. Given that there is a dramatic decrease in intensity at the low Q range, this motion is due to larger motions or jumps in real space (Q < ∼ 2.6 Å−1), which also matches with the temperature of the dielectric transition and the onset of the motion of the entire TEA cation.
Given the interesting temperature and Q dependence of the intensity of the data in Fig. 2, it is worth further analysing I(Q) at each individual temperature. With this in mind, it is noted that there are only two distinct and sizeable proton environments, with the dielectric transition being due to the onset of the motion of the whole TEA molecule. Therefore, it is reasonable to treat the I(Q) vs. Q data as the elastic incoherent structure factor (EISF) and model the data as such to extract more information related to the motion of the molecular structure of TEA.
Since the type of motion that the protons may undergo is ambiguous, we have attempted to find the best fits to the data using different models of the EISF33 by comparing the quality of the fits of each model. The adjusted-R2 value, that takes into account additional independent variables within a model and allows a comparison between these different models, is shown in Fig. 3A, with the fits to the data shown in Fig. 3B. We believe there are three regions that can be described by slightly different fitting functions and these are illustrated in Fig. 3A. The first region to consider is that at low temperatures (<100 K); it is extremely likely that the first motion of protons that unfreezes within the time scale of the measurement is that of the methyl group protons and one can assume all these protons to be equivalent. Therefore the EISF model that describes a 3-site jump, or methyl rotation, model was used. The formula to account for a 3-jump rotation is
 | (1) |
 | ||
| Fig. 3 EISF analysis of the incoherent elastic line scattering from IN13. (A) The adjusted R2 parameters illustrating the quality and applicability of each model to each spectra. The solid lines are purely a guide to the eye. (B) Examples of fits (solid red lines) to the I(Q) data at selected temperatures. Eqn (1) was fitted to the 50 K data. (C) The temperature dependence of the respective amplitude of each component from the fits to the data. The solid lines are guides to the eye. (D) The radius associated with the two component fits to the data where r1 is for the CH3 jump rotation and r2 is for the spherical diffusion model. The solid lines are guides to the eye. | ||
Above 100 K, there is an intensity change in the high Q tail as can be seen in Fig. 2 where one can assume that eqn (1) is no longer solely a valid model. For temperatures above 100 K, we fit the data using two models. The first was a summation of the 3-site jump model (for the CH3 rotations) and a 2-site jump model, which we believed may account for the onset of ethyl group motion, the equation is shown below;
 | (2) |
 | (3) |
As the temperature is increased, and one moves into region 3, the best fit is achieved by using eqn (3). Within error the value of r1 stays the same up until 225 K, afterwhich there is a dramatic change to ∼1 Å, the value one would expect for a full methyl group rotation. Concomitantly, the value of r2 drops slowly and flattens out at 1.4 Å above 225 K, the temperature of the dielectric transition. The value of r2 in this case is the radius of a sphere that the protons are able to move around. The fact that the value of r2 decreases and then plateaus at 1.4 Å is curious. Given that the distance from the nitrogen at the centre of the TEA molecule to the methyl carbon on the edge is around 2.5 Å, then the value of r2 at these high temperatures is too short to account for the TEA molecule simply diffusing in a spherical motion. However, the value of ∼1.4 Å is similar to the distance between the ethyl and methyl carbon atoms. Therefore, perhaps, this result is pointing more towards the idea that it is the methyl group moving and not the entire TEA molecule. As the methyl groups flip between positions, it could simply be that this motion freezes out as opposed to the entire TEA cation rotating about the nitrogen atom. Additionally, the fact that r1 increases to ∼1 Å at the transition is also indicating that the motion of the methyl group protons are no longer restricted above the transition.
Lastly, given that there are two very different processes occurring within the molecule at very different values of Q, it is sensible to plot out the change in intensity at a value at high and low Q, which can be seen in Fig. 4. In both cases, there is a very slow decrease in intensity across the whole Q range. At the high value of Q, the decrease in intensity is fairly broad but there is perhaps a change in slope at approximately 225 K, which again indicates that although there is onset of this process at low temperatures, there is a change in this motion, which we believe is the methyl group rotation, at the dielectric transition. For the change in intensity at lower values of Q, this begins above 100 K, which matches up with what we saw from the EISF fits and rather than there being a change at the dielectric transition, this larger length scale process is more gradual across the temperature range. Therefore, this larger length scale process does not appear to begin at the dielectric transition at 220 K, but far below this. There is a slight difference between the 3.43 and 3.75 Å−1 data above 200 K and this may be given as an indication of a length scale (approximately 1.6 Å) of a motion, however it should be noted that this should be taken lightly. Perhaps, the most one may take away from these values is that in a time-averaged state, the proton motion may not have a strong temperature dependence, perhaps supporting the idea that a lot the behaviour is governed by the expansion of the spacing between TCNQ anions.
4 Dynamics at the transition
Whilst the conformational changes at the transition are described above. In order to fully understand the transition, one must also probe the dynamics. This has primarily focused on two techniques, QENS, that follows on from the above EINS experiment, and NMR, able to probe both T1 (400 MHz) and T1ρ (50 kHz).4.1 Quasielastic neutron scattering
Fixed window, or elastic window, energy scans, integrated over all of Q, confirms the transition at 220 K and that this transition involves the motion of the protons. The broadness of the transition indicates that there are multiple processes occurring. The mean squared displacement (MSD) response, generated by modelling the EINS data and assuming the Gaussian approximation at low Q values, also shows evidence of the dielectric transition at 220 K (see Fig. 5A and B). Above 200 K, the MSD data can be fit using the Arrhenius equation where Ea/kB = 544(12) K and the pre-exponent is 6.8(3) Å2. This is a low value for Ea/kB. However given the number of processes this could probe, this may not be surprising.Detailed QENS spectra were taken at five temperatures between 150–300 K and these were summed over all of Q, minus any detectors that showed Bragg peaks, and converted from S(Q,ω) to I(Q,t) (see Fig. 5C). The best fits to the data were found to be by a summation of two exponential relaxations:
 | (4) |
4.2 NMR
Both 1H T1 and T1ρ measurements were performed, since these are sensitive to molecular motions at complementary frequencies: the 1H NMR frequency (400 MHz) and 1H nutation frequency (50 kHz) respectively.The T1 data could be fit using two components in a roughly fixed ratio of 0.75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.25. Since the sample is not spatially imhomogeneous, the populations of the individual fitting components are unlikely to be physically meaningful. We have therefore taken the approach of Carignani et al.37 and used a weighted average to obtain a single motionally sensitive parameter, the Population Weighted Rate Average (PWRA), which is defined as:
0.25. Since the sample is not spatially imhomogeneous, the populations of the individual fitting components are unlikely to be physically meaningful. We have therefore taken the approach of Carignani et al.37 and used a weighted average to obtain a single motionally sensitive parameter, the Population Weighted Rate Average (PWRA), which is defined as:
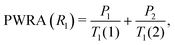 | (5) |
| R1 = K[J(ν) + 4J(2ν)], | (6) |
 | (7) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (f0/Hz) = 10.4(2) (f0 ≈ 2.4 × 1010 Hz). The activation energy for methyl group rotation is highly variable,38,39 depending on the degree of steric hindering, and the value obtained is consistent with a relatively hindered group. The overall T1 data imply that there is a single dominant fast motional process (most likely methyl rotation) present below the dielectric transition, but that other processes must be active (in the same 100 s of MHz frequency scale) above the transition; the relaxation stays short (about 0.2 s) above 225 K. The absence of a clear additional maximum strongly suggests that these involve multiple potentially correlated motions, as might be expected if the ethyl chains of the TEA cation were unconstrained.
(f0/Hz) = 10.4(2) (f0 ≈ 2.4 × 1010 Hz). The activation energy for methyl group rotation is highly variable,38,39 depending on the degree of steric hindering, and the value obtained is consistent with a relatively hindered group. The overall T1 data imply that there is a single dominant fast motional process (most likely methyl rotation) present below the dielectric transition, but that other processes must be active (in the same 100 s of MHz frequency scale) above the transition; the relaxation stays short (about 0.2 s) above 225 K. The absence of a clear additional maximum strongly suggests that these involve multiple potentially correlated motions, as might be expected if the ethyl chains of the TEA cation were unconstrained.
 | ||
| Fig. 6 The temperature dependence of the parameters extracted from the NMR experiments for TEA(TCNQ)2, where (A) is the PWRA for the T1 data with a Larmor frequency of 400 MHz, (B) is the PWRA for the T1ρ data, where the data shows maxima when the molecular motion is about 50 kHz. The solid blue line is the dielectric loss at 50 kHz, with data shown between 150 and 220 K, showing remarkable agreement between the two data sets. (C) is the full width at half maximum associated with the NMR peak. The red solid lines are fits to the data using equations eqn (6)–(8). | ||
The T1ρ data was also fitted to two component decays and again using the PWRA, now of R1ρ, that can be seen in Fig. 6B. The R1ρ data show two clear maxima, which can be modelled in a similar way to the R1 data, except in this case,40
 | (8) |
The blue solid line in Fig. 6B shows the dielectric loss between 150 and 220 K at 50 kHz showing remarkable agreement between the two techniques. This shows that the T1ρ NMR relaxation data and the dielectric spectroscopy are measuring the same process below the phase transition, which is assumed to be the unfreezing of the TEA cations. It is also clear from Fig. 6A that multiple dynamic procesess are active above the phase transition. It is also important to note that the dielectric spectroscopy only observes processes that change local dipole moments, whereas the 1H NMR measurements are sensitive to any dynamics of the hydrogen atoms. Hence the methyl group rotation is observed by NMR and not dielectric spectroscopy.
Lastly, the FWHM of the NMR peak can be seen in Fig. 6C. As expected, this has strong similarities with the measurements of second moments of 1H lineshapes conducted by Travers et al.25 (assuming a consistent lineshape, the second moment, or rather its square root, would be proportional to the FWHM). The measurements within this paper were performed on a sample where the TCNQ moeity was deuterated, therefore the one expected difference is that we should not see a flattening out of the FWHM at high temperatures. The FWHM, in our case, will tend to zero as there are no static protons within the structure. It is difficult to interpret the FWHM quantitatively, however, one can see from the flattening of the curve in Fig. 6C at 220 K, that the overall fluctuation rate is exceeding 15 kHz. This is consistent with the FWHM being sensitive to the same motional process as observed in the T1ρ experiment. Moreover, the FWHM data show that this motion must involve relatively large re-orientations of the TEA cations, since a small-amplitude libration-type motion would not result in significant changes to 1H linewidths. The merit of these measurements on the deuterated sample is that they reveal a continuous decrease of the linewidth associated with the cation as the temperature increases. This is consistent with a gradual evolution from a restricted flip-type motion to a more isotropic re-orientation of the cations as the TCNQ host structure expands.
5 Discussion
All the measurements described above span a wide range of frequencies or time scales and in all cases we have followed the temperature dependence of an experimental parameter as described using the Arrhenius equation, | (9) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (−Ea/kBT) part of the equation that defines the probability that the system is able to transition between exited states, i.e. when the protons are able to undergo different types of motion. In all cases, with the exception of the MSD data shown in Fig. 5B and the temperature-dependent I(Q) results shown in Fig. 4, we have been able to get values of the attempt frequency. For the MSD data, the intercept and the slope from the Arrhenius plot provide parameters in terms of a length scale and an intensity respectively and so one is limited to extracting an activation energy.
(−Ea/kBT) part of the equation that defines the probability that the system is able to transition between exited states, i.e. when the protons are able to undergo different types of motion. In all cases, with the exception of the MSD data shown in Fig. 5B and the temperature-dependent I(Q) results shown in Fig. 4, we have been able to get values of the attempt frequency. For the MSD data, the intercept and the slope from the Arrhenius plot provide parameters in terms of a length scale and an intensity respectively and so one is limited to extracting an activation energy.
A graph summarising the different activation energies against experimental frequencies/timescales is shown in Fig. 7A. One should note that despite the logarithmic scale on the ordinate, there are clusters of points pointing to correlations between the different techniques.
 | ||
| Fig. 7 (A) Plot of the fitted activation energy against the experimental frequencies or timescales from different techniques. (B) A comparison of the activation energies for each respected technique with their respective attempt frequencies. The values for the dielectric data have been taken from ref. 27. | ||
Previous work, using electrical conductivity and structural studies, has estimated the energy gap to be ∼2000 K42,43 and it is likely that the processes we are measuring are related.
The values of activation energy from the dielectric data supports this but the technique does have some huge limitations. Dielectric spectroscopy is a bulk technique and averages over all of the sample and every different molecular environment. As such we may see both the motions of the TEA cations but also the polarisation of the electronic moments on the TCNQ dimers. There is also the question of which type of analysis is correct; the simple Arrhenius model or Vogel–Fulcher model. However, the frequency dependence of the dielectric data clearly shows there are two process present at different frequencies when going through the transition. It should also be remembered that the dielectric measurements may also be sensitive to any polarisation set-up by hydrogen bonding of the N–H on the TEA cation to the N atom on a TCNQ molecule. The H-bonding may provide an anchor to prevent the full flipping of the entire TEA cation, but there will still be motion associated with the N–H and TCNQ interactions and this could show an activated behaviour. Therefore it is important to consider the behaviour of the more local techniques across the range of frequencies.
At the higher frequencies, both the QENS and the T1 data, show activation energies that are close and lie within the range 500 K–750 K, Fig. 7A. It is likely that the behaviour of the T1 (or R1) data is indicative of methyl group rotation, and that this process onsets below the dielectric transition; although the EINS data do illustrate that the rotation of the methyl groups is hindered. The QENS measurements also account for some fairly fast dynamics associated with the protons within the TEA cation, with one process (τs) accounting for a fast process that is just within the experimental time window. The second process (τl) comes into the experimental timescale as the sample goes through the dielectric transition. Paired with the EINS data this confirms that there are two different regimes for methyl group mobility; hindered confinement below the transition and unhindered unconfinement above the transition. This is the reason that the T1 and τl result in similar activation energies.
For μSR (see ESI†), the frequency or time-scale of the measurement is very different to that of the NMR and QENS. Sitting within the MHz window, this is generally too slow to observe methyl group rotation or other local C–H motions, but it is faster than the T1ρ and toward the limit of the dielectric measurements. Therefore, μSR is likely providing us with unique information. The activation energy is lower then that of both the QENS and T1 experiment, and one may not expect a correlation. The muons observe all motions, electronic or nuclear, that cause a large enough change in the local field distribution that are on the experimental time scale within the TEA cation. The muon interacts with a TCNQ molecule by forming a σ-bond with a nitrogen on one of the cyano groups, resulting in a hyperfine interaction between the quadrupole moment on the nitrogen nuclei and the muon. This interaction is particularly sensitive to local changes across the strongly coupled TCNQ dimer as well as along the entire 1D stack if electrons are able to hop from one dimer to another, i.e. the sample transitions out of a Mott insulator state, or if the wavefunction of the electrons become more diffuse along these stacks. Given the unique time region that the muons probe, the behaviour does not match up with the T1ρ or the QENS/T1 measurements. It is therefore likely that the muons provide additional evidence of a change in spin dynamics at the dielectric transition.
Moving down into the kHz frequency region, one encounters the activation energies from the T1ρ and the dielectric spectroscopy measurements. The T1ρ experiment showed two activation energies, yet these activation energies are high when compared with other techniques. The T1ρ measurements probe much slower time scales than many of the other frequency-dependent techniques and this will exclude faster process that will be detected within the QENS, T1 and possibly μSR data. However, the dielectric loss at 50 kHz and the T1ρ do show agreement with the maximum of the peak and so this is confirmation that below 220 K they are probing the same dynamic process. As one goes above 220 K, there are no obvious signatures within the dielectric loss that would suggest the measurements are sensitive to the higher temperature T1ρ process, probably because this process does not involve a change in the net polarisation. From previous dielectric data, the activation energies calculated using the Arrhenius model, agree well with the the T1ρ data. This could question whether both the Vogel–Fulcher and Arrhenius analysis are a valid models within this system. The high activation energies are perhaps telling us that the processes are most likely related to a single energy barrier, as opposed to multiple processes all moving into the experimental time scale. As mentioned in a previous section, the two peaks in the T1ρ (or R1) data could be related to the motion of the whole cation above and below the dielectric transition. The fact that the value of the fitted attempt frequency (see Fig. 7B) for the high temperature T1ρ and T1 are similar could indicate that the processes probed are related, with the number of attempted excitations roughly equal, just on very different time scales, pointing to a continuum of energies. This may be supported by the EINS data showing that there is a change in the motion of the methyl groups at the dielectric transition.
Lastly, within the 500 K–750 K band of activation energies is the value calculated from the MSD data. Both the IN13 EINS data and IRIS MSD measurements represent the scattering condition ΔE = Δω = 0. This scattering condition is related to the structure or position of the protons at different values of Q, which when integrated over time result in an average representation of the geometry of motion and indicates where one may find the protons at a given time. The MSD, generated by modelling the IRIS EINS data, represents all the protons within the system. Since it is possible that the methyl group rotation and the entire cation motion have a similar activation energy, this may explain why the fitted value is within the lower band. In contrast, the EINS data probes the change in intensity at different length scales, the higher of the two activation energies being related to the high Q data. The higher values of Q will probe the more local motions such as that of the methyl groups and the low values of Q probe the larger motions of the TEA cation. Thus within the EINS data one can probe both the methyl group rotation as well as the motion of the whole cation. The change in intensity at these different Q values allows one to pick the processes apart. If a fit to these changes in intensity to gain an activation energy is attempted, one ends up with unphysical energies that are lower than the temperature range that is being fitted. Therefore, these processes do not seem to represent a single process with an activated behaviour. This may point to the processes not being strongly dependent on temperature and as the spacing between the TCNQ molecules increases, due to thermal expansion, the TEA cation (including the methyl groups) are free to move. So in a time averaged state, the behaviour of the protons at high and low Q may be a consequence of the thermal expansion of the TCNQ chains. As the TCNQ chains expand, this may also disrupt the hydrogen bonding between the ammonium proton of the TEA cation and an individual TCNQ molecule. It is this disruption that may then also free up the TEA cation to undergo motion as it is no longer restricted. Ultimately pushing the sample through the dielectric transition.
6 Conclusion
Within this work, we have been able to map out activation energy as a function of measurement time scale and have show how Ea depends on the length scale of the measurement. By mapping the different techniques onto each other we have been able to reveal the different behaviours and processes that are activated when passing through the dielectric transition.One main result has been to show that, although the methyl group rotation may exist below the dielectric transition, it is only at the transition that the methyl groups become unconfined. Additionally, the length scale of the lower Q process is not indicative of the whole TEA cation moving but, from looking at the atomic distances calculated from diffraction measurements, one can infer that it is the carbon–carbon bonds which are moving between positions. This is a large step forward in understanding not only this compound, but related materials. It is hoped that by understanding the dynamic behaviour of TEA(TCNQ)2 one is able to apply this fundamental knowledge to future device fabrication as well as providing better understanding of other organic-based systems where similar behaviour is seen.
Author contributions
A. B. conceived, coordinated and led the work; M. S. and A. B. synthesised the sample; A. B., D. Z. and M. T. performed and analysed the QENS and EINS measurements; D. A. and P. H. collected and, along with A. B., analysed the NMR data; and A. B. and I. T. performed the μSR experiment and analysed the data. A. B. wrote the paper with input from I. T., M. S. and P. H.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the ISIS neutron and Muon Source, STFC for beam time on IRIS and RIKEN for access to the RIKEN-RAL Muon Facility. Our thanks also go to Dr Stephen Cottrell for valuable advice and Dr Ian Silverwood for help with performing the experiment on IRIS. We also thank the ILL for beam time on IN13 as well as Dr Francesca Natali for advice on data analysis.Notes and references
- J. Brebels, J. V. Manca, L. Lutsen, D. Vanderzande and W. Maes, High dielectric constant conjugated materials for organic photovoltaics, J. Mater. Chem. A, 2017, 5, 24037 RSC.
- S. Horiuchi and Y. Tokura, Organic Ferroeletrics, Nat. Mater., 2008, 7, 357 CrossRef CAS PubMed.
- D. A. Bonnell, Ferroelectric organic materials catch up with oxides, Science, 2013, 339, 401 CrossRef CAS PubMed.
- D.-W. Fu, H.-L. Cai, Y. Liu, Q. Ye, W. Zhang, Y. Zhang, X.-Y. Chen, G. Giovannetti, M. Capone, J. Li and R.-G. Xion, Diisopropylammonium bromide is a high-temperature molecular ferroelectric crystal, Science, 2013, 339, 425 CrossRef CAS PubMed.
- K. Miyagawa, A. Kawamoto, Y. Nakazawa and K. Kanoda, Antiferromagnetic Ordering and Spin Structure in the Organic Conductor, κ-(BEDT-TTF)2Cu[N(CN)2]Cl, Phys. Rev. Lett., 1995, 75, 1174 CrossRef CAS PubMed.
- P. Lunkenheimer, J. Muller, S. Krohns, F. Schrettle, A. Loidl, B. Hartman, R. Rommel, M. de Souza, C. Hotta, J. A. Schlueter and M. Lang, Multiferroicity in an organic charge-transfer salt that is suggestive of electric-dipole-driven magnetism, Nat. Mater., 2012, 11, 755 CrossRef CAS PubMed.
- M. Poirier, M. de Lafontaine, C. Bourbonnais and J.-P. Pouget, Charge, spin, and lattice effects in the spin-Peierls ground state of MEM(TCNQ)2, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 245134 CrossRef.
- D. S. Acker, R. J. Harder, W. R. Hertler, W. Mahler, L. R. Melby, R. E. Benson and W. E. Mochel, 7, 7, 8, 8-Tetracyanoquinodimethane and its electrically conducting anion-radical derivatives, J. Am. Chem. Soc., 1960, 82, 6408 CrossRef CAS.
- D. S. Acker and W. R. Hertler, Substituted quinodimethans. I. Preparation and chemistry of 7, 7, 8, 8-tetracyanoquinodimethan, J. Am. Chem. Soc., 1962, 84, 3370 CrossRef CAS.
- L. R. Melby, R. J. Harder, W. R. Hertler, W. Mahler, R. E. Benson and W. E. Mochel, Substituted quinodimethans. II. Anion-radical derivatives and complexes of 7, 7, 8, 8-tetracyanoquinodimethan, J. Am. Chem. Soc., 1962, 84, 3374 CrossRef CAS.
- W. R. Hertler, H. D. Hartzler, D. S. Acker and R. E. Benson, Substituted quinodimethans. III. Displacement reactions of 7, 7, 8, 8-tetracyanoquinodimethan, J. Am. Chem. Soc., 1962, 84, 3387 CrossRef CAS.
- J. S. Miller and A. J. Epsteinn, Organic and organometallic molecular magnetic materials-designer magnets, Angew. Chem., Int. Ed. Engl., 1994, 33, 385 CrossRef.
- J. S. Miller, Magnetically ordered molecule-based materials, Chem. Soc. Rev., 2011, 40, 3266 RSC.
- R. S. Potember, T. O. Poeheler and D. O. Cowan, Electrical switching and memory phenomena in Cu-TCNQ thin films, Appl. Phys. Lett., 1979, 34, 405 CrossRef CAS.
- S. A. O'Kane, R. Clérac, H. Zhao, X. Ouyang, J. R. Galan-Mascaros, R. Heintz and K. R. Dunbar, New crystalline polymers of Ag(TCNQ) and Ag(TCNQF4): structures and magnetic properties, J. Solid State Chem., 2000, 152, 159 CrossRef.
- R. A. Heintz, H. Zhao, X. Ouyang, G. Grandinetti, J. Cowen and K. R. Dunbar, New insight into the nature of Cu(TCNQ): solution routes to two distinct polymorphs and their relationship to crystalline films that display bistable switching behavior, Inorg. Chem., 1999, 38, 144 CrossRef CAS.
- A. Berlie, I. Terry, M. Szablewski and S. R. Giblin, Separating the ferromagnetic and glassy behavior within the metal-organic magnet Ni(TCNQ)2, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 184431 CrossRef.
- R. Clérac, S. O’Kane, J. Cowen, X. Ouyang, R. Heintz, H. Zhao, M. J. Bazile and K. R. Dunbar, Glassy Magnets Composed of Metals Coordinated to 7,7,8,8-tetracyanoquinodimethane: M(TCNQ)2 (M = Mn, Fe, Co, Ni), Chem. Mater., 2003, 15, 1840 CrossRef.
- J. R. Kirtley and J. Mannhart, When TTF met TCNQ, Nat. Mater., 2008, 7, 520 CrossRef CAS PubMed.
- H. Alves, A. S. Molinari, H. Xie and A. F. Morpurgo, Metallic conduction at organic charge-transfer interfaces, Nat. Mater., 2008, 7, 574 CrossRef CAS PubMed.
- A. Berlie, I. Terry, S. Cottrell, F. L. Pratt and M. Szablewski, Magnetic ordering of defects in a molecular spin-Peierls system, J. Phys.: Condens. Matter, 2017, 29, 025809 CrossRef PubMed.
- A. Filhol and M. Thomas, Structural evolution of the one-dimensional organic conductor triethylammonium-7,7,8,8-tetracyano-p-quinodimethane (1
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2)[TEA(TCNQ)2] in the temperature, Acta Crystallogr., Sect. B: Struct. Sci., 1984, 40, 44 CrossRef.
2)[TEA(TCNQ)2] in the temperature, Acta Crystallogr., Sect. B: Struct. Sci., 1984, 40, 44 CrossRef. - A. Berlie, I. Terry and M. Szablewski, A 3D antiferromagnetic ground state in a quasi-1D π-stacked charge-transfer system, J. Mater. Chem. C, 2018, 6, 12468 RSC.
- J. P. Farges and A. Brau, Study at 108 and 2 × 108 Hz of the Electrical Conductivity and Dielectric Constant of the Highly Anisotropic Organic Semiconductor TEA(TCNQ)2, Phys. Status Solidi B, 1974, 61, 669 CrossRef CAS.
- J. P. Travers, F. Devreux and M. Nechtschein, NMR Studies of molecular motion and spin dynamics in TEA(TCNQ)2, J. Phys., Colloq., 1983, 44, C3–1295 CrossRef.
- S. Takagi, An anomaly in the magnetic susceptibility of an organic ion-radical salt: triethylammonium-[TCNQ]2, J. Phys. Soc. Jpn., 1987, 56, 1123 CrossRef CAS.
- A. Berlie, I. Terry, Y. Liu and M. Szablewski, Dipolar glass and magneto-electric coupling within a π-stacked organic system, J. Mater. Chem. C, 2016, 4, 6090 RSC.
- R. A. Cowley, S. N. Gvasaliya, S. G. Lushnikov, B. Roessli and G. M. Rotaru, Relaxing with relaxors: a review of relaxor ferroelectrics, Adv. Phys., 2011, 60, 229 CrossRef CAS.
- D. Dolphin, W. Pegg and P. Wirz, The Preparation of Protio and Deuterio Derivatives of the Tetracyanoquinodimethane-Tetrathiofulvalene Complex, Can. J. Chem., 1974, 52, 4078 CrossRef CAS.
- A. Berlie, et al., Looking at the motion associated with the cation and their freezing in TEA(TCNQ)2 using QENS, STFC ISIS Neutron and Muon Source, 2017 DOI:10.5286/ISIS.E.RB1710079.
-
A. Berlie, et al., An Attempt To Unravel Critical Behaviour in 1
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 TCNQ Salts TEA(TCNQ)2 and MEM(TCNQ)2, STFC ISIS Neutron and Muon Source, 2016 DOI:10.5286/ISIS.E.RB1670540.
2 TCNQ Salts TEA(TCNQ)2 and MEM(TCNQ)2, STFC ISIS Neutron and Muon Source, 2016 DOI:10.5286/ISIS.E.RB1670540. - H. Cavaye, Neutron Spectroscopy: An Under-Utilised Tool for Organic Electronics Research?, Angew. Chem., Int. Ed., 2019, 58, 9338 CrossRef CAS PubMed.
- A Practical Guide to Quasi-elastic Neutron Scattering, ed. M. T. F. Telling, Royal Society of Chemistry, London, 2020 Search PubMed.
- R. Zorn, B. Frick and L. J. Fetters, Quasielastic neutron scattering study of the methyl group dynamics in polyisoprene, J. Chem. Phys., 2002, 116, 845 CrossRef CAS.
- B. Gabryi, J. S. Higgins, K. T. Ma and J. E. Roots, Rotational motion of the ester-methyl group in stereoregular poly(methylmethacrylate): a neutron scattering study, Macromolecules, 1984, 17, 560 CrossRef.
- D. Zeller, M. T. F. Telling, M. Zamponi, V. García Sakai and J. Peters., Analysis of elastic incoherent neutron scattering data beyond the Gaussian approximation, J. Chem. Phys., 2018, 149, 234908 CrossRef CAS PubMed.
- E. Carignani, S. Borsacchi and M. Geppi, Detailed characterization of the dynamics of ibuprofen in the solid state by a multi-technique NMR approach, ChemPhysChem, 2011, 12, 974 CrossRef CAS PubMed.
- A. J. Horsewill, Quantum tunnelling aspects of methyl group rotation studied by NMR, Prog. Nucl. Magn. Reson. Spectrosc., 1999, 35, 359 CrossRef CAS.
- D. C. Apperley, A. F. Markwell, I. Frantsuzov, A. J. Ilott, R. K. Harris and P. Hodgkinson, NMR characterisation of dynamics in solvates and desolvates of formoterol fumarate, Phys. Chem. Chem. Phys., 2013, 15, 6422 RSC.
- Solid-State NMR Basic Principles and Practise, ed. D. C. Apperley, R. K. Harris and P. Hodgkinson, Momentum Press, New York, 2012 Search PubMed.
- M. R. Hampson, J. S. O. Evans and P. Hodgkinson, Characterization of Oxygen Dynamics in ZrW2O8, J. Am. Chem. Soc., 2005, 127, 15175 CrossRef CAS PubMed.
- A. Brau and J.-P. Farges, Further Aspects of the Electrical Conduction in the Highly Anisotropic Organic Semiconductor TEA(TCNQ)2, Phys. Status Solidi B, 1974, 61, 257 CrossRef CAS.
- J.-P. Farges, Descriptive analysis of the crystal structure of the 1-D semiconducting TCNQ salt: TEA(TCNQ)2, as a function of temperature. - I. Intermolecular distortions of the conducting TCNQ columns, J. Phys., 1985, 46, 465 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d2cp00142j |
| This journal is © the Owner Societies 2022 |



