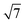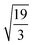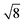Effective medium theory for bcc metals: electronically non-adiabatic H atom scattering in full dimensions
Received
7th January 2022
, Accepted 30th March 2022
First published on 4th April 2022
Abstract
We report a newly derived Effective Medium Theory (EMT) formalism for bcc metals and apply it for the construction of a full-dimensional PES for H atoms interacting with molybdenum (Mo) and tungsten (W). We construct PESs for the (111) and (110) facets of both metals. The EMT-PESs have the advantage that they automatically provide the background electron density on the fly which makes incorporation of ehp excitation within the framework of electronic friction straightforward. Using molecular dynamics with electronic friction (MDEF) with these new PESs, we simulated 2.76 eV H atoms scattering and adsorption. The large energy losses at a surface temperature of 300 K is very similar those seen for H atom scattering from the late fcc metals and is dominated by ehp excitation. We see significant differences in the scattering from different surface facets of the same metal. For the (110) facet, we see strong evidence of sub-surface scattering, which should be observable in experiment and we predict the best conditions for observing this novel type of scattering process. At low temperatures the MD simulations predict that H atom scattering is surface specific due to the reduced influence of the random force.
1 Introduction
Adsorption is a prerequisite to most surface chemistry and requires that the incident molecule transfers kinetic energy to the solid, either via excitations of phonons or electron–hole pairs (ehp). H-atom adsorption on transition metals is of special interest1–4 as the efficiency of energy transfer to phonons is reduced, a result of the light mass of hydrogen compared to the surface atoms. This makes an accurate description of ehp excitation essential and H atom scattering from metal surfaces an excellent test case for modeling electronically non-adiabatic dynamics beyond the Born–Oppenheimer approximation.5
Two theoretical frameworks to accomplish this have evolved over the last decades: (i) independent electron surface hopping6 and (ii) mean-field methods like the effective Hamiltonian approach7,8 or molecular dynamics with electronic friction.9–11 Electronic friction—the most commonly used approach for H atom interactions with metals—treats the electrons as a bath, which is well-suited to describe a metal's electronic continuum.10,11 The coupling between the translational degrees of freedom of the atom and metal electrons is then described by a frictional drag force upon the classically moving nuclei. The friction tensor is commonly treated simply as a coefficient, which can then easily be calculated from the background electron density at the location of the nuclei. This is referred to as the local density friction approximation (LDFA).10–13 Using this model of ehp excitations, a Langevin equation is used to propagate classical trajectories. This introduces a temperature dependent random force that ensures detailed balance.14 Despite the LDFA works well in modeling the ehp influence on the dynamics of atoms at metal surfaces, it is not applicable for molecule-surface scattering. The contribution due to the molecular electronic structure into the friction can be taken into account by the orbital-dependent friction approach.15,16
The critical step in carrying out molecular dynamic simulations with LDFA electronic friction is the simultaneous acquisition of reliable configuration–dependent energies and background electron densities. Many-body potentials like the Embedded Atom Method (EAM)17,18 or Effective Medium Theory (EMT)19–22 have the advantage that their energy expressions contain an electron density model, allowing potential gradients and LDFA based friction coefficients to be computed on the fly. By parameterizing an EMT expression by fitting to DFT data, full-dimensional potential energy surfaces (PES) and electron density functions can be derived.23 In recent studies, this approach was used to investigate the scattering dynamics of H and D atoms from six late fcc (111) transition metal surfaces and comparisons of predicted energy losses were in excellent agreement with experiment.23–25 Remarkably, the scattering dynamics of H and D from these six metals were quite similar, prompting the authors to speak of “universal behavior”.24
In this work, we investigate how the surface and crystal structure influence the H and D translational energy losses resulting from collisions at metal surfaces. This required us to extend the EMT formalism22 to the bcc crystal symmetry, the formalism for which we also present. We parameterized these newly derived energy formulae by fitting them to ab initio energies for two bcc metals, Mo and W, both with (111) surface structures. We also showed that the same EMT parameters accurately describe the H interactions with the (110) surfaces of W and Mo. Finally, we used the PESs and electron densities to perform LDFA electronic friction molecular dynamics simulations of H atoms scattering and computed energy loss distributions. We find, as before, that there are only small differences in the H atom energy losses when comparing different metals. However, scattering from different facets—even for the same metal—leads to significantly different scattering dynamics. In contrast to (111) facets, H scattering from (110) facets leads to deep H atom penetration followed by scattering back to the vacuum. This produces a large energy loss that should be observable in experiment. We make the prediction that H scattering from W(110) at liquid nitrogen temperature is the best possibility to observe this novel scattering process.
2 Theory
2.1 Effective medium theory
The Effective Medium Theory (EMT) has proven useful to describe gas-surface interactions for fcc metals.2,14,22–24,26–30 Here, we extend the previously formulated EMT formalism to the case of bcc metals.
EMT represents the energy of a real system relative to a reference system.22 Hence, the total energy E of a system consisting of N atoms is the sum of the energy of the reference system and a correction term ΔE:
| |  | (1) |
where
Ei (
![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) i
i) represents the cohesive energy of atom
i and depends on the average background electron density
![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) i
i surrounding the atom.
Ei (
![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) i
i) is calculated by considering atom
i to be an impurity embedded in a metal host. Jacobsen
et al.
22 and Janke
et al.
2 chose a perfect fcc crystal as a reference system, but other choices are possible. In our new formalism, we choose a perfect bcc crystal to serve as an effective medium, and follow the derivation used for fcc metals.
22
The correction term ΔE is often represented in the following form:
| |  | (2) |
where
Vij(
rij) is the pairwise correction term due to the interaction between atoms
i and
j separated by the distance
rij.
Vrefi (
![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) i
i) is the many-body correction term for the reference system. The background electron density
![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) i
i, averaged over the volume inside a sphere with the radius
si, serves as a connection between the real system and the reference system and is calculated as
| |  | (3) |
where Δ
nj(
si,
rij) is the electron density tail of atom
j contributing to the background electron density in the location of atom
i. These density tails can be approximated by exponential functions resulting in the following equation:
| |  | (4) |
where
η1 and
η2 describe the fall-off of the many-body and the pairwise contributions to the average electron density
![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) i
i, respectively. Δ
n0,j is assumed to be a constant. On the other hand, the DFT calculations on the level of local density approximation lead to the following relation:
21| | ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) i = n0e−η(si−s0), i = n0e−η(si−s0), | (5) |
where
s0 defines a sphere of the same volume as the Wigner–Seitz cell of a perfect fcc or bcc crystal in equilibrium. Setting
si =
s0 and assuming that only nearest neighbors contribute to the background electron density,
eqn (4) and (5) give
| |  | (6) |
Here,
b1 denotes the number of nearest neighbors. The geometric factor
β relates the neutral sphere radius
s0 to the nearest-neighbor equilibrium distance
In general, it can be shown that the interatomic distance to the neighbors situated in the
q-th shell in a perfect lattice is given by
For the fcc metal the coefficients
dq are related to the number of shell
q by a simple formula
| |  | (9) |
It is slightly more complex for the bcc lattice: the values of
d(bcc)q can be calculated numerically with the aid of the primitive lattice vectors.
Table 1 shows the radii and the number of atoms for the first 10 shells.
Table 1 Radius dq of the q-th shell in the units of βs0 and the corresponding number of the atoms bq belonging to it for both the fcc and bcc crystal
|
q
|
d
fcc
q
|
b
fcc
q
|
d
bcc
q
|
b
bcc
q
|
| 1 |
1 |
12 |
1 |
8 |
| 2 |

|
6 |

|
6 |
| 3 |

|
24 |

|
12 |
| 4 |

|
12 |

|
24 |
| 5 |

|
24 |
2 |
8 |
| 6 |

|
8 |

|
6 |
| 7 |
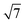
|
48 |
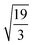
|
24 |
| 8 |
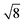
|
6 |

|
24 |
| 9 |

|
36 |

|
24 |
| 1 |

|
24 |
3 |
32 |
The geometrical factor β entering eqn (8) is defined by:
| | 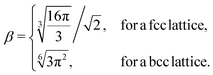 | (10) |
Substituting eqn (6) into eqn (4) and comparing with eqn (5) we obtain the equation:
| |  | (11) |
which implies, for the sake of consistency, that
Rose et al.31 developed a functional producing the cohesive energy for a crystal lattice of the following form
| | | Ei = E0 [1 + λ (si − s0)]e−λ(si−s0) − E0. | (13) |
The expression for the neutral sphere radius
si can be obtained from
eqn (11):
| |  | (14) |
with
σi being the short hand notation for
| | 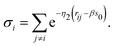 | (15) |
E0 is the cohesive energy for the equilibrium geometry. The pairwise correction term and the potential energy of the reference system entering
eqn (2) can be represented in the following form
| |  | (16) |
and
| | | Vref = −b1V0e−κ(si−s0), | (17) |
respectively.
22
The above formalism allows the straightforward extension to two-component systems like metal alloys or a hydrogen atom at metal surfaces. Then, the total cohesive energy of the system consists of the sum of the partial (species-specific) cohesive energies
| | 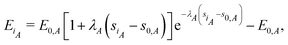 | (18) |
where index
A labels species
A. In a two-component system the neutral sphere radius of atom
iA belonging to species
A is defined by the following formula:
| |  | (19) |
where index
B runs over the species. The important difference between
eqn (19) and (14) resides in the quantity
| | 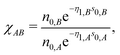 | (20) |
which accounts for the contribution of cross-terms between two different species to the neutral sphere radius. Note, that
χAA = 1 in the case of
A =
B.
| |  | (21) |
is the sum of exponential pair-wise contributions of the atoms belonging to species
B to the neutral sphere radius
siA. The sum in
eqn (21) runs over all atoms of species
B, and in case of
B =
A the self-interacting term (
jA =
iA) is excluded from the sum.
The pairwise correction term in eqn (2) is constructed in a similar way to eqn (21),
| |  | (22) |
Finally, the reference energy contribution to
eqn (2)| |  | (23) |
is defined as in
eqn (17).
The factor
| |  | (24) |
in the formulas above serves as a smooth cut-off function needed for molecular dynamics simulations.
2 The falloff parameter
| |  | (25) |
dictates the steepness of the cut-off function,
rc =
r3 is the cut-off radius set to the third-nearest neighbor distance in equilibrium, and
| |  | (26) |
where
d3 and
d4 are given in
Table 1. The normalization coefficients
| |  | (27) |
and
| |  | (28) |
in
eqn (21) and (22) ensure that for the perfect bulk structure the total energy is zero.
2,22 The sums in the above equations run over the first three shells.
bq is the number of atoms in shell
q. For a perfect fcc crystal
b1 = 12,
b2 = 6, and
b3 = 24, while for a bcc crystal
b1 = 8,
b2 = 6 and
b3 = 12.
EMT characterizes each atomic species in the system with seven parameters: E0, n0, s0, λ, η2, V0 and κ. All parameters except for n0 are connected to bulk properties that can be obtained experimentally.2,21,22E0 is the cohesive energy. s0 is related to the lattice constant a0 by expressions:
| |  | (29) |
which were obtained from
eqn (8) noting that
a0 =
r2 for both fcc and bcc lattice.
The remaining parameters λ, V0, η2 and κ are related to the elastic moduli of a metal (see Appendix).
2.2 Electronic structure calculations
The optimal EMT parameters must be found by fitting the EMT energy function to energy values obtained from ab initio calculations, using a large number of configurations. These were determined using VASP5.3.532–35 with the PBE functional36,37 and with the electron-core interactions treated within the framework of the projector-augmented wave (PAW) approach.38 The plane-wave basis set cutoff energy was set to 400 eV. Partial occupancies were modeled with the method of Methfessel–Paxton39 (N = 1) with a smearing width of 0.1 eV. We calculated the energy for both (111) and (110) facets of W and Mo metals. The simulation cell contained a (2 × 2) six-layered slab with the bottom layer held stationary. The k-point grid for the Brillouin zone for W(111) and Mo(111) was sampled with the (6 × 6 × 1) Monkhorst–Pack mesh,40 while for W(110) and Mo(110) the (12 × 12 × 1) and the (10 × 10 × 1) mesh were used, respectively.
The system geometries were sampled in two ways: (i) H atoms were placed at nodes of a 3D grid consisting of about 1000 points, while the metal atoms were fixed at their equilibrium lattice positions (Fig. 1); (ii) configurations were taken from ab initio molecular dynamics trajectories simulating the scattering of an H atom from a surface at 120 K. The initial positions of H atom for these AIMD simulations were set to be 6 Å above the surface at random lateral coordinates. The initial velocity of the H atom was set to correspond to the incidence kinetic energy of 5 eV and the incidence angle of 30°. The time step was set to 0.1 fs and the H atom was considered to be scattered when it was more than 6.05 Å above the surface. The initial positions and velocities of the surface atoms were sampled from the equilibrium NVE MD simulations of a metal slab at 120 K. The snapshots were taken from a 1 ps MD trajectory with an interval of 100 fs.
2.3 Fitting procedure
A genetic algorithm developed in our group23 was used to fit the EMT function to the DFT energies described above. We used the relations of the fitting parameters to the bulk properties of metals discussed in Subsection 2.1 to constrain values of the following parameters. s0,M was calculated from eqn (29) using the lattice constant a0 obtained from the DFT calculations. The cohesive energy of the metal E0,M was set to its experimental value.41λM was set to a value ensuring a good agreement with the literature value of the bulk modulus.41 This leaves eleven parameters remaining, which were optimized to fit the DFT data. We also used MD simulations to check that the metal slab remained intact up to 900 K for 100 ps. Finally, we compared the EMT background electron density to that of the DFT calculations. Although these two physical quantities are not strictly comparable, they agree well within one another.
2.4 Non-adiabatic molecular dynamics simulations
We treat electronically non-adiabatic effects in terms of a drag force and a random force, using the Langevin equation to govern the motion of the H atom| |  | (30) |
Here, m and r are the projectile's mass and position, respectively; 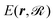 is the ground-state potential energy surface provided by the optimized EMT energy expression that depends not only on the projectile coordinates r but on the coordinates of the surface atoms
is the ground-state potential energy surface provided by the optimized EMT energy expression that depends not only on the projectile coordinates r but on the coordinates of the surface atoms  . Eqn (30) can be derived from the time-dependent Schrödinger equation using a mean-field approximation in the limit of weak non-adiabatic couplings.42 In that case, the friction term
. Eqn (30) can be derived from the time-dependent Schrödinger equation using a mean-field approximation in the limit of weak non-adiabatic couplings.42 In that case, the friction term 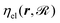 is obtained by Fermi's golden rule with perturbations defined first-derivative non-adiabatic couplings of the electronic states. In this work, we are operating within the framework of the local density friction approximation (LDFA),10–12i.e., we are dealing with a single friction coefficient instead of a friction tensor. The friction coefficient is calculated with the aid of the background densities associated with the EMT-PES. The detailed mapping procedure between friction coefficient and background electron density is described elsewhere.2 The random force FL (t) is modeled by a stochastic process with a Gaussian white noise of zero mean valueand the variance being characterized by the second fluctuation-dissipation theorem43
is obtained by Fermi's golden rule with perturbations defined first-derivative non-adiabatic couplings of the electronic states. In this work, we are operating within the framework of the local density friction approximation (LDFA),10–12i.e., we are dealing with a single friction coefficient instead of a friction tensor. The friction coefficient is calculated with the aid of the background densities associated with the EMT-PES. The detailed mapping procedure between friction coefficient and background electron density is described elsewhere.2 The random force FL (t) is modeled by a stochastic process with a Gaussian white noise of zero mean valueand the variance being characterized by the second fluctuation-dissipation theorem43| |  | (32) |
Here, I denotes the 3D unity matrix and T is the surface temperature. We emphasize that neglecting the random force, as has sometimes been done,44 can lead to spurious results.14 The EMT-PES and the Langevin propagator integrating eqn (30) are implemented in our homemade program md_tian2 available at a public repository.45
The MD trajectories simulating H scattering from a metal surface were started with a H atom placed at 6 Å above the surface with a lateral position chosen randomly. The time step was 0.1 fs and the trajectory was stopped once the projectile was more than 6.05 Å above the surface. The metal surface was equilibrated to 70 K and 300 K in the following way: for 100 ps the slab was equilibrated with an Anderson-thermostat,46 and then propagated microcanonically for additional 100 ps, using the velocity-Verlet algorithm.47,48 Afterwards, we ran a 1 ns-equilibrium trajectory and took a snapshot every picosecond. These shapshots sample the equilibrium slab geometries at the desired temperature which served as slab initial conditions for the scattering dynamics simulations.
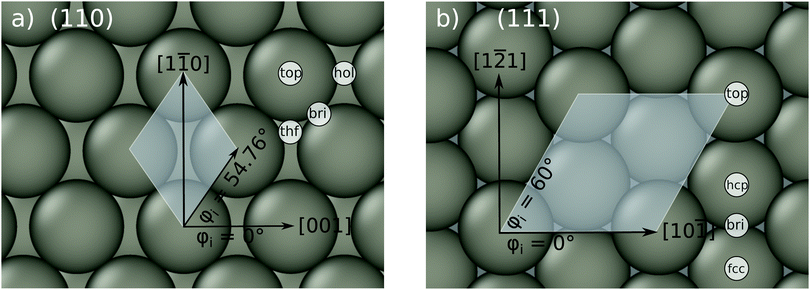 |
| | Fig. 1 Top view on the bcc (110) surface, shown in panel (a), and the bcc (111) surface in panel (b). The cartesian coordinate system, the incidence azimuth and the most important high symmetry sites are also shown. The white shaded areas mark the p(1 × 1) unit cell. | |
3 Results and discussion
3.1 Full dimensional PES for H on W(111) and Mo(111)
Table 2 shows the optimized EMT parameter sets for atomic hydrogen interacting with both W(111) and Mo(111). Fig. 2 shows cuts through the EMT-PESs for the two metals. The root mean-square error (RMSE) for H/W(111) and H/Mo(111) is 0.25 eV and 0.26 eV, respectively. Fig. 3 shows comparisons of EMT-PESs to DFT results as AIMD trajectories that include structures with surface atoms displaced from their equilibrium positions. The resulting EMT-PESs for H/Mo and H/W show an overall RMSE of 0.27 eV and 0.30 eV, respectively. Fig. 4 shows cuts of the EMT background electron density 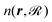 for four surface symmetry sites along the surface normal, as well as the corresponding electron densities obtained from the DFT calculations absent the H atom. Again, the agreement is good.
for four surface symmetry sites along the surface normal, as well as the corresponding electron densities obtained from the DFT calculations absent the H atom. Again, the agreement is good.
Table 2 EMT parameters defining the H/W and H/Mo interaction energies and background electron density
|
|
η
2/Å−1 |
n
0/Å−3 |
E
0/eV |
λ/Å−1 |
V
0/eV |
κ/Å−1 |
s
0/Å |
| W |
3.546 |
0.051 |
−8.90 |
3.505 |
1.518 |
2.296 |
1.564 |
| H |
7.049 |
0.141 |
−3.36 |
7.701 |
0.482 |
8.047 |
0.680 |
| Mo |
2.782 |
0.051 |
−6.82 |
3.738 |
2.595 |
3.899 |
1.554 |
| H |
5.371 |
0.066 |
−2.33 |
6.236 |
0.407 |
8.767 |
0.844 |
 |
| | Fig. 2 Interaction energy of H atom with the metal as a function of the projectile's height z over the surface shown for several high-symmetry sites (see Fig. 1). The gray crosses mark the DFT energies of H/W(111) and H/Mo(111), which served as input data for the fit. The black line represents the EMT fitting function. Note that the metals were held fixed at their lattice coordinates. | |
 |
| | Fig. 3 Interaction energies corresponding to configurations sampled from AIMD trajectories. The gray crosses represent the ab initio energies along the trajectories for H/W(111) (left panels) and H/Mo(111) (right panels), respectively. The black line stands for the energy from EMT fitting function. | |
 |
| | Fig. 4 Background EMT and DFT electron densities for Mo(111) and W(111) as a function of the H atom height over the surface at four different high-symmetry sites shown in Fig. 1a. Note that the metal atoms were kept fixed at their equilibrium lattice coordinates. | |
3.2 EMT-PES transferability to the (110)-facet
The EMT energy expression is independent of the surface facet; hence, the EMT parameters of Table 2 can just as easily be used to produce a PES for H interacting with a (110) surface. This is an advantage over other methods like neural networks, which need to be retrained for each facet. Fig. 5 and 6 show comparisons of DFT data to the EMT energies for H on W and Mo(110) facet. Agreement between the (111)-fitted EMT-PES and DFT is good. We emphasize that these comparisons sample a wide variety of configurations including those corresponding to single bounce scattering as well as penetration of H atom into the bulk. In all cases the EMT-PESs are in a good agreement with the DFT calculations with the RMSE of about 330 meV (13.2 meV per atom) without no adjustment to the fitting parameters.
 |
| | Fig. 5 EMT energy dependence on z coordinate of the H-atom at W(110) (left panels) and Mo(110) (right panels) shown for several high-symmetry sites. The gray crosses mark the corresponding DFT energies. Note, the EMT-PES was fitted to the (111) data. | |
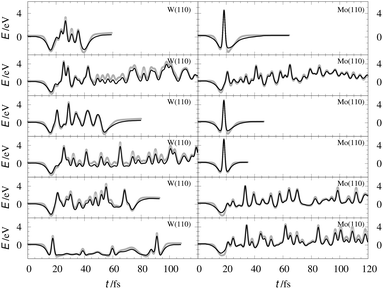 |
| | Fig. 6 H/W(110) and H/Mo(110) interaction energies calculated for the configurations sampled from AIMD scattering trajectories. The gray crosses represent the DFT energies. The black line stands for the EMT-PES. | |
We also checked the accuracy of the EMT electron densities against DFT calculations—see Fig. 7. As in the (111) case, agreement is good. In case of H/Mo(110), the EMT background electron density (filled circles) is systematically ∼30% lower than the one from DFT (solid line). However, this does not influence the predicted energy loss distributions appreciably.
 |
| | Fig. 7 Background EMT and DFT electron densities for Mo(110) and W(110) as a function of the H atom height over the surface at four different high-symmetry sites shown in Fig. 1b. | |
Nowadays, it is possible to craft Neural-Network potentials with fitting errors (RMSE) less than 1 meV per atom.49 So, our potentials may seem by comparison inaccurate. But the high accuracy of Neural-Network potentials comes at a cost of complexity. It requires far more DFT data to be trained, and it must be retrained from facet to facet. Furthermore, it delivers no background electron density information necessary for computing electronic friction forces. The EMT approach presented here is by comparison extremely simple, transferable between facets and, as has been shown, despite the reduced accuracy in reproducing DFT data, accurate enough to reproduce experimental energy loss distributions.24 Another strength of the EMT-PES is that the projectile cannot enter out-of sampling regions of the configuration space during MD simulations—an aspect which needs to be always checked when using Neural-Network potentials.
3.3 MD simulations of H scattering
Using the EMT-PESs described above, we performed LDFA frictional based molecular dynamics simulations to compute energy-loss distributions for hydrogen atom scattering from tungsten and molybdenum. We launched 106 trajectories with incidence energy of Ein = 2.76 eV and incidence angle ϑin= 45°. To reflect typical experimental conditions,50 we selected trajectories scattered at the specular angle with the in-plane and out-of-plane tolerance of ±5°. We refer to these distributions as specular energy loss distributions.
Fig. 8 shows simulations for H scattering from both surface facets of Mo and W at 70 K and 300 K. The energy loss distribution obtained from electronically adiabatic MD simulations are also shown. The MDEF simulations predict a much larger energy loss dominated by ehp excitation. The mean energy losses are all about 1 eV, consistent with experimental observations for H atom scattering from fcc metals24 and similar in magnitude to predictions of another calculation using a reduced dimensional PES.51 When comparing the four scattering calculations at two temperatures, we see that there is very little difference in the energy loss distributions for Mo and W, when other factors are the same. On the other hand, there is a distinct difference in the energy loss distributions when comparing different surface facets or different temperatures. The effect of temperature has been reported previously14 and arises from the reduced influence of the random force at low temperature.
 |
| | Fig. 8 Specular energy loss distributions of H atoms scattered from molybdenum and tungsten surfaces. Upper panels show results for the surface temperature of 300 K and lower panels for 70 K. The gray dashed line represent adiabatic simulations for H atom scattering from tungsten, demonstrating the crucial contribution of electrons to the energy loss of the scattered particles. The initial conditions are: Ein = 2.76 eV, ϑin = 45°, and φin = 0° (see Fig. 1). | |
The differences seen in the H-atom energy loss distributions for different surface facets—compare Fig. 8(a)–(d)—are due to differences in surface structure. This can be inferred from results presented in Fig. 9. Here, contour plots report the number of specular scattering events as a function of the energy loss and depth of penetration for trajectories of panels Fig. 8(c) and (d), where the surface temperature was 70 K. A clear correlation between energy loss and the depth of penetration is seen for both surface geometries—the deeper the H atom moves into the bulk, the more kinetic energy is lost to the metal.
 |
| | Fig. 9 Distribution of specular scattering events as a function of the energy loss and the depth of penetration of H atom scattered from (a) Mo(110), (b) Mo(111), (c) W(110), and (d) W(111). The surface temperature is 70 K. The other conditions are the same as in Fig. 8. The signal above the black, dashed line indicate from which layer the projectiles repelled. The labels top, hcp and fcc refer to the high-symmetry sites of the (111) facet and are shown in Fig. 1(b). The bin sizes are 0.027 eV and 0.063 Å. | |
This can be qualitatively understood from the structures of the surfaces. The (111) surfaces allow access to three surface sites—top, fcc-hollow and hcp-hollow—broadening the energy-loss distribution as the three sites allow for different degrees of surface penetration. For (110) surfaces, the surface density is higher—over 70% of the specular scattered H atoms do not penetrate the surface. But, the (110) facets also exhibit geometric channels that allow very deep penetration that results in a better resolved high energy loss feature in the energy loss distributions. It is noteworthy that subsurface-penetration scattering processes are predicted by these calculations, and hints are provided how these might best be observed experimentally. Specifically, we suggest that H atom scattering experiments using W(110) held at liquid nitrogen temperature would provide clear signatures of subsurface scattering. Tungsten is more favorable to these proposed experiments and it exhibits higher background electron density (see Fig. 4): resulting in higher values of the friction coefficient, which in turn leads to larger energy losses for deep penetration.
3.4 MD simulations of H adsorption
Finally, we report the sticking probabilities for H under the incidence conditions of this work—see Table 3. Remarkably, the sticking probability is uniformly about 0.4 regardless of the identity of the metal, the surface facet or the temperature. This reflects the mechanism of adsorption previously identified for H adsorption to Au(111).2,4 In this mechanism, adsorption results from trajectories that sample the high electron density below the surface of the metal and subsequently resurface with less than enough energy to desorb. In our case, for the (110) surface, resurfacing originates predominantly from the underlying subsurface and—to a minor extend—from the third layer, while for the (111) surface the resurfacing occurs even from the sixth metal layer. This strong migration reflects the small distance between the individual layers in the (111) surface along with a variety of easy accessible diffusion pathways due to the low packing density.
Table 3 Sticking coefficient S0 computed from the same set of trajectories that were used for the calculation of the specular energy loss distributions shown in Fig. 8
| System |
300 K |
70 K |
| H/Mo(110) |
0.44 |
0.44 |
| H/Mo(111) |
0.40 |
0.41 |
| H/W(110) |
0.42 |
0.41 |
| H/W(111) |
0.40 |
0.40 |
4 Conclusion
In summary, we have extended the EMT formalism derived for fcc metals22 to the bcc case. We then fit the newly derived formulae to DFT data for H interacting with W and Mo, which led to full dimensional PESs and electron densities. We employed the PESs and the electron densities to carry out electronically non-adiabatic MD simulations of H atom scattering, following previous work that used the LDFA approximation with a Langevin propagator. Specifically, we predict energy loss distributions for H scattering from (111) and (110) facets of these two metals at 2.76 eV incidence energy. Although no experiments are currently available for bcc metals, our results are similar to what has been seen for H scattering from fcc metals. This suggests that the current results are likely to be a reliable prediction of experiment. We find only subtle differences in the energy loss distributions arising from the scattering of H atom with these two metals; however, scattering from the (111) and (110) facets are distinctly different. Remarkably, on the (110) facet, we predict a clearly resolvable energy loss peak that arises from sub-surface scattering. The calculations predict that the subsurface scattering is most easily seen for H scattering from W(110) at reduced surface temperatures.
Conflicts of interest
There are no conflicts to declare.
Appendix
Derivation of elastic constants with contributions from the first shell
The components of the elastic tensor can be obtained as follows:| |  | (33) |
where Ω0 is the volume per metal atom at equilibrium conditions, ε is the energy per atom, rk,ρ is the Cartesian component ρ of the position vector of neighbor k, NB is the total number of neighbors. In case of a fcc lattice it is sufficient to include only the neighbors located in the first shell. For a bcc lattice on the other hand, it is necessary to include the second shell, too. Due to the symmetry of the elastic tensor, defined by eqn (33), there are only three independent components: C11 = {Cxxxx,Cyyyy,Czzzz}, C12 = {Cxxyy,Cxxzz,Cyyzz}, and C44 = {Cxyxy,Cxzxz,Cyzyz}. The bulk modulus of the system can be obtained with the following relationship that holds for all cubic metals| |  | (34) |
Now, when we insert the EMT energy expression (1) for a one-component fcc metal system into eqn (33), we derive the bulk modulus| |  | (35) |
and the shear modulus| |  | (36) |
Considering only the nearest neighbors, i.e. neglecting many-body contributions, one can derive the other elastic constants for a fcc lattice| |  | (37) |
| |  | (38) |
and a bcc lattice| |  | (39) |
| |  | (40) |
Thus, the bulk modulus reads the same as for the fcc case| |  | (41) |
whereas the third elastic constant for a bcc lattice in EMT is| |  | (42) |
Accounting the second shell contributions into elastic constants
If a perfect bcc crystal is used as effective medium and only the nearest neighbors are considered, the elastic constants, given in eqn (39), (40) and (42), violate the elastic stability criteria.52 As a consequence, we also took the next-nearest neighbors into account. The three elastic constants and the bulk modulus then have the following expressions:| |  | (43) |
| | | C12 = A + Ω [−γ1 (κs0 + 1) + γ2 (βη2s0 + 1)], | (44) |
| |  | (45) |
and| | | B = A + Ω (−γ1κs0 (1 + Mκ) + γ2βη2s0 (1 + Mη2)). | (46) |
The factors A and Ω are the abbreviation for the following expressions:
| | 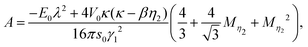 | (47) |
| |  | (48) |
with
Mη2 and
Mκ being
| |  | (49) |
and
| |  | (50) |
respectively.
Acknowledgements
This work was performed in the framework of the Elementary Dynamical Processes at Model Catalytic Surfaces (EDPMCS) Experiment, a part of the Molecular Physics at Interfaces Initiative at the Dalian Coherent Light Source. The authors acknowledge support for this project from the Max Planck Society Central Funds, the international partnership program of the Chinese Academy of Science (No. 121421KYSB20170012) as well as the Max Planck Institute for Multidisciplinary Sciences and the Georg-August University of Goettingen. We further acknowledge support from the Deutsche Forschungsgemeinschaft under Grant number 217133147, which is part of the Collaborative research Center 1073 operating Project A04. AK acknowledges European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (grant agreement no. 833404).
Open Access funding provided by the Max Planck Society.
References
- M. Pavanello, D. J. Auerbach, A. M. Wodtke, M. Blanco-Rey, M. Alducin and G.-J. Kroes, J. Phys. Chem. Lett., 2013, 4, 3735–3740 CrossRef CAS
 .
.
- S. M. Janke, D. J. Auerbach, A. M. Wodtke and A. Kandratsenka, J. Chem. Phys., 2015, 12, 124708 CrossRef PubMed
 .
.
- M. Blanco-Rey, J. I. Juaristi, R. D. Muino, H. F. Busnengo, G. J. Kroes and M. Alducin, Phys. Rev. Lett., 2014, 112, 103203 CrossRef CAS PubMed
 .
.
- O. Bünermann, H. Jiang, Y. Dorenkamp, A. Kandratsenka, S. M. Janke, D. J. Auerbach and A. M. Wodtke, Science, 2015, 350, 1346–1349 CrossRef PubMed
 .
.
- M. Born and R. Oppenheimer, Ann. Phys., 1927, 84, 0457–0484 CrossRef CAS
 .
.
- N. Shenvi, S. Roy and J. C. Tully, J. Chem. Phys., 2009, 130, 174107 CrossRef PubMed
 .
.
- S. Mandal, T. Sahoo, S. Ghosh and S. Adhikari, J. Theor. Comput. Chem., 2015, 14, 1550028 CrossRef CAS
 .
.
- S. Mandal, T. Sahoo, S. Ghosh and S. Adhikari, Mol. Phys., 2015, 113, 3042–3056 CrossRef CAS
 .
.
- M. Head-Gordon and J. C. Tully, J. Chem. Phys., 1995, 103, 10137–10145 CrossRef CAS
 .
.
- Y. Li and G. Wahnström, Phys. Rev. Lett., 1992, 68, 3444–3447 CrossRef CAS PubMed
 .
.
- Y. Li and G. Wahnström, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 14528–14542 CrossRef CAS PubMed
 .
.
- J. Juaristi, M. Alducin, R. Díez Muiño, H. Busnengo and A. Salin, Phys. Rev. Lett., 2008, 100, 116102 CrossRef CAS PubMed
 .
.
- G.-J. Kroes, Phys. Chem. Chem. Phys., 2021, 23, 8962–9048 RSC
 .
.
- N. Hertl, R. Martin-Barrios, O. Galparsoro, P. Larrégaray, D. J. Auerbach, D. Schwarzer, A. M. Wodtke and A. Kandratsenka, J. Phys. Chem. C, 2021, 125, 14468–14473 CrossRef CAS PubMed
 .
.
- R. J. Maurer, M. Askerka, V. S. Batista and J. C. Tully, Phys. Rev. B, 2016, 94, 115432 CrossRef
 .
.
- P. Spiering, K. Shakouri, J. Behler, G. J. Kroes and J. Meyer, J. Phys. Chem. Lett., 2019, 10, 2957–2962 CrossRef CAS PubMed
 .
.
- M. S. Daw and M. I. Baskes, Phys. Rev. B: Condens. Matter Mater. Phys., 1984, 29, 6443–6453 CrossRef CAS
 .
.
- M. S. Daw, S. M. Foiles and M. I. Baskes, Mater. Cience Rep., 1993, 9, 251–310 CrossRef CAS
 .
.
- J. K. Nørskov and N. D. Lang, Phys. Rev. B: Condens. Matter Mater. Phys., 1980, 21, 2131–2136 CrossRef
 .
.
- J. K. Nørskov, Phys. Rev. B: Condens. Matter Mater. Phys., 1982, 26, 2875–2885 CrossRef
 .
.
- K. W. Jacobsen, J. K. Nørskov and M. J. Puska, Phys. Rev. B: Condens. Matter Mater. Phys., 1987, 35, 7423–7442 CrossRef CAS PubMed
 .
.
- K. W. Jacobsen, P. Stoltze and J. K. Nørskov, Surf. Sci., 1996, 366, 394–402 CrossRef CAS
 .
.
- M. Kammler, S. M. Janke, A. Kandratsenka and A. M. Wodtke, Chem. Phys. Lett., 2017, 683, 286–290 CrossRef CAS
 .
.
- Y. Dorenkamp, H. Jiang, H. Köckert, N. Hertl, M. Kammler, S. M. Janke, A. Kandratsenka, A. M. Wodtke and O. Bünermann, J. Chem. Phys., 2018, 148, 034706 CrossRef PubMed
 .
.
- O. Bünermann, A. Kandratsenka and A. M. Wodtke, J. Phys. Chem. A, 2021, 125, 3059–3076 CrossRef PubMed
 .
.
- N. Chetty, K. Stokbro, K. W. Jacobsen and J. K. Nørskov, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 3798–3809 CrossRef PubMed
 .
.
- J. Strömquist, L. Bengtsson, M. Persson and B. Hammer, Surf. Sci., 1998, 397, 382–394 CrossRef
 .
.
- S. M. Janke, M. Pavanello, G.-J. Kroes, D. J. Auerbach, A. M. Wodtke and A. Kandratsenka, Zeitschrift für Physikalische Chemie, 2013, 227, 1467–1490 CAS
 .
.
- A. Kandratsenka, H. Jiang, Y. Dorenkamp, S. M. Janke, M. Kammler, A. M. Wodtke and O. Bünermann, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 680–684 CrossRef CAS PubMed
 .
.
- N. Hertl, A. Kandratsenka, O. Bünermann and A. M. Wodtke, J. Phys. Chem. A, 2021, 125, 5745–5752 CrossRef CAS PubMed
 .
.
- J. H. Rose, J. Ferrante and J. R. Smith, Phys. Rev. Lett., 1981, 47, 675–678 CrossRef CAS
 .
.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed
 .
.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS
 .
.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558 CrossRef CAS PubMed
 .
.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251 CrossRef CAS PubMed
 .
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed
 .
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396 CrossRef CAS
 .
.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed
 .
.
- M. Methfessel and A. T. Paxton, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 3616–3621 CrossRef CAS PubMed
 .
.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192 CrossRef
 .
.
- M. J. Zhu, D. M. Bylander and L. Kleinman, Phys. Rev. B: Condens. Matter Mater. Phys., 1987, 36, 3182–3185 CrossRef CAS PubMed
 .
.
- M. Head-Gordon and J. C. Tully, J. Chem. Phys., 1995, 103, 10137–10145 CrossRef CAS
 .
.
-
R. Kubo, M. Toda and N. Hashitsume, Statistical Physics II, Springer Verlag, Berlin Heidelberg, 1985 Search PubMed
 .
.
- M. Alducin, R. Díez Muiño and J. I. Juaristi, Prog. Surf. Sci., 2017, 92, 317–340 CrossRef CAS
 .
.
-
D. J. Auerbach, N. Hertl, S. M. Janke, M. Kammler, A. Kandratsenka, L. Lecroart and S. Wille, Molecular Dynamics Tian Xia 2 (MDT2): program for simulating the scattering of atoms and molecules from surfaces, 2021, available at https://github.com/akandra/md_tian2, https://github.com/akandra/md_tian2.git.
- H. C. Andersen, J. Chem. Phys., 1980, 72, 2384 CrossRef CAS
 .
.
- L. Verlet, Phys. Rev., 1967, 159, 98–103 CrossRef CAS
 .
.
- L. Verlet, Phys. Rev., 1968, 165, 201–214 CrossRef
 .
.
- J. Behler, Chem. Rev., 2021, 121, 10037–10072 CrossRef CAS PubMed
 .
.
- O. Bünermann, H. Jiang, Y. Dorenkamp, D. J. Auerbach and A. M. Wodtke, Rev. Sci. Instrum., 2018, 89, 094101 CrossRef PubMed
 .
.
- R. Martin Barrios, O. Galparsoro, A. Martínez Mesa, L. Uranga-Piña, C. Crespos and P. Larregaray, J. Phys. Chem. C, 2021, 125, 14075–14081 CrossRef CAS
 .
.
- Z. Zhou and B. Joós, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 3841–3850 CrossRef CAS PubMed
 .
.
|
| This journal is © the Owner Societies 2022 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *ab,
Alexander
Kandratsenka
*ab,
Alexander
Kandratsenka
 ab and
Alec M.
Wodtke
ab and
Alec M.
Wodtke
 abc
abc

![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) i) represents the cohesive energy of atom i and depends on the average background electron density
i) represents the cohesive energy of atom i and depends on the average background electron density ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) i surrounding the atom. Ei (
i surrounding the atom. Ei (![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) i) is calculated by considering atom i to be an impurity embedded in a metal host. Jacobsen et al.22 and Janke et al.2 chose a perfect fcc crystal as a reference system, but other choices are possible. In our new formalism, we choose a perfect bcc crystal to serve as an effective medium, and follow the derivation used for fcc metals.22
i) is calculated by considering atom i to be an impurity embedded in a metal host. Jacobsen et al.22 and Janke et al.2 chose a perfect fcc crystal as a reference system, but other choices are possible. In our new formalism, we choose a perfect bcc crystal to serve as an effective medium, and follow the derivation used for fcc metals.22

![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) i) is the many-body correction term for the reference system. The background electron density
i) is the many-body correction term for the reference system. The background electron density ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) i, averaged over the volume inside a sphere with the radius si, serves as a connection between the real system and the reference system and is calculated as
i, averaged over the volume inside a sphere with the radius si, serves as a connection between the real system and the reference system and is calculated as

![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) i, respectively. Δn0,j is assumed to be a constant. On the other hand, the DFT calculations on the level of local density approximation lead to the following relation:21
i, respectively. Δn0,j is assumed to be a constant. On the other hand, the DFT calculations on the level of local density approximation lead to the following relation:21![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) i = n0e−η(si−s0),
i = n0e−η(si−s0),

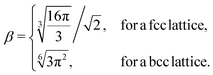


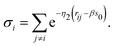

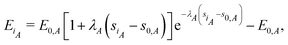

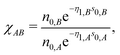










 is the ground-state potential energy surface provided by the optimized EMT energy expression that depends not only on the projectile coordinates r but on the coordinates of the surface atoms
is the ground-state potential energy surface provided by the optimized EMT energy expression that depends not only on the projectile coordinates r but on the coordinates of the surface atoms 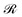 . Eqn (30) can be derived from the time-dependent Schrödinger equation using a mean-field approximation in the limit of weak non-adiabatic couplings.42 In that case, the friction term
. Eqn (30) can be derived from the time-dependent Schrödinger equation using a mean-field approximation in the limit of weak non-adiabatic couplings.42 In that case, the friction term 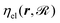 is obtained by Fermi's golden rule with perturbations defined first-derivative non-adiabatic couplings of the electronic states. In this work, we are operating within the framework of the local density friction approximation (LDFA),10–12i.e., we are dealing with a single friction coefficient instead of a friction tensor. The friction coefficient is calculated with the aid of the background densities associated with the EMT-PES. The detailed mapping procedure between friction coefficient and background electron density is described elsewhere.2 The random force FL (t) is modeled by a stochastic process with a Gaussian white noise of zero mean value
is obtained by Fermi's golden rule with perturbations defined first-derivative non-adiabatic couplings of the electronic states. In this work, we are operating within the framework of the local density friction approximation (LDFA),10–12i.e., we are dealing with a single friction coefficient instead of a friction tensor. The friction coefficient is calculated with the aid of the background densities associated with the EMT-PES. The detailed mapping procedure between friction coefficient and background electron density is described elsewhere.2 The random force FL (t) is modeled by a stochastic process with a Gaussian white noise of zero mean value
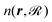 for four surface symmetry sites along the surface normal, as well as the corresponding electron densities obtained from the DFT calculations absent the H atom. Again, the agreement is good.
for four surface symmetry sites along the surface normal, as well as the corresponding electron densities obtained from the DFT calculations absent the H atom. Again, the agreement is good.

















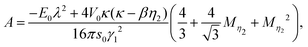



.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.