Stereodynamics of rotational energy transfer in NO(A²Σ⁺) + Kr collisions

Abstract

A crossed molecular beam, velocity-map ion imaging apparatus has been used to determine differential cross sections (DCSs) and angle-resolved rotational angular momentum alignment moments for the state-resolved rotationally inelastic scattering of NO(A²Σ⁺, v = 0, j = 0.5 f₁) with Kr at an average collision energy of 785 cm⁻¹. The experimental results are compared to close-coupled quantum scattering (QS) calculations performed on a literature ab initio potential energy surface (J. Kłos et al., J. Chem. Phys., 2008, 129, 244303). DCSs are very strongly forward scattered, with weaker side and backward scattered peaks becoming progressively more important at higher-N′. Good agreement is found between experimental and QS DCSs, indicating that the PES is an accurate reflection of the NO(A)–Kr interaction energies. Partial wave analysis of the QS DCSs isolates multiple scattering mechanisms contributing to the DCSs, including L-type rainbows and Fraunhofer diffraction. Measured alignment moments are not well described by a hard-shell kinematic apse scattering model, showing deviations in the forward scattering hemisphere that are in agreement with QS calculations and arise from attractive regions of the PES. These discrepancies emphasise that established scattering mechanisms for molecules such as NO with lighter noble gases cannot be extrapolated safely to heavier, more polarisable members of the series.

---

Introduction

Rotational energy transfer (RET) resulting from bimolecular collisions is a ubiquitous process in the gas phase.¹ Systems that have seen extensive experimental and theoretical study are relatively limited, but include small reactive radical species that are important in atmospheric and combustion environments, notably OH, and the focus of this study, NO.^2,3

Developing understanding of the processes underlying RET and providing accurate predictions of scattering cross sections and rate constants requires potential energy surfaces (PESs) which describe the forces acting between the collision partners. These PESs can come from ab initio theory, but necessarily require testing and validation. One of the best, and most established, ways to test the accuracy of a PES is to make measurements of the scattering dynamics via the differential cross section (DCS) and rotational polarization moments, i.e. stereodynamics measurements, and compare these to the results of Quasi-Classical Trajectory (QCT) or Quantum Scattering (QS) calculations.⁴

The collisions of NO(X²Π) with the rare gases (Rg) have been benchmark systems for this approach, with a very wide range of measurements of ground-state NO(X) + Rg scattering. Most recently, the state-of-the-art in such scattering measurements has combined selection of a single initial rotational quantum state of NO(X) in a crossed molecular beam scattering apparatus, followed by resonance-enhanced multiphoton ionisation velocity-map imaging (REMPI-VMI) to detect the scattered product NO(X).^5–7 The resulting systematic work on collisions with He, Ne, Ar and Kr has provided very stringent tests of the latest ab initio PESs, confirming the high degree of accuracy attained by modern coupled cluster methods for these systems.^5,6,8–16 The measurements have also provided great insight into the process of inelastic scattering. This includes the importance of interference effects, both in the forward direction, where high-frequency oscillations are observed that can be viewed as arising from diffraction effects, and as low-frequency oscillations across sideways and backwards scattering that can be explained through interference from multiple paths arising from collisions at the ends and the sides of the NO.^6,7,17,18

A striking feature of the alignment moments arising from inelastic scattering in the NO(X) + Rg systems is their simple dependence on scattering angle. The majority of observed moments for all final states in all systems studied can be reproduced by a simple classical model of angular momentum conservation, in which the angular momentum along a specific direction, the kinematic apse (KA), is conserved.¹⁹ Angular momentum generated in the collision is therefore necessarily applied orthogonal to the KA. The KA model is classically exact for a sudden collision, i.e. one between rigid bodies. The excellent agreement of the KA model with the observed NO(X) + He, Ne and Ar scattering is consistent with the very steep repulsive walls reported by ab initio PESs for these systems, together with shallow attractive wells relative to the typical collision energies in the experiments.^5,10,13 However, the NO(X)–Kr and NO(X)–Xe PESs display substantially deeper attractive wells, as expected with these larger and more polarizable colliders. In these systems significant deviations from the KA model have been observed, and attributed to the attractive interactions.^14–16

In contrast to the extensive work on NO(X) + Rg rotational energy transfer discussed above, there has been substantially less work on scattering of electronically excited species, i.e. the complementary NO(A²Σ⁺) + Rg systems. This is a result of the inherently challenging nature of experiments on short-lived electronically excited states, with NO(A) having a fluorescence lifetime of ca. 200 ns. However, following our initial demonstration of the combination of optical state preparation of NO(A) with crossed molecular beams and VMI detection,^20–22 we have performed a series of systematic experimental and theoretical studies of rotationally inelastic collisions of NO(A).^23–27 In these experiments we have measured both DCSs and angle-resolved rotational alignment moments for the NO(A) + He, Ne and Ar systems. We observed quantitative agreement between experiment and theory for NO(A) + He, and very good agreement for NO(A) + Ar.^25,27 There are larger discrepancies between QS calculations and experiment for NO(A) + Ne.^23,26 In particular, we observe a strong forward scattered peak in the 0–10° range in the experimental DCSs for a wide range of final rotational states, which is not reproduced by QS calculations. The experimental results are consistent with the presence of a shallow attractive well in a linear geometry, something seen in the NO(A)–Ar, Kr and Xe ab initio PESs, but absent from the literature NO(A)–Ne PESs.^28–30 There are also experiment-theory disagreements in the angular location and relative intensities of rainbow scattering peaks in the NO(A) + Ne DCSs, which imply inaccuracies in the shape of the repulsive wall of the literature PESs.

More generally, the dynamics of the NO(A) + Rg systems show substantial differences when compared to the equivalent NO(X) + Rg. Perhaps most noticeable is the difference in the form of the scattering-angle-resolved rotational angular momentum. In contrast to the relatively simple KA behaviour observed for the NO(X) + Rg scattering, all of the NO(A) + Rg systems studied to date show strong deviations from the KA model, in both experiment and theoretical results.^{22,23,25–27} A striking observation for collisions with Ne and Ar are strong, angle-dependent, deviations from the KA model, which are most pronounced at scattering angles close to the rainbow maxima in the DCS. Only in the backward scattering hemisphere, at angles greater than 150°, does the observed rotational alignment fit the KA model.

The surprising angular momentum polarization dynamics of the NO(A) + Rg systems extends to novel measurements of the transfer of rotational orientation in NO(A) + Ne.²⁶ By preparing NO(A) in the N = 2, j = 1.5 state, using circularly polarised light, with an initial orientation of the rotational angular momentum parallel to the collision vector, k, and then probing the rotational orientation of the product N′ states relative to k, we were able to make the first direct measurement of the k-k′–j-j′ correlation in rotationally inelastic scattering. A strong scattering-angle dependence was found for this propensity, including the unexpected observation of a change in sign in rotational orientation for sideways scattering in the N′ = 5 state. These experimental observations are qualitatively reproduced by both QS and QCT calculations on two different ab initio NO(A)–Ne PESs, and close inspection shows that this 4-vector measurement is more sensitive to the details of the PESs than a more conventional, although still challenging, k-k′–j′ correlation measurement.

In this paper, we extend the sequence of measurement and QS calculation to the more strongly interacting NO(A) + Kr system. We have prepared the non-rotating NO(A, v = 0, N = 0, j = 0.5) level, and have performed crossed molecular beam scattering experiments with velocity-map imaging detection. We report experimental measurements of DCSs and the scattering-angle-resolved rotational alignment moments A^{2}_q+ for the product rotational states N′ = 3 and 5–11, together with the results of collision-energy-averaged QS calculations on the most-recent literature PES for the system.²⁹

Materials and methods

Experiment

The experimental apparatus and methodology have been described in detail in previous recent papers, and only the essential details are therefore reproduced here.^23,25,27 Experiments were performed in a crossed molecular beam velocity-map ion-imaging apparatus specifically designed for studies of inelastic scattering of electronically excited radicals. Skimmed pulsed molecular beams were crossed in the centre of the VMI optics. The first beam, a mix of 10% NO (BOC, 99.5% purity) seeded in Ne (BOC, 99.999%) at 3 bar total backing pressure, had a Gaussian NO velocity distribution with a mean of 831 ms⁻¹ and a full width at half maximum (FWHM) of 52 ms⁻¹. The second beam, consisting of pure Kr (BOC, 99.999%) at 5 bar backing pressure, had a mean velocity of 398 ms⁻¹ and a FWHM of 45 ms⁻¹. Mean speeds were determined from fitting 2-d Gaussian distributions to images of the beam spots, with the FWHM determined in a separate measurement described in detail previously.^23,25,27 These conditions resulted in a Gaussian distribution of centre-of-mass collision energies, E_col, with a mean of 785 cm⁻¹ and a FWHM of 86 cm⁻¹.

The output of a pulsed Nd : YAG pumped dye laser (Continuum Surelite II-10/Sirah Cobra-Stretch) at 226.05 nm was used to excite NO via the A²Σ⁺–X²Π(0,0) Q₁(0.5) transition to prepare a sample of NO(A²Σ⁺, v = 0, N = 0, j = 0.5) in the crossing region of the molecular beams. After a 370 ns delay, the products of rotational energy transfer within the NO(A, v = 0) state were probed using 1 + 1′ REMPI via the E²Σ⁺–A²Σ⁺ (0,0) band. The ca. 600 nm resonant probe light was produced by a Nd : YAG pumped dye laser (Continuum Surelite I-10 and Sirah Cobra-Stretch), with the 532 nm non-resonant ionization radiation being also produced by the same Nd : YAG laser. The resonant probe laser fluence was maintained in the linear perturbative regime, as previously determined (≤0.65 μJ cm⁻²), and the non-resonant ionization pulse was set to a strongly saturating fluence.²⁷ A photo-elastic modulator (PEM-90, Hinds Instruments inc.) was used to switch the probe laser linear polarization between horizontal (H), in which the electric vector was in the plane of the molecular beams and the ion image, and vertical (V), perpendicular to this plane. Scattering images were acquired for both probe polarizations, together with background images in which the neat collider beam was delayed by 1 ms, so that it is effectively completely absent when the images are taken, in an interleaved fashion. The wavelength of the probe laser was step-scanned over the relevant R(N′) transition to remove Doppler selection, in 20 steps of 0.0005 nm increments. Note that the spin-rotation levels j′ = N′ ± ½ are not resolvable in the NO(E–A) spectrum, and we therefore measure and report N′-dependent dynamics. 200 laser shots were acquired in each phase of the measurement cycle at each wavelength point, with the cycle performed 3 times over the Doppler profile, totalling 48 000 camera shots per individual image. In total, 5–8 independent measurements were made for each final N′ state across multiple days, depending on the overall signal levels for different N′ states. Contributions from unscattered incident beam populations, arising from direct excitation on the NO(A–X) Q₁(1.5, 2.5 and 4.5) transitions by the wings of the excitation laser frequency profile, contaminated product measurements for N′ = 1, 2 and 4 to an unacceptable degree, and we do not report measurements for these states. Signal levels further restricted the range of N′ reported to N′ = 3 and 5 to 11.

The data were fitted using an extension of our previously published analysis.^23,25,27 In brief, this simulates basis images for both V and H polarizations including all experimentally relevant parameters using a Monte-Carlo (MC) approach, and fits a linear combination of the images to the data using a simplex algorithm. The basis images are generated for basis functions in either the DCS or scattering-angle dependent alignment moments, with separability assumed between the DCS and alignment moments. An iterative procedure is used to refine the DCS and polarization moments independently until they are converged within a user-defined tolerance, with the DCS constrained to be positive at all angles and the alignment moments constrained to lie within their physical limits.

In our previous work, we used Legendre polynomials as the basis functions, either P_λ(cos θ) or P_λ(1 − θ/90°), where θ is the scattering angle and λ is the order of the polynomial.^23,25,27 These are convenient, as they are orthogonal functions that span the full 180° scattering range and can often represent the full range of the DCS or polarization moments with a limited (e.g. < 15) number of parameters. However, they are poorly suited to the representation of scattering distributions which are strongly localized, for example DCSs which simultaneously display an intense peak at small scattering angles and also low intensity structure over the remaining angular range. In these circumstances a large number of Legendre moments are required to fit the sharp forward peak, and convergence of the fit to both this, and any low intensity wide-angle scattering, becomes difficult to achieve. We have therefore implemented an alternative basis set for NO(A) + Kr, using localized basis functions based on triangles, applied to both the DCS and alignment moments. Each triangle has a value of 1 at its peak, decreasing to a value of 0 at the peak position of the neighbouring basis function, with the two end basis functions peaking at 0° and 180°, respectively. MC simulation and inspection of the basis images, together with trial fitting, was used to determine an appropriate angular range for each basis function. In the results presented here, the DCS basis functions were spaced by 5°, with the angular momentum basis functions on a 10° (A^{2}₀(θ)) or 20° spacing (A^{2}₁₊(θ) and A^{2}₂₊(θ)), respectively. Basis functions of this form have been used in related image-fitting approaches previously, and as we will show below, can successfully parameterize strongly localized scattering-angle distributions.^31,32

Theory

The DCSs and scattering-angle-dependent alignment moments have been calculated via time-independent quantum scattering theory using the Hibridon suite of programs.³³ Scattering calculations were performed using the PES of Kłos et al., computed at the RCCSD(T)/aug-cc-pVTZ + bf level of theory.²⁹ In the scattering calculations, the NO(A) molecule was treated as an open-shell rigid rotor, with a rotational constant, B = 1.987 cm⁻¹, and spin-rotation coupling constant, γ = −0.0027 cm⁻¹.³⁴ Calculations were only performed for the ⁸⁴Kr isotope, which has a natural abundance of 57%. Partial waves up to J_tot = 400.5 were included, with propagation from 5 to 300 Bohr. A rotational basis up to N = 21 was employed. Because we only detect individual rotational states N′, DCSs calculated for individual spin-rotation levels, j′ = N′ ± ½, were summed to give N′-dependent DCSs. The angular momentum moments for each N′ were then calculated as the DCS-weighted average of the corresponding f₁ and f₂ spin-rotation states. Calculations were performed at 17 individual energies in 15 cm⁻¹ steps spanning a range of ± 3 σ of the experimentally determined collision-energy distribution about the mean collision energy, and were then averaged over the Gaussian collision-energy distribution.

Results

A representative Newton diagram for the NO(A) + Kr scattering to form N′ = 10 is shown in Fig. 1, superimposed on the sum of images recorded in both the V and H geometries. Also included in the figure is the probe laser beam propagation vector, k_p. The average angle between k_p and the relative collision velocity, k, is 109°. As a consequence, the images are weakly sensitive to the A^{2}₁₊(θ) alignment moment, similar to our previous measurements of NO(A) + He scattering, and in contrast to those of NO(A) + Ne scattering.^23,25,26

Fig. 1 Newton diagram for NO(A) + Kr scattering, superimposed on the average of all experimental data for the N′ = 10 final state. The propagation direction of the probe laser beam, k_p, is shown, as well as the vectors of the NO and Kr molecular beams, v_NO and v_Kr, the velocity of the centre of mass, v_CM, and the relative collision velocity, k. The circle represents the in-plane final velocity for this product state.

Fig. 2 shows the final velocity-map images for the product states N′ = 3, 5–11, for both H and V polarizations, summed over all of the independent measurements, together with the equivalent summed results of the fitting procedure as applied to individual measurements. Note that the same colour-map, scaled to the image maximum is applied to all four images for each N′, so that differences between data and fit, or H and V, are apparent. However, total intensity comparisons between different N′, and hence determination of the relative integral cross sections are not possible.

Fig. 2 Experimental images for the inelastic collision of NO(A, v = 0, N = 0, j = 0.5 f₁) with Kr at 〈E_coll〉 = 785 cm⁻¹ for product states N′ = 3 and 5–11, for both H and V probe laser polarizations, summed over all independent image measurements. Also shown are the results of the fitting procedure applied to individual measurements and summed over all independent fits. The colour map scale is the same for all images (H and V, data and fit) for each N′, but is different for different N′.

It is immediately obvious that the images are dominated by extremely strong forward scattering, for all except the highest states, N′ = 10 and 11. However, there is low-intensity sideways and backwards scattering also present in essentially all of the data and fit images. Fig. 3 shows the same summed images as Fig. 2, but with the colour intensity scale remapped so that this weak sideways and backwards scattering is visible; the forward scattering region is hence strongly saturated in all cases. We emphasize that this strong forward-scattered signal is not an artefact caused by incomplete subtraction of a ‘beam spot’ caused by background NO that has not undergone scattering. As described in the experimental methods, background measurements taken without the collider beam have been subtracted in all cases. The natural reduction in the radius of the scattering ring as increasing energy is directed into rotation also results in a clear separation of the ‘beam-spot’ region from the scattered products for N′ = 7 and above. This is particularly clear for high-N′ in Fig. 3, where the beam-spot region has been masked in the fitting procedure, and is indicated by the irregular black area immediately to larger radius of the forward scattering. The angular range of this forward scattered signal increases with increasing N′. The low-intensity scattering at larger angles generally moves from sideways to backwards with increasing N′ while simultaneously increasing in relative magnitude. The fitted images quantitatively reproduce the experimental results with no significant systematic residuals, providing confidence that we have successfully extracted the DCSs and alignment moments in the fitting procedure.

Fig. 3 Experimental images for the inelastic collision of NO(A, v = 0, N = 0, j = 0.5 f₁) with Kr at 〈E_coll〉 = 785 cm⁻¹ for product states N′ = 3 and 5–11, for both H and V probe laser polarizations, summed over all independent image measurements. Also shown are the results of the fitting procedure applied to individual measurements and summed over all independent fits. Images for each N′ state have been plotted on an independent colour scale, magnified by the indicated factor from the equivalent images in Fig. 2. For each N′ the relative scales for H and V and data and fit are the same.

Fig. 4 shows the averaged results from fitting all individual data sets for all final states, namely the DCSs, and the A^{2}₀(θ), and A^{2}₂₊(θ) alignment moments, together with the results of the QS calculations described above. The experimental DCS results have been normalized to the integral cross section determined in the QS calculations to enable easy comparison of experiment and theory. We have not presented the resulting A^{2}₁₊(θ) moments in Fig. 4, because our relatively low sensitivity to this moment makes its determination particularly difficult, and we therefore have low confidence in the results.

Fig. 4 Differential cross sections and angular momentum alignment moments, A^{k}_q+(θ), for rotational energy transfer of NO(A, v = 0, N = 0, j = 0.5 f₁) to final states NO(A, v = 0, N′ = 3, 5–11) in collisions with Kr. First column, differential cross sections, with different x and y scales for main graph and inset; second column, A^{2}₀(θ) also with different x-scale for the insets for N′ = 3 and 5; third column, A^{2}₂₊(θ). Results of fitting to experimental data (black lines, error bars are 1 standard error of the mean), collision-energy-averaged quantum scattering calculations (red line) and kinematic apse model calculations (blue line) at 〈E_col〉 = 785 cm⁻¹. The alignment moments have been truncated to angular ranges for which there was sufficient scattering intensity to determine them.

As expected from inspection of the images, the measured DCSs are very strongly forward scattered for all reported N′. The DCS plots are presented with insets to enable both the magnitude, range and fine structure of the large amplitude forward-scattered peak, and the form of the low-amplitude wide-angle scattering, to be displayed in detail. For N′ ≤ 7, the QS calculations display strong, high-frequency oscillations in the 0–15° range. The angular resolution of the experimental measurements is not high enough to resolve these oscillations, but the overall form of the QS results in this angular range do show good agreement with the experimental DCSs. At larger scattering angles, low-amplitude peaks are observed, with the peaks moving steadily to larger scattering angle as N′ increases. Good general agreement is also found between the experiment and the QS calculations for this wider-angle scattering, with the latter reproducing the observed angle and magnitude of these weak features for the majority of N′.

Turning to the alignment moments, we note their measurement is dependent on the difference of the relative intensities of the V and H images as a function of scattering angle. It is therefore not possible to accurately determine the alignment moments at all scattering angles, and we therefore only report them over angular ranges where sufficient scattering intensity is observed for each N′. However, we do report the alignment moments resulting from the QS calculations at all scattering angles. We also show the results of a calculation of the alignment moments assuming KA conservation for each final state.

It is immediately obvious that the QS and KA calculations predict very different forms of the alignment moments. This is best illustrated in the A^{2}₀(θ) results. Positive A^{2}₀(θ) reflects an angular momentum distribution that is preferentially parallel or anti-parallel to k, while negative A^{2}₀(θ) results from a distribution that is preferentially perpendicular to k. The KA calculation, as is observed in all previous KA predictions of related systems,^10,23,25,27 results in a smooth variation in A^{2}₀(θ) from the negative limit (A^{2}₀(θ) = −1) at 0° to a positive maximum at a moderate forward hemisphere scattering angle, followed by a steady decline to the negative limit again at 180°. In contrast, the QS calculations predict much more complicated structures, with high frequency oscillations for forward-scattered products at low-N′ (shown in the insets for N′ = 3 and 5), and with multiple inflections and secondary maxima present on a larger angular scale. For final N′ ≥ 9 the experimental measurements of A^{2}₀(θ) can clearly distinguish between the QS and KA models, as there is sufficient scattering into wider angles to accurately determine the alignment moments over a significant angular range. The QS calculations agree well with the experimental measurements, while the KA model does not predict the experimental results successfully. At lower-N′ there is weaker agreement between the measurements and the QS calculations, although in general the QS calculations are also a better prediction than the KA model here.

The A^{2}₂₊(θ) moment, the measurement of which depends on the variation of the intensity of the images with azimuthal scattering angle, is harder to determine than the A^{2}₀(θ) moment. The experimental measurements, QS and KA calculations all agree that this moment is negative for essentially all scattering angles for all final states. In general, the QS calculations are again a better overall prediction of the experiment than the KA model. However, the uncertainty in the measured A^{2}₂₊(θ) precludes any stronger conclusions about the relative agreement between experiment and QS or KA calculations.

Discussion

We first discuss the differential cross sections. These are very strongly forward scattered for essentially all measured N′. The strength of attractive interactions on the PESs clearly increase with increasing polarizability of the collider, and hence the most directly comparable of our previous measurements is of NO(A) + Ar scattering.²⁷ The NO(A)–Kr PES of Kłos et al., used in the QS calculations here, is shown as a polar contour plot in the upper panel of Fig. 5, together with the radial dependence of the Legendre moments of the PES, V_λ(R) in the lower panel.²⁹ The NO(A)–Kr PES has a global minimum of −138 cm⁻¹ for N-end approach occurring around R = 4 Å, with a secondary minimum (−63 cm⁻¹) for O-end approach at slightly larger distances. In comparison, the NO(A)–Ar PES has a shallower global minimum for N-end approach of −70 cm⁻¹.²⁹ The doubling of the well depth on going from Ar to Kr is consistent with the higher proportion of forward scattering observed in the NO(A) + Kr system.

Fig. 5 (Top) Contour plot of the ab initio potential energy surface for NO(A)–Kr described by Kłos et al. and used in the quantum scattering calculations. Blue contours, negative energies in 10 cm⁻¹ intervals. Red contours, positive energies in 100 cm⁻¹ intervals. Black contour, 0 cm⁻¹. (Bottom) Radial dependence of the Legendre moments, V_λ(R), of the PES, with the inset showing an expanded y-axis for R = 5 to 7 Å.

Comparisons may also be drawn with NO(X) + Kr scattering, which also displays strong forward scattering for multiple final states.¹⁵ The NO(X)–Kr V_sum PES, which largely determines spin–orbit-conserving scattering, has a global minimum of −140 cm⁻¹ in a T-shaped geometry, with slightly shallower −130 and −120 cm⁻¹ wells at the N- and O-end approaches. Overall, although the global minima of the NO(X)–Kr and NO(A)–Kr PESs are very similar, the attractive wells on the NO(A)–Kr PES are significantly more anisotropic, which may contribute to the stronger forward scattering observed here for NO(A) + Kr, as anisotropy is required for collisions to result in a change in rotational state.

The QS calculations are close-coupled and open-shell, are fully converged, and within the approximation of the fixed NO bond length are exact. The excellent overall agreement between the experimental and QS DCSs, including for the weaker sideways and backwards scattering, therefore implies that the ab initio PES is an accurate prediction of interaction energies over the experimentally accessible range. We have therefore performed further analysis of the QS calculations to provide deeper insight into the scattering mechanisms involved.

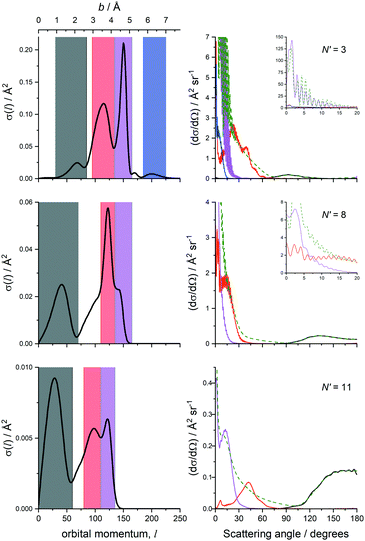
The QS calculations reported in Fig. 4 show clear oscillations from interference effects in the forward 20°, even though the calculations are averaged over the experimental collision energy distribution. The origins of these oscillations and the other features of the DCSs can be illustrated by further analysis of the QS calculations. Fig. 6 shows the scattering cross sections as a function of initial orbital angular momentum, l, or so-called partial cross sections (PCSs), for three representative final states, N′ = 3, 8 and 11, at a single collision energy, specifically the average collision energy, E_col = 785 cm⁻¹. For all three states the PCSs are strongly structured, with multiple clear peaks. The orbital angular momentum can be related to the classical impact parameter, b, also shown on Fig. 6. The range of l or b for which scattering is significant decreases with increasing N′, as expected from classical models of linear to angular momentum transfer. However, even for N′ = 11, there is a clear peak in the PCS around l = 125, b = 3.9 Å. As shown in Fig. 5, the attractive minimum for N-end approach is located at R = 4.2 Å, which alone suggests that the forward scattering may result from this peak in the PCS.

Fig. 6 Left column, partial cross sections for final states N′ = 3, 8 and 11 from quantum scattering calculations at a collision energy of 785 cm⁻¹. The top axis shows the equivalent impact parameter. Right column, differential cross sections with contributions for the respective black, red, magenta and blue coloured ranges of partial waves in the left hand column. The insets for N′ = 3 and 8 show an expanded view of the large amplitude forward scattering. Green dashed line, differential cross sections with contributions from l = 0 to 300.

Direct support from this interpretation can be found in the right-hand column of Fig. 6. This shows DCSs for specific ranges of l, specifically those illustrated in the left-hand column PCS plots which are also given in Table 1. Also shown is the DCS including all partial waves in the range l = 0 to 300.

Table 1 Ranges of partial waves shown in Fig. 6 for which DCSs were calculated, as a function of final state

N′	l-Range
	Black	Red	Magenta	Blue
3	30–85	95–135	135–165	185–225
8	0–70	110–135	135–165
11	0–60	80–110	110–135

---

Taking N′ = 11 first, it is clear that the l = 110 to 135 range of partial waves leads to a strongly forward-scattered DCS that represents well the overall DCS from 0–20°. The second peak in the PCS from l = 80 to 110 leads to a DCS peak around 45°, while the lowest-range peak, l = 0 to 60, provides the backward-hemisphere scattering. The total DCS is well reproduced by an incoherent sum of these partial ranges, suggesting that interference between these ranges of partial waves is not very significant, and that they can be considered to arise from independent scattering mechanisms to a first approximation.

Turning to N′ = 3, there are four ranges of l shown. The first, l = 30 to 85, gives rise to the small peak centred around 90°, the classical rotational rainbow peak. The second range, l = 95 to 135 results in scattering over a substantial range in the forward hemisphere, between 0 and 30°, with a secondary peak at 22°. This corresponds to an impact parameter range of 3 to 4.2 Å, covering the transition from attractive to repulsive scattering. There are then two outer peaks in the PCS. The first, from l = 135 to 165, gives rise to the large and high frequency oscillations observed from 0 to 20°. These are very similar to the Fraunhofer oscillations previously reported in NO(X) + Rg scattering, caused by diffraction of the incident plane wave from the edges of the NO.^{17,18,35–38} The Fraunhofer model specifically treats the diatom as a rigid shell, typically taken as the relevant repulsive contour of the PES for the collision energy. However, Fig. 6 clearly shows that for NO(A) + Kr this scattering process is occurring for partial wave ranges that correspond to scattering from the outer attractive well, between 4.2 and 5 Å. We note, however, that very similar oscillations are observed in NO(X) + Kr scattering on a PES with broadly similar well depths at relatively low collision energies, leading to our identification of these as diffraction oscillations. The final PCS range identified is l = 185 to 225, corresponding to b = 5.8 to 7 Å. In this range, as the inset plot of the Legendre moments in the lower panel of Fig. 5 shows, there are only very weak anisotropic components to the PES. Only anisotropic components can cause inelastic scattering, and hence the scattering here results from the small (≈5 cm⁻¹) λ = 1 and 2 terms. The resulting scattering peaks at 0° and extends to ≈15°. This peak in the PCS is beyond a clear, near-zero minimum at l = 180. In a classical scattering calculation, such a minimum would be identified as the ‘glory’ impact parameter, and scattering at higher impact parameter would result in an ‘L-type’ rainbow.¹⁷ We therefore assign the scattering in this highest PCS range to an L-type rainbow.

Finally, for the intermediate N′ = 8 final state we again find that the lowest range of l from 0 to 70 results in the backward-scattered rotational-rainbow peak. The large sharp peak in the PCS from l = 110 to 135 gives rise to scattering in the 0 to 30° range, with clear oscillatory structure that we would again assign to diffraction effects. The shoulder at highest l corresponds to the range of the deepest part of the attractive well, and gives rise to the large peak in the DCS observed at ≈4°. Overall, the scattering observed is intermediate between that seen for N′ = 3 and 11, and clearly shows that the influence of the attractive potential can extend to dominate the scattering mechanisms even for this relatively high-N′ final rotational state.

Although it is difficult to measure the alignment moments over significant angular ranges for these strongly forward-scattered DCSs, comparison of experimental values of A^{2}₀(θ) and A^{2}₂₊(θ) to the QS and KA models in general show better agreement with the QS calculations, particularly for N′ = 9, 10 and 11. We observed similar systematic disagreements between QS and KA models for NO(A) + He and Ne, which we attributed to the ‘soft’ repulsive walls of these systems, which have only very weak attractive interactions.^23,25 In contrast the KA model is very successful at predicting product alignment in NO(X) + He, Ne and Ar scattering, where the PESs have very steep repulsive walls.^5,10,13 However, it has been shown to break down in NO(X) + Kr and Xe scattering, attributed to the stronger attractive forces in these more polarizable systems.^14–16 In these measurements of NO(A) + Kr scattering, there is good agreement between QS and KA models for backward scattering for all N′, indicating that collisions at low-l that probe the repulsive wall are well described by the KA model. In contrast, significant disagreements are seen between QS and KA models for forward scattering, which the PCSs show is arising for all N′ from the attractive regions of the PES. We therefore conclude that the failure of the KA model to predict the product alignment in NO(A) + Kr scattering is primarily a consequence of the stronger attractive forces on the NO(A)–Kr PES, similar to the behaviour found for the NO(X) + Kr system.

At small scattering angles, the QS predictions of the alignment moments in Fig. 4 display rapid oscillations. Closer inspection on an expanded scale shows that these are in phase with the equivalent oscillations in the respective DCS predictions, with the more positive alignment moment peaks coinciding with the peaks in the DCS, and the most negative alignment moments coinciding with minima in the DCS. This is consistent with Fraunhofer diffraction being the origin of this structure. It has been shown for the NO(X) + Rg systems that the diffraction oscillations observed are strongly dependent on final angular-momentum-projection state, m′.¹⁸ Specifically, the scattering amplitude is largest for collisions that result in the largest change in |m|. Since the scattering initiates in j = 0.5, |m| = 0.5, conservation such that |m| = |m′| results in a negative product A^{2}₀(θ), while transfer to large |m′| results in a positive product A^{2}₀(θ). Within the Fraunhofer model, this can be correlated with diffraction from different orientations of the bond axis, r, relative to the collision vector, k. Collisions where k is parallel to r lead to |m| conservation, while collisions where k is perpendicular to r lead to the diffraction peaks with large |m′|. The observed negative excursions in A^{2}₀(θ) for diffraction minima and positive A^{2}₀(θ) for diffraction maxima in our QS calculations are therefore consistent with the interpretation of these oscillations in the DCS arising from Fraunhofer diffraction.

Conclusions

We have studied the stereodynamics of rotationally inelastic scattering of NO(A²Σ⁺, v = 0, j = 0.5 f₁) + Kr, at a mean collision energy of 785 cm⁻¹, and have reported differential cross sections and angle-resolved rotational angular momentum alignment moments for a range of final N′ states. Comparison with QS calculations has allowed us to test the best-available ab initio PES. The observation of strongly forward scattering for essentially all of the N′ states probed is consistent with the deep attractive wells observed in the system. The generally good agreement in the location and magnitude of the rotational rainbow scattering peaks implies that the repulsive wall of the PES is accurately modelled. Partial wave analysis of the QS calculations reveals the distinct scattering mechanisms that underlie the total DCSs. At low-N′ the forward scattering arising purely from attractive regions of the PES can be separated into multiple components. Through partial-wave analysis, we assign the two longest-range of these to Fraunhofer diffraction and L-type rainbow scattering, respectively. Shorter range scattering mechanisms give rise to more sideways and backwards rotational rainbow scattering. The measured alignment moments are not consistent with a kinematic apse conservation model, but in general agreement with the QS calculations. Rapid oscillations in the alignment moments for small angle scattering are consistent with the assignment of this scattering to Fraunhofer diffraction. NO(A) + Kr scattering provides an interesting example of how the complex interplay of attractive and repulsive interactions can be interpreted through stereodynamical measurements and modelling.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the U.K. EPSRC via Grants EP/J017973/01, EP/P001459/1 and EP/T021675/1.

References

1. A. Schiffman and D. W. Chandler, Int. Rev. Phys. Chem., 1995, 14, 371–420.
2. H. Chadwick, M. Brouard, T. Perkins and F. J. Aoiz, Int. Rev. Phys. Chem., 2014, 33, 79–123.
3. G. Paterson, M. L. Costen and K. G. McKendrick, Int. Rev. Phys. Chem., 2012, 31, 69–109.
4. M. L. Costen, S. Marinakis and K. G. McKendrick, Chem. Soc. Rev., 2008, 37, 732–743.
5. A. Gijsbertsen, H. Linnartz, G. Rus, A. E. Wiskerke, S. Stolte, D. W. Chandler and J. Kłos, J. Chem. Phys., 2005, 123, 224305.
6. C. J. Eyles, M. Brouard, C. H. Yang, J. Kłos, F. J. Aoiz, A. Gijsbertsen, A. E. Wiskerke and S. Stolte, Nat. Chem., 2011, 3, 597–602.
7. A. von Zastrow, J. Onvlee, S. N. Vogels, G. C. Groenenboom, A. van der Avoird and S. Y. T. van de Meerakker, Nat. Chem., 2014, 6, 216–221.
8. S. N. Vogels, J. Onvlee, S. Chefdeville, A. van der Avoird, G. C. Groenenboom and S. Y. T. van de Meerakker, Science, 2015, 350, 787–790.
9. T. de Jongh, M. Besemer, Q. Shuai, T. Karman, A. van der Avoird, G. C. Groenenboom and S. Y. T. van de Meerakker, Science, 2020, 368, 626–630.
10. M. Brouard, H. Chadwick, C. J. Eyles, B. Hornung, B. Nichols, F. J. Aoiz, P. G. Jambrina and S. Stolte, J. Chem. Phys., 2013, 138, 104310.
11. B. Nichols, H. Chadwick, S. D. S. Gordon, C. J. Eyles, B. Hornung, M. Brouard, M. H. Alexander, F. J. Aoiz, A. Gijsbertsen and S. Stolte, Chem. Sci., 2015, 6, 2202–2210.
12. C. G. Heid, V. Walpole, M. Brouard, P. G. Jambrina and F. J. Aoiz, Nat. Chem., 2019, 11, 662–668.
13. M. Brouard, H. Chadwick, C. J. Eyles, B. Hornung, B. Nichols, J. M. Scott, F. J. Aoiz, J. Kłos, S. Stolte and X. Zhang, Mol. Phys., 2013, 111, 1759–1771.
14. H. Chadwick, B. Nichols, S. D. S. Gordon, B. Hornung, E. Squires, M. Brouard, J. Kłos, M. H. Alexander, F. J. Aoiz and S. Stolte, J. Phys. Chem. Lett., 2014, 5, 3296–3301.
15. M. Brouard, H. Chadwick, S. D. S. Gordon, B. Hornung, B. Nichols, J. Kłos, F. J. Aoiz and S. Stolte, J. Chem. Phys., 2014, 141, 164306.
16. M. Brouard, H. Chadwick, S. D. S. Gordon, C. G. Heid, B. Hornung, B. Nichols, J. Kłos, P. G. Jambrina and F. J. Aoiz, Chin. J. Chem. Phys., 2020, 33, 217–233.
17. J. Onvlee, S. N. Vogels, A. D. van der Avoird, G. C. Groenenboom and S. Y. T. van de Meerakker, New J. Phys., 2015, 17, 055019.
18. J. Onvlee, S. D. S. Gordon, S. N. Vogels, T. Auth, T. Karman, B. Nichols, A. van der Avoird, G. C. Groenenboom, M. Brouard and S. Y. T. van de Meerakker, Nat. Chem., 2017, 9, 226–233.
19. V. Khare, D. J. Kouri and D. K. Hoffman, J. Chem. Phys., 1981, 74, 2275–2286.
20. J. J. Kay, G. Paterson, M. L. Costen, K. E. Strecker, K. G. McKendrick and D. W. Chandler, J. Chem. Phys., 2011, 134, 091101.
21. J. J. Kay, J. D. Steill, J. Kłos, G. Paterson, M. L. Costen, K. E. Strecker, K. G. McKendrick, M. H. Alexander and D. W. Chandler, Mol. Phys., 2012, 110, 1693–1703.
22. J. D. Steill, J. J. Kay, G. Paterson, T. R. Sharples, J. Kłos, M. L. Costen, K. E. Strecker, K. G. McKendrick, M. H. Alexander and D. W. Chandler, J. Phys. Chem. A, 2013, 117, 8163–8174.
23. T. F. M. Luxford, T. R. Sharples, K. G. McKendrick and M. L. Costen, J. Chem. Phys., 2016, 145, 174304.
24. T. F. M. Luxford, T. R. Sharples, K. G. McKendrick and M. L. Costen, J. Chem. Phys., 2017, 147, 013912.
25. T. F. M. Luxford, T. R. Sharples, D. Townsend, K. G. McKendrick and M. L. Costen, J. Chem. Phys., 2016, 145, 084312.
26. T. R. Sharples, J. G. Leng, T. F. M. Luxford, K. G. McKendrick, P. G. Jambrina, F. J. Aoiz, D. W. Chandler and M. L. Costen, Nat. Chem., 2018, 10, 1148–1153.
27. T. R. Sharples, T. F. M. Luxford, D. Townsend, K. G. McKendrick and M. L. Costen, J. Chem. Phys., 2015, 143, 204301.
28. H. Cybulski and B. Fernandez, J. Phys. Chem. A, 2012, 116, 7319–7328.
29. J. Kłos, M. H. Alexander, R. Hernandez-Lamoneda and T. G. Wright, J. Chem. Phys., 2008, 129, 244303.
30. P. Pajon-Suarez, G. Rojas-Lorenzo, J. Rubayo-Soneira and R. Hernandez-Lamoneda, Chem. Phys. Lett., 2006, 421, 389–394.
31. J. Winterhalter, D. Maier, J. Honerkamp, V. Schyja and H. Helm, J. Chem. Phys., 1999, 110, 11187–11196.
32. K. T. Lorenz, D. W. Chandler and G. C. McBane, J. Phys. Chem. A, 2002, 106, 1144–1151.
33. HIBRIDON is a package of programs for the time-independent quantum treatment of inelastic collisions and photodissociation written by M. H. Alexander, D. E. Manolopoulos, H.-J. Werner, B. Follmeg, and P. J. Dagdigian, with contributions by D. Lemoine, P. Vohralik, G. Corey, B. Johnson, T. Orlikowski, A. Berning, A. Degli-Esposti, C. Rist, B. Pouilly, J. Kłos, Q. Ma, G. van der Sanden, M. Yang, F. de Weerd, S. Gregurick, and F. Lique. More information and/or a copy of the code can be obtained from the website http://www2.chem.umd.edu/groups/alexander/hibridon/hib43.
34. J. Danielak, U. Domin, R. Kepa, M. Rytel and M. Zachwieja, J. Mol. Spectrosc., 1997, 181, 394–402.
35. M. Faubel, J. Chem. Phys., 1984, 81, 5559–5569.
36. M. Lemeshko and B. Friedrich, J. Chem. Phys., 2008, 129, 024301.
37. M. Lemeshko and B. Friedrich, Phys. Chem. Chem. Phys., 2010, 12, 1038–1041.
38. M. Lemeshko, P. G. Jambrina, M. P. de Miranda and B. Friedrich, J. Chem. Phys., 2010, 132, 161102.

---